Heritable changes in division speed accompany the diversification of single T cell fate

Significance

Rapid clonal expansion of antigen-specific T cells is a fundamental feature of adaptive immune responses. Here, we utilize continuous live-cell imaging in vitro to track the division speed and genealogical connections of all descendants derived from a single naive CD8⁺ T cell throughout up to ten divisions of activation-induced proliferation. Bayesian inference of tree-structured data reveals that clonal expansion is divided into a homogenously fast burst phase encompassing two to three divisions and a subsequent diversification phase during which T cells segregate into quickly dividing effector T cells and more slowly cycling memory precursors. Our work highlights cell cycle speed as a major heritable property that is regulated in parallel to key lineage decisions of activated T cells.

Abstract

Rapid clonal expansion of antigen-specific T cells is a fundamental feature of adaptive immune responses. It enables the outgrowth of an individual T cell into thousands of clonal descendants that diversify into short-lived effectors and long-lived memory cells. Clonal expansion is thought to be programmed upon priming of a single naive T cell and then executed by homogenously fast divisions of all of its descendants. However, the actual speed of cell divisions in such an emerging “T cell family” has never been measured with single-cell resolution. Here, we utilize continuous live-cell imaging in vitro to track the division speed and genealogical connections of all descendants derived from a single naive CD8⁺ T cell throughout up to ten divisions of activation-induced proliferation. This comprehensive mapping of T cell family trees identifies a short burst phase, in which division speed is homogenously fast and maintained independent of external cytokine availability or continued T cell receptor stimulation. Thereafter, however, division speed diversifies, and model-based computational analysis using a Bayesian inference framework for tree-structured data reveals a segregation into heritably fast- and slow-dividing branches. This diversification of division speed is preceded already during the burst phase by variable expression of the interleukin-2 receptor alpha chain. Later it is accompanied by selective expression of memory marker CD62L in slower dividing branches. Taken together, these data demonstrate that T cell clonal expansion is structured into subsequent burst and diversification phases, the latter of which coincides with specification of memory versus effector fate.

The smallest unit from which an adaptive immune response can originate is an individual antigen-specific lymphocyte (1). For both CD4⁺ and CD8⁺ T cells, it has been shown that single-cell–derived immune responses in vivo are subject to immense variation, despite being directed against the same epitope and unfolding within the same host (2–6). Upon vaccination or infection, even naive T cells harboring identical T cell receptors (TCRs) will generate “T cell families” (i.e., immune responses derived from a single T cell) of highly distinct size and phenotypic composition (2, 3, 6). Interestingly, within a given T cell family, clonal expansion and T cell differentiation are interdependent; at the peak of expansion, larger T cell families harbor lower percentages of long-lived central memory precursors (CMPs) and higher percentages of shorter-lived effector memory precursors (EMPs) and terminal effectors (TEs) than smaller T cell families (2, 7).

To account for the variation in single-cell–derived expansion and the interdependency of T cell phenotype and family size, we have put forward a stochastic developmental framework in which naive T cells first give rise to slowly dividing CMPs, which can then differentiate into more quickly dividing but shorter-lived progeny (2). This framework proved to be efficient in describing features of single-cell–derived T cell responses in vivo, such as the relative independence of a T cell family’s memory capacity from its acute size of clonal expansion. In fact, the acute size of clonal expansion is dictated by shorter-lived EMPs and TEs and does not reflect the underlying prevalence of CMPs within a T cell family. This framework is further supported by direct measurements of division speed in vivo, showing that, already by day 4 after vaccination, CD62L⁺ CMPs undergo, on average, one division less per day than their CD62L^– counterparts (8). Moreover, recent work confirmed the largely unidirectional differentiation of CMPs into non-CMPs during the expansion phase of a T cell response (9) and the role of CMPs as the major source of long-lasting CD8⁺ T cell memory (10–12).

However, certain features of our originally proposed stochastic framework are at odds with observations made during the very early phase of T cell activation. First, directly after activation in vivo, CD8⁺ T cells have been found to divide particularly fast (13, 14), conflicting with the idea of an initial emergence of slowly dividing CMPs. Second, elegant in vitro experiments have shown that division activity is strongly correlated among the members of a given T or B cell family, arguing against the emergence of distinct expansion kinetics within the same family (15–18). However, these latter studies mainly investigated the first three to four cell divisions executed by an expanding lymphocyte family and compared division speed only between close relatives within the family tree (i.e., sibling or mother–daughter correlations). We reasoned that to investigate the gradual cross-generational emergence of slower- or faster-dividing genealogical branches, division speed and T cell kinship must be tracked across longer genealogical distances than done before.

Therefore, we performed continuous in vitro imaging of single-cell–derived clonal expansion for up to 5 d after T cell activation. In contrast to previous studies, we utilized a culture system that allowed us to faithfully track the genealogical connections within expanding T cell families for up to ten generations. We found that after completing their first cell cycle, CD8⁺ T cells underwent a burst phase of two to three uniformly quick divisions. Mean division speed then slowed down in the absence of continued TCR stimulation and remained high when TCR stimulation was maintained. However, even upon continuous TCR stimulation, distinctly proliferating branches emerged in the later generations of a family tree. To better quantify the hereditary nature of this process, we developed a computational framework that enabled a model-based analysis of the tree-structured data obtained from live-cell imaging. We combined branching process modeling with a Bayesian inference approach for models with hidden states. This framework enabled us to test various hypotheses about the diversification pattern of proliferating T cells into subsets with distinct interdivision times. These analyses identified a model in which naive T cells first differentiate into a quickly proliferating early activated state, which then transits into slowly and quickly dividing branches that heritably maintain their distinct division activity. Further investigating the molecular regulation of these processes, we found that distinct expression levels of the high-affinity interleukin-2 (IL-2) receptor alpha chain (CD25), established during the burst phase, preceded the adoption of distinct division activities. Moreover, we found that CD62L, as a marker of CMP differentiation, was preferentially expressed in slowly dividing T cells that emerged beyond the burst phase.

Taken together, our work shows that after a short burst phase, the division speed of activated CD8⁺ T cells segregates into slow- and fast-cycling branches. Moreover, it provides mathematical methodology suited to test models of heredity within tree-structured data generated by an expanding T cell family or any other proliferating and continuously imaged cell type.

Results

Continuous In Vitro Imaging Reveals That Distinct Division Speeds Emerge within the Same T Cell Family.

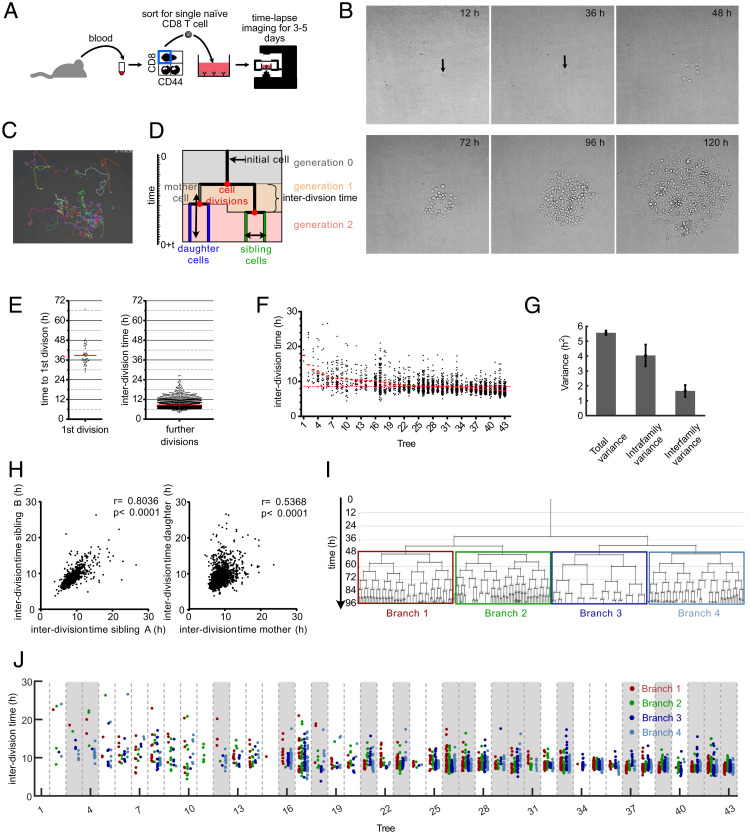
To comprehensively map clonal expansion in vitro starting out from individual naive CD8⁺ T cells, we utilized a continuous imaging platform (19, 20). Naive CD44^low CD8⁺ T cells were individually sorted via flow cytometry from peripheral blood of C57BL/6 mice, transferred to culture wells coated with anti-CD3 and anti-CD28 antibodies, and supplemented with IL-2 (Fig. 1A). This treatment enabled TCR restimulation throughout the expansion phase and induced vigorous proliferation that we monitored via continuous imaging for up to 5 d (Fig. 1B and Movie S1). Importantly, IL-2 concentrations remained at saturating levels throughout the whole observation period (SI Appendix, Fig. S1). Since overcrowding of microwells (20 to 100 μm in diameter) and clustering of T cells can be a problem for tracking the individual members of an expanding T cell family tree (16, 17), we sorted single T cells into relatively large wells with a diameter of 1,840 μm and imaged the complete well (Movie S2). These “macrowells” allowed for freer migration and reduced overlay phenomena of activated T cells. This enabled reliable tracking of individual T cells for up to ten cell generations (Fig. 1 C and D and Movie S3). We found that activated T cells required, on average, 39 h to complete their first cell division (Fig. 1E). The average interdivision time for subsequent cell cycles amounted to 8.6 h but showed strong variation ranging from 5 to 28 h per cell cycle (Fig. 1F). Interestingly, while some of this variation could be attributed to differences between the overall division speed of distinct T cell families (interfamily variance), most of it was derived from differences in division speed between individual T cells belonging to the same family (intrafamily variance) (Fig. 1G). To explore whether these differences arose as random fluctuations or were heritably maintained, we first investigated correlations of division speed between close relatives in a family tree. As previously reported (14–17), we found that T cell siblings shared similar division speeds with one another and with the mother cell from which they were derived (Fig. 1 D and H). To then investigate more distant genealogical relationships, we grouped the progeny of an individual T cell into four main branches, emerging from the second generation of each family tree (Fig. 1I). In more than 40% of family trees (18 of 43), the average T cell division speed differed significantly between these branches (Fig. 1J). We also identified distinct average division speeds in branches derived from the first generation of T cell family trees, albeit at a lower incidence (SI Appendix, Fig. S2). These data show that slow- versus fast-cycling T cells can segregate onto distinct branches of the same T cell family tree. To more formally explore whether this segregation could be accounted for by differentiation of proliferating T cells into heritably distinct subsets, we next performed computational modeling.

Fig. 1.

Continuous in vitro imaging reveals that distinct cell cycle speeds emerge within the same T cell family. (A) Blood was taken from an OT-I mouse and sorted for naive CD8⁺, CD44^low cells. A single naive OT-I cell was sorted into a well that was coated with anti-CD3 and anti-CD28 in the presence of 25 U/mL IL-2. The cell culture plate was transferred to a live-cell imaging microscope and imaged for the next 3 to 5 d. (B) Pictures, taken at different time points from the same single cell–derived progeny. The length of each micrograph edge is 250 μm. (C) Snapshot of a single cell–derived progeny at 3 d, 17 h, and 45 min after start of acquisition. Colored lines represent migration pattern of individual cells. (D) Definitions of family tree–associated data; y axis, time; generation, the number of cell divisions that have occurred from the naive T cell until the respective cell was created by division of its respective mother cell; mother and daughter cells, the two cells that originate from the same cell division are daughter cells in respect of the original cell that divided (mother cell); sibling cells, cells that have the same mother cell; interdivision time, time between the creation of an individual cell due to the division of its mother cell into two daughter cells and the end of the respective cell due to its own division into two new daughter cells. (E) Time for first and subsequent divisions. Single naive (CD44^low) CD8⁺ T cells were sorted into separate wells of an anti-CD3/CD28–coated 384-well plate and imaged for 5 d in a live-cell imaging microscope. The fate of each cell was tracked, and the interdivision time for the first division and all subsequent divisions was determined for 43 single-cell–derived progenies (in total, 43 cells for first division and 2,710 cells for subsequent cell divisions). Red lines indicate the means. (F) Intra- and interclonal variability of interdivision times. The interdivision times from E (first division excluded) are arranged according to their mean interdivision time; red bars, mean interdivision time within family tree; red dotted line, mean for all cells. Of note, very little cell death was observed in these experiments. Thus, differences in the number of displayed data points per family are mainly due to differences in the average division speed and the efficiency of continuous tracking (Materials and Methods). (G) Total variance of interdivision times from further divisions in E as well as the contribution of intrafamily and interfamily variances are shown. Intrafamily variance is calculated as the weighted mean of the variances of interdivision times within all different families. Interfamily variance is calculated as the weighted variance of the mean interdivision times of different families (SI Appendix, Supplementary Methods); total variance, 5.57 ± 0.15; intrafamily variance, 4.045 ± 0.73; interfamily variance, 1.66 ± 0.39. The distribution of intrafamily variance is significantly larger than that of interfamily variance (P < 1 × 10⁻³). (H) Interdivision times from E were plotted against the interdivision times of their sibling cell (Left, 1,201 pairs) or their direct daughter cells (Right, 2,630 pairs). The correlation coefficients (r) and the P values for Spearman correlations are indicated. (I) A representative family tree was divided into four branches starting from generation 2; loose ends, no further tracking possible for the respective cell. (J) Interdivision time of cells in the four branches starting from the second generation (as depicted in I) are color coded for all trees in F. In 18 of 43 trees (∼42%; trees highlighted in gray), interdivision times differed significantly between the four branches. For every tree, a P value was calculated based on one-way ANOVA. We then estimated positive false discovery rates (pFDR) for multiple hypothesis testing based on these P values and used a cutoff of pFDR < 0.05 for significance.

Computational Analysis of T Cell Family Trees Identifies a Model in Which Early Activated T Cells Diverge into Slow- and Fast-Cycling Subsets.

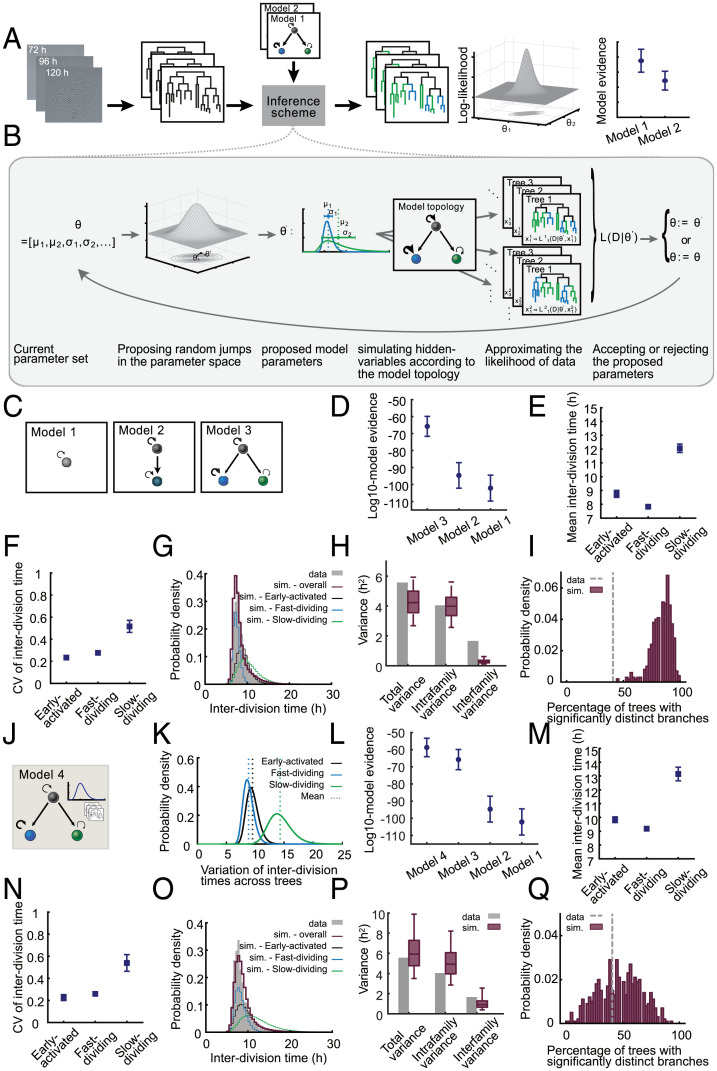
To test whether differentiation of proliferating T cells into subsets with heritably distinct division speeds indeed accounted for the variability of interdivision times and the resulting interior structure of T cell family trees, we used a branching process framework (21). Since we could not monitor the underlying differentiation processes directly, we modeled the differentiation state of each cell as a hidden variable (i.e., its belonging to a slow- or fast-cycling subset). To infer the parameters of the branching process, we then developed a Bayesian inference framework for tree-structured data comprised of a Markov chain Monte Carlo sampling approach with hidden layers (22, 23). Our inference framework takes as input the genealogical trees obtained from live-cell imaging movies as well as a model hypothesis describing the underlying branching process. As output, it returns the posterior distribution of model parameters as well as the model evidence for every assumed model hypothesis. These model evidences and corresponding Bayes factors are then used for model selection (Fig. 2A and SI Appendix, Supplementary Methods). The individual steps of our iterative scheme are depicted in Fig. 2B (SI Appendix, Supplementary Methods).

Fig. 2.

Computational analysis of T cell family trees identifies a model in which early activated T cells diverge into slow- and fast-cycling subsets. (A) Schematic of the workflow of our inference scheme. The scheme requires as input 1) lineage trees obtained from successive two-dimensional microscopy images and 2) one or more model hypotheses describing the underlying branching process. For every model hypothesis, it returns posterior distribution of model parameters and an approximation of the model evidence. The model evidences are used for model selection. (B) Individual steps of the iterative inference scheme. In every iteration, a new set of model parameters is proposed based on the current parameter values and a proposal distribution. These proposed parameters (e.g., the mean and CV of subset-specific interdivision time distribution) are used to simulate several samples of hidden variables of the model. For instance, the shown model topology includes three different subsets (black, blue, and green). The simulated hidden variables in this case are the subset that is assigned to each cell in the tree. For every tree and every simulated sample, the likelihood of the data is calculated given the current value of parameters and hidden variables. A Monte Carlo approximation method is used to calculate the overall likelihood of the data given the parameters. The proposed parameter set is accepted with the acceptance probability calculated based on the likelihood and is rejected otherwise. (C) Schematic of different model hypotheses used for the analysis of T cell family trees. Model 1 assumes a homogenous population with one proliferation speed. Model 2 assumes an early expanding subset that later differentiates into another subset with a distinct proliferation speed. Model 3 assumes an early expanding subset that diversifies into slow- and fast-dividing subsets. (D) The model evidences for the models in C indicate the following hierarchy: model 3 > model 2 > model 1; model 3, having the highest evidence, explains the data best, and model 1, having the lowest evidence, is least matching to the data. The circles show the mean of log₁₀ model evidences of the eight data groups (SI Appendix, Supplementary Methods). The error bars show the SEM. The (Akaike and Bayesian) information criteria confirmed the same model hierarchy presented here. (E and F) Inferred mean (E) and CV (F) of the interdivision time distribution for “early activated”, “slow-dividing”, and “fast-dividing” subsets based on model 3. For every data group, the median of the posterior distribution of the respective parameters is calculated; the squares denote the mean of these medians (SI Appendix, Supplementary Methods). The error bars show the SEM. (G) The distribution of interdivision times in 10,000 simulated trees based on model 3 compared to that of the experimental data (gray). The red histogram shows the overall distribution in the simulated data, while the black, blue, and green histograms show the distribution of “early activated”, “fast-dividing”, and “slow-dividing” subsets, respectively. The results are shown for one data group; sim, simulation. (H) Total variance of the interdivision times and the contribution of intrafamily and interfamily sources as observed in the experimental data (gray bars) and simulated data (red boxes). Intrafamily variance is calculated as the weighted mean of the variances of interdivision times within different families. Interfamily variance is calculated as the weighted variance of the family mean interdivision times (SI Appendix, Supplementary Methods). The simulated data consist of 500 datasets of each 44 trees simulated based on model 3. The boxes show the 90% confidence interval of the simulated data. The total variance and intrafamily variance of the experimental data are contained within the 90% confidence interval of the simulated data, while for interfamily variance, the simulated data do not contain the experimental data point. The following are the three variance terms from left to right for the experimental data: 5.57, 4.05, and 1.66. The 5th percentile, median, and 95th percentile for the three variance terms for simulated data from left to right are 2.68, 4.23, and 5.93; 2.56, 3.98, and 5.61; and 0.11, 0.27, and 0.61, respectively. The results are shown for one data group. (I) Percentage of the trees whose four branches (as in Fig. 1I) have significantly distinct interdivision times. The gray line shows the experimental data, and the red histogram shows the distribution of this percentage in the simulated data, as in H (SI Appendix, Supplementary Methods). The results are shown for one data group. (J) Model 4 adopts the topology of model 3 and incorporates variability between trees. The mean interdivision times of subsets early activated, slow-dividing, and fast-dividing are assumed to differ between trees, and this variation is assumed to be log-normally distributed. The inset shows the stack of different trees and a sample log-normal distribution for the variation of subset-specific mean interdivision times between these trees. (SI Appendix, Supplementary Methods). (K) Inferred variation of subset-specific mean interdivision times among different families based on model 4. The black, blue, and green curves show the distribution for “early activated,” “fast-dividing,” and “slow-dividing” subsets, respectively. The results are shown for one data group. (L) Model evidences for the models in C and J indicate that model 4 explains the data best. The circles show the mean of the log₁₀ of model evidences of eight data groups (SI Appendix, Supplementary Methods). The error bars show the SEM. A difference of seven between the mean log₁₀ model evidences for model 4 and model 3 indicates the significant superiority of model 4. The mean Bayes factor, as well as individual Bayes factors in every data group, show at least strong evidence for choosing model 4 over model 3 (SI Appendix, Figs. S5 and S12). The (Akaike and Bayesian) information criteria confirmed the same model hierarchy presented here. (M and N) Same as E and F, with parameters inferred based on model 4. (O–Q) Same as G to I, with simulated data based on model 4. (P) The total variance, intrafamily variance, and interfamily variance of the experimental data are all contained within the 90% confidence interval of the simulated data. The three variance terms from left to right for the experimental data are 5.57, 4.045, and 1.66. The 5th percentile, median, and 95th percentile for the three variance terms for simulated data from left to right are 3.5, 5.92, and 9.89; 2.86, 4.92, and 8.21; and 0.39, 0.91, and 2.55, respectively.

We assumed that the interdivision times of cells belonging to every subset are distributed according to a log-normal distribution with a specific mean and coefficient of variation (CV). To allow for efficient computation, we divided our dataset into eight groups of five family trees each and for each group inferred the posterior distribution of model parameters as well as the model evidences. We then selected the models fitting best to our data by calculating Bayes factors based on the model evidences. To further assess how well the best-fitting model represented our data, we tested whether model-based simulations recapitulated the statistical characteristics of the experimental data (SI Appendix, Supplementary Methods).

We first investigated three basic model topologies. In model 1, naive T cells gave rise to one proliferating subset. In model 2, naive T cells gave rise to one proliferating subset that could differentiate into another subset proliferating at a distinct speed. In model 3, naive T cells gave rise to one proliferating subset that could differentiate into two others, each proliferating at distinct speeds (Fig. 2C). As expected, model 1, which assumed that proliferation of all activated T cells could be described by one division speed (i.e., one distribution of division speed learned from the data) was insufficient to account for the specific structure of T cell family trees (model evidences and Bayes factors are shown in Fig. 2D and SI Appendix, Figs. S3–S6). Interestingly, model 2, which relied on the differentiation of one proliferating subset into another, was also insufficient to account for the measured data. Only model 3, which assumed that a proliferating early activated subset differentiates into a slowly or a quickly dividing one, provided an adequate fit to the measured data (Fig. 2D and SI Appendix, Figs. S3–S6). Mean interdivision times of these subsets were predicted at 8.8 h, 7.8 h, and 12 h for the early activated, fast-dividing, and slow-dividing subsets, respectively (Fig. 2E and SI Appendix, Fig. S7). The learned distribution of division speed for the slow-dividing subset was relatively wide, while those of the early activated and fast-dividing subsets showed considerably less variation (Fig. 2F and SI Appendix, Fig. S7). To rule out the possibility that model 3 was the preferred model only due to its increased number of parameters and the resulting additional flexibility, we compared it to a mixture model in which, once leaving the early activated state, cell cycle speeds are taken from two overlaid distributions without considering the topological restraints of the proposed differentiation process, meaning that switching between fast and slow division activities is possible within a given branch (SI Appendix, Supplementary Methods). The resulting mixture model could not explain the experimental data as well as model 3, which accounts for the topological relationships and heritable features within a T cell family tree. Additionally, we opted to test whether the variations in division times could be explained by a correlation between the division times of mother and daughter cells, without any underlying topological subsets. Therefore, we considered the topology of model 1 and modeled the division time of every cell dependent on the division time of its mother cell, with the correlation coefficient being an additional model parameter (SI Appendix, Supplementary Methods). The model evidence and Bayes factors obtained by our Bayesian framework indicated that solely a correlation in mother–daughter division times could not explain the variability observed in the experimental data, and indeed distinct subsets were required (the model evidences and Bayes factors are shown in SI Appendix, Figs. S3–S6). Thus, the topological diversification of cells into distinct subsets and the maintenance of distinct division speeds within every subset, as considered in model 3, were crucial for explaining the data. Using the simulation analysis mentioned earlier, we found that the best-fit “early activated to slow-dividing or fast-dividing” model (model 3), although adequately reproducing the overall distribution of interdivision times (Fig. 2G and SI Appendix, Fig. S8), underestimated the contribution of interfamily differences to the overall variation of T cell division speed (Fig. 2H and SI Appendix, Fig. S9). It further overestimated the percentage of trees with branches showing significantly distinct division speeds (Fig. 2I and SI Appendix, Fig. S10). This indicated that division speed of activated T cells may not only depend on their current differentiation state (early activated, slow-dividing, or fast-dividing) but also on an ancestral imprinting received by the starting cell and passed down to its descendants. To account for this clonal imprinting of division speed, we allowed for a log-normally distributed factor in the model formalism that could modify all subset-specific proliferation rates (for subsets early activated, slow-dividing, and fast-dividing) of a given T cell family by a certain value (SI Appendix, Supplementary Methods). Fitting this extended model (model 4; Fig. 2J) to the data, we quantified the variation of subset-specific mean interdivision times between different families (Fig. 2K and SI Appendix, Fig. S11) and found that this model was best supported by the data. A difference of seven in the average log₁₀ model evidences indicated that model 4 was significantly better than model 3 in explaining the data (Fig. 2L). Furthermore, the corresponding Bayes factors showed that in six of eight data groups, there was decisive evidence for choosing model 4 over model 3 (log₁₀ Bayes factors > 2), with the remaining two data groups providing strong evidence for model 4 (log₁₀ Bayes factors > 1) (SI Appendix, Figs. S3–S5 and S12). Importantly, despite the additional variation introduced by this factor, the distinct division speeds of the early activated, fast-dividing, and slow-dividing subsets were maintained according to the best-fit parameters of model 4 (Fig. 2 M and N and SI Appendix, Fig. S13). We noted that the overall distribution of interdivision times in simulated data based on model 4 (Fig. 2O and SI Appendix, Fig. S14) was similar to the results of model 3 (Fig. 2G and SI Appendix, Fig. S8), and this statistical feature alone would not have been enough to distinguish between the two models. Instead, more elaborate structural features of the T cell family trees could demonstrate differences between the two models. Indeed, model 4 now correctly captured both intra- and interfamily variability (Fig. 2P and SI Appendix, Fig. S15) and generated a realistic fraction of T cell family trees whose second-generation branches proliferated at distinct average speeds (Fig. 2Q and SI Appendix, Fig. S16). The inferred model parameters and model evidences for all models and data groups are depicted in SI Appendix, Figs. S7, S13, and S17–S20. Interestingly, when taking into account initial variation of T cell recruitment measured in vivo (3), simulations based on the topology and parameters identified for model 4 in vitro also replicated the variation of T cell family sizes previously found in vivo (2) (SI Appendix, Fig. S21 and Supplementary Methods).

Taken together, these computational analyses suggested that T cell clonal expansion is not a homogenous process programmed exclusively upon T cell priming. Instead, the emergence of multiple T cell subsets proliferating at distinct speeds appeared necessary to correctly capture the evolution of an expanding T cell family tree.

Diversification of Division Speed Occurs after a Homogenous Burst Phase and Is Preceded by Differences in CD25 Expression.

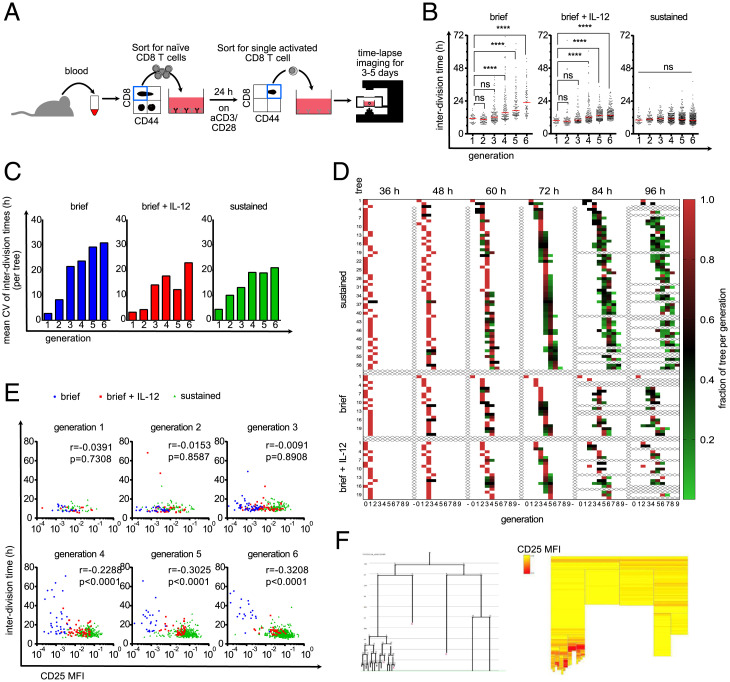
The experimental conditions, under which the above-mentioned results were gathered, allowed both the starting cell as well as its descendants to receive TCR stimulation. This raised the question of whether the emergence of slow- and fast-dividing branches within the same T cell family tree was the consequence of TCR stimuli incidentally accumulating in one branch but not the other. Thus, we next asked whether distinct division speeds would also emerge when TCR stimuli are restricted to the starting cell. To achieve this, we activated T cells in bulk via plate-bound anti-CD3 and anti-CD28 antibodies in the presence of IL-2 and IL-12 and, 24 h later, sorted single undivided T cells into wells containing no further TCR stimuli. To sustain proliferation for an extended period of time, wells, were supplemented with saturating doses of IL-2 only (“brief”) or IL-2 and IL-12 (“brief + IL-12”). Since IL-12 induces the expression of CD25, we were expecting a synergistic effect of both cytokines jointly added. As before, we tracked T cell proliferation via continuous imaging for up to 5 d (Fig. 3A). Upon brief TCR stimulation, first- and second-generation T cells divided at the same average speed as those cultured in the sustained presence of TCR stimuli (“sustained”). After this initial burst phase, the average division speed of briefly stimulated T cells significantly slowed down, albeit less in the group supplemented with IL-2 and IL-12 (Fig. 3 B and C). Importantly, the variation in division speed of both the “brief” and “brief + IL-12” groups matched or even exceeded that of T cells receiving sustained TCR stimuli (Fig. 3 B and C). If this variation arose due to random fluctuations in division speed, one would expect that, over time, short and long interdivision times cancel each other out, and all members of a growing T cell family occupy the same or adjacent generations. However, we found that upon acquiring an increasing number of divisions, the generational range between the most- and least-divided members of a T cell family constantly widened (increasing length of colored rows from 36 to 96 h), arguing in favor of distinct family branches heritably maintaining slower and faster cell cycle activity (Fig. 3D). Our Bayesian model inference on the “brief” and “brief + IL-12” groups showed a tendency that models 3 and 4 are generally more adequate than models 1 and 2 in explaining the data (SI Appendix, Fig. S22). However, decisive model selection on these groups was not possible (SI Appendix, Fig. S23), likely because fewer divisions in these stimulation conditions than in the continuous stimulation setting do not allow for observation of diversification events into slow- and fast-dividing subsets (that are characteristics of models 3 and 4) often enough. To more closely investigate the mechanistic origin of these distinct division speeds, we measured the expression of CD25 during continuous imaging. We achieved this by addition of very low concentrations of fluorophore-conjugated anti-CD25 antibody, as described previously (20, 24). We found that addition of very low antibody concentrations had negligible effects on proliferative activity of activated T cells (SI Appendix, Fig. S24) while generating robust and reliable fluorescent signals (Movie S4). Interestingly, T cells receiving brief versus sustained TCR stimulation showed distinct levels of CD25 surface expression already within the first and second generation but still proliferated at the same speed. Only from the fourth generation onward did lower or higher CD25 expression levels begin to correlate with lower or higher T cell division speed (Fig. 3E). In fact, closer inspection of individual T cell family trees showed that changes in CD25 expression levels can be allocated to specific branches and can precede changes in division speed that develop across multiple generations (Fig. 3F and SI Appendix, Fig. S25). Taken together, these data indicate that during the first two generations of T cell proliferation, division speed is largely independent of sustained TCR stimuli, IL-12 availability, or CD25 expression levels. Thereafter, however, distinct levels of CD25 surface expression begin to correlate with distinct division speeds and are heritably maintained within distinct branches of an expanding family tree.

Fig. 3.

Diversification of division speed occurs after a homogenous burst phase and is preceded by differences in CD25 expression. (A) Live-cell imaging with brief TCR stimulation. Blood was taken from an OT-I mouse and sorted for naive CD8⁺ T cells. Ten thousand cells/well were activated for 24 h with plate-bound anti-CD3/CD28 and 25 U/mL IL-2. Cells were sorted again for activated (CD44^high) cells, and a single cell was sorted in each well of a 384-well plate that was coated with ICAM-1 or anti-CD28 to enable attachment. The cells were imaged for 3 to 5 d. (B) Cells were stimulated as described in A. After the brief stimulation and segregation, 10 ng/mL IL-12 was added to the medium (Middle) or not (Left). Cells were stimulated continuously with anti-CD3/anti-CD28 as in Fig. 1 (Right). The interdivision times of all cells are plotted for the respective generations. Red lines indicate the median. Kruskal–Wallis test; ****P < 0.0001. (C) Data points from B were allocated to the different family trees, and the CVs of the interdivision times within the trees were calculated within each generation. The mean of these CVs is plotted as a bar graph, on average, 15.45 trees per bar (range of 4 to 27). (D) For all three conditions, it is shown how the individual cells within a tree are distributed over the generations at different time points. The fraction of tree per generation is calculated by dividing the number of cells in a specific generation at the given time point by the maximum number of cells potentially present in the respective generation (number of cells in generation X/2^{generation X}). For example, for a potential tree that consists after 48 h of one cell in generation 2 and six cells in generation 3, the respective fractions of tree per generation are for generation 2, 1/2² = 0.25, and for generation 3, 6/2³ = 0.75. For incompletely tracked trees (e.g., when cells died or the identity of cells is unclear), the fractions of tree per generation is corrected so that the sum of all fractions of tree per generation sum up to 1.0 (corrected fraction of tree per generation = fraction of tree per generation/sum of all fractions of tree per generation at the same time point). Each square represents the cells of a tree that are in the respective generation at the given time point. The redder the box is, the higher is the fraction of the tree in the respective generation. Thus, red boxes indicate synchronized cell divisions, whereas green boxes indicate desynchronization. Samples from the continuous stimulation setting are depicted at the Top. Below that are the short stimulation samples. The short stimulation + IL-12 samples are depicted at the Bottom. (E) As in A, but anti-CD25–APC was added to the culture. The interdivision times of all cells from all investigated trees were separated according to their generation, and their interdivision times were plotted against their CD25 expression; blue, brief stimulation without IL-12; red, brief stimulation with IL-12; green, continuous stimulation. Spearman r and P values are as indicated; generation 1, 80 cells; generation 2, 138 cells; generation 3, 232 cells; generation 4, 313 cells; generation 5, 422 cells; generation 6, 583 cells; MFI, mean fluorescence intensity. (F) Exemplary tree (brief stimulation + IL-12) shown as family tree (Left, loose ends with red X indicate that the cell died) and heat tree (Right). Each box represents a cell as in the family tree; yellow, low CD25 expression; red, high CD25 expression; blank, no CD25 quantification possible.

Adoption of Slower Division Speed Coincides with Expression of CMP Marker CD62L.

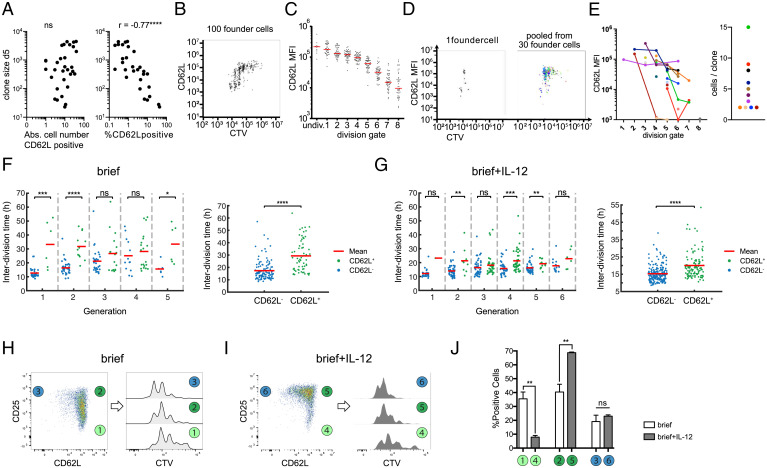
Finally, we aimed to investigate whether these linked changes in IL-2 receptivity and division speed also correlated with memory versus effector T cell differentiation. Since CD62L⁺ CMPs have been identified as early as day 4 after immunization in vivo and have been shown to divide slower than their CD62L^– counterparts (8), we decided to investigate expression of this memory marker in our experimental system. First, we analyzed single-cell–derived T cell responses via flow cytometry at day 5 after in vitro activation. In line with previous observations made in vivo, we found that T cell family size did not significantly correlate with the absolute number of CD62L⁺ T cells but inversely correlated with the percentage of CD62L⁺ T cells found per family (Fig. 4A). Moreover, when tracking T cell responses derived from populations of 100 T cells via intracellular dye dilution, we found that those T cells that had undertaken more divisions expressed lower levels of CD62L than their less-divided counterparts (Fig. 4 B and C). Vice versa, reduction of accumulated divisions due to shortened initial TCR signaling reduced the fraction of CD62L^– cells (SI Appendix, Fig. S26). When tracking single-cell–derived T cell responses in the same manner, we found that T cell families stretched out across multiple generations and that CD62L^– cells accumulated in the more strongly divided offspring of the same starting cell (Fig. 4 D and E). While these observations could indicate that CD62L^– T cells divide faster, they could also mean that differentiation into CD62L^– T cells happens only after a certain generation is reached. To resolve this question, we again turned to continuous imaging. Immediately after T cell activation, CD62L is enzymatically removed from the surface of activated T cells (25). In line with this shedding of CD62L, we found virtually no surface expression of this molecule immediately after T cell activation. However, CD62L surface expression reappeared in subsequent generations and coincided with a slower division speed relative to CD62L^– T cells found in the same generation (Fig. 4F). Importantly, division speed of CD62L⁺ T cells remained relatively fixed throughout generations, arguing that the gradual slowdown of T cell families that we had observed from generations 3 to 6 resulted from an increasing number of T cells switching into the CD62L⁺ state. The same differentiation-associated reduction of cell cycle speed occurred in the presence of IL-12, albeit with CD62L⁺ T cells maintaining substantially faster division activity than in the absence of this inflammatory cytokine (Fig. 4G), which may be due to IL-12 driving increased CD25 expression among CD62L⁺ T cells (Fig. 4 H–J). Finally, we found that incorporating the measured differences between division speed of CD62L⁺ and CD62L^– T cells into our Bayesian modeling scheme described the data as well but with fewer parameters than the initial model 3 (SI Appendix, Fig. S27). This provides further evidence that CD62L is indeed an indicator of cell state as it relates to division speed.

Fig. 4.

Adoption of slower division speed coincides with expression of CMP marker CD62L. (A) Cell numbers of single-cell–derived progenies are plotted against the absolute number of CD62L-expressing cells (Left) or the percentage of CD62L-expressing cells (Right) (determined by flow cytometry) within the respective T cell family (continuous TCR stimulation). Spearman correlation coefficient, r = −0.7569; P < 0.0001, n = 31 (cells with %CD62L = 0% excluded from analysis); Abs, absolute. (B) Representative Cell Trace Violet plot of the offspring of 100 OT-I cells that had been stained with Cell Trace Violet and activated for 24 h. After a further 3 d of cell culture, the cells were stained for CD62L and analyzed by flow cytometry. (C) On the basis of the vertical lines in the Cell Trace Violet plot in B, the number of cell divisions for each cell in the plot can be estimated. The mean CD62L expression within each division peak is shown for all cells of the 100 cell-derived progenies. (D) Representative Cell Trace Violet plot as in B but from a single progenitor cell (Left). Overlay of 30 single-cell Cell Trace Violet plots (Right). Each color represents a different single-cell–derived progeny. (E) CD62L expression in division peaks as in C but from single-cell–derived progenies. Single-cell–derived progenies distributed across more than one division peak are connected with a line (Left). Corresponding scatter plot showing the number of recovered cells for each single-cell–derived progeny distributed across more than one division peak (Right). Single-cell–derived progenies that were present in only one division peak are not displayed in the Right plot (i.e., 13 progenies containing 1 cell, 1 progeny with 2 cells, 2 progenies with 3 cells, and 1 progeny with 7 cells). (F) Interdivision times in different generations (Left) and from all generations together (Right) in the “brief” stimulation condition. The two-sided Wilcoxon rank sum test is used to determine if the interdivision times of CD62L⁺ (green) and CD62L⁻ (blue) cells are significantly different; ns, P > 0.05; *P ≤ 0.05; **P ≤ 0.01; ***P ≤ 0.001; ****P ≤ 0.0001. (G) Same as F for the “brief + IL-12” stimulation condition. (H) Representative pseudocolor plot showing expression of CD25 and CD62L for population-derived responses in the “brief” stimulation condition and definition of three subpopulations based on their CD25/CD62L profile (Left) and corresponding overlaid histograms showing intracellular dye dilution profiles for each of these three subpopulations (Right). (I) Same as H for the “brief + IL-12” stimulation condition. (J) Corresponding bar graph depicting the percentage of cells in each subpopulation defined in H and I under both stimulation conditions. The unpaired t test is used to determine statistical significance between both stimulation conditions; ns, P > 0.05; **P ≤ 0.01.

Discussion

It is a hallmark of adaptive immunology that single antigen-specific T cells can generate progeny that diversifies into both terminally differentiated effector cells and precursors of long-lived memory cells (26). This fate diversification occurs in parallel to rapid T cell proliferation, and computational modeling of single-cell–derived T cell responses has suggested that memory precursors and short-lived effector T cells are set apart by fundamentally distinct cell cycle speeds (2). Recently, we have shown that 4 d after initial T cell priming, memory precursors are characterized by a slower division speed than their effector counterparts in vivo (8). Early clonal expansion, however, was found in vitro to occur in a highly synchronized manner (15–18). Here, we set out to close the gap between these early in vitro observations and the later diversification of division speed and T cell fate observed in vivo. Therefore, we utilized continuous live-cell imaging and tracked the division speed, differentiation status, and genealogical connections of all descendants derived from a single naive T cell for up to ten divisions of activation-induced proliferation in vitro. We find that initial T cell proliferation indeed occurs in a burst-like manner, with rapid execution of T cell divisions being largely independent of further TCR and cytokine stimuli received beyond priming. At two to three cell divisions, the average duration of this burst is similar to that previously described for in vitro settings in which stimuli were stringently restricted to the starting cell (18, 27, 28). Upon restriction of subsequent stimuli, including blockade of endogenous IL-2, T cell proliferation abruptly subsides after completion of this burst (18, 27, 28). This homogenous programming of proliferation activity, termed “division destiny”, has been attributed to a division counter (18, 27) or division timer (28) set in the starting cell and transmitted to all of its progeny. Here, we deliberately chose culture conditions that maintained T cell proliferation beyond the initial burst phase and closely monitored the evolution of cell cycle speed within the resulting family trees. Interestingly, we found evidence for a heredity of cell cycle speed that was in part programmed in the starting cell but also critically required the emergence of distinct T cell subsets proliferating at distinct speeds. One of these, the early activated subset, was of transient nature, and its lifetime coincided with the duration of the initial proliferative burst. Thereafter, slow- and fast-cycling subsets emerged that were characterized by distinct CD25 and CD62L expression levels, two markers that have been found to characterize the early subdivision of long-lived CMPs (CD62L⁺CD25^–) and non-CMPs (CD62L^–CD25⁺) in vivo (29, 30). In keeping with a concept of asymmetric cell divisions (31), the segregation of these subsets has been proposed to occur as early as the first cell division. While our in vitro data cannot exclude such an immediate segregation, they rather support a developmental model in which lineage segregation begins somewhat later after a burst-like expansion of two to three cell divisions. Thereafter, we find that individual branches within an expanding T cell family tree can maintain slower or faster cell cycle speeds that coincide with differences in expression of CD25 and CD62L. Programmed division destiny and subset-specific division speed may thus act in concert, with the prior dictating cellular behavior throughout the first divisions following TCR engagement and the latter emerging after this phase and coinciding with lineage segregation of CMPs and non-CMPs. Of note, expression of CD62L and CD25 is not mutually exclusive. In fact, CD25 coexpression identifies CD62L⁺ cells that show intermediate division activity between slow-dividing CD62L⁺CD25^– and fast-dividing CD62L^–CD25⁺ cells. However, rather than constituting a stable subset, we would currently speculate that these cells occupy an activation state within the CD62L⁺ CMP lineage that is transiently induced by IL-12 treatment. Taken together, our study puts renewed focus on the intertwined nature of cell cycle activity and T cell differentiation (32, 33). While previously, this relation has been mainly explored with respect to the accumulated number of divisions, we now highlight the actual speed of cell division as a major heritable property that appears to be regulated in parallel to key lineage decisions of activated T cells. From a methodological point of view, we provide a computational inference framework optimally suited for analyzing tree-structured data obtained by live-cell imaging. Due to the complexity of such tree-structured data, previous studies have mostly utilized summary statistics from live-cell imaging experiments to infer underlying kinetics (15, 34, 35). Our framework, however, exploits full structural information from this data type. As opposed to few other model-based analyses of lineage trees, where phenotypic measurements were assumed to inform about cellular differentiation (36–39), our framework does not rely on phenotypic observations and instead links division speed to underlying hidden states. Unlike similar studies (38), an important feature of our computational modeling is the simultaneous analysis of complete genealogical trees without partitioning into smaller “subtrees”; this ensures that no long-ranged structural information is lost. Our inference framework allows for investigation of the complex kinetic structure of expanding T cell family trees and enables hypothesis testing as to the hereditary nature of cell cycle activity and the topological organization of T cell differentiation. It will likely be of similar utility in deciphering the interdependence of differentiation and division activity in other rapidly proliferating cell types, such as hematopoietic stem and progenitor cells or B cells undergoing activation-induced class switch recombination and memory development. Moreover, it will be exciting to investigate whether the developmental framework proposed here will hold true in vivo and to more closely examine how T cell differentiation and cell cycle speed are connected on the molecular level. Subtle fluctuations in division activity may in fact serve as the initial spark, triggering the diversification of cellular phenotypes in the context of T cell immunology and beyond (40).

Materials and Methods

Mice.

C57BL/6 wild-type mice were purchased from Envigo. OT-I Rag1^−/− matrix donor mice expressing combinations of the congenic markers CD45.1/2 and CD90.1/2 were bred under specific pathogen-free conditions at the mouse facility of the Institute for Medical Microbiology, Immunology and Hygiene, Technical University of Munich, Munich, Germany. Animal care and procedures were in accordance with institutional protocols as approved by the relevant local authorities.

Cell Sorting.

Cells were isolated from peripheral blood or spleens of C57BL/6 or OT-I Rag1^−/− matrix donor mice and sorted for a naive phenotype (CD8⁺CD44^low) on a MoFlo Legacy or MoFlo XDP cell sorter. For experiments with sustained anti-CD3/CD28 stimulation, a single naive CD8⁺ T cell was sorted per well of an anti-CD3/CD28–coated (10 µg/mL at 4 °C overnight) plate (384 Well Small Volume LoBase med. Binding µClear microplate) containing 25 µL of Roswell Park Memorial Institute (RPMI) cell culture medium, penicillin/streptomycin (Pen/Strep), 10% heat-inactivated fetal calf serum (FCS), and 25 U/mL recombinant human IL-2. For experiments with limited anti-CD3/CD28 stimulation, 10,000 naive CD8⁺CD44^low T cells were sorted per well of an anti-CD3/CD28–coated (10 µg/mL at 4 °C overnight) plate (384 Well med. Binding µClear microplate) containing 100 µL of RPMI cell culture medium, Pen/Strep, 10% heat-inactivated FCS, 25 U/mL recombinant human IL-2, and 10 ng/mL murine IL-12. After 24 h at 37 °C, 5% CO₂, and 95% H₂O, the cells were pooled and sorted again. This time, cells were sorted for activated (CD8⁺CD44^high) T cells, and a single activated cell was sorted per well of an anti-CD28–coated 384-well plate (384 Well Small Volume LoBase med. binding µClear microplate) containing 25 µL of RPMI cell culture medium, Pen/Strep, 10% heat-inactivated FCS, and 25 U/mL recombinant human IL-2 with or without 10 ng/mL murine IL-12.

Continuous Single-Cell Imaging.

Live-cell imaging was performed by the ETH Zurich, as described by Eilken et al. (20). Briefly, the microplates were imaged using a Nikon-Ti Eclipse with a linear encoded motorized stage, Orca Flash 4.0 V2 (Hamamatsu), and Spectra X fluorescent light source (Lumencor) and a 10× chrome free infinity (CFI) Plan Apochromat λ objective (numerical aperture of 0.45). White light emitted by Spectra X was collimated and used as a transmitted light for brightfield illumination via a custom-made motorized mirror controlled by Arduino UNO Rev3 (Arduino), and images were taken every 1 to 3 min. For experiments in which the expression of a surface antigen was measured, the respective dye-conjugated antibody was added at a very low concentration to the culture medium (e.g., 1:20,000 for anti-CD25–allophycocyanin (APC), corresponding to 10 ng/mL), and, in addition to the brightfield images, the respective fluorescent channel was acquired approximately once every 45 min using filter sets for phycoerythrin (PE) (546/10; 560LP; 577/25) and APC (620/60; 660LP; 700/75; both from AHF analysentechnik AG). The cells were observed for 3 to 5 d at 37 °C, 5% CO₂, and 5% O₂. All images were acquired as a 16-bit lossless .png and linearly transformed using optimal black

Cell Tracking.

Generation of T cell family trees and heat trees was performed by manually tracking the cells using “The Tracking Tool” and the semiautomatic fluorescence intensity measurement software “qTFy” (19). Dead cells were identified by protracted motionlessness and apoptotic blebbing and designated with a red cross in the respective family trees. Failure of continuous tracking of individual T cells, due to overlay phenomena between T cells or escape of T cells into the imaging shadow of the culture well’s rim, is designated by a blind end of the respective branch of the family tree that terminates before the end of the imaging period.

Cell Proliferation Dye Staining and Flow Cytometry.

Cell proliferation dye staining was performed using the CellTrace Violet Cell Proliferation kit by Thermo Fisher Scientific, according to the manufacturer’s instructions. Cells were sorted, activated for 24 h, and sorted again, as described in Cell Sorting. After 3 d, the cells were stained with anti-CD62L–fluorescein isothiocyanate (FITC) (MEL-14) and acquired using a Cytoflex S cytometer.

Enzyme-Linked Immunosorbent Assay (ELISA).

The IL-2 ELISA was performed using the IL-2 Human ELISA kit by Thermo Fisher Scientific, according to the manufacturer’s instructions.

Antibodies and Cytokines.

Anti-murine CD3 (145-2C11), anti-murine CD28 (37.51), and anti-murine CD25-APC (PC61) were purchased from BD Biosciences, and anti-murine CD8 (53.6.7), anti-murine CD44 (IM7), and anti-murine CD62L-FITC (MEL-14) were purchased from BioLegend. Recombinant murine IL-12 was purchased from Peprotech. Recombinant human IL-2 was purchased from Thermo Fisher Scientific.

Statistical Analysis.

All non–in silico experiments were analyzed using Prism 7, 8, and 9 (GraphPad software). P values were assessed using a two-tailed unpaired Student’s t test, one-way analysis of variance (ANOVA), Spearman nonparametric test, or Pearson test, as specified in the figure legends.

Data Availability

All study data are included in the article and/or supporting information or will be made available upon request.