Design of Experiments, Chemometrics, and Raman Spectroscopy for the Quantification of Hydroxylammonium, Nitrate, and Nitric Acid

Abstract

Selecting optimal combinations of preprocessing methods is a major holdup for chemometric analysis. The analyst decides which method(s) to apply to the data, frequently by highly subjective or inefficient means, such as user experience or trial and error. Here, we present a user-friendly method using optimal experimental designs for selecting preprocessing transformations. We applied this strategy to optimize partial least square regression (PLSR) analysis of Stokes Raman spectra to quantify hydroxylammonium (0–0.5 M), nitric acid (0–1 M), and total nitrate (0–1.5 M) concentrations. The best PLSR model chosen by a determinant (D)-optimal design comprising 26 samples (i.e., combinations of preprocessing methods) was compared with PLSR models built with no preprocessing, a user-selected preprocessing method (i.e., trial and error), and a user-defined design strategy (576 samples). The D-optimal selection strategy improved PLSR prediction performance by more than 50% compared with the raw data and reduced the number of combinations by more than 95.5%.

1. Introduction

Raman spectroscopy is commonly used for qualitative and quantitative analysis of molecular species in aqueous solutions. It has been applied in numerous process-monitoring applications from micro to industrial scales. It has even been applied to processing that occurs in harsh and restrictive locations, such as shielded hot cell environments.¹⁻³ Industrial Raman applications are primarily used in the food and pharmaceutical industries, but other fields, such as the nuclear industry, could benefit from process monitoring using this and other optical techniques.³⁻⁹ Several Raman applications in the nuclear fuel cycle have been considered.⁶⁻⁹ Monitoring redox reagents for stabilizing Pu and Np valences is an important application to consider.

Hydroxylammonium is a common redox reagent for reducing Pu(IV) to Pu(III) and Np(VI) to Np(V) for radiochemical separations.¹⁰ It is a highly reactive species, and performance is highly dependent on nitrous acid (HNO₂) and nitric acid (HNO₃) concentrations.^11,12 Real-time monitoring using quantum cascade laser infrared analysis has been considered.^13,14 Raman spectroscopy, a technique that could provide better detection limits and several operational benefits for practical glove box and hot cell applications (e.g., fiber launched), has not been considered.³

Quantitative Raman analysis is primarily based on the proportional relationship between the intensity of Raman scattered light and analyte concentration. Changes in Raman band position, width, or shape can also be used for quantitative analysis.¹⁵ Applying spectroscopic analysis can be difficult in complex systems with overlapping bands, noise, matrix effects, chemical interactions, and baseline offsets. However, data preprocessing and multivariate chemometrics can be applied to these systems to quantify species in complex conditions.^8,16−21

Multivariate chemometrics allows the researcher to create regression models that correlate the entire spectrum to the analyte concentration. One of the most established supervised methods is partial least squares regression (PLSR).^5,8,21 PLSR relates the independent (X matrix [i.e., spectra]) and dependent (Y matrix [i.e., concentrations]) variables iteratively using combinations of orthogonal linear functions. PLSR models are created using a training set that represents the expected analyte concentrations. The prediction performance of the PLSR model is normally evaluated by testing how well it predicts samples that are not included in the training set (i.e., by using a validation set).²² The samples included in the training and validation sets significantly affect model performance and are normally selected subjectively by the user using a one-factor-at-a-time approach.²³ However, several works have shown that design of experiments can be used to select these sample concentrations within an objective statistical framework.^3,5,24−26 A logical extension of design of experiments, explored in this paper, is the selection of preprocessing strategies.

Applying a preprocessing transformation (e.g., baseline, scattering, scaling) to spectral data can significantly improve the performance of PLSR models. Each method attempts to adjust the measured spectral variables to optimize the regression analysis. Preprocessing spectral data comprises multiple steps that correct for specific artifacts. These steps generally include (1) identifying outlier spectra by observation or an outlier detecting algorithm, (2) reducing noise artifacts, (3) correcting for baseline fluctuations, (4) normalizing, and (5) an optional data reduction step.¹⁶ Steps 2–4 would benefit from optimization the greatest because they are the most customizable and subject to user bias. Generally, the analyst must decide which transformations to include; this task can be daunting because thousands of combinations are available. Preprocessing transformations are commonly chosen by trial and error; the researcher tries several methods and selects the one that looks the best. This highly subjective procedure rarely finds the true optimum and is time consuming.¹⁷

Recent studies have applied the design of experiments or machine learning algorithms to select preprocessing strategies.^27,28 Several full factorial design approaches appear to provide an efficient means to select transformations, but they typically require either thousands of trials to select which methods to include in the design or the inclusion of software default parameters. Other machine learning methods are promising, but these methods can be computationally expensive, require specialized coding experience, and typically use cross-validation to assess the predictive ability of multivariate models, even though a more robust test of prediction performance uses validation samples not included in the training set.⁵

Optimal designs are the most flexible and effective option when a small number of experimental runs are desired; they encompass both mixture and process variables, they contain different high and low components, and they accommodate constraints with factor limits.^29,30 This work demonstrates that determinant (D)-optimal designs can provide an efficient, flexible, and user-friendly option for selecting several well-chosen preprocessing strategies to optimize PLSR prediction performance. Calibration and validation Raman spectral data sets that correspond to hydroxylammonium (0–0.5 M) and HNO₃ (0–1 M) concentrations highly relevant to nuclear fuel cycle applications were used to test this approach. This may represent the first time that D-optimal designs have been applied to select preprocessing techniques.

2. Results and Discussion

2.1. Raman Spectra

The vibrational structure of the hydroxylammonium cation has been examined with Raman spectroscopy in several studies,^12,15 but monitoring applications are very limited. The ionic pairing of a protonated hydroxylamine group and nitrate forms hydroxylammonium nitrate (HAN). The hydroxylammonium (HA⁺) cation (pK_a = 5.96) in HNO₃ is highly reactive and undergoes several autocatalytic reactions.¹¹ The HA⁺ must be handled carefully, and fine-tuning the HNO₃ concentration is imperative for successful implementation.¹⁰ The reduction of Pu(IV) using hydroxylammonium is highly dependent on solution acidity (HNO₃); therefore, fluctuations in HNO₃ concentration, which are inevitable in an industrial process, could significantly affect the reduction rate of Pu and overall performance. Monitoring HAN and HNO₃ concentration using Raman spectroscopy could provide timely feedback and inform adjustments.

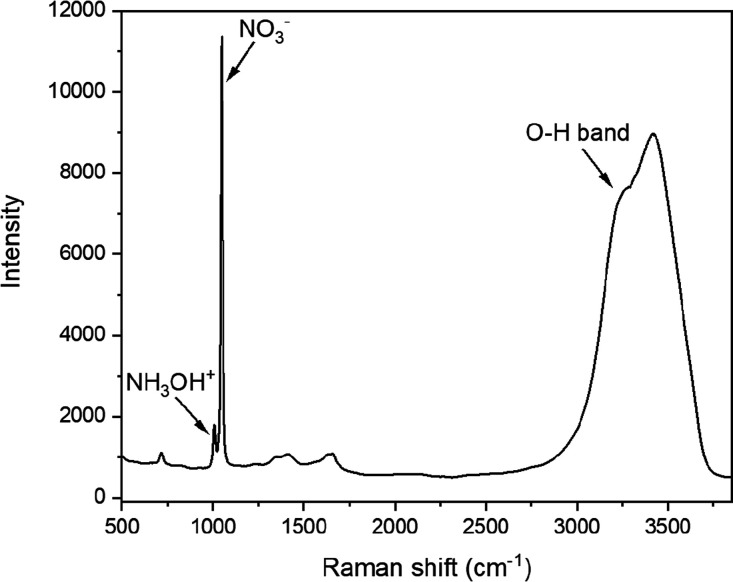
The HA⁺ (NH₃OH⁺) ion and its conjugate base hydroxylamine (NH₂OH) both belong to the C_s symmetry group. Each molecule has numerous Raman active vibrational bands with distinct peak frequencies.¹⁵ Three vibrational bands for free HA⁺ ions include the strong N–O symmetric stretch (ν₅) at 1007 cm^–1, a weak O–H plane bending (ν₈) peak at 1236 cm^–1, and a broad NH₃ asymmetric deformation (ν₄) shoulder at 1564 cm^–1 (Figure 1). Several symmetric stretching modes, assigned to NH₃OH⁺ ion, appear from approximately 2900 to 3050 cm^–1 (e.g., O–H symmetric stretch, N–H₃ symmetric stretch, and N–H₃ asymmetric stretch) but were not unambiguously identified because of overlap with the O–H stretching region of H₂O. The Raman spectra indicated that NH₂OH was not present in any sample because its primary N–O symmetric stretching mode near 955 cm^–1 was not identified.

Figure 1.

Stokes Raman spectrum of an aqueous solution containing 0.65 M HNO₃ and 0.5 M HAN. The most intense peaks are labeled and correspond to the NH₃OH⁺ symmetric N–O stretch at 1007 cm^–1, the NO₃^– symmetric N–O stretch at 1048 cm^–1, and the O–H stretching band from approximately 2700 to 3800 cm^–1.

Raman spectral signatures for free acid (H⁺) and nitrate (NO₃^–) ions and the O–H stretching band are well established.^8,9 At concentrations less than or equal to approximately 1 M HNO₃, it fully dissociated to H⁺ and NO₃^– ions.³¹ H⁺ is not Raman active; however, it can be quantified indirectly because it distorts water structure and affects the O–H stretching region (2700–3800 cm^–1).⁹ Unperturbed nitrate ions have four possible vibrational bands and D_3h symmetry, although only ν₁ (∼1048 cm^–1), ν₃ (∼1415 cm^–1), and ν₄ (∼717 cm^–1) are Raman active. The primary HA⁺ peak corresponding to the N–O symmetric stretching band (at 1007 cm^–1) partially overlapped with the most intense NO₃^– ν₁ symmetric peak at 1048 cm^–1 (Figure 1). Nitrate ions undergo deformations in the presence of polar solvents, cations (e.g., H⁺ and HA⁺), or both, which reduce the symmetry from D_3h to C_2v. This reduction splits the degenerate ν₃ and ν₄ modes into A₁ and B₂ pairs. The ν₃ asymmetric stretching A₁ and B₂ pairs were clearly identified at 1345 and 1658 cm^–1 (Figure 1). Very weak peaks related to the ν₄ in-plane deformation A₁ and B₂ pairs were identified around 650 and 700 cm^–1, respectively. The intensities of these bands are expected to increase as cation concentration increases.

Water molecules have three Raman active modes and C_2v symmetry. These modes correspond to a totally symmetric ν₁ O–H stretching (∼3280 cm^–1), the ν₂ O–H bending (∼1643 cm^–1) modes (A₁), and the depolarized ν₃ O–H antisymmetric stretch (∼3408 cm^–1). The O–H vibrational stretching region consists of several overlapping bands attributed to various H₂O and O–H (free and bound) vibrations. The complexity of this region is caused by an intricate hydrogen bonding network.⁹ This broad band (Figure 1) is sensitive to inter- and intramolecular modes of the water molecule (H₂O). Spectral variations resulting from changes in solution chemistry and temperature are generally best described using multivariate data analysis.

2.2. Transformation Strategies

PLSR models were built using no preprocessing (NP) or a variety of combinations to optimize prediction performance. The user-selected (U-S) preprocessing method was chosen based on user experience and trial and error.³² The models were evaluated by the root mean square error (RMSE) of the calibration (C) cross-validation (CV) and optimized by minimizing the RMSE of prediction (P) through numerous reiterations. A D-optimal design (26 points) and U-DD (576 points) were used to select preprocessing steps. Constraints were included in both the D-optimal and U-DD to ensure that the polynomial order was greater than or equal to the derivative order and less than or equal to the sum of left and right smoothing points. This well-chosen set of preprocessing combinations included SNV, SG smoothing/derivatives, and mean centering (MC) for several reasons. SNV is one of the most popular scatter correction algorithms, and it uses only the data within each spectrum. SG derivatives are commonly used to remove baseline offsets but can also provide a smoothing feature to the data. Although other derivative algorithms are available (e.g., gap–segment), SG is the most popular, and studies suggest that the prediction performance is nearly the same as gap–segment when applied to first and second derivatives.¹⁷ MC is by far the most common form of scaling for PLSR analysis, but it may not always improve performance.¹⁹

The preprocessing strategies selected by D-optimal design, run space type, and build type are shown in Table 1. Factor levels can be varied using the D-optimal approach, which is an attractive option for this application and one that is not possible using simpler full factorial designs.²⁷ The design comprised 19 required model points, 3 additional model points, and 4 lack-of-fit points for a total of 26 runs. The fraction of design space (FDS) was assessed to evaluate design suitability.³⁰ The FDS for this D-optimal design was 0.99, which indicates good prediction capability over the entire range of factors. A minimum FDS ≥ 0.8 with δ = 2 is generally recommended for optimal designs.

Table 1. D-Optimal Design Matrix for Preprocessing Transformations^a.

run	scatter	der. order	poly. order	left/right	scaling	space type	build type
1	1	0	1	2	1	vertex	model
2	0	1	5	3	0	interior	model
3	1	0	7	4	0	edge	model
4	1	0	3	2	0	edge	model
5	1	2	3	20	0	vertex	lack of fit
6	0	0	1	2	0	vertex	model
7	1	0	5	24	0	plane	lack of fit
8	0	0	3	17	1	plane	model
9	0	2	7	4	0	edge	model
10	0	2	7	30	1	vertex	model
11	1	1	7	17	0	plane	model
12	1	2	3	30	1	vertex	model
13	1	0	7	30	1	vertex	model
14	0	0	7	4	1	edge	model
15	0	2	3	30	0	vertex	model
16	0	0	5	13	0	plane	lack of fit
17	1	2	7	4	1	edge	model
18	1	1	3	13	1	interior	lack of fit
19	1	2	3	2	0	vertex	model
20	0	0	1	30	1	vertex	model
21	0	2	3	2	1	vertex	model
22	1	0	1	15	0	vertex	model
23	1	2	7	30	0	vertex	model
24	1	0	1	30	0	vertex	model
25	0	1	7	30	1	edge	model
26	0	0	7	30	0	vertex	model

^aAbbreviations used in this table are derivative (der.) and polynomial (poly.). Left/right smoothing points are for a SG smoothing or derivative. Scatter and scaling refer to SNV and MC.

2.3. PLSR Model Development

PLSR analysis was used to correlate spectral features to the analyte concentration. The concentrations for each species in the training and validation sets were selected using D-optimal design (Supporting Information). Most training sets selected by the one-factor-at-a-time approach include many samples.^3,9,23 Because the anticipated application would take place in restrictive glove box or hot cell environments, the number of samples in the training set was minimized to evaluate model performance and to minimize time and resource consumption.⁵ At the concentrations used in this work, HAN and HNO₃ fully dissociate into HA⁺, H⁺, and NO₃^– ions.^11,12 Concentrations of HA⁺, H⁺, and total NO₃^– were treated separately when building the PLSR models (i.e., as distinct columns in the Y concentration matrix) because the nitrate concentration depended on the concentrations of both HAN and HNO₃. The predictor matrix X comprised the entire spectrum (500–3850 cm^–1). Statistically insignificant differences in prediction performance were found when noise regions were omitted from the analysis and when only certain regions of the spectrum corresponding to molecular vibrational modes were included in the model (data not shown here).

RMSE and R² values are highly dependent on the number of factors included in a PLSR model. Including too many factors risks overfitting the model, which introduces noise. Variance and RMSE plots are helpful when determining the optimal number of factors. Variance plots represent the percentage of the original Y variance in the data that is accounted for by the model vs the number of factors. Models with a total explained variance close to 100% explain most of the variations in the data set. The optimal number of factors for each PLSR model was chosen by the software and confirmed by evaluating the explained variance and RMSE plots. The optimal number of factors was chosen as the last factor prior to the plateau in total RMSE and Y-explained variance (Figure 2). Calibration variance/RMSE was determined by fitting the calibration data to the model, and the validation variance/RMSE was computed by testing the model on data that were not included in the model. PLSR models from all the various preprocessing combinations used either three or four factors. Models with the lowest RMSEP values normally contained three factors.

Figure 2.

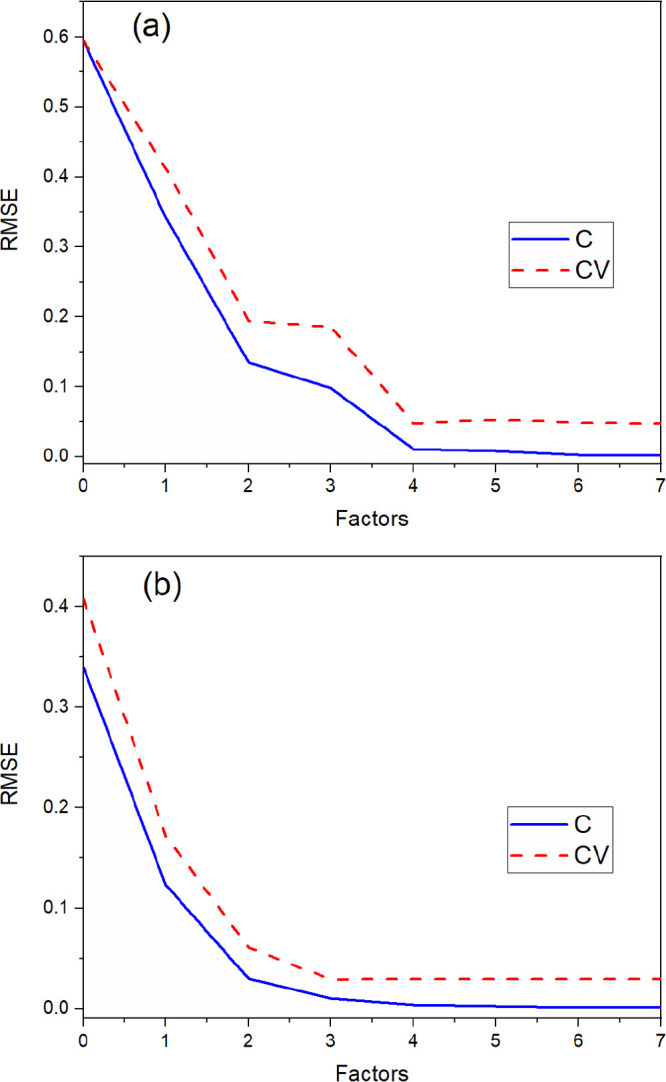
Plot of total Y-variable RMSEC (C) and RMSECV (CV) vs the number of factors for PLSR models built (a) without preprocessing and (b) with the optimal strategy selected using D-optimal design.

The total calibration and validation RMSE for all Y-variables was plotted as a function of the number of factors in the model to visually show the optimal number of factors (Figure 2). This plot more clearly shows where to select the optimal number of factors than the Y-variance plots. The point where the RMSECV curve reached a minimum was chosen as the optimal number of factors. This point occurred at three factors for the D-optimal model and four factors for the NP model, but the RMSEC continued to decrease past this point. This decrease is likely attributed to the introduction of artifacts (e.g., noise) in the model that would not improve prediction performance. The explained calibration and validation Y-variance plots for PLSR models built from the NP and D-optimal approach are shown in Figure S2. The optimal number of factors for the NP and D-optimal model was four (99.94% variance) and three (99.89% variance), respectively.

The calibration and validation curves were closer together for the PLSR model built using transformations selected by D-optimal design than the NP model, which suggest that the D-optimal model is more representative than the NP model and can describe new data well. If two models explain nearly the same amount of variance but one has fewer factors than the other, the simpler model is generally considered to be more robust. Including three factors in a D-optimal model is reasonable because it describes three species (HA⁺, H⁺, and NO₃^–). The first factor describes nearly all the variations in NO₃^– and most of the variations in H⁺, the second factor primarily accounts for HA⁺, and the third factor describes some variations in both HA⁺ and H⁺. Including a fourth factor in the NP model is reasonable because it may describe scatter artifacts in the spectra that are not removed by preprocessing.

2.4. Calibration and Prediction Metrics

The calibration and validation statistics for PLSR models corresponding to each preprocessing approach are summarized in Table 2. Performance was also demonstrated in parity plots comparing the measured concentration with the reference concentrations (Figure S2). Models were evaluated by calibration/CV (i.e., R², RMSEC, RMSECV) and by validation (RMSEP, RMSEP%, bias, and SEP) criteria. RMSEC, RMSECV, RMSEP, RMSEP%, SEP, and bias values closest to zero indicate better models. The best PLSR model for the U-S, D-optimal, and U-DD approach was chosen based on the lowest RMSEP for HA⁺ concentration because that was the primary analyte of interest. The performance metrics for these models are summarized in Table 2. A common threshold for a satisfactory PLSR model is an RMSEP value below 10% of the median value of the concentration range used in the calibration matrix. The U-S, D-optimal, and U-DD models satisfied this criterion, but the NP PLSR model did not. Thus, applying transformations was essential to improve the regression analysis in this circumstance.

Table 2. PLSR Model Calibration and Validation Statistics for Each Analyte Derived from Multiple Preprocessing Strategies^a.

design	NP	U-S	D-optimal	U-DD
no. samples	1	undefined	26	576
preprocessing	none	SNV/derivative/MC	derivative/MC	derivative/MC
no. factors	4	3	3	3
Calibration/CV statistics
R2 (HA+)	0.9992096	0.9995188	0.9993514	0.9994043
RMSEC	0.0060845	0.0042479	0.0049315	0.0047265
RMSECV	0.0454421	0.0184775	0.015596	0.0147932
R2 (H+)	0.9990751	0.9996105	0.9991647	0.9991879
RMSEC	0.0123394	0.0076351	0.0111814	0.0110249
RMSECV	0.0588891	0.0204559	0.032528	0.0315437
R2 (NO3–)	0.9991027	0.9995734	0.9989014	0.9989355
RMSEC	0.0147092	0.0090814	0.0145736	0.014346
RMSECV	0.0393324	0.0232106	0.0384820	0.0380667
Validation statistics
RMSEP (HA+)	0.032912	0.018964	0.0108452	0.0105082
RMSEP%	12.28	7.09	4.29	3.79
bias	0.014777	0.0143382	–0.0004326	–0.0019518
SEP	0.029910	0.0126239	0.0110218	0.0105019
RMSEP (H+)	0.0523674	0.0362628	0.0215038	0.0209245
RMSEP%	10.05	6.83	4.24	4.57
bias	0.019598	0.0296535	0.0056263	–0.0032218
SEP	0.049392	0.0212292	0.0211095	0.0210284
RMSEP (NO3–)	0.045651	0.0534647	0.0244241	0.0240554
RMSEP%	5.78	6.69	3.21	3.22
bias	0.034373	0.0439889	0.0051911	–0.0051765
SEP	0.030556	0.0309078	0.0242741	0.0238934

^aR² of the calibration, CV, different SG derivatives for U-S, D-optimal (D), and U-DD strategies. Abbreviated model with no preprocessing (NP).

RMSEP values for each species (i.e., HA⁺, H⁺, and NO₃^–) tended to increase or decrease relatively uniformly when applying the various transformations. However, NO₃^– RMSEP values did not change as substantially with changes in preprocessing combinations compared with HA⁺ and H⁺. For example, the D-optimal processing run number 2 (Table 1) resulted in intolerably high RMSEP values for HA⁺ (0.255) and H⁺ (0.283), whereas the RMSEP value for NO₃^– (0.036) was acceptable. The U-S preprocessing combinations (RMSEP 0.18 for HA⁺) included SNV, an SG first derivative with a third-order polynomial and 15 smoothing points, and MC. The D-optimal model with the lowest RMSEP (0.108) for HA⁺ was run number 25 (Table 1), which consisted of a first derivative with a seventh-order polynomial and 61 smoothing points and MC. The U-DD model with the lowest RMSEP (0.105) for HA⁺ consisted of a very similar combination of preprocessing methods, including a first derivative with a seventh-order polynomial and 57 smoothing points and MC. The calibration, CV, and validation statistics were the largest for the PLSR built using the raw data for both HA⁺ and H⁺, whereas these values were the largest using the U-S model for NO₃^–. The calibration and CV statistics for H⁺ and nitrate concentrations were the lowest for the U-S approach, even though this model did not have the lowest RMSEP. The U-DD model had the lowest RMSECV for HA⁺ concentration, and it also had the lowest RMSEP. On the other hand, the U-S model had the lowest RMSECV for H⁺ and NO₃^–, but it did not have the lowest RMSEP values. If CV was used to approximate predictive capability, then the U-S model would have been chosen as the best option despite the better prediction performances of both the D-optimal and U-DD models.

An estimate of PLSR prediction capability is often determined by calculating the RMSECV. This value is calculated by removing a data point from the original training set and using the regression model to predict that data point. However, this statistic does not always accurately represent how a PLSR model will predict concentrations from spectra that the model has not previously encountered.⁵ The true measure of prediction performance is the RMSEP, which has the same units as the analyte concentration. RMSEP represents the error between the actual concentration value and the predicted values. Most PLSR models are built to make predictions on unknown samples in the future; therefore, testing the prediction performance on samples not included in the training set is best. Previous work demonstrated that using a minimal number of samples in the training set has a greater tendency to cause artificially low CV statistics, indicating better prediction performance than reality.⁵ Contrary effects were indicated by comparing RMSECV and RMSEP values for each analyte in this study. PLSR models with the most disparate RMSECV and RMSEP values were built using strategies 6, 7, 20, and 24. The HA⁺ RMSEP values for models 6 and 7 were approximately one-third of their RMSECV values, and the RMSEP values for models 20 and 24 were approximately 2.5 times greater than their RMSECV values. Although the RMSECV values may have indicated satisfactory or poor prediction performance, determining RMSEP was essential to evaluate this criterion with confidence. The difference between RMSEP and RMSECV for each analyte generally decreased as a more optimal model was developed because the RMSEP decreased (Figure S6). This agreement is desirable because stable models generally have similar RMSECV and RMSEP values. This effect was evident when the RMSECV and RMSEP values were compared for each strategy in the D-optimal set (Figure S6). However, RMSEP generally had better agreement with RMSEC for the best selection methods. RMSEC was usually much lower than RMSEP, which indicates that calibration statistics with few samples in the training set may be prone to mislead optimizations by indicating excellent calibration statistics but poor prediction performance (Figure S7).

RMSEC and RMSEP values for the D-optimal and U-DD models were generally in good agreement. However, the RMSECV values overestimated the prediction error and were much larger than RMSEC (i.e., greater than a factor of 2). During cross-validation, one of the six samples in the training set was left out of the analysis. Normally, training sets comprise many samples, which provide redundant information, so leaving one sample out has a minor effect on RMSECV.³ In this example, RMSECV might be high because each of the six samples is essential for describing the variation of the factor space, suggesting that the number of samples in the training set was effectively minimized by the D-optimal selection process and contains only the information necessary for an effective regression analysis.

2.5. Statistical Comparison

Stating that one PLSR model is better than another simply by observing a decrease in RMSEP is a relatively ambiguous assertion. A statistical comparison is necessary to have confidence that RMSEP values are statistically similar or different.⁵ Therefore, the prediction performance of each PLSR model was compared by separating RMSEP into bias and SEP. Each model was compared pairwise: if the bias and the SEP confidence interval contained 0 and 1, respectively, then the models were considered statistically similar. If either interval did not meet these criteria, then the models were considered statistically different. The order of each comparison is listed in Tables S3, S4, and S5 (Supporting Information).

The confidence intervals for each pairwise comparison are shown in Figures 3–5. These comparisons verify that the prediction performances of the D-optimal and U-DD designs were different from the NP and U-S models, which imply that applying the selected preprocessing strategies successfully improved performance. The prediction performance of the U-S PLSR model was statistically superior to NP for both HA⁺ and H⁺. For nitrate, both the bias and SEP confidence intervals contained 0 and 1, respectively, so the prediction performance was statistically equivalent. However, the U-S model contained fewer factors, which imply that the model was simpler and therefore more robust than the NP model. Thus, the prediction performance was improved by user experience and trial and error. However, additional comparisons revealed that this strategy did not achieve the optimal approach. Both the D-optimal and U-DD models performed better than the U-S model.

Figure 3.

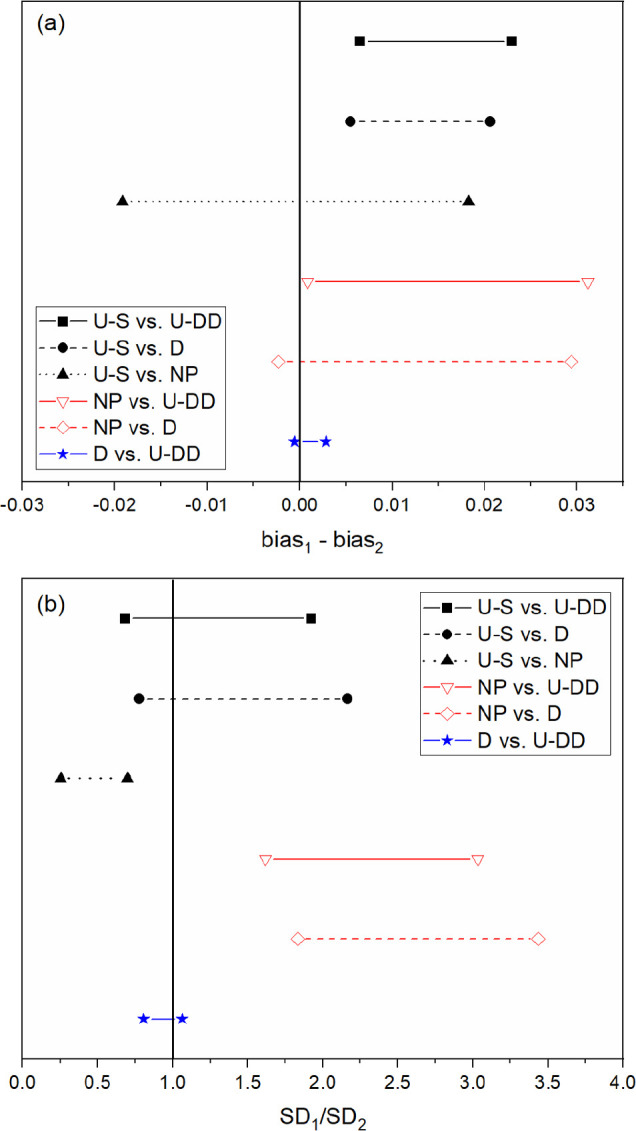
Confidence intervals for HA⁺ (a) bias and (b) SEP for all six comparisons. Prediction performance is statistically similar between designs if the confidence interval crosses the solid vertical line for bias and SEP.

Figure 5.

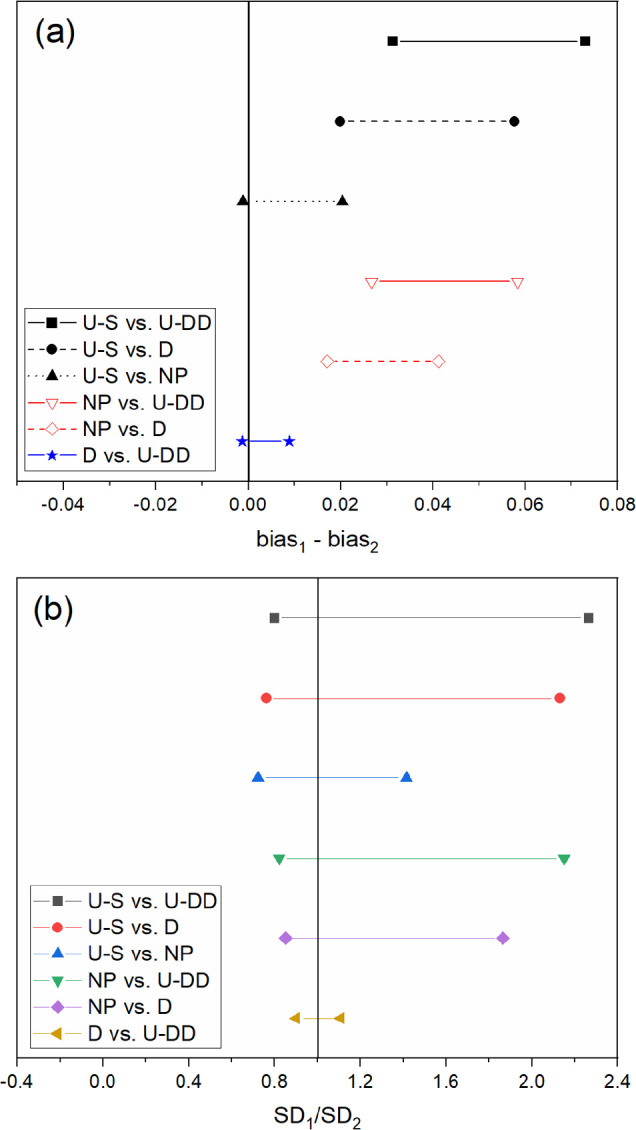
Confidence intervals for NO₃^– (a) bias and (b) SEP for all six comparisons. Prediction performance is statistically similar between designs if the confidence interval crosses the solid vertical line for bias and SEP.

Figure 4.

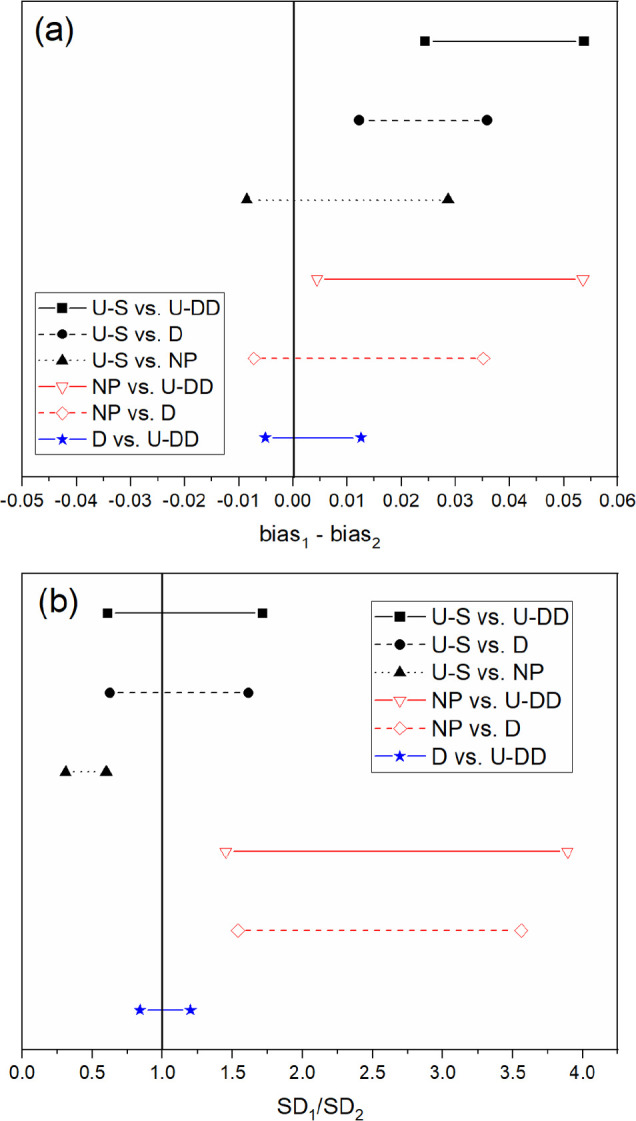
Confidence intervals for H⁺ (a) bias and (b) SEP for all six comparisons. Prediction performance is statistically similar between designs if the confidence interval crosses the solid vertical line for bias and SEP.

The predictive capability of D-optimal and U-DD was compared statistically for each analyte (HA⁺, H⁺, and NO₃^–). Although the U-DD RMSEP values for each analyte were marginally lower than the D-optimal approach, the prediction performance was statistically identical. Even though the U-DD probed a much greater range of combinations (576 samples), the prediction performance of the D-optimal design (26 samples) was statistically identical. Because the D-optimal approach was much more efficient (i.e., 95.5% fewer strategies), it was chosen as the best approach for the intended purpose. Therefore, the rank of prediction performance for HA⁺, H⁺, and NO₃^– is D-optimal > U-DD > U-S > NP.

Several preprocessing combinations selected by the D-optimal design decreased prediction performance compared to the model built without preprocessing (Figure S7). Even though these combinations did not improve the regression between spectra and concentration in this work, they could be useful for data sets with different spectral signals and instrument settings (e.g., resolution). Future work will include testing the D-optimal preprocessing selection approach on disparate spectral data sets (e.g., Raman, near-IR, and Fourier-transform IR) to evaluate how the optimal combination of preprocessing strategies may vary between systems.

3. Conclusions

The D-optimal preprocessing selection approach significantly improved PLSR model prediction performance and reduced the number of trials by more than 95.5% compared with a U-DD. The D-optimal strategy provides a method that can simultaneously vary the combinations of preprocessing strategies and the levels within each factor. Raman spectroscopy and multivariate chemometrics offer an excellent means to simultaneously monitor hydroxylammonium, nitrate, and HNO₃ concentrations. Furthermore, the PLSR models were built using only six samples in the training set selected by D-optimal design. Results from this study indicate that this approach is promising for glove box and hot cell applications for which minimizing time and resources is essential to make the application simpler to operate and more attractive for widespread use. When minimizing samples in the training set, CV statistics may not always accurately represent the error in PLSR model predictions. Caution should be applied when optimizing PLSR model performance based on the RMSECV because it is only an estimate of the true prediction error. Therefore, an independent validation data set should be used when applying this strategy. Future work will test this preprocessing selection approach on disparate spectral data sets.

Future work may also include testing this selection approach, Raman spectroscopy, and PLSR analysis in a system with additional factors (e.g., temperature and Pu). Temperature, another important variable affecting the kinetics and equilibrium of HA⁺ redox reactions, can be measured indirectly by Raman analysis of the O–H stretching region.⁹ Additionally, the Pu(III/IV) concentration could be varied to measure the effect of Raman self-absorption on the spectra and subsequent regression analysis. Self-absorption occurs when the incident (i.e., laser) and/or Raman scattered light coincides with the absorption cross section of a species. This self-absorbance phenomenon can make quantitative Raman analysis more challenging yet still feasible.³³ The Pu(III/IV) ions are not Raman active but could be quantified by analyzing the O–H stretching band.⁹

4. Methods

All chemicals were commercially obtained (ACS grade) and used as received unless otherwise stated. Concentrated HNO₃ (70%) and HAN (24 wt %) were purchased from Sigma-Aldrich. Samples were prepared using deionized water with Milli-Q purity (18.2 MΩ·cm^–1 at 25 °C).

4.1. Sample Preparation

Solutions containing HAN (0–0.5 M) and HNO₃ (0–1 M) were prepared using volumetric glassware. Calibration and validation sample concentrations were selected using the design of experiments. Each solution was pipetted into individual 1.8 mL borosilicate glass vials (VWR Scientific, 66009-882) for Raman analysis.

4.2. Raman Spectroscopy

A fully automated imaging iHR 320 spectrometer (Horiba Scientific) was used to collect Stokes Raman spectra with a 532 nm laser source (Cobalt Samba 150) operating at 90 mW. Static measurements were recorded in triplicate from 500 to 3850 cm^–1 using a 1200 grooves/mm grating with a resolution of 0.9 cm^–1. Each spectrum comprised 3984 data points. A general-purpose Raman probe made by Spectra Solutions, Inc., was used to collect Raman spectra in reflection mode at 24 s intervals (8 s integration time and three acquisitions). The probe had a 9 mm focal length and a 7 mm working distance. It was placed approximately 5 mm from the edge of each sample vial in a probe and sample cuvette holder made by Spectra Solutions, Inc. (Figure S1). Each spectrum was collected at 22 °C.

4.3. Design of Experiments

The Design-Expert (v.11.0.5.0) by Stat-Ease, Inc., within the Unscrambler software package by Camo Analytics was used to build each experimental design. Analyte concentrations in the training and validation sets were selected by D-optimal design with a quadratic process order. Design points were selected using the Best search option, which explores the design space using both point and coordinate exchange. D-optimal designs choose runs by iteratively minimizing the determinant of the variance–covariance matrix X^TX.²⁹ The fraction of design space (FDS) was calculated by mean error type, δ = 2, σ = 1, and α = 0.05. These values were used to calculate an acceptable maximum standard error threshold and evaluate the model.³⁰ Six required model points for two numeric factors (i.e., HAN and HNO₃ concentration) were used for the calibration set (Table S1). Required model points are the minimum number of points necessary to estimate each coefficient in the design model. The validation set comprised 10 lack-of-fit points, which were chosen to maximize the distance to other runs while maintaining the optimality criterion (Table S2).

The D-optimal design and user-defined design (U-DD) were used to select preprocessing transformations. Preprocessing combinations were applied in the following order: (1) scatter correction (standard normal variate [SNV]), (2) smoothing/derivative, and (3) scaling (mean centering [MC]). The D-optimal design built to select preprocessing strategies comprised three numeric and two categorical factors. Scaling and scatter factors included two levels corresponding to no transformation (0) or applying the transformation (1). The derivative (3 levels), polynomial order (4 levels), left/right points (29 levels), scaling (2 levels), and scatter (2 levels) were included in the design. Therefore, a total of 26 combinations (default software settings) were possible, including 19 required model points, 3 additional model points, and 4 lack-of-fit points. Additional model points improve the precision of the estimates, and lack-of-fit points improve the accuracy of the coefficients in the design. U-DD includes all possible factor and component combinations from the candidate points included in the design. The U-DD comprised three numeric and two categorical factors. The derivative (3 levels), polynomial order (4 levels), and left/right smoothing points (15 levels) were included as discrete variables, and the scatter (2 levels) and scaling (2 levels) were included as nominal variables. Every other level for smoothing, starting at 2 left/right and ending at 30 left/right, was included in this design to help reduce the number of samples. Including every left/right combination would likely have been redundant (data not shown here). This design resulted in 720 possible categorical points (i.e., preprocessing combinations), but 144 combinations were invalid because they fell outside the constraints placed on the design. These constraints prevented impossible combinations of preprocessing from being created in the design (i.e., a derivative with a higher order than the smoothing polynomial order). Thus, the design contained 576 valid points.

4.4. Multivariate Analysis and Preprocessing

The Unscrambler X (version 10.4) software package from CAMO Software AS was used for PLSR analysis and preprocessing. PLSR models were optimized by applying a variety of transformations selected by either the user or experimental design. A full cross-validation (CV) was used to estimate the usefulness of a model for future observations (i.e., estimated predictive ability). The CV was computed by leaving out each sample (i.e., the entire triplicate), one at a time, and testing how well the model predicted the sample that was left out. The optimal number of factors included in each PLSR model was determined by evaluating RMSE and explained Y-variance plots.

An SNV transformation removes scatter effects from spectra and centers and scales each spectrum using only the data from that spectrum. It does not use the mean spectrum of a set, as is the case for multiplicative scatter corrections. Savitzky–Golay (SG) smoothing and derivative methods fit a polynomial to the data based on a user-defined number of left/right smoothing points and polynomial order. The polynomial order must be greater than or equal to the derivative order, and the polynomial order must be less than or equal to the sum of left and right smoothing points. The total number of smoothing points was calculated as the sum of left-side and right-side points plus 1. Derivative orders higher than first and second order were not included here because they are more commonly used to study fundamental component(s) of a spectrum.³³ The SG algorithm is the most common smoothing/derivatization option. Both SNV and SG transformations are row-oriented, meaning that the contents of each cell are influenced by horizontal neighbors.

4.5. Statistical Comparison

Model performance was evaluated using calibration, CV, and validation (i.e., prediction) metrics. The most important calibration/validation statistics typically include R² correlation values, root mean square error (RMSE) of the calibration (RMSEC), and RMSE of the CV (RMSECV). Although these statistics may suggest that a PLSR model is satisfactory, testing the prediction performance of PLSR models on samples not included in the training set is important because RMSECV is only an estimate.⁵ Prediction statistics typically include RMSE of the prediction (RMSEP), RMSEP%, bias, and standard error of prediction (SEP). RMSEs for the calibration, CV, and validation were calculated using eq 1.

1

where ŷ_i is the predicted concentration, y_i is the measured concentration, and n is the number of samples. RMSEP% was calculated by dividing the RMSEP by the average model values using eq 2.

2

where y_m® represents the total mean value of each measured concentration. Each RMSE value is in units of analyte concentration. Lower RMSEC, RMSECV, RMSEP, and RMSEP% values indicate better model performance. SEP is like RMSEP, except that it is corrected for bias. Bias values lie either systematically above or below the regression line, and a value close to 0 indicates a random distribution about the regression line.

The validation metrics for each PLSR model were compared using the Tukey–Kramer method.^34,35 A parametric two-way analysis of variance between the prediction errors is the most suitable comparison method.³⁶ Bias and SEP t values were compared at the 95% confidence interval following previous methods.^5,26 A full description of the statistical comparison can be found elsewhere,⁵ and additional details are provided in the Supporting Information. Briefly, if the bias confidence interval contained 0 (eq 3) and the confidence interval of the SEP contained 1 (eq 5), then the prediction performance of the two models being compared was considered statistically similar. The value s_e represents the standard error of the difference between models being compared (eq 4, where d_i is the difference in error between models being compared and d̅ is the mean difference).

3

4

5

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c07111.

• Extended statistical methods section and additional experimental results including PLSR parity plots and root mean square error comparisons (PDF)

Author Contributions

The manuscript was written using contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Notes

This manuscript has been authored by UT-Battelle, LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).