Abstract
Social epidemiology aims to identify social structural risk factors, thus informing targets and timing of interventions. Ascertaining which interventions will be most effective and when they should be implemented is challenging because social conditions vary across the life course and are subject to time-varying confounding. Marginal structural models (MSMs) may be useful but can present unique challenges when studying social epidemiologic exposures over the life course. We describe selected MSMs corresponding to common theoretical life-course models and identify key issues for consideration related to time-varying confounding and late study enrollment. Using simulated data mimicking a cohort study evaluating the effects of depression in early, mid-, and late life on late-life stroke risk, we examined whether and when specific study characteristics and analytical strategies may induce bias. In the context of time-varying confounding, inverse-probability–weighted estimation of correctly specified MSMs accurately estimated the target causal effects, while conventional regression models showed significant bias. When no measure of early-life depression was available, neither MSMs nor conventional models were unbiased, due to confounding by early-life depression. To inform interventions, researchers need to identify timing of effects and consider whether missing data regarding exposures earlier in life may lead to biased estimates.
Keywords: bias, confounding, inverse probability weighting, life course, marginal structural models, simulation, social epidemiology
Abbreviation
- AUD
alcohol use disorder
- CI
confidence interval
- IPW
inverse probability weighting
- IPWs
inverse probability weights
- MSM
marginal structural model
While there is conclusive evidence that social exposures are associated with health outcomes, causal inference remains a central challenge in social epidemiology (1–3). It is typically infeasible and/or unethical to randomize many social or psychological exposures, which often present early in life and persist for decades. Therefore, many studies in life-course epidemiology rely on observational data from longitudinal cohorts. Though cohort studies often enroll participants in mid- or late life, many investigators are interested in the lifetime effects of a given exposure—that is, contrasting the anticipated adult health outcome under exposure from conception to adulthood with that of no exposure or a shorter exposure period. For example, numerous studies have examined stroke risk in relation to depression or social support, and while most investigators acknowledge that these exposures do not appear de novo in midlife, often studies cannot directly account for earlier exposures (4, 5).
In the context of marginal structural models (MSMs), inverse probability weights were initially proposed as a method of estimating causal effects of time-dependent exposures in the presence of time-dependent covariates that could simultaneously be confounders and intermediate variables (6–8). MSMs have been adopted by researchers investigating the effects of social or psychological exposures on health (9–21), but data commonly used to assess such exposures may be insufficient to identify causal effects. Here, we provide a systematic consideration of MSMs to evaluate whether and when they improve causal inference for social epidemiologic research. First, we describe how MSMs can be used to encode standard life-course conceptual models. We then discuss methodological challenges related to 1) adjustment for time-varying confounders that also mediate effects of prior social exposures, 2) “late–study-start confounding” (where early-life exposures are not assessed), and 3) situations in which both scenarios occur simultaneously. Second, we illustrate how well MSMs and conventional models account for these challenges through simulations, which provide the “true” effects of an exposure on an outcome. Our simulations are designed to ensure that bias is due only to structural biases and not to model misspecification.
The well-studied relationship between depression and stroke across the life course serves as a motivating example (5, 9, 10, 22). The onset of depression typically occurs by adolescence (23), and the illness can follow a remitting-recurring pattern (24). We draw on commonly used conceptual frameworks and corresponding models to examine the relationship between depression and stroke risk. We adopt a counterfactual approach to causation assuming a well-defined outcome value under every possible exposure history for each individual. In the case of a point exposure D, Yd=0 denotes the outcome the individual would have if, possibly contrary to fact, the exposure were set to 0 (i.e., unexposed), and Yd=1 denotes the outcome the individual would have if, possibly contrary to fact, the exposure were set to 1 (i.e., exposed). Under the consistency assumption, only the outcome corresponding to the individual’s actual exposure is observed (25). See Web Appendix 1 (available at https://doi.org/10.1093/aje/kwab253) for details on MSM definitions and identifying assumptions.
In this paper, we evaluate bias induced or mitigated by use of conventional models versus MSMs to assess the role of social exposures in health. We also demonstrate problems that can occur due to late–study-start confounding. By discussing these issues, we aim to provide investigators with a clearer picture of the trade-offs involved when choosing one analytical method over another or in making opportunistic use of existing data. Armed with this information, researchers will be better positioned to interpret and extrapolate their results in the most rigorous possible way.
BACKGROUND
Encoding causal effects using MSMs
A mean MSM is a parametric model for the marginal (i.e., population-wide) mean of a counterfactual outcome corresponding to a joint intervention on a time-varying exposure (i.e., if the exposure was intervened upon at multiple time points), possibly conditional on a subset of baseline covariates (6, 7, 26, 27). It is important to distinguish between the causal model (MSM) and the estimation procedure (inverse probability weighting (IPW)). To the extent that the joint intervention is well-defined, MSM parameters have specific causal interpretations as the joint effects of exposure over time on a given outcome. A point in time is represented by t, and we focus on the following time points: early life (t = e), midlife (t = m), and late life (t = l). An individual’s observed binary exposure status at time t is represented by Dt, while history of exposure is represented by 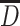 . In our example,
. In our example, 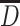 encompasses depression status in early life (
encompasses depression status in early life (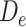 ), midlife (
), midlife (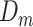 ), and late life (
), and late life (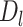 ).
). 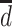 represents a hypothetical depression history that identifies depression at specific times (i.e.,
represents a hypothetical depression history that identifies depression at specific times (i.e., 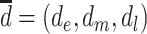 ).
). 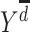 is the potential stroke outcome in late life if, possibly contrary to fact, a person experienced depression history
is the potential stroke outcome in late life if, possibly contrary to fact, a person experienced depression history 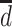 . For simplicity, we assume no dropout or death. The causal relationship between depression history and late-life stroke risk (given that one has not experienced stroke in early or midlife) is specified by the following MSM:
. For simplicity, we assume no dropout or death. The causal relationship between depression history and late-life stroke risk (given that one has not experienced stroke in early or midlife) is specified by the following MSM:
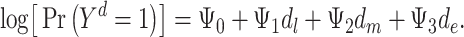 |
(model 1) |
Here, 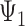 represents the effect (expressed as the log of the risk ratio) of late-life depression on stroke risk under an intervention that sets depression in early life (
represents the effect (expressed as the log of the risk ratio) of late-life depression on stroke risk under an intervention that sets depression in early life (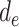 ) and midlife (
) and midlife (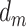 ) to specific values. Similarly,
) to specific values. Similarly, 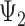 and
and 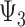 represent the controlled direct effect of depression in mid- and early life on late-life stroke risk, respectively, setting the other depression exposures to a specific value. MSM parameters do not capture the indirect effect of the given exposure mediated by another exposure at a later occasion when the latter exposure is included in the model. For example,
represent the controlled direct effect of depression in mid- and early life on late-life stroke risk, respectively, setting the other depression exposures to a specific value. MSM parameters do not capture the indirect effect of the given exposure mediated by another exposure at a later occasion when the latter exposure is included in the model. For example, 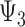 captures only the effect of
captures only the effect of 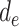 on Y not mediated by
on Y not mediated by 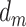 or
or 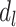 , even though such effects may be present. Model 1 assumes that the effects of
, even though such effects may be present. Model 1 assumes that the effects of 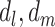 , and
, and 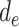 are additive on the log scale. This assumption could be relaxed by including interactions (e.g.,
are additive on the log scale. This assumption could be relaxed by including interactions (e.g., 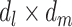 or
or 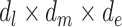 ). By imposing certain constraints on possible values of
). By imposing certain constraints on possible values of 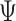 , incorporating versus omitting interactions, MSMs can represent the main life-course models used in social epidemiology.
, incorporating versus omitting interactions, MSMs can represent the main life-course models used in social epidemiology.
Estimating effects encoded in MSMs
MSMs define marginal effects, contrasting the population outcomes under 2 distinct hypothetical joint interventions (e.g., when all individuals are exposed vs. when no individuals are exposed). For example, under the model 1 MSM, stroke risk under a joint intervention in which all individuals are exposed to depression at all 3 life stages versus none of the life stages would be
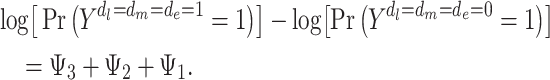 |
(1) |
In the context of time-varying confounding, MSM parameters will generally differ from the corresponding parameters estimated in conventional conditional mean models, which contrast people within a particular covariate stratum with and without the exposure of interest in each life-course period. Conventional models are biased away from the causal effects specified in the MSM regardless of whether they adjust for the time-varying confounders (6, 7). MSMs can be estimated by means of inverse probability weights (IPWs) through the joint probability law of a person’s observed exposure history. Provided that exposure models are correctly specified, IPWs appropriately account for observed time-varying confounders, eliminating the need for covariate adjustment in the outcome regression model (6, 28). In our example, each observation would be weighted by the inverse of the probability of an individual’s observed depression history up to that time point, given the individual’s time-constant and time-varying covariates. Reweighting renders time-varying confounders and exposure history statistically independent, eliminating potential confounding bias by observed confounders (7, 28). The MSM estimate calculated in the weighted sample provides an unbiased (i.e., consistent) estimate of the average causal effect of depression on stroke risk when time-varying confounders are also mediators of the exposure-outcome relationship, assuming no unmeasured confounding or model misspecification. More formally, an MSM can be viewed as a parametric model for the g-formula, and therefore IPWs provide an alternative to the g-computation algorithm (29). Although time-varying confounding is a common concern in social and psychosocial epidemiology, use of this approach is still somewhat infrequent (but see references 9–15 for examples). In many settings, MSMs are clearly preferable to conventional models. However, we will illustrate situations in which standard assumptions required to identify MSMs may be hard to meet due to confounding biases common to life-course epidemiology.
Common life-course models described as MSMs
Conceptual models commonly used to describe how exposures across the life course may affect late-life outcomes include the accumulation model, the early-life critical period model, and the pathway model (12, 30–33). Some aspects of these models can be represented graphically using causal directed acyclic graphs and algebraically as MSMs. In our example, the accumulation model is a special case of Figure 1A which posits that each exposure to depression has a separate direct effect on stroke, with all effects being nonzero and in the same direction. Model 2 is an example of the accumulation model with separate, direct, and equal effects of depression on stroke, with 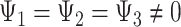 .
.
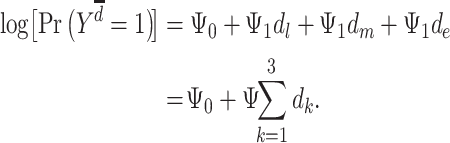 |
(model 2) |
Figure 1.
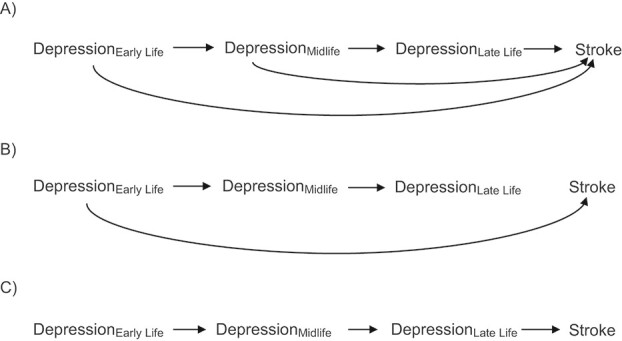
Causal diagrams reflecting the application of life-course theories (in the absence of time-varying confounding) to the example of depression in early, mid-, and late life and subsequent stroke risk (in the absence of time-varying confounding). A) The accumulation model, in which each exposure to depression has a direct effect on stroke; B) the early-life critical period model, in which only early-life depression affects stroke; C) the pathway model, in which early- and midlife depression influence stroke only via their impact on late-life depression. Note that all 3 panels show early-life depression being associated with late-life depression only through midlife depression; the plausibility of this assumption must be considered on a case-by-case basis.
According to the early-life critical period model (Figure 1B), only early-life exposures affect outcomes later in life, with effects occurring regardless of later exposures. Under this model’s assumptions, neither depression in midlife (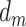 ) nor depression in late life (
) nor depression in late life (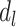 ) will affect stroke risk; thus, coefficients representing mid- (
) will affect stroke risk; thus, coefficients representing mid- (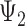 ) and late life (
) and late life (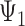 ) are 0 (model 3).
) are 0 (model 3).
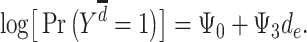 |
(model 3) |
Lastly, the pathway model posits that only late-life exposures have direct effects on outcomes, with effects of any early- and midlife exposures being fully mediated by late-life exposure. This model is represented by Figure 1C and the following MSM:
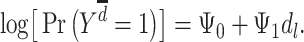 |
(model 4) |
The pathway model entails that only depression in late life (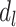 ) directly influences the probability of stroke, and
) directly influences the probability of stroke, and 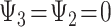 . The effects of early- and midlife depression on late-life depression are not specified in model 4, so a full representation of the pathway model would need to additionally include a model for the effect of early- and midlife depression on late-life depression.
. The effects of early- and midlife depression on late-life depression are not specified in model 4, so a full representation of the pathway model would need to additionally include a model for the effect of early- and midlife depression on late-life depression.
Regardless of which model is true, under certain assumptions researchers could estimate the effect of depression throughout the life course (henceforth called the lifetime effect) if they were provided information regarding depression at all 3 time points. While models 2–4 are structural models representing different life-course models, model 5 is a statistical regression model, and the coefficients of this model might be estimated in observed data, ignoring any potential confounders:
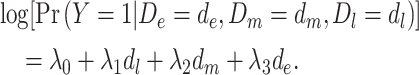 |
(model 5) |
In model 5, 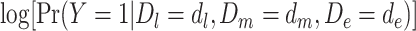 is the observed log risk of stroke conditional on depression status in late, middle, and early life. Specifically,
is the observed log risk of stroke conditional on depression status in late, middle, and early life. Specifically, 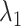 captures the log risk ratio comparing average stroke risk observed in the subset of people who were depressed in late life with the stroke risk observed in people who were not depressed in late life, assuming both groups shared the same early- and midlife depression history. Without additional adjustment for confounders, these groups are not necessarily comparable; thus, these regression coefficients are merely descriptive of observed associations that may not be causal. Model 5 implies a statistical (not causal) accumulation model with equal effects at each exposure time point if
captures the log risk ratio comparing average stroke risk observed in the subset of people who were depressed in late life with the stroke risk observed in people who were not depressed in late life, assuming both groups shared the same early- and midlife depression history. Without additional adjustment for confounders, these groups are not necessarily comparable; thus, these regression coefficients are merely descriptive of observed associations that may not be causal. Model 5 implies a statistical (not causal) accumulation model with equal effects at each exposure time point if 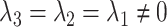 ; an early-life critical period statistical model is implicated if
; an early-life critical period statistical model is implicated if 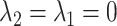 but
but 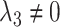 ; and a pathway model may be implicated if
; and a pathway model may be implicated if 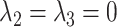 but
but 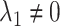 . It is also possible that none of these 3 archetypal models will fit perfectly (e.g., there is an early-life sensitive (as opposed to critical) period (
. It is also possible that none of these 3 archetypal models will fit perfectly (e.g., there is an early-life sensitive (as opposed to critical) period (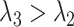 ,
, 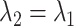 , and
, and 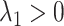 )). Even when correctly specified, the parameters of simple regression models such as model 5 can only be interpreted as an MSM in the absence of confounding. An alternative approach is needed for estimating MSMs in the likely context of time-varying confounders.
)). Even when correctly specified, the parameters of simple regression models such as model 5 can only be interpreted as an MSM in the absence of confounding. An alternative approach is needed for estimating MSMs in the likely context of time-varying confounders.
METHODOLOGICAL CHALLENGES
Appropriate adjustment for time-varying confounding
If all confounders occurred prior to depression onset, researchers could estimate causal effects by directly including these variables in standard statistical regression models. However, many confounders vary over time and may partially mediate effects of prior exposures on outcome. For example, alcohol use disorder (AUD) often develops after depression onset, has been associated with subsequent depression (34), and is a well-established risk factor for stroke (Figure 2A). Adjusting for confounding effects of AUD through inclusion of AUD in a conventional regression model (i.e., conditioning on AUD) blocks the indirect effect of depression on stroke mediated by AUD, thereby underestimating the total effect of depression. Adjusting for a confounder that also behaves as a mediator may also induce collider bias when there is an unmeasured common cause of the confounder and the outcome (i.e., conditioning on We); the net bias induced by adjustment for a mediating confounder could be in either direction.
Figure 2.
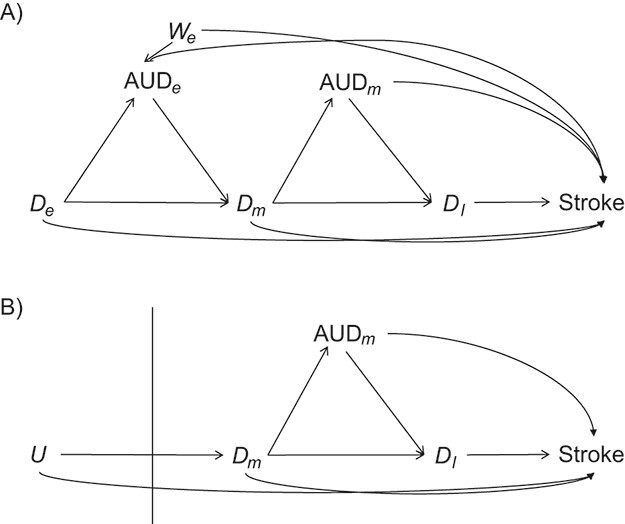
Possible causal structures for the associations of depression status in early life (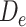 ), midlife (
), midlife (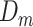 ), and late life (
), and late life (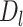 ) with risk of stroke, assuming that depression has cumulative effects on stroke risk and that alcohol use disorder (AUD) is a time-varying confounder that partially mediates the effect of time-varying depression on stroke. AUD status in early life (AUDe) and midlife (AUDm) is depicted in panel A, which shows associations as captured by a cohort followed since early life. We represents an unmeasured common cause of AUD in early life and stroke. Panel B shows a directed acyclic graph (DAG) consistent with panel A but representing all early-life variables as unknown (U), as they would be for a cohort study beginning in midlife (the vertical line represents study initiation). In this setting, both depression in early life and AUD in early life would behave as confounders of the mid- and late-life depression-stroke associations. In the modified DAG, we represent early-life AUD and depression with a single “U,” since these variables have the same structural associations with measured variables represented in the DAG.
) with risk of stroke, assuming that depression has cumulative effects on stroke risk and that alcohol use disorder (AUD) is a time-varying confounder that partially mediates the effect of time-varying depression on stroke. AUD status in early life (AUDe) and midlife (AUDm) is depicted in panel A, which shows associations as captured by a cohort followed since early life. We represents an unmeasured common cause of AUD in early life and stroke. Panel B shows a directed acyclic graph (DAG) consistent with panel A but representing all early-life variables as unknown (U), as they would be for a cohort study beginning in midlife (the vertical line represents study initiation). In this setting, both depression in early life and AUD in early life would behave as confounders of the mid- and late-life depression-stroke associations. In the modified DAG, we represent early-life AUD and depression with a single “U,” since these variables have the same structural associations with measured variables represented in the DAG.
Late–study-start bias
In the majority of cohort studies examining diseases in mid- to late adulthood, researchers begin capturing prospective data on social and psychological exposures and potential confounders at a somewhat arbitrary time in midadulthood or later. Capturing only mid- or late-life measures of depression restricts us to estimating the coefficients of model 6, an abbreviated version of model 1:
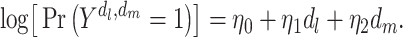 |
(model 6) |
This MSM represents the causal effects of hypothetical interventions on mid- and late-life depression on late-life stroke risk. This differs from model 1 because it does not represent any causal effect of early-life depression. Correct specification of model 1 requires that there be no effect modification of mid- or late-life depression by early-life depression on the risk ratio scale; however, model 6 is completely agnostic to such an assumption. Model 6 is a well-defined counterfactual model even if early-life depression has a nonnull controlled direct effect on stroke after controlling for mid- and late-life depression. However, without collecting data on early-life depression, it may not be possible to correctly estimate the parameters in model 6, because early-life depression predicts mid- or late-life depression and therefore may confound the joint effects of mid- or late-life depression on stroke risk.
Combined effects of time-varying exposures and unmeasured confounders under late–study-start conditions
Often researchers encounter issues of both late–study-start and time-varying confounding within a single project. In a late–study-start setting, exposure history prior to study start often operates as an unobserved confounder (Figure 2B). Estimating MSMs with IPWs will not fully address potential biases in these situations, since IPWs can only adjust for time-varying confounders when those confounders are measured.
Below we present simulations demonstrating the potential magnitude, direction, and type of biases that can occur and consider how commonly used methods may or may not adequately address these concerns.
METHODS FOR SIMULATION STUDY
Data-generation
Time-varying confounding simulation.
We mimicked a birth cohort with all relevant measures of exposures and confounders to assess possible differences in estimates obtained from conventional models versus MSM modeling of the effect of depression under the accumulation model. We assumed the following (details are provided in Web Appendix 2 and Web Appendix 3):
In each exposure period (early, mid-, or late life), depression had a direct effect that doubled stroke risk.
At each time point, having depression increased the odds of having depression at the subsequent time point by 50%.
AUD was a time-varying confounder that also behaved as a mediator. We assumed that depression approximately tripled the odds of AUD, and we varied the association between AUD and stroke. We generated stroke risk under the following model, where Lk represents AUD at time k (model 7; additional details are provided in Web Appendix 2):
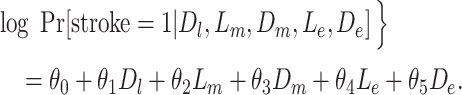 |
(model 7) |
We considered the following 6 scenarios:
No confounding (risk ratio (RR) for the association between AUD and stroke (RRAUD-stroke) = exp(θ4) =exp(θ2) = 1.0)
Moderate positive confounding (RRAUD-stroke =exp(θ4) = exp(θ2) = 1.5)
Strong positive confounding (RRAUD-stroke exp(θ4) = exp(θ2) = 2)
Negative confounding (RRAUD-stroke exp(θ4) = exp(θ2) = 0.67)
Strong positive confounding in early life (RRAUD-stroke = exp(θ4) = 2) and moderate confounding in midlife (RRAUD-stroke = exp(θ2) = 1.5)
Moderate positive confounding in early life (RRAUD-stroke = exp(θ4) = 1.5) and strong confounding in midlife (RRAUD-stroke = exp(θ2) = 2)
We modified scenario 2 (moderate positive confounding) such that the time-varying confounder was unaffected by prior exposure (i.e., depression did not affect AUD; scenario 7). Lastly, we modified scenario 2 by adding an unmeasured confounder that was strongly positively associated with both AUD in early life (RRWe-AUD = 1.65) and stroke (RRWe-stroke = 0.22) (scenario 8; details are provided in Web Appendix 4). In our example of depression and stroke confounded by AUD, US state of early-life residence is an example of such an unmeasured confounder, since state of early-life residence is associated with binge drinking and stroke (35). We generated stroke risk under model 8, where We represents state of residence in early life.
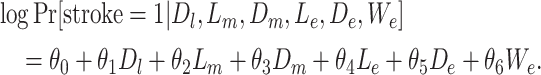 |
(model 8) |
For all models, we generated 10,000 data sets (n = 100,000 people per data set).
Late–study-start bias simulation.
We generated data to illustrate the effect of a late study start in the absence of time-varying confounding. We assessed how the estimated midlife, late-life, and total effect of depression differed from the true effects according to the 3 life-course models outlined above. We also considered 2 hybrid models: 1) an accumulation model incorporating an increasing effect of depression with age and 2) an accumulation model incorporating a decreasing effect with age. Data were generated using early-, mid-, and late-life depression and assumed no confounders of the effect of depression on stroke. For each life-course model, we generated 10,000 data sets (n = 100,000 people per data set; details are provided in Web Appendices 2 and 3). For all scenarios, depression at each time point increased the odds of depression in the subsequent period by 50%.
Accumulation model: The direct effect of early-, mid-, and late-life depression each doubled stroke risk.
Critical period during early life model: The direct effect of early-life depression tripled stroke risk, and depression during the remaining periods had no direct effect on stroke.
Pathway model: The direct effect of late-life depression tripled stroke risk, and depression during the remaining periods had no direct effect on stroke.
We also conducted simulations under the hybrid models described above.
Late–study-start scenario with time-varying confounding simulation.
Under the accumulation model described above, we generated data to assess possible differences in estimates obtained from conventional models versus MSM coefficients fitted with IPW when information on early-life depression was not available (details are provided in Web Appendix 3). We assumed that depression approximately tripled the odds of AUD; that AUD increased the odds of depression at the subsequent time point by 50%; and that AUD also doubled stroke risk.
Statistical analysis
Time-varying confounding simulation.
Effect estimates for early-, mid-, and late-life depression were calculated using conventional logistic regression to approximate log-linear models under the rare disease assumption with regression adjustment for AUD. Next, the coefficients of the MSMs were estimated using IPW. Stabilized IPWs were created for depression, with depression at each time point being conditional on depression and AUD at the prior time point (e.g., the probability of depression at midlife was conditional on depression and AUD in early life). We calculated the percent bias of the estimates, the standard error of the estimated bias (i.e., the standard deviation of the estimates across iterations of the simulation), the mean squared error, and the 95% confidence interval (CI) coverage (SAS code (SAS Institute, Inc., Cary, North Carolina) is provided in Web Appendix 5).
Late–study-start bias simulation.
For each scenario, we approximated log-linear models with conventional logistic models under under the rare disease assumption to estimate the lifetime effect of depression on stroke, contrasting “depressed throughout life” with “not depressed at any point.” We then reestimated the lifetime effect using information only from mid- and late life to mimic a real-world setting where follow-up started in midlife. The percent bias was calculated comparing the estimated effects with the “true” effects on the log odds scale. We also calculated the standard error of estimated bias, the mean squared error, and the 95% CI coverage (SAS code is provided in Web Appendix 5).
Late–study-start scenario with time-varying confounding simulation.
Effect estimates for mid- and late-life depression were calculated with conventional logistic regression to approximate log-linear models under the rare disease assumption and MSMs using information only from mid- and late life. Conventional models adjusted for AUD by directly including it in the regression model, and the MSM coefficients were estimated using IPW methods. Stabilized IPWs were created for depression, with depression at each time point being conditional on depression and AUD at the prior time point. The percent bias was calculated for the midlife, late-life, and lifetime effects for each set of analyses. We also calculated the standard error of the estimated bias, the mean squared error, and the 95% CI coverage (SAS code is provided in Web Appendix 5).
RESULTS
Time-varying confounding simulation results
Under the accumulation model, effect estimates for early-, mid-, and late-life depression provided by the conventional model versus the MSM were the same if no confounding was present (Table 1, scenario 1) or if the confounder was unaffected by prior depression (scenario 7). After introducing time-varying mediating confounders (Figure 2A; Table 1, scenarios 2 and 3), effects for early life and midlife estimated in conventional models were closer to the null than the true effect. Conversely, the estimate of late-life effects from the conventional model and all of the estimates from the MSMs closely approximated the true effect of depression at the corresponding time points. A similar pattern was shown in the context of negative confounding (scenario 4) but with conventional model estimates for early- and midlife being further from the null than the true effect. When greater time-varying confounding occurred in early life (scenario 5), conventional regression underestimated the effect of early-life versus midlife depression more severely. The opposite was true when time-varying confounding was greatest later in life (scenario 6). In the presence of an unmeasured confounder of AUD and stroke (scenario 8), conventional estimates of the effect of early- and midlife depression were underestimated while late-life estimates were unbiased.
Table 1.
Bias in Estimates of the Causal Direct Effect of Depression in Early, Mid-, and Late Life on Stroke Risk Under the Accumulation Model Using Conventional Regression Versus Inverse Probability Weighting in the Presence or Absence of Time-Varying Confounding by Alcohol Use Disordera
| Estimated Effect (Log RR) of Depression on Stroke Risk | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Conventional Regression | Inverse Probability Weighting | |||||||||||
| Type of Magnitude Change and Scenario No. |
Early-Life
Depression (  )
)
|
% Bias b |
Midlife
Depression (  )
)
|
% Bias |
Late-Life
Depression (  )
)
|
% Bias |
Early-Life
Depression ( 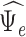 )
)
|
% Bias |
Midlife
Depression ( 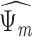 )
)
|
% Bias |
Late-Life
Depression ( 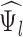 )
)
|
% Bias |
| Varying the magnitude of the effect of AUD on stroke | ||||||||||||
| 1. No confounding | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 |
| 2. Moderate positive confounding | 0.58 | −16 | 0.58 | −16 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 |
| 3. Strong positive confounding | 0.51 | −26 | 0.51 | −26 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 |
| 4. Negative confounding | 0.81 | 17 | 0.81 | 17 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 |
| 5. Greater confounding earlier in life | 0.51 | −26 | 0.58 | −16 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 |
| 6. Greater confounding later in life | 0.58 | −16 | 0.51 | −26 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 |
| Varying the magnitude of the effect of depression on AUD | ||||||||||||
| 7. No effect of depression on AUD | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 | 0.69 | 0 |
| Unmeasured confounding of both AUD and stroke | ||||||||||||
| 8. Moderate positive unmeasured confounder of AUD and stroke | 0.62 | −10 | 0.58 | −16 | 0.69 | 0 | 0.68 | −1 | 0.69 | 0 | 0.69 | 0 |
Abbreviations: AUD, alcohol use disorder; RR, risk ratio.
a Data were generated to mimic the effect of depression on stroke under the accumulation model: The true direct effect of depression at each time point doubled the odds of stroke, and depression increased the odds of depression at the subsequent time point by 50%. Data were generated with 10,000 replications and 100,000 people in each sample.
b Percent bias = [(average of 10,000 estimated effect − true effect of 0.69)/true effect of 0.69] × 100.
Late–study-start bias simulation results
With a late study start, under the 3 accumulation models and the early-life critical period models, the estimated mid- and late-life effects were inflated compared with the true mid- and late-life effects (Table 2). Under these theoretical models, individuals with early-life depression had elevated risks of mid- and late-life depression and of stroke, so early-life depression was a confounder that was positively associated with the measured exposure and the outcome. However, under these theoretical models, the effects of early-life depression were not completely mediated by later depression; thus, the mid- and late-life estimates only partially captured the effects of early-life depression. As a result, the accumulation and early-life critical period models underestimated the lifetime effect by 27% and 82%, respectively. Under the pathway model, the direct effects of mid- and late life were estimated correctly even in a model without information on early-life depression, and the estimated lifetime effect was minimally biased.
Table 2.
Difference in “True” Versus Estimated Effects of Depression on Stroke Risk on the Log Odds Scale Under Different Theoretical Life-Course Models When Information Regarding Early-Life Exposure Is Missinga
| Effect (Log RR) of Depression on Stroke Risk | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Direct Effect of Depression | Lifetime Effect of Depression | |||||||||
| Depression in Midlife | Depression in Late Life | |||||||||
| Theoretical Model Under Which Data Were Generated |
Depression in Early Life (“True” Effect (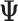 3)) 3))
|
“True”
Effect ( 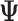 2
)
2
)
|
Estimated Effect (
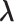 2
)
2
)
|
% Bias b |
“True”
Effect ( 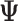 1
)
1
)
|
Estimated Effect (
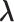 1
)
1
)
|
% Bias b |
“True” Effect (
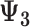 +
+ 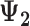 + + 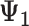 ) )
|
Estimated Effect (
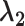 +
+ 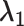 ) )
|
% Bias b |
| Accumulation model | 0.69 | 0.69 | 0.75 | 9 | 0.69 | 0.76 | 10 | 2.07 | 1.51 | −27 |
| Early-life critical period model | 1.10 | 0.00 | 0.09 | 0.00 | 0.10 | 1.10 | 0.20 | −82 | ||
| Pathway model | 0.00 | 0.00 | 0.00 | 1.10 | 1.10 | 0 | 1.10 | 1.10 | 0 | |
| Accumulation model with increasing effect across the life course | 0.41 | 0.69 | 0.73 | 6 | 0.92 | 0.96 | 5 | 2.02 | 1.69 | −16 |
| Accumulation model with decreasing effect across the life course | 0.92 | 0.69 | 0.77 | 122 | 0.41 | 0.50 | 22 | 2.02 | 1.27 | −37 |
Abbreviation: RR, risk ratio.
a The true direct effect of depression on stroke was set to 0.69, and there were 10,000 replications with 100,000 people in each sample unless otherwise stated. Estimates were obtained from conventional logistic regression models.
b Percent bias = [(average of 10,000 estimated effect − true effect)/true effect] × 100.
Late–study-start scenario with time-varying confounding simulation under the accumulation model
When time-varying confounding occurred in the context of a late study start under the accumulation model, neither conventional models nor MSMs could recover true effects for all parameters of interest (Table 3). While the conventional model ignoring early-life depression provided an almost unbiased estimate of late-life depression effects on stroke, it underestimated the effect of midlife depression. Thus, it underestimated the lifetime effect of depression, which was based on unbiased estimates of late-life depression and underestimated midlife depression. In contrast, the MSM overestimated the midlife effect of depression, correctly estimated the late-life effect, and underestimated the lifetime effect.
Table 3.
Estimated Effects of Depression on Stroke Risk Under an Accumulation Model (Expressed on the Log Odds Scale) Comparing Conventional Regression and Inverse Probability Weighting to Estimate Marginal Structural Model Parameters in the Presence of a Late Study Start and Time-Varying Confoundersa
| Estimated Effect (Log RR) of Depression on Stroke Risk | |||||||
|---|---|---|---|---|---|---|---|
| Depression in Midlife | Depression in Late Life | Lifetime Effect of Depression | |||||
| Analytical Method |
Log RR (
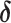 2)
2)
|
% Bias b |
Log RR (
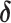 3)
3)
|
% Bias b |
Method of
Calculation |
Log RR | % Bias b |
| True effects | 0.69 | 0.69 |
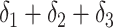
|
2.07 | |||
| Conventional regression | 0.56 | −19 | 0.69 | 0 |
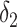 +
+ 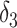
|
1.25 | −40 |
| IPW estimation of MSM | 0.74 | 7 | 0.69 | 0 |
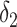 +
+ 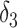
|
1.43 | −31 |
Abbreviations: AUD, alcohol use disorder; IPW, inverse probability weighting; MSM, marginal structural model; RR, risk ratio.
a Data were generated to mimic the effect of depression on stroke under the accumulation model: The true direct effect of depression at each time point doubled the odds of stroke, and depression increased the odds of depression at the subsequent time point by 50%. We assumed that depression approximately tripled the odds of AUD, that AUD increased the odds of depression at the subsequent time point by 50%, and that AUD doubled the odds of stroke. Data were generated with 10,000 replications and 100,000 people in each sample.
b Percent bias = [(average of 10,000 estimated effect − true effect of 0.69)/true effect of 0.69] × 100.
Accuracy and precision of estimates across simulations
Web Tables 1–3 present the standard error of estimated bias, the mean squared error, and the 95% CI coverage of effect estimates obtained under the 3 sets of scenarios described above. In general, the larger the percent bias, the lower was the 95% CI coverage and the greater the mean squared error. There did not appear to be an association between the percent bias and the standard error. The difference in standard errors between estimates obtained from conventional models versus MSMs varied by simulation.
DISCUSSION
We examined whether MSMs can provide unbiased estimates of the association between depression and stroke risk under different life-course models and in the context of 2 often co-occurring methodological challenges: time-varying confounding and initiation of data collection in midlife. Bias introduced by time-varying confounding can be appropriately addressed using MSMs, but the extent of bias due to a late study start depends on the true underlying life-course model. In our simulations, conventional models and MSMs provided unbiased estimates when time-varying confounders were not present or when time-varying confounders were unaffected by prior levels of depression. When a time-varying confounder was affected by prior depression levels, regression adjustment of the confounder resulted in underestimation of depression’s effect on stroke. MSM estimates using IPW provided unbiased estimates in the context of time-varying confounding but not in the scenario with a late study start.
When cohort studies begin in mid- to late life, researchers are only able to estimate effects of observed mid- to late-life exposures rather than lifetime effects. In simulations assuming no confounders, the estimated effect of late-life depression from conventional models provided an unbiased estimate of the true lifetime effect of depression only under the pathway model (i.e., when early- and midlife depression had no direct effects on stroke). Under the accumulation and early-life critical periods models, early-life depression acted as a positive confounder, resulting in overestimation of the relationships between mid- and late-life depression and stroke. Moreover, the lifetime effects were underestimated, since the effects of early-life depression on stroke were not completely mediated by mid- and late life.
In real-world research on psychosocial factors, often time-varying exposures and a late study start co-occur. When simulated concurrently, MSM estimates were generally less biased than those from conventional models, though both underestimated the lifetime effect of depression on stroke. The correlation of exposures over time implies that midlife exposures may serve as a good proxy for early-life exposures. However, it also means that effect estimates of midlife exposures could be confounded by the effects of early-life exposures. Disentangling the time-specific exposure effect from potentially confounding effects of prior exposure becomes critical when trying to inform the timing of potential interventions. When conducting research in which exposures are measured only in mid- to late life, researchers should acknowledge that omitting early-life exposures could bias estimates and should describe how the estimated late-life effect may differ from the lifetime effect (8). In these cases, it may be useful to include estimates of the plausible direction and magnitude of bias using sensitivity analyses. Although, in principle, we expect IPW of exposures to increase the variance of the estimates, whether conventional models or MSMs had more precise estimates varied by simulation. The optimal choice when balancing bias and variance will be specific to the scientific question at hand.
Conventional epidemiologic methods are often inappropriate for estimating effects of psychosocial factors on life-course health because these effects may accumulate across the life course, differ depending on age of exposure, or are subject to complex, time-varying confounding by other exposures. While MSMs can ameliorate some bias due to these methodological challenges, they cannot completely account for bias induced by late study entry, a common complication in this field. The best time to handle missing early-life exposure data is during the study design phase. Our findings reinforce the importance of supporting birth cohort studies and other types of studies that capture information on exposures across the life course. For example, cohort data could be linked to preexisting data sources such as US Census data, Social Security claims, vital records, military veterans’ records, and other government records. Retrospective collection of data on prior exposures may help mitigate confounding of later-life exposures, but misclassification and recall bias become concerns.
During the analytical phase, methods such as the use of negative controls can be implemented to detect bias in observational studies (36, 37). Other sources of information regarding the likely distribution of the exposure within the population of interest could be used to estimate a weighted average of the different exposure categories in late life. Mendelian randomization uses genetic variants as instrumental variables and under certain assumptions provides causal estimates. Such estimates may be useful but should not be misinterpreted as providing precise estimates for effects of exposure at a specific age. In principle, instrumental variables with age-specific effects on exposure could be used to ameliorate this problem. For example, policy changes are often used as instrumental variables in social epidemiology if the policy alters access or exposure to specific social resources or adversities. Such policy changes will occur at different ages for different individuals and could—with sufficient data and strong assumptions—be used to estimate age-specific effects of social determinants of health.
Left-truncation of outcomes is another possible source of bias if people who have already experienced an outcome are excluded from the cohort. In the presented scenarios, it is unlikely that left-truncation of the outcomes was a serious concern, since the outcome (stroke) rarely occurs before the start of follow-up in midlife. However, researchers should consider the possible effects of left-truncation of the outcome if relevant to their studies, since it may result in selection bias (38, 39). Though the causal structures we present are oversimplifications of a series of complex relationships occurring across the life course, our scenarios highlight the importance of addressing these methodological challenges, since biases illustrated in simplified scenarios will likely be evident in more complicated scenarios.
Our findings underscore the importance of clearly identifying and discussing what effects can and cannot be estimated without bias. A more refined understanding of each study’s results will provide the clearest possible indication of what future studies are needed to advance the field and what important questions remain.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Kaiser Permanente Division of Research, Oakland, California, United States (Paola Gilsanz, Chloe W. Eng); Department of Epidemiology and Biostatistics, School of Medicine, University of California, San Francisco, San Francisco, California, United States (Paola Gilsanz, M. Maria Glymour, Chloe W. Eng); Department of Population Medicine, Harvard Medical School and Harvard Pilgrim Health Care Institute, Boston, Massachusetts, United States (Jessica G. Young); Department of Epidemiology, Harvard T.H. Chan School of Public Health, Harvard University, Boston, Massachusetts, United States (Jessica G. Young, Karestan C. Koenen); CAUSALab, Harvard T.H. Chan School of Public Health, Harvard University, Boston, Massachusetts, United States (Jessica G. Young); Department of Statistics and Data Science, The Wharton School, University of Pennsylvania, Philadelphia, Pennsylvania, United States (Eric J. Tchetgen Tchetgen); and Department of Social and Behavioral Sciences, Harvard T.H. Chan School of Public Health, Harvard University, Boston, Massachusetts, United States (Laura D. Kubzansky).
This study was supported by the National Institutes of Health (grants R01AI104459, R01AI27271, RF1AG050782, RF1AG052132, RF1AG055486, R01AG065276, R01AG066132, R01CA222147, R01GM139926, R01MH101269, T32MH017119, and T32AG049663) and the Yerby Postdoctoral Fellowship Program.
These analyses were conducted on simulated data. SAS code for generating these data can be found in Web Appendix 5.
Conflict of interest: none declared.
REFERENCES
- 1. Kaufman JS, Cooper RS. Seeking causal explanations in social epidemiology. Am J Epidemiol. 1999;150(2):113–120. [DOI] [PubMed] [Google Scholar]
- 2. Koenen KC, Sumner JA, Gilsanz P, et al. Post-traumatic stress disorder and cardiometabolic disease: improving causal inference to inform practice. Psychol Med. 2017;47(2):209–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Glymour MM, Rudolph KE. Causal inference challenges in social epidemiology: bias, specificity, and imagination. Soc Sci Med. 2016;166:258–265. [DOI] [PubMed] [Google Scholar]
- 4. Nagayoshi M, Everson-Rose SA, Iso H, et al. Social network, social support, and risk of incident stroke: Atherosclerosis Risk in Communities Study. Stroke. 2014;45(10):2868–2873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Pan A, Sun Q, Okereke OI, et al. Depression and risk of stroke morbidity and mortality: a meta-analysis and systematic review. JAMA. 2011;306(11):1241–1249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Hernán MA, Brumback BA, Robins JM. Estimating the causal effect of zidovudine on CD4 count with a marginal structural model for repeated measures. Stat Med. 2002;21(12):1689–1709. [DOI] [PubMed] [Google Scholar]
- 7. Hernán MA, Brumback B, Robins JM. Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology. 2000;11(5):561–570. [DOI] [PubMed] [Google Scholar]
- 8. Mansournia MA, Naimi AI, Greenland S. The implications of using lagged and baseline exposure terms in longitudinal causal and regression models. Am J Epidemiol. 2019;188(4):753–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Gilsanz P, Kubzansky LD, Tchetgen Tchetgen EJ, et al. Changes in depressive symptoms and subsequent risk of stroke in the Cardiovascular Health Study. Stroke. 2017;48(1):43–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Gilsanz P, Walter S, Tchetgen Tchetgen EJ, et al. Changes in depressive symptoms and incidence of first stroke among middle-aged and older US adults. J Am Heart Assoc. 2015;4(5):e001923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Cerdá M, Diez-Roux AV, Tchetgen Tchetgen E, et al. The relationship between neighborhood poverty and alcohol use: estimation by marginal structural models. Epidemiology. 2010;21(4):482–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Nandi A, Glymour MM, Kawachi I, et al. Using marginal structural models to estimate the direct effect of adverse childhood social conditions on onset of heart disease, diabetes, and stroke. Epidemiology. 2012;23(2):223–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Li S, Stampfer MJ, Williams DR, et al. Association of religious service attendance with mortality among women. JAMA Intern Med. 2016;176(6):777–785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Krishna Rao S, Mejia GC, Roberts-Thomson K, et al. Estimating the effect of childhood socioeconomic disadvantage on oral cancer in India using marginal structural models. Epidemiology. 2015;26(4):509–517. [DOI] [PubMed] [Google Scholar]
- 15. Capistrant BD, Moon JR, Berkman LF, et al. Current and long-term spousal caregiving and onset of cardiovascular disease. J Epidemiol Community Health. 2012;66(10):951–956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Marden JR, Tchetgen Tchetgen EJ, Kawachi I, et al. Contribution of socioeconomic status at 3 life-course periods to late-life memory function and decline: early and late predictors of dementia risk. Am J Epidemiol. 2017;186(7):805–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Rhew IC, Fleming CB, Vander Stoep A, et al. Examination of cumulative effects of early adolescent depression on cannabis and alcohol use disorder in late adolescence in a community-based cohort. Addiction. 2017;112(11):1952–1960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Hope S, Pearce A, Chittleborough C, et al. Temporal effects of maternal psychological distress on child mental health problems at ages 3, 5, 7 and 11: analysis from the UK Millennium Cohort Study. Psychol Med. 2019;49(4):664–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. VanderWeele TJ, Hawkley LC, Thisted RA, et al. A marginal structural model analysis for loneliness: implications for intervention trials and clinical practice. J Consult Clin Psychol. 2011;79(2):225–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Zhong QY, Gelaye B, VanderWeele TJ, et al. Causal model of the association of social support with antepartum depression: a marginal structural modeling approach. Am J Epidemiol. 2018;187(9):1871–1879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Yakubovich AR, Heron J, Feder G, et al. Long-term exposure to neighborhood deprivation and intimate partner violence among women: a UK birth cohort study. Epidemiology. 2020;31(2):272–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Dong JY, Zhang YH, Tong J, et al. Depression and risk of stroke: a meta-analysis of prospective studies. Stroke. 2012;43(1):32–37. [DOI] [PubMed] [Google Scholar]
- 23. Zisook S, Lesser I, Stewart JW, et al. Effect of age at onset on the course of major depressive disorder. Am J Psychiatry. 2007;164(10):1539–1546. [DOI] [PubMed] [Google Scholar]
- 24. Hardeveld F, Spijker J, De Graaf R, et al. Prevalence and predictors of recurrence of major depressive disorder in the adult population. Acta Psychiatr Scand. 2010;122(3):184–191. [DOI] [PubMed] [Google Scholar]
- 25. Hernan MA, Robins JM. Causal Inference: What If. Boca Raton, FL: Chapman & Hall/CRC Press; 2020. [Google Scholar]
- 26. Robins JM, Hernán MÁ, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–560. [DOI] [PubMed] [Google Scholar]
- 27. Young JG, Hernán MA, Robins JM. Identification, estimation and approximation of risk under interventions that depend on the natural value of treatment using observational data. Epidemiol Methods. 2014;3(1):1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Cole SR, Hernán MA. Constructing inverse probability weights for marginal structural models. Am J Epidemiol. 2008;168(6):656–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Robins JM. Causal inference from complex longitudinal data. In: Berkane M, ed. Latent Variable Modeling and Applications to Causality. New York, NY: Springer-Verlag New York; 1997. [Google Scholar]
- 30. Berkman LF. Social epidemiology: social determinants of health in the United States: are we losing ground? Annu Rev Public Health. 2009;30:27–41. [DOI] [PubMed] [Google Scholar]
- 31. Kuh D, Ben-Shlomo Y. A Life Course Approach to Chronic Disease Epidemiology. New York, NY: Oxford University Press; 1997. [Google Scholar]
- 32. Power C, Hertzman C. Social and biological pathways linking early life and adult disease. Br Med Bull. 1997;53(1):210–221. [DOI] [PubMed] [Google Scholar]
- 33. De Stavola BL, Daniel RM. Marginal structural models: the way forward for life-course epidemiology? Epidemiology. 2012;23(2):233–237. [DOI] [PubMed] [Google Scholar]
- 34. Pacek LR, Martins SS, Crum RM. The bidirectional relationships between alcohol, cannabis, co-occurring alcohol and cannabis use disorders with major depressive disorder: results from a national sample. J Affect Disord. 2013;148(2-3):188–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Howard VJ, McClure LA, Glymour MM, et al. Effect of duration and age at exposure to the Stroke Belt on incident stroke in adulthood. Neurology. 2013;80(18):1655–1661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Lipsitch M, Tchetgen Tchetgen E, Cohen T. Negative controls: a tool for detecting confounding and bias in observational studies. Epidemiology. 2010;21(3):383–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Shi X, Miao W, Tchetgen Tchetgen E. A selective review of negative control methods in epidemiology. Curr Epidemiol Rep. 2020;7(4):190–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Cain KC, Harlow SD, Little RJ, et al. Bias due to left truncation and left censoring in longitudinal studies of developmental and disease processes. Am J Epidemiol. 2011;173(9):1078–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Mayeda ER, Banack HR, Bibbins-Domingo K, et al. Can survival bias explain the age attenuation of racial inequalities in stroke incidence? A simulation study. Epidemiology. 2018;29(4):525–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


