Slow waves form expanding, memory-rich mesostates steered by local excitability in fading anesthesia

Summary

In the arousal process, the brain restores its integrative activity from the synchronized state of slow wave activity (SWA). The mechanisms underpinning this state transition remain, however, to be elucidated. Here we simultaneously probed neuronal assemblies throughout the whole cortex with micro-electrocorticographic recordings in mice. We investigated the progressive shaping of propagating SWA at different levels of isoflurane. We found a form of memory of the wavefront shapes at deep anesthesia, tightly alternating posterior-anterior-posterior patterns. At low isoflurane, metastable patterns propagated in more directions, reflecting an increased complexity. The wandering across these mesostates progressively increased its randomness, as predicted by simulations of a network of spiking neurons, and confirmed in our experimental data. The complexity increase is explained by the elevated excitability of local assemblies with no modifications of the network connectivity. These results shed new light on the functional reorganization of the cortical network as anesthesia fades out.

Graphical abstract

Highlights

• •Complexity of isoflurane-induced slow waves reliably determines anesthesia level
• •In deep anesthesia, the propagation strictly alternates between front-back-front patterns
• •In light anesthesia, there is a continuum of directions and faster propagation
• •Local excitability underpins the cortical reorganization in fading anesthesia

Neuroscience; Experimental models in systems biology

Introduction

During sleep and anesthesia, the brain generates patterns of low-frequency, synchronized activity, referred to as slow wave activity (SWA) (Destexhe et al., 1999; Massimini et al., 2004; Mohajerani et al., 2010; Steriade et al., 1993a). This activity coordinates large portions of the cortex into a coherent rhythmic sequence of recurring cortical and corticothalamic activations (Destexhe and Sejnowski, 2003; Grenier et al., 1998; Muller et al., 2016, 2018; Sheroziya and Timofeev, 2014). In this state, cortical neurons undergo a slow alternation between periods of depolarization and firing (Up or On states) and periods of almost-silent hyperpolarization (Down or Off states) (Steriade et al., 1993b; Torao-Angosto et al., 2021; Vyazovskiy et al., 2009). This is accompanied by reduced amounts of neuronal excitability and enhanced segregation of cortical areas (Bettinardi et al., 2015; Compte et al., 2003; Fernandez et al., 2017; Fischer et al., 2018; Levenstein et al., 2019; Liu et al., 2013; Massimini et al., 2004, 2005; Mattia and Sanchez-Vives, 2012; Muller and Destexhe, 2012; Sanchez-Vives and Mattia, 2014; Sanchez-Vives and McCormick, 2000). Slow oscillations are believed to interact with the other characteristic signatures of sleep, like spindles reaching the cortex from the thalamus. These nested oscillations might be responsible for cognitive processes such as memory consolidation (Muller et al., 2016, 2018). However, a characterization of the modes of propagation of the slow oscillations at the level of local neuronal assemblies during the process of emergence to consciousness is still missing.

In the last two decades, several studies have approached the transition between the unconscious and the awake state, by means of recordings at various depths of either natural sleep or anesthesia, as well as during the process of awakening (Barttfeld et al., 2015; Bettinardi et al., 2015; Dasilva et al., 2021; Fischer et al., 2018; Hahn et al., 2012; Hudetz et al., 2015; Hudson et al., 2014; Lee et al., 2020; Li and Mashour, 2019; Liu et al., 2013; Schartner et al., 2017; Tort-Colet et al., 2021). Results from single – or a small number of simultaneously recorded – areas (including primary visual (Hudetz et al., 2015; Lee et al., 2020; Vizuete et al., 2012), cingulate (Hudson et al., 2014), retrosplenial (Hudson et al., 2014), temporo-parieto-occipital (Fischer et al., 2018) cortices and the thalamus (Hudson et al., 2014)), as well as from the whole cortex (Barttfeld et al., 2015; Bettinardi et al., 2015; Dasilva et al., 2021; Grandjean et al., 2014; Li and Mashour, 2019; Liu et al., 2013; Schartner et al., 2017), showed that during the emergence from deep anesthesia and NREM sleep the frequency of the slow oscillations increases and the network activity strengthens its integration and complexity dynamical properties, possibly starting to wander among so-called microstates that involve a varying number of frequency bands (Brodbeck et al., 2012; Dasilva et al., 2021; Hudson et al., 2014; Lee et al., 2020; Liu et al., 2013). These studies support the hypothesis that the anesthetized (sleeping) brain is not confined to a static-dynamical state, but actually explores a more complex landscape, eventually operating a rather progressive state transition to wakefulness (Barttfeld et al., 2015; Dasilva et al., 2021; Li and Mashour, 2019; Stevner et al., 2019). However, these studies investigated the features of the brain activity during the recovery of consciousness either at a coarse spatial scale, or focused on general signatures of the neuronal activity. How the activity of local neuronal assemblies propagates through the cortex, and which mechanisms lead to its emergence and transmission, is still to be elucidated.

Several mechanisms are thought to play a role during the emergence of slow wave states and during the inverse process that leads to awakening (Deco et al., 2014; Destexhe and Sejnowski, 2003; Längkvist et al., 2012; Mattia and Sanchez-Vives, 2012; Pearlmutter and Houghton, 2009; Sanchez-Vives et al., 2017; Stevner et al., 2019; Tort-Colet et al., 2021). These include corticothalamic loops (Crunelli and Hughes, 2010; Crunelli et al., 2015; Destexhe and Sejnowski, 2003; Grenier et al., 1998; Merica and Fortune, 2004; Sheroziya and Timofeev, 2014; Steriade et al., 1993a) and the balance between local dynamical features and global connectivity of the brain network shaping its integration and segregation capabilities (Barttfeld et al., 2015; Deco et al., 2014, 2015; Mohajerani et al., 2013). At the cellular and local cortical assembly level, various experimental and modeling studies pointed to two main players playing a critical role in the process of awakening: firing adaptation of excitatory cortical neurons and neuronal excitability (Compte et al., 2003; Lee et al., 2020; Levenstein et al., 2019; Mattia and Sanchez-Vives, 2012; Muller and Destexhe, 2012; Sanchez-Vives and McCormick, 2000). However, the network mechanisms underlying these state transitions remain to be conclusively elucidated. In particular, an open question is the role played by the restored levels of local excitability and long-range connectivity in shaping the activity observed at different levels of anesthesia as the awake state is approached. Importantly, the presence and the properties of the traveling wavefronts underlying the well-established slow oscillations and how their propagation mode throughout the cortex changes during the awakening process has not yet fully been understood and characterized.

Here, by probing the electrophysiological activity of neuronal populations across a wide area of the mouse cortical surface at various anesthesia levels, we addressed the following question: what are the mechanisms and network features that steer the brain activity emerging from deep anesthesia? We analyzed recordings from different mice and at varying levels of slow wave anesthesia sorting them on a common fine-grained scale. For that purpose, we used a cocktail of anesthetics that allowed us to modulate the SWA regime in a controlled way. We developed an objective and quantitative measure of the level of complexity of the slow waves based on their frequency and the entropy of the wavefronts of propagation through the cortex, referred to as the wave entropy index (WEI). We described the progression from the simple, irregular spatiotemporal patterns of multiunit activity (MUA) characteristic of deep anesthesia to the spatially complex, albeit temporally regular patterns that are encountered at low isoflurane levels. We found a significant correlation between the WEI and the number of spontaneously expressed modes of propagation, and the progressive loss and recovery of sequential memory between consecutive waves. Resorting to a spatially extended spiking neuron network modeling the cortical surface probed in experiments, we show how the rise of complexity is obtained without modifying the underlying “structure”; that is, the cortico-cortical connectivity. Changes in the local excitability alone suffice to explain the dynamical transition of the global cortical network in the arousal process from deep anesthesia, supporting the hypothesis of a tight binding between scales in the brain.

Results

Lightening up of anesthesia increases frequency and complexity of slow waves

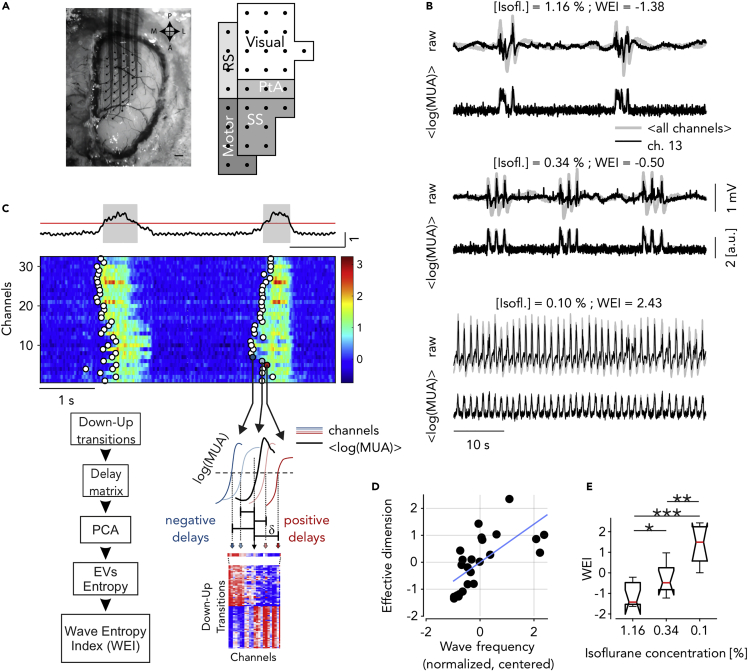
To understand the local and global changes underpinning the progressive transition of the cortical network in the arousal process from deep anesthesia, we recorded the ongoing neuronal activity across three levels of anesthesia (isoflurane) in the intact mouse brain. We placed a multielectrode array (MEA) of 32 channels on the cortical surface of $n=8$ wild-type mice (Figure 1A, left; see STAR Methods). The probed surface spanned several cortical areas including both sensory and motor cortices of a single hemisphere (Figure 1A, right). Anesthesia levels were finely tuned to induce slow wave activity, that is, the quasiperiodic alternation between slowly propagating onsets of high-firing up states and almost-quiescent down periods across the probed surface (Figure 1B). Spontaneously occurring spatiotemporal patterns were well visible in the multiunit activity (MUA) signals, although electrophysiological recordings were epicortical and not intraparenchymal (Figure 1B and 1C-top). This allowed us to characterize the changes in the onsets and offsets of the Up states with the lightening up of the anesthesia levels at multiple spatial and temporal scales. The timing of Down-Up transitions for every channel led to a time lag matrix (TLM) (Capone et al., 2019; Ruiz-Mejias et al., 2011), where each row corresponds to a wavefront containing the relative delays in the channels activation (Figure 1C-bottom, Materials and Methods). Computing the principal components (Jolliffe and Cadima, 2016) of the TLM and transforming the eigenvalue distribution of the covariance matrix into probabilities, we estimated the number of the effective dimensions (i.e., the principal components) of the space embedding the activation wavefronts. The number of effective dimensions strongly correlates with the frequency of the slow waves across experiments and anesthesia levels (Figure 1D, $n=24$). Interestingly, the projection of each of these points onto the first principal component of the distribution (blue line in Figure 1D) is not only coherent with the corresponding isoflurane level (Figure 1E), but it also allows us to finely classify the experiments according to their effective level of slow wave anesthesia. We called the projected value on this axis the “wave entropy index” (WEI), and used it to visualize the progression of other relevant quantities across the different anesthesia levels.

Figure 1.

Extraction of the wave entropy index (WEI) from dimensionality and frequency during slow waves

(A) Superficial 32-channel multielectrode array placed on the cortical surface of anesthetized mice (left) and schematic representation of the recorded cortical areas (right, as in (Dasilva et al., 2021)).

(B) Representative raw recordings and log(MUA) for one experiment in three anesthesia levels. Gray: average of all channels; black: representative channel.

(C) Top: representative average log(MUA) (black), threshold used to extract the Up states (red) and identified Up and Down states (gray and white periods, respectively). Middle: single-channel log(MUA) of activation fronts (Down-Up transitions) from example slow waves (circles). Bottom right: time lags δ of each state transition from the center of a wave comprise the rows of the blue-red time lag matrix (TLM, bottom). Bottom left: flow chart of the method used to work out the wave entropy index (WEI) based on measure of the effective dimension of the TLM and the frequency of Down-Up waves occurrence. EV: eigenvalues.

(D) Effective dimension (see STAR Methods) and mean frequency of the Down-Up transitions (normalized by their variances and centered around their means) for each recording ($n=24$, eight mice, and three anesthesia levels each). Blue line: first principal component, onto which the single recordings are projected thus defining the wave entropy index (WEI).

(E) WEI values versus anesthesia concentration (stars indicate significance for Wilcoxon test, P<0.05, <0.01, <0.001, respectively).

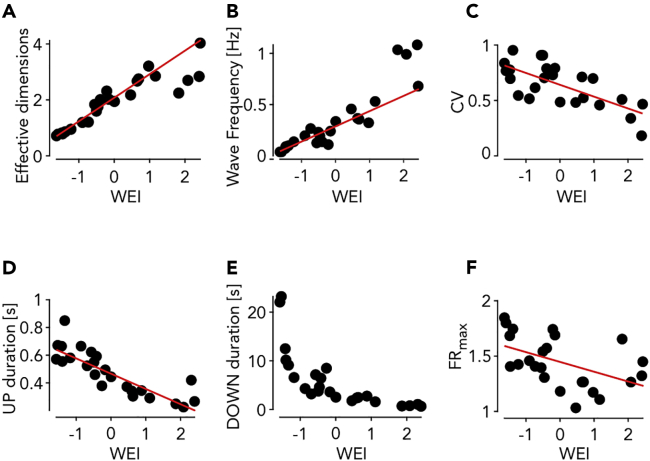
As expected, both the number of effective dimensions and the frequency of Down-Up transitions fit well with the WEI (Figures 2A and 2B). Furthermore, both the coefficient of variation of the Up-Down cycles (CV) and the duration of the Up states have a significant linear correlation with the WEI (Figures 2C and 2D). The increase in SWA frequency is mainly because of the modulation of the Down state duration, which shows the largest exponential-like reduction with the WEI (Figure 2E). The maximal firing rate of the cortical assemblies, measured as the peak amplitude of the Up states, shows a significant decrease as a function of the WEI (Figure 2F).

Figure 2.

Statistical properties of the slow wave activity (SWA) as a function of the WEI

(A–F) Number of effective dimensions (A), wave frequency (Down-Up transitions) (B), coefficient of variation of Down-Up cycles (C), mean Up (D), Down (E) state durations and maximal firing rate during the Ups versus the WEI (F). Red lines: linear regression (P < 10^˗9, P < 10^˗9, P < 0.001, P < 10^˗6, P < 0.05 for panels (A–D and F), respectively).

These results highlight the acceleration and regularization in time of the slow rhythm associated with the SWA with the lightening up of the anesthesia, similarly to what has been observed at the single-column level in cortex under ketamine-medetomidine anesthesia in rats (Tort-Colet et al., 2021). The fading of the anesthesia is accompanied by a rise of a form of complexity of the spontaneously occurring wavefronts, here defined as the number of dimensions necessary to embed them.

Modes of propagation increase in number and speed as anesthesia fades out

Regularity in time and increase in wavefront complexity could appear as contradicting features of the slow waves. Therefore, we took a closer look at the changes occurring to the spatiotemporal patterns of neuronal activity across anesthesia levels. We did this by making use of the simultaneous acquisition of the MUA of local cortical assemblies, and by projecting their relative time of Down-Up transition into a single, common multidimensional space.

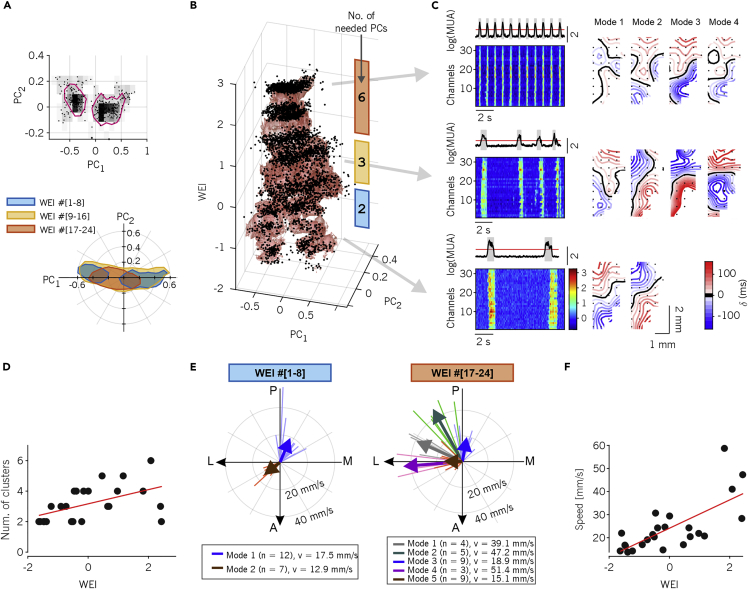
Specifically, we projected the individual Down-Up wavefronts onto the space of the principal components extracted after concatenating all TLMs (Dasilva et al., 2021), and pooling the set of recordings (n = 24) in three equally populated groups, based on their WEI (Figure 3A). For the group with smallest WEI (WEI ranking 1 to 8, corresponding to WEI values in the range [-1.63, -0.73] and associated with the deepest anesthesia level), we found a bimodal distribution of propagation modes in the (PC₁, PC₂) plane, highlighting the existence of two preferred spatiotemporal patterns. In the second group, having a higher WEI (ranking 9–16, corresponding to WEI in the range [-0.55, 0.46]), the distribution of waves slightly moves and increases in size, whereas in the last group of recordings (WEI ranking 17–24, in the range [0.65, 2.43]) the distribution became smaller and unimodal further approaching the origin of the (PC₁, PC₂) plane. By visualizing the points in a three dimensional representation that included the WEI, such changes become even more apparent, as a clear progression can be observed from two “legs” (small WEI, two modes), through a fat “belly” (intermediate WEI) to a small “head” (high WEI, Figure 3B).

Figure 3.

Speed and wave diversity increases as anesthesia fades out

(A) Top: representative distribution of time lags (i.e., rows of the TLM) in the space of the first two principal components (PC₁, PC₂). All transitions from experiments with WEI ranking one to eight are shown. Magenta contours represent 66% isodensity levels of the distribution. Bottom: 65% isodensity contours for the activation waves from experiments and anesthesia levels pooled in three equally-sized groups according to the WEI ranking.

(B) Activation waves (dots) for all experiments projected on the first 2 PCs versus WEI. Red shading: smoothed 65% isodensity surface. The colored bars on the right show the WEI ranges that define the three groups used in panel (A). The number written on each bar shows the number of PCs needed to obtain a value of Pearson correlation $\ge 0.8$ between the TLM reconstructed with this very number of PCs only and the original, full TLM.

(C) Average and single-channel MUA for three experiments and anesthesia levels representative of the WEI groups in (A) and (B). Right: resulting average spatiotemporal propagating patterns of activation waves clustered in different “modes of propagation” (see also supplemental movies S1 and S2).

(D) Number of propagation modes per experiment and anesthesia level. Red line: linear regression (P < 0.05).

(E) Direction and velocity of the modes of propagation from the experiment’s eight lowest and highest values of WEI. Modes are colored according to the results of k-means clustering. Clusters with less than three patterns are not shown (number of excluded modes = 1, number of excluded patterns = 2). Thick arrows: average directions and velocities of each mode.

(F) Mean propagation velocity for each experiment and anesthesia level. Red line: linear regression (P < 10^˗4).

Although the contraction of the distributions at higher WEIs might suggest that the waves are more similar to each other, this is not the case as is apparent from the representative experiment shown in Figure 3C, where for the three recordings at different anesthesia levels, similar patterns of propagation are grouped together resorting to automatic clustering (see STAR Methods). Indeed, the number of propagation modes, that is, the clusters of activation wavefronts (Figure 3C-right), increases with the WEI together with the frequency of the slow waves (see MUA rasters, Figure 3C-left): a correlation also confirmed at the population level (Figure 3D, R² = 0.26, P = 0.01). This apparent contradiction between wave distribution and number of clusters is explained by the fact that at high WEI the effective dimension is greater than two and the plane (PC₁, PC₂) is no more adequate to represent the variability of the activation wavefronts. Indeed, by computing for each experiment the number of PCs necessary to reconstruct with a similar level of approximation the original (raw) TLM we obtained a monotonically increasing (with the WEI) number (Figure 3B).

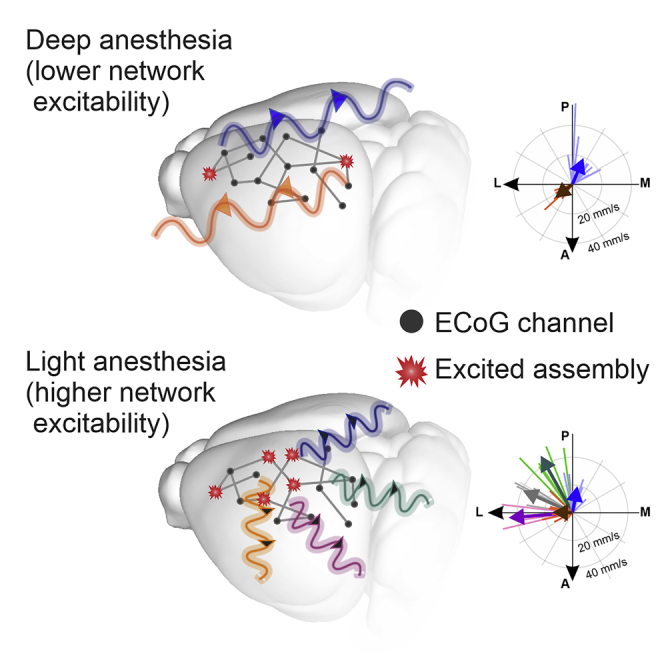
We also found a similar WEI-dependent segregation and coalescence of the directions of singled-out propagation modes. By computing the average wavefront for each cluster of waves (i.e., propagation mode) and plotting the resulting average vector speeds (Figure 3E), a prevalence of anterior-to-posterior and posterior-to-antero/lateral propagation was apparent for deep anesthesia levels (small WEI, Figure 3E-left), as previously reported in (Greenberg et al., 2018). For lighter anesthesia levels, several medial to lateral modes appeared (Figure 3E-right), with rare slow waves with caudal or lateral origin. Importantly, slow waves displayed a mode-independent increase of the speed with the WEI (Figure 3F, R² = 0.51, P < 10^˗4). Faster waves implies that relative delays in the TLM become progressively smaller, which in turn leads to relatively small PC₁ and PC₂, partly explaining why in Figure 3B the wave distributions shrink close to the plane origin.

These results show that the rise of wavefront complexity occurring as the anesthesia fades out is because of a widening of the repertoire of the propagation modes of the SWA. Intriguingly, at low isoflurane levels such diversity is constrained to have slow waves with anteromedial origin, similar to that is found in humans under slow wave (NREM) sleep (Massimini et al., 2004; Nir et al., 2011). In the time domain, a kind of temporal compression takes place making the slow waves more frequent and faster with the lightening up of the anesthesia.

Wavefronts are shaped by previous waves differently across anesthesia levels

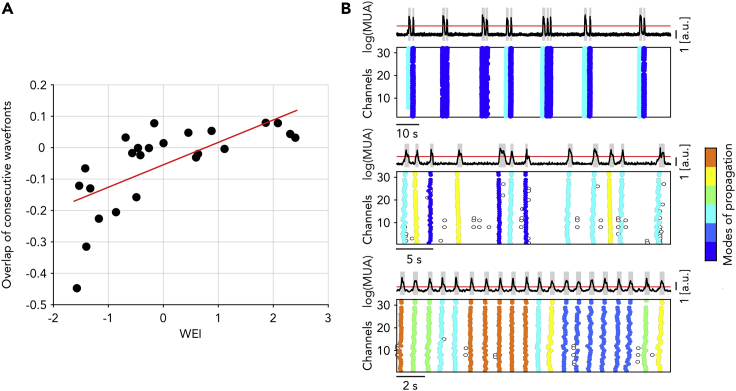
We have shown that slow waves are faster and occur closer in time during the lightening of anesthesia. Under this condition, the transit of slow waves across the cortical surface may leave a trace on the ongoing neuronal activity. This in turn could modulate the degree of wavefront complexity, thus linking together the spatial and temporal domain. To investigate such a possibility, we quantified the overlap of consecutive propagation modes for the different anesthesia levels.

We measured the overlap by calculating the similarity of subsequent activation waves as the detrended correlation between the associated time lag arrays (TLM, see STAR Methods for details). Surprisingly, for deep anesthesia levels we found a strong negative correlation of the wavefronts similarity (Figure 4A). For decreasing levels of anesthesia, the influence from the shape of previous waves firstly vanished, eventually increasing to positive overlap values giving rise to a significant correlation with the WEI. A negative correlation can be explained by a nonrandom alternation between the two modes of propagation spontaneously expressed under deep anesthesia (Figure 4B-top). In contrast, for lighter anesthesia a propagation mode was more frequently followed by a similar one, thus leading to positive values of the overlap (Figure 4B-bottom).

Figure 4.

Propagation modes alternate as anesthesia level gets deeper

(A) Autocorrelation (i.e., overlap) of the time lags associated with consecutive activation waves for experiment and anesthesia levels with increasing WEI. Red line: linear regression (P < 0.001).

(B) Average log(MUA) and single-channel Down-Up transitions for three representative experiments, showing (from top to bottom) negative, null, and positive consecutive overlap. Colors represent different modes of propagations as in Figure 3.

These results suggest that past events impact differently the onset of the current activation wave depending on the state the global network is in. The persistence and the alternation of propagation modes under light and deep anesthesia, respectively, are likely because of different mechanisms at the network and single-neuron levels. Interestingly, the former and the latter are associated with a more regular and irregular SWA rhythm, respectively, as recently pointed out in cortical slices (Capone et al., 2019).

Leading and following assemblies differentially contribute to the rise in complexity

Having observed that the lightening of anesthesia leads to the emergence of a greater variability of the paths followed by the slow waves, we wanted to investigate whether this might be because of changes in the exogenous drive from other cortical and/or subcortical areas. Indeed, it has been previously shown that the transition to wakefulness is accompanied by a progressive restoration of the functional integration between cortical and subcortical areas (Alkire et al., 2008; Bettinardi et al., 2015; Hudetz, 2012). If this was the case, the local cell assemblies probed by the MEA would display activation and silencing MUA profiles independent from the singled-out propagation modes.

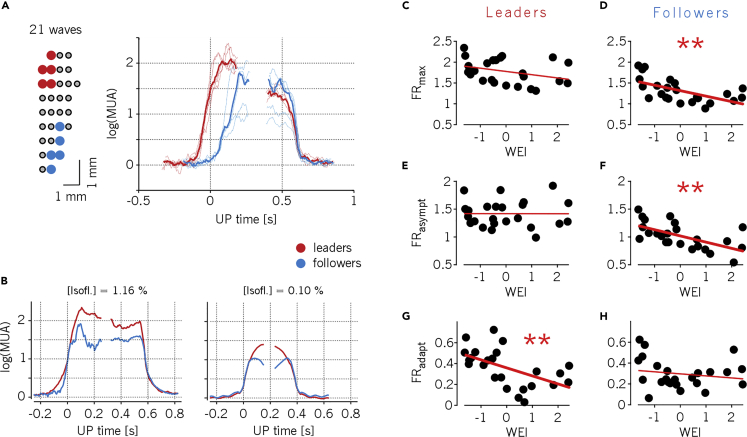
To test this hypothesis, we characterized the Down-Up and Up-Down activity transitions of both the channels initiating and the very last channels being recruited by a traveling wave (referred to as leading and following channels, respectively). We observed that although there was a consistent temporal delay between leading and following channels at the Down-Up transition (activation wavefront), all channels ended the Up state simultaneously (Figure 5A) (Sheroziya and Timofeev, 2014; Volgushev et al., 2006). In agreement with our previous results, the average amount of time the neuronal populations fired action potentials increased with the lightening of the anesthesia (because of more frequent Up states), revealing an increasing excitability of the network (Dasilva et al., 2021). However, the maximum MUA amplitude of the Up states decreased with the lightening of the anesthesia (Figure 5B, see also Figure 2F). Furthermore, leading channels systematically displayed a maximum MUA significantly larger than followers (Figures 5C and 5D, Wilcoxon rank-sum test, P < 10^˗4). Note that leaders and followers change from wave to wave, thus proving that the probed network contribute actively to shape the modes of propagation of the slow waves.

Figure 5.

Neuronal assemblies leading wave propagations are the most excitable

(A) Left: mapping of the five channels leading (red) and following (blue) a representative mode of propagation (in this case going posterior-anterior, and containing 21 activation waves). Right: average log(MUA) of the leading and following channels in their Down-Up and Up-Down transitions (thin lines), and their grand-averages (thick lines). The average time of Down-Up transitions in a wave is considered as time origin.

(B) Representative average log(MUA) during Down-Up and Up-Down transitions of leading and following channels for two anesthesia levels in the same animal. Differently from panel (A), time origin refers to state transitions for each group of channels. WEI values are −1.63 and 0.46 for deep and light anesthesia levels, respectively.

(C–F) Maximum (C, D) and asymptotic (E, F) firing rate (FR_max and FR_asympt, respectively) during Up states for leading and following channels across all experiments and anesthesia levels (n = 24). (stars in panels D,F: P < 0.01.)

(G and H) Firing rate adaptation measured as the difference FR_asympt - FR_max from panels (C–F) for leading (G) and following (H) channels. (P < 0.01 for panel G.)

Surprisingly, it turned out that the firing rate of leading channels stays constant at all anesthesia levels (Figures 5C and 5E, P = 0.11 and P = 0.99, respectively), despite the fact the Down periods progressively shrink, hence reducing the recovery time of the spiking resources responsible for the spike-frequency adaptation, that is, determining in turn a net increase of the mean adaptation-related hyperpolarizing potassium currents. In contrast, following channels featured a strong decrease of both the maximal and the asymptotic firing rate with the WEI (Figures 5D and 5F, R² = 0.35 and 0.37, respectively, and P < 0.01). Consistent with these observations, the adaptation leading to a reduction of the firing rate from its maximum to its asymptotic value is stronger for leading than for following channels (Figures 5G and 5H, R² = 0.30 and 0.03, P < 0.01 and P = 0.4, respectively).

These results suggest that as anesthesia fades out, the excitability of local cortical assemblies is diversely affected depending on the role they have in contributing to the activation wavefronts. In this way, SWA exploits the maximally available resources in terms of state-dependent excitability to find its preferential pathways of propagation.

Changes in local excitability explain the increase in SWA complexity

To further investigate the question whether the spatiotemporal patterns observed during SWA are initiated by inputs from other (possibly subcortical) brain structures and shed light on the mechanisms underlying the initiation of the slow waves in our system, we modulated the excitability in a relatively simple network model capable of retaining the relevant characteristics of the studied cortical structures. Indeed, if the observed excitability modulation of local cell assemblies was not responsible for initiating the increasingly variable propagating patterns as anesthesia is lightened, we predict that the network would need additional external input to produce these patterns, and not a mere change in local excitability.

The in silico network aimed to model a wide region of the cortical surface as a $13\times 13$ grid of local cell assemblies composed of 500 excitatory and 125 inhibitory randomly connected integrate-and-fire neurons (see STAR Methods). Each of these cell assemblies modeled the cortical columns contributing to the MUA we assumed to have been recorded by a single channel of the MEA (Figure 6A-top). We analyzed the spatiotemporal distribution of the firing activity of a $5\times 5$ subset of the grid representing the cortical area probed by a schematized MEA (Bazhenov et al., 2008). We varied the working point of the model network by changing two key parameters of the local assemblies modeling the anesthesia fading out (Destexhe, 2009; Tort-Colet et al., 2021): i) the intensity of the excitatory synaptic current received from external (non-modeled) brain regions, and modulated by changing the firing rate ${\nu }_{ext}$ of Poisson-like upstream neurons; and ii) the strength $g_a$ of the spike-frequency adaptation because of after-hyperpolarizing potassium currents (Figure 6A-middle, Materials and Methods).

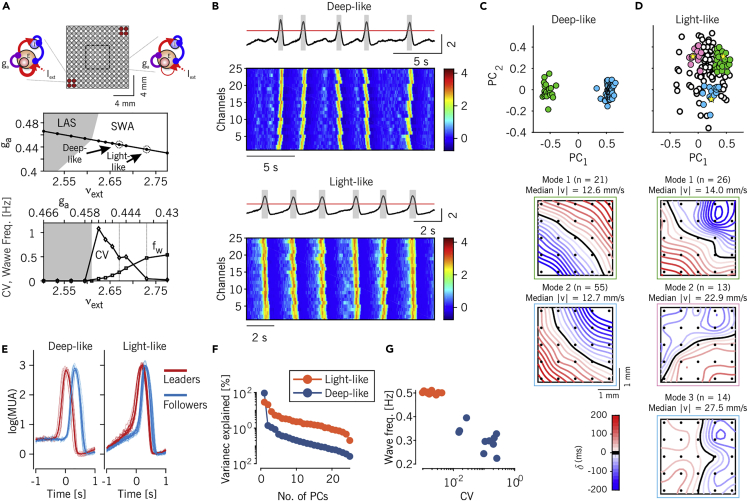
Figure 6.

Increased excitability in model explains observed changes as anesthesia lightens

(A) Top: schematic representation of the simulated network, consisting of 13 × 13 local cell assemblies. Cell assemblies are composed of excitatory and inhibitory integrate-and-fire neurons and are sketched on the left those with increased excitability (stronger synaptic self-excitation, red circles) and on the right the ones with reference excitability in the rest of the grid. The internal square shows the portion of the network used for the analysis. Middle: bifurcation diagram showing the different activity regimes displayed by spiking neuron network simulations as the level g_a of the firing rate adaptation and the rate v_ext of incoming excitatory spikes from other (external) areas are changed. To model anesthesia fading, these parameters are changed according to the depicted black line connecting the low-firing asynchronous (LAS) and the slow wave state. The arrows point to the parameter combinations used in the rest of the figure. Bottom: coefficient of variation of Up-Down cycles (circles) and frequency of waves (f_w, squares) measured in simulations along the above black trajectory.

(B) Representative average and single-channel log(MUA) in the simulated network for low wave frequency/high CV (top, “deep-like”), and high frequency/low CV (bottom, “light-like”) modeling deep and light levels of anesthesia, respectively.

(C and D) Distributions of time lag arrays of spontaneously occurring activation waves in the model network in the plane (PC₁, PC₂) as in Figures 3A and 3B for in vivo recordings. Model networks in both the deep-like and the light-like conditions are shown (panel C and D, respectively). Colored dots highlight the wavefronts belonging to the modes of propagations singled out in bottom panels, relying on k-means clustering as in Figure 3C. For the “light-like” case (panel D) three representative groups of wavefronts were selected; these included the points centered at the yellow stars (see STAR Methods for details).

(E) Average log(MUA) of the five leading (red) and five following (blue) channels (thin) and averages (thick) around the Down-Up transitions for all modes shown in panel C, for the “deep-like” (left) and “light-like” (right) conditions.

(F) Percentage of explained variance as a function of the number of PCs for the TLMs extracted from the simulated data.

(G) Frequency of the activation waves versus the CV of the Up-Down cycles for the simulated data obtained from 10 equally-sized nonoverlapping intervals of time.

In the plane $\left({\nu }_{ext},g_a\right)$ the network followed a linear trajectory moving its working point from the low-firing asynchronous (LAS) region reminiscent of a “burst suppression” global state, to the SWA regime. In this way, the lightening of the anesthesia is modeled as a simultaneous reduction of the strength of the activity-dependent adaptation $g_a$ and an increase of the external excitation ${\nu }_{ext}$, which in turn can be proven to be equivalent to causing an unbalance between synaptic excitation and inhibition (Levenstein et al., 2019). This increase of local excitability in the SWA regime led to a rise of the wave frequency $f_W$ occurring more regularly in time, thus lowering the coefficient of variation CV of Up-Down slow oscillations (Figure 6A-bottom) (Sancristóbal et al., 2016). We selected two points (referred to as deep-like and light-like) on this trajectory, where the resulting CV and $f_W$ matched the experimental values (arrows on panel 6A, middle). The firing rates of the cell assemblies converted in $\log \left(MUA\right)$ (see STAR Methods for details) showed spatiotemporal patterns closely resembling the experimental data (Figure 6B). The internal variability of the patterns (i.e., the wavefront complexity) was lower under the “deep-like” condition with high CV and low $f_W$, as demonstrated by the presence of two narrow clusters in the wave projections onto the $({\text{PC}}_1,{\text{PC}}_2)$ plane (Figure 6C). These two propagation modes (Figure 6C-bottom) originated by the more excitable opposite corners of the $13\times 13$ grid, as this was the only structural element of heterogeneity implemented in the cortical field model.

In contrast, in the low CV/high $f_W$ (“light-like”) case, wavefront complexity was higher, as demonstrated by the wider distribution of waves in the $({\text{PC}}_1,{\text{PC}}_2)$ plane (Figure 6D). In this state, activation wavefronts had a rather homogeneous distribution of propagation directions (Figure 6D-bottom), highlighting the possibility to have the onset of a wave from any point of the grid. The average MUA size of the Up states was comparable for the deep-like and the light-like conditions (Figure 6E). Importantly, both the decay of variance explained by the principal components (related to the effective dimensions of the wavefront space), and the dynamics in the CV-frequency plane were good markers to differentiate the two dynamical regimes (Figures 6F and 6G, respectively).

These results show that the modeled cortical field was capable of reproducing the large majority of the changes observed in the SWA as anesthesia fades out. This was obtained by simply modulating the local excitability of the cell assemblies composing the network. No changes in the cortico-cortical connectivity seem to be requested. Instead, some structural heterogeneity of the local excitability needs to be incorporated as it plays a role under relatively deep levels of anesthesia. Indeed, our model highlights the necessity to have a structural modulation along the rostro-caudal and mediolateral axis (the axis connecting the two excitable corner of 13 × 13 grid) in order to obtain two preferred modes of wave propagation. Intriguingly, this is not enough to reproduce the anticorrelation of consecutive wavefronts observed in Figure 4A at negative WEIs (overlap values: 0.16 and 0.72 for light-like and deep-like, respectively). An additional component would have to be included that takes into account active interactions with other subcortical brain structures (Adamantidis et al., 2019).

Anesthesia fading out induces increasing fluctuations of SWA features

Our simulations confirmed the presence of a multiplicity of patterns when the excitability is bigger, that is, in the state corresponding to light anesthesia. Together with the associated positive values of the overlap of consecutive wavefronts (Figure 4) this could underlie fluctuations in time of the complexity of the associated dynamical state. Think of sampling a short time segment from a pot of many possible spatiotemporal patterns with some memory and then repeating the procedure for the length of the recording. This process could result in either picking only a subset of patterns (with little variability) or picking many different ones. In the first case, the embedding space (and thus, the WEI) would be small, whereas in the second case it would be high. Repeating the procedure, we would therefore expect a high variability of the WEI in time.

To investigate whether our data are in such a dynamical condition, we analyzed the WEI values at a finer-grained temporal scale along the whole time of the recordings. This was done by computing the effective dimension and the frequency of the slow waves in sliding windows containing a fixed number of waves (Figure 7A). Only a few recordings (3 out of 24) showed a marked non-stationarity, highlighted by the isolated trajectories in the frequency-effective dimension plane starting in one point but ending up somewhere else on the plane (see also an example of trace in Figure 7A, inset). When analyzing the WEI values resolved in time for the rest of the recordings, these were segregated in two groups, pretty much separating those with the WEI<1 from those with the WEI>1 (Figure 7B). This effect was quantified by fitting the WEI distribution for the first 200 s versus the last 200 s of the acquisition time with a mixture of up to four Gaussian distributions (Figure 7C, see STAR Methods for details). In addition, the recordings having average WEI above $1$ tended to further increase their WEI at later times (Figure 7B). Critically, the size of the fluctuations around the fitted trend of the WEIs significantly increased with the WEI itself (Figure 7D R² = 0.49, P = 0.001). Importantly, when computing the WEI value resolved in time for our network simulations, these are nicely fitted in the high-value and low-value groups (Figure 7B, green traces). Furthermore, the fluctuations of the simulated data also showed a clear increase for the “light-like” case (Figure 7D, green crosses).

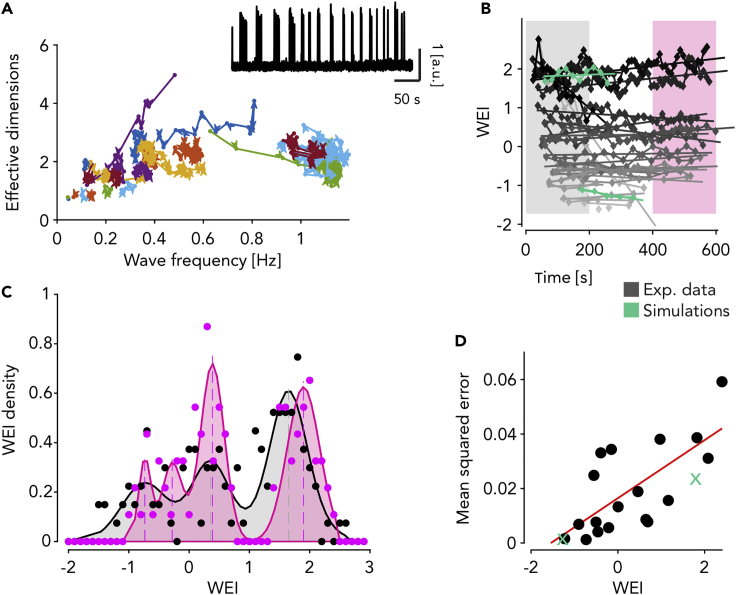
Figure 7.

WEI drifts in time toward two preferred values at fixed anesthesia levels

(A) Time-resolved relationship between effective dimension of activation waves and their frequency of occurrence for all experiments and anesthesia levels (n = 24) each identified by a different color. Points of the trajectories are computed from time windows including 30 consecutives activation waves. Adjacent time windows have 10 waves of overlap. Inset: example experiment with log(MUA) displaying nonstationary frequency of wave occurrence.

(B) Time-resolved WEI computed in the same time window as in (A). Time values are the centers of the time windows. Lines are linear fits for each experiment and anesthesia level. Colored intervals highlight the first and the last 200 s of the experiments. Gray levels represent the average WEI value. Green: simulations.

(C) Distribution of WEI values for the first and the last 200 s of the experiments (highlighted in panel B). Colored shading, fit of the distribution with up to four Gaussian probability densities.

(D) Mean squared error of the linear fits shown in (B) as a function of the mean WEI per experiment and anesthesia levels (n = 24). Red line: linear regression (P<0.05). Green: simulations.

In summary, the lightening of the anesthesia leads to larger fluctuations of the WEI in time, compatible with the hypothesis that the increased complexity of the slow waves is because of spatiotemporal patterns of activation (i.e., states) that are more prone to wander across their state space, as perfectly predicted by network simulations. Intriguingly, such a dynamical condition appears to be strengthened in the recordings having values of the WEI above $1$.

Discussion

The unconscious state experienced in NREM sleep and anesthesia is characterized by slow waves of brain activity spanning a continuum of dynamical features, for example, frequency of occurrence and distribution of their propagation speed and directions (Dasilva et al., 2021). In the present work we investigated how these dynamics emerge in a network of cortical cell assemblies as the level of isoflurane anesthesia reduces. Anesthesia was induced by ketamine and medetomidine, and maintained by the inhalation of isoflurane in 100% oxygen. Therefore, we relate our results to changes in isoflurane concentrations. Besides a progressive increase of the “spatial” richness of the spontaneously expressed propagation modes, we found an unexpected change of their sequential memory: while at deep anesthesia, consecutive waves consistently inverted their direction of propagation (front to back vs back to front); however, at light anesthesia, consecutive waves were on average more similar to each other. The rise of spatial complexity with lighter anesthesia levels, measured here as an increase of the effective dimension of the space embedding the activation wavefronts, could seem to be in contradiction with the observed temporal “simplicity” associated with the fact that consecutive waves tend to be more similar to each other. In a previous study we argued that a repetition of similar-shaped waves can be because of adaptation effects (Capone et al., 2019). Indeed, the propagation of more frequent slow waves leads to a more fatigued cortical tissue. Here, excitability is more readily recovered in locations where the last wave initiated, such that the next activation will likely start from the same place as the previous one. In this way, the increased overlap of consecutive wavefronts reported here corresponds to the longer time scales needed to “forget” previous events (Zilio et al., 2021). Having longer time scales does not mean that the space embedding the activation wavefronts cannot be fully explored. It rather means that more time is needed to express the available dynamical richness, represented by waves of different origin and trajectory of propagation. Note that longer time scales imply stronger correlations between spatiotemporal patterns, which is a typical fingerprint of the critical dynamics arising when the transition from the synchronized to the desynchronized global state is approached (di Santo et al., 2018): a possible other side of the “complexity” coin. Interestingly, recent literature backs up our observations about a rise of complexity of the awake vs. anesthetized state (Pal et al., 2020).

Our network simulations of cell assemblies in a large cortical field closely reproduced the large majority of our experimental observations. The fact that this was obtained without modifying the underlying “structure”, that is, the connections between the elements of the network, highlights the local excitability —modulated by activity-dependent adaptation— as a key element to explain the functional changes observed during the arousal from deep anesthesia. Interestingly, these conclusions fit nicely with experimental works demonstrating the ability of restricted cortical regions to produce a switch of global brain state (Li et al., 2009; Pal et al., 2018). In this regard, the channels leading (in time) the onset of Up states were those with the highest firing rates (Figure 5C), similarly to what we found in cortical slices where the leaders of the activation wavefront lie in layer 5, and have longer Up states (Capone et al., 2019). Excitability of leading channels is expected to be because of activity reverberation in the high-firing state which can persist in time like in bistable units (Jercog et al., 2017; Levenstein et al., 2019; Mattia and Sanchez-Vives, 2012). Even if traveling waves do not originate from the cortical location probed by the multielectrode array and hosting the wave-dependent leading channels, they likely find a preferential pathway through the most excitable cell assemblies.

The changes in local excitability predicted by the model match the evidence collected in our experiment, provided that the MUA measured from each contact of our epidural micro-electrocorticogram (ECoG) faithfully represents the spiking activity of a nearby, spatially limited (thus, local) cell assembly. Clearly, superficial recordings from an ECoG might acquire signals from a bigger cortical volume than an electrode deep in a cortical layer. If this was the case, one would expect that the contributions from local as well as more distant sources of spikes would determine, for example, a degree of smoothing in the (locally) highly synchronized SWA Down-Up transitions. However, we found Down-Up transitions having similar profiles as the ones measured with intracortical recording in similar experiments (Ruiz-Mejias et al., 2011; Mattia et al., 2021), thus backing up our assumption of “locality”. Experiments of simultaneous epidural and intracortical recordings would be needed to exactly quantify the locality and the layer(s) contributing to the ECoG.

Switch of global brain state associated with anesthesia

The changes in the memory/correlation about the preceding slow waves can also explain the increase in variability of the WEI as the anesthesia fades out. Indeed, under light anesthesia the small bunches of consecutive slow waves considered to produce single points of Figure 7 are often composed of similar wavefronts (thus yielding positive overlap values) residing in a limited region of the whole embedding space, which in turn is rich and wide. The size of this region varies from bunch to bunch, resulting in a highly variable WEI in time (Figure 7B). Differently, under deep anesthesia the slow waves are concentrated in two focused clusters and consecutive wavefronts are anticorrelated: the dynamics jump back and forth from one cluster to the other. In this condition each bunch of waves is sufficient to probe the whole embedding space, leading to small changes in the WEI.

Our finding of divergent trajectories above and below the WEI $\approx 1$ shown in Figure 7 corroborates the hypothesis of a repulsive barrier between anesthesia and wakefulness, highlighting a possible destabilization of the (attractive) unresponsive state as the anesthesia level lowers below a threshold dose. This would be compatible with the hypothesis that unconscious (sleep) and conscious (wake) states are two distinct conditions coexisting as attractors of a global brain dynamics (Adamantidis et al., 2019; Saper et al., 2010). Similar to a flip-flop ‘switch’, intermediate states tend to be avoided as the global attractors are separated by a repulsive barrier. A similar bistability has been invoked to explain the hysteresis loop observed in the switch from anesthesia to wakefulness and vice versa (Friedman et al., 2010; Hudson et al., 2014; McKay et al., 2006; Proekt and Kelz, 2018). Of course, further and more focused experiments are required to confirm such a theoretical framework.

Our model predicts that local excitability of cortical assemblies is one of the main players in modulating the global spontaneous activity as anesthesia fades out. The hysteresis loop mentioned above is expected to be related to the nonlinear dynamics associated with the proposed local excitability, as it can support the coexistence of two local states, as recently demonstrated by (Tort-Colet et al., 2021). In this framework the switch of activity regime in local cell assemblies can elicit a chain reaction affecting the global network and thus eliciting a global state transition, as reported in (Li et al., 2009) following stimulations of very single neurons.

Role of subcortical regions in the presence of anticorrelated slow waves

Another intriguing aspect of our work is again related to the significant negative correlation between consecutive wavefronts found under deep anesthesia. Although SWA features like mean frequency and Up (Down) durations measured in these conditions are quantitatively similar to those we observed in isolated cortical slices (Sanchez-Vives and McCormick, 2000; Sanchez-Vives et al., 2010), we had never found an anticorrelation of consecutive slow waves in vitro (Capone et al., 2019). Furthermore, our network model was unable to reproduce such negative memory effects in deep-like dynamical conditions, although a suited degree of heterogeneity in the cell assembly organization was incorporated to have two clusters of propagation modes (see Figure 6). Thus, a question arises: where does this anticorrelation come from?

The presence of isolated Up states (bursts) of cortical activity under deep anesthesia can in principle provide suprathreshold input to other subcortical areas. More specifically, the back-to-front waves ending in the frontal cortex could for example elicit a reaction, say, in the hippocampal network. If this activity persisted long enough (i.e., beyond the refractory period, after which the full excitability is recovered) and fed back to the cortex, this would ignite a new wave propagating backward. Evidence of such cortico-hippocampal interaction has been described in rodents with simultaneous recordings in the hippocampus (CA1) and in parietal (Hahn et al., 2007), temporal (entorhinal) (Hahn et al., 2012), visual (Ji and Wilson, 2007), and in the whole (Busche et al., 2015) cortex. In a similar way, other subcortical structures, like first-order thalamus, could be involved when fronto-caudal propagation modes occur (Sheroziya and Timofeev, 2014; Steriade et al., 1993a), giving rise to a rebound activity, which is then back-projected onto cortical neurons (Steriade et al., 1993c).

We remark that, although our model has the intrinsic limitation of being a heterogeneous cortical network that does not include the thalamus or the hippocampus, pursing a kind of Occam's razor argument, this approach allowed us to make a prediction of a possible multiscale scenario. If such a scenario was confirmed, negative correlations between consecutive slow waves under burst suppression would be the result of a state-dependent communication between cortical and subcortical structures. A multiscale system like that could in principle be replicated in a more detailed model. We would then expect to find a recognizable fingerprint: activity bursts would occur often as duplets interspersed by relatively long Down (suppression) periods (as in the example recording shown in Figure 1B-top).

Relationship between slow waves and EEG microstates

As cortical Down-Up transitions during slow wave activity are known to induce thalamic-generated spindle oscillations (7—16 Hz) (Andrillon et al., 2011; Mak-Mccully et al., 2017; Muller et al., 2016), in view of our current results, a possible relationship may be seen between spatiotemporal phase patterns of these two rhythms. Indeed, in ECoG recordings during quiet wakefulness in humans and macaques, alpha oscillations (7—13 Hz) display a preferential direction of propagation from anterosuperior to posteroinferior cortex (Halgren et al., 2019). This distribution of directions widely overlaps with the ones we found for slow waves under relatively high WEI, that is, under light isoflurane levels, compatible with the evidence that quiet wakefulness is a kind of nonstationary wandering between first sleep stages and wakefulness (Reimer et al., 2014; Vyazovskiy et al., 2011).

A second analogy comes from the field of EEG electrophysiology, where alpha oscillations are associated with the so-called EEG microstates, that is, spatial snapshots of the field potential phases captured at the peaks of these waves, eventually clustered in a small number of stereotyped spatiotemporal patterns (Brodbeck et al., 2012; Lehmann et al., 1987; von Wegner et al., 2017). Here, the spontaneous brain activity (i.e., sleep and quiet wakefulness) is hypothesized to be a continuous transition between such EEG microstates (Brodbeck et al., 2012; Lehmann et al., 1987). Intriguingly, EEG microstates display some degree of memory about past events, analogously to what we report here for cortical slow waves. Furthermore, EEG microstates are non-Markovian (von Wegner et al., 2017), with each microstate likely persistently reoccurring for about half a second: a timescale remarkably reminiscent of the Up state duration measured during SWA. In addition, this timescale is not independent from the brain state: EEG microstates persist for a longer time in deep sleep (stage N3) compared to wakefulness and N1 stage (Brodbeck et al., 2012). This in turn is reminiscent of the elongation of the Up state duration we found as the WEI decreases from light to deep slow wave anesthesia.

In summary, we propose that slow waves can be seen as “mesostates”, probably embedding coherent spindle-related EEG microstates, which coarse-grain the richness of propagation modes we observed in invasive recordings. Such a picture is confirmed by recent findings showing that parietal and cortical networks under anesthesia are not confined to a static dynamical state but rather wander across a complex landscape expressing a relatively wide range of spectral features (Li et al., 2019). According to this, the fine-grained resolution characterizing the slow waves we report here allows us to generalize the idea that the rise of complexity associated with the transition from the unconscious to the conscious brain state is because of a continuous widening and reshaping of the landscape of such mesostates, which by the way can be fully described by a parametric modulation of the local excitability of cortical assemblies.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Ketamine	Pfizer	PC: 08470007762119; SN: 555864387401
Medetomidine	Ecufar	CN: 570686.3; GTIN: 06432100017529
Isofluorane	Ecufar	CN: 571329.8; GTIN: 05414736031378
Deposited data
Raw data	EBRAINS repository	(Sanchez-Vives, 2020; Vijayan et al., 2010)
Experimental models: Organisms/strains
Mouse C57BL/6J	Envigo
Software and algorithms
Analysis code	EBRAINS repository	EBRAINS: https://drive.ebrains.eu/d/cfe55579f07c44d68586/
Python version 2.7.13	Python Software Foundation	https://www.python.org/ RRID:SCR_008394
MATLAB	The MathWorks, Inc.	http://www.mathworks.com/products/matlab/ RRID:SCR_001622
NEST 2.12.0	The NEST Initiative	http://www.nest-simulator.org/ RRID:SCR_002963

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Maurizio Mattia (maurizio.mattia@iss.it).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Animals

All procedures were approved by the Ethics Committee at the Hospital Clinic of Barcelona and were carried out to the standards laid down in Spanish regulatory laws (BOE 34/11370-421, 2013) and in the European Union directive 2010/63/EU. Recordings were performed in eight adult male C57BL/6J mice bred in-house at the University of Barcelona and kept under 12h light/dark cycle with food and water ad libitum. All experiments were performed in the animal’s subjective daytime.

Surgical procedures

Anesthesia was induced with an intraperitoneal injection of ketamine (75 mg/kg) and medetomidine (1.3 mg/kg) and maintained by the inhalation of isoflurane in 100% oxygen. Atropine (0.3 mg/kg), methylprednisolone (30 mg/kg) and mannitol (0.5 g/kg) were administered subcutaneously to avoid respiratory secretions and edema. Body temperature was constantly monitored and kept at 37°C using a thermal blanket (RWD Life Science, China). Once under the surgical plane of anesthesia, mice were placed on a stereotaxic frame (SR-6M, Narishige, Japan) and a craniotomy and durotomy were performed over either the right or left hemisphere from −3.0 mm to +3.0 mm relative to bregma and +3.0 mm relative to midline. This broad craniotomy and durotomy were chosen to allow access to a large area of the targeted hemisphere, either left or right. Three levels of anesthesia were reached that were classified according to the provided isoflurane concentrations: Deep = 1.16 ± 0.08% (mean ± s.e.m); Medium = 0.34 ± 0.06%; Light = 0.1–0% (Dasilva et al., 2021). The volume delivered was 0.8 L/min and the animals were breathing freely via a tracheotomy. Each anesthesia level was maintained for 20–30 minutes and recordings were each of 300–500 s duration consistently obtained in a stable slow oscillatory regime (∼10 minutes after the change in concentration) and thus, before microarousals appeared due to lighter anesthesia (Tort-Colet et al., 2021). Furthermore, the absence of reflexes was regularly checked. With respect to the extreme of the depth of anesthesia, we had already determined in previous experiments the range of anesthetic that could be used to ensure the maintenance of a bistable pattern of activity, while avoiding respiratory depression.

Electrophysiological recordings

Extracellular LFP activity was recorded by means of 32-channel multi-electrode arrays (Pazzini et al., 2018) (550 μm spacing between recording points) covering the entire exposed area of the cortex. The single electrodes' diameter was 50μm. The signal was amplified by 100 and high-pass filtered above 0.1 Hz (Multichannel Systems, GmbH), digitized at 5 kHz and fed into a computer via a digitizer interface (CED 1401 and Spike2 software, Cambridge Electronic Design, UK). We ensured that all 32 channels were working and recording good signal during the experiments.

Method details

MUA estimate and detection of the state transitions

Up and Down states and multi-unit activity (MUA) were estimated from the recorded raw signals (Mattia et al., 2010; Reig et al., 2010; Sanchez-Vives et al., 2010). Briefly, the power spectra were computed from 5-ms sliding windows of the raw signal. MUA was estimated as the relative change of the power in the [0.2, 1.5] kHz frequency band. Such spectral estimate of the MUA was not affected by the electrode filtering properties, and it provided a good estimate of the relative firing rate of the pool of neurons near the electrode tip. In a second step, the MUA was logarithmically scaled to compensate for the high positive fluctuations due to the neurons closest to the electrode, thus obtaining the log(MUA) signal. We then smoothed the log(MUA) by performing a moving average with a sliding window of $40$ ms. The average activity during Down states was subtracted from the resulting log(MUA) signal, so that the activity associated with the Down state fluctuates around 0. From the long-tailed histogram of log(MUA), an optimal threshold separating Up and Down activity states was set at the absolute value of $0.4$. The threshold for detecting both Down-to-Up and Up-to-Down transitions was the same.

The frequency of the SO was the inverse of the duration of the entire Up-Down cycle. We reconstructed the activation waves from the detected Down-to-Up state transitions as in Capone et al. (2019) and in Dasilva et al. (2021). Briefly, each wave was reconstructed pooling together the transitions occurring in multiple electrodes in a reasonable time interval that was iteratively reduced until each wave contained no more than one transition per channel. Each reconstructed wave was associated with a vector of relative time lags computed as the difference between the time of occurrence of the wave in each electrode and the average time of occurrence across all the electrodes taking part in the wave propagation. We rejected the waves occurring in less than twelve channels, otherwise we replaced the missing values with the result of a nearest-neighbor interpolation using the five nearest points in terms of Euclidian distance of wavefronts/time lag vectors. Using the resulting vectors describing the detected activation wavefronts, for each animal and anesthesia level we composed a time-lag matrix (TLM) having a number of rows equal to the number of waves and a number of columns equal to the number of recording channels of the experiment. We refer to the rows of the TLM, representing relative Down-Up transitions for each channel, also as time-lag arrays. The spatiotemporal course of the wavefronts was then obtained by spatially interpolating the time lags without smoothing, using a thin-plate spline method.

Extraction of the wave entropy index (WEI)

In order to determine with more accuracy, the level of anesthesia as perceived by the animal, we introduced an index based on the data, referred to as the wave entropy index (WEI). This was computed with the following steps: first, we computed for each dataset the fraction of variance $p_k={\lambda }_k/{\sum }_j{\lambda }_j$ explained by each principal component (λ_k are the eigenvalues of the covariance matrix) of the TLM. Next, we computed the effective dimension as $D=e^{(H-1)}$ where $H=-\sum _k{p}_k\log p_k$ is the Shannon entropy of the variance distribution. Under the hypothesis of an exponential distribution of the variance, $p_k\propto e^{-k/D}$ provided that $D\ll N$, where N is the number of recording channels considered (N ≤ 32). Both these conditions where well satisfied by all recording sessions analyzed in this work, and according to (Schiff et al., 2007), D is the minimum number of modes explaining the 90% of the system energy, thus representing the number of dimensions needed to describe its dynamics. We then defined a two-column matrix W, whose columns contain the wave frequencies and the effective dimension D for each wave, both normalized by their respective standard deviations. Finally, we computed the principal components of W and the WEI was defined as the projection of each row/dataset of $W$ onto the resulting first principal component. See Figure S1 for a schematic representation of the computation of the WEI.

Modes of propagation and speed of the modes

Relying on the first principal component of TLM we clustered waves/rows sharing similar features with a k-means algorithm. The optimal number of clusters to be used to group the waves in each anesthesia level was chosen using a Silhouette method. For each cluster, we obtained the mean wavefront and its spatiotemporal profile by averaging the waves belonging to it. The mean wavefront extracted from each cluster was used to compute the mean velocity and direction of propagation of the cluster as in (Capone et al., 2019). This was done relying on the smoothed surface T(x, y) (thin-plate smoothing spline) of the relative time lags associated with each cluster and distributed according to the electrode positions, and computing the local velocity as $V\left(x,y\right)=1/\left({\partial }_x{T}^2+{\partial }_y{T}^2\right)$. The gradient of this field points out the direction of the wave propagation. Mean values are computed across the 32 electrode positions.

Overlap of the patterns

We defined the overlap (sometimes referred to as memory) of the spatiotemporal patterns as the average overlap of consecutive wavefronts, where for the latter we used the rows of the TLM defined above, corrected with a shuffling method. Specifically, for each dataset we computed the dot product of the unitary vector containing the Down-Up lag times and all subsequent lag vectors. In order to prevent large effects of noise, we replaced the rows of the TLM with the average over the nearest (in the Euclidean sense) five other rows. Next, we subtracted from the average distance to the following waves the mean of a shuffled version of the distance to each wave. The latter was computed as the average of 25 repetitions of the distance between every wave and a randomly chosen other wave in the experiment.

Leaders/followers analysis

For the analyses related to the leading and following cell assembly reported in Figure 5, we extracted from the TLM of each dataset the first and the last five channels participating to every wavefront and defined them as leaders and followers, respectively. In Figures 5A and 5B the average waveforms of the leaders and the followers for representative clusters (as defined above) of wavefronts are shown. The maximal firing rate during the Up states (Figures 2F, 5C and 5D) was then computed as the maximal amplitude of the log(MUA), whereas the asymptotic firing rate (panels E, F) is the average log(MUA) amplitude in the interval [200, 100] ms before the Up—Down transition.

Network model and simulations

The network model shown in Figure 6 was composed of standard point-like integrated-and-fire (LIF) neurons. It was organized as a set of interacting modules, each consisting of two interconnected pools of excitatory and inhibitory spiking neurons. Similarly to (Mattia et al., 2013), each cortical module was composed of 250 inhibitory (I, 20%) and 1,000 excitatory (E, 80%) neurons with spike frequency adaptation (SFA). The neurons in the excitatory population were divided into a “foreground” (F, 25%) and “background” (B, 75%) sub-pools. Such modules were spatially distributed on a two-dimensional grid of 13 × 13 sites. The inter-modular connectivity was greater than zero only between pairs of populations displaced at relative distance less than 3, thus modeling cortico-cortical horizontal connections. The membrane potential V(t) of each neuron evolved according to $\dot{V}\left(t\right)=-V\left(t\right)/\tau +I\left(t\right)-a\left(t\right)$ where $I\left(t\right)=\sum _{i,k}{J}_{iki}\delta \left(t-t_{i,k}-d_{ik}\right)+\sum _k{J}_{ext}\delta \left(t-t_{ext,k}{t}_{ext}^k\right)$ is the synaptic current from recurrent (i) and external (ext) presynaptic neurons emitting their k-th at time $t_{i,k}$ and $t_{ext,k}$, and transmitted with efficacy J_i and J_ext, respectively. Recurrent spikes were delivered with axonal transmission delay d_i. The adaptation current ${\tau }_a\dot{a}\left(t\right)=-a\left(t\right)+g_a{\tau }_a\sum _{ik}\delta \left(t-t_{ik}\right)$ modeled the activity-dependent afterhyperpolarizing K⁺ current underlying SFA, increasing by g_a = 0.04 mV/ms at each spike emission time t_k of the neuron and relaxing with a characteristic time τ_a = 500 ms. No SFA was incorporated in inhibitory neurons. Membrane potential decay constant was τ = 20 and 10 ms E and I neurons, respectively. Spikes were emitted when V(t) crossed the threshold ϴ = 20 mV, after which potential was reset to 16 mV for an absolute refractory period τ₀ = 2 and 1 ms for E and I neurons, respectively. External spikes mimicked the input from the other cerebral areas and were implemented as a Poisson process from C_ext independent source firing at rate v_ext. We chose C_ext = 800, v_ext = 3 Hz, J_ext = 0.43 mV and 0.56 mV for E and I neurons, respectively, in order to have a fixed point with firing rates (for E and I neurons) v_E = 3 Hz and v_I = 6 Hz, respectively, under mean-field approximation (Amit and Brunel, 1997). To this purpose the synaptic efficacies were randomly chosen from a Gaussian distribution with mean $J_{\alpha \beta }$ and standard deviation $\Delta J_{\alpha \beta }$ depending on the type of presynaptic ($\beta =E,I$β = E, I) and postsynaptic (α = E, I) neurons, whereas $\Delta J_{\alpha \beta }=0.25J_{\alpha \beta }$ for any α and $\beta$. Inhibitory connections were set to J_II = J_EI = 1.5 mV, J_EE = 0.43 mV and J_IE = 0.56 mV. In the same mean-field framework we structured the cortical module to have an additional high-frequency fixed point for the F excitatory neurons by potentiating synaptic self-excitation J_FF and depressing the other excitatory connections J_FB and J_BF compared to J_EE as in (Amit and Brunel, 1997): J_FF = 0.61 mV and J_FB = J_BF = 0.39 mV. Intra-modular connectivity between excitatory neurons (i.e., the probability be synaptically coupled) was c_EE = 0.8, whilst the inter-modular connectivity decreased with distance (Ercsey-Ravasz et al., 2013) assuming the values (0.03, 0.018, 0.007, 0.004, 0.001, 0.001). Axonal transmission delays were drawn from an exponential distribution with mean d_αE = 22.6 ms and d_αI = 5.7 ms (α = E, I). In the 13 × 13 grid, the modules in the two opposite 2 × 2 corners shown in Figure 6A had an enhanced self-excitation among F neurons (J_FF = 0.65 mV) to increase their excitability. Analyses were performed in the 5 × 5 subset of modules in the center of the grid. In order to use the same analytical approach developed for in vivo recordings, we transduced the simulated activity in an in silico representation of MUA. MUA was computed from the firing rates v_F(t) of each module, subsampled at 5 ms, by adding a white noise $\zeta \left(t\right)$ with $\zeta \left(t\right)=0$ and ${\zeta }^2\left(t\right)={\eta }^2$, where η = 0.4 min (v_F(t)), to mimic the fluctuations observed in the experiments

Simulations were performed with NEST (Kunkel et al., 2017). All Python code including all model parameters are freely available in EBRAINS (https://wiki.ebrains.eu/bin/view/Collabs/slow-waves-in-fading-anesthesia).

Quantification and statistical analysis

All the analyses were performed in MATLAB (The MathWorks, Natick, MA). Linear fits shown throughout the manuscript were computed using a linear regression model reporting both R² and P values of the fits.

Sample size, statistical tests and outcomes are indicated in the results section and/or figure legends.

Published: March 18, 2022

Data and code availability

• •All experimental data have been deposited at the EBRAINS repository and are publicly available as of the date of publication. The DOI is listed in the key resources table.
• •All original code has been deposited at the EBRAINS repository and is publicly available as of the date of publication, at the following link: EBRAINS: https://drive.ebrains.eu/d/cfe55579f07c44d68586/ .
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.