Deep Ensemble Machine Learning Framework for the Estimation of $\mathbf{P}{\mathbf{M}}_{2.5}$ Concentrations

Abstract

Background:

Accurate estimation of historical ${\mathrm{PM}}_{2.5}$ (particle matter with an aerodynamic diameter of less than $2.5\mathrm{\mu }\mathrm{m}$) is critical and essential for environmental health risk assessment.

Objectives:

The aim of this study was to develop a multiple-level stacked ensemble machine learning framework for improving the estimation of the daily ground-level ${\mathrm{PM}}_{2.5}$ concentrations.

Methods:

An innovative deep ensemble machine learning framework (DEML) was developed to estimate the daily ${\mathrm{PM}}_{2.5}$ concentrations. The framework has a three-stage structure: At the first stage, four base models [gradient boosting machine (GBM), support vector machine (SVM), random forest (RF), and eXtreme gradient boosting (XGBoost)] were used to generate a new data set of ${\mathrm{PM}}_{2.5}$ concentrations for training the next-stage learners. At the second stage, three meta-models [RF, XGBoost, and Generalized Linear Model (GLM)] were used to estimate ${\mathrm{PM}}_{2.5}$ concentrations using a combination of the original data set and the predictions from the first-stage models. At the third stage, a nonnegative least squares (NNLS) algorithm was employed to obtain the optimal weights for ${\mathrm{PM}}_{2.5}$ estimation. We took the data from 133 monitoring stations in Italy as an example to implement the DEML to predict daily ${\mathrm{PM}}_{2.5}$ at each $1\mathrm{km}\times 1\mathrm{km}$ grid cell from 2015 to 2019 across Italy. We evaluated the model performance by performing 10-fold cross-validation (CV) and compared it with five benchmark algorithms [GBM, SVM, RF, XGBoost, and Super Learner (SL)].

Results:

The results revealed that the ${\mathrm{PM}}_{2.5}$ prediction performance of DEML [coefficients of determination $\left(R^2\right)=0.87$ and root mean square error $\left(\text{RMSE}\right)=5.3{8\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$] was superior to any benchmark models (with $R^2$ of 0.51, 0.76, 0.83, 0.70, and 0.83 for GBM, SVM, RF, XGBoost, and SL approach, respectively). DEML displayed reliable performance in capturing the spatiotemporal variations of ${\mathrm{PM}}_{2.5}$ in Italy.

Discussion:

The proposed DEML framework achieved an outstanding performance in ${\mathrm{PM}}_{2.5}$ estimation, which could be used as a tool for more accurate environmental exposure assessment. https://doi.org/10.1289/EHP9752

Introduction

Both short-term and long-term exposure to ambient fine particulate matter (PM) with an aerodynamic diameter of $2.5\mathrm{\mu }\mathrm{m}$ or less (${\mathrm{PM}}_{2.5}$) are related to a broad range of adverse health outcomes, such as cardiovascular and respiratory diseases (Guo et al. 2016; Hoek et al. 2013; Soriano et al. 2020), neurological disorders (Shi et al. 2020), mental disorders (Lu et al. 2020), type 2 diabetes (Liu et al. 2019a), and premature mortality (Liu et al. 2019b; Yu et al. 2020), even at a concentration below the World Health Organization (WHO) air quality guideline (WHO 2021). However, in most regions of the world, the design of air quality monitoring networks tends to give priority to urban areas with a lack of homogeneity at regional and national levels (Alsahli and Al-Harbi 2018; Duyzer et al. 2015). Therefore, it is important to monitor the spatial and temporal changes of ${\mathrm{PM}}_{2.5}$ concentrations in areas not covered by monitoring stations. Especially in suburban and rural areas, monitoring stations are spread sparsely, whereas the levels of air pollution might be different from urban areas due to disparate socioeconomic levels and human activities (Bravo et al. 2017; Zhao et al. 2021).

Over the last few decades, a large body of research has put forward efforts to integrate the air quality monitoring networks with air pollution modeling approaches to assess air pollution exposure. Apart from the traditional statistical regression algorithms, like the mixed-effect model (Kloog et al. 2011) and generalized additive model (GAM) (Liu et al. 2009), machine learning methods have been widely used in the ${\mathrm{PM}}_{2.5}$ estimation because of their ability to achieve a better prediction performance by capturing the nonlinear relationships and complicated interactions between predictors (Chen et al. 2018; Di et al. 2016; Stafoggia et al. 2017).

The ensemble learning technique is a machine learning method that has been increasingly applied in air pollutant estimation (Shtein et al. 2020; Wichard 2006; Zhou 2012). The basic idea of ensemble learning is to establish a prediction model by combining the predictions of multiple base learning algorithms to achieve a better performance than any of the constituent algorithms alone (Requia et al. 2020; Rokach 2010; Zhou 2012). The strategic combination of these base learning algorithms can reduce the total exposure assessment errors and make it robust to noise (Polikar 2006). Several ensemble models in the estimation of ${\mathrm{PM}}_{2.5}$ have been developed to achieve a better performance than that of only a single machine learning model (Di et al. 2019; Lyu et al. 2019; Shtein et al. 2020). For example, Shtein et al. used four base models: linear mixed effects model (LME), random forest (RF), eXtreme gradient boosting (XGBoost), and chemical transport models (CTMs) integrated with a GAM combiner to estimate the daily average concentrations of ${\mathrm{PM}}_{2.5}$ and particles with an aerodynamic diameter of $10\mathrm{\mu }\mathrm{m}$ or less (${\mathrm{PM}}_{10}$) across Italy, and the results of the ensemble model outperformed any of these four separate base models (Shtein et al. 2020).

The stacked ensemble model is a generalization of the ensemble method, where the first-level learners (called the base models) are used to generate a new data set for training the next-level learner. In contrast to a typical ensemble approach, which involves training a combiner algorithm (called meta-model) to make a final prediction by using all the predictions of the other individual base models as additional inputs (Wolpert 1992), a stacked multilevel ensemble model could boost the models’ prediction accuracy by constructing the multiple-level architecture and improving the diversity of the component learners (Young et al. 2018; Zhou 2012).

The super learner (SL) method is a stacked ensemble method proposed by Van der Laan et al. (Van der Laan et al. 2007). This algorithm provides a system of combining many base learners into an improved estimator along with the optimal set of weights for those learners (Davies and Van Der Laan 2016; Polley and Van Der Laan 2010). It estimated the performances of multiple machine learning models by cross-validation (CV), finetuned the hyperparameters of each algorithm, and created an optimal nonnegative weighted average of those models by minimizing a loss function (Naimi and Balzer 2018; Van der Laan et al. 2007; Young et al. 2018). It has been used in many aspects in epidemiology to improve prediction accuracy and avoid overfitting (Naimi and Balzer 2018), including improving high-dimensional propensity score estimation (Ju et al. 2019; Wyss et al. 2018), causal inference (Van der Laan and Rose 2011), and mortality risk assessment (Luque-Fernandez et al. 2018; Pirracchio et al. 2015; Zheng et al. 2018).

In this study, we proposed a novel three-level stacked ensemble model called the Deep Ensemble Machine Learning model (DEML) based on such a theoretically validated SL algorithm to improve the estimation of the concentrations of ${\mathrm{PM}}_{2.5}$. It can be viewed as an extension of SL by combining the strengths of SL with a diverse hierarchy structure. The DEML technology could be used to evaluate the performance of all constructed individual models simultaneously and generate optimal performance with a combination of these models. This study used Italy as an example to apply the proposed DEML approach to improve the estimation of the daily concentrations of ${\mathrm{PM}}_{2.5}$ based on local meteorological factors, satellite data, and land cover data in Italy from 2015 to 2019.

Methods

DEML Framework

The DEML framework proposed in this study is a three-level stacked ensemble approach. It is based on the SL ensemble algorithm (Naimi and Balzer 2018; Polley and Van Der Laan 2010; Van der Laan et al. 2007) introduced in the neural network hierarchy structure. Figure 1 illustrates the overall training procedure of our DEML algorithm.

Figure 1.

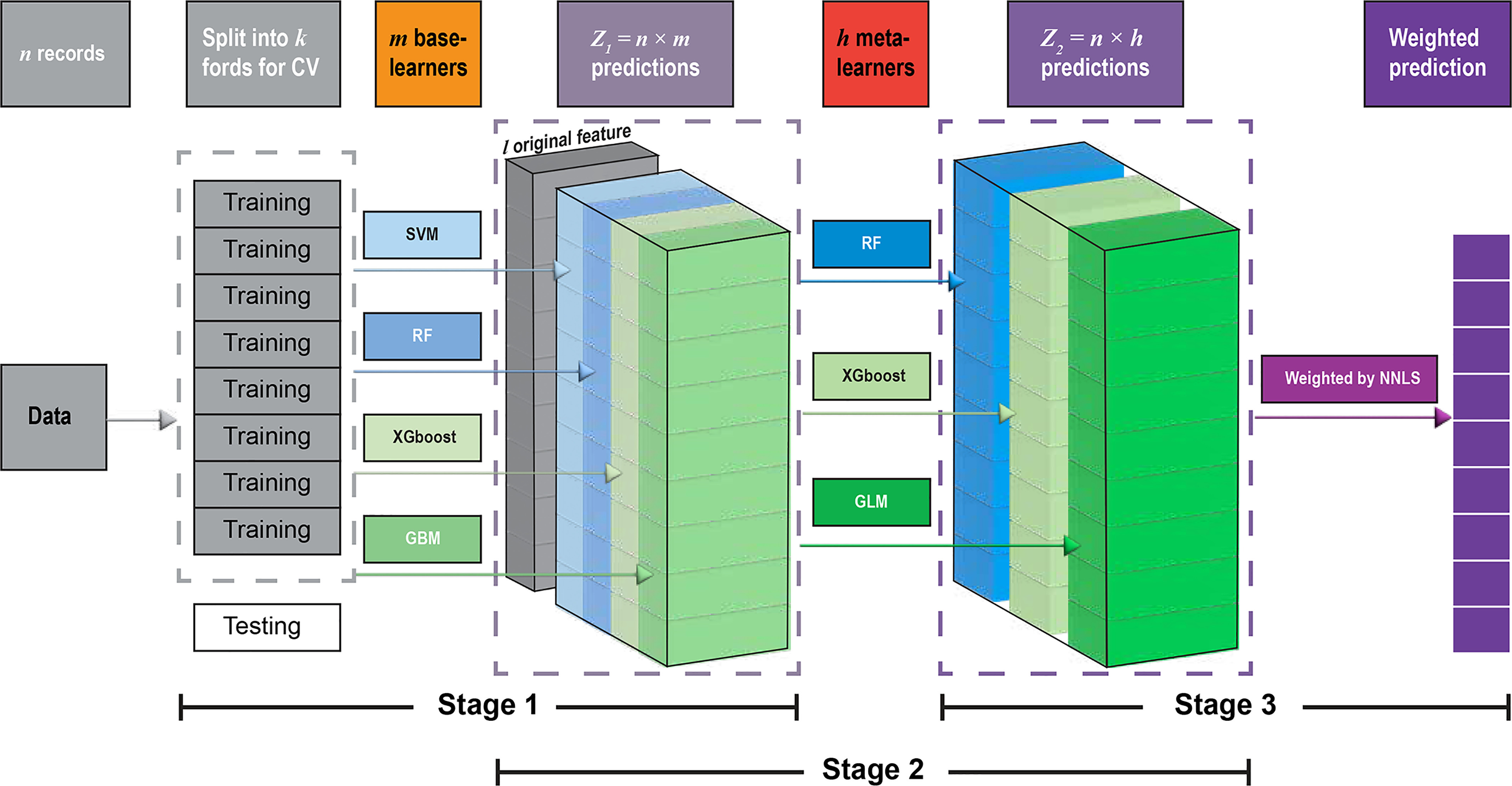
The framework of the DEML algorithm. $Z_1$ is a matrix with $n$ rows and $m$ columns, which is the combination of ${\mathrm{PM}}_{2.5}$ predictions for each base model; l represents the original features; h denotes the number of meta-models; $Z_2$ is a matrix with $n$ row and $h$ columns, which is the combination of ${\mathrm{PM}}_{2.5}$ predictions for each meta model. We finally get $Z_2$ as the input to obtain the weights of the meta models by using the NNLS algorithm and get the final ${\mathrm{PM}}_{2.5}$ prediction; k is the number of folds for CV, and we select the same valid rows for the base and meta models; $n$ is the number of records of all data; $m$ denotes the number of base models. Note: CV, cross-validation analysis; DEML, the three-stage stacked deep ensemble machine learning method; GBM, gradient boosting machine; GLM, generalized linear model; NNLS, nonnegative least squares algorithm; RF, random forest; SVM, support vector machine; XGBoost, extreme gradient boosting.

Specifically, the DEML has a three-stage structure. At the first stage, $m$ base machine learning methods are built and trained after the cross-validation is used on the entire training set (with $n$ records). The predictions of $m$ base-learners are collected by bringing each $k$-fold CV data set together to form the input data of stage 2 (a $Z_1$ matrix with $n\times m$ predictions). At the second stage, $h$ meta-learning algorithms are trained simultaneously on the data set combined with the $Z_1$ matrix and the original training data set $l$ with the $k\text{-fold}$ CV to form another input data of stage 3 (a $Z_2$ matrix with $n\times h$ predictions). At the third stage, a nonnegative least squares (NNLS) algorithm is employed in the $Z_2$ matrix to calculate the contribution of each candidate algorithm and find the optimal weights of the meta-learners in DEML. The ultimate predictions were generated by combining the predictions of meta-learners with the estimated optimized weights.

For a typical ensemble model, we have:

$$\widehat{f}\left(x\right)=\sum _{i=1}^m{w}_i{f}_i\left(x\right),\sum _{j=i}^m{w}_i=1,$$ (1)

where $f_i\left(x\right)$ denotes $m$ different base models; the model weights $w_i$ sum to one (Wichard 2006). In this study, we selected four representative machine learning models ($m=4$) as the base learners from different learning schemes to increase the model diversity, including the gradient boosting machine (GBM) and XGBoost models from boosting algorithms, support vector machine (SVM) from kernel-based algorithms, and RF from bagging algorithms. In our DEML algorithm, the combined outputs ($Z_1$) of four base models $f_i\left(x\right)$ and the original features $l$ were further integrated by stacking with 3 meta-models ${\widehat{g}}_j\left(x\right)$ to extend with a cascading hierarchy structure:

$$g\left(x\right)=\sum _{j=1}^h{w}_j{\widehat{g}}_j\left(f_i\left(x\right)\right),w_j\ge 0,\sum _{j=1}^h{w}_j=1,$$ (2)

where RF, XGBoost, and generalized linear model (GLM) ($h=3$) were selected as the meta-learners in the DEML algorithm. We finally used an NNLS optimization algorithm to obtain the optimal weights of meta-learners ${\widehat{g}}_j\left(x\right)$ from the combined matrix $Z_2$ as input. Different from the ordinary least squares (OLS), which seek a vector of coefficients $\mathrm{W}\in \mathrm{R}$ to make $\widehat{\mathrm{W}}=\text{argmin\hspace{0.17em}}\Vert \mathrm{y}-\mathbf{X}{\mathrm{W}\Vert }_2^2$, NNLS minimizes the same subject with an additional constraint that each element of $\widehat{w}$ is nonnegative so that it could ensure the weight $w_j$ in the ensemble algorithms are nonnegative. The details of SVM, RF, XGBoost, GBM, and GLM machine learning algorithms can be found elsewhere (Alpaydin 2020; Bishop 2006). The hyperparameters of each model in this study were set to their default values (Table S1). All statistical analyses and model establishments were performed using R software (version 3.5.3; R Development Core Team). The newly built R package called “deeper” (Yu and Guo 2021) was used to implement the DEML approach.

Practice Example of the Data from Italy

Study area.

Italy is a boot-shaped peninsula located in southern Europe and the Mediterranean with a total area of $\mathrm{301,230}{\mathrm{km}}^2$. Because more than one-third of the Italian territory is mountainous, along with a long coastline, the climate in Italy displays remarkably varied features (Fratianni and Acquaotta 2017). In most of the inland northern and central regions in Italy, the climate ranges from humid subtropical to humid continental and oceanic climates. There is a Mediterranean climate in most of the coastal and southern areas across Italy, with mild winters and warm and dry summers. At the same time, the higher altitudes tend to be cold, wet, and often snowy in winter and are hot and humid in summer (Beck et al. 2018). The variable climatic characteristics combined with diverse anthropogenic and natural air pollution sources lead to a large spatial and temporal variability of ${\mathrm{PM}}_{2.5}$ in Italy (Shtein et al. 2020). The Po Valley in northern Italy is one of the most polluted areas in Europe. However, the distribution of monitoring stations in Italy is uneven, with more stations in northern Italy and in urban areas. Therefore, it is necessary to capture the spatial and temporal variability of ${\mathrm{PM}}_{2.5}$ through the DEML framework for air pollution risk assessment in Italy.

Station-based PM data.

We extracted daily average station-based concentrations of ${\mathrm{PM}}_{2.5}$ and ${\mathrm{PM}}_{10}$ from the Italian National Institute for Environmental Protection and Research (Istituto Superiore per la Protezione e la Ricerca Ambientale 2021). We included data for 133 monitoring stations in the study area for 5 years (from 1 January 2015 to 31 December 2019). The spatial distribution of the monitoring sites is shown in Figure S1 and Figure S2.

Satellite-retrieved aerosol optical depth (AOD) data.

AOD is a measure of the extinction of the solar beam by particles like dust, smoke, and pollution in the atmosphere. The daily average AOD data were retrieved from the MCD19A2-V6 data product in the Google Earth Engine (GEE) platform, which is a product by the Moderate Resolution Imaging Spectroradiometer (MODIS) Terra and Aqua combined Multi-angle Implementation of Atmospheric Correction (MAIAC) algorithm (Lyapustin et al. 2018). The daily AOD at $470\text{\hspace{0.17em}nm}$ (blue band) at $1\mathrm{km}\times 1\mathrm{km}$ spatial resolution was used.

Meteorological conditions.

The climate data at $0.1°\times 0.1°$ spatial resolution were obtained from the E-OBS data set (Haylock et al. 2008), which has accuracy with the root mean square error (RMSE) values of $1.15°\mathrm{C}\text{\hspace{0.17em}to\hspace{0.17em}}2.41°\mathrm{C}$ for temperature and $2.74\mathrm{mm}-3.63\mathrm{mm}$ for precipitation when validated against weather station observations (Cornes et al. 2018). We included daily maximum, mean, and minimum ambient temperature (at $2\mathrm{m}$ above the land surface), total daily precipitation, relative humidity, and solar radiation measured at the earth’s surface.

Land cover data and population density.

The land-use status data at $100\text{\hspace{0.17em}meters}$ spatial resolution in 2018 was obtained from the Copernicus CORINE land cover data set through the GEE platform (Congedo et al. 2016). The digital elevation data with the spatial resolution of $90\mathrm{m}$ was from the Shuttle Radar Topography Mission (SRTM) project (Jarvis et al. 2008). The annual residential population density data at $100\mathrm{m}$ spatial resolution from 2015 to 2019 was collected from the WorldPop Global Project (Sorichetta et al. 2015). We upscaled the land cover, elevation, and population density data and downscaled the AOD and climate conditions to $1\mathrm{km}\times 1\mathrm{km}$ spatial resolution for further grid cell estimation by the bilinear interpolation resampling approach (Manjunatha and Malini 2018). All the collected data details and sources can be found in Table S2.

Modeling strategy.

Overall process.

We used the proposed DEML framework with a three-level stacked structure, in which the predictions of four base models (GBM, SVM, RF, and XGBoost) ($m=4$), and three second-level models (RF, XGBoost, and GLM) ($h=3$) with 10-fold CV ($k=10$) were concatenated with an NNLS algorithm (the third-level model) to obtain the optimal ${\mathrm{PM}}_{2.5}$ prediction. Specifically, we first evaluated the proposed DEML to interpolate the missing ${\mathrm{PM}}_{2.5}$ concentrations using the existed ${\mathrm{PM}}_{10}$ data in monitor stations. After that, another DEML with the same structure was trained by including all collected meteorological conditions, AOD, land cover, and population density variables (except for ${\mathrm{PM}}_{10}$) to establish their relationship with the observed and imputed daily ${\mathrm{PM}}_{2.5}$. Finally, we applied this established DEML model to predict daily ${\mathrm{PM}}_{2.5}$ at each $1\mathrm{km}\times 1\mathrm{km}$ grid cell from 2015 to 2019 across Italy.

Using DEML to impute missing ${\mathrm{PM}}_{2.5}$ by ${\mathrm{PM}}_{10}$.

Based on previous studies (Shtein et al. 2020; Stafoggia et al. 2019) and our initial analysis, there was a high correlation (with a Spearman correlation coefficient of 0.58 in this study) between daily observed ${\mathrm{PM}}_{10}$ and ${\mathrm{PM}}_{2.5}$ in the ground stations. Therefore, we used the observed ${\mathrm{PM}}_{10}$ to estimate the missing ${\mathrm{PM}}_{2.5}$ concentrations with the proposed DEML approach when ${\mathrm{PM}}_{10}$ data were available in monitor stations. Specifically, we used the proposed three-level stacked DEML structure where the daily ${\mathrm{PM}}_{10}$ concentrations, the coordinate positions of ground stations (latitude and longitude), and the recording date (year, month, day of the week) were included as independent variables (predictors) to estimate the corresponding ${\mathrm{PM}}_{2.5}$ concentrations in the monitor stations. The DEML model was trained with a 10-fold CV based on 112,604 daily observations from 77 stations where both ${\mathrm{PM}}_{2.5}$ and ${\mathrm{PM}}_{10}$ were available. We compared the performance of the DEML model with that of the RF and XGBoost imputation models at the same data set. Finally, a total of 23,003 daily missing ${\mathrm{PM}}_{2.5}$ (accounting for 6% of the total cases) were imputed by the established DEML model in the stations where the corresponding daily ${\mathrm{PM}}_{10}$ existed.

Using DEML to predict ${\mathrm{PM}}_{2.5}$.

Because the purpose of this study is to estimate the daily concentrations of ${\mathrm{PM}}_{2.5}$ in locations without monitoring stations in Italy from 2015 to 2019, we developed the DEML model by establishing the potential association between the observed and imputed ${\mathrm{PM}}_{2.5}$ and the local meteorological conditions, satellite data, and land cover data to predict daily ${\mathrm{PM}}_{2.5}$ at every $1\mathrm{km}\times 1\mathrm{km}$ grid cell across Italy. Briefly, our predictors included all collected meteorological variables, land use data, and population density. Other input variables in our study included the latitude and longitude of the monitoring stations; daily, weekly, and monthly dummy variables; and elevation. We tested the performance of DEML in different seasons to investigate the seasonal variation of ${\mathrm{PM}}_{2.5}$ in Italy. To test the impact of AOD on the model performance, we built the DEML models with and without AOD separately to compare the contribution of AOD to daily ${\mathrm{PM}}_{2.5}$ estimation in our study. The loss of RMSE was selected to measure how much a model’s performance would change if the effect of AOD were removed (Biecek and Burzykowski 2021). We selected 10 permutations to repeat the process 10 times to compute the mean values of RMSE loss using the DALEX R package (Biecek 2018). The RF and XGBoost models were selected to calculate the variable importance separately. We deleted all missing values cases in the input predictors instead of filling them with certain spatial interpolation technologies like the inverse distance weight interpolation or kriging interpolation methods (Li and Heap 2014) to reduce the uncertainties of interpolation for models. The extreme value of AOD and ${\mathrm{PM}}_{2.5}$ above 500 and $100{\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$ separately were dropped out. A total of 202,001 records were included in the DEML model establishment to predict the concentrations of ${\mathrm{PM}}_{2.5}$ across Italy.

Assessment of model performance.

We evaluated the model performance of ${\mathrm{PM}}_{2.5}$ estimation by the hold-out method and 10-fold CV to prevent overfitting. Specifically, we randomly selected 10% of the whole data set as the unseen independent testing data set to compare models and get unbiased estimations. Then, the remaining data were randomly split into 10 equally sized subsets to conduct the 10-fold CV to obtain the best model performance and weights. For each training process, 90% of data were randomly selected to train the base models as well as the meta-models with the same uniform separations, and the remaining data were used to validate the model performance and determine the optimal super parameters. The process would be repeated 10 times, and the average of the 10 estimates was used to assess the quality of the models. Because the ground ${\mathrm{PM}}_{2.5}$ stations in Italy were spatially highly imbalanced, where most of the stations were located in northern and central Italy and few stations in southern Italy and the island of Sardinia, we introduced a dissimilarity index (DI) (Meyer and Pebesma 2021) to measure the dissimilarity and uncertainties of new spatial prediction locations (that were not covered with stations) with those in the ground stations. The DI is the normalized and weighted minimum distance to the nearest training data point divided by the average distance within the training data (Meyer and Pebesma 2021). We randomly selected one specific day in our study period and estimated the relative variable importance as the variable weights by RF to investigate the DI on a specific day in Italy (Figure S3). We validated the potential spatial and temporal overfitting by conducting the spatial CV and temporal CV separately. For the spatial CV, we randomly selected 5% of monitor stations as a testing data set to examine the spatial generalization ability. Furthermore, we conducted a cluster-based spatial CV region to test the spatial variations in the region not covered by the ground monitors (Xue et al. 2020). The observations from all ground monitors in the same region were simultaneously selected as the testing data, and 7 out of 20 Italian regions were involved in the study (Figure S2). With regard to the temporal CV, we selected the last 7 d of each year to test the temporal forecasting ability of the DEML model.

To verify the performance of the proposed DEML approach, a series of benchmark models were implemented for comparison, including GBM, SVM, RF, XGBoost, and an SL model, which was composed of the above four machine learning methods with an optimal nonnegative weight using NNLS. All models were independently trained with the same training data set, and the fitness of models was then tested with the same unseen independent testing observations. The performance of models was assessed by two performance indices: RMSE and coefficients of determination ($R^2$).

Results

The basic statistics of the daily mean ${\mathrm{PM}}_{2.5}$ concentrations at 133 monitor stations across Italy in the period 2015–2019 are presented in Table 1. In general, the annual average concentrations of ${\mathrm{PM}}_{2.5}$ in the period 2015–2019 ranged from $17.2{5\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$ to $24.3{8\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$, whereas the concentrations in summer tended to be lower than in other seasons (Table S3). For the ${\mathrm{PM}}_{2.5}$ imputation results, our DEML approach achieved a 10-fold CV $R^2$ of 0.91 and RMSE of $4.{55\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$, which was better than the benchmark RF and XGBoost models, which had a 10-fold CV $R^2$ of 0.88 and 0.71, respectively (Figure S4).

Table 1.

The descriptive statistics for the daily average ${\mathrm{PM}}_{2.5}$ (micrograms per cubic meter) from 2015 to 2019 based on 113 air quality stations in Italy.

Year	Mean	SD	${\mathrm{P}}_{2.5}$	${\mathrm{P}}_{25}$	${\mathrm{P}}_{50}$	${\mathrm{P}}_{75}$	${\mathrm{P}}_{97.5}$
2015	24.38	28.40	4.08	11.76	18.76	31.12	70.99
2016	20.34	18.68	3.12	10.08	15.90	24.94	63.25
2017	22.61	20.11	3.12	10.08	16.38	28.27	74.87
2018	20.78	15.18	4.08	11.04	16.86	26.84	55.50
2019	17.25	18.22	3.12	8.16	13.05	20.18	55.50
Total	21.11	20.81	3.36	10.08	15.90	25.89	65.18

Note: ${\mathrm{P}}_{2.5}$, ${\mathrm{P}}_{25}$, ${\mathrm{P}}_{50}$, ${\mathrm{P}}_{75}$, and ${\mathrm{P}}_{97.5}$ are the 2.5th, 25th, 50th, 75th, and 97.5th percentile of ${\mathrm{PM}}_{2.5}$ concentrations in the study period separately. ${\mathrm{PM}}_{2.5}$, particulate matter with aerodynamic diameter $<2.5\mathrm{\mu }\mathrm{m}$; SD: standard deviation.

In terms of the ${\mathrm{PM}}_{2.5}$ estimation, the overall ${\mathrm{PM}}_{2.5}$ model performances of DEML and five benchmark models in Italy are presented in Table 2. In summary, our DEML algorithm exhibited higher performance in estimating ${\mathrm{PM}}_{2.5}$ (with an $R^2=0.87$ and $\text{RMSE}=5.3{8\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$) than any of the competitors. The performance of the ensemble SL model and RF were achieved with an $R^2=0.83$, $\text{RMSE}=6.23{\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$, which were followed by the performance of SVM and XGBoost models (with an $R^2=0.76$ and 0.70, respectively). The ${\mathrm{PM}}_{2.5}$ distribution estimated by DEML had a stronger correlation with the observed values than other benchmark models, with a Spearman’s rank correlation of 0.91 (Table S4). The performance of our DEML algorithm in different years in Italy was stable, with $R^2$ ranging from 0.87 to 0.89 (Table 2).

Table 2.

${\mathrm{PM}}_{2.5}$ prediction performances of DEML model and five benchmark models from 2015 to 2019 in Italy.

Year	Measurement	GBM	SVM	RF	XGBoost	SLa	DEMLb
2015	$R^2$	0.69	0.79	0.85	0.81	0.85	0.89
	RMS E (${\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$)	9.25	6.42	6.49	7.23	6.47	5.54
2016	$R^2$	0.72	0.80	0.84	0.81	0.84	0.87
	RMSE (${\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$)	7.74	6.51	5.84	6.33	5.82	5.18
2017	$R^2$	0.74	0.81	0.85	0.81	0.85	0.89
	RMSE (${\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$)	8.20	7.19	6.41	7.09	6.38	5.37
2018	$R^2$	0.70	0.78	0.86	0.82	0.86	0.89
	RMSE (${\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$)	7.44	6.22	5.18	5.69	5.13	4.43
2019	$R^2$	0.68	0.76	0.84	0.79	0.84	0.87
	RMSE (${\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$)	7.34	6.42	5.13	5.78	5.12	4.55
Total	$R^2$	0.51	0.76	0.83	0.70	0.83	0.87
	RMSE (${\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$)	10.4	7.42	6.23	8.20	6.23	5.38

Note: DEML, the three-stage stacked deep ensemble machine learning method; GBM, gradient boosting machine; ${\mathrm{PM}}_{2.5}$, particulate matter with aerodynamic diameter $<2.5\mathrm{\mu }\mathrm{m}$; $R^2$, coefficients of determination for unseen independent data; RF, random forest; RMSE, root mean square error; SL, super learner algorithm; SVM, support vector machine; XGBoost, extreme gradient boosting.

^a SL was constructed with four machine learning models (GBM, SVM, RF, and XGBoost) using a nonnegative least squares (NNLS) approach to achieve the optimal weight.

^b DEML was a three-stage stacked ensemble model by constructing with four base models (GBM, SVM, RF, and XGBoost), three second-level models (RF, XGBoost, and GLM), and an NNLS algorithm.

We also evaluated the performance of our DEML model in different seasons in the study period. As shown in Figure 2, the DEML model appeared to perform well in different seasons with an $R^2$ above 0.81 except for in summer ($R^2=0.70$).

Figure 2.

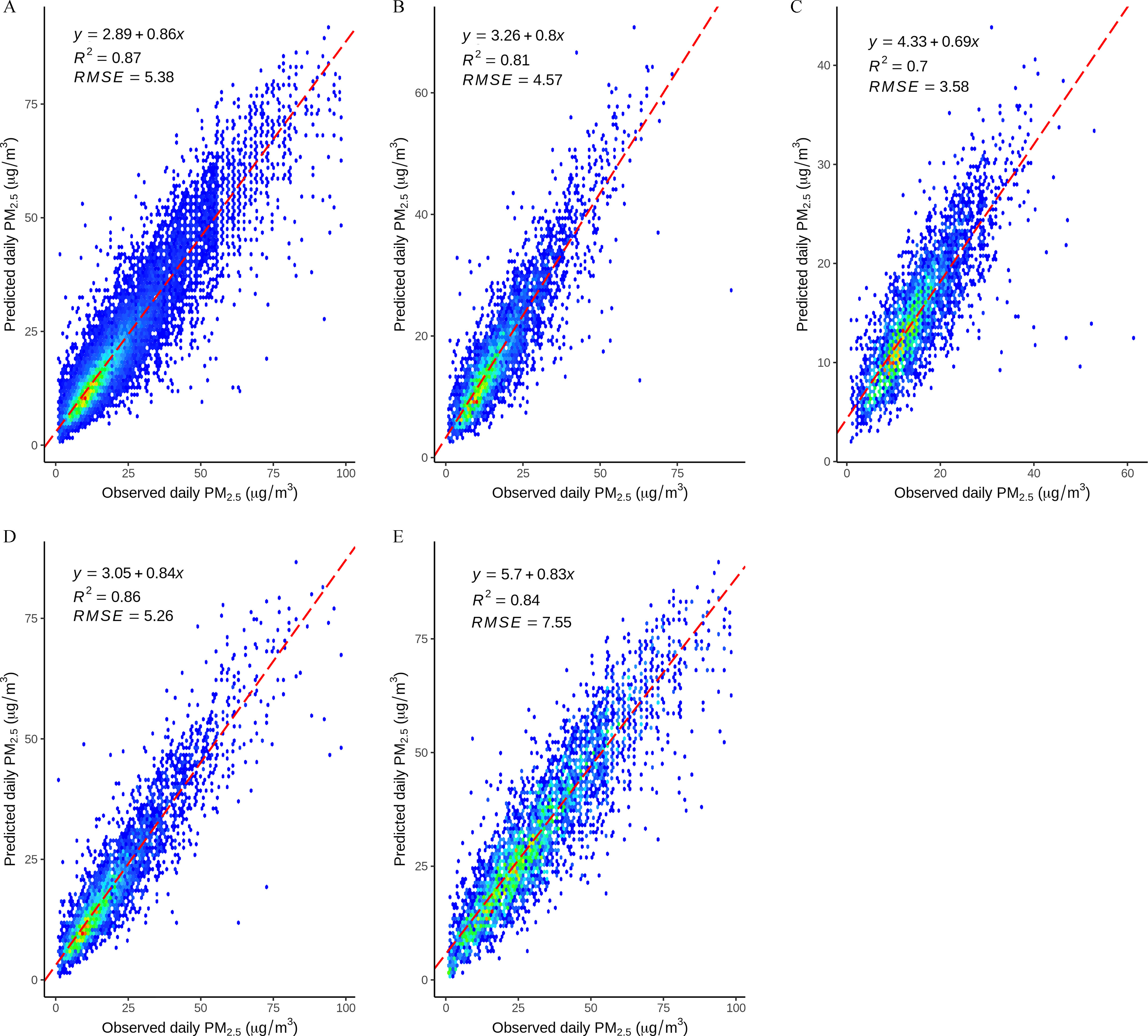
The ${\mathrm{PM}}_{2.5}$ prediction performance of the DEML model in different seasons of 2015–2019 in Italy. The x-axis indicates the observed daily ${\mathrm{PM}}_{2.5}$ in the monitor stations; y-axis indicates the estimated ${\mathrm{PM}}_{2.5}$ by the DEML model; the points represent the corresponding ${\mathrm{PM}}_{2.5}$ for both observed and predicted values. The solid line represents a regression line for the observed and predicted ${\mathrm{PM}}_{2.5}$ by using the simple linear regression. $R^2$ is the coefficients of determination for the unseen independent data. (A) Overall performance. (B) Spring means from March to May; (C) Summer means from June to August; (D) Autumn means from September to November; and (E) Winter means from December to February. Note: DEML, the three-stage stacked deep ensemble machine learning method; ${\mathrm{PM}}_{2.5}$, particulate matter with an aerodynamic diameter $<2.5\mathrm{\mu }\mathrm{m}$; RMSE, the root mean square error (micrograms per cubic meter).

We conducted the spatial and temporal cross-validation test to evaluate the spatiotemporal variations and reliability of the DEML. Table 3 displays the results of spatial and temporal cross-validation for each model. The results of the spatial and cluster-based spatial CV $R^2$ in DEML were 0.90 and 0.79, respectively. The temporal CV results presented the fitness of the DEML algorithm in ${\mathrm{PM}}_{2.5}$ estimation with the temporal CV $R^2$ of 0.96. We also calculated the adjusted $R^2$ at each monitoring station in the study area with a range of 0.61 to 0.97 (Figure S1). The DEML model obtained a high adjusted $R^2$ in the northern plain, where the concentrations of ${\mathrm{PM}}_{2.5}$ tended to be high, whereas it gained a slightly low adjusted $R^2$ at higher altitudes around the Apennine mountains (Figure S1). The DI distribution indicated that most of the predicted regions in Italy had a DI value lower than one, which means that the spatial difference to the nearest station point was smaller than the average dissimilarity of all station data (Figure S3).

Table 3.

The performance of the spatial and temporal cross-validation for DEML model and five benchmark models from 2015 to 2019 in Italy.

Type	Measurement	GBM	SVM	RF	XGBoost	SL	DEMLa
Spatial CVb	$R^2$	0.54	0.61	0.89	0.73	0.89	0.90
	RMSE (${\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$)	10.26	9.70	5.33	8.02	5.33	4.84
Cluster spatial CVc	$R^2$	0.37	0.49	0.50	0.43	0.50	0.79
	RMSE (${\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$)	11.64	12.69	10.45	11.23	10.45	7.46
Temporal CVd	$R^2$	0.24	0.49	0.96	0.36	0.96	0.96
	RMSE (${\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$)	12.28	10.61	3.30	10.83	3.30	2.84

Notes: CV, cross-validation; DEML, the three-stage stacked deep ensemble machine learning method; GBM, gradient boosting machine; ${\mathrm{PM}}_{2.5}$, particulate matter with aerodynamic diameter $<2.5\mathrm{\mu }\mathrm{m}$; $R^2$, coefficients of determination for the spatial and temporal cross-validation; RF, random forest; RMSE, the root mean square error; SL, super learner algorithm; SVM, support vector machine; XGBoost, extreme gradient boosting.

^a The spatial and temporal CV were conducted in both base models and meta models with the same uniform separations.

^b Randomly selected 5% of monitors and put the observations in these monitors as the testing data and others as training data. The process would repeat 20 times.

^c The observations from all ground monitors in the same region were simultaneously selected as the testing data and others as training data. The process would repeat seven times because seven regions were involved.

^d Selected the last 7 days of each year as testing data and others as training data for each year. The process would repeat five times.

The estimated annual average concentrations of ${\mathrm{PM}}_{2.5}$ for each year from 2015 to 2019 at $1\mathrm{km}\times 1\mathrm{km}$ spatial resolution in Italy is shown in Figure 3. The highest level of observed ${\mathrm{PM}}_{2.5}$ was present in the valley of the Po Valley in northern Italy, whereas the lower concentrations of ${\mathrm{PM}}_{2.5}$ were observed in the central and southern regions in Italy. A similar distribution of the annual average concentrations of ${\mathrm{PM}}_{2.5}$ in study years was found in Italy, even though 2019 witnessed a slight decrease in ${\mathrm{PM}}_{2.5}$ concentrations.

Figure 3.

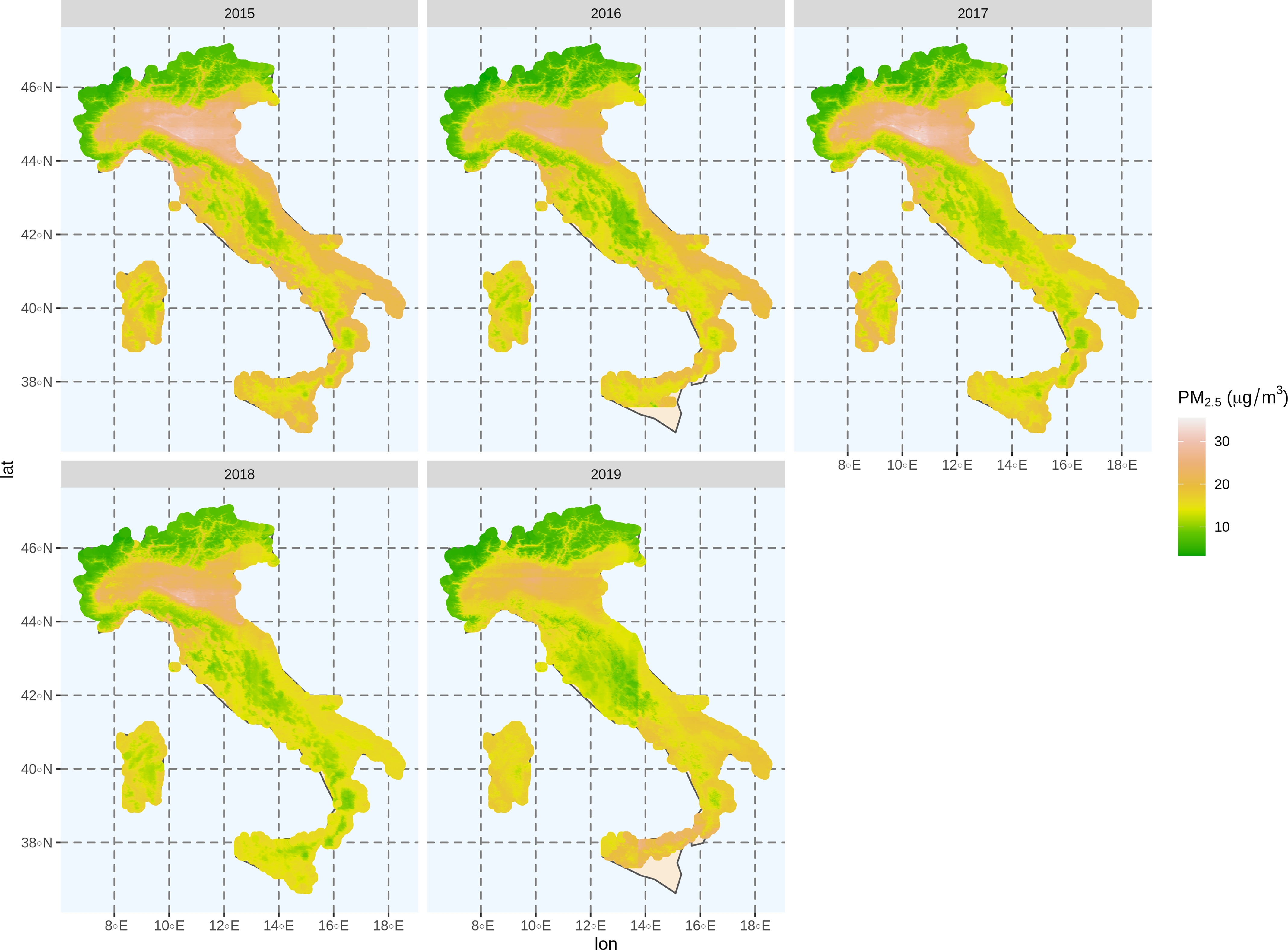
The estimated annual average concentrations of particulate matter with an aerodynamic diameter $<2.5\mathrm{\mu }\mathrm{m}$ (${\mathrm{PM}}_{2.5}$) (micrograms per cubic meter) from 2015 to 2019 in Italy at $1\mathrm{km}\times 1\mathrm{km}$ spatial resolution.

The comparison results for AOD and non-AOD DEML models are shown in Figure 4. With the same data in both DEML models, there was a similar performance for both AOD and non-AOD models with an $R^2$ of 0.85. We tested the importance of the AOD in the ${\mathrm{PM}}_{2.5}$ prediction with RF and XGBoost models, and the results showed that the loss of RMSE was $7.{7\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$ and $9.{3\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$ when AOD was removed from the models, which ranked the seventh and third most important explanatory variables for RF and XGBoost model, respectively (Figure S5).

Figure 4.

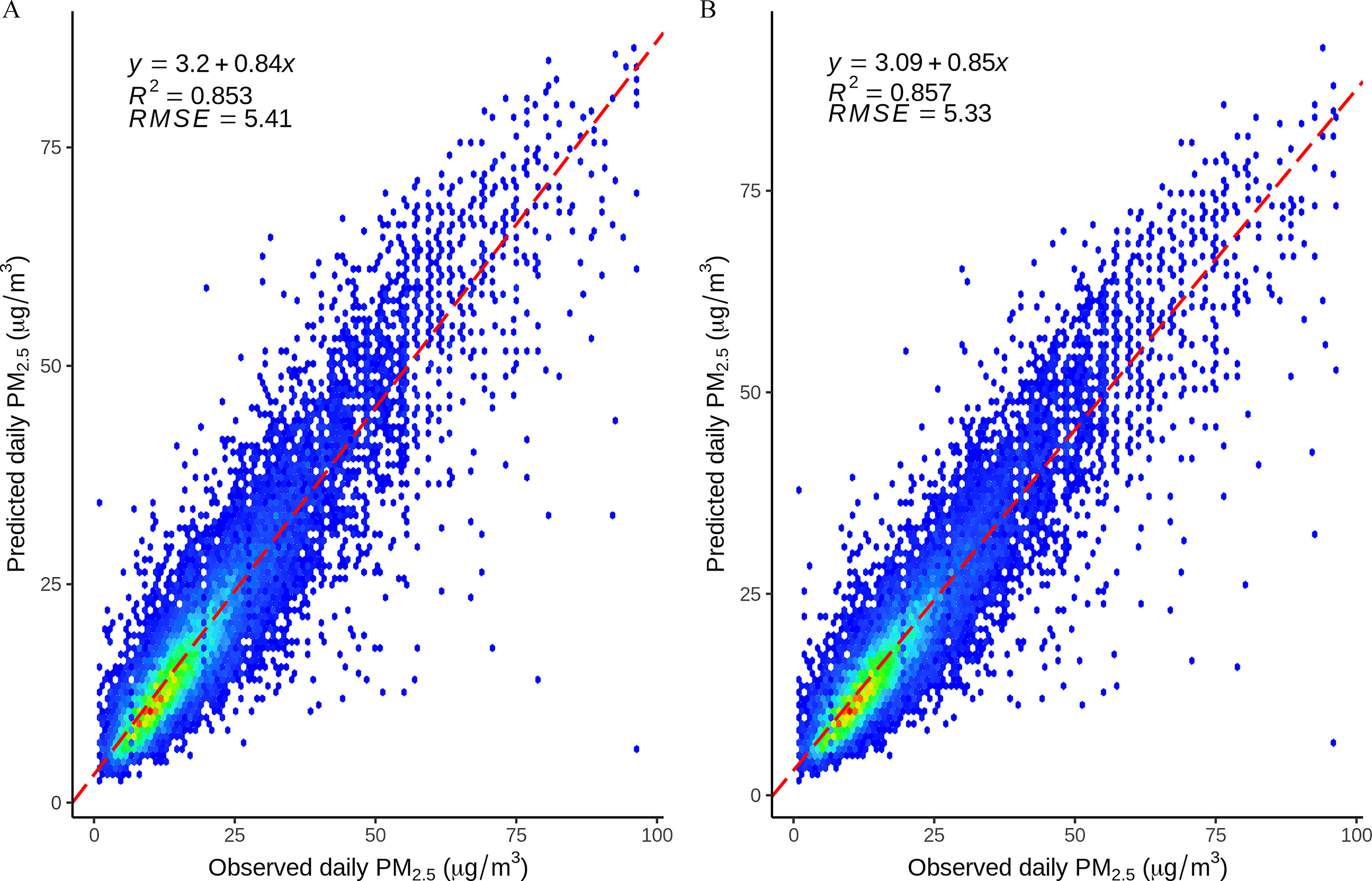
The ${\mathrm{PM}}_{2.5}$ prediction performance of the DEML models with and without AOD as a predictor from 2015–2019 in Italy. The x-axis indicates the observed daily ${\mathrm{PM}}_{2.5}$ in the monitor stations; the y-axis indicates the estimated ${\mathrm{PM}}_{2.5}$ by the DEML model. The points represent the corresponding ${\mathrm{PM}}_{2.5}$ for both observed and predicted values. The solid line represents a regression line for the observed and predicted ${\mathrm{PM}}_{2.5}$ by using the simple linear regression. $R^2$ is the coefficients of determination for the unseen independent data. (A) The DEML prediction model including AOD. (B) The DEML prediction model without AOD. Note: DEML, the three-stage stacked deep ensemble machine learning method; ${\mathrm{PM}}_{2.5}$, particulate matter with aerodynamic diameter $<2.5\mathrm{\mu }\mathrm{m}$; RMSE, the root mean square error (micrograms per cubic meter).

Discussion

A novel three-level DEML was developed in this study to estimate the daily concentrations of ${\mathrm{PM}}_{2.5}$ in Italy, in which four base models GBM, SVM, RF, and XGBoost, and three second-level models (RF, XGBoost, and GLM) were constructed with an NNLS algorithm (the third-level model) to obtain the optimal weights for prediction. Our DEML model showed better performance (with $R^2=0.87$, $\text{RMSE}=5.38$) than many previous methodologies, such as the traditional data-fusion model (Friberg et al. 2016), machine learning methods (Chen et al. 2019a; Nordio et al. 2013; Stafoggia et al. 2017, 2019), and some ensemble learning algorithms (Gariazzo et al. 2020; Shtein et al. 2020). The performance of DEML in cluster CV also showed a meaningful improvement in comparison with SL model ($R^2$ of 0.79 VS. 0.50), indicating that the spatial prediction ability of DEML is better than any base models. The DEML model displayed reliable promising performance in ${\mathrm{PM}}_{2.5}$ imputation by ${\mathrm{PM}}_{10}$ and was able to capture above 90% of the spatial and temporal variability of ${\mathrm{PM}}_{2.5}$, especially in the Po Valley in northern Italy, which is one of Europe’s most polluted areas, with severe ${\mathrm{PM}}_{2.5}$ air pollution (Khomenko et al. 2021).

Even though a growing body of ensemble learning models have been reported to estimate the concentrations of air pollutants (Di et al. 2019; Li et al. 2017; Lyu et al. 2019; Shtein et al. 2020; Xiao et al. 2018; Zhai and Chen 2018), few studies have used a multilevel stacked ensemble approach to estimate the daily concentrations of ${\mathrm{PM}}_{2.5}$. Di et al. integrated neural networks, RF, and XGBoost algorithms with a two-stage model to estimate ${\mathrm{PM}}_{2.5}$ across the United States in the period 2005–2015 and reached an $R^2$ of 0.86 for daily ${\mathrm{PM}}_{2.5}$ (Di et al. 2019). Shtein et al. used an ensemble modeling approach by combining LME, RF, XGBoost, and CTMs with a geographically weighted GAM to estimate the daily average concentrations of ${\mathrm{PM}}_{2.5}$ and ${\mathrm{PM}}_{10}$ in Italy from 2013 to 2015 and achieved an $R^2$ from 0.79 to 0.81 (Shtein et al. 2020). In the current study, we found that the performance of the DEML model was comparable to these previous studies by training with a three-level stacked ensemble model in daily ${\mathrm{PM}}_{2.5}$ prediction with an $R^2$ of 0.87. The DEML approach, like the structure of artificial neural networks, consists of layer-by-layer processing of features with a cascading hierarchy structure, in which the ${\mathrm{PM}}_{2.5}$ prediction results processed by four base models are fed to the following three meta-models for further processing. The hierarchical architecture of DEML could enrich the diversity of component learners so that the diverse decision boundaries of the estimators are able to complement each other (Polikar 2012). For example, our constructed learners include boosting (e.g., GBM and XGBoost), bagging (e.g., RF), kernel-based algorithms (e.g., SVM), and regression-based approaches (e.g., GLM). These disparate but complementary algorithms in DEML could produce estimation errors on different instances and make ${\mathrm{PM}}_{2.5}$ prediction contributions varying by locations and concentrations (Zhou 2012). The strategy in our ensemble learning system is, therefore, able to effectively combine several outputs of meta-models to improve the performance of ${\mathrm{PM}}_{2.5}$ estimation.

Consistent with previous ensemble studies (Bai et al. 2019; Di et al. 2019; Lyu et al. 2019; Xiao et al. 2018), our DEML results indicate that hybrid or stacked ensemble models could achieve a better ${\mathrm{PM}}_{2.5}$ prediction performance than a single machine learning model. Much compelling evidence suggests that ensemble models could yield better prediction results when they constitute diverse models (Chandra and Yao 2006; Kuncheva and Whitaker 2003). Like many ensemble models, the disparate models in our DEML could capture the features of complex relationships and spatiotemporal variations between ${\mathrm{PM}}_{2.5}$ and predictors to improve the model performance. For example, the association between temperature and ${\mathrm{PM}}_{2.5}$ tends to be highly nonlinear with complex interactions (Wang et al. 2016). The component nonparametric models in the DEML have the ability to learn complex, nonlinear relationships when given enough data (Chen et al. 2018). Therefore, the advanced combination of several diverse machine learning models in the DEML could present the spatiotemporal variation in ${\mathrm{PM}}_{2.5}$ concentration estimation.

Our DEML technique is an extension of the ensemble SL method, which is an ensemble algorithm increasingly used in epidemiology to improve prediction accuracy and avoid overfitting (Naimi and Balzer 2018). The general SL algorithm involves a two-level ensemble structure using k-fold cross-validation to build the optimal combination of predictions from a library of candidate learners. Compared with SL, the DEML method was constructed with a stacked three-level model structure with an optimal combination of several meta-models and achieved a better ${\mathrm{PM}}_{2.5}$ estimation performance than SL (with an $R^2$ of 0.87 vs. 0.83). Stacking multiple SL models in a hierarchical structure has been proposed previously. Steven Young used a deep super learner (DSL) approach in 2018 by repeating the SL process in a hierarchical structure and achieved accurate results (Young et al. 2018). In the study case, we found that the three-level stacked model can obtain a stable performance in ${\mathrm{PM}}_{2.5}$ estimation.

Our DEML algorithm inherited several key advantages of ensemble SL. First, the DEML relies on the cross-validation to avoid overfitting. In the DEML, both raw input data and subsequent mid-outputs ($Z_1$ matrix) were processed with the k-fold cross-validation analysis to detect the overfitting and selection bias. Another significant advantage of the proposed DEML is its adaptive model selection and asymptotical optimality. Learning from SL (Polley and Van Der Laan 2010), the constituted machine learning algorithms in DEML would be trained simultaneously on the same data set, and the underperformed models will be discarded with a weight of zero. For example, three meta-models (RF, XGBoost, and GLM) in the study were trained independently at the second stage, and the contribution of the GLM algorithm was dropped out with a weight of zero in the final DEML results because of its underperformance. In addition, we used the NNLS algorithm to obtain the optimal combination of a collection of the individual models in DEML. In contrast to GLM (Lyu et al. 2019) and GAM model (Di et al. 2019; Shtein et al. 2020), in which negative contribution may appear in a component model, NNLS could ensure that a nonnegative weight with a minimal loss function can be obtained. The nonnegativity constraint was crucial to guarantee the performance of the DEML model to be better than its constructed single best learner (Zhou 2012) and asymptotically outperform any of its competitors (Polley and Van Der Laan 2010). It is also reasonable to weigh the individual models with a positive coefficient to assess their contributions and importance in air pollution estimation. Therefore, the DEML methodology could evaluate the performance of all constructed models simultaneously and automatically select an optimal integration of a collection of candidate models to reduce the errors due to empirical experience.

Several previous studies (Shtein et al. 2020; Stafoggia et al. 2019) used co-located ${\mathrm{PM}}_{10}$ as the main predictor to fill the missing ${\mathrm{PM}}_{2.5}$ concentrations based on their high correlation. For example, an RF model was applied for ${\mathrm{PM}}_{2.5}$ imputation from the corresponding available ${\mathrm{PM}}_{10}$ in stations across Italy, in which it achieved a CV $R^2$ of 0.87–0.90 for different years in 2013–2015 (Shtein et al. 2020). The performance of our benchmark model, RF, was in line with this previous study with a CV $R^2$ of 0.88 in the study period, whereas the accuracy of our DEML imputation was slightly higher than that of RF, with a CV $R^2$ of 0.91. Therefore, our DEML could be used as an interpolation technique to deal with missing ${\mathrm{PM}}_{2.5}$ data. It was noteworthy that the correlation between the ${\mathrm{PM}}_{10}$ and ${\mathrm{PM}}_{2.5}$ may vary in different meteorological conditions (Munir et al. 2017) and certain transient air pollution events like dust storms and bushfire events (Pereira et al. 2017), which might inflate the variations of DEML estimations in the scenario of ${\mathrm{PM}}_{2.5}$ imputation by ${\mathrm{PM}}_{10}$.

Satellite retrieved AOD has been widely used as a predictor in the estimation of the spatio-temporal distribution of ${\mathrm{PM}}_{2.5}$ (Chen et al. 2019b; Van Donkelaar et al. 2006). However, the large proportion of AOD missing values due to the cloud coverage, water, and snow glint reflectance has become one of the challenges in the application of PM estimation (Di et al. 2019). Additionally, the relationship between AOD and ${\mathrm{PM}}_{2.5}$ concentrations could be affected by many factors, such as meteorological conditions, air pollutants’ spatiotemporal distribution, the decomposition of aerosol types, and different structures in algorithms (Kumar 2010). Several recent studies indicate a disparate contribution of satellite-based AOD on PM prediction in different regions (Chen et al. 2021; Meng et al. 2016; Munir et al. 2017; Pereira et al. 2017). For example, Chen et al. indicated a similar performance by comparing AOD and non-AOD RF models in China. One possible explanation for the limited contribution of AOD in the RF model is that certain predictors such as meteorological variables could explain most of the spatial and temporal variation and the relationship between ${\mathrm{PM}}_{2.5}$ and AOD (Chen et al. 2021). Our study in Italy also revealed a result that is consistent with that previous study by using DEML with and without AOD as one of the predictors. Because RF is an integral part of our DEML model, our algorithm could leverage some advantages from RF and achieved a similar performance in ${\mathrm{PM}}_{2.5}$ prediction without AOD in the model. However, such findings should be interpreted with caution because of the potential uncertainties involved. For example, only the nonmissing values of the satellite AOD had been taken into consideration in the AOD and non-AOD DEML models. Such cloud-free sampling may induce biases in the association with ${\mathrm{PM}}_{2.5}$ (Li et al. 2015).

The DEML algorithm framework can be used in many other domains or other exposure estimation tasks. Because this approach could combine the advantages of each diverse individual learner and adaptively select their combination to produce one optimal predictive model, users can freely adjust the architecture of the DEML framework based on different prediction tasks both for regression and classification to boost the diversity of ensemble model, such as selecting different algorithms or setting different hyperparameters in the same algorithm. Therefore, this DEML framework could minimize the extent of the empirical model selection and parametric assumptions by automatically providing an optimal set of weights for the combination of algorithms to improve the estimation of any environmental exposure or other prediction scenarios.

Several limitations of the DEML approach in the implementation of ${\mathrm{PM}}_{2.5}$ estimation warrant a brief discussion. Although the DEML algorithm showed promising results, we acknowledge that the model performance was biased in some scenarios in Italy with daily average ${\mathrm{PM}}_{2.5}$ concentration above the 95th percentile in this study and in the places that present higher spatial dissimilarity and uncertainties than the average dissimilarity of ground stations. For example, predictions in southern Italy may be less reliable because of fewer monitoring sites and high spatial variability. Additionally, the heteroscedasticity (Gelfand 2015; Rosopa et al. 2013) in ${\mathrm{PM}}_{2.5}$ missing value interpolation should be mentioned. That is to say, the estimation variance increased as the ${\mathrm{PM}}_{2.5}$ observation increased in the range above $5{0\mathrm{\mu }\mathrm{g}/\mathrm{m}}^3$ in this study (Figure S4). The biased prediction was expected because of the high variations in the retrieved ${\mathrm{PM}}_{10}$ and ${\mathrm{PM}}_{2.5}$ concentrations, especially in a certain season like summer when variable atmospheric conditions (Fratianni and Acquaotta 2017) and certain transient air pollution events such as Saharan dust appear frequently in Italy (Mallone et al. 2011). Logarithmic transformations for the depend variable and quantile-based probabilistic models could be applied in the correction of the heteroscedasticity (O’Sullivan et al. 2016; Tofallis 2009; Vasseur and Aznarte 2021). Furthermore, our DEML could not directly deal with missing values. Even though our approach can be regarded as a potential imputation method, using improved missing value imputation technologies is recommended prior to the use of the DEML model. Finally, the specific sources and chemical profile of ${\mathrm{PM}}_{2.5}$ are not available in this study. The implementation of the DEML in other scenarios with various toxicities of ${\mathrm{PM}}_{2.5}$ chemical components is worth further investigation.

In this study, we proposed a novel multiple-level DEML by integrating GBM, SVM, RF, and XGBoost with three meta-models (RF, XGBoost, and GLM) to estimate the daily ${\mathrm{PM}}_{2.5}$ concentrations from 2015 to 2019 in Italy. Benchmarking analysis showed that our model performance is superior to any constructed individual machine learning methods and the SL approach. Our results exhibited that the combination of multiple-level models could improve prediction accuracy. This powerful ensemble learning framework will likely shed more light on the advantage of the ensemble approach in estimating air pollutants and can be regarded as an important extension for SL. It is worth exploring our DEML with other machine learning methods in other realistic scenarios.