Sparse linear discriminant analysis for multiview structured data

Abstract

Classification methods that leverage the strengths of data from multiple sources (multiview data) simultaneously have enormous potential to yield more powerful findings than two-step methods: association followed by classification. We propose two methods, sparse integrative discriminant analysis (SIDA), and SIDA with incorporation of network information (SIDANet), for joint association and classification studies. The methods consider the overall association between multiview data, and the separation within each view in choosing discriminant vectors that are associated and optimally separate subjects into different classes. SIDANet is among the first methods to incorporate prior structural information in joint association and classification studies. It uses the normalized Laplacian of a graph to smooth coefficients of predictor variables, thus encouraging selection of predictors that are connected. We demonstrate the effectiveness of our methods on a set of synthetic datasets and explore their use in identifying potential nontraditional risk factors that discriminate healthy patients at low versus high risk for developing atherosclerosis cardiovascular disease in 10 years. Our findings underscore the benefit of joint association and classification methods if the goal is to correlate multiview data and to perform classification.

1 |. INTRODUCTION

With advancements in technologies, multiple diverse but related high-throughput data, such as gene expression, metabolomics, and proteomics data, are often times measured on the same subject. A common research goal is to effectively synthesize information from these sources of data in a way that goes beyond simply stacking the data to exploit the overall dependency structure among views to identify associated factors (e.g., genetic and environmental [e.g., metabolites ]) that potentially separate subjects into different groups. Popular approaches in the literature for integrative analysis and/or classification studies can broadly be grouped into three categories: association, classification, or joint association and classification methods. The literature on the first two is numerous, but the literature on the latter is rather limited. We focus on developing integrative analysis and classification methods to identify multiview variables that are highly associated and optimally separate subjects into different groups.

1.1 |. Motivating application

Cardiovascular diseases (including atherosclerotic cardiovascular disease (ASCVD)) continue to be the leading cause of death in the United States and have become the costliest chronic disease (American Heart Association, 2016). It is projected that nearly half of the U.S. population will have some form of cardiovascular disease by 2035 and will cost the economy about $2 billion/day in medical costs (American Heart Association, 2016). Established environmental risk factors for ASCVD (e.g., age, gender, and hypertension) account for only half of all cases of ASCVD (Bartels et al., 2012). Finding other novel risk factors of ASCVD unexplained by traditional risk factors is important and may help prevent cardiovascular diseases. Trans-omics integrative analysis can leverage the strengths of omics to further our understanding of the molecular architecture of ASCVD. We integrate gene expression, metabolomics, and/or clinical data from the Emory University and Georgia Tech Predictive Health Institute (PHI) study to identify potential biomarkers beyond established risk factors that can distinguish between subjects at high versus low risk for developing ASCVD in 10 years.

1.2 |. Existing methods

As mentioned earlier, the literature for integrative analysis and/or classification studies can be broadly grouped into three categories: association, classification, or joint association and classification methods. Association-based methods (Hotelling, 1936; Witten and Tibshirani, 2009; Min et al., 2018; Safo et al., 2018) correlate multiple views of data to identify important variables as a first step. This is followed by independent classification analyses that use the identified variables. These methods are largely disconnected from the classification procedure and oblivious of the effects class separation has on the overall dependency structure. The classification-based methods either stack the views and perform classification on the stacked data, or individually use each view in classification algorithms and pool the results. Several classification methods, including Fishers linear discriminant analysis (LDA) (Fisher, 1936) and its variants, may be used. These techniques take no consideration of the dependency structure between the views, and may be computationally expensive if the dimension of each view is large. Finally, the joint association- and classification-based methods (Witten and Tibshirani, 2009; Luo et al., 2016; Li and Li, 2018; Zhang and Gaynanova, 2018) link the problem of assessing associations between multiple views to the problem of classifying subjects into one of two or more groups within each view. The goal is then to identify linear combinations of the variables in each view that are correlated with each other and have high discriminatory power. The method we propose in this paper falls into this category.

1.3 |. Overview of the proposed methods

Our proposal is related to existing joint association- and classification-based methods but our contributions are multifold. First, our formulation of the problem is different from the regression approach largely considered by existing methods; this provides a different insight into the same problem. More importantly, our methods rely on summarized data (i.e., covariances) making them applicable if the individual view cannot be shared due to privacy concerns. Second, while existing association and classification methods concentrate on sparsity (i.e., exclude nuisance predictors), which is mainly data-driven, our SIDANet method is both data- and knowledge-driven. Third, our formulation makes it easy to include other covariates without enforcing sparsity on the coefficients corresponding to the covariates. This is rarely done in integrative analysis and classification methods. Fourth, our formulation of the problem can be solved easily with any off-the-shelf convex optimization software. We develop computationally efficient algorithms that take advantage of parallelism.

The rest of the paper is organized as follows. In Section 2, we briefly discuss the motivation of our proposed methods. In Section 3, we present the proposed methods for two views of data. In Section 4, we introduce the sparse versions of the proposed methods. In Section 5, we present the algorithm for implementing the proposed methods. In Section 6, we conduct simulation studies to assess the performance of our methods in comparison with other methods in the literature. In Section 7, we apply our proposed methods to a real dataset. Discussion and concluding remarks are given in Section 8. Extensions of the methods to more than two views are provided in the Supporting Information.

2 |. MOTIVATION

Suppose that there are two sets of high-dimensional Data ${\mathbf{X}}^1={\left({\mathbf{x}}_1^1,\cdots ,{\mathbf{x}}_n^1\right)}^{\text{T}}\in {\Re }^{n\times p}$ and ${\mathbf{X}}^2={\left({\mathbf{x}}_1^2,\cdots ,{\mathbf{x}}_n^2\right)}^{\text{T}}\in {\Re }^{n\times q}$, $p,q>n$, all measured on the same set of n subjects. For subject $i,i=1,\dots ,n$, let y_i be the class $k(k=1,\dots K)$ membership. Given these data, we wish to predict the class membership y_j of a new subject j using their high-dimensional information ${\mathbf{z}}_j^1\in {\Re }^p$ and ${\mathbf{z}}_j^2\in {\Re }^q$. Several supervised classification methods, including Fishers LDA (Fisher, 1936), may be used to predict class membership when there is only one view of data, but not when there are two views of data. Of note, naively stacking the data and performing LDA on the stacked data does not model the correlation structureamong the different views. On the other hand, unsupervised association methods, including canonical correlation analysis (CCA) (Hotelling, 1936) may be used to study association between the two views of data, but are not suitable when classification is the ultimate goal. We propose two methods for joint association and classification problems that bridge the gap between LDA and CCA. We briefly describe LDA and CCA.

2.1 |. Linear discriminant analysis

For the description of LDA, we suppress the superscript in X. Let ${\mathbf{X}}_k={\left({\mathbf{x}}_{1k},\dots ,{\mathbf{x}}_{n_k,k}\right)}^{\text{T}}\in {\Re }^{n_k\times p}$, ${\mathbf{x}}_k\in {\Re }^p$ be the data matrix for class $k,k=1,\dots ,K$, and n_k is the number of samples in class k. Then, the mean vector for class k, common covariance matrix for all classes, and the between-class covariance are, respectively, given by ${\widehat{\mathit{\mu }}}_k=\left(1/n_k\right){\sum }_{i=1}^{n_k}{\mathbf{x}}_{ik}$; ${\mathbf{S}}_w=\sum _{k=1}^K\sum _{i=1}^n\left({\mathbf{x}}_{ik}-{\widehat{\mathit{\mu }}}_k\right){\left({\mathbf{x}}_{ik}-{\widehat{\mathit{\mu }}}_k\right)}^{\text{T}}$; ${\mathbf{S}}_b=\sum _{k=1}^K{n}_k\left({\widehat{\mathit{\mu }}}_k-\widehat{\mathit{\mu }}\right){\left({\widehat{\mathit{\mu }}}_k-\widehat{\mathit{\mu }}\right)}^{\text{T}}$. Here, $\widehat{\mathit{\mu }}$ is the combined class mean vector and is defined as $\widehat{\mathit{\mu }}=(1/n)\sum _{k=1}^K{n}_k{\widehat{\mathit{\mu }}}_k$. For a k class prediction problem, LDA finds k − 1 direction vectors, which are linear combinations of all available variables, such that projected data have maximal separation between the classes and minimal separation within the classes. Mathematically,the solution to the optimization problem: ${\max }_{{\mathit{\beta }}_k}{\mathit{\beta }}_k^{\text{T}}{\mathbf{S}}_b{\mathit{\beta }}_k$ subject to ${\mathit{\beta }}_k^{\text{T}}{\mathbf{S}}_w{\mathit{\beta }}_k=1$, ${\mathit{\beta }}_l^{\text{T}}{\mathbf{S}}_w{\mathit{\beta }}_k=0\forall l<k$, $k=1,2,\dots ,K-1$ yields the LDA directions that optimally separate the K classes, and these are the eigenvalue–eigenvector pairs $\left({\widehat{\lambda }}_k,{\widehat{\mathit{\beta }}}_k\right),{\widehat{\lambda }}_1>\cdots >{\widehat{\lambda }}_k$ of ${\mathbf{S}}_w^{-1}{\mathbf{S}}_b$ for ${\mathbf{S}}_w\succ 0$.

2.2 |. Canonical correlation analysis

Without loss of generality, we assume that X¹ and X² have zero means for each variable. The goal of CCA (Hotelling, 1936) is to find linear combinations of the variables in X¹, say X¹α and in X², say ${\mathbf{X}}^2\mathit{\beta }$, such that the correlation between these linear combinations is maximized. If S₁ and S₂ are sample covariances of X¹ and X², respectively, and S₁₂ is the p × q sample cross-covariance between X¹ and X²,then mathematically, CCA finds α and β that solve the optimization problem: ${\max }_{\mathit{\alpha },\mathit{\beta }}{\mathit{\alpha }}^{\text{T}}{\mathbf{S}}_{12}\mathit{\beta }$ subject to ${\mathit{\alpha }}^{\text{T}}{\mathbf{S}}_1\mathit{\alpha }=1$ and ${\mathit{\beta }}^{\text{T}}{\mathbf{S}}_2\mathit{\beta }=1$. The solution to the CCA problem is given as $\widehat{\mathit{\alpha }}={\mathbf{S}}_1^{-1/2}{\mathbf{e}}_1$, $\widehat{\mathit{\beta }}={\mathbf{S}}_2^{-1/2}{\mathbf{f}}_1$, where e₁ and f₁ are the first left and right singular vectors of ${\mathbf{S}}_1^{-1/2}{\mathbf{S}}_{12}{\mathbf{S}}_2^{-1/2}$, respectively. Note that maximizing the correlation is equivalent to maximizing the square of the correlation. Hence, the CCA objective can be written as ${\mathit{\alpha }}^{\text{T}}{\mathbf{S}}_{12}\mathit{\beta }{\mathit{\beta }}^{\text{T}}{\mathbf{S}}_{12}^{\text{T}}{\mathit{\alpha }}^{\text{T}}$; we use this in our proposed method.

3 |. DISCRIMINANT ANALYSIS FORTWO VIEWS OF DATA

Consider a K-class classification problem with two sets of variables ${\mathbf{X}}^1\in {\Re }^{n\times p}$ and ${\mathbf{X}}^2\in {\Re }^{n\times q}$ and the class membership vector y. Let S₁₂ be the covariance between X¹ and X². Our goal is to find linear combinations of X¹ and X² that explain the overall association between these views while optimally separating the k classes within each view. These optimal discriminant vectors could be used to effectively classify a new subject into one of the k classes using their available data. We propose a method that combines LDA and CCA. Specifically, we consider the optimization problem below for $\tilde{\mathbf{A}}=\left[{\tilde{\mathit{\alpha }}}_1,\dots ,{\tilde{\mathit{\alpha }}}_{K-1}\right]$ and $\tilde{\mathbf{B}}=\left[{\tilde{\mathit{\beta }}}_1,\dots ,{\tilde{\mathit{\beta }}}_{K-1}\right]$:

$$\begin{gathered} \underset{\mathbf{A},\mathbf{B}}{\max }\rho \text{tr}\left({\mathbf{A}}^{\text{T}}{\mathbf{S}}_b^1\mathbf{A}+{\mathbf{B}}^{\text{T}}{\mathbf{S}}_b^2\mathbf{B}\right) \\ +(1-\rho )\text{tr}\left({\mathbf{A}}^{\text{T}}{\mathbf{S}}_{12}\mathbf{B}{\mathbf{B}}^{\text{T}}{\mathbf{S}}_{12}^{\text{T}}\mathbf{A}\right) \\ \text{subject to}\text{tr}\left({\mathbf{A}}^{\text{T}}{\mathbf{S}}_w^1\mathbf{A}\right)/(K-1)=1, \\ \text{tr}\left({\mathbf{B}}^{\text{T}}{\mathbf{S}}_w^2\mathbf{B}\right)/(K-1)=1. \end{gathered}$$ (1)

Here, tr(.) is the trace function, and ρ is a parameter that controls the relative importance of the first (i.e., “separation”) and second (i.e., “association”) trace terms in the objective. The first trace term in Equation (1) considers the discrimination between classes within each view and the second trace term models the dependency structure between the views through the squared correlation. Essentially, the goal here is to uncover some basis directions that influence both separation and association.We note that the “separation” and “association” terms are loosely defined as the objective could be rewritten so that the separation term also accounts for the covariance between the views. In particular, the cross-covariance, S₁₂, can be decomposed as ${\mathbf{S}}_{12}={\mathbf{S}}_b^{12}+{\mathbf{S}}_w^{12}$ where ${\mathbf{S}}_w^{12}$ and ${\mathbf{S}}_b^{12}$ are defined as follows: ${\mathbf{S}}_w^{12}=\sum _{k=1}^K\sum _{i=1}^n\left({\mathbf{x}}_{ik}^1-{\widehat{\mathit{\mu }}}_k^1\right){\left({\mathbf{x}}_{ik}^2-{\widehat{\mathit{\mu }}}_k^2\right)}^{\text{T}}$; ${\mathbf{S}}_b^{12}=\sum _{k=1}^K{n}_k({\widehat{\mathit{\mu }}}_k^1-{\widehat{\mathit{\mu }}}^1){\left({\widehat{\mathit{\mu }}}_k^2-{\widehat{\mathit{\mu }}}^2\right)}^{\text{T}}$. Here ${\widehat{\mathit{\mu }}}_k^j=\left(1/n_k\right){\sum }_{i=1}^{n_k}{\mathbf{x}}_{ik}^j$, $j=1,2$ and ${\widehat{\mathit{\mu }}}^j$ is the combined class mean vector for view $j,j=1,2$, and is defined as ${\widehat{\mathit{\mu }}}^j=(1/n)\sum _{k=1}^K{n}_k{\widehat{\mathit{\mu }}}_k^j$. We also note that ${\mathbf{S}}_w^{12}$ measures the covariance within the classes and across the two views (we term this within-class cross-covariance), and ${\mathbf{S}}_b^{12}$ measures the covariance between the classes and across the two views (we refer to this as between-class cross-covariance). Ignoring the weights ρ and (1 − ρ) in Equation (1) for now, substituting ${\mathbf{S}}_{12}={\mathbf{S}}_b^{12}+{\mathbf{S}}_w^{12}$ into the second trace term (i.e., association term) in Equation (1), and expanding, we obtain the objective function: ${\max }_{\mathbf{A},\mathbf{B}}\text{tr}({\mathbf{A}}^{\text{T}}{\mathbf{S}}_b^1\mathbf{A}+{\mathbf{B}}^{\text{T}}{\mathbf{S}}_b^2\mathbf{B}+{\mathbf{A}}^{\text{T}}{\mathbf{S}}_b^{12}\mathbf{B}{\mathbf{B}}^{\text{T}}{{\mathbf{S}}_b^{12}}^{\text{T}}\mathbf{A}+2{\mathbf{A}}^{\text{T}}{\mathbf{S}}_b^{12}\mathbf{B}{\mathbf{B}}^{\text{T}}{{\mathbf{S}}_w^{12}}^{\text{T}}\mathbf{A})+\text{tr}\left({\mathbf{A}}^{\text{T}}{\mathbf{S}}_w^{12}\mathbf{B}{\mathbf{B}}^{\text{T}}{{\mathbf{S}}_w^{12}}^{\text{T}}\mathbf{A}\right)$. This and the objective function in Equation (1) both account for the covariance between the views. The “separation” term (first trace term) in this decomposition also models the covariance between the views through both ${\mathbf{S}}_b^{12}$ and ${\mathbf{S}}_w^{12}$, while the “association” term in Equation (1) models the covariance, also through ${\mathbf{S}}_b^{12}$ and ${\mathbf{S}}_w^{12}$. We prefer Equation (1) because when we add in the weights ρ and $(1-\rho )$, respectively, to the first and second terms in this new decomposition, and we let ρ = 1 or ρ = 0, our objective in Equation (1) has a nice property in that it reduces to LDA or CCA, respectively, while this decomposition does not. Consider optimizing Equation (1) above using Lagrangian multipliers. One can show that the solution reduces to a set of generalized eigenvalue (GEV) problems. Theorem 1 gives a formal representation of the solution to the optimization problem (1).

Theorem 1.

Let ${\mathbf{S}}_w^1$, ${\mathbf{S}}_w^2$ and ${\mathbf{S}}_b^1$, ${\mathbf{S}}_b^2$, respectively, be withinscatter and between-scatter covariances for X¹ and X². Let S₁₂ be the covariance between the two views of data. Assume ${\mathbf{S}}_w^1\succ 0$, ${\mathbf{S}}_w^2\succ 0$. Then $\mathbf{A}={\left({\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_r\right)}^T\in {\Re }^{p\times r}$, $\mathbf{B}={\left({\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_r\right)}^T\in {\Re }^{q\times r}$, $k=1,\dots ,r$ are eigenvectors corresponding respectively to eigenvalues ${\mathbf{\Lambda }}_1=diag\left({\lambda }_{1_k},\dots ,{\lambda }_{1_r}\right)$ and ${\mathbf{\text{Λ}}}_2=diag\left({\lambda }_{2_k},\dots ,{\lambda }_{2_r}\right)$, ${\lambda }_{1_k}>\cdots >{\lambda }_{1_r}>0$, ${\lambda }_{2_k}>\cdots >{\lambda }_{2_r}>0$ that iteratively solve the geGEV system:

$$\begin{gathered} \left(\rho {\mathbf{S}}_b^1+\rho {{\mathbf{S}}_b^1}^T+(1-\rho ){\mathbf{\Omega }}^1+(1-\rho ){{\mathbf{\Omega }}^1}^T\right) \\ \mathbf{A}=\left({\mathbf{S}}_w^1+{{\mathbf{S}}_w^1}^T\right){\mathbf{\text{Λ}}}_1\mathbf{A}, \end{gathered}$$ (2)

$$\begin{gathered} \left(\rho {\mathbf{S}}_b^2+\rho {{\mathbf{S}}_b^2}^T+(1-\rho ){\mathbf{\Omega }}^2+(1-\rho ){{\mathbf{\Omega }}^2}^T\right) \\ \mathbf{B}=\left({\mathbf{S}}_w^2+{{\mathbf{S}}_w^2}^T\right){\mathbf{\Lambda }}_2\mathbf{B}, \end{gathered}$$ (3)

where ${\mathbf{\Omega }}^1={\mathbf{S}}_{12}\mathbf{B}{\mathbf{B}}^{\text{T}}{\mathbf{S}}_{12}^{\text{T}}$ and ${\mathbf{\Omega }}^2={\mathbf{S}}_{12}^{\text{T}}\mathbf{A}{\mathbf{A}}^{\text{T}}{\mathbf{S}}_{12}$. Equations (2) and (3) may be solved iteratively by fixing B and solving an eigensystem for A, and then fixing A and solving an eigensystem in (3) for B. The algorithm may be initialized using any arbitrary normalized nonzero vector. With B fixed at B* in (2), the solution is the eigenvalue–eigenvector pair of ${\left({\mathbf{S}}_w^1+{{\mathbf{S}}_w^{\text{1}}}^T\right)}^{-1}(\rho {\mathbf{S}}_b^1+\rho {{\mathbf{S}}_b^1}^T+(1-\rho ){\mathbf{\Omega }}^1+(1-\rho ){{\mathbf{\Omega }}^1}^{\text{T}})$. With A fixed at A* in (3), the solution of (3) is the eigenvalue–eigenvector pair of ${\left({\mathbf{S}}_w^2+{{\mathbf{S}}_w^2}^{\text{T}}\right)}^{-1}\left(\rho {\mathbf{S}}_b^2+\rho {{\mathbf{S}}_b^2}^{\text{T}}+(1-\rho ){\mathbf{\Omega }}^2+(1-\rho ){{\mathbf{\Omega }}^2}^T\right)$.

We rewrite the optimization problem (1) and the generalized eigensystems (2) and (3) equivalently so that we solve a system of eigenvalue problems to facilitate computations. We omit its proof for brevity sake because it follows easily from (1). Let ${\mathcal{M}}^1={\mathbf{S}}_w^{1^{-1/2}}{\mathbf{S}}_b^1{\mathbf{S}}_w^{1^{-1/2}}$, ${\mathcal{M}}^2={\mathbf{S}}_w^{2^{-1/2}}{\mathbf{S}}_b^2{\mathbf{S}}_w^{2^{-1/2}}$. Also, let ${\mathcal{N}}_{12}={\mathbf{S}}_w^{1^{-1/2}}{\mathbf{S}}_{12}{\mathbf{S}}_w^{2^{-1/2}}$ and ${\mathcal{N}}_{21}={\mathbf{S}}_w^{2^{-1/2}}{\mathbf{S}}_{12}^{\text{T}}{\mathbf{S}}_w^{1^{-1/2}}$.

Proposition 1.

The maximizer (1) is equivalent to $(\tilde{\mathbf{A}},\tilde{\mathbf{B}})=\left({\mathbf{S}}_w^{1-1/2}\tilde{{\mathbf{\text{Γ}}}^1},{\mathbf{S}}_w^{2^{-1/2}}\tilde{{\mathbf{\text{Γ}}}^2}\right)$ where

$$\left(\widetilde{{\mathbf{\Gamma }}^1},\widetilde{{\mathbf{\Gamma }}^2}\right)=\underset{{\mathbf{\Gamma }}^1,{\mathbf{\Gamma }}^2}{\max }\rho tr\left({\mathbf{\Gamma }}^{1T}{\mathcal{M}}^1{\mathbf{\Gamma }}^1+{\mathbf{\Gamma }}^{2T}{\mathcal{M}}^2{\mathbf{\Gamma }}^2\right)$$

$$+(1-\rho )tr\left({\mathbf{\Gamma }}^{1T}{\mathcal{N}}_{12}{\mathbf{\Gamma }}^2{\mathbf{\Gamma }}^{2T}{\mathcal{N}}_{21}{\mathbf{\Gamma }}^1\right)$$

$$subject\mathit{\text{to}}tr\left({\mathbf{\Gamma }}^{1T}{\mathbf{\Gamma }}^1\right)/(K-1)=1,$$

$$tr\left({\mathbf{\Gamma }}^{2T}{\mathbf{\Gamma }}^2\right)/(K-1)=1.$$

Furthermore, this yields the equivalent eigensystem problems of (4) and (5)

$$\left(\rho {\mathcal{M}}^1+\rho {{\mathcal{M}}^1}^T+(1-\rho ){\overline{\mathcal{N}}}_{12}+(1-\rho ){\overline{\mathcal{N}}}_{12}^T\right){\mathbf{\Gamma }}^1={\mathbf{\Lambda }}_1{\mathbf{\Gamma }}^1,$$ (4)

$$\left(\rho {\mathcal{M}}^2+\rho {{\mathcal{M}}^2}^T+(1-\rho ){\overline{\mathcal{N}}}_{21}+(1-\rho ){\overline{\mathcal{N}}}_{21}^T\right){\mathbf{\Gamma }}^2={\mathbf{\Lambda }}_2{\mathbf{\Gamma }}^2,$$ (5)

where ${\overline{\mathcal{N}}}_{12}={\mathcal{N}}_{12}{\mathbf{\Gamma }}^2{\mathbf{\Gamma }}^{2^T}{\mathcal{N}}_{21}$ and ${\overline{\mathcal{N}}}_{21}={\mathcal{N}}_{21}{\mathbf{\text{Γ}}}^1{\mathbf{\text{Γ}}}^{1^T}{\mathcal{N}}_{12}.$.

3.1 |. SPARSE LDA FOR TWO VIEWS OF DATA

In the high-dimensional setting where $n\ll p$, ${\mathbf{\Gamma }}^1$ and ${\mathbf{\text{Γ}}}^2$ are weight matrices of all available variables in X¹ and X². These coefficients are not usually zero (i.e., not sparse) making interpreting the discriminant functions challenging. We propose to make ${\mathbf{\Gamma }}_1$ and ${\mathbf{\Gamma }}_2$ sparse by imposing convex penalties subject to modified eigensystem constraints. Our approach follows ideas in Safo et al. (2018), which is, in turn, motivated by the Dantzig selector (DS) (Candes and Tao, 2007). The DS was designed for linear regression models where the number of variables is large but the set of regression coefficients is sparse, and it was shown to have desirable theoretical properties. It has successfully been used for LDA (Cai and Liu, 2011) and has also shown impressive performance in real world applications for large p. It is easy to understand and is readily solved by any off-the-shelf convex optimization software. We impose penalties that depend on whether or not prior knowledge in the form of functional relationships is available. In what follows, for a vector $\mathbf{v}\in {ℝ}^p$, we define $\parallel \mathbf{v}{\parallel }_{\infty }={\max }_{i=1,\cdots ,p}\left|v_i\right|$, $\parallel \mathbf{v}{\parallel }_1={\sum }_{i=1}^p\left|v_i\right|$, and $\parallel \mathbf{v}{\parallel }_2=\sqrt{{\sum }_{i=1}^p{v}_i^2}$. For a matrix $\mathbf{M}\in {ℝ}^{n\times p}$, we define ${\mathbf{m}}_i$ to be its ith row, m_ij to be its i,jth entry, and define the maximum absolute row sum $\parallel \mathbf{M}{\parallel }_{\infty }={\max }_{1\le i\le n}{\sum }_{j=1}^p\left|m_{ij}\right|$.

3.1.1 |. Sparse integrative discriminant analysis (SIDA)

Let ${\mathbf{\Gamma }}^1={\left({\gamma }_1^1,\dots ,{\gamma }_p^1\right)}^{\text{T}}\in {\Re }^{p\times K-1}$ and ${\text{Γ}}^2={\left({\gamma }_1^2,\dots ,{\gamma }_q^2\right)}^{\text{T}}\in {\Re }^{q\times K-1}$ denote the collection of basis vectors that solve the eigensystems (4). To achieve sparsity, we define the following block l₁∕l₂ penalty functions that consider the length of row elements in ${\mathbf{\Gamma }}^1$ and ${\mathbf{\text{Γ}}}^2$ and shrinks the row vectors of irrelevant variables to zero:

$$\mathcal{P}\left({\mathbf{\Gamma }}^d\right)=\sum _{i=1}^{p\text{ or }q}{\parallel {\gamma }_i^d\parallel }_2,d=1,2.$$ (6)

We note that variables with null effects are encouraged to have zero coefficients simultaneously in all basis directions. This is because the block l₁∕l₂ penalty applies the l₂-norm ${\parallel {\mathit{\gamma }}_i^d\parallel }_2$ within each variable, and the l₁-norm across variables, and thus, shrinks the row length to zero. This results in coordinate-independent variable selection, making it appealing for screening irrelevant variables. With penalty (6), we obtain sparse solutions ${\widehat{\mathbf{\text{Γ}}}}^1$ and ${\widehat{\mathbf{\text{Γ}}}}^2$ by iteratively solving the following convex optimization problems for fixed ${\mathbf{\text{Γ}}}^1$ or ${\mathbf{\Gamma }}^2$:

$$\begin{gathered} \underset{{\mathbf{\text{Γ}}}^1}{\min }\sum _{i=1}^p{\parallel {\mathit{\gamma }}_i^1\parallel }_2\text{s.t}\parallel (\rho {\mathcal{M}}^1+\rho {\mathcal{M}}^{1^{\text{T}}} \\ +(1-\rho ){\overline{\mathcal{N}}}_{12}+(1-\rho ){\overline{\mathcal{N}}}_{12}^{\text{T}}){\tilde{\mathbf{\Gamma }}}^1-{\tilde{\mathbf{\Lambda }}}_1{\mathbf{\Gamma }}^1{\parallel }_{\infty }\le {\tau }_1 \\ \underset{{\mathbf{\text{Γ}}}^2}{\min }\sum _{i=1}^q{\parallel {\mathit{\gamma }}_i^2\parallel }_2\text{s.t}\parallel (\rho {\mathcal{M}}^2+\rho {{\mathcal{M}}^2}^{\text{T}} \\ +(1-\rho ){\overline{\mathcal{N}}}_{21}+(1-\rho ){\overline{\mathcal{N}}}_{21}^{\text{T}}){\tilde{\mathbf{\Gamma }}}^2-{\tilde{\mathbf{\Lambda }}}_2{\mathbf{\Gamma }}^2{\parallel }_{\infty }\le {\tau }_2. \end{gathered}$$ (7)

Equation (7) essentially constrains the first and second eigensystems (4) to be within τ₁ and τ₂, respectively. It can be easily shown that naively constraining the eigensystems result in trivial solutions. Hence, we substitute ${\mathbf{\Gamma }}^1$ and ${\mathbf{\text{Γ}}}^2$ in the left-hand side (LHS) of the eigensystem problems in (4), respectively, with ${\tilde{\mathbf{\Gamma }}}^1$ and ${\tilde{\mathbf{\Gamma }}}^2$, the nonsparse solutions that solve equation (4). Here, $\left({\widetilde{\mathbf{\text{Λ}}}}_1,{\widetilde{\mathbf{\text{Λ}}}}_2\right)$ are the eigenvalues corresponding to ${\tilde{\mathbf{\Gamma }}}^1$ and ${\widetilde{\mathbf{\text{Γ}}}}^2$. Also, $\left({\tau }_1,{\tau }_2\right)$ are tuning parameters controlling the level of sparsity; their selection will be discussed in Section 6. ${\widehat{\mathbf{\Gamma }}}^1$ may be obtained from (7) by fixing ${\mathbf{\text{Γ}}}^2$ (definition of ${\overline{\mathcal{N}}}_{12}$ involves ${\mathbf{\text{Γ}}}^2$). Similarly, ${\widehat{\mathbf{\text{Γ}}}}^2$ may be obtained by fixing ${\mathbf{\Gamma }}^1$. The solutions $\left({\widehat{\mathbf{\text{Γ}}}}^1,{\widehat{\mathbf{\text{Γ}}}}^2\right)$ may not necessarily be orthogonal, as such we use Gram–Schmidt orthogonalization on $\left({\widehat{\mathbf{\Gamma }}}^1,{\widehat{\mathbf{\Gamma }}}^2\right)$. We note that Equation (7) can be equivalently written as ${\min }_{{\mathbf{\Gamma }}^1}{\parallel (\rho {\mathcal{M}}^1+\rho {\mathcal{M}}^{1^T}+(1-\rho ){\overline{\mathcal{N}}}_{12}+(1-\rho ){\overline{\mathcal{N}}}_{12}^T){\tilde{\mathbf{\Gamma }}}^1-{\tilde{\mathbf{\Lambda }}}_1{\mathbf{\Gamma }}^1\parallel }_{\infty }+{\tau }_1^{\ast }{\sum }_{i=1}^p{\parallel {\mathbf{\Gamma }}_i^1\parallel }_2,{\tau }_1^{\ast }>0$ (similarly for solving ${\mathbf{\text{Γ}}}^2$), but we use our current formulation as it follows closely the DS approach.

Remark 1. Inclusion of covariates:

Our optimization problems in (7) make it easy to include other covariates to potentially guide the selection of relevant variables likely to improve classification accuracy. Assume that τ₂ is set to zero (no penalty on the corresponding coefficients). Then ${\widetilde{\mathbf{\text{Γ}}}}^2$ solves the second optimization problem. But the basis discriminant directions ${\widehat{\mathbf{\Gamma }}}^1$ for the first view of data depend on the second view (X²) through the covariance matrix S₁₂. Thus, to account for the influence of covariates in the optimal basis discriminant directions, one could always include the available covariates (as a separate view) and set the corresponding tuning parameter to zero. This forces data from the covariates to be used in assessing associations and discrimination without necessarily shrinking their effects to zero. For binary (e.g., biological sex) or categorical covariates (assumes no ordering), we suggest the use of indicator variables (Gifi, 1990). RRefer to Section 10.4 in the Supporting Information for a simulation example.

3.1.2 |. SIDA for structured data (SIDANet)

We introduce SIDANet for structured or network data. SIDANet utilizes prior knowledge about variable–variable interactions (e.g., protein–protein interactions) in the estimation of the sparse integrative discriminant vectors. Incorporating prior knowledge about variable–variable interactions can capture complex bilateral relationships between variables. It has potential to identify functionally meaningful variables (or network of variables) within each view for improved classification performance, as well as aid in interpretation of variables.

Many databases exist for obtaining information about variable–variable relationships. One such database for protein–protein interactions is the human protein reference database (HPRD) (Peri et al., 2003). We capture the variable–variable connectivity within each view in our sparse discriminant vectors via the normalized Laplacian (Chung and Graham, 1997) obtained from the underlying graph. Let ${\mathcal{G}}^d=\left(V^d,E^d,W^d\right)$, $d=1,2$ be a network given by a weighted undirected graph. V^d is the set of vertices corresponding to the p^d variables (or nodes) for the dth view of data. Let $E^d=\{u\sim v\}$ if there is an edge from variable u to v in the dth view of data. W^d is the weight of an edge for the dth view satisfying $w(u,v)=w(v,u)\ge 0$. Note that if $\{u,v\}\notin E(G)$, then $w(u,v)=0$. Denote r_v as the degree of vertex v within each view; $r_v={\sum }_{u}w(u,v)$. The normalized Laplacian of ${\mathcal{G}}^d$ for the dth view is

$${\mathcal{L}}_n(u,v)$$ (8)

$$=\{\begin{array}{ll}1-w(u,v)/r_v& \text{if}u=v\text{and}{r}_v\ne 0\\ -\frac{w(u,v)}{\sqrt{r_u{r}_v}}& \text{if}u\ne v\text{and variables}u\text{and}vareadjacent\\ 0& \text{otherwise}.\end{array}$$

The matrix ${\mathcal{L}}_n(u,v)$ is usually sparse (has many zeros) and so can be stored with sparse functions in any major software programs such as R or Matlab. For smoothness while incorporating prior information, we impose the following penalty:

$$\mathcal{P}\left({\mathbf{\Gamma }}^d\right)=\eta \sum _{i=1}^{p^d}{\parallel {\gamma }_i^{{\mathcal{L}}_n}\parallel }_2+(1-\eta )\sum _{i=1}^{p^d}{\parallel {\gamma }_i\parallel }_2.$$ (9)

${\gamma }_i^{{\mathcal{L}}_n}$ is the ith row of the matrix product ${\mathcal{L}}_n{\mathbf{\Gamma }}^d$. Note that ${\mathcal{L}}_n(u,v)$ is different for each view. The first term in Equation (9) acts as a smoothing operator for the weight matrices ${\mathbf{\Gamma }}^d$ so that variables that are connected within the dth view are encouraged to be selected or neglected together. Note that because we use the normalized laplacian, the coefficients of variables that are connected may not be the same; this will capture each variable’s contribution to overall objective. The second term in Equation (9) enforces sparsity of variables within the network; this is ideal for eliminating variables or nodes that contribute less to the overall association and discrimination relative to other nodes within the network. $\eta$ balances these two terms. Several $\eta$ values in the range (0,1) can be considered with the $\eta$ that yields higher classification accuracy and/or correlation chosen.

3.2 |. INITIALIZATION, TUNING PARAMETERS, AND ALGORITHM

In Section 6 of the Supporting Information, we extend the proposed methods to more than two views. The optimization problems in Equations (7) and (6) in the Supporting Information are biconvex. With ${\mathbf{\text{Γ}}}^d$ fixed at ${\mathbf{\Gamma }}^{d^{\ast }}$, the problem of solving for ${\widehat{\mathbf{\Gamma }}}^j$, $j\ne d$ is convex, and may be solved easily with any-off-the shelf convex optimization software. At the first iteration, we fix ${\mathbf{\Gamma }}^{d^{\ast }}$ as the classical LDA solution from applying LDA on ${\mathbf{X}}^d$. We can initiate ${\mathbf{\Gamma }}^{d^{\ast }}$ with random orthonormal matrices, but we choose to initialize with regular LDA solutions because the algorithm converges faster. Algorithm 1 in the Supporting Information gives an outline of our proposed methods. The optimization problems depend on tuning parameters τ_d, which need to be chosen. We fix ρ = 0.5 to provide equal weight on separation and association. Without loss of generality, assume that the Dth (last) view is the covariates, if available. We fix τ_D = 0 and select the optimal tuning parameters for the other views from a range of tuning parameters. Note that searching the tuning parameters hyperspace can be computationally intensive. To overcome this computational bottleneck, we follow ideas in Bergstra and Bengio (2012) and randomly select some grid points (from the entire grid space) to search for the optimal tuning parameters; we term this approach random search. Our simulations with random search produced satisfactory results (Tables 2–4) compared to grid search. A detailed comparison of random and grid search is found in Section 7 in the Supporting Information. Our approach for classifying future observations is found in the Supporting Information.

TABLE 2.

Scenario 1: all four networks contribute to separation of classes within each dataset and association between the three views of data. Scenario 2: two networks contribute to both separation and association. FNSLDA (Ens) applies fused sparse LDA on separate views and perform classification on the combined discriminant vectors. FNSLDA (Stack) applies fused sparse LDA on stacked views. TPR-1; true positive rate for X¹. Similar for TPR-2 and TPR-3. FPR; false positive rate for X². Similar for FPR-2 and FPR-3; F-1 is F-measure for X¹. Similar for F-2 and F-3

Method	Error (%)	$\widehat{\rho }$	TPR-1	TPR-2	TPR-3	FPR-1	FPR-2	FPR-3	F-1	F-2	F-3
Scenario 1
SIDANet (RS)	1.57	0.87	99.88	99.25	98.00	1.49	4.12	2.28	87.79	67.88	80.24
SIDANet (GS)	1.81	0.87	99.25	98.88	94.25	1.92	1.31	0.92	85.26	88.94	89.93
FNSLDA (Ens)	1.59	0.88	100.00	100.00	100.00	7.25	2.00	2.83	75.80	85.29	82.01
FNSLDA (Stack)	1.50	0.87	100.00	100.00	100.00	8.95	9.04	8.81	79.34	78.67	79.15
Scenario 2
SIDANet (RS)	3.69	0.88	99.50	100.00	91.75	1.40	2.31	1.01	78.85	65.16	74.21
SIDANet (GS)	3.78	0.88	100.00	99.75	86.50	1.39	0.95	0.31	79.18	86.05	85.05
FNSLDA (Ens)	4.03	0.87	100.00	100.00	100.00	7.01	4.46	12.55	52.43	52.91	44.25
FNSLDA (Stack)	3.73	0.85	100.00	100.00	100.00	16.63	16.46	16.80	38.52	38.52	38.49

TABLE 4.

Comparison of AUCs using genes and m/z features identified. We run a logistic regression model on the training data to obtain effect sizes (logarithm of the odds ratio of the probability that ASCVD risk group is high) for each gene or m/z feature. The genetic risk score (GRS) or metabolomic risk score (MRS) are each obtained as a sum of the genes or m/z features in the testing data set, weighted by the effect sizes. Model 1 (M1): Age + gender; Model 2 (M2): Age + gender + gene risk score (GRS); Model 3 (M3): Age + gender + metabolomic risk score (MRS). Model 4 (M4): Age + gender + gene risk score (GRS) + metabolomic risk score (MRS). The genes and m/z features identified by the methods on the training datasets are used to calculate GRS and MRS

	Minimum	Mean	Median	Maximum
M1	0.71	0.79	0.79	0.86
M2: M1 + GRS
SIDA	0.82	0.89	0.90	0.94
SIDANet	0.86	0.94	0.94	0.98
JACA	0.87	0.93	0.93	0.97
sCCA	0.71	0.80	0.80	0.90
M3: M1 + MRS
SIDA	0.79	0.85	0.84	0.91
SIDANet	0.81	0.87	0.86	0.95
JACA	0.81	0.90	0.92	0.97
sCCA	0.72	0.80	0.81	0.87
M4: M1 + GRS + MRS
SIDA	0.84	0.91	0.91	0.95
SIDANet	0.89	0.95	0.95	1.00
JACA	0.89	0.96	0.96	1.00
sCCA	0.71	0.81	0.81	0.90

3.3 |. SIMULATIONS

We consider two main simulation examples to assess the performance of the proposed methods in identifying important variables and/or networks that optimally separate classes while maximizing association between multiple views of data. In the first example, we simulate a D = 2, K = 3 class discrimination problem and assume that there is no prior information available. Refer to the Supporting Information for more simulation scenarios including a scenario with covariates as a third view. In the second example, we simulate a D = 3 and K = 3 class problem and assume that prior information is available in the form of networks. In each example, we generate 20 Monte Carlo datasets for each view.

3.3.1 |. Example 1: Simulation settings when no prior information is available

Scenario 1 (multiclass, equal covariance with class). : The first view of data X¹ has P variables and the second view X² has q variables, all drawn on the same samples with size n = 240. Each view is a concatenation of data from three classes, that is, ${\mathbf{X}}^d=\left[{\mathbf{X}}_1^d,{\mathbf{X}}_2^d,{\mathbf{X}}_3^d\right]$, $d=1,2$. The combined data $\left({\mathbf{X}}_k^1,{\mathbf{X}}_k^2\right)$ for each class are simulated from $N\left({\mathit{\mu }}_k,\mathbf{\text{Σ}}\right)$, where ${\mathit{\mu }}_k={\left({\mathit{\mu }}_k^1,{\mathit{\mu }}_k^2\right)}^{\text{T}}\in {\Re }^{p+q}$, $k=1,2,3$ is the combined mean vector for class $k;{\mathit{\mu }}_k^1\in {\Re }^p$, ${\mathit{\mu }}_k^2\in {\Re }^q$ are the mean vectors for ${\mathbf{X}}_k^1$ and ${\mathbf{X}}_k^2$, respectively. The true covariance matrix Σ is partitioned as

$$\mathbf{\Sigma }=\left(\begin{array}{cc}{\mathbf{\Sigma }}^1& {\mathbf{\Sigma }}^{12}\\ {\mathbf{\Sigma }}^{21}& {\mathbf{\Sigma }}^2\end{array}\right),{\mathbf{\Sigma }}^1=\left(\begin{array}{cc}{\widetilde{\mathbf{\text{Σ}}}}^1& \mathbf{0}\\ \mathbf{0}& {\mathbf{I}}_{p-20}\end{array}\right),{\mathbf{\Sigma }}^2=\left(\begin{array}{cc}{\widetilde{\mathbf{\text{Σ}}}}^2& \mathbf{0}\\ \mathbf{0}& {\mathbf{I}}_{q-20}\end{array}\right),$$

where ${\mathbf{\text{Σ}}}^1$ and ${\mathbf{\text{Σ}}}^2$ are, respectively, the covariance of X¹ and X², and ${\mathbf{\text{Σ}}}^{12}$ is the cross covariance between the two views. ${\widetilde{\mathbf{\text{Σ}}}}^1$ and ${\widetilde{\mathbf{\text{Σ}}}}^2$ are each block diagonal with two blocks of size 10, between-block correlation 0, and each block is a compound symmetric matrix with correlation .8. We generate ${\mathbf{\text{Σ}}}^{12}$ as follows. Let ${\mathbf{V}}^1={\left[{\mathbf{V}}_1^1,{\mathbf{0}}_{(p-20)\times 2}\right]}^{\text{T}}\in {\Re }^{p\times 2}$ where the entries of $V_1^1\in {\Re }^{20\times 2}$ are i.i.d. samples from U(0.5,1). We similarly define V² for the second view, and we normalize such that ${\mathbf{V}}^{1^T}{\mathbf{\Sigma }}^1{\mathbf{V}}^1=\mathbf{I}$ and ${{\mathbf{V}}^2}^{\text{T}}{\mathbf{\Sigma }}^2{\mathbf{V}}^2=\mathbf{I}$. We then set ${\mathbf{\text{Σ}}}^{12}={\mathbf{\text{Σ}}}^1{\mathbf{V}}^1\mathbf{D}{{\mathbf{V}}^2}^T{\mathbf{\Sigma }}^2$, $\mathbf{D}=\text{diag}\left({\rho }_1,{\rho }_2\right)$. We vary ρ₁ and ρ₂ to measure the strength of the association between X¹ and X². For separation between the classes, we take μ_K to be the Kth column of $\left[\mathbf{\Sigma }\mathbf{A},{\mathbf{0}}_{p+q}\right]\in {\Re }^{(p+q)\times 3}$, and $\mathbf{A}={\left[{\mathbf{A}}^1,{\mathbf{A}}^2\right]}^{\text{T}}\in {\Re }^{(p+q)\times 2}$. Here, the first column of ${\mathbf{A}}^1\in {\Re }^{p\times 2}$ is set to $\left(c{\mathbf{1}}_{10},{\mathbf{0}}_{p-10}\right)$; the second column is set to $\left({\mathbf{0}}_{10},-c{\mathbf{1}}_{10},{\mathbf{0}}_{p-20}\right)$. We set ${\mathbf{A}}^2\in {\Re }^{q\times 2}$ similarly. We vary c to assess discrimination between the classes, and we consider three combinations of $\left({\rho }_1,{\rho }_2,c\right)$ to assess both discrimination and strength of association. For each combination, we consider equal class size n_k = 80, and dimensions (p∕q = 2000∕2000). The true integrative discriminant vectors are the generalized eigenvectors that solve Theorem 1. Figure S1 in the Supporting Information is a visual representation of random data projected onto the true integrative discriminant vectors for different combinations of c, ρ₁, and ρ₂.

Competing methods

We compare SIDA with classification- and/or association-based methods. For the classification-based method, we consider Multi-Group Sparse Discriminant Analysis (MGSDA) (Gaynanova et al., 2016) and either apply MGSDA on the stacked data (MGSDA (Stack)), or apply MGSDA on separate datasets (MGSDA (Ens)). To perform classification for MGSDA (Ens), we pool the discriminant vectors from the separate MGSDA applications, and apply the pooled classification algorithm discussed in the Supporting Information. For association-based methods, we consider the sparse CCA (sCCA) method (Safo et al., 2018). We perform sCCA using the Matlab code the authors provide, pool the canonical variates, and perform classification in a similar way as MGSDA (Ens). We also compare SIDA to JACA (Zhang and Gaynanova, 2018), a method for joint association and classification studies. We use the R package provided by the authors, and set the number of cross-validation folds as 5.

Evaluation criteria

We evaluate the methods using the following criteria: (1) test misclassification rate, (2) selectivity, and (3) estimated correlation. We consider three measures to capture the methods ability to select true signals while eliminating false positives: true positive rate (TPR), false positive rate (FPR), and F₁ score defined as follows: $TPR=\frac{TP}{TP+FN}$, $FPR=\frac{FP}{FP+TN}$, $F_1\text{score}=\frac{2TP}{2TP+FP+FN}$, where TP, FP, TN,and FN are defined, respectively, as true positives, false positives, true negatives, and false negatives. We estimate the overall correlation, $\widehat{\rho }$, by summing estimated pairwise unique correlations obtained from the R-vector (RV) coefficient (Robert and Escoufier, 1976). The RV coefficient for two centered matrices $\mathcal{X}\in {\Re }^{n\times k}$ and $\mathcal{Y}\in {\Re }^{n\times k}$ is defined as $RV(\mathcal{X},\mathcal{Y})=\frac{tr\left({\text{Σ}}_{\mathcal{X}\mathcal{Y}}{\text{Σ}}_{\mathcal{Y}\mathcal{X}}\right)}{\sqrt{tr\left({\text{Σ}}_{\mathcal{X}\mathcal{X}}^2\right)tr\left({\text{Σ}}_{\mathcal{Y}\mathcal{Y}}^2\right)}}$. The RV coefficient generalizes the squared Pearson’s correlation coefficient to multivariate data sets. We obtain the estimated correlation as $\widehat{\rho }=\frac{2}{D(D-1)}{\sum }_{d=1,d\ne j}^{D}RV\left({\mathbf{X}}_{test}^d{\widehat{\mathbf{\Gamma }}}^d,{\mathbf{X}}_{test}^j{\widehat{\mathbf{\Gamma }}}^j\right)$, $\widehat{\rho }\in [0,1]$

Results

Tables 1 shows the averages of the evaluation measures from 20 repetitions, for scenarios 1 and 2 (refer to the Supporting Information for other scenarios). We first compare SIDA with random search (SIDA(RS)) to SIDA with grid search (SIDA(GS)). We note that across all evaluation measures, SIDA (RS) tends to be better or similar to SIDA (GS). In terms of computational time, SIDA (RS) is faster than SIDA (GS) (refer to the Supporting Information). This suggests that we can choose optimal tuning parameters at a lower computational cost by randomly selecting grid points from the entire tuning parameter space and searching over those grid values, and still achieve similar or even better performance compared to searching over the entire grid space. We next compare SIDA with an association-based method, sCCA. In scenario 1, across all settings, we observe that SIDA (especially SIDA (RS)) tends to perform better than sCCA. Compared to a classification-based method, MGSDA (either Stack or Ens), SIDA has a lower error rate, higher estimated correlations (except in setting 3), higher TPR, and higher F₁ scores. Similar results hold for scenarios 2 and 3 (Supporting Information). When compared to JACA, a joint association- and classification-based method, for scenarios 1 and 2, SIDA has lower error rates in setting 1, and comparable error rates in settings 2 and 3. In terms of selectivity, SIDA has comparable TPR in setting 1, lower TPR in setting 2, higher TPR in setting 3, lower or comparable FPR, comparable estimated correlations, and higher F₁ scores in settings 1 and 2. These simulation results suggest that joint integrative- and classification-based methods, SIDA and JACA, tend to out-perform association- or classification-based methods. In addition, the proposed method, SIDA, tends to be better than JACA in the scenarios where the views are moderately or strongly correlated,and the separation between the classes is not weak.

TABLE 1.

Scenario 1: RS; randomly select tuning parameters space to search. GS; search entire tuning parameters space. MGSDA (Ens) applies sparse LDA method on separate views and perform classification on the pooled discriminant vectors. MGSDA (Stack) applies sparse LDA on stacked views. TPR-1; true positive rate for X¹. Similar for TPR-2. FPR; false positive rate for X². Similar for FPR-2; F-1 is F-measure for X¹. Similar for F-2. ρ₁ and ρ₂ control the strength of association between X¹ and X². c controls the between-class variability within each view

Method	Error (%)	$\widehat{\rho }$	TPR-1	TPR-2	FPR-1	FPR-2	F-1	F-2
Setting 1
(ρ1 = 0.9, ρ2 = 0.7, c = 0.5)
SIDA (RS)	0.04	0.99	100.00	100.00	0.00	0.00	100.00	100.00
SIDA (GS)	0.05	0.99	100.00	100.00	0.00	0.00	100.00	100.00
sCCA	0.05	0.99	100.00	100.00	1.04	1.32	69.89	69.19
JACA	0.11	1.00	100.00	100.00	3.42	3.86	42.37	38.07
MGSDA (Stack)	0.19	0.84	7.50	8.50	0.00	0.00	16.82	16.20
MGSDA (Ens)	0.33	0.95	14.25	13.50	0.00	0.05	24.65	22.46
Setting 2
(ρ1 = 0.4, ρ2 = 0.2, c = 0.2)
SIDA (RS)	11.32	0.58	100.00	100.00	1.17	1.90	86.56	80.51
SIDA (GS)	11.42	0.58	100.00	99.75	2.28	1.57	68.82	81.85
sCCA	16.20	0.65	100.00	100.00	2.44	1.14	66.70	70.81
JACA	11.32	0.58	100.00	100.00	2.23	1.94	75.92	76.38
MGSDA (Stack)	12.52	0.55	34.25	32.50	0.04	0.06	48.22	46.29
MGSDA (Ens)	17.05	0.61	39.00	37.00	0.04	0.07	53.34	50.09
Setting 3
(ρ1 = 0.15, ρ2 = 0.05, c = 0.12)
SIDA (RS)	31.03	0.14	98.50	97.00	5.07	2.93	41.43	58.05
SIDA (GS)	29.61	0.26	99.00	99.75	2.48	2.85	53.88	56.07
sCCA	34.80	0.20	92.75	93.75	1.10	1.47	74.66	77.45
JACA	29.84	0.19	97.25	97.00	0.74	0.85	81.51	82.53
MGSDA (Stack)	31.55	0.15	28.00	27.00	0.07	0.05	41.53	40.25
MGSDA (Ens)	35.31	0.16	30.75	28.50	0.17	0.01	41.92	43.09

3.3.2 |. Example 2: Simulation settings when prior information is available

In this setting, there are three views of data X^d, d = 1,2,3, and each view is a concatenation of data from three classes. The true covariance matrix Σ is defined as in Model 1 but with the following modifications. We include Σ₃, Σ₁₃, and Σ₂₃. ${\widetilde{\mathbf{\text{Σ}}}}^1$, ${\widetilde{\mathbf{\text{Σ}}}}^2$, and ${\widetilde{\mathbf{\text{Σ}}}}^3$ are each block diagonal with four blocks of size 10 representing four networks, between-block correlation 0, and each block is a compound symmetric matrix with correlation .7. Each block has a 9 × 9 compound symmetric submatrix with correlation .49 capturing the correlations between other variables within a network. The cross-covariance matrices ${\mathbf{\text{Σ}}}_{12}$, ${\mathbf{\Sigma }}_{13}$, and ${\mathbf{\text{Σ}}}_{23}$ follow Model 1, but to make the effect sizes of the main variables larger, we multiply their corresponding values in V^d, d = 1,2,3 by 10. We set D =diag(0.9,0.7) when computing the cross-covariances.

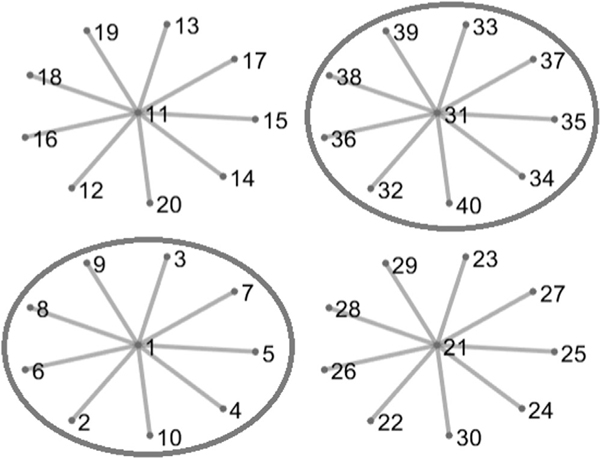
We consider two scenarios in this example that differ by how the networks contribute to both separation and association. In the first scenario, all four networks contribute to separation of classes within each view and association between the views. Thus, there are 40 signal variables for each view, and P₁ − 40, P₂ − 40, and P₃ − 40 noise variables. In the second scenario, only two networks in the graph structure contribute to separation and association; hence, there are 20 signal variables and P₁ − 20, P₂ − 20, and P₃ − 20 noise variables. Figure 3 is a pictorial representation for the two scenarios. For each scenario, we set n_k = 40, k = 1,2,3, and generate the combined data $\left({\mathbf{X}}_k^1,{\mathbf{X}}_k^2,{\mathbf{X}}_k^3\right)$ from $MVN\left({\mathit{\mu }}_k\cdot \mathbf{\Sigma }\right)$. We set c (refer to Model 1) to 0.2 when generating the mean matrix μ_k In both scenarios, the weight for connected variables is set to 1.

Competing methods and results

We compare SIDANet with fused sparse LDA (FNSLDA) (Safo and Long, 2019), a classification-based method that incorporates prior information in sparse LDA. We apply FNSLDA on the stacked views (FNSLDA (Stack)) and use the classification algorithm proposed in the original paper. We also perform FNSLDA on separate views and perform classification on the combined discriminant vectors (FNSLDA (Ens)) using the approach described in the Supporting Information. Compared to FNSLDA, SIDANet tends to have competitive TPR, lower FPR, higher F₁ scores, and competitive error rates and estimated correlations (refer to Table 2). These findings, together with the findings when there are no prior information, underscore the benefit of considering joint integrative and classification methods when the goal is to both correlate multiple views of data and perform classification simultaneously.

3.4 |. REAL DATA ANALYSIS

We focus on analyzing the gene expression, metabolomics, and clinical data from the PHI study. Our main goals are to (i) identify genes and metabolomics features (mass-tocharge ratio [m/z]) that are associated and optimally separate subjects at high versus low risk for developing ASCVD, and (ii) assess the added benefit of the identified variables in ASCVD risk prediction models that include some established risk factors (i.e., age and gender).

3.4.1 |. Application of the proposed and competing methods

We used data for 142 patients for whom gene expression and metabolomics data are available and for whom there were clinical and demographic variables to compute ASCVD risk score. The ASCVD risk score for each subject is dichotomized into high (ASCVD > 5%) and low (ASCVD ≤ 5%) risks based on guidelines from the American Heart Association. Because of the skewed distributions of most metabolomic levels, we log2 transformed each feature. We obtained the gene–gene interactions from the HPRD (Peri et al., 2003). The resulting network had 519 edges. Both datasets were normalized to have mean 0 and variance 1 for each variable. We divided each view of data equally into training and testing sets. We selected the optimal tuning parameters that maximized average classification accuracy from fivefold cross-validation on the training set. The selectedtuningparameterswerethenapplied tothetesting set to estimate test classification accuracy. The process was repeated 20 times and we obtained average test error, variables selected, and RV coefficient using the training data.

3.4.2 |. Average misclassification rates, estimated correlations, and variables selected

Table 3 shows the average results for the 20 resampled datasets. Of note, (+ covariates) refers to when the covariates age, gender, BMI, systolic blood pressure, low-density lipoprotein (LDL), and triglycerides are added as a third dataset to SIDA or SIDANet; we assess the results with and without covariates. For SIDANet, we only incorporated prior information from the gene expressions data (i.e., protein–protein interactions).

TABLE 3.

SIDA (+covariates) uses RS and includes other covariates (see text) as a third dataset. SIDANet uses prior network information from the gene expression data alone. sLDA (Ens) separately applies sparse LDA on the gene expression and metabolomics data and combines discriminant vectors when estimating classification errors. sLDA (Stack) applies sparse LDA on the stacked data. SIDA and SIDANet have competitive error rate and higher estimated correlations. It seems that including covariates does not make the average classification accuracy and correlation any better

	Error (%)	# Genes	# m/z features	Correlation
SIDA	22.54	166.05	123.60	0.61
SIDA (+ covariates)	22.46	69.05	33.35	0.31
SIDANet	21.83	247.30	111.90	0.67
SIDANet (+ covariates)	22.75	64.05	33.80	0.31
sCCA	46.48	139.75	336.25	0.43
JACA	25.49	637.20	871.65	0.52
sLDA (Ens)	30.28	14.20	11.60	0.23
sLDA (Stack)	19.15	4.25	6.20	0.09

We observe that SIDA and SIDANet offer competitive results in terms of separation of the ASCVD risk groups. They also yield higher estimated correlations between the gene expressions and metabolomics data. SIDANet yields higher estimated correlation and competitive error rate when compared to SIDA, which suggests that incorporating prior network information may be advantageous. It seems that including covariates in this example does not make the average classification accuracy and correlation any better. From this application, stacking the data results in better classification rate, but the estimated correlation is poor,which is not surprising because this approach ignores correlation that exists between the datasets. Among the methods compared, sLDA (Ens) and sLDA (Stack) identify fewer number of genes and m/z features. This agrees with the results from the simulations where these methods had lower false and TPRs.

3.4.3 |. Variable stability and enrichment analysis

To reduce false findings and improve variable stability in identifying variables that potentially discriminate persons at high versus low risk for ASCVD, we used resampling techniques and chose variables that were selected at least 12 times (≥60%) out of the 20 resampled datasets. SIDANet and JACA selected 28 and 45 genes (and 7 and 20 m/z features), respectively, of which 17 genes (6 m/z features) overlap. Additionally, all genes identified by SIDA were also selected by SIDANet; there were six overlapping m/z features selected by SIDA and SIDANet. sLDA (Ens) and sLDA (Stack) did not identify any gene and m/z feature (refer to the Supporting Information).

We also used ToppGene Suite (Chen et al.,2009) to investigate the biological relationships of these “stable” genes. These genes were taken as input in ToppGene online tools for pathway enrichment analysis. The pathways that are significantly enriched (Bonferonni p-value <= .05) in the 28 genes selected by SIDANet include Sphingolipid signaling and RNA Polymerase 1 Promoter Opening pathways (see Supporting Information). These pathways play essential roles in some important biological processes including cell proliferation, maturation, and apoptosis (Borodzicz et al., 2015). For instance, several experimental and clinical studies suggest that sphingolipids are implicated in the pathogenesis of cardiovascular diseases and metabolic disorders (Borodzicz et al., 2015).

We also assessed whether including the “stable” genes and/or m/z features identified by our methods is any better than a model with only age and gender. We observe that including genes and/or m/z features as a risk score to a model with age and gender results in better discrimination of the ASCVD risk groups compared to association or classification-based methods, and when compared to a model with only age and gender. By integrating gene expression and m/z features and simultaneously discriminating ASCVD risk group, we have identified biomarkers that potentially may be used to predict ASCVD risk, in addition to a few established ASCVD risk factors.

3.5.|. CONCLUSION

We have proposed two methods for joint integrative analysis and classification studies of multiview data. Our framework combines LDA and CCA and is aimed at finding linear combination(s) of variables within each view that optimally separate classes while effectively explaining the overall dependency structure among multiple views. Of the methods we compared our approach to, JACA (Zhang and Gaynanova, 2018) with the same end goal and use of both LDA and CCA, emerged as the strongest competitor. However, our methods have several advantages over JACA. One such advantage is that our methods rely on summarized data (i.e., covariances) making them applicable if the individual view cannot be shared due to privacy concerns. Another advantage is that our algorithms provide the users the option to include covariates (such as clinical covariates) to guide the selection of predictors without putting those covariates up for selection. It is possible to include covariates in Zhang and Gaynanova (2018) as another view but the coefficients would be penalized and potentially excluded. Finally, SIDANet is both data- and knowledge-driven, while JACA (Zhang and Gaynanova (2018)) is mainly data-driven. The use of both data and prior knowledge allows us to assess variable– variable interactions and leads to biologically interpretable findings. In addition, our tuning parameters selection and our use of parallel computing make our algorithm computationally efficient. The encouraging findings from the real data analysis motivate further applications. We acknowledge some limitations in our methods. The methods we propose are only applicable to complete data and do not allow for missing values. The Laplacian matrix encourages smoothing in the same direction. In some applications, it is possible that the variables are connected but they have opposite signs. In such instances, our approach may fail; a penalty that encourages $\left|{\beta }_i\right|\approx \left|{\beta }_j\right|$ for connected variables i and j might be appropriate. Despite these limitations,our proposed methods advance statistical methods for joint association and classification of data from multiple sources.

FIGURE 1.

Simulation setup when network information is available. In scenario 1, all four networks contribute to both separation and association. In the second scenario, two networks (circled and in red color [this figure appears in color in the electronic version of this article, and any mention of color refers to that version]) contribute to both separation and association