Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Feb 15;34(5):2146–2160. doi: 10.1021/acs.chemmater.1c03593

Crystal Structure and Thermoelectric Properties of Novel Quaternary Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) Thiospinels with Low Thermal Conductivity

Oleksandr Cherniushok †, Oleksandr V Smitiukh ‡, Janusz Tobola §, Rafal Knura †,∥, Oleg V Marchuk ‡, Taras Parashchuk †,*, Krzysztof T Wojciechowski †,*
PMCID: PMC8910496  PMID: 35281971

Abstract

graphic file with name cm1c03593_0011.jpg

Uncovering of the origin of intrinsically low thermal conductivity in novel crystalline solids is among the main streams in modern thermoelectricity. Because of their earth-abundant nature and environmentally friendly content, Cu-based thiospinels are attractive functional semiconductors, including thermoelectric (TE) materials. Herein, we report the crystal structure, as well as electronic and TE properties of four new Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) thiospinels. The performed density functional theory calculations predicted the decrease of the band gap and transition from p- to n-type conductivity in the Mn–Fe–Co–Ni series, which was confirmed experimentally. The best TE performance in this work was observed for the Cu2NiHf3S8 thiospinel due to its highest power factor and low thermal conductivity. Moreover, all the discovered compounds possess very low lattice thermal conductivity κlat over the investigated temperature range. The κlat for Cu2CoHf3S8 has been found to be as low as 0.8 W m–1 K–1 at 298 K and 0.5 W m–1 K–1 at 673 K, which are significantly lower values compared to the other Cu-based thiospinels reported up to date. The strongly disturbed phonon transport of the investigated alloys mainly comes from the peculiar crystal structure where the large cubic unit cells contain many vacant octahedral voids. As it was evaluated from the Callaway approach and confirmed by the speed of sound measurements, such a crystal structure promotes the increase in lattice anharmonicity, which is the main reason for the low κlat. This work provides a guideline for the engineering of thermal transport in thiospinels and offers the discovered Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) compounds, as new promising functional materials with low lattice thermal conductivity.

1. Introduction

The unique ability to convert heat into electrical power makes thermoelectric (TE) materials very promising for improving energy utilization and management.1,2 The efficiency of this compelling technology is determined by the TE materials’ figure of merit, ZT = σS2T/(κlat + κel), where σ is the electrical conductivity, S is the Seebeck coefficient, κlat and κel are the lattice and electronic components of the thermal conductivity, respectively, and T is the absolute temperature.3 To provide a high ZT parameter, the simultaneous enhancement of the power factor (PF = S2σ) and low lattice thermal conductivity κlat is necessary.4−6 The difficulty of producing high-performance TE materials is that the parameters σ, S, and κel are interdependent through the carrier concentration n. Moreover, the toxic nature of most well-established TE materials, that is, Bi2Te3, PbTe, and GeTe, and the drastic cost increase of tellurium in the last years, restrict their widespread utilization. Therefore, the search for new earth-abundant and Te-free TE materials is a great challenge.

Up to date, many efforts were applied for the development of materials that consist of earth-abundant and environmentally friendly elements. Following this idea, a lot of attention was focused on the development of sulfides, especially the copper-based sulfide compounds such as Cu2–xS,7 ternary Cu–Sn–S semiconductors,8,9 chalcopyrites,10 cubanites,11 colusites,12 stannoidites,13 tetrahedrites,14 argyrodites,15,16 and some other Cu-based sulfides.17−20 Despite good TE performance, some of these compounds (e.g., Cu2–xS and argyrodites) are superionic conductors and their practical application is restricted due to low thermal stability accompanied by cation migration, which causes the structure degradation of the material.21,22

The finding of more stable sulfides leads to ternary and quaternary transition metal thiospinels23,24 as the derivatives of the spinel MgAl2O4 structure type.25 Thiospinel compounds with the general formula AB2S4 can accommodate variable metal elements, which significantly tunes physical properties and demonstrates the playground for the designing of promising materials with high functionality.26 As an example, ternary Cu-based CuM2S4 (M—Ti, Cr, Co, etc.) thiospinels and their derivatives have gained significant interest due to their diversity of magnetic,27,28 catalytic,29,30 electrical,28 and TE properties.19,31−35 Moreover, the density ρ of thiospinels usually does not exceed ∼5.0 g/cm3, which is significantly lower compared to the other well-established TE materials, that is, Bi2Te3 (7.7 g/cm3),36 PbTe (8.24 g/cm3),37 GeTe (6.18 g/cm3),38 CoSb3 (7.6 g/cm3),39 and half-Heuslers (8.0–11.0 g/cm3).40 The use of low-density materials for the construction of TE modules can decrease the overall weight of devices. Only one trap that may occur here is that the low mass of elements usually corresponds with the high thermal conductivity of materials.41

Because of the aforementioned reasons, many studies related to the investigation of the crystal and TE properties of ternary and quaternary thiospinels have occurred recently. Wyzga et al. performed a systematic study on indium-based ternary thiospinels to explore their potential for TE applications. The high resistivity of the studied MIn2S4 (M—Mn, Fe, Co, and Ni) thiospinels together with quite high κlat (∼2.5–3.5 W m–1 K–1 at 298 K) lead to a low ZT < 0.1 at 760 K.42,43 Only In0.67–0.33In2S4 thiospinel alloyed with selenium showed improvement in the power factor and together with relatively low κlat (∼1.1–1.4 W m–1 K–1 at 298 K) resulted in a higher ZTmax = 0.25 at 760 K.44−46 However, Chen et al. reported for In2.67–xCuxS4ZTmax = 0.5 at 700 K due to the increased power factor and suppressed κlat (∼1.1–1.4 W m–1 K–1 at 298 K).47 Hashikuni et al. recently reported n-type Cu2MTi3S8 (M—Mn, Fe, Co, and Ni) quaternary thiospinels as a TE material with a large power factor of 0.6 mW m–1 K–2. However, the relatively high κlat (1.4–2.3 W m–1 K–1 at 298 K) also results in a low ZT = 0.2 at 650 K for Cu2CoTi3S8.31,48,49

The performed analysis indicates that the first step in the optimization of the TE performance of the thiospinel materials and the other TE materials is connected with the intrinsically low thermal conductivity.50 The thermal conductivity of semiconductors is usually dominated by lattice thermal conductivity κlat.51,52 Thus, the effective method for finding new, advanced TE materials is to search for semiconductors with low lattice thermal conductivity κlat.24

The reported Cu2CoTi3S8 thiospinel compound crystallizes in the space group Fd3̅m (no 227, Pearson symbol cF56) and is characterized by a large number of atoms (N = 56 per cubic cell with a ∼ 10 Å) distributed over three crystallographic sites, that is, one tetrahedral site for Cu (8b), a mixed octahedral site for Ti/Co (16c), and one site for S (32e). The (CuS4) tetrahedra are corner shared with four [(Co/Ti)S6] octahedra, which share their edges. According to Spitzer,41 the relatively high coordination number of the M atoms in such a structure may favor low lattice thermal conductivity. Aiming to reduce lattice thermal conductivity, Bourges et al. substituted Ti for Sn, and showed that Cu2CoSn3S8 possesses lower κlat ∼ 1.0 W m–1 K–134 compared with ∼1.9 W m–1 K–1 at 298 K for Cu2CoTi3S8.31 According to the radii of the Ti atom and the size factor of the octahedral form, the site that is occupied by Ti(Sn) atoms can be replaced by Hf atoms. Because of the higher atomic mass, a more effective reduction of lattice thermal conductivity than in the cases of Ti and Sn is expected.

The purpose of this study was to find environmentally friendly and mechanically stable materials with high earth abundance characterized by low lattice thermal conductivity, as this is the major request for high TE performance. Keeping this in mind, we successfully synthesized and characterized four new thiospinels with the chemical composition Cu2MHf3S8 (M—Mn, Fe, Co, and Ni). The structure of these compounds is based on the three-layer close packing of sulfur atoms. The nature of filling 1/2 octahedral voids with the statistical mixture of atoms L = Hf + M (M—Mn, Fe, Co, and Ni) and 1/8 tetrahedral voids with Cu, respectively, causes the differentiation of the unit cell in the structure into octants and the formation of smaller F-cubes. The large cubic unit cells full of vacant octahedral voids have been found extremely useful for the reduction of the lattice thermal conductivity through increased lattice anharmonicity. As a result, the thermal conductivity for the Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) compounds shows significantly lower values compared to the other Cu-based thiospinels reported up to date.

2. Experimental Details

2.1. Materials and Synthesis

Samples with the nominal compositions of Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) were prepared by melting high-purity Cu (shot, 99.99%), Mn (shot, 99.99%), Fe (shot, 99.99%), Co (shot, 99.99%), Ni (shot, 99.99%), Hf (shot, 99.99%), and S (shot, 99.99%) in quartz containers evacuated to a residual pressure of 10–2 Pa. The total mass of every sample was 3 g. The ampules with the stoichiometric mixtures of elements were heated up to 1423 K at the rate of 12 K/h, kept at this temperature for 4 h, and cooled down to room temperature at the same rate. To obtain homogeneous samples, obtained ingots were crushed and milled into fine powders, compacted using a cold-press, heated in evacuated quartz ampules up to 773 K with a rate of 12 K/h, annealed at this temperature for 500 h, and quenched in cold water without breaking the containers.

2.2. Sintering

After the annealing process, the samples were crushed into fine powders by hand milling using an agate mortar and then densified by the pulsed electric current sintering (PECS) technique at 1073 K for 60 min in a 12.8 mm diameter graphite mold under an axial compressive stress of 40 MPa in an argon atmosphere. The heating and cooling rates were 70 and 50 K/min, respectively. Highly dense (ρ > 95% of crystallographic density) pellets with a diameter of 12.8 mm and a height of ∼2 mm were obtained and polished for transport property measurements.

2.3. Powder X-Ray Diffraction and Scanning Electron Microscopy

Phase identification was performed using a BRUKER D8 ADVANCE X-ray diffractometer using Cu Kα radiation (λ = 1.5418 Å, Δ2Θ = 0.005°, and 2Θ range of 10–120°) with the Bragg–Brentano geometry. The Rietveld refinement of the crystal structure was carried out using WinCSD program package.53

For scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDS) analyses, the samples were embedded in conductive resin and subsequently polished, finally using 0.1 μm of diamond powder in a slurry. The analysis of the chemical composition was performed using SEM (JEOL JSM-6460LV scanning electron microscope) equipped with EDX spectroscopy.

2.4. Electrical and Thermal Transport Properties

The Seebeck coefficient S and electrical conductivity σ were measured using the commercial apparatus NETZSCH SBA 458 Nemesis. The measurements were performed in an argon flow at a temperature range of 298 to 673 K. The thermal diffusivity αD was measured using a NETZSCH LFA 457 equipment, and the specific heat capacity Cp was estimated from the Dulong–Petit limit. The samples were first spray-coated with a thin layer of graphite to minimize errors from the emissivity of the material and laser beam reflection caused by a shiny pellet surface. Thermal conductivity was calculated using the equation κ = ρCpαD, where ρ is the density obtained by the Archimedes principle at the disks from PECS. The uncertainty of the Seebeck coefficient and electrical conductivity measurements was 7 and 5%, respectively, whereas that of the thermal diffusivity measurements was 3%. The combined uncertainty for the determination of the TE figure of merit ZT was ∼20%.54 The Hall effect was investigated by applying the four-probe method in constant electric and magnetic fields (H = 0.9 T) and current through a sample of 50 mA. The uncertainty of Hall measurements was ∼10%. The speed of sound was measured at T = 298 K using the ultrasonic flaw detector Olympus Panametrics Epoch 3. The Vickers hardness of sintered samples was measured using a microhardness tester FM-700 developed by Future-Tech Corp., applying a load of 100 g. The optical absorbance spectra were measured using a Fourier transform infrared spectroscope (BRUKER VERTEX 70 V) at room temperature.

2.5. Electronic Band Structure Calculations

The electronic densities of states (DOSs) of Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) were calculated using the Korringa–Kohn–Rostoker (KKR) method with the coherent potential approximation (CPA) that enables us to treat the chemical disorder induced by M substitution on the Hf site as a random atom distribution.55,56 In our calculations, the crystal potential was constructed within the local density approximation (LDA), employing the parameterization of Perdew and Wang for the exchange–correlation part.57 The position of the Fermi level EF was determined accurately from the generalized Lloyd formula.58 For all the compositions, the experimental lattice parameters (Table 1) and atomic coordinates (Table 2), determined from Rietveld refinements against the powder X-ray diffraction (PXRD) data, were used. For well-converged crystal potential and atomic charges (below 1 meV and 10–3e, respectively), the total-, site-, and l-decomposed DOS (truncated at lmax = 2) were computed using a tetrahedron method for integration in the reciprocal k-space.58 The electronic band structure was also computed for all the investigated compounds in the framework of the complex energy KKR-CPA calculations, where the real part of the E(k) dispersion curves was extracted to plot electronic bands along high-symmetry directions in the fcc Brillouin zone.

Table 1. Results of the Crystal Structure Determination of the Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) Compounds.

  Cu2MnHf3S8 Cu2FeHf3S8 Cu2CoHf3S8 Cu2NiHf3S8
space group Fd3̅m (no. 227)
a (Å) 10.39759(3) 10.33404(3) 10.32084(2) 10.30074(2)
V (Å3) 1124.083(8) 1103.597(8) 1099.372(6) 1092.963(6)
number of atoms in a cell 56 56 56 56
calculated density (g/cm3) 5.78 5.95 6.07 6.08
absorption coefficient (1/cm) 773.1 802.0 822.0 733.4
radiation and wavelength Cu Kα 1.54185 Å
diffractometer BRUKER D8 ADVANCE
mode of refinement full profile
number of atom sites 4
number of free parameters 1
2θ and sin θ/γ (max) 120.00 0.562
RI 0.0520 0.0384 0.0244 0.0306
RP 0.0818 0.0823 0.0533 0.1000
scale factor 0.09818 0.13065 0.09678 0.12190
Open in a new tab

Table 2. Atomic Coordinates and Isotropic Temperature Displacement Parameters for the Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) Compounds.

atom x/a y/b z/c Biso×102, Å2 N
Cu2MnHf3S8
Cu 1/8 1/8 1/8 0.69(8) 8
Mn* 1/2 1/2 1/2 0.63(1) 16
Hf* 1/2 1/2 1/2 0.87(3) 16
S 0.7472(3) 0.7472(3) 0.7472(3) 0.67(6) 32
*—Occupancy: Mn—0.241(3) Mn; Hf—0.759(3) Hf
Cu2FeHf3S8
Cu 1/8 1/8 1/8 0.91(5) 8
Fe* 1/2 1/2 1/2 0.4(3) 16
Hf* 1/2 1/2 1/2 0.99(2) 16
S 0.7455(2) 0.7455(2) 0.7455(2) 0.78(4) 32
*—Occupancy: Fe—0.220(2) Fe; Hf—0.780(2) Hf
Cu2CoHf3S8
Cu 1/8 1/8 1/8 1.65(6) 8
Co* 1/2 1/2 1/2 0.2(2) 16
Hf* 1/2 1/2 1/2 0.89(2) 16
S 0.7444(2) 0.7444(2) 0.7444(2) 0.98(5) 32
*—Occupancy: Co—0.220(7) Co; Hf—0.780(3) Hf
Cu2NiHf3S8
Cu 1/8 1/8 1/8 1.03(5) 8
Ni* 1/2 1/2 1/2 0.53(14) 16
Hf* 1/2 1/2 1/2 0.97(2) 16
S 0.7437(1) 0.7437(1) 0.7437(1) 0.71(4) 32
*—Occupancy: Ni—0.228(6) Ni; Hf—0.772(2) Hf
Open in a new tab

3. Results and Discussion

3.1. Crystal Structure and Microstructural Properties

The determination and refinement of the crystal structure of the Cu2MHf3S8 chalcogenide phases (M—Mn, Fe, Co, and Ni) were performed using X-ray powder diffraction. The diffraction patterns were indexed in cubic symmetry (SG Fd3̅m, Pearson symbol cF56). The conditions and results of the X-ray experiments are presented in Table 1. The analysis of hkl indices, reflections, and intensities indicated that the synthesized chalcogenide phases belong to the MgAl2O425 structure type. The atomic coordinates of the Cu7.38Mn4Sn12S3259 compound were used as the starting computation model. The structural parameter refinement was performed by the Rietveld method using a gradual approximation of the calculated diffraction pattern profiles to the experimental patterns (Figure S1).

In Table 1, we can observe that the unit cell parameter of the Cu2MnHf3S8 compound is significantly higher than the unit cell for the other investigated thiospinels. It is connected with the variation of the ionic radii of transition metals (Mn, Fe, Co, and Ni). According to the data of Vainshtein et al.,60 the ionic radii of Mn2+ (0.91 Å) is significantly larger than the ion radii of Fe2+ (0.80 Å), Co2+ (0.78 Å), and Ni2+ (0.74 Å). Therefore, the compositional dependence of the unit cell parameter is in good agreement with the change of the M ionic radii for the investigated Cu2MHf3S8 thiospinels.

The refinement of coordinates and isotropic thermal displacement parameters of atoms (Table 2) yields satisfactory values of the fit factors and proves the validity of the model. A somewhat higher value of the Biso for Cu atoms in the Co-containing specimen, compared to the other investigated samples, can be caused by the presence of specific Co atoms that occupy close octahedral voids. As it was reported for homologous Cu2CoTi3S8 using single-crystal data,61 the isotropic thermal displacement parameter of the Cu atom Ueq = 2.17 × 10–2 Å2 is almost two times higher than the corresponding value Ueq = 1.25 × 10–2 Å2 of Cu atoms in unsubstituted Cu2Ti4S8.62 Moreover, for the case of Cu2M0.6Ti3.4S8, it was reported that the increase of the isotropic thermal displacement parameter of the Cu atom in the series Mn–Fe–Co (Ueq = 1.32 × 10–2 Å2 for M = Mn, Ueq = 1.51 × 10–2 Å2 for M = Fe, and Ueq = 1.96 × 10–2 Å2 for M = Co).61 A similar tendency in the isotropic thermal displacement parameter of the Cu atom is observed in the case of our compounds (Table 2).

As the losses of copper or sulfur are highly expected during the high-temperature preparation of Cu-based sulfides, we took into account the different weighting schemes for the deviation of these elements during Rietveld refinement. Nevertheless, the best agreement between the experimental and calculated PXRD patterns corresponds to the site occupancy factor of 1.0 for these elements in the investigated samples. Therefore, we conclude that no losses of Cu and S during synthesis were observed.

The experimental and calculated diffraction patterns of Cu2MHf3S8 chalcogenides and their difference are shown in Figure 1a–d.

Figure 1.

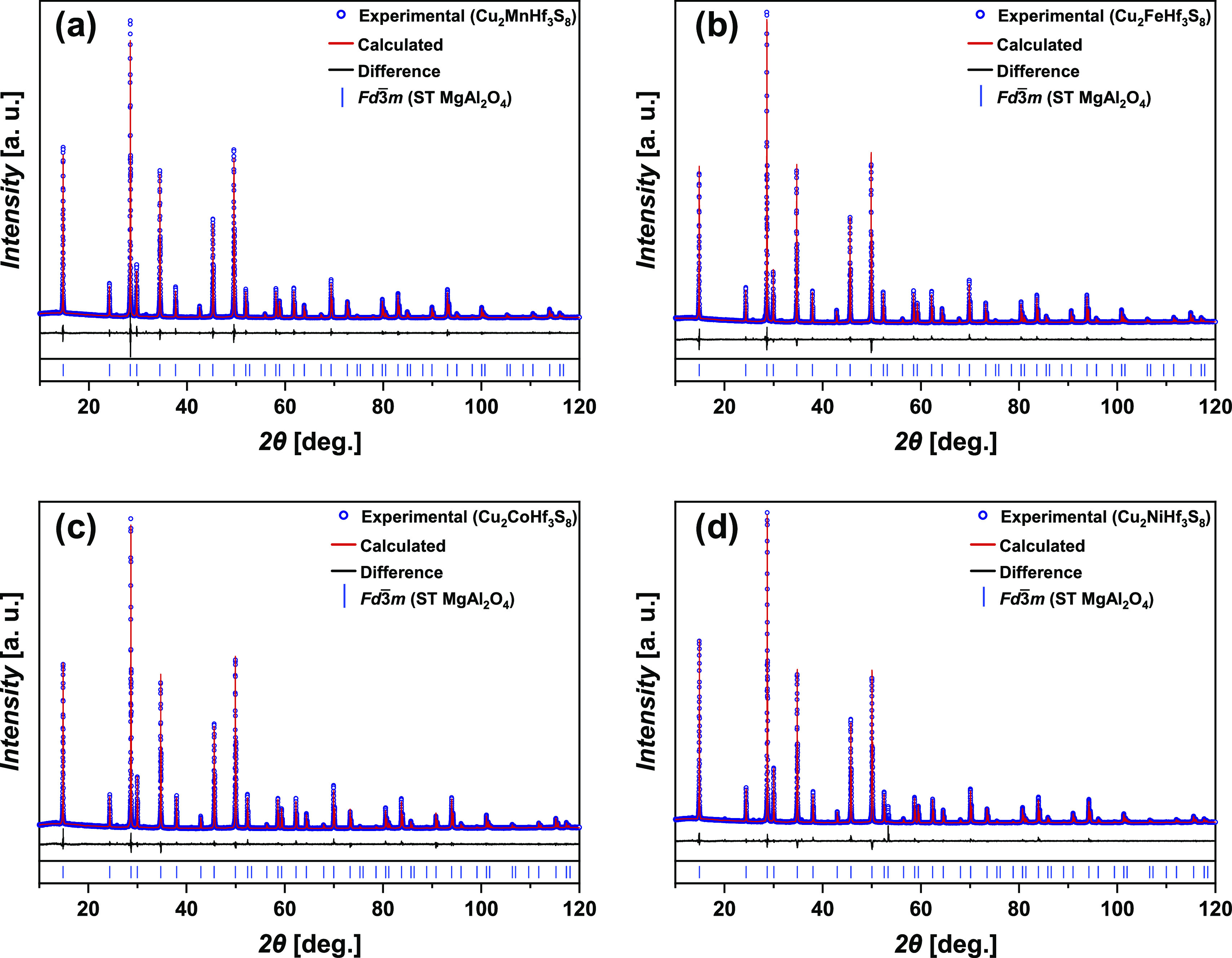
Figure 1

Open in a new tab

Results of the Rietveld refinement of the Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) compounds.

The results of the calculation of interatomic distances and coordination numbers of atoms in the Cu2MHf3S8 structures are presented in Table 3. The interatomic distances correlate well with the sums of the corresponding ionic radii.63

Table 3. Interatomic Distances (δ) and Coordination Numbers (C.N.) of Atoms in the Structure of Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) Compounds.

 
 Cu2MnHf3S8 Cu2FeHf3S8 Cu2CoHf3S8 Cu2NiHf3S8  
atoms δ (Å) δ (Å) δ (Å) δ (Å) C.N.
Cu – 4 S 2.302(2) 2.318(1) 2.334(2) 2.343(1) 4
M – 6 S 2.571(2) 2.538(1) 2.524(2) 2.511(1) 6
Hf – 6 S 2.571(2) 2.538(1) 2.524(2) 2.511(1) 6
S – 1 Cu 2.302(2) 2.318(1) 2.334(2) 2.343(1) 4
  – 3 La 2.571(2) 2.538(1) 2.524(2) 2.511(1)  
Open in a new tab
a

L = M + Hf.

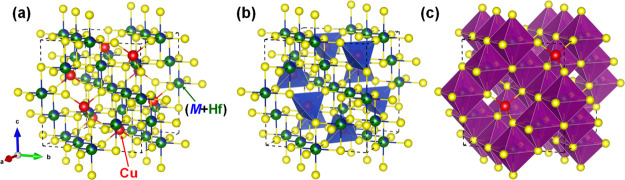
The structure of discovered compounds is based on the three-layer close packing of sulfur atoms. The nature of filling 1/2 octahedral voids with the statistical mixture of atoms L = M + Hf (M—Mn, Fe, Co, and Ni) and 1/8 tetrahedral voids with Cu, respectively, causes the differentiation of the unit cell in the structure into octants and the formation of smaller F-cubes. Cu atoms in such an eightfold cell are located in the tetrahedral surroundings of sulfur atoms (Figure 2).

Figure 2.

Figure 2

Open in a new tab

Unit cell (a), representation of the coordination environment of Cu atoms (b), and (M + Hf) atoms (c) for the Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) crystal structure.

The atoms of the statistical mixture are located in centrosymmetric sites and S atoms in monovariant sites on the third-order axes (Bravais lattice 3m). The first coordination sphere of sulfur is the tetrahedron. The cation–anion distances for the octahedral sites are averaged, and for Cu, the distances correspond to the sum of the tetrahedral radii. Quaternary copper-containing sulfides of transition 3d elements belong to the phases with mixed coordination. The ordered occupation of tetrahedral and octahedral positions in the structure attributes them to normal chalcogenide spinels.

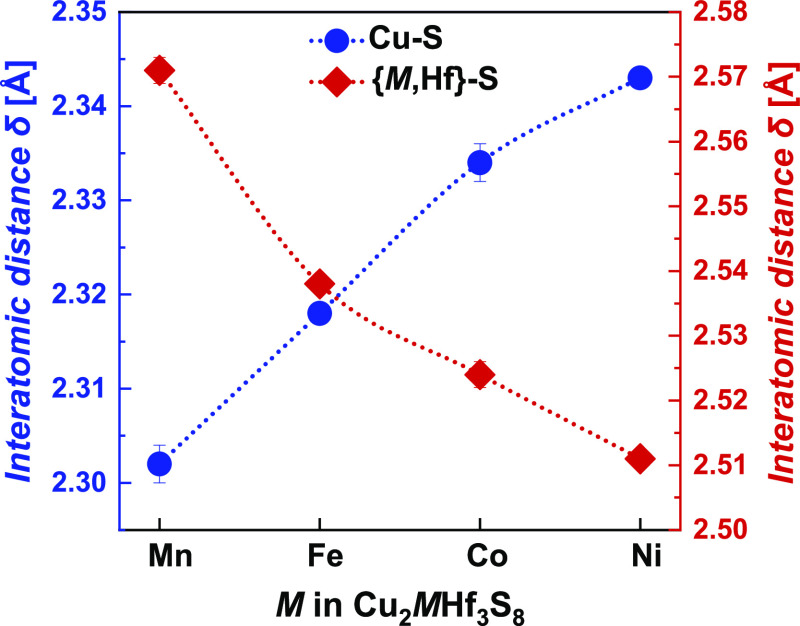
The gradual increase of the interatomic distance Cu–S and the decrease of the interatomic distance (M/Hf)–S are observed in the Mn → Fe → Co → Ni series (Figure 3). The latter is associated with the decrease of the ionic radius of M atoms in the series.

Figure 3.

Figure 3

Open in a new tab

Change of the Cu–S and (M + Hf)–S interatomic distances for Cu2MHf3S8 compounds.

Figure 4 shows backscattered electron (BSE) images of Cu2MHf3S8 samples (M—Mn, Fe, Co, and Ni). All the samples were generally single phase, however, with a small presence of Hf-rich sub-micro precipitates. The Co- and Ni-containing samples (Figure 4c,d) additionally have some minor traces of Co–S and Ni–S phases. The chemical composition of the main phase for all the investigated samples was very close to the nominal composition, as determined by Rietveld refinements and EDS analysis. Co- and Ni-rich precipitates were found to have a chemical composition close to Co9S8 and Ni9S8, respectively, in agreement with PXRD data. The precise identification of the chemical composition of Hf-rich sub-micro precipitates was problematic due to their small dimensions. However, the amount of secondary phases is very small, therefore we do not expect any modification of physical properties due to these phases. Figure 4e,f shows EDS element distribution mapping, where only small agglomerations of Co-rich and Hf-rich phases were detected.

Figure 4.

Figure 4

Open in a new tab

BSE images of Cu2MHf3S8 samples: (a) M—Mn, (b) M—Fe, (c) M—Co, and (d) M—Ni. BSE image of the Cu2CoHf3S8 sample (e) with EDS element mapping (f).

3.2. Electronic Transport Properties

The transport properties of Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) specimens at T = 298 K are shown in Table 4. The absolute values of the carrier concentration nH for all the studied compounds are in the range of 1016–1017 cm–3.

Table 4. Seebeck Coefficient S, Electrical Conductivity σ, Thermal Conductivity κ, Hall Carrier Concentration nH, and Carrier Mobility μ for the Cu2MHf3S8 Polycrystalline Samples at T = 298 K.

compound S [μV K–1] σ [S m–1] κ [W m–1 K–1] nH [cm–3] μ [cm2 V–1 s–1]
Cu2MnHf3S8 357 0.031 1.15 4.0 × 1016 (p) 0.1
Cu2FeHf3S8 172 2.4 0.96 2.3 × 1016 (p) 6.5
Cu2CoHf3S8 –322 8.7 0.79 6.8 × 1016 (n) 8.0
Cu2NiHf3S8 –120 775 0.79 6.4 × 1017 (n) 75.7
Open in a new tab

As suggested by Kariya et al.,27 the charge balance for Cu2Hf4S8 can be written as Cu2+Hf2+Hf3S82– with two configurations of hafnium: Hf2+–5d2 and Hf4+–5d0. In our case, Hf2+ is substituted by M (M—Mn, Fe, Co, and Ni) in Cu2MHf3S8. Cu2MnHf3S8 possesses a very high positive Seebeck coefficient (357 μV K–1 at 298 K), which is typical for an intrinsic semiconductor with a low carrier concentration (4.0 × 1016 cm–3). The density functional theory (DFT) calculations of the electronic structure also confirm that EF is lying in the valence band (VB) close to the band gap edge. Cu2FeHf3S8 shows a lower positive Seebeck coefficient with a lower concentration of holes of 2.3 × 1016 cm–3 compared with the Cu2MnHf3S8. The lower carrier concentration can be connected to the electrons introduced into the system due to an additional d-electron in Fe2+ (3d6) compared to Mn2+ (3d5). The lower Seebeck coefficient can originate from the effect of the minority carriers, which is highly probable in the undoped compounds with a narrow band gap. The DFT calculations also indicate that the EF is tending to fall into the band gap, which is in line with the abovementioned explanation. Cu2CoHf3S8 shows a negative Seebeck coefficient with a low concentration of dominant charge carriers (electrons) of 6.8 × 1016 cm–3. This can be explained by the shift of the Fermi level toward the conduction band (CB) in contrast with the Cu2FeHf3S8 and Cu2MnHf3S8. This observation is also in agreement with the electron configuration of Co2+ (3d7). More d-electrons first cause the self-compensation of holes, and later change the material from p- to n-type. As a result, Cu2NiHf3S8 shows a lower negative Seebeck coefficient (−120 μV K–1). The dominant carriers are electrons, and the measured Hall concentration nH = 6.4 × 1017 cm–3 is higher compared to the case of Cu2CoHf3S8, where nH = 6.8 × 1016 cm–3. The larger number of d-electrons (3d8) shifts the Fermi level deeper into the CB, decreases the absolute value of the Seebeck coefficient, and enhances electrical conductivity. The performed analysis indicates that further steps (i.e., deviation from stoichiometry and doping) should be performed to tune the concentration to the optimal value for the maximum energy conversion efficiency,50 which can be the object of future studies.

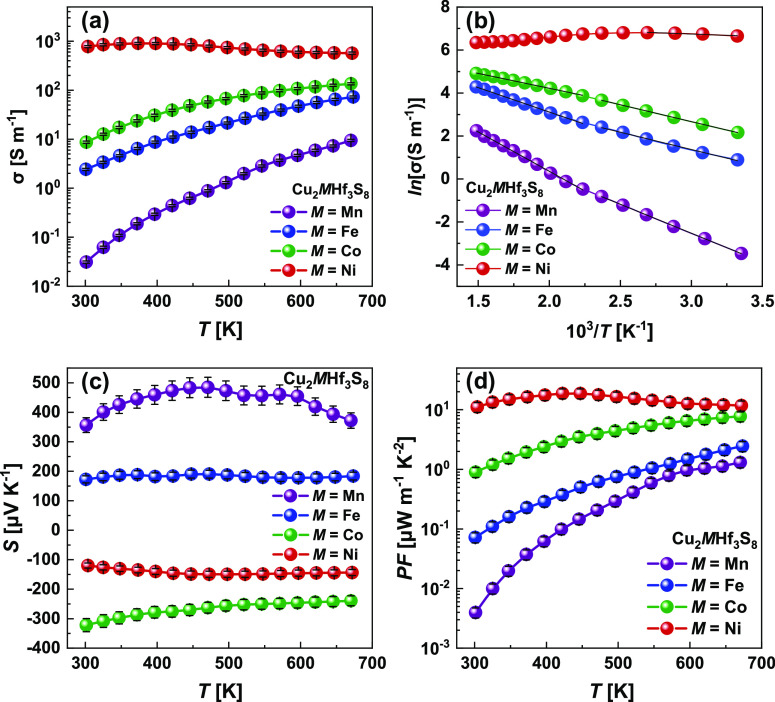
Figure 5 shows the electrical conductivity (panel a) and the Arrhenius plot of electrical conductivity (panel b) for Cu2MHf3S8 polycrystalline samples over the entire temperature range of 298–673 K. The electrical conductivity σ for the Cu2MnHf3S8 sample increased from ∼0.03 S m–1 at 298 K to ∼9.4 S m–1 at 673 K (Figure 5a). The electrical conductivity of Cu2FeHf3S8 and Cu2CoHf3S8 increase from ∼2.4 S m–1 at 298 K to ∼73 S m–1 at 673 K and from ∼8.7 S m–1 at 298 K to ∼135 S m–1 at 673 K for Fe- and Co-containing thiospinels, respectively. The electrical conductivity of Cu2NiHf3S8 shows the highest values and just slightly increases with temperature from ∼775 S m–1 at 298 K to ∼900 S m–1 at 373 K, and then decreases to ∼570 S m–1 at 673 K, showing weak metallic behavior (Figure 5a). The values of σ for Cu2MHf3S8 samples are lower than other Cu-based thiospinels, especially homologous Cu2MTi3S8 (M = Mn, Fe, Co, and Ni), studied by Hashikuni et al.,48 which shows electrical conductivity in the range of ∼4.3 × 104–1.1 × 105 S m–1 at 298 K. However, the obtained values of σ are similar to Sn-based thiospinels, especially the Cu2CoSn3S8 compound, which increases from ∼200 S m–1 at 323 K to ∼700 S m–1 at 673 K.34

Figure 5.

Figure 5

Open in a new tab

Electrical conductivity (a), Arrhenius plot of electrical conductivity (b), Seebeck coefficient (c), and TE power factor PF (d) for Cu2MHf3S8.

Electrical conductivity activation energies Ea, estimated from the Arrhenius plot of electrical conductivity (Figure 5b) for Cu2MHf3S8 polycrystalline samples are given in Table 5. The values of Ea for Cu2MnHf3S8 are in the range of 0.46–0.63 eV, which is in good agreement with the lowest electrical conductivity and the highest Seebeck coefficient for this sample. The activation energies for Cu2FeHf3S8 and Cu2CoHf3S8 are higher and vary in a range of 0.24–0.39 eV. The values of Ea for Cu2NiHf3S8 are very small at low temperatures, probably due to hopping conductivity or the presence of some in-gap states. Considering the low values of the activation energies, we can conclude that the poor electrical conductivity observed for the investigated Cu2MHf3S8 alloys originates from the low charge carrier concentration.

Table 5. Activation Energy Ea in the Given Temperature Range for Studied Thiospinels.

compound Ea [eV] temp. range [K]
Cu2MnHf3S8 0.46(1) 298–423
  0.63(1) 448–623
Cu2FeHf3S8 0.28(1) 298–423
  0.39(1) 448–673
Cu2CoHf3S8 0.27(1) 298–423
  0.24(1) 448–673
Cu2NiHf3S8 0.06(1) 298–373
Open in a new tab

Figure 5c represents the measured Seebeck coefficient for Cu2MHf3S8 polycrystalline samples prepared by the PECS technique at 1073 K. Two samples containing manganese and iron possess a positive Seebeck coefficient S throughout the entire temperature range, indicating that holes are the dominant carriers. The Seebeck coefficient for the pristine Cu2MnHf3S8 is monotonously increasing from 357 to 485 μV K–1 at 473 K and then decreases to 372 μV K–1 at 673 K due to the effect of minority carriers. The Seebeck coefficient for pristine Cu2FeHf3S8 shows roughly temperature-independent behavior, with values in the range of 170–190 μV K–1. The different temperature gradients of S for these two samples can be explained by the different band structures of the investigated compounds and differences in the Hall carrier concentration. Cobalt- and nickel-containing materials possess a negative Seebeck coefficient over the entire temperature range, indicating that electrons are the dominant charge carriers. The Seebeck coefficient for pristine Cu2CoHf3S8 shows a decreasing tendency from −322 to −239 μV/K and is much higher compared with the Seebeck coefficient of Cu2NiHf3S8 (from −120 to −150 μV K–1) at the temperature range of 298–673 K. The low Seebeck coefficient accompanied by the low carrier concentration can be connected with the compensation effect of majority carriers (electrons) by the minority carriers (holes) in Cu2NiHf3S8.

Based on the measured S and σ, the power factors (PF = S2σ) of all the studied Cu2MHf3S8 polycrystalline samples are calculated and presented in Figure 5d. Because of the increase of electrical conductivity in the series Mn–Fe–Co–Ni in a few orders of magnitude and simultaneously with considerably high Seebeck coefficients,64 the Cu2NiHf3S8 sample showed the highest values of PF over the whole temperature range. The heating/cooling cycles of the electronic transport properties for the investigated samples are shown in Figure S2 (Supporting Information). The electrical conductivity, Seebeck coefficient, and power factor are repeatable for all the materials, except Cu2MnHf3S8, where the properties disagreed under heating and cooling. Such a tendency for this sample can be related to some chemical composition change or non-repeatable growth of intrinsic carrier concentration, as it was also observed for other thiospinels42,44 and some other chalcogenides.65−67

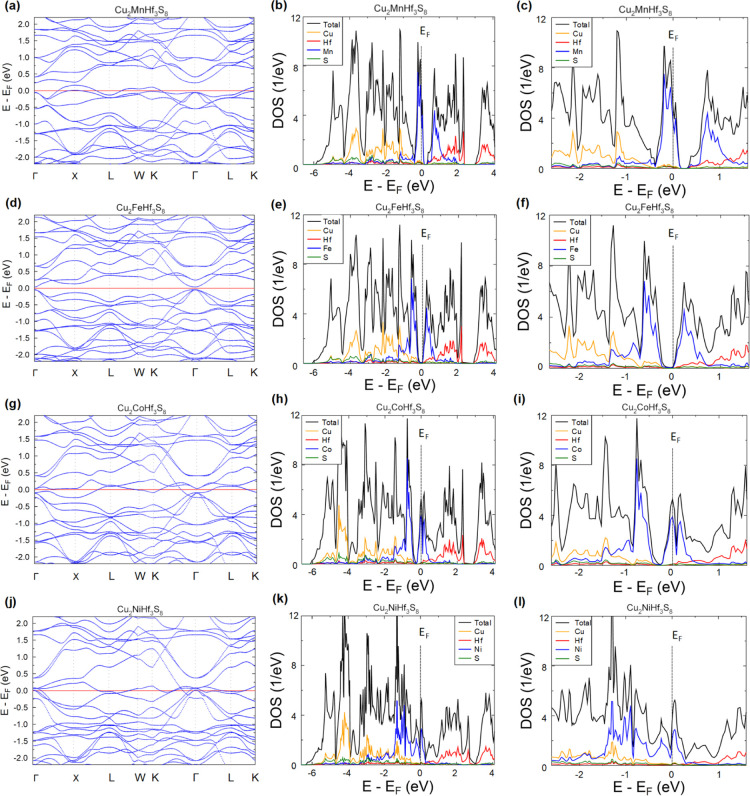
Electronic structure calculations using the KKR-CPA method were performed for the studied Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) thiospinel compounds to have an insight into measured electrical transport properties strongly varying with M substitution. Accordingly, Figure 6a–l presents the comparison of total- and site-decomposed DOS and electronic dispersion curves E(k) for Cu2MnHf3S8 as Cu2FeHf3S8, Cu2CoHf3S8, and Cu2NiHf3S8 alloys. Looking at the DOSs of these systems, one can distinguish a common feature, that is, the appearance of a deep minimum or an energy gap in the electronic spectra (appearing around the Fermi level), which divides the block of the strongly hybridized d-states of transition metal atoms Cu, Hf, and M and the p-states of S into valence-like and conduction-like bands. Inspecting in more detail the dispersion curves, one can notice that the energy gap (DOS minimum) tends to be formed above the 45th VB (enabling to accommodate 90 electrons), if accounting for eight bands (16 electrons s-symmetry originating from S) lying c.a. 6 eV below the valence edge located at about energy −6 eV. Hence, the visible p–d block of valence states consists of 37 bands accommodating 74 electrons.

Figure 6.

Figure 6

Open in a new tab

Electronic dispersion curves E(k) along the high-symmetry fcc Brillouin zone (left panel) and total- and site-decomposed DOS (middle panel) and DOS zoomed near EF (right panel) for Cu2MHf3S8 thiospinels: M = Mn (a–c); M = Fe (d–f); M = Co (g–i); and M = Ni (j–l) from the non-spin-polarized KKR-CPA calculations. The Fermi level was set to zero (EF = 0).

As mentioned above, the relatively open structure of the Cu2MHf3S8 thiospinels with variable interatomic distances and specific atomic coordination leads to the formation of tetrahedral bonds and sp3 hybridization around p-elements, favoring bonding between d-metals. The propensity of some systems to form the energy gap at a specific number of electrons (VEC—valence electron counts) can be compared to, for example, ternary half-Heusler systems, crystallizing in a similar F4̅3m structure and exhibiting semiconducting-like properties for VEC = 18. In the case of the thiospinel structure, it appears to have 90 valence electrons calculated for the primitive unit cell (or per chemical formula). In particular, the VEC condition is satisfied in Cu2FeHf3S8, where VEC = 2 × 11e (Cu) + 3 × 4e (Hf) + 1 × 8e (Fe) + 8 × 6e (S) = 90, and as a consequence, the Fermi level falls into the energy gap (or deep DOS minimum), responsible for semiconducting-like transport behaviors. Bearing in mind such electronic structure features of Cu2MHf3S8 thiospinels, the variety of electron transport behaviors with different M elements can be partly interpreted in terms of the number of electrons in the system.

Hence, Cu2MnHf3S8 also has a narrow band gap in the X point of the Brillouin zone, but due to one electron less in the system with respect to the VEC = 90 criterion, the Fermi level is located in the VB in agreement with measured p-type conductivity for this compound. As aforementioned, Cu2FeHf3S8 also has a very narrow band gap, however, the Γ point and Fermi level are shifted up to the band gap due to the additional d-electron of Fe2+ in comparison with Mn2+. Furthermore, the addition of d-electrons in the case of Cu2MHf3S8 (M—Co and Ni) makes them more metallic-like alloys (semimetals) with the Fermi level located in the CB, which is in agreement with the observed n-type conductivity for these compounds. The KKR-CPA results of the Cu2NiHf3S8 compound suggest that its ground state is metallic, which correlates well with the experimentally measured metallic-like character of the temperature-dependent electrical conductivity and the low Seebeck coefficient. The partial DOS shows that the VB and CB near EF, are mainly built up by M–3d states in Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) compounds. That is why the substitution of the M atom in Cu2MHf3S8 has such a strong effect on electronic transport, observed during measurements. This observation also suggests that the substitution of M atoms can be the most effective way to modify the band structure for the investigated alloys. All the compounds show a multivalley band structure near the EF, however, the low values of electrical conductivity can be explained by the undesirable intervalley scattering of electrons. In contrast with Cu2MTi3S8 compounds, where mostly Ti forms states near the EF,48 Hf has a very small contribution in this region in Cu2MHf3S8 thiospinels. This can also be a reason for the low electrical conductivity of Cu2MHf3S8 thiospinels in comparison to Cu2MTi3S8 because the [M/Ti(Hf)]S6 network bears the electrical conduction in such kinds of compounds, as suggested in ref. (48)

Because of the LDA used, we expect that the calculated band gap energy is underestimated. Hence, the evolution of the electron structure of Cu2MHf3S8, as obtained from the KKR-CPA calculations, suggests the change in electrical conductivity from hole-like to electron-like and in thermopower from positive to negative with an increasing number of electrons (M = Mn, Fe, Co, and Ni), should be treated more qualitatively than quantitatively. It can be assumed that extending first principles calculations to the LDA + U approach, with extra repulsion on-site term U on transition metal elements, should be used to better explain the semiconducting character of the electrical conductivity measured for M = Mn and M = Co. Our KKR-CPA-LDA calculations rather indicate the proximity of the band gap (or the pseudogap) and the Fermi level lying on a strongly varying DOS slope. So that, the main goal of KKR(CPA) calculations in this work was to observe the evolution of the band structure in Cu2MHf3S8 compounds, not to provide the precise values of the Eg. In the investigated series Mn–Fe–Co–Ni, it was found to have a decrease in conduction activation energies in agreement with such a tendency from KKR(CPA) calculations and with the literature reports for other similar thiospinels.42

The infrared absorption spectroscopy measurements have been performed to estimate the optical band gap for the investigated materials (Figure S3). From the dependence of optical absorption spectra versus photon energy, we observe at least two absorption edges in line with the complex electronic band structure of the investigated compounds. The measured smallest direct transitions correspond to 0.32 eV for the Cu2MnHf3S8 and 0.22 eV for Cu2FeHf3S8, Cu2CoHf3S8, and Cu2NiHf3S8 materials. The estimated band gaps are correlated with the activation energies calculated using temperature-dependent electrical conductivity. The values of Eg are also roughly consistent with the estimates obtained using the DFT calculations, where the decrease of the band gap can be detected; however, the LDA values of the Eg are lower compared with the optical data.68

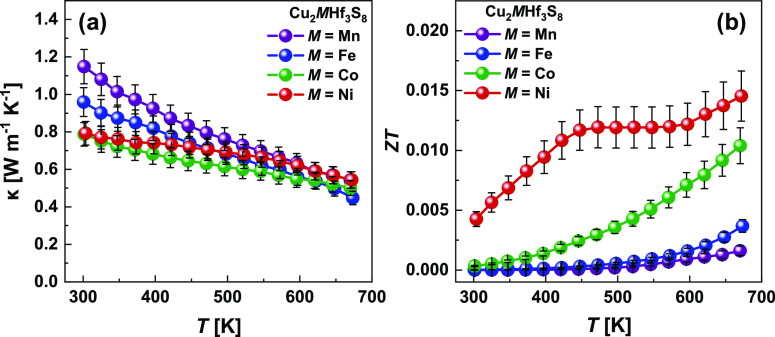
Figure 7a shows the total thermal conductivity (κ) of the studied Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) samples after sintering. All specimens possess very low thermal conductivities, in the range of 0.79–1.15 W m–1 K–1 at 298 K, decreasing to 0.45–0.54 W m–1 K–1 at 673 K, which are among the lowest values observed in spinel-type materials. In our case, the total κ is mainly contributed by the lattice thermal conductivity (κlat) due to the very low electrical conductivity of the investigated samples. The origin of the remarkable reduction in thermal conductivity observed for the investigated alloys is discussed in the following section.

Figure 7.

Figure 7

Open in a new tab

Thermal conductivity (a) and dimensionless figure of merit ZT (b) as a function of temperature for Cu2MHf3S8 polycrystalline samples.

Combining the measured S, σ, and κ, the TE figure of merit (ZT) of the Cu2MHf3S8 polycrystalline samples are calculated and shown in Figure 7b. The beneficial effects of lower κ, however, have been negated by the poor PF, thus resulting in a low figure of merit ZT value of ∼0.015 at 673 K for the Cu2NiHf3S8 compound. Nevertheless, the highest PF and the low lattice thermal conductivity of Cu2NiHf3S8, makes this compound the most interesting for further investigation and tuning of carrier concentration, which can significantly improve the TE figure of merit.

The good TE performance requires a high power factor and low lattice thermal conductivity. If the κ for the investigated alloys shows very low values, the power factor is rather moderated, mainly due to the unoptimized carrier concentration. Therefore, to obtain a higher TE figure of merit ZT for the investigated thiospinels, the carrier concentration must be increased through proper doping or deviation from stoichiometry.

3.3. Origins of the Low Thermal Conductivity

Recent work by Hashikuni et al. shows that Cu2MTi3S8 (M—Mn, Fe, Co, and Ni) spinels possess much higher κlat ∼ 1.4–2.3 W m–1 K–1 at 298 K48 compared to the investigated Cu2MHf3S8 materials (κlat ∼ 0.79–1.15 W m–1 K–1 at 298 K). The explanation of this issue can be connected with the significant mass difference between Hf and M (M—Mn, Fe, Co, and Ni) compared to Ti vs. M. In this case, the large phonon scattering on point defects is expected, which may cause a reduction of the lattice thermal conductivity. On the other hand, the aforementioned features of the crystal structure, particularly the mixed occupation of octahedral voids by Hf and M, and the occupation of only three of six octahedra in the structure, provoke an increase in bond anharmonicity, which has recently been reported as one of the most powerful instruments for disturbing phonon transport.69

To shed some light on the measured thermal conductivity of the investigated alloys, we conjugated the ultrasonic measurements of longitudinal and transverse sound velocities at room temperature with the theoretical calculations based on the Callaway approach. The measured data of the longitudinal vl and transverse vt, velocity and results of the calculations of the average velocities vm, Debye temperatures ΘD, the Poisson ratio ν, Grüneisen parameter γ, bulk modulus B, Young modulus E, phonon mean free path lph, and the minimum thermal conductivity κglass and κdiff for Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) samples investigated in this work are shown in Table 6.

Table 6. Elastic and Thermal Transport Properties for Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) Thiospinels.

compound vl, m/s vt, m/s vm, m/s ΘD, K ν γ B, GPa E, GPa lph, Å κglass, W/(m K) κdiff, W/(m K)
Cu2MnHf3S8 4094 2209 2466 263.8 0.29 1.74 55.0 49.5 6.95 0.64 0.40
Cu2FeHf3S8 4237 2229 2493 270.2 0.31 1.83 63.2 56.9 5.56 0.66 0.42
Cu2CoHf3S8 4072 2172 2427 261.3 0.30 1.78 56.5 50.8 4.29 0.64 0.41
Cu2NiHf3S8 3712 2009 2242 240.2 0.29 1.73 45.5 40.9 6.53 0.59 0.37
Open in a new tab

The measured speed of sound shows relatively high values compared to the other well-established TE materials, that is, PbTe,69 Bi2Te3,70 and GeTe.3 This may indicate that scattering of acoustic phonons is not the dominant mechanism that affects the phonon transport in the investigated materials.71 On the other hand, the quite high difference between the longitudinal vl and transverse vt speeds of sound causes the high Grüneisen parameters for the investigated materials. Such high values of γ, ranging from 1.73 to 1.83 (Table 6), are in line with the aforementioned hypothesis of the high degree of bond anharmonicity in the investigated compounds. Moreover, using inelastic neutron scattering, the anharmonicity has been experimentally demonstrated to be at the origin of the low lattice thermal conductivity in other sulfur-based compounds, for example, tetrahedrites.72 As shown in Figure 2, the studied structures are characterized by the (M + Hf)S6 octahedra. Introducing a heavier atom Hf instead of Ti or Sn in octahedra is evidently responsible for the evolution of bond anharmonicity.69,73 These lead to a very short phonon mean free path lph ∼4–7 Å that is about twice shorter than lattice parameters and can be a dominant mechanism responsible for disturbed phonon transport in our compounds. On the other hand, copper atoms form CuS4 tetrahedra with strong atomic interactions, which contribution to phonon scattering is rather small.

To examine the effect of M substitution on the mechanical properties of Cu2MHf3S8 samples, Vickers microhardness measurements were carried out, as shown in Figure 8a. In the series Mn–Fe–Co–Ni, the Vickers microhardness is generally decreasing; however, the Fe-containing sample shows the maximum value. On the other hand, such a compositional dependence of the measured microhardness excellently correlates with Young’s modulus determined from ultrasonic measurements, as shown in Figure 8b. Cu2MHf3S8 samples exhibit superior Young’s modulus and Vickers hardness, which is comparable (or even higher) to other well-established TE materials, suggesting their good mechanical stability.

Figure 8.

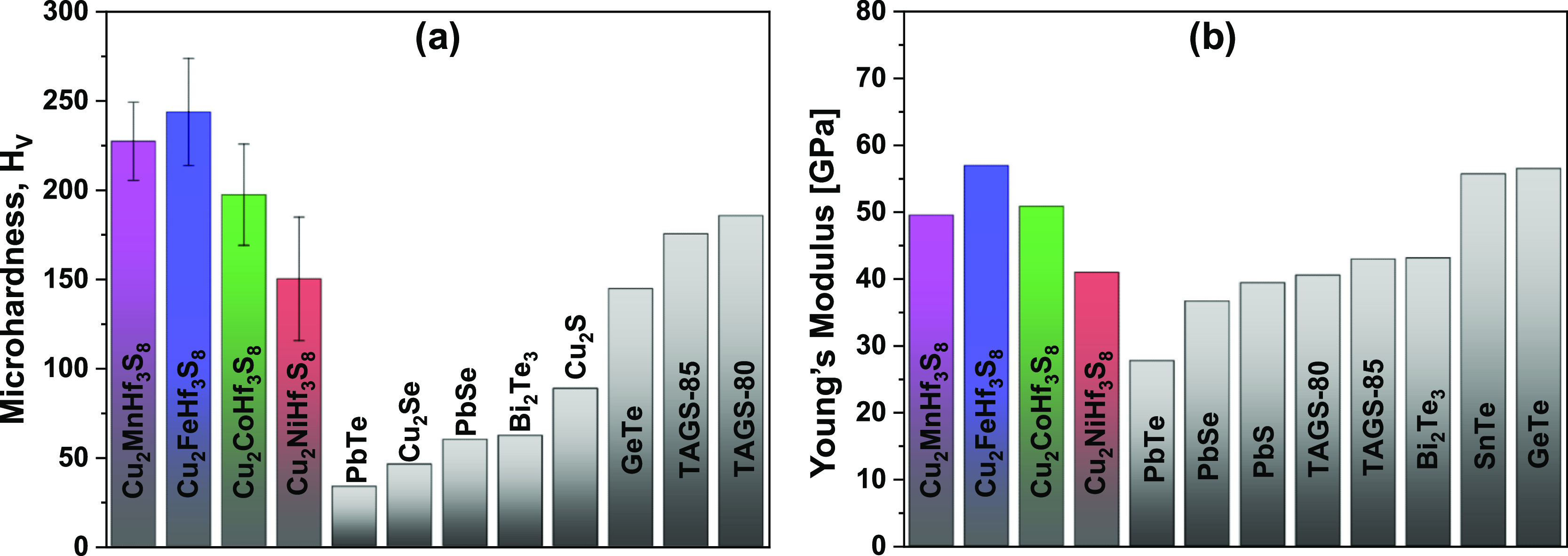
Figure 8

Open in a new tab

Microhardness of Cu2MHf3S8 samples in comparison to other conventional TE materials (a). Young’s modulus of Cu2MHf3S8 samples compared with the literature data (b).74−76

We also calculated the “minimum thermal conductivity” using Cahill’s formulation77

3.3. 1

where V is the average volume per atom calculated from the refined lattice parameters and kB is the Boltzmann constant. As the calculated values of the lattice thermal conductivity were found to be higher than the experimental points, the diffusive-based minimum of the thermal conductivity κdiff was calculated using the formalism proposed by Agne et al.78

3.3. 2

We see that the measured samples showed κ values that are close to the minimum of the thermal conductivity estimated from the assumption of diffuson-mediated thermal transport.78 The performed analysis also suggests that the complexity of the crystal structure caused by Hf atoms, that are introduced into the octahedral voids leads to a remarkable reduction of lattice thermal conductivity.79 Moreover, the abundance of structural voids and cationic disorder on the Hf/M site further contributes to the lowering of lattice thermal conductivity, as it was also recently shown for other Cu-based chalcogenides, for example, Cu2SnS380−82 and colusites.83−85 However, the realistic mechanism that can describe the origin of the observed ultralow κlat is still unclear.

To further understand the role of Hf on the thermal transport properties of Cu2MHf3S8 (M—Mn, Fe, Co, and Ni), we used the Callaway approach.86 In this case, the phonon relaxation time (τc) is calculated using contributions related to scattering on point defects86 and four-phonon processes87

3.3. 3
3.3. 4

where, ℏ = h/(2π) and t = ℏω/(kBT), A and B are adjustable fitting parameters related to point defect scattering and four-phonon Umklapp scattering processes, respectively. The materials considered in this work have large values of the Grüneisen parameter, this indicating high anharmonicity, which was identified as a factor that promotes the influence of the four-phonon Umklapp scattering processes.87,88 The use of the four-phonon Umklapp process allowed for much better fit quality over the fitting with the three-phonon Umklapp process and for obtaining smaller uncertainties of the fitted variables.

All the investigated lattice thermal conductivity dependences were reasonably well fitted by the Callaway model. The fitting parameters A and B (Table 7) quantify the strength of phonon scattering on point defects89 and four-phonon scattering processes,87 respectively. Therefore, their comparative analysis might provide a deeper insight into the origins of lattice thermal conductivity reduction.

Table 7. Fitted A and B Parameters of Cu2MX3S8 in the Callaway Model for the Calculation of Lattice Thermal Conductivity [A = (10–38 s3) and B = (10–43 s3 K–2)].

    (I)
  X→ Hf
 Sn
 Ti
  M↓ A B A B A B
(IIa) Mn 1.465(20) 0.613(11)     1.305(18) 0.145(08)
  Fe 1.737(30) 0.609(16)        
(III) Co 2.646(33) 0.449(15) 2.240(99) 0.058(36) 1.099(20) 0.143(08)
(IIb) Ni 3.091(43) 0.378(19)     0.908(19) 0.144(09)
Open in a new tab

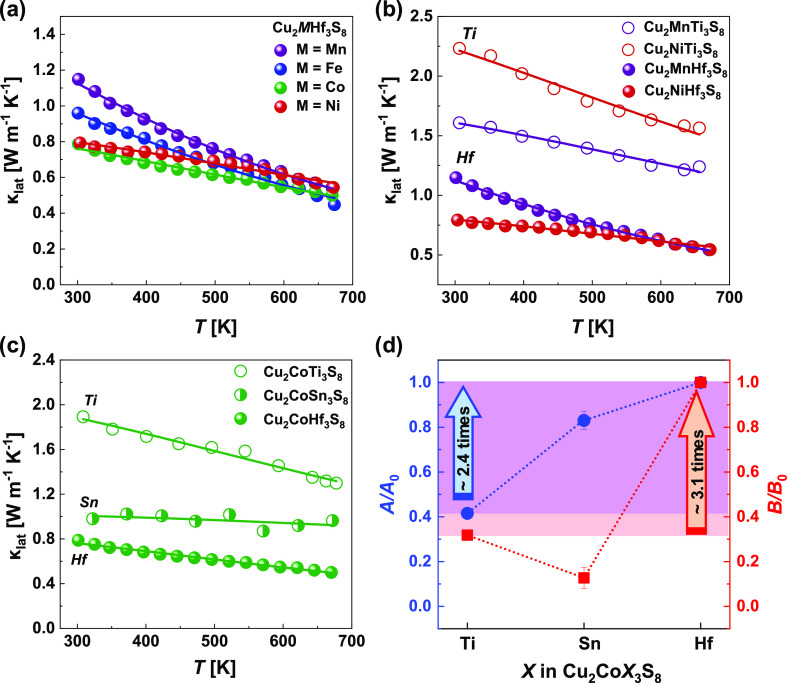
In the case of Hf-based samples investigated in this work (Figure 9a, Table 7I), the A parameter increases in the Mn → Fe → Co → Ni series, which could be related to the observed decrease in atomic radius in this series, and thus an increase in the difference between the atomic radii of Hf and X, which increases strain in the material. At the same time, parameter B decreases in the Mn → Fe → Co → Ni series, indicating a slight reduction of the anharmonic scattering with the decrease of interatomic distances (M/Hf)–S.

Figure 9.

Figure 9

Open in a new tab

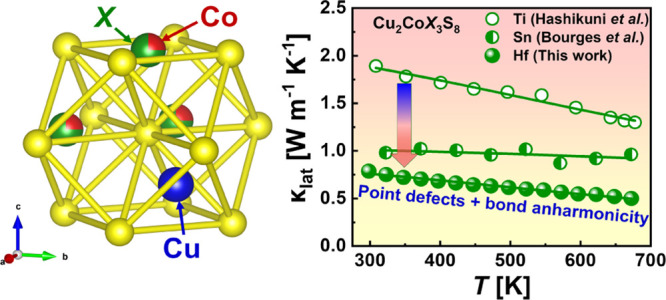
(a) Lattice thermal conductivity for Cu2MHf3S8 (M—Mn, Fe, Co, and Ni). (b) Comparison of lattice thermal conductivity of Hf-contained samples with the Ti-contained ones. (c) Comparison of lattice thermal conductivity for Cu2CoX3S8 (X = Hf, Sn, and Ti). The reduction of lattice thermal conductivity for the series Ti → Sn → Hf is obvious. In panels a–c, points indicate experimental data received in the present work or taken from refs.,31,34,48 lines correspond to the calculations using the Callaway approach. (d) Fitting parameters A and B, which were used for the calculation of lattice thermal conductivity by the Callaway approach for the Cu2CoX3S8 (X = Hf, Sn, and Ti). Parameter A quantifies the strength of phonon scattering on point defects89 and parameter B denotes the four-phonon scattering processes.87 Therefore, the reduction of the lattice thermal conductivity for investigated samples is coming from both mechanisms; however, the latter one is dominant.

A much more interesting observation has occurred after the comparison of the lattice thermal conductivity of spinels with Hf (this work) and Sn34 and Ti31,48 (Figure 9b–d, Table 7IIa,b). The Hf-induced large atom mass and size differences significantly increase the strength of phonon scattering on point defects (A parameter) by more than ∼2.3 times. However, the B parameter in the case of Hf-based spinels investigated in this work shows even more than ∼3.1 times difference compared with the Sn- and Ti-based compounds, suggesting a significantly larger effect of four-phonon scattering. As the four-phonon scattering is largely defined by bond anharmonicity, we can conclude that this effect could be determinative for the phonon transport in the Cu2MHf3S8 (M = Mn, Fe, Co, and Ni) spinels.

4. Conclusions

Thermal transport engineering through understanding the role of structural properties is among the newest ways to increase the functionality of TE materials. In this work, we successfully synthesized and investigated the crystal structure and electronic and band structure properties, and established the TE performance for four new Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) thiospinels. It was found, that the discovered compounds crystallize in the space group Fd3̅m (No 227, Pearson symbol cF56) with a large number of atoms in the unit cell [N = 56 per cubic cell with a from 10.398 Å (for Mn) to 10.301 Å (for Ni)].

The DFT calculations using the KKR-CPA method suggest that the main contribution to the total density of electronic states, close to the Fermi energy, comes from M–3d electrons (Mn, Fe, Co, and Ni). Besides, the computed electronic band structure features near EF reveal an apparent correlation between the number of valence electrons in the system and its strongly changing physical properties. Therefore, the significant modification of the electronic transport properties for the investigated Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) thiospinels is expected due to substitution or partial substitution of these atoms. In line with the DFT results, the decrease in the activation energies and the transition from p- to n-type conductivity were observed in the Mn–Fe–Co–Ni series. The best dimensionless TE figure of merit ZT in this work was determined for the Cu2NiHf3S8 thiospinel due to the highest power factor and low thermal conductivity.

If the electrical transport properties for the investigated compounds are moderated mainly due to low electrical conductivity, the thermal conductivity shows very low values (as low as 0.50 W m–1 K–1 at 673 K for Cu2CoHf3S8) compared to the other reported thiospinels. The origins of such low thermal conductivity are connected with the introduction of Hf to the structure and particularities of the crystal lattice. On the one hand, the heavy Hf atoms cause a large mass difference effect between Hf and the other atoms in the structure, which reduces the lattice thermal conductivity. On the other hand, the atoms of Hf are located in the (Hf/M)S6 octahedral voids, and only half of these voids are occupied. Such a combination of crystal structure properties promotes large bond anharmonicity. The estimated from the speed of sound measurements high values of the Grüneisen parameters γ (1.73–1.83) are in line with this statement. Moreover, using the Callaway approach, we were able to evaluate that the contribution of the bond anharmonicity to the reduction of the thermal conductivity is much larger than the mass difference effect for the investigated alloys. This intriguing finding suggests Cu2MHf3S8 (M—Mn, Fe, Co, and Ni) thiospinels as novel and promising functional materials with intrinsically low lattice thermal conductivity. Moreover, the work offers bond anharmonicity as a powerful instrument for disturbing phonon transport in TE materials, particularly in lightweight thiospinels.

Acknowledgments

The research was funded by the Foundation for Polish Science (TEAM-TECH/2016-2/14 grant “New approach for the development of efficient materials for direct conversion of heat into electricity”) and cofinanced by the European Union under the European Regional Development Fund. T.P. acknowledges support from the program “Excellence Initiative—Research University” for the AGH University of Science and Technology.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemmater.1c03593.

  • Cu2CoHf3S8 (CIF)

  • Cu2FeHf3S8 (CIF)

  • Cu2MnHf3S8 (CIF)

  • Cu2NiHf3S8 (CIF)

  • PXRD patterns of samples after synthesis and pellets after measurements; heating and cooling data of electronic transport properties; optical absorption spectra; and details of the elastic and thermal transport properties calculations (PDF)

The authors declare no competing financial interest.

Supplementary Material

cm1c03593_si_001.cif (10.7KB, cif)
cm1c03593_si_002.cif (10.7KB, cif)
cm1c03593_si_003.cif (10.7KB, cif)
cm1c03593_si_004.cif (10.7KB, cif)
cm1c03593_si_005.pdf (588.7KB, pdf)

References

  1. Snyder G. J.; Toberer E. S. Complex Thermoelectric Materials. Nat. Mater. 2008, 7, 105–114. 10.1038/nmat2090. [DOI] [PubMed] [Google Scholar]
  2. Zhang Q. H.; Huang X. Y.; Bai S. Q.; Shi X.; Uher C.; Chen L. D. Thermoelectric Devices for Power Generation: Recent Progress and Future Challenges. Adv. Eng. Mater. 2016, 18, 194–213. 10.1002/adem.201500333. [DOI] [Google Scholar]
  3. Kumar A.; Bhumla P.; Parashchuk T.; Baran S.; Bhattacharya S.; Wojciechowski K. T. Engineering Electronic Structure and Lattice Dynamics to Achieve Enhanced Thermoelectric Performance of Mn–Sb Co-Doped GeTe. Chem. Mater. 2021, 33, 3611–3620. 10.1021/acs.chemmater.1c00331. [DOI] [Google Scholar]
  4. Parashchuk T.; Horichok I.; Kosonowski A.; Cherniushok O.; Wyzga P.; Cempura G.; Kruk A.; Wojciechowski K. T. Insight into the Transport Properties and Enhanced Thermoelectric Performance of N-Type Pb1-xSbxTe. J. Alloys Compd. 2021, 860, 158355. 10.1016/j.jallcom.2020.158355. [DOI] [Google Scholar]
  5. Parashchuk T.; Wiendlocha B.; Cherniushok O.; Knura R.; Wojciechowski K. T. High Thermoelectric Performance of P-Type PbTe Enabled by the Synergy of Resonance Scattering and Lattice Softening. ACS Appl. Mater. Interfaces 2021, 13, 49027–49042. 10.1021/acsami.1c14236. [DOI] [PubMed] [Google Scholar]
  6. Knura R.; Parashchuk T.; Yoshiasa A.; Wojciechowski K. T. Evaluation of the Double-Tuned Functionally Graded Thermoelectric Material Approach for the Fabrication of n-Type Leg Based on Pb0.75Sn0.25Te. Appl. Phys. Lett. 2021, 119, 223902. 10.1063/5.0075126. [DOI] [Google Scholar]
  7. He Y.; Day T.; Zhang T.; Liu H.; Shi X.; Chen L.; Snyder G. J. High Thermoelectric Performance in Non-Toxic Earth-Abundant Copper Sulfide. Adv. Mater. 2014, 26, 3974–3978. 10.1002/adma.201400515. [DOI] [PubMed] [Google Scholar]
  8. Fiechter S.; Martinez M.; Schmidt G.; Henrion W.; Tomm Y. Phase Relations and Optical Properties of Semiconducting Ternary Sulfides in the System Cu–Sn–S. J. Phys. Chem. Solids 2003, 64, 1859–1862. 10.1016/s0022-3697(03)00172-0. [DOI] [Google Scholar]
  9. Pavan Kumar V.; Lemoine P.; Carnevali V.; Guélou G.; Lebedev O. I.; Boullay P.; Raveau B.; Al Rahal Al Orabi R.; Fornari M.; Prestipino C.; Menut D.; Candolfi C.; Malaman B.; Juraszek J.; Guilmeau E. Ordered Sphalerite Derivative Cu5Sn2S7: A Degenerate Semiconductor with High Carrier Mobility in the Cu–Sn–S Diagram. J. Mater. Chem. A 2021, 9, 10812–10826. 10.1039/d1ta01615f. [DOI] [Google Scholar]
  10. Ang R.; Khan A. U.; Tsujii N.; Takai K.; Nakamura R.; Mori T. Thermoelectricity Generation and Electron-Magnon Scattering in a Natural Chalcopyrite Mineral from a Deep-Sea Hydrothermal Vent. Angew. Chem. Int. Ed. 2015, 54, 12909–12913. 10.1002/anie.201505517. [DOI] [PubMed] [Google Scholar]
  11. Barbier T.; Berthebaud D.; Frésard R.; Lebedev O. I.; Guilmeau E.; Eyert V.; Maignan A. Structural and Thermoelectric Properties of N-Type Isocubanite CuFe2S3. Inorg. Chem. Front. 2017, 4, 424–432. 10.1039/c6qi00510a. [DOI] [Google Scholar]
  12. Bourgès C.; Bouyrie Y.; Supka A. R.; Al Rahal Al Orabi R.; Lemoine P.; Lebedev O. I.; Ohta M.; Suekuni K.; Nassif V.; Hardy V.; Daou R.; Miyazaki Y.; Fornari M.; Guilmeau E. High-Performance Thermoelectric Bulk Colusite by Process Controlled Structural Disordering. J. Am. Chem. Soc. 2018, 140, 2186–2195. 10.1021/jacs.7b11224. [DOI] [PubMed] [Google Scholar]
  13. Pavan Kumar V.; Barbier T.; Caignaert V.; Raveau B.; Daou R.; Malaman B.; Caër G. L.; Lemoine P.; Guilmeau E. Copper Hyper-Stoichiometry: The Key for the Optimization of Thermoelectric Properties in Stannoidite Cu8+xFe3-xSn2S12. J. Phys. Chem. C 2017, 121, 16454–16461. 10.1021/acs.jpcc.7b02068. [DOI] [Google Scholar]
  14. Zazakowny K.; Kosonowski A.; Lis A.; Cherniushok O.; Parashchuk T.; Tobola J.; Wojciechowski K. T. Phase Analysis and Thermoelectric Properties of Cu-Rich Tetrahedrite Prepared by Solvothermal Synthesis. Materials 2022, 15, 849. 10.3390/ma15030849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fan Y.; Wang G.; Wang R.; Zhang B.; Shen X.; Jiang P.; Zhang X.; Gu H.-s.; Lu X.; Zhou X.-y.X. Enhanced Thermoelectric Properties of P-Type Argyrodites Cu8GeS6 through Cu Vacancy. J. Alloys Compd. 2020, 822, 153665. 10.1016/j.jallcom.2020.153665. [DOI] [Google Scholar]
  16. Cherniushok O.; Parashchuk T.; Tobola J.; Luu S. D. N.; Pogodin A.; Kokhan O.; Studenyak I.; Barchiy I.; Piasecki M.; Wojciechowski K. T. Entropy-Induced Multivalley Band Structures Improve Thermoelectric Performance in p-Cu7P(SxSe1–x)6 Argyrodites. ACS Appl. Mater. Interfaces 2021, 13, 39606–39620. 10.1021/acsami.1c11193. [DOI] [PubMed] [Google Scholar]
  17. Zhang R.-Z.; Gucci F.; Zhu H.; Chen K.; Reece M. J. Data-Driven Design of Ecofriendly Thermoelectric High-Entropy Sulfides. Inorg. Chem. 2018, 57, 13027–13033. 10.1021/acs.inorgchem.8b02379. [DOI] [PubMed] [Google Scholar]
  18. Pavan Kumar V.; Paradis-Fortin L.; Lemoine P.; Caignaert V.; Raveau B.; Malaman B.; Le Caër G.; Cordier S.; Guilmeau E. Designing a Thermoelectric Copper-Rich Sulfide from a Natural Mineral: Synthetic Germanite Cu22Fe8Ge4S32. Inorg. Chem. 2017, 56, 13376–13381. 10.1021/acs.inorgchem.7b02128. [DOI] [PubMed] [Google Scholar]
  19. Bourgès C.; Ventrapati P.; Nagai H.; Miyazaki Y.; Raveau B.; Guilmeau E. Role of Cobalt for Titanium Substitution on the Thermoelectric Properties of the Thiospinel CuTi2S4. J. Alloys Compd. 2019, 781, 1169–1174. 10.1016/j.jallcom.2018.12.102. [DOI] [Google Scholar]
  20. Lemoine P.; Guélou G.; Raveau B.; Guilmeau E. Crystal Structure Classification of Copper-Based Sulfides as a Tool for the Design of Inorganic Functional Materials. Angew. Chem. Int. Ed. 2022, 61, e202108686 10.1002/anie.202108686. [DOI] [PubMed] [Google Scholar]
  21. Shen X.; Yang C.-C.; Liu Y.; Wang G.; Tan H.; Tung Y.-H.; Wang G.; Lu X.; He J.; Zhou X. High-Temperature Structural and Thermoelectric Study of Argyrodite Ag8GeSe6. ACS Appl. Mater. Interfaces 2019, 11, 2168–2176. 10.1021/acsami.8b19819. [DOI] [PubMed] [Google Scholar]
  22. Baumer F.; Nilges T. Phase Segregation of Polymorphic Solid Ion Conducting Cu7PSe6 during Thermoelectric Experiments. Z. Anorg. Allg. Chem 2018, 644, 1519–1524. 10.1002/zaac.201800108. [DOI] [Google Scholar]
  23. Strick G.; Eulenberger G.; Hahn H. Über Einige Quaternäre Chalkogenide Mit Spinellstruktur. Z. Anorg. Allg. Chem. 2004, 357, 338–344. 10.1002/zaac.19683570421. [DOI] [Google Scholar]
  24. Snyder G. J.; Caillat T.; Fleurial J.-P. Thermoelectric Properties of Chalcogenides with the Spinel Structure. Mater. Res. Innovat. 2001, 5, 67–73. 10.1007/s100190100133. [DOI] [Google Scholar]
  25. Hill R. J.; Craig J. R.; Gibbs G. V. Systematics of the Spinel Structure Type. Phys. Chem. Miner. 1979, 4, 317–339. 10.1007/bf00307535. [DOI] [Google Scholar]
  26. Kuhs W. F.; Nitsche R.; Scheunemann K. The Argyrodites - A New Family of Tetrahedrally Close-Packed Structures. Mater. Res. Bull. 1979, 14, 241–248. 10.1016/0025-5408(79)90125-9. [DOI] [Google Scholar]
  27. Kariya F.; Ebina K.; Hasegawa K.; Koshimizu K.; Wuritunasitu B.; Hondou K.; Ebisu S.; Nagata S. Magnetic Properties of the Spinel-Type Cu(Cr1-xHfx)2S4. J. Solid State Chem. 2009, 182, 2018–2023. 10.1016/j.jssc.2009.05.012. [DOI] [Google Scholar]
  28. Matsumoto N.; Hagino T.; Taniguchi K.; Chikazawa S.; Nagata S. Electrical and Magnetic Properties of CuTi2S4 and CuZr2S4. Phys. B Condens. Matter 2000, 284–288, 1978–1979. 10.1016/s0921-4526(99)02946-4. [DOI] [Google Scholar]
  29. Chauhan M.; Reddy K. P.; Gopinath C. S.; Deka S. Copper Cobalt Sulfide Nanosheets Realizing a Promising Electrocatalytic Oxygen Evolution Reaction. ACS Catal. 2017, 7, 5871–5879. 10.1021/acscatal.7b01831. [DOI] [Google Scholar]
  30. Kormosh Z.; Fedorchuk A.; Wojciechowski K.; Tataryn N.; Parasyuk O. The Cu2FeTi3S8 and Cu2FeZr3S8 Compounds: Crystal Structure and Electroanalytical Application. Mater. Sci. Eng., C 2011, 31, 540–544. 10.1016/j.msec.2010.11.015. [DOI] [Google Scholar]
  31. Hashikuni K.; Suekuni K.; Usui H.; Chetty R.; Ohta M.; Takabatake T.; Ohtaki M. A Comparative Study of Thermoelectric Cu2TrTi3S8 (Tr = Co and Sc) Thiospinels: Enhanced Seebeck Coefficient via Electronic Structure Modification. J. Alloys Compd. 2021, 871, 159548. 10.1016/j.jallcom.2021.159548. [DOI] [Google Scholar]
  32. Lang Y.; Pan L.; Chen C.; Wang Y. Thermoelectric Properties of Thiospinel-Type CuCo2S4. J. Electron. Mater. 2019, 48, 4179–4187. 10.1007/s11664-019-07182-x. [DOI] [Google Scholar]
  33. Hashikuni K.; Suekuni K.; Usui H.; Chetty R.; Ohta M.; Kuroki K.; Takabatake T.; Watanabe K.; Ohtaki M. Thermoelectric Properties and Electronic Structures of CuTi2S4 Thiospinel and Its Derivatives: Structural Design for Spinel-Related Thermoelectric Materials. Inorg. Chem. 2019, 58, 1425–1432. 10.1021/acs.inorgchem.8b02955. [DOI] [PubMed] [Google Scholar]
  34. Bourgès C.; Srinivasan B.; Fontaine B.; Sauerschnig P.; Minard A.; Halet J. F.; Miyazaki Y.; Berthebaud D.; Mori T. Tailoring the Thermoelectric and Structural Properties of Cu-Sn Based Thiospinel Compounds [CuM1+xSn1-xS4 (M = Ti, V, Cr, Co)]. J. Mater. Chem. C 2020, 8, 16368–16383. 10.1039/D0TC04393A. [DOI] [Google Scholar]
  35. Khan A. U.; Orabi R. A. R. A.; Pakdel A.; Vaney J.-B.; Fontaine B.; Gautier R.; Halet J.-F.; Mitani S.; Mori T. Sb Doping of Metallic CuCr2S4 as a Route to Highly Improved Thermoelectric Properties. Chem. Mater. 2017, 29, 2988–2996. 10.1021/acs.chemmater.6b05344. [DOI] [Google Scholar]
  36. Goltsman B. M.; Kudinov V. A.; Smirnov I. A.. Thermoelectric Semiconductor Materials Based On Bi2Te3; Nauka: Moskow, 1972. [Google Scholar]
  37. Ravich Y. I.; Efimova B. A.; Smirnov I. A.. Semiconducting Lead Chalcogenides; Springer US, 1970. [Google Scholar]
  38. Goldak J.; Barrett C. S.; Innes D.; Youdelis W. Structure of Alpha GeTe. J. Chem. Phys. 1966, 44, 3323–3325. 10.1063/1.1727231. [DOI] [Google Scholar]
  39. Kosonowski A.; Kumar A.; Parashchuk T.; Cardoso-Gil R.; Wojciechowski K. T. Thermal Conductivity of PbTe-CoSb3 bulk Polycrystalline Composite: Role of Microstructure and Interface Thermal Resistance. Dalton Trans. 2021, 50, 1261–1273. 10.1039/d0dt03752d. [DOI] [PubMed] [Google Scholar]
  40. Graf T.; Felser C.; Parkin S. S. P. Simple Rules for the Understanding of Heusler Compounds. Prog. Solid State Chem. 2011, 39, 1–50. 10.1016/j.progsolidstchem.2011.02.001. [DOI] [Google Scholar]
  41. Spitzer D. P. Lattice Thermal Conductivity of Semiconductors: A Chemical Bond Approach. J. Phys. Chem. Solids 1970, 31, 19–40. 10.1016/0022-3697(70)90284-2. [DOI] [Google Scholar]
  42. Wyżga P.; Veremchuk I.; Bobnar M.; Hennig C.; Leithe-Jasper A.; Gumeniuk R. Ternary MIn2S4 (M = Mn, Fe, Co, Ni) Thiospinels – Crystal Structure and Thermoelectric Properties. Z. Anorg. Allg. Chem. 2020, 646, 1091–1098. 10.1002/zaac.202000014. [DOI] [Google Scholar]
  43. Wyżga P.; Veremchuk I.; Koželj P.; Leithe-Jasper A.; Gumeniuk R. Mn-for-Fe Substitution in Fe1-xMnxIn2S4 Thiospinel – Crystal Structure and Thermoelectric Properties. J. Phys. Chem. Solids 2021, 152, 109984. 10.1016/j.jpcs.2021.109984. [DOI] [Google Scholar]
  44. Wyżga P.; Veremchuk I.; Bobnar M.; Koželj P.; Klenner S.; Pöttgen R.; Leithe-Jasper A.; Gumeniuk R. Structural Peculiarities and Thermoelectric Study of Iron Indium Thiospinel. Chem.—Eur J. 2020, 26, 5245–5256. 10.1002/chem.201905665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Wyżga P.; Grimm S.; Garbe V.; Zuñiga-Puelles E.; Himcinschi C.; Veremchuk I.; Leithe-Jasper A.; Gumeniuk R. Improving Thermoelectric Performance of Indium Thiospinel by Se- And Te-Substitution. J. Mater. Chem. C 2021, 9, 4008–4019. 10.1039/D1TC00291K. [DOI] [Google Scholar]
  46. Wyżga P.; Carrillo-Cabrera W.; Akselrud L.; Veremchuk I.; Wagler J.; Hennig C.; Tsirlin A. A.; Leithe-Jasper A.; Kroke E.; Gumeniuk R. Crystal Structure, Phase Transition and Properties of Indium(Iii) Sulfide. Dalton Trans. 2020, 49, 15903–15913. 10.1039/d0dt03302b. [DOI] [PubMed] [Google Scholar]
  47. Chen Y.-X.; Li F.; Wang W.; Zheng Z.; Luo J.; Fan P.; Takeuchi T. Optimization of Thermoelectric Properties Achieved in Cu Doped β-In2S3 Bulks. J. Alloys Compd. 2019, 782, 641–647. 10.1016/j.jallcom.2018.12.138. [DOI] [Google Scholar]
  48. Hashikuni K.; Suekuni K.; Usui H.; Ohta M.; Kuroki K.; Takabatake T. High Power Factor in Thiospinels Cu2TrTi3S8 (Tr = Mn, Fe, Co, Ni) Arising from TiS6 Octahedron Network. Appl. Phys. Lett. 2016, 109, 182110. 10.1063/1.4966955. [DOI] [Google Scholar]
  49. Hashikuni K.; Suekuni K.; Watanabe K.; Bouyrie Y.; Ohta M.; Ohtaki M.; Takabatake T. Carrier Concentration Tuning in Thermoelectric Thiospinel Cu2CoTi3S8 by Oxidative Extraction of Copper. J. Solid State Chem. 2018, 259, 5–10. 10.1016/j.jssc.2017.12.031. [DOI] [Google Scholar]
  50. Parashchuk T.; Kostyuk O.; Nykyruy L.; Dashevsky Z. High Thermoelectric Performance of P-Type Bi0.5Sb1.5Te3 Films on Flexible Substrate. Mater. Chem. Phys. 2020, 253, 123427. 10.1016/j.matchemphys.2020.123427. [DOI] [Google Scholar]
  51. Parashchuk T.; Dashevsky Z.; Wojciechowski K. Feasibility of a High Stable PbTe:In Semiconductor for Thermoelectric Energy Applications. J. Appl. Phys. 2019, 125, 245103. 10.1063/1.5106422. [DOI] [Google Scholar]
  52. Wojciechowski K. T.; Parashchuk T.; Wiendlocha B.; Cherniushok O.; Dashevsky Z. Highly Efficient N-Type PbTe Developed by Advanced Electronic Structure Engineering. J. Mater. Chem. C 2020, 8, 13270–13285. 10.1039/d0tc03067h. [DOI] [Google Scholar]
  53. Akselrud L.; Grin Y. WinCSD: Software Package for Crystallographic Calculations (Version 4). J. Appl. Crystallogr. 2014, 47, 803–805. 10.1107/s1600576714001058. [DOI] [Google Scholar]
  54. Borup K. A.; De Boor J.; Wang H.; Drymiotis F.; Gascoin F.; Shi X.; Chen L.; Fedorov M. I.; Müller E.; Iversen B. B.; Snyder G. J. Measuring Thermoelectric Transport Properties of Materials. Energy Environ. Sci. 2015, 8, 423–435. 10.1039/c4ee01320d. [DOI] [Google Scholar]
  55. Bansil A.; Kaprzyk S.; Mijnarends P. E.; Toboła J. Electronic Structure and Magnetism of Fe3-xVxX (X=Si, Ga, and Al) Alloys by the KKR-CPA Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 60, 13396–13412. 10.1103/physrevb.60.13396. [DOI] [Google Scholar]
  56. Stopa T.; Kaprzyk S.; Toboła J. Linear Aspects of the Korringa-Kohn-Rostoker Formalism. J. Phys. Condens. Matter 2004, 16, 4921–4933. 10.1088/0953-8984/16/28/012. [DOI] [Google Scholar]
  57. Perdew J. P.; Wang Y. Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 45, 13244–13249. 10.1103/physrevb.45.13244. [DOI] [PubMed] [Google Scholar]
  58. Kaprzyk S.; Bansil A. Greens Function and a Generalized Lloyd Formula for the Density of States in Disordered Muffin-Tin Alloys. Phys. Rev. B: Condens. Matter Mater. Phys. 1990, 42, 7358–7362. 10.1103/physrevb.42.7358. [DOI] [PubMed] [Google Scholar]
  59. Garg G.; Bobev S.; Ganguli A. K. Single Crystal Structures of Two New Cation-Deficient Thiospinels: Cu7.38(11)Mn4Sn12S32 and Cu7.07(6)Ni4Sn12S32. Solid State Ionics 2002, 146, 195–198. 10.1016/s0167-2738(01)01006-2. [DOI] [Google Scholar]
  60. Vainshtein B. K.; Fridkin V. M.; Indenbom V. L.. Modern Crystallography 2: Structure of Crystals; Springer Berlin Heidelberg, 2000; Vol. 520. [Google Scholar]
  61. Barahona P.; Galdámez A.; López-Vergara F.; Manríquez V.; Peña O. Crystal Structure and Magnetic Properties of Titanium-Based CuTi2–xMxS4 and CuCr2–xTixSe4 Chalcospinels. J. Solid State Chem. 2014, 212, 114–120. 10.1016/j.jssc.2014.01.017. [DOI] [Google Scholar]
  62. Soheilnia N.; Kleinke K. M.; Dashjav E.; Cuthbert H. L.; Greedan J. E.; Kleinke H. Crystal Structure and Physical Properties of a New CuTi2S4 Modification in Comparison to the Thiospinel. Inorg. Chem. 2004, 43, 6473–6478. 10.1021/ic0495113. [DOI] [PubMed] [Google Scholar]
  63. Shannon R. D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1976, 32, 751–767. 10.1107/s0567739476001551. [DOI] [Google Scholar]
  64. Hong M.; Lyu W.; Wang Y.; Zou J.; Chen Z.-G. Establishing the Golden Range of Seebeck Coefficient for Maximizing Thermoelectric Performance. J. Am. Chem. Soc. 2020, 142, 2672–2681. 10.1021/jacs.9b13272. [DOI] [PubMed] [Google Scholar]
  65. Lin S.; Li W.; Bu Z.; Shan B.; Pei Y. Thermoelectric P-Type Ag9GaTe6 with an Intrinsically Low Lattice Thermal Conductivity. ACS Appl. Energy Mater. 2020, 3, 1892–1898. 10.1021/acsaem.9b02330. [DOI] [Google Scholar]
  66. Lin S.; Li W.; Bu Z.; Gao B.; Li J.; Pei Y. Thermoelectric Properties of Ag9GaS6 with Ultralow Lattice Thermal Conductivity. Mater. Today Phys. 2018, 6, 60–67. 10.1016/j.mtphys.2018.09.001. [DOI] [Google Scholar]
  67. Weldert K. S.; Zeier W. G.; Day T. W.; Panthöfer M.; Snyder G. J.; Tremel W. Thermoelectric Transport in Cu7PSe6 with High Copper Ionic Mobility. J. Am. Chem. Soc. 2014, 136, 12035–12040. 10.1021/ja5056092. [DOI] [PubMed] [Google Scholar]
  68. Perdew J. P. Density Functional Theory and the Band Gap Problem. Int. J. Quantum Chem. 1985, 28, 497–523. 10.1002/qua.560280846. [DOI] [Google Scholar]
  69. Knura R.; Parashchuk T.; Yoshiasa A.; Wojciechowski K. T. Origins of Low Lattice Thermal Conductivity of Pb1-xSnxTe Alloys. Dalton Trans. 2021, 50, 4323–4334. 10.1039/d0dt04206d. [DOI] [PubMed] [Google Scholar]
  70. Chen X.; Parker D.; Singh D. J. Acoustic Impedance and Interface Phonon Scattering in Bi2Te3 and Other Semiconducting Materials. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 045317. 10.1103/physrevb.87.045317. [DOI] [Google Scholar]
  71. Skelton J. M.; Parker S. C.; Togo A.; Tanaka I.; Walsh A. Thermal Physics of the Lead Chalcogenides PbS, PbSe, and PbTe from First Principles. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 205203. 10.1103/physrevb.89.205203. [DOI] [Google Scholar]
  72. Lai W.; Wang Y.; Morelli D. T.; Lu X. From Bonding Asymmetry to Anharmonic Rattling in Cu12Sb4S13 Tetrahedrites: When Lone-Pair Electrons Are Not So Lonely. Adv. Funct. Mater. 2015, 25, 3648–3657. 10.1002/adfm.201500766. [DOI] [Google Scholar]
  73. Cherniushok O.; Cardoso-Gil R.; Parashchuk T.; Grin Y.; Wojciechowski K. T. Phase Equilibria and Thermoelectric Properties in the Pb–Ga–Te System in the Vicinity of the PbGa6Te10 Phase. Inorg. Chem. 2021, 60, 2771–2782. 10.1021/acs.inorgchem.0c03549. [DOI] [PubMed] [Google Scholar]
  74. Suwardi A.; Lim S. H.; Zheng Y.; Wang X.; Chien S. W.; Tan X. Y.; Zhu Q.; Wong L. M. N.; Cao J.; Wang W.; Yan Q.; Tan C. K. I.; Xu J. Effective Enhancement of Thermoelectric and Mechanical Properties of Germanium Telluride: Via Rhenium-Doping. J. Mater. Chem. C 2020, 8, 16940–16948. 10.1039/d0tc04903d. [DOI] [Google Scholar]
  75. Gelbstein Y.; Gotesman G.; Lishzinker Y.; Dashevsky Z.; Dariel M. P. Mechanical Properties of PbTe-Based Thermoelectric Semiconductors. Scr. Mater. 2008, 58, 251–254. 10.1016/j.scriptamat.2007.10.012. [DOI] [Google Scholar]
  76. Davidow J.; Gelbstein Y. A Comparison Between the Mechanical and Thermoelectric Properties of Three Highly Efficient P-Type GeTe-Rich Compositions: TAGS-80, TAGS-85, and 3% Bi2Te3-Doped Ge0.87Pb0.13Te. J. Electron. Mater. 2012, 42, 1542–1549. 10.1007/s11664-012-2316-y. [DOI] [Google Scholar]
  77. Cahill D. G.; Pohl R. O. Lattice Vibrations and Heat Transport in Crystals and Glasses. Annu. Rev. Phys. Chem. 1988, 39, 93–121. 10.1146/annurev.pc.39.100188.000521. [DOI] [Google Scholar]
  78. Agne M. T.; Hanus R.; Snyder G. J. Minimum Thermal Conductivity in the Context of Diffuson-Mediated Thermal Transport. Energy Environ. Sci. 2018, 11, 609–616. 10.1039/c7ee03256k. [DOI] [Google Scholar]
  79. Dawahre L.; Lu R.; Djieutedjeu H.; Lopez J.; Bailey T. P.; Buchanan B.; Yin Z.; Uher C.; Poudeu P. F. P. Lone-Electron-Pair Micelles Strengthen Bond Anharmonicity in MnPb16Sb14S38 Complex Sulfosalt Leading to Ultra-Low Thermal Conductivity. ACS Appl. Mater. Interfaces 2020, 12, 44991–44997. 10.1021/acsami.0c12938. [DOI] [PubMed] [Google Scholar]
  80. Baranowski L. L.; Zawadzki P.; Lany S.; Toberer E. S.; Zakutayev A. A Review of Defects and Disorder in Multinary Tetrahedrally Bonded Semiconductors. Semicond. Sci. Technol. 2016, 31, 123004. 10.1088/0268-1242/31/12/123004. [DOI] [Google Scholar]
  81. Shen Y.; Li C.; Huang R.; Tian R.; Ye Y.; Pan L.; Koumoto K.; Zhang R.; Wan C.; Wang Y. Eco-Friendly p-Type Cu2SnS3 Thermoelectric Material: Crystal Structure and Transport Properties. Sci. Rep. 2016, 6, 32501. 10.1038/srep32501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  82. Lohani K.; Nautiyal H.; Ataollahi N.; Maji K.; Guilmeau E.; Scardi P. Effects of Grain Size on the Thermoelectric Properties of Cu2SnS3: An Experimental and First-Principles Study. ACS Appl. Energy Mater. 2021, 4, 12604–12612. 10.1021/acsaem.1c02377. [DOI] [Google Scholar]
  83. Guélou G.; Lemoine P.; Raveau B.; Guilmeau E. Recent Developments in High-Performance Thermoelectric Sulphides: An Overview of the Promising Synthetic Colusites. J. Mater. Chem. C 2021, 9, 773–795. 10.1039/D0TC05086E. [DOI] [Google Scholar]
  84. Pavan Kumar V.; Guélou G.; Lemoine P.; Raveau B.; Supka A. R.; Al Rahal Al Orabi R.; Fornari M.; Suekuni K.; Guilmeau E. Copper-Rich Thermoelectric Sulfides: Size-Mismatch Effect and Chemical Disorder in the [TS4]Cu6 Complexes of Cu26T2Ge6S32 (T = Cr, Mo, W) Colusites. Angew. Chem. Int. Ed. 2019, 58, 15455–15463. 10.1002/anie.201908579. [DOI] [PubMed] [Google Scholar]
  85. Candolfi C.; Guélou G.; Bourgès C.; Supka A. R.; Al Rahal Al Orabi R.; Fornari M.; Malaman B.; Le Caër G.; Lemoine P.; Hardy V.; Zanotti J.-M.; Chetty R.; Ohta M.; Suekuni K.; Guilmeau E. Disorder-Driven Glasslike Thermal Conductivity in Colusite Cu26V2Sn6S32 Investigated by Mössbauer Spectroscopy and Inelastic Neutron Scattering. Phys. Rev. Mater. 2020, 4, 025404. 10.1103/physrevmaterials.4.025404. [DOI] [Google Scholar]
  86. Callaway J. Model for Lattice Thermal Conductivity at Low Temperatures. Phys. Rev. 1959, 113, 1046. 10.1103/physrev.113.1046. [DOI] [Google Scholar]
  87. Feng T.; Lindsay L.; Ruan X. Four-Phonon Scattering Significantly Reduces Intrinsic Thermal Conductivity of Solids. Phys. Rev. B 2017, 96, 161201. 10.1103/physrevb.96.161201. [DOI] [Google Scholar]
  88. Feng T.; Ruan X. Quantum Mechanical Prediction of Four-Phonon Scattering Rates and Reduced Thermal Conductivity of Solids. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 045202. 10.1103/physrevb.93.045202. [DOI] [Google Scholar]
  89. Abeles B. Lattice Thermal Conductivity of Disordered Semiconductor Alloys at High Temperatures. Phys. Rev. 1963, 131, 1906–1911. 10.1103/physrev.131.1906. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cm1c03593_si_001.cif (10.7KB, cif)
cm1c03593_si_002.cif (10.7KB, cif)
cm1c03593_si_003.cif (10.7KB, cif)
cm1c03593_si_004.cif (10.7KB, cif)
cm1c03593_si_005.pdf (588.7KB, pdf)

Articles from Chemistry of Materials are provided here courtesy of American Chemical Society

RESOURCES