Integration of biology, mathematics and computing in the classroom through the creation and repeated use of transdisciplinary modules

Abstract

The integration of biology with mathematics and computer science mandates the training of students capable of comfortably navigating among these fields. We address this formidable pedagogical challenge with the creation of transdisciplinary modules that guide students toward solving realistic problems with methods from different disciplines. Knowledge is gradually integrated as the same topic is revisited in biology, mathematics, and computer science courses. We illustrate this process with a module on the homeostasis and dynamic regulation of red blood cell production, which was first implemented in an introductory biology course and will be revisited in the mathematics and computer science curricula.

1. INTRODUCTION

Since the turn of the millennium, the mathematical analysis of biological systems (MABS) has become a widely accepted approach to understanding the living world. More broadly, a vision for A New Biology for the 21^st Century was articulated in a National Research Council (NRC) report (NRC, 2009), whereby traditional biology must be integrated with physics, mathematics, computer science and engineering in order to solve complex, real-world problems in biology, medicine, and other fields. According to the report, this New Biology “has the potential to meet critical societal goals” in terms of providing food and energy for a growing world population, conserving a sustainable environment, and achieving affordable and personalized health care. It calls for “new approaches that tackle traditional and systems level questions in new, interdisciplinary, and especially, quantitative ways”.

Along with its exciting new potential, however, NRC warns that this New Biology requires systemic rethinking which, combined with the need for new teaching paradigms, is “a staggeringly difficult challenge.” The same sentiments were conveyed in numerous reports that specifically emphasized undergraduate education, such as the National Science Foundation’s Shaping the future (1996), the National Academies of Science’s Bio2010 (NRC,2003), the Mathematical Association of America’s Math & Bio 2010 (Steen, 2005), the Association of American Medical Colleges and Howard Hughes Medical Institute’s recommendations regarding Scientific Foundations for Future Physicians (2009), and the American Association for the Advancement of Science’s report Vision and Change (2010). Collectively, these and other reports have served as a roadmap for reform in undergraduate education in biology. All identify the ability to integrate various STEM (science, technology, engineering, and mathematics) disciplines as a key competency for all life sciences students, whether they intend to join the workforce, pursue research or advance toward professional schools.

These reports, as well as articles in the biological literature (e.g., Savageau, 1991a; Savageau, 1991b) conclude that innovative, computationally supported, system-based strategies can only emerge in due time if a new generation of students, “bilingual” in the biological and computational sciences, is drawn into the field through effective education. In response to these calls for change, a variety of projects and resources, such as BioQuest (https://bioquest.org/), the National Institute for Mathematical and Biological Synthesis (NIMBioS, http://www.nimbios.org/), Project Kaleidoscope https://www.aacu.org/pkal ) and the Quantitative Undergraduate Biology Education and Synthesis (QUBES, https://qubeshub.org), are focused on supporting the implementation of approaches ranging from interdisciplinary modules to interdisciplinary courses (e.g., Jungck, 2011; Jungck, 2012; Waldrop et al., 2015), and several universities, including the Universities of Delaware, Richmond, Washington, and others, have begun to implement curricula toward this goal (Marsteller et al., 2010).

The complexity of the new biology, combined with the astounding growth in information and an increasing specialization, mandates the design and implementation of new strategies for integrating and sharing information from different fields. For future generations of biologists, scientists and physicians to achieve these goals, the traditional reductionist teaching paradigm must be complemented with transdisciplinarity, integration, systems thinking, and the education and nurture of students who are at least rudimentarily versed in both biology and the mathematical and computational sciences. Indeed, new types of questions must be asked for the field to move forward effectively, such as:

• How can we change the current biomedical mindset from reductionism to systems thinking, where components are in dynamic interactions?

• How can we foster a new genre of bidialectical individuals who have the cognitive flexibility to reach across traditional scientific boundaries between biology, mathematics, computer science, engineering and other disciplines?

• How can newcomers entering the field of biological systems analysis be trained to acquire and master, with reasonable effort, what they need to know?

• How should we teach students to evaluate the quality of the abundant information that is readily available?

Current efforts for addressing these questions generally consist of (i) incorporating biological problems into existing mathematics courses such as calculus, (ii) incorporating mathematical tools into existing biology courses, (iii) creating new hybrid courses incorporating both disciplines, or (iv) creating new interdisciplinary majors (e.g., Marsteller et al., 2010; Usher et al., 2010; Gentils et al., 2012). Often, courses like ‘Introduction to Systems Biology’ are taught as senior-level capstone courses where students finally integrate their knowledge base in the different disciplines. Here we present an alternative approach - the use of small transdisciplinary modules that are revisited in the context of different courses - to foster the appreciation and integration of skills from different disciplines, starting at the introductory level. Of course, not every biology student will be interested in mathematics, and vice versa, but it seems very desirable that all biology and math students develop a feel or intuition for how the two seemingly disparate disciplines can cross-pollinate each other (Voit et al., 2012).

Three substantial challenges toward fostering such cross-pollination are that: (1) current curricula are already cramped with “absolutely mandatory” topics; (2) a true understanding of the systemic nature of life sciences requires not only biology and math, but also computational science, physics, chemistry, basic engineering, and a host of other aspects; and (3) reaching beyond the boundaries of a discipline requires dedicated effort and flexibility on the side of instructors (Voit and Kemp, 2011).

The fields of cognitive science and epistemology have established that complex topics are often learned best in a problem-based, hands-on fashion (e.g., Hmelo, 1998; Sahin, 2010; Belland et al., 2019). Embracing this mode of learning, we have begun to guide undergraduates toward transdisciplinarity with minimal disruption of their existing curricula. These efforts are definitively not intended to turn biologists or mathematicians into systems analysts but to offer both, through carefully selected modules, a systems-based view of the living world and to provide them with a fundamental intuition of how mathematics and computing can be valuable approaches toward solving challenges in the life sciences. We consider this intuition a significant step toward an appreciation of the functioning of living systems, even if the students learning from the modules are not quite ready to execute mathematical modeling tasks on their own. We are at the beginning of implementing means toward these goals and, in this paper, describe these initial efforts. This approach expands the repertoire of practices for implementing interdisciplinary education and can be of interest to undergraduate deans, innovative instructors and, in particular, individuals interested in interdisciplinary curriculum development.

2. DESIGNING FOR A TRANSDISCIPLINARY CLASSROOM EXPERIENCE

Transdisciplinarity refers to the process of creating knowledge forged from different disciplines (Hoffmann et al., 2017). In the process of solving complex real-life problems, participants from various disciplines begin to formulate a problem space informed by their disciplinary perspectives. Rigorous knowledge coproduction and synthesis eventually result in transdisciplinary integration and ultimately in new ways of solving problems that transcend disciplinary boundaries.

From an epistemological point of view, transdisciplinarity, for instance in MABS, addresses “boundary objects” at the intersection of different scientific worlds, which are, nonetheless, of interest to different groups of stakeholders (Star and Griesemer, 1989). Specifically, mathematical and computational models link experimental biologists, whose data might benefit from quantitative analysis, with computer scientists and mathematicians who are looking for new applications and are equipped to provide the required analytical tools. For their models to be fruitful elements of interdisciplinary research or teaching, i.e., effective boundary objects, mathematicians, computational scientists and biologists need to be able to consider a model from each other’s perspective. Driven by the different backgrounds of stakeholders, dealing with boundary objects leads to the creation of a space of interaction between disciplines, called a “trading zone” or “agora” (Galison, 1997; Voit, 2016; Wikipedia, 2018). As Galison (1997) vividly explains, such a space between disciplines allows researchers and instructors to come together for a period of time and exchange scientific ideas. Importantly, this meeting of disciplines initially faces difficult challenges, including substantial language barriers and different value systems. As an example for the former, what is a biologist to do with a term like “eigenvalue”? In the latter category, impact factors and h-indices, which are highly prized in biology, have little importance in mathematics. As ethnographers have known for some while, and as it is intuitively presented by Galison (1997), such epistemological and language barriers are initially addressed with an impromptu and highly unstable “pidgin” language that is provisional, dynamic, and full of neologisms and vaguely defined terminologies (Wikipedia, 2018). Driven by the desire for scientific exchange and advance, and not necessarily trusting a few translators, the initial ad hoc conversations between trading partners steadily morph and solidify into a fully defined and refined combination language, which linguists call a “creole” (Wikipedia, 2018). This creole matures and eventually becomes the means of effective communication in the agora. It is not difficult to imagine that, as a first step, some future mathematicians and biologists will become bilingual (Savageau, 1991a; Savageau, 1991b). However, for enhanced efficiency, the community as a whole will ultimately create and use a “systems biology creole.”

Indeed, many reports emphasize that the New Biology for the 21^st Century critically depends on interdisciplinary collaboration, which mandates suitable “language skills” and new ways of education and learning. Acquiring these capabilities requires that students develop cognitive flexibility. Naturally, different profiles of integration will emerge for different students, and at the end of the training, each student will ideally have developed some set of transdisciplinary core competencies and concepts, including the rudiments of a common language. We believe that the revisiting of the same problem space within different courses will enhance the students’ cognitive flexibility and teach them the basics of the systems biology creole we envision.

One essential ingredient for designing transdisciplinary learning experiences is the selection of an authentic problem that requires knowledge integration from different disciplines. In the course of solving the problem, students acquire various complementary aspects of knowledge and terminology from different fields and subsequently integrate these in a more comprehensive view than would otherwise be possible. This progression is accomplished by revisiting the problem in different courses over an extended period of time that spans multiple semesters (Figure 1). The disciplinary contexts promote cognitive apprenticeship and ultimately facilitate comprehension and retention (Collins et al., 1989).

Figure 1.

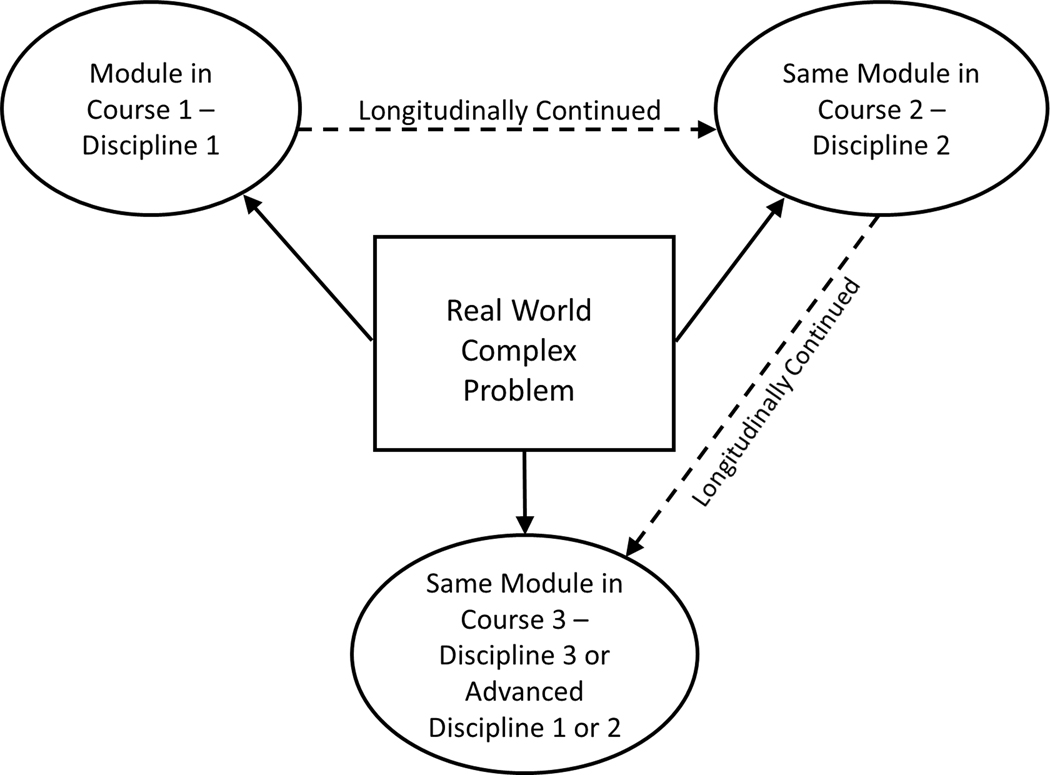
Implementation of transdisciplinary modules. Students are introduced to a real complex problem requiring the integration of knowledge from several disciplines. The problem is longitudinally continued by revisiting the module over an extended period of time that spans multiple semesters and disciplinary perspectives.

Authentic knowledge integration requires students to answer questions by effectively drawing from all disciplines (Hoffmann et al., 2017). Such knowledge integration does not truly emerge if a learning topic is solely presented as a singular application of one set of discipline-specific tools in the context of another discipline. For instance, using bacterial growth to illustrate the concept of exponential growth does not bridge biology and mathematics, since that growth pattern only holds for the short term, as long as resources such as food are not limiting factors. However, modifying the exponential growth to incorporate processes that stop the population from growing quickly approaches transdisciplinarity, because the specific resources needed by living organisms, such as nutrients and suitable environments in order to survive and reproduce are taken into account. Thus, to model bacterial growth, a student needs to consider concepts and principles from both mathematics and biology.

3. PILOT MODULE ON HOMEOSTASIS

Implementing the conceptual framework of a revisited problem space (Figure 2), we designed a stand-alone module that discusses compensatory action of the human body if the blood oxygen level is too low. The module was primarily established for an introductory biology course mostly taken by first-year biology majors, but also by students with an interest in pursuing health careers. The general course content aligns with the ‘Animal Form and Function’ and ‘Plant Form and Function’ units typically found in introductory biology textbooks. Fundamental, overarching concepts covered in the course include homeostasis, feedback regulation, and the role of hormones in maintaining homeostasis. Other important concepts in the course address cellular respiration and the role of the components of the circulatory system, including red blood cells (RBCs) and the transport of oxygen (O₂). Thus, the relative simplicity of the regulation of blood oxygenation, mediated by the hormone erythropoietin (Epo), implicitly or explicitly revisits and reinforces core concepts and lends itself particularly well for illustrating the power of transdisciplinary learning (Figure 3). Of note is that the students in this class had so far not received much college-level training in mathematics or computing.

Figure 2.

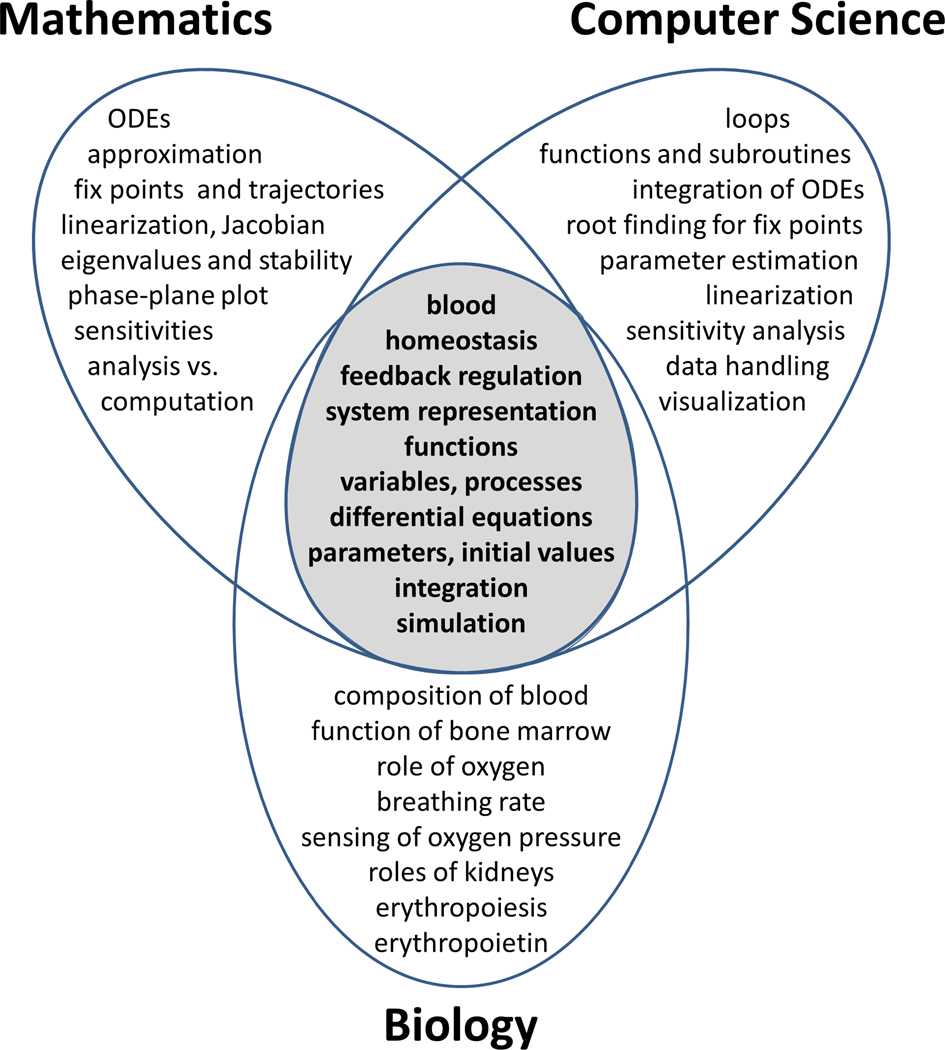
Several disciplines use the same problem space (shaded) with its fundamental concepts, components, and terminology, but then branch out into subject-specific tasks, methods, and techniques, as shown here for mathematics, computer science, and an advanced biology course.

Figure 3.

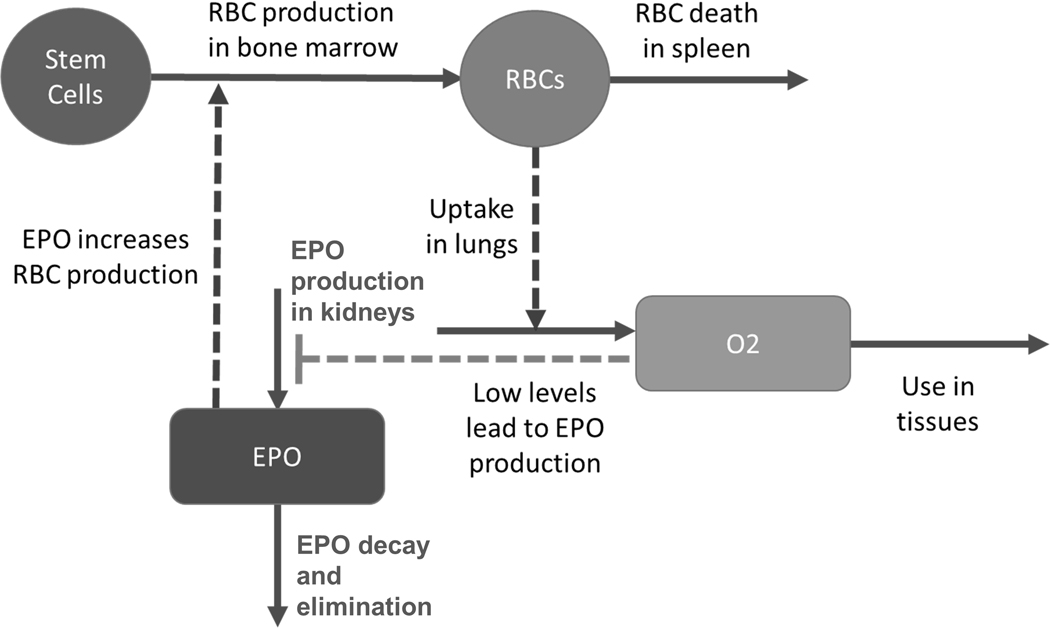
Core structure of a model for exploring homeostasis within the context of RBC regulation. Solid arrows indicate material flow, while dashed arrows represent activating processes and the dashed T-line represents an inhibitory effect.

3.1. Design of the Epo Module

Epo was discovered decades after the observation that journeys in high altitudes cause a substantial increase in the number of RBCs. The physiological role of Epo is by now well established (Jelkmann, 2011; Bunn, 2013). Briefly, Epo is essential for triggering the production of RBCs from stem cells in the bone marrow. Only small amounts of Epo are needed to maintain the baseline level in healthy persons. When the O₂ content in the blood plasma and tissues decreases, Epo production is stimulated in kidney cells and, following a rise in plasma Epo levels, it takes 3–4 days before the production of new RBCs in bone marrow becomes apparent. Once production begins, plasma RBC numbers increase rapidly. The response is dynamic, with initially high Epo values that drop towards normal values before tissue O₂ content normalizes.

The dynamic interplay between RBCs, tissue O₂ levels and Epo can be mathematically modeled relatively easily and intuitively, thus allowing simulations or predictions of outcomes under a number of conditions in health or disease (Erslev et al., 1987; Shander et al., 2014; Erslev and Besarab, 1997; Ballas and Marcolina, 2000; Shander et al., 2014). For instance, such a dynamical systems model may be based on three ordinary differential equations (ODEs) that involve functions of the system variables and their derivatives with respect to time. In our model, the following three generic equations define the system:

$$\frac{d\mathrm{ }RBC}{dt}=\mathrm{ }{F}_1\left(RBC,O_2,\mathrm{ }Epo\right),$$

$$\frac{d\mathrm{ }{O}_2}{dt}=\mathrm{ }{F}_2(RBC,O_2,\mathrm{ }Epo)\mathrm{ },$$

$$\frac{d\mathrm{ }Epo}{dt}=\mathrm{ }{F}_3\left(RBC,O_2,\mathrm{ }Epo\right).$$

Here F_1, F_2, and F₃ are suitably chosen functions that model the processes of the system. Because most students have not seen differential equations before, these equations are restated in terms of rates of change as follows:

$\frac{d RBC}{dt}=$ overall rate of change of RBC = rate of RBC production − rate of RBC death,

$\frac{d O_2}{dt}=$ overall rate of change of O₂ = rate of O₂ binding in RBCs − rate of O₂ use,

$\frac{d Epo}{dt}=$ overall rate of change of Epo = rate of Epo production − rate of Epo breakdown.

It is quite obvious that the specific functions governing this system are in truth not known in detail. For the students, this fact, and the subsequent use of approximations, tends to be troublesome at first and therefore requires explanation and assurance, as described next.

3.2. Implementation

The students had earlier been introduced to hormones and their role in homeostasis via negative feedback loops. As a specific example, Epo is presented in class during this time. Some basic physiology regarding the role of RBCs and their life-span is reviewed either in class or as a short assignment before class. Students are gradually introduced to the model by focusing on a single term in one of the equations at a time. The first topic to be addressed is the control of the number of RBCs in the body. The students are invited to think about how the number of RBCs at any given time might change and what might affect it. In particular, they should be brought to the insight (which in hindsight may be trivial) that this number can be increased (decreased) by increasing (decreasing) the rate of production or by decreasing (increasing) the rate of removal.

Because the details of these processes are convoluted, we found it helpful first to discuss the simile of fluctuations in the water level of a lake. Students readily realize that inflow from upstream tributaries or efflux into downstream rivers, rain, pumping water in or out, evaporation, and many other processes can affect the amount of water in a lake. This understanding is represented and intuitively reframed as a single overall rate of change equation (ODE), in which certain events or phenomena increase the water level while others decrease it.

Once the students understand this example, they are encouraged to work in small groups, maybe of 3 to 4 students, to transfer their insights into an appropriate overall representation of the numbers of RBCs, their dynamics, and what might affect these dynamics. In a similar vein, equations for O₂ and Epo and their drivers are established. Emphasis is put on the fact that the model is a vast simplification and that that is ok, at least initially. The instructor reviews the students’ models and wraps up the model design step by mentioning that details of the model implementation, along with alternatives, will be revisited in their future calculus course.

Within the biology module, appropriate functions are pre-defined for the students. By and large, they consist of mass-action and power-law functions (the rationale for choosing these types can be found in Voit (2013) and Voit et al.(2015)). It might be tempting to go into more depth on each of the biological, mathematical or computational components of the module, such as the regulation of Epo production at the molecular level, but the students will readily accept that simplicity is key to getting started. This need for simplicity shifts the focus on the interplay among RBCs, O₂ and Epo.

It is important that students during this first step become somewhat familiar with the notion of modeling and translating their understanding of the biological phenomenon into the form of a computable structure that captures their quantitative thinking. In the second phase of the module, the students’ understanding of the model is reinforced when they are given different biological scenarios and tasked to identify which aspects of the model are affected (Supplemental File). For this task, the students are given a fully functional Python code that generates numerical solutions and automatically displays graphs of RBC, O₂ and Epo levels over time. Example output graphs are shown when simulating blood donation and iron deficiency anemia (Figure 4). The actual solving of the ODEs remains in the background, except that the students are informed what “solving ODEs” means and that several options for this purpose are available and will be discussed in their computer science course.

Figure 4.

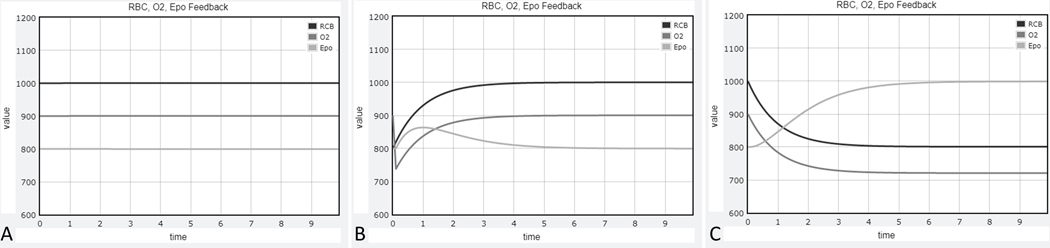
Example graphical outputs obtained when running the provided Python script to simulate various biological scenarios. (A) Default parameters and initial conditions, (B) initial condition for RBC changed from1000 to 800 to simulate blood donation, (C) rate of RBC production changed from 1 to 0.8 to simulate anemia due to iron deficiency.

3.3. Module Assessment

Our overarching goal is to make the students understand the system’s qualitative dynamics (in response to a perturbation, what goes up or down and why?) and to answer quasi-realistic questions via analysis and simulation.

The specific learning goals for the module are for students to:

• gain an appreciation for modeling as an approach for solving biological problems;

• gain an appreciation for the interdisciplinary nature of modeling.

To achieve these goals, the students start by interpreting every key term in the model and continue by predicting—per intuition—how the RBC, O₂ and Epo levels might change under a given scenario. They learn to identify the variable(s) or parameter(s) that might be affected, change each affected model component, run the Python script, thereby generating graphical renderings of RBC, O₂, and Epo levels over time, and interpret results. Importantly, the students are asked to reflect on the outcome, both from the perspective of biology and modeling. In particular, they are asked to assess the simulation results against their predictions and to explain why some predictions may have been wrong. If appropriate, the students are encouraged to execute further simulations to test their explanations.

In our experience, some of the most salient discussions centered on the return of RBC, O₂ and Epo levels to normal basal levels and the observation that these levels may actually not return to normal levels in some diseases, such as anemia. This discrepancy further reinforced the concept of homeostasis and opened up additional conversations about disease states. The students also tended to become aware of limitations of the model. For instance, delays in responses (new RBC production beginning much later than the increase of Epo) are notoriously difficult to model with ordinary differential equations (see math course), which demonstrates to the students that these models are not a panacea.

The reflection on the usefulness of the model, the ease of executing what-if-simulations, and the possibility of improving the model often lead students to appreciate the flexibility of modeling and also suggest that realistic values and units are needed for setting the parameters. At times, students also suggested that the models could be improved to capture more complexity, which led to discussions of the trade-off between usefulness and complexity of the model. In the end, the small student groups turned in their assignment worksheets, which included their reflections.

The following representative quotes illustrate student responses to the question “What is the advantage of using a model?”

• “It is a great learning tool”

• “Model allows us to be more quantitative, explain what is actually happening in such a given scenario, and predict parameters and outcomes”

• “To be able to experiment with different scenarios in ways we couldn’t observe in real life”

• “It allows us to be able to explain or hypothesize underlying mechanisms”

• “We received quicker results”

• “You can see how different factors interact with each other”

Further, the students’ appreciation for modeling was captured in a pre-post survey where they were asked two questions (Figure 5):

Figure 5.

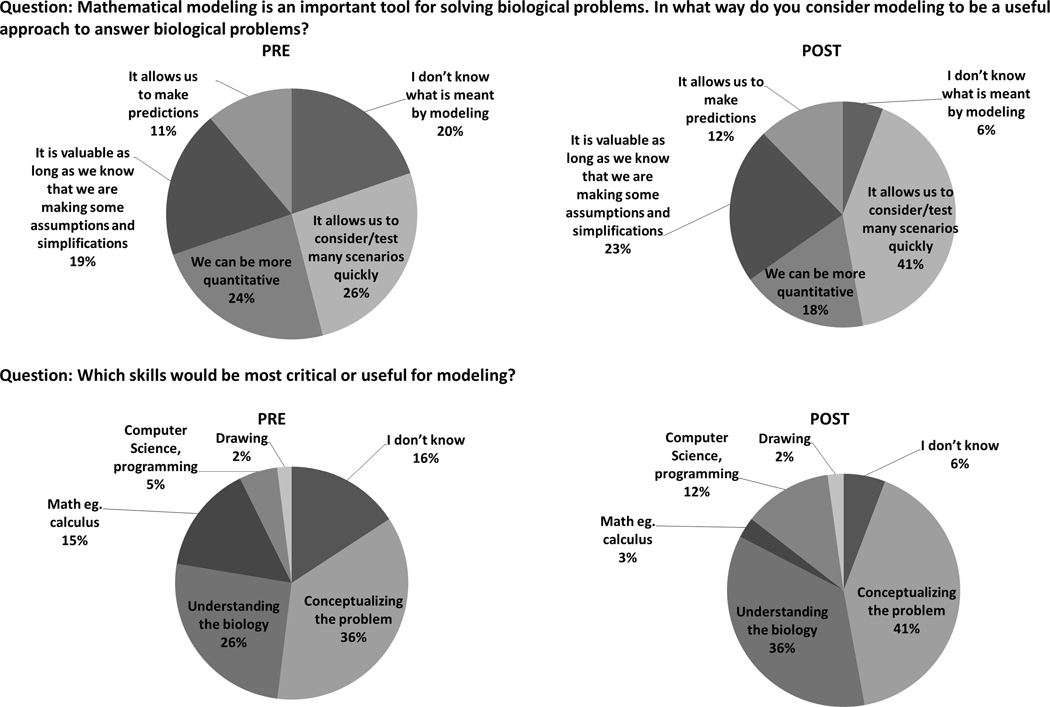
Student response to two survey questions asked in the introductory biology course pre (n = 152) and post (n = 138) implementation of the Epo and RBC modeling activity.

1. Mathematical modeling is an important tool for solving biological problems. In what way do you consider modeling to be a useful approach to answer biological problems?

   Assessment of answers:

   The choice of “I don’t know the meaning of modeling” decreased substantially from 20% to 6%, which indicates that the modeling module made students more aware of the meaning and value of mathematical modeling. The other substantial changes are for the choice “It allows us to consider/test many scenarios quickly”, which went from 26% to 41%; and for the choice “We can be more quantitative”, which declined from 24% to 18%. Since the students were only allowed to select one choice, the combined total of these two choices remained about the same, which indicated that the students kept their understanding of the power of mathematical modeling and tended to appreciate the speed at which various ideas can be tested. Overall, these data indicate that we accomplished our goal of bringing awareness and reinforcing the power and value of mathematical modeling.

2. Which skills would be more critical or useful for modeling?

   Assessment of answers:

   Again, the choice of “I don’t know” decreased substantially from 16% to 6%. This suggests that the students were made more aware of the essentials of mathematical modeling, and what it would entail for them to pursue this area, especially since the choice of “Computer Science, programming” increased from 5% to 12%. They also realized the value of such an activity, since the choice “Understanding the Biology” increased from 26% to 36%. It was troubling that the choice “Math, e.g., calculus” decreased from 15 to 3%. This may be explained by the fact that students could only choose one answer. When this result is coupled with an increase in the choice “Conceptualizing the problem” from 36% to 41%, we may be seeing a shift in attitude towards mathematical modeling, as its value and benefits become clear to the student.

Overall, the student responses indicate an appreciation for modeling, a deeper awareness for its uses and the many skills needed. Their responses clearly reflect the context and approach used for introducing the modeling activity in the biology course. They heavily emphasize the importance of understanding the biology and conceptualizing it in the form of a model. A similar survey administered in a mathematic or computer science course would likely have a very different outcome and reveal the emphasis of the modules on concepts from these disciplines.

4. CONTINUED IMPLEMENTATION AND FUTURE DIRECTIONS

Corresponding modules focusing on the same problem space will be introduced in mathematics and computer science courses, and there is no reason not to use them also in other STEM disciplines, such as physics, chemistry, or engineering. While using the exact same problem space, the specific design of the module in such courses is of course informed by the learning goals and objectives that would best be served by the module (Figure 2). These goals and objectives, in turn, dictate where the emphasis of each module would be. For example, in a mathematics course, this module could be used to illustrate the conceptual meaning of a derivative as a rate of change, the behavior of the functions used in the modeling process (mass action, power-law with different positive and negative exponents), questions of fix points, and linearization as a tool for assessing the stability of a homeostatic state. It is also necessary to adjust the content and delivery depending on whether any of the courses serve a unique population of students (e.g., mathematics majors only) or whether other courses are taught where the module could be a prerequisite.

4.1. Module within a mathematics course

In a calculus course that is typically taken by students from various majors in their second or third semester, the chosen focus will be on the differential equations of the model. Specifically, the lake water model and the oxygen regulation model may be used to introduce and illustrate the concept of rate change. In the former case, analytical solutions of the ODE can be discussed, especially for constant input, while the latter case requires numerical solutions. This difference might immediately lead to the important contrasting of the elegance of analytical mathematics versus the brute-force, but powerful use of computational methods.

It is easily possible to provide students with realistic data containing the production and removal of RBCs over time for several example scenarios that slightly differ from the original module, such as blood donation, iron deficiency anemia, or sickle cell anemia. Students are then asked to calculate the total number of RBCs, plot the data and analyze the observed trends for each scenario. Further, they calculate the average rate of change for the respective datasets and investigate the rate at which RBCs are increasing or decreasing. Based on this analysis of rates of change, the students address the question: are the production or death, and thus the number of RBCs, increasing or decreasing, and are their results intuitive for the specific scenario? To fully answer such a question, students are (re-)introduced to the biological importance of RBCs and their relationship with O₂ levels and Epo hormone levels. If desired, students could also research these connections with an independent assignment, for example through reading a news article (Wedro, 2016).

As a follow-up, the mathematical details of the model are gradually recapitulated. For instance, the instructor could note that the initial values and parameter values of the ODE model were chosen arbitrarily. Thus, students could be invited to edit the Python script using more realistic values for their analyses. They could be asked to examine the graphical output and assess to what degree it conforms to their expectations, closely analyzing the relationships between rate of red blood cells, oxygen levels and the hormone Epo. The students could also be asked to replace the functions in the model with alternative functions. The module might conclude with a wrap-up discussion on red blood cells, oxygen levels and the hormone Epo, and the value of using a mathematical modeling to examine these relationships under various scenarios.

Thus, in this model, students will achieve the following calculus learning goals:

• Graph functions using mathematical software

• Define and illustrate the ideas of differentiation

• Estimate derivatives from numerical or graphical data

• Calculate derivatives of functions using mathematical software

• Solve simple ODEs analytically

• Model physical, biological, business and social science applications using derivatives

In addition, the same module could be revisited in an advanced math course. Just one pertinent but quite difficult topic for such a class could be how to account for delays between sensing oxygen loss and remedial action of the bone marrow; in reality, this delay very clearly exist, but it was ignored in the ODE model. Some options could be the insertion of artificial intermediates, the jump toward the much harder delay differential equations, the capturing of delays through a Padé approximation that creates a larger ODE system (e.g., Lam, 1993; Mocek et al., 2005) or the switch to discrete recursive systems, which have their own advantages and drawbacks (for a comparison of methods in the context of red blood cells, see Fonseca et al. 2015). The latter would furthermore afford the opportunity to introduce matrices in the model formulation, and to compute the dynamics of the systems by using matrix multiplication, potentiation, and the computation of dominant eigenvalues as drivers of such systems.

4.2. Module in a computer science course

The Epo module can also be used in a Computing for Biologists course, which at our institution is typically taken by biology sophomores and juniors. Our course emphasizes the use of existing bioinformatics tools as well as reading, editing, and creating beginner-level Python scripts to solve biological problems. The module may be used to address the latter. It re-introduces the biological concepts of RBC production from stem cells and their stimulation by Epo, which was explored in the freshmen course. However, instead of focusing on and changing a single variable, students are introduced to several new computational concepts. First, students identify the key elements of a Python program (including variable assignments, block structure, iterative loops and graphing functions) by writing summary comments describing each section of the Epo module script. Second, students are asked to account and construct the code for a new variable that was ignored in the original assignment: breathing rate. Students could also be asked to use matplotlib to label parts of the resulting graph using Python. As such, the new components help students build new knowledge of computing and programming skills using a familiar concept. One could also compare different ODE integrators, of which there are many, in terms of ease of use, accuracy, and speed. The module could moreover be used for simple Monte-Carlo simulations. Finally, the computing course could discuss methods of linearization, computation of the Jacobian, analyses of eigenvalues, steady–state stability and sensitivity, input-output data handling, and visualization of results. It would even be possible to introduce simple estimation methods for the model parameters from (artificial or real) data.

4.3. Assessment of modules

The modules in each course can be evaluated using standard formative or summative assessment tools such as written reflections, response to essay questions, pre/post answer to test questions to ensure that the learning objectives are met. However, the interdisciplinary knowledge integration and changes in attitude are expected to be gradual and occur over the course of multiple semesters. The successful implementation of a transdisciplinary problem space is best demonstrated through multiple knowledge transfer (Newell, 2000; NRC, 2014). Namely, if students have learned how to integrate concepts and principles from different disciplines to solve a particular task, their problem solving mastery can be validated by posing another problem that borrows from the same or similar concepts. Students’ solutions to a new problem can be assessed by evaluating whether information or analyses from one or more disciplines were effectively applied, validly adapted to the novelty of the new problem, and integrated. One should note that such assessments of student outcomes in transdisciplinary education are often difficult tasks (Howes et al., 2013), because standard instruments designed to assess disciplinary understanding may not be suitable for assessing learning from a transdisciplinary module.

Recently, the core elements of an interdisciplinary science have been articulated (Tripp and Shortlidge, 2019) to provide a framework for assessment. These include disciplinary humility (or the acknowledgement that one single discipline may not be sufficient to solving a given problem), disciplinary grounding, the acquisition of different research methods, knowledge integration and collaboration. These elements strongly align with our learning goals for the module across the disciplines and will serve as guides for further assessing student attitudes and skills towards our learning goals.

5. CONCLUSION

In designing different versions of the same module, for biology, math, and computer science, principles and methods of scientific teaching, such as active knowledge acquisition, scaffolding, assessment, alignment and inclusion, are taken into account and incorporated (Handelsman et al., 2006). Short but compelling scenarios, to which students can relate, are used to engage students with the activity. It is critical to stress that students are not taught to do modeling for the sake of modeling, but to learn a new tool that may answer biological questions they care about. In the introductory biology module, the activity is scaffolded and broken down as a two-step process, with a first step where students relate the biological question to the model and a second step where they exploit the model. During both steps, students work collaboratively in teams of 3 or 4, and all are expected to contribute to the final product. In addition to the principles and methods of scientific teaching, the choice of using an online platform (www.glowscript.org) makes it easy to use Python without the need to download and install it on classroom computers or personal laptops. This way, all students and instructors across sections work with the same version and their experience is therefore uniform. Several similar online platforms such as those provided through QUBES exist and are convenient for a one time use in the classroom. Moreover, many colleges and universities have begun to maintain clouds containing a wide spectrum of software packages, to which students have access.

From the perspective of the instructors, the interdisciplinary nature of the module is a unique challenge requiring that everyone gain some degree of comfort with the components of the module in its different manifestations. For example, a biology instructor naturally emphasizes the biological aspects of the module and teaches the students how they might approach the problem—or a similar problem in the future—as a biologist. At the same time, biology students are not truly accountable for the mathematical or computational components, as long as they develop a basic intuition of what the model can or cannot do. By the same token, the emphasis in the mathematics or computer science classes is naturally different. Nevertheless, every instructor needs to acquire some familiarity and a minimal comfort level with all components of the module. This familiarity is best achieved by co-developing and co-teaching a new module with instructors across disciplines.

Transdisciplinary modules offer a pedagogical framework in which students gradually acquire the language, skills and expertise to tackle complex problems at the intersection of the life sciences, mathematics, and computer science, as well as other STEM disciplines. These modules serve as connectors across courses in various disciplines and break down the educational silos students typically experience. From the perspective of curricular change, the use of transdisciplinary modules enables gradual modification as the modules are designed to be relatively small, only lasting one or two class sessions. This effort should be compared to the massive curricular overhaul that might be needed for an interdisciplinary curriculum. Ideally, the transdisciplinary modules should be self-standing, and prior exposure to the module in a previous course should not be required or expected. This structure makes it easy to introduce modules across disciplines in no particular order. In our pilot study, the Epo module was first introduced in an introductory biology course, and corresponding modules emphasizing the mathematical and computational aspects are under development as case studies in Calculus I and in a Computing for Biologists course. Ultimately, we anticipate training students to develop the cognitive flexibility to reach across disciplines in order to solve actual problems in the life sciences.

Biography

Mentewab Ayalew is an Associate Professor Biology at Spelman College. Her interests include the infusion of quantitative and computational thinking in the Biology curriculum as well as faculty development in these areas. Her research focus is on understanding antibiotic resistance in plants. She earned a Ph.D. in Plant Cellular and Molecular Biology at Ecole Nationale Superieure d’Agronomie de Toulouse, France.

Derrick J. Hylton is an Associate Professor of Physics at Spelman College. He was the founding faculty member of the Physics Department at Spelman College. He earned a Ph.D. in physics at Yale University in the theory of atomic structure. Other research interests are in Physics Education and Computational Physics. At Spelman, he has worked on infusing a problem-based pedagogy in the physics curriculum.

Jeticia Sistrunk is an Assistant Professor in the Department of Biology at Spelman College. Her work addresses questions towards understanding the pathogenic mechanisms of microorganisms using microbial genomics and metagenomics approaches. Her interests include STEM outreach and developing innovative curriculum for integrating computing techniques in biology courses.

James Melton is a Course-based Undergraduate Research Experiences (CURE) postdoctoral fellow in the Biology Department at Spelman College. His research has focused on diversity, molecular systematics, and genomics of green algae and Amoebozoa. He has also been involved with designing biology courses to improve student training in evolution and bioinformatics.

Kiandra Johnson is a Senior Instructor of Mathematics at Spelman College. Her interests include infusion of active learning and technology in foundational mathematics course. Her research focus is primarily on hybrid courses and project-based learning’s impact on Intermediate Algebra and Precalculus course achievement. She earned a Master’s of Science in Applied and Computational Mathematics at Emory University in Atlanta, GA.

Eberhard O. Voit is a chair professor and Georgia Research Alliance Eminent Scholar in biological systems. He studied at Cologne University in Cologne, Germany, where he received Master’s degrees in biology and mathematics, as well as Ph.D. in developmental and theoretical biology. His interests focus on research and education in complex biomedical systems and, in particular, computational analyses of metabolic pathway systems.