Percolation across households in mechanistic models of non-pharmaceutical interventions in SARS-CoV-2 disease dynamics

Abstract

Since the emergence of the novel coronavirus disease 2019 (COVID-19), mathematical modelling has become an important tool for planning strategies to combat the pandemic by supporting decision-making and public policies, as well as allowing an assessment of the effect of different intervention scenarios. A proliferation of compartmental models were developed by the mathematical modelling community in order to understand and make predictions about the spread of COVID-19. While compartmental models are suitable for simulating large populations, the underlying assumption of a well-mixed population might be problematic when considering non-pharmaceutical interventions (NPIs) which have a major impact on the connectivity between individuals in a population. Here we propose a modification to an extended age-structured SEIR (susceptible–exposed–infected–recovered) framework, with dynamic transmission modelled using contact matrices for various settings in Brazil. By assuming that the mitigation strategies for COVID-19 affect the connections among different households, network percolation theory predicts that the connectivity among all households decreases drastically above a certain threshold of removed connections. We incorporated this emergent effect at population level by modulating home contact matrices through a percolation correction function, with the few additional parameters fitted to hospitalisation and mortality data from the city of São Paulo. Our model with percolation effects was better supported by the data than the same model without such effects. By allowing a more reliable assessment of the impact of NPIs, our improved model provides a better description of the epidemiological dynamics and, consequently, better policy recommendations.

1. Introduction

Mathematical models, upon which decision-making and public policies can be based, have become important tools with which to plan mitigating strategies during the SARS-CoV-2 pandemic, and there has been a recent proliferation of such models (Adam, 2020, Aguas et al., 2020, Anirudh, 2020, Panovska-Griffiths et al., 2021). Several of these compartmental models, which are typically age-structured SEIR (susceptible–exposed–infected–recovered)-like models, have been proposed and used to assess the effects of multiple interventions (Davies et al., 2020b, Ferguson et al., 2020, Flaxman et al., 2020, Fumanelli et al., 2016). As simplified representations of reality, these models come with assumptions regarding the nature of the underlying network of interactions (Rahmandad and Sterman, 2008). More explicitly, most SEIR compartmental models assume that the population is homogeneously-mixed, meaning that every individual in each compartment has the same probability of coming into contact with other individuals.

Although these underlying assumptions might be appropriate to make robust predictions for well-mixed populations, they may not be suitable in a context with significant contact network heterogeneity. Therefore, several methods have been proposed to enable compartmental models to take contact structure heterogeneities into account (min Liu et al., 1987, Roy and Pascual, 2006, Stroud et al., 2006). However, these methods usually consider static underlying network structures, which are only good approximations for slowly spreading epidemics, in which neither the contact rates nor the network structure change significantly over time (Volz and Meyers, 2007, Bansal et al., 2007). This is not the case in a pandemic situation such as the one caused by SARS-CoV-2, where governments were compelled to impose wide-ranging contact and movement restrictions that essentially resulted in a large reduction in connectivity among individuals. As we discuss below, this leads to the need for a more flexible and dynamic approach, which motivated the present study.

In this context, network theory provides a picture of a homogeneously mixed population as a (highly connected) regular random network of individuals (vertices) connected through possible disease transmission contacts (edges) with long-range connectivity properties (Bansal et al., 2007). During an outbreak, the disease would spread across these links. Non-pharmaceutical interventions (NPIs) that involve social distancing could, therefore, be thought of as modulators of the strength and even persistence of such links. One of the main outcomes of network theory is that, as contact networks become less connected, a critical transition occurs, and the network becomes fragmented into disconnected (or weakly connected) sub-networks. This phenomenon is known as percolation (Chen et al., 2007, Essam, 1980), and the existence of a critical percolation threshold in the mean number of contacts can be established for many types of networks. Once this threshold has been crossed, even small changes in the number of contacts can lead to large changes in the connectivity of the network.

In compartmental models, SARS-CoV-2 mitigation strategies are modelled by altering contact rates, thus changing the force of infection. This can be performed at varying degrees of granularity, depending on the level of detail of the contact matrices. For instance, many studies (Aguas et al., 2020, Noll et al., 2020, Davies et al., 2020a) have used the categorisation employed by Prem et al. (2021), which divides contacts into four settings, namely home, work, school, and other. In this way, the effectiveness of various NPIs are reflected in reductions in the contact rates for each setting, depending on the nature of the intervention, e.g. school closures reduce contact rates in schools. As the overall contact matrix is a linear combination of the contact matrices for each setting, with coefficients dependent on the coverage and efficiency of NPIs, each NPI contributes linearly to reduce the infection force. By itself, this change in contacts among individuals does not affect the relationship between the mean number of contacts in the underlying network and the force of infection in the compartmental model. This is adequate if the structure of the network is not greatly affected. However, when social distancing NPIs are applied with a high degree of coverage and connections among individuals are continuously being removed, this approximation is prone to break down, and the compartmental model may no longer provide a satisfactory portrayal of the epidemiological dynamics.

Although the issues above may seem largely theoretical, it became evident, when attempting to fit compartmental models to data in a situation where there were strong and time-varying NPIs, that such a task was not feasible while keeping parameters within reasonable ranges. There are two current alternatives in such a situation: first, to allow for a greater number of degrees of freedom for model fitting, which may lead to overfitting; this is usually done by fitting the epidemic effective reproduction number ($R_t$) as a function of time, or allowing wider ranges for parameters in spite of knowledge from other sources. The second option is to build more complex models incorporating network structure, such as individual-based models. Neither of these solutions retain the simplicity coupled with the explanatory power of traditional compartmental models, so we sought instead to adapt these model to incorporate the effects of a fluctuating network structure.

Here, we propose an approach that modifies how compartmental models incorporate the effects of NPIs to account for changes in network structure and any consequent reduction in the force of infection. We integrate results from percolation theory into an age-structured SEIR model by using a non-linear correction function dependent on the adherence to NPIs that multiplies the resulting contact matrix, thus directly affecting the force of infection.

In the following sections, we build on the previously implemented and widely used COVID-19 Modelling Consortium (CoMo) model (Aguas et al., 2020), adapting its compartmentalisation to the Brazilian hospital system. Then, we present a nested model version that takes into account the loss of long-range connectivity (percolation) effect. Finally, we fit both model versions to hospitalisation and mortality data for SARS-CoV-2 during 2020 in São Paulo, Brazil. This is the country’s most populous city, with more than 12 million inhabitants and was the city in Brazil first to detect COVID-19 cases. By making a model comparison using the Akaike Information Criterion (AIC) (Burnham and Anderson, 2013) we found that the data strongly support the model that incorporates percolation effect.

2. Methods

2.1. Standard model

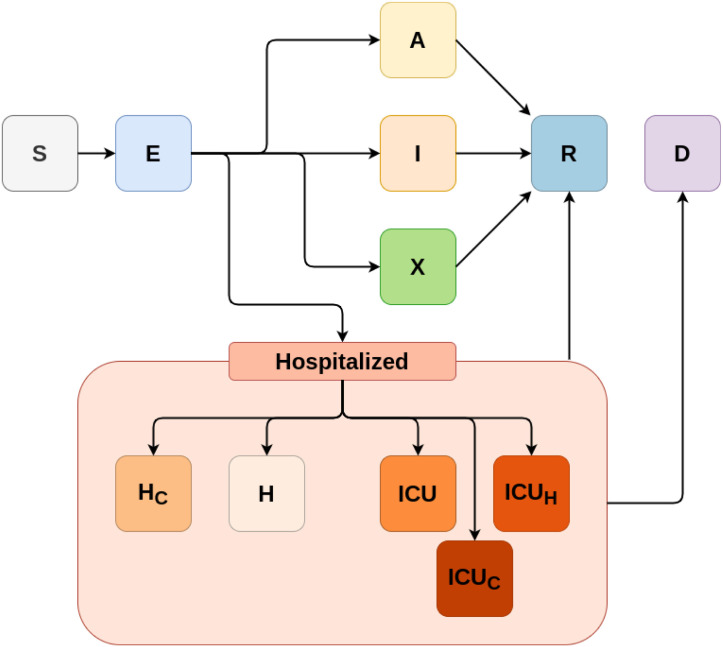
To model the epidemiological dynamics of COVID-19 in São Paulo, we apply an age-structured SEIR model with infected compartments stratified by severity of symptoms, treatment requirement and accessibility to healthcare. The main framework for this SARS-CoV-2 epidemic model was developed in collaboration with the CoMo Consortium (Aguas et al., 2020) with slightly different treatment seeking compartments, an adaptation applied to better represent the Brazilian organisation of hospital beds. The progression of individuals through the infection cycle, for this version of the CoMo model, is represented in Fig. 1.

Fig. 1.

A diagram of the baseline model structure for SARS-CoV-2 in Brazil, representing the unmitigated epidemic spread scenario. The variables in the compartments represent individuals as follows. S: susceptible, E: presymptomatic infectious, A: asymptomatic infectious, I: infectious with mild symptoms, X: infectious with mild symptoms and self-isolated, H${}_C$: infectious, requiring hospital treatment but denied, H: infectious and hospitalised, ICU: infectious, receiving intensive care, ICU${}_C$: infectious, requiring intensive care but denied, ICU${}_H$: infectious, requiring intensive care but being admitted to a regular hospital bed, R: recovered, D: deceased. All compartments are further subdivided into 5 year age classes from 0 to 90+ years old.

Each model compartment depicted in Fig. 1 is divided into 19 sub-compartments, comprising all 19 age classifications used by the Brazilian Institute of Geography and Statistics (IBGE, 2016). Transmission between each pair of age classes is evaluated using estimated contact rates, which are encoded into contact matrices for different settings (school, work, home and others, denoted as $c$) in Brazil, as estimated by Prem et al. (2021). Each matrix accounts for any contacts within each specific setting. For example, if an individual has a contact in a household other than their own household, this contact would still be counted as a “household contact”. Prem et al. (2021)’s study extrapolates from the measurements made during the POLYMOD project (Mossong et al., 2008), so a more complete definition of a contact can be found in the original study.

We considered NPI scenarios such as social distancing, working from home, and school closures. The interventions are given by:

• •Self-isolation: symptomatic individuals who do not require hospitalisation voluntarily isolate themselves during the time of their infection and thus reduce the chance of infecting others. This is modelled as the proportion of individuals that enters the isolated compartment (X) instead of symptomatic compartment (I), as shown in Fig. 1.
• •Social distancing: this intervention comprises reductions in contacts in churches, markets, social events and gatherings, shopping activities, gyms, and others. It requires adherence of the population to the NPI to be estimated for a given time, as well as how effective it is in reducing contacts in the “other” setting. It is modelled as a linear reduction in the “other” contact matrix, given by $a_{other}\left(t\right)$.
• •Use of masks: this intervention comprises individual protection measures, gained through the adoption of mask usage. It requires adherence of the population to the NPI to be estimated for a given time, along with the effectiveness of mask usage. It is modelled as a direct reduction in the attack rate and is given by $mask\left(t\right)$.
• •Work from home: this intervention models workers performing their normal work activities from home. It requires adherence of the population to the NPI to be estimated, as well as how effective it is at reducing contacts among workers. It is modelled as a linear reduction in “work” contact matrix given by $a_{work}\left(t\right)$.
• •School closure: this intervention reduces contacts in the school setting due to limitation of in-school activities or school closures. It requires the adherence of schools and students to the NPI to be estimated, as well as the effectiveness of reducing contacts in the “school” environment. It is modelled as a linear reduction in “school” contacts given by $a_{school}\left(t\right)$.
• •Cocoon the elderly: this intervention reduces the contacts with a proportion of the older adult population, given a minimum age $D$. It requires the adherence of older individuals to the NPI to be estimated, as well as how effective isolating older individuals is. This is modelled as a linear reduction in contacts with and within older individuals and is further described in Section 2 of the Supplementary Material (SM).
• •Travel ban: this intervention involves the interruption of inward travel from outside of the city and the isolation of cases coming from the outside, which reduces or eliminates imported cases. It is modelled as a linear reduction in the number of infected individuals that are imported to the study site (which is also a model parameter).

Here, the effect of some of the mitigation strategies (namely, work from home, school closure and social distancing) are modelled as linear corrections to the contact matrices, since these interventions aim to reduce contact rates or the risk of contagion at each possible contact. Thus, the effective contact matrix is given by:

$$\hat{c}={\hat{c}}_{home}+(1-a_{work}\left(t\right)){\hat{c}}_{work}+(1-a_{school}\left(t\right)){\hat{c}}_{school}+(1-a_{other}\left(t\right)){\hat{c}}_{other}$$ (1)

where the caret ($\stackrel{ˆ}{}$  ) stands for the contact matrices affected by the “cocoon elderly” NPI.

It is reasonable to assume that the contact rates would decrease linearly with increasing adherence to mitigating strategies in schools, workplaces or other settings. Nevertheless, owing to the fact that SEIR-like models assume underlying homogeneously mixed populations, this assumption might not hold for household settings as their connectivity structure is dynamically affected by NPIs in a non-homogeneous fashion. In the next section, we discuss our proposed implementation of such an effect.

2.2. Model with percolation

The model described in the previous section introduced a phenomenological implementation to account for the effects of NPIs through a proportional reduction in contact rates in the matrices. NPIs affected all contact matrices in the standard model, with the exception of the household matrix (which accounts for both contacts within and between households, indistinguishably), implying that the dynamics among households persisted as fully well-mixed, even under high coverage of NPIs. In reality, however, the contact network among households should become more sparse as connecting pathways are removed, in such a way that the “effective” contact rates should be considerably reduced. We draw a comparison with percolation theory to address the fact that, above a certain threshold value of combined NPI adherence, inter-household contacts are much less common.

In a non-NPI scenario, we can picture the entire population as a collection of households assigned as vertices with links among households (created due to interactions at work, schools, or other places) represented by edges. This highly connected network would form one giant connected component, which could therefore be approximated as a homogeneously mixed population (Bansal et al., 2007). However, by introducing social distancing measures and increasing their coverages, we break connections in the network until long-range connectivity is lost. The critical value of the number of connections (or edge density) where this transition happens is the so-called percolation threshold (Essam, 1980). Above the percolation threshold of contact loss, i.e. in a high coverage social distancing scenario, we would expect to see the emergence of small household clusters that, although well connected within themselves, would be poorly connected between them.

Here we model the percolation effect on home contact matrices assuming that, while contacts outside households are kept above the percolation threshold, the effect of mitigation strategies is less apparent in home settings. On the other hand, the overall probability of infection of a susceptible individual decreases drastically when their mean number of contacts drops below a certain threshold (Pastor-Satorras et al., 2015). Mathematically, we correct the home contact matrix by a factor dependent on all the coverage and efficiency of all NPI, which we denote as a percolation correction function, $f_{perc}$, that must satisfy several requirements:

• •$0\le f_{perc}\le 1$;
• •$f_{perc}\to 0$ as NPIs are completely lifted; for low adherence to NPIs, no connectivity loss should be noticed as different households would still be strongly connected;
• •$1-f_{perc}\ll 1$ for high adherence to NPIs; as connections among different households are widely severed, so $f_{perc}$ approaches its maximum value.

A hyperbolic functional form, as follows, is proposed to model this effect:

$$f_{perc}\left(t\right)=\frac{h_{eff}}{2}\left[1+tanh\left(h_{steep}(W_{NPI}\left(t\right)-T_{perc})\right)\right]$$ (2)

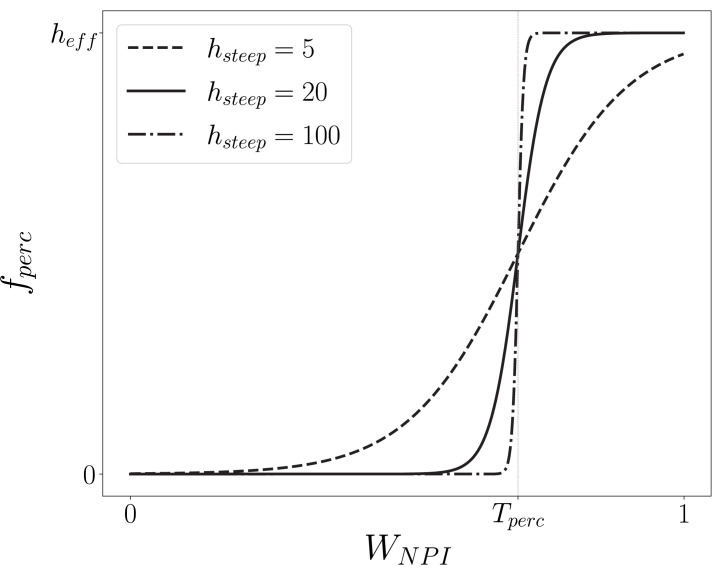
where $0\le h_{eff}\le 1$ is the maximum reduction in contacts, a parameter introduced to control the amplitude of the percolation effect (for simplicity, we adopt $h_{eff}=1$); $0\le T_{perc}\le 1$ is the percolation threshold, i.e. the fraction of connections we need to remove so that the network no longer percolates; and $h_{steep}$ is the steepness of the percolation correction function determining how fast the network percolates: a large $h_{steep}$ implies $f_{perc}$ changing abruptly from 0 to $h_{eff}$ in the vicinity of $W_{NPI}\approx T_{perc}$ (see Fig. 2).

Fig. 2.

Percolation correction as a function of the combined adherence to interventions ($W_{NPI}$). We plot the resultant curve for different values of $h_{steep}$, which is the steepness of the hyperbolic tangent in the definition of $f_{perc}$ (Eq. (2)). For low $W_{NPI}$, $f_{perc}\to 0$, meaning no connectivity is lost at low levels of adherence. Near $W_{NPI}=T_{perc}$, $f_{perc}$ increases rapidly. Under the high $W_{NPI}$ regime, where more connections are lost, $f_{perc}\to h_{eff}\approx 1$. Here we used $T_{perc}=0.6$ for the percolation threshold, which is indicated as the curve’s inflexion point. Note that changing the $T_{perc}$ value simply translates the curve along the $x$-axis.

Finally, $W_{NPI}$ is defined as the combined adherence to NPI, where the resulting reduction of contacts due to each type of intervention are weighted by the age and contact structure of the population they are applied to, namely

$$W_{NPI}\left(t\right)=p_{work}{a}_{work}\left(t\right)+p_{school}{a}_{school}\left(t\right)+p_{other}{a}_{other}\left(t\right)$$ (3)

The weights $p_j$, $j=\{work,school,other\}$, are calculated as

$$p_j=\frac{\mathbf{P}(t=0){\hat{c}}_j{\mathbf{P}}^T(t=0)}{\mathbf{P}(t=0)({\hat{c}}_{work}+{\hat{c}}_{school}+{\hat{c}}_{other}){\mathbf{P}}^T(t=0)},$$ (4)

where $\mathbf{P}(t=0)$ is the initial age distribution of the population and $c_j$ the contact matrices in each setting.

Now, clearly, $0<W_{NPI}\left(t\right)<1$. Note also that $W_{NPI}\left(t\right)$ has this specific form to consider population structure, accounting for how much each of these NPIs effectively reduce contacts in each age-class. Also note that $W_{NPI}\left(t\right)$ can vary according to the current implemented interventions, adding flexibility to the model.

Finally, considering all effects due to NPIs and percolation ($f_{perc}$), the effective contact matrix, $\hat{c}$, is written as

$$\hat{c}=(1-f_{perc}\left(t\right)){\hat{c}}_{home}+(1-a_{work}\left(t\right)){\hat{c}}_{work}+(1-a_{school}\left(t\right)){\hat{c}}_{school}+(1-a_{other}\left(t\right)){\hat{c}}_{other}$$ (5)

This resultant matrix can, therefore, be used to simulate the overall contact rates between age groups, throughout all settings. In the simulations presented here, the populations and setting-specific contact matrices for Brazil were obtained from publicly available data (IBGE, 2016, Prem et al., 2021); all $a_j$ are estimated based on the effect of mitigation strategies adopted by the city of São Paulo (Toscano et al., 2020, Secretaria Municipal de Mobilidade e Transportes, Cidade de São Paulo, 2020, Google, 2020); whereas $h_{steep}$ and $T_{perc}$ are obtained through fitting to epidemiological data.

2.3. Data sources

The data used were time-series of hospitalisations and deaths for severe acute respiratory illness (SARI) in São Paulo, Brazil, reported in the 2020 SIVEP-Gripe database (Datasus, 2020). To be certain records had already been consolidated, i.e. did not suffer from delayed reporting (which can be a significant issue in the Brazilian SARI notification system, demanding corrections that take into account delay distributions, McGough et al., 2020), we restricted the data to weekly aggregate data points comprising the first 23 weeks of the pandemic in the city, from 15 March to 31 August 2020.

Based on the current literature and proxy data for mobility and coverage of NPIs (Google, 2020, Toscano et al., 2020, Secretaria Municipal de Mobilidade e Transportes, Cidade de São Paulo, 2020), we set values for all parameters using reasonable data sources or proxies (see SM Tables III–V for all parameter values and references). Thus, there were just a few parameters that could not be inferred from the literature and therefore required to be fitted to epidemiological data. These fitted parameters were the probability of infection given a contact ($p$), start date of community transmission ($startdate$), and both $h_{steep}$ and $T_{perc}$ from Eq. (2) for the model that takes percolation into account.

2.4. Fitted models

We used a Levenberg–Marquardt non-linear least square regression fitting algorithm (Elzhov et al., 2016) to minimise the squared residuals of the predicted number of weekly cases with to the observed values. This is equivalent to maximising the likelihood of the model under the assumption that the data point errors are normally distributed (details in SM Section 3). With that, we obtained the maximum likelihood estimates (mle) for $p$, $startdate$, $h_{steep}$ and $T_{perc}$. This procedure was applied to test the two versions of the model, in three different scenarios:

• •Standard model: derived from the CoMo model (Aguas et al., 2020), without including the percolation effect, which in practice meant setting $T_{perc}=h_{steep}=h_{eff}=0$ and fitting only $p$ and $startdate$ to the data.
• •Standard model + 30% NPI adherence: the model equations and parameters are the same as the standard model, but we consider a much greater (30%) adherence to all NPIs. This potentially unrealistic instance was included here to show that an underestimated NPI adherence in the standard version would not by itself favour the model with percolation — given that we already know that it always reduces the contact rates.
• •Model with percolation: derived from standard model, including the percolation effect, where $T_{perc}$, $h_{steep}$, $p$ and $startdate$ were fitted to the data.

As the model with percolation introduces two extra parameters fitted to data into the standard model, we can consider them nested models and therefore compare the quality of the fittings using the AIC.

3. Results

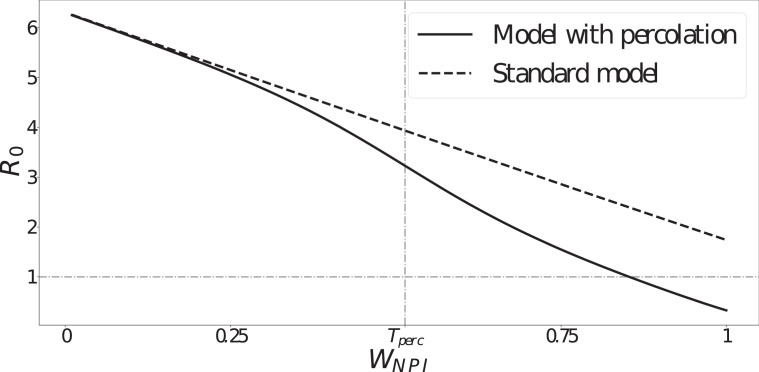
We compare the model implementations with and without percolation by calculating an NPI-dependent basic reproduction number ( $R_0\left(W_{NPI}\right)$ ) using the next generation matrix (NGM) method (Allen et al., 2008 Chapter 6). This resultant $R_0\left(W_{NPI}\right)$ would represent the epidemic basic reproduction number in a hypothetical fully susceptible population under the NPI corresponding to $W_{NPI}$.

The basic reproduction number is a quantity determined by the population affected by a pathogen in a specific environment, rather than a variable that is exclusively determined by the biology of a pathogen. Hence, we can interpret this $R_0\left(W_{NPI}\right)$ as an indicator of the pathogen’s transmissibility in an environment subjected to the combined NPI adherence $W_{NPI}$.

From Fig. 3, we can see that $R_0\left(W_{NPI}\right)$ diverges between the two model versions (standard model and model with percolation) as the combined NPI adherence approaches the fitted percolation threshold (indicated as $T_{perc}$). Percolation implies considerably lower $R_0$ values for greater NPI adherence, which is consistent with the sharp decrease in the effect of NPIs near the percolation threshold modelled by the percolation correction function (Eq. (2)). In summary, this result shows that, near to and above the percolation threshold ($T_{perc}$), i.e. for high combined NPI adherence and effectiveness, the standard model will always overestimate transmission rates.

Fig. 3.

NPI-dependent epidemic basic reproduction number ($R_0\left(W_{NPI}\right)$) as a function of the combined NPI adherence for both model versions. Note the sharp divergence near the percolation threshold ($T_{perc}=0.514$, as a result of fitting the model with percolation to data).

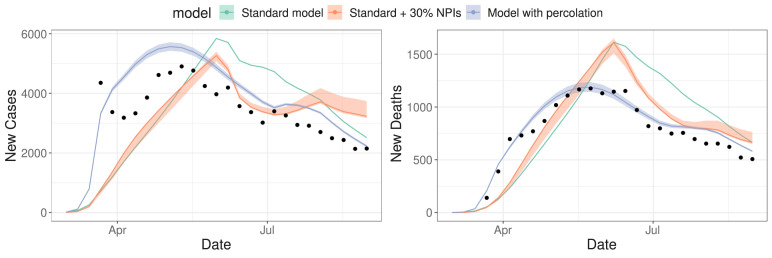
After implementing both model versions with equivalent fixed parameter sets, and also with increased NPIs in one scenario (see Tables III–V in the SM), we fitted the free parameters (among $T_{perc}$, $h_{steep}$, $p$ and $startdate$) in each model to weekly new cases and new deaths from SARI data for São Paulo during 2020. Fig. 4 shows the resulting curves for all fitted models, with confidence intervals assuming that fitted parameters follow a multivariate normal distribution. These confidence intervals are estimated by parametric bootstrap using the covariance matrix from the Levenberg–Marquardt algorithm (details in SM Section 3). The comparison between the two standard model curves shows that increasing intervention coverages (even to the point of assuming unrealistic values) can modulate the epidemic curve to a certain extent, but still does not result in a good fit to data.

Fig. 4.

Results from simultaneous model fitting to SARI new cases and new deaths data, for each of the proposed model versions: the model with percolation (blue) and the standard model (green), using the same parameter sets, apart from the fitted parameters ($p$, $startdate$, $T_{perc}$, $h_{steep}$), and the standard model version with additional 30% adherence to all NPIs (red) (also fitted to data); dots represent data points from the SIVEP-Gripe database (15 March to 31 August 2020) (Datasus, 2020); and shaded areas represent bootstrapped confidence intervals based on parameter uncertainty from the fitting (too thin to see for the green curve). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The resulting parameters and the computed AIC for each model version are shown in Table 1. Comparing the standard model, the standard model + 30% NPI and the model with percolation (curves shown in Fig. 4), the AIC clearly shows a much higher level of empirical support for the model featuring percolation. Furthermore, we can see from Fig. 4 that the percolation model better captures the timing and the size of both case and death peaks.

Table 1.

Fitted parameter values and AIC evaluated for each of the model versions, as they were fitted to the same dataset of weekly SARI cases and deaths for São Paulo, which consisted of 23 data points.

Model	$p$	$startdate$	$h_{steep}$	$T_{perc}$	AIC	$\Delta$AIC
Standard	0.0294	2020-01-15	–	–	−756	191
Standard + 30% NPI adherence	0.0401	2020-01-30	–	–	−793	154
Percolation	0.0461	2020-01-30	4.83	0.516	−947	0

$\Delta$AIC is the difference between the AIC for each model and the minimum overall AIC.

4. Discussion

Modelling the ongoing COVID-19 pandemic represented an unprecedented challenge, as we attempted to make urgent recommendations and predictions based on scarce information about the underlying biology of the virus, its main mechanisms of spread, and severity and fatality rates (Davey Smith et al., 2020, Cyranoski, 2020). Furthermore, we lacked individual-level data on mobility patterns to accurately understand the dynamic effect of social distancing NPIs on individual behaviour and contact patterns.

Although previous studies considered heterogeneous contact structures in epidemiological models (min Liu et al., 1987, Roy and Pascual, 2006, Stroud et al., 2006), and many others accounted for the effects of NPIs on transmissibility (Davies et al., 2020b, Ferguson et al., 2020, Flaxman et al., 2020, Adam, 2020, Aguas et al., 2020, Anirudh, 2020, Panovska-Griffiths et al., 2021, Fumanelli et al., 2016), few to none of them made the connection between both phenomena. Strictly speaking, NPIs can affect the underlying network structure over time due to large-scale social distancing interventions. In this context, we identified a demand for more flexible and dynamic modelling approaches taking into account the non-linear phenomena emerging from social distancing NPIs.

In the case of the COVID-19 pandemic, governments enforced restrictions on movement and contacts, which essentially aimed to remove connections among individuals. To take into account the structural heterogeneities introduced by these social distancing measures on a population’s contact network, we proposed an optional improvement to compartmental models that only depends on quantities already computed when modelling NPIs, without the addition of an excessive number of parameters which could lead to model over-fitting.

The effect of our proposed implementation of an NPI-induced percolation effect was clearly shown by the evaluation of the NPI-dependent basic reproduction number, which resulted in a distinctive discrepancy in the transmissibility when comparing model versions with and without percolation. We determined that for high combined NPI adherence, the model without percolation highly overestimates transmission rates. Using the AIC we found a $\Delta \text{AIC}=191$, between the model versions with and without the percolation effect (Table 1), which is orders of magnitude higher than the conventional threshold of $\Delta \text{AIC}\le 2$ to consider both models equally plausible (Fabozzi et al., 2014). That is, the model with percolation correction had support from the data analysed. It should be noted that the AIC takes into account biases caused by over-fitting (Anderson, 2008). Therefore, the stronger support of the percolation model cannot be attributed to a spurious effect caused by a few additional parameters.

One alternative solution to the data fitting difficulty would consist of adjusting other model parameters. However, with further exploration of the parameter space, even considering less realistic parameter sets (e.g. tampering with the coverage parameters of NPIs), we could not obtain a good fit to data. For instance, a 30% increase in NPI adherence in the standard model (red curve in Fig. 4) did not result in better model fitness, compared to the model version including percolation.

These results highlight the importance of implementing this non-linear response to NPIs in compartmental models to obtain a better representation of the effect of those interventions on a large population.

5. Conclusion

The proposed improvement to an age-structured SEIR compartmental model described here, although motivated by the need to better represent the dynamics of how COVID-19 spreads, was inspired by network theory and general individual level considerations that could be applied to any population whose underlying network structure has been affected by similar fragmentation processes.

We implemented the effect of individuals’ behavioural changes on a population’s macroscopic dynamics without drastically increasing the number of fitted parameters in our compartmental model. Specifically, only two parameters were added to the equations governing the dynamic model and these were fitted to epidemiological data. Hence, the increased model fitness obtained would not imply additional efforts for decision-makers in terms of data collection.

The usefulness of incorporating this fragmentation process into our SARS-CoV-2 epidemiological compartmental model was evident, but it should also be noted that its flexible implementation also permits it to be applied when modelling the transmission dynamics of other communicable diseases under similarly high NPI coverage regimes.

Therefore, our framework may be applied to any compartmental models trying to represent the dynamics of a homogeneously mixed population suffering drastic changes in its connectivity patterns during an epidemic. This result contributes to a more accurate epidemic modelling, potentially implying better control and prevention policy recommendations at a public health level.

CRediT authorship contribution statement

Caroline Franco: Conceptualization, Formal analysis, Software, Writing – original draft, Writing – review & editing. Leonardo Souto Ferreira: Writing – original draft, Writing – review & editing, Conceptualization, Formal analysis, Software. Vítor Sudbrack: Conceptualization, Writing – original draft, Writing – review & editing. Marcelo Eduardo Borges: Formal analysis, Software. Silas Poloni: Conceptualization, Formal analysis, Software, Writing – original draft, Writing – review & editing. Paulo Inácio Prado: Data curation. Lisa J. White: Supervision, Writing – review & editing. Ricardo Águas: Supervision, Writing – review & editing. Roberto André Kraenkel: Conceptualization, Supervision, Writing – review & editing. Renato Mendes Coutinho: Conceptualization, Formal analysis, Software, Writing – original draft, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

The following is the Supplementary material related to this article.

MMC S1

.