Deep learning-based identification of genetic variants: application to Alzheimer’s disease classification

Abstract

Deep learning is a promising tool that uses nonlinear transformations to extract features from high-dimensional data. Deep learning is challenging in genome-wide association studies (GWAS) with high-dimensional genomic data. Here we propose a novel three-step approach (SWAT-CNN) for identification of genetic variants using deep learning to identify phenotype-related single nucleotide polymorphisms (SNPs) that can be applied to develop accurate disease classification models. In the first step, we divided the whole genome into nonoverlapping fragments of an optimal size and then ran convolutional neural network (CNN) on each fragment to select phenotype-associated fragments. In the second step, using a Sliding Window Association Test (SWAT), we ran CNN on the selected fragments to calculate phenotype influence scores (PIS) and identify phenotype-associated SNPs based on PIS. In the third step, we ran CNN on all identified SNPs to develop a classification model. We tested our approach using GWAS data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) including (N = 981; cognitively normal older adults (CN) = 650 and AD = 331). Our approach identified the well-known APOE region as the most significant genetic locus for AD. Our classification model achieved an area under the curve (AUC) of 0.82, which was compatible with traditional machine learning approaches, random forest and XGBoost. SWAT-CNN, a novel deep learning–based genome-wide approach, identified AD-associated SNPs and a classification model for AD and may hold promise for a range of biomedical applications.

Introduction

Deep learning is a representative machine learning algorithm that enables nonlinear transformations to extract features of high-dimensional data [1], unlike traditional machine learning models that predict a linear combination of weights by assuming a linear relationship between input features and a phenotype of interest. Deep learning has been used to predict disease outputs by handling original high-dimensional medical imaging data without feature selection procedures [2, 3]. In genetic research, deep learning frameworks have been used to investigate molecular phenotypes that predict the effects of noncoding variants [4–10], differential gene expression [11] and potential transcription factor binding sites [12]. These tools use CHIP-Seq or DNase-Seq data as training data to predict chromatin features such as transcription factor binding or DNase hypersensitivity from DNA sequences. More recently, deep learning has been employed in the capture of mutations and the analysis of gene regulations, demonstrating its potential for furthering our understanding of epigenetic regulation [13]. Furthermore, deep learning is being used in gene therapy to design CRISPR guide RNAs using deep learning–based gene features [14–19].

Genome-wide association studies (GWAS) use a statistical approach by considering one single nucleotide polymorphism (SNP) at a time across the whole genome to identify population-based genetic risk variation for human diseases and traits [20, 21]. However, deep learning has not yet been used to perform GWAS, as it is challenging due to the so-called high-dimension low-sample-size (HDLSS) problem [22], which is known to impact phenotype prediction using genetic variation. Feature reduction approaches have been commonly used [23–25] to resolve this problem, but feature reduction using high-dimensional genomic data is also challenging due to an NP-hard problem [26, 27]. Therefore, it is necessary to develop a deep learning framework to identify genetic variants using whole genome data.

Here we proposed a novel three-step deep learning–based approach to select informative SNPs and develop classification models for a phenotype of interest. In the first step, we divided the whole genome into nonoverlapping fragments of an optimal size and then used deep learning algorithms to select phenotype-associated fragments containing phenotype-related SNPs. Different sized fragments and several deep learning algorithms were tested to select the optimal size for fragments and the optimal algorithm. In the second step, we ran the optimal deep learning algorithm using an overlapping Sliding Window Association Test (SWAT) within selected fragments to calculate phenotype influence scores (PIS) using SNPs and the phenotype of interest to identify informative SNPs. In the third step, we ran the optimal algorithm again on all identified informative SNPs to develop a classification model.

Alzheimer’s disease (AD), the most common form of dementia, is a neurodegenerative disorder that causes progressive deterioration of memory and cognitive function. The pathological hallmarks of the disease are toxic amyloid-β plaques and neurofibrillary tau tangles in the brain [28, 29], with the strongest genetic risk factor being the ε4 allele of apolipoprotein E (APOE). APOE ε4 allele carriers are more prone to amyloid deposition and have a 3- to 4-fold increased risk of AD [30–32]. In addition to amyloid, tau and APOE, many other aging- and neurodegeneration-associated biological pathways are being actively investigated for their role in AD pathogenesis and for their potential as targets for therapeutic development. Examples include inflammation, cellular senescence, telomere shortening, altered neurogenesis, dysregulated lipid metabolism, altered mitochondrial function and brain energetics, and other age-associated factors [33–39]. In addition, processes related to clearance of misfolded proteins are important including autophagy, the primary mechanism that removes protein aggregates [40] [41]. Relatedly, mitophagy plays an essential role in maintaining mitochondrial homeostasis and when impaired may contribute to AD-related pathophysiology [42, 43]. As amyloid-β is clearly linked to the initiation and progression of AD, it has been targeted for drug treatment. Despite longstanding global efforts and numerous failed trials, the FDA recently granted accelerated approval of aducanumab, the first potentially disease-modifying antiamyloid treatment [44]. In addition, it is of fundamental importance to identify biomarkers for the detection of AD at presymptomatic stages to slow or prevent disease progression [45–47]. In the past few years, artificial intelligence (AI) approaches have been used to identify AD biomarkers through brain image analysis [2, 3, 48], cerebrospinal fluid (CSF) AD biomarkers [49] and plasma metabolites [50]. Using high-throughput bioassays, AI technology has been used to repurpose known drugs to treat Alzheimer’s disease [51, 52]. Though these AI applications are growing rapidly, only a few have reached the clinical stage.

We tested our approach using only whole genome data for AD (N = 981; cognitively normal older adults (CN) = 650 and AD = 331). Our approach identified the known APOE region as the most significant genetic locus for AD. Using the identified region, we made a classification model with CNN. To determine if the algorithm is comparable to traditional machine learning algorithms, we also applied XGBoost and random forest. Our classification model yielded 75.2% accuracy, which was generally compatible with a modest gain in accuracy of 3.8% and 9.6% relative to XGBoost and random forest, respectively. Our classification model yielded 75.2% accuracy over traditional machine learning methods, being 3.8% and 9.6% higher than XGBoost and random forest, respectively. Our novel deep learning–based approach can identify informative SNPs and develop a classification model for AD by combining nearby SNPs and testing their aggregation.

Materials and methods

Study participants

All individuals used in the analysis were participants of the Alzheimer’s Disease Neuroimaging Initiative (ADNI) cohort [53, 54]. The ADNI initial phase (ADNI-1) was launched in 2003 to test whether serial magnetic resonance imaging (MRI), position emission tomography (PET), other biological markers, and clinical and neuropsychological assessment could be combined to measure the progression of mild cognitive impairment (MCI) and early AD. ADNI-1 has been extended in subsequent phases (ADNI-GO, ADNI-2 and ADNI-3) for follow-up of existing participants and additional new enrollments. Demographic information, APOE and whole genome genotyping data, and clinical information are publicly available from the ADNI data repository (www.loni.usc.edu/ADNI/). Informed consent was obtained for all subjects, and the study was approved by the relevant institutional review board at each data acquisition site.

Genotyping and imputation

ADNI participants were genotyped using several Illumina genotyping platforms including Illumina Human610-Quad BeadChip, Illumina HumanOmni Express BeadChip and Illumina HumanOmni 2.5M BeadChip [54]. As ADNI used different genotyping platforms, we performed quality control procedures (QC) on each genotyping platform data separately and then imputed un-genotyped single nucleotide polymorphisms (SNPs) separately using MACH and the Haplotype Reference Consortium (HRC) data as a reference panel [55]. Before imputation, we performed QC for samples and SNPs as described previously: (1) for SNP, SNP call rate < 95%, Hardy–Weinberg P value < 1 × 10⁻⁶, and minor allele frequency (MAF) < 1% and (2) for sample, sex inconsistencies, and sample call rate < 95% [56]. Furthermore, in order to prevent spurious associations due to population stratification, we selected only non-Hispanic participants of European ancestry that clustered with HapMap CEU (Utah residents with Northern and Western European ancestry from the CEPH collection) or TSI (Toscani in Italia) populations using multidimensional scaling (MDS) analysis and the HapMap genotype data [56, 57]. After imputation, we performed standard QC on imputed genotype data as described previously [58]. Specifically, we imposed an r² value equal to 0.30 as the threshold to accept the imputed genotypes. In the study, imputed genome-wide genotyping data from 981 ADNI non-Hispanic participants (650 cognitive normal older adults (CN) and 331 AD patients) were used with a total of 5,398,183 SNPs (minor allele frequency (MAF) > 5%).

Genome-wide association study (GWAS)

Using imputed genotypes, a GWAS for AD was conducted. For the GWAS, logistic regression with age and sex as covariates was performed using PLINK [59] to determine the association of each SNP with AD. To adjust for multiple testing, a conservative threshold for genome-wide significant association (P < 5 × 10⁻⁸) was employed based on a Bonferroni correction.

Fragmentation of whole genome data

Whole genome data for 981 participants were divided into nonoverlapping fragments of varying sizes from 10 SNPs to 200 SNPs to determine the optimal fragmentation size. The subdatasets consisting of fragments of the same size were divided into train–test–validation sets (60:20:20), and convolutional neural network (CNN) [60], long short-term memory (LSTM) [61], LSTM-CNN [62] and attention [63] algorithms were applied to each. Early stopping using a validation set was applied to prevent overfitting, followed by the measurement of training time and accuracy (ACC).

Deep learning on fragments

Deep learning is the result of continuous development such as perceptron [64, 65], which adds the concept of weight adjustment to the theory that it can behave like a human brain when neurons with on–off functions are connected in a network form [66], and Adaline [67], which uses gradient descent to update weights. These early neural nets were advanced to a multilayer perceptron, which includes hidden layers to solve the famous XOR problem [68], marking a theoretical turning point with the concept of backpropagation to update the weight of the hidden layer [69–72]. The inherent problem of backpropagation, in which vanishing gradients occur when there are many layers [73], has been alleviated through activation functions, such as sigmoid function and ReLU [74, 75], as well as optimization methods for better gradient descent methods, such as Ada-Grad [76], RMSprop [77] and Adam [78]. These developments, along with the advancement of GPU hardware, have created an era of deep learning as it is now.

Deep learning has laid the theoretical foundation for backpropagation, the application of activation functions and the development of optimizers for better gradient descent. Common deep learning algorithms, such as CNN, LSTM and attention, have a hierarchical structure that implements an enhanced version of the basic principles of deep learning. The detailed technical description of each algorithm is described extensively in the relevant paper, so here we focus on the core of the deep learning technology commonly applied to the algorithm used in the experiment.

We used ReLU as an activation function that underlies the deep learning algorithms used in our experiments. ReLU, the most used activation function in the deep learning community, replaces the given value with zero if the value is <0 and uses the given value if it is >0. Thus, if the given value is greater than zero, the derivative becomes one, and the weight can be adjusted without vanishing the gradient to the first layer through the hidden layer. We used Adam as the optimization method. Adam is currently the most popular optimization method for deep learning, as it takes advantage of momentum SGD [79] and RMSprop, which are expressed as follows: G_t is the sum of the square of the modified gradient and ε is a very small constant that prevents the equation from being divided by zero.

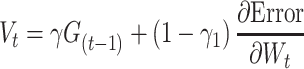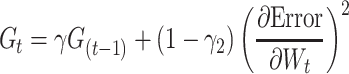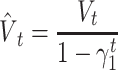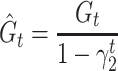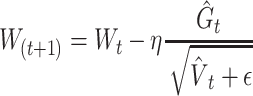Backpropagation is used to calculate the initial error value from a given random weight using the least squares method and then to update the weight using a chain rule until the differential value becomes zero. Here, the differential value of zero means that the weight does not change when the gradient is subtracted from the previous weight.

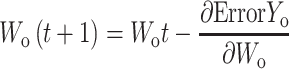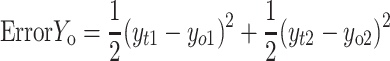If y_o1 and y_o2 are the output values of the output layer coming through the hidden layer and the actual values of the given data are y_t1 and y_t2, the partial derivative of the error ErrorY_o to the weight of the output layer can be calculated using the chain rule as follows:

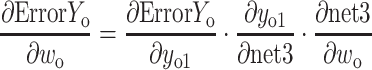The partial derivative of the error ErrorY_o to the weight of the hidden layer can be calculated as follows:

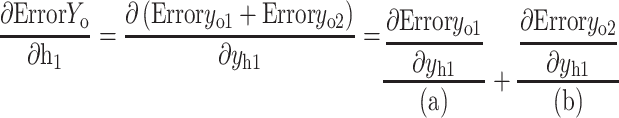• (a)

  
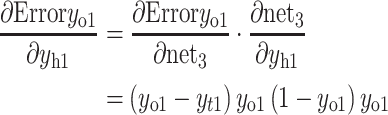
• (b)

  

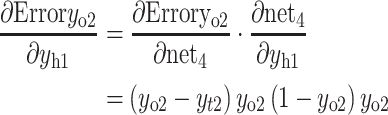
Accordingly, the weight w_h of the hidden layer is updated as follows:

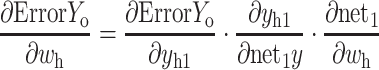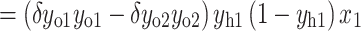Calculation of phenotype influence score using deep learning

Prediction accuracy was calculated from deep learning applied to each fragment and converted to a z-score. The z-score follows a normal distribution with μ = 1 and σ = 0, under the hypothesis that there is no relationship between the variables in the population. Fragments with a z-score higher than the median were selected. An overlapping SWAT for the calculation of PIS is applied to these fragments. When the length of the fragment is w, the window is positioned w − 1 from the first SNP of the fragment and moves by one SNP and stops at the last SNP of the fragment. Each region within the SWAT is divided into a train–test–validation set (60:20:20), and early stopping using a validation set is applied to prevent overfitting. When the kth SNP is S_k, PIS is calculated as follows.

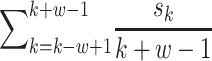This SWAT is applied to all selected fragments, resulting in a PIS for all SNPs.

Phenotype classification using deep learning

We selected the top 100 to 10,000 SNPs based on the PIS. For the AD-CN classification, we used a CNN consisting of convolution layers with a kernel size of 5, pooling the layer with a max-pool size of 2, a fully connected layer of 64 nodes, and an output layer with a softmax activation function. Due to gradient vanishing and explosion issues caused by the repeated multiplication of the recurrent weight matrix, RNN or its variants had difficulty training. In order to compare the performance, we also applied random forest and XGBoost, which are traditionally used for tabular data classification. XGBoost is a tree-based ensemble algorithm, one of popular implementations of gradient boosting. We trained XGBoost using an ‘xgboost’ package for python (https://xgboost.readthedocs.io/). Random forest is another ensemble learning method that uses many decision trees as its classifiers [80, 81]. We trained random forest using the scikit-learn package for python by setting the number of trees as 10 and the maximum depth of each tree as 3.

Results

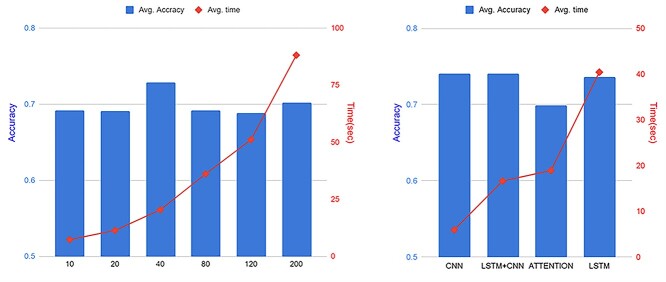
Our deep learning–based approach consists of three steps to select informative SNPs and develop an accurate classification model. In the first step, we divided the whole genome into nonoverlapping fragments of an optimal size. To choose an optimal fragment size and an optimal deep learning algorithm, we calculated the mean accuracy and computation time for classification of AD using various fragment sizes containing 10 to 200 SNPs and several deep learning algorithms (CNN, LSTM, LSTM-CNN, Attention). In this analysis, we used 10–200 SNPs located within a region surrounding the APOE gene, the strongest and most robust AD genetic risk locus. Figure 1 shows the average accuracy and computation time for CNN, LSTM, LSTM-CNN and attention as a function of the fragment size. As shown in Figure 1A, the analysis yielded the highest accuracy for classification of AD for a fragment size with 40 SNPs (Figure 1A). Figure 1B shows the average accuracy and time as a function of the deep learning algorithm on window size of 40 within a region surrounding the APOE gene. CNN and LSTM-CNN models had the highest accuracy for classification of AD, followed by LSTM. However, the computation time of CNN and LSTM models were 5.9 and 40.4 s, respectively. The computation time of LSTM, LSTM-CNN and attention models sharply increased compared to CNN because the fragment contains more SNPs; therefore, we chose a fragment with 40 SNPs as the optimal fragment size for the CNN and optimal deep learning algorithm, respectively. The whole genome was divided into 134,955 fragments, each with 40 SNPs. We ran CNN on each fragment to calculate z-scores based on classification accuracy and selected phenotype-associated fragments. We selected 1802 fragments with z-scores higher than a median z-score.

Figure 1.

Selection of an optimal fragment size and an optimal deep learning algorithm. In order to choose an optimal fragment size and an optimal deep learning algorithm, the mean accuracy and computation time was calculated for the classification of AD using various fragment sizes containing 10 to 200 SNPs in the APOE region and several deep learning algorithms (CNN, LSTM, LSTM-CNN and attention). (A) Average accuracy and time as a function of the fragment size. The highest accuracy for classification of AD was obtained with a fragment having 40 SNPs in CNN, LSTM-CNN and LSTM models. The accuracy difference was not large according to window size, but the processing time increased with window size. (B) Average accuracy and time as a function of the deep learning algorithm using a widow size of 40. The computation time of LSTM, LSTM-CNN and attention models increases sharply compared to CNN as they include more SNPs in their fragments.

In the second step, using a SWAT, we ran CNN on the selected fragments to calculate the PIS of each SNP in the selected fragments and identify phenotype-associated SNPs based on the PIS, as shown in Figure 2. For each SNP, we calculated a mean accuracy of 40 windows, which is the PIS of the SNP. Using PIS values, we calculated the z-scores and one-tailed P-values. Figure 3 shows a Manhattan plot with the −log10 P-values on the y-axis against the SNP position in the genome on the x-axis. The SNP with the smallest P-value was rs5117 in the APOC1 gene (P-value = 1.04E−22) and rs429358 in the APOE gene (P-value of 1.41E-16). The genetic region including APOE/APOC1/TOMM40 genes is known as the strongest genetic risk locus for AD [30, 82–84]. The next highest genetic loci were located at SNX14, SNX16, BICD1, WDR72 and GLT1D1 genes.

Figure 2.

Sliding Window Association Test (SWAT) for genetic variants. (A) Inside view of a sliding window that traverses the entire genome sequence to find a location that is associated with a specific phenotype. A CNN consisting of a convolutional layer with a kernel size of 10, a pooling layer with a maximum pool size of 2, a fully connected layer of 64 nodes, and an output layer with softmax activation was used. (B) Framework to calculate phenotype influence scores of SNPs. We divided the whole genome into 134 955 fragments, each with 40 SNPs. To calculate a phenotype influence score for each of the 40 SNPs included in one fragment, we used an overlapping window approach and CNN. w is the number of SNPs in the fragment and Sk is the kth SNP in the fragment.

Figure 3.

Manhattan plot of P-values of SNPs by our deep learning-based approach in AD. The X-axis shows SNP positions in the genome. The Y-axis shows −log10 of P-values. The genetic region including APOE, APOC1 and TOMM40 genes is known as the strongest genetic risk locus for Alzheimer’s disease. The SNP with the smallest P-value was rs5117 in APOC1 gene (P = 1.04E−22). rs429358 in APOE has a P-value of 1.41E−16. Next identified genetic loci were located at SNX14, SNX16, BICD1, WDR72 and GLT1D1 genes.

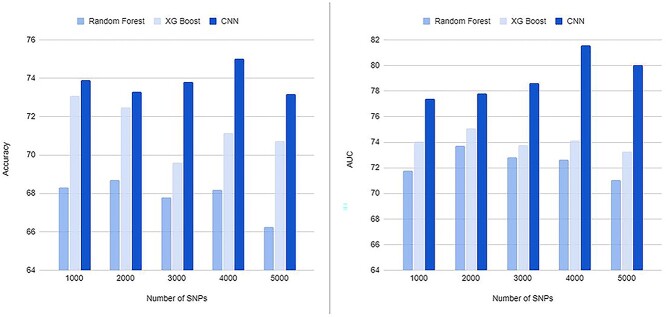
In the third step, we ran CNN on the identified SNPs to develop an AD classification model. Table 1 shows the classification results of AD versus CN using subsets containing the top 100 to 10,000 SNPs based on PIS. For comparison with traditional machine learning methods, we used two popular algorithms as classifiers, XGBoost and random forest. The highest mean accuracy of 10 cross-validation in classifying AD from CN by CNN was 75.02% (area under the curve [AUC] of 0.8157) for a subset containing 4000 SNPs, which had a 6.3% higher accuracy than random forest for a subset containing 2000 SNPs and a 1.94% higher accuracy than XGBoost for a subset containing 1000 SNPs. When we calculated the classification accuracy of AD using only the number of APOE ε4 alleles, the classification accuracy was 66.7%, which was 8.3% lower than our method. Our CNN models outperformed two traditional machine learning models, random forest and XGBoost, in all cases as shown in Figure 4.

Table 1.

Results of classification of AD from CN

Top	Random forest				XGBoost				CNN
	Accuracy	STD(±)	AUC	STD(±)	Accuracy	STD(±)	AUC	STD(±)	Accuracy	STD(±)	AUC	STD(±)
100	66.46	7.79	0.7137	0.0576	70.24	2.80	0.7266	0.0281	68.29	2.87	0.7216	0.0603
200	67.18	3.88	0.7175	0.0386	67.99	1.52	0.7166	0.0245	69.52	5.08	0.7182	0.0494
300	66.26	3.80	0.7098	0.0377	68.20	3.32	0.7029	0.0272	70.64	2.20	0.7250	0.0585
400	67.58	4.67	0.7074	0.0428	69.42	3.43	0.7177	0.0234	67.99	4.65	0.7167	0.0412
500	67.59	7.79	0.7111	0.0457	71.05	2.56	0.7381	0.0325	71.56	6.58	0.7411	0.0614
1000	68.31	5.22	0.7178	0.0445	73.08	2.89	0.7407	0.0372	73.91	3.87	0.7741	0.0444
2000	68.70	3.13	0.7372	0.0424	72.48	2.61	0.7509	0.0365	73.29	2.77	0.7782	0.0409
3000	67.78	3.59	0.7282	0.0351	69.62	4.27	0.7376	0.0328	73.80	2.40	0.7862	0.0282
4000	68.19	4.69	0.7263	0.0469	71.15	4.07	0.7412	0.0368	75.02	3.17	0.8157	0.0261
5000	66.25	5.41	0.7105	0.0399	70.74	3.14	0.7330	0.0305	73.19	4.72	0.8003	0.0506
10 000	66.26	5.59	0.6919	0.0528	69.63	3.27	0.7248	0.0211	71.05	6.57	0.7083	0.1424

Notes: The table shows the number of top SNPs selected based on phenotype influence score for AD classification and the accuracy and AUC of 10-fold cross-validation. Our CNN-based approach yielded the highest accuracy and AUC of 75.02% and 0.8157, respectively, for 4000 SNPs. In all cases, our CNN models outperformed two traditional machine learning models, random forest and XGBoost

Figure 4.

Results of classification of AD from CN. The X-axis shows the number of top SNPs selected based on phenotype influence score for AD classification. The Y-axis shows the accuracy (A) and AUC (B) of 10-fold cross-validation. Our CNN-based approach yielded the highest accuracy and AUC of 75.02% and 0.8157, respectively, for 4000 SNPs. In all cases, our CNN models outperformed two traditional machine learning models, random forest and XGBoost.

Figure 5 shows LocusZoom plots [85] for SNPs located at 300 kb upstream and downstream regions from the boundary of the APOE gene. The horizontal axis is the location of SNPs, and the vertical axis is −log10 of the P-values. Each dot represents a SNP, and the color represents the squared correlation coefficient (r²) with the most significant SNP. Figure 5A shows P-values calculated using PLINK, and the most significant SNP was rs429358 in APOE. Figure 5B shows P-values calculated using our deep learning approach, and the most significant SNP was rs5117 in APOC1. Figure 5B shows a linear increase on the left side of rs5117 and a linear decrease on the right side of rs5117, which was different from PLINK results (Figure 5A), which have no linear patterns. In addition, Figure 5B shows three strongly correlated SNPs (r² > 0.8), with rs5117 on the left side of rs5117 but no SNPs on the right side of rs5117.

Figure 5.

LocusZoom plots for SNPs located at the 300 kb upstream and downstream region from the boundary APOE gene. The horizontal axis is the location of SNPs and the vertical axis is −log10 of P-values. Each dot represents an SNP and the color represents the squared correlation coefficient (r²) with the most significant SNP. (A) shows P-values calculated using PLINK and the most significant SNP was rs429358 in APOE. (B) shows P-values calculated using our deep learning approach and the most significant SNP was rs5117 in APOC1. In (B), we can see linear increase on the left side of rs5117 and linear decrease on the right side of rs5117, which was different from PLINK results (A), which has no linear patterns. In addition, in (B), we can see three strongly correlated SNPs (r² > 0.8) with rs5117 on the left side of rs5117 but no SNPs on the right side of rs5117.

Discussion

Although deep learning has solved many real-world problems, few deep learning approaches have been used in GWAS or sequence data to identify genetic variants and for disease/risk classification due to the high dimensionality of the genomic data [22]. In this study, we propose a novel deep learning–based sliding window approach to identify and select disease-associated SNPs and develop an accurate classification model using high dimensional genomic data that we tested using the ADNI cohort (N = 981). The proposed method successfully identified significant genetic loci for AD that included the well-known APOE genetic locus and highlighted several other risk loci. Our deep learning–based approach was compatible to traditional machine learning methods for classification of AD.

The deep learning–based approach for identification of genetic variants consists of three steps. In the first step, we divided the whole genome into nonoverlapping fragments of an optimal size, creating a fragmentation and windowing approach that, to the best of our knowledge, is the first deep learning–based method for identifying genetic variants.

In the second step, we calculated a PIS of each SNP within the selected fragments by using an overlapping window and CNN algorithm. Our method calculates PIS, a novel index that is used to find disease-related variants and predict disease. Furthermore, we calculated the z-scores and one-tailed P-values using PIS, which yielded a Manhattan plot showing the most significant genetic loci in APOE/APOC1/TOMM40 genes that are known as the strongest genetic risk factors for AD. Our method also identified several novel candidate genetic loci, including sorting nexin (SNX) 14 and SNX16, located on chromosomes 6 and 8, respectively, that have not been previously identified to be associated with AD, though there may be special relevance for neurodegeneration as SNX12 [86], SNX17 [87], SNX27 [88] and SNX33 [89] are involved in neuronal survival. Bicaudal D1 (BICD1) on chromosome 12 is a susceptibility gene in chronic obstructive pulmonary disease [90] and lissencephaly [91], but there are no reports of it being associated with AD.

In the third step, we selected top SNPs based on PIS to develop classification models for AD. We selected sets of highly AD-related SNPs and classified AD from CN using CNN, as well as two popular traditional machine learning algorithms, XGBoost and random forest. We found the accuracy of classification was changed with the number of the selected SNPs and the classification algorithms. The highest mean accuracy of the classification was 75.0% when CNN was used on the top 4000 SNPs, which was comparable to two traditional machine learning algorithms. It was also 8.3% higher than the accuracy of the classification using only the number of APOE ε4 alleles. Classification is the first step toward achieving a better understanding of the genetic architecture of AD. The proposed method will benefit from future studies that use deep learning with quantitative phenotypes and baseline values to predict future disease trajectories.

We plotted the SNPs selected by PIS and PLINK for comparison using LocusZoom. We found that there were no SNPs with r² greater than 0.8 in the PLINK results, but three strongly associated SNPs were identified using our method. This is because the PLINK method finds statistical significance SNP by SNP, whereas the deep learning approach uses multiple inputs to adjust weights through the training process. Deep learning uses adjacent SNPs to compute gradients at every epoch and uses a loss function to adjust the weights in the backpropagation process. Unlike PLINK, our method shows that SNPs related to a phenotype can be extracted by considering surrounding SNPs, which means that both methods might be complementary because they identify different variants, though notably in the same region around APOE.

In summary, our novel deep learning–based approach can identify AD-related SNPs by using genome-wide data to develop a classification model for AD. The heritability of AD is estimated to be up to 80%. Accordingly, it is important to identify novel genetic loci related to the disease. Using a modest sample size, we found a significant genetic locus and a classification accuracy of 75%. In future work, we plan to apply our method to large-scale whole genome sequencing datasets that are expected to become available soon to identify novel AD-related SNPs and develop more accurate classification models. We also plan to study early stages of disease including mild cognitive impairment and subjective cognitive decline, where there is considerable heterogeneity, and more refined classification of risk for progression to AD would be valuable. In addition, future studies will investigate use of quantitative endophenotypes that may be more informative than binary classification given their potential to elucidate genetic risk related to specific disease pathways and mechanisms.

Key Points

• Although deep learning has been successfully applied to many scientific fields, deep learning has not been used in genome-wide association studies (GWAS) in practice due to the high dimensionality of genomic data.

• To overcome this challenge, we propose a novel three-step approach (SWAT-CNN) for identification of genetic variants using deep learning to identify phenotype-related single nucleotide polymorphisms (SNPs) that can be applied to develop accurate disease classification models.

• To accomplish this, we divided the whole genome into nonoverlapping fragments of an optimal size and ran a deep learning algorithm on each fragment to select disease-associated fragments.

• We calculated phenotype influence scores (PIS) of each SNP within selected fragments to identify disease-associated significant SNPs and developed a disease classification model by using overlapping window and deep learning algorithms.

• In the application of our method to Alzheimer’s disease (AD), we identified well-known significant genetic loci for AD and achieved higher classification accuracies than traditional machine learning methods.

Taeho Jo is an assistant research professor in the Department of Radiology and Imaging Sciences at the Indiana University School of Medicine. His research focuses on developing machine learning, deep learning methods to analyze large-scale biomedical data, including neuroimaging, genetics and other omics modalities.

Kwangsik Nho is an associate professor in the Department of Radiology and Imaging Sciences at the Indiana University School of Medicine. His main research focus is on computational strategies for integrative analysis of genomic, transcriptomic and metabolomic data in relation to multimodal MRI and PET neuroimaging, as applied to Alzheimer’s disease.

Paula Bice is an assistant research professor in the Department of Radiology and Imaging Sciences and the Indiana Alzheimer’s Disease Research Center, at the Indiana University School of Medicine. As a neuroscientist, her research focuses on studies using neuroimaging, omics and systems biology approaches.

Andrew J. Saykin is the Raymond C. Beeler Professor of Radiology and Imaging Sciences and of Medical and Molecular Genetics at the Indiana University School of Medicine where he directs the NIA-designated Indiana Alzheimer’s Disease Research Center. His research focuses on integrative analysis of multimodal imaging, omics and other biomarker data in support of precision medicine.

Author contributions

T.J., K.N. and A.S.: Conceptualization. A.S.: Acquisition of Data and Interpretation of Results. T.J., K.N.: Data Curation. T.J.: Formal Analysis, Investigation, Methodology, Validation, Visualization. T.J., K.N., P.B. and A.S.: Writing—Original Draft Preparation. T.J., K.N., P.B. and A.S.: Review & Editing.

Funding

Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). In addition, this work was supported, in part, by grants from the National Institutes of Health (NIH) and includes the following sources: P30 AG010133, P30 AG072976, R01 AG019771, R01 AG057739, U01 AG024904, R01 LM013463, R01 AG068193, T32 AG071444, U01 AG068057, R01 LM012535 and R03 AG063250. The funders played no role in the design of the study, analysis and interpretation of the data or in writing the manuscript.