Abstract
Water potential directly controls the function of leaves, roots, and microbes, and gradients in water potential drive water flows throughout the soil-plant-atmosphere continuum. Notwithstanding its clear relevance for many ecosystem processes, soil water potential is rarely measured in-situ, and plant water potential observations are generally discrete, sparse, and not yet aggregated into accessible databases. These gaps limit our conceptual understanding of biophysical responses to moisture stress and inject large uncertainty into hydrologic and land surface models. Here, we outline the conceptual and predictive gains that could be made with more continuous and discoverable observations of water potential in soils and plants. We discuss improvements to sensor technologies that facilitate in situ characterization of water potential, as well as strategies for building new networks that aggregate water potential data across sites. We end by highlighting novel opportunities for linking more representative site-level observations of water potential to remotely-sensed proxies. Together, these considerations offer a roadmap for clearer links between ecohydrological processes and the water potential gradients that have the ‘potential’ to substantially reduce conceptual and modeling uncertainties.
Gradients in the water potential (Ψ) of soils and plants form the energetic basis for the transport of water, and elements contained therein, through a connected continuum linking the deepest soil layers to the top of plant canopies (Figure 1). Ψ can be a positive or negative pressure, though it is typically negative -- a tension force -- in unsaturated soils and within plant hydraulic systems. Ψ gradients have been recognized as the fundamental driver of water fluxes between soils, streams, and groundwater for more than a century, and they appear in some of the most foundational equations in hydrology1 (e.g. Darcy’s Law, Richard’s Equation). Likewise, the critical role of Ψ gradients in driving water flows through the soil-plant-atmosphere continuum has been known for decades2.
Figure 1: Water potential links environmental drivers to biophysical responses.
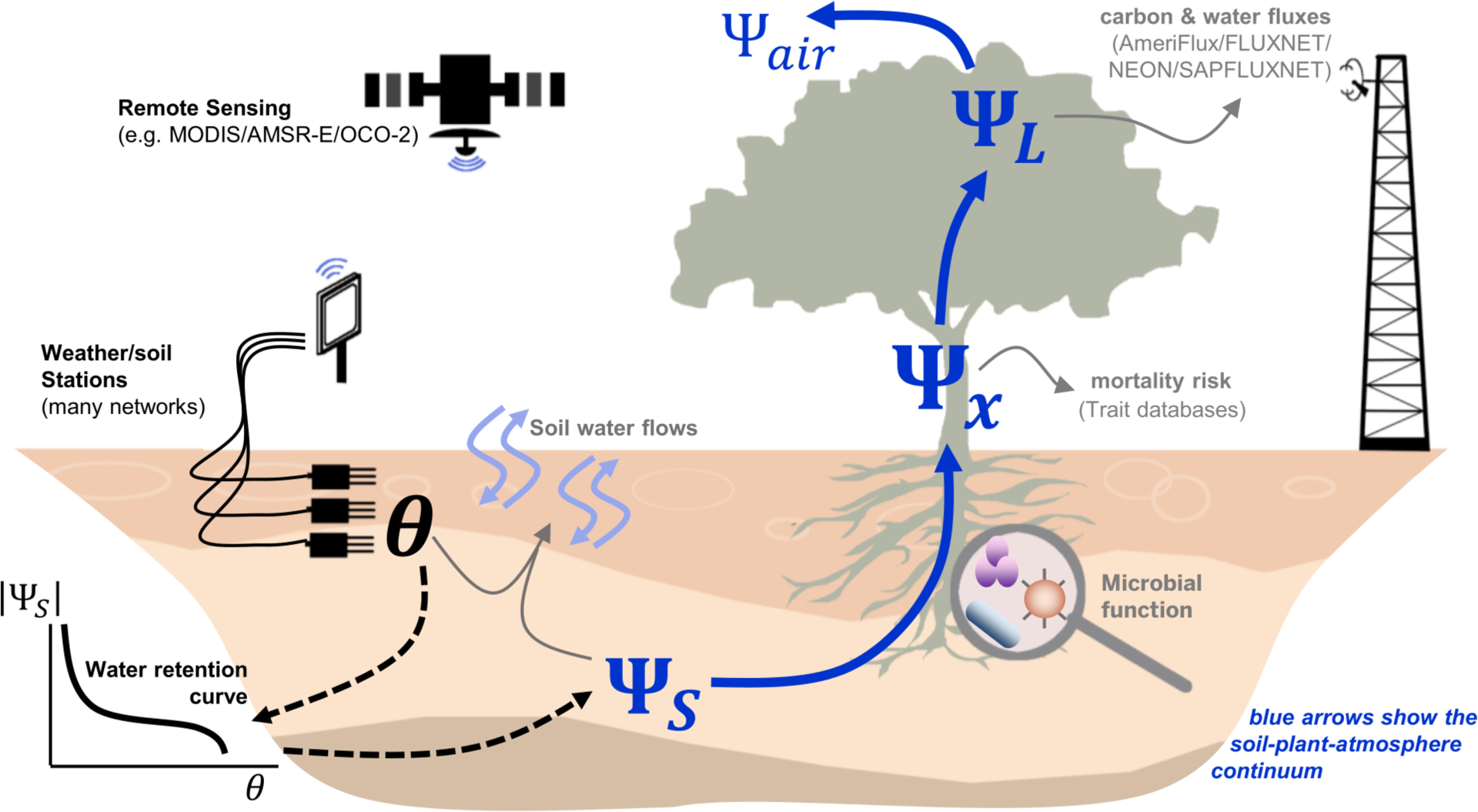
Water flows “downhill” along gradients of water potential in the soils (ΨS, where water potential is relatively high, often >-1 MPa) through the stems (Ψx) to the leaves (ΨL, where potential is relatively low) and eventually to the air (Ψair, where it can be as low as −100 MPa). Water potential also directly controls key biological processes, including microbial function, mortality risk arising from damaged plant xylem, and plant-atmosphere gas exchange. While observations of environmental drivers, soil moisture content (θ) and carbon and water fluxes are broadly accessible from environmental networks and remote sensing, Ψ timeseries are more discrete, sparse, and generally not coordinated or discoverable.
Beyond redistributing water through ecosystems, Ψ is also a direct control of many biophysical processes. Soil water potential (ΨS) regulates flow of water into and out of soil microbe cells and determines their metabolism3. In plants, leaf water potential (ΨL) is a key driver of stomatal conductance and photosynthetic carbon uptake4,5, and its close connection to branch and stem water potential (ΨX) controls the risk of drought-driven xylem embolism and mortality6,7. Consequently, most ecosystem services, including water storage, food and fiber supply, and water and climate regulation, are fundamentally linked to Ψ.
While undeniably important for soil and plant function, for reasons discussed in more detail below, ΨS is rarely measured in-situ8,9, and observations of plant Ψ have historically been limited to destructive and disjunct manual measurements. The objective of this paper is to demonstrate key uncertainties linked to the dearth of soil and plant Ψ data, and to discuss the theoretical and modeling progress that could be enabled with richer and more discoverable information about Ψ. We begin by discussing issues surrounding the measurement, modeling, and synthesis of soil water potential, and then address additional considerations linked to the measurement and prediction of water potential in plants. We then present a road map for creating accessible and open Ψ databases and discuss promising new approaches for detecting Ψ using remote sensing.
Concepts and uncertainties linked to soil water potential
Water flows “downhill” energetically, moving from areas of higher-to-lower potential, such that ΨS gradients are the driving force of subsurface water flows1. In most unsaturated soils, ΨS is dominated by the matric potential, which becomes more negative when soils dry, and the effective radii of water-filled pore spaces in the soil become smaller. This process produces the general shape of the water retention curve (also known as the ‘moisture characteristic’ or ‘water release’ curve), which relates ΨS to volumetric soil moisture content (θ). Critically, variation in soil physical properties can cause ΨS to differ by an order of magnitude across soil types, even if soil moisture content is the same10,11 (Figure 2a).
Figure 2: Water retention curve and pedotransfer function (PTF) uncertainty.
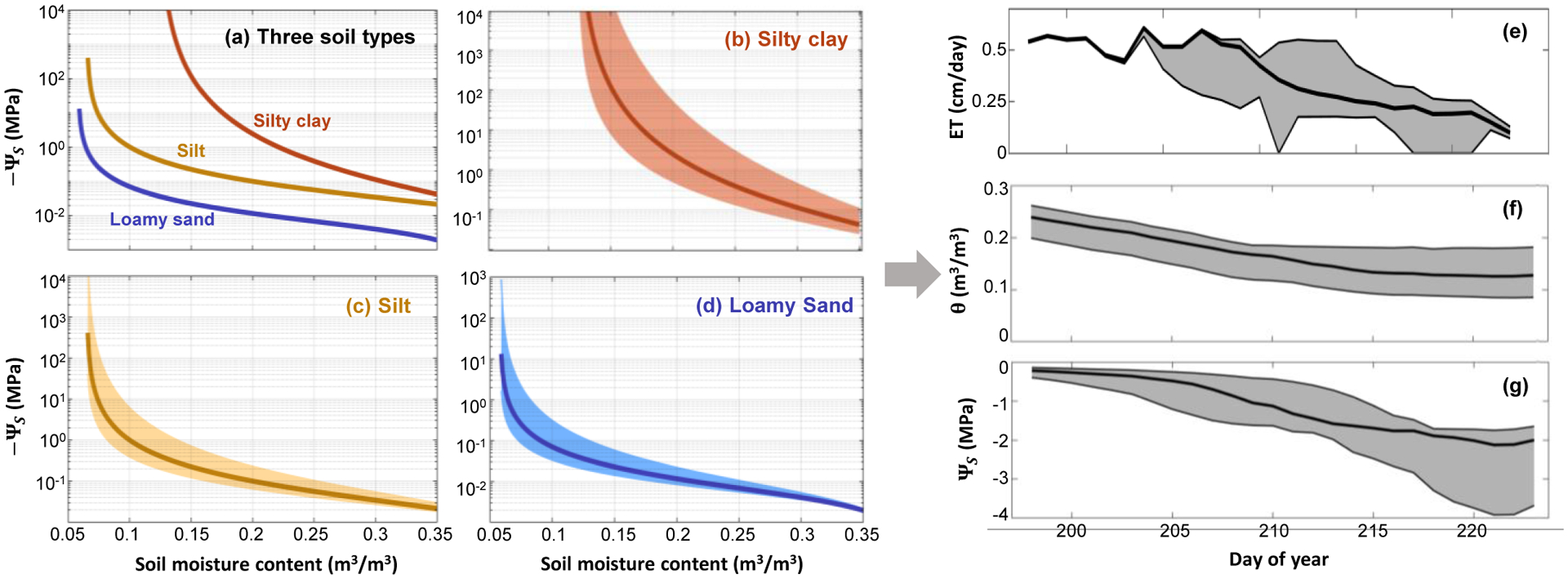
Across soil types, ΨS can differ by an order of magnitude for a given soil moisture content (panel a, with curves generated from the van Genutchen model11,, see methods). Panels b-d illustrate the uncertainty in the water retention curve attributable to PTF parameter uncertainty. The shaded area shows the 90% confidence interval due solely to variation in a single parameter of the van Genuchten model (the ‘n’ shape parameter, which is linked to pore size) within just one standard deviation of its reported distribution for each soil class from a popular PTF18. Thick lines in panels b-d are the same as in panel a. The PTF-driven uncertainty in the water retention curve propagates into large uncertainty for modeled fluxes and pools. Specifically, variation in the van Genuchten ‘n’ parameter within again just one standard deviation of its reported range18 causes the 90% confidence intervals on modeled evapotranspiration (ET), soil moisture content (θ, and ΨS (shaded gray areas, panels e-f) to vary by a magnitude comparable to the mean value of each parameter (thick black line). Simulations were run using the HYDRUS 1-D79 model for a forest site in Indiana, US80 during a drought event (see methods for details).
Field observations of θ are common12, but with a few exceptions9,13, ΨS is rarely measured systematically in field research settings8,9. The reasons why θ became the predominant metric for describing soil water status are not entirely clear8, but may reflect the fact that no single instrument captures the entire range of ΨS (from saturation to the very dry end), and sensors for measuring ΨS in the field have historically been associated with unique limitations and uncertainty8,14.
Even if ΨS data were plentiful, strategies for relating θ to ΨS would still be necessary in models to connect water balance equations with potential-driven flows. Most hydrologic and land surface models thus rely on water retention curve models15, with those proposed by Campbell (1974)10 or van Genuchten (1980)11 ranking high in popularity. Pedotransfer functions (PTFs) predict the parameters of water retention curve models using empirical equations driven by a limited set of soil characteristics (typically %sand, %clay, and bulk density16–18).
While developing PTFs is an active field15, PTF parameter distributions are poorly constrained and prevent confident transformation of θ to ΨS. For example, even relatively small variations in a single parameter of the van Genuchten model cause ΨS to vary by an order of magnitude over a wide range of θ (Figure 2b–2d). Soil structure, which differs from soil texture and is governed by biophysical properties, may be a key omission in PTFs19 explaining some of this uncertainty. For example, growth of roots and mycorrhizae into soil pores, and deposition of root exudates, increase overall water retention20,21, and macropores can create preferred flow pathways that are challenging to incorporate into PTFs. Moreover, depth into the soil may also affect hydraulic properties by controlling connectivity with root systems and through slowly-evolving changes in soil morphology. Finally, most PTFs assume that the water retention curve is static; but many relevant processes occurring in natural landscapes (including drying-rewetting cycles, fire, and management shifts) may cause time-dependent hysteresis of the water retention curve22–24.
This uncertainly linked to PTFs propagates through water cycle models in highly consequential ways.25–26 Prior work performed in the Shale Hills Critical Zone Observatory confirms that van Genuchten model parameters are the dominant source of model uncertainty in a coupled 3-D land-surface and hydrological model27, and that water retention curve parameters must be measured locally and optimized through data assimilation28 for watershed hydrologic variables to be predicted with any degree of certainty29. Here, using a popular 1-D water balance model, we further demonstrate that uncertainty in a single PTF parameter drives large uncertainty in modeled predictions of evapotranspiration, soil moisture, and ΨS (Figure 2e).
The parameters of the water retention curve are also key sources of uncertainty explaining variability in carbon cycle fluxes from global-scale land surface models. Here, we used a global sensitivity experiment30 to explore the variability of these parameters along with other key parameters of the ORCHIDEE land surface model31,32 (see methods for details). The parameters of the water retention curve explained between 10–32% of the modelled GPP variance across three diverse sites (Figure 3). Moreover, when considering the wider set of soil hydrology parameters (including the hydraulic conductivity, field capacity, and permanent wilting point of the soil), the percentage of explained GPP variance increased to 22–53% across sites.
Figure 3. Water retention curve parameters are a key source of land surface model uncertainty.
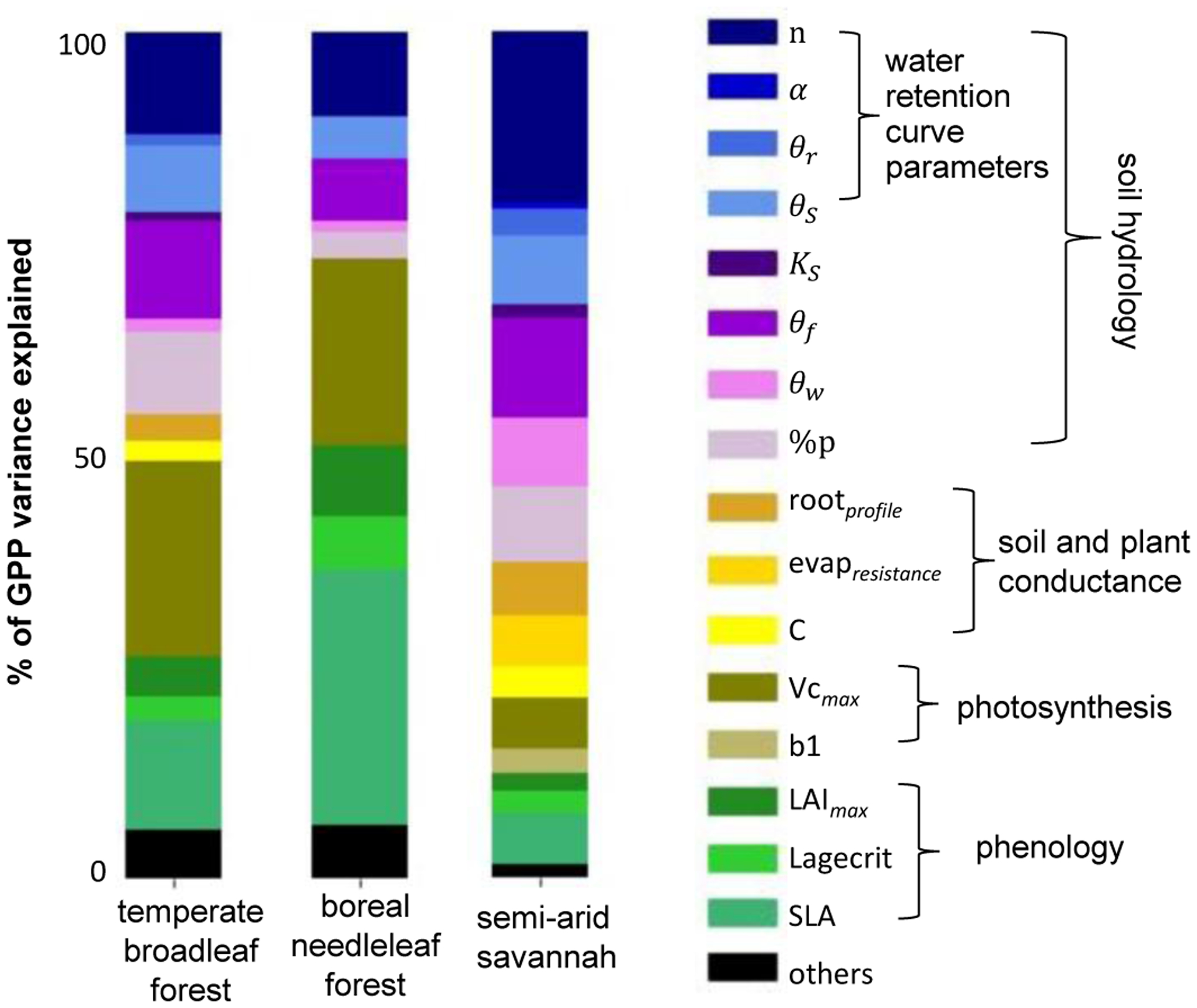
A sensitivity analysis of key model parameters of the ORCHIDEE land surface model31,32 was performed to demonstrate the relative importance of each parameter in simulating daily GPP at three contrasting FLUXNET sites: a) a temperate broadleaf forest (Harvard Forest, FLUXNET code US-Ha182); b) a boreal needleleaf forest (Sodankyla, FI-Sod,83); and c) a semi-arid savanna (Demokeya, SD-Dem84). The Sobol method30 was used to perform the sensitivity analysis; this method is based on variance decomposition and is able to capture interactions between parameters. More details can be found in the methods.
The dearth of information about ΨS is not only a problem for models, but also confounds observation-driven work. Because θ is widely measured, and ΨS is not, it is extremely common to see key response variables like carbon and water fluxes explained as a function of measured θ33–35. These relationships are usually non-linear and threshold driven36–37. This is not surprising, as these responses embed site-to-site variability in the water retention curve, which itself is nonlinear and threshold-driven (Fig. 2a–d). The shape of these response functions thus depends very much on whether ΨS or θ is chosen as the driving variable38. Indeed, the relationship between gross primary productivity (GPP) and soil water status is more linear and less spatially heterogeneous when ΨS, as opposed to θ, appears on the x-axis (Figure 4). Likewise, substantial skill in predicting soil respiration can be gained when model functions are driven explicitly by ΨS3. Thus, more abundant and aggregated site-level ΨS information could reduce conceptual uncertainty about how ecosystem fluxes respond to soil water deficits, and permit other sources of spatio-temporal variability to be more discernable.
Figure 4: Soil water potential better explains variability in GPP when compared to soil moisture content.
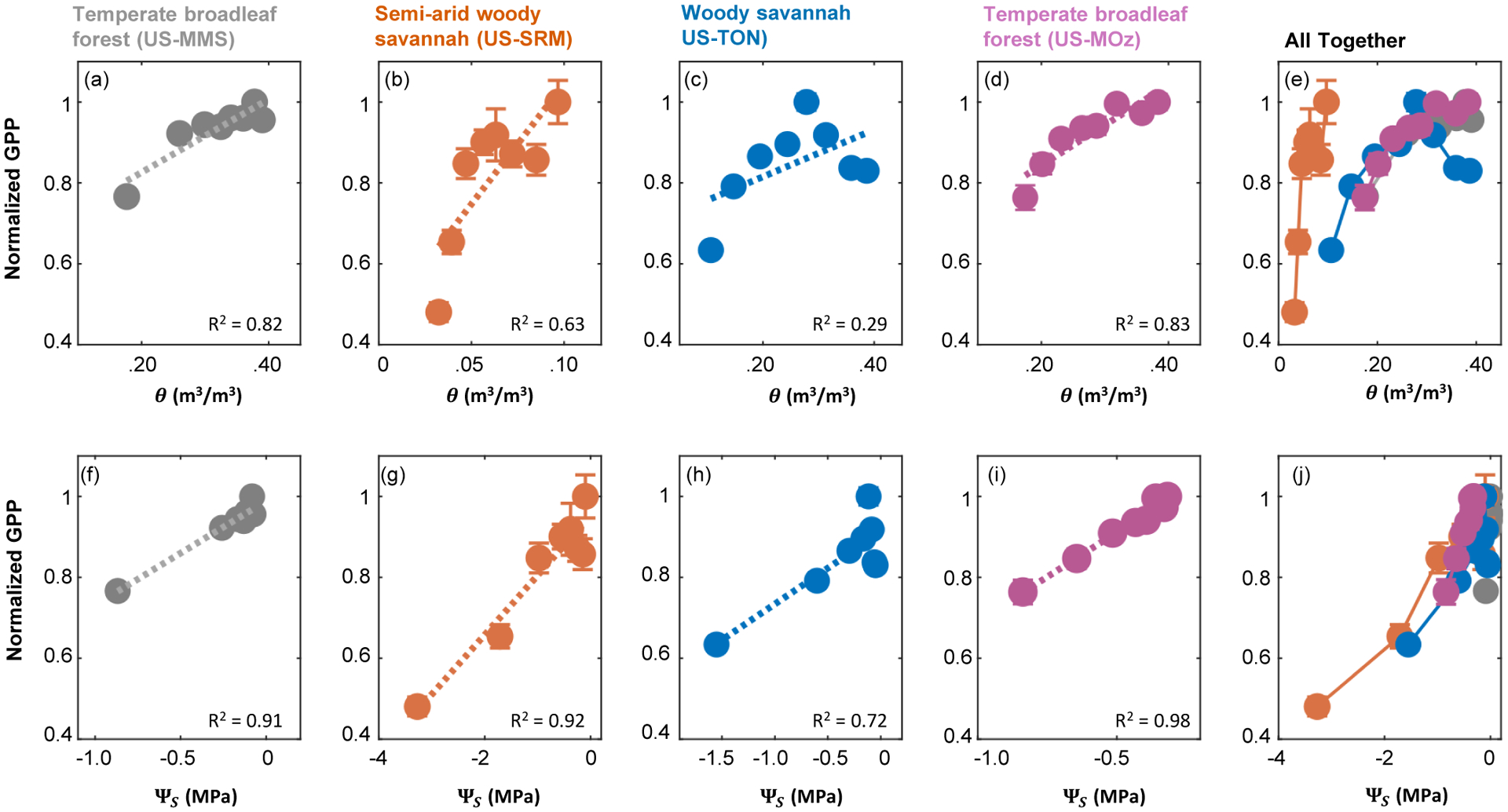
Across four AmeriFlux sites for which site-specific water retention curves were measured38,85–87, the relationship between GPP (normalized by its well-watered rate) and ΨS (bottom row) is more linear than the relationship between GPP and θ (top row). Moreover, cross-site heterogeneity in the response functions is reduced when it is ΨS, as opposed to θ, on the x-axis (compare panel e to panel j). GPP estimates were obtained from AmeriFlux, with site codes given in parentheses. Error bars indicate one standard error of the mean, which is quite small for some of the binned averages. See methods for more details.
Plant water potential: Key concepts and controversies
The effective radii of evaporating water surfaces within plant cell walls are extremely small, resulting in tension forces strong enough to pull water upwards from soils, where it is already tightly bound, to the leaves. Thus, the difference between ΨL and ΨS is the driving force for transpiration, which is closely coupled with photosynthetic carbon uptake. Moreover, branch and stem water potential (ΨX), which are coupled with ΨL, interact with anatomical features of the plant’s water transport system to determine the risk of xylem embolism that can lead to mortality6,7,39–41. Stomatal regulation of gas exchange is also critical for buffering plants from the very low water potential of the atmosphere (see Figure 1), which is extremely sensitive to relative humidity.
Historically, observations of plant Ψ have been limited to manually collected “snapshots” (e.g. with a pressure chamber43). These data have proven indispensable for shaping our theoretical understanding of how plants respond to soil water stress6,7,40,44. However, because pressure chamber measurements are destructive and labor intensive, they are typically limited to weekly or seasonal temporal resolutions. While the weekly timescale is well matched to soil drying, it is too coarse to capture faster-acting hydrodynamic processes, including stomatal response to vapor pressure deficit (VPD45) and the depletion and refilling of plant water pools over the course of a day46. Moreover, with some exceptions47, ΨL and ΨX are not often monitored over long time periods (e.g. years to decades), and centralized databases and networks for time series of Ψ do not yet exist.
The discrete and undiscoverable nature of plant Ψ observations limit our ability to characterize the distributions of the minimum plant water potentials that are so critical for determining plant mortality risk41. The gap also limits understanding of how plant and soil water potential are coordinated and coupled. For example, a fundamental assumption in plant eco-physiology is that ΨL and ΨX are equilibrated with ΨS across the root zone in pre-dawn hours48. This assumption has allowed eco-physiologists to circumvent the ΨS data scarcity problem by relying on pre-dawn ΨL observations as a proxy for root-zone ΨS – an approach that treats the plants as an instrument for recording the soil water environment. Yet experiments have shown that nighttime transpiration – while small – can still occur49,50, lowering pre-dawn ΨL and decoupling it from ΨS51. Synthetic assessments of pre-dawn equilibrium are hindered by the absence of nocturnal ΨL observations collected together with data on ΨS and/or stem water flows (e.g. from sap flux), or at least often enough to determine if stationarity in pre-dawn ΨL, which should be a hallmark of equilibrium, has been achieved.
Likewise, the water potential information gap limits understanding of how soil and plant water potential are coupled at mid-day. The relationship between mid-day ΨL and the root-zone ΨS is frequently used to classify plant water use strategies44,52,53. For example, plants with conservative water use strategies (“isohydric” species) close stomata quickly as ΨS declines, whereas “anisohydric” plants keep stomata open longer, sustaining gas exchange but with more rapid declines in ΨL that may increase the risk of xylem embolism. The (an)isohydry framework is popular but controversial, with several studies highlighting critical interactions with other environmental drivers beyond ΨS54–56, including VPD57. Moreover, coordinated observations of sapflow, enhanced with data on soil and stem water potentials, hold great promise for understanding how the dynamics of hydraulic conductance of different plant organs influence whole-plant hydraulic physiology58. Plant hydraulics schemes relying on concepts like isohydry are rapidly being incorporated in hydrologic and Earth system models59–61. Benchmarking and testing these schemes would benefit from open and spatially representative databases of plant and soil Ψ timeseries, measured together at a temporal frequency (e.g. hourly) over which key drivers like VPD vary.
Coordinated observation of plant and soil Ψ could also offer new perspectives on the critical role of root hydraulic function. Pre-dawn observations of ΨL and ΨS from multiple depths could reveal interspecific patterns in functional rooting depth – a trait that is difficult to measure by other means and partially responsible for model difficulty in capturing plant drought responses62. When complemented with data on Ψx and/or root sap flow, profile observations of ΨS would also illuminate the important but poorly understood consequences of hydraulic redistribution of water from wetter to drier soil layers through plant roots63–64. While root Ψx is difficult to measure with pressure chambers, it could be monitored more easily with psychrometers or other techniques for continuous observation of plant Ψx. Data on root Ψx, especially when paired with laboratory-derived root xylem vulnerability curves, would also be useful for understanding the dynamics of root hydraulic conductance, noting that roots may be among the most vulnerable components of the plant hydraulic system65–66. Finally, differences in ΨS and root Ψx could also improve our understanding of gradients in Ψ occurring at the root-soil interface67.
Strategies to address the water potential information gap
Recent advances in measurement technology have substantially improved the ease and reliability of ΨS observations. In the lab, sensor improvement has reduced the time necessary to generate the “wet end” of the water retention curve68. A second instrument, typically a dew-point potentiometer, is required to capture the dry end of the curve, but this step proceeds relatively quickly. While the instrumentation and expertise necessary to characterize water retention curves may be siloed within soil science disciplines, this barrier could be easily overcome through cooperative arrangements and/or knowledge transfer. At the same time, technology is improving for more confident observation of ΨS in-situ8. Tensiometers, which are accurate when soil is relatively wet (e.g. ΨS > −0.1 MPa), are widely used in agricultural settings for the purposes of irrigation scheduling. In the drier range, soil matric potential can be measured using psychrometry or from dielectric measurements, with several commercial sensors available at a relatively low cost (e.g. the Teros 21 product, Meter Group). While the accuracy of sensors like these is greatest when ΨS is above −2 MPa, this is still lower than the wilting point of many plant species8.
With respect to plants, psychrometers permitting continuous and long-term observation of both ΨL and ΨX are becoming more widely and commercially available (e.g. the PSY1 products, ICT International), drawing from a long history of psychrometric approaches for measuring plant water potential69. Stem psychrometers can now be deployed on branches and boles of some species for weeks to months at a time55, and evidence is mounting that high-frequency ΨL and Ψx data can indeed improve our understanding of plant water use strategies and dynamics55,70. Psychrometers are still relatively expensive, best suited for broadleaf and non-resinous species, and sensitive to biases linked to temperature fluctuations and wounding effects. Thus, for now, psychrometer data is best viewed as complimentary to pressure chamber measurements. Nonetheless, for many plants, these instruments allow for the collection of ΨL and/or Ψx data at the hourly timescales necessary to be harmonized with observed carbon and water fluxes (e.g. from sap flux and flux towers) and to more rigorously test model frameworks.
Ultimately, addressing environmental questions at policy- and management-relevant scales requires the collection and standardization of observations across many sites. This need has motivated the recent development of many environmental observation networks, including highly-centralized initiatives like NSF’s National Ecological Observatory Network (NEON71), as well as more bottom-up networks like AmeriFlux72 and FLUXNET73 and the new international SAPFLUXNET network74. Other approaches include “network-of-networks” cyberinfrastructure like the International Soil Moisture Network,13 which aggregates soil moisture observations from dozens of individual networks.
Both bottom-up and top-down approaches could be useful for building new Ψ networks. On the one hand, centralized and standardized deployment of new Ψ sensors, ideally in locations that are already nodes of other networks, would have the advantage of uniformity in instrumentation and data quality control that facilitates cross-site synthesis. On the other, a community-driven effort to aggregate and redistribute both existing and new Ψ data could follow the highly successful ‘coalition’ model employed by networks like AmeriFlux72, increasing the discoverability of data while allowing room for innovation at the site level. Even a concerted effort to generate and/or collect laboratory-based water retention curves from existing network sites could substantially constrain how much of the non-linearity in the response of fluxes to observed soil water content can be explained by soil physics (e.g. see Fig. 4). The success of a water potential network would be maximized with: a) a focus on collecting data from sites that also support continuous plant- and/or stand-scale carbon and water fluxes, b) cyberinfrastructure to support the discoverability and distribution of these databases; c) a focus in at least some locations on within-site spatial heterogeneity in Ψ dynamics, to better understand of how many observation points (and at what depths) are necessary to substantially improve model skill; and d) training programs, such as summer short-courses or distributed graduate seminars, to transfer knowledge about how to interpret network observations and to share best practices for sensor deployment.
Even with well-developed observation networks, it is not possible to measure key physiological variables like Ψ everywhere and all the time. Thus, strategies for linking these variables to proxies observable from space are required for regional- and continental-scale work, with microwave remote sensing representing a particularly promising approach. Microwave observations can be used to determine vegetation optical depth (VOD), which is sensitive to plant water content75 and should be monotonically related to ΨL76,77. Comparison of observed ΨL with either spaceborne78 or tower-based70 radiometry confirms that VOD and ΨL follow similar dynamics, especially after accounting for the effect of changing biomass and leaf area. However, the exact relationship between VOD and ΨL is influenced by vegetation type76, and further study of this relationship is currently hindered by the sparsity of ΨL data.
Importantly, microwave remote sensing observations can be made at night, which raises the question: can nocturnal microwave remote sensing of ΨL be used to infer dynamics of root-zone ΨS? Answering this question requires a critical understanding of when and where pre-dawn ΨL is equilibrated with root-zone ΨS. This knowledge gap can be addressed with network observations of ΨL from psychrometry, or observations of plant and soil water potential collected in the same site, which could then guide the design and interpretation of both tower- and satellite-mounted microwave remote sensing systems. The approach will also require further refinement of retrieval algorithms for separating the contribution of plant and soil water content, for example by leveraging emerging approaches for the remote sensing of vegetation structure77.
In conclusion, we have highlighted how more numerous, discoverable, and continuous observations of soil and plant Ψ can improve not only our conceptual understanding of biophysical processes throughout the soil-plant-atmosphere continuum, but also serve as a much-needed new tool for benchmarking and calibrating hydrologic and land-surface models and remote sensing products. While in-situ and site-specific observations of ΨS, ΨL, and Ψx may not yet be “easy,” recent advancements in sensor technology have certainly made them easier than in decades past. The time is right for a new focus on the collection of these data in the field, and the development of new networks to aggregate observations across sites complemented by new approaches for integrating these observations into Earth system models.
Methods
Water retention curve uncertainty:
The water retention curves in Figure 2 were created using the van Genuchten water retention curve model11 relating ΨS to θ. As described in more detail in the Supplementary Information, most parameters of the model were held constant within each soil type, specified as the mean values reported in the updated ROSETTA pedotransfer function18 (see Supplementary Table S1). The ‘n’ parameter was allowed to vary by randomly selecting a value from a uniform distribution bounded by ±1 standard deviation as reported for the ROSETTA PTF18. Overall, this was a conservative approach; drawing the values of n from the full distribution reported for each soil type expands the range of predicted ΨS by orders of magnitude.
The HYDRUS 1-D simulations:
Uncertainty in the water retention curve linked to pedo-transfer uncertainty (e.g. as Figure 2a–d) was propagated through predictions of ΨS and θ (at depths of 15 cm) and surface evapotranspiration (ET, cm day) using the HYDRUS 1D soil water dynamics model79. Fifty simulations were performed for the Bradford Woods deciduous forest site in south-central Indiana, where the HYDRUS 1D model had been previously calibrated80. In general, model settings were left unchanged, with a few exceptions as discussed in more detail in the Supplementary Information. The soil at Bradford Woods is characterized by a 40 cm depth AP horizon dominated by sandy loam, and a BW Horizon dominated by silt loam from a depth of 40 cm to 208 cm. The very bottom of the soil layer (depths 208 – 230 cm) was prescribed to be clay loam. The parameters of the van Genuchten model used in the HYDRUS simulations are shown in Supplementary Table S2, where again most were held constant, but n varied for the sandy and silt loam layers by drawing it from within one standard deviation of its distribution reported in the updated ROSETTA PTF18. The shaded areas in Figure 2e–f thus illustrate the resulting variation in ET, ΨS, and θ due solely to variability in n.
The ORCHIDEE GPP sensitivity analysis:
The ORCHIDEE land surface model (CMIP6 version)31,32, which is the terrestrial part of the IPSL (Institute Pierre-Simon Laplace) Earth system model, was used to explore the sensitivity of modeled GPP to uncertainty in a wide range of parameters. ORCHIDEE relies on the van Genuchten model to calculate ΨS, as well as the hydraulic conductivity and diffusivity required to solve the Richard’s diffusion equation. ORCHIDEE discretizes the first 2 m of the soil column over 11 layers. For this experiment, we ran ORCHIDEE over three single mesh locations using local half-hourly forcing data to drive the model at each site (see Table Supplementary Table S3), and considered modelled GPP at a daily time-step. The sensitivity analysis results shown in Figure 3 were generated using Sobol’s method30, using the SALib python package81 to sample the parameter space and execute the SA algorithms. Briefly, the model was run using different parameter ensembles, with parameters varied within their reported ranges of uncertainty. Then, each modeled GPP timeseries was compared to GPP derived from flux tower observations. The variance of simulated GPP was then decomposed into fractions which can be attributed to each parameter tested. These results shown in Figure 3 capture both independent and interactive contributions of each parameter to the total variance. When interactions are removed, the independent contribution of water retention curve parameters is still significant, and actually increases for the semi-arid site (see details in Supplementary Section 3).
The AmeriFlux GPP analysis:
Half-hourly or hourly data from the four flux towers referenced in Figure 4 were acquired from the AmeriFlux network (ameriflux.lbl.gov) and subjected to a standardized quality control, gapfilling, and partitioning approaches. The sites and quality control procedures are described in more detail in Supplementary Table S5. The methods used to determine the relationship between GPP and soil moisture are similar to those previously used to explore the relationship between surface conductance and soil moisture35. Briefly, analysis was constrained to the peak of the growing season to limit bias linked to phenological variation in LAI. Estimates of ΨS for each site were determined from site-specific water retention curves38,82–84. The data were then sorted into nine bins representing the 15th, 30th, 45th, 60th, 70th, 80th, 90th, and 100th quantiles of the observed values of soil moisture content in each site. Within each bin, data were constrained to relatively high light (net radiation > 300 W/m2) conditions with VPD limited to 1 ≤ VPD ≤ 1.5 Pa in US-MMS, US-TON, and US-MOz, and 1.5 ≤ VPD ≤ 2 kPa in the more arid US-SRM site. The mean GPP, ΨS, and θ were then calculated for each bin using the filtered data, and normalized by the maximum bin-averaged value observed at each site.
Supplementary Material
Acknowledgments
KAN acknowledges support from NSF (DEB, Grant 1552747) and the AmeriFlux Management Project via the US Department of Energy, Office of Science Lawrence Berkeley National Laboratory. AGK was supported by NASA Terrestrial Ecology (award 80NSSC18K0715). JDW acknowledges support from the U.S. Department of Energy, Office of Science, through Oak Ridge National Laboratory’s Terrestrial Ecosystem Science Focus Area. KJD and YS were supported by National Science Foundation Grant EAR - 1331726 (S. Brantley) for the Susquehanna Shale Hills Critical Zone Observatory.
Footnotes
Competing interests: The authors declare no competing interests.
Code availability Statement: The HYDRUS-1D program used to create the results of Figure 2e–g is available for public download from https://www.pc-progress.com/en/Default.aspx?hydrus-1d. A reference version of the ORCHIDEE land-surface model, used for Figure 3, is available at https://orchidee.ipsl.fr/. Details on the parameterizations of these models are presented in the Supplementary Information.
Data availability statement:
The FLUXNET tower data appearing in Fig. 3 are from the FLUXNET 2015 dataset (DOIs 10.18140/FLX/1440186 for SD-Dem, 10.18140/FLX/1440071 for US-HA1, and 10.18140/FLX/1440160 FI-SOD. The AmeriFlux tower data appearing in Fig. 4 are available from the AmeriFlux network with the following DOIs: 10.17190/AMF/1246080 for US-MMS, 10.17190/AMF/1246081 for US-MOz, 10.17190/AMF/1246104 for US-SRM, and DOI: 10.17190/AMF/1245971 for US-TON.
References
- 1.Brutsaert W Hydrology: An Introduction. Cambridge University Press; (2005). [Google Scholar]
- 2.Philip J Plant water relations: some physical aspects. Annual Review of Plant Physiology 17, 245–268 (1966). [Google Scholar]
- 3.Ghezzehei TA, Sulman B, Arnold CL, Bogie NA & Berhe AA On the role of soil water retention characteristic on aerobic microbial respiration. Biogeosciences 16, 1187–1209 (2019). [Google Scholar]
- 4.Boyer J Differing sensitivity of photosynthesis to low leaf water potentials in corn and soybean. Plant Physiology 46, 236–239 (1970). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jarvis P The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philosophical Transactions of the Royal Society of London. B, Biological Sciences 273, 593–610 (1976). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Choat B et al. Global convergence in the vulnerability of forests to drought. Nature 491, 752–755 (2012). [DOI] [PubMed] [Google Scholar]
- 7.Tyree MT & Sperry JS Vulnerability of xylem to cavitation and embolism. Annual Review of Plant Biology 40, 19–36 (1989). [Google Scholar]
- 8.Whalley W, Ober E & Jenkins MJJ Measurement of the matric potential of soil water in the rhizosphere. Journal of Experimental Biology 64, 3951–3963 (2013). [DOI] [PubMed] [Google Scholar]
- 9.Yu H, Yang P & Lin H Spatiotemporal patterns of soil matric potential in the Shale Hills Critical Zone Observatory. Vadose Zone Journal 14, 1–18 (2015). [Google Scholar]
- 10.Campbell GS A simple method for determining unsaturated conductivity from moisture retention data. Soil Science 117, 311–314 (1974). [Google Scholar]
- 11.van Genuchten MT A closed‐form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal 44, 892–898 (1980). [Google Scholar]
- 12.Dorigo W et al. The International Soil Moisture Network: a data hosting facility for global in situ soil moisture measurements. Hydrology and Earth System Sciences 15, 1675–1698. [Google Scholar]
- 13.Scott BL et al. New soil property database improves Oklahoma Mesonet soil moisture estimates. Journal of Atmospheric and Oceanic Technology 30, 2585–2595 (2013). [Google Scholar]
- 14.Campbell GS Soil water potential measurement: An overview. Irrigation Science 9, 265–273 (1988). [Google Scholar]
- 15.Van Looy K et al. Pedotransfer functions in Earth system science: challenges and perspectives. Reviews of Geophysics 55, 1199–1256 (2017). [Google Scholar]
- 16.Clapp RB & Hornberger GM Empirical equations for some soil hydraulic properties. Water Resources Research 14, 601–604 (1978). [Google Scholar]
- 17.Cosby B, Hornberger G, Clapp R & Ginn T A statistical exploration of the relationships of soil moisture characteristics to the physical properties of soils. Water Resources Research 20, 682–690 (1984). [Google Scholar]
- 18.Zhang Y & Schaap MG Weighted recalibration of the Rosetta pedotransfer model with improved estimates of hydraulic parameter distributions and summary statistics (Rosetta3). Journal of Hydrology 547, 39–53 (2017). [Google Scholar]
- 19.Fatichi S et al. Soil structure is an important omission in Earth System Models. Nature Communications 11, 1–11 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ghezzehei TA & Albalasmeh AA Spatial distribution of rhizodeposits provides built-in water potential gradient in the rhizosphere. Ecological Modelling 298, 53–63 (2015). [Google Scholar]
- 21.Leung AK, Garg A & Ng CWW Effects of plant roots on soil-water retention and induced suction in vegetated soil. Engineering Geology 193, 183–197 (2015). [Google Scholar]
- 22.Caplan JS et al. Decadal-scale shifts in soil hydraulic properties as induced by altered precipitation. Science Advances 5, eaau6635 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Peña-Sancho C, López M, Gracia R & Moret-Fernández D Effects of tillage on the soil water retention curve during a fallow period of a semiarid dryland. Soil Research 55, 114–123 (2017). [Google Scholar]
- 24.Stoof CR, Wesseling JG & Ritsema CJ Effects of fire and ash on soil water retention. Geoderma 159, 276–285 (2010). [Google Scholar]
- 25.Gutmann E & Small E The effect of soil hydraulic properties vs. soil texture in land surface models. Geophysical Research Letters 32 (2005). [Google Scholar]
- 26.Weihermüller L, Lehmann P, Herbst M, Rahmati M, Verhoef A, Or D, Jacques D & Vereecken H Choice of pedotransfer functions matters when simulating soil water balance fluxes. Journal of Advances in Modeling Earth Systems 13, p.e2020MS002404. (2021). [Google Scholar]
- 27.Shi Y, Davis KJ, Zhang F & Duffy CJ Evaluation of the parameter sensitivities of a coupled land surface hydrologic model at a critical zone observatory. Journal of Hydrometeorology 15, 279–299 (2014). [Google Scholar]
- 28.Shi Y, Davis KJ, Zhang F, Duffy CJ & Yu XJ Parameter estimation of a physically-based land surface hydrologic model using an ensemble Kalman filter: A multivariate real-data experiment. Advances in Water Resources 83, 421–427 (2015). [Google Scholar]
- 29.Shi Y et al. Simulating high‐resolution soil moisture patterns in the Shale Hills watershed using a land surface hydrologic model. Hydrological Processes 29, 4624–4637 (2015). [Google Scholar]
- 30.Sobol IM Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Mathematics and Computers in Simulation 55, 271–280 (2001). [Google Scholar]
- 31.Boucher O et al. Presentation and evaluation of the IPSL‐CM6A‐LR climate model. Journal of Advances in Modeling Earth Systems 12, e2019MS002010 (2020). [Google Scholar]
- 32.Lurton T et al. Implementation of the CMIP6 Forcing Data in the IPSL‐CM6A‐LR Model. Journal of Advances in Modeling Earth Systems 12, e2019MS001940 (2020). [Google Scholar]
- 33.Green JK et al. Large influence of soil moisture on long-term terrestrial carbon uptake. Nature 565, 476–479 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jung M et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 467, 951–954 (2010). [DOI] [PubMed] [Google Scholar]
- 35.Novick KA et al. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nature Climate Change 6, 1023–1027 (2016). [Google Scholar]
- 36.Feldman AF, Short Gianotti DJ, Trigo IF, Salvucci GD & Entekhabi D Satellite‐based assessment of land surface energy partitioning–soil moisture relationships and effects of confounding variables. Water Resources Research 55, 10657–10677 (2019). [Google Scholar]
- 37.Stocker BD et al. Quantifying soil moisture impacts on light use efficiency across biomes. New Phytologist 218, 1430–1449 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Baldocchi DD, Xu L & Kiang N How plant functional-type, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak–grass savanna and an annual grassland. Agricultural and Forest Meteorology 123, 13–39 (2004). [Google Scholar]
- 39.Trugman AT, Anderegg LD, Shaw JD & Anderegg WR Trait velocities reveal that mortality has driven widespread coordinated shifts in forest hydraulic trait composition. Proceedings of the National Academy of Sciences 117, 8532–8538 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.McDowell N et al. Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytologist 178, 719–739 (2008). [DOI] [PubMed] [Google Scholar]
- 41.Martínez-Vilalta J, et al. Towards a statistically robust determination of minimum water potential and hydraulic risk in plants. New Phytologist 232, 404–417. [DOI] [PubMed] [Google Scholar]
- 42.Taiz L, Zeiger E, Møller IM & Murphy A Plant physiology and development (No. Ed. 6). Sinauer Associates Incorporated. (2015). [Google Scholar]
- 43.Scholander PF, Bradstreet ED, Hemmingsen E & Hammel H Sap pressure in vascular plants: negative hydrostatic pressure can be measured in plants. Science 148, 339–346 (1965). [DOI] [PubMed] [Google Scholar]
- 44.Martínez‐Vilalta J, Poyatos R, Aguadé D, Retana J & Mencuccini M A new look at water transport regulation in plants. New Phytologist 204, 105–115 (2014). [DOI] [PubMed] [Google Scholar]
- 45.Grossiord C et al. Plant responses to rising vapor pressure deficit. New Phytologist 226, 1550–1566 (2020). [DOI] [PubMed] [Google Scholar]
- 46.Matheny AM, Bohrer G, Garrity SR, Morin TH, Howard CJ & Vogel CS Observations of stem water storage in trees of opposing hydraulic strategies. Ecosphere 6, 1–13 (2015). [Google Scholar]
- 47.Wood JD, Knapp BO, Muzika R-M, Stambaugh MC & Gu L The importance of drought–pathogen interactions in driving oak mortality events in the Ozark Border Region. Environmental Research Letters 13, 015004 (2018). [Google Scholar]
- 48.Hinckley TM, Lassoie JP & Running SW Temporal and spatial variations in the water status of forest trees. Forest Science 24, a0001–z0001 (1978). [Google Scholar]
- 49.Marks CO & Lechowicz MJ The ecological and functional correlates of nocturnal transpiration. Tree Physiology 27, 577–584 (2007). [DOI] [PubMed] [Google Scholar]
- 50.O’Keefe K & Nippert JB Drivers of nocturnal water flux in a tallgrass prairie. Functional Ecology 32, 1155–1167 (2018). [Google Scholar]
- 51.Donovan L, Linton M & Richards J Predawn plant water potential does not necessarily equilibrate with soil water potential under well-watered conditions. Oecologia 129, 328–335 (2001). [DOI] [PubMed] [Google Scholar]
- 52.Kannenberg SA, et al. Opportunities, challenges and pitfalls in characterizing plant water‐use strategies. Functional Ecology. In press. DOI: 10.1111/1365-2435.13945. [DOI] [Google Scholar]
- 53.Oliveira RS, et al. Linking plant hydraulics and the fast–slow continuum to understand resilience to drought in tropical ecosystems. New Phytologist 230, 904–923. [DOI] [PubMed] [Google Scholar]
- 54.Feng X et al. Beyond isohydricity: the role of environmental variability in determining plant drought responses. Plant, Cell & Environment 42, 1104–1111 (2019). [DOI] [PubMed] [Google Scholar]
- 55.Guo JS, Hultine KR, Koch GW, Kropp H & Ogle K Temporal shifts in iso/anisohydry revealed from daily observations of plant water potential in a dominant desert shrub. New Phytologist 225, 713–726 (2020). [DOI] [PubMed] [Google Scholar]
- 56.Hochberg U, Rockwell FE, Holbrook NM & Cochard H Iso/anisohydry: a plant–environment interaction rather than a simple hydraulic trait. Trends in Plant Science 23, 112–120 (2018). [DOI] [PubMed] [Google Scholar]
- 57.Novick KA, Konings AG & Gentine P Beyond soil water potential: An expanded view on isohydricity including land–atmosphere interactions and phenology. Plant, Cell & Environment 42, 1802–1815 (2019). [DOI] [PubMed] [Google Scholar]
- 58.McCulloh KA et al. A dynamic yet vulnerable pipeline: Integration and coordination of hydraulic traits across whole plants. Plant, Cell & Environment 42, 2789–2807 (2019). [DOI] [PubMed] [Google Scholar]
- 59.Kennedy D et al. Implementing plant hydraulics in the community land model, version 5. Journal of Advances in Modeling Earth Systems 11, 485–513 (2019). [Google Scholar]
- 60.Mirfenderesgi G, Matheny AM & Bohrer G Hydrodynamic trait coordination and cost–benefit trade‐offs throughout the isohydric–anisohydric continuum in trees. Ecohydrology 12, e2041 (2019). [Google Scholar]
- 61.Xu X, Medvigy D, Powers JS, Becknell JM & Guan K Diversity in plant hydraulic traits explains seasonal and inter‐annual variations of vegetation dynamics in seasonally dry tropical forests. New Phytologist 212, 80–95 (2016). [DOI] [PubMed] [Google Scholar]
- 62.De Kauwe MG et al. Do land surface models need to include differential plant species responses to drought? Examining model predictions across a mesic-xeric gradient in Europe. Biogeosciences 12, 7503–7518 (2015). [Google Scholar]
- 63.Meinzer FC, Brooks JR, Bucci SJ, Goldstein G, Scholz FG, & Warren JM Converging patterns of uptake and hydraulic redistribution of soil water in contrasting woody vegetation types. Tree Physiology 24, 919–928 (2004). [DOI] [PubMed] [Google Scholar]
- 64.Scott RL, Cable WL, & Hultine KR The ecohydrologic significance of hydraulic redistribution in a semiarid savanna. Water Resources Research 44, W02440 (2008). [Google Scholar]
- 65.Tyree MT, & Ewers FW The hydraulic architecture of trees and other woody plants. New Phytologist 119, 345–360 (1991). [Google Scholar]
- 66.Johnson DM, Wortemann R, McCulloh KA, Jordan-Meille L, Ward E, Warren JM, Palmroth S & Domec JC A test of the hydraulic vulnerability segmentation hypothesis in angiosperm and conifer tree species. Tree physiology 36, 983–993 (2016). [DOI] [PubMed] [Google Scholar]
- 67.Lehto T & Zwiazek JJ Ectomycorrhizas and water relations of trees: a review. Mycorrhiza 21, 71–90 (2011). [DOI] [PubMed] [Google Scholar]
- 68.Bezerra-Coelho CR, Zhuang L, Barbosa MC, Soto MA & Van Genuchten MT Further tests of the HYPROP evaporation method for estimating the unsaturated soil hydraulic properties. Journal of Hydrology and Hydromechanics 66, 161–169 (2018). [Google Scholar]
- 69.Wullschleger S, Dixon M & Oosterhuis D Field measurement of leaf water potential with a temperature‐corrected in situ thermocouple psychrometer. Plant Cell & Environment 11, 199–203 (1988). [Google Scholar]
- 70.Holtzman NM et al. L-band vegetation optical depth as an indicator of plant water potential in a temperate deciduous forest stand. Biogeosciences 18, 739–753 (2021). [Google Scholar]
- 71.Nagy RC, et al. 2021. Harnessing the NEON data revolution to advance open environmental science with a diverse and data‐capable community. Ecosphere 12, e03833. [Google Scholar]
- 72.Novick KA et al. The AmeriFlux network: A coalition of the willing. Agricultural and Forest Meteorology 249, 444–456 (2018). [Google Scholar]
- 73.Baldocchi D ‘Breathing’of the terrestrial biosphere: lessons learned from a global network of carbon dioxide flux measurement systems. Australian Journal of Botany 56, 1–26 (2008). [Google Scholar]
- 74.Poyatos R et al. Global transpiration data from sap flow measurements: the SAPFLUXNET database. Earth System Science Data Discussions, 1–57 (2020). [Google Scholar]
- 75.Jackson T & Schmugge T Vegetation effects on the microwave emission of soils. Remote Sensing of Environment 36, 203–212 (1991). [Google Scholar]
- 76.Konings AG, Rao K & Steele‐Dunne SC Macro to micro: microwave remote sensing of plant water content for physiology and ecology. New Phytologist 223, 1166–1172 (2019). [DOI] [PubMed] [Google Scholar]
- 77.Konings AG, et al. Detecting Forest Response to Droughts with Global Observations of Vegetation Water Content. Global Change Biology (2021). DOI: 10.1111/gcb.15872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Momen M et al. Interacting effects of leaf water potential and biomass on vegetation optical depth. Journal of Geophysical Research: Biogeosciences 122, 3031–3046 (2017). [Google Scholar]
- 79.Simunek J, Van Genuchten MT & Sejna M The HYDRUS-1D software package for simulating the one-dimensional movement of water, heat, and multiple solutes in variably-saturated media. University of California-Riverside Research Reports 3, 1–240 (2005). [Google Scholar]
- 80.Naylor S, Letsinger S, Ficklin D, Ellett K & Olyphant G A hydropedological approach to quantifying groundwater recharge in various glacial settings of the mid‐continental USA. Hydrological Processes 30, 1594–1608 (2016). [Google Scholar]
- 81.Herman J & Usher W SALib: An open-source Python library for sensitivity analysis. Journal of Open Source Software 2, doi: 10.21105/joss.00097. (2017) [DOI] [Google Scholar]
- 82.Urbanski S et al. Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest. Journal of Geophysical Research: Biogeosciences 112 (2007). [Google Scholar]
- 83.Thum T et al. Parametrization of two photosynthesis models at the canopy scale in a northern boreal Scots pine forest. Tellus B: Chemical and Physical Meteorology 59, 874–890 (2007). [Google Scholar]
- 84.Ardö J, Mölder M, El-Tahir BA & Elkhidir HAM Seasonal variation of carbon fluxes in a sparse savanna in semi arid Sudan. Carbon Balance and Management 3, 1–18 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Roman DT, et al. The role of isohydric and anisohydric species in determining ecosystem-scale response to severe drought. Oecologia 179, 641–654 (2015). [DOI] [PubMed] [Google Scholar]
- 86.Fu C, et al. Combined measurement and modeling of the hydrological impact of hydraulic redistribution using CLM4. 5 at eight AmeriFlux sites. Hydrology and Earth System Sciences 20, 2001–2018 (2016). [Google Scholar]
- 87.Liang J, et al. Evaluating the E3SM land model version 0 (ELMv0) at a temperate forest site using flux and soil water measurements. Geoscientific Model Development 12, 1601–1612. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The FLUXNET tower data appearing in Fig. 3 are from the FLUXNET 2015 dataset (DOIs 10.18140/FLX/1440186 for SD-Dem, 10.18140/FLX/1440071 for US-HA1, and 10.18140/FLX/1440160 FI-SOD. The AmeriFlux tower data appearing in Fig. 4 are available from the AmeriFlux network with the following DOIs: 10.17190/AMF/1246080 for US-MMS, 10.17190/AMF/1246081 for US-MOz, 10.17190/AMF/1246104 for US-SRM, and DOI: 10.17190/AMF/1245971 for US-TON.


