Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Nov 30;14(12):16743–16754. doi: 10.1021/acsnano.0c04570

Cross-Sections of Nanocellulose from Wood Analyzed by Quantized Polydispersity of Elementary Microfibrils

Tomas Rosén †,‡,§, HongRui He †, Ruifu Wang †, Chengbo Zhan †, Shirish Chodankar ∥, Andreas Fall ⊥, Christian Aulin ⊥, Per Tomas Larsson ⊥,§, Tom Lindström †, Benjamin S Hsiao †,*
PMCID: PMC8926302  PMID: 33253525

Abstract

graphic file with name nn0c04570_0007.jpg

Bio-based nanocellulose has been shown to possess impressive mechanical properties and simplicity for chemical modifications. The chemical properties are largely influenced by the surface area and functionality of the nanoscale materials. However, finding the typical cross-sections of nanocellulose, such as cellulose nanofibers (CNFs), has been a long-standing puzzle, where subtle changes in extraction methods seem to yield different shapes and dimensions. Here, we extracted CNFs from wood with two different oxidation methods and variations in degree of oxidation and high-pressure homogenization. The cross-sections of CNFs were characterized by small-angle X-ray scattering and wide-angle X-ray diffraction in dispersed and freeze-dried states, respectively, where the results were analyzed by assuming that the cross-sectional distribution was quantized with an 18-chain elementary microfibril, the building block of the cell wall. We find that the results agree well with a pseudosquare unit having a size of about 2.4 nm regardless of sample, while the aggregate level strongly depends on the extraction conditions. Furthermore, we find that aggregates have a preferred cohesion of phase boundaries parallel to the (110)-plane of the cellulose fibril, leading to a ribbon shape on average.

Keywords: nanocellulose, elementary microfibrils, polydispersity, small-/wide-angle X-ray scattering, biosynthesis

There is an increased demand for renewable and sustainable materials that are biodegradable with a low carbon footprint, having a low environmental impact as well as low human/animal health and safety risks. In this regard, cellulose is the most important source of sustainable materials that can meet this demand. Cellulose is an almost inexhaustible natural polymer with annual production rate that is over 2 orders of magnitude higher than that of synthetic plastics,1 where wood is a key source of cellulosic materials on an industrial scale. The general perception of the high value in woody plants is mainly due to the strong mechanical properties and good structural integrity of wood.

Nanoscale cellulose, or nanocellulose, can be extracted from any higher plants, including both wood and nonwood biomasses. During the past decades, nanocellulose has shown many applications, although some are only at the initial stages. Typically, nanocellulose can be divided into three categories,2,3 including microfibrillar cellulose or cellulose nanofibers (CNFs), nanocrystalline cellulose or cellulose nanocrystals (CNCs), and bacterial nanocellulose (BNC), each with different fibrillar structure and thus applications. CNCs and CNFs are manufactured in a top-down manner from the biomass, while BNC is made from the bottom-up approach.

Typically, CNCs are manufactured through a harsher chemical route (e.g., acid hydrolysis), resulting in relatively greater degradation of cellulose chains and thus shorter fibril length, whereas CNF is produced through a milder route (e.g., oxidation), leading to a higher degree of polymerization in cellulose chains and longer fibril length.4 The average cross-sectional dimensions of CNCs are also larger than those of CNFs. As a result, we chose to focus on the investigation of CNFs in this work because this material may better preserve the nascent state of elementary microfibrils.

CNFs were first demonstrated using comminution equipment, such as high-pressure homogenizers, microfluidizers, and grinding equipment etc.,5,6 but it was soon found that such equipment consumed too much energy for most applications. The impediment of the high energy can be alleviated by the use of varying chemical schemes, such as TEMPO-mediated oxidation (with 2,2,6,6-tetramethylpiperidinyloxyl),7 chemical modification with carboxymethylation,8 or mild acid or enzymatic treatments.2 These treatments introduce charged groups on the cellulose surface, resulting in repulsive forces that greatly facilitate the fiber delamination process and produce nanocellulose materials. Due to the complex interactions between charge repulsion and van der Waals attraction on the surface, nanocellulose materials are notoriously difficult to characterize, especially when the end products consist of a mixture of microfibers (partially defibrillated) and nanofibers, as well as a wide range of length scales from nano- to millimeters. This has constituted an impediment for commercialization of cellulose nanomaterials.

Recently, an extensive review on characterization methods of cellulose nanomaterials has been published.9 In spite of the thorough discussion of varying methods in this review, the use of small-angle X-ray scattering (SAXS) on nanocellulose dispersion was missing, even though the technique is ideally suited to obtain statistical information about the individual nanofiber morphology and dimensions (i.e., the form factor) in dilute suspension (the structure factor = 1). It has been shown that a typical cross-section of CNFs extracted from wood determined by SAXS revealed a ribbon shape with an average thickness between 1 and 3 nm and an average width between 4 and 8 nm, depending on the extraction condition.10−13 These results are generally consistent with the average width determined by transmission electron microscopy (TEM), and the average thickness determined by atomic force microscopy (AFM). However, these results are quite different from our knowledge of the elementary microfibril, i.e., the cellulosic building block of any plant cell.

The structure of the elementary microfibril is determined by the structure of cellulose synthase complexes (CSCs) in the plasma membrane of the plant cell wall. Although the CSC structure can vary among algae,14 it is well-known within the biological community that the elementary microfibrils in higher land plants (e.g., the wood samples in this work) are synthesized by rosette-shaped CSCs. Both structure and properties of the individual microfibrils have also been extensively studied with various methods.15 However, there has still been an argument with respect to the number of cellulose chains inside the elementary microfibril, with a number between 18 to 36.16 There is now a growing consensus that as the rosette-shaped CSC contains six groups of three synthase units (so-called the “hexamer of trimers” model; see Figure 1A),17,18 the elementary microfibril should contain only 18-chains.19,20 Nevertheless, the average dimension of an 18-chain microfibril should be on the order of 2.3–3.6 nm, depending on the chain arrangement;21,22 this dimension is quite different from the cross-sectional dimensions typically observed in nanocellulose.

Figure 1.

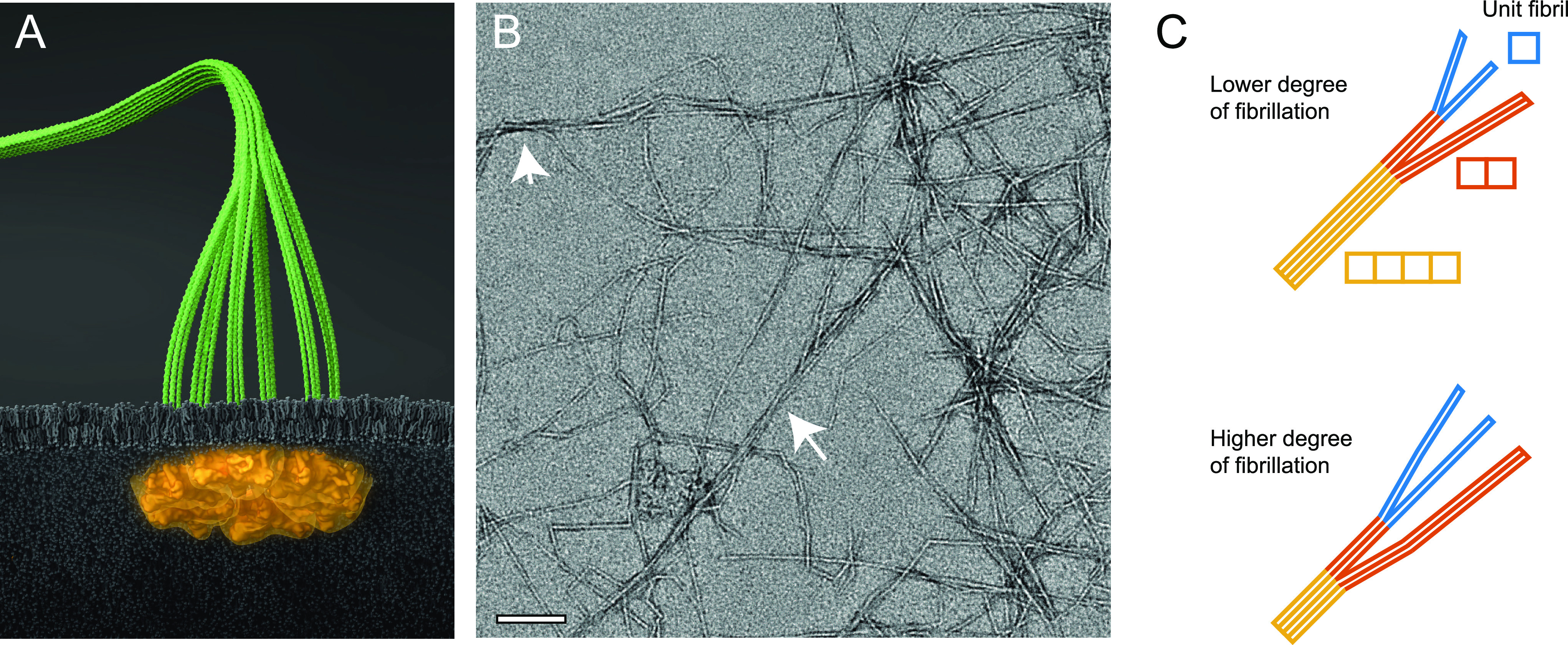
Figure 1

Open in a new tab

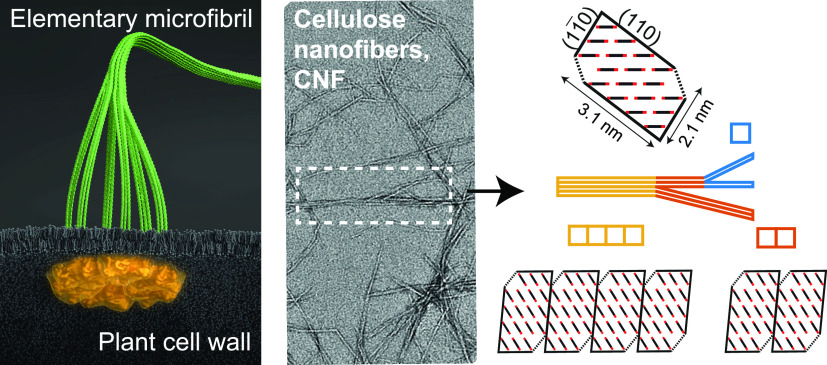
Illustration of cellulose nanofibers (CNFs). (A) Six proteins arranged in rosette complexes in the cell wall of plants synthesize three cellulose chains per protein continuously that assemble into an elementary microfibril (containing 18 cellulose chains). (B) Representative TEM image of CNFs extracted from wood (sample no. 3 in Table 1). The arrows highlight regions of aggregated microfibrils; the scale bar indicates 100 nm. (C) Cross-section distribution of CNFs dependent on the degree of fibrillation (DOF), where lower DOF means that a larger mass fraction of microfibrils are part of cross-sectional aggregates. The model system in this work assumes the microfibrils form aggregates of 2 of 4 unit fibrils. (Illustration (A) was created by Dr. Thomas Splettstößer of SCISTYLE, Berlin.)

Although, it has been well-known that macroscale cellulose fibers can be defibrillated by comminution treatments, the nanoscale material can also aggregate into macrofibrils,23 akin to the concept of hornification.24 Typically, the average cross-sectional dimension of nanocellulose obtained from kraft pulps using only mechanical treatments is in the range of 18 and 20 nm,25,26 which can be determined by TEM and cross-polarization magic angle spinning CP/MAS13C NMR studies.27 However, with the assistance of chemical modifications, such as oxidation and carboxymethylation, by introducing charged groups on the cellulose surface, the cross-sectional dimension of nanocellulose can be drastically decreased. In one study, the TEMPO-assisted defibrillation process showed that cellulose nanostrips containing a single layer of parallel chains, holding mostly by interchain van de Waals forces, could be obtained.11 The thickness of the nanostrip (around 0.5 nm) was thinner than that of an elementary microfibril, indicating that intense oxidation conditions can further delaminate the integrity of the microfibril.

The main purpose of this work is to provide a comprehensive description of the morphology of extracted CNFs on a nanometer scale and how it relates to elementary microfibrils. The key focus is to understand the aggregation behavior of elementary microfibrils, leading to different cross-sectional shapes and dimensions, in nanocellulose samples prepared by different extraction methods. In specific, two types of CNFs prepared by TEMPO-mediated oxidation and carboxymethylation methods were used. On the basis of TEM imaging (Figure 1B and Supporting Information), the chosen samples all exhibited larger cross-sectional dimensions than that of the elementary microfibril. This indicated that the resulting CNFs contained aggregates of microfibrils. This is in line with previous studies,11,28 where complementary AFM examination indicated that CNFs are ribbon shape; findings that clearly suggest that these aggregates are likely favoring an aggregation direction. To gain insights into the above subject, combined SAXS and wide-angle X-ray diffraction (WAXD) measurements of CNF dispersions and freeze-dried samples, respectively, were carried out. The complementary data were analyzed assuming that the cross-sectional distribution of CNFs consists of aggregates of a discrete number of elementary microfibrils, where a system with higher degree of fibrillation will approach the shape of an individual unit microfibril according to Figure 1C. The obtained results agree well with the unit microfibril with a size of 2.4 nm as well as provide us with the information on the degree of fibrillation, which would be very useful as a characterization quantity for nanocellulose. We further discuss the relationship between the structure and microfibril aggregation mechanisms of CNFs.

Results and Discussion

Preparation of Cellulose Nanofibers

The samples in this study were prepared from never-dried wood pulp using either TEMPO-mediated oxidation or carboxymethylation (CM) methods to incorporate charged carboxylate groups on the cellulose surface. Through subsequent high-pressure homogenization, nanofibers were liberated and kept in a stable dispersion through electrostatic repulsion. In this study, 18 different samples were prepared, where the chemical method used, degree of homogenization, and the resulting charge (degree of substitution, DS) are listed in Table 1 (details are given in Methods).

Table 1. List of CNF Samples Obtained with Different Oxidation Methods (i.e., TEMPO-Oxidized CNF, Noted ”TEMPO”, or Carboxymethylated CNF, Noted ”CM”), Homogenization Conditions, and Total Charge/Degree of Substitution (DS).

sample no. oxidation homogenization charge/DS
1 TEMPO 1 pass at 550 bar 0.15
2 TEMPO 1 pass at 1700 bar 0.15
3 TEMPO 2 passes at 1700 bar 0.15
4 TEMPO 1 pass at 550 bar 0.19
5 TEMPO 1 pass at 1700 bar 0.19
6 TEMPO 2 passes at 1700 bar 0.19
7 CM 1 pass at 550 bar 0.06
8 CM 1 pass at 1700 bar 0.06
9 CM 2 passes at 1700 bar 0.06
10 CM 1 pass at 550 bar 0.11
11 CM 1 pass at 1700 bar 0.11
12 CM 2 passes at 1700 bar 0.11
13 CM 1 pass at 550 bar 0.22
14 CM 1 pass at 1700 bar 0.22
15 CM 2 passes at 1700 bar 0.22
16 CM 1 pass at 550 bar 0.34
17 CM 1 pass at 1700 bar 0.34
18 CM 2 passes at 1700 bar 0.34
Open in a new tab

Small-Angle X-ray Scattering of CNF Dispersions

The samples were diluted to a concentration of 0.1 wt %, and the resulting dispersions were injected in quartz capillaries and measured using the solution SAXS technique at the National Synchrotron Light Source II (NSLS-II), Brookhaven National Laboratory, USA. The structure was determined using the scattered intensity profile at different scattering vectors 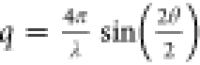Inline graphic (λ is the wavelength and 2θ is the scattering angle). The scattered intensity profile mainly resulted from the form factor of a single nanofiber (the structure factor in such a dilute suspension is near unity). Since the length scales studied with SAXS were in the range 1–50 nm, significantly shorter than the CNF length, the intensity profile only reflected the cross-sectional distribution of CNFs.13

Quantized Polydispersity Fitting of SAXS Data from CNF Dispersions

The method developed in this work relies on a simulated SAXS intensity profile of parallelepiped-shaped CNF particles (Figure 2). The scattered intensity of a single parallelepiped with cross-section A × B and length L (volume V = ABL) has an analytical form of29,30

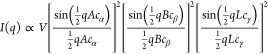graphic file with name nn0c04570_m002.jpg 1

with

graphic file with name nn0c04570_m003.jpg 2

In eqs 1 and 2, the cosine operations (cα, cβ, and cγ) represent the projection of particle unit axes on the detector coordinates. Many parallelepipeds are sampled with random orientations to simulate a 2D SAXS detector image, whereby the average intensity I(q) is obtained. In this work, we assume that the cross-section of an elementary microfibril can be considered as a square unit fibril with side dimension of d. Furthermore, the allowed aggregate cross-section will have to be multiples of the unit fibril, i.e., A × B = (1 × 1)d, (2 × 1)d, and (2 × 2)d, etc. With this approach, we can obtain the volume-averaged (proportional to the mass-average, which will be used from hereafter, assuming a constant density of CNFs) scattering curves I(q) of a predefined set of cross-sectional aggregates. In Figure 3, we choose to only describe the cross-section distribution by a set of three allowed aggregates: (1 × 1)d, (2 × 1)d, and (4 × 1)d. The fitting procedure thus relied on finding the optimal prefactors c1×1, c2×1, and c4×1 in the expression

graphic file with name nn0c04570_m004.jpg 3

given a fixed value of d. Normalizing the prefactors with their sum equal to 1, the fitted mass fractions ϕ1×1, ϕ2×1, and ϕ4×1 of each aggregate type could be estimated. An example of the procedure is illustrated in Figure 3A. By iteratively looping through different values of d in the range 1.5–4 nm, we find the value of d that minimizes the residuals (Figure 3B). Even though the system probably could allow for a wider variety of cross-sections, the more possibilities we add to the model, the less accurate the fitting becomes as many different solutions could match the data (since the set of form factors does not form an orthogonal basis). This is clearly visible in Figure 3B, where a set with more allowed shapes results in lower residuals. However, already at a set with three different shapes as used in this evaluation, we find indications of nearby solutions with similar residuals (gray areas in Figure 3B) that provide clear jumps in the residual curve. This problem becomes even more severe with a larger set of allowed cross-sections. To maintain a residual curve with a clear minimum, this set of three shapes was chosen to represent the system. More details of the fitting method are provided in Methods.

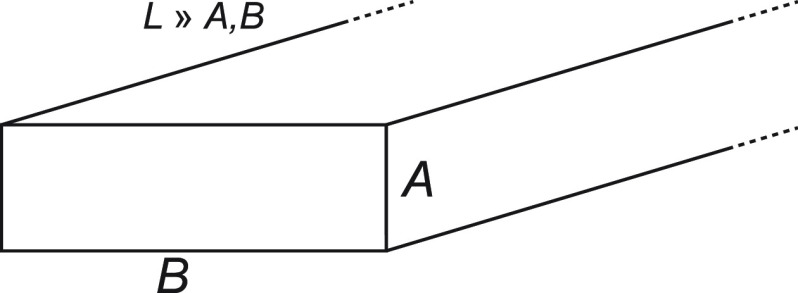
Figure 2.

Figure 2

Open in a new tab

Illustration of a parallelepiped model to represent a cellulose nanofiber with dimensions A, B, and L, with L ≫ A, B.

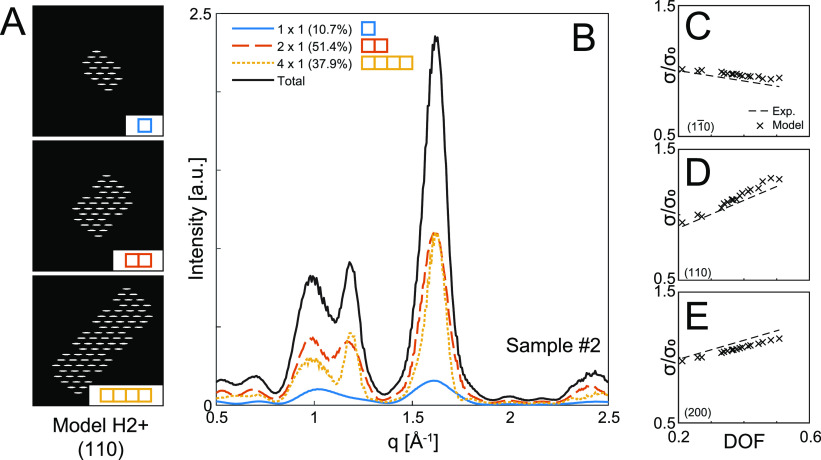
Figure 3.

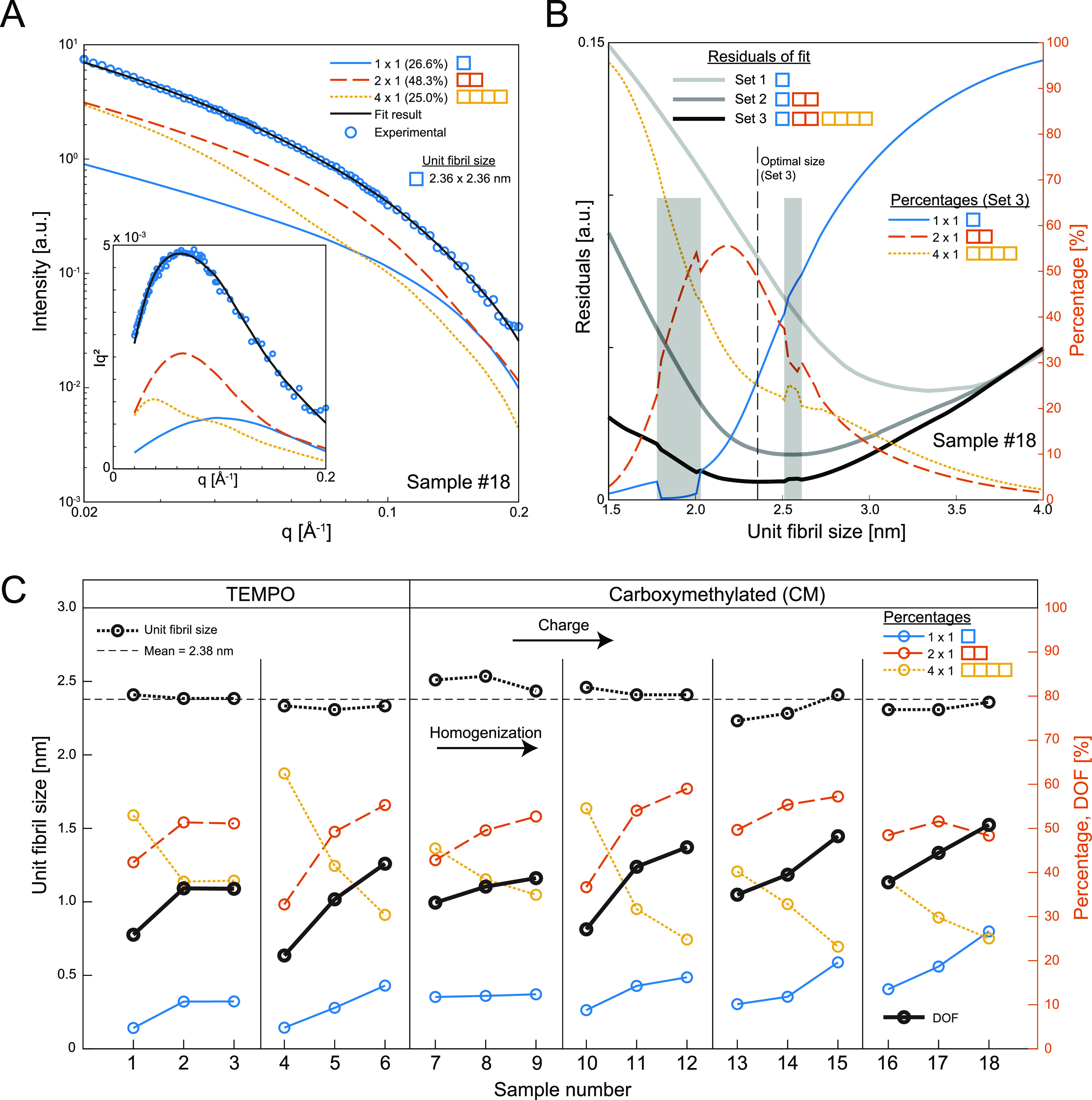
Figure 3

Open in a new tab

Analysis of CNF cross-section distributions using small-angle X-ray scattering (SAXS) and fitting of the data using the assumption of quantized polydispersity. (A) The experimental SAXS data are fitted with the contributions from 1 × 1, 2 × 1, and 4 × 1 unit fibrils to find the optimal mass fractions of these aggregates; the inset shows the corresponding Lorentz-corrected curves. (B) Unit fibril size found by minimizing the residuals of the best fit given a certain set of cross-sectional aggregates (thick gray/black curves). Every given unit fibril size provides an optimal combination of aggregate mass fractions (thin colored curves); the gray highlighted region indicates unit fibril size intervals where an alternate solution is found as optimal. (C) Results of the analysis for all samples (1–18) where every group of three corresponds to increasing homogenization, and each group to the right has a higher degree of surface charge; samples 1–6 are TEMPO-oxidized, and samples 7–18 are carboxymethylated (CM); the fitting results yield unit fibril size and mass fractions of aggregates from which a degree of fibrillation (DOF) is calculated; the mean unit fibril size is found to be 2.4 nm.

The SAXS data from all samples in Table 1 were fitted with this procedure. The resulting values of the unit fibril size d as well as mass fractions ϕ1×1, ϕ2×1, and ϕ4×1 are summarized in Figure 3C. The mass fractions are further used to define a degree of fibrillation (DOF):

graphic file with name nn0c04570_m005.jpg 4

Since the mass fraction of ϕ4×1 in essence describes all larger aggregates, the DOF is thus defined as zero when ϕ4×1 = 1. Similarly, DOF = 1 if the material is completely fibrillated; i.e., ϕ1×1 = 1.

As expected, the best fit of all samples results in an increasing DOF, which also increases with a higher degree of homogenization and charge but independent of the chemical modification scheme. More interestingly, the best fit of all samples results in a unit fibril around d = 2.4 nm, which is in full agreement with the dimension expected of the elementary microfibril consisting of 18 cellulose chains.

Wide-Angle X-ray Diffraction of Freeze-Dried CNF Samples

The cellulose chains inside the CNFs have a crystalline arrangement that can be characterized through the diffraction signals at wide angles (q > 0.5 Å–1). However, due to the strong scattering of water molecules at similar q-values, it is difficult to extract these signals in aqueous dispersions, especially at low concentrations. Thus, for high-quality WAXD data, the samples need to be dried. However, normal air-drying often leads to cocrystallization/hornification, thus influencing the chain arrangement in the material.31,32 In order to maintain the internal structure, the CNF dispersions were freeze-dried (detailed procedure provided in Methods) and the structure was analyzed using the WAXD technique. 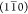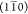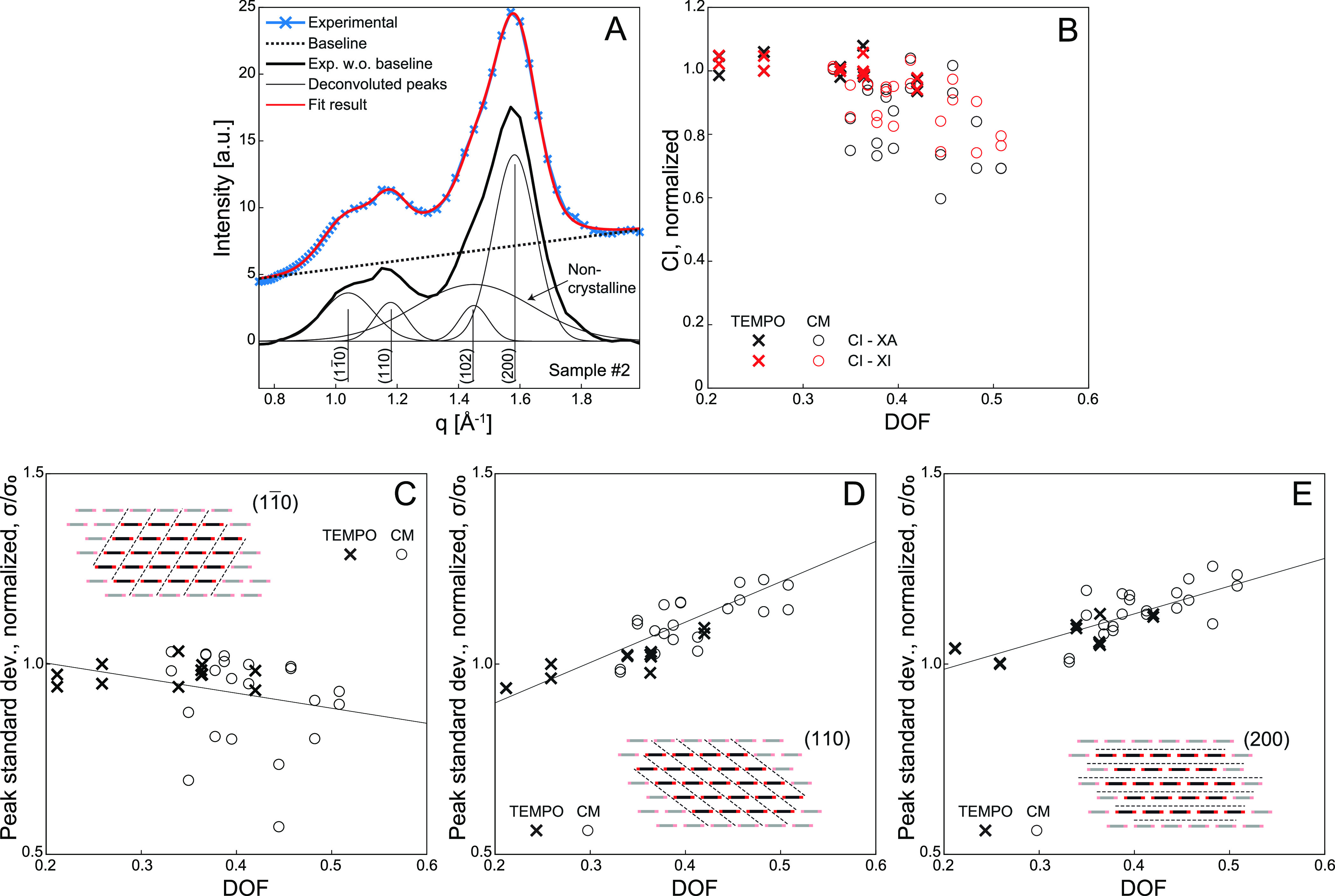Given the monoclinic unit cell arrangement in the native cellulose crystal, we can assign the three prominent diffraction peaks as the result of Inline graphic, (110), and (200) planes in the cellulose Iβ structure (Figure 4A). In fact, the baseline-corrected WAXD profile can be deconvoluted into five Gaussian peaks using Inline graphic, (110), (200), and (102) reflections as well as a broad background peak (commonly referred to as a noncrystalline peak although likely also including higher order reflections in the crystal;33 more details about the deconvolution are given in Methods). The diffraction intensity I and standard deviation σ of each deconvoluted peak can then be extracted for each sample to assess the structural changes on a molecular level as a function of DOF. Each sample was measured twice, with all results plotted in Figure 4.

Figure 4.

Figure 4

Open in a new tab

Analysis of unit fibril internal structure by wide-angle X-ray diffraction (WAXD) of freeze-dried CNFs. (A) Illustration of the deconvolution procedure. The baseline is subtracted from the experimental data, which is subsequently fitted with five Gaussian functions corresponding to known Bragg reflections of cellulose, Iβ. (B) Crystallinity index (CI) based on deconvoluted peak area (XA) or intensity (XI) versus degree of fibrillation normalized with the value of sample 1. (C–E) Standard deviation of deconvoluted peaks normalized with sample 1 (inset indicates the reflection plane in the cellulose Iβ lattice).

The crystallinity of dried cellulose is often assessed by calculating a crystallinity index (CI), based on either the area under the diffraction profile (CI-XA) or relative intensity (CI-XI) of the deconvoluted peaks. However, it has been found previously that the absolute values of these measures are somewhat unreliable,21 but the relative trends remain the same. Here, we also calculate the CI based on previous methodology21 and normalizing the value with the value of sample 1 (i.e., the first measurement). The results are shown in Figure 4B. It was found that the crystallinity decreased quite dramatically as DOF increased. This trend was also observed from the previous work of Daicho et al.,21 where the phenomenon could be attributed to the effect of surface chains being more disordered. In other words, with higher DOF, more surface is exposed and, consequently, there are more disordered chains in the sample. It has been proposed that less crystalline domains could be located in discrete regions along the fibril giving rise to a “kinked” shape of fibrils.34 We will make no further assumption about the origin of the amorphous scattering and, rather, focus on the cross-sectional arrangement of chains giving rise to the primary peaks 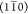Inline graphic, (110), and (200).

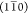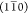To assess more specifically how the molecular arrangement changes with increasing DOF, we evaluated the shape of the deconvoluted primary peaks corresponding to the Inline graphic, (110) and (200) reflections. Although no trend was found in terms of relative peak height, the width of the deconvoluted (Gaussian) peaks showed a clear trend in Figure 4C–E: the Inline graphic peak became narrower, while the (110) and (200) peaks became broader.

With respect to the WAXD analysis, we emphasize that the deconvolution method applied here is just a way of parametrizing the WAXD signal and observing trends in the extracted parameters. Although the ”true” peak shapes might not be Gaussian and the spectra might include other minor peaks, including more parameters to the fitting will lead to overfitting, resulting in a large uncertainty of the parameters. We find that 5 peaks (i.e., 10 free parameters) including the baseline subtraction are sufficient to describe the WAXD profile and therefore a more complicated deconvolution is not performed.

Modeling the Molecular Arrangement of CNFs

The main results from the SAXS analysis of the CNF dispersions revealed a likely fibrillation scenario with gradual breakdown of larger, flat aggregates into single elementary microfibrils. We speculate that the cohesion of the microfibrils are likely formed shortly after the biosynthesis between nearby rosette complexes and would therefore be arranged in parallel. Although other cross-sectional aggregates might form during processing, the electrostatic repulsion from the charged carboxylate groups and Brownian motion would probably render them short-lived. Furthermore, the WAXD analysis (Figure 4C–E) revealed certain trends of the deconvolution parameters describing the primary peaks, indicating that the chain arrangement in the cross-section also changes with the degree of fibrillation.

With these considerations in mind, we made a simple model of the internal unit fibril structure to simulate the WAXD profile. Since the primary peaks arise from the structure factor of cellulose chains in a cross-sectional segment, we could assume any variation along the fibril axis negligible and only consider the 2D arrangement of chains. Furthermore, the chain itself including the arrangement on an atomistic scale is modeled with a simple coarse-grained form factor but is also playing a minor role as will be demonstrated later.

We first define a large number of hypothesized scenarios of the unit fibril shape and preferred aggregation directions based on the surfaces of the unit fibril. Note that, throughout this work, we will denote the aggregation direction (hkl) as the direction perpendicular to the (hkl)-diffraction planes. Five different types of unit fibrils were tested, which are summarized in Figure 5:

  • Model H1: an irregular hexagonal 18-chain model described by, e.g., Daicho et al.,21 which has surfaces parallel to all three reflection planes, 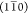Inline graphic, (110), and (200).

  • Model H2: a semihexagonal 18-chain model, with primary surfaces parallel to 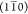Inline graphic and (110) planes.

  • Model R1: a rectangular 20-chain model, with primary surfaces parallel to 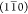Inline graphic and (110) planes.

  • Model R2: A rectangular 18-chain model described by, e.g., Newman,35 with primary surfaces parallel to 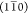Inline graphic and (110) planes.

  • Model Rh1: A rhomboidal 18-chain model, with primary surface parallel to (200) and either 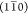Inline graphic or (110) planes.

  • Model Rh2: A rhomboidal 18-chain model similar to a model proposed by Fernandes et al.,23 with primary surface parallel to (200) and (010) planes.

Figure 5.

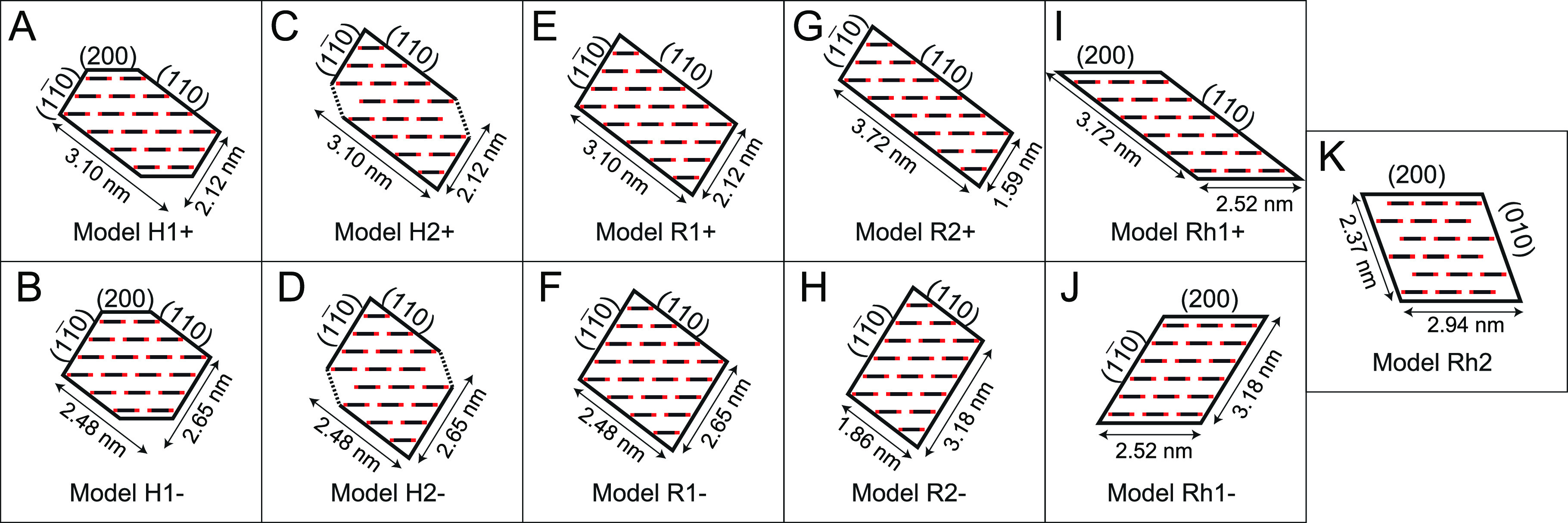
Figure 5

Open in a new tab

Cross-sectional models of the unit fibril noting the orientation of surface planes. (A, B) Irregular hexagonal 18-chain model H1+ and H1–. (C, D) Semihexagonal 18-chain model H2+ and H2–. (E, F) Rectangular 20-chain model R1+ and R1–. (G, H) Rectangular 18-chain model 5a and 5b. (I, J) Rhomboidal 18-chain model Rh1+ and Rh1–. (I) Rhomboidal 18-chain model Rh2.

Each model has two possible arrangements to promote either a larger (110) surface (models denoted “+”) or a larger 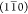Inline graphic surface (models denoted “–”), except model Rh2. The simulated WAXD profiles using 11 proposed models (Figure 5) under the above assumptions are illustrated in the Supporting Information, where the most likely scenario (the results are shown in Figure 6) is found using the following procedure.

Figure 6.

Figure 6

Open in a new tab

Modeling of WAXD profiles from CNFs. (A) Internal cellulose structure of the different cross-sectional aggregates modeled by a unit fibril (model H2+ in Figure 5) and cohesion/aggregation of phase boundaries parallel to the (110) plane. (B) Structures in panel A Fourier-transformed to yield approximations of the WAXD signals given the mass fractions extracted from the SAXS analysis in Figure 3. (C–E) Standard deviation of deconvoluted peaks of simulated WAXD curves normalized with sample 1, compared with mean experimental trends from Figure 4C–E.

First, the cross-sectional arrangement (structure factor) of the cellulose chains is decided by the specific model in Figure 5. The cross-sectional (projected) electron distribution of a chain is modeled as a binary ellipse (major axis aligned with the 200 planes), with three different dimensions (semiaxes): 3 Å × 0.5 Å, 2 Å × 0.75 Å, and 1 Å × 1 Å.

In Figure 6A, three types of fibril aggregates are shown, using the scenario of unit fibril model H2+ and chain form factor of 3 Å × 0.5 Å with cohesion of the surfaces parallel to the (110) plane. The cellulose chain projection image for each aggregate is then Fourier-transformed to obtain the approximate mass-averaged WAXD signal, which is shown in Figure 6B (more details are given in Methods). Given the extracted mass fraction of each aggregate obtained from the SAXS analysis, we can simulate the total WAXD profile for each sample (black curve in Figure 6B).

Given the 11 unit fibril models with varying aggregation directions and three different chain form factors, the simulation study resulted in 72 different hypothetical scenarios. The simulated WAXD profile of each scenario was parametrized with the same deconvolution method as that for the experimental data. This allowed us to evaluate the shape of the deconvoluted peaks in the simulations and compare them with the experimental results. The comparison of the width of the deconvoluted peaks from the simulations with the trends from Figure 4C–E are shown in Figure 6C–E. It was found that only a few scenarios followed the correct trend; i.e., the 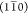Inline graphic peak became narrower while the (110) and (200) peaks become broader. These scenarios are summarized in Table 2.

Table 2. Resulting Simulated WAXD Data from Hypothetical Scenarios (Figure 5C–E) Matching the Trends Found in Experimental WAXD Data (Figure 4C–E).

model aggregation direction modeled cross-sectional CNF chain dimensions
H1+ (110) 3 Å × 0.5 Å
H2+ (110) 3 Å × 0.5 Å
R1+ (110) 3 Å × 0.5 Å
Rh1+ (110) 3 Å × 0.5 Å
H1+ (110) 2 Å × 0.75 Å
H2+ (110) 2 Å × 0.75 Å
H2– (110) 2 Å × 0.75 Å
R1+ (110) 2 Å × 0.75 Å
R1– (110) 2 Å × 0.75 Å
R2– (110) 2 Å × 0.75 Å
H2+ (110) 1 Å × 1 Å
R1+ (110) 1 Å × 1 Å
R1– (110) 1 Å × 1 Å
R2+ (110) 1 Å × 1 Å
Open in a new tab

It is interesting to see that the results in Table 2 are highly consistent with preferred aggregation/cohesion of surfaces parallel to the (110) plane and, thus, clearly favor the unit fibril models having larger surfaces parallel to this plane (models denoted with “+”). Given that the dimensions of the unit fibril models in this study are very close to those of the native elementary fibril, we assume that the model should consist of 18-chains, ruling out model R1. If we furthermore assume that CNFs should only have two surfaces as argued by, e.g., Wickholm et al.,36 and Bergenstråhle et al.,37 using the results from CP/MAS13C NMR spectroscopy and atomistic simulations, we can also rule out model H1.

In the remaining scenarios, models Rh1+, H2–, R2+, and R2– are also not favored, as their surface ordering does not apply generally to the fit between simulated and experimental results, where only a specific chain form factor can meet the selection criteria. The model that is most likely is model H2+, since all chain form factors can generate the observed trends in the WAXD signals.

Physical Implications of CNFs and the Elementary Microfibril

The best fit of SAXS results from all samples, with three types of aggregates (1 × 1, 2 × 1, and 4 × 1 unit fibrils) and optimal mass fractions, results in a unit fibril of size 2.4 nm (Figure 3C), which is consistent with the dimensions of a native elementary fibril with 18 cellulose chains. We note that the best fit model H2+ from our WAXD analysis, containing 5 layers of cellulose chains in a 34443 arrangement, is different from the model (H1+) endorsed by Kubicki et al.,22 and Daicho et al.,21 both also contain 5 layers in a 34443 arrangement. The latter is the same as model H1+, which possesses two hydrophobic surfaces parallel to the (200) plane, while the model H2+ only possesses hydrophilic surfaces parallel to either 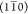Inline graphic or (110) planes.

In Figure 6C–E, the good agreement between experimental and simulated WAXD profiles by the most likely model H2+ indicated the preferred cohesion of surfaces parallel to the (110) plane. Perhaps, this can be understood by the following argument. In the cellulose Iβ crystal structure, the (200) plane is held together by intrasheet hydrogen bonds, while both 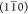Inline graphic and (110) planes are held together by van der Waals (hydrophobic) interactions and weak intersheet hydrogen bonds.38,39 Recent molecular dynamics simulation studies suggested that the hydrophobic pairing energy between cellulose chains are much stronger than intermolecular hydrogen bonds.40,41 The observation of favorable aggregation/cohesion of elementary microfibril surfaces parallel to the (110) plane can greatly enhance van der Waals interactions in crystalline fibrils, leading to insolubility in common organic solvents.40

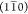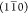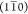In this study, the chosen schemes (TEMPO-mediated oxidation and carboxymethylation) for CNF extraction both seem to preferentially occur at the hydroxymethyl groups present on the elementary fibril phase boundaries parallel to the Inline graphic plane, possibly resulting in a selective weakening of cohesion between neighboring elementary fibrils in the Inline graphic-direction. A selective weakening of cohesion could be an explanation to the result obtained from the simulations of the WAXD diffractograms. Weakening the cohesion between neighboring elementary fibril phase boundaries in the direction of the Inline graphic planes could give a preferential delamination in this direction of aggregates held together by the less affected cohesion between adjacent (110) elementary fibril phase boundaries. The fact that one of the interfibrillar surfaces is more resistant to the pretreatment naturally results in the average cross-section of CNFs being flat or becoming a ribbon shape, which has been the source of a long-standing puzzle.

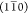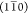The seeming preference of TEMPO oxidation to occur at the fibril phase boundaries parallel to the Inline graphic plane has also been previously observed by CP/MAS13C NMR. In a study of TEMPO-oxidized fibers, prior to homogenization, the major impact was observed on the signal assigned to C4 atoms in surface polymers belonging to the fibril phase boundary parallel to the Inline graphic plane.42

With stronger treatment (e.g., higher charge or stronger homogenization), the DOF would increase in CNF dispersions due to further weakening of the cohesion of the phase boundaries parallel to (110) planes. This interfibrillar cohesion would eventually break, as seen by the broadening of both (110) and (200) peaks in freeze-dried CNF samples with higher DOF. This process could lead to the narrowing of the cross-section distribution, allowing it to approach the dimensions of the native elementary microfibril. It is interesting to note that, under even stronger treatment conditions, the elementary microfibril itself can be further delaminated into a single-layer cellulose nanostrip.11

Conclusions

In this study, we have investigated the cross-sectional structure of CNFs in 18 different dispersions extracted from the same raw material (wood) using different chemical methods (TEMPO and CM) with different surface charges and different degrees of homogenization. The system was analyzed both in the dispersion state with solution SAXS to capture the average cross-section shape and dimensions and in the freeze-dried state with WAXD to capture the arrangement of cellulose chains in the elementary microfibril.

The SAXS data were analyzed by approximating the elementary microfibril with a square-shaped unit fibril that can aggregate and result in ribbon-shaped CNFs in agreement with images from TEM. By analyzing the SAXS data with an assumption of quantized polydispersity, we were able to resolve different-sized aggregates of unit fibrils and provide estimates of corresponding mass fractions. We further defined a degree of fibrillation (DOF) based on these mass fractions. The unit fibril was found to have a mean cross-sectional dimension of 2.4 nm, consistent with the dimensions of an 18-chain elementary microfibril. Complementary WAXD analysis revealed that the elementary microfibrils have a preferred aggregation of phase boundaries parallel to the (110) plane, resulting in the enhanced van der Waals interactions and stability of a larger CNF cross-section. With cellulose modification (e.g., TEMPO-mediated oxidation and carboxymethylation) and homogenization, we can break down cellulose microfibers by disrupting the interfibrillar bonds between surfaces parallel to the 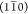Inline graphic plane, creating ribbon-shaped cross-sections. With stronger treatment, the interfibrillar bonds between surfaces parallel to the (110) planes are also broken, and the material can approach a dispersion of completely liberated elementary fibrils.

Furthermore, our results favor a 18-chain model, containing 5 layers of cellulose chains in a 34443 arrangement and two hydrophilic surfaces parallel to the 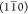Inline graphic and (110) planes. This model is slightly different from that endorsed by Daicho et al.,21 and Kubicki et al.,22 which contains two hydrophobic (200) surfaces. It is necessary to point out that the specific elementary fibril model endorsed here remains only a hypothesis. It is highly likely that real CNF dispersions contain much more variability of cross-sectional aggregates, microfibril structures, and cohesion directions as well as various degrees of chain disorder instead of the highly idealized model system presented here. Nevertheless, we argue that the present work contributes toward the full understanding of the origin of nanocellulose, where more detailed experiments and models are needed to verify or revise the hypothesized scenarios presented here.

Furthermore, we believe that this work provides a comprehensive explanation for the different CNF cross-sections obtained from different extraction methods and their relationships with the elementary microfibril in wood.

Methods

Materials

A commercial sulfite softwood dissolving pulp (Domsjö Dissolving plus; Domsjö Fabriker AB, Domsjö, Sweden) from 60 wt % Norwegian spruce and 40 wt % Scots pine, with a hemicellulose content of 4.5 wt % and a lignin content of 0.6 wt %, was supplied in a never-dried form and was used for the preparation of CNFs. The fiber composition and dimensions are very similar for the two species43 and the dissolving pulp used in the present study are ultrapure and with very low variability. Ethanol (Rectapur) was purchased from VWR (Sweden). Monochloroacetic acid (99%, ACS reagent, ClCH2COOH), acetic acid (ACS reagent), 2-propanol (ACS reagent), sodium hydroxide (ACS reagent), sodium hydrogen carbonate (ACS reagent), and methanol (ACS reagent) were purchased from Sigma-Aldrich (Sweden). Deionized water was used throughout the studies.

Preparation of Carboxymethylated Cellulose

The CM CNF samples were prepared by a carboxymethylation pretreatment of fibers followed by a high-pressure homogenization technique similar to a previously described procedure.8,44 A total of 90 g of fibers were pretreated. The never-dried fibers were first dispersed in deionized water at 30,000 revolutions in an ordinary laboratory reslusher. This was conducted with batches of 30 g of fibers in 2 L of deionized water. The fibers were then solvent-changed to ethanol by washing 90 g of fibers in 1 L of ethanol four times with an intermediate filtration step. The fibers were then impregnated for 30 min with a solution of 4.1, 8.2, 24.6, or 36.1 g of monochloroacetic acid in 409 mL of 2-propanol, targeting four different degrees of substitution (DS). These fibers were then added in portions to a solution of 13.3, 13.3, 30.0, or 36.3 g of NaOH in 409 mL of methanol mixed with 1636 mL of 2-propanol that had been heated to just below its boiling temperature in a 5 L reaction vessel fitted with a condenser. This carboxymethylation reaction was allowed to continue for 1 h.

Following this carboxymethylation step, the fibers were filtered and washed in several steps: first with 20 L of deionized water, then with 1636 mL of acetic acid (0.1 M), and then with 10 L of deionized water. Finally, the fibers were impregnated with a 1636 mL of NaHCO3 solution (4 wt % solution) for 60 min in order to convert the carboxyl groups to their sodium form, and then washed with 15 L of deionized water and drained on a Büchner funnel.

Preparation of TEMPO-Oxidized Cellulose

The TEMPO-oxidzed CNF samples were prepared using the TEMPO/NaBr/NaClO procedure established by Saito and Isogai.45 In order to prepare 10 g of TEMPO-oxidized cellulose nanofibers (CNFs), 26.3 g of the same pulp with 38 wt % cellulose content is first dissolved and dispersed in 1 L of deionized water. Then, 0.125 g of TEMPO with concentration of 0.0125 g of TEMPO per 1 g of cellulose and 1 g of NaBr with concentration of 0.1 g of NaBr per 1 g of cellulose are added before the solution is adjusted to pH = 10 with 0.5 M NaOH. To have a comparison in DS, to the sample expected with higher DS will be added 42 g of NaClO solution and the one with lower DS will be added 21 g of NaClO. After 24 h of TEMPO oxidation under room temperature, the reaction is quenched with 100 mL of ethanol and the samples are washed through centrifugation and dialysis.

Preparation of CNF Dispersions

After these pretreatment steps, the fibers were homogenized using a high-pressure microfluidizer (Microfluidizer M-110EH, Microfluidics Corp., USA). The fluidizer was equipped with two chambers of different sizes connected in series (200 and 100 μm). Pulp fiber slurries of 2 wt % concentration were passed once or twice at operating pressures of 550 and 1700 bar, respectively.

The dispersion was then diluted to 0.1 wt % and subjected to magnetic stirring overnight. In order to remove any fiber residuals of fibril fragments, the diluted CNF dispersions were transferred to 45 mL flasks and submitted to centrifugation (Multifuge 3L Centrifuge, Heraeus, Germany) for 15 min at 1000g. The clear dispersion was removed by pipet and transferred to a solvent resistant press-based stirred cell ultrafiltration unit (300 mL, Millipore, USA) equipped with membrane with a molecular weight cutoff of 100 kDa. The stirred cell concentrated the CNF dispersions rapidly but gently, using magnetic stirring, to minimize concentration polarization and shear-stress-induced denaturation. The final concentration of the dispersions was 0.2–0.3 wt %.

Pulp Total Charge Determination

The total charge of the pulp was measured by conductometric titration of the fibers prior to homogenization.46 Before titration, the fibers were washed at low pH, to remove unwanted adsorbed metal ions. The measured DS values for the four charges of carboxymethylated CNFs were determined to be 0.06, 0.11, 0.22, and 0.34. For TEMPO-oxidized CNFs, the DS values were determined to be 0.15 and 0.19 for the low and high charged samples, respectively.

Freeze-Drying of CNF Samples

Tubes containing dispersed CNF samples were dropped in liquid nitrogen and taken out after thermal equilibration (e.g., when boiling stops). The tubes with frozen samples were then put in the freeze-drier (Millrock Technology. Inc. with model of BT48A) below −40 °C and 500 Pa for 3 days. For the freeze-drying, the lids of the tubes are replaced by perforated aluminum foil to allow for sublimation.

Transmission Electron Microscopy

To ensure the fiber morphology of the CNF dispersions, transmission electron microscopy (TEM) experiments were performed at the Center of Functional Nanomaterials, Brookhaven National Laboratory. The equipment used was a JEOL JEM-1400 TEM instrument with a Ruby camera with operating voltage set to 120 kV. The CNF dispersions were diluted to ≈0.01 wt % and a small droplet (≈2.2 μL) was dropped on a carbon-coated copper grid. To obtain sufficient contrast, the samples were stained using a 2 wt % aqueous uranyl acetate solution. A total of 5–10 images were taken per sample, where an example image for each sample is provided in the Supporting Information.

X-ray Scattering/Diffraction Experiments

Small-angle X-ray scattering and wide-angle X-ray-diffraction experiments were performed at the LiX beamline (16-ID), Brookhaven National Laboratory, National Synchrotron Light Source (NSLS-II), USA.

For the SAXS experiments, the aqueous CNF samples were diluted to 0.1 wt % and slowly flowing through MICA tubes, where the X-ray beam is focused, and the scattered light is detected by a Pilatus3 1 M detector (Dectris). The X-ray wavelength is λ = 0.92 Å, and the sample–detector distance is 3.6 m. Background subtraction is done by subtracting the scattering from deionized (DI) water.

For the WAXD experiments, freeze-dried samples are mounted on a sample stage where the X-ray beam is focused. The scattered light is detected by a custom Pilatus 900k detector (Dectris), which essentially is a 1 M detector with one module removed to allow for simultaneous SAXS/WAXD measurements. The X-ray wavelength λ = 0.91 Å, and the sample–detector distance is 28.6 cm. Background subtraction is done by subtracting the scattering from air, i.e., measuring at the same setup without the sample mounted on the stage. The isotropy of the sample was verified by analyzing the angular intensity distribution of the (110) peak (see Supporting Information for details).

Quantized Polydispersity Fitting of SAXS Data

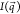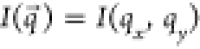The quantized polydispersity (QPD) fitting method of the SAXS data relies on the simulated form factor of the three allowed fibril/aggregate shapes: d × d (square cross-section), and 2d × d and 4d × d (rectangular cross-sections). For each aggregate shape, we sample 5000 parallelepipeds with random orientations and calculate the intensity Inline graphic according to eq 1, where the contributions of each particle are summed. The 2D detector plane is chosen to be in the xy-plane, such that Inline graphic. The exact particle dimensions are sampled from Gaussian distributions with mean d0 = 2.5 nm and L = 1000 nm (thus ensuring L ≫ d) and standard deviation taken as 5% of the mean. The simulated 2D data are converted to polar coordinates and then averaged in the azimuthal direction to get the intensity I as a function of Inline graphic. Each of the three curves I1×1,0(q), I2×1,0(q), and I4×1,0(q) at d = d0 are found by applying a smoothing spline to the simulated intensity and averaging them with the total mass. To obtain the curves for other values of d, the curves are scaled accordingly:

graphic file with name nn0c04570_m030.jpg 5

The fitting relies on finding the optimal prefactors c1×1, c2×1, and c4×1 in eq 3 given a fixed value of d. The fitting procedure is repeated for values of d between 1.5 and 4 nm, with steps of 0.025 nm, with the best fit of d and corresponding optimal prefactors found by minimizing the fit residuals (see Figure 3B). The optimal prefactors are normalized to find the resulting mass fractions ϕ1×1, ϕ2×1, and ϕ4×1 of each type of aggregate.

WAXD Peak Deconvolution and Crystallinity Index

It is important to note that scattering angles in WAXD were quantified with the scattering vector q, due to the possibility to tune the X-ray wavelength, λ. In conventional X-ray-diffraction (XRD) measurement, the wavelength is usually generated by Cu Kα radiation (λXRD = 0.1548 nm), where the scattering angle is given as 2θXRD. For readers with more experience with XRD using Cu Kα radiation, the conversion can easily be made through

graphic file with name nn0c04570_m031.jpg 6

The data points that applied in the WAXD deconvolution were within a q-range from 0.75 to 2 Å–1 (2θXRD = 10.6° to 28.5°). First, data points from q = 0.76 to 0.85 Å–1 and from q = 1.9 to 2 Å–1 were considered as a baseline, which were fitted with a linear function and removed from the raw data. The baseline-subtracted data were subsequently fitted with 5 Gaussian peaks with limited range of the peak center corresponding to known crystalline planes of cellulose,21 including (200) at 1.59 Å–1 (2θXRD = 22.6°), 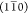Inline graphic at 1.03 Å–1 (2θXRD = 14.6°), (110) at 1.16 Å–1 (2θXRD = 16.4°), and (102) and “noncrystalline” peak with both centers at 1.45 Å–1 (2θXRD = 20.6°). Note that the broader noncrystalline peak likely includes both amorphous contributions and secondary peaks. The deconvolution here provided a way to parametrize the spectra. To minimize the uncertainty of the parameters, no other peaks were taken into consideration and the Gaussian shape was assumed for all crystalline/amorphous peaks. The crystallinity index was calculated in two ways. CI-XI was determined on the basis of the sum of the deconvoluted peak intensities Itotal and calculated through21,47

graphic file with name nn0c04570_m033.jpg 7

This equation corresponds to the estimates of the relative difference between the (200) peak and the amorphous (noncrystalline) peak. CI-XA was determined on the basis of the area A(hkl) of the individual deconvoluted Gaussian functions:21,47

graphic file with name nn0c04570_m034.jpg 8

WAXD Simulations of CNF Crystallite Structure

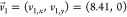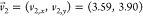The 2D crystal lattice of the cellulose chains is described by lattice vectors Inline graphic Å and Inline graphic Å (obtained through Figure 9 in Daicho et al.(21)), where 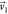Inline graphic is assumed parallel to the plane of the glucose units. Binary representations of the electron distribution in the fibril cross-section were created by assuming the cross-section of each cellulose chain as a binary ellipse with defined semiaxes (either 3 Å × 0.5 Å, 2 Å × 0.75 Å, or 1 Å × 1 Å) and placing them on the predefined lattice nodes. 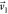The major axis of the ellipse is aligned with Inline graphic. A binary image of the cross-sectional arrangement was created using this procedure, which can be seen in Figure 6A, representing the electron density difference distribution Δρ(x,y). 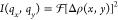The squared amplitude of the 2D Fourier transform of the image was taken to represent the scattering intensity Inline graphic using the fft2 function in Matlab R2019a. By converting this image to polar coordinates and averaging over all angles, we obtain a simulated curve of I(q) seen in Figure 6B. Note that since we assume no variation along the fibril axis (z), the 3D Fourier transform is zero where qz ≠ 0. Therefore, the averaging of all possible angles in 3D space is equivalent to the 2D angular averaging in the qx, qy-plane. By matching the mass fractions of the difference aggregates extracted by SAXS, we can obtain a representation of the WAXD signal from the same sample (black curve in Figure 6B). All 72 hypotheses with variations of unit fibril shape, aggregation direction, and form factors, as well as resulting WAXD profiles for sample 1, are given in the Supporting Information. Movie S1 is also provided to further explain the simulation procedure.

Acknowledgments

The authors acknowledge financial support from the DMR Polymer Program of the National Science Foundation (DMR-1808690), the Alf de Ruvo Foundation (SCA) and the Hans Werthén Foundation (IVA). Experimental assistance by S. Samadnouri, L. Yang and F. Camino is also greatly acknowledged along with helpful discussions with R. Joshi and D. Söderberg. The SAXS/WAXD experiments were performed at the LiX beamline (16-ID) in NSLS-II at Brookhaven National Laboratory, USA. The LiX beamline is part of the Life Science Biomedical Technology Research resource, primarily supported by the National Institute of Health, National Institute of General Medical Sciences (NIGMS) under grant P41 GM111244, and by the DOE Office of Biological and Environmental Research under grant KP1605010, with additional support from NIH under grant S10 OD012331. As a National Synchrotron Light Source II facility resource at Brookhaven National Laboratory, work performed at the LSBR is supported in part by the U.S. Department of Energy, Office of Basic Energy Sciences Program under contract number DE-SC0012704. Transmission electron microscopy (TEM) experiments were performed at the Center of Functional Nanomaterials, Brookhaven National Laboratory. The Center for Functional Nanomaterials, which is a U.S. DOE Office of Science Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 761000. The publication reflects only the author’s view and the Commission is not responsible for any use that may be made of the information it contains.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.0c04570.

  • Video S1 illustrating the WAXD simulation procedure (MP4)

  • Example TEM images of all 18 CNF samples along with mean width and standard deviation of >60 measured nanofibrils; results from WAXD simulations of all 72 hypotheses and subsequent WAXD deconvolution results; assessment of sample isotropy in WAXD experiments (PDF)

The authors declare no competing financial interest.

Supplementary Material

nn0c04570_si_001.mp4 (7.1MB, mp4)
nn0c04570_si_002.pdf (40.5MB, pdf)

References

  1. French A. D.; Bertoniere N. R.; Brown R. M.; Chanzy H.; Gray D.; Hattori K.; Glasser W. In Kirk–Othmer Encyclopedia of Chemical Technology, 5th ed.; Kirk-Othmer, Ed.; Wiley: New York, 2004. [Google Scholar]
  2. Klemm D.; Kramer F.; Moritz S.; Lindström T.; Ankerfors M.; Gray D.; Dorris A. Nanocelluloses: A New Family of Nature-Based Materials. Angew. Chem., Int. Ed. 2011, 50, 5438–5466. 10.1002/anie.201001273. [DOI] [PubMed] [Google Scholar]
  3. Moon R. J.; Martini A.; Nairn J.; Simonsen J.; Youngblood J. Cellulose Nanomaterials Review: Structure, Properties and Nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. 10.1039/c0cs00108b. [DOI] [PubMed] [Google Scholar]
  4. Blanco A.; Monte M. C.; Campano C.; Balea A.; Merayo N.; Negro C. In Handbook of Nanomaterials for Industrial Applications; Hussain C. M., Ed.; Elsevier: Amsterdam, 2018; pp 74–126. [Google Scholar]
  5. Herrick F. W.; Casebier R. L.; Hamilton J. K.; Sandberg K. R. Microfibrillated Cellulose: Morphology and Accessibility. J. Appl. Polym. Sci.: Appl. Polym. Symp. 1983, 37, 797–813. [Google Scholar]
  6. Turbak A. F.; Snyder F. W.; Sandberg K. R. Microfibrillated Cellulose, A New Cellulose Product: Properties, Uses, and Commercial Potential. J. Appl. Polym.: Appl. Polym. Symp. 1983, 37, 815–827. [Google Scholar]
  7. Isogai A.; Saito T.; Fukuzumi H. TEMPO-Oxidized Cellulose Nanofibers. Nanoscale 2011, 3, 71–85. 10.1039/C0NR00583E. [DOI] [PubMed] [Google Scholar]
  8. Wågberg L.; Decher G.; Norgren M.; Lindström T.; Ankerfors M.; Axnäs K. The Build-Up of Polyelectrolyte Multilayers of Microfibrillated Cellulose and Cationic Polyelectrolytes. Langmuir 2008, 24, 784–795. 10.1021/la702481v. [DOI] [PubMed] [Google Scholar]
  9. Foster E. J.; Moon R. J.; Agarwal U. P.; Bortner M. J.; Bras J.; Camarero-Espinosa S.; Chan K. J.; Clift M. J. D.; Cranston E. D.; Eichhorn S. J.; et al. Current Characterization Methods for Cellulose Nanomaterials. Chem. Soc. Rev. 2018, 47, 2609–2679. 10.1039/C6CS00895J. [DOI] [PubMed] [Google Scholar]
  10. Su Y.; Burger C.; Hsiao B. S.; Chu B. Characterization of TEMPO-Oxidized Cellulose Nanofibers in Aqueous Suspension by Small-Angle X-Ray Scattering. J. Appl. Crystallogr. 2014, 47, 788–798. 10.1107/S1600576714005020. [DOI] [Google Scholar]
  11. Su Y.; Burger C.; Ma H.; Chu B.; Hsiao B. S. Exploring the Nature of Cellulose Microfibrils. Biomacromolecules 2015, 16, 1201–1209. 10.1021/bm501897z. [DOI] [PubMed] [Google Scholar]
  12. Su Y.; Burger C.; Ma H.; Chu B.; Hsiao B. S. Morphological and Property Investigations of Carboxylated Cellulose Nanofibers Extracted from Different Biological Species. Cellulose 2015, 22, 3127–3135. 10.1007/s10570-015-0698-8. [DOI] [Google Scholar]
  13. Mao Y.; Liu K.; Zhan C.; Geng L.; Chu B.; Hsiao B. S. Characterization of Nanocellulose Using Small-Angle Neutron, X-ray, and Dynamic Light Scattering Techniques. J. Phys. Chem. B 2017, 121, 1340–1351. 10.1021/acs.jpcb.6b11425. [DOI] [PubMed] [Google Scholar]
  14. Tsekos I. The Sites of Cellulose Synthesis in Algae: Diversity and Evolution of Cellulose-Synthesizing Enzyme Complexes. J. Phycol. 1999, 35, 635–655. 10.1046/j.1529-8817.1999.3540635.x. [DOI] [Google Scholar]
  15. Nishiyama Y. Structure and Properties of the Cellulose Microfibril. J. Wood Sci. 2009, 55, 241–249. 10.1007/s10086-009-1029-1. [DOI] [Google Scholar]
  16. Turner S.; Kumar M. Cellulose Synthase Complex Organization and Cellulose Microfibril Structure. Philos. Trans. R. Soc., A 2018, 376, 20170048. 10.1098/rsta.2017.0048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Vandavasi V. G.; Putnam D. K.; Zhang Q.; Petridis L.; Heller W. T.; Nixon B. T.; Haigler C. H.; Kalluri U.; Coates L.; Langan P.; Smith J. C.; Meiler J.; O’Neill H. A Structural Study of CESA1 Catalytic Domain of Arabidopsis Cellulose Synthesis Complex: Evidence for CESA Trimers. Plant Physiol. 2016, 170, 123–135. 10.1104/pp.15.01356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Purushotham P.; Ho R.; Zimmer J. Architecture of a Catalytically Active Homotrimeric Plant Cellulose Synthase Complex. Science 2020, 369, 1089–1094. 10.1126/science.abb2978. [DOI] [PubMed] [Google Scholar]
  19. Nixon B. T.; Mansouri K.; Singh A.; Du J.; Davis J. K.; Lee J.-G.; Slabaugh E.; Vandavasi V. G.; O’Neill H.; Roberts E. M.; Roberts A. W.; Yingling Y. G.; Haigler C. H. Comparative Structural and Computational Analysis Supports Eighteen Cellulose Synthases in the Plant Cellulose Synthesis Complex. Sci. Rep. 2016, 6, 28696. 10.1038/srep28696. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Jarvis M. C. Structure of Native Cellulose Microfibrils, the Starting Point for Nanocellulose Manufacture. Philos. Trans. R. Soc., A 2018, 376, 20170045. 10.1098/rsta.2017.0045. [DOI] [PubMed] [Google Scholar]
  21. Daicho K.; Saito T.; Fujisawa S.; Isogai A. The Crystallinity of Nanocellulose: Dispersion-Induced Disordering of the Grain Boundary in Biologically Structured Cellulose. ACS Appl. Nano Mater. 2018, 1, 5774–5785. 10.1021/acsanm.8b01438. [DOI] [Google Scholar]
  22. Kubicki J. D.; Yang H.; Sawada D.; O’Neill H.; Oehme D.; Cosgrove D. The Shape of Native Plant Cellulose Microfibrils. Sci. Rep. 2018, 8, 13983. 10.1038/s41598-018-32211-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Fernandes A. N.; Thomas L. H.; Altaner C. M.; Callow P.; Forsyth V. T.; Apperley D. C.; Kennedy C. J.; Jarvis M. C. Nanostructure of Cellulose Microfibrils in Spruce Wood. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, E1195–E1203. 10.1073/pnas.1108942108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jayme G. Mikro-Quellungsmessungen an Zellstoffen. Wochenbl. Papierfabr. 1944, 6, 187–194. [Google Scholar]
  25. Bardage S.; Donaldson L.; Tokoh C.; Daniel G. Ultrastructure of the Cell Wall of Unbeaten Norway Spruce Pulp Fibre Surfaces. Nord. Pulp Pap. Res. J. 2004, 19, 448–452. 10.3183/npprj-2004-19-04-p448-452. [DOI] [Google Scholar]
  26. Donaldson L. Cellulose Microfibril Aggregates and Their Size Variation With Cell Wall Type. Wood Sci. Technol. 2007, 41, 443. 10.1007/s00226-006-0121-6. [DOI] [Google Scholar]
  27. Hult E.-L.; Larsson P. T.; Iversen T. Cellulose Fibril Aggregation - An Inherent Property of Kraft Pulps. Polymer 2001, 42, 3309–3314. 10.1016/S0032-3861(00)00774-6. [DOI] [Google Scholar]
  28. Geng L.; Peng X.; Zhan C.; Naderi A.; Sharma P. R.; Mao Y.; Hsiao B. S. Structure Characterization of Cellulose Nanofiber Hydrogel as Functions of Concentration and Ionic Strength. Cellulose 2017, 24, 5417–5429. 10.1007/s10570-017-1496-2. [DOI] [Google Scholar]
  29. Nayuk R.; Huber K. Formfactors of Hollow and Massive Rectangular Parallelepipeds at Variable Degree of Anisometry. Z. Phys. Chem. 2012, 226, 837–854. 10.1524/zpch.2012.0257. [DOI] [Google Scholar]
  30. SasView 4.2.2. Documentation, 2017; http://www.sasview.org/docs/user/models/parallelepiped.html (Accessed 2020–02–04).
  31. Newman R. H. Carbon-13 NMR Evidence for Cocrystallization of Cellulose as a Mechanism for Hornification of Bleached Kraft Pulp. Cellulose 2004, 11, 45–52. 10.1023/B:CELL.0000014768.28924.0c. [DOI] [Google Scholar]
  32. Peng Y.; Gardner D. J.; Han Y.; Kiziltas A.; Cai Z.; Tshabalala M. A. Influence of Drying Method on the Material Properties of Nanocellulose I: Thermostability and Crystallinity. Cellulose 2013, 20, 2379–2392. 10.1007/s10570-013-0019-z. [DOI] [Google Scholar]
  33. French A. D. Increment in Evolution of Cellulose Crystallinity Analysis. Cellulose 2020, 27, 5445–5448. 10.1007/s10570-020-03172-z. [DOI] [Google Scholar]
  34. Usov I.; Nyström F.; Adamcik J.; Handschin S.; Schütz C.; Fall A.; Bergström L.; Mezzenga R. Understanding Nanocellulose Chirality and Structure–Properties Relationship at the Single Fibril Level. Nat. Commun. 2015, 6, 7564. 10.1038/ncomms8564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Newman R. H. Simulation of X-Ray Diffractograms Relevant to the Purported Polymorphs Cellulose IVI and IVII. Cellulose 2008, 15, 769–778. 10.1007/s10570-008-9225-5. [DOI] [Google Scholar]
  36. Wickholm K.; Larsson P. T.; Iversen T. Assignment of Non-Crystalline Forms in Cellulose I by CP/MAS 13C NMR Spectroscopy. Carbohydr. Res. 1998, 312, 123–129. 10.1016/S0008-6215(98)00236-5. [DOI] [Google Scholar]
  37. Bergenstråhle M.; Wohlert J.; Larsson P. T.; Mazeau K.; Berglund L. A. Dynamics of Cellulose-Water Interfaces: NMR Spin-Lattice Relaxation Times Calculated from Atomistic Computer Simulations. J. Phys. Chem. B 2008, 112, 2590–2595. 10.1021/jp074641t. [DOI] [PubMed] [Google Scholar]
  38. Nishiyama Y.; Langan P.; Chanzy H. Crystal Structure and Hydrogen-Bonding System in Cellulose Iβ from Synchrotron X-Ray and Neutron Fiber Diffraction. J. Am. Chem. Soc. 2002, 124, 9074–9082. 10.1021/ja0257319. [DOI] [PubMed] [Google Scholar]
  39. Nishiyama Y. Molecular Interactions in Nanocellulose Assembly. Philos. Trans. R. Soc., A 2018, 376, 20170047. 10.1098/rsta.2017.0047. [DOI] [PubMed] [Google Scholar]
  40. Medronho B.; Romano A.; Miguel M. G.; Stigsson L.; Lindman B. Rationalizing Cellulose (In)Solubility: Reviewing Basic Physicochemical Aspects and Role of Hydrophobic Interactions. Cellulose 2012, 19, 581–587. 10.1007/s10570-011-9644-6. [DOI] [Google Scholar]
  41. Kumar R.; Hu F.; Hubbell C. A.; Ragauskas A. J.; Wyman C. E. Comparison of Laboratory Delignification Methods, Their Selectivity, and Impacts on Physiochemical Characteristics of Cellulosic Biomass. Bioresour. Technol. 2013, 130, 372–381. 10.1016/j.biortech.2012.12.028. [DOI] [PubMed] [Google Scholar]
  42. Sjöstedt A.Preparation and Characterization of Nanoporous Cellulose Fibres and Their Use in New Material Concepts. Ph.D. thesis; KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
  43. Ilvessalo-Pfäffli M.-S. In Fiber Atlas: Identification of Papermaking Fibers; Timell T. E., Ed.; Springer Series in Wood Science; Springer-Verlag: Berlin, Heidelberg, 1995. [Google Scholar]
  44. Wågberg L.; Winter L.; Ödberg L.; Lindström T. On the Charge Stoichiometry Upon Adsorption of a Cationic Polyelectrolyte on Cellulosic Materials. Colloids Surf. 1987, 27, 163–173. 10.1016/0166-6622(87)80140-3. [DOI] [Google Scholar]
  45. Saito T.; Isogai A. TEMPO-Mediated Oxidation of Native Cellulose. The Effect of Oxidation Conditions on Chemical and Crystal Structures of the Water-Insoluble Fractions. Biomacromolecules 2004, 5, 1983–1989. 10.1021/bm0497769. [DOI] [PubMed] [Google Scholar]
  46. Katz S.; Beatson R. P.; Scallon A. M. The Determination of Strong and Weak Acidic Groups in Sulfite Pulps. Sven. Papperstidn. 1984, 87, R48–R53. [Google Scholar]
  47. Terinte N.; Ibbett R.; Schuster K. C. Overview on Native Cellulose and Microcrystalline Cellulose I Structure Studied by X-Ray Diffraction (WAXD): Comparison between Measurement Techniques. Lenzinger Berichte 2011, 89, 118. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn0c04570_si_001.mp4 (7.1MB, mp4)
nn0c04570_si_002.pdf (40.5MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES