Using single-cell models to predict the functionality of synthetic circuits at the population scale

Significance

At the single-cell level, biochemical processes are inherently stochastic. For many natural systems, the resulting cell-to-cell variability is exploited by microbial populations. In synthetic biology, however, the interplay of cell-to-cell variability and population processes such as selection or growth often leads to circuits not functioning as predicted by simple models. Here we show how multiscale stochastic kinetic models that simultaneously track single-cell and population processes can be obtained based on an augmentation of the chemical master equation. These models enable us to quantitatively predict complex population dynamics of a yeast optogenetic differentiation system from a specification of the circuit’s components and to demonstrate how cell-to-cell variability can be exploited to purposefully create unintuitive circuit functionality.

Abstract

Mathematical modeling has become a major tool to guide the characterization and synthetic construction of cellular processes. However, models typically lose their capacity to explain or predict experimental outcomes as soon as any, even minor, modification of the studied system or its operating conditions is implemented. This limits our capacity to fully comprehend the functioning of natural biological processes and is a major roadblock for the de novo design of complex synthetic circuits. A common cause of this problem is that cell-to-cell variability creates couplings between single-cell circuits and population processes such as selection or growth. Altering the circuit may then have unforeseen consequences inside growing populations. Here we construct a yeast optogenetic differentiation system that exploits cell-to-cell variability to enable external control of the population composition. We show that a simple deterministic model can explain the dynamics of the core system. However, modifying the context of the circuit by expressing system components from plasmids leads to failure of model predictions. Subsequently, we deploy theory from stochastic chemical kinetics to construct models of the system’s components that simultaneously track single-cell and population processes and demonstrate that this allows us to quantitatively predict emerging dynamics of the plasmid-based system without any adjustment of model parameters. We conclude that carefully characterizing the dynamics of cell-to-cell variability using appropriate modeling theory may allow one to unravel the complex interplay of stochastic single-cell and population processes and to predict the functionality of complex synthetic circuits in growing populations before the circuit is constructed.

At the heart of rational circuit design in synthetic biology lies the assumption that the functionality of complex circuits can be predicted from known properties of their components. Yet in practice, we routinely fail to make predictions of circuit dynamics that would agree with the data at the level expected in physics or engineering. A core reason for this is cell-to-cell variability inside genetically identical cell populations. Such population heterogeneity is often a consequence of the inherent stochasticity of biochemical processes inside cells (1). Cell-to-cell variability may lead to unexpected and undesirable circuit dynamics and has been identified as one of the major roadblocks for designing synthetic circuits with in silico predictable functionality (2, 3). However, it has been shown that identifying and carefully characterizing sources of variability at the single-cell scale allows one to design remarkably robust synthetic circuits (4) or to exploit stochasticity for creating features of cell populations, such as bimodal phenotype distributions, that would otherwise be difficult to engineer (5).

While the single-cell perspective has certainly helped to advance our understanding of cellular processes (6–9), what eventually matters for most applications in synthetic biology is how a particular circuit functions inside growing populations. At the population scale, synthetic circuits may intentionally [e.g., circuits to control growth (10)] or unintentionally [e.g., toxicity or burden caused by the circuit (11, 12)] affect traits of cells that can be selected during population growth. If this is the case, we need to expect that variability that is generated at the single-cell scale (e.g., stochastic production of the burdensome protein) will lead to consequences at the population scale that cannot be predicted solely based on a characterization of the circuit inside single cells (13). However, despite the apparent prevalence of problems where single-cell and population processes are coupled, multiscale models that capture both single-cell stochastic chemical kinetics and population dynamics are rarely used to predict, or even just to explain, how population-scale functionality emerges from single-cell characteristics of synthetic circuits. Presumably, this is because the classically used modeling framework for single-cell processes, that is, the chemical master equation (CME) (14, 15), is only directly applicable at the population scale whenever the population phenotype distribution is equivalent to the distribution of the single-cell process and not additionally shaped by population-level processes (16, 17).

Here we construct an artificial yeast differentiation system in which a Cre-recombinase is expressed from a light-inducible promoter and used to create dynamically controllable yeast communities of differentiated and undifferentiated cell types (18). The system is equipped with four fluorescent reporter proteins to allow for simultaneous measurements of cellular processes and the differentiation state of cells. The core feature of our system is that varying the duration of applied light pulses allows one to modulate the fraction of cells that differentiate even though the entire population is exposed to the same global light stimulation. The system therefore exploits heterogeneity in the response of cells to light to enable external control of population dynamics but by doing so creates a complex coupling between population dynamics and the single-cell process that leads to the production of recombinase. It can therefore serve as an ideal test bed to study what types of models are needed to explain and predict complex dynamics of synthetic circuits at the population scale. We find that a simple deterministic model that ignores all sources of variability can explain dynamics of a chromosomally integrated system version fairly well. However, modifying sources of variability and growth conditions, by expressing the system from plasmids and growing cells in selective media, leads to structural incapacity of the deterministic model to match measured population dynamics. To remedy this shortcoming, we derive a nonlinear version of the CME that tracks conditional probabilities and that can be used to simultaneously model single-cell and population processes. Subsequently, we develop one such nonlinear CME model to represent the chromosomally integrated differentiation system and another to track plasmid copy number fluctuations, plasmid loss, and growth in selective media. We find that composing these two models allows one not only to match but to in silico predict complex emerging dynamics of the plasmid-based differentiation system without any modification of model parameters. Together with similar findings that have been obtained in the past for other systems that affect cellular growth rates (11, 13, 19, 20), our results suggest that the frequently encountered failure of model predictions for composed circuits may in some cases be resolvable with appropriate component models that are carefully constructed to track the coupled dynamics of single-cell and population processes via multiscale stochastic kinetic models.

A Yeast Optogenetic Differentiation System

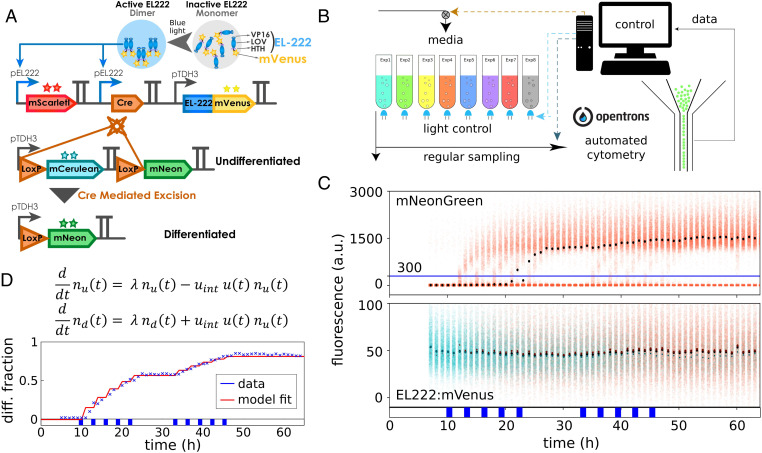
To be able to study the role of cell-to-cell variability in the design and functionality of synthetic circuits, we constructed a yeast optogenetic recombination system whose dynamics can be well observed at the single-cell level thanks to the simultaneous presence of four different fluorescent reporters. Concretely, we started from a circuit design that we recently published (18) and used a Cre-recombinase (Cre) under control of the EL222 promoter (21) to trigger recombination in controllable population fractions using global light stimulation patterns (Fig. 1). When expressed, Cre excises a DNA fragment that is designed such that upon recombination, cells switch from constitutively producing blue fluorescent protein (mCerulean) to producing green fluorescent protein (mNeonGreen). Furthermore, red fluorescent protein (mScarlet-I) is produced alongside Cre from a second copy of the EL222 promoter and provides an observable readout that reports on Cre expression levels in response to light. Finally, EL222 transcription factor is constitutively expressed from a pTDH3 promoter and fused to a yellow fluorescent protein (EL222:mVenus). Fusion of EL222 to mVenus leads to significantly reduced gene expression from the EL222 promoter in response to light (unless light intensity or duration is increased), but this does not impair functionality of our recombination system. In summary, the system allows one to trigger and monitor recombination in cells and to observe correlations of the probability for cells to recombine with cellular amounts of EL222:mVenus. To highlight functional differences between the two emerging cell types and the analogy of our system to natural differentiation systems, we will henceforth refer to cells as differentiated and undifferentiated cells. To test system functionality, we performed experiments using a platform of LED-equipped and fully computer-controlled parallel bioreactors (22). Single-cell measurements are automatically taken by flow cytometry with the help of a programmable pipetting robot (Fig. 1B). Using deconvolution to extract amounts of the different reporter proteins in cells from measured spectral signatures (SI Appendix, section S9), we find that all cells gradually switch from blue to green when sufficient light is applied. However, exposing cell populations to pulses of light leads to bimodal mNeonGreen distributions (Fig. 1C and SI Appendix, Fig. S1), which shows that only a fraction of the population recombines in response to light pulses. Applying a threshold in mNeonGreen fluorescence to classify cells into differentiated and undifferentiated, we can quantify the differentiation dynamics of the system (Fig. 1 C and D). We find that the system’s response to light can be captured fairly well by a simplistic population dynamics model that relates differentiated and undifferentiated cells via a constant differentiation rate in the presence of light (Fig. 1D and SI Appendix, section S1). To test if the probability for a cell to recombine is correlated with single-cell levels of EL222:mVenus and Cre, we analyzed mVenus and mScarlet-I fluorescence distributions shortly after applied light pulses. We find only minor differences in EL222:mVenus levels of undifferentiated cells before and after light induction that are difficult to distinguish from small inaccuracies in deconvolution or reactor-to-reactor variability of the experimental platform (Fig. 1C and SI Appendix, Fig. S1). Overall, we are led to conclude that cell-to-cell variability in EL222:mVenus and Cre can be safely ignored and that the functionality of the system can readily be characterized by a simple deterministic model. However, past experience in synthetic biology has shown that most circuits only function reliably in tightly constrained operating conditions and even seemingly good models retain their predictive power only in the precise context that has been used to construct the model.

Fig. 1.

A yeast optogenetic differentiation system. (A) EL222:mVenus is constitutively produced from a pTDH3 promoter. In the dark, the LOV domain binds the HTH domain and inhibits dimerization and DNA binding. Upon exposure of cells to blue light, this inhibition is disrupted, and EL222:mVenus dimerizes, binds to the pEL222 promoter, and triggers the expression of mScarlet-I and Cre-recombinase. Cre excises a DNA fragment placed between two target LoxP sites that is designed such that cells switch from producing mCerulean to mNeonGreen from a second pTDH3 promoter. (B) Yeast cells harboring the differentiation system are grown in parallel, fully automated bioreactors that are equipped with controllable blue LEDs. Average optical density of cultures is maintained constant, and flow cytometry measurements are taken at regular intervals via a custom-programmed pipetting robot. (C) Upon exposure of the population to short light pulses, some cells recombine as indicated by increasing mNeonGreen levels in a part of the population (Top). Cells are classified as differentiated when they exceed 300 arbitrary units (a.u.) mNeonGreen fluorescence after deconvolution of signals from the four fluorescent proteins (blue line; SI Appendix, section S9). EL222:mVenus is constitutively expressed in all cells, and there are no clearly noticeable differences in EL222:mVenus levels between differentiated and undifferentiated cells (Bottom). Dots show median fluorescence (black, all cells; cyan, undifferentiated cells; orange, differentiated cells). The applied light sequence is shown at the bottom (two times five 1-h pulses with 2 h between subsequent pulses). The data of all four fluorescent reporters are visualized as fluorescence histograms in SI Appendix, Fig. S1. (D) A simple model is capable of capturing population dynamics of differentiated and undifferentiated cells very well. The applied light sequence is shown at the bottom.

Modifying Circuits Leads to Unpredictable Functionality

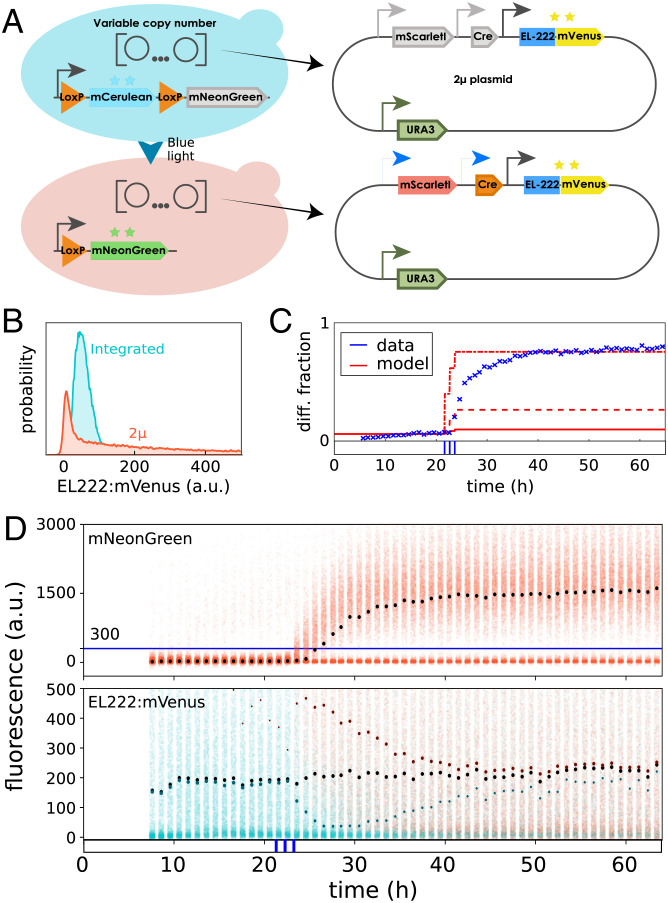
To test if functionality of our differentiation system remains predictable when the circuit is modified, we constructed a variant of the system in which EL222:mVenus and Cre genes are placed on a 2-µ m plasmid instead of being chromosomally integrated (Fig. 2A).

Fig. 2.

Expressing the differentiation system from plasmids breaks straightforward predictability. (A) To analyze consequences of changes in cell-to-cell variability, a new strain was constructed in which Cre and EL222:mVenus genes are placed on 2-µ m plasmids instead of being chromosomally integrated. (B) Measuring stationary EL222:mVenus distributions in the dark for the plasmid-based version of the system (orange) shows that cell-to-cell variability in the amount of EL222:mVenus is strongly increased compared to the integrated version of the system (blue). (C) The simple model of Fig. 1D fails to capture population dynamics for the plasmid-based version of the system. Crosses indicate measured differentiated population fractions. Solid line indicates model predictions using the same parameter values as in Fig. 1D for the integrated system. Dashed line indicates model predictions after adjusting the differentiation rate parameter to account for the presence of multiple copies of the system. Dash-dotted line shows that refitting the model to match final stationary differentiated fractions (30 to 40 h after first light induction) leads to significant model mismatch during early transient dynamics. The applied light sequence is shown at the bottom (three 5-min pulses with 55 min between subsequent pulses). (D) Cell-to-cell variability in EL222:mVenus is strongly increased with some cells displaying much higher fluorescence compared to the integrated system version (Bottom; fivefold increased scale on y axis compared to Fig. 1C). Using mNeonGreen fluorescence (Top) to classify cells into differentiated and undifferentiated (blue line) shows that light causes a transient split in EL222:mVenus distributions of the two subpopulations. The applied light sequence is shown at the bottom. The data of all four fluorescent reporters are visualized as fluorescence histograms in SI Appendix, Fig. S5.

Since plasmid copy numbers vary between cells, we expect this change to lead to significant differences in EL222:mVenus and Cre average levels and additional cell-to-cell variability. Indeed, growing cells in the dark, we find that EL222:mVenus distributions are very different from the integrated system version and characterized by much heavier tails and a mode that is shifted to lower levels (Fig. 2B). Taken together, these two features imply that on average, cells in the population contain more EL222:mVenus (almost sixfold), but at the same time more cells contain less EL222:mVenus compared to the integrated system version (which notably falsifies the a priori expectation that all cells would have higher EL222:mVenus levels due to the presence of multiple plasmids in cells). We may therefore wonder if and how these differences impact functionality of the circuit and if emerging dynamics of the population composition can still be predicted by the simple model in Fig. 1D. Exposing cells to different light patterns, we find that the same amount of light leads to differentiation of more cells for the plasmid-based version of the system (SI Appendix, Fig. S3), which is in line with higher average levels of EL222:mVenus in the population and the presumable presence of multiple plasmids in cells, each carrying a copy of the promoter driving Cre. Adjusting the differentiation rate parameter in the simple deterministic model to account for the on-average presence of multiple copies of the system, however, does not lead to agreement of model predictions and data, nor is it at all possible to obtain any precise fit of this model to the population dynamics that emerge from the plasmid-based differentiation system (Fig. 2C). Analyzing EL222:mVenus distributions, we find that differentiated cells shortly after applied light pulses are characterized by high EL222:mVenus levels, whereas the EL222:mVenus distribution of the undifferentiated subpopulation is shifted to lower levels compared to the total EL222:mVenus population distribution (Fig. 2D). Since EL222:mVenus is constitutively expressed from the same promoter and plasmids in all cells, we conclude that these differences must be caused by selective differentiation of cells with high amounts of EL222:mVenus. Differences between subpopulations gradually disappear over time but are still noticeable up to days after the last application of light to the population (Fig. 2D). This is quite remarkable as it is difficult to comprehend, at a first glance, how a constitutively expressed gene can display a cellular memory of a stimulus that is retained over several tens of cell generations. In conclusion, cell-to-cell variability in EL222:mVenus, which previously seemed to be negligible for the characterization of the system, suddenly appears to be of key importance for understanding how population dynamics emerge from the differentiation system. We may thus ask ourselves if a dedicated characterization of the system with a multiscale stochastic kinetic model that takes into account both single-cell and population processes would have allowed us to retain predictable functionality.

Single-Cell Modeling of the Differentiation System

To test if consequences of changes in the system can be understood and predicted, we constructed a multiscale stochastic kinetic model of the integrated differentiation system and a model of plasmid copy number fluctuations and asked if the models can be composed to predict emerging single-cell and population dynamics when the differentiation system is expressed from plasmids. Concretely, since variability in EL222:mVenus appeared to be of key importance, we deployed a model of bursty production of EL222:mVenus (EL222) and cell differentiation to represent the differentiation system:

$$\begin{array}{ll}\varnothing \stackrel{a}{\to }Z·\text{EL222}& \text{EL222}\stackrel{\lambda }{\to }\varnothing \\ \text{undifferentiated}\stackrel{u_s·u(t)·f(\text{EL222})}{\to }\text{differentiated},& \end{array}$$ [1]

where u_s is the maximal single-cell differentiation rate for given fixed light intensity, u(t) is equal to one in the presence of light and equal to zero otherwise, λ is the cells’ growth rate, and a is the rate at which protein bursts occur. Protein production bursts are of size Z and assumed to be geometrically distributed with average burst size b, $Z\sim \text{Geo}\left(\frac{1}{b}\right)$, as dictated by classical results for modeling stochastic gene expression (23, 24). Since there is no active degradation, EL222:mVenus levels are only reduced by dilution due to cell growth and division, which we incorporated in the model following the standard simplifying approach to represent dilution as a continuously occurring reaction instead of explicitly tracking cell growth and division (see ref. 25 for a comparison of continuous dilution models to more complex models that aim to explicitly represent random distribution of molecules upon cell division). To keep the model as simple as possible, we neglected possible delays or noise caused by the production and action of recombinase or the experimental detection of recombined cells. Instead, we assumed that the probability per unit time for a cell to differentiate in the presence of light is directly a function of the amount of EL222:mVenus, $f(\text{EL222})$, in the cell. When u(t) = 0, the stochastic model in Eq. 1, is a standard model of bursty gene expression ([23]), and the EL222:mVenus distribution follows the master equation

$$\begin{array}{l}\frac{d}{dt}p(x,t)=-(a+\lambda x)p(x,t)+\lambda (x+1)p(x+1,t)\\ +a{\displaystyle \sum _{y=1}^x\frac{1}{b}{\left(1-\frac{1}{b}\right)}^{y-1}p(x-y,t)},\end{array}$$

where $p(x,t)≔\mathbf{P}\left(\text{EL222}(t)=x|\text{EL222}(0)=x_0\right)$. Truncating the state space at some maximal number of proteins $x_{\text{m}}$ and collecting the probabilities of all states in a vector $\mathbf{p}(t)≔{\left[p(0,t)\hspace{0.17em}\cdots \hspace{0.17em}p(x_{\text{m}},t)\right]}^T$, the master equation can be written in vector form as

$$\begin{array}{l}\frac{d}{dt}\mathbf{p}(t)=\mathbf{A}\mathbf{p}(t),\hspace{0.17em}\text{where}\\ {\mathbf{A}}_{x+1,y+1}=\{\begin{array}{ll}-(a+\lambda x)\hspace{0.17em}\hfill & \text{if}\hspace{0.17em}y=x<x_m,\hfill \\ -\lambda x\hspace{0.17em}\hfill & \text{if}\hspace{0.17em}y=x=x_m,\hfill \\ \lambda (x+1)\hspace{0.17em}\hfill & \text{if}\hspace{0.17em}y=x+1,\hfill \\ \frac{a}{b}{(1-\frac{1}{b})}^{x-y-1}\hspace{0.17em}\hfill & \text{if}\hspace{0.17em}y<x<x_m,\hfill \\ {\displaystyle \sum _{z=x-y}^{\infty }\frac{a}{b}{(1-\frac{1}{b})}^{z-1}}\hspace{0.17em}\hfill & \text{if}\hspace{0.17em}y<x=x_m.\hfill \end{array}\end{array}$$

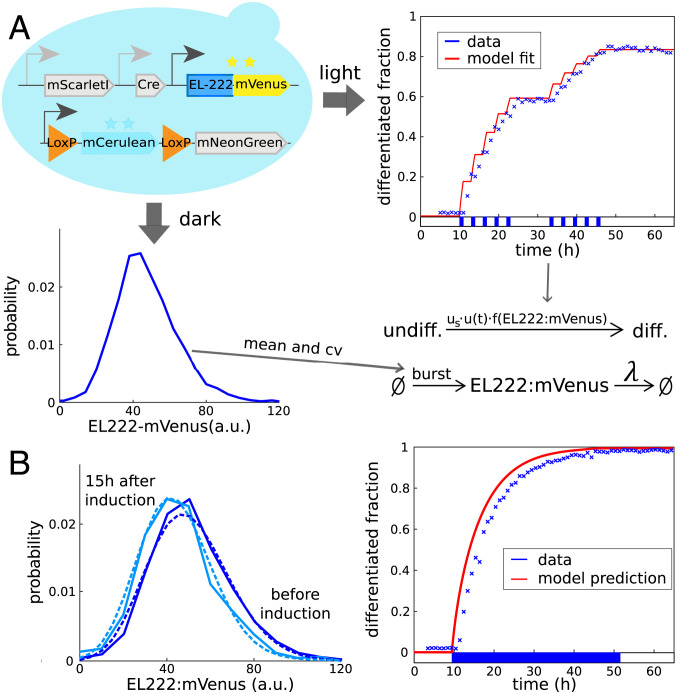
If u(t) remains zero for sufficiently long, the EL222:mVenus distribution converges to a negative binomial distribution that is determined by average burst size and frequency (23, 24). Growing cells in the dark and measuring their mVenus fluorescence by flow cytometry then allows one to determine burst size and frequency (up to a fluorescence scaling factor) from mean and coefficient of variation of measured fluorescence distributions (Fig. 3A, Left).

Fig. 3.

(A) Characterization of the differentiation system. (Bottom) Extracting mean (=50.6 arbitrary units [a.u.]) and coefficient of variation (=0.35) from measured stationary EL222:mVenus distributions before light induction allows one to determine burst frequency and average burst size of the EL222:mVenus production model up to a fluorescence scaling factor (SI Appendix, section S2). (Right) Exposing cell populations to light pulses and measuring dynamics of the resulting population composition (crosses indicate data, line indicates model fit, and applied light sequence is shown at the bottom) then allows one to determine parameters of the differentiation function $u_s·f(\text{EL222})$ (SI Appendix, section S2). (B) Dynamics in continuous light. (Right) Exposing cells to continuous light eventually leads to differentiation of the entire population. (Left) Cells that remain undifferentiated after light induction (light blue) seem to be characterized by slightly lower EL222:mVenus levels compared to initial levels (dark blue) according to both model predictions (dashed) and data (solid). Data from further time points are provided in SI Appendix, Fig. S2.

When light is applied to the population, u(t) = 1, the dynamics of the EL222:mVenus distribution of the undifferentiated cell population are not captured anymore by the plain bursty protein production model. However, Eq. 1 can be augmented with an absorbing state, D, that represents differentiation and transitions to which occur at a rate $u_s·u(t)·f(\text{EL222})$. Denoting this new absorbing state by D and its probability by p(D, t) and defining a new vector of all probabilities ${\mathbf{p}}_s(t)≔{\left[p(D,t)\hspace{0.17em}p(0,t)\hspace{0.17em}\cdots \hspace{0.17em}p(x_{\text{m}},t)\right]}^T$, we obtain the augmented master equation

$$\frac{d}{dt}{\mathbf{p}}_s(t)=\left[\begin{array}{cc}0& {\mathbf{c}}_1\\ \mathbf{0}& \mathbf{C}\end{array}\right]{\mathbf{p}}_s(t),$$

where ${\mathbf{c}}_1=u_s·u(t)·\left[f(0)\hspace{0.17em}f(1)\hspace{0.17em}\cdots f(x_m)\right]$ and matrix C is the same as matrix A except that the outflow terms due to differentiation in ${\mathbf{c}}_1$ are subtracted from the diagonal of A. We can now define conditional probabilities $p_c(x,t)≔\mathbf{\mathbb{P}}\left(\text{EL222}(t)=x|\text{cell}\ne D,\text{EL222}(0)=x_0\right)$ for cells to contain x EL222:mVenus molecules at time t given that differentiation has not occurred yet and deduce that the EL222:mVenus distribution in the subpopulation of undifferentiated cells follows a nonlinear master equation that can be stated in vector form as

$$\frac{d}{dt}{\mathbf{p}}_c(t)=\mathbf{C}{\mathbf{p}}_c(t)+{\mathbf{p}}_c(t)·\left({\mathbf{c}}_1{\mathbf{p}}_c(t)\right),$$ [2]

where ${\mathbf{p}}_c(t)≔{[p_c(0,t)\hspace{0.17em}\cdots \hspace{0.17em}{p}_c(x_{\text{m}},t)]}^T$. Eq. 2 couples the variability generating process at the single-cell scale (stochastic production of EL222:mVenus) to a population process that selectively differentiates cells with high levels of EL222:mVenus. We thus expect that upon light exposure, the EL222:mVenus distribution of the undifferentiated cell population gradually shifts to lower levels. However, this population process is counteracted by the fact that the same variability generating process is operating in all cells and that this process will always drift to the original EL222:mVenus distribution in both subpopulations at a time scale that is determined by the cells’ growth rate. In the absence of light, we therefore expect distributions to trend toward the stationary negative binomial distribution of the bursty protein production model while the continuous presence of light should lead to a quasi-stationary condition in which single-cell and population process are dynamically balanced until eventually all cells will have differentiated. Solving Eq. 2 (numerically) allows us to determine these distribution dynamics in response to varying light inputs u(t). The net population differentiation rate can then be obtained from the solution of Eq. 2 according to

$$k(t)≔{\mathbf{c}}_{\mathbf{1}}{\mathbf{p}}_c(t)={\displaystyle \sum _{i=0}^{m}f(x_i)·p_c(x_i,t)}.$$

Using the data for the light pattern in Fig. 1D, we find that choosing $f(\text{EL222})$ as a steep Hill function with a threshold significantly larger than average amounts of EL222:mVenus leads to good agreement of model and data (Fig. 3A, Right, and SI Appendix, section S2A).

According to this model, we find that the maximum possible shift in EL222:mVenus distributions of undifferentiated cells that can potentially be observed in experiments (in continuous presence of light) is fairly small and of similar size as experimental errors due to inaccurate deconvolution or reactor-to-reactor variability. To test whether such a shift can nevertheless be detected, we exposed cells to continuous light and collected measurements at time points early enough after induction such that sufficiently many cells remain undifferentiated to allow for reliable quantification of EL222:mVenus distributions. We find that experimental EL222:mVenus distributions of undifferentiated cells indeed seem to show a small shift toward lower levels in response to continuous light (SI Appendix, Fig. S2). This shift is in good agreement with distribution dynamics predicted from the model (Fig. 3B, Left, and SI Appendix, Fig. S4). As a side note, the model provides a very good prediction of the increase in the differentiated fraction in response to continuous light (Fig. 3B, Right). Despite the possible presence of small selection effects, we can overall conclude that sufficiently low noise in EL222:mVenus production coupled to sufficiently fast fluctuations implies that cell-to-cell variability has only small consequences for emerging population dynamics. It is now clear, however, that this conclusion will change if either noise levels or time scales of the single-cell process are modified.

Consequences of Plasmid Copy Number Fluctuations

In addition to a single-cell model of the differentiation system, we require a model that captures cell-to-cell variability in plasmid copy numbers. Many, often detailed, models of plasmid copy number fluctuations exist in the literature (26, 27). In order to keep the system characterization as simple as possible, we decided to omit any detailed mechanistic description of processes such as replication failure or unequal division of plasmids between mother and daughter cell (28). Instead, we chose to represent plasmid copy number fluctuations by a simple stochastic birth–death process with both birth rate (representing replication) and death rate (representing dilution due to cell growth) being linear in the plasmid copy number:

$$\begin{array}{ll}P\stackrel{a_p}{\to }P+P& P\stackrel{\lambda }{\to }\varnothing \\ \text{cell}\stackrel{\mu ·{\mathbf{1}}_{\left\{P=0\right\}}}{\to }\text{removed},& \end{array}$$ [3]

where a_p is the plasmid replication rate, λ is the growth rate of cells, and μ is the rate at which cells that have lost the plasmid (${\mathbf{1}}_{\left\{P=0\right\}}$) are removed from the population when cells are growing in selective media. Replication failure can be implicitly incorporated by choosing the replication rate smaller than the cells’ growth rate, which is in any case a necessary feature of a birth–death process model since expected plasmid copy numbers in cells would diverge to infinity if plasmids are replicated faster than cells divide. For $a_p<\lambda$ (and μ = 0), however, the process will eventually reach zero plasmids with probability 1. The rate at which cells in the population lose the (last copy of the) plasmid is then determined by the difference between replication and growth rate. When selective media is used for growth, $\mu >0$, cells that have lost the plasmid will either die or be outgrown, and the plasmid copy number distribution of the population will remain stable. However, this neither implies that there exist no cells without plasmids in the population nor do plasmid copy numbers remain constant from the perspective of single cells. Instead, we should expect a dynamic equilibrium and a quasi-stationary plasmid copy number distribution in which the single-cell plasmid loss process is balanced with selective removal of cells without plasmids (SI Appendix, section S3B). From a mathematical perspective, this result is equivalent to what was obtained previously for EL222:mVenus distributions in the undifferentiated cell population. In both cases, a variability generating process at the single-cell scale (EL222:mVenus fluctuations vs. plasmid copy number fluctuations) is coupled to a state-dependent removal process at the population scale (differentiation vs. removal of cells that have lost the plasmid) and leads to the same type of nonlinear master equation for the cells that have not been removed yet (compare SI Appendix, sections S2B and S3B).

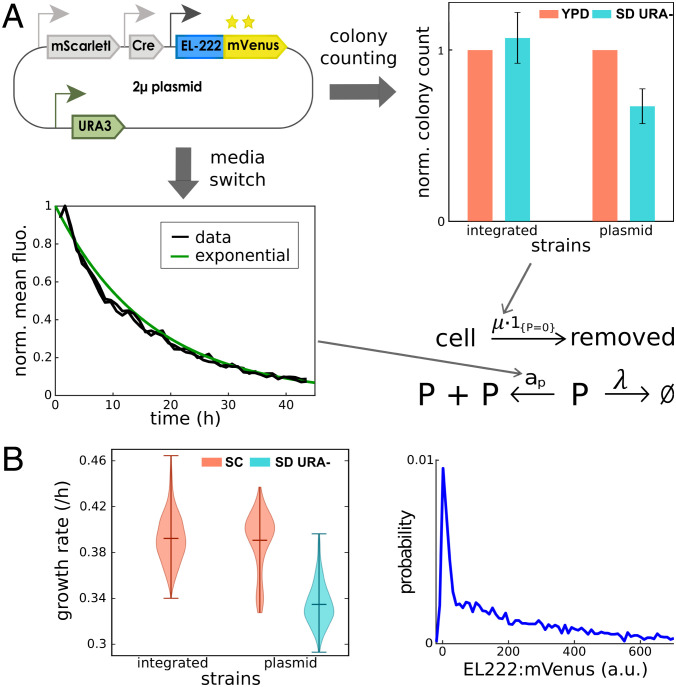
To characterize the full multiscale dynamics of plasmid copy numbers and cell populations, we switched cells from selective to nonselective media and measured how the average abundance of a constitutively expressed protein decays over time. We found that average fluorescence decays approximately exponentially with a rate that is 15% of the cells’ growth rate λ (Fig. 4A, Bottom). Mathematical analysis of the single-cell model (SI Appendix, section S3B) shows that this is a direct consequence of the plasmid replication rate, a_p, being 15% smaller than the cells’ growth rate $a_p=0.85\lambda$. Somewhat counterintuitively, the net population growth rate in selective media is independent of μ. Faster removal of cells that have lost the plasmid means faster reduction (or slower increase) in the total number of cells, but this is compensated by the fact that in stationary growth conditions, the population fraction of cells without plasmids becomes smaller when their removal rate is increased. Therefore, to determine μ, stationary growth rate measurements are insufficient. Instead, it is necessary to directly measure what fraction of the population has plasmids in stationary growth conditions since it can be shown (SI Appendix, section S3A) that this fraction must be equal to $\frac{\mu -\lambda +a_p}{\mu }$ for $a_p<\lambda$ (plasmid numbers do not diverge) and $\mu >\lambda -a_p$ (cells with plasmids can be maintained in the population). Correspondingly, we performed a colony counting experiment (SI Appendix, section S3A) and observed that approximately one-third of all cells do not contain plasmids in stationary growth conditions (Fig. 4A, Right), which allowed us to determine that the removal rate of cells without plasmids, μ, must be approximately 45% of the growth rate, $\mu =0.45\lambda$. Together, the parameters a_p, μ, and λ completely characterize the multiscale dynamics of plasmid copy number fluctuations and growth in selective media.

Fig. 4.

(A) Characterization of plasmid copy number dynamics. (Bottom) After switching cells from selective to nonselective media, the rate of exponential decay of average levels of a protein that is constitutively expressed from plasmids (here EL222:mVenus) can be measured to determine the population plasmid loss rate and to fix the plasmid replication rate in the model. Mean fluorescence (normalized by its maximum) of two replicates is shown. (Right) Stationary fractions of cells without plasmids determine the removal rate in selective media of cells that have lost the plasmid. These fractions can be measured by a colony counting experiment as described in SI Appendix, section S3A. (B) Consequences of plasmid copy number fluctuations. Expressing the differentiation system from plasmids leads to modified population distributions of EL222:mVenus (Right) as well as changes in the effective population growth rate (Left). Violin plots are composed of growth rate estimates based on cell density averaged over all reactors of the turbidostat and multiple experiments (in total 19 reactors for the strain with the integrated system, 12 for the strain with the plasmid-based system in selective media, and 6 in nonselective media).

To test the model and to better understand possible consequences of plasmid copy number fluctuations, we experimentally determined effective population growth rates of our cells in selective and nonselective media. We found that after preculture in selective media, populations of cells carrying the plasmid-based differentiation system quickly adopt the same growth rate as populations of cells carrying the integrated system version when transferred to nonselective media. Subsequently, the population growth rate remained constant, and no dependence on the fraction of cells that still carry plasmids was detected. When grown in selective media, however, populations of cells carrying the plasmid-based differentiation system display an effective growth rate that is reduced by approximately 15% (Fig. 4B, Left). Analyzing the model, we find that the reduction in growth is a consequence of removal of cells that have lost the (last copy of) the plasmid and that the observed reduction by 15% is in quantitative agreement with model predictions and another consequence of the plasmid replication rate, a_p, being 15% smaller than the single-cell growth rate λ. Overall, we should expect that placing the differentiation system on plasmids will significantly alter variability in EL222:mVenus levels (Fig. 4B, Right) and also modify effective population growth.

Having constructed single-cell models of the differentiation system and plasmid copy number fluctuations, we are now in a position to ask the central question of this manuscript: is it possible to quantitatively predict functionality of the plasmid-based differentiation system without having to change the model or even just to reidentify model parameters for the new conditions?

Prediction of Circuit Functionality

To test if the dynamics of the plasmid-based differentiation system can be predicted by combining models calibrated on parts of the system, we coupled the single-cell model of the integrated differentiation system, Eq. 1, to the model of plasmid copy number fluctuations, Eq. 3, to obtain a composed model that can be stated in reaction network form as

$$\begin{array}{l}\begin{array}{ll}P\stackrel{a_p}{\to }P+P& P\stackrel{\lambda }{\to }\varnothing \\ P\stackrel{a}{\to }P+Z·\text{EL222}& \text{EL222}\stackrel{\lambda }{\to }\varnothing \end{array}\\ \begin{array}{cc}\begin{array}{l}\text{undifferentiated}\stackrel{u_{int}·u(t)·f(\text{EL222})}{\to }\text{differentiated}\\ \text{undifferentiated}\stackrel{\mu ·{\mathbf{1}}_{\left\{P=0\right\}}}{\to }\text{removed}\\ \text{differentiated}\stackrel{\mu ·{\mathbf{1}}_{\left\{P=0\right\}}}{\to }\text{removed}.\end{array}& \end{array}\end{array}$$ [4]

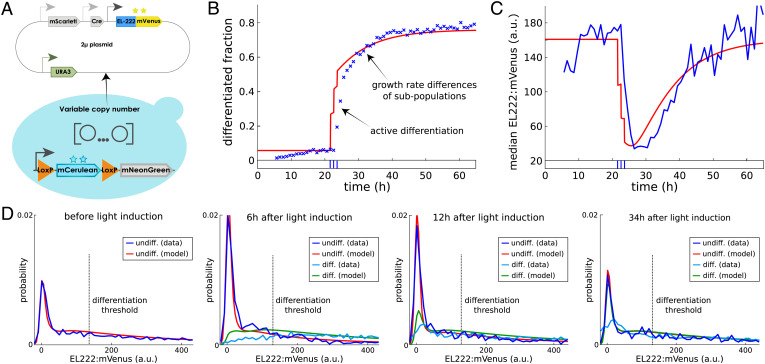
We highlight that the coupling of the two models is very natural and does not introduce any new parameters: the protein burst rate is now scaled by the plasmid copy number since production can occur from any copy of the plasmid, while all other model parts are exactly the same as previously characterized. To test if complex functionalities of our circuit such as population dynamics emerging from single-cell stochastic biochemical processes can be predicted without any adjustment of model parameters, we used the composed model to predict the dynamics of the plasmid-based version of the differentiation system for the light stimulation pattern in Fig. 2D and compared the results to data. We find that population dynamics of differentiated and undifferentiated cells are very well predicted without any adjustment of model parameters (Fig. 5B).

Fig. 5.

Prediction of emerging population dynamics for the plasmid-based differentiation system. (A) Sketch of the plasmid-based differentiation system. (B) Emerging dynamics of the differentiated fraction according to the composed model (red) for the same light input as in Fig. 2D are compared to experimental data (blue). According to the model, late increases in the differentiated fraction are due to varying subpopulation growth rates and not caused by active differentiation. (C) Upon light induction, median EL222:mVenus levels of undifferentiated cells drop fivefold to sixfold as predicted by the composed model. a.u., arbitrary units. (D) In the first panel, the model-predicted EL222:mVenus distribution in the dark agrees very well with experimental data even though these data were not used to parametrize the model. According to the model, the peak of the distribution close to zero corresponds to the $\sim 33\%$ of cells without plasmids (Fig. 4A). In the second and third panels, shortly after the application of light, cells with EL222:mVenus levels above the threshold parameter of the differentiation Hill function (dashed line) are enriched in the differentiated population while the undifferentiated population contains more cells without plasmids (increased peak close to zero). In the fourth panel, when cells are subsequently kept in the dark, EL222:mVenus distributions converge back to the initial condition. Model predictions show remarkable agreement with measured EL222:mVenus distribution dynamics, except for seemingly lower numbers of differentiated cells without plasmids in the data (in particular after 34 h). This small mismatch is presumably caused by inaccuracies in deconvolution (the presence of mNeonGreen in cells makes it difficult to precisely quantify low mVenus levels in cells; SI Appendix, section S9). Full time-varying distribution data of all fluorescent reporters for this experiment are displayed in SI Appendix, Fig. S8.

Comparing EL222:mVenus distributions in the two subpopulations between model and data shows that the high quality of population-level predictions is a consequence of the fact that the model predicts correctly how single-cell processes will operate in union with population-level processes to shape the full dynamics of EL222:mVenus distributions in undifferentiated cells (Fig. 5 C and D and SI Appendix, Fig. S5). In particular, the heavy tails of EL222:mVenus distributions for cells growing in darkness (observed already in Fig. 2B) emerge naturally from the fact that plasmid copy numbers can fluctuate significantly in the model. These heavy tails imply that significantly more cells have EL222:mVenus levels above the threshold of the differentiation Hill function $f(\text{EL222})$ and will recombine quickly upon light induction. Shortly after light induction, the remaining undifferentiated cell population is therefore shifted to significantly lower EL222:mVenus levels (fivefold to sixfold reduction of the median; Fig. 5C), while the differentiated cell population inherits the heavy tail of the original distribution (Fig. 5D). While not experimentally measurable, it can be deduced that according to the model the same holds true for plasmid copy number distributions in subpopulations (SI Appendix, Fig. S6). As a consequence, the population differentiation rate spikes very high upon first light induction but is significantly reduced when subsequent light pulses are applied before the EL222:mVenus distribution of the undifferentiated cell population has converged back to its initial condition (SI Appendix, Fig. S7). When the light stimulus is maintained for some time, fluctuations in plasmid copy numbers create larger fluctuations in EL222:mVenus amounts compared to the integrated version of the system, which leads to more frequent threshold crossing events and therefore larger population differentiation rates.

Eventually, the plasmid-based version of the system reaches differentiated population fractions close to 100% very quickly when light is maintained (SI Appendix, Fig. S10) despite the fact that a large part of the population (around a third) displays EL222:mVenus levels that are close to zero at all time points. According to the model, these are cells that have lost the plasmid (SI Appendix, Fig. S6), cannot differentiate, but are likely to be removed at subsequent time points due to growth in selective media (see SI Appendix, section S7.2 for experimental results in nonselective media). The coupling of plasmid loss dynamics and selective media with the differentiation system therefore leads to unintuitive population dynamics in which seemingly the entire population can recombine despite a continuous presence of many cells that are not carrying any copy of the differentiation system. Another complex consequence of the coupling of single-cell and population processes is that the split in plasmid copy numbers between subpopulations that follows from selective differentiation of cells with high EL222:mVenus levels leads to different subpopulation growth rates in selective media (SI Appendix, Fig. S7) since cells that have lost the plasmid (or are close to losing it) are enriched in the undifferentiated subpopulation. This implies that the differentiated population fraction will continue to increase even if light is removed and no more active differentiation takes place, which explains why the assumption of the simple deterministic model in Fig. 1D, that the differentiated population fraction can only increase due to active differentiation, led to structural incapacity of the model to explain the slow transient differentiation dynamics and significantly increasing differentiated fractions up to 10 h after last light induction (Fig. 5B). If the light stimulus is removed, EL222:mVenus subpopulation distributions converge back to the original distribution (Fig. 5D) but remain noticeably different for at least a day after last light induction. This experimental observation is in good agreement with slow convergence of subpopulation plasmid copy numbers to their quasi-stationary distribution in selective media, which creates a surprisingly long subpopulation memory of applied light stimuli (SI Appendix, Fig. S6).

To provide further experimental backup for these model-based results, we constructed a third version of our differentiation system where the system components are expressed from more tightly regulated centromeric plasmids. Regulation of plasmids copy numbers leads to less cell-to-cell variability in the population and an effectively decreased time scale of fluctuations and plasmid loss (SI Appendix, Fig. S14). As expected based on the modeling and theory, we observe that the centromeric strain displays a reduction of EL222:mVenus levels in undifferentiated cells that is less pronounced but sustained for longer (SI Appendix, Fig. S17B). Since subpopulation plasmid copy number distributions require more time to reequilibrate to initial conditions after the application of light, growth rate differences between differentiated and undifferentiated cells are sustained for even longer compared to the 2-µ m version of the system, and the differentiated population fraction continues to increase in the dark for several days (SI Appendix, Fig. S17A). Switching the media of the bioreactor to nonselective stops the gradual increase of the differentiated fraction but leads to cells without plasmids accumulating in the population (SI Appendix, Fig. S18). We conclude that deploying multiscale stochastic chemical kinetics models for understanding the interplay of single-cell and population processes allows us to understand and predict complex emerging dynamics when the differentiation system is placed on plasmids and cells are grown in selective media. Population dynamics for plasmid strains, despite being shaped by cell-to-cell variability, are deterministically reproducible (SI Appendix, Fig. S12). Thus, the capacity to predict such dynamics implies that the interplay of single-cell and population processes can be exploited for creating features of microbial community dynamics that would otherwise be difficult to engineer.

Optogenetic Control of Constitutive Gene Expression

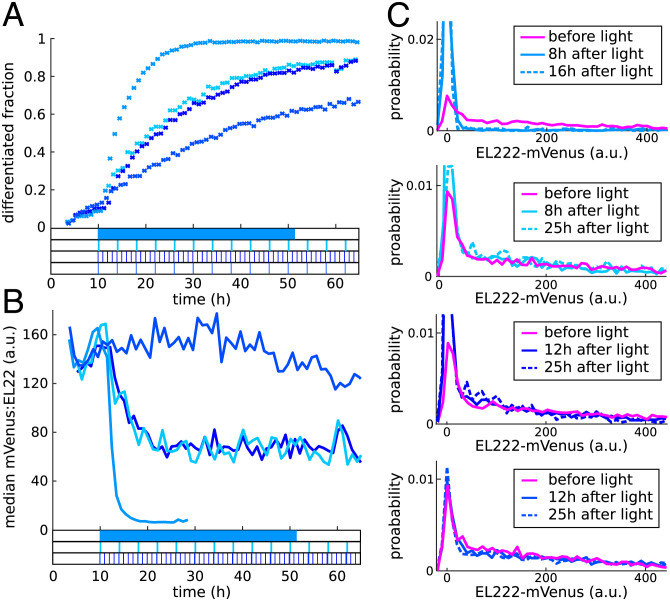
In the previous section, we demonstrated that coupling of single-cell and population processes may lead to outcomes that are fairly unintuitive such as dynamically changing distributions of a constitutively expressed gene or increasing fractions of differentiated cells in the absence of active differentiation. In practice, such couplings will often be seen as a nuisance, but we may also ask if the interplay of stochastic single-cell processes and population dynamics can be exploited to create and control features of cell populations that would otherwise be impossible to engineer. For instance, in light of the results of this paper, we may ask if it is possible to use light to regulate constitutive gene expression, plasmid copy numbers, and growth rates of subpopulations via targeted differentiation of cells with high EL222:mVenus levels. Since neither plasmid copy numbers nor subpopulation growth rates are directly measurable on our experimental platform, we set ourselves the goal to regulate the constitutively expressed EL222:mVenus. Concretely, according to our theoretical results (convergence to a quasi-stationary distribution; SI Appendix, sections S2B and S3B), it should be possible to maintain EL222:mVenus levels in the undifferentiated cell population at reduced constant levels by applying continuous light for sufficiently long. Indeed, we find that EL222:mVenus distributions in undifferentiated cells quickly reach a distribution that remains invariant when the population is exposed to continuous light (Fig. 6C, Top). However, this distribution is characterized by a median of almost zero (Fig. 6B), which indicates that only cells that have no EL222:mVenus (and presumably no plasmids) remain undifferentiated. Furthermore, 15 to 20 h after the start of light application, almost all cells are differentiated, and the population displays a slightly reduced net growth rate, presumably due to toxicity of DNA-bound EL222:mVenus (SI Appendix, section S8 and refs. 11, 13). To test if also low but nonzero EL222:mVenus levels in undifferentiated cells can be stably maintained, we exposed cells to a number of different light sequences that mimic continuous light with short pulses that are regularly repeated with an interpulse duration that is short in comparison to the duration of the experiment. We find that applying light for 2 min every 4 h or for 1 min every 1 h leads to approximately halved median EL222:mVenus levels in undifferentiated cells (Fig. 6B). In both cases, the full EL222:mVenus distribution of undifferentiated cells remains approximately invariant after around 12 h have passed from first light application (Fig. 6C, Middle; see also SI Appendix, Fig. S13). Finally, we applied a light sequence with only half-minute light pulses applied every 4 h and found that in this case, the EL222:mVenus distribution of undifferentiated cells differs only very moderately from the initial population distribution at all time points (Fig. 6C, Bottom) despite the fact that the differentiated population fraction increases (Fig. 6A).

Fig. 6.

Optogenetic control of constitutive gene expression. (A) Regularly repeated short light pulses (shown at the bottom) lead to a slow steady increase in the differentiated population fraction while the differentiated fraction increases fairly quickly in response to continuous light. (B) Over intermediate time periods, repeated selective differentiation and reversion to the mean balance each other, which leads to approximately constant EL222:mVenus medians in all cases. (C) After transient dynamics in response to the start of the light sequence, EL222:mVenus distributions in undifferentiated cells reach a quasi-stationary form that remains invariant for extended time periods (see also SI Appendix, Fig. S13). Color coding of distributions labels corresponds to the light sequences and data in A and B.

To conclude, understanding and characterizing the consequences of cell-to-cell variability allowed us to optogenetically regulate the (subpopulation) expression level of a constitutively expressed gene, a feat that seems quite counter intuitive at a first glance and that is not realizable in any obvious way by other means.

Discussion

Quantitatively predicting the dynamics of complex synthetic circuits before the circuit is constructed is the key challenge that needs to be mastered to turn synthetic biology into a true engineering discipline. Yet, while our capacity to construct complex circuits is continuously increasing, our capability to predict circuit functionality from supposedly known and characterized circuit components remains, at best, limited to very tightly constrained operating conditions and qualitative and/or stationary outputs (29). We exemplified this problem for the case of our optogenetic differentiation system by showing that predictions obtained from a simple deterministic model break down as soon as the context in which the system is used (plasmid-based expression of proteins and growth in selective media) is modified (Fig. 2). The concrete reasons for the failure of model predictions may be manifold and caused by unexpected component-to-component interactions [e.g., retroactivity (30) or resource competition (31)] or couplings of the circuit to processes of the host [e.g., burden (12), growth (32, 33), or saturation of the host’s degradation machinery (4)]. Eventually, however, all these reasons are but different facets of a common problem: our incapacity to foresee the consequences of complex interdependencies of a circuit in vivo.

For our optogenetic differentiation system, expressing proteins from plasmids led to unforeseen couplings of plasmid copy number fluctuations, growth in selective media, and selective differentiation, which, for instance, created seemingly slow differentiation dynamics that remained mysterious (even to us) in the absence of an explanatory model (Fig. 2D). We thus set out to construct dedicated multiscale stochastic kinetic models of the circuit’s components in their population context (Figs. 3 and 4). Since the CME in its standard form does not capture population processes, it was necessary to augment the CME and to derive a nonlinear version for conditional probabilities to correctly capture dynamics of population distributions (SI Appendix, sections S2B and S3B). We then used our theoretical results to determine experiments that can be used to readily extract parameters of the two component models from data (Figs. 3A and 4A). Merging the so-obtained models to construct a model of the plasmid-based differentiation system (Eq. 4), we found that the composed model does not only resolve the previously not understood features but quantitatively predicts the consequences of complex component interactions without any adjustment of model parameters (Fig. 5). This is a particularly encouraging finding as it demonstrates that, at least for the system studied in this paper, our incapacity to foresee the consequences of complex interdependencies of circuit components and couplings of single-cell and population processes can be remedied by appropriate characterization of circuit components. Importantly, with the ability to foresee consequences comes the possibility to exploit such couplings in the design (34). This is evidenced by our result that the circuit allows one to modulate constitutive gene expression (and presumably plasmid copy numbers and net growth rates) in subpopulations via the application of light (Fig. 6), a feat that seems impossible upon a first glance at the circuit’s wiring diagram (Fig. 1A).

To conclude, we highlight that for the application considered in this paper, the crucial ingredient for obtaining a faithful model was to augment the CME to incorporate population processes in addition to single-cell dynamics that are classically tracked in stochastic models. It is to be expected that the same will hold true for many other applications where couplings of single-cell and population processes are likely to be at play (35–39). This is notably the case for synthetic circuits that are constructed to produce proteins in large quantities since this creates a burden for cells that may lead to growth rate variability between cells and a dynamical enrichment of low-producing cells upon induction of protein production. Furthermore, similar couplings between scales are likely also present in many natural systems such as selective killing of cancer cells with particular states of internal processes in response to treatments that induce the apoptotic pathway (40) or differential responses of bacteria to antibiotic treatments (41), to name but two possible examples. We therefore expect that our approach for calculating with multiscale stochastic kinetic models will be of use far beyond the particular case study considered here. It needs to be noted, however, that for cases where the single-cell model is more high-dimensional than the fairly small models considered here, tracking the entire solution of the corresponding master equation will be computationally infeasible. Further work is thus necessary to develop and test approaches for approximately calculating with multiscale stochastic kinetic models (17, 42).

Data Availability

Raw data and software are publicly available as CSV and MATLAB files in Zenodo (DOI: 10.5281/zenodo.5155290).