A Revisit of the k-Space Filtering Effects of Magnetization-Prepared 3D FLASH and Balanced SSFP Acquisitions: Analytical Characterization of the Point Spread Functions

Abstract

Purpose:

3D FLASH and balanced SSFP (bSSFP) are increasingly used in quantitative MRI after contrast preparation. The acquired k-space data are modulated by T₁ relaxation (or additional T₂ for bSSFP). Three separate sequence parameters including the number of phase-encoding steps per shot (N), flip angle (FA), and TR have made the transient state of rapid gradient echo (GRE) imaging difficult for analysis and optimization. Here we aim to analytically characterize the k-space filtering effect of magnetization-prepared FLASH and bSSFP with the point spread functions (PSF).

Methods:

The amplitude effect is characterized with the peak magnitude of the PSF, i.e. PSF(0), which, due to their approaching from transient state to steady-state for the GRE acquisitions, obeys a linear (with a slope and an intercept, not proportional) relationship with the prepared longitudinal magnetization (M_prep). The blurring effect is characterized by the FWHM of the PSF. The magnetization-prepared acquisition-dependent image contrast efficiency is characterized with the relative contrast-to-noise ratio (CNR) per unit time (ruCNR).

Results:

The slope of PSF(0) characterizes the relative contrast between different M_prep levels. The intercept of PSF(0) could lead to quantification bias for magnetization-prepared imaging. FLASH and bSSFP experience very little blurring effect, which is to the contrary of conventional fast spin echo (FSE). Analytical selections of N, FA, and TR are provided to optimize ruCNR for different scenarios.

Conclusions:

PSFs of the FLASH and bSSFP acquisitions are analytically derived and numerically validated, and compared with the FSE acquisition, thus providing a useful tool for optimizing magnetization-prepared GRE acquisitions.

1. Introduction

A straightforward approach to obtain many MR contrast with 3D volumetric coverage is to apply a magnetization-preparation module followed by a rapid acquisition module, which could be EPI, fast spin echo (FSE), gradient and spin echo (GRASE), FLASH, and balanced SSFP (bSSFP), etc. It is desirable to choose a 3D acquisition scheme with high SNR efficiency while filling as many phase-encoding (PE) k-lines as possible right after each magnetization-preparation module. The signal decay or recovery due to T₂*, T₂ or T₁ relaxation through an extended acquisition duration imposes a k-space filtering effect, which depends on the acquisition scheme, as well as the low-high (centric, center k-lines first) or linear (sequential) profile order being used.

This k-space filtering effect is described as a real modulation transfer function (MTF) in the k-space and a symmetric point spread function (PSF) in the image space as a Fourier transform pair. The PSF has been analytically derived for T₂ exponential decay during a long echo train [1] for FSE type of sequences (including GRASE) with 180° refocusing pulses. The amplitude of the signal can be represented by the maximum magnitude of a PSF function. When considering both the amplitude-loss effect induced by the T₂ decay and the SNR gain from the long acquisition duration based on MR sampling theory, the maximum SNR per unit time can be obtained when the echo train duration is about 1.2T₂ for a Cartesian PE direction (for example, any phase encoding direction in Cartesian scans, partition dimension in stack-of-radial or stack-of-spiral scans) [1]. The blurring of the image can be characterized in terms of FWHM of the PSF function, which describes the broadness of the peak at half of the maximum magnitude. FWHM increases with longer echo train duration following a quadratic function [1]. Similar analysis has been conducted for 1D, 2D, and 3D radial k-space trajectories in ultrashort echo-time imaging [2] and could be expanded to the T₂* decay effect through PE lines of EPI readout. These analyses indicate that EPI or FSE/GRASE sequences suffer strong signal loss and image blurring with a prolonged acquisition window, with its optimal duration on the order of T₂* or T_2, respectively.

Rapid gradient-echo (GRE) imaging [3] such as FLASH and bSSFP are alternative acquisition strategies that are often selected for steady-state imaging [4, 5]. FLASH applies gradient- and/or RF-spoiling at the end of each short TR to eliminate transverse magnetization, yielding pure T₁ weighting [3]. bSSFP does not apply spoiling gradients between alternating excitation pulses and its steady-state signal is known to exhibit a T₂/T₁ contrast [6, 7]. GRE sequences are typically short in each k-line readout and thus do not have severe distortion or signal drop in areas with severe B₀ field inhomogeneity.

Magnetization-prepared methods always acquire transient magnetization before the steady-state is reached, with low-high profile order typically employed [8]. FLASH, or called as spoiled gradient echo (SPGR), turbo FLASH (TFL), turbo field echo (TFE) by different vendors, has been incorporated for magnetization-prepared sequences to generate different contrast, e.g., T₁ [8–12], T₂ [13–16], diffusion [17–19], perfusion [20, 21], functional MRI [19, 20, 22], MT [23, 24], CEST [25], MRA [26–29], and water-fat separation [30, 31]. bSSFP has also been applied immediately after different contrast preparations, e.g., T₂ [32–34], diffusion [35, 36], T₁ rho [37], and MRA [38–40].

It is understood that the signal evolution of the GRE acquisitions influences the obtained image contrast in the PE direction [3, 8, 41]. The k-space filtering effects with regard to MTF have been analytically described for the transient phase of FLASH during the late 1990’s [12, 14, 17, 18] and of bSSFP in the early 2000’s [42], respectively. Their MTFs depend on TR, flip angle (FA), the number of PE steps per shot (N), and T₁ (additional T₂ factor for bSSFP). As observed in these earlier studies about the MTF transitioning from the prepared magnetization (M_prep) toward the steady-state (M_ss) [12, 14, 17, 18], the signal acquired at the later excitation steps is a summation of one M_prep-proportional term and one M_prep-independent term. The postulation was made subsequently that the image contrast of FLASH would also carry such a linear (not proportional) relationship with M_prep, and the M_prep-independent term as an intercept should be either fitted or corrected for quantitative parameter mapping [12, 14, 17, 18].

However, as no detailed analysis of the PSF was ever given, the quantification bias was gradually overlooked by many following works employing transient 3D GRE acquisitions, and blurring is still commonly mentioned in numerous papers as an adverse effect of 3D GRE sequences without specification of its relative degree. Choosing an optimal 3D acquisition scheme for a wide range of applications with contrast preparation will benefit from a full understanding of its PSF. Here we aim to provide rigorous analytical derivations of PSFs of both FLASH and bSSFP acquisitions based on general sequence parameters and relaxation values, and characterize their relative contrast, quantification bias and blurring effect. Note that, for GRE, relative contrast instead of relative signal is investigated for PSF analysis due to its signal eventually approaching a steady-state regardless of M_prep. Furthermore, the properties in terms of contrast loss and image blurring will be compared among FLASH, bSSFP and FSE based acquisitions with strategies discussed for optimizing the respective sequence parameters.

2. Methods

2.1. General framework

2.1.1. Modulation transfer function (MTF) and point spread function (PSF)

Since the k-space filtering effect due to magnetization relaxation manifests mainly along the slowest PE direction in each echo train (assumed as z-direction), the following derivations are limited in 1D along this direction. The MTF applies a multiplication filter onto the original k-space:

$$S\left(k\right)=S_{ori}\left(k\right)\cdot MTF\left(k\right),$$ (1)

where k is the k-space location, S(k) is the signal acquired within the k-space, S_ori(k) is the original signal without magnetization-relaxation induced signal evolution through these k-space locations, which is described as MTF(k). For simplicity, the k-space location is normalized to the entire range of the k-space along the assumed z-direction [-π/∆z, π/∆z] by dividing 2π/∆z, such that k ϵ [-0.5, 0.5].

With N as the number of PE steps acquired in the echo train per shot (also referred to as echo train length (ETL) for FSE, or turbo factor for FLASH and bSSFP), and the function M_xy(n) as the transverse signal acquired at the n^th PE step, the MTF of a linear (LN) and low-high (LH) profile orders are:

$$MT{F}^{LN}\left(k\right)=M_{xy}\left(n\left(k\right)\right)=M_{xy}\left(\left(k+0.5\right)N+1\right),$$ (2)

$$MT{F}^{LH}\left(k\right)=M_{xy}\left(2\left|k\right|N+1\right).$$ (3)

The PSF is the Fourier transform of the MTF:

$$PSF\left(z\right)={\int }_{-0.5}^{0.5}MTF\left(k\right)e^{i2\pi kz}dk,$$ (4)

where z is the index of image pixels, and i is the imaginary unit. The range of z here is the reciprocal of the k-space resolution (∆k = 1/N), so z ϵ [-N/2, N/2], The image (I) is a circular convolution of the original image (I_ori) and the PSF:

$$I\left(z\right)=I_{ori}\left(z\right)\otimes PSF\left(z\right),$$ (5)

The convolution with PSF results in two effects on the images as mentioned in the Introduction section: an amplitude effect that can be characterized with the peak magnitude of the main lobe of the PSF, i.e. PSF(0), and a blurring effect that can be characterized with the FWHM of the main lobe of the PSF.

Note that PSF(0) is the integral of the transverse signal acquired at all echoes, which is not affected by the profile order:

$$PS{F}^{LN}\left(0\right)=PS{F}^{LN}\left(0\right)={\int }_{-0.5}^{0.5}\text{MTF}\left(k\right)dk={\int }_1^N{M}_{xy}\left(n\right)dn.$$ (6)

Because the MTF is real, the PSF is an even function. Therefore, the FWHM satisfies abs(PSF(FWHM/2)) = PSF(0)/2. As it is difficult to find the analytical solution of the FWHM due to the complexity of the PSF formula, the FWHM is obtained numerically in this work.

2.1.2. Relative contrast-to-noise ratio (CNR) per unit time (ruCNR)

Following a contrast-preparation module, the prepared magnetization is established, M_prep ϵ [-M⁰, M⁰], with M⁰ as the equilibrium magnetization. For simplicity, only gradient echoes or spin echoes are taken into account in this work, and stimulated echoes or other coherent echoes resulted from applying multiple RF pulses between preparation and acquisition are considered to be mitigated by adequate gradient or RF spoiling. Likewise, off-resonance effects are also ignored here assuming sufficient shimming. We will confirm in the following sections that PSF(0) and the initial longitudinal magnetization, M_prep, always obeys a linear relationship for different acquisition sequences:

$$PSF\left(0\right)=a\cdot M_{prep}+b$$ (7)

where a is the slope and b is the intercept, when M_prep = 0, PSF(0) = b.

Based on MR sampling theory, the SNR per unit time (uSNR) per voxel for the image signal is proportional to the square root of the acquisition window duration [43], which can be approximated as N∙TR through N PE steps for FLASH and bSSFP (the readout time is assumed to be close to TR for the maximal efficiency). If the signal being acquired is constant, such as in steady-state, then uSNR is increased with higher N or longer TR. However, the uSNR is also proportional to PSF(0), which is modulated by both M_prep and the signal relaxation during the acquisition (Eq. (7)). Hence, the uSNR is proportional to the multiplication of two factors, PSF(0) and $\sqrt{N\cdot TR}$:

$$uSNR\propto PSF\left(0\right)\cdot \sqrt{N\cdot TR}.$$ (8)

As indicated in the Introduction section and explained in more details below, the transient signal of FLASH and bSSFP eventually approach a steady-state regardless of M_prep.

The contrast-to-noise ratio (CNR) is used as a measure of the image contrast of the imaging sequences. A relative CNR per unit time (ruCNR) can be defined as the ratio of the difference of uSNR over the difference of M_prep at two prepared longitudinal magnetizations, M_prep,1 and M_prep,2.

$$\begin{array}{l}ruCNR=\frac{uSN{R}_{prep,1}-uSN{R}_{prep,2}}{M_{prep,1}-M_{prep,2}}\propto \frac{PS{F}_{prep,1}\left(0\right)-PS{F}_{prep,2}\left(0\right)}{M_{prep,1}-M_{prep,2}}\cdot \sqrt{N\cdot TR}\\ =\frac{\left(a\cdot M_{prep,1}+b\right)-\left(a\cdot M_{prep,2}+b\right)}{M_{prep,1}-M_{prep,2}}\cdot \sqrt{N\cdot TR}=a\cdot \sqrt{N\cdot TR}.\end{array}$$ (9)

The expression of ruCNR is proportional to slope a. The uSNR is a special case for ruCNR when intercept b is zero, such as for FSE in the following analysis. An imaging sequence with higher ruCNR can better preserve the image contrast set by the preparation pulses.

2.2. FSE

2.2.1. MTF and PSF of FSE

Conventional FSE refers to the acquisition consisting of a 90° excitation pulse and N 180° refocusing pulses with an echo space of TE and N PE steps centered at the formed spin echoes. The analytical expression of MTF and PSF of FSE sequence was derived previously [1] and, in order for more consistent comparison with FLASH and bSSFP, is slightly modified here with the new framework with respect to the normalized k-space location and the M_prep. The transverse magnetization M_xy(n) acquired at the n^th spin echo is:

$$M_{xy}\left(n\right)=M_{prep}\cdot e^{-\left(n-1\right)TE/T_2}=M_{prep}\cdot E_2^{n-1},$$ (10)

with $E_2=e^{-TE/T_2}$.

The MTF of FSE with linear and low-high profile orders are derived from Eq. (2) and (3), respectively:

$$MT{F}_{FSE}^{LN}\left(k\right)=M_{xy}\left(\left(k+0.5\right)N+1\right)=M_{prep}\cdot E_2^{\left(k+0.5\right)N}.$$ (11)

$$MT{F}_{FSE}^{LH}\left(k\right)=M_{xy}\left(2\left|k\right|N+1\right)=M_{prep}\cdot E_2^{2\left|k\right|N}.$$ (12)

Corresponding PSFs of FSE with linear and low-high profile orders are derived from Eqs. (4) and (11), (12), respectively (Supporting Information S1):

$$PS{F}_{FSE}^{LN}\left(z\right)=M_{prep}\cdot \frac{E_2^N{e}^{i\pi z}-e^{-i\pi z}}{N\ln E_2+i2\pi z},$$ (13)

$$PS{F}_{FSE}^{LH}\left(z\right)=M_{prep}\cdot \frac{E_2^{N}N\ln E_2\cos \left(\pi z\right)+{E_2}^N\pi x\sin \left(\pi z\right)-N\ln E_2}{N^2{\ln }^2{E}_2+{\pi }^2{z}^2}.$$ (14)

The amplitude-loss effect of an FSE sequence, characterized with PSF(0), is equivalent for linear and low-high profile orders. Based on Eq. (14):

$$PS{F}_{FSE}\left(0\right)=PS{F}_{FSE}^{LN}\left(0\right)=M_{prep}\cdot \frac{E_2^N{e}^0-e^0}{N\ln E_2+0}=M_{prep}\cdot \frac{E_2^N-1}{N\ln E_2}.$$ (15)

Note that Eq. (15) is consistent with Eq. (28) of the previous work [1] when M_prep = 1. Hence PSF_FSE(0) is proportional to M_prep, and following Eq. (7), the slope a and intercept b of the linear relation between PSF_FSE(0) and M_prep for FSE are:

$${\alpha }_{FSE}=\frac{E_2^N-1}{N\ln E_2},b_{FSE}=0.$$ (16)

2.2.2. ruCNR of FSE

Note that for FSE, the acquisition window duration is proportional to N∙TE (the readout time is assumed to be close to TE for the maximal efficiency). The ruCNR of the FSE sequence is derived from Eqs. (9) and (16) with TR replaced by TE:

$$ruCN{R}_{FSE}\propto a_{FSE}\cdot \sqrt{N\cdot TE}=\frac{E_2^N-1}{N\ln E_2}\cdot \sqrt{N\cdot TE}=\frac{1-E_2^N}{\sqrt{-N\ln E_2}}\sqrt{T_2}.$$ (17)

It can be found that there is a maximal ruCNR_FSE (Supporting Information S2), when

$$N\cdot TE=1.26T_2.$$ (18)

The maximal ruCNR_FSE is:

$$ruCN{R}_{FSE}^{\ast }\propto 0.64\sqrt{T_2},$$ (19)

The optimal ruCNR is obtained when the echo train duration (N·TE) is 1.26 times the T₂ value, which is consistent with the numerical result of the previous work for optimal uSNR [1].

2.3. FLASH

2.3.1. MTF and PSF of FLASH

FLASH refers to the acquisition consisting of N excitation pulses with a constant small FA of α, short TR and N PE steps which are centered at the gradient echoes with an echo time of TE. It is assumed that the transverse magnetization before the next FLASH excitation pulses are fully spoiled. Based on the Bloch equation, the longitudinal magnetization at the end of the n^th TR is:

$$M_z\left(n\right)=M_z\left(n-1\right)\epsilon +M^0\left(1-E_1\right),$$ (20)

with $E_1=e^{-TR/T_1}$ and ε = E₁ cos α. This recurrent equation is a typical first-order non-homogeneous linear recurrence relation with constant variables. The solution of M_z(n) is (Supporting Information S3):

$$\begin{array}{l}{M}_z\left(n\right)=\left(M_{prep}-M^0\frac{1-E_1}{1-\epsilon }\right){\epsilon }^{n-1}+M^0\frac{1-E_1}{1-\epsilon }\\ =M_{prep}\cdot {\epsilon }^{n-1}+M^0\frac{1-E_1}{1-\epsilon }\cdot \left(1-{\epsilon }^{n-1}\right).\end{array}$$ (21)

Therefore, using $E_2^{\ast }=e^{-TE/T_2^{\ast }}$ the transverse magnetization acquired at the n^th gradient echo is given by:

$$\begin{array}{l}{M}_{xy}\left(n\right)=M_z\left(n-1\right)E_2^{*}\sin \alpha \\ =M_{prep}\cdot {\epsilon }^{n-1}{E}_2^{*}\sin \alpha +M^0\frac{1-E_1}{1-\epsilon }{E}_2^{*}\sin \alpha \\ \cdot \left(1-{\epsilon }^{n-1}\right),\end{array}$$ (22)

It is obvious from Eq. (22) that, when n→∞, the well-known steady-state transverse magnetization (M_ss) for FLASH is:

$$M_{ss}=M_{xy}\left(\infty \right)=M^0\frac{1-E_1}{1-\epsilon }{E}_2^{*}\sin \alpha .$$ (23)

Note that the Ernst angle for FLASH that maximizes M_ss is α_E = arccos(E₁). Eq. (22) can then be expressed as:

$$\begin{array}{l}{M}_{xy}\left(n\right)=M_{prep}\cdot {\epsilon }^{n-1}{E}_2^{*}\sin \alpha +M_{ss}\cdot \left(1-{\epsilon }^{n-1}\right)\\ =M_{ss}+\left(M_{prep}{E}_2^{*}\sin \alpha -M_{ss}\right)\cdot {\epsilon }^{n-1}.\end{array}$$ (24)

Note that Eq. (24) is consistent with similar derivations in previous work with T₁, T₂ or diffusion preparations [12, 14, 17, 18]. Based on Supporting Information S3, the effective decay time of a FLASH sequence from the transient state to the steady state equals $TR/\left(-ln\epsilon \right)=1/\left(\frac{1}{T_1}-\frac{ln\cos \alpha }{TR}\right)$, which is T₁/2 when using the Ernst angle.

Hence, the MTF of FLASH with the linear and low-high profile orders are derived from Eq. (2) and (3), respectively:

$$MT{F}_{FLASH}^{LN}\left(k\right)=M_{xy}\left(\left(k+0.5\right)N+1\right)=M_{prep}\cdot {\epsilon }^{\left(k+0.5\right)N}{E}_2^{*}\sin \alpha +M_{ss}\cdot \left(1-{\epsilon }^{\left(k+0.5\right)N}\right).$$ (25)

$$\begin{array}{l}MT{F}_{FLASH}^{LH}\left(k\right)=M_{xy}\left(2\left|k\right|N+1\right)\\ =M_{prep}\cdot {\epsilon }^{2\left|k\right|N}{E}_2^{*}\sin \alpha +M_{ss}\cdot \left(1-{\epsilon }^{2\left|k\right|N}\right).\end{array}$$ (26)

Corresponding PSFs of the FLASH with the linear and low-high profile orders are derived from Eqs. (4), and (25), (26), respectively (Supporting Information S4):

$$PS{F}_{FLASH}^{LN}\left(z\right)=\left(M_{prep}\cdot E_2^{*}\sin \alpha -M_{ss}\right)\cdot \frac{{\epsilon }^N{e}^{i\pi z}-e^{-i\pi z}}{N\ln \epsilon +i2\pi z}+M_{ss}\cdot \sin \text{c}\left(\pi z\right),$$ (27)

$$\begin{array}{l}PS{F}_{FLASH}^{LH}\left(z\right)={\int }_{-0.5}^{0.5}MT{F}_{FLASH}^{LH}\left(k\right)e^{i2\pi kz}dk\\ =\left(M_{prep}\cdot E_2^{*}\sin \alpha -M_{ss}\right)\cdot \frac{{\epsilon }^{N}N\ln \epsilon \cos \left(\pi z\right)+{\epsilon }^N\pi x\sin \left(\pi z\right)-N\ln \epsilon }{N^2{\ln }^2\epsilon +{\pi }^2{z}^2}\\ +M_{ss}\cdot \sin \text{c}\left(\pi z\right).\end{array}$$ (28)

The amplitude effect of a FLASH sequence, characterized with PSF(0), is equivalent for linear and low-high profile orders. Based on Eq. (27):

$$\begin{array}{l}PS{F}_{FLASH}\left(0\right)=\left(M_{prep}\cdot E_2^{*}\sin \alpha -M_{ss}\right)\cdot \frac{{\epsilon }^N{e}^0-e^0}{N\ln \epsilon +0}+M_{ss}\cdot \sin \text{c}\left(0\right)\\ =\left(M_{prep}\cdot E_2^{*}\sin \alpha -M_{ss}\right)\cdot \frac{{\epsilon }^N-1}{N\ln \epsilon }+M_{ss}\\ =M_{prep}\cdot \frac{{\epsilon }^N-1}{N\ln \epsilon }{E}_2^{*}\sin \alpha +M_{ss}\cdot \left(1-\frac{{\epsilon }^N-1}{N\ln \epsilon }\right).\end{array}$$ (29)

Following Eq. (7), the slope a and intercept b of the linear relation between PSF(0) and M_prep for FLASH are:

$${\alpha }_{FLASH}=\frac{{\epsilon }^N-1}{N\ln \epsilon }{E}_2^{*}\sin \alpha ,b_{FLASH}=M_{ss}\cdot \left(1-\frac{{\epsilon }^N-1}{N\ln \epsilon }\right).$$ (30)

2.3.2. ruCNR of FLASH

The ruCNR of the FLASH sequence is derived from Eqs. (9) and (30):

$$ruCN{R}_{FLASH}\propto a_{FLASH}\cdot \sqrt{N\cdot TR}=\frac{{\epsilon }^N-1}{\ln \epsilon }\frac{\sqrt{TR}}{N}{E}_2^{*}\sin \alpha .$$ (31)

Hence ruCNR_FLASH has a complicated dependence on TR, N, and FA. When considering 1.5 ms ≤ TR ≤ 30 ms, 0 < α ≤ 90°, it can be found that there is a maximal ruCNR_FLASH for each TR (Supporting Information S5), when optimal N* and FA* are:

$$\begin{array}{l}{N}_{FLASH}^{*}\left(TR\right)=\frac{-2.51}{1+W_{-1}\left(-E_1^2/e\right)},\\ {\alpha }_{FLASH}^{*}\left(TR\right)=\arccos \frac{1}{\sqrt{-W_{-1}\left(-E_1^2/e\right)}},\end{array}$$ (32)

where W_-1(x) is the negative branch of the Lambert W function, and both N and α need to be rounded to the nearest integer. And the maximal ruCNR_FLASH is:

$$ruCN{R}_{FLASH}^{*}\left(\text{TR}\right)\propto \frac{0.90E_2^{*}\sqrt{TR}}{\sqrt{-W_{-1}\left(-E_1^2/e\right)}}.$$ (33)

To achieve a smaller FA and a larger optimal N, we allow a minor sacrifice of ruCNR, Which is characterized by a factor η ≤ 1 (Supporting Information S6):

$$ruCN{R}_{FLASH}^{\eta }=\eta \cdot ruCN{R}_{FLASH}^{*}.$$ (34)

Typically we chose η ≥ 0.9. In this case, the optimal N* and FA* are:

$$\begin{array}{l}{N}_{FLASH}^{\eta }=\frac{-2.51}{x{E}_1^2-W_{-1}\left(x{e}^{x{E}_1^2}\right)}\\ {\alpha }_{FLASH}^{\eta }=\arccos \left(\sqrt{\frac{W_{-1}\left(x{e}^{x{E}_1^2}\right)}{x{E}_1^2}}\right).\\ x=\frac{W_{-1}\left(-E_1^2/e\right)}{{\eta }^2{E}_1^2}\end{array}$$ (35)

Note that Eq. (35) is equivalent to Eq. (32) when η = 1.

2.4. bSSFP

2.4.1. MTF and PSF of bSSFP

bSSFP here refers to the acquisition consisting of N alternating excitation pulses with FAs of ±α, short TR and N PE steps which are centered in the middle of the TR with an echo time of TE = TR/2. To smooth the oscillation of the transient magnetization, the bSSFP acquisition is often preceded by a short preparation with an α/2 excitation pulse and TR/2 period. It is assumed that there is ideal dephasing between consecutive excitation pulses and some very small oscillations not fully smoothed by the α/2─TR/2 preparation are neglected.

The steady-state transverse magnetization (M_ss) for bSSFP is [42]:

$$M_{ss}=\frac{M^0\left(1-E_1\right)\sqrt{E_2}\sin \alpha }{1-\left(E_1-E_2\right)\cos \alpha -E_1{E}_2},$$ (36)

with $E_1=e^{-TR/T_1}$, $E_2=e^{-TR/T_2}$.

Based on the previous formulation [42], the transient-state magnetization M_xy(n) acquired at the n^th echo is:

$$\begin{array}{l}{M}_{xy}\left(n\right)=\left(M_{prep}\cdot \sin \left(\frac{\alpha }{2}\right)-M_{ss}\right){\lambda }^{n-1}+M_{ss}=M_{prep}\cdot {\lambda }^{n-1}\sin \left(\frac{\alpha }{2}\right)+M_{ss}\cdot \left(1-{\lambda }^{n-1}\right)\\ =M_{ss}+\left(M_{prep}\sin \left(\frac{\alpha }{2}\right)-M_{ss}\right)\cdot {\lambda }^{n-1}\mathrm{..}\end{array}$$ (37)

where the parameter λ is:

$$\lambda =E_1{\cos }^2\left(\alpha /2\right)+E_2{\sin }^2\left(\alpha /2\right),$$ (38)

Note that the power of λ being n-1 in Eq. (37) instead of n in the original work [42] is because the definition of n is the index of echo (acquisition) in this work rather than the index of excitation pulses used previously [42], which included the additional α/2 excitation pulse. Similar to the derivation in Supporting Information S3, the effective decay time of a bSSFP sequence from the transient state to the steady state equals TR/(−lnλ), which is a weighted average between T₁ and T₂.

Hence, the MTF of bSSFP with the linear and low-high profile orders are derived from Eq. (2) and (3), respectively:

$$MT{F}_{bSSFP}^{LN}\left(k\right)=M_{prep}\cdot {\lambda }^{\left(k+0.5\right)N}\sin \left(\alpha /2\right)+M_{ss}\cdot \left(1-{\lambda }^{\left(k+0.5\right)N}\right).$$ (39)

$$MT{F}_{bSSFP}^{LN}\left(k\right)=M_{prep}\cdot {\lambda }^{2\left|k\right|N}\sin \left(\alpha /2\right)+M_{ss}\cdot \left(1-{\lambda }^{2\left|k\right|N}\right).$$ (40)

Corresponding PSFs of the bSSFP with the linear and low-high profile orders are derived from Eqs. (4), and (39), (40), respectively (Supporting Information S7):

$$PS{F}_{bSSFP}^{LN}\left(z\right)=\left(M_{prep}\cdot \sin \left(\alpha /2\right)-M_{ss}\right)\cdot \frac{{\lambda }^N{e}^{i\pi z}-e^{-i\pi z}}{N\ln \lambda +i2\pi z}+M_{ss}\cdot \sin \text{c}\left(\pi z\right),$$ (41)

$$\begin{array}{l}PS{F}_{bSSFP}^{LN}\left(z\right)=\left(M_{prep}\cdot \sin \left(\alpha /2\right)-M_{ss}\right)\cdot \frac{{\lambda }^{N}N\ln \lambda \cos \left(\pi z\right)+{\lambda }^N\pi x\sin \left(\pi z\right)+N\ln \lambda }{N^2{\ln }^2\lambda +{\pi }^2{z}^2}.\\ =M_{ss}\cdot \sin \text{c}\left(\pi z\right).\end{array}$$ (42)

The amplitude effect of a bSSFP sequence, characterized with PSF(0), is equivalent for linear and low-high profile orders. Based on Eq. (41):

$$\begin{array}{l}PS{F}_{bSSFP}\left(0\right)=\left(M_{prep}\cdot \sin \left(\alpha /2\right)-M_{ss}\right)\cdot \frac{{\lambda }^N{e}^0-e^0}{N\text{\hspace{0.17em}ln\hspace{0.17em}}\lambda +0}+M_{ss}\cdot \sin \text{c}\left(0\right)\\ =\left(M_{prep}\cdot \sin \left(\alpha /2\right)-M_{ss}\right)\cdot \frac{{\lambda }^N-1}{N\text{\hspace{0.17em}ln\hspace{0.17em}}\lambda }+M_{ss}\\ =M_{prep}\cdot \frac{{\lambda }^N-1}{N\text{\hspace{0.17em}ln\hspace{0.17em}}\epsilon }\sin \left(\alpha /2\right)+M_{ss}\cdot \left(1-\frac{{\lambda }^N-1}{N\text{\hspace{0.17em}ln\hspace{0.17em}}\lambda }\right).\end{array}$$ (43)

Following Eq. (7), the slope a and intercept b of the linear relation between PSF(0) and M_prep for bSSFP are:

$${\alpha }_{bSSFP}=\frac{{\lambda }^N-1}{N\text{\hspace{0.17em}ln\hspace{0.17em}}\lambda }\sin \left(\alpha /2\right),b_{bSSFP}=M_{ss}\cdot \left(1-\frac{{\lambda }^N-1}{N\text{\hspace{0.17em}ln\hspace{0.17em}}\lambda }\right).$$ (44)

2.4.2. ruCNR of bSSFP

The ruCNR of the bSSFP sequence is derived from Eqs. (9) and (44):

$$ruCN{R}_{bSSFP}\propto a_{bSSFP}\cdot \sqrt{N\cdot \text{TR}}=\frac{{\lambda }^N-1}{ln\lambda }\frac{\sqrt{\text{TR}}}{\sqrt{N}}\sin \left(\alpha /2\right).$$ (45)

Similarly, ruCNR_bSSFP has a complicated dependence on TR, N, and FA. When considering 3 ms ≤ TR ≤ 10 ms, 0 < α ≤ 180°, it can be found that the maximal ruCNR_bSSFP is a continuous and piecewise function with two segments w.r.t TR separating at a shared endpoint $\left(\overline{TR}\right)$ defined by T₁ and T₂ (Supporting Information S8):

$$\overline{TR}=\frac{T_1{T}_2}{T_2-T_1}{W}_{-1}\left(\frac{T_2-T_1}{T_1}{e}^{\frac{T_2-T_1}{T_1}}\right)-T_2,$$ (46)

To obtain the maximal ruCNR_bSSFP for each TR, the optimal N* and FA* are:

$$\begin{gathered} N_{bSSFP}^{*}\left(TR\right)=\{\begin{array}{l}\begin{array}{l}1.26\frac{T_2}{\text{TR}}\text{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{0.17em}}TR\le \overline{TR,}\\ 1.26\frac{-1}{1+W_{-1}\left(-E_1/e\right)}\text{\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}}TR>\overline{TR,}\end{array}\hfill \end{array} \\ {\alpha }_{bSSFP}^{*}\left(TR\right)=\{\begin{array}{l}\begin{array}{l}{180}^{\circ }\text{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{0.17em}}TR\le \overline{TR,}\\ \arccos \left(\frac{2E_1+\left(E_1+E_2\right)W_{-1}\left(-E_1/e\right)}{\left(E_2-E_1\right)W_{-1}\left(-E_1/e\right)}\right)\text{\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}}TR>\overline{TR,}\end{array}\hfill \end{array} \end{gathered}$$ (47)

where W_-1(x) is the negative branch of the Lambert W function, and both N and α need to be rounded to the nearest integer. And the maximal ruCNR_bSSFP is:

$$ruCN{R}_{bSSFP}^{*}\left(TR\right)=\{\begin{array}{l}\begin{array}{l}0.64\sqrt{T_2}\text{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{0.17em}}TR\le \overline{TR,}\\ 0.64\frac{\sqrt{TR\cdot E_1}}{\sqrt{\left(E_2-E_1\right)W_{-1}\left(-E_1/e\right)}}\text{\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}}TR>\overline{TR,}\end{array}\hfill \end{array}$$ (48)

To achieve a smaller optimal FA and a larger optimal N, we allow a minor sacrifice of ruCNR, which is characterized by a factor 0.9 < η ≤ 1 (Supporting Information S9):

$$ruCN{R}_{bSSFP}^{\eta }=\eta \cdot ruCN{R}_{bSSFP}^{*}.$$ (49)

In this case, the optimal N* and FA* are:

$$\begin{array}{l}{N}_{bSSFP}^{\eta }=1.26\frac{1}{W_{-1}\left(x{e}^{x{E}_1}\right)-x{E}_1}\\ {\alpha }_{bSSFP}^{\eta }=\arccos \left(\frac{2W_{-1}\left(x{e}^{{\text{xE}}_1}\right)/x-E_1-E_2}{E_1-E_2}\right).\\ x=\{\begin{array}{l}\frac{\ln E_2}{{\eta }^2\left(E_1-E_2\right)}\text{\hspace{1em}if\hspace{0.17em}}TR\le \overline{TR}\\ \frac{W_{-1}\left(-E_1/e\right)}{{\eta }^2{E}_1}\text{\hspace{1em}if\hspace{0.17em}}TR>\overline{TR}\end{array}\end{array}$$ (50)

Note that Eq. (50) is equivalent to Eq. (47) when η = 1.

2.5. Numerical validation

Numerical simulations based on Bloch equations using Matlab (MathWorks, Inc., Natick, MA, USA) were conducted for validation purposes. MTFs of FSE, FLASH, and bSSFP were generated with different sequence parameters such as TR, TE, FA (α), N, as well as various T₁ and T₂ values. Only the low-high profile order is simulated as it is the choice for most magnetization-preparation sequences. Infinitely short RF pulses were assumed with instant flipping and no phase or frequency encoding was applied in this simulation. To be aligned with the symmetric MTFs in the analytical format, the negative k-space locations were shifted for half a k-space pixel (0.5/N) to compensate for the asymmetric modulation due to interleaved sampling between positive and negative k-space locations. The corresponding PSFs are obtained following the Fourier transform of the MTFs. Note that the Lambert’s W function, W_-1(x), used in describing ruCNR optimization of FLASH and bSSFP is solved as ‘lambertw(-1, x)’ in Matlab.

3. Results

Figure 1 shows (a, b) MTF and (c, d) PSF of FSE acquisitions with a low-high profile order with different (a, c) N and (b, d) T₂ values, following Eqs. (12) and (14) in Section 2.2.1, respectively. For FSE, larger N or shorter T₂ values lead to both notable signal loss and blurring effect.

Figure 1:

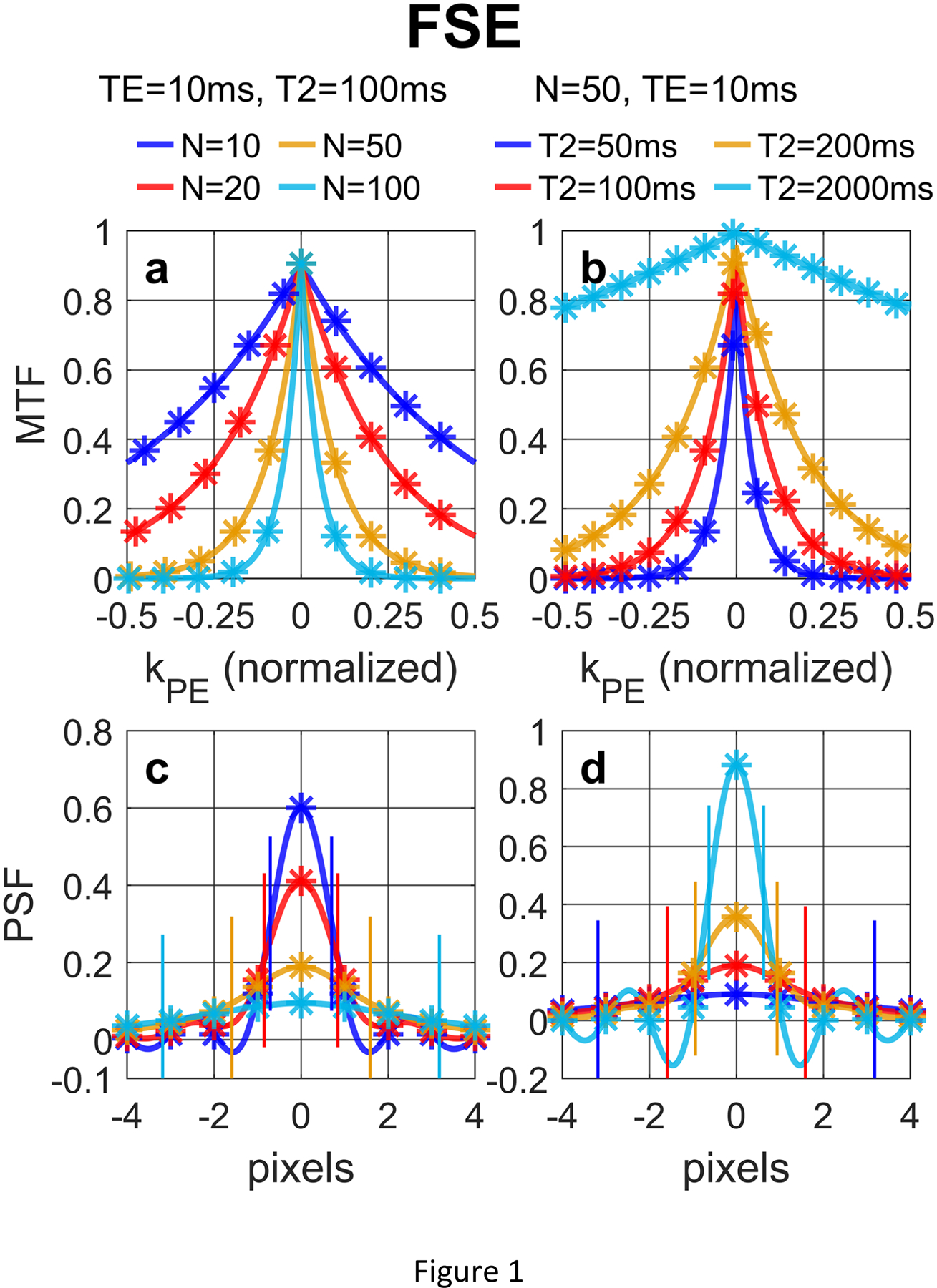
(a, b) MTF and (c, d) PSF of FSE acquisition with a low-high profile order with different (a, c) N and (b, d) T₂ values, following Eqs. (12) and (14), respectively. The analytical results (solid lines) align well with the numerically computed and discretely sampled values (stars) generated via Bloch equation simulations. For FSE, larger N or shorter T₂ values lead to both notable signal loss (reduced signal at the center of the PSF) and blurring effect (FWHM labeled with paired vertical bars).

Figure 2 shows (a, b, c, d) MTF and (e, f, g, h) PSF of FLASH acquisitions with a low-high profile order with different (a, e) N, (b, f) TR, (c, g) FA, (d, h) T₁ values, following Eqs. (26) and (28) in Section 2.3.1, respectively. For FLASH, larger N leads to notable signal loss at the center of the PSF but little blurring effect (FWHM labeled with paired vertical bars).

Figure 2:

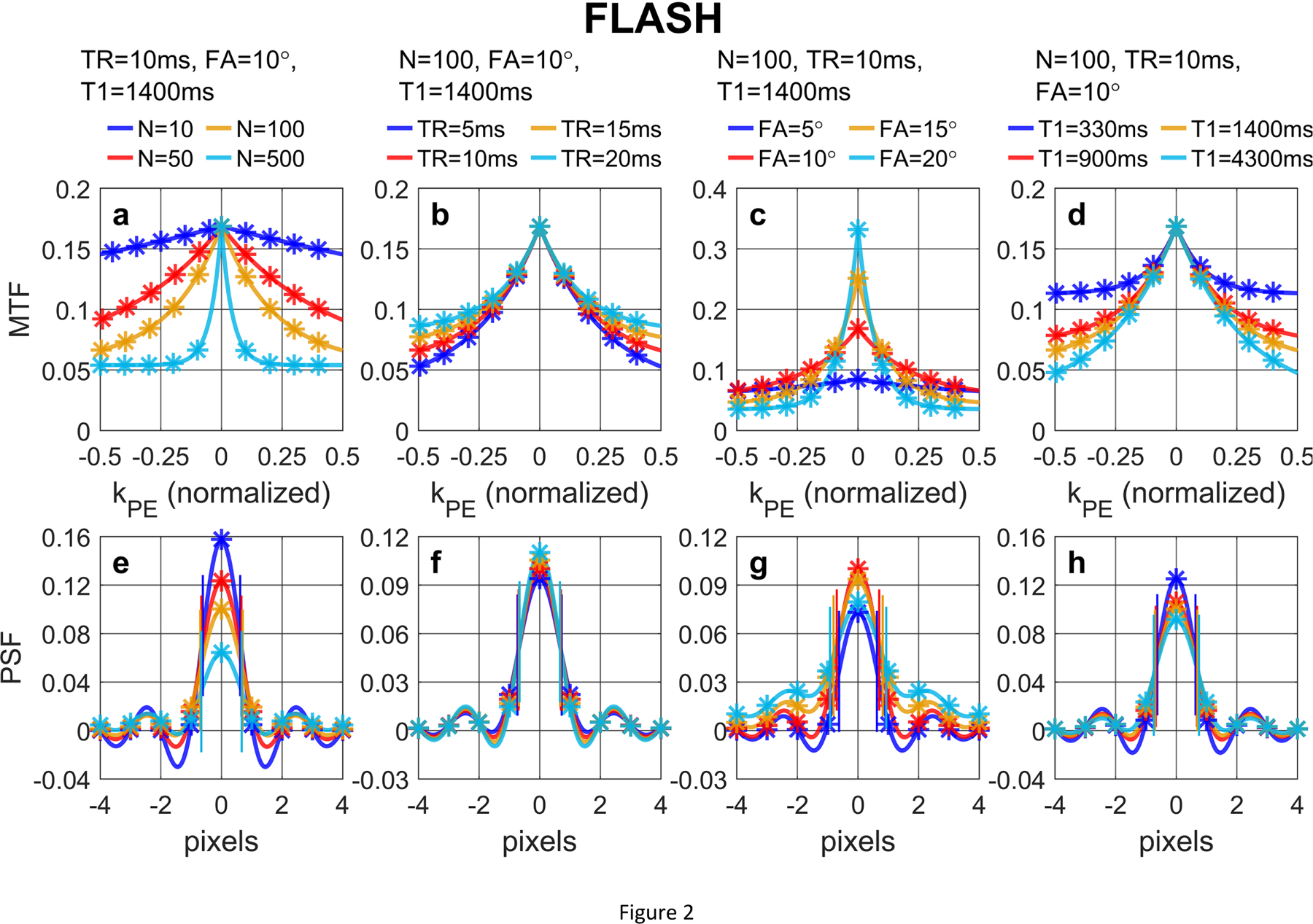
(a, b, c, d) MTF and (e, f, g, h) PSF of FLASH acquisition with a low-high profile order with different (a, e) N, (b, f) TR, (c, g) FA, (d, h) T₁ values, following Eqs. (26) and (28), respectively. The analytical results (solid lines) align well with the numerically computed and discretely sampled values (stars) generated via Bloch equation simulations. For FLASH, larger N leads to notable signal loss at the center of the PSF but little blurring effect (FWHM labeled with paired vertical bars).

Figure 3 shows (a, b, c, d) MTF and (e, f, g, h) PSF of bSSFP acquisitions with a low-high profile order with different (a, e) N, (b, f) TR, (c, g) FA, (d, h) T₁/T₂ values, following Eqs. (40) and (42) in Section 2.4.1, respectively. For bSSFP, larger N leads to notable signal loss at the center of the PSF and a small blurring effect. In these conditions, bSSFP also displays various dependence of the PSF on different N, TR, FA, and T₁/T₂ values. Larger N leads to notable signal loss at the center of the PSF; FWHM shows small blurring effects with larger N and longer TR, while broader FWHM is induced by higher FA.

Figure 3:

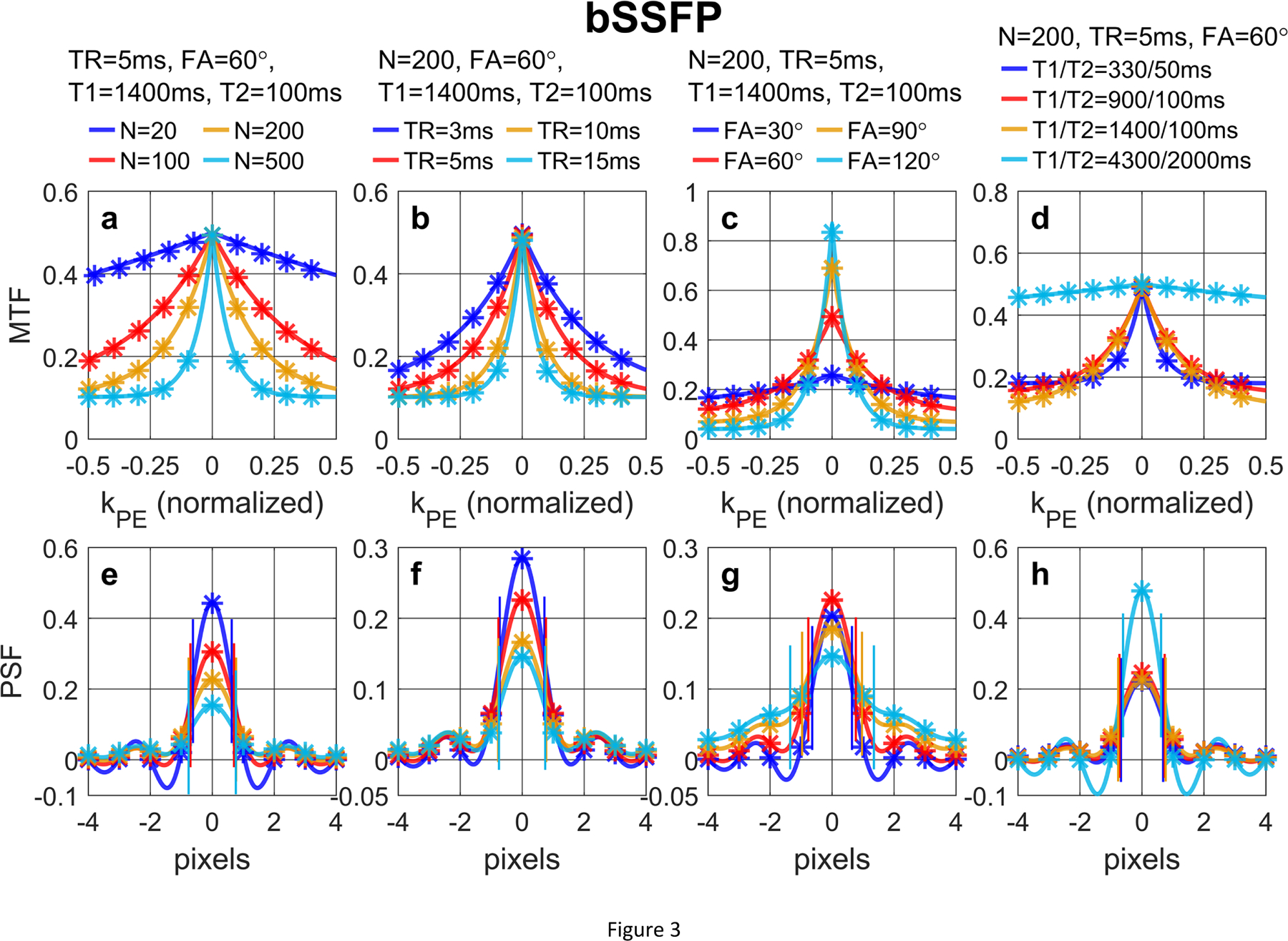
(a, b, c, d) MTF and (e, f, g, h) PSF of bSSFP acquisition with a low-high profile order with different (a, e) N, (b, f) TR, (c, g) FA, (d, h) T₁/T₂ values, following Eqs. (40) and (42), respectively. The analytical results (solid lines) align well with the numerically computed and discretely sampled values (stars) generated via Bloch equation simulations. For bSSFP, larger N leads to notable signal loss at the center of the PSF and a small blurring effect (FWHM labeled with paired vertical bars).

Note that the sequences in Figures 1–3 are without contrast-preparation (M_prep = 1). Figure 4 compares analytical MTFs and corresponding PSFs of (a, d) FSE, (b, e) FLASH, and (c, f) bSSFP on their dependence on different M_prep values. When M_prep = 0, (a) MTF of FSE decay to zero and (d) the center of its PSF is zero, while MTFs of (b) FLASH and (c) bSSFP all converge towards the steady-state signals and (e, f) the center of their PSFs are nonzero. FWHM shows little variations with different M_prep values.

Figure 4:

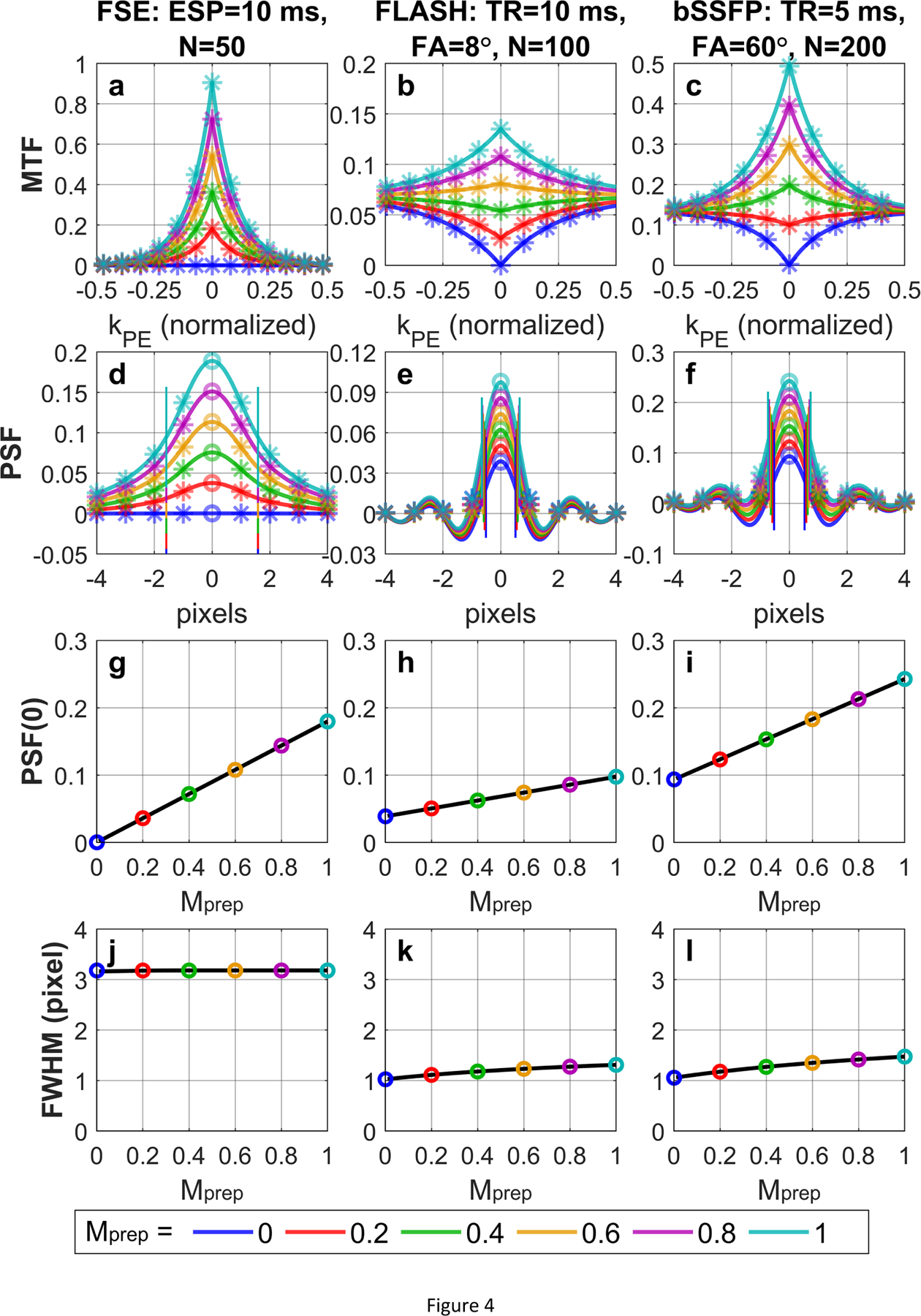
(a, b, c) MTF and (d, e, f) PSF of (a, d) FSE, (b, e) FLASH, and (c, f) bSSFP acquisitions with low-high profile orders with different M_prep values. The analytical results (solid lines) align well with the numerically computed and discretely sampled values (stars) generated via Bloch equation simulations. When M_prep = 0, (a) MTF of FSE decay to zero and (d) the center of its PSF is zero, while MTFs of (b) FLASH and (c) bSSFP all converge towards the steady-state signals and (e, f) the center of their PSFs are nonzero. FWHM (labeled with paired vertical bars) shows little variations with different M_prep values. The analytically derived linear functions of PSF(0) and the numerically solved FWHM (y-axis) vs M_prep (x-axis) are displayed with the solid lines, which fit closely with the PSF(0) and FWHM for exemplary M_prep values (colored circles) for (g, j) FSE, (h, k) FLASH, and (i, l) bSSFP.

In Figures 1–4, the analytical expressions (solid lines) of MTFs (Eqs. (12), (26), (40)) and PSFs (Eqs. (14), (28), (42)) for FSE, FLASH, and bSSFP in Sections 2.2.1, 2.3.1, 2.4.1, respectively, display minimal differences from the numerically computed values (stars) generated via Bloch equation simulations sampled at discrete k-space locations and image pixels with above sequence parameters and relaxation times. In Figure 4, the linear functions of PSF(0) vs M_prep for (g) FSE, (h) FLASH, and (i) bSSFP are displayed with the solid lines using the slope and intercept described by Eqs. (15), (29), (43) respectively. These linear equations fit closely with the PSF(0) for exemplary M_prep values for different acquisition schemes. Clearly, there are small intercepts for PSF(0) with respect to M_prep for (h) FLASH and (i) bSSFP. The numerically solved FWHM vs M_prep for (j) FSE, (k) FLASH, and (l) bSSFP also correspond with the FWHM of exemplary M_prep values as well. Beyond the main lobes of the PSFs, their side lobes for FSE, FLASH, and bSSFP all decay to zero with oscillating phases (Figures 1–4).

Figure 5 illustrates the dependence of slopes and intercepts for PSF(0) described by Eq. (30) in Section 2.3.1 for FLASH (red curves) and Eq. (44) in Section 2.4.1 for bSSFP (green curves) on varying (a, e) N, (b, f) TR, (c, g) FA, and (d, h) T₁ values, respectively. For comparison, the dependence of slop for FSE described by Eq. (16) (blue curves) on varying (a, e) N and (b, f) TE is also displayed. The default parameters are the same as in Figure 4. The numerically solved FWHMs with respect to these different factors are shown in (i, j, k, l), respectively. The corresponding ruCNR, analytically derived from Eqs. (17), (31), and (45) in Sections 2.2.2, 2.3.2, 2.4.2 as the multiplications between the slopes and $\sqrt{N\cdot TR}$ are exhibited in (m, n, o, p). With these conditions, the slopes of FLASH and bSSFP both reduce with longer (a) N and (b) TR, and do not vary much with respect to (c) FA and (d) T₁; intercept of FLASH and bSSFP increase with (e) larger N and (f) longer TR, are highest when (g) FA is around 20° or 75°, and increase quickly with (h) shorter T₁; FWHM of FLASH and bSSFP are less than 1.5 pixels for (i, j, k, l) most of the parameters except when (k) FA is larger than 90° for bSSFP; ruCNR of FLASH and bSSFP are highest for certain (m) N, (n) TR and (o) FA, respectively, and increases with longer (p) T₁.

Figure 5:

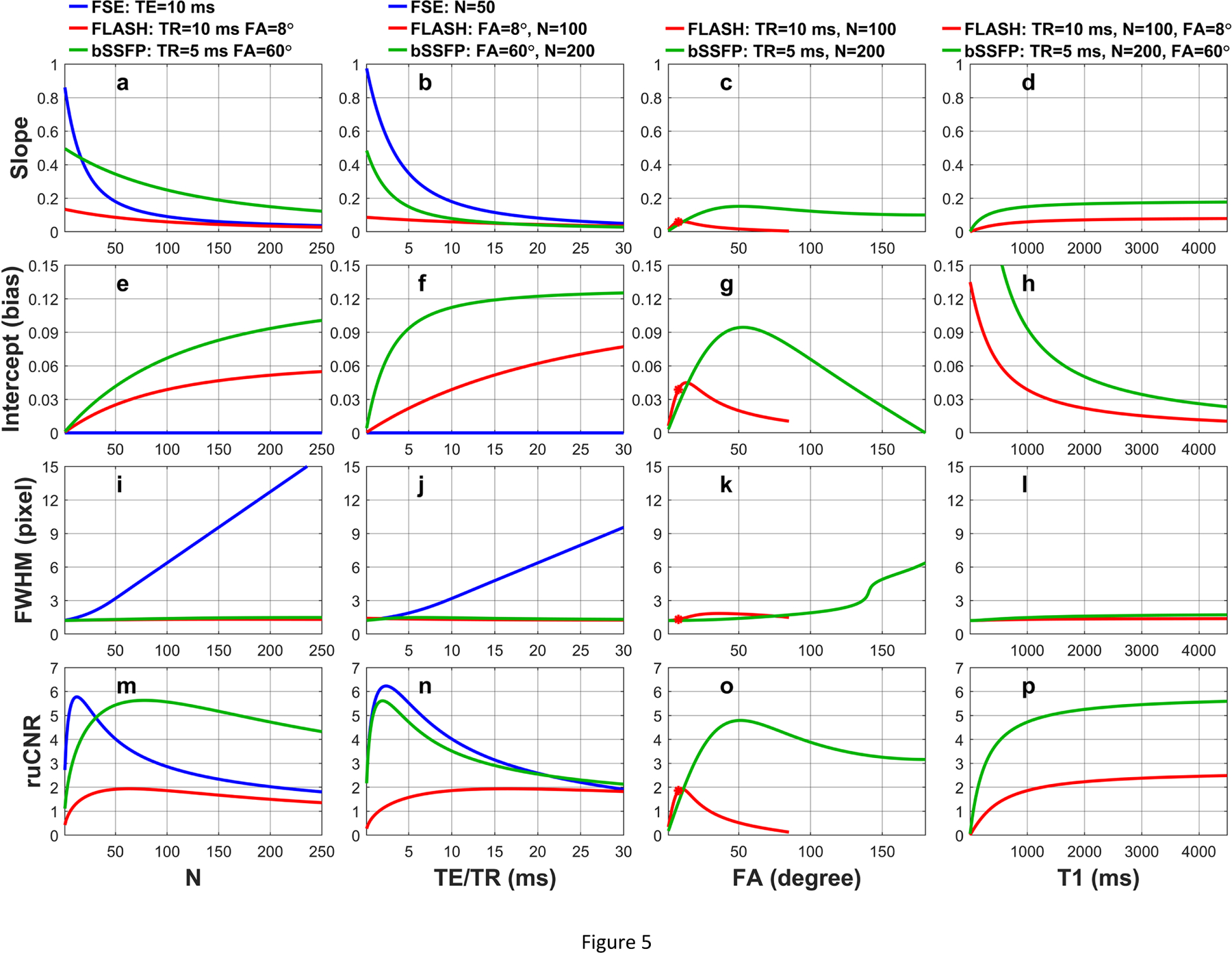
The dependence of slopes and intercepts for PSF(0) on varying (a, e) N, (b, f) TR, (c, g) FA, and (d, h) T₁ values for FSE (blue curves, Eq. (16)), FLASH (red curves, Eq. (30)), and bSSFP (green curves, Eq. (44)), respectively. The numerically solved FWHMs with respect to these different factors are shown in (i, j, k, l). The corresponding ruCNR, analytically derived from Eqs. (17), (31), and (45), are exhibited in (m, n, o, p). Slopes of (a) FLASH and (b) bSSFP both reduce with larger N and longer TR and (e, f) their intercepts yield opposite trend. (i, j, k, l) FWHM of FLASH and bSSFP are less than 1.5 pixels for most of the conditions. (m, n, o) ruCNR of FLASH and bSSFP display plateau for certain N, TR and FA parameters.

The ruCNR_FLASH based on Eq. (31) in Section 2.3.2 is displayed in Figure 6a over the plane of N versus FA with TR fixed to 10 ms and T₁ / T₂* values assumed to be 1000 / 50 ms. The optimal N* and FA* expressed by Eq. (32) are plotted with respect to TR in Figures 6b, 6c respectively. The corresponding echo train duration N*·TR is plotted in Figure 6d. The maximal ruCNR_FLASH as a function of TR (Eq. (33)) is displayed in Figure 6e. When TR = 10 ms, the maximal ruCNR* = 2.51 is achieved at N* = 12 and FA* = 25° (white star in Figure 6a), which match the optimal N*, FA*, echo train duration, and ruCNR* as labeled with black circles in respective plots (Figure 6b,c,d,e). Note that this ruCNR* is monotonically increasing with TR (Figure 6e), as analytically proved in Supporting Information S5. These represent the original optimization results when η = 1. In Fig. 6a, Contours are drawn for sacrificed ruCNR when η = 0.99, 0.95, 0.9; In Figure 6b,c,d,e, the red dashed lines, green dash-dot lines and blue dotted lines represent the corresponding optimization results based on Eq. (35) for optimal N*, FA*, echo train duration, and ruCNR* with varying TR, respectively. When TR = 10 ms and η = 0.99, 0.95, 0.9, the maximal ruCNR* = η · 2.51 = 2.48, 2.38, 2.26 are achieved at larger N* = 18, 30, 40, and lower FA* = 20°, 15°, 12° (black star in Figure 6a), which match the optimal N*, FA*, echo train duration, and ruCNR* as labeled with colored circles in respective plots (Figure 6b,c,d,e).

Figure 6:

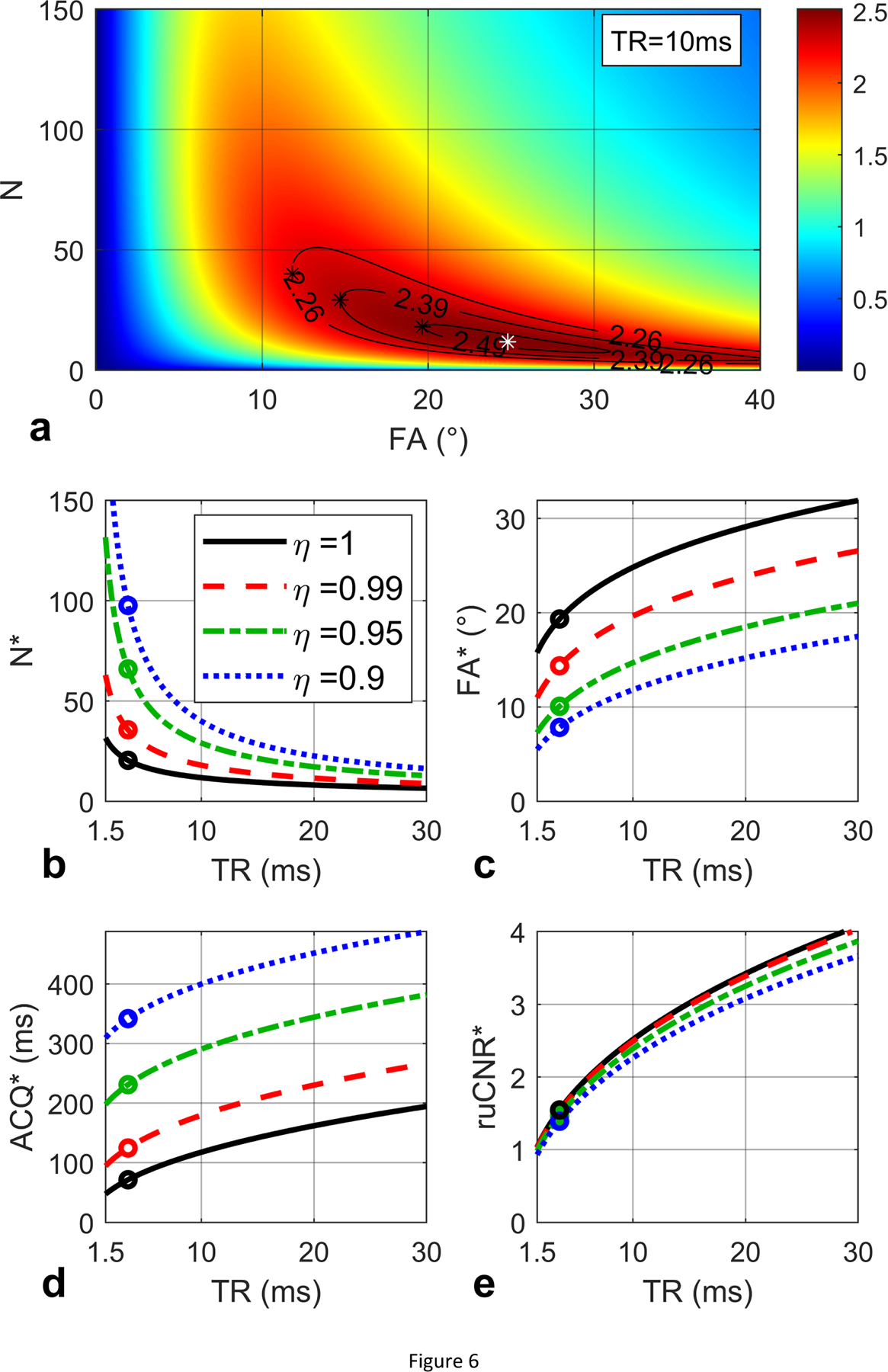
(a) ruCNR of FLASH is displayed as a function of N and FA (Eq. (31)) with given TR (10 ms), T₁ (1000 ms) and T₂* (50 ms) values. An optimal N and FA pair (12, 25°) is found to maximize ruCNR (2.51, white star). Contours are shown for sacrificed ruCNR when η = 0.99, 0.95, 0.9. (b, c, d, e) The optimal N* and FA* (Eq. (32)), echo train duration N*·TR, and the maximal ruCNR_FLASH (Eq. (33)) are plotted with respect to TR, with black circles indicating the values for TR = 10 ms, which match the white star in (a), and the solid black lines represent the original optimization results when η = 1. The red dashed lines, green dash-dot lines and blue dotted lines represent the corresponding optimization results (Eq. (35)) for optimal N*, FA*, echo train duration, and ruCNR* with varying TR, when η = 0.99, 0.95, 0.9, respectively. For TR = 10 ms and η = 0.99, 0.95, 0.90, (a) the maximal ruCNR* = η · 2.51 = 2.48, 2.38, 2.26 are achieved at N* = 18, 30, 40 and lower FA* = 20°, 15°, 12° (black stars), which match (b, c, d, e) the colored circles in the red dashed, green dash-dot and blue dotted lines.

One example for the ruCNR_bSSFP based on Eq. (45) in Section 2.4.2 is displayed in Figure 7a over the plane of N versus FA with TR fixed to 5 ms and T₁ / T₂ values assumed to be 1000 / 100 ms. Based on Eq. (46) $\overline{TR}=23.0$ ms. For TR ranging from 3 to 10 ms, $\text{TR}<\overline{TR}$. The optimal N* = 1.26T₂/TR and FA* = 180° (Eq. (47)) are plotted with respect to TR in Figure 7b, 7c respectively. The corresponding echo train duration N*·TR = 1.26T₂ =126 ms is plotted in Figure 7d. The maximal ${\text{ruCNR}}_{\text{bSSFP}}=0.64\sqrt{T_2}=6.40$ (Eq. (48)) is displayed in Figure 7e. When TR = 5 ms, the maximal ruCNR* = 6.38 is achieved at N* = 25 and FA* = 180° (white star in Figure 7a), which match the optimal N*, FA*, echo train duration, and ruCNR* as labeled with black circles in respective plots (solid black lines, Figure 7b,c,d,e). These represent the original optimization results when η = 1. In Fig. 7a, Contours are drawn for sacrificed ruCNR when η = 0.99, 0.95, 0.9; In Figure 7b,c,d,e, the red dashed lines, green dash-dot lines and blue dotted lines represent the corresponding optimization results based on Eq. (50) for optimal N*, FA*, echo train duration, and ruCNR* with varying TR, respectively. When TR = 5 ms and η = 0.99, 0.95, 0.9, the maximal ruCNR* = η · 6.38 = 6.32, 6.06, 5.74 are achieved at larger N* = 31, 50, 71, and lower FA* = 128°, 85°, 65° (black star in Figure 7a), which match the optimal N*, FA*, echo train duration, and ruCNR* as labeled with colored circles in respective plots (Figure 7b,c,d,e).

Figure 7:

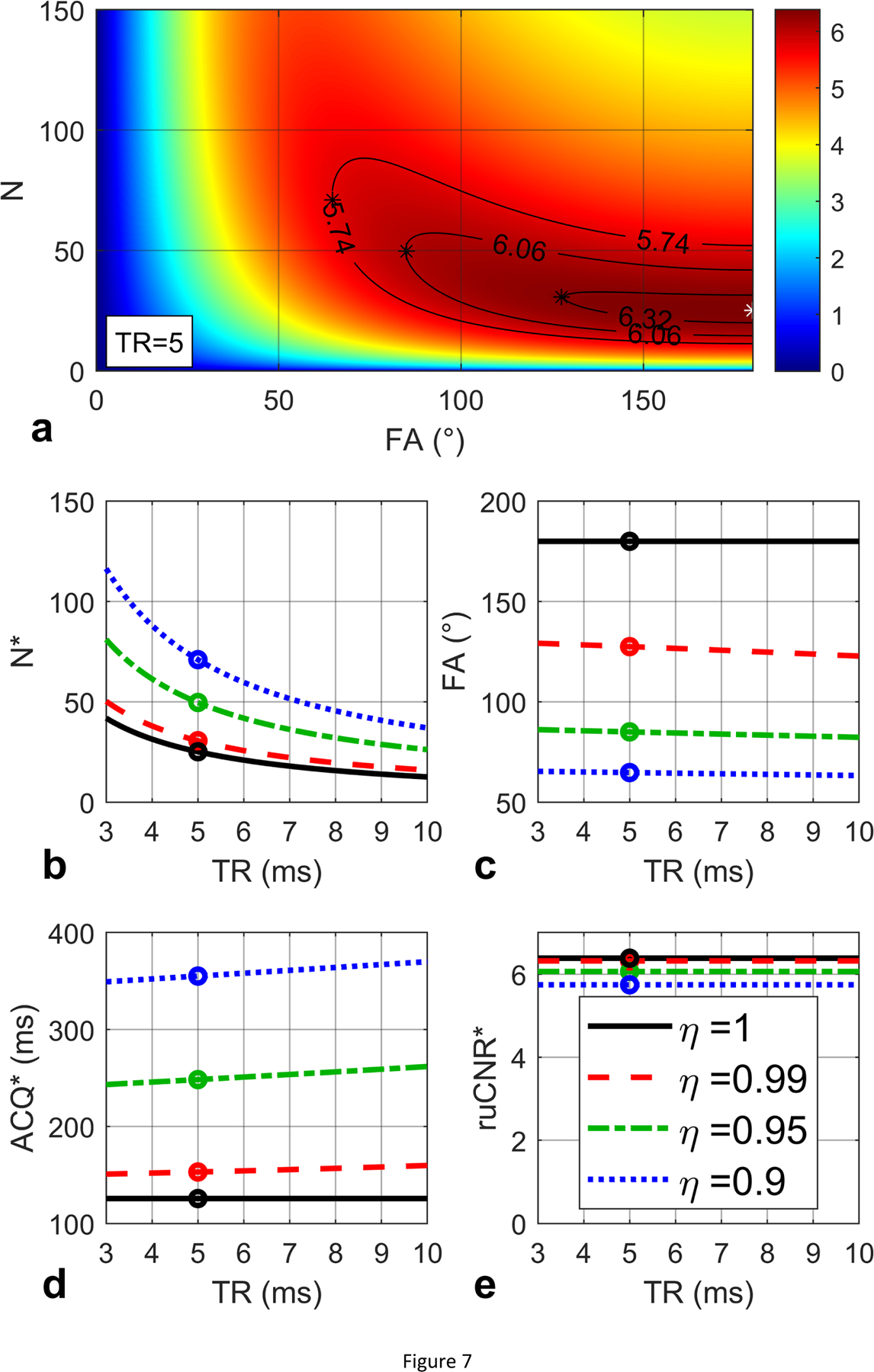
(a) ruCNR of bSSFP is displayed as a function of N and FA (Eq. (45)) with given TR (5 ms), T₁ (1000 ms) and T₂ (100 ms) values, for a condition of $\text{TR}<\overline{TR}$ (23.0 ms). An optimal N and FA pair (25, 180°) is found to maximize ruCNR (6.38, white star). Contours are shown for sacrificed ruCNR when η = 0.99, 0.95, 0.9. (b, c, d, e) The optimal N* and FA* (Eq. (47)), echo train duration N*·TR, and the maximal ruCNR_bSSFP (Eq. (48)) are plotted with respect to TR, with black circles indicating the values for TR = 5 ms, which match the white star in (a), and the solid black lines represent the original optimization results when η = 1. The red dashed lines, green dash-dot lines and blue dotted lines represent the corresponding optimization results (Eq. (50)) for optimal N*, FA*, echo train duration, and ruCNR* with varying TR, when η = 0.99, 0.95, 0.9, respectively. For TR = 5 ms and η = 0.99, 0.95, 0.90, (a) the maximal ruCNR* = η · 6.38 = 6.32, 6.06, 5.74 are achieved at N* = 31, 50, 71 and lower FA* = 128°, 85°, 65° (black stars), which match (b, c, d, e) the colored circles in the red dashed, green dash-dot and blue dotted lines.

Another example is provided in Figure 8a for the ruCNR_bSSFP (Eq. (45) in Section 2.4.2) with T₁ / T₂ values assumed to be 1000 / 40 ms. Based on Eq. (46), $\overline{TR}=3.4$ ms. For TR = 3 ms, $\text{TR}<\overline{TR}$; for TR ranging from 4 to 10 ms, $\text{TR}>\overline{TR}$. Similar plots as Figure 7b,c,d,e are shown in Figure 8b,c,d,e. When TR = 5 ms, For η = 1.00, the maximal ruCNR* = 4.04 is achieved at larger N* = 12 and FA* = 131°; For η = 0.99, 0.95, 0.90, the maximal ruCNR* = η · 4.04 = 4.00, 3.84, 3.64 are achieved at larger N* = 22, 43, 66 and lower FA* = 83°, 55°, 41°.

Figure 8:

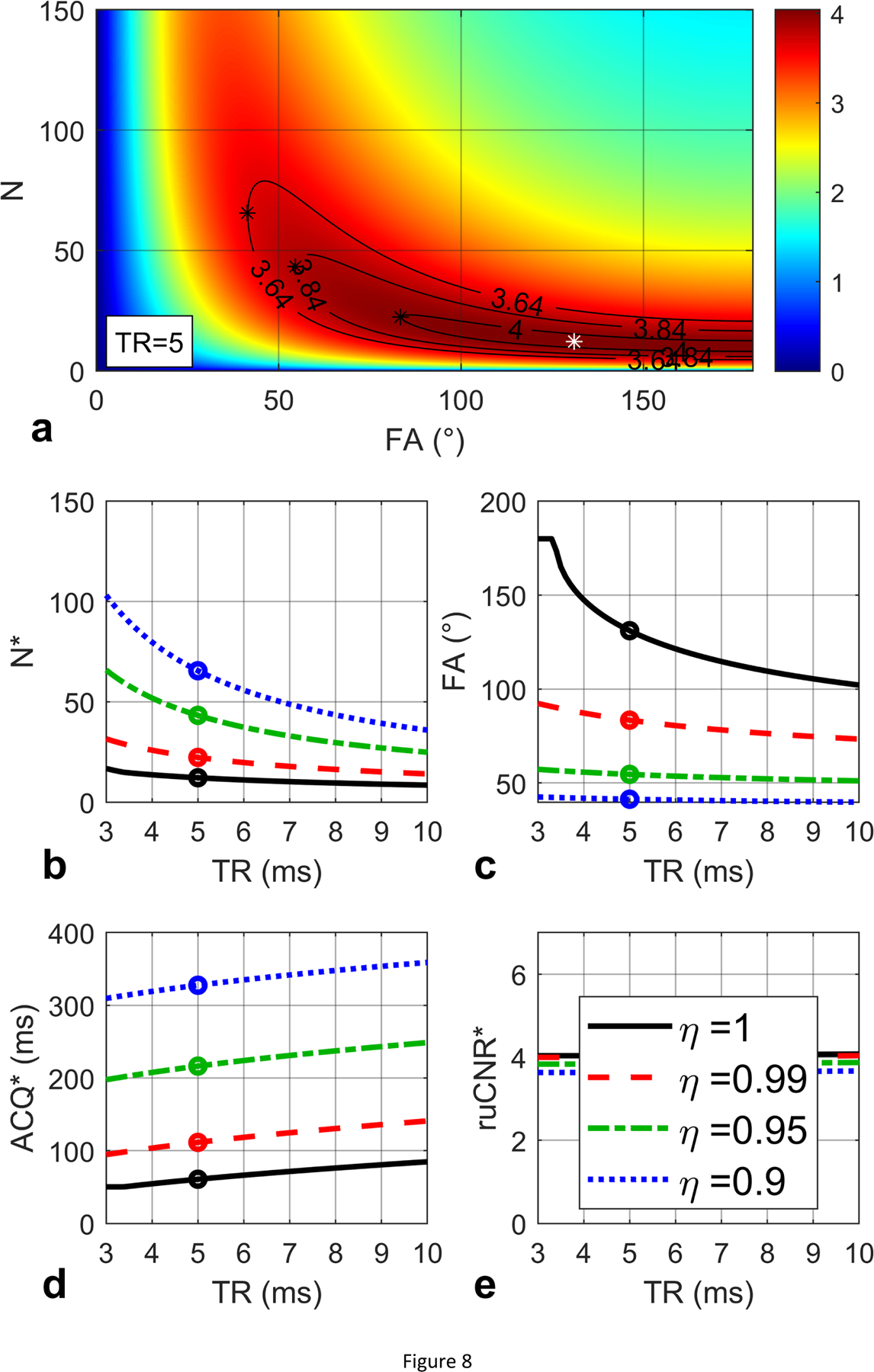
(a) ruCNR of bSSFP is displayed as a function of N and FA (Eq. (45)) with given TR (5 ms), T₁ (1000 ms) and T₂ (40 ms) values, for a condition of $\text{TR}\ge \overline{TR}$ (3.4 ms). An optimal N and FA pair (12, 131°) is found to maximize ruCNR (4.04, white star). Contours are shown for sacrificed ruCNR when η = 0.99, 0.95, 0.9. (b, c, d, e) The optimal N* and FA* (Eq. (47)), echo train duration N*·TR, and the maximal ruCNR_bSSFP (Eq. (48)) are plotted with respect to TR, with black circles indicating the values for TR = 5 ms, which match the white star in (a), and the solid black lines represent the original optimization results when η = 1. The red dashed lines, green dash-dot lines and blue dotted lines represent the corresponding optimization results (Eq. (50)) for optimal N*, FA*, echo train duration, and ruCNR* with varying TR, when η = 0.99, 0.95, 0.9, respectively. For TR = 5 ms and η = 0.99, 0.95, 0.90, (a) the maximal ruCNR* = η · 4.04 = 4.00, 3.84, 3.64 are achieved at N* = 22, 43, 66 and lower FA* = 83°, 55°, 41° (black stars), which match (b, c, d, e) the colored circles in the red dashed, green dash-dot and blue dotted lines.

4. Discussion

To the best of our knowledge, the present work is the only study that conducted a comprehensive MTF and PSF analysis in the same framework of three fundamental acquisition schemes widely adopted after magnetization-preparation, FSE, FLASH, and bSSFP, based on the respective k-space filtering effect due to magnetization relaxation from transient state to steady state. Their properties in terms of signal level (PSF(0)), image blurring (FWHM), and CNR efficiency (ruCNR) were derived with respect to sequence parameters such as the number of PE steps per shot (N), TR/TE, FA, as well as T₁/T₂ values. Compared to FSE acquisition, whose amplitude-loss effect and image blurring effect (Figures 1, 5) can be simply expressed as functions of the ratio of the echo train duration over T₂ (N∙TE/T₂) [1]. PSFs of FLASH and bSSFP acquisitions are shown to have more complexed dependence on N, TR, FA, and T₁/T₂ values (Figures 2, 3, 5). The characterization of their PSFs could provide full understanding of image signal and contrast resulting from the magnetization relaxation during the k-space acquisition and further benefit respective image interpretation and sequence optimization for a varieties of applications.

When quantification of the magnetization-prepared contrast is desired, the signal level (PSF(0)) of FLASH and bSSFP should not be treated as directly proportional to the M_prep as in FSE (Eq. (15)), rather, their PSF(0) should be described as a summation of one M_prep-proportional term with a slope a and one M_ss-proportional term as an intercept b (Eqs. (29,30), (43,44)). These intercepts are considered as a source of quantification bias for magnetization-prepared GRE imaging,^12,14,16,17 which would increase with larger N, TR, or shorter T₁ values (Figure 5e,f,h). In the examples given in Figure 5e, when N increase from 100 to 200, the bias of the magnetization (when M_prep = 0) for FLASH is 26% higher (0.043 vs 0.054) and the one for bSSFP is 40% higher (0.067 vs. 0.093); in Figure 5h, when T₁ is lowered from 1500 ms to 800 ms, the bias for FLASH is 70% higher (0.030 vs 0.051) and the one for bSSFP is 74% higher (0.065 vs. 0.113).

With larger N and longer echo trains, all acquisition schemes have reduced contrast between different M_prep levels, as the slope a of PSF(0) decreases with increasing N (Figure 5a). However, it is worth noting that FLASH and bSSFP experience very little blurring effect even with very large N (FWHM < 1.5 pixels. Figure 5i). This is to the contrary of FSE with FWHM broadened from 3 pixels at N = 50 to 13 pixels at N = 200 (Figure 5i).

When choosing the optimal N of the acquisition after the magnetization-preparation module, one needs to maximize the newly introduced metric for relative image contrast efficiency (ruCNR) (Eq. (9)). The ruCNR of FLASH and bSSFP exhibit plateaus specific to each acquisition parameters (Figure 5m). When plotted against both N and FA, the ruCNR of FLASH and bSSFP show TR-dependent plateaus that can be predicted by Eqs. (32,33), and (47,48) (Figures 6–8). Using Eqs. (35) and (50), minor ruCNRs can be achieved with larger N and lower FA (Figures 6–8). For FLASH readout, Ernst angle could be a default choice for FA, despite that it is not calculated for the transient state. As shown in Figures 5m and 6a with TR = 10 ms and T₁ = 1000 ms, compared to the FLASH with N = 50 at Ernst angle = 8°, achieved ruCNR could be 25% higher (2.5 vs 2.0) by choosing a shorter N* =12 and higher FA* = 25°. It is notable that, with TR of FLASH extended to 15–30 ms when using fast imaging such as stack-of-spirals [15, 20]. its ruCNR* could gain 50–100% improvement (Figure 6e).

Compared to FLASH, bSSFP offers higher ruCNR with large N factors (Figure 5), but at the cost of higher specific absorption rate (SAR) due to the higher FA used. bSSFP also requires shorter TR as it is limited by its susceptibility to B₀ field inhomogeneity [6]. bSSFP is posed for wider utilizations at low field strength where both SAR and B₀ field inhomogeneity are of less concerns [44, 45].

5. Conclusions

In this work, MTFs and PSFs of the FLASH and bSSFP acquisitions are analytically derived and numerically validated, and compared with the FSE acquisition. The prepared longitudinal magnetization before the GRE acquisitions and the image signal obeys a linear (not proportional) relationship with a slope and intercept. The effects on relative contrast (slope), the quantification bias (intercept), and the image blurring (FWHM) are characterized with different sequence parameters and relaxation values. The strategy for optimizing magnetization-prepared FLASH and bSSFP acquisitions with regard to the relative contrast per unit time would be facilitated with the analytical formulas derived in this work in terms of the number of phase-encoding factors (N), flip angles (FA), TR, and the knowledge of the relaxation parameters for a wide range of applications.