Modulation of Cathodoluminescence Emission by Interference with External Light

Abstract

Spontaneous processes triggered in a sample by free electrons, such as cathodoluminescence, are commonly regarded and detected as stochastic events. Here, we supplement this picture by showing through first-principles theory that light and free-electron pulses can interfere when interacting with a nanostructure, giving rise to a modulation in the spectral distribution of the cathodoluminescence light emission that is strongly dependent on the electron wave function. Specifically, for a temporally focused electron, cathodoluminescence can be canceled upon illumination with a spectrally modulated dimmed laser that is phase-locked relative to the electron density profile. We illustrate this idea with realistic simulations under attainable conditions in currently available ultrafast electron microscopes. We further argue that the interference between excitations produced by light and free electrons enables the manipulation of the ultrafast materials response by combining the spectral and temporal selectivity of the light with the atomic resolution of electron beams.

Coherent laser light provides a standard tool to selectively create optical excitations in atoms, molecules, and nanostructures with exquisite spectral resolution.¹ Additional selectivity in the excitation process can be gained by exploiting the light polarization and the spatial distribution of the optical field to target, for example, modes with specific angular momentum in a specimen.² However, the diffraction limit constrains our ability to selectively act on degenerate excitation modes sustained by structures that are separated by either less than half the light wavelength when using far-field optics (unless ingenious, sample-dependent schemes are adopted³⁻⁵) or a few tens of nanometers when resorting to near-field enhancers such as metallic tips.⁶⁻⁸ In contrast to light, electron beams, which are also capable of producing optical excitations,⁹ can actuate with a spatial precision roughly determined by their lateral size, currently reaching the sub-angstrom domain in state-of-the-art electron microscopes.¹⁰⁻¹² Indeed, the evanescent electromagnetic field accompanying a fast electron spans a broadband spectrum that mediates the transfer of energy and momentum to sample excitation modes with such degree of spatial accuracy.⁹ However, spectral selectivity is unfortunately lost because of the broadband nature of this excitation source, unless postselection is performed by energy filtering of the electrons, as done for instance in electron energy-loss spectroscopy.^9,13,14

Photons and electrons team up to extract the best of both worlds in the rapidly evolving field of ultrafast transmission electron microscopy (UTEM), whereby the high spatial precision of electron microscopes is combined with the time resolution and spectral selectivity of optical spectroscopy. In this technique, ultrashort electron pulses created by photoelectron emission are used to track structural or electronic excitations with picosecond and femtosecond temporal resolution.¹⁵⁻²⁵ Regarding electron–photon interaction, UTEM allows us to exploit the evanescent optical field components created by light scattering at nanostructures, so that the interaction is facilitated by passing the free electron beam through these fields, thus enabling spectrally and temporally resolved imaging with combined resolution in the nanometer–femtosecond–millielectronvolt domain via the so-called photon-induced near-field electron microscopy (PINEM) technique.^{17,20,22,26−54} This approach has been exploited to investigate the temporal evolution of plasmons^30,31 and optical cavity modes,^50,51 as well as a way to manipulate the electron by exchanging transverse linear^36,39,55 and angular^40,44 momentum with the photon field.

Following concepts from accelerator physics,⁵⁶ temporal compression of the electron beam into a train of attosecond pulses can be achieved by periodic momentum modulation and free-space propagation, using either ponderomotive forces⁵⁷⁻⁵⁹ or PINEM-like inelastic electron-light scattering interactions.^{20,37,41,42,60,61} Accompanying these advances in our ability to manipulate free electrons, recent theoretical studies have explored the use of modulated free electrons to gain control over the density matrix of excitations created in a sample.⁶²⁻⁹⁹⁹ Intriguingly, the cathodoluminescence (CL) emission produced by a PINEM-modulated electron has been predicted to bear coherence with the laser used to achieve such modulation, which could be revealed through correlations in an interferometer.⁶³ This scenario holds the potential to combine light and electrons as coherent probes acting on a sample, possibly enabling practical applications in pushing the space–time–energy levels of resolution beyond their current values. Although we refer to coherence in a precise way in what follows (i.e., the interference of two phase-locked signals), this term can have various meanings when applied to different types of processes, so we provide a discussion of possible interpretations in the context of electron microscopy in the Supporting Information.

The CL intensity is extremely low in most samples (≲10^–5 photons per electron), unless we restrict ourselves to special classes of targets (e.g., those enabling phase matching between the emitted radiation and the electron^45,49,66). When measuring far-field radiation, the visibility of the interference between CL emission and external light could be enlarged by dimming the latter to match the former. Shot noise that could potentially mask the resulting interference is avoided if photon measurements are performed at a single detector (i.e., after the amplitudes of CL and external light have been coherently superimposed). Based on this idea, we anticipate that the use of dimmed illumination in combination with CL light emission represents a practical route toward the sought-after push in space–time–energy resolution with which we can image and manipulate optical excitations at the nanoscale.

Here, we show that the optical excitations produced in a structure by the combined effect of light and free electrons can add coherently, therefore providing a tool for actively manipulating sample excitations. The combination of light and electrons adds the spatial resolution of the latter to the spectral selectivity of the former in our ability to manipulate and probe nanoscale materials and their optical response. Specifically, we illustrate this possibility by showing that the CL emission produced by a free electron can be coherently controlled by simultaneously exciting the sample with suitably modulated external light. We demonstrate that it is possible to strongly modulate the CL emission using currently existing technology, while complete cancellation of CL is physically feasible using tightly compressed electron wavepackets, which act as classical external point charges. The present work thus capitalizes on the correlation between CL from modulated electrons and synchronized external light as discussed in ref (63), so we propose a disruptive form of ultrafast electron microscopy based on the direct observation of interference between CL emission and dimmed light scattering at a single photon spectrometer. We anticipate the application of interference in the excitations produced by the simultaneous action of light and electrons as a route toward spectrally resolved imaging and selective excitation of sample optical modes with an improved level of space–time–energy resolution. The sensitivity provided by the measurement of the relative phases between electron and laser waves could be further enhanced through lock-in amplification schemes that isolate the interference effects to gain information on both the electron density profile and the temporal evolution of the targeted optical excitations.

Results and Discussion

First-Principles Description of CL Interference with External Light

We consider the combined action of external light and free electrons on a sampled structure, such as schematically illustrated in Figure 1. Under common conditions met in electron microscopes, the electrons can be prepared with well-defined velocity, momentum, and energy, such that their wave functions consist of components that have a narrow spread relative to those values. Additionally, we adopt the nonrecoil approximation by assuming that any interaction with the specimen produces negligible departures of the electron velocity with respect to its average value (i.e., small momentum transfers relative to the central electron momentum). Under these conditions, we calculate the far-field radiation intensity produced by the combined contributions of interaction with the electron and scattering from a laser, based on the far-field Poynting vector. In a fully quantum treatment of radiation, the angle- and frequency-resolved far-field (ff) photon probability reduces to

1

where k = ω/c (see detailed derivation in Methods). This expression is the quantum counterpart of a classical result for CL,⁹ now involving the position- and frequency-dependent positive-energy part of the electric and magnetic field operators 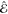(r,ω) and 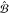(r,ω), respectively. We follow a quantum electrodynamics formalism in the presence of dispersive and absorptive media^67,68 to calculate this quantity for a free electron of incident wave function ψ⁰(r) and external light characterized by a spectrally resolved electric field amplitude E^ext(r,ω). After some analysis (see Methods), taking the electron velocity vector v along z, we find

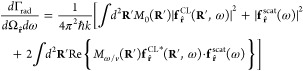2

where

3

is the Fourier transform of the electron probability density, which acts as a coherence factor. Here, we use the notation r = (R, z) with R = (x, y), and we define the electric far-field amplitudes f_r̂^CL(R, ω) and f_r̂(ω) through the asymptotic expressions

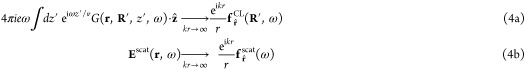corresponding to the classical CL and laser-scattering contributions, respectively. It should be noted that we only retain the 1/r radiative components of the far field in dΓ_rad/dΩ_r̂dω (see eqs 2 and 4), which is a legitimate procedure when considering directions in which they do not interfere with the external illumination. Nevertheless, interference between the incident and forward 1/r radiative components produces an additional contribution dΓ_forward/dΩ_r̂dω (i.e., dΓ_ff/dΩ_r̂dω = (dΓ_rad/dΩ_r̂dω) + (dΓ_forward/dΩ_r̂dω)), as we discuss below in relation to the energy pathways associated with the interaction. The specimen is assumed to be characterized by a linear and local electromagnetic response, which enters this formalism through the Green tensor, implicitly defined by

5

where ϵ(r,ω) is the position- and frequency-dependent permittivity. The first and second terms in eq 2 describe the separate contributions from CL and light scattering, respectively, whereas the third term accounts for interference between them. We remark that this result relies on the nonrecoil approximation for the electron, which allows us to replace its associated current operator by the average expectation value under the assumption that v remains unaffected by the interaction.

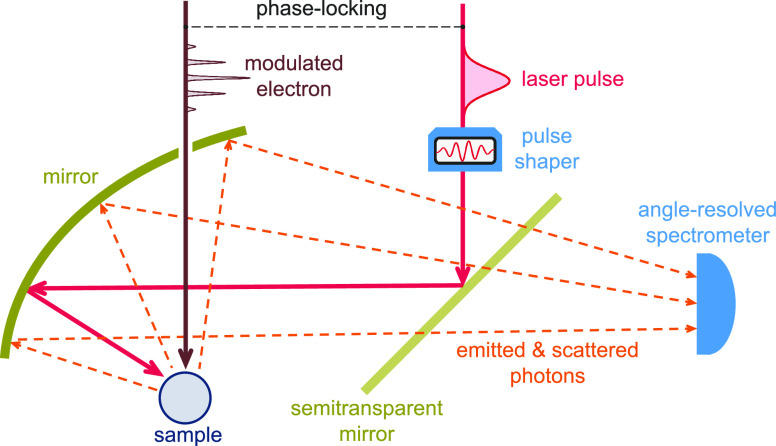
Figure 1.

Sketch of the system under consideration. A laser pulse and a modulated electron are made to interact with a sample and produce light scattering and cathodoluminescence (CL) emission, respectively. The electron is synchronized with the laser pulse to maintain mutual phase coherence. The resulting emitted and scattered photons are collected by a spectrometer. A laser pulse shaper is inserted in this scheme to bring the scattered light amplitude to a level that is commensurate with the CL emission field.

Interestingly, the CL emission in the absence of external illumination (i.e., the first term in eq 2) is constructed as an incoherent sum of contributions from different lateral positions R′ across the electron beam^69,70 (i.e., no interference remains in this signal between the CL emission from different lateral positions of the beam). In contrast, the signal associated with the interference between CL and light scattering (third term in eq 2) contains additive contributions from different lateral electron-beam positions R′. Interestingly, this effect is genuinely associated with interference between different lateral positions of the beam because the light scattering amplitude f_r̂^scat(ω) in that equation does not depend on R′.

For completeness, we note that eq 2 can be written in the more compact form

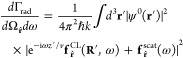which directly reflects the interference between CL and laser scattering. In addition, our results can easily be generalized to deal with several distinguishable electrons (labeled by superscripts j), for which we have (see derivation in Methods)

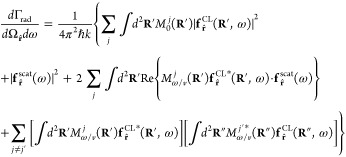6

where M_ω/v^j is given by eq 3 with ψ⁰ replaced by ψ^j (the wave function of electron j). In the absence of external light (i.e., with f_r̂ = 0), this expression converges to the multielectron excitation probability described elsewhere.⁷⁰

While the above results are derived for electrons prepared in pure states (i.e., with well-defined wave functions), the extension to mixed electron states is readily obtained by evaluating the averages in eqs 32 as Tr{ĵ^el(r′,ω)ĵ^el†(r″,ω)ρ̂^j} and Tr{ĵ^el(r′,ω)ρ̂^j}, respectively, where ρ̂^j is the electron density matrix of electron j. This leads exactly to the same expressions as above but replacing |ψ^j(r)|² by the probability densities ⟨r|ρ̂^j|r⟩, which allow us to describe electrons that have undergone decoherence processes before interacting with the sample.

We present results below for nanoparticles whose optical response can be described through an isotropic, frequency-dependent polarizability α(ω). Considering a well-focused electron with impact parameter R₀ relative to the particle position r = 0 (i.e., an electron probability density |ψ⁰(r)|² ≈ δ(R – R₀)|ψ_∥(z)|²), we find that eq 2 then reduces to

7

where

8

Here, 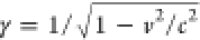is the Lorentz factor, and we now have

9

for the electron coherence factor. These expressions clearly reveal that, although the phase of the electron wave function is erased because only the probability density appears in eq 9, the mutual electron-light coherence is controlled by the temporal profile of that density, as well as its timing with respect to the light field, which produces a global phase in M_ω/v relative to the light field that in turn enters through the first term inside the square brackets in eq 7 (e.g., to partially cancel the CL emission). Obviously, without electron-laser timing, averaging over this phase difference cancels such interference.

Reassuringly, eq 7 reduces to well-known expressions for the CL emission when setting E^ext = 0 (i.e., in the absence of external light). This result is independent of the electron wave function.^63,64,70,71 Conversely, we recover the photon scattering probability ∝ ω³|α|² when E^el = 0 (i.e., without the electron). An additional element of intuition is gained by the fact that the expression for E^el(R₀,ω) corresponds to the spectrally resolved evanescent field produced by a classical point electron,⁹ which decays exponentially away from the trajectory, as described by the modified Bessel functions K₀ and K₁.

The electron coherence factor M_ω/v in eq 9 (and similarly M_ω/v(R) in eq 3) determines the degree of coherence (DOC) of the electron excitation (i.e., the CL emission) relative to the signal originating in the laser (i.e., light scattering). This factor enters eq 7 through terms proportional to DOC(ω) = |M_ω/v|², where we use the definition of DOC introduced in ref (63). Indeed, for M_ω/v = 0, the scattered light field does not mix at all with the CL emission field, so they are mutually incoherent. In contrast, if M_ω/v = 1, we have a maximum of coherence, so that the external illumination can fully suppress the CL emission. Specifically, we stress that the point-particle limit of the electron (i.e., |ψ⁰(r)|² → δ(r)) produces M_ω/v = 1, thus recovering an intuitive result for a classical point charge: the radiation from the passage of the electron is then a deterministic solution of the Maxwell equations, and thus, it can be suppressed by an external light field with the same frequency-dependent amplitude and opposite phase. This is not the case in general, so for arbitrarily distributed electron wave functions, the degree of coherence is partially reduced. We also stress that the phase of the electron wave function is entirely removed from the coherence factor (see eq 3).

We have shown that the CL emission can be modulated by interference with external laser light. As a way to illustrate this effect, we discuss in what follows the maximum achievable minimization of the overall far-field (scattered + emitted) photon intensity by appropriately selecting the external incident-field amplitude. If we have complete freedom to choose the external field, we readily find from eq 7 that dΓ_rad/dω is minimized by taking

10

Alternatively, when one adopts light pulses E^ext(0,ω) = f(ω)E₀ with a predetermined spectral profile f(ω) (e.g., a Gaussian f(ω) = e^{–(ω–ω₀)2σ_t2/2}), the minimization condition at a given sample resonance frequency ω = ω₀ is readily achieved by setting the field amplitude to E₀ = −M_ω0/v^*E^el(R₀,ω₀)/f(ω₀). As an estimate of the laser intensity needed to optimally modulate the CL emission, we take |M_ω/v| = 1 and consider the electric field amplitude from eq 8 for a 100 keV electron passing at a distance R₀ = 50 nm (10 nm) away from the dipolar particle, so that, setting ℏω = 1 eV, we have |E^el(R₀,ω)|Δω ∼ 50 kV/m (280 kV/m), assuming a depletion bandwidth ℏΔω = 0.1 eV; also, the corresponding laser fluence is (c/4π²)|E^el(R₀,ω)|²Δω ∼ 10 nJ/m² (400 nJ/m²).

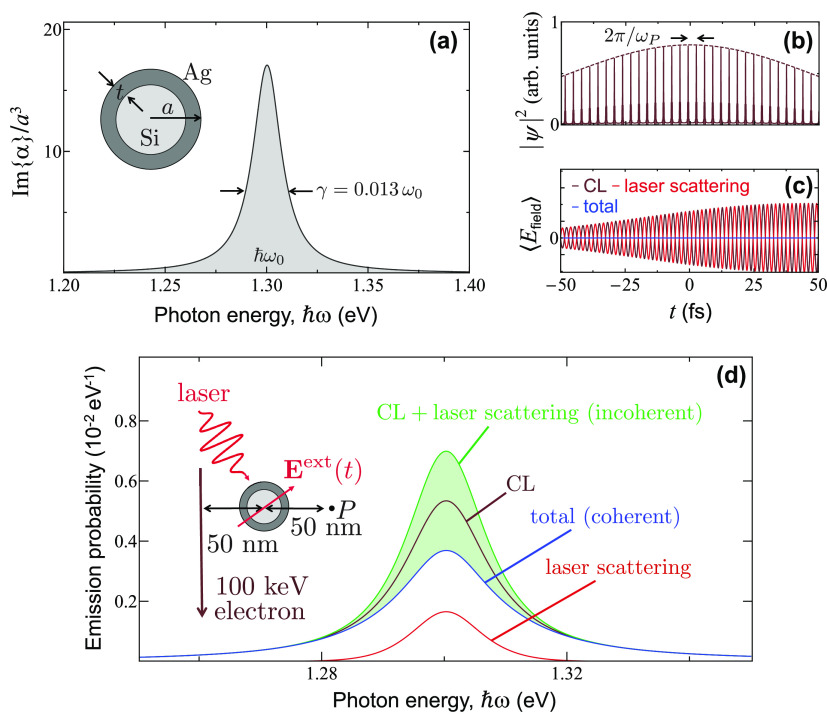
Motivated by the potential application of electron beams in controlling the excitations of small elements in a sample (e.g., molecules), we consider a dipolar scatterer as that depicted in Figure 2a, consisting of a 60 nm silicon sphere coated with a silver layer of 5 nm thickness (i.e., an outer radius a = 35 nm), which exhibits a spectrally isolated plasmon resonance at a photon energy ℏω₀ = 1.3 eV. In practice, we calculate the dipolar polarizability of small spheres from the corresponding electric Mie scattering coefficient as α = (3/2k³)t₁^E.⁹ The relatively low level of ohmic losses in silver produces a narrow resonance, with 14% of its fwhm (ℏγ = 0.013ℏω₀ ≈ 17 meV) attributed to radiative losses, as estimated from the ratio (≈0.86) of peak absorption to extinction cross sections. Similar dipolar resonances can be found in other types of samples, such as metallic nanoparticles of different morphology^73,74 and dielectric cavities,⁷⁵ for which we anticipate a variability in their coupling strength to light and electrons that should not, however, affect the qualitative conclusions of the present work.

Figure 2.

Interference between cathodoluminescence and external light scattering. (a) We consider a sample consisting of a small isotropic scatterer described through a frequency-dependent polarizability α(ω) that is dominated by a single resonance of frequency ω₀ and width γ. For concreteness, we take a nanosphere (see inset) comprising a silicon core (60 nm diameter, ϵ = 12 permittivity) coated with a silver layer (5 nm thickness, permittivity taken from optical data⁷²), for which ℏω₀ = 1.3 eV and γ = 0.013ω₀. In the plot, the polarizability is normalized using the outer particle radius a = 35 nm. (b) Electron density profile of a 100 keV electron Gaussian wavepacket (50 fs standard deviation duration in probability density) after modulation through PINEM interaction (coupling coefficient |β| = 5, central laser frequency tuned to ω_P = ω₀) followed by free propagation over a distance d = 2.5 mm, which produces a train of temporally compressed density pulses. (c) Time dependence of the CL, laser scattering, and total field amplitudes for the electron in (b) and a laser Gaussian pulse of 50 fs duration in amplitude. The light amplitude is optimized to deplete the CL signal at frequency ω₀. (d) Spectral dependence of the resulting angle-integrated far-field CL (maroon curve), laser scattering (red curve), and total (blue curve) light intensity for the optimized amplitude of the Gaussian laser pulse. The incoherent sum of CL emission and laser scattering signals is shown for comparison (green curve). The shaded region corresponds to spectra obtained with partially optimized laser pulses. The inset in (d) shows details of the geometry under consideration, also indicating the position P at which the field in (c) is calculated.

In what follows, we consider modulated electrons, focusing on their interaction with a particle under simultaneous laser irradiation. The production of sub-femtosecond-modulated electrons has become practical thanks to PINEM-related advances in ultrafast electron microscopy, whereby an ultrashort laser pulse is used to mold each electron into a train of pulses,^{37,41,42,59,60,76} from which an individual wavepacket can be extracted by applying a streaking technique.⁶¹ Specifically, we consider either Gaussian electron wavepackets defined by the wave function

11

where the duration is expressed in terms of the standard deviation σ_t of the electron pulse probability density |ψ_∥(z)|² and q₀ is the central wave vector, or electrons modulated by PINEM interaction with scattered laser light followed by free-space propagation over a macroscopic distance d before reaching the sampled particle. The wave function of the so modulated electron consists of a Gaussian wavepacket envelope (i.e., eq 11) multiplied by an overall modulation factor^64,70

12

where l labels a periodic array of energy sidebands separated by multiples of the laser photon energy ℏω_P from the zero-loss peak; the modulation strength is quantified by a single complex coupling parameter β that is proportional to the laser amplitude and whose phase determines the reference position z_P, and we have introduced a sideband-dependent recoil correction phase ∝ l² to account for propagation over d, involving a Talbot distance z_T = 4πm_ev³γ³/ℏω_P². These expressions are valid under the assumption that the laser is quasi-monochromatic (i.e., its frequency spread is small compared with ω_P). Then, for an optimum value of d, the factor 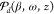renders a temporal comb of periodically spaced pulses (time period 2π/ω_P) that are increasingly compressed as |β| is made larger, eventually reaching attosecond duration.^{37,41,42,59,60,76} We remark that mutual electron-laser phase coherence can be achieved using the same laser to both modulate the electron and subsequently interact with the sample. For concreteness, we set the electron energy to 100 keV and tune the PINEM laser frequency to the resonance of the aforementioned sample (i.e., ℏω_P = ℏω₀ = 1.3 eV). The corresponding Talbot distance is then z_T ≈ 211 mm.

Optical Modulation of CL from a Dipolar Scatterer

An example of the PINEM-modulated electron density profile is shown in Figure 2b for σ_t = 50 fs, |β| = 5, and d = 2.5 mm. Direct application of eq 7 to this electron allows us to calculate the CL emission spectrum, along with its modulation due to interference with light scattering from a phase-locked Gaussian pulse (50 fs duration in field amplitude), as shown in Figure 2d, where the inset depicts further details of the geometrical arrangement and configuration parameters. Starting from the CL spectrum in the absence of external illumination (maroon curve, which we insist is independent of electron wave function profile^63,64,70,71), we then superimpose the phase-locked laser pulse in which we optimize the light field amplitude E₀ as prescribed above in eq 5 to produce a maximum of depletion in the resulting photon intensity at the peak maximum (blue curve). The achievable depletion is not complete because we have DOC(ω₀) = |M_ω0/v|² ≈ 0.31 for the considered electron, which differs from the limit of perfect coherence (see below), so a fraction of the original CL signal given by 1 – DOC(ω₀) ≈ 69% remains after complete cancellation of the coherent part. If the electron and light pulses are not phase-locked, relative phase averaging renders M_ω/v = 0, so the resulting probability of detecting CL or scattered photons (green curve) is just the incoherent sum of the probabilities associated with these two processes (i.e., the sum of the blue and red curves).

It is instructive to compare the electric near-field associated with CL versus light scattering by computing the quantum average of the total electric field operator Ê^H(r,t). Although this quantity is an observable, we note that its measurement is not straightforward. Following the approach explained in the Methods section and retaining only terms that are linear in the electron current operator ĵ(r,ω), we find the average field to be given by

which under laser and electron exposure becomes

where E^CL is defined in Methods (eq 34). The scattered part of the resulting time-dependent field is plotted in Figure 2c as calculated from this equation at the position P indicated in the inset of Figure 2d. We corroborate that the optimized laser scattering field (red) can be made to cancel the CL field (maroon), therefore producing a nearly vanishing total field (blue) that is consistent with the depletion of CL observed in Figure 2d. It is important to stress that the average of the electric field amplitude cancels, while nonvanishing fluctuations give rise to the incoherent part of the emission, which is not suppressed.

CL Modulation for Gaussian Electrons

In Figure 3, we consider an electron prepared in a Gaussian wavepacket with standard deviation duration σ_t of either 0.3 or 0.9 fs (Figure 3a). These values are consistent with those achieved in recent experiments.⁶¹ The corresponding coherence factor M_ω/v = e^{–ω2σ_t2/2} (Figure 3b, as calculated from eqs 9 and 11) quickly dies off as the electron pulse duration exceeds the optical period 2π/ω of the targeted excitation. In the point-electron limit (σ_t → 0), full coherence is obtained in accordance with the intuitive picture that the electron then generates a classical field that is well described by the solution of Maxwell’s equations for a classical external source. The corresponding CL emission probability (Figure 3c, maroon curve) is again independent of electron wave function, while maximal depletion can be obtained upon sample irradiation with an optimum spectral profile of the external field amplitude (eq 10), so that only a fraction 1 – |M_ω/v|² of the CL emission remains (see eq 7). Consequently, the level of depletion depends dramatically on pulse duration, as illustrated by comparing solid and dashed curves in Figure 3c.

Figure 3.

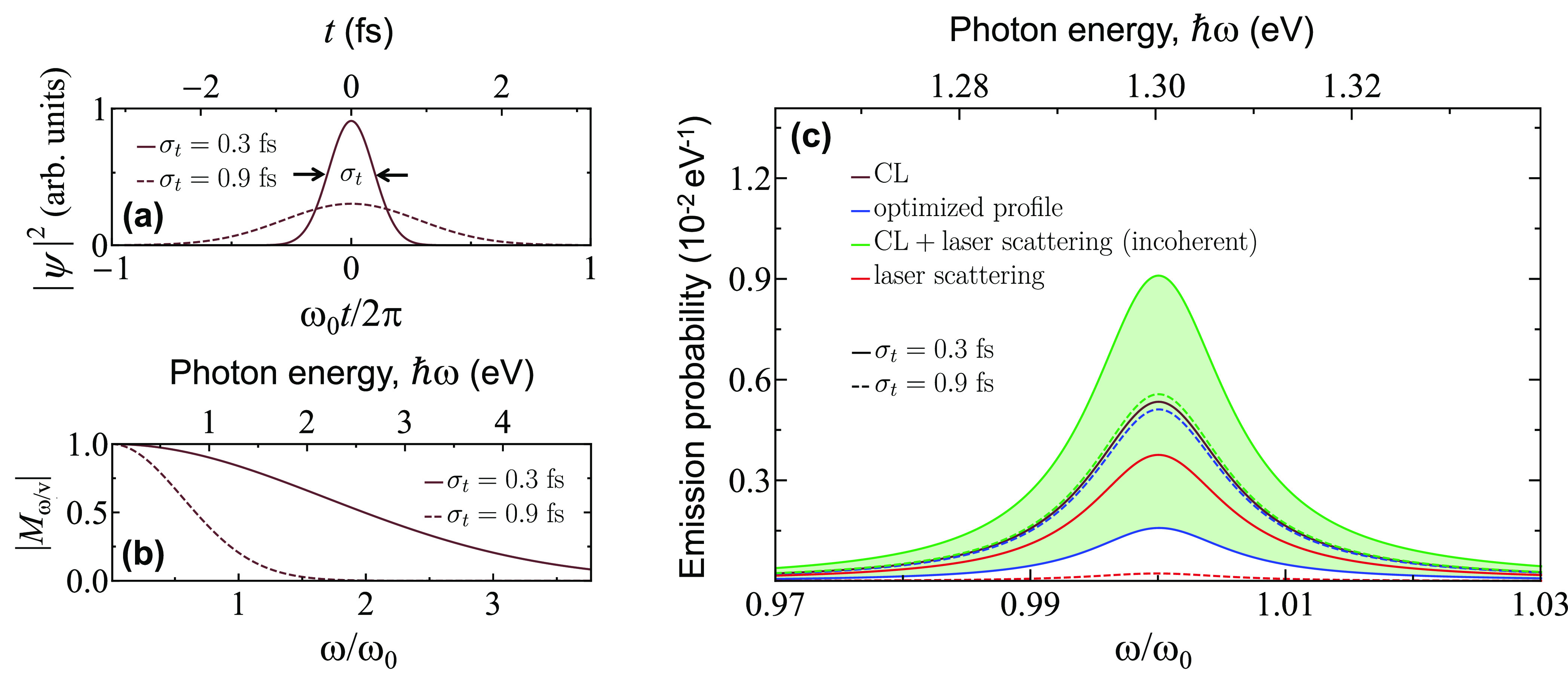
Modulation of the CL emission by Gaussian electron and laser pulses. (a) Gaussian electron wavepackets of 0.3 and 0.9 fs duration. (b) Frequency dependence of the electron coherence factor M_ω/v (i.e., the Fourier transform of the profiles in (a)). (c) Angle-integrated CL, laser scattering, and total far-field photon intensity using the electron pulses in (a), the same particle and geometrical configuration as in Figure 2, and an optimized spectral profile of laser field amplitude. We also show the incoherent sum of CL emission and laser scattering signals for comparison (green curves).

CL Modulation for PINEM-Compressed Electrons

The wave function of a PINEM-modulated electron at the sample interaction region is given by the product of eqs 11 and 12 when using a quasi-monochromatic laser. The corresponding coherence factor, calculated from eq 9 as explained in the Methods section, is a function of the PINEM coupling coefficient β, the free-propagation distance d, the excitation frequency ω, the electron velocity v, and a slowly varying envelope profile that we take here to be a Gaussian of temporal width σ_t. In the ωσ_t ≫ 1 limit, which is reached in practice with σ_t ∼ 2 fs for sample excitations of ℏω = 1.3 eV energy (see supplementary Figure S1), we obtain the universal plot for |M_ω/v| shown in Figure 4a, where the dependence on ω, d, and v is fully encapsulated in the d/z_T ratio, using the Talbot distance z_T defined above. Importantly, we find a region of maximum coherence (blue contour) in which |M_ω/v| ≈ 0.582, and therefore, the fraction of excitations produced by the electron that are coherent with respect to the external phase-locked laser is limited to DOC(ω) = |M_ω/v|² ≤ 34%. This maximum value can be reached for coupling parameters |β| ≥ 0.46, while the corresponding free-propagation distance d can be controlled by changing the modulating laser intensity. We note that the d position at which maximum coherence is found does not coincide with that of maximal temporal compression of the electron pulse train due to a substantial electron probability density remaining in the region between consecutive peaks.⁶⁴

Figure 4.

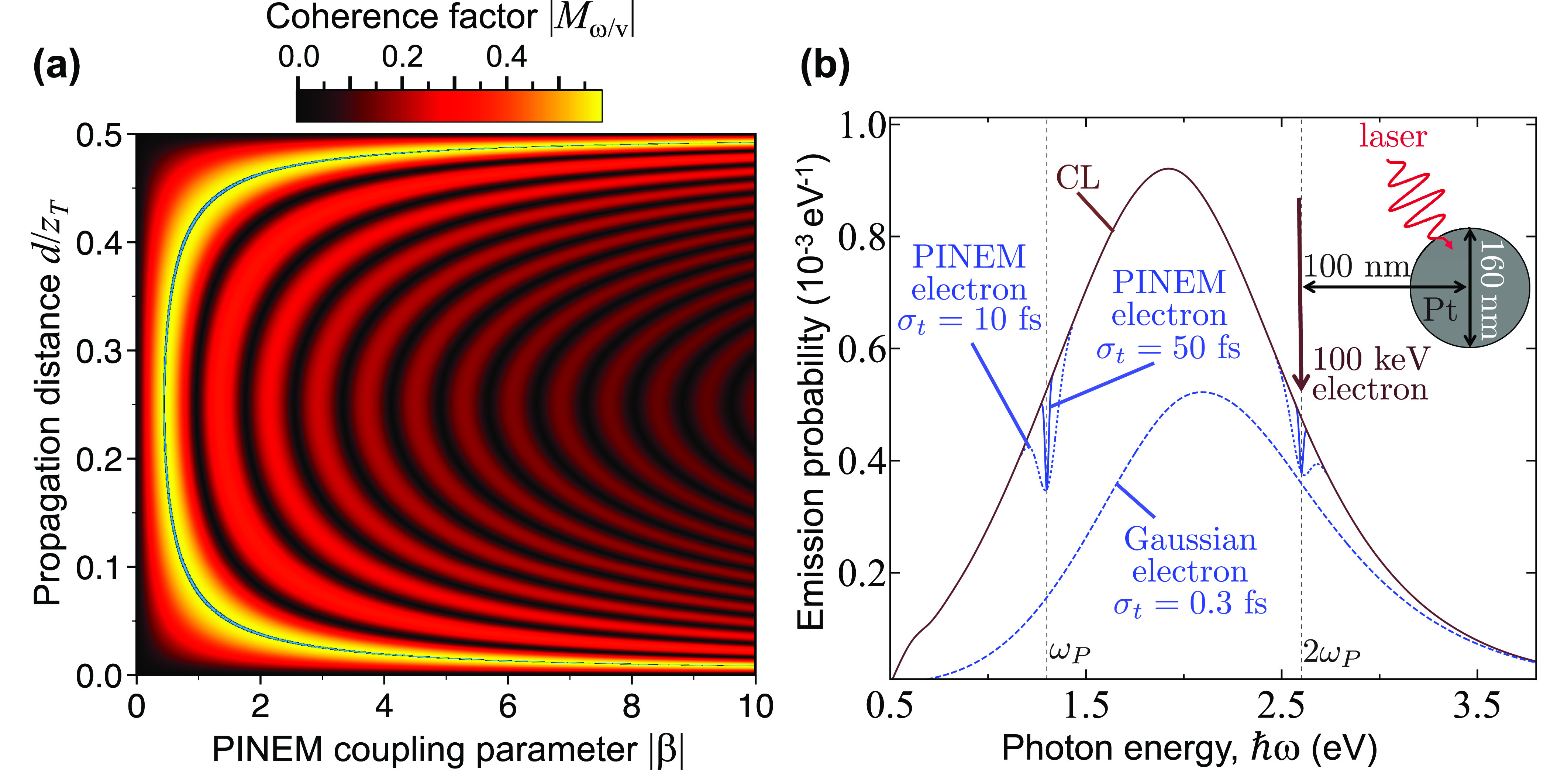
Coherence factor of PINEM-modulated electrons. (a) We show the coherence factor |M_ω/v| for modulated electrons in the limit of long pulse duration (ωσ_t ≫ 1) as a function of the PINEM coupling parameter β and free-propagation distance d. This function is periodic along d with a period given by half the Talbot distance z_T. Additionally, |M_ω/v| presents an absolute maximum of ≈0.582 along the blue contour superimposed on the density plot. (b) Unperturbed (maroon curve) and optically depleted (blue curves) CL spectra from a 160 nm Pt spherical particle for electrons prepared in Gaussian wavepacket (dashed blue curve, σ_t = 0.3 fs) or PINEM-modulated (solid and dotted blue curves obtained with |β| = 5 and either σ_t = 50 fs or σ_t = 10 fs; see labels) states. The inset shows the geometrical arrangement and parameters. The laser amplitude is taken to be optimized for all emission frequencies.

In Figure 4b, we consider a dipolar scatter with a broad spectral response to better illustrate the optically driven depletion of CL for PINEM-compressed electrons. In particular, we take a 160 nm Pt spherical particle, which produces a wide CL emission peak (maroon curve). For comparison, we show the depletion obtained under optimized laser irradiation (i.e., with the external light field amplitude given in eq 10) for a Gaussian electron wavepacket of 0.3 fs duration (Figure 4b, dashed curve), showing a stronger effect at lower photon energies in accordance with Figure 3b. In contrast, for a nearly optimum PINEM-modulated electron (the same as in Figure 2b), we find instead discrete depletion features, corresponding to the PINEM energy (i.e., ℏω_P = 1.3 eV in this case) and its harmonics ω = mω_P (only m = 1 and 2 peaks are visible in the solid and dotted curves of Figure 4b). We note that the leftmost depletion does not reach as deep as that produced by the Gaussian wavepacket electron, whereas the second one has nearly the same magnitude. In the ωσ_t ≫ 1 limit, the depletion observed at the excitation frequencies ω = mω_P is equally ruled by universal plots of M_ω/v analogous to that in Figure 4a (see supplementary Figure S2), showing a similar dependence on β and d but with an increasingly reduced magnitude as the harmonic order m is increased. When the envelope of the PINEM-modulated electron is reduced from 50 fs (solid blue curved) to 10 fs (dotted curve), the depletion features are broadened, but their depth is maintained, directly mimicking the behavior of DOC(ω). In other words, shorter electron pulses allow us to suppress a larger fraction of the CL power, and of course, this suppression requires illuminating the sample with a synchronized, amplitude-optimized laser that covers the range of sampled excitation frequencies ω.

Temporal Control of the Emission

The studied CL modulation strongly depends on the timing between the laser and electron interactions with the sampled structure, as illustrated in Figure 5. To elaborate on this point, we reduce the number of parameters by considering electron wavepackets with a Gaussian profile (i.e., without an additional PINEM modulation) and vary their temporal delay relative to the laser pulses (see sketch in Figure 5a), using the same standard deviation duration σ_t = 10 fs both for the electron probability density and for the light field amplitude. We consider the same particle as in Figure 1 and integrate the CL signal over frequency to cover the resonance region. The result is plotted in Figure 5b. For optimal CL suppression, the polarization induced in the particle by the electron and the laser must have overlapping envelopes with a temporal delay precision well below an optical cycle. For finite delay, we show that the interference signal oscillates as a function of τ with a period that coincides with the resonance optical period 2π/ω₀. Additionally, the amplitude of these oscillations is effectively attenuated by a factor e^–γ|τ|/2 away from zero delay; this attenuation takes place at a pace that is half of the resonance decay rate γ because interference is governed by the resonance amplitude rather than the intensity.

Figure 5.

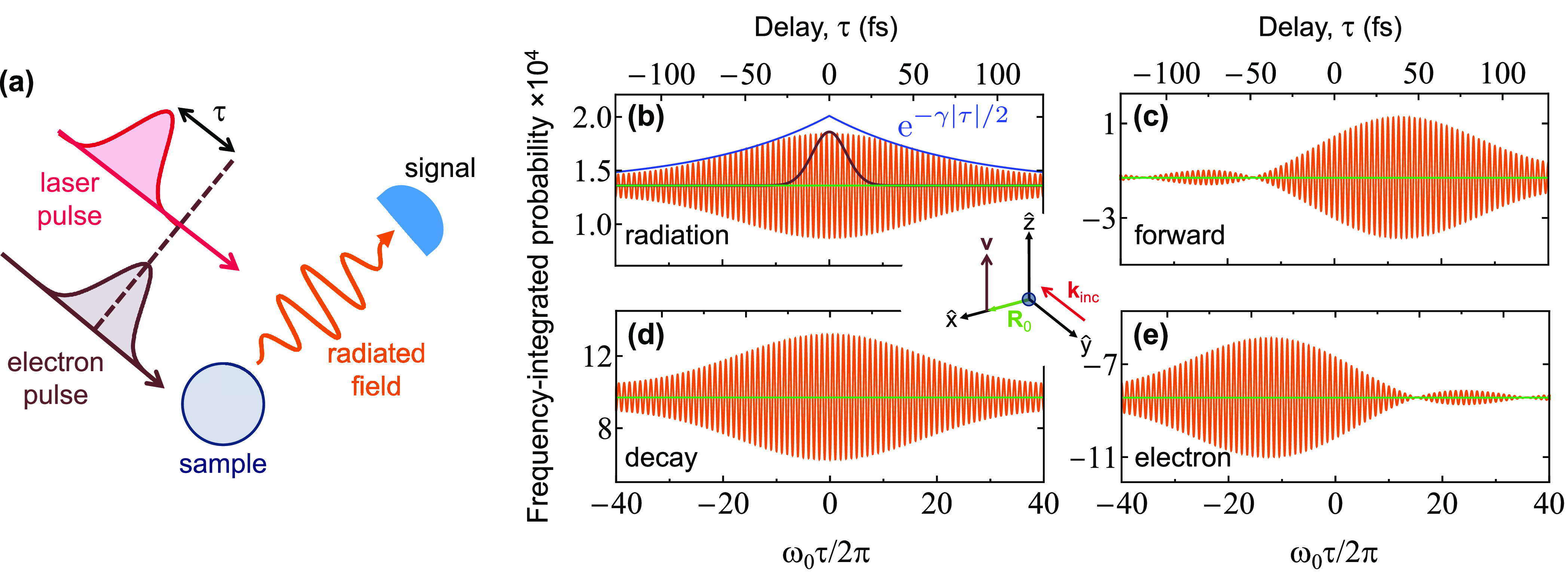
Control of the far-field photon intensity and energy pathways through the electron-laser temporal delay. (a) We consider the same configuration as in Figure 2, using electron and laser Gaussian pulses that act on the sample with a relative time delay τ. (b) Angle- and frequency-integrated photon intensity (orange, in units of photons per electron, multiplied by 10⁴), showing oscillations of period 2π/ω₀ as a function of τ, as calculated for 100 keV electrons, 10 fs Gaussian pulse durations (i.e., f(ω) = e^{–(ω–ω₀)2σ_t2/2}; see black profile for comparison, corresponding to the profiles of electron density and laser field amplitude), and the same particle as in Figure 2a. The interference attenuation for γτ ≫ 1 is indicated by the blue curve, where γ is the decay rate of the sampled resonance. The laser field amplitude is fixed to (1.4 eω₀/v²γ)f(ω). (c−e) Frequency-integrated probability associated with additional energy pathways: laser-stimulated forward scattering (c), total decay following excitation of the particle plasmon (d), and change in the electron energy (e). Calculations in (b−e) correspond to the orientations of the light (incident wave vector k_inc) and the electron (velocity v) shown in the central inset.

Energy Pathways

We present an alternative density-matrix formalism in the Supporting Information to describe the combined electron and light interaction with an isotropic dipolar sample that hosts a triply degenerate optical mode of frequency ω₀. This allows us to obtain partial probabilities for processes associated with energy changes in the electron (Γ_el), accumulated excitations and subsequent decays of the particle mode (Γ_decay), emission of radiation along forward (Γ_forward) and non-forward (Γ_rad) directions, and inelastic absorption events (Γ_abs). This analysis leads to the following expressions for the corresponding frequency-resolved probabilities:

13a

13b

13c

In addition, it reproduces eq 7 for dΓ_rad/dω, whereas the probability of any remaining process leading to absorption (e.g., ohmic losses in the particle material) is given by dΓ_abs/dω = (dΓ_decay/dω) − (dΓ_rad/dω). Importantly, the probabilities in eqs 13 satisfy the energy-conservation condition

14

To corroborate the correctness of these results, we have obtained an independent derivation of eqs 13 based on an extension of the quantum-electrodynamics formalism followed in the Methods section, as succinctly described in the Supporting Information.

We interpret Γ_forward as the change in photon forward emission (i.e., toward the direction of propagation of the incident light beam) associated with interference between emitted and externally incident photons (i.e., the type of stimulated process that is neglected in the non-forward far-field radiation probability Γ_rad). In particular, the first term inside the squared brackets of eq 13c coincides with the depletion of the incident light that is described by the optical theorem⁷⁹ (i.e., (1/πℏ)Im{α(ω)}|E^ext(0,ω)|² = σ_ext(ω)I(ω)/ℏω, where σ_ext(ω) = (4πω/c)Im{α(ω)} is the extinction cross section and I(ω) = (c/4π²)|E^ext(0,ω)|² is the light intensity per unit frequency), whereas the remaining term originates in electron-light interference. The probabilities given above are derived for isotropic dipolar particles, but a similar analysis leads to expressions corresponding to a particle characterized by a polarizability tensor α(ω)û ⊗ û (i.e., linear induced polarization along a certain direction û), for which the partial probabilities are still given by eqs 7 and 13 after substituting û·E^ext and û·E^el for E^ext and E^el, respectively.

We explore the aforementioned energy pathways in Figure 5b−e, where we plot the frequency-integrated probabilities Γ_rad, Γ_forward, Γ_decay, and Γ_el, respectively, as a function of electron-light pulse delay τ. We find that the decay probability follows a similar symmetric profile as the radiative emission (cf. panels b and d, both of them independent of the sign of τ). In contrast, the electron energy-change probability (Figure 5e) is markedly asymmetric (and so is the forward-emission probability (Figure 5c) as a result of energy conservation viaeq 14): we obtain the intuitive result that the electron energy remains nearly unmodulated if the electron arrives before the optical pulse, while the opposite is true for the forward light emission component.

Conclusions

Electron-beam-based spectroscopy techniques provide unrivaled spatial resolution for imaging sample excitations by measuring electron energy losses (EELS) or light emission (CL) associated with them. In this study, we propose the opposite approach: suppression of sample excitations produced by free electrons through combining them with mutually coherent laser irradiation. Indeed, our first-principles theory confirms that electrons and light can both be treated as mutually coherent tools for producing optical excitations. They form a synergetic team that combines optical spectral selectivity with the high spatial precision of electron beams. In contrast to EELS, where free electrons act as a broadband electromagnetic source, so that only a posteriori selection of specific mode frequencies can be performed by spectrally resolving the inelastically scattered probes, the methods here explored allow us to target designated mode frequencies with sub-angstrom control over the excitation process. In addition, the excitation of on-demand nanoscale optical modes through the combined use of modulated electrons and tailored light pulses is amenable to the implementation of coherent control schemes^77,78 for the optimization of the desired effects on the specimen.

From a practical viewpoint, the PINEM interaction provides a way of molding the electron wave function to produce the temporally compressed pulses that are required to address specific sample frequencies. However, this method has a limited degree of achievable coherence in the electron-driven excitation process when using quasi-monochromatic light, quantified through the degree of coherence⁶³ 0 < DOC(ω) = |M_ω/v|² ≤ 1; more precisely, it can produce values DOC(ω) ≲ 34%, as we show above. We remark that the frequency-dependent function DOC(ω) is a property of the electron: this function is univocally determined by the probability density profile. Full coherence at a frequency ω, corresponding to the DOC(ω) → 1 limit, can be delivered by δ-function-like combs of electron pulses (i.e., for an electron probability density |ψ(z)|² ≈ ∑_mb_mδ(z – 2πmv/ω) along the beam,⁷⁰ with arbitrary coefficients b_m, including single pulses for b_m = δ_m,0), the synthesis of which emerges as a challenge for future research.

By putting free electrons and light on a common basis as tools for creating excitations in a specimen, one could additionally envision the combined effect of multiple electron and laser pulses, which would increase the overall probability of exciting an optical mode, provided that their interactions take place within a small time interval compared with the mode lifetime. This idea capitalizes on the concept of super-radiance produced by PINEM-modulated electrons,⁶² which our first-principles theory supports for probing and manipulating nanoscale excitations including the extra degrees of freedom brought by synchronized light and electron probes.

We remark that CL is just one instance of sample excitation, but the present study can be straightforwardly extended to optically bright modes in general (see independent analysis in ref (70)), including two-level resonances of different multipolar character. A key ingredient of our work is the use of dimmed illumination, so that the weak probability amplitude that the electron typically imprints on the sample has a magnitude that is commensurate with the effect of the external light. Because the measurement is performed once interference between electron- and light-driven excitation amplitudes takes place (i.e., at the far-field photospectrometer in CL or by the effect of any subsequent inelastic process following the decay of the excited sample mode in general), the studied electron–light mutual coherence is unaffected by additional sources of shot noise other than the intrinsic ones associated with the detection process (e.g., like in conventional CL).

Our prediction of unity-order effects in the modulation of electron–sample interactions through the use of external light enables applications in the manipulation of optical excitations at the atomic scale. Additionally, it suggests an alternative approach to damage-free sensing, whereby the spectral response of a specimen could be monitored through the modulation produced by the combined action of light and electrons, involving a reduced level of sample exposure to electrons because the targeted interference is proportional to the polarization amplitudes that they induce, so the outcome of a weak electron interaction could be amplified by applying a lock-in technique to the laser. This approach could be useful for imaging biomolecules, as well as strongly correlated materials in which probing without invasively perturbing the system is essential and remains a challenge in the exploration of spin and electronic ultrafast dynamics. In addition to the experimental configuration proposed in Figure 1, one could alternatively flip the semitransparent mirror horizontally to mix the external laser light with the CL emission at the detector instead of undergoing scattering at the specimen.

We find it interesting the possibility of adjusting the amplitude of the external light field (for example, through a temporal light shaper) to determine the frequency-dependent magnitude and phase of the CL amplitude field (f_r̂^CL(R,ω) in our formalism), thus providing temporal resolution when probing the specimen by direct Fourier transformation of this quantity. This method could yield a time resolution limited by the width of the frequency window in the CL measurement at the spectrometer, without affecting the intrinsic temporal resolution associated with the short duration of the electron and light pulses, and likewise, retaining the sub-angstrom spatial resolution associated with tightly focused electron beams. In a related direction, spatial light modulation and raster scanning of the electron beam could also be employed to gain further insight into the symmetry and nanoscale spatial dependence of the sample response. Additionally, for a sample in which f_r̂(R,ω) is well characterized (e.g., a dielectric sphere⁷⁵ or a thin film), the modulation of CL by varying the external field could be used to resolve the coherence factor M_ω/v, thus allowing us to retrieve the electron density profile from the Fourier transform of this quantity. In addition to far-field optical measurements, the present analysis can also be extended to alternative ways of probing optical excitations that are coherently created by light and electrons, such as electrical or acoustic detection of the modifications produced in the specimen.

Methods

Quantization of the Electromagnetic Field in the Presence of Material Structures

We follow ref (67) for the quantization of the electromagnetic field in the presence of linearly responding materials characterized by a position- and frequency-dependent local permittivity ϵ(r,ω). Without loss of generality to deal with free electrons that do not traverse any material, we adapt this formalism to a gauge in which the scalar potential is zero, as detailed elsewhere.⁶⁸ The response of the media is represented through a noise current distribution operator ĵ^noise(r,ω), in terms of which the vector potential operator reduces to

15

where G(r, r′, ω) is the classical electromagnetic Green tensor at frequency ω, implicitly defined by eq 5. The noise operator is chosen to be bosonic and satisfy the fluctuation–dissipation theorem for the current. These two conditions are fulfilled by writing

16

in terms of bosonic ladder operators f̂(r,ω) satisfying the commutation relations

17a

17b

where f̂_i=x,y,z denotes the Cartesian components of f̂. The Hamiltonian governing the free evolution of the radiation degrees of freedom is then expressed in terms of these operators as

Using eqs 15 and 16, the time-dependent quantum vector potential takes the form

18

Of particular interest for the rest of the calculation are the different-times commutators between the quantum electromagnetic vector potential and the fields. These quantities can easily be obtained using eqs 15–18, together with the relations Ê(r,t) = (−1/c)∂_t Â(r,t) and B̂(r, t) = ∇ × Â(r,t), which lead to

19a

19b

Here, we use the Levi-Civita symbol ϵ_ii″i‴, as well as the identity⁶⁷

20

It is important to remark that the commutators between fields and potentials are c-numbers, only dependent on the time difference t – t′. In the calculation of the CL emission probability, we also need the retarded Green tensors constructed from the commutators in eqs 19 as

21a

21b

in the time domain, or equivalently

22a

22b

in the frequency domain. In the derivation of eqs 22, we have used the fact that the electromagnetic Green tensor G(r,r′,ω) satisfies the Kramers–Kronig relations and the causality property G(r,r′,−ω) = G*(r,r′,ω).

Far-Field Radiation Emission: Derivation of Equation 1

We now calculate the far-field emission produced by quantum currents taking into consideration the quantum nature of the electromagnetic excitations. To this aim, we define the average electromagnetic energy flow through a solid angular region ΔΩ as

23

where k = ω/c, Ŝ^H(r,t) = (c/8π)[Ê^H(r,t) × B̂^H(r,t) – B̂^H(r,t) × Ê^H(r,t)] is the quantum mechanical counterpart of the classical Poynting vector,⁷⁹ and |ψ(−∞)⟩ is the initial quantum state at time t = –∞. The superscript H indicates that operators have to be calculated in the Heisenberg picture, and thus evolved with the total Hamiltonian

where 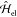describes the free evolution of the electron degrees of freedom (or charge currents, in general) and 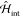represents the light–current interaction. Equation 23 can be expressed in terms of the scattering operator (t,–∞) by incorporating an adiabatic switching of the interaction, which leads to the relation ,⁸⁰ and from here, eq 23 becomes

24

We now describe the interaction between the electromagnetic field and a total quantum current ĵ(r,t) through the minimal coupling Hamiltonian in the zero scalar potential gauge as

25

where the time dependence in indicates that it is expressed in the interaction picture (i.e., the free part of the Hamiltonian, , is taken care of through the scattering matrix). Because the commutator [Â(r,t), Â(r′,t′)] is a c-number (this is a direct consequence of eqs 15–18), if we assume that the current operators commute at different times and positions (see below), the scattering operator can be written as^68,80,81 (see detailed derivation below)

26

where the operator 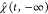only acts on the current degrees of freedom, and consequently, we can ignore it within this Methods section, but it must be taken into account when calculating quantities related to the electron probe (see Supporting Information). From here, we plug eq 26 into eq 24 and then use twice the identity [Â,e^B̂] = Ce^B̂ (valid if [Â, B̂] = C is a c-number) to bring the rightmost scattering operator to cancel its Hermitian conjugate on the left. This leads us to

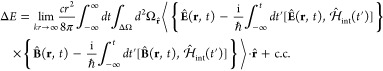27

where we have defined the quantum average as

The term Ê(r,t) × B̂(r,t) in eq 27, which is independent of the sources, represents the contribution from the zero-point energy, so it bears no relevance to this analysis. In addition, since the commutators between the vector potential and the field operators are c-numbers, the terms linear in the currents (i.e., through 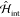) in eq 27 vanish when they are averaged over an initial state |ψ(−∞)⟩ in which the radiation part is prepared in the photonic vacuum. Now, we use the retarded Green functions (eqs 21) and their Fourier transforms (eqs 22) to obtain

where

28

is the angle- and frequency-resolved, time-integrated, far-field (ff) photon emission probability. Here, we have defined the new field operators

and we have introduced ĵ(r,ω) = ∫_–∞^∞dte^iωt ĵ(r,t). We note that eq 28 resembles its classical counterpart,⁹ but now the currents are commuting quantum mechanical operators.

Photon Intensity Produced by a Single Free Electron Combined with a Dimmed Laser: Derivation of Equation 2

We consider that the quantum current operator ĵ is the sum of a classical term j^ext (i.e., the source of the external laser light) and the quantum part associated with the free electrons ĵ^el. For a highly energetic electron with central relativistic energy E₀ = 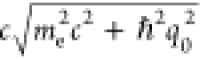and initial wave function consisting of momentum components that are tightly focused around a central value ℏq₀, the free-electron Hamiltonian 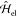can be approximated as⁴⁸ 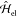= ∑_q[E₀ + ℏv·(q − q₀)]ĉ_q^†ĉ_q, where v = ℏc²q₀/E₀ is the central electron velocity, and we have introduced anticommuting creation and annihilation operators ĉ_q and ĉ_q of an electron with momentum ℏq. We remind that the momentum operator, written in the space basis set as −iℏ∇ in ref (48), now becomes 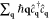in the second quantization formalism that we use here. Then, the electron current reduces to

29

where L is the side length of the quantization box, so wave vector sums can be transformed into integrals using the prescription ∑_q → (L/2π)³∫d³q (i.e., we have ⟨r|ĉ_q^†|0⟩ = e^iq·r/L^3/2). By repeatedly using the anticommutation relations to pull all electron creation operators to the left, we find the commutation relation

30

which is a property used above in the derivation of eq 28. Without loss of generality, we take v along the z and calculate the Fourier transform

31

where k_⊥⊥ ẑ is the transverse component of the exchanged wave vector k. This allows us to evaluate the average in eq 28 for an initial state consisting of an electron prepared in a wave function ψ⁰ = ∑_qα_q⟨r|ĉ_q^†|0⟩ and zero photons (i.e., 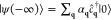) by first computing the intermediate results

32a

32b

where we use the notation r = (R, z). Also, M_ω/v(R), defined in eq 3, is a coherence factor that captures the dependence on the electron wave function through the probability density |ψ⁰(r)|². We note that there is no dependence on the phase of ψ⁰(r). By using eqs 32 to work out the evaluation of eq 28, we obtain

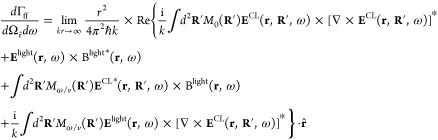33

where we have defined the CL-related vector

34

and the total (external + scattered) light fields

and B^light(r,ω) = (−i/k)∇ × E^light(r,ω). At this point, it is convenient to separate the light field into external and scattered components as E^light(r,ω) = E^ext(r,ω) + E^scat(r,ω), where the first term arises from the free-space part of the Green tensor, whereas the second term decays as 1/r far from the sample. First, we consider emission directions in which the external light does not interfere with the scattered and CL fields. Then, in the far-field limit (kr ≫ 1), we can approximate ∇ ≈ ikr̂ in the above expressions, and the electric and magnetic fields only retain components perpendicular to r. This allows us to rewrite eq 33 in the form given by eq 2 in terms of far-field electric field amplitudes f_r̂^CL(R′,ω) and f_r̂(ω) associated with CL emission and laser scattering contributions (see definitions in eqs 4). Under typical electron microscope conditions, for a well-focused electron beam, we can factorize the electron wave function as ψ⁰(r) = ψ_⊥(R)ψ_∥(z) and approximate |ψ_⊥(R)|² ≈ δ(R – R₀), where R₀ defines the beam position. Inserting this wave function into eq 2, we find

35

where now M_ω/v is defined in eq 9. There is an additional component in dΓ_ff/dΩ_r̂dω (eq 33) arising from the interference between the external light field E^ext(r,ω) and the scattered + CL far-field amplitudes. For plane wave light incidence with wave vector k_inc, the former can be written as E^ext(0,ω)e^ik_inc·r, which contributes to dΓ_ff/dΩ_r̂dω through the three last terms of eq 33. After integration over emission directions, and considering a dipolar scatterer (see below), this contribution becomes dΓ_forward/dω (eq 13c) (see Supporting Information for more details).

Generalization to Multiple Electrons: Derivation of Equation 6

The above formalism can be readily extended to deal with more than one electron by taking the initial state as 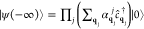, where j runs over different electrons and the photonic field is prepared in the vacuum state. Then, using the definition of the electron current operator ĵ^el(r, ω) in eq 31, the averages in eqs 32 can be readily computed for the multielectron state to yield

36a

36b

where M_ω/v^j is given by eq 9 with ψ⁰(r) substituted by ψ ^j(r) = Σ_qα_q⟨r|ĉ_q^†|0⟩ (the wave function of electron j). Finally, plugging eqs 36 into eq 28 and following similar steps as done above for a single electron, we obtain eq 6 in the main text.

Cathodoluminescence from a Dipolar Sample Object: Derivation of Equation 7

We present results in the main text for sample objects whose responses are dominated by an electric dipolar mode represented through an isotropic polarizability α(ω) placed at r = 0. We now carry out the limit in eq 4a by realizing that the free-space component of the Green tensor to the z′ integral vanishes exponentially away from the electron beam (i.e., just like the electromagnetic field accompanying a freely moving classical charge), so we only need to account for the contribution from the scattering part:

Plugging this expression into eq 4a, we can carry out the z′ integral using the identities ∫_–∞^∞dze^{iω(z/υ+r/c)}/r = 2K₀(ωR/υγ) and ∫_–∞dz(1 + i/kr)e^{iω(z/υ+r/c)}/r² = (2ic/Rυγ)K₁(ωR/υγ), where 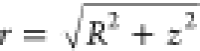and 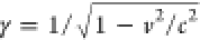(see eqs 3.914–4 and 3.914–5 in ref (82)). This leads to

37

where E^el(R′,ω), defined in eq 8, coincides with the electric field produced at the particle position r = 0 by a classical point electron whose trajectory crosses (R′,0) at time t = 0.⁹ Similarly, from eq 4b, the scattered external field amplitude is readily found to be

38

where E^ext(0,ω) is the external laser field acting on the particle. Finally, by inserting eqs 37 and 38 into eq 35, we obtain

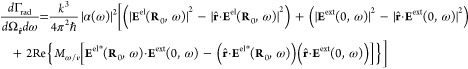39

The total far-field photon probability per unit frequency is then obtained by integrating eq 39 over solid angles, leading to

40

This expression can readily be recast in the form of eq 7 in the main text.

Scattering Operator: Derivation of Equation 26

We describe our system through the interaction Hamiltonian in eq 25 and use the commutation relation in eq 30 to write

Additionally, eqs 15 and 17 directly imply that [Â(r,t), Â(r′,t′)] is a c-number, which in turn leads to the nested commutation relation

41

This expression is important to derive eq 26 for the scattering operator starting from its definition⁸⁰

where T denotes time ordering. Following a well-established procedure,⁸¹ we discretize the time integral (with a set of equally spaced times t_i with i = 1, ..., N) and explicitly implement time ordering to write

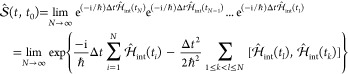with Δt = (t – t₀)/N, where we have used the relation e^X̂e^Ŷ = e^{X̂+Ŷ+[X̂,Ŷ]/2}, which is valid if [X̂[X̂,Ŷ]] = [Ŷ,[X̂,Ŷ]] = 0 (i.e., like in eq 41). Using this identity again, we readily find eq 26 by setting t₀ = –∞ and defining the phase operator

Interestingly, since the commutator between the electromagnetic potentials is a c-number, the operator 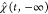acts only on the degrees of freedom associated with the currents and represents the effect of the image potential acting on the free charges.⁶⁸

One is often interested in calculating asymptotic quantities such as electron spectra at t = ∞. We then need to know the scattering operator 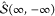, which can be obtained using eqs 15 and 29, leading to

Here

(see definition of  in eq 15) describes the total time evolution of electron-light states in the nonrecoil approximation if we disregard the effect of the image potential (i.e., the phase operator 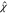). When the electron is focused around a point R = R₀ and its wave function can be separated in longitudinal and transverse components, as we do in the main text, we can approximate ĉ_q ≈ ĉ_q⊥ĉ_qz and replace the operator in the exponent of 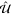by its average over a transverse electron state 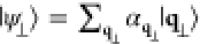satisfying the relation 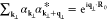, from which we find

42

Here, we have introduced the operators

and

as well as the coupling coefficient 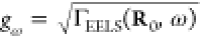, which reduces to the square root of the classical EELS probability⁹

We define these operators in such a way that they satisfy the commutation relations [â_ω,â_ω′^†] = δ(ω – ω′) and [b̂_ω, b̂_ω′] = 0, where the former can be proven using eq 20. Importantly, eq 42 allows us to quickly compute observables after electron–sample interaction. As an example of this, we find that the average of the positive-energy electric field operator 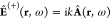over the state

with

(proportional to the photonic vacuum) reduces to

where 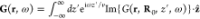. To derive this result, we made use of the relation [Â,e^B̂] = Ce^B̂ (valid if [Â,B̂] = C is a c-number), as well as the commutation relation

together with the fact that the operators b̂_ω and b̂_ω^† commute.

Calculation of the Coherence Factor for PINEM-Modulated Electrons

For an electron whose wave function is the product of eqs 11 and 12, the coherence factor defined in eq 9 readily reduces to the expression

which we evaluate numerically for finite σ_t. In the ω_Pσ_t ≫ 1 limit, M_ω/v takes negligible values unless the excitation frequency is a multiple of the PINEM laser frequency (i.e., ω = mω_P). Then, only l′ = l + m terms contribute to the above sum, which reduces to

and using Graf’s addition theorem, we have |M_ω/v| = |J_m[4|β|sin(2πmd/z_T)]|, in agreement with ref (999). We use this equation with m = 1 to obtain the map shown in Figure 4a, and with m = 1–3 to produce the supplementary Figure S2.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.1c00549.

• Discussion on the meaning of coherence in electron microscopy (section S1); alternative description for a dipolar scatterer and analysis of energy pathways (section S2); dependence of the coherence factor on Gaussian wavepacket duration (Figure S1); coherence factor at harmonic frequencies of the PINEM laser frequency ω_P (Figure S2) (PDF)

The authors declare no competing financial interest.