A vesicle microrheometer for high-throughput viscosity measurements of lipid and polymer membranes

Abstract

Viscosity is a key property of cell membranes that controls mobility of embedded proteins and membrane remodeling. Measuring it is challenging because existing approaches involve complex experimental designs and/or models, and the applicability of some methods is limited to specific systems and membrane compositions. As a result there is scarcity of systematic data, and the reported values for membrane viscosity vary by orders of magnitude for the same system. Here, we show how viscosity of membranes can be easily obtained from the transient deformation of giant unilamellar vesicles. The approach enables a noninvasive, probe-independent, and high-throughput measurement of the viscosity of membranes made of lipids or polymers with a wide range of compositions and phase state. Using this novel method, we have collected a significant amount of data that provides insights into the relation between membrane viscosity, composition, and structure.

Significance

Cell membranes are thin sheets whose fluidity is essential for processes that involve deformations or diffusion of membrane-associated biomolecules. Despite its importance, membrane fluidity remains poorly characterized because existing methods to determine membrane viscosity rely on complex experimental designs and analyses. Here, we devise a noninvasive, high-throughput method capable of measuring the viscosity of membranes with a wide range of compositions and phase state. The amassed data provide insights into the relation between membrane viscosity, composition, and structure. The method paves the way to quantify membrane fluidity in a fast and consistent manner, which will advance the understanding of cell membrane dynamics.

Introduction

Cells and cellular organelles are enveloped by membranes, whose main structural component is a lipid bilayer (1). The lipid bilayer endows membranes with fluidity that is essential for functions that depend on biomolecule mobility, e.g., signaling (2, 3, 4). Fluidity is modulated by membrane composition, and this homeoviscous adaptation is crucial for the survival of organisms that cannot regulate their body temperature, such as bacteria (5,6). Viscosity is the common measure for fluidity, yet for membranes this property has been challenging to assess. Data for viscosity of lipid membranes are limited and reported values vary significantly, sometimes by orders of magnitude for the same system (Appendix Table 1).

For example, reported values for the surface shear viscosity of membranes made of a typical lipid such as dioleoylphosphatidylcholine (DOPC) span two orders of magnitude: (0.197 ± 0.0069) × 10⁻⁹ Pa·s·m (7), (1.9 ± 11) × 10⁻⁹ Pa·s·m (8), (16.72 ± 1.09) × 10⁻⁹ Pa·s·m (9). For a similarly structured lipid, palmitoyloleoylphosphatidylcholine (POPC), the surface viscosity measured by shear rheology of Langmuir monolayers is 3 × 10⁻⁴ Pa·s·m (10). Experimental methods that utilize free-standing bilayer membranes, e.g., vesicles or black lipid membranes, rely on estimates from the rate of tether formation (11), diffusion coefficients of domains (12, 13, 14) or membrane-anchored particles (15,16,17), domain shape fluctuations (18), domain motion on vesicles induced by applied flow (8,19), bilayer thickness fluctuations or lipid dynamics measured with neutron spin echo spectroscopy (20, 21, 22), fluorescence quantum yield or lifetime of viscosity-sensitive fluorescent dyes (23,24), and the forced motion of colloidal particles in the membrane (25, 26, 27). In silico approaches, using molecular dynamics simulations, have also been developed to determine membrane viscosity (7,28,29). Despite these advances, the systematic study of membrane viscosity has been hindered by various limitations of the proposed methodologies. For example, domain-based methods (8,12,13,18,19) are limited to phase-separated membranes, and the measured viscosity reflects the continuous phase, not the membrane as a two-phase fluid. Bilayer thickness fluctuations (20) depend on both shear and dilational monolayer viscosities. In particle-based methods (15,16,25, 26, 27), the probe perturbs the membrane and the data interpretation requires complicated analysis that discerns the contributions to the particle mobility from the flow in the membrane and the surrounding fluids (30, 31, 32). Furthermore, since membrane surface viscosity is a macroscopic quantity defined on scales where the bilayer can be modeled as a two-dimensional incompressible fluid, methods utilizing measurements at the micro- or nano-scale and/or based on molecular probes may not report the effective continuum viscosity but a quantity, often called “microviscosity,” which is local and depends on the immediate environment (22). These complexities are likely the source of the huge variability in reported values of viscosity for lipid bilayer membranes, making it challenging to compare data obtained by different methods.

Here, we show that the time-dependent deformation of giant unilamellar vesicles (GUVs) can be employed to obtain the surface ”macroviscosity,” i.e., the shear viscosity of the membrane treated as a two-dimensional incompressible fluid. Upon application of an extensional stress, e.g., generated by an uniform electric field (33, 34, 35, 36), extensional flow (37, 38, 39), or an optical stretcher (40,41) a quasi-spherical vesicle deforms into a prolate ellipsoid. The aspect ratio, ν = a/b (see sketch in Fig. 1 A), increases and reaches a steady state. When the stress is removed, the vesicle relaxes back to its equilibrium spherical shape. Fig. 1 B and Video S1 illustrate this process for a vesicle in a uniform electric field. Vesicle electrodeformation has been used to measure bending rigidity of membranes from the steady-state shapes (maximum deformation at a given electric field strength) (42, 43, 44, 45). Here, we show that the time-dependent shapes can yield membrane viscosity. Even though the applied stress is extensional and vesicle deformation is axisymmetric, material transported on the vesicle surface undergoes shear because the membrane is area-incompressible (46, 47, 48, 49, 50). The rate at which the vesicle elongates while the field is on, and relaxes back to its equilibrium shape after the field is turned off, is related to the membrane shear viscosity. For small deformations, $\nu \lesssim 1.5$, the evolution of the aspect ratio is described by (35,50, 51, 52) (see Supporting material, section 1 for a summary of the theory)

$$\dot{\nu }=\frac{1}{\eta \left(55+16{\chi }_m\right)}\left(3p-\frac{24\sigma }{R}\left(\nu -1\right)\right),$$ (1)

where χ_m = η_m/ηR is the dimensionless surface viscosity η_m, η is the viscosity of the solution inside and outside the vesicle (assumed to be the same), σ is the membrane tension, and R is the vesicle radius. In an applied extensional flow with strain rate $\dot{\gamma }$, $p=60\eta \dot{\gamma }$. In the case of a charge-neutral vesicle in a uniform DC electric field with amplitude E₀, $p=9\epsilon E_0^2/4$, where ε is the permittivity of the solution, and in an AC field with frequency ω, p(ω) is given in Supporting material, section 1 (note that the permittivity is constant in the frequency range used for the experiments). Thus, from the vesicle dynamics in response to an extensional flow or a uniform electric field it is straightforward to obtain the membrane viscosity. Note that the dynamics does not involve dilational viscosity because vesicle deformation and the accompanying increase in apparent area come from ironing of suboptical thermally excited membrane undulations, while the area per lipid remains the same.

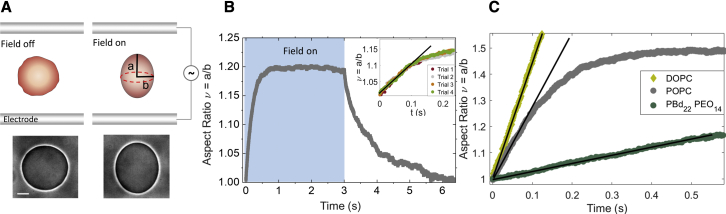
Figure 1.

Vesicle electrodeformation reveals differences in membrane viscosity. (A) A uniform electric field deforms a GUV into a prolate ellipsoid by pulling out area stored in suboptical thermally excited membrane undulations. Snapshots of the vesicle during the experiment. Imaging with phase contrast microscopy. Scale bar, 15 μm. (B) Prolate deformation of a POPC GUV in an electric field with amplitude E₀ = 10 kV/m and frequency of 1 kHz. Time zero in all graphs corresponds to turning the field on. The inset shows that repeated deformation does not alter the initial slope of the deformation curve. Because of the applied field forcing, deformation while the electric field is on is much faster than the relaxation driven by the membrane tension; the characteristic timescale of electrodeformation, $\eta /\epsilon E_0^2$, is much shorter than the relaxation timescale, ηR/σ. (C) Vesicles made of lipids (DOPC, POPC) and the diblock copolymer PBD₂₂PEO₁₄ deform at a different rate indicating different membrane viscosity. The field strength and frequency are 8 kV/m and 1 kHz. The solid lines correspond to the theoretical fit with Eq. 2. To see this figure in color, go online.

Video S1. Videos showing the deformation and relaxation of GUVs made of POPC (left) and PBd₃₃-b-PEO₂₀ (right) with radii of 31 and 24 μm, respectively

The videos were acquired with phase contrast microscopy at E₀ = 10 kV/m at 1 kHz. The time stamps show the actual time.

Materials and methods

Vesicle preparation

GUVs are formed from lipids and polymers such as POPC, DOPC, oleoylmyristoylphosphatidylcholine (OMPC), cholesterol (Chol), stearoyloleoylphosphatidylcholine (SOPC), dipalmitoylphosphatidylcholine (DPPC), and poly(butadiene)-b-poly(ethylene oxide) diblock copolymers, PBd_x-b-PEO_y. The lipids and diblock copolymers were purchased from Avanti Polar Lipids (Alabaster, AL) and Polymer Source (Montreal, Canada), respectively. The multicomponent vesicles made of DOPC:DPPC:Chol were fluorescently marked with 0.1 mol % of Liss Rhod PE. The lipid vesicles were produced using the electroformation method (53). The stock solutions of 12 mM lipid in chloroform are diluted to 5 mM from which 10 μL of the solution is spread on the conductive sides of the ITO slides (Delta Technologies, Loveland, CO). The slides are stored in a vacuum for 2–4 h to evaporate all the organic solvents. The two slides are then sandwiched with a 2-mm-thick Teflon spacer, and the electroformation chamber is filled with 40 mM sucrose solution in 0.3 mM of NaCl. The conductivity conditions were chosen to ensure prolate deformation (34). The chamber is connected to a signal generator (Agilent, Santa Clara, CA) for 2 h at 50 Hz and voltage 1.5 V at 60°C, which ensures that all lipids are above their main phase transition temperatures. The harvested vesicles are diluted in isotonic glucose solution without salt. Three independent GUV batches for every lipid composition were analyzed. Polymer vesicles were produced from a spontaneous swelling method. Initially, 50 μL of 6–10 mg/mL (in chloroform) polymer solution was dissolved in 200–300 μL of chloroform in a 20 mL vial. Polymer films were formed from evaporation by blowing with a nitrogen stream while swirling the solution inside. Thereafter, the vials were dried under vacuum for 2–4 h. The polymer films were hydrated in the suspending solutions (40 mM sucrose solution in 0.3 mM NaCl) and placed at 60°C in an oven for 18–24 h.

Electrodeformation

The electrodeformation experiments are conducted in the electrofusion chamber (Eppendorf, Hamburg, Germany). The chamber is made from Teflon with two 92 μm cylindrical parallel electrodes 500 μm apart. The field is applied using a function generator (Agilent 3320A). The function generator is controlled using a custom-built MATLAB (MathWorks, Natick, MA) program. This gives precise control over the strength and duration of applied electric fields (45). Electric fields with amplitude up to 10 kV/m and frequency up to 1 kHz were used.

Optical microscopy and imaging

The vesicles are visualized using a phase contrast microscope (A1 Axio Observer; Zeiss, Jena, Germany) with 63× objective 0.75 NA (air). Imaging is performed using a Photron (San Diego, CA) SA1.1 camera. The image acquisition rate for electrodeformation recordings is kept to a constant of 500–2000 frames per second (fps) for lipid vesicles and 60–200 fps for polymer vesicles, and the shutter speed is fixed to 500 μs. The time evolution of the vesicle is analyzed using home-made image analysis software. The software uses a Fourier series to fit around the vesicle contour, $r_s={\sum }_{n=0}^{\infty }{\alpha }_n\text{cos}\left(n\theta \right)+{\beta }_n\text{sin}\left(n\theta \right)$. The second mode in the series is used to determine the major axis (a) and minor axis (b) of the deformed vesicles to evaluate $\nu =\frac{a}{b}=\left(1+{\alpha }_2\right)/\left(1-{\alpha }_2\right)$.

Bending rigidity and tension measurements

Flickering spectroscopy is a popular technique to extract membrane rigidity and tension, due to its nonintrusive nature and well-developed statistical analysis criteria. The details of the technique are given in (44,54,55). Essentially, a time series of fluctuating vesicle contours is recorded on the focal plane. The quasi-circular contour is represented in Fourier modes, $r\left(\phi \right)=R\left(1+{\sum }_q{u}_q\left(t\right)\text{exp}\left(\text{i}q\phi \right)\right)$. The fluctuating amplitudes u_q have mean square amplitude dependence on the membrane bending rigidity κ and the tension σ, $⟨|u_q{|}^2⟩\sim \frac{k_{B}T}{\kappa \left(q^3+\overline{\sigma }q\right)}$, where k_BT is the thermal energy (k_B is the Boltzmann constant and T is the temperature), and $\overline{\sigma }=\sigma R^2/\kappa$. The integration time effect of the camera was reduced by acquiring images at a low shutter speed of 100–200 μs. At least 5000 images were obtained for each vesicle for good statistics.

Results

We illustrate the implementation of the approach with the example of a quasi-spherical vesicle subjected to a uniform AC electric field. The electric field is advantageous over extensional flow or radiation pressure (as in optical stretchers) because of the simplicity of the experimental setup and the ability to analyze multiple vesicles at the same time, which highly speed up the measurements. The use of an AC field is preferable because a DC field could cause Joule heating and electro-osmotic flows, whose effect on vesicle deformation and stability is difficult to account for (56). We applied the method to fluid membranes composed of the phosphatidylcholine lipids palmitoyloleoyl (POPC), dioleoyl (DOPC), oleoylmyristoyl (OMPC), stearoyloleoyl (SOPC), and dipalmitoyl (DPPC), Chol, and diblock copolymers PBd_x-b-PEO_y with varying hydrophobic molecular weight, M_h, from 0.7 kDa to 6.8 kDa.

Vesicle transient deformation yields membrane viscosity

Fig. 1 summarizes the experiment. The elongation curves of a GUV initially show linear increase (Figs. 1 C and S4). The linear slope is predicted by Eq. 1 if the second term, which describes the action of the tension opposing the deformation, is neglected:

$$\nu =1+\frac{t}{t_{\text{d}}}\left(\frac{3p\left(\omega \right)}{\left(55+16{\chi }_m\right)}\right),$$ (2)

where $1/t_{\text{d}}=\epsilon E_0^2/\eta$ is the characteristic rate of strain imposed by the electric field. Thus, the slope of the aspect ratio plotted as a function of the rescaled time t/t_d, at the same field frequency, depends solely on the membrane viscosity. Vesicles made of different lipids or diblock copolymers show different initial slopes (see Fig. 1 C), indicating different membrane viscosities. The linear response is observable only if the restoring force of the membrane tension is negligible compared with the deforming electric stress, i.e., $\sigma /R\epsilon E_0^2\ll 1$, which is indeed the case for typical values of the applied electric field E₀ = 8 kV/m, equilibrium membrane tension σ = 10⁻⁸ N/m, and vesicle radius R = 10 μm. The time up to which the linear approximation is reasonable (see Supporting material, section 1B) is estimated to be $t_c/t_{\text{d}}\sim \epsilon E_0^{2}R\left(55+16{\chi }_m\right)/\left(12\sigma \right)$. Using times up to 0.1t_c/t_d (or equivalently ν up to 1.1) minimizes the error in the linear fit. Even though the whole deformation curve could be fitted using Eq. 1, the nonlinear fit with two parameters (viscosity and tension) or three parameters, if bending rigidity is also unknown, is challenging. Since Eq. 2 implies single-parameter fitting, we consider its use to yield more reliable viscosity results (especially for more viscous membranes). Furthermore, it eases the implementation of data fitting. The reproducibility of the results was tested by repeated measurements with the same vesicle (see Fig. 1 B, inset), showing identical slope of the aspect ratio curves for small deformations. Fig. S3 demonstrates that analyzing vesicles made in different preparations and on different days also results in consistent values.

Effects of field frequency and amplitude

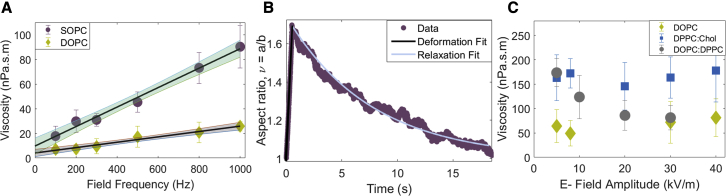
Intriguingly, measurements at the same field amplitude but different frequencies revealed an apparent increase of viscosity with frequency (Fig. 2 A). Viscosity values in the literature obtained by methods that do not involve electric fields (Appendix Table 1) are at least a factor of 10 smaller than the value of the viscosity measured at 1 kHz but comparable with the zero-frequency limit obtained from the linear extrapolation at low frequencies. We hypothesize that the zero-frequency viscosity is representative of the viscosity of the membrane in the absence of electric field. As a test, we analyzed the vesicle relaxation back to its equilibrium shape after the field is turned off (Fig. 2 B). That analysis, however, is complicated by the fact that unlike the initial elongation upon application of the field, the relaxation is driven by and thus depends on the membrane tension. To leave the membrane viscosity as the only fitting parameter for the relaxation curve, the tension needs to be independently determined. In this experiment, the tension was obtained from the analysis of the equilibrium thermally excited membrane undulations (flickering spectroscopy) in the absence of an electric field before the electrodeformation experiment. The fit of the relaxation curve with Eq. 1 yielded viscosity 21.1 ± 29.4 nPa·s·m. The large error is due to the uncertainty in the tension. The viscosity value is close to the zero-frequency limit of the viscosity obtained from the frequency sweep (9.73 ± 5.80 nPa·s·m) for SOPC. We adopt the frequency sweep to determine the initial linear dependence of the viscosity and its “no-field” limit.

Figure 2.

(A) Viscosity measured at different frequencies at a fixed field strength 8 kV/m increases with frequency. Extrapolating to zero frequency yields the shear surface viscosity. The symbols on the vertical-axis intercept refer to the extrapolated values of 4.11 ± 2.63 nPa·s·m and 9.73 ± 5.80 nPa·s·m for DOPC and SOPC, respectively. The R-squared value of the linear fit is 0.98 and 0.97 for the SOPC and DOPC, respectively. The shaded band represents a 95% confidence interval. (B) Shape relaxation after the field is turned off yields a similar value for the viscosity as the zero-frequency limit obtained from the frequency sweep. Data for SOPC, E₀ = 8 kV/m and ω = 1 kHz. Tension obtained from flickering spectroscopy is 5.7 ± 2.6 × 10⁻⁹ N/m. Viscosity obtained from initial deformation and relaxation is 164 nPa·s·m and 21.1 ± 29.4 nPa·s·m, respectively. (C) Viscosity of single-component (DOPC) and single-phase multicomponent (DPPC:Chol 1:1) bilayers is independent of field magnitude, in contrast to the viscosity of phase-separated multicomponent (DPPC:DOPC 1:1) bilayers. To see this figure in color, go online.

Electric field decreases the melting temperature of DPPC:DOPC:Chol bilayers (57), thus suggesting field-dependent membrane fluidity. We find that bilayers made of only one lipid or a homogeneous mixture, either in the liquid-disordered (e.g., DOPC or POPC) or liquid-ordered (e.g., DPPC:Chol 1:1) state, exhibit field-independent viscosity. However, the phase-separated bilayers such as DPPC:DOPC (1:1), which have solid domains coexisting with liquid-disordered continuous phase (58, 59, 60), showed viscosity decrease with increasing field amplitude (Fig. 2 C).

Method summary

To summarize, the method involves measuring apparent viscosities at different frequencies in the range 0.1–1 kHz and extrapolating to zero frequency (as in Fig. 2 A) to obtain the value of the viscosity in the absence of an electric field. An electric field of 8 kV/m produces a good range of data in the initial linear deformation regime. The method is high-throughput as it allows measurement of several vesicles at the same time; measurement and data analysis of each vesicle typically take about 10 min. We analyze 10–50 vesicles per viscosity value. The viscosity obtained for 14 different bilayer compositions is reported in Table 1. The values are in the range reported in previous studies (Appendix Table 1). For example, the bilayer viscosity for SOPC is in good agreement with previously reported values from 3 to 13 nPa·s·m (27,28,61).

Table 1.

Membrane viscosity and bending rigidity for various bilayer systems at 25.0°C and E₀ = 8 kV/m

Composition	Viscosity (nPa·s·m)	Bending rigidity (kBT)
DOPC	4.11 ± 2.63	22.2 ± 2.0
OMPC	7.73 ± 3.09	27.1 ± 2.6
POPC	9.32 ± 5.95	27.8 ± 2.3
SOPC	9.73 ± 5.80	30.1 ± 3.1
DOPC:Chol	7.00 ± 4.77	27.8 ± 4.6
DPPC:DOPC:Chol (1:1:1)	17.7 ± 3.06	72.0 ± 8.4
DPPC:DOPC:Chol (1:1:2)	15.4 ± 2.40	69.2 ± 7.9
DPPC:Chol (1:1)	56.4 ± 4.63	121.3 ± 11.0
PBd13-b-PEO11	14.4 ± 4.40	17.1 ± 1.5
PBd22-b-PEO14	686 ± 51.0	31.0 ± 5.1
PBd33-b-PEO20	2890 ± 670	54.4 ± 6.4
PBd46-b-PEO24	20,600 ± 4700	NA
PBd54-b-PEO29	46,700 ± 900	154.0 ± 16.0
PBd120-b-PEO78	157,000 ± 54,500	NA

Viscosity correlation with lipid diffusivity, membrane composition, and thickness

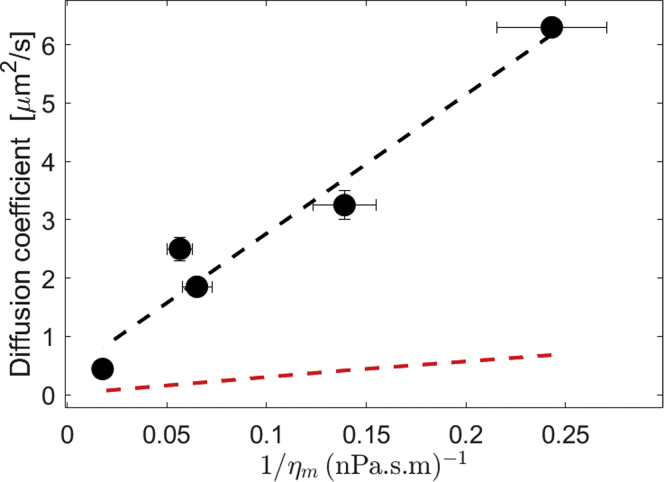
Since mobility of lipids or domains is often used to assess membrane fluidity (12, 13, 14), we have compared our results for membrane viscosity with measurements of the diffusion coefficient of a lipid dye (DiI-C18) using fluorescence correlation spectroscopy (FCS) in the same ternary system (62). The diffusion coefficient scales inversely with surface viscosity (Fig. 3), a trend expected from the Saffman-Delbrück model (63), $D=k_{\text{B}}T\left(\text{log}\left({\eta }_m/\left(\eta r\right)\right)-0.5772\right)/\left(4\pi {\eta }_m\right)$. However, there is a quantitative disagreement: using lipid dye radius r = 0.5 nm (comparable with the radius of DOPC estimated from the area per lipid head, 67.4–75.4 Å² (64, 65, 66, 67, 68, 69)), the Saffman-Delbrück equation predicts much lower diffusivities. These results suggest that while increasing viscosity does correlate with decreasing diffusivity, it is not trivial to relate membrane viscosity and the diffusion constant because diffusion of molecular probes is sensitive to the probe itself as well as the bilayer structure (11,14,22).

Figure 3.

Membrane viscosity as a function of diffusivity values obtained with FCS (62) for membrane compositions DOPC, DOPC:Chol (1:1), DPPC:DOPC:Chol (1:1:2), DPPC:DOPC:Chol (1:1:1), and DPPC:Chol (1:1). Values of the diffusion coefficient are listed in Table S2. The red dashed line corresponds to the prediction from the Saffman-Delbrück model with probe radius r = 0.5 nm. The black dashed line is a linear fit with intercept 0.383 μm²/s and slope 23.83 μm³·mPa. To see this figure in color, go online.

The viscosity values compiled in Table 1 highlight that in pure lipid systems membrane viscosity decreases with the number of unsaturated bonds in the hydrophobic tail. POPC, OMPC, and SOPC have a single unsaturated bond while DOPC has two double bonds in the hydrophobic tails. DOPC bilayers exhibit much smaller viscosity than the other single unsaturated lipid bilayers. In the mixed systems, adding DPPC or/and Chol to DOPC increases the viscosity. Adding Chol (molar ratio 1:1) to DOPC increases the bilayer viscosity as Chol increases the packing of the liquid-disordered (L_d) phase. For the liquid-ordered (L_o) phase, such as DPPC:Chol (1:1), the bilayer viscosity is much higher due to the tight packing provided by saturated acyl chains. The effect is less pronounced in the ternary L_o system DOPC:DPPC:Chol (1:1:2) and DOPC:DPPC:Chol (1:1:2). For a phase-separated system of coexisting solid and fluid phases DOPC:DPPC (1:1) (see Fig. 2 B), the viscosity also increases relative to pure DOPC. The increase agrees with an estimate of the viscosity of a two-dimensional (2D) suspension, η_eff = η_DOPC(1 + 2φ), where φ ∼ 0.4 is the fraction of the solid phase (70).

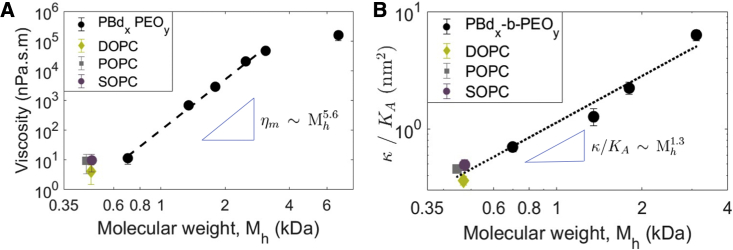
Using our method we examined the commonly assumed relation between the 2D viscosity (η_m) and three-dimensional (3D) viscosity (η_3D), η_m = η_3Dh, where h is the membrane thickness. The thickness of diblock-polymer bilayers increases with the molecular weight of the hydrophobic part, $h\sim M_h^n$ (71,72), where n lies within the theoretical bounds of 0.5 (random Gaussian coil) and 1 (full stretch). The polymers' molecular weight varies in a wide range (1–8 kDa), thereby resulting in bilayers with greater range of thicknesses, unlike lipids. The diblock polymers showed membrane viscosity spanning four orders of magnitude, from 14 nPa·s·m to 157,000 nPa·s·m. The lowest-molecular-weight polymer membrane exhibits a viscosity similar to that of POPC. Fig. 4 A shows that the membrane viscosity does follow a power-law dependence on M_h, but the power 5.6 is much larger than the expected range of 0.5–1. In contrast, as seen from Fig. 4 B, the bending rigidity follows a power law consistent with the expected $\kappa \sim M_h^{2n}$, since κ/K_A ∼ h², where K_A is the area-compressibility modulus (73). The K_A value is relatively insensitive to the molecular weight; its value for the lipids was taken to be 250 mN/m and for the polymer membranes 100 mN/m (74,75). The polymer 3D viscosity η, however, varies with the polymer molecular weight, and this may be the source of the unexpectedly higher exponent in the power-law dependence of η_m on M_h.

Figure 4.

(A) Viscosity of PBd_x-b-PEO_y bilayers as a function of the M_h of the hydrophobic part (PBd). Viscosities of phospholipids are also shown for comparison. (B) Bending rigidity κ (scaled by the area-compressibility modulus K_A) of PBd_x-b-PEO_y and phospholipid bilayer membranes as a function of molecular weight. The power law obtained is $\kappa /K_A\sim M_h^{1.3}$. The values of the bending rigidity are listed in Table S1. To see this figure in color, go online.

Conclusions

We developed a novel method to measure the shear viscosity of membranes using the transient deformation of a giant vesicle. The approach is inspired by the interfacial rheology measurements using deformation of droplets and capsules (76). The method is able to interrogate a wide range of bilayer compositions and phase states, and the measured membrane viscosities span a range of more than four orders of magnitude. The collected data show that decreasing viscosity leads to increasing probe diffusivity, although the relation is not captured by the celebrated Saffman-Delbrück equation. Membrane viscosity is also found to nontrivially depend on bilayer thickness. Using diblock-copolymer systems with different molecular weight to modulate bilayer thickness revealed a power-law relation between viscosity and molecular weight that is much stronger than the power predicted from the assumption that the membrane viscosity is equal to the bulk viscosity multiplied by bilayer thickness. Our study also reveals that viscosity is sensitive to membrane electric polarization. In an applied uniform electric field, membrane viscosity increases with frequency, while in some systems electric field amplitude has the opposite effect. For example, the macroviscosity of phase-separated gel-fluid membranes decreases with the field magnitude. These findings open new questions for future exploration.

The ease of implementation, high throughput, minimal experimental equipment and effort, as well as robustness make the electrodeformation viscometry developed by us easy to adopt in every lab. The method can also be applied to obtain interfacial properties of lipid monolayers using deformation of droplets and fitting the shape evolution with the theoretical model in (52). Such study will hopefully shed some light on the observed discrepancies between monolayer and bilayer viscosities (77,78). We envision that our approach will become a standard tool for characterization of membrane fluidity that will help address questions of biological and engineering importance such as synthetic cell design.

Author contributions

H.A.F., R.D., and P.M.V. designed the research; H.A.F. performed the research; H.A.F., R.D., and P.M.V. analyzed the data; H.A.F., R.D., and P.M.V. wrote the paper.

Editor: Andreas Janshoff.

Appendix

See Appendix Table 1.

Appendix Table 1.

Membrane viscosity obtained using different experimental methods and simulations

Method	Membrane composition	Viscosity (nPa·s·m)	Temperature (K)	System
Falling ball viscometry (27)	SOPC	3	298	GUVs
Coarse-grained simulations (28)	SOPC	3	323	bilayer
Electrodeformation (this study)	SOPC	9.73 ± 5.80	298	GUVs
Probe diffusion (61)	SOPC	13.2 a	293	GUVs
Optical dynamometry (26)	DMPC	5 ± 2	298	GUVs
Neutron spin echo (20)	DMPC	75	298	SUVs
Coarse-grained simulations (28)	DMPC	5	323	bilayer
Fluorescence spectroscopy (79)	DMPC	0.36 a	298	SUVs
Tether pulling (11)	EPC	2.7–88	295–298	GUVs
Shear surface rheology (10)	POPC	300,000	NA	monolayer
Electrodeformation (this study)	POPC	9.32 ± 5.95	298	GUVs
Shear surface rheology (10)	POPC:Chol (7:3)	10,000	NA	monolayer
Shear surface rheology (10)	DPPC	900,000	NA	monolayer
Optical tweezers (80)	DOPC	<0.6	293	bilayer
Fluorescence spectroscopy (79)	DOPC	0.20 a	298	SUVs
Fluorescence quantum yield (23)	DOPC	0.84 a	298	LUVs
Fluorescence lifetime of dye (24)	DOPC	0.15 a	298	LUVs
All-atom simulations (7)	DOPC	0.197 ± 0.0069	297	bilayer
Coarse-grained simulations (28)	DOPC	0.17	323	bilayer
Membrane-anchored particles (16)	DOPC	15.3 ± 3.4	297	GUVs
Electrodeformation (this study)	DOPC	4.11 ± 2.63	298	GUVs
Probe diffusion (15)	DOPC	0.59 ± 0.2	298	GUVs
Neutron spin echo (9)	DOPC	16.7 ± 1.1	298	SUVs
Electrodeformation (this study)	OMPC	7.73 ± 3.09	298	GUVs
Membrane-anchored particles (16)	13:0 PC	14.7 ± 6.9	297	GUVs
Neutron spin echo (9)	DOPC:Chol (8:2)	31.9 ± 3.5	298	SUVs
Electrodeformation (this study)	DOPC:Chol (1:1)	7.00 ± 4.77	298	GUVs
Electrodeformation (this study)	DPPC:Chol (1:1)	56.4 ± 4.63	298	GUVs
Optical tweezers (80)	DOPC:DPPC (2:1), Lo	2.1	293	bilayer
Shear-driven flow (8)	DOPC:DPPC (85:15), Ld	1.9 ± 11.9	296	GUVs
Shear-driven flow (8)	DiPhyPC:Chol:DPPC (5:40:55), Lo	15.7 ± 9.9	296	GUVs
Domain fluctuations (18)	DiPhyPC:Chol:DPPC (25:55:20)	4 ± 1	293	GUVs
Diffusion of domains (12)	DPPC:DOPC:Chol (3.5:3.5:3), Lo	10–500	295	GUVs
Diffusion of domains (13)	DiPhyPC:DPPC (1:1)	2.2 ± 0.1	296.5	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (3:6:1), Lo domain	4.1	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (4:5:1), Lo domain	14	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (2:6:2), Lo domain	9.6	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (4:4:2), Lo domain	4.3	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (5:3:2), Lo domain	54	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (6:2:2), Ld domain	1200	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (2:5:3), Lo domain	7.7	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (5:2:3), Ld domain	85	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (6:1:3), Ld domain	1200	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (3:3:4), Ld domain	0.63	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (4:2:4), Ld domain	65	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (5:1:4), Ld domain	71	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (4:3:3), Ld domain	98	293	GUVs
Shear-driven flow (19)	DPPC:DOPC:Chol (3:5:2), Lo domain	65	293	GUVs
Electrodeformation (this study)	DPPC:DOPC:Chol (1:1:1)	17.7 ± 3.06	298	GUVs
Electrodeformation (this study)	DPPC:DOPC:Chol (1:1:2)	15.4 ± 2.40	298	GUVs
Falling ball viscosimetry (81)	PBd33-b-PEO20	1500 ± 120	298	GUVs
Electrodeformation (this study)	PBd33-b-PEO20	2890 ± 670	298	GUVs
Micropipette aspiration (82)	PEG-b-PA6ester1	7,900,000 ± 200,000	298	GUVs
Micropipette aspiration (82)	PEG-b-PA444	4,000,000 ± 200,000	298	GUVs
Atomic force microscopy (83)	PBd130-b-PEO66	5,000,000	298	bilayer
Atomic force microscopy (83)	PBd130-b-PEO66 (cross-linked)	20,000,000	298	bilayer
Electrodeformation (this study)	PBd13-b-PEO11	14.4 ± 4.40	298	GUVs
Electrodeformation (this study)	PBd22-b-PEO14	686 ± 51.0	298	GUVs
Electrodeformation (this study)	PBd46-b-PEO24	20,600 ± 4700	298	GUVs
Electrodeformation (this study)	PBd54-b-PEO29	46,700 ± 900	298	GUVs
Electrodeformation (this study)	PBd120-b-PEO78	157,000 ± 54,500	298	GUVs

L_d and L_o refer to liquid-disordered and liquid-ordered phases, respectively. GUVs, LUVs, and SUVs refer to giant unilamellar vesicles, large unilamellar vesicles, and small unilamellar vesicles, respectively.

^aFor DMPC, SOPC, and DOPC, the bilayer thicknesses are 3.67 nm, 4.00 nm (84), and 3.67 nm (69), respectively. Denotes membrane viscosity obtained from the bulk viscosity, η, using the relation η_m = ηh, where h is the bilayer thickness.