Extracellular and intracellular components of the impedance of neural tissue

Abstract

Electric phenomena in brain tissue can be measured using extracellular potentials, such as the local field potential, or the electro-encephalogram. The interpretation of these signals depends on the electric structure and properties of extracellular media, but the measurements of these electric properties are still debated. Some measurements point to a model in which the extracellular medium is purely resistive, and thus parameters such as electric conductivity and permittivity should be independent of frequency. Other measurements point to a pronounced frequency dependence of these parameters, with scaling laws that are consistent with capacitive or diffusive effects. However, these experiments correspond to different preparations, and it is unclear how to correctly compare them. Here, we provide for the first time, impedance measurements (in the 1–10 kHz frequency range) using the same setup in various preparations, from primary cell cultures to acute brain slices, and a comparison with similar measurements performed in artificial cerebrospinal fluid with no biological material. The measurements show that when the current flows across a cell membrane, the frequency dependence of the macroscopic impedance between intracellular and extracellular electrodes is significant, and cannot be captured by a model with resistive media. Fitting a mean-field model to the data shows that this frequency dependence could be explained by the ionic diffusion mainly associated with Debye layers surrounding the membranes. We conclude that neuronal membranes and their ionic environment induce strong deviations to resistivity that should be taken into account to correctly interpret extracellular potentials generated by neurons.

Significance

The electro-encephalogram recorded at the scalp surface and local field potentials recorded within neural tissue are generated by electric currents in neurons, and thus depend on the impedance of neural tissue. Different measured values were proposed, and it is currently unclear what is the real impedance of neural tissue. Here, we show that the impedance depends on the measurement technique. If the measurement is exclusively extracellular, the system appears as equivalent to a simple resistor. However, if the measurement includes an intracellular electrode, a more complex impedance is observed, because the current must flow through the membrane, as happens in the brain. Thus, we provide an explanation for apparent disagreements, and indicate in which cases each impedance should be used.

Introduction

The genesis of extracellular electric potentials in the brain depends on the electric properties of the extracellular medium. The exact nature of these electric properties is important, because nonresistive media will necessarily impose frequency-filtering properties to electric signals (1,2) and therefore will influence any source localization. Early studies modeled the genesis of extracellular potentials assuming that the medium is analogous to a resistance (3). Evidence for such resistive media was provided by different measurements (4, 5, 6), while other measurements (7, 8, 9) revealed a more complex situation, where the measured electric parameters displayed a dependence on frequency in contrast to the frequency-independence of resistive systems. Computational models showed that such a dependence on frequency can be obtained if there are strong spatial variations of conductivity and/or permittivity (10). Further models showed that frequency-dependent electric parameters can also result from electric polarization of the medium (11), or from ionic diffusion (12).

The extracellular medium properties were also estimated indirectly by correlating intracellular and local field potentials (LFPs) (13) or by the frequency dependence between electro-encephalogram (EEG) and magneto-encephalogram signals (MEG) (14). Although a framework was proposed to explain the contradictory measurements (15), the electric nature of the extracellular medium is still debated (15, 16, 17).

The main problem to resolve this debate is that different experiments correspond to very different preparations, and it is not clear how to correctly compare them. For example, impedance was either measured intracellularly (9) or extracellularly (5,6). Could this account for discrepancies observed across studies? In the present study, we provide for the first time, impedance measurements, either with an intracellular electrode or extracellularly, in different preparations, in acute brain slices, in primary cell cultures, and we compare to measurements using the same setup in artificial cerebrospinal fluid (ACSF).

Materials and methods

In vitro electrophysiology

Animals

C57BL/6 and Swiss mice were housed by groups of 3 to 5 mice, in a 12-h light/dark cycle, with food and water available ad libitum. All experiments were performed in accordance with local animal welfare committee (Center for Interdisciplinary Research in Biology, and Institut de Biologie Paris-Seine, IBPS, Ethical Committees) and EU guidelines (Directive 2010/63/EU). Every precaution was taken to minimize stress and the number of animals used in each series of experiments.

Neuronal primary cultures

The brains (from Swiss mice) were removed from day 14 embryos, and striata were isolated and dissociated by gently pipetting in phosphate-buffered saline-0.6% glucose. Cells were collected by centrifugation at 1000 × g for 5 min. Cell pellets were resuspended in Neurobasal medium supplemented with B27 (Invitrogen, Thermo Fisher Scientific, Illkirch, France), 500 nM L-glutamine, 60 μg/mL penicillin-streptomycin, and 25 μM β-mercaptoethanol (Sigma, Saint-Quentin Fallavier, France), and then plated into 24-well (1.8 × 10⁵ cells per well) plates coated with 50 μg/mL poly-d-lysine (Sigma). After removal of the coating solution, cells were seeded in the Neurobasal medium on glass coverslips and cultured at 37°C in 95% air and 5% CO₂. When placed in the recording chamber, the cell culture was initially superfused with a 95% O₂/5% CO₂-bubbled Neurobasal medium, and then progressively diluted in ACSF solution. Patch-clamp recordings were made from day 3 to day 10 after seeding.

Brain slices preparation

Horizontal brain slices (from C57BL/6) with a thickness of 300 μm were prepared from postnatal P30-40 mice using a vibrating blade microtome (VT1200S; Leica Biosystems, Nussloch, Germany). Brains were sliced in a 95% O₂/5% CO₂-bubbled, ice-cold cutting ACSF solution containing NaCl 125 mM, KCl 2.5 mM, glucose 25 mM, NaHCO₃ 25 mM, NaH₂PO₄ 1.25 mM, CaCl₂ 1 mM, MgCl₂ 1 mM, and pyruvic acid 1 mM, and then transferred into the same solution at 34°C for 1 h before cell recording.

Whole-cell patch-clamp recordings and experimental setup

Electrophysiological recordings were performed in the dorsal striatum, which has the advantage of having no laminar organization (with neurons presenting a relatively constricted dendritic arbor with a spherical distribution), which hence limits the influence on the current trajectories and avoids strong anisotropic equipotential surfaces. Patch-clamp recordings were combined with extracellular recording using a 2- to 3.5-MΩ patch-clamp glass pipette. The latter was located within a close vicinity (≈5–10 μm) of the patched neuron (Fig. 1 A). In the primary cell culture experiments, the average distance separating neighboring cells was on average 17.4 μm (±7.1, n = 14) and 12.8 μm (±6.4, n = 25) for immature and mature cells, respectively, thus about three times larger than the distance separating the two pipettes. Borosilicate glass pipettes of 5- to 7-MΩ impedance contained for whole-cell recordings: K-gluconate 122 mM, KCl 13 mM, HEPES 10 mM, phosphocreatine 10 mM, ATP-Mg 4 mM, GTP-Na 0.3 mM, and EGTA 0.3 mM (adjusted to pH 7.35 with KOH). The composition of the extracellular solution and inside the extracellular pipette was the same ACSF solution that was used for brain slice incubation. Signals were amplified using EPC9-2 amplifiers (HEKA Elektronik, Lambrecht, Germany) with a very high input impedance (1 TΩ) to ensure there was no appreciable signal distortion imposed by the high-impedance electrode (18,19). All recordings were performed at 34°C using a temperature control system (Bath-Controller V; Luigs & Neumann, Ratingen, Germany) and brain slices or primary cell cultures were continuously superfused at 2 mL/min with the extracellular solution. The extracellular solution used in the recording chamber had the same ionic composition for all the experimental conditions. Neurons were visualized on a BX51WI microscope (Olympus, Rungis, France) using a 40×/0.80 water-immersion objective for localizing cells for whole-cell recordings and extracellular electrode positioning. Series resistance was not compensated. Current-clamp recordings were sampled at 50 kHz using the Patchmaster v2x73 program (HEKA Elektronik).

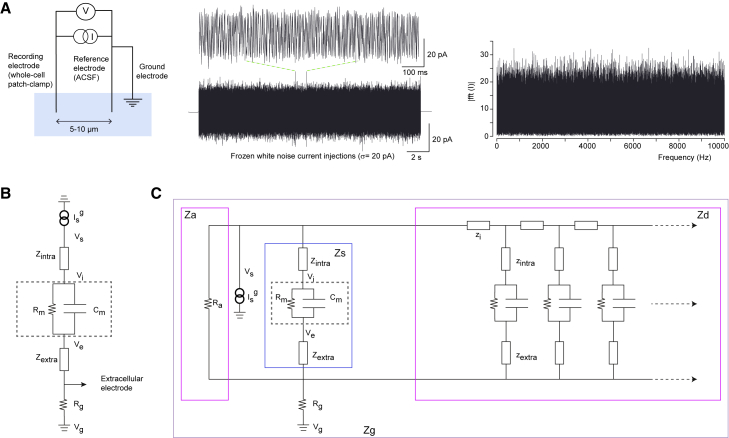
Figure 1.

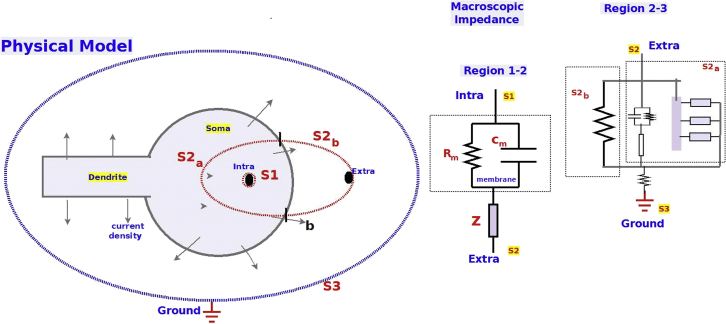
Method used for macroscopic impedance measurements and numerical simulations in different preparations. (A) Scheme of the experimental setup. Left: Two borosilicate micropipettes with silver-chloride electrodes and a ground electrode are placed in the ACSF solution. One electrode is used in whole-cell configuration to send white-noise current and simultaneously measure the voltage response of the recorded neuron (acquisition sampling rate: 50 kHz); the other electrode used as a reference is located 5 to 10 μm away from the recorded neuron. Middle: Frozen Gaussian white noise (amplitude: ± 5 to 20 pA; duration: 20 s) is injected repeatedly into patched neurons. Right: Fourier modulus of the injected current as a function of frequency confirms that each frequency from 0 to 10,000 Hz is uniformly sampled. (B) Equivalent electrical circuit between intracellular and extracellular electrodes. (C) Equivalent electrical circuit between the extracellular electrode and the ground. Z_a is the impedance of the region defined by the isopotential surface ${\mathcal{S}}_1$ passing through the extracellular electrode and the first isopotential surface ${\mathcal{S}}_g$ that totally includes the neuron, $Z_s$ is the impedance of the part of the soma included between ${\mathcal{S}}_1$ and ${\mathcal{S}}_g$, Z_d is the input impedance of the dendrite between surfaces ${\mathcal{S}}_1$, ${\mathcal{S}}_g$, and Z_g is the impedance of the region between ${\mathcal{S}}_g$ and the ground. $Z_g=\left(Z_a\left|\left|Z_s\right|\right|Z_d\right)\oplus R_g$ where $\parallel$ means “in parallel” and $\oplus$ “in series.” To see this figure in color, go online.

White noise stimulation protocols and signal analyses

Frozen white noise stimuli were applied via the recording patch-clamp electrode in current-clamp mode. A quantity of 20 s of Gaussian white noise with zero mean and 5, 10, or 20 pA variance was injected. For each cell, we injected up to 71 times the same sequence of white noise (Fig. 1 A). For each neuron, we computed the IV-curve by applying hyperpolarizing current steps of different intensities in current-clamp. Neurons for which the recording voltage of the responses was not inside the linear region of the IV-curve were excluded (only two neurons from brain slices had to be excluded for this reason in this study). For each trial, we calculated as a function of the frequency the modulus and Fourier phase of the voltage difference between the intracellular recording and extracellular reference electrode, as well as between the extracellular reference and ground electrode. We then averaged these measures to obtain a Fourier spectrum, ranging from 1 to 10 kHz, for each cell. Going at higher frequencies was challenging because of the limitations in sampling frequency of our electrophysiological setup and because the power of the signal becomes weak and dominated by instrumental noise. In addition, the 10 kHz upper limit was sufficient to observe the capacitive effect between the extracellular and intracellular electrodes, because of their close proximity.

Importantly, the numerical measurement of the phase induces a small delay Δt between the real and digitally measured voltage, and this delay depends on the sampling frequency. This delay is likely due to the electronics and does not affect the modulus of the impedance, but is proportional to frequency. We have measured and corrected for this effect by using the measurement of the resistance between the two electrodes in ACSF. Without this correction, we would have Φ(ν) = 0 because saline is resistive for ν between 0 and 10 kHz. With the delay, we have $\text{Φ}\left(\nu \right)=-\frac{0.5}{{\nu }_e}\nu$, where ν_e is the sampling frequency.

We have fitted the models on the experimentally measured phase values to minimize the mean square distance between experimental and theoretical values. To do this, we computed the average values on small intervals of frequency (≈1 Hz) in the impedance modulus of the experimental data in each example. In other words, we calculated $min\left[\frac{1}{N-1}{\sum }_{i=1}^N{\left(Y_i-Z_i\right)}^2\right],$ where Z and Y are, respectively, the average value over a segment of length equal to 1 Hz in the model and experimental data. We adjusted the parameters of the different models to minimize the largest absolute distance between the modulus of the average experimental and model values over the ensemble of intervals. This choice simplifies the comparison between the different models and experimental results. Importantly, log-log graphs give the false impression that there is more noise at high frequencies, but this is due to the high density of points.

Finally, we fitted numerically the polar representation of the experimental data in Fourier frequency space, using a filtering with the cubic spline method (20). This method has a smooth derivative, which is appropriate for very noisy modulus and phase values. Also, the data were fit to models that are plausible biophysically (resistive, diffusive, etc.), so that the parameters have a clear biological or physical interpretation. In all cases, each biophysical model has a few parameters (which number remains very small compared with the data set), and provides us with estimates of these parameters, as we describe in the results section.

Mathematical and physical models used to simulate the experimental data

To model the experimental data, we use Maxwell equations under the electric quasistatic approximation, which was formulated in mean-field in previous studies (12,21). (The electric quasistatic approximation consists of neglecting electromagnetic induction such that we have $\nabla \times \overrightarrow{E}=0$. It is important to note that in this approximation, the displacement current is taken into account and accumulation of charges can occur. There exists another approximation, the magnetic quasistatic approximation, in which electromagnetic induction is not neglected (22)). At the first order of this mean-field theory, the macroscopic impedance (corresponding here to the definition of the impedance as in electronics, and different from the macroscopic impedance used at large scales, in the centimeter range) of a point neuron in a heterogeneous medium is given by the following:

$$Z\left(\omega \right)=\frac{V\left(\omega \right)}{I^g\left(\omega \right)}=\frac{R_m}{1+i\omega {\tau }_m}+\frac{A_w}{1+\sqrt{i\frac{\omega }{{\omega }_{wT}}}}+R_{asymp}+F\left(\omega \right)$$ (1)

where $A_w=A_o+\frac{B_o}{1+i\omega {\tau }_{mw}}$. This expression was written by explicitly following physical phenomena. The first right-hand term corresponds to the usual R-C circuit of the membrane, and the second term is due to ionic diffusion (in a linear approximation), as well as to electric polarization (if the polarization relaxation time is negligible). The last term F(w) takes into account other physical phenomena that may introduce a frequency dependence in the extracellular medium, such as electromagnetic induction, electric viscosity, etc., but these phenomena seem to have a negligible impact on the impedance values for the frequency range <1000 Hz investigated here (7). The physical meaning of the parameters is as follows: R_m is the macroscopic membrane resistance, τ_m = R_mC_m is the membrane time constant, A_ω is the amplitude of the diffusive impedance, which is a real number when the polarization relaxation time (Maxwell-Wagner time τ_MW) is negligible, R_asymp is the asymptotic resistance for very high frequencies, and ν_wT = ω_wT/2π is its Warburg threshold frequency (for details, see Online Appendix C).

The model used to take into account the effect of dendrites is the same as used previously (9), and consists of a model with a soma and a dendrite. Because we have a monopolar current source (electrode injection), the electrotonic length of a dendritic branch is given by the following:

$$\lambda =\sqrt{\frac{r_m}{z_i}\left[1+\frac{z_e^{\left(m\right)}}{r_m}\left(1+i\omega {\tau }_m\right)\right]}$$ (2)

where the following quantities are defined in the generalized cable: z_i is the cytoplasm impedance per unit length, r_m is the specific membrane resistance, and $z_e^{\left(m\right)}$ is the specific input impedance of the extracellular medium as seen by the membrane.

We have $z_e^{\left(m\right)}=z_{intra}+z_{extra}$ (from Fig. 1). The physical link between the generalized cable is the following. The current density in the dendritic stick has a component in parallel to the axis of the stick, and a component perpendicular to it. However, the electric conductivity is different for these two components. z_i is associated with the parallel component, where the current density is physically related to the cytoplasm, and z_intra is associated with the perpendicular component, which is physically related to the Debye layers in the inner side of the membrane. We have

$$\{\begin{array}{l}\frac{V_m}{I^g}=\frac{\lambda z_i}{\kappa }coth\left(\frac{\kappa l}{\lambda }\right)\left(a\right)\\ \frac{V_i}{I^g}=\frac{Z_a{Z}_s{Z}_d}{Z_a{Z}_s+Z_s{Z}_d+Z_d{Z}_a}+R_g\left(b\right)\end{array}$$ (3)

where the neuronal cable model in an “open configuration” (i.e., without return current) was used, as defined in (23).

Because the current that goes from the neuron to the extracellular space separates into several parts, one part that flows through the soma membrane, and another part that flows in the dendrite, we have used several impedances (Fig. 1): Z_a: the impedance of the extracellular medium in contact with the isopotential surface S (which touches the extracellular electrode and surrounds the intracellular electrode), Z_s: the impedance of the current flowing through the soma membrane (in contact with this surface S), and Z_d: the input impedance of the dendritic tree. When measuring the equivalent impedance, we have $\left(Z_a\left|\left|Z_s\right|\right|Z_d\right)\oplus R_g$, where R_g is the impedance between the ground and the first isopotential surface, which comprises the neuron (Online Appendix A). Note that the isopotential surfaces are necessarily continuous, but may be more irregular in shape than that schematized.

The electric potentials V_i and V_e are taken at the inside and outside borders of the membrane, respectively, at the level of the soma and relative to a reference point outside the neuron. According to the law of generalized current conservation, we have $\frac{V_e}{z_e^{\left(m\right)}}=\frac{V_m\left(1+i\omega {\tau }_m\right)}{r_m}$. Note that the parameters R_m = r_m/ΔS and $Z_e^{\left(m\right)}=z_e^{\left(m\right)}/\text{Δ}S$ (where ΔS is an element of surface area of the membrane) are macroscopic parameters, whereas r_m and $z_e^{\left(m\right)}$ characterize the membrane at a microscopic level. This explains the difference between expressions 3a and 3b, because by definition we have V_i = Vm + V_e. Note that if $\left|z_e^{\left(m\right)}\right|\ll r_m$, then expression 3b becomes equivalent to the input impedance of the dendrite (stick) in parallel with a portion of soma membrane (Fig. 1).

$z_e^{\left(m\right)}$ is the specific input impedance of the extracellular medium, as sensed by the membrane, as also defined by the generalized cable theory (23). This parameter also can be applied to the intracellular medium, in case of a current source from an intracellular electrode, to take into account the impedance of the intracellular medium between the tip of the electrode and the membrane. In the open configuration, $z_e^{\left(m\right)}$ can be a resistance for a resistive extracellular medium, but can be more complex when taking into account effects such as polarization, ionic diffusion, capacitive effects, etc. Thus, the form of this frequency dependence contains the contribution from the extracellular medium. Note that the expression in Eq. 2 shows that, in the open configuration, the electrotonic length depends on frequency, even for a resistive extracellular medium.

Also, in a “closed configuration” (where the neuron is electrically a closed system, where all currents loop back to the neuron), for a resistive medium, we have $z_e^{\left(m\right)}=-\frac{r_m{r}_e}{\left(r_i+r_e\right)\left(1+i\omega {\tau }_m\right)}$ and $\lambda =\sqrt{\frac{r_m}{r_i+r_e}}$. z_i = r_i is the cytoplasm resistance per unit length and r_e is the extracellular medium resistance per unit length, as defined in the Rall-Tuckwell model. In this simplified and resistive model of the neurons, one assumes that the extracellular current flows parallel to the axis of the dendrite. In this case, we see that λ does not depend on frequency. This is in accordance with the classic Rall-Tuckwell cable theory (24,25). In contrast, in an open configuration with resistive media ($z_e^{\left(m\right)}$ and z_i are real positive), the modulus of λ increases with frequency (Eq. 2). Thus, in general, the electrotonic length ($\left|\lambda \right|$) of a ball-and-stick neuron depends on frequency, which is not the case in the Rall-Tuckwell model, as shown above.

An interesting consequence of this is that, if one measures the impedance $z_e^{\left(m\right)}$ in a resistive configuration (for example in an isolated neuron embedded in ACSF), one should see the frequency dependence, which would validate the open configuration, as we describe in the results section.

Results

We first describe the experimental results and the different experimental configurations, then we propose different models to fit the experimental measurements.

Experimental measurements

The experimental protocol consisted of in vitro whole-cell patch-clamp recordings of striatal neurons, either from primary cell cultures or in acute brain slices, while simultaneously recording the potential in the vicinity (5–10 μm) of the neuron using a second reference electrode (Figs. 1 A and 2). The setup thus consists of three electrodes: the intracellular electrode, the reference electrode, and the ground. Frozen white Gaussian noise is injected in the cell via the patch-clamp electrode, and is measured according to two configurations: either one measures the intracellular-to-extracellular (intracellular electrode with respect to reference electrode) potential, or the extracellular-to-ground (reference electrode with respect to ground).

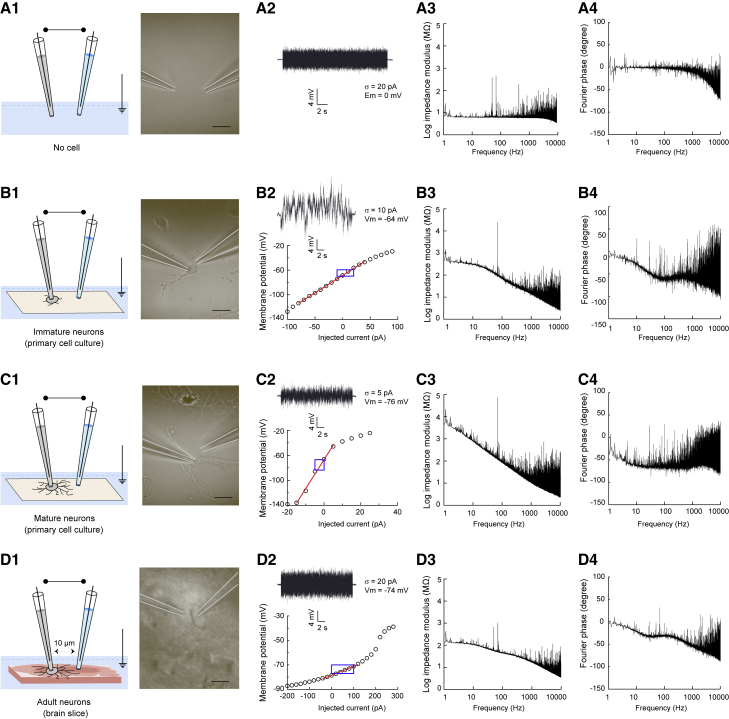
Figure 2.

Impedance measurements in different preparations using a three-electrode setup. (A) Measurement in ACSF. Description of the (1) experimental preparation (no biological sample is present in the ACSF solution) with (2) an example voltage response and for neuronal recordings, the corresponding I-V curve with the linear fit in red and the window of the voltage amplitudes during the current injection in blue. (3) and (4) show respectively the Fourier modulus and phase spectra of the voltage difference between whole-cell patch electrode and reference electrode as a function of frequency. (B–D) same setup for different experimental preparations: recordings were made in primary cell cultures of striatal tissue (day 3 to day 10 after seeding) from neurons with almost no neurites (B), with extended dendrites (C), and from striatal neurons in acute horizontal brain slices (D). To see this figure in color, go online.

Several templates (from 1 to 71) of the same Gaussian white noise with a flat spectrum between 0 and 10,000 Hz, were injected into each recorded neuron. Importantly, for the subthreshold range of voltage responses considered here (−67 mV ± 2.3 mV), the membrane I-V curve of striatal neurons was linear and only subthreshold responses to current injections (±5 to 20 pA, adjusted according to the membrane resistance) were considered for analysis. More precisely, recordings, using the very same electrophysiological setup, were obtained in four different experimental preparations (Figs. 2 and 3). We describe below the experimental results from the simplest experimental preparation in which two electrodes were added to a homogeneous ACSF solution without biological sample (Fig. 2 A1), to a more complex preparation, in which recordings were obtained from neurons within an acute brain slice (Fig. 2 D1). We also tested the influence of the dendritic arborization by recording either in nonarborized neurons with almost no neurites (Fig. 2 B1) or in arborized neurons with extended dendrites (Fig. 2 C1) in primary cell cultures. For each experiment, the Fourier modulus and phase of the voltage difference between the whole-cell recording electrode and the reference electrode were calculated and then averaged (as illustrated in Figs. 1 and 2). The same analysis was also applied to the voltage difference between the reference and ground electrodes (Fig. 3).

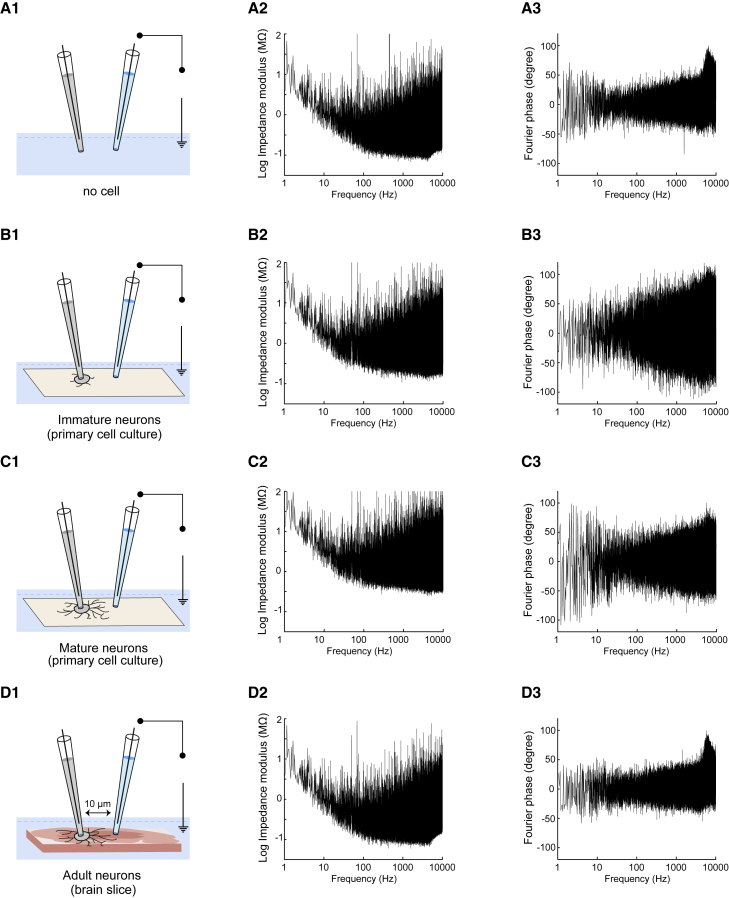
Figure 3.

Measurements between the extracellular electrode and the ground (extracellular-to-ground impedance). Same arrangement of panels as in Fig. 2. Left: scheme of the recordings in the different preparations; Middle: modulus of the impedance; Right: phase of the impedance. To see this figure in color, go online.

We describe below the experimental results from the simplest configuration of the two electrodes in ACSF, then primary cell cultures in a quasi-homogeneous medium (to to contrast with the high heterogeneity seen in acute brain slices), and finally a more complex configuration of neurons in acute brain slices.

Measurements in ACSF

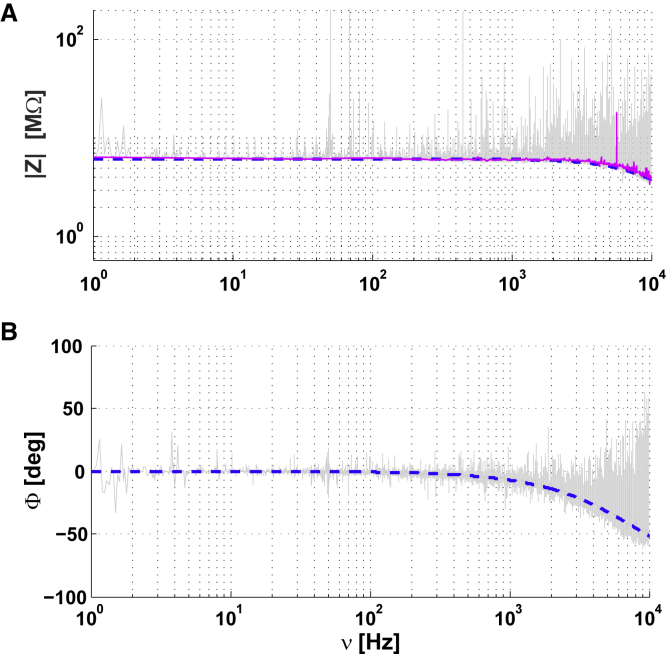
In this section, we examine the simplest configuration consisting of two electrodes in a homogeneous medium solely constituted by ACSF (Figs. 2 A and 3 A). The glass pipettes containing the electrodes were situated at a distance of 5 to 10 μm. Fig. 4 shows the measured impedance between the two electrodes. The observed frequency dependence appears above 2 kHz for the modulus (Fig. 4 A) and above 500 Hz for the phase (Fig. 4 B). This frequency dependence of the impedance modulus is negligible for frequencies lower than 2 kHz, but not for higher frequencies because Δlog₁₀V ≈ 50% between 2 kHz and 10 kHz, similar to previous measurements using patch electrodes in the extracellular medium (6). The phase of the impedance also shows a frequency dependence. It is negligible for frequencies smaller than 0.5 kHz, but for frequencies between 0.5 and 10 kHz, it varies by about 50°. Our interpretation is that these frequency dependences come from the capacitive effect between the two electrodes (which was estimated of C ≈ 3.25 pF). We found that this capacitive effect is present in all experiments shown in the next sections, for intracellular and extracellular recordings.

Figure 4.

Impedance between two electrodes in ACSF. The distance between the two electrodes was of the order of 5 to 10 μm. The modulus (A) and the phase (B) are represented as a function of frequency ν. A frequency dependence can be seen for ν > 2 kHz (A) and for ν > 500 Hz (B). The blue curve shows a capacitive effect of 3.25 pF. The magenta curve is a cubic spline fit of the experimental data (gray). To see this figure in color, go online.

Importantly, in this part of the experiments, we observe a linear phase lag Φ = −kν on the phase Φ of the impedance, as if electrode polarization had a non-negligible impact on the measurement. However, we observe that the constant k is inversely proportional to the sampling frequency, which rules out a polarization effect (because with polarization, we would have Φ = −(k + k_p)ν, with k_p independent of sampling frequency). Thus, the phenomenon of electrode polarization seems negligible here, contrary to Miceli et al. (6). This difference probably occurs because we applied smaller amplitude currents (about 20 pA here, compared with 175–500 pA in (6)). Note that the linear phase lag was removed in Fig. 3 A3.

According to Miceli et al. (6) and Wagner et al. (8), the electric conductivity of ACSF (“ACSF_c” in Miceli et al. (6)) is similar to the conductivity measured between two points in the extracellular medium (around 0.5 S/m). We did not evaluate the value of this conductivity here, because the very short distance between electrodes (5–10 μm) induces capacitive effects. In this case, one would have to solve the Laplace equation to estimate the conductivity from the macroscopic impedance measurement. In previous experiments, such as (6), the interelectrode distance (100–125 μm) was sufficiently large to avoid capacitive effects.

Measurements in primary cell culture

Nonarborized neurons

In this section, we first examine a relatively simplified system of immature neurons with little dendritic arborization, and laying in a simplified extracellular medium (primary cell culture); n = 6 neurons (with few or no dendrites) were recorded in this quasi-homogeneous medium (Fig. 2 B).

Figs. 5, 6, and 7 show the fitting of different models to experimental measurements obtained with isolated cells immersed in saline, which is a medium that can be considered as homogeneous and resistive as a first approximation. The fitting to these measurements shows that the intracellular-to-extracellular and extracellular-to-ground macroscopic impedance clearly depends on frequency.

Figure 5.

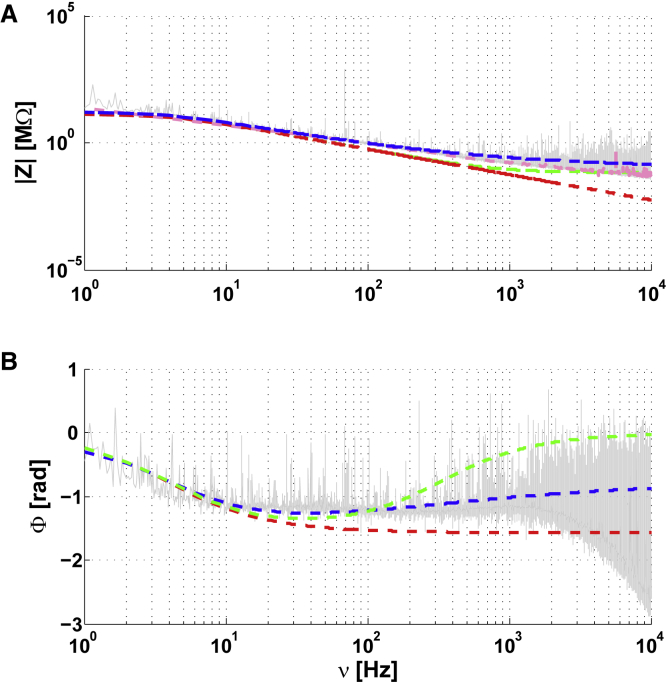
Cell-to-extracellular impedance Z as a function of frequency ν for a non-arborized neuron (no dendrites) in a primary culture (quasi-homogeneous medium). (A) Modulus of Z as a function of ν. (B) phase of Z as a function of ν. The different models tested were Red: $\left(R_m\left|\right|C_m\right)$ model, Blue: $\left(R_m\left|\right|C_m\right)\oplus Z_w\oplus R_{asymp}$, Gray: experimental measurement, Green: $\left(R_m\left|\right|C_m\right)\oplus R_{extra}$ (Online Appendix B). The symbol $\oplus$ means “in series with” and the symbol $\left|\right|$ means “in parallel with.” Magenta: cubic spline fit of the experimental data. Parameters: R_m = 810 MΩ, τ_m = 30 ms; A_w = 495 MΩ, ν_wT = 0.1 Hz, R_extra = 4 MΩ and R_asymp ≈ 0.5 MΩ. To see this figure in color, go online.

Figure 6.

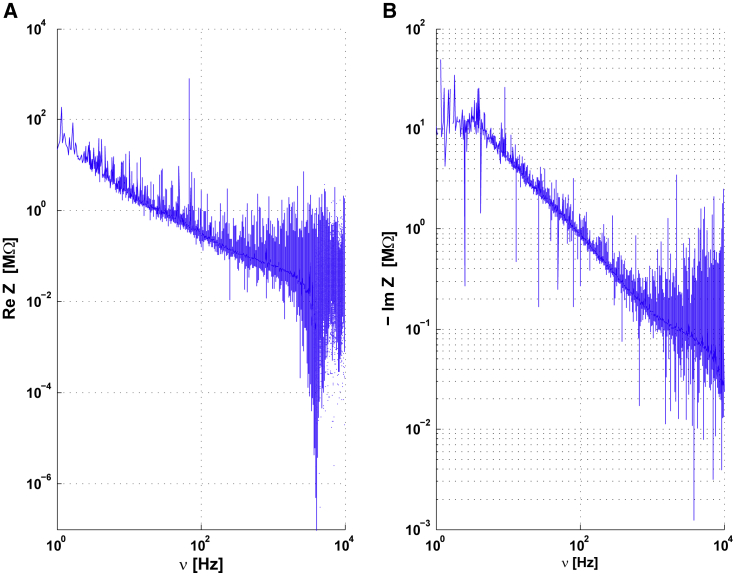
Impedance in polar coordinates for cell-to-extracellular measurements using experimental data from Fig. 5 of the manuscript. (A) Re(Z) versus frequency from the data of (A). (B) -Im(Z) versus frequency from the same data. To see this figure in color, go online.

Figure 7.

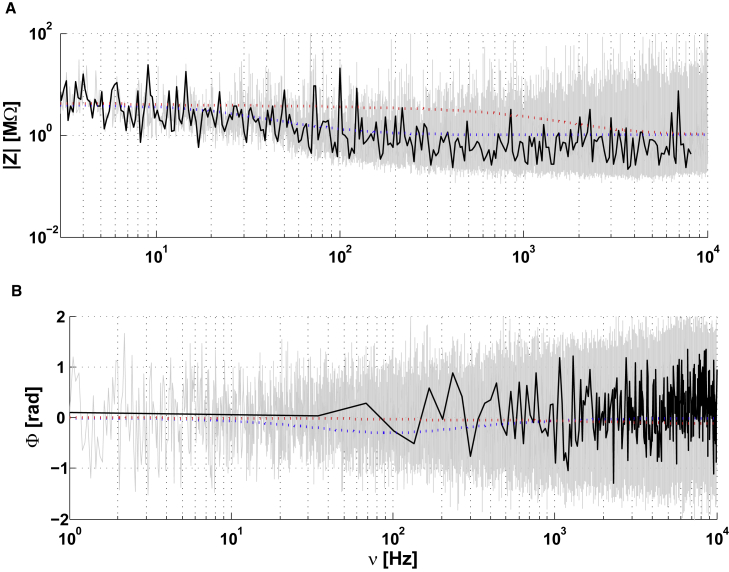
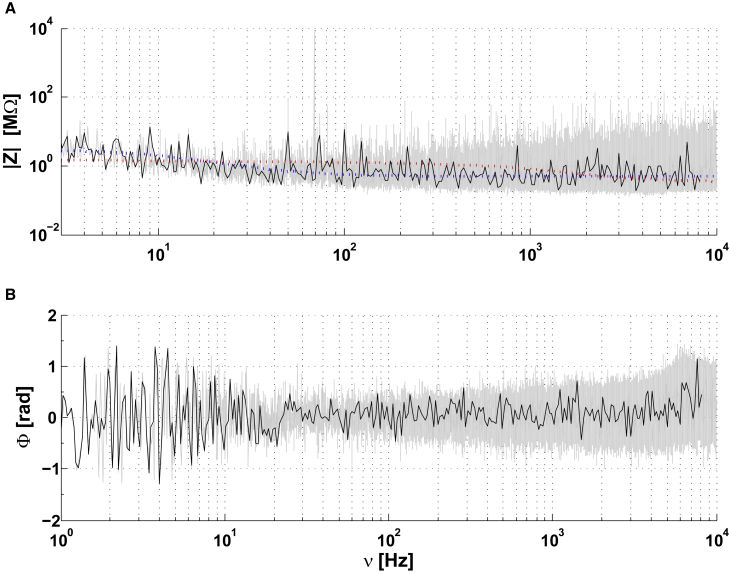
Extracellular-to-ground impedance for a nonarborized neuron in culture. (A) Modulus of the impedance as a function of frequency. (B) Phase of the impedance as a function of frequency. Dotted lines correspond to the mathematical model given by Eq. 3b (Fig. 5 and Online Appendix A). The different fits shown are: Blue: NMD - Membrane + diffusive intracellular and extracellular media; Red: NMR - Neuron in a non-negligible resistive medium $z_e^{\left(m\right)}\ne 0$; Gray: experimental measurement; Black: For (A), cubic spline of the logarithm of the modulus and frequency of experimental data; for (B): cubic spline of the phase and logarithm of frequency. Parameters: in all models, R_m = 10 MΩτ_m = 25 ms, r_d = 2 μm, l_d = 100 μm and Z_g = 0.1 MΩ; NMR: ${\sigma }_e^i=5S/m$, $\frac{z_m^{\left(e\right)}}{r_m}=0.5$, NMD: ν_wT = 0.01 Hz, $\frac{z_e^{\left(m\right)}}{r_m}=0.5+\frac{0.5}{1+\sqrt{i\frac{\omega }{{\omega }_{wT}}}}$, $\pi r_d^2\cdot z_i=\frac{1}{{\sigma }_e^i}+\frac{1}{1+\sqrt{i\frac{\omega }{{\omega }_{wT}}}}$. To see this figure in color, go online.

Fig. 6 also depicts the real and imaginary part of the impedance. Note that the instrumental noise on the phase is large compared with that on the modulus, the real $\left|Z\right|cos\text{Φ}$ and imaginary $\left|Z\right|sin\text{Φ}$ components are both more noisy than the modulus. However, the representations of Im(Z)/ν(Z) and Re(Z)/ν(Z) complement well the analyses given in the paper.

The gray curve in Fig. 5 shows the measured impedance between the intracellular and extracellular electrodes. An RC circuit (membrane) in series with a resistance R_medium (medium) cannot account for these impedance measurements (green curves in Fig. 5). Simulating the impedance with different values of R_medium (Online Appendix B), could not mimic the experimental results. The red curve corresponds to R_medium = 0, which is equivalent to consider that the membrane impedance is much larger than that of the extracellular medium. In this case also, it was not possible to properly fit the measurements.

The magenta curves in Fig. 5 are cubic spline fits of the experimental data. We observed a capacitive effect between the two intracellular and extracellular electrodes, as observed in ACSF, but larger. This indicates that the mean electric permittivity of the intracellular medium is larger than that of ACSF. This capacitive effect is responsible for a steep decrease of the phase values at high frequencies. This is consistent with a diffusive effect, because a resistive model with membrane would have a phase around π/2 rad. for ν > 100 Hz, which is difficult to reconcile with this phase measurement.

The gray curve in Fig. 7 shows the measured impedance between the extracellular electrode and the ground. A model with a simple dendrite (stick) with resistive intracellular and extracellular media could not account for these experimental measurements. The red curve corresponds to an extracellular medium with negligible resistivity compared to that of the membrane ($z_e^{\left(m\right)}\approx 0$). This case is equivalent to applying expression 3a. The green curve is such that $z_e^{\left(m\right)}=0.5r_m\ne 0$.

In contrast, for the intracellular-extracellular measurement, we observed that the NMD model (F(ω) = 0 and $A_w\in \mathbb{R}$; see Eq. 1) simulates (with some error) these experimental measurements with a macroscopic RC circuit in series with a resistance and a diffusive impedance (blue curve in Fig. 5). However, the residual error between experimental measurements and the diffusive model is very similar to what we observed for two electrodes in ACSF (Fig. 4). This model also fits the extracellular-to-ground measurement, despite the noise on the phase, for a stick where both intracellular and extracellular Debye layers are modeled with a diffusive model (blue curve in Fig. 7). We propose an interpretation of these results in the analysis of the experiments section.

Arborized neurons

We now follow the same approach as in the previous section, but in the case of recordings made from more mature neurons with extended dendritic arborizations, in primary cell cultures (n = 6 cells), which corresponds to Fig. 2 C. Using the same scheme as in Fig. 5, we also investigate how the presence of dendrites influences the measured macroscopic impedance in this quasi-homogeneous medium.

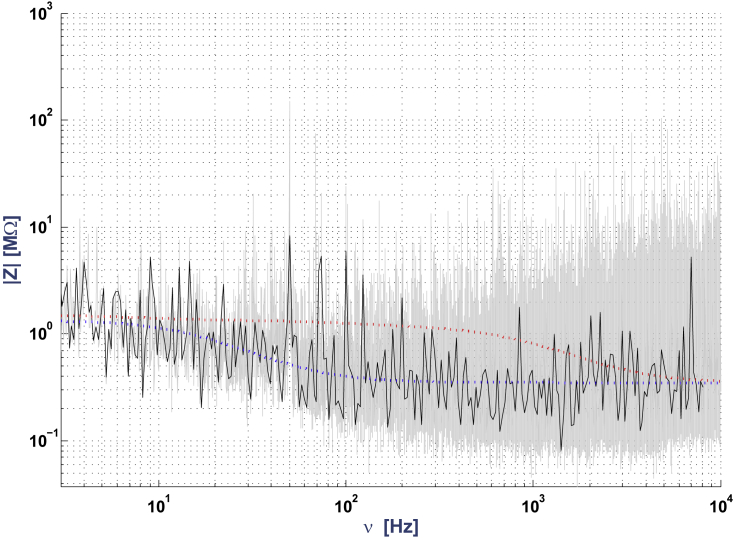
By comparing the intracellular-to-extracellular impedances in Figs. 5 and 8, one can observe that the presence of dendrites has a negligible influence on the measured intracellular-to-extracellular impedance. The quality of the fit of the extracellular-to-ground impedance in the extracellular-to-ground impedance in Fig. 9 is very similar to that of Fig. 7. We considered a stick radius of 2 μm (as in nonarborized neurons) and a stick length of 600 μm (instead of 100 μm) to take into account the presence of a more extended dendritic arborescence (Online Appendix E). Note that the values of radius and length of the stick are not unique because the simulations can fit the experimental results equally well with a large number of dendritic parameters. However, the area of the dendritic stick is fixed when we fix the ratio $z_e^{\left(m\right)}/r_m$, r_i and τ_m (see Eqs. 3 and 2; for more details, see (23)). Thus, keeping the same stick diameter as in the previous section, the fact that the length of the stick is much larger than in immature neurons, indicates that, in these experiments, the presence of dendrites has a much larger impact on the extracellular-to-ground impedance compared with the previous section. We have used a dendrite length that is six times larger for arborized neurons, which corresponds to visual inspection, but the results were weakly dependent on the exact value of this parameter (not shown).

Figure 8.

Intracellular-to-extracellular impedance Z as a function of frequency ν for an arborized neuron in a primary cell culture (homogeneous medium). Magenta: cubic spline fit of the experimental data. Similar description as in Fig. 5 with parameters R_m = 1350 MΩ, τ_m = 28 ms; A_w = 450 MΩ,τ_mw ≈ 0 s, ν_W = 0.3 Hz, R_extra = 1MΩ, R_asymp = 1MΩ. To see this figure in color, go online.

Figure 9.

Extracellular-to-ground impedance for an arborized neuron in culture. (A) Modulus of the impedance as a function of frequency. (B) Phase of the impedance as a function of frequency. Same color code as in Fig. 7. Dotted lines correspond to the mathematical model given by Eq. 3b (for details, see Fig. 7 and Online Appendix A). Parameters: r_d = 2 μml_d = 600 μm, R_m = 12 MΩ τ_m = 35 ms, ${\sigma }_e^i=5S/m$, and Z_g = 0.2 MΩ. NMR: $\frac{z_m^{\left(e\right)}}{r_m}=.5$; NMD: ν_wT = 0.1 Hz, $\frac{z_e^{\left(m\right)}}{r_m}=0.5+\frac{0.5}{1+\sqrt{\frac{i\omega }{{\omega }_{wT}}}}$, $\pi r_d^2\cdot z_i=\frac{1}{{\sigma }_e^i}+\frac{1}{1+\sqrt{\frac{i\omega }{{\omega }_{wT}}}}$. To see this figure in color, go online.

Thus, the fits of different theoretical models to experimental measurements of (arborized) neurons with dendrites give very similar results to those obtained in neurons without dendrites (nonarborized) examined in the previous section. In other words, the mean square error of the fit of the diffusive model is about 50 times smaller than that of the resistive model (with or without dendrites; Online Appendix G). The same capacitive effect as in ACSF was observed here for both arborized and nonarborized neurons (Fig. 4 in measurements in ACSF and Figs. 5 and 8 in measurements in primary cell culture). It is thus important to stress that the 3-point measurement used here allowed us to directly measure the physical effect of the presence of dendrites on experimental measurements.

Analysis of the experiments

The measurements from neurons in primary cell culture can be analyzed according to the electrical configuration depicted in Fig. 10. The isopotential surfaces indicated are central to our analysis. S_i is the isopotential surface that corresponds to the potential measured at point i, where S₁ corresponds to the potential measured by the intracellular electrode, S₂ corresponds to the potential measured by the extracellular electrode, and S₃ corresponds to the ground potential. For simplicity, we call Region i−j the domain delimited by surfaces S_i and S_j.

Figure 10.

Electrical configuration of the cell and electrodes. Left: Physical model. The cell is schematized in gray, and the isopotential surfaces are labeled as S₁, S₂, S₃. Right: equivalent electric circuits for the impedances calculated between the intracellular and extracellular electrodes, as well as between extracellular and ground electrodes. This corresponds to the isopotential surfaces S₁−S₂ (Region 1–2) and S₂−S₃ (Region 2–3), respectively. S_2b is the part of surface S₂ where the current directly goes to the extracellular medium, whereas S_2a is the part of S₂ where the current that passes through the intracellular medium before going extracellular (soma + dendrite). In other words, in Region 2–3, we have taken Eq. 3b where Z_g is a resistance. R_g is the resistance between the ground and the first isopotential surface which includes the neuron. Note that the drawing with equipotential surfaces (left) is a schematic drawing where the only goal is to illustrate the link between equivalent electric circuits (right), the physical models and the experimental measurements (Online Appendix A). To see this figure in color, go online.

First, because the extracellular medium surrounding the cell is mostly homogeneous and resistive, its macroscopic impedance cannot depend on frequency (10). (Note that in (10), we have shown that if there is a strong spatial dependence of the electric parameters, a frequency dependence of the impedance appears. The equation used is equivalent to the generalized current conservation law. The latter can be written as $\nabla \cdot {\overrightarrow{j}}^g=0$, where ${\overrightarrow{j}}^g=-\left({\sigma }_e+i\omega \epsilon \nabla V\right)$, and we have $\nabla \cdot {\overrightarrow{j}}^g=\left({\sigma }_e+i\omega \epsilon \right){\nabla }^{2}V+\nabla \left({\sigma }_e+i\omega \epsilon \right)\cdot \nabla V=0,$ which is equivalent to (10)). We thus conclude that the surface S₂ does not totally include the neuron, but cuts part of the soma, such that we have a portion of membrane over Region 2–3. Indeed, if the neuron was completely included into Region 1–2, then Region 2–3 would only consist of extracellular fluid, and would not exhibit (or exhibit negligible) frequency dependence, which was not what was observed (Fig. 7). This is in agreement with the fact that the intracellular and extracellular electrodes are very close to each other (between 5 and 10 μm), compared with the size of the soma (estimated around 15 μm).

Second, the graph of the modulus of the impedance as a function of frequency in Region 1–2 (Fig. 5) is very different from Region 2–3 (Fig. 7). We thus conclude that the physical model is similar to the one represented in Fig. 10. Because the two points 1 and 2 are very close to each other, we can simulate the impedance of Region 1–2 by an RC circuit in series with a diffusive impedance. However, the equivalent circuit of Region 2–3 cannot be the same because the current of the intracellular electrode divides into three parts: $I_{intra}^g=I_a^g+I_s^g+I_d^g$, where $I_s^g+I_d^g$ flows through the soma membrane and the dendrite, to the extracellular medium, while $I_a^g$ directly goes to the extracellular medium. Thus, the impedance of Region 2–3 is equivalent to expression 3b (Online Appendix A). Because this equivalent impedance is much smaller than the input impedance of the stick and of the soma membrane, the extracellular-to-ground impedance is also much smaller than the intracellular-to-extracellular impedance. Despite this small value, the frequency dependence of the modulus of this impedance can be clearly seen (Fig. 7). The experimental measurement of the impedance of Region 1–2 shows an additional capacitive effect similar to that seen in the previous section between intracellular and extracellular electrodes. However, this capacitive effect is negligible for the impedance measured in Region 2–3, which is coherent with the fact that the distance between the extracellular electrode and the ground is much larger than the distance between intracellular and extracellular electrodes.

Third, the growth of the modulus of the impedance of Region 2–3 for frequencies above 20 Hz is in full agreement with the diffusive model, as in Eq. 3b. This is not the case with the other models considered here. The minimum of the modulus is directly linked to the membrane time constant. The longer the time constant, the higher the frequency of the minimum. We estimate from the position of the minimum, a membrane time constant of about 30 ms, which is consistent with the membrane time constant estimated in this configuration. The growth of the modulus shows that $\frac{z_e^{\left(m\right)}}{r_m}$ cannot be neglected (Fig. 5). The value of this ratio is estimated between 0.5 and 1 for null frequency (Online Appendix D).

Fourth, the values of the ratio α = R_m/A_w (model NMD for ν = 0) are approximately α ≈ 1–2 for both Region 1–2 and Region 2–3. Here, NMD stands for a model in which each differential element of membrane is equivalent to a parallel RC circuit and where the intracellular and extracellular media are diffusive. These ratios do not correspond to a singular case, but were similar in all examined cells (Online Appendix G) in the same experimental conditions. Because neglecting A_w would amount to having the NMR model of Fig. 5, these experimental results show that the intracellular and external Debye layers cannot be assimilated to a simple resistance. In contrast to NMD, the NMR configuration has resistive extracellular and intracellular media, but with the same membrane impedance. Moreover, the threshold frequency cannot be considered as infinitely large (ν_wT = 0.1 Hz in Fig. 4 and ν_wT = 0.001 Hz in Fig. 5) because in this case, we would also have the NMR model. The threshold frequency ν_wT of the diffusive impedance between surfaces S₁ and S₂ is greater than that between surfaces S₂ and S₃. This shows that surfaces S₁ and S₂ have very different curvatures. The small value of the Warburg threshold frequency (ν_wT = ω_wT/2π) indicates that the curvature radius of the isopotential surface S₂ is much larger than the surface S₁, which is consistent with the fact that surface S₁ is at a zero distance from the tip of the intracellular electrode, which is not the case for surface S₂ (Fig. 5; Online Appendix D).

Fifth, even for zero frequency, one does not observe the typical resistance of ACSF. If we calculate the resistance sensed by a fictive spherical source of diameter equivalent to the intracellular electrode (∼1 μm), embedded in ACSF with an electric conductivity of σ_e = 0.5 S/m (6), we have $\approx \frac{1}{4\pi {\sigma }_e}\left[\frac{1}{r_1}-\frac{1}{r_2}\right]\approx 40k\text{Ω}$. Here, r₁ is the diameter of the fictive source, and r₂ is the average distance between the membrane and the spherical source. This value of 40 kΩ is smaller than the value in Region 1–2 predicted by the diffusive model for a near-zero frequency, because this value is much smaller than the estimated A_w, which is about 30% to 45% of that of the membrane. This result is surprising, and different from the approximation usually made, assuming that the intracellular impedance is much smaller in amplitude compared with the membrane impedance for near-zero frequencies.

How to explain this result? According to the theory and experimental measurements of the electric conductivity of heterogeneous media (26,27), the phenomenon of polarization occurs when an electric field is applied, and this contributes to lower the electric conductivity of the medium. Similar considerations apply to the phenomenon of ionic diffusion, which also lowers the conductivity (9,23). In the polarization effect, the electric field polarizes the intracellular medium, which determines an electric resistivity that is larger than the most conductive part of the medium. Thus, electric polarization diminishes the apparent electric conductivity in a heterogeneous medium, which directly affects the value of A_w (Online Appendix C). Nevertheless, the present measurements show that the characteristic relaxation time of polarization (also called Maxwell-Wagner time), is negligible in these experimental conditions because the diffusive model alone can fit very well the experimental results. (Note that the diffusive model stems from the application of quasistatic statistical thermodynamics to the model of Gouy-Chapmann-Stern-Debye (21,28)). If the polarization relaxation time was not negligible, there would be an additional frequency dependence to take into account in addition to the diffusive model. Note that the diffusive model is equivalent to a model in which the polarization relaxation time becomes very large when the frequency tends to zero (Online Appendix F). We conclude that the intracellular medium is such that the cutoff frequency f_c = 1/2πτ_mw of the low-pass filter due to electric polarization (11) is larger than 10 kHz in this experiment.

The large extracellular medium impedance also can be explained by the tortuous structure of the intracellular medium. Because the electric field lines cannot follow this tortuous structure, the charges that are moving in the extracellular space due to the electric field are subject to various obstacles (29). To move away from these obstacles, ionic diffusion is necessary in addition to the electric field. Thus, it is expected that the impedance modulus of such a tortuous medium is larger than ACSF.

The high value of the impedance (high value of A_w) is also due to the fact that the size of the soma is much larger than the plasmic membrane thickness. The ratio between the two is of the order of 1000, because the membrane has a thickness around 7.5 nm while the soma has a typical size around 10 μm. If we consider a slice inside the soma, we get approximately R_{soma internl} < A_w/1000 = 4 MΩ/1000 ≈ 4 kΩ, which is much smaller than R_m. We can repeat this for further slices in series of similar thickness. Because A_w contains the contribution of external and internal Debye layers, the value of R_{soma internal} evaluated is smaller than 4 kΩ. (By definition, the external (or internal) Debye layer is the region at the interface between the membrane and the extracellular (or intracellular) medium. It was estimated that the electric potential over this region attenuates by e ≈ 2.718 times its value on the membrane surface. Its thickness is called the Debye length. For more details on the notion of Debye layers, see (28)). Thus, the medium inside the soma is much more conductive than the membrane, as postulated by the standard model, but the difference is not as large as assumed by that model (red curve in Fig. 5).

Finally, we observed that the impedance measured between the extracellular electrode and the ground is much noisier than the intracellular-to-extracellular impedance. This is, in part, due to the smaller amplitude of the latter impedance, and to the fact that the power falls off at higher frequencies, where instrumental noise becomes dominant. However, it should be noted that, besides the presence of this higher level of noise, the measurements also show that the modulus of the two theoretical diffusive impedances in Regions 1–2 and 2–3 are in full agreement with the experimental results. This indicates that the extracellular electrode is sufficiently far away from the membrane and does not disturb its ionic environment (Debye layers). It is nevertheless close enough so that the isopotential surface S₂ only cuts a portion of the soma.

To conclude this analysis, the present measurements from neurons in primary cell culture cannot be made compatible with a resistive system, both for the modulus and phase of the impedance. However, both seem compatible with the impedance profile predicted by a diffusive system, which we interpret as being essentially due to the presence of Debye layers surrounding the membrane. However, to be rigorous, we must also mention the influence of the multiple obstacles inside and outside the neuron, which also have Debye layers and will influence the current flow. Importantly, the lack of major differences between the measurements from immature nonarborized neurons and those obtained from neurons with an extended dendritic tree argues against the hypothesis that the presence of dendrites could have a significant impact on impedance measurements.

Measurements in acute brain slices

In this section, we present and analyze impedance measurements of mature and fully arborized neurons (n = 9 cells) recorded in acute brain slices (Fig. 2 D). In this case, the tissue surrounding the neuron is quasi-intact, and the extracellular medium is the neuropil, which is very heterogeneous (30). We analyzed the effect of such an environment on the frequency dependence of the macroscopic impedance.

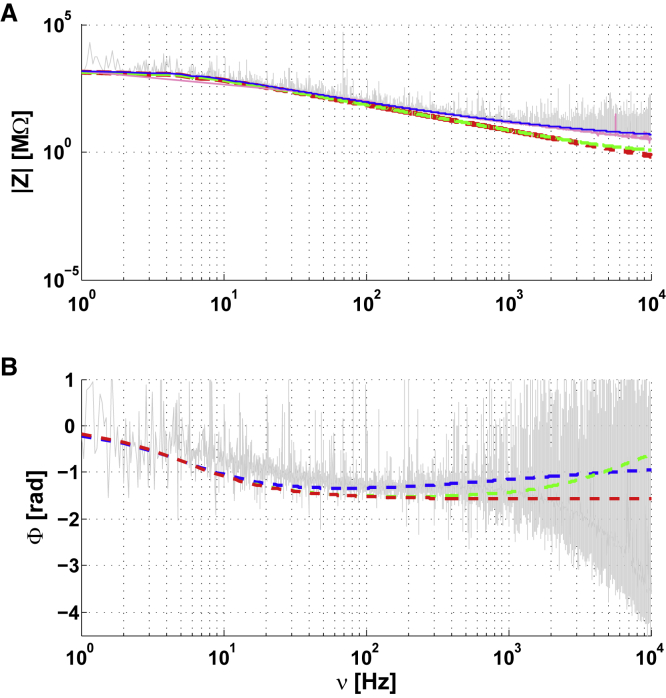
We used the same experimental method (three-point recording) as in previous sections. We observe a different frequency dependence for the impedance of Region 1–2 (compare Figs. 5, 8, and 11). This shows that the presence of a complex extracellular medium (neuropil) causes more complex effects in the vicinity of the neuronal membrane. However, if we consider two different threshold frequencies for intracellular and extracellular media, we obtain the following:

$$Z=\underset{membrane}{\underbrace{\frac{R_m}{1+i\omega {\tau }_m}}}\oplus \stackrel{intracellularmedium}{\overbrace{\underset{diffusivemodel}{\underbrace{\frac{A_w^{\alpha }}{1+\sqrt{i\frac{\omega }{{\omega }_{wT}^{\alpha }}}}\oplus R_{asymp}^{\alpha }}}}}\oplus \stackrel{extracellularmedium}{\overbrace{\underset{diffusivemodel}{\underbrace{\frac{A_w^{\beta }}{1+\sqrt{i\frac{\omega }{{\omega }_{wT}^{\beta }}}}\oplus R_{asymp}^{\beta }}}}},$$ (4)

which gives excellent fits (Fig. 11). Note that we have kept the characteristics (parameters) of the previous experiments for modeling the intracellular medium.

Figure 11.

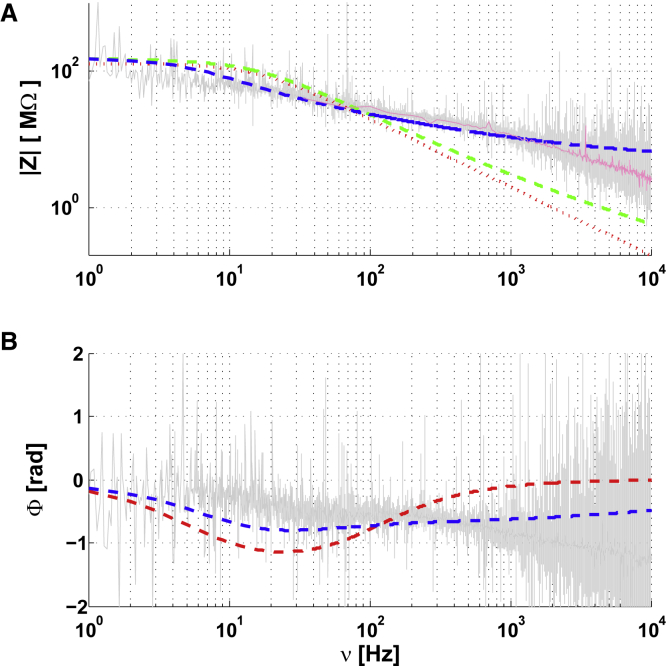
Intracellular-to-extracellular impedance Z as a function of frequency ν for a neuron recorded in acute brain slice. (A) Modulus of Z as a function of ν. (B) Phase of Z as a function of ν. Parameters: τ_m = 10ms, R_m = 128 MΩ; $A_w^{\alpha }=60M\text{Ω}$, ${\nu }_{wT}^{\alpha }=0.5Hz$, $R_{asymp}^a=6M\text{Ω}$; $A_w^{\beta }=16M\text{Ω}$, ${\nu }_{wT}^{\beta }=40Hz$ and $R_{asymp}^{\beta }=6M\text{Ω}$. The color code is red: fit with resistive intracellular and extracellular media (16 MΩ); green: fit with a diffusive intracellular medium (a) and a resistive extracellular medium (16 MΩ); blue: fit diffusive intracellular and extracellular media (Eq. 4); Magenta: cubic spline fit of the experimental data. The latter case best fits the experimental measurements. The mean square error of the diffusive model is about threefold less that than of the resistive model (Online Appendix G). To see this figure in color, go online.

In Region 2–3, we observed a similar frequency dependence as in previous configurations (compare Figs. 7, 9 and 12). In the case of the diffusive model, we used a model of the macroscopic impedance Z_b (impedance of the extracellular medium as sensed by Surface S₂; Fig. 10), which was taken from a previous study (9), with the difference that we added a series resistance (8 MΩ). This addition is justified in Online Appendix C (Eq. C.5). This impedance is necessarily macroscopic because it is given by the ratio of the measured current between two points separated by macroscopic distances (as defined by the region in between the two isopotential surfaces going through each point). Accordingly, we used $Z_b=8+\frac{8}{1+\sqrt{\frac{i\omega }{w_{wT}}}}M\text{Ω}$, where ν_wT = 40 Hz, as determined in (9). Note that the particular choice of the parameters (A_w = R_asymp = 8 M and w_wT) can be varied (by approximately ± 50%) with no qualitative change in the results (Online Appendix G). While many combinations of parameters fit the data for diffusive models, we did not find a single parameter set of resistive models that could fit the data.

Figure 12.

Extracellular-to-ground impedance for a neuron recorded in acute brain slice. The same color code as in Fig. 7 was used. Dotted lines correspond to the mathematical model given by Eq. 3b (for details, see Fig. 11 and Online Appendix A). The modulus of the impedance is represented as a function of frequency. Parameters: R_m = 5 MΩ, τ_m = 10ms, r_d = 2 μm, l_d = 600 μm, ${\sigma }_e^i=5S/m$, and Z_g = .2 MΩ. NMR: $\frac{z_m^{\left(e\right)}}{r_m}=.5$; NMD: ν_wT = 0.01 Hz, $\frac{z_e^{\left(m\right)}}{r_m}=0.5+\frac{0.25}{1+\sqrt{i\frac{\omega }{{\omega }_{wT}}}}$, $\pi r_d^2\cdot z_i=\frac{1}{{\sigma }_e^i}+\frac{1}{1+\sqrt{i\frac{\omega }{{\omega }_{wT}}}}$. To see this figure in color, go online.

The modulus of the extracellular impedance between the extracellular electrode and the ground (Region 2–3) in acute brain slices can be different from that in primary cell culture. The impedance sensed by the current source that does not flow through the dendrite and the cell membrane (Fig. 10) on Region 2–3 (between the extracellular electrode and the ground) are experimental conditions similar to extracellular measurements performed in other studies (5,6). Thus, for Region 2–3, we have chosen a similar model as for the experiments in primary cell culture.

Analysis of the brain slice experiments

In the acute brain slice preparation, the observations are similar to the observations in primary cell culture, except that the best fit is obtained here when we use different threshold frequencies for intracellular and extracellular media. We now focus on the analysis and interpretation of such different threshold frequencies.

According to Gomes et al. (9), the extracellular impedance in brain slices has a threshold frequency between 40 and 60 Hz. Compared with the present experiments, the thickness of the extracellular medium was much larger in (9), because the extracellular electrode was located at a distance about 10 times larger. Indeed, in (9), the macroscopic impedance of the extracellular medium was larger than that of the intracellular medium. Thus, the present results, together with Gomes et al. (9), suggest that the threshold frequency of the extracellular medium is larger than that of the intracellular medium. This larger threshold may indicate that the medium is more tortuous inside the cell compared with the extracellular medium.

This result is also in qualitative agreement with the experimental measurements of Gabriel et al. (7) and Wagner et al. (8) because the apparent conductivity and permittivity of the diffusive model are respectively very low and very high, which gives a very large dielectric relaxation time (Online Appendix F). According to the experimental results of (7), the electric permittivity of the extracellular medium is much larger in the neuropil, compared with that of the extracellular fluid in cultures. The value of the permittivity is in agreement with the experimental measurements (7,8) and is estimated to be 10⁵ to 10⁷ times larger than that of ACSF. Notice that the results of Wagner et al. (8) were obtained in vivo and are not identical to that of Gabriel et al. (7) obtained in vitro. This difference may be because the linear approximation of the medium impedance may be valid in vitro but not in vivo. Can the linear approximation be considered as a first estimate? Is the deviation due to the presence of ongoing (spike) activity? These questions await experimental testing.

The correspondence between the theoretical models presented in mathematical and physical models used to simulate the experimental data and the different experimental configurations is summarized in Table 1.

Table 1.

The different biophysical models used for fitting the experimental data in the different figures of the manuscript

	Fig.	Zeq.	Resistive model	Diffusive model
ACSF	4	$\text{R}\Vert \text{C}$
Culture (immature)
intra-extra	5		Zm	$Z_m\oplus Z_w$
extra-ground	6		$\left(Z_a\left|\left|Z_s\right|\right|Z_d\right)\oplus R_g$	$\left(Z_a\left|\left|Z_s\right|\right|Z_d\right)\oplus R_g$
Culture (mature)
intra-extra	8		Zm	$Z_m\oplus Z_w$
extra-ground	9		$\left(Z_a\left|\left|Z_s\right|\right|Z_d\right)\oplus R_g$	$\left(Z_a\left|\left|Z_s\right|\right|Z_d\right)\oplus R_g$
In vitro
intra-extra	11		Zm	$Z_m\oplus Z_w$
extra-ground	12		$\left(Z_a\left|\left|Z_s\right|\right|Z_d\right)\oplus R_g$	$\left(Z_a\left|\left|Z_s\right|\right|Z_d\right)\oplus R_g$

1: $Z_m=R\parallel C$ corresponds to the impedance of a portion of membrane where R and C are respectively the resistance and capacitance. 2: $Z_w$ is given by expression $\frac{A_w^{\alpha }}{1+\sqrt{\frac{\omega }{{\omega }_{w_T}^{\alpha }}}}+\frac{A_w^{\beta }}{1+\sqrt{\frac{\omega }{{\omega }_{w_T}^{\beta }}}}+R_{asym}$, where $A_w^{\alpha }\ne 0$ and $A_w^{\beta }\ne 0$ and ${\omega }_{w_T}\ne \infty$. In primary cell cultures, we have used $A_w=2A_w^{\alpha }=2A_w^{\beta }$ and ${\omega }_{w_T}^{\alpha }={\omega }_{w_T}^{\beta }$. In the in vitro conditions, we have used $A_w^{\alpha }\ne 0$, $A_w^{\beta }\ne 0$, and $A_w^{\alpha }\ne A_w^{\beta }$, with ${\omega }_{w_T}^{\alpha }\ne {\omega }_{w_T}^{\beta }$ and different from infinity. $Z_a$ is the impedance of the region defined by the isopotential surface ${\mathcal{S}}_1$ passing through the extracellular electrode and the first isopotential surface ${\mathcal{S}}_g$ that totally includes the neuron, $Z_s$ is the impedance of the part of the soma included between ${\mathcal{S}}_1$ and ${\mathcal{S}}_g$, $Z_d$ is the input impedance of the dendrite between surfaces ${\mathcal{S}}_1$, ${\mathcal{S}}_g$, and $Z_g$ is the impedance of the region between ${\mathcal{S}}_g$ and the ground. $Z_g=\left(Z_a\left|\left|Z_s\right|\right|Z_d\right)\oplus R_g$ where $\parallel$ means “in parallel” and $\oplus$ “in series” (Fig. 1).

Discussion

In this study, we provide impedance measurements around neurons, in different experimental preparations and a comparison between extracellular and intracellular impedance measurements. The aim was to determine which is the most plausible physical model that accounts for the electric properties of the extracellular medium. We used an experimental measurement consisting of three points, an intracellular electrode, an extracellular electrode in the close vicinity of the membrane (a few microns), and a ground electrode located far away. Using the same recording setup, we considered different preparations ranging from acute brain slices, primary cell cultures with neurons of different morphological complexity, and measurements in ACSF solution as control. In addition to these measurements, we have provided a detailed fitting of the measured impedance using several biophysical models of the extracellular medium. The main conclusions are that (1) in no circumstance, is the resistive model able to fit the whole data set; (2) the measurements point to a dominant role of ionic diffusion, as soon as a membrane is present; (3) the measurements suggest that the underlying mechanism is the ionic diffusion associated to the Debye layers around the membrane; and (4) additional capacitive effects may be needed to explain the differences between experimental preparations.

Regarding the first conclusion, a resistive medium cannot account for any of the measurements, except when electrodes are placed in ACSF. The resistive nature of the impedance measured in ACSF is expected because this saline solution is the simplest case of a resistive medium. In this case, we had to consider an additional capacitive effect in parallel with the two electrodes (measurements in ACSF). This shows that the measurements with the micropipettes do not create an apparent frequency dependence of the measured medium, and once the capacitive effect is removed, one recovers the correct resistive measurement in this case.

The second conclusion, that ionic diffusion plays a prominent role, is supported by our fitting analysis considering different model alternatives. This suspected presence of ionic diffusion (and the associated Warburg impedance) agrees with previous studies showing a role for ionic diffusion. Macroscopic measurements of the impedance of brain tissue (7,8) showed a frequency dependence of the electric parameters that is consistent with ionic diffusion, as pointed out by a theoretical study (21). This study developed a mean-field formalism of Maxwell equations, which was necessary to properly account for macroscopic measurements that imply averages over large spatial volumes. In this mean-field framework, the predicted frequency scaling of ionic diffusion was found to be consistent with the experimental observations. It was further shown, using a two-electrode measurement setup with intracellular and extracellular electrodes, that ionic diffusion also accounted for the observed frequency dependence (9). However, as pointed out in (16), the dendrites were neglected in our previous study. We provide here new data on this issue by showing that there was little difference between the impedance measured in intact (arborized) neurons or in (nonarborized) neurons with greatly simplified dendritic morphology. Therefore, the presence of dendrites is not a plausible cause to explain the deviations from resistivity.

The third conclusion, that the underlying mechanism is the ionic diffusion in Debye layers around the membrane, is mostly supported by the experiments in primary cell cultures where no intact neuropil is present. In these conditions, the medium is almost devoid of glial cells or neighboring neurons, and can be considered close to homogeneous saline. We also observed a frequency dependence in such conditions, when an intracellular recording was present, but not in saline with two electrodes in ACSF (measurements in ACSF). Therefore, we find that the presence of a membrane induces a frequency dependence, which we attribute as mainly due to the presence of Debye layers around the membrane. Debye layers not only constitute the basis of the membrane capacitance, but they also are characterized by ionic diffusion that participates to maintain the membrane potential. Our interpretation is that, when current flows from the intracellular electrode, the corresponding ions induce local concentration changes in Debye layers, which will re-equilibrate by ionic diffusion. This increases the modulus of the impedance and introduces a frequency dependence which signature can be seen as a diffusive (Warburg) impedance. Importantly, this impedance is a linear approximation, and thus, cannot capture the ratio V/I^g for large variations of the membrane potential (such as during spikes; see discussion in (21)).

The fourth conclusion is that it was necessary to include capacitive effects to account for differences between the different preparations. These effects were not necessary for a cell in a homogeneous medium (in culture), but were required to fit acute brain slice conditions when the electrodes were very close (about 10 μm). On the other hand, no additional capacitive effect was seen between the extracellular electrode and the ground. This suggests the possibility that both intracellular and extracellular media have a significant diffusive component. We could fit the measurements assuming a different cutoff frequency between the media (about 5 Hz intracellular, and 40 Hz extracellular). This difference suggests that the medium is more tortuous intracellularly compared with the extracellular medium.

Importantly, the present results seem in agreement with the principle of least constraint of Gauss, according to which the introduction of constraints modifies the least as possible the movement of a system. In electromagnetism, the application of this principle means that most charges will follow the path with the lowest impedance. (For example, if we have two resistances in parallel, most of the charges will go through the smallest resistance. In electromagnetism, the principle of least constraint can be seen as a generalization of this example (31)). In the measurements of Logothetis et al. and Miceli et al. (5,6), the magnitude of the minimal extracellular impedance would be of the same order as ACSF, which is a similar situation as our measurement between the extracellular electrode and the ground. In Gomes et al. (9), as in the present paper, the modulus of the minimal impedance between the intracellular and extracellular electrodes would be much larger because the charges are constrained to flow across the cell membrane, and not just flowing exclusively in the extracellular medium.

Taking together our results in different preparations, we conclude that, for the frequency range of electrophysiological phenomena (frequencies ν < 10 kHz), there is a very significant frequency dependence of the electric parameters in intracellular and extracellular media. Our experiments show that this significant frequency dependence should be taken into account when current flows across a cell membrane. On the other hand, there is very little frequency dependence if the current does not flow across a membrane. (Note that one study (8)) reports a frequency-dependent extracellular impedance, but a very different frequency range, between 4.7 kHz and 2 MHz, was used). This major difference suggests that impedance measurements should necessarily give different results if they are performed extracellularly, or using an intracellular recording. This could potentially reconcile contradictory measurements and also answer some of the questioning about the origin of the LFP signal (32).

This raises the question of which impedance is the most physiologically pertinent, the impedance of the medium alone, measured with extracellular electrodes, or the impedance between intracellular and extracellular media? If the point of interest is to relate neuronal activity (ionic currents) with the extracellular potentials, then the relevant impedance is the intracellular-extracellular impedance as measured here. Indeed, the ionic currents in the membrane must flow through a complex environment (Debye layers, various obstacles), which are important to generate the extracellular potential (which “sense” the current after its interaction with the complex environment). The impedance measured here correctly captures this effect and is the closest to the natural conditions. On the other hand, impedances measured with extracellular electrodes inform about how the extracellular medium reacts to currents injected extracellularly and does not reflect the situation with natural (membrane) currents. Thus, our study complements previous extracellular measurements, and goes further in biophysical realism by measuring the impedance pertinent for the genesis of extracellular potentials.

Our results may call for a redefinition of the classic “neuronal dipole” mechanism underlying LFP or EEG signals. However, such an extrapolation is not immediate, because our measurements were made in the linear regimen, whereas the LFP and EEG signals are generated by active networks that involve nonlinear phenomena such as action potentials. Nevertheless, our experiments indicate that LFP and EEG signals should be affected by the frequency filtering measured here, because the formation of the neuronal dipoles will depend on currents flowing through the membrane/Debye layers complex. In other words, the currents forming the neuronal dipole should include the frequency filtering due to the flow through the membrane/Debye layers complex, and that can only be revealed by intracellular measurements.

Author contributions

C.P. and L.V. did the experiments, A.D. and C.B. conceptualized the study, C.B. did the analysis, and all authors contributed to interpret the analysis and to write the manuscript.

Editor: Arthur Sherman.