Skip to main content
PMC home page
PLOS Biology logoLink to PLOS Biology
. 2022 Mar 14;20(3):e3001575. doi: 10.1371/journal.pbio.3001575

An estimation of the absolute number of axons indicates that human cortical areas are sparsely connected

Burke Q Rosen 1,*, Eric Halgren 1,2
Editor: Claus C Hilgetag3
PMCID: PMC8947121  PMID: 35286306

Abstract

The tracts between cortical areas are conceived as playing a central role in cortical information processing, but their actual numbers have never been determined in humans. Here, we estimate the absolute number of axons linking cortical areas from a whole-cortex diffusion MRI (dMRI) connectome, calibrated using the histologically measured callosal fiber density. Median connectivity is estimated as approximately 6,200 axons between cortical areas within hemisphere and approximately 1,300 axons interhemispherically, with axons connecting functionally related areas surprisingly sparse. For example, we estimate that <5% of the axons in the trunk of the arcuate and superior longitudinal fasciculi connect Wernicke’s and Broca’s areas. These results suggest that detailed information is transmitted between cortical areas either via linkage of the dense local connections or via rare, extraordinarily privileged long-range connections.

Using data from Human Connectome Project to estimate the absolute number of axons linking cortical areas yields surprisingly sparse connectivity; reconciling large-scale functional synchronization with sparse anatomical connectivity presents a challenge for our present understanding of human brain organization.

Introduction

The major tracts connecting cortical areas have long been central to models of information processing in the human brain [1]. Such models have been refined and applied to development and disease with the advent of diffusion MRI (dMRI) [2]. However, dMRI only provides relative connectivity, not the absolute number of axons. Relative connectivity is very useful in many circumstances, but more constraints would be possible if the absolute number of axons connecting different cortical areas could be estimated. Here, we describe and apply a novel method for translating from dMRI-derived streamlines to axon counts.

The ratio between these 2 measures is obtained by comparing the number of streamlines pass through the corpus callosum to the number of axons, as measured with histology. The corpus callosum is uniquely well suited for this purpose. Electron microscopy (EM) can be used to unambiguously count the total number of callosal axons because the limits of the callosum are well defined, axons are aligned, and sections can be cut perpendicular to their axis. Likewise, dMRI-derived streamlines can be unambiguously and exhaustively assigned to the callosum because the source and destination of all axons passing through the callosum as a whole are well defined. In contrast to the ipsilateral fiber tracts, in which the majority of axons enter or leave the tract at point between the fascicular terminals, commissural axons must all be connecting the 2 hemispheres. Fortunately, despite these differences, the mean and variability of cross-sectional axon density of the corpus callosum are quite similar to that of telencephalic white matter (WM) in general [3–5], permitting the streamline:axon ratio calculated from callosal fiber to be applied to intrahemispheric connections.

It has long been recognized that as the number of cortical neurons increases, maintaining the same probability of connectivity between neurons would require that axon number increase approximately with the square of neuron number, and this would require too much volume, impose an unsustainable metabolic load [6], and actually decrease computational power due to conduction delays [7]. The consequent imperative to minimize long-distance corticocortical fibers has been posited to be reflected in exponential decline in cortical connectivity with distance [8] and to be partially compensated for with a small-world graph architecture [9], granting special properties to rare long-distance fibers in a log-normal neural physiology and anatomy [10]. However, this organizing principle is rarely explicitly addressed in terms of individual axon counts, nor in a manner both granular and exhaustive with respect to cortical areas. In our histologically calibrated dMRI-derived estimation of these intercortical axon counts, we find that the widespread cortical integration implied by behavioral and mental coherence, and routinely observed in widespread physiological synchronization, belies a surprising small absolute number of long-range axons connecting cortical areas.

Materials and methods

The basic principle of our method is very simple. Given a dMRI-based measure of total interhemispheric connectivity in arbitrary units and the physical number of axons traversing the corpus callosum, the conversion factor between the 2 can be obtained by dividing the first by the second. Specifically, we started with the total interhemispheric tractography strength reported in our dMRI connectome of the Human Connectome Project (HCP) cohort [11]. For each individual, the cross-sectional area of the corpus callosum was obtained using the standard FreeSurfer structural MRI pipeline [12]. Multiplying this number by a histologically ascertained callosal fiber density [3] yields an estimate of the number of axons traversing an individual’s corpus callosum. Dividing this count by individuals’ interhemispheric dMRI streamline value yields the conversion ratio from the arbitrarily scaled dMRI metric to the absolute number of axons. Note that this procedure is independent from the scale of the dMRI metric, requiring only that it be proportional to the absolute number of fibers. A moderate proportionality has been observed in comparisons of dMRI and retrograde tracing in macaque [13,14]. Therefore, while the ratio itself is study specific, the procedure can be applied to any dMRI tractography method or parameter set, provided that the dMRI method returns a continuous distribution of connectivity values and has reasonably similar sensitivity to callosal and ipsilateral fiber tracts. To demonstrate this, we repeated the analysis using data from an alternate tractography of the HCP cohort [15]. For detailed methodology, see S1 Appendix.

Results

Our previous dMRI study [11] includes estimated tractography streamlines between all 360 parcels of the HCP-MMP1.0 atlas [16] for each of the 1,065 individuals in the HCP dMRI cohort. The sum connectivity between the 180 left hemisphere cortical parcels and the 180 right (1802 parcel pairs) constitutes the total callosal connectivity, on average 1.25 × 108 streamlines. Based on our assumed fiber density of 3.7 × 105 axons/mm2 [3] and measured callosal cross-sectional area (mean = 689.45mm2), we estimate this cohort to have 2.6 × 108 callosal fibers on average. The mean quotient between these 2 quantities is 2.00 axons per streamline, a ratio specific to the dMRI methodology and parameters used.

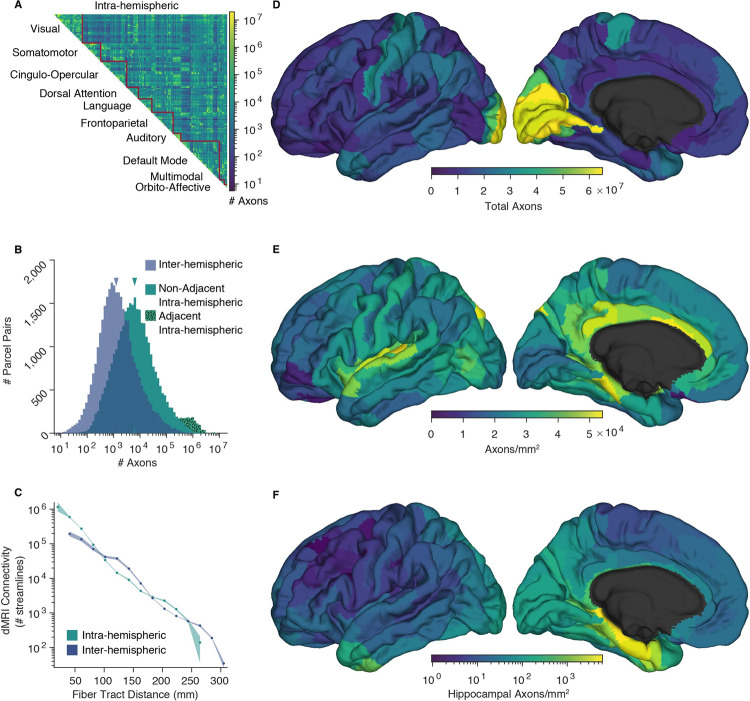
Applying the conversion factor to the interparcel connectivity from our prior study yields an estimate of the absolute number of axons connecting different cortical areas (Fig 1A), 2.43 × 109 axons in total. This implies that <22% of the approximately 11.5 × 109 cortical pyramidal cells [17,18] project outside their parcel with the remainder being short-range horizontal or U-fibers. Furthermore, because 51% of interareal axons are to adjacent areas, <11% of pyramidal cells project beyond the adjacent parcel. Axons are approximately log normally distributed among nonadjacent parcel pairs, with adjacent pairs having disproportionally high axon counts (Fig 1B). Median connectivity is approximately 6,200 axons between cortical areas in the same hemisphere and approximately 1,300 interhemispherically. The number of axons in the median interhemispheric connection is approximately 20% of that in the median intrahemispheric connection, similar to that found with histological tracing in macaques [19]. The number of callosal axons is not significantly affected by participant sex, although participants ages 26 to 30 have slightly more interhemispheric axons than participants ages 22 to 15 (S2 Fig). This sparse long-range connectivity is consistent with its exponential falloff measured with dMRI in humans and histologically in other mammals [8,11] and with previous statistical estimates based on traditional neuroanatomy [20]. In comparison to the number of axons that would be necessary for complete interconnectivity of neurons in different cortical areas with each other, the estimated number is approximately 1011 times smaller (see S1 Appendix for calculation).

Fig 1. The number of axons estimated to interconnect the 360 cortical parcels of the HCP-MMP1.0 atlas.

Fig 1

Open in a new tab

(A) Connectivity matrix of intrahemispheric axon counts, averaged across the 2 hemispheres. Parcels are ordered into 10 functional networks. (B) Histograms showing the distribution of inter- and intrahemispheric pairwise axon counts. Physically adjacent and nonadjacent parcel pair intrahemispheric histograms are stacked. Median connectivity, indicated, is approximately 6,200 axons between cortical areas in the same hemisphere and approximately 1,300 interhemispherically. (C) Comparison of intra- and interhemispheric dMRI connectivity as a function fiber tract distance. Pairwise values averaged within 15 fiber length bins. Shading shows bootstrapped 95% confidence intervals. (D–F) Axon counts and densities averaged across the 2 hemispheres and visualized on the left fsaverage template cortex [12]. (D) Total axons connecting each parcel to all others. (E) Axons connecting each parcel to all others, normalized by the reference parcel’s area. (F) Axons connecting the hippocampus to the rest of the cortex, normalized by the area of the cortical parcel, shown in log scale. HCP, Human Connectome Project. The source data for this figure can be found at https://doi.org/10.5281/zenodo.6097026.

Our method requires that dMRI tractography performs in a roughly similar manner when applied to intra- versus interhemispheric connections. We evaluated this similarity by comparing linear regressions of distance-matched log-transformed streamlines and found no difference between the slope or intercept of inter- and intrahemispheric connections (Fig 1C); within the common distance domain a paired r test showed no difference in correlation, p = 0.58. The total count of a parcel’s axons to or from all other areas is much less variable when normalized by the parcel’s area (Fig 1D and 1E). Multiplying the total number of fibers by the effective fiber cross-sectional area (the inverse callosal packing density, 2.7 × 10−6 mm2/axon) yields 6.6 × 103 mm2 of cortex or 3.7% of the total white gray interface. Note that the effective axonal area includes myelin, supporting cells and intercellular space in addition to the axon proper. The cross-sectional packing density of human prefrontal WM is quite similar to callosal values with an average of 3.5 × 105 myelinated axons/mm2 [4] after correction for tissue shrinkage, and this varies among prefrontal regions by a less than factor of 2 [5]. The percent of fiber-allocated cortical area is quite similar to the approximately 4% of total cortical fibers Schüz and Braitenberg estimated [20] are contained in the corpus callosum and long fascicles. The remaining approximately 95% of the cortical gray white interface area is likely occupied by the short range U-fiber system which is difficult to assess with dMRI.

We estimated the fraction of axons traversing the entire length of the arcuate/superior lateral fasciculus (AF/SLF) between termination fields centered on Broca’s and Wernicke’s areas. The total number of AF/SLF axons was derived by multiplying the tracts’ cross-sectional areas by mean axon density of ipsilateral tracts. Using published estimates of the cross-sectional areas of 160.6 mm2 and 51.5 mm2 for the left and right AF and 213.8 mm2 and 174.4 for the left and right SLF [21], and a shrinkage-corrected axon density of 3.5 × 105 axons/mm2 [4], yields a total of 1.3 × 108 and 0.8 × 108 axons in the left and right AF/SLF. These values were compared to the number of tractography-derived axons connecting AF/SLF termination fields [16] according to consensus definitions from reference [22]; see S3 Fig. When the anterior termination field, centered on Broca’s area is defined as HCP-MMP1.0 parcels 44, 45, 6r, IFSa, IFSp, and FOP4 and the posterior termination field, centered on Wernicke’s area as parcels PSL, RI, STV, and PFcm, trans-terminal axons account for only 0.6% and 0.8% of tract axons in the left and right hemispheres. If the termination fields are liberally expanded to also include parcels 47l and p47r in Broca’s and parcels PF, PFm, and PGi in Wernicke’s then these percentages increase to a still modest 1.9% and 2.9% of total tract axons. Please note that in this calculation, all axons between Broca’s and Wernicke’s areas are assumed to pass through the AF/SLF; to the degree that some pass outside the AF/SLF, our estimates should be decreased.

The volume of hemispheric WM occupied by axons between cortical parcels is equal to the sum of all axons’ lengths multiplied by their cross-sectional areas. The mean fiber tract lengths of connections were taken from our prior dMRI analysis [11]. For the effective cross-sectional area of axons, we again assumed an effective cross-sectional area equivalent to the inverse of the callosal fiber density [3]. So calculated, the volume occupied by corticocortical and hippocampocortical fibers is 4.3 × 105 mm3 or about 96% of the total MRI-assessed WM volume. This implies that the number of long-range fibers cannot be larger than our estimate unless the axon density calculated from the corpus callosum histology is mistakenly low, but this is a linear effect that would need to be unrealistically inaccurate for it to change our main conclusions. Another possibility is that axon density was correctly measured for the corpus callosum but is higher for intrahemispheric fibers and the number of axons per streamline is higher intra- than interhemispherically. These both need to be the case because there is no space available in the hemispheric WM to contain more axons unless they are smaller. However, the histological data indicate that axonal density is approximately the same intra- and interhemispherically [3,4], and the comparison of distance-matched streamlines (Fig 1C) suggests that the number of axons per streamline intra- and interhemispherically is also approximately equal. The remaining WM volume may seem insufficient for connections with subcortical structures. However, the major subcortical structures known to communicate with the cortex (thalamus, amygdala, striatum, nucleus basalis, locus coeruleus, etc.) contain, in sum, less than 1% of the number of cortical neurons [23–25]; see S1 Appendix. Even under the unlikely assumption that all excitatory thalamic neurons project to the cortex with a density across all cortical parcels proportionally to their area, their axons would only comprise approximately 4% of the total WM volume.

We conducted a series of simulations examining the consequences of possible errors in axonal packing density and axon-to-streamline ratio. As noted above, these parameters are coconstrained by the physical volume available for WM. At our derived ratio and assumed packing density, the volume of interareal axons is just under the observed total WM volume. Large net errors in the assumed packing density would result in total interareal axon volumes that are inconsistent with the hemispheric WM volume, a value that is well established. Consequently, in our simulations, axonal packing density and axon-to-streamline ratio were reciprocally changed in order to maintain a constant total cerebral WM volume. Since our parameter estimates are based primarily on fibers passing through the callosum, which are longer in general than intrahemispheric fibers, parameter inaccuracies are more likely for short fibers. In order to evaluate the effect of such inaccuracies, we first simulated the effect of assuming that dMRI sensitivity is systematically reduced (and thus axon count underestimated) for shorter fibers. Uniformly doubling the number of axons with lengths <40 mm in this way yields only a 37.5% increase in the total number of interareal axons and because rank order of observations is not altered the median axon counts are unchanged. Conceivably, our parameter estimates are accurate for the longest fibers (which tend to pass through the callosum) but are progressively less accurate for shorter interareal distances. Consequently, we simulated assuming that our packing density and dMRI sensitivity estimates at the longest fiber lengths were as in our base model and then increased the dMRI streamline-to-axon ratio linearly as the fibers got shorter. Axon density was adjusted to maintain WM volume constant. Even with unrealistically large systematic and matched errors in the 2 estimates, median interareal axon count are only modestly increased; see S4 Fig. For example, adjustments resulting in twice the axon density and half the sensitivity of dMRI to axons at short interparcel distances increase the median number of interparcel axons by only approximately 36%. As reviewed below, errors in interareal axon count due to misestimation of axonal packing density are likely to be relatively unbiased with respect to interareal fiber length, and reported measures vary less than a factor of 2. Our simulations indicate that such errors would have only marginal effects on the median number of interareal axons.

In order to demonstrate that the key principles and findings of this report are robust to the details of tractography procedure, we repeated our analysis on the tractography data of Arnatkeviciute and colleagues [15]. These data consist of a 972-participant subset of the HCP cohort and use the same parcellation but a different method to reconstruct the fiber streamlines. These data contain fewer streamlines and the estimated numbers of axons per connection are broadly comparable, being somewhat fewer but within an order of magnitude of our primary estimate. We find 8.4 × 108 total axons and 1.1 × 108 callosal axons per participant on average, with medians of approximately 1,100 and approximately 130 axons for pairwise intra- and interhemispheric connections between cortical areas (S1 Fig), i.e., even more sparse than those calculated from our tractography data. These data confirm that, independent of tractography procedure, cortical areas are sparsely connected.

Discussion

In this study, we estimated the absolute number of axons interconnecting cortical areas by calibrating dMRI-based tractography using the histologically ascertained cross-sectional fiber density of the corpus callosum and found that long-range corticocortical connections are quite sparse. Our method depends on histological estimates of callosal axon packing density and leverages the unique properties of the callosum. It assumes proportionality between the number of axons connecting 2 areas and the number of dMRI tractography streamlines for the areal pair, and it assumes approximate parity between dMRI sensitivity to inter- and intrahemispheric connections. In order to estimate the volume occupied by interparcel corticocortical connections, we make the further assumption that the effective axonal packing density is reasonably uniform across the hemispheric WM.

Although there are few reports of axonal density in the corpus callosum [3,26], they are consistent with each other and with reports of axonal density of intrahemispheric tracts [4]. Our study relies on the data reported by Aboitiz and colleagues [3], because it is the most systematic count of which we are aware. There is a later study, [26], which provides a value only slightly lower, 2.83 × 105 versus 3.7 × 105 axons/mm2 after correction for tissue shrinkage [27]. However, since this later study was primarily a survey of axon diameter with packing density only incidentally recorded, it is conceivable that density values derived from could be small underestimates. Misestimated tissue shrinkage is possible but likely to be <10% and callosal areas were measured with a well-validated and widely used in vivo method [12]. The axon count estimate does not require that the packing densities of the corpus callosum and ipsilateral WM be the same, but rather the lesser assumption that the axon to dMRI streamline ratio be reasonably uniform across the various instances of long-distance corticocortical connectivity. However, if the packing densities of ipsilateral and callosal long-distance connections are also similar, then the total hemispheric WM volume provides an absolute constraint on the number of long-distance connections, and this provides a powerful validation of our estimate.

The literature provides converging evidence that the fiber packing density of WM varies by at most a factor of 2 across the cortex, including the corpus callosum. A histological study of human cortex found only a 7% difference in the axon densities of the callosum versus the superior longitudinal and inferior occipitofrontal fasciculi [26]. Zikopoulos and Barbas [4] found that the cross-sectional packing density of human prefrontal WM is remarkably similar to callosal values with an average of 3.5 × 105 myelinated axons/mm2 after correction for tissue shrinkage and that this varies among prefrontal regions by a less than factor of 2 [5]. In addition, while dMRI-based estimates of axon density and caliber are imperfect, they suggest that axon density varies by less than 2-fold both between major ipsilateral tracts and within each tract along their length [28]. While packing density is not directly equivalent to axon caliber, the 2 are likely inversely related. Axon diameter, as estimated with dMRI, varies by 20% among ipsilateral tracts and by at most a factor of 2.2 among WM voxels, including those of the corpus callosum [29,30]. Overall, distributions of dMRI-derived axon diameter for the callosum [31] and whole cerebrum [30] are similar with the bulk of values between 2.5 and 5 μm. Histological measurements in macaques concur that axon diameters are very similar within the callosal and noncallosal segments of major fasciculi and vary by less than 2-fold across the cortex [32]. Furthermore, even this limited variation in diameter is not systematically dependent on the length of axons but rather on their regions of origin and termination [33].

Concerning dMRI to axon count proportionality, it has been shown that there is a moderate linear correlation between dMRI-traced streamlines and the number of fibers identified with histological tracers connecting cortical regions in macaques [13,14] and a strong correlation in ferrets [34]. Based on these data, Donahue and colleagues [13] concluded that dMRI tractography was capable of quantitively describing corticocortical WM tracts with approximately order of magnitude precision using a high-quality dataset such as the HCP. In line with previous statistical estimates of whole-cortex axon counts based on traditional neuroanatomy [20], the numbers of axons in pairwise connections are probably correct within an order of magnitude. Estimates of this precision are useful as we find that that interareal connectivity derived from dMRI varies over more than 7 orders of magnitude.

While we derive a single dMRI to axon count factor, it is likely that the true conversion ratio varies somewhat among connections due to local microstructural differences other than axon count such as axon caliber, packing density, or myelination. However, the major fasciculi (including the corpus callosum) have similar axon calibers and packing densities, varying by only a factor of approximately 2 across the cortex when examined in humans histologically [4,5,26] or with dMRI [28–30] and histologically in macaques [32]. More generally, packing density is a function of local cellular interactions, especially with oligodendrocytes, and because these are the same in the corpus callosum and intrahemispheric WM, the a priori expectation is that packing density would be similar, as histological data support. Myelination has only a modulatory effect on dMRI-detected anisotropy, with most of the effect derived from axonal membranes [35]. Nevertheless, microstructural variation in dMRI to axon count ratio may be a source of noise in our estimates. Our simulations of misestimation of dMRI to axon ratio and packing density show that these errors only marginally affect estimated axon counts and do not alter our conclusions. Our findings were also similar when we repeated our analysis on an alternative, somewhat sparser dMRI tractography dataset [15], demonstrating that the details of the tractography algorithm do not affect the overall tenor of our results. While the scope of this study is limited to long-range fibers, we note that shorter, more superficial U-fibers are systematically less myelinated and of lesser caliber than their interareal counterparts [5], and, therefore, the procedure outlined here may require modification before being applied to them.

As previously stated, this methodology assumes a reasonable degree of parity in the sensitivity of the dMRI tractography to intra- and interhemispheric fiber tracts. Consistent with this assumption, we found little difference between distance-matched dMRI connectivity for callosal versus ipsilateral connections. If callosal axons were more easily detectable, this would be reflected as an upward displacement of the interhemispheric trace (blue) above the intrahemispheric trace (green) across the entire distance domain in Fig 1C, which is not evident. This parity is perhaps unsurprising because over most of their trajectories, interhemispheric fibers are subjected to the same crossing fiber issues as intrahemispheric. Specifically, the corpus callosum is a distinct tract for only about 15 to 35 mm, but its fibers range in length up to about 300 mm. Thus, the fraction of an interhemispheric tract that resides within the callosum is inversely proportional to its total length. Consequently, if there were enhanced detection of callosal fibers as streamlines by dMRI, one would expect the interhemispheric (blue) trace in Fig 1C to be elevated primarily at short fiber lengths and depressed at long fiber lengths, resulting in a noticeably steeper slope for the interhemispheric than the intrahemispheric trace, which is not observed. These data support the applicability of the scaling factor derived from interhemispheric fibers to intrahemispheric fibers.

The corpus callosum was used to calibrate the estimate because of its unique properties: It has a well-defined cross-sectional area, more than approximately 99% of interhemispheric corticocortical axons are routed through it [3,36], and essentially no fibers leave or enter the tract between the 2 hemispheres. This is in sharp contrast to noncommissural fasciculi. While it may be commonly assumed that within major cortical fasciculi the majority of axons terminate or originate at the ends of the tract and thus carry information along its entire length, an alternative conception is that these large bundles are composed mostly of axons shorter than the total fascicular length which enter and exit the tract at various points. By analogy, the former assumption likens a tract to a tunnel, where all traffic is trans-terminal, whereas the latter conceives of tracts as like interstate highways, where very few vehicles travel the entire route. In a supplementary analysis, we compared these models for the AF/SLF system. The total number of AF/SLF axons was estimated using the tract diameters [21] and packing densities [4] taken from the literature. The number of trans-terminal axons was determined by defining termination field parcels centered on restricted and inclusive definitions of Broca’s and Wernicke’s areas [22]. Depending on the assumptions, only about 1% to 5% of the axons in a middle section of these fasciculi are trans-terminal. These percentages may be overestimates since they assume that all fibers between the posterior and anterior areas travel through the AF/SLF. However, even if these values are a 2-fold underestimate, it suggests that only a small fraction of the axons in the ipsilateral fasciculi are trans-terminal. The evidence indicates that the “highway” model is more apt for the ipsilateral fiber tracts, and this conception is consistent with neural wiring being driven, in large part, by exponential distance rules [8]. This of course, does not apply to the corpus callosum, as there is no interterminal cortex to project into.

Importantly, the reconceptualization of major intrahemispheric tracts as containing few fibers connecting their distant terminals is still consistent with the long and well-established impression from blunt dissection [37] and dMRI orientation maps [38] that the hemispheric WM is largely composed of well-defined long-distance tracts. Indeed, we estimate that approximately 96% of the WM is composed of interareal axons. What these observations suggest is that the major tracts arise from the tendency of axons to grow in alignment with axons that are already present using established mechanisms of adhesion and fasciculation [39]. Thus, axons are free to join tracts at various points, and tend to proceed together (fasciculate), but again are free to leave whenever they approach their own target. In other words, axons are joined in a given tract because they share a direction rather than an origin and destination.

The interareal axon counts we derive here permit other interesting quantitative estimates that may inform models of cortical neurophysiology. For example, the connections between Wernicke’s and Broca’s areas are thought to integrate receptive and expressive aspects of language, but we estimate that there are only approximately 58,000 axons between the core cortical parcels in these regions (parcels 44 and PSL), fewer than 2 for each word in an average university student’s vocabulary [40]. Another example where quantitative appreciation of direct axonal connections may influence neurocognitive models are the hippocampocortical interactions subserving recent memory, which are commonly posited to carry information regarding the contents of the memory trace during memory formation, consolidation, and retrieval. We estimated that areas distant from the hippocampus, notably the dorsolateral prefrontal cortex, may be connected to it by <10 axons/mm2 (Fig 1F), including both efferent and afferent axons, yet hippocampo–prefrontal interactions are considered crucial for contextual recall [41]. We estimated the average neural density in the cortex as approximately 92,300 neurons/mm2 by dividing the 16.34 × 109 cortical neurons (including interneurons) from [17] by the 1.77 × 105 mm2 mean white gray surface area of the HCP cohort used. If the sparse connectivity suggested by our calculations is correct, it implies that hippocampo–dorsolateral prefrontal interactions in memory are likely mediated by polysynaptic pathways.

These constraints encourage consideration of models of cortical function where connections are dense but mainly local, i.e., a small-world network with intense interconnections within modules and sparse projections between them. While this general principle is widely accepted, the scale of the vast gulf in absolute connectivity between local and long-range connections is startling. This network architecture provides for the wide and efficient distribution of information created by local processing within modules [8,9]. A more uniformly connected cortex would require more WM, necessitating a more voluminous cerebrum and the human cortex is near the limit after which an increase in size reduces computational power [6,7]. Functionally, a deep reservoir of weak connections enables a large number of states and eases state transitions [10]. Modeling suggests that long-range covariance and even synchrony can be achieved through activation of multisynaptic pathways rather than direct connections [42,43], and possible signs of these have been observed experimentally in humans [44,45].

While the long-range direct corticocortical axons are few in number, we note that axons are heterogeneous and that these counts are a limited proxy for true interareal connectivity. Axons, especially those connecting architectonically similar regions, may have a disproportionate impact on the flow of information despite their rarity [46–48], by virtue of their morphology (e.g., greater diameter, larger termination fields, greater axonal arborization, or more numerous en passant varicosities) or by molecular synaptic specializations. For example, while only approximately 5% of the synapses to V1 layer 4 come from the lateral geniculate body in the macaque [49], they have an outsized effect on their firing [50]. The importance of rare intermodule connections might also be enhanced if they are focused on a small location within cortical parcels (i.e., the rich club [51]), but this has not been convincingly demonstrated. Last, it is useful to note that these quantitative considerations are radically different in other species, where the smaller number of cortical neurons and shorter interareal distances allow greater connectivity between cortical areas, as well as a larger proportion of subcortical connectivity [7].

Supporting information

S1 Appendix. Extended methods and results.

(PDF)

Click here for additional data file. (236.2KB, pdf)
S1 Fig. Replication results.

Results obtained by repeating the analysis using an alternative tractography dataset [15]. (A) Connectivity matrix of intrahemispheric axon counts, averaged across the 2 hemispheres. Parcels are ordered into 10 functional networks [11]. (B) Histograms showing the distribution of inter- and intrahemispheric pairwise axon counts. Physically adjacent and nonadjacent parcel pair intrahemispheric histograms are stacked. Median connectivity, shown in gray, is approximately 2,500 axons between cortical areas in the same hemisphere and approximately 300 interhemispherically. Parcel pairs with zero axons connecting them are represented by the bars left of the y-axis. (C) dMRI connectivity as a function fiber tract distance. Pairwise values averaged within 15 fiber length bins. Shading shows bootstrapped 95% confidence intervals. (D–F) Axons counts and densities averaged across the 2 hemispheres and visualized on the left fsaverage template cortex [12]. (D) Total axons connecting each parcel to all others. (E) Axons connecting each parcel to all others, normalized by the reference parcel’s area. (F) Axons connecting the hippocampus to the rest of the cortex, normalized by the area of the cortical parcel, shown in log scale. dMRI, diffusion MRI.

(PDF)

Click here for additional data file. (1.2MB, pdf)
S2 Fig. Effects of sex and age on the interhemispheric connectivity.

Each individual’s total number of estimated interhemispheric axons is shown with a marker. The black horizonal bars show the group means and vertical bars the bootstrapped 95% confidence intervals these means. Shading shows a kernel density estimate of the group distributions. Note that while the number of pairwise axons is approximately log normally distributed across areal pairs, it is approximately normally distributed across individuals. The only significant group difference is between the 22 to 15 and 25 to 30 age groups, F1,1064 = 7.646, p = 0.0058. Interactions between sex and age effect were not significant. As we assume a constant fiber density, our estimate the total number of interhemispheric fibers is a linear multiple of the callosal cross-sectional area.

(PDF)

Click here for additional data file. (151.5KB, pdf)
S3 Fig. AF/SLF termination fields.

In order to estimate the fraction of tract axons that travel the entire length of the tract, its termination fields, centered on Broca’s and Wernicke’s areas, were manually defined in terms of HCP-MMP1.0 parcels [16] according to consensus definitions [22]. (A) Conservative definitions where the anterior termination field, in teal, is composed of parcels 44, 45, 6r, IFSa, IFSp, and FOP4 and the posterior termination field, in yellow, is composed of parcels PSL, RI, STV, and PFcm. For this definition, trans-terminal axons account for 0.6% and 0.8% of tract axons in the left and right hemispheres. (B) Liberal definitions in which parcels 47l and p47r were added anteriorly and parcels PF, PFm, and PGi were added posteriorly, resulting in trans-terminal axons accounting for 1.9% and 2.9% of tract axons in the left and right hemispheres. Gray lines indicate the approximate locations at which the tract diameter, used to estimate the total number of tract axons were ascertained [21]. Areas are rendered on the fsaverage template cortex [12]. AF/SLF, arcuate/superior lateral fasciculus; HCP, Human Connectome Project.

(PDF)

Click here for additional data file. (675.3KB, pdf)
S4 Fig. Simulated effect of short axon underestimation on pairwise axon counts.

In order to explore the possibility that dMRI tractography is less sensitive to shorter connections the streamline-to-axon ratio was increased linearly with inverse fiber length using a range of slope parameters. Packing density was assumed to be reciprocally decreased in order to fix a constant total cerebral WM volume. (A) Distributions of intra- and interhemispheric interareal axons counts. Gray histograms show the effect of uniformly halfling the ratio and doubling the assumed packing density. (B) Intrahemispheric and (C) interhemispheric adjustments to the # of pairwise axons as a function of inverse fiber tract length and the resultant increase in median axon count as a function of the adjustments’ slope parameter. At slope = 0, values are unadjusted from the primary analysis. Large adjustments only increase median counts modestly in the context of the log-normal distribution. For example, for intrahemispheric connections (B), at a slope of 0.004, the number of the shortest axons is about doubled (i.e., corresponding to doubling the axon density and halving the sensitivity of dMRI to axons), but the median number of interparcel axons only increases by approximately 36%. dMRI, diffusion MRI; WM, white matter.

(PDF)

Click here for additional data file. (241.9KB, pdf)

Acknowledgments

Data were provided, in part, by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 National Institutes of Health (NIH) Institutes and Centers that support the NIH Blueprint for Neuroscience Research and by the McDonnell Center for Systems Neuroscience at Washington University.

Abbreviations

AF/SLF

arcuate/superior lateral fasciculus

dMRI

diffusion MRI

EM

electron microscopy

HCP

Human Connectome Project

WM

white matter

Data Availability

The processed data used in this study are available at https://doi.org/10.5281/zenodo.6097026. Datafiles are in Matlab v7.3 format. The Human Connectome Project’s raw imaging data and FreeSurfer outputs may be downloaded from https://db.humanconnectome.org.

Funding Statement

This work was supported by the by National Institute of Mental Health grant RF1MH117155 (EH) and National Institute of Neurological Disorders and Stroke grant R01NS109553 (EH). The funders had no role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

  • 1.Geschwind N. Disconnexion syndromes in animals and man. Brain. 1965;88:237–94. doi: 10.1093/brain/88.2.237 [DOI] [PubMed] [Google Scholar]
  • 2.Assaf Y, Johansen-Berg H, Thiebaut de Schotten M. The role of diffusion MRI in neuroscience. NMR Biomed. 2019;32:e3762. doi: 10.1002/nbm.3762 [DOI] [PubMed] [Google Scholar]
  • 3.Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. Brain Res. 1992;598:143–53. doi: 10.1016/0006-8993(92)90178-c [DOI] [PubMed] [Google Scholar]
  • 4.Zikopoulos B, Barbas H. Changes in prefrontal axons may disrupt the network in autism. J Neurosci. 2010;30:14595–609. doi: 10.1523/JNEUROSCI.2257-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Zikopoulos B, García-Cabezas MÁ, Barbas H. Parallel trends in cortical gray and white matter architecture and connections in primates allow fine study of pathways in humans and reveal network disruptions in autism. PLoS Biol. 2018;16:e2004559. doi: 10.1371/journal.pbio.2004559 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Bullmore E, Sporns O. The economy of brain network organization. Nat Rev Neurosci. 2012;13:336–49. doi: 10.1038/nrn3214 [DOI] [PubMed] [Google Scholar]
  • 7.Hofman MA. Evolution of the human brain: when bigger is better. Front Neuroanat. 2014;8:15. doi: 10.3389/fnana.2014.00015 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Markov NT, Ercsey-Ravasz M, Van Essen DC, Knoblauch K, Toroczkai Z, Kennedy H. Cortical high-density counterstream architectures. Science. 2013:1238406–6. doi: 10.1126/science.1238406 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Bassett DS, Bullmore ET. Small-world brain networks revisited. Neuroscience. 2017;23:499–516. doi: 10.1177/1073858416667720 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Buzsáki G, Mizuseki K. The log-dynamic brain: how skewed distributions affect network operations. Nat Rev Neurosci. 2014;15:264–78. doi: 10.1038/nrn3687 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Rosen BQ, Halgren E. A Whole-Cortex Probabilistic Diffusion Tractography Connectome. eNeuro. 2021;8: ENEURO.0416-20.2020. doi: 10.1523/ENEURO.0416-20.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Fischl B. FreeSurfer. Neuroimage. 2012;62:774–81. doi: 10.1016/j.neuroimage.2012.01.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Donahue CJ, Sotiropoulos SN, Jbabdi S, Hernandez-Fernandez M, Behrens TE, Dyrby TB, et al. Using Diffusion Tractography to Predict Cortical Connection Strength and Distance: A Quantitative Comparison with Tracers in the Monkey. J Neurosci. 2016;36:6758–70. doi: 10.1523/JNEUROSCI.0493-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.van den Heuvel MP, de Reus MA, Feldman Barrett L, Scholtens LH, Coopmans FMT, Schmidt R, et al. Comparison of diffusion tractography and tract-tracing measures of connectivity strength in rhesus macaque connectome. Hum Brain Mapp. 2015;36:3064–75. doi: 10.1002/hbm.22828 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Arnatkeviciute A, Fulcher BD, Oldham S, Tiego J, Paquola C, Gerring Z, et al. Genetic influences on hub connectivity of the human connectome. Nat Commun. 2021;12:4237. doi: 10.1038/s41467-021-24306-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, et al. A multi-modal parcellation of human cerebral cortex. Nature. 2016;536:171–8. doi: 10.1038/nature18933 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Azevedo FAC, Carvalho LRB, Grinberg LT, Farfel JM, Ferretti REL, Leite REP, et al. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J Comp Neurol. 2009;513:532–41. doi: 10.1002/cne.21974 [DOI] [PubMed] [Google Scholar]
  • 18.DeFelipe J, Fariñas I. The pyramidal neuron of the cerebral cortex: Morphological and chemical characteristics of the synaptic inputs. Prog Neurobiol. 1992;39:563–607. doi: 10.1016/0301-0082(92)90015-7 [DOI] [PubMed] [Google Scholar]
  • 19.Barbas H, Hilgetag CC, Saha S, Dermon CR, Suski JL. Parallel organization of contralateral and ipsilateral prefrontal cortical projections in the rhesus monkey. BMC Neurosci. 2005;6:32. doi: 10.1186/1471-2202-6-32 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Schüz A, Braitenberg V. The human cortical white matter: quantitative aspects of cortico-cortical long-range connectivity. In: Areas Cortical. 2002. p. 377–85. doi: 19810944 [DOI] [Google Scholar]
  • 21.Yeh F-C. Shape analysis of the human association pathways. Neuroimage. 2020;223:117329. doi: 10.1016/j.neuroimage.2020.117329 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Tremblay P, Dick AS. Broca and Wernicke are dead, or moving past the classic model of language neurobiology. Brain Lang. 2016;162:60–71. doi: 10.1016/j.bandl.2016.08.004 [DOI] [PubMed] [Google Scholar]
  • 23.Xuereb JH, Perry RH, Candy JM, Perry EK, Bonham JR. Nerve cell Loss in the thalamus in Alzheimer’s disease and Parkinson’s disease. Brain. 1991;114:1363–79. doi: 10.1093/brain/114.3.1363 [DOI] [PubMed] [Google Scholar]
  • 24.Arcelli P, Frassoni C, Regondi MC, De Biasi S, Spreafico R. GABAergic neurons in mammalian thalamus: a marker of thalamic complexity? Brain Res Bull. 1997;42:27–37. doi: 10.1016/s0361-9230(96)00107-4 [DOI] [PubMed] [Google Scholar]
  • 25.Avino TA, Barger N, Vargas MV, Carlson EL, Amaral DG, Bauman MD, et al. Neuron numbers increase in the human amygdala from birth to adulthood, but not in autism. Proc Natl Acad Sci U S A. 2018;115:3710–5. doi: 10.1073/pnas.1801912115 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Liewald D, Miller R, Logothetis N, Wagner HJ, Schüz A. Distribution of axon diameters in cortical white matter: an electron-microscopic study on three human brains and a macaque. Biol Cybern. 2014;108:541–57. doi: 10.1007/s00422-014-0626-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Schüz A, Palm G. Density of neurons and synapses in the cerebral cortex of the mouse. J Comp Neurol. 1989;286:442–55. doi: 10.1002/cne.902860404 [DOI] [PubMed] [Google Scholar]
  • 28.De Santis S, Drakesmith M, Bells S, Assaf Y, Jones DK. Why diffusion tensor MRI does well only some of the time: variance and covariance of white matter tissue microstructure attributes in the living human brain. Neuroimage. 2014;89:35–44. doi: 10.1016/j.neuroimage.2013.12.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Huang SY, Tian Q, Fan Q, Witzel T, Wichtmann B, McNab JA, et al. High-gradient diffusion MRI reveals distinct estimates of axon diameter index within different white matter tracts in the in vivo human brain. Brain Struct Funct. 2020;225:1277–91. doi: 10.1007/s00429-019-01961-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Fan Q, Nummenmaa A, Witzel T, Ohringer N, Tian Q, Setsompop K, et al. Axon diameter index estimation independent of fiber orientation distribution using high-gradient diffusion MRI. Neuroimage. 2020;222:117197. doi: 10.1016/j.neuroimage.2020.117197 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Horowitz A, Barazany D, Tavor I, Bernstein M, Yovel G, Assaf Y. In vivo correlation between axon diameter and conduction velocity in the human brain. Brain Struct Funct. 2015;220:1777–88. doi: 10.1007/s00429-014-0871-0 [DOI] [PubMed] [Google Scholar]
  • 32.Tomasi S, Caminiti R, Innocenti GM. Areal differences in diameter and length of corticofugal projections. Cereb Cortex. 2012;22:1463–72. doi: 10.1093/cercor/bhs011 [DOI] [PubMed] [Google Scholar]
  • 33.Innocenti GM, Vercelli A, Caminiti R. The Diameter of Cortical Axons Depends Both on the Area of Origin and Target. Cereb Cortex. 2014;24:2178–88. doi: 10.1093/cercor/bht070 [DOI] [PubMed] [Google Scholar]
  • 34.Delettre C, Messé A, Dell L-A, Foubet O, Heuer K, Larrat B, et al. Comparison between diffusion MRI tractography and histological tract-tracing of cortico-cortical structural connectivity in the ferret brain. Netw Neurosci. 2019;3:1038–50. doi: 10.1162/netn_a_00098 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Beaulieu C. The basis of anisotropic water diffusion in the nervous system–a technical review. NMR Biomed. 2002;15:435–55. doi: 10.1002/nbm.782 [DOI] [PubMed] [Google Scholar]
  • 36.Highley JR, Esiri MM, McDonald B, Roberts HC, Walker MA, Crow TJ. The size and fiber composition of the anterior commissure with respect to gender and schizophrenia. Biol Psychiatry. 1999;45:1120–7. doi: 10.1016/s0006-3223(98)00323-0 [DOI] [PubMed] [Google Scholar]
  • 37.Schmahmann JD, Pandya DN. Cerebral White Matter—Historical Evolution of Facts and Notions Concerning the Organization of the Fiber Pathways of the Brain. J Hist Neurosci. 2007;16:237–67. doi: 10.1080/09647040500495896 [DOI] [PubMed] [Google Scholar]
  • 38.Hagler DJ, Ahmadi ME, Kuperman J, Holland D, McDonald CR, Halgren E, et al. Automated white-matter tractography using a probabilistic diffusion tensor atlas: Application to temporal lobe epilepsy. Hum Brain Mapp. 2009;30:1535–47. doi: 10.1002/hbm.20619 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Spead O, Poulain FE. Trans-axonal signaling in neural circuit wiring. Int J Mol Sci. 2020;21:5170. doi: 10.3390/ijms21145170 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Brysbaert M, Stevens M, Mandera P, Keuleers E. How Many Words Do We Know? Practical Estimates of Vocabulary Size Dependent on Word Definition, the Degree of Language Input and the Participant’s Age. Front Psychol. 2016:1116. doi: 10.3389/fpsyg.2016.01116 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Jin J, Maren S. Prefrontal-Hippocampal Interactions in Memory and Emotion. Front Syst Neurosci. 2015. doi: 10.3389/fnsys.2015.00170 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Bazhenov M, Rulkov NF, Timofeev I. Effect of synaptic connectivity on long-range synchronization of fast cortical oscillations. J Neurophysiol. 2008;100:1562–75. doi: 10.1152/jn.90613.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Vicente R, Gollo LL, Mirasso CR, Fischer I, Pipa G. Dynamical relaying can yield zero time lag neuronal synchrony despite long conduction delays. Proc Natl Acad Sci U S A. 2008;105:17157–62. doi: 10.1073/pnas.0809353105 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Dickey CW, Verzhbinsky IA, Jiang X, Rosen BQ, Kajfez S, Stedelin B, et al. Widespread ripples synchronize human cortical activity during sleep, waking, and memory recall. bioRxiv. 2021; 2021.02.23.432582. doi: 10.1101/2021.02.23.432582 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Mak-McCully RA, Deiss SR, Rosen BQ, Jung KY, Sejnowski TJ, Bastuji H, et al. Synchronization of Isolated Downstates (K-Complexes) May Be Caused by Cortically-Induced Disruption of Thalamic Spindling. PLoS Comput Biol. 2014;10. doi: 10.1371/journal.pcbi.1003855 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Beul SF, Barbas H, Hilgetag CC. A Predictive Structural Model of the Primate Connectome. Sci Rep. 2017;7:1–12. doi: 10.1038/s41598-016-0028-x [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Deco G, Sanz Perl Y, Vuust P, Tagliazucchi E, Kennedy H, Kringelbach ML. Rare long-range cortical connections enhance human information processing. Curr Biol. 2021;31: 4436–48.e5. doi: 10.1016/j.cub.2021.07.064 [DOI] [PubMed] [Google Scholar]
  • 48.Aboitiz F, López J, Montiel J. Long distance communication in the human brain: timing constraints for inter-hemispheric synchrony and the origin of brain lateralization. Biol Res. 2003;36:89–99. doi: 10.4067/s0716-97602003000100007 [DOI] [PubMed] [Google Scholar]
  • 49.Peters A, Payne BR, Budd J. A numerical analysis of the geniculocortical input to striate cortex in the monkey. Cereb Cortex. 1994;4:215–29. doi: 10.1093/cercor/4.3.215 [DOI] [PubMed] [Google Scholar]
  • 50.Chung S, Ferster D. Strength and orientation tuning of the thalamic input to simple cells revealed by electrically evoked cortical suppression. Neuron. 1998;20:1177–89. doi: 10.1016/s0896-6273(00)80498-5 [DOI] [PubMed] [Google Scholar]
  • 51.Van Den Heuvel MP, Sporns O. Rich-club organization of the human connectome. J Neurosci. 2011;31:15775–86. doi: 10.1523/JNEUROSCI.3539-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]

Decision Letter 0

Gabriel Gasque

12 Aug 2021

Dear Dr Rosen,

Thank you for submitting your manuscript entitled "Human cortical areas are sparsely connected: Combining histology with diffusion MRI to estimate the absolute number of axons" for consideration as a Short Report by PLOS Biology.

Your manuscript has now been evaluated by the PLOS Biology editorial staff, as well as by an academic editor with relevant expertise, and I am writing to let you know that we would like to send your submission out for external peer review.

However, before we can send your manuscript to reviewers, we need you to complete your submission by providing the metadata that is required for full assessment. To this end, please login to Editorial Manager where you will find the paper in the 'Submissions Needing Revisions' folder on your homepage. Please click 'Revise Submission' from the Action Links and complete all additional questions in the submission questionnaire.

Please re-submit your manuscript within two working days, i.e. by Aug 16 2021 11:59PM.

Login to Editorial Manager here: https://www.editorialmanager.com/pbiology

During resubmission, you will be invited to opt-in to posting your pre-review manuscript as a bioRxiv preprint. Visit http://journals.plos.org/plosbiology/s/preprints for full details. If you consent to posting your current manuscript as a preprint, please upload a single Preprint PDF when you re-submit.

Once your full submission is complete, your paper will undergo a series of checks in preparation for peer review. Once your manuscript has passed all checks it will be sent out for review.

Given the disruptions resulting from the ongoing COVID-19 pandemic, please expect delays in the editorial process. We apologise in advance for any inconvenience caused and will do our best to minimize impact as far as possible.

Feel free to email us at plosbiology@plos.org if you have any queries relating to your submission.

Kind regards,

Gabriel Gasque

Senior Editor

PLOS Biology

ggasque@plos.org

Decision Letter 1

Gabriel Gasque

16 Sep 2021

Dear Dr Rosen,

Thank you very much for submitting your manuscript "Human cortical areas are sparsely connected: Combining histology with diffusion MRI to estimate the absolute number of axons" for consideration as a Short Report at PLOS Biology. Your manuscript has been evaluated by the PLOS Biology editors, by an Academic Editor with relevant expertise, and by three independent reviewers. Reviewer 2 is Basilis Zikopoulos and reviewer 3 is Almut Schüz.

The reviews of your manuscript are appended below. You will see that the reviewers find the work potentially interesting. However, based on their specific comments and following discussion with the Academic Editor, I regret that we cannot accept the current version of the manuscript for publication. We remain interested in your study and would be willing to consider resubmission of a comprehensively revised version that thoroughly addresses all the reviewers' comments. We cannot make any decision about publication until we have seen the revised manuscript and your response to the reviewers' comments. Your revised manuscript would be sent for further evaluation by the reviewers.

Reviewers 2 and 3 expressed significant enthusiasm about the approach, while reviewer 1 raises several methodological concerns. We think that the request made by reviewers 1 and 2 that the relationships established for the fibers of the human corpus callosum need to be carefully cross validated for other fiber systems, and ideally in animal models where ground truth tractography data are available, would be strictly required for a successful revision. Together with the Academic Editor, we think this point is critical, but may be difficult to address, as it depends on the availability of matched histological and noninvasive diffusion imaging data. However, we do not think that such a cross validation can be postponed to a later study, as one of the reviewers suggested. First, as the reviewers pointed out, projection systems are indeed highly diverse in terms of axonal diameters, myelination, trajectories, etc., and what is true for callosal projections does not necessarily need to hold for short- or long-range corticocortical projections within the hemispheres. Second, if the present paper is published, we expect it to be widely cited and used in many further analyses and modeling; therefore, the numbers presented here need to be reliable. Without these additional analyses, we will not be prepared to move forward with your manuscript.

You will see that in addition there is a long list of specific methodological issues put forward by the three reviewers, but we think you should be able to address most of them through additional analyses or with explicit caveats in an extended discussion. This includes the appropriate scaling of the conversion factor –which is central to this study– that was debated by reviewer 3. As this reviewer states, a scaling of the conversion factor by factor two may not actually alter the principal conclusions of the paper; nonetheless, proper accounting for tissue shrinking of the used literature data is still important.

We appreciate that our requests represent a great deal of extra work and are willing to relax our standard revision time to allow you six months to revise your manuscript.

Please email us (plosbiology@plos.org) if you have any questions or concerns, or would like to request an extension. At this stage, your manuscript remains formally under active consideration at our journal; please notify us by email if you do not intend to submit a revision so that we may end consideration of the manuscript at PLOS Biology.

**IMPORTANT - SUBMITTING YOUR REVISION**

Your revisions should address the specific points made by each reviewer. Please submit the following files along with your revised manuscript:

1. A 'Response to Reviewers' file - this should detail your responses to the editorial requests, present a point-by-point response to all of the reviewers' comments, and indicate the changes made to the manuscript.

*NOTE: In your point by point response to the reviewers, please provide the full context of each review. Do not selectively quote paragraphs or sentences to reply to. The entire set of reviewer comments should be present in full and each specific point should be responded to individually, point by point.

You should also cite any additional relevant literature that has been published since the original submission and mention any additional citations in your response.

2. In addition to a clean copy of the manuscript, please also upload a 'track-changes' version of your manuscript that specifies the edits made. This should be uploaded as a "Related" file type.

*Resubmission Checklist*

When you are ready to resubmit your revised manuscript, please refer to this resubmission checklist: https://plos.io/Biology_Checklist

To submit a revised version of your manuscript, please go to https://www.editorialmanager.com/pbiology/ and log in as an Author. Click the link labelled 'Submissions Needing Revision' where you will find your submission record.

Please make sure to read the following important policies and guidelines while preparing your revision:

*Published Peer Review*

Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out. Please see here for more details:

https://blogs.plos.org/plos/2019/05/plos-journals-now-open-for-published-peer-review/

*PLOS Data Policy*

Please note that as a condition of publication PLOS' data policy (http://journals.plos.org/plosbiology/s/data-availability) requires that you make available all data used to draw the conclusions arrived at in your manuscript. If you have not already done so, you must include any data used in your manuscript either in appropriate repositories, within the body of the manuscript, or as supporting information (N.B. this includes any numerical values that were used to generate graphs, histograms etc.). For an example see here: http://www.plosbiology.org/article/info%3Adoi%2F10.1371%2Fjournal.pbio.1001908#s5

*Blot and Gel Data Policy*

We require the original, uncropped and minimally adjusted images supporting all blot and gel results reported in an article's figures or Supporting Information files. We will require these files before a manuscript can be accepted so please prepare them now, if you have not already uploaded them. Please carefully read our guidelines for how to prepare and upload this data: https://journals.plos.org/plosbiology/s/figures#loc-blot-and-gel-reporting-requirements

*Protocols deposition*

To enhance the reproducibility of your results, we recommend that if applicable you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols

Thank you again for your submission to our journal. We hope that our editorial process has been constructive thus far, and we welcome your feedback at any time. Please don't hesitate to contact us if you have any questions or comments.

Sincerely,

Gabriel Gasque

Senior Editor

PLOS Biology

ggasque@plos.org

*****************************************************

REVIEWS:

Reviewer #1: The authors present a potentially interesting paper that proposes a relationship between probabilistic tractography streamlines and absolute axon counts after having related the data to the prior histological literature, particularly Aboitiz et al., 1992, but also Arcelli et al., 1997 and Liewald et al., 2014. I am not convinced of the authors' claims at this point.

Major Concerns:

1) The authors cite Donahue et al., 2016 Journal of Neuroscience as evidence of a strong relationship between histological and tractography connection strengths. However, their data shows a strong correlation only for the short distance strong connections (see their Figs 4A and 5). Long-distance (e.g., such as the corpus callosum) and weak connections had many discrepancies between tractography and tracers (see Figure 4a). Thus, I am not sure that this citation is good evidence for the authors' point.

2) The authors use a single value for the total number of axons crossing the corpus callosum; however, it is known (e.g., shown in Aboitiz et al., 1992) that there are major differences in axonal density in different parts of the corpus callosum, with larger, lower density axons in the posterior midbody and posterior splenium of the corpus callosum with higher axonal density in the genu and rostrum. If we are to believe that tractography streamlines can be scaled to represent axonal density, we would expect a similar pattern to be present in the tractography data as the axons cross the midsagittal plane of the corpus callosum. Was this indeed the case in the study carried out by the authors? Also, it is not clear to me that the authors have internalized this important point from Aboitiz et al., given the statement "However, the major fasciculi (including the corpus callosum) have similar axon calibers and packing densities," as it would seem that the corpus callosum at least is not a good example of such properties.

3) It was not immediately clear to me how the authors derived axonal values from Arcelli et al., 1997 and Liewald et al., 2014 on a quick review of these papers.

4) I had some concerns about the tractography methods: a) It seems that the authors did not use the surface-based tractography available in probtrackx2 despite the fact that it is more accurate than the 3D volume-based approach (e.g., voxel corners do not stick out into deep white matter) and the 360 cortical areas exist natively on cortical surface meshes. b) More to the point, the authors seem not to have understood how to use the data as released by the HCP for such purposes and produced a convoluted and potentially error prone process for getting the 360 cortical areas aligned with the bedpostX data that requires mapping from the 32k fs_LR space to fsaverage ico5 space, then to the FreeSurfer volume space, and then finally to the bedpostX space. Even if they had chosen not to use surface-based tractography, they could simply have mapped the cortical areas directly from the 32k fs_LR surfaces in the ${StudyFolder}/${Subject}/T1w/fsaverage_LR32k folder to the volume space in the ${StudyFolder}/${Subject}/T1w/Diffusion.bedpostX folder using a single command wb_command -label-to-volume-mapping. A simple question on the HCP-Users mailing list could have clarified the correct approach before large scale computations had been undertaken. c) Similarly, it was not clear how the authors prevented axons from crossing CSF spaces bounded by the pial surface or through the ventricles. Thus, it is not clear that the streamlines being studied here were forced to even cross the corpus callosum.

5) Inadequate consideration of alternative explanations. The authors state key assumptions regarding fiber diameter distributions and the 'conversion ratio' in several places:

a. line 81 "Note that this procedure does not at all depend on the scale of the dMRI metric, requiring only that it be proportional to absolute number of fibers."

b. line 84: "It only requires that the dMRI method return a continuous distribution of connectivity values and have reasonably similar sensitivity to callosal and ipsilateral fiber tracts."

c. Line 153 "While we derive a single dMRI-to-axon count factor, it is possible that the true conversion ratio varies somewhat among connections due to local microstructural differences other than axon count such as axon caliber, packing density, or myelination. However, the major fasciculi (including the corpus callosum) have similar axon calibers and packing densities [12]."

The main experimental support of these statements is the Liewald et al. (2014) EM study reporting roughly similar fiber diameter distributions for two large intrahemispheric tracts compared to the callosum. However, an alternative hypothesis is that short-distance pathways, particularly those connecting sulcal banks with a thin white matter gyral blade in between are mediated by axons having substantially smaller average diameter. Suppose, for example, that there is a two-fold difference in average diameter for axons shorter than ~4 cm (never reaching the major tracts) vs axons that do reach major tracts. Since these account for the majority of intrahemispheric connections (Fig. 1C), this would imply a many-fold greater number of inter-areal axons than the 1.05 x 10^9 value proposed by the authors. In principle, the disparity between short and long distance axonal diameters could be even greater. Hence, without high quality empirical data on axonal diameters as a function of axonal length, it behooves the authors to be far more circumspect in their claims.

6) Issues of scaling. There is an apparent mismatch between the reported tractography-based streamline distances and the physical size of the human brain.

a. Line 112: "The mean fiber tract lengths of connections were taken from our prior dMRI analysis [3]." This mean length is not stated in the present ms and does not appear to have been mentioned in ref 3. Please state what that value is.

b. Line 145 "Specifically, the corpus callosum is a distinct tract for only about 15-35 mm, but its fibers range in length up to about 300 mm". This is consistent with Fig 1C of the current study, which shows a maximum length >300mm for interhemispheric and >250mm for intrahemispheric fiber tract distance. This is very puzzling insofar as the maximum tract length shown in Fig. 7 of Rosen & Halgren 2020 is <180 mm, which is consistent with the known A-P length of human brains. The authors need to explain the apparent discrepancy between the two studies and to provide evidence that these extreme lengths represent plausible anatomical trajectories within the white matter.

7) Confusing wording. Line 145 "Of course, short interhemispheric trajectories are dominated by the callosal segment, and long by the intrahemispheric segments. Generally, the proportion of their trajectories that are within the callosum is roughly proportional to their length. Consequently, if there were enhanced detection of callosal fibers as streamlines by dMRI, the green trace in figure 1C would be expected to be elevated primarily at short fiber lengths, resulting in a noticeably steeper slope for the blue than the green trace, which again is not observed. These data support the applicability of the scaling factor derived from interhemispheric fibers to intrahemispheric fibers."

These statements are confusing - please explain them more clearly.

8) Tractography false positives. Fig 1D: V1 has one of the highest apparent interhemispheric connectivity values among all parcels. Yet in the macaque few if any V1 neurons project contralaterally (Van Essen et al., J. Neuroscience, 1982). Hence, this is a likely example of artifactually large number of false positive connections revealed by tractography.

Reviewer # 2, Basilis Zikopoulos: The paper entitled "Human cortical areas are sparsely connected: Combining histology with diffusion MRI to estimate the absolute number of axons" provides estimates of the number of long-range axons connecting cortical areas within and between hemispheres, using the myelinated fiber density of the corpus callosum, measured histologically, to calibrate whole-cortex diffusion MRI (dMRI) connectivity data. The authors conclude that cortical areas within hemispheres are sparsely connected, with an average of about 2,700 axons, whereas connections of areas between hemispheres involve about five times fewer axons.

This is a very timely, interesting, straight-forward, and well written study and I want to commend the authors on their excellent idea to perform this, much needed work, and analysis. The strengths of this manuscript include (1) the high quality of the data analyzed (from detailed high-resolution histological studies and a large dMRI dataset) and (2) the theoretical framework used to correlate data from sets at multiple scales for the analysis, which is based on the key relationship between structural features and connectivity of the cortex.

The main apparent limitations that will need to be addressed in this or future experimental and theoretical work include the lack of cross-validation of the findings using additional approaches for calibration and combination of the two datasets, the dearth of high-quality, high-resolution histological data, and the low resolution and threshold sensitivity, especially of the dMRI dataset for the detection of short- and some medium-range connections that also include significant numbers of thin, branching, and unmyelinated axons. Despite these limitations, the findings are novel, highly significant, and the manuscript is poised to be an outstanding contribution to our field and of general interest.

Below few comments and suggestions that in my opinion will further increase the value and clarity of the manuscript, strengthen reported findings, and place them in the context of key principles that underlie functional and structural cortical network organization and connectivity:

1. The last sentence in the abstract (lines 59-61) and relevant discussion part (last paragraph, lines 180-188) are somewhat problematic, or a narrow interpretation that can be misinterpreted or misleading and should be modified. The authors' interpretation that the sparseness of long-range connectivity suggests that cortical integration relies mainly on extremely dense local connections and that models that require direct long-range connectivity are somehow challenged by these findings, is not justified, because that would assume that all pathway interactions with different types of excitatory and inhibitory neurons, receptors, distal or proximal dendritic segments, numbers of axon branches and terminals are similar across the cortex. Another equally plausible interpretation based on these findings would be that sparse, in terms of axons, long-range connectivity can still produce major effects postsynaptically, which can integrate information and direct cortical activity, due to specialized interactions with key elements of local circuits. In addition, the last statement of the abstract also suggests that direct transmission of information between cortical areas may be substituted by indirect connections (serial multisynaptic steps of short-range connections) overlooking differences in conduction velocity and variable key interactions with distinct local inhibitory and other microenvironments for each set of pathways. As such, the following statement in the discussion "In such models, cortical locations interact through activation of multi-synaptic pathways rather than direct connections, and the key to connectivity is physiological selection under multiple constraints rather than anatomical projections" wrongly implies that long-range pathways do not lead to connectivity that is physiologically selected under multiple constraints and complex interactions, and should be modified.

2. Methods and Results sections: the authors compare linear regressions of distance-matched streamlines to find no difference between inter- and intrahemispheric connections, as shown in Fig. 1C. Even though this is a previously used approach, it must be noted that although distance is often correlated with the strength and/or presence of connections in some studies, it is well-established that it doesn't accurately and fully capture the relationship between connections, and in many cases, it falls apart when describing long-range connections, especially between frontal and parietal lobes, which together constitute a large chunk of the cortex. On the other hand, structural (dis)similarity between areas is a much better predictor of connectivity strength in most mammals studied, including primates, as shown in several studies using golden-standard tract-tracing and structural imaging approaches (see relevant work by Hilgetag, Barbas, Zikopoulos etc.). As the authors likely know, the Structural Model for Connections, also known as Architectonic Type Principle, was initially proposed by Helen Barbas after multiple tract tracing studies in non-human primates; later, this model was extended to other mammalian species and, since then, predictions based on the Structural Model have been consistently confirmed across all cortical lobes and systems in non-human primates and other species. Therefore, we can assume that the relational principle of the Structural Model obtained from animal research applies to the human cerebral cortex. Based on this large body of work we know that cortical areas tend to be connected primarily with other areas that are relatively similar in type (structure etc.), most of which happen to be nearby, but some are quite distant, as for example in the case of the relatively strong connections between lateral prefrontal and parietal cortices that do not fit and overrun distance models. Therefore, several tract tracing studies in non-human primates show that long-range cortico-cortical connections across lobes are far from weak and do involve lots of axons. See for instance the summary figures (Figures 15 & 16) in Cavada & Goldman-Rakic, 1989 J Comp Neurol 287: 422-445. Cavada and Goldman-Rakic showed that projections from prefrontal areas to posterior parietal areas, which are long range connections, are denser than short-range projections from other areas that are closer to the parietal areas injected by these authors. Actually, dense long-range cortico-cortical connections have been shown for multiple areas across the cerebral cortex of the macaque (see Morecraft et al 2004 J Comp Neurol for posterior cingulate and posterior parietal areas, Morecraft et al 2012 Brain Res Bull for frontal motor and anterior cingulate areas, Morecraft et al 2015 Brain Res Bull for insular and parietal somatosensory areas; Zikopoulos et al 2018 PLOS Biol for prefrontal connections with all other lobes; Cavada et al 2000 Cerebral Cortex for orbital areas; Medalla and Barbas, 2006 for frontal and parietal areas; or Joyce and Barbas, 2018 for especially strong long-range connectivity between anterior cingulate areas in the frontal lobe and area prostriata in the occipital lobe of primates). Based on connectivity patterns in primates, the laminar architecture of the cortex, and the principles of the Structural Model, Zikopoulos et al. in 2018 (PLOS Biol) showed that eulaminate areas have comparatively more and stronger long-range connections than limbic cortices and went one step further to predict that this would also apply to the human cortex, especially since the human cortex includes more eulaminate cortices. These findings from tract tracing studies should be taken into consideration and since this study deals primarily with long-range connectivity it would be appropriate and more accurate to correlate dMRI connectivity with structural features of the connected parcels, if possible. Several recent studies in humans have parcellated the human cortex using relevant structural features that could be used to explore dMRI connectivity relationships. If not possible, at the very least, this should be briefly noted in the Discussion or Appendix.

3. The axon density in the corpus callosum estimated in previous histological studies (Aboitiz et al., or Liewald et al.) was used and was combined with dMRI data to estimate axon numbers in pathways. The second study referenced has also reported axon density in other major long-distance pathways of the brain, including the superior longitudinal fasciculus or the uncinate fasciculus. In addition, several other high-resolution histopathology studies at the light and electron microscopic level have examined and reported axon features and density in the white matter below prefrontal and temporal cortices (e.g. Zikopoulos and colleagues in 2010, or 2018; Liu and Schumann, 2014) that participate in short- or long-range cortical connections. Combined, some of these data on other major white matter pathways in the human brain could be used to calibrate dMRI connectivity data and cross-validate estimates derived from the callosal calibration. Some of these studies also include very relevant information on the relative prevalence of short- vs long-range connections that could support and strengthen the authors' findings.

4. Discussion, page 7, lines 174-178: this statement can be misconstrued and should be reworded. I recommend stating that <5% of cortical pyramidal cells project outside their immediate neighborhood instead of using the word "area". This is because many short-range white matter connections that are below the resolution of dMRI approaches and are not included in this analysis are between adjacent, relatively small areas or neighboring columns within an area. In addition, a study by Zikopoulos et al., 2018 in PLOS Biology has also shown a clear relationship between the number of neurons and the density of white matter pathways in non-human primates and humans and could be relevant to this statement.

5. The authors show that interhemispheric connectivity constitutes on average about 20% of intrahemispheric connectivity (540 vs 2,700 axons). This estimate is in line with similar estimates from Barbas et al., 2005 for non-human primates (estimated that less than 30% of connections are contralateral in rhesus monkeys).

6. Since this study focuses on analysis of long-range connectivity, and uses long-range callosal connections to calibrate dMRI data, it is important to highlight key, relevant differences between long- and short-range connections and U-fibers, something that is now missing. The authors do briefly state that dMRI methods cannot reliably resolve short-range connections, but I think the readers would appreciate a specific comment in the discussion/supplement regarding key features of pathways, other than axon density and number such as: proportion of thin vs thick axons that correlate well with short- and long-range pathways, proportion of myelinated vs unmyelinated axons (more unmyelinated axons in limbic cortical pathways), myelin thickness data for short- vs long-range connections, which is relevant for conduction velocity and function, axonal branching patterns and size of termination fields that may disproportionately amplify the effects of some connections over others, and how some of these features change as we move from the superficial to the deep white matter (e.g. see Liewald et al., 2014; Zikopoulos and Barbas 2010; Zikopoulos et al., 2018; Caminiti and Innocenti, 2009; LaMantia and Rakic 1990; Makris et al., 1999; Rademacher et al., 1992).

7. Reference list (page 10): references 5 and 11 refer to the same study and one of them should be deleted, and in-text citations corrected appropriately. Same for references 12 and 14.

8. S1 Appendix, page 14, lines 359-360: The authors state that they used estimates on thalamocortical connections from histological counts in reference [12] - Arcelli P, Frassoni C, Regondi MC, De Biasi S, Spreafico R. GABAergic neurons in mammalian thalamus: a marker of thalamic complexity? Brain Res Bull. 1997;42: 27-37. As I have carefully read this paper several times I am not sure how the authors got estimates about volume of thalamocortical axons and total axon count (22.6x106) from this study, which only reports local inhibition in the thalamus. Perhaps they meant to cite reference [11] instead - Ji JL, Spronk M, Kulkarni K, Repovš G, Anticevic A, Cole MW. Mapping the human brain's cortical subcortical functional network organization. Neuroimage. 2019;185: 35-57. doi:10.1016/j.neuroimage.2018.10.006. Please clarify and correct, as needed.

Reviewer #3:

Review by Almut Schüz, see attached file

Summary

This is a fascinating paper. It quantifies in an elegant way cortico-cortical connections between distant cortical areas in the human brain. The results are in support of findings which indicate a preponderance of connectivity between closely located areas (Schüz and Braiten- berg, 2002), also in other species (Scannell et al., 1995; Schüz at al., 2006). The study by Rosen and Halgren is outstanding since - in contrast to previous studies – it is able to provide an astonishingly concrete estimate for the median number of axons between distant cortical areas in the human brain.

The study uses the parcellation into 180 areas in each hemisphere by Glasser et al. (2016). This parcellation is based on a combination of neuroanatomical (mainly myelin) and functional features, by way of MRI and fMRI. The number of areas comes close to that of the myeloarchitectonic areas by the Vogt and Vogt school. The present study is based on diffusion MRI data from the database of the Human Connectome Project.

In this paper, the relative connectivity provided by dMRI (number of streamlines) is transformed into absolute numbers of axons. This transformation is based on a comparison with histological data from the literature on the density of axons in the Corpus callosum (Aboitiz et al, 1992). It leads to a conversion factor of 0.87 axons per streamline. The authors assume that the same factor can be applied to both, the Corpus callosum and to the other long range systems via the white matter. This is a reasonable assumption.

Presentation of data:

It would be good to visualize not only the median:

The HCP data contain a family structure with genetic related and unrelatedness and many

other behavioral measures (Van Essen et al., 2012). The data also vary with age (22-36 years). Thus, the number of streamlines (Page 11, Line 292) between cortical areas shows inter- individual variability, affecting axon estimation. It would be essential to visualize a scatter

plot (e.g. for the Corpus callosum) how the spread of the number of axons is depicted in the healthy HCP sample. Are these values in an acceptable range? As tractography relies on coarser spatial resolution, partial volume effects, and may be erroneous due to false- positive/negative estimation of streamlines.

The conversion factor

The conversion factor is the crucial point in this paper. Re-reading Aboitiz’ paper and based on my own histological experience I come to the conclusion that your cobersion factor is at the lower end and is rather around 1.6. This does not invalidate the paper – a factor of 2 is negligible in this kind of statistical neuroanatomy – but it gives an idea of the possible range.

Let me explain. In Line 307 to 313 you describe your approach. In line 308 you say “electron microscopic study”, but it is both light and electron microscopic. The shrinkage factor mentioned in the method’s part of Aboitiz’ paper is only valid for his light microscopic material, embedded in paraffin. He does not mention any shrinkage factor for his electron microscopic material (embedded in Epon), and – according to our own experience – there is hardly any shrinkage in such material. (The volume in our EM-material is about 96% of the original tissue after fixation; Schüz and Palm. 1989).

The number you mention for light microscopy of 1.57x105/mm2 is not mentioned explicitly in

Aboitiz paper as far as I can see, but you probably calculated it from the data given in his table I and corrected it for areal shrinkage. Correct?

Aboitiz estimates that about 20% of fibers were not detected in the light microscope. So we end up with a range of about 1.6x105/mm2 from light microscopy and about 3.8 x 105/mm2 from electron microscopy. The reality is probably somewhere between these values.

This is supported when looking at the total number of axons in the Corpus callosum. Aboitiz estimates 2 x108 fibers. This is twice the number you get when using his light microscopic density of about 1.6x105mm2 and your average areal size. (He does not give an areal size as

far as I can see). This speaks in favour of a density between the LM and EM-data, and it leads to a conversion factor of 1.6 rather than 0.87.

The inverse packing density (area per axon) in line 104 would then be lower, but well within the possible range. The average axonal diameter is below 1 m in most cortico-cortical long- range systems (Liewald et al, 2014).

Some points to be clarified

In the discussion in lines 130 and in line 165 the authors quote Liewald et al. (2014) for an alternative value for packing density in the corpus callosum of 1.23 x 105 /mm2. I cannot find this number in the quoted paper. Did the authors somehow calculate this value from the fiber diameters given there? Or did I overlook something?

Another point: in line 176 the authors quote Azevedo et al. (2009) for a number of 11.5x109 cortical pyramidal cells. I cannot find a number for cortical pyramidal cells in this paper. Did the authors derive this from the total number of cortical neurons mentioned on p.535 (16.34x109 ) and perhaps subtract a percentage of non-pyramidal cells?

Also, in some cases the same paper is quoted under 2 different numbers in the reference list: Liewald et al. under 12 and 14, Aboitiz et al under 5 and 11.

Finally, on line 107 the names Schüz and Braitenberg are misprinted. (And thanks to this quotation I discovered a serious printing error in our own paper: on p.381, first line, it should be 6x109 not 6x103)

References:

Aboitiz at al. (1992), as quoted under [5] and [11]

Glasser et al. (2016), as quoted under [7]

Liewald et al. (2014), as quoted under [12] and [14]

Scannell MP, Blakemore C, Young MP (1995) Analysis of connectivity in the cat cerebral cortex. The J. of Neuroscience 15, 1463-1483

Schüz A., Chaimow D, Liewald D and Dortenmann M (2006) Quantitative Aspects of

Corticocortical Connections: A Tracer Study in the Mouse. Cerebral Cortex October 2006;

16:1474--1486 , doi:10.1093/cercor/bhj085

Schüz and Braitenberg (2002), as quoted under [8]

Schüz A. and Palm G (1989) Density of neurons and synapses in the cerebral cortex of the mouse. The J. Comp. Neurol. 286: 442-455

Glasser, M.F., Coalson, T.S., Robinson, E.C., Hacker, C.D., Harwell, J., Yacoub, E., Ugurbil, K., Andersson, J., Beckmann, C.F., Jenkinson, M., Smith, S.M., Essen, D.C.V., 2016. A

multi-modal parcellation of human cerebral cortex. Nature 536, 171–178. https://doi.org/10.1038/nature18933

Van Essen, D.C., Ugurbil, K., Auerbach, E., Barch, D., Behrens, T.E.J., Bucholz, R., Chang, A., Chen, L., Corbetta, M., Curtiss, S.W., Della Penna, S., Feinberg, D., Glasser, M.F., Harel, N., Heath, A.C., Larson-Prior, L., Marcus, D., Michalareas, G., Moeller, S., Oostenveld, R., Petersen, S.E., Prior, F., Schlaggar, B.L., Smith, S.M., Snyder, A.Z., Xu, J., Yacoub, E., WU- Minn HCP Consortium, 2012. The Human Connectome Project: a data acquisition perspective. NeuroImage 62, 2222–2231. https://doi.org/10.1016/j.neuroimage.2012.02.018

Attachment

Submitted filename: Review on the manuskript Rosen Halgren.pdf

Click here for additional data file. (327.6KB, pdf)

Decision Letter 2

Gabriel Gasque

8 Feb 2022

Dear Dr Rosen,

Thank you for submitting your revised Short Report entitled "Human cortical areas are sparsely connected: Combining histology with diffusion MRI to estimate the absolute number of axons" for publication in PLOS Biology. I have now discussed this new version with the Academic Editor. I am pleased to let you know that we will probably accept this manuscript for publication, provided you satisfactorily address the remaining minor points raised by the Academic Editor, which are included below my signature. Please also make sure to address the following data and other policy-related requests:

1) Title:

We would like to suggest a more direct title that might be more appealing to a broad readership. We recommend: “An estimation of the absolute number of axons indicates that human cortical areas are sparsely connected”

However, we would be happy to work with you on an alternative if you think our suggestion misrepresents your findings.

2) Data:

2.1) Please upload to Zenodo the data for all supporting figures and include a README file that explains how these data were analyzed to generate the plots and graphs displayed in those figures.

2.2) Please also ensure that each figure legend in your manuscript includes information on where the underlying data can be found: https://doi.org/10.5281/zenodo.5204805

3) Peer review history:

We think it would be extremely useful for future readers to make the peer-review history of your manuscript accessible, so they can read and assess your thoughtful answers to the reviewers. You will be offered this option later on during the production process, and we ask that you take it.

As you address these items, please take this last chance to review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the cover letter that accompanies your revised manuscript.

We expect to receive your revised manuscript within two weeks.

To submit your revision, please go to https://www.editorialmanager.com/pbiology/ and log in as an Author. Click the link labelled 'Submissions Needing Revision' to find your submission record. Your revised submission must include the following:

-  a cover letter that should detail your responses to any editorial requests, if applicable, and whether changes have been made to the reference list

-  a Response to Reviewers file that provides a detailed response to the reviewers' comments (if applicable)

-  a track-changes file indicating any changes that you have made to the manuscript. 

NOTE: If Supporting Information files are included with your article, note that these are not copyedited and will be published as they are submitted. Please ensure that these files are legible and of high quality (at least 300 dpi) in an easily accessible file format. For this reason, please be aware that any references listed in an SI file will not be indexed. For more information, see our Supporting Information guidelines:

https://journals.plos.org/plosbiology/s/supporting-information  

*Published Peer Review History*

Please note that you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out. Please see here for more details:

https://blogs.plos.org/plos/2019/05/plos-journals-now-open-for-published-peer-review/

*Early Version*

Please note that an uncorrected proof of your manuscript will be published online ahead of the final version, unless you opted out when submitting your manuscript. If, for any reason, you do not want an earlier version of your manuscript published online, uncheck the box. Should you, your institution's press office or the journal office choose to press release your paper, you will automatically be opted out of early publication. We ask that you notify us as soon as possible if you or your institution is planning to press release the article.

*Protocols deposition*

To enhance the reproducibility of your results, we recommend that if applicable you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols

Please do not hesitate to contact me should you have any questions.

Sincerely,

Gabriel

Gabriel Gasque, Ph.D.,

Senior Editor,

ggasque@plos.org,

PLOS Biology

------------------------------------------------------------------------

Academic Editor's comments:

To reiterate the main point of this paper, the authors compared post-mortem axon density in the human corpus callosum with estimates of callosal streamline density from non-invasive diffusion tractography and found that their calculations suggest that most cortical areas in the human brain are linked by a surprisingly small absolute number of projection neurons. As the authors state, this is a result that will be very widely debated and referenced and may form the basis of a reevaluation of models of cortical activity and function, which currently assume a more massive neuronal communication system. (Metaphorically speaking, right now we assume that the cortex is quite well-connected by a far-reaching multi-lane highway system, when in fact there may exist just a few foodpaths between most areas. Naturally, this change of perspective strongly affects how we understand signalling mechanisms in the brain.) The finding crucially hinges on the inferred conversion factor of streamlines to axons. Therefore, the reviewers and authors were chiefly concerned with getting this conversion factor right. I think the authors have made a reasonable case that, while there are several constraints on the reliability of the conversion, the conversion factor that they derived is largely accurate.

Generally, I think that the authors responded to the reviewers’ comments very thoroughly, and while they did not take up every suggestion, they addressed the essence of the criticism that centered on the correct determination of the conversion factor between DTI streamlines and axons. I do think the authors have done a good job in this respect, reassuring the reviewers that their calculations are at least correct within an order of magnitude. There are still a number of caveats (particularly concerning whether the relations established for the corpus callosum translate also to other fiber systems within each cortical hemisphere), but at least these caveats are explicitly addressed in the manuscript. Moreover, there is a main issue of interpretation of the findings which was brought up by R2, of whether the findings imply that cortical signals only propagate between adjacent areas, or whether long-distance projections may have a functional role after all. These issues will likely be the subject of many studies starting from these findings, and they are more cautiously discussed now.

As a minor point, the authors may find this additional reference useful, which I think further strengthens their case: Delettre et al. 2019, Comparison between diffusion MRI tractography and histological tract-tracing of cortico-cortical structural connectivity in the ferret brain. Netw Neurosci 3(4):1038-1050. doi: 10.1162/netn_a_00098.

Moreover, I was confused by this statement of the authors in their response letter: “…the data in figure 5A indicates that, relative to histological tracing, dMRI tends to underestimate the presence of long-range connections. This implies that long range cortical connectivity may be even sparser than our dMRI-based evidence indicates…” — I think they mean “overestimate”.

Decision Letter 3

Gabriel Gasque

17 Feb 2022

Dear Dr Rosen,

On behalf of my colleagues and the Academic Editor, Claus Hilgetag, I am pleased to say that we can in principle accept your Short Report "An estimation of the absolute number of axons indicates that human cortical areas are sparsely connected" for publication in PLOS Biology, provided you address any remaining formatting and reporting issues. These will be detailed in an email that will follow this letter and that you will usually receive within 2-3 business days, during which time no action is required from you. Please note that we will not be able to formally accept your manuscript and schedule it for publication until you have any requested changes.

Please take a minute to log into Editorial Manager at http://www.editorialmanager.com/pbiology/, click the "Update My Information" link at the top of the page, and update your user information to ensure an efficient production process.

PRESS

We frequently collaborate with press offices. If your institution or institutions have a press office, please notify them about your upcoming paper at this point, to enable them to help maximise its impact. If the press office is planning to promote your findings, we would be grateful if they could coordinate with biologypress@plos.org. If you have not yet opted out of the early version process, we ask that you notify us immediately of any press plans so that we may do so on your behalf.

We also ask that you take this opportunity to read our Embargo Policy regarding the discussion, promotion and media coverage of work that is yet to be published by PLOS. As your manuscript is not yet published, it is bound by the conditions of our Embargo Policy. Please be aware that this policy is in place both to ensure that any press coverage of your article is fully substantiated and to provide a direct link between such coverage and the published work. For full details of our Embargo Policy, please visit http://www.plos.org/about/media-inquiries/embargo-policy/.

Thank you again for choosing PLOS Biology for publication and supporting Open Access publishing. We look forward to publishing your study. 

Sincerely, 

Gabriel Gasque, Ph.D. 

Senior Editor 

PLOS Biology

ggasque@plos.org

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Supplementary Materials

    S1 Appendix. Extended methods and results.

    (PDF)

    Click here for additional data file. (236.2KB, pdf)
    S1 Fig. Replication results.

    Results obtained by repeating the analysis using an alternative tractography dataset [15]. (A) Connectivity matrix of intrahemispheric axon counts, averaged across the 2 hemispheres. Parcels are ordered into 10 functional networks [11]. (B) Histograms showing the distribution of inter- and intrahemispheric pairwise axon counts. Physically adjacent and nonadjacent parcel pair intrahemispheric histograms are stacked. Median connectivity, shown in gray, is approximately 2,500 axons between cortical areas in the same hemisphere and approximately 300 interhemispherically. Parcel pairs with zero axons connecting them are represented by the bars left of the y-axis. (C) dMRI connectivity as a function fiber tract distance. Pairwise values averaged within 15 fiber length bins. Shading shows bootstrapped 95% confidence intervals. (D–F) Axons counts and densities averaged across the 2 hemispheres and visualized on the left fsaverage template cortex [12]. (D) Total axons connecting each parcel to all others. (E) Axons connecting each parcel to all others, normalized by the reference parcel’s area. (F) Axons connecting the hippocampus to the rest of the cortex, normalized by the area of the cortical parcel, shown in log scale. dMRI, diffusion MRI.

    (PDF)

    Click here for additional data file. (1.2MB, pdf)
    S2 Fig. Effects of sex and age on the interhemispheric connectivity.

    Each individual’s total number of estimated interhemispheric axons is shown with a marker. The black horizonal bars show the group means and vertical bars the bootstrapped 95% confidence intervals these means. Shading shows a kernel density estimate of the group distributions. Note that while the number of pairwise axons is approximately log normally distributed across areal pairs, it is approximately normally distributed across individuals. The only significant group difference is between the 22 to 15 and 25 to 30 age groups, F1,1064 = 7.646, p = 0.0058. Interactions between sex and age effect were not significant. As we assume a constant fiber density, our estimate the total number of interhemispheric fibers is a linear multiple of the callosal cross-sectional area.

    (PDF)

    Click here for additional data file. (151.5KB, pdf)
    S3 Fig. AF/SLF termination fields.

    In order to estimate the fraction of tract axons that travel the entire length of the tract, its termination fields, centered on Broca’s and Wernicke’s areas, were manually defined in terms of HCP-MMP1.0 parcels [16] according to consensus definitions [22]. (A) Conservative definitions where the anterior termination field, in teal, is composed of parcels 44, 45, 6r, IFSa, IFSp, and FOP4 and the posterior termination field, in yellow, is composed of parcels PSL, RI, STV, and PFcm. For this definition, trans-terminal axons account for 0.6% and 0.8% of tract axons in the left and right hemispheres. (B) Liberal definitions in which parcels 47l and p47r were added anteriorly and parcels PF, PFm, and PGi were added posteriorly, resulting in trans-terminal axons accounting for 1.9% and 2.9% of tract axons in the left and right hemispheres. Gray lines indicate the approximate locations at which the tract diameter, used to estimate the total number of tract axons were ascertained [21]. Areas are rendered on the fsaverage template cortex [12]. AF/SLF, arcuate/superior lateral fasciculus; HCP, Human Connectome Project.

    (PDF)

    Click here for additional data file. (675.3KB, pdf)
    S4 Fig. Simulated effect of short axon underestimation on pairwise axon counts.

    In order to explore the possibility that dMRI tractography is less sensitive to shorter connections the streamline-to-axon ratio was increased linearly with inverse fiber length using a range of slope parameters. Packing density was assumed to be reciprocally decreased in order to fix a constant total cerebral WM volume. (A) Distributions of intra- and interhemispheric interareal axons counts. Gray histograms show the effect of uniformly halfling the ratio and doubling the assumed packing density. (B) Intrahemispheric and (C) interhemispheric adjustments to the # of pairwise axons as a function of inverse fiber tract length and the resultant increase in median axon count as a function of the adjustments’ slope parameter. At slope = 0, values are unadjusted from the primary analysis. Large adjustments only increase median counts modestly in the context of the log-normal distribution. For example, for intrahemispheric connections (B), at a slope of 0.004, the number of the shortest axons is about doubled (i.e., corresponding to doubling the axon density and halving the sensitivity of dMRI to axons), but the median number of interparcel axons only increases by approximately 36%. dMRI, diffusion MRI; WM, white matter.

    (PDF)

    Click here for additional data file. (241.9KB, pdf)
    Attachment

    Submitted filename: Review on the manuskript Rosen Halgren.pdf

    Click here for additional data file. (327.6KB, pdf)
    Attachment

    Submitted filename: Numbers_respReviewers_7.pdf

    Click here for additional data file. (369KB, pdf)
    Attachment

    Submitted filename: Numbers_PLoSBIO_respReviewers_v8_clean.pdf

    Click here for additional data file. (269.4KB, pdf)

    Data Availability Statement

    The processed data used in this study are available at https://doi.org/10.5281/zenodo.6097026. Datafiles are in Matlab v7.3 format. The Human Connectome Project’s raw imaging data and FreeSurfer outputs may be downloaded from https://db.humanconnectome.org.

    Articles from PLoS Biology are provided here courtesy of PLOS

    RESOURCES