Abstract
Pulsatile insulin secretion by pancreatic beta cells is necessary for tight glucose control in the body. Glycolytic oscillations have been proposed as the mechanism for generating the electrical oscillations underlying pulsatile insulin secretion. The glycolytic enzyme 6-phosphofructokinase-1 (PFK) synthesizes fructose-1,6-bisphosphate (FBP) from fructose-6-phosphate. It has been proposed that the slow electrical and Ca2+ oscillations (periods of 3–5 min) observed in islets result from allosteric feedback activation of PFKM by FBP. Pancreatic beta cells express three PFK isozymes: PFKL, PFKM, and PFKP. A prior study of mice that were engineered to lack PFKM using a gene-trap strategy to delete Pfkm produced a mosaic reduction in global Pfkm expression, but the islets isolated from the mice still exhibited slow Ca2+ oscillations. However, these islets still expressed residual PFKM protein. Thus, to more fully test the hypothesis that beta cell PFKM is responsible for slow islet oscillations, we made a beta-cell-specific knockout mouse that completely lacked PFKM. While PFKM deletion resulted in subtle metabolic changes in vivo, islets that were isolated from these mice continued to exhibit slow oscillations in electrical activity, beta cell Ca2+ concentrations, and glycolysis, as measured using PKAR, an FBP reporter/biosensor. Furthermore, simulations obtained with a mathematical model of beta cell activity shows that slow oscillations can persist despite PFKM loss provided that one of the other PFK isoforms, such as PFKP, is present, even if its level of expression is unchanged. Thus, while we believe that PFKM may be the main regulator of slow oscillations in wild-type islets, PFKP can provide functional redundancy. Our model also suggests that PFKM likely dominates, in vivo, because it outcompetes PFKP with its higher FBP affinity and lower ATP affinity. We thus propose that isoform redundancy may rescue key physiological processes of the beta cell in the absence of certain critical genes.
Significance
Pancreatic beta cells ( cells) secrete insulin in pulses, reflecting bursting electrical activity and subsequent oscillations in the intracellular Ca2+. It has been hypothesized that these events are generated by intrinsic glycolytic oscillations. We investigated the role of the muscle isoform of the glycolytic enzyme phosphofructokinase (PFKM) in the oscillatory activity of cells. PFKM is subjected to allosteric regulation conducive to glycolytic oscillations and has been previously shown to dominate other PFK isoforms in total enzymatic activity in situ. We show that -cell-specific depletion of Pfkm in mice does not affect the slow electrical bursting, Ca2+ oscillations, or glycolytic oscillations of islets ex vivo. Mathematical modeling provides an explanation for these results based on compensation by existing PFK isoforms of cells.
Introduction
In both human and mouse, pancreatic islets secrete insulin in a pulsatile fashion, and this pulsatility is lost in type 2 diabetes, thus reflecting its importance in the regulation of blood glucose (1). Pulsatile insulin release is necessary for the efficacious action of insulin without provoking insulin resistance in its target tissues, which include liver, fat, and skeletal muscle (2).
In isolation, mouse islets are capable of robust oscillations over a range of periods from less than 1 min (e.g., 15 s) to 3–5 min (3). While the faster oscillations are likely mediated by interactions between ion channels and sustained by increases in ATP/ADP triggered by glucose metabolism (4), the origin of the slower oscillations has been more elusive. An interesting and compelling early hypothesis for their generation is that they are triggered by slow oscillations in ATP/ADP due to intrinsic glycolytic oscillations in beta cells ( cells). Tornheim and associates proposed that the glycolytic enzyme phosphofructokinase, specifically its muscle isoform (PFKM), was responsible. This conjecture was based on the fact that autocatalytic activity of this enzyme wherein its product, fructose-1,6-bisphosphate (FBP), provides positive feedback to PFKM in an allosteric manner and that the accelerated depletion of its substrate, fructose-6-phosphate (F6P), provides negative feedback (5,6). They also demonstrated that PFKM activity dominates that of the other isoforms in cells (5), even though later studies (including studies using RNA sequencing) reported similar levels of expression of M- and P-type isoforms (7, 8, 9) or even more P than M (10); most all found that L is the least-expressed isoform. Mathematical modeling of this process (11) was incorporated into two previous models from our group, the dual oscillator model (4) and, more recently, the integrated oscillator model (12,13). While both models are capable of accounting well for the oscillations observed experimentally in mouse islets, several issues remained unclear, prompting the current investigation.
To test the hypothesis that slow oscillations are driven by glycolytic oscillations mediated by PFKM, Richard et al. (8) made a whole-body mouse model using a gene trap to knock down PFKM. They found that reducing PFKM did not abolish or even significantly change the oscillatory properties of Ca2+ or insulin oscillations. However, PFKM expression was not completely abolished by this approach, raising the possibility that residual PFKM protein was sufficient to support oscillatory activity. In addition, this knockdown approach was not cell specific, meaning that the contributions of other tissues could not be ruled out.
To critically revisit this issue, we constructed a mouse using contemporary genetic approaches to delete PFKM specifically and completely in cells, which we refer to as -PFKM-knockout (KO) mice. To further improve on the earlier study, we not only measured free Ca2+ oscillations with fura-2 and electrical oscillations using patch clamp but directly tested for changes in glycolytic oscillations using a fluorescent resonance energy transfer probe of glycolytic activity of our own design, the pyruvate kinase activity reporter (PKAR), which monitors the FBP level in the cell (14). We report here that the electrical activity, the slow oscillations in islet free Ca2+, and the FBP level remained largely undisturbed in the islets of the KO mice in which PFKM was completely knocked out in cells, and, consequently, the metabolic phenotype of the animals was also largely unaffected, although some small changes were observed. These results indicate that other PFK isoforms (PFKP or PFKL) provide the FBP needed for glucose metabolism in cells. Indeed, it is well established that mouse islets contain multiple PFK isoforms (5). The question then becomes, can a non-M-type PFK isoform take over the role played by PFKM in generating oscillations in cell activity? These other isoforms have a lower affinity for the allosteric activator FBP and a higher affinity for the inhibitor ATP (5). Could a PFK enzyme having these properties sustain oscillations driven by oscillations in ATP, as has been proposed for PFKM?
In the second part of our study, we use the Integrated Oscillator Model (IOM) mathematical model to show that when PFKM is absent, a non-PFKM isoform (which we refer to for specificity as PFKP, though PFKL could work as well) can assume the role of PFKM quite successfully. That is, with a model that incorporates both PFKM and PFKP, the activity of the former dominates under normal conditions by virtue of the increased activity, not by the increased expression of PFKM. If PFKM is removed, however, PFKP takes over the role of PFKM and provides the FBP necessary for sustaining metabolic oscillations. These results thus support the hypothesis that while PFKM likely dominates the other isoforms in ATP production necessary for slow oscillations in wild-type animals, the other isoforms are able to supply an alternative pathway when PFKM is disabled.
Materials and methods
Mathematical model
We used a modified version of the IOM to investigate the contribution of different PFK isoforms to the generation of cell oscillatory activity. The model is described in detail in the Supporting material. The differential equations were integrated numerically using MATLAB v.2020b (The MathWorks, Natick, MA), and the computer code can be downloaded from https://www.math.fsu.edu/∼bertram/software/islet/.
The basic model for PFK activity that we employed was developed by Smolen (11). We modified this model, which includes only one PFK isoform, to account for a second PFK isoform. This isoform, which could be either the liver (PFKL) or platelet (PFKP) type, has a lower affinity for FBP (15) and a higher affinity for ATP (16,17) than PFKM. Due to the similar affinities of PFKL and PFKP, we included only one of the non-PFKM enzymes, PFKP.
In our model, the total flux through the PFK reaction, , is the sum of the contributions of each of the two isoforms (PFKM and PFKP):
| (1) |
where and are portions of flux mediated by PFKM and PFKP, respectively. Each component , where I can be M or P, is described by
| (2) |
where the indices i, j, k, and l take on values of 0 and 1, and the maximum rate and weights are isoform specific. The weights are given by
| (3) |
The weights of the two isoforms differ only in their affinities for FBP and ATP. In Equation (3), these affinities are represented by the parameters and , which identify the FBP and ATP dissociation constants, respectively. We therefore set to reflect the lower affinity of PFKP for FBP than PFKM, and to account for the higher affinity for ATP of PFKP than PFKM. The parameter values are shown in Table 1.
Table 1.
Parameters used for the PFK subsystem of the model
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 2 μM | |||||
| 5×104 μM2 | |||||
| 1,000 μM2 | |||||
| 100 μM2 | |||||
| 0.02 |
The knockout of PFKM was simulated by decreasing the maximum rate through the PFK reaction mediated by the M-type isoform, , from 0.01 μM ms–1 (baseline value) to 0 μM ms–1, while was unchanged.
Molecular biology
Construction of -cell-specific PFKM-null mice
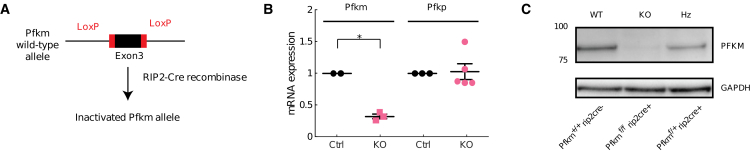
CRISPR-Cas9 was used to identify a suitable target for Cas9 endonuclease by submitting a genomic Pfkm DNA sequence to an algorithm (http://www.crispor.tefor.net; (18)). Single-guide RNAs (sgRNAs) for Cas9 targets were obtained from Synthego.com (19), and recombinant Cas9 endonuclease was obtained from MilliporeSigma (20). Mouse zygotes microinjected with Cas9/sgRNA ribonucleoprotein complexes identified a sgRNA to cleave exon 3 of Pfkm. DNA from blastocysts was subjected to PCR and DNA sequencing to identify small insertions/deletions at Cas9/sgRNA cut sites (21), and a single-stranded DNA donor replaced the critical exon with a floxed exon (22,23). Premature termination codons introduced using this approach have been shown to block protein production (24,25). Ribonucleoprotein and single-stranded DNA donors were microinjected into mouse zygotes (50 ng/μL Cas9 protein, 30 ng/μL sgRNA, 10 ng/μL single-stranded DNA donor) as described (26). Surviving zygotes were then transferred to pseudopregnant females. Potential G0 founder pups were screened for floxed Pfkm using PCR (21,27, 28, 29). G0 founders carrying floxed Pfkm were mated to wild-type mice, and the resulting G1 pups were screened for floxed Pfkm transmission. The sequences of G1 pups were determined by the cloning of genomic DNA flanking the insertion site (29). A floxed Pfkm mouse line derived from independent founders was crossed with RIP2-cre (expressing rat insulin promoter 2) mice to generate -cell-specific Pfkm nulls. Islets isolated from these mice had selective loss of PFKM mRNA and protein, compared with Cre-positive wild-type PFK mice, as shown by RT-PCR and western blotting, respectively.
Gene expression analysis
Total RNA was extracted from isolated islets using miRNeasy micro kit and treated with DNase I according to the manufacturer's instructions (Qiagen). cDNA was synthesized using High-Capacity cDNA Reverse Transcription Kit (Thermo Fisher). Quantitative real-time RT-PCR was performed on a StepOnePlus System (Applied biosystem) using TaqMan Universal PCR Master Mix (Thermo Fisher). Each sample was run in duplicates, and the gene expression was calculated using the change in threshold method with TATA-box binding protein as an internal control. The TaqMan gene expression probes used in the study are summarized in Table S1. Genotyping was done on a regular basis by sending tail samples to a commercial lab (Transnetyx, Cordova, TN).
Islet preparation
Islets were isolated from 3- to 4-month-old mice using collagenase injection using an established protocol (30). The animal protocol used was approved by the University of Michigan Committee on the Use and Care of Animals. Islets were handpicked into saline and then transferred into culture media consisting of RPMI1640 supplemented with FBS (10%), glutamine, and pen/strep. Islets were kept in culture overnight in an incubator at 37°C.
Live cell imaging methods
Adenoviruses were used to express the PKAR fluorescent resonance energy transfer biosensor in pancreatic islet cells under control of the rat insulin promoter as in (30). Islets were placed in a glass-bottomed chamber (54 mL volume) (Warner Instruments, Hamden, CT) on a model no. IX71 inverted microscope (Olympus, Melville, NY) equipped with a 20×/0.75 numeral aperture objective (Nikon Instruments, Melville, NY). The chamber was perfused at 0.3 mL/min, and temperature was maintained at 33°C using inline solution and chamber heaters (Warner Instruments). Excitation was provided by a TILL Polychrome V monochromator set to 10% output. Excitation (x) or emission (m) filters (ET type; Chroma Technology, Bellows Falls, VT) were used in combination with an FF444/521/608-Di01 dichroic (Semrock, Lake Forest, IL) as follows: 430/24x, 470/24 m, and 535/30 m (430x – R535m/470 m). Fluorescence emission was collected with a QuantEM:512SC camera (PhotoMetrics, Tucson, AZ) or an ORCA-Flash4.0 V2 Digital CMOS camera (Hamamatsu, Skokie, IL) at 0.125–0.2 Hz. A single region of interest was used to quantify the average response of individual cells using MetaMorph (Molecular Devices, San Jose, CA) software.
Ca2+ measurements
Islets were loaded with fura-2/AM (2.5 μM) for 45 min in medium containing 5 mM glucose prior to imaging. Islets were then transferred to a 1 mL perfusion chamber containing 5 mM glucose imaging buffer for 6 min, followed by 10–30 min perfusion with this solution at approximately 1 mL/min. Imaging buffer contained (in mM) 140 NaCl, 3CaCl2, 5 KCl, 2 MgCl2, 10 HEPES, and 5 glucose. Ratiometric fura-2 imaging was carried out using 340/380 nm excitation and collecting 502 nm emission, as previously described (30).The fluorescence data were acquired using Metafluor, with a single region of interest used to quantify the average response of individual islets.
Electrophysiology
Patch pipettes were pulled from filament-containing borosilicate glass capillaries (WPI Instruments) using a Sutter P-97 puller (Sutter Instruments, Novato, CA) and had resistances of 4–6 M when filled with solution containing an internal buffer containing (in mM) 28.4 K2SO4, 63.7 KCl, 11.8 NaCl, 1 MgCl2, 20.8 HEPES, and 0.5 EGTA at pH 7.2. Electrodes were then backfilled with the same solution but containing amphotericin B at 0.36 mg/mL to allow membrane perforation. Islets were transferred from culture dishes into a 0.5 mL recording chamber. Solutions held at 32°C–34°C were driven through the bath by a gravity system at a rate of 1 mL/min. Islets were visualized using an inverted microscope (Olympus IX50). Pipette seals obtained were >2 G. Perforation was judged to be successful when the series resistance decreased to a steady-state level and the membrane capacitance increased. Recordings were made using an extracellular solution containing (in mM) 140 NaCl, 3 CaCl2, 5 KCl, 2 MgCl2, 10 HEPES, and 11.1 or 2.8 glucose. cells were identified by their lack of activity in 2.8 mM glucose and by the appearance of regular electrical bursting in external solution containing 11.1 mM glucose. Drugs were dissolved directly into saline solution daily using DMSO stocks; the final concentration of DMSO used was always <0.1%.
One cell in each intact islet was typically patched. After the perforated patch configuration in voltage clamp mode was established, membrane potential was recorded in the current clamp mode.
RT-PCR
Total RNA was extracted from islets using the RNeasy Mini Kit (Qiagen, Ann Arbor, MI) according to the manufacturer's instructions. Total inslet RNA (0.4 μg) was reverse transcribed using Superscript RT II. Real-time experiments were carried out using an SYBR green PCR master mix (Applied Biosystems) with the primers shown in Table S1. Raw threshold-cycle values were obtained using Step One software, and mean threshold-cycle values were calculated from triplicate PCR reactions for each sample. Data were presented as RQ values (2-DD threshold-cycle), with expression presented relative to an endogenous control, HPRT1.
Western blotting
Islets were handpicked in ice-cold PBS immediately after isolation and gently spun to remove the supernatant. Next, islets were lysed in radioimmunoprecipitation assay lysis buffer supplemented with total protease inhibitor cocktail and stored at -80°C. Next, islet lysate was prepared by passing through a 30G needle. Protein concentration was determined using BCA reagent kit. Next, 25 μg protein lysate was mixed with loading buffer and boiled at 70°C for 10 min and separated by electrophoresis on NuPAGE 4%–12%, Bis-Tris mini gels. Next, proteins from the gels were transferred on nitrocellulose membrane (iBlot2 transfer stacks) using iBlot 2 Gel Transfer Device with a preset 7 min transfer protocol. Next, the membrane was incubated in in 5% BSA in TBS tween 20 (TBST) 0.1% for the blocking of non-specific epitopes. Next, PFKM (1:1,000 in TBST 0.1%) isoform and GAPDH (Rb 1:10,000 in 5% BSA in TBST 0.1%) primary antibodies were used overnight at 4°C. The primary antibodies were probed with secondary rabbit HRP (1:5,000 5% BSA TBST 0.1%) by incubation at room temperature for 1 h. HRP signals was detected by incubating membranes in SuperSignal West Femto Chemiluminescent Substrate for 5 min at room temperature, and membranes were subsequently imaged on ChemiDoc System (BioRad). The protein ladder was used to locate protein on the membrane. Islets were collected from 10 control and five animals.
Chemicals and reagents
Gels (Thermo Fisher Scientific, cat. no. NP0321PK2), RIPA (Boston Bioproduct, cat. no. BP-115), iBlot transfer stack nitrocellulose membrane (Invitrogen, cat. no. IB23002), PFKM (Invitrogen; #PA5-29336), GAPDH (CST; G9545), protease inhibitor (CST, cat#5872), Rb HRP (Invitrogen, cat. no. 7074P2), protein ladder (BioRad, cat. no. 1610377), SuperSignal West Femto Chemiluminescent Substrate (Thermo Fisher Scientific, cat. no. 62237), iBlot2 transfer stacks (Thermo Fisher Scientific, #IB23002), and BCA protein assay kit (Thermo Fisher Scientific, cat. no. 23225).
Metabolic measurements and data analysis
Whole animal measurements were made by the University of Michigan Animal Phenotyping Core. For intraperitoneal glucose tolerance tests (IPGTTs), mice were fasted for 5 h, given 1.25 g/kg glucose intraperitoneally, and tail-vein blood was sampled before and then 0, 5, 15, 30, 60, or 120 min after injection. Blood glucose was measured using a glucometer (Accucheck, Roche) and plasma insulin using ELISA (Millipore). Tail-vein blood was sampled before and then 0, 15, 30, 45, 60, 75, and 90 min after injection of glucose.
Analysis of membrane potential and live cell imaging data
Quantitative analysis of membrane potential, islet free Ca2+, and PKAR oscillations was performed using MATLAB to measure the oscillation period and plateau fraction. For membrane potential and free Ca2+, traces were linearly detrended within time intervals corresponding to a fixed glucose level then lightly low-pass filtered (Savitzky-Golay filter, cutoff period of ∼45–60 s). Oscillation periods were detected as repeated crossings of a threshold value of 55% of the trace amplitude. Plateau fraction was recorded as the time between the beginning of a period and the subsequent time when the trace dropped below 45% of trace amplitude. The mean period and plateau fraction of all oscillations at each applied glucose level were then computed.
For PKAR recordings, traces corresponding to individual cells were first normalized to deviations from the trace mean value, . Traces were then detrended using a low-pass filtered trend line (Savitzky-Golay filter, cutoff period of ∼15 min), and traces from cells corresponding to the same islet were averaged. The islet-averaged traces were then low-pass filtered (Savitzky-Golay filter, cutoff period of ∼2 min), and oscillation properties were detected as described above.
Statistics were done with R (v.4.0.3) and MATLAB. Repeated measures ANOVA was done with R command aov, followed by t test. Linear mixed effect models were fit with the R commands lm and lmer to assess the dependence of the oscillation period and plateau fraction on PFKM KO status, sex, and glucose concentration. Details of those results are in Supporting material.
Results
Oscillations persist in islets from -PFKM-KO mice
Mouse islets have been previously shown to express PFKP, L, and M isoforms (5,8). As shown diagrammatically in Fig. 1 A, exon 3 of Pfkm was floxed using CRISPR-Cas9, and the resulting progeny were crossed with RIP2-cre mice to generate -cell-specific Pfkm-null mice. Islets from Pfkm-null mice (KO) show the depletion of Pfkm transcripts compared with islets from littermate controls. Conversely, we found no statistically significant difference in Pfkp mRNA between islets from controls or Pfkm-null mice (Fig. 1 B). Western blot analysis done with a PFKM-specific antibody (Fig. 1 C) confirmed a loss of PFKM protein in the KO mice, whereas reduced protein was present in islets from heterozygotes. Taken together, our -PFKM-null mice exhibit -cells-specific depletion of PFKM and are an appropriate model to investigate the role of PFKM in generating glycolytic oscillation (8).
Figure 1.
Creation of beta cell specific PFKM null line. -PFKM-KO mice were generated using CRISPR-Cas9 to flox exon 3 of the Pfkm gene (A). Employing this method, we were able to selectively delete the Pfkm mRNA transcript in KO mouse islets, while no statistically significant difference in Pfkp mRNA was observed between wild-type controls and the KO islets (B). Western blot analysis done using a PFKM-specific antibody confirmed the loss of the PFKM protein in the KO islets, while reduced PFKM protein was evident in islets from heterozygous mice (C). To see this figure in color, go online.
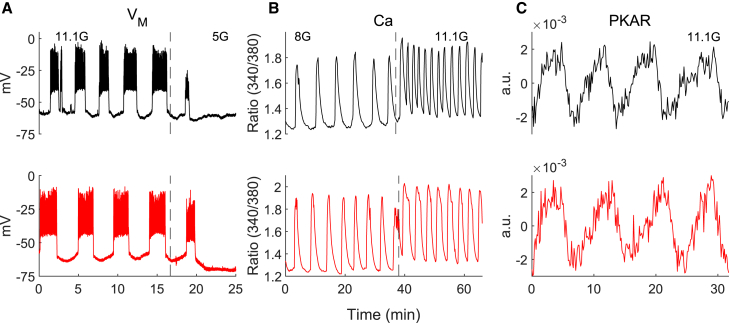
To test whether the loss of PFKM in cells altered the oscillatory properties of the islet, as has been previously predicted (6), we used perforated patch clamp to record oscillations of islet membrane potential, fura-2 to monitor islet Ca2+ and PKAR to dynamically monitor FBP in both KO and wild-type mouse islets. As shown in Fig. 2, there were no obvious changes in the oscillations of electrical activity (Fig. 2 A, black traces correspond to wild-type [WT] and red to KO) or Ca2+ (Fig. 2 B), which are typically observed in response to glucose concentrations >∼7 mM. Furthermore, reducing the glucose concentration from 11.1 to 5 mM promptly shut off the oscillations, as is typically seen in normal islets, and increasing glucose from 8 to 11.1 mM led to similar changes in the oscillations.
Figure 2.
-PFKM-KO islets exhibit typical oscillations. (A–C) Representative examples of oscillations at several glucose levels in control (black) and -PFKM-KO islets for membrane potential (VM, A), intracellular Ca2+ concentration (Ca, B), and normalized, detrended PKAR fluorescent resonance energy transfer ratio (C). Traces are representative of 21 VM recordings, 10 Ca recordings, and 23 PKAR recordings. Control traces shown were from Cre+ control mice. To see this figure in color, go online.
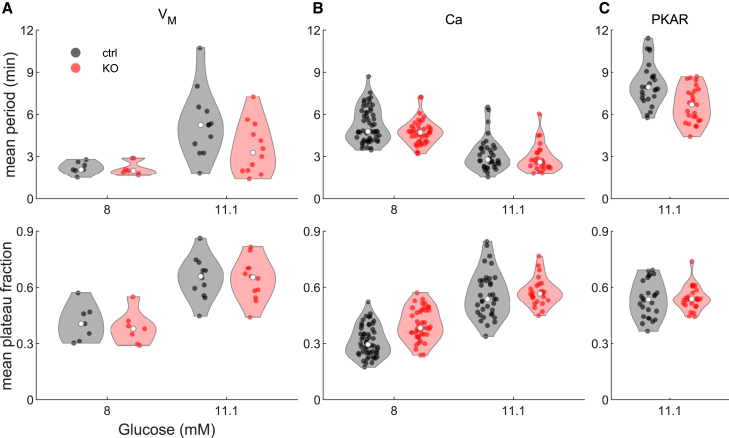
Finding that loss of PFKM did not strongly affect islet oscillations suggested that there may be redundant mechanisms regulating glycolytic oscillations and concomitant insulin release that are revealed by the absence of PFKM. To address this as well as further improve on the earlier study, we next examined the glycolytic oscillations of WT and KO islet cells using PKAR, a probe of our own design that was described previously (14). Quantitative analysis of the periods and plateau fractions of islet membrane potential recordings from a total of 21 islets from 14 mice, Ca2+ recordings of 112 islets from 6 mice (10 recordings), and PKAR recordings of 52 islets from 14 mice (23 recordings) was carried out (as described in Table S7). Fig. 3 summarizes this analysis, showing that -PFKM-KO islets (red) had oscillations with similar periods and plateau fractions to control islets (black) for membrane potential (Fig. 3 A), Ca2+ (Fig. 3 B), and PKAR oscillations (Fig. 3 C) at different glucose levels. To statistically analyze islet oscillations across different groups, we needed to account for the hierarchical nature of islet measurements at three levels: islets were exposed to one or more glucose levels (repeated measures), batches of one or more islets from an animal were recorded in each recording, and one or more recordings were made from each animal. We addressed this using linear mixed effects modeling of oscillation properties as a function of glucose stimulus, PFKM status, and sex, with random effects for islet, recording, and mouse (see Tables S4–S6 and Fig. S1 for details). This analysis indicated that there was a significant dependence on glucose concentration, as expected. However, only a slightly smaller period was detected in the -PFKM-KO islets, which was close to, but did not achieve, statistical significance at the p = 0.05 level (VM: –1.12 min, p = 0.067; Ca: –0.71 min, p = 0.15; PKAR: –1.44 min, p = 0.053). Plateau fraction effect sizes were very small and not different statistically between -PFKM-KO and control (VM: –0.02, p = 0.58; Ca2+: 0.0, p = 0.98; PKAR: –0.02, p = 0.40). These results are consistent across all three recording types. We did note that the islets of male mice tended to have slightly higher oscillation periods (∼0.63–0.72 min higher than control), but this was not significant in any assay. Plateau fraction was slightly higher in islets from male animals for VM and Ca recordings (VM: +0.13, p = 0.046; Ca: +0.13, p = 0.088) but was slightly lower in the PKAR recordings (–0.06, p = 0.029). These results show that PFKM is clearly not needed to produce slow oscillations. It should be noted that the differences in oscillation periods reported here, especially between VM or Ca2+ oscillations and those of PKAR, reflect the differing experimental conditions used, as viral induction of PKAR required adenoviral transduction followed by 3 days in culture (14). In contrast to the results reported here, when simultaneous recordings of VM and PKAR were made, the periods measured were strikingly similar (30).
Figure 3.
Comparison of oscillation period and plateau fraction between -PFKM-KO and control islets. (A–C) Violin plots showing mean oscillation period (top panels) and plateau fraction (bottom panels) for islets exposed to specific glucose levels: 8 and 11.1 mM glucose for membrane potential (A) and Ca2+ concentration (B) or at 11.1 mM glucose for PKAR (C). White dots indicate the median across all islets. All -PFKM-KO islets were oscillated at 8 and 11.1 mM glucose. Linear mixed effects modeling (see Materials and methods and Supporting material) found that the modest reduction in period in -PFKM-KO compared with control oscillations was close to, but did not achieve, statistical significance at the p = 0.05 level. The differences in plateau fraction were not significant. Control islets consisted of mostly +/+ Cre + islets (59%), with the remaining from WT or fl/fl Cre − mice. As no differences were noted among the controls, the results were pooled. To see this figure in color, go online.
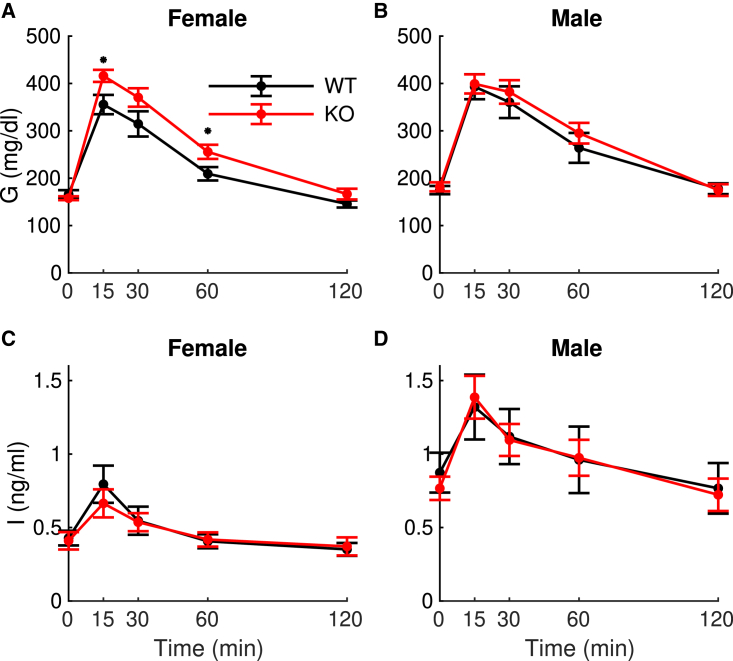
To test whether the very small differences we observed in the properties of isolated islets were reflected in the in vivo metabolic profile of WT (n = 21; 11 female, 10 male) and null mice (n = 25; 15 female, 10 male), we conducted IPGTTs on the mice. Female mice with the -cell-specific PFKM deletion showed a slight increase in glucose but no difference in their insulin (Fig. 4), suggesting a mild impairment in insulin secretion. We tested this using the homeostasis model assessment of β-cell function (31) and the insulinogenic index (increment of insulin/increment of glucose during the first 30 min of the IPGTT) (32), and, though both measures of beta-cell function were numerically smaller in KO mice, neither was statistically significant (homeostasis model assessment of β-cell function: 2.35 ± 1.7 control versus 2.00 ± 1.2 KO, p = 0.4; insulinogenic index: 0.0024 ± 0.004 control versus 0.0020 ± 0.001 KO, p = 0.5).
Figure 4.
In vivo metabolic measurements using intraperitoneal glucose tolerance tests. (A–D) Female mice (A and B), male mice (C and D), glucose (A and C), and insulin (B and D). The only significant difference is glucose for the females (p = 0.04) by repeated measures ANOVA. The values at t = 15 min and t = 60 min are different by unpaired t test (p < 0.05). To see this figure in color, go online.
The overall increase in glucose was significant (p = 0.04), as assessed by repeated measures ANOVA, and the glucose values taken at the 15 and 60 min time points were significantly different by t test (p < 0.05). There was no significant difference in the insulin, however, by repeated measures ANOVA. Male mice showed no effect of PFKM deletion in either their glucose or insulin (repeated measures ANOVA was not significant).
The lack of effect of deleting PFKM in cells that are known to express other PFK isoforms suggests the possibility that another PFK isoform could be more functionally important in cells. While this is a tempting conclusion, we instead asked a subtler question: could these other isoforms take over the role of PFKM in driving metabolic oscillations, despite their differences in biochemical properties and despite the fact that PFKP expression, at least in terms of mRNA transcript levels, was unchanged in the KOs (Fig. 1 B)? To answer this, we next sought to take advantage of what is known biochemically about the differences between the isoforms and their regulation and examine their ability to generate oscillations in a mathematical model.
Slow oscillations may persist because PFKP takes over from PFKM
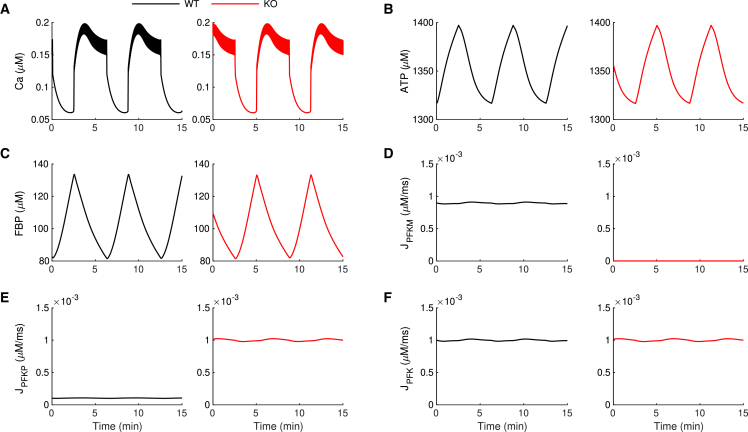
In the IOM, modified to include equations for PFKP as well as PFKM (see Materials and methods), slow bursting electrical activity and associated slow Ca2+ oscillations occur under WT conditions (Fig. 5 A, black trace). This activity is accompanied by slow oscillations in the ATP level (Fig. 5 B). The rapid changes in VM and contrasting slow changes in ATP have been universally seen in experiments, such as in (30,33), and have also been replicated in previous models, such as in (34). This is a consequence of the much slower kinetics of ATP than of Ca2+. During the active phase of each burst, the cytosolic Ca2+ concentration is elevated, so ATP is utilized to power Ca2+ pumps in the plasma membrane and endoplasmic reticulum membrane (35), resulting in a decline in the ATP concentration due to ATP consumption. Between bursts (i.e., silent phase), the Ca2+ concentration is low, reducing the ATP utilization and resulting in a rise in the ATP concentration. The fast jumps of Ca2+ in Fig. 5 occur when the slow changes in ATP push the spiking dynamics back and forth across its thresholds for activity. The Ca2+ oscillations also induce oscillations in the FBP level through Ca2+ activation of pyruvate dehydrogenase (36) (Fig. 5 C). We refer to this mechanism as a passive metabolic oscillator (PMO), in which metabolic oscillations passively result from the Ca2+ oscillations. Although both PFKP and PFKM are present under WT conditions, the majority of the metabolic flux is through the M-type isoform (Fig. 5 D–F), reflecting the fact that PFKM is the most active isoform (37).
Figure 5.
Simulations showing the mechanism for persistence of slow oscillations in -PFKM-KO islets. In the IOM, slow oscillations persist when PFKM is knocked out due to increased activity of PFKP. The black traces are for WT conditions (with PFKM present), and the red traces are after PFKM knockout. (A) The free cytosolic Ca2+ concentration exhibits slow oscillations for both WT and KO conditions. (B and C) The ATP (B) and FBP (C) concentrations exhibit slow oscillations before and after the KO. (D) Metabolic flux through the PFKM enzymatic reaction is eliminated once the PFKM enzyme is knocked out. (E) The metabolic flux through PFKP is very small in the WT case but in the KO is comparable to the WT PFKM flux. (F) The total PFK metabolic flux is the same before and after the removal of PFKM. The time courses were generated with and . For the WT simulation (black), and . PFKM is knocked out (red) by setting . To see this figure in color, go online.
When PFKM KO is simulated, by setting the maximum activity rate of PFKM to 0 (see Materials and methods), the oscillations in intracellular Ca2+, ATP, and FBP concentrations persist with no significant changes (Fig. 5 A–C, red traces). This surprising result can be explained with an analysis of the distribution of PFK flux through the two isoforms. The total flux through PFK is the same after the KO of PFKM as before its KO (compare the black and red traces in Fig. 5 F). However, the scenario at the single-isoform level changes significantly once the PFKM is knocked out. In WT conditions, the flux through PFKP (Fig. 5 E, black trace) is negligible compared with the PFKM flux (Fig. 5 D). However, after the PFKM KO, the PFKP flux reaches a level equal to that of the PFKM flux prior to its removal (compare the red trace in Fig. 5 E to the black trace in Fig. 5 D), while the PFKM flux is now zero.
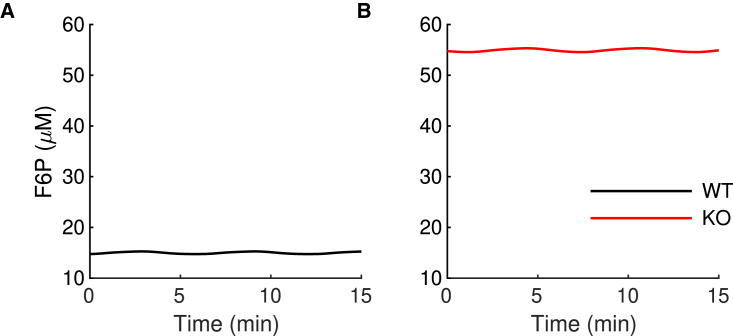
One may expect the flux through PFK to be lower after the removal of PFKM. How was it possible for PFKP to completely compensate for the loss of PFKM? This occurs because when PFKM is knocked out, the level of the PFK substrate F6P increases dramatically (Fig. 6). This higher substrate level compensates for the less-favorable allosteric affinities of PFKP, allowing it to produce the same metabolic flux as PFKM. We note that none of the PFKP parameters were altered in this simulation. In particular, there is no upregulation of the PFKP enzyme. It is simply more active following the KO of PFKM because the substrate level is much higher than before the KO. This is consistent with mRNA expression data that show that PFKP expression is not affected by the PFKM KO (Fig. 1 B).
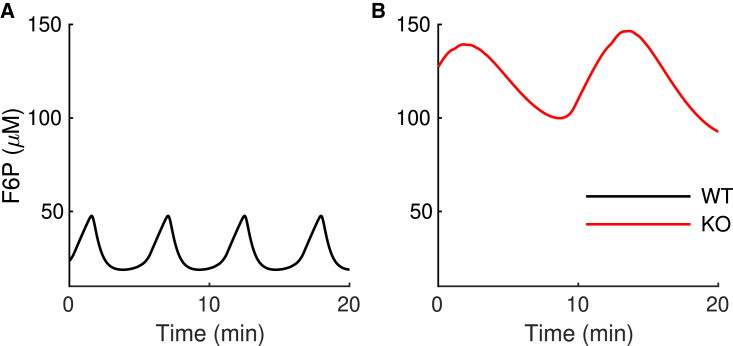
Figure 6.
The mathematical model predicts an increase in the F6P concentration in the -PKFM-KO during slow bursting. (A and B) The mean value of the F6P concentration is lower in the WT model islet (A) than in the model -PFKM-KO islet (B). To see this figure in color, go online.
Compound oscillations also occur in -PFKM-KO islets
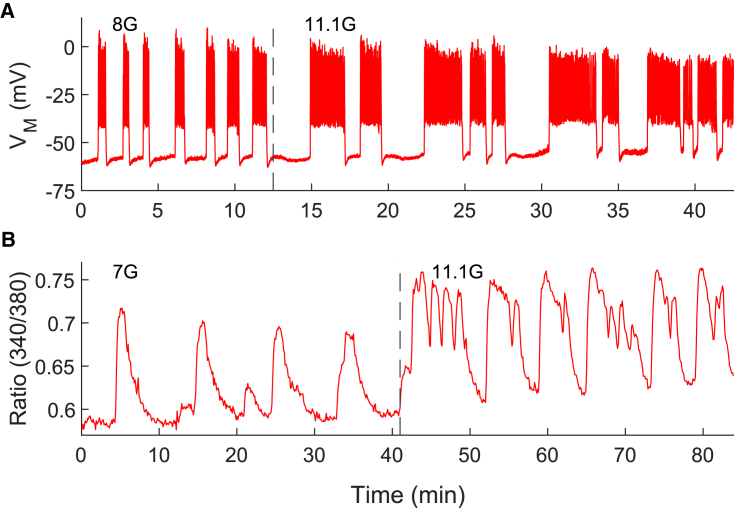
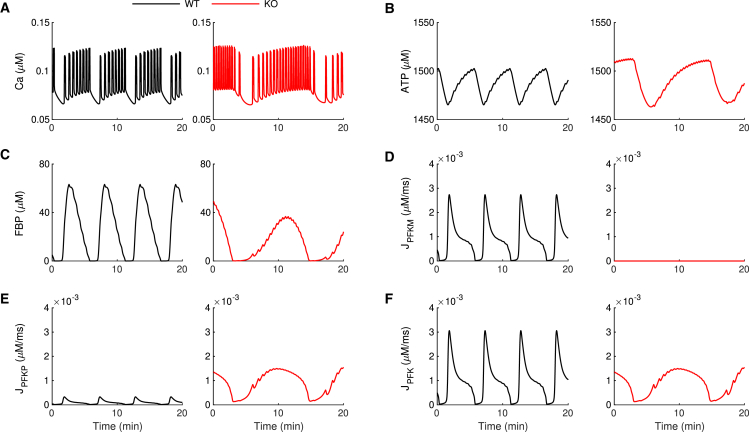
In addition to the PMO mechanism presented in the previous section, the model can exhibit active metabolic oscillations (AMOs). In this case, the intrinsic, AMOs modulate the bursting activity. We have proposed that the AMO mode is required to generate compound bursting, which consists of fast bursts of electrical activity grouped into episodes of typically 3–5 min (38,39). Indeed, we have hypothesized that the slow wave that groups the fast bursts into episodes is due to intrinsic glycolytic oscillations, driven by the positive feedback of FBP onto PFKM and the subsequent depletion of substrate F6P (40). Can this still work if PFKM is knocked out? Fig. 7 shows that compound bursting does occur in -PFKM-KO islets. Fig. 7 A shows a patch-clamp recording of the electrical activity of a cell within an islet from a -PFKM-KO mouse with several episodes of fast bursts. The number of bursts per episode is highly variable, as is typical for compound bursting oscillations. Fig. 7 B shows the same phenomenon in an independent recording of Ca2+ oscillations. To test whether the IOM with two PFK isoforms can replicate this finding, we first set model parameters so that the model cell was in a compound bursting mode prior to simulated -PFKM KO (Fig. 8, black trace). In the WT, there are FBP pulses (Fig. 8 C) due to the pulsatile activity of PFKM (Fig. 8 D), and the ATP level oscillates both due to the pulsatile production as well as the Ca2+-dependent consumption (Fig. 8 B). The oscillation amplitude of PFKP flux is very small in the WT condition, but it increases dramatically when PFKM is knocked out (red trace) and PFKP is the only isoform present (Fig. 8 E). In this scenario, compound oscillations in Ca2+ (Fig. 8 A, red trace) and FBP pulses (Fig. 8 C) persist. These pulses are now driven entirely by PFKP (Fig. 8 E). As in the WT, the FBP pulses give rise to oscillations in ATP (Fig. 8 B, red trace), which drive the episodes of electrical activity in compound bursting. As with slow bursting (Fig. 5), the P-type isoform of PFK provides the total PFK metabolic flux necessary to drive oscillations (Fig. 8 F, red trace).
Figure 7.
Compound bursting oscillations are observed in -PFKM-KO islets. (A and B) Examples of compound bursting oscillations in membrane potential (A) and Ca2+ concentration (B) from two independent experiments. To see this figure in color, go online.
Figure 8.
Simulations showing the mechanism for persistence of compound oscillations in -PFKM-KO islets. In the model, compound oscillations persist when PFKM is knocked out due to increased activity of PFKP. (A) The free cytosolic Ca2+ concentration exhibits compound oscillations for both WT and KO conditions. (B and C) The ATP (B) and FBP (C) concentrations exhibit slow oscillations before and after the KO. (D) Metabolic flux through the PFKM enzymatic reaction is eliminated once the PFKM enzyme is knocked out. (E) The metabolic flux through PFKP is very small in the WT case but in the KO is comparable to the WT PFKM flux. (F) Unlike the case of slow bursting (Fig. 5), the total PFK metabolic flux is different in the model WT and -PFKM-KO islet; however, values are comparable. The time courses were generated using and . For the WT simulation (black), and . PFKM is knocked out (red) by setting . In cases of compound bursting such as those shown here, active phases of bursting are short relative to that of the compound oscillation and during the fast phase of activity; fast declines in ATP level due to Ca2+ influx drive very brief transient fluctuations, as described in (4). To see this figure in color, go online.
The PFKP isoform is again capable of rescuing oscillations in spite of its lower affinity for FBP allosteric feedback because the F6P substrate level rises to a much higher level when PFKM is removed (Fig. 9). While this prediction could, in theory, be measurable experimentally, we are not aware of any experimental approaches that have the requisite sensitivity and dynamics needed to perform this type of experiment at present.
Figure 9.
The mathematical model predicts an increase in the F6P concentration in the PKFM-KO during compound bursting. (A and B) Both the mean and the amplitude of oscillations in the F6P concentration are lower in the WT model islet (A) than in the model -PFKM-KO islet (B). To see this figure in color, go online.
There are profound oscillations in the F6P concentration both before and after the removal of PFKM. These reflect the active glycolytic oscillation that drives the slow episodes of compound oscillations. These active glycolytic oscillations produce substrate oscillations of much greater amplitude than passive glycolytic oscillations (Fig. 6). We once again note that the only parameter change made in the simulation of the KO was to set the maximum PFKM flux rate, , to 0. In particular, no upregulation of the PFKP protein is necessary to rescue the compound oscillations.
Discussion
A previous study found that slow oscillations in mouse islets persisted when PFKM levels were reduced using a gene-trapping technique (8). Our study used a gene KO approach to determine whether oscillations persisted after the complete removal of PFKM (Fig. 1). We showed that oscillations in VM, Ca2+, and FBP are indeed present in -PFKM-KO islets (Figs. 2 and 3) and therefore do not rely on the M-type isoform. In addition, IPGTTs performed on -PFKM-KO mice revealed little or no difference in glucose or insulin responses when compared with WT mice (Fig. 4).
Previously, we predicted that oscillations could persist in PFKM KO islets if the KO of this isoform was compensated by increased protein expression of a different PFK isoform (13,34,41). Since we showed here that the PFKP expression appeared to be the same in WT and KO islets (Fig. 1), it is clear that a different compensation strategy must be involved.
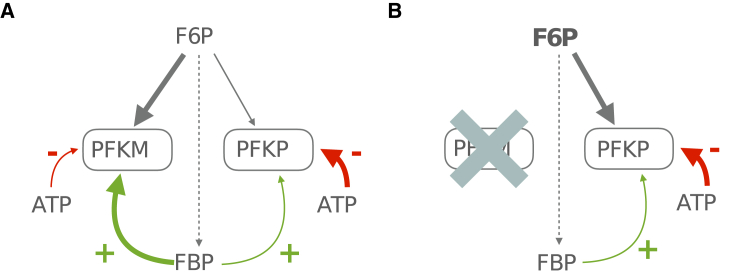
Our explanation for how PFKP takes over from PFKM once the latter is knocked out is illustrated in the “competition scheme” shown in Fig. 10. Both PFK isoforms compete for the substrate F6P (Fig. 10 A) and are subject to allosteric activation by FBP (green arrows) and inhibition by ATP (red arrows). However, because of the different affinities of PFKM and PFKP for FBP and ATP, the effects of activation and inhibition are different for the two isoforms (15,16). The M-type isoform has a high affinity for FBP (thick green arrow) and a low affinity for ATP (thin red arrow), while the P-type has low affinity for FBP (thin green arrow) and a high affinity for ATP (thick red arrow). When both isoforms are present (Fig. 10 A), PFKP loses the competition for the substrate F6P because of the differences in these affinities, and the majority of PFK activity in this case is mediated by PFKM. Conversely, when PFKM is absent (Fig. 10 B), PFKP is the only competitor for the substrate and thus wins the competition by default. However, since PFKP has weaker allosteric activation and stronger allosteric inhibition than PFKM, the substrate level must now reach a much higher level (Fig. 10, bold font in F6P) to produce the same metabolic flux through the enzyme.
Figure 10.
Proposed mechanism for compensation to -PFKM KO. Gray arrows represent substrate flux (thicker arrows indicate greater flux). Other arrows represent positive (green) or negative (red) allosteric regulation (thicker arrows indicate greater affinity). (A) Wild type. (B) -PFKM KO, leading to an increase in the F6P level. To see this figure in color, go online.
For simplicity, we model PFKP here as being modified allosterically by FBP in the same manner as PFKM but using a different parameter for FBP (and ATP) affinity. However, a possible alternative mechanism is that FBP increases PFKP activity instead by stabilizing PFKP in the active tetrameric form. FBP has in fact been shown to stabilize all three human PFK isoforms (42, 43, 44). Having demonstrated the proof of concept in the present paper that PFKP can act as a reserve enzyme that takes over when PFKM is absent, we can explore this alternate mechanism in future versions of the model.
Our model predicts that the metabolic oscillations that occur during the slow bursting oscillations shown in Fig. 2 reflect a PMO in which oscillations in FBP and downstream ATP oscillations reflect the effects of Ca2+ on pyruvate dehydrogenase and the Ca2+ removal process that uses ATP hydrolysis to power Ca2+ pumps. The oscillations in Fig. 5 are generated in this way. This oscillation mechanism is robust to changes in the PFK parameters, so replacing the PFKM isoform with the PFKP isoform has little effect on the VM, Ca2+, and FBP oscillations. It does, however, result in an increase in the level of F6P substrate (Fig. 6), and indeed, this is an important model prediction whose validation awaits new methods having sufficient sensitivity for measuring the F6P levels of islets.
We hypothesize that compound oscillations, those where both fast and slow oscillations coexist simultaneously, are fundamentally different from the slow oscillations, and their generation requires intrinsic glycolytic oscillations. That is, there is an active glycolytic oscillator that packages fast bursts into episodes through the action of ATP on K(ATP) channels. We showed, for the first time, that compound oscillations are produced even when PFKM is removed by genetic KO (Fig. 7). These data therefore suggest that another PFK isoform is capable of producing the oscillations previously attributed to PFKM alone (6). Here, we used mathematical modeling to demonstrate that the AMO can indeed be driven by PFKP (Figs. 8 and 9). This AMO is, however, more sensitive to the parameter values of PFK than are PMOs. For example, for larger values of the maximum pyruvate dehydrogenase reaction rate, , and/or lower values of the PFKP reaction rate, , the compound oscillations present in simulated WT islets may be lost if PFKM is knocked out (data not shown). If the FBP production is too low (low ) or its consumption too high (high ), PFKP cannot sustain the amount of PFK activity necessary to generate intrinsic glycolytic oscillations, and compound bursting is replaced by fast bursting. If compound oscillations persist, however, then the model predicts that F6P levels will be elevated in -PFKM-KO islets relative to WT islets. This key prediction is therefore independent of whether oscillations are driven by PMOs or AMOs.
Conclusion
The redundancy of the PFK isoforms expressed in cells allows glycolytic and Ca2+ oscillations to persist even if one of the isoforms is not expressed or is otherwise active. Thus, despite PFKM being the physiologically most responsive isoform because of its higher affinities for FBP and ATP (5), it is dispensable for the production of oscillations. This molecular redundancy may reflect the importance of maintaining pulsatility in the actions of insulin in the maintenance of glucose homeostasis.
Author contributions
All authors contributed to the experimental design as well as the writing and editing of the manuscript. V.S.P., B.T., J.R., and X.T. performed the experiments. I.M., A.S., R.B., and P.A.F. generated the mathematical models. P.A.F., J.H., and A.S. performed statistical analysis.
Acknowledgments
The authors gratefully acknowledge Drs. Keith Tornheim, Bradley Webb, Scott Soleimanpour, and Nathan Qi for providing valuable comments, discussion, and/or their scientific expertise. The University of Michigan Transgenic Core, the Vector Core, and the UM Advanced Genomics Core provided excellent technical service. The UM Phenotyping Core of the Diabetes Center (NIDDK/MDRC P30DK020572) performed glucose tolerance testing and insulin assays. I.M. acknowledges the financial support of the University of Birmingham Dynamic Investment Fund. V.S.P. acknowledges the support of the Upjohn Fellowship program of the UM Department of Pharmacology. R.B. was supported by NSF (DMS 1853342), A.S., J.H., and P.A.F. by the Intramural Research Program of the National Institutes of Health (NIDDK), and L.S.S. by NIH (RO1 DK46409).
Editor: Brian Salzberg.
Footnotes
Vishal Parekh's present address is Broad Institute of Massachusetts Institute of Technology and Harvard University, Cambridge, Massachusetts.
Isabella Marinelli and Vishal Parekh contributed equally to this work.
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.01.027.
Supporting material
References
- 1.Satin L.S., Butler P.C., et al. Sherman A.S. Pulsatile insulin secretion, impaired glucose tolerance and type 2 diabetes. Mol. Aspects. Med. 2015;42:61–77. doi: 10.1016/j.mam.2015.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Matveyenko A.V., Liuwantara D., et al. Butler P.C. Pulsatile portal vein insulin delivery enhances hepatic insulin action and signaling. Diabetes. 2012;61:2269–2279. doi: 10.2337/db11-1462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nunemaker C.S., Bertram R., et al. Satin L. Glucose modulates [Ca2+]i oscillations in pancreatic islets via ionic and glycolytic mechanisms. Biophys. J. 2006;91:2082–2096. doi: 10.1529/biophysj.106.087296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bertram R., Satin L., et al. Sherman A. Calcium and glycolysis mediate multiple bursting modes in pancreatic islets. Biophys. J. 2004;87:3074–3087. doi: 10.1529/biophysj.104.049262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yaney G.C., Schultz V., et al. Tornheim K. Phosphofructokinase isozymes in pancreatic islets and clonal β-cells (INS-1) Diabetes. 1995;44:1285–1289. doi: 10.2337/diab.44.11.1285. [DOI] [PubMed] [Google Scholar]
- 6.Tornheim K. Are metabolic oscillations responsible for normal oscillatory secretion? Diabetes. 1997;46:1375–1380. doi: 10.2337/diab.46.9.1375. [DOI] [PubMed] [Google Scholar]
- 7.DiGruccio M.R., Mawla A.M., et al. Huising M.O. Comprehensive alpha, beta and delta cell transcriptomes reveal that ghrelin selectively activates delta cells and promotes somatostatin release from pancreatic islets. Mol. Metab. 2016;5:449–458. doi: 10.1016/j.molmet.2016.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Richard A.M., Webb D.L., et al. Tornheim K. Tissue-dependent loss of phosphofructokinase-M in mice with interrupted activity of the distal promoter: impairment in insulin secretion. Am. J. Physiol. Endocrinol. Metab. 2007;293:E794–E801. doi: 10.1152/ajpendo.00168.2007. [DOI] [PubMed] [Google Scholar]
- 9.Blodgett D.M., Nowosielska A., et al. DiIorio P. Novel observations from next-generation rna sequencing of highly purified human adult and fetal islet cell subsets. Diabetes. 2015;64:3172–3181. doi: 10.2337/db15-0039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Adriaenssens A.E., Svendsen B., et al. Gribble F.M. Transcriptomic profiling of pancreatic alpha, beta and delta cell populations identifies delta cells as a principal target for ghrelin in mouse islets. Diabetologia. 2016;59:2156–2165. doi: 10.1007/s00125-016-4033-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Smolen P. A model for glycolytic oscillations based on skeletal muscle phosphofructokinase kinetics. J. Theor. Biol. 1995;174:137–148. doi: 10.1006/jtbi.1995.0087. [DOI] [PubMed] [Google Scholar]
- 12.Bertram R., Satin L.S., Sherman A.S. Closing in on the mechanisms of pulsatile insulin secretion. Diabetes. 2018;67:351–359. doi: 10.2337/dbi17-0004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Marinelli I., Vo T., et al. Bertram R. Transitions between bursting modes in the integrated oscillator model for pancreatic β-cells. J. Theor. Biol. 2018;454:310–319. doi: 10.1016/j.jtbi.2018.06.017. [DOI] [PubMed] [Google Scholar]
- 14.Merrins M.J., Van Dyke A.R., et al. Satin L.S. Direct measurements of oscillatory glycolysis in pancreatic islet β-cells using novel fluorescence resonance energy transfer (FRET) biosensors for pyruvate kinase M2 activity. J. Biol. Chem. 2013;288:33312–33322. doi: 10.1074/jbc.M113.508127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Boscá L., Aragón J.J., Sols A. Specific activation by fructose 2,6-bisphosphate and inhibition by P-enolpyruvate of ascites tumor phosphofructokinase. Biochem. Biophys. Res. Commun. 1982;106:486–491. doi: 10.1016/0006-291x(82)91136-6. [DOI] [PubMed] [Google Scholar]
- 16.Dunaway G.A., Kasten T.P., et al. Trapp R. Analysis of the phosphofructokinase subunits and isoenzymes in human tissues. Biochem. J. 1988;251:677–683. doi: 10.1042/bj2510677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Foe L.G., Kemp R.G. Isolation and characterization of phosphofructokinase C from rabbit brain. J. Biol. Chem. 1985;260:726–730. [PubMed] [Google Scholar]
- 18.Haeussler M., Schönig K., et al. Concordet J.P. Evaluation of off-target and on-target scoring algorithms and integration into the guide RNA selection tool CRISPOR. Genome Biol. 2016;17:148. doi: 10.1186/s13059-016-1012-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hendel A., Bak R.O., et al. Porteus M.H. Chemically modified guide RNAs enhance CRISPR-Cas genome editing in human primary cells. Nat. Biotechnol. 2015;33:985–989. doi: 10.1038/nbt.3290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Slaymaker I.M., Gao L., et al. Zhang F. Rationally engineered Cas9 nucleases with improved specificity. Science. 2016;351:84–88. doi: 10.1126/science.aad5227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sakurai T., Watanabe S., et al. Shindo T. A single blastocyst assay optimized for detecting CRISPR/Cas9 system-induced indel mutations in mice. BMC Biotechnol. 2014;14:69. doi: 10.1186/1472-6750-14-69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Quadros R.M., Miura H., et al. Gurumurthy C.B. Easi-CRISPR: a robust method for one-step generation of mice carrying conditional and insertion alleles using long ssDNA donors and CRISPR ribonucleoproteins. Genome Biol. 2017;18:92. doi: 10.1186/s13059-017-1220-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Miyasaka Y., Uno Y., et al. Mashimo T. CLICK: one-step generation of conditional knockout mice. BMC Genomics. 2018;19:318. doi: 10.1186/s12864-018-4713-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Popp M.W., Maquat L.E. Leveraging rules of nonsense-mediated mRNA decay for genome engineering and personalized medicine. Cell. 2016;165:1319–1322. doi: 10.1016/j.cell.2016.05.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Skarnes W.C., Rosen B., et al. Bradley A. A conditional knockout resource for the genome-wide study of mouse gene function. Nature. 2011;474:337–342. doi: 10.1038/nature10163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ittner L.M., Gotz J. Pronuclear injection for the production of transgenic mice. Nat. Protoc. 2007;2:1206–1215. doi: 10.1038/nprot.2007.145. [DOI] [PubMed] [Google Scholar]
- 27.Ralser M., Querfurth R., et al. Krobitsch S. An efficient and economic enhancer mix for PCR. Biochem. Biophys. Res. Commun. 2006;347:747–751. doi: 10.1016/j.bbrc.2006.06.151. [DOI] [PubMed] [Google Scholar]
- 28.Stratman J.L., Barnes W.M., Simon T.C. Universal PCR genotyping assay that achieves single copy sensitivity with any primer pair. Transgenic Res. 2003;12:521–522. doi: 10.1023/a:1024225408961. [DOI] [PubMed] [Google Scholar]
- 29.Aida T., Chiyo K., et al. Tanaka K. Cloning-free CRISPR/Cas system facilitates functional cassette knock-in in mice. Genome Biol. 2015;16:87. doi: 10.1186/s13059-015-0653-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Merrins M.J., Poudel C., et al. Satin L.S. Phase analysis of metabolic oscillations and membrane potential in pancreatic islet β-cells. Biophys. J. 2016;110:691–699. doi: 10.1016/j.bpj.2015.12.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Matthews D.R., Hosker J.P., et al. Turner R.C. Homeostasis model assessment: insulin resistance and β-cell function from fasting plasma glucose and insulin concentrations in man. Diabetologia. 1985;28:412–419. doi: 10.1007/BF00280883. [DOI] [PubMed] [Google Scholar]
- 32.Utzschneider K.M., Prigeon R.L., et al. Kahn S.E. Within-subject variability of measures of beta cell function derived from a 2 h OGTT: implications for research studies. Diabetologia. 2007;50:2516–2525. doi: 10.1007/s00125-007-0819-5. [DOI] [PubMed] [Google Scholar]
- 33.Li J., Shuai H.Y., et al. Tengholm A. Oscillations of sub-membrane ATP in glucose-stimulated beta cells depend on negative feedback from Ca(2+) Diabetologia. 2013;56:1577–1586. doi: 10.1007/s00125-013-2894-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.McKenna J.P., Ha J., et al. Bertram R. Ca2+ effects on ATP production and consumption have regulatory roles on oscillatory islet activity. Biophys. J. 2016;110:733–742. doi: 10.1016/j.bpj.2015.11.3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Detimary P., Gilon P., Henquin J.C. Interplay between cytoplasmic Ca2+ and the ATP/ADP ratio: a feedback control mechanism in mouse pancreatic islets. Biochem. J. 1998;333:269–274. doi: 10.1042/bj3330269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Denton R.M. Regulation of mitochondrial dehydrogenases by calcium ions. Biochim. Biophys. Acta. 2009;1787:1309–1316. doi: 10.1016/j.bbabio.2009.01.005. [DOI] [PubMed] [Google Scholar]
- 37.Fernandes P.M., Kinkead J., et al. Walkinshaw M.D. Biochemical and transcript level differences between the three human phosphofructokinases show optimisation of each isoform for specific metabolic niches. Biochem. J. 2020;477:4425–4441. doi: 10.1042/BCJ20200656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Henquin J.C., Meissner H.P., Schmeer W. Cyclic variations of glucose-induced electrical activity in pancreatic B cells. Pflügers Arch. 1982;393:322–327. doi: 10.1007/BF00581418. [DOI] [PubMed] [Google Scholar]
- 39.Cook D.L. Isolated islets of Langerhans have slow oscillations of electrical activity. Metabolism. 1983;32:681–685. doi: 10.1016/0026-0495(83)90124-5. [DOI] [PubMed] [Google Scholar]
- 40.Bertram R., Sherman A., Satin L.S. Metabolic and electrical oscillations: partners in controlling pulsatile insulin secretion. Am. J. Physiol. 2007;293:E890–E900. doi: 10.1152/ajpendo.00359.2007. [DOI] [PubMed] [Google Scholar]
- 41.Bertram R., Satin L.S., et al. Sherman A. Interaction of glycolysis and mitochondrial respiration in metabolic oscillations of pancreatic islets. Biophys. J. 2007;92:1544–1555. doi: 10.1529/biophysj.106.097154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Meienhofer M.C., Cottreau D., et al. Kahn A. Kinetic-properties of human F4-phosphofructokinase - poor regulatory enzyme. FEBS Lett. 1980;110:219–222. doi: 10.1016/0014-5793(80)80077-9. [DOI] [PubMed] [Google Scholar]
- 43.Tornheim K. Activation of muscle phosphofructokinase by fructose 2,6-bisphosphate and fructose-1,6-bisphosphate is differently affected by other regulatory metabolites. J. Biol. Chem. 1985;260:7985–7989. [PubMed] [Google Scholar]
- 44.Sanchez-Martinez C., Estevez A.M., Aragon J.J. Phosphofructokinase C isozyme from ascites tumor cells: cloning, expression, and properties. Biochem. Biophys. Res. Commun. 2000;271:635–640. doi: 10.1006/bbrc.2000.2681. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.