Temporal and spatial topography of cell proliferation in cancer

Abstract

Proliferation is a fundamental trait of cancer cells but its properties and spatial organization in tumors are poorly characterized. Here we use highly multiplexed tissue imaging to perform single-cell quantification of cell cycle regulators and then develop robust, multivariate, proliferation metrics. Across diverse cancers, proliferative architecture is organized at two spatial scales: large domains, and smaller niches enriched for specific immune lineages. Some tumor cells express cell cycle regulators in the (canonical) patterns expected of freely growing cells, a phenomenon we refer to as “cell cycle coherence”. By contrast, the cell cycles of other tumor cell populations are skewed toward specific phases or exhibit non-canonical (incoherent) marker combinations. Coherence varies across space, with changes in oncogene activity and therapeutic intervention, and is associated with aggressive tumor behavior. Thus, multivariate measures from high-plex tissue images capture clinically significant features of cancer proliferation, a fundamental step in enabling more precise use of anti-cancer therapies.

Although cell proliferation is a defining feature of cancer¹ much of our understanding of the cell cycle comes from studying cell monocultures grown in vitro where nutrients and growth factors are abundant. These conditions commonly result in doubling times of 24–48 hours². By contrast, most solid tumors do not grow uniformly or according to exponential kinetics^3,4 and even aggressive tumors such as metastases can have a doubling time of >90 days⁵. While mutations in oncogenes and tumor suppressors are a prerequisite for cancer growth, cell-intrinsic growth signals arising from genetic changes are only one component of a complex set of factors that determine whether or not any specific cancer cell will divide in vivo⁶. Across space and over time, cancer cells are exposed to different levels of nutrients, oxygen, and metabolites, receive signals from neighboring immune and stromal cells, and must navigate the physical constraints of tissue architecture^7–9; each of these potentially imposes conditions that foster proliferative, non-proliferative, and arrested states¹⁰.

Tumors removed during clinical care contain valuable information about tumor cell proliferation and the ways in which it is controlled. Tumor cell proliferation is primarily assessed in biopsies and resections using two features detectable by conventional tissue imaging: the frequency of mitotic figures as judged visually in hematoxylin and eosin stained tissue sections and the fraction of Ki-67-positive cells as measured using immunohistochemistry¹¹. Both measures have substantial limitations. Mitotic figures reflect one brief phase of the cell cycle, and do not always represent active proliferation as they can also accumulate during mitotic arrest; their detection is also highly dependent on staining and fixation quality¹². Ki-67 is not an essential cell-cycle regulator but rather a protein that organizes chromatin during mitosis and whose levels correlate with proliferation^13,14. Studies in cultured cells show that Ki-67 levels change in a graded manner throughout the cell cycle, rising gradually during S phase, peaking during mitosis, and falling during anaphase and G1^15,16. Nonetheless, in clinical practice the proliferative index of tumors is scored as the percentage of Ki-67 positive cells, with each cell assigned a dichotomous Ki-67 positive (proliferating) or Ki-67 negative (non-proliferating) score. The imprecision of this approach underestimates the proportion of cells that are actually proliferating and is subject to a range of confounders^16,17. Multiple studies have demonstrated the potential of proliferative index to serve as both a prognostic and predictive cancer biomarker, but the analytic and pre-analytic variability of Ki-67 staining has made it difficult to realize this promise^18,19. A more accurate and comprehensive means to assay proliferation that accounts for the complexities of cell-cycle dynamics is therefore needed for applications as diverse as tissue and tumor atlas construction²⁰, biomarker assessment in clinical trials, and routine clinical decision-making. To be widely useful, approaches must be compatible with formalin-fixed paraffin-embedded (FFPE) preparations universally used with human biopsies and tissue from murine cancer models.

The multiplexed tissue imaging methods necessary to characterize cell proliferation in FFPE specimens have only recently become available^20–24. These methods measure the levels of 10–60 antigens at single-cell resolution and permit the identification and quantification of cell types and cell states as well as the description of cell-cell interactions and higher-order spatial relationships²⁵. Multiplexed protein imaging is well-suited to studying processes that are controlled in a combinatorial manner by multiple protein factors. This is true of cell-cycle progression which is regulated by periodic synthesis and proteolysis of phase-specific proteins whose biological activities can be assessed with considerable accuracy using protein-level measurements alone^26,27. For example, the inverse oscillations of DNA licensing factors CDT1²⁸ and Geminin²⁹ through G1/S/G2 are widely used to delineate cell-cycle phase transitions in cultured cells³⁰. The availability of information on many different proteins provided by multiplexed measurements makes it possible to compute single-cell patterns of correlation and decorrelation among cell-cycle regulators and obtain insight into the fidelity of cell division.

In this study we use multiplexed measurements of cell-cycle regulators from fixed tissues in two ways. First, we develop a Multivariate Proliferation Index (MPI) that categorizes tumor cells as proliferative, non-proliferative or arrested based on information from multiple cell-cycle markers. This corrects for biases arising from the use of Ki-67 alone as a measure of proliferation. Second, we create a framework for studying cell-cycle dynamics using images of fixed tissues. This framework (cell cycle difference combined with classical multidimensional scaling; ccD-CMD) is based on time inference, a computational method for modeling dynamic processes in the absence of temporal data. Time inference methods have previously been described for inferring dynamics from images of cells grown in culture^31,32 and from single-cell RNAseq data^33–36; the ccD-CMD framework extends the time inference approach to multiplexed tissue images. Using these two approaches, we address fundamental questions about cell proliferation in cancer tissues.

Results

Using tissue-based cyclic immunofluorescence (CyCIF)²⁴, we quantified 20–30 protein markers at subcellular resolution and localized cells within intact surgical specimens of multiple human carcinomas (breast, lung, colon, ovarian), mesothelioma, and gliomas (representing a total of ~27.9 million cells from >680 specimens; Supplementary-Table-1,2). We distinguished tumor cells from immune and stromal cells using lineage-specific markers (e.g., E-cadherin, pan-cytokeratin, SOX2, CD45, vimentin), and characterized the spatial organization of proliferating and non-proliferating tumor cells (Fig.1–2). We mapped cells to a multi-dimensional marker space, before and after perturbation, by interpreting marker combinations in light of known protein expression patterns across the cell cycle (Fig.3–7).

Figure 1. Multivariate Proliferation Index (MPI) is linked to clinical parameters.

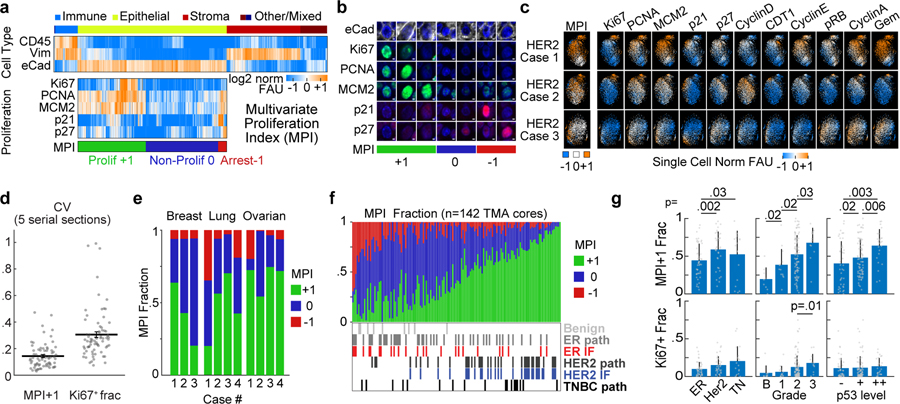
a. Top, clustered heat map of normalized log2 fluorescence signal intensities of cell lineage markers from CyCIF images (one cell per column, breast tumor tissues n = 2.5 million cells). Bottom, clustered heat map of signal intensities of five markers in epithelial/tumor population (n = 1.4 million cells), sorted by MPI categories: +1 (proliferative, green), 0 (non-proliferative, blue), or −1 (arrested, red). b. Representative immunofluorescence images of individual tumor cells from breast cancer (from panel a., E-cadherin+) showing MPI marker expression and corresponding MPI category (scale bar 2 μm, example from three biologically independent breast cancer specimens). c. t-SNE plots for the three breast carcinoma tissues with proliferation and cell cycle markers mapped to color (MPI categories were not used as t-SNE variables, n = 2,500 cells/tissue). d. Coefficient of variation of the MPI +1 and Ki-67+ fractions across 5 serial sections of Pantomics BRC15010 TMA; each dot represents a core with ≥500 cells in each section (n=74 cores, mean + SEM). e. Stacked bar graph of MPI categories from epithelial/tumor cells from three types of carcinomas (n = 3 breast, 4 lung, 4 ovarian cases). f. Stacked bar graph of MPI categories from epithelial/tumor cells from 142 breast samples from 75 patients (Pantomics BRC15010). The receptor status of each tumor is indicated as reported by the vendor (‘path’) and from direct CyCIF measurements (‘IF’). g. Comparison of MPI +1 and Ki-67+ fraction of epithelial/tumor cells across different classifiers of breast cancer (n = 142 samples from panel f, mean + SD, 2-sided KS p-values, all other comparisons were above 0.05 significance cutoff).

Figure 2. MPI reveals two proliferative domains of cancer proliferative architecture.

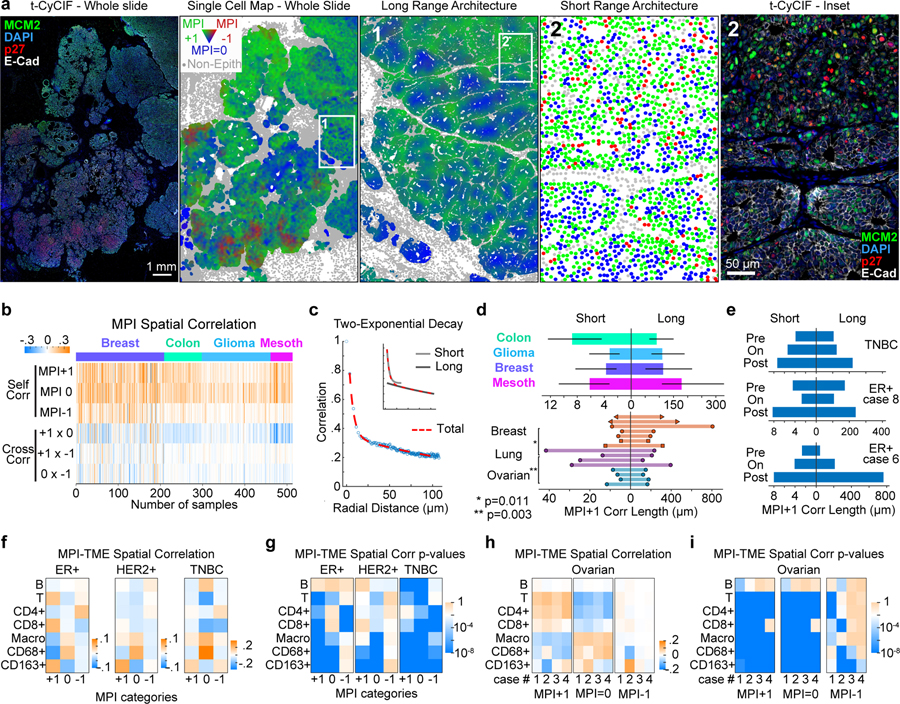
a. Spatial maps of MPI categories (the whole slide and inset 1 were smoothed over 40 neighboring cells, for visualization purposes only) and corresponding composite CyCIF images (left) from a HER2-positive breast tumor (white = E-Cadherin, green = MCM2, red = p27, blue = DNA). b. Heat map of spatial correlations within and across MPI categories (“self corr” and “cross corr” respectively, k = 5^th neighbor, n = 513 samples). c. Spatial correlation plot and two-exponential fit. Inset depicts the two exponential curves that composed the fit (“short “and “long” scales). d. Spatial correlation decay lengths for multiple cancer types (n = 53 breast, 73 colon carcinoma, 122 glioma, 32 mesothelioma samples from four tissue microarrays; median +/− 25th percentile) and 15 whole slide cancer tissues (7 breast, 4 lung, 4 ovarian). e. Spatial correlation lengths through treatment (see Supplementary Table 4 for details). f-i. Spatial correlation between epithelial tumor cells and immune cells (f and h), and corresponding p-values (g and i) for breast cancer cohort (ER+ n = 46, HER2+ n = 37, TNBC n = 18 samples, Pantomics BRC15010) and individual ovarian whole tumor slides (n = 4). Pearson correlation p-values are displayed in log10 color scale.

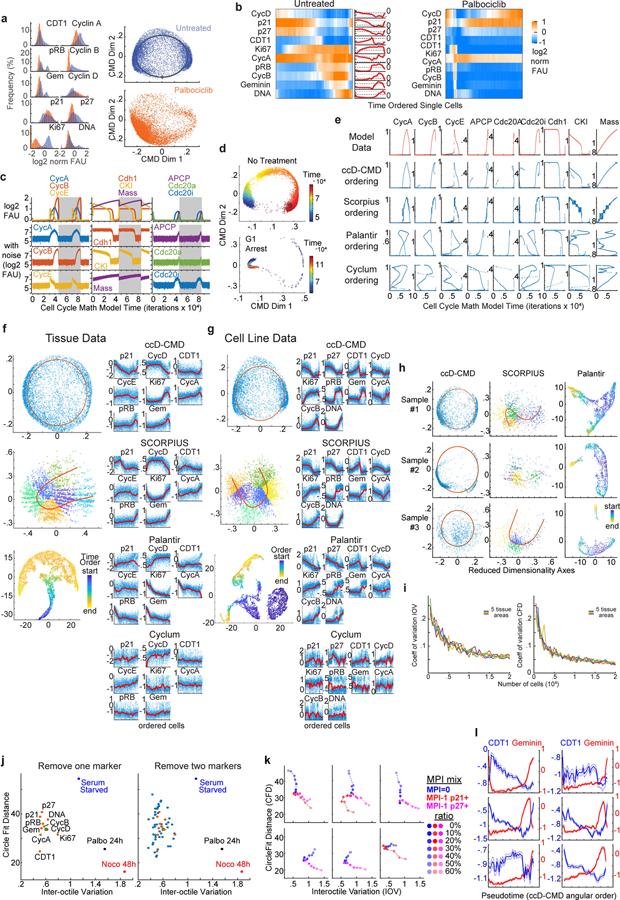
Figure 3. A framework for inferring cell cycle dynamics from multiplexed imaging data.

a. Composite fluorescence image of a subset of cell-cycle markers and E-cadherin (breast tumor, scale bar, 50μm). b-e. ccD-CMD algorithm computational steps to order cells along cell-cycle pseudotime (n=10,000 cells from a HER2+ breast cancer tissue). b. Histograms of the fluorescence signal of cell-cycle markers measured at single-cell level. c. Hierarchical clustering of pairwise cell cycle Difference (ccD). d. Plot of ccD with classical multidimensional scaling to two dimensions (ccD-CMD) (left, n=10,000 cells) with expression of cell-cycle markers mapped to color (right). e. Schematic of best-fit circle of ccD-CMD scatter (red dashed line, top) and time ordering of cell cycle from ccD-CMD from G1 start (inferred from marker expression). Heat map and time plot of single-cell normalized signal intensity measurements of cell-cycle markers from the time-ordered cells (n=10,000 cells; moving mean over 200 cells). f. Derivation of Inter-Octile Variation (IOV) and Circle Fit Distance (CFD) metrics. g. ccD-CMD plot of single-cell multiplexed data of cell-cycle markers from p-CyCIF from fixed untreated MCF10A cells (Control), serum starved for 48h (Starv), and exposed for 24 and 48h to nocodazole or palbociclib. Colors represent 3 biological replicates, n=1000 cells each. h-i. Bar graphs of IOV and mean +/−25^th percentile CFD (2-sided KS p-value). j. IOV-CFD scatter plot for each treatment in panels h and i (lines connect mean treatment values). k-l. IOV-CFD scatter plots from p-CyCIF data from k. MCF-7 cells treated for 24h (n=3 biological replicates; mean indicated by larger circle), and l. panel of cell lines treated with palbociclib 1μM (n=1000 cells each). m. IOV-CFD scatter plots from t-CyCIF data from MCF-7 xenografts treated daily for four days with vehicle (n=14 tumors from 7 mice) or with abemaciclib dosing (n=6 tumors from 3 mice/dose) or palbociclib (n=8 tumors from 5 mice). Doses are in mg/kg. Median +/− SEM. Multiplexed images of human HER2 breast cancer used in Fig. 3a viewable in Minerva Story^73,74 interpretive guide https://tinyurl.com/minerva-proliferation.

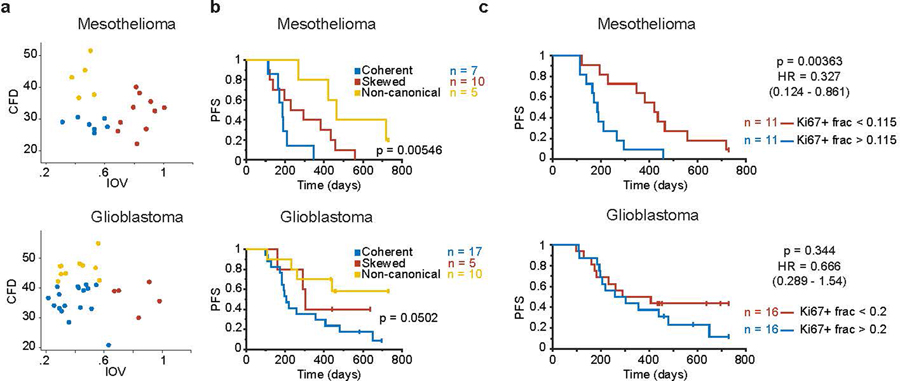
Figure 7. Coherence metrics are associated with clinical outcome.

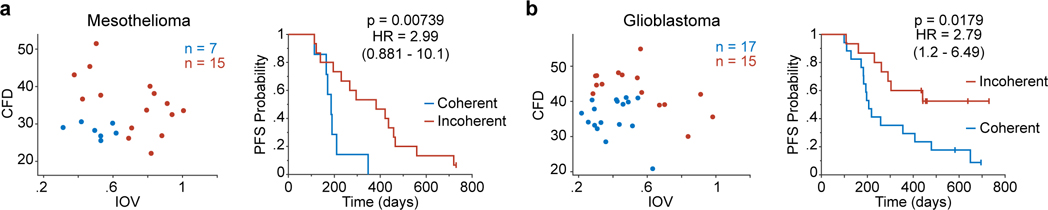
a. Left, scatter plot of CFD versus IOV from a mesothelioma sample cohort (n = 22 patients). Colors represent binning into coherence groups according to IOV and CFD metrics. Right, corresponding Kaplan Meier estimation of progression-free survival (PFS) for the patients (logrank p-value). b. Left, scatter plot of CFD versus IOV from a glioblastoma sample cohort (n = 32 patients). Colors represent binning into coherence groups according to IOV and CFD metrics. Right, corresponding Kaplan Meier estimation of progression-free survival (PFS) for the patients (logrank p-value).

A Multivariate Proliferation Index from multiplexed images

As a robust means to score cell proliferation based on a multivariate feature, we generated a categorical Multivariate Proliferation Index (MPI) based on staining intensities for three proliferation markers (Ki-67, PCNA, MCM2)^37–40 and two cell-cycle arrest markers (p21, p27)^41,42 (Fig.1a,b, Extended-Data-Fig.1a–c). An MPI value was assigned to each tumor cell based on the following rule: cells were scored as proliferative (MPI +1) if they expressed a positive balance of proliferation markers; non-proliferative (MPI 0) if they lacked expression of proliferation markers; and arrested (MPI −1) if they expressed high levels of one or both of the arrest markers, even if proliferation markers were also expressed.

The MPI classifications were consistent with those obtained by unsupervised clustering of single-cell data based on the same markers (Fig.1c,d, Extended-Data-Fig.1d,e), but we found that using MPI was advantageous because parameter tuning was not required to identify subpopulations (Supplementary-Note1). The quantification of proliferation by MPI was highly reproducible across adjacent sections from the same samples (R²= 0.88–0.96) and robust to errors in single-marker normalization (Extended-Data-Fig.1f–j). Notably, the robustness of an MPI+1 measurement across serial sections of the same tissue sample (median CV=0.14, maximum CV=0.47) substantially exceeded the robustness of the Ki-67 positive fraction (median CV=0.33, maximum CV=0.99) (Fig.1d). This occurs because no single marker is sufficient for identifying a proliferative cell (Fig.1a,b, Extended-Data-Fig.1a–c). For example, although Ki-67 is the most widely used measure of proliferation in diagnostic and research settings^43,44, we found that 39–72% of MPI+1 cells were Ki-67 negative but positive for PCNA or MCM2, depending on the tumor type (Extended-Data-Fig.1b–c). This is consistent with data from cultured cells showing that Ki-67 expression is highest in the G2 phase of the cell cycle and that, when dichotomous scoring is imposed, proliferating cells prior to G2 can be scored ‘Ki-67 negative’^15,16.

The frequency of proliferative cells (MPI+1) varied between tumor types (Fig.1e,f). To determine whether the variation in MPI across patient samples is associated with clinically-relevant features of tumor behavior, we focused on breast cancer, where tumor subtype⁴⁵, histological grade⁴⁶, and p53 status⁴⁷ are known predictors of outcome. In samples from 75 patients, the fraction of MPI+1 cells varied from 0 to 1 and was highest in aggressive molecular subtypes such as HER2-amplified and triple-negative breast cancer (KS test, p<0.035, Fig.1g). The MPI+1 cell fraction also increased significantly with tumor grade and p53 status (KS test, p<0.035, Fig.1g, Extended-Data-Fig.1k). These associations were not observed for the Ki-67 positive fraction (Fig.1g).

Two length scales of proliferation in tumors

To determine whether proliferating and non-proliferating tumor cells are organized into distinct spatial domains, we quantified the spatial correlation within MPI categories (“self-correlation”) and between MPI categories (“cross-correlation”) across 513 tumor specimens including carcinomas, mesothelioma and gliomas. Visual inspection of multiplexed images and corresponding single-cell maps of MPI values revealed a variety of spatial patterns (Fig.2a, Extended-Data-Fig.2a–c). Across tumor types, self-correlations between proliferative (MPI+1) and non-proliferative (MPI 0) states were positive, strong, and highly significant, while cross-correlations were weak and variable (Fig.2b, Extended-Data-Fig.2d–f). Thus, proliferating cells clustered together with other proliferating cells and away from non-proliferating and arrested cells.

Spatial self-correlation decreased with distance and was well fit by a two-exponential decay model (Fig.2c, validated by Ripley’s L metric, Extended-Data-Fig.2g–h). The fitting revealed that proliferation is organized at two physical scales: small niches spanning short length scales of ~10–30μm within larger structured neighborhoods spanning long length scales of ~100–300μm (Fig.2d).

In tissues from three breast cancer patients biopsied before, on, and after treatment, both short and long correlation lengths increased following therapy (Fig.2e). At short length scales in breast tissue from 75 patients (from Fig.1f,g above), MPI 0 tumor cells clustered away from T lymphocytes and were more frequently found in proximity to CD68-expressing macrophages, whereas MPI+1 tumor cells were associated with CD163-expressing macrophages (correlation p<10⁻⁸) (Fig.2f,g). In estrogen receptor positive breast cancer, MPI+1 cells were significantly proximal to cytotoxic T cells (correlation p<10⁻⁸); this strong association was also observed in ovarian cancer but was absent in HER2+ and triple negative breast (TNBC) cancers (Fig.2f–i). We speculate that the short length scales observed in MPI data correspond to small clones that are also influenced by interaction with immune cells. Large proliferative neighborhoods may be organized by environmental conditions such as hypoxia^48,49, nutrient availability, or tissue structure⁵⁰.

Time inference of cell-cycle dynamics

To further characterize cells with different MPI values we stained tissues using antibodies against 10 well-established cell-cycle regulators including cyclins A1/A2, B1, D1 and E1, CDK inhibitors p21 and p27 and DNA replication regulators CDT1, Geminin, and phospho-RB (Supplementary-Table3). Single-cell intensity data revealed a wide range of marker intensities, but most markers did not have clearly separated high and low states (Fig.3a–b, Extended-Data-Fig.3a–c,4). Using this data, neither multidimensional gating nor conventional dimensionality reduction methods such as t-SNE provided obvious insight into the likely order of cell-cycle events (Fig.1c, Extended-Data-Fig.3d, Supplementary-Note1). We therefore sought an alternative approach informed by knowledge of cell-cycle dynamics.

Because the molecular events driving the cell cycle are mediated by coordinated fluctuations in cell-cycle regulators, correlation and anti-correlation in marker expression can be used to identify cell-cycle stage in a data-driven manner. As a first step we focused on proliferative MPI+1 epithelial cells and calculated a pairwise cell-cell correlation distance matrix in the space of cell-cycle markers (the “cell cycle Difference” matrix; ccD; Fig.3c, Supplementary-Note1). We then transformed the data using classical multidimensional scaling (CMD) to enable visualization of the ccD in two dimensions. In the resulting “ccD-CMD” representation, proliferating cells from a breast tumor sample lay within a torus (Fig.3d). Moreover, by mapping single markers onto the ccD-CMD representation it was evident that the toroidal organization of the data was driven by fluctuations in the expression of cell-cycle regulators expected for proliferating cells (Fig.3d).

In keeping with previous theoretical work on the cell cycle⁵¹, we assume that progression can be described by a deterministic dynamical system and that sampling is sufficiently dense to apply the ergodic principle. In this case the difference in cell-cycle position for two cells is proportional to their distance in ccD-CMD space. A circular trajectory through the toroidal landscape of the ccD-CMD (Fig.3d,e) therefore corresponds to prototypical progression from G1 to S to M and then back to G1. Leveraging this relationship we computed a best fit circle in the ccD-CMD landscape to order the cells in time, effectively reconstructing cell-cycle dynamics (Fig.3e, Extended-Data-Fig.5a–b). Conceptually similar time inference algorithms^32–35 have previously been described for reconstruction of cell-cycle dynamics, development, and other dynamic processes from fixed-time data. When we compared our ccD-CMD time inference algorithm to existing methods using synthetic data or real data from multiplexed imaging of a breast epithelial cell line grown in culture, we found that the ccD-CMD algorithm outperformed other inference algorithms in all settings (Extended-Data-Fig.5c–l; Supplementary-Note1).

Cell cycle coherence metrics from multiplexed images

Fitting a circle to the ccD-CMD data yielded two useful parameters: the uniformity of the distribution along the circumference of the circle which we described using the Inter-Octile Variation (IOV – the coefficient of variation of distribution of cells across pi/4 sections of the circle), and the average distance of data points from the best-fit circle (the circle fit distance, CFD) (Fig.3f). A low IOV indicates that cells in a population are evenly distributed through the cell cycle. CFD measures the dispersion of cells in ccD-CMD space: when the value is low, data from individual cells lie on or close to the best-fit circle. An even distribution of cells in ccD-CMD space corresponds to low IOV and low CFD values. This distribution is one in which the order of states is consistent with current understanding of cell-cycle dynamics²⁶ as observed in freely growing cultured cells; we refer to this state as a “coherent” cell cycle (human tissue Fig.3e, cell culture Extended-Data-Fig.5b, Fig.3f). Loss of coherence indicates a loss of canonical cell-cycle dynamics either by increased accumulation of cells in a specific cell-cycle phase (increased IOV) or by a loss of molecular coordination between cell-cycle regulators (increased CFD).

To confirm these interpretations of IOV and CFD we performed plate-based CyCIF⁵² with non-transformed MCF10A mammary epithelial cells and MCF-7 breast cancer cells grown in culture and exposed to CDK4/6 inhibitors (palbociclib or abemaciclib), or the microtubule inhibitor nocodazole, or subjected to serum starvation (Fig.3g–k, Extended-Data-Fig.6a–c). CDK4/6 inhibitors are expected to cause G1/S arrest, nocodazole to cause G2/M arrest, and serum starvation to cause cell cycle exit; the induction of these responses was confirmed using EdU incorporation and cell-cycle assays (Extended-Data-Fig.6a–d). When CyCIF data were plotted in a ccD-CMD landscape, control untreated MCF10A and MCF-7 cells exhibited an IOV^low CFD^low (coherent) state consistent with unrestrained, normally ordered cell proliferation (Fig.3g,k Extended-Data-Fig.5a). Cells treated with CDK4/6 inhibitors or nocodazole were skewed toward specific quadrants of the ccD-CMD landscape, representing IOV^high CFD^low states (Fig.3g–k). By contrast, when cells were serum starved, data fell in a point cloud corresponding to an incoherent IOV^high CFD^high state. Thus, the higher the value of IOV and CFD the greater the deviation from unrestrained proliferation (Fig.3h–k). Moreover, changes in IOV and CFD tracked with genotype-predicted responses to CDK4/6 inhibitors in Rb wild-type and mutant breast cancer cell lines⁵³: palbociclib induced a IOV^high state in Rb wild-type cells (MCF-7, SUM159, BT20) which arrested in the presence of CDK4/6 inhibitors. Rb-mutant cells (BT549, HCC1937), which are resistant to palbociclib, remained IOV^low CFD^low and cycling (Fig.3l). Additionally, MCF-7 mouse xenografts treated with CDK4/6 inhibitors⁵⁴ exhibited a dose-dependent decrease in MPI+1 fraction which correlated strongly with inhibition of tumor growth (Extended-Data-Fig.6e–f). As in MCF-7 cell culture, CDK4/6 inhibitors induced a IOV^high state in MCF-7 xenografts (Fig.3m, Extended-Data-Fig.6g). Based on these observations, we conclude that the transformations involved in generating a ccD-CMD landscape and scoring IOV and CFD metrics faithfully capture key features of the cell cycle from fixed cell images.

HER2 levels modulate cell cycle coherence in breast cancer

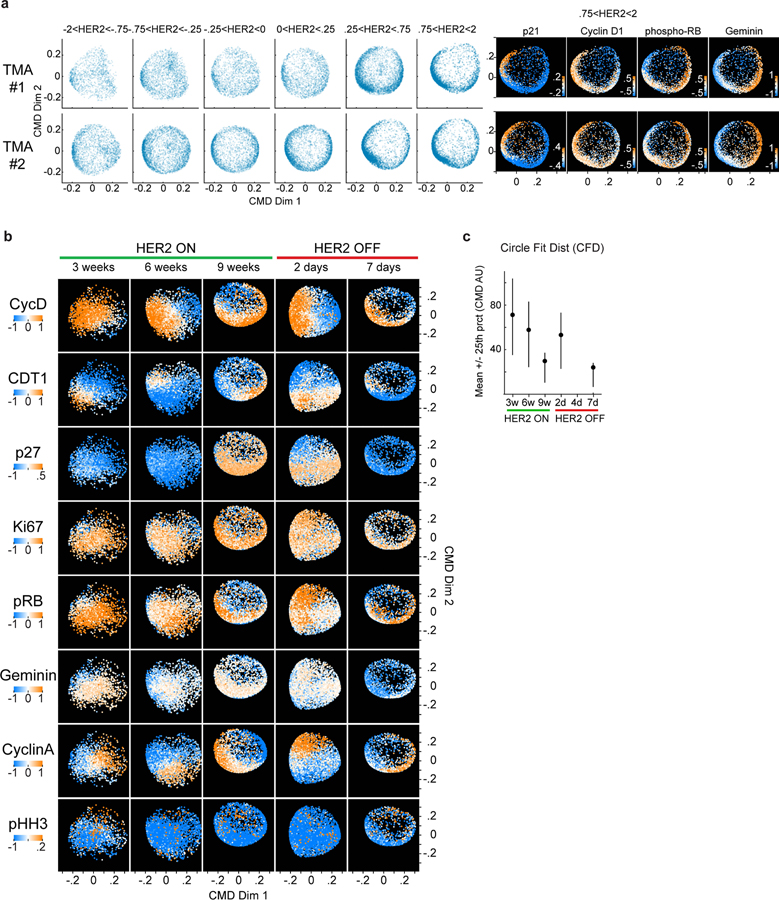
We applied CyCIF and coherence analysis to study cell-cycle dynamics in human breast cancer tissues overexpressing the HER2 growth factor receptor⁵⁵. HER2 overexpression promotes proliferation of mammary epithelial cells via receptor-mediated mitogenic signaling^55,56 and high HER2 expression defines a major subclass of breast cancer and is routinely assessed using immunohistochemistry⁵⁷. Both the magnitude and heterogeneity of HER2 protein expression are known to predict response to HER2-directed therapy^58,55,59,60. We performed CyCIF on a cohort of 26 breast cancer specimens (TMA1, TMA2), identified MPI+1 epithelial cells, and used the ccD-CMD algorithm to quantify IOV and CFD for individual patients (Fig.4a,b). A subset of tumors was found to be in an IOV^low CFD^low state (e.g., Sample 1 in Fig.4c) and inspection of time-ordered cell-cycle markers confirmed prototypical “coherent” cell-cycle dynamics with a balanced distribution of proliferative tumor cells in both G1 and G2 phases (Fig.4c–e). However, other samples deviated substantially from this pattern. For example, in Sample 2 IOV^high cells were ‘skewed’ towards G1 and in Sample 3 a CFD^high high state was observed (Fig.4c,d) and cells expressed combinations of cell-cycle proteins that are not found in normally cycling cells. These unexpected combinations included CDT1 plus Geminin without detectable Ki-67, or a combination of high p21, Cyclin A, Cyclin D and phospho-Rb (Fig.4e). Across all specimens we observed a continuum of IOV and CFD values and, within a single specimen, coherence also varied in space with gradual transitions occurring over length scales of several millimeters (Fig.4f, Extended-Data-Fig.7). We combined the proliferative cells from four regions of interest (ROIs) within a single tissue and used the ccD-CMD algorithm to order cells by their cell-cycle positions, thereby obtaining insight into relative cell-cycle distribution in each ROI (Fig.4g). In ROI1, which had the highest coherence, cells were evenly distributed through the cell cycle whereas in ROI2–4, IOV was higher and cells were concentrated in different parts of the cycle (Fig.4g). Thus, proliferating breast cancers expressing the same oncogenic driver (HER2) can exhibit different cell-cycle dynamics within a single specimen and these can range from a canonical IOV^low CFD^low state, to skewed distributions consistent with cell-cycle phase imbalance (skewed: IOV^high CFD^low), as well as states not normally encountered in normally growing cells (non-canonical: IOV^low CFD^high).

Figure 4. Extraction of cell cycle coherence metrics from multiplexed images of human cancer tissues.

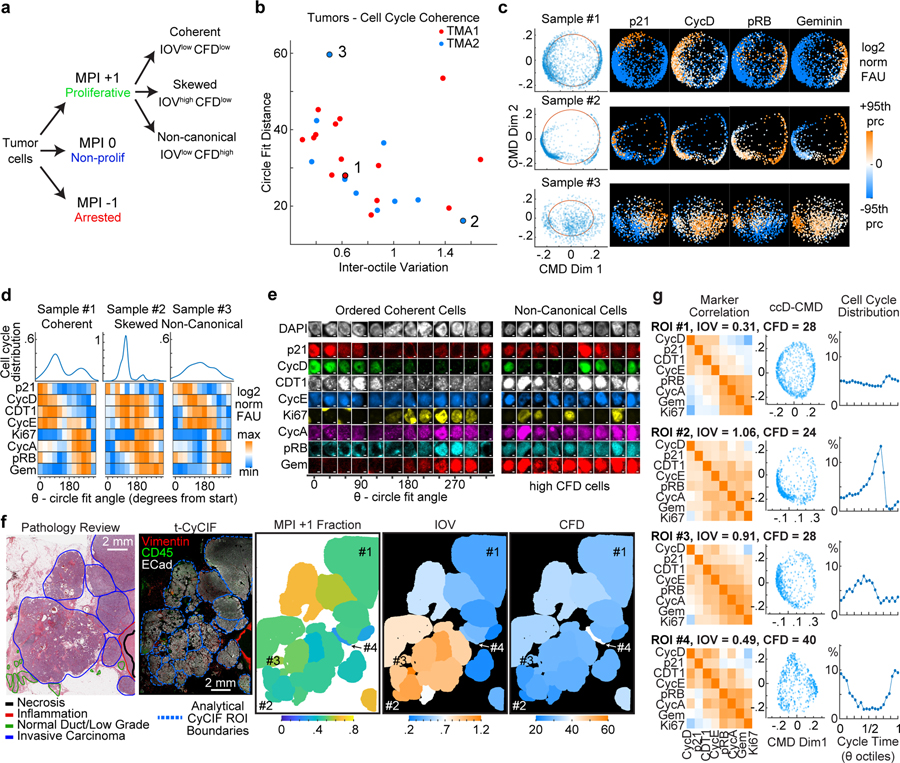
a. Scheme to classify tumor cell populations using the MPI and characterize cell cycle coherence states. b. Scatter plot of cell cycle coherence metrics IOV and CFD for 25 HER2+ breast samples. c. Examples of ccD-CMD plots for 3 samples (indicated in panel b) with cell cycle markers (+/−95th percentile range in sample, log2 normalized FAU). d. Distribution of cell density and heat maps of cell cycle markers with cells binned by the circle fit angle for the 3 samples in panel c. (color, median bin intensity, normalized maximum to minimum). e. Representative immunofluorescence images of individual tumor cells from Sample 1 (Ordered Coherent Cells) and Sample 3 (Non-Canonical Cells). (scale bar 2 μm, example from 25 biologically independent specimens in b.). f. (Left to Right) Scanned image of hematoxylin and eosin (H&E) stained section from a HER2+ positive breast tumor with pathology annotations. Composite CyCIF images of tissues with annotated regions of interest (ROI) used for analysis (scale bar 2mm). Spatial ROI maps of MPI and coherence metrics IOV and CFD. g. Comparison of selected ROIs from panel f. Left, Pearson correlation matrix of cell cycle markers. Middle, ccD-CMD plot for each ROI. Right, plot of distribution of cells along cell cycle time from ccD-CMD performed on data from the 4 combined ROIs.

To explore the relationship between HER2 expression and coherence we used TMA1 and TMA2 (n = 26, known HER2 positive). We binned single cells by HER2 protein levels and inferred cell-cycle dynamics (Fig.5a). Cells having the lowest HER2 levels were typically CFD^high. Optimal coherence (IOV^low, CFD^low) was observed in cells expressing intermediate levels of HER2. By contrast, cells with the highest HER2 levels were also CFD^low; their cell-cycle dynamics were however skewed to late G1 and IOV was high (IOV^high, CFD^low) (Fig.5a, Extended-Data-Fig.8a). Similar results were observed in biopsies from patients enrolled in a clinical trial (NCT02326974) of neoadjuvant dual HER2 therapy (n=5, Fig.5b,c).

Figure 5. Coherence metrics are modulated by HER2 expression in human breast cancer tissues and HER2-driven mouse model of breast cancer.

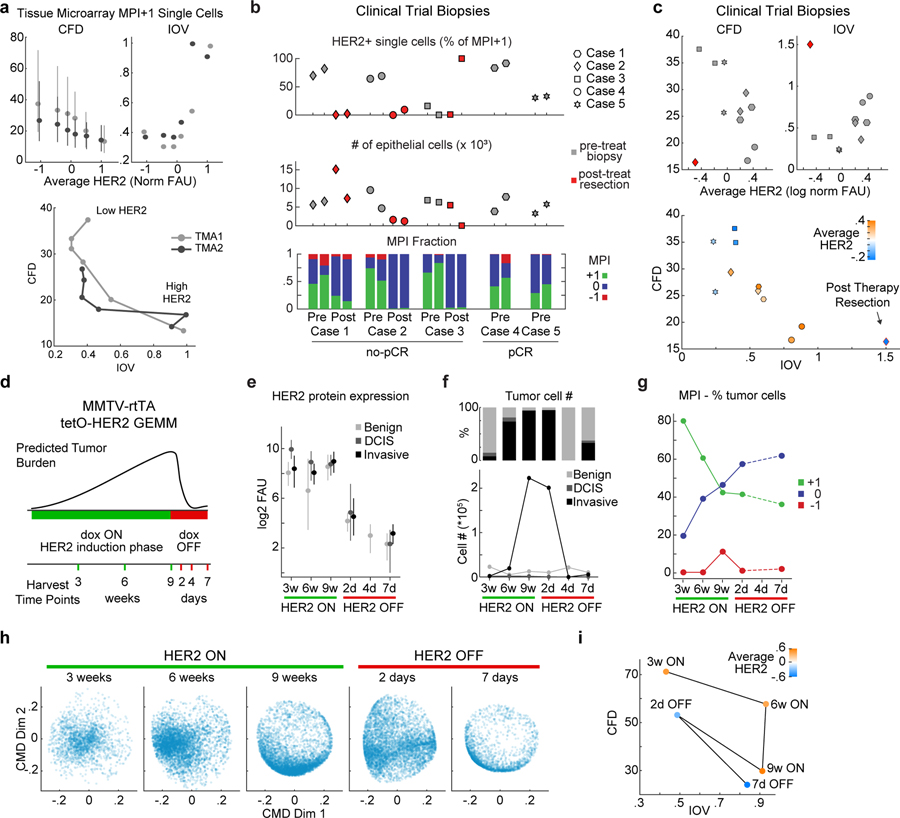
a. Top, Coherence metrics CFD and IOV for HER2+ TMA1 and TMA2 cells (MPI +1 cells only) binned by HER2 levels (CFD mean +/− 25th percentile, n = 5000 cells per bin). Bottom, CFD versus IOV per HER2 bin, lines connect data from increasing HER2 mean levels. b. Single-cell data summary for a 5-patient HER2+ breast cancer cohort enrolled in an anti-HER2 clinical trial (gray markers are 2 pre-treatment biopsies, red markers are two areas of post-treatment resections). Top, percent HER2 positive cells in MPI +1 set per sample. Middle, total number of epithelial/tumor cells per sample. Bottom, fraction of cells in each MPI category. Cases 4 and 5 had a pathological complete response (pCR) to neoadjuvant therapy and did not have tumor cells in the matched resection samples. c. CFD and IOV versus average HER2 levels for clinical trial samples from panel b, and plot of CFD versus IOV with HER2 level in color scale (mean log2 normalized FAU). Shapes represent patients (n = 2 biopsies per patients). Red diamond is a post-therapy resection sample. d-h. MMTV-rtTA tetO-HER2 genetically engineered mouse model (GEMM, n=2 mice per experiment, cell numbers in panel f.). d. Schematic diagram of HER2 induction (dox ON) and repression (dox OFF) and tissue harvest times. e. HER2 protein fluorescence in regions of normal epithelium, and in situ and invasive breast carcinoma of HER2 GEMM as defined by histology review (median +/− 25th percentile). n=2 mice per experiment, exact number of cells plotted in panel f. f. Cell number and fraction of total cells present as benign duct epithelium, and in situ or invasive breast carcinoma in time. g. Fraction of tumor cells (in situ and invasive) in time in the three MPI categories. h. ccD-CMD plot of the MPI +1 cells for each time point (n = 5,000 cells per sample, day 4 did not have enough MPI +1 tumor cells). i. CFD versus IOV for time points of the GEMM experiment from panel h.

To determine if altering HER2 expression affects cell cycle coherence, we used a genetically engineered mouse model (GEMM) of breast cancer in which HER2 expression can be induced ~100-fold and then silenced in mammary tissue using a doxycycline-regulated construct (MMTV-rtTA/tetO-HER2; Fig.5d)⁵⁶. HER2-expressing mice develop ductal carcinoma in situ (DCIS) after three weeks of Dox-On, and palpable invasive carcinoma with a median latency of 53 days. Upon doxycycline withdrawal (Dox-Off), tumor regression is apparent with 100% penetrance. However, more than two-thirds of mice exhibit tumor recurrence within 120 days⁵⁶. This murine model therefore mimics important aspects of tumor dynamics in response to HER2-targeted therapy in patients, although on a faster time scale.

Mammary tissues collected over a nine-week period of HER2 induction and seven days of subsequent HER2 repression underwent CyCIF to assay tumor cell-cycle dynamics (Fig.5d–i). After nine weeks of HER2 overexpression tumors adopted a proliferative state with a skewed cell cycle (IOV^high CFD^low, Fig.5h,i). This state resembles established human tumors expressing high HER2 (Fig.5a). Within two days of HER2 withdrawal, cell-cycle dynamics changed to an incoherent state (IOV^low CFD^high; Fig.5h–i, Extended-Data-Fig.8b,c), even though neither proliferation (MPI+1 fraction) nor tumor cellularity had yet decreased (Fig.5f,g). Seven days after HER2 withdrawal, only ~2.5% of tumor cells remained and these exhibited skewed IOV^high CFD^low cell-cycle dynamics (Fig.5h,i). For comparison, we examined a residual tumor having a detectable population of proliferating cells following neoadjuvant dual HER2 therapy in a patient enrolled in a clinical trial (NCT02326974) (Fig.5b). In this specimen, HER2 levels were lower than in any pre-treatment sample and the state was IOV^high CFD^low (Fig.5c). These data suggest that the relationship between HER2 levels and cell cycle coherence is bell shaped, with the highest coherence observed at intermediate receptor levels. In both humans and mice, HER2-independent residual disease adopted the skewed cell-cycle dynamics observed in pre-treatment tissues having high HER2 expression.

Coherence metrics are associated with clinical outcome

To study how coherence changes with therapy, we assayed specimens from three patients with localized breast cancer biopsied before, during, and after treatment (these patient samples were also analyzed in Fig.2e). In one patient with TNBC biopsied prior to treatment (pre), following 12 weeks of neoadjuvant paclitaxel (on), and after 20 additional weeks of treatment with doxorubicin-cyclophosphamide (post) (Fig.6a), we found that either paclitaxel or doxorubicin-cyclophosphamide induced only small changes in the MPI+1 fraction (Fig.6b), even though the Ki-67+ fraction fell ~50% in the on-paclitaxel specimen (Fig.6c). ccD-CMD analysis of the three longitudinal TNBC samples showed that the resulting cell-cycle dynamics were mostly coherent throughout the treatment (CFD<40, IOV<0.6, Fig.6d). However, the dynamics of the “on” sample skewed towards the G1 phase of the cell cycle (Fig.6e–g), consistent with data from intravital imaging of xenograft models treated with paclitaxel⁶¹. G1 accumulation in the presence of paclitaxel explains why Ki-67 staining alone underestimated the proliferative fraction (Fig.6c). In another type of breast cancer (ER+ HER2−) two other “pre-on-post” sample sets collected longitudinally over time showed drastic changes in coherence metrics induced by therapy (Fig.6h,i), even when treatment lasted for as little as two weeks (“pre” to “on” samples). Changes in coherence were independent of changes in the fraction of proliferating cells (Fig.6h). We conclude that cell cycle coherence is a plastic phenotype that provides a sensitive measure of therapy-induced changes independent of significant reductions in proliferative index.

Figure 6. Coherence metrics change with treatment.

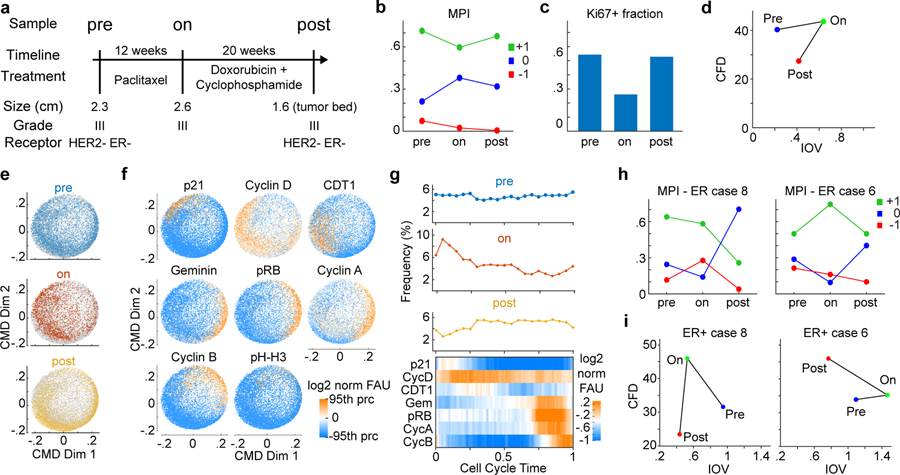
a. Clinical and pathologic features of biopsy/resection tissues from a patient with triple negative breast cancer (TNBC) characterized by CyCIF imaging. Three samples include the diagnostic biopsy (pre) and two samples after indicated treatments (on, post). b-c. Plot of b. fraction of cells in the three MPI categories and c. Ki-67 positive fraction through the treatment course for samples in panel a. d. Scatter plot of CFD versus IOV for triple-negative breast cancer (TNBC) patient (pre n = 5,000, on n=2,250, post n = 5,000 single MPI +1 cells). e-f. ccD-CMD plot of combined data from TNBC pre, on, and post samples with data e. corresponding to time of biopsy indicated by color, and f. with single marker normalized intensities mapped to color (n = 5,000 cells per plot, phospho-histone H3 (pH-H3) was not used by the ccD-CMD algorithm). g. Distribution of cells along cell cycle time in the three samples and heat map of marker expression for single cells across cell cycle time combined for the three samples (moving mean over 100 cells). Upper panels, single time point cell frequency distribution. h. Plot of fraction of cells in the three MPI categories through the treatment course for samples from two ER+ breast cancer patients pre-, on-, and post-treatment (see Supplementary Table 4 for treatment details). i. Scatter plot of CFD versus IOV for two ER+ breast cancer patients pre-, on-, and post-treatment from panel h.

To determine if differences in cell cycle coherence are associated with differences in outcome we assayed specimens from patient cohorts diagnosed with two different lethal malignancies (mesothelioma, glioblastoma). Patients were stratified into a coherent IOV^low, CFD^low group and an incoherent group encompassing either IOV^high or CFD^high states (Fig.7a,b). Patients whose tumors exhibited coherent cell-cycle dynamics had significantly worse outcomes (logrank p<0.02). Similar results were obtained if tumors were stratified into three groups (coherent, skewed, non-canonical; Extended-Data-Fig.9). We conclude that cell cycle coherence in mesothelioma and glioblastoma is associated with aggressive tumor behavior.

Discussion

Cancer is a disease of excess cell proliferation but cell-cycle progression, even in highly malignant cells, is still subject to regulation by both cell-intrinsic and cell-extrinsic factors^27,1,62. The effects of such regulation on tumor cell proliferation is largely unexplored in the setting of intact human tumors. Instead, in the vast majority of studies involving human tumors and mouse models, proliferative fraction is captured via a dichotomous assessment of the signal intensity of a single marker: Ki-67. This approach incorrectly makes some dividing cells appear non-proliferative and fails to capture the wide-ranging states that proliferating tumor cells can assume. Here we present a multiplexed approach for determining the emergent features of dynamic processes in tumors that provides a foundation for understanding how tumors integrate microenvironmental, cell-intrinsic, and physical signals to grow in different niches.

Specifically, a Multivariate Proliferation Index (MPI) provides a means to quantify proliferative index based on the expression of multiple cell-cycle regulators – not just Ki-67 – and cell cycle coherence measures how closely cell-cycle dynamics conform to those of the well understood cell cycles in freely dividing cancer cells. We show that only a subset of tumors grows with ”canonical” dynamics while others are skewed towards specific cell-cycle phases or express unanticipated combinations of regulators. In both humans and mice, we find that intermediate levels of HER2 expression promote coherent cell-cycle dynamics, whereas higher levels of oncogene overexpression lead to skewed dynamics, potentially resulting from phase-specific deceleration or acceleration involving skipped restriction points^63,64. High coherence may not necessarily translate into faster growth, but skewed and non-canonical dynamics are associated with more favorable outcomes in two highly lethal malignancies. This finding is also consistent with evidence that many oncogenes are toxic to tumor cells when expressed at very high levels⁶⁵. We anticipate that MPI and coherence will be broadly useful concepts even through the precise cell-cycle regulators used to compute these parameters are likely to change with further study.

We observe diverse cell-cycle states within and across specimens. By contrast, the spatial organization of cells into proliferative and non-proliferative domains of two characteristic lengths appears to be conserved across cancers of diverse histology. We speculate that small-scale proliferative structures correspond to cells and their daughters arising after a few relatively rapid cell divisions, perhaps corresponding to well-adapted clones or to favorable mitogenic gradients, nutrient availability, or mitogenic cell-cell interactions. Large neighborhoods likely arise from differences in environmental conditions that extend across tumors and from structural constraints. These neighborhoods contain thousands of either proliferating or non-proliferating cells, reminiscent of developmental patterning by morphogen gradients⁶⁶.

Basic research, clinical trials, and precision cancer medicine require new quantitative measurements and computational approaches to correctly quantify cancer cell states and phenotypes, and their spatial organization in tissues^20,67,68. This information is orthogonal but complementary to characterization of genomic heterogeneity in tumors, and is expected to provide new means to understand response to treatment and the evolution of drug resistance^69–72.

Methods:

Our research complies with all relevant ethical regulations and was reviewed and approved by the Institutional Review Boards (IRB) at BWH, HMS and DFCI.

Data availability

Images, generated datasets and corresponding analysis are available in the Synapse.org repository syn22300771⁷⁵. Multiplexed images of human HER2 breast cancer used in Fig. 3a can be viewed in Minerva Story^73,74 an interpretive guide for interacting with multiplexed tissue imaging data https://tinyurl.com/minerva-proliferation. Imaging data and other data supporting the findings of this study are available from the corresponding author on reasonable request.

Code availability

MATLAB codes used to process and analyze the plate-based CyCIF (p-CyCIF) and tissue-based CyCIF (t-CyCIF; shortened as ‘CyCIF’) and the codes used for ccD-CMD analysis are available at https://github.com/santagatalab.

Experimental model and subject details

Cell Lines

BT20, BT549, HCC1937, MCF-7, MCF10A, SUM159 cells were purchased from ATCC and grown in medium (Gibco) supplemented with 10% fetal bovine serum and 1% penicillin/streptomycin (Gibco, 15070–063). Cell lines were regularly retested for identity using short tandem repeat (STR) markers. Growth medium details: EMEM (BT20), RPMI-1640 + 1μg/mL Insulin (BT549), RPMI-1640 (HCC1937), DMEM (MCF-7). MCF10A cells were grown with 5% horse serum (Gibco, 16050–122), 1% P/S, 0.1% Insulin (IN, Sigma, #I1882), 0.05% hydrocortisone (HC, Sigma, #H0888), 0.02% human-EGF (Sigma, E5036), and 0.01% cholera toxin (Sigma, #C8052). SUM159 cells were grown with F-12 + 5% FBS + 1% P/S, 1 μg/ml HC, 5 μg/ml IN, 10 mM HEPES. Cells were incubated at 37°C and 5% CO2.

Human Tissue Sections

Whole slide tissue sections of breast, ovarian, and squamous cell lung carcinoma, and sections of tissue microarrays (TMAs) of breast carcinoma (HTMA226, 227, 240; triplicate 0.6mm diameter cores per case; courtesy of DFCI Breast Oncology Group), glioma (HTMA399; quadruplicate 0.6mm cores), colorectal carcinoma (HTMA402; triplicate 0.6mm), and mesothelioma (HTMA403, triplicate 1.0mm cores) were prepared from formalin-fixed, paraffin-embedded (FFPE) tissue blocks from the archives of BWH Pathology. See Supplementary Table 5 for clinical information of cases analyzed as whole sections. Progression free survival analysis was performed on a subset of cases from HTMA399 and HTMA403 and included only patients with clinical follow-up following resection of primary tumors that were treated using standard-of-care regimens (therapy information: Supplementary Tables 6–7); in the case of gliomas (HTMA399), only IDH-wt glioblastoma were used. FFPE sections of breast carcinoma TMA BRC15010 and eight TMAs comprising case sets 14–17 of the Cancer Diagnosis Program Breast Cancer Stage II TMA were acquired from Pantomics, Inc. and the Mid-Atlantic Division of the Cooperative Human Tissue Network at University of Virginia (clinical data available at https://chtn.sites.virginia.edu/tissue-microarrays#CDPProgn2).

Animal experiments

MMTV-rtTA/tetO-HER2 mice were previously generated⁵⁶; the transgene was induced by introducing a doxycycline containing diet to 8 week-old female FVB MMTV-rtTA/tetO-HER2 mice⁵⁶. Two mice were sacrificed at 3, 6, and 9 weeks following introduction of the doxycycline diet and 2, 4, and 7 days after withdrawal of doxycycline by switching to a standard diet. Mice were euthanized using CO2 inhalation, and all mouse experiments were performed in accordance with protocol 06–034 approved by the DFCI and HMS IUCAC. Multiple primary tumors were excised from each mouse and processed into FFPE blocks. The TMA of MCF-7 cell xenograft used in Fig.3m and Extended-Data-Fig.6e–g was created for a prior publication⁵⁴ and analyzed with CyCIF. Tumor change was calculated as the difference in size between the end of the 4-day treatment and the tumor size before treatment. Tumor size=(length × width²)/2 measured using calipers.

METHOD DETAILS

Experimental methods

Plate-based Cyclic Immunofluorescence (p-CyCIF)

MCF10A cells were plated in flat-bottom polystyrene 96-well plates at ~1e6 cells/mL. Two plates were seeded for two treatment times; 12 wells were seeded (triplicates × 4 treatments). After 24h, cells were either given fresh media or treated with serum-free media, 1μM palbociclib (Sigma, #PZ0383), or 5μM nocodazole (Cell Signaling Technology, 2190S) and incubated at 37°C for 24 or 48h. After treatment, Click-iT™ EdU Alexa Fluor™ 488 solution (Molecular Probes, PZ0383) was added (final concentration 10 μM) and incubated at 37°C for 2h. Cells were washed in Dulbecco’s phosphate-buffered saline (DPBS; Gibco, 14190–250) and fixed with 3.7% paraformaldehyde (Electron Microscopy Science, C993M23) for 30min. Cells were washed and permeabilized with 0.5% Triton® X-100 (Sigma, X100) in PBS (Gibco, 10010023) for 15min.

Other cell lines (BT20, BT549, HCC1937, MCF-7, SUM159) were seeded at densities ranging from 8,000–12,000 cells/well in 96 well plates (Corning 3603, Corning, NY). Drugs were added 24h later with an HP D300e Digital Dispenser (HP, Palo Alto, CA). Serum starvation of MCF-7 cells used 1% FBS. Following 24h of treatment, cells were pulsed with EdU in 10% OptiPrep for 1h and then fixed with 4% formaldehyde in 20% OptiPrep for 1h. Stain/fix solutions were replaced with PBS and plates were sealed.

p-CyCIF was performed using multiple cycles of incubation with primary-labeled antibody, imaging, and fluorophore inactivation as per ref.52. Primary conjugated antibodies and Hoechst 33342 (Thermo Fisher Scientific, 62249) were diluted in Odyssey Blocking Buffer (LI-Cor, cat. no. P/N 927–40003) and incubated at 4°C overnight (Supplementary Table 8 list the antibodies and dilutions ranging from 1:10–1:500). Cells were washed and placed in PBS for imaging using DAPI, FITC, Cy3, and Cy5 channels on GE IN Cell Analyzer 6000. Fluorophores were inactivated with 200μL of bleaching solution (4.5% H2O2, 20 mM NaOH in PBS; Sigma, 216763, Sigma, 221465) for 1h under LED lights (Amazon, cat. no. B078JCBW9S) and washed before adding a new cycle of three antibodies. After completing all cycles, EdU Click-iT Reaction was performed and imaged.

Deep Dye Drop

Cell lines were maintained in recommended conditions and seeded at densities ranging from 1,500–2,000 cells/well in 384-well CellCarrier plates (Perkin Elmer, Waltham, MA) using a Multidrop Combi Reagent Dispenser (Thermo Fisher Scientific, Waltham, MA). 24h later cells were drugs were added with an HP D300e. Cells were stained and fixed for analysis at the time of drug delivery and after 24h treatment according to the Deep Dye Drop protocol⁷⁶. Cells were pulsed with 10μM EdU (Lumiprobe, Waltham, MA) and stained with LIVE/DEAD Far Red Dead Cell Stain (LDR, 1:2000) (Thermo Fisher Scientific, Waltham, MA) in 10% OptiPrep (Sigma Aldrich, St Louis, MO) for 1h. Cells were then fixed with 4% formaldehyde (Sigma Aldrich, St. Louis, MO) in 20% OptiPrep for 30 min. Following aspiration with an EL406 automated plate washer (Biotek, Winooski, VT), cells were permeabilized with 0.5% Triton-X1000 (Sigma Aldrich, St. Louis, MO) in 10% OptiPrep for 20min and EdU was labeled by Click-chemistry (2mM copper sulfate, 4μM sulfo-cy3-azide, 20 mg/ml ascorbic acid, 20% OptiPrep) for 30min. Staining reagents were aspirated and cells were blocked with Odyssey buffer (LI-COR Biosciences, Lincoln, NE) for 1h and stained overnight at 4°C with an Alexa-488 conjugated anti-phospho-histone H3 (pH-H3; clone D2C8) antibody (1:2000 in Odyssey buffer, Cell Signaling Technology, Danvers, MA) and 2 μg/ml Hoechst 33342 (Sigma Aldrich, St. Louis, MO). Cells were washed once with PBS-T (0.1% Tween 20) and twice with PBS and plates were sealed. Fixed cells were imaged with a 10x objective using an ImageXpress confocal microscope (Molecular Devices, San Jose, CA). MetaXpress software was used to segment nuclei based on Hoechst signal, and LDR, EdU and pH-H3 intensities within nuclear masks were extracted. LDR intensity was used to classify live and dead cells, EdU and pH-H3 intensities were used to assign cells to the S- and M- cell cycle phases, and Hoechst signal for DNA quantification.

Tissue Cyclic Immunofluorescence (t-CyCIF)

CyCIF was conducted following published protocols^24,77 on full slide tissues and TMAs. FFPE slides were baked at 60°C for 30min, dewaxed using Bond Dewax solution at 72°C, and antigen retrieval was performed with Epitope Retrieval 1 solution at 100°C for 20min using the BOND RX Automated IHC/ISH Stainer. Antibodies for each cycle were diluted in Odyssey Blocking Buffer and incubated overnight at 4°C in the dark (Supplementary Table 8 lists antibodies). After antibody incubation, slides were stained with Hoechst 33342 for 10 min at RT. Slides were coverslipped using 20–50% glycerol solution (Sigma, G5516) in PBS. Images were taken using DAPI, FITC, Cy3, and Cy5 channels either on the GE IN Cell Analyzer 6000 (20x/0.75NA objective) or on the RareCyte CyteFinder (20x/0.75NA objective). After imaging, fluorophores were inactivated (4.5% H2O2, 20mM NaOH in PBS, 45 min) under LED lights, and the next cycle was performed.

Image processing

p-CyCIF and t-CyCIF image processing is organized in the following steps detailed further below. Additional details and access to the underlying code can be found at https://github.com/labsyspharm/ashlar and https://github.com/santagatalab.

1. stitching, registration, correction of acquisition artifacts were performed using ASHLAR and the BaSiC algorithm. ASHLAR outputs a single pyramid ome.tiff file;

2. the ome.tiff file is re-cut into tiles (typically 5000×5000 pixels) containing only the highest resolution image for all channels. One random cropped image (250×250 pixels) per tile is outputted for segmentation training (using Fiji); for p-CyCIF steps i-ii are optional;

3. ilastik software is trained on cropped images to label nuclear, cytoplasmic, and background areas. Ilastik outputs a 3-color RGB image with label probabilities;

4. RBG probability images are thresholded and watershed in MATLAB to segment the nuclear area. Cytoplasmic measurements are derived by dilating the nuclear mask;

5. single-cell measurements are extracted for each channel (cell-pixel median and mean for both nuclear- and cytoplasmic-area) as well as morphological measurements of area, solidity, and cell location coordinates.

BaSiC

The BaSiC ImageJ plugin tool is used to perform background and shading correction of images⁷⁸. The BaSiC algorithm calculates the flatfield, the change in effective illumination across an image, and the darkfield, which captures camera offset, thermal noise. The dark field correction image is subtracted from the original image, and the result is divided by the flatfield image correction.

ASHLAR

ASHLAR is used to stitch and register image tiles in subsequent layers to those in the first layer⁷⁹ and outputs an OME-TIFF file containing a multi-channel mosaic of the full image across all imaging cycles (https://github.com/labsyspharm/ashlar).

ilastik

ilastik is used to generate nuclear and cytoplasmic segmentation masks from OME-TIFF files⁸⁰. For increased processing speed, randomly selected 250 × 250 pixel regions from the original OME-TIFF are used for training. User annotations are used to train non-linear classifiers that are applied to the entire image to obtain masks describing probabilities of each pixel belonging to nuclear, cytoplasmic, or background areas. A MATLAB (version 2018a) script uses these masks to construct binary masks for nuclear and cytoplasmic area.

Data analysis workflow

Data analysis is divided in a set of pre-processing steps in which data from different tissues is i) log2-transformed and aggregated together, ii) filtered for image analysis errors, and iii) normalized on a channel-by-channel basis across the entire data from a single experiment (performed in MATLAB).

Data aggregation

The processing workflow outputs one ome.tiff image and one data file (.mat) for each tissue area imaged. The data matrices from each .mat file are concatenated into a single matrix for measured metrics (median/mean, nuclear/cytoplasmic) into a single structure (“AggrResults”). The morphological data (i.e., area, solidity, and centroid coordinates) are concatenated into a single structure (“MorpResults”), also containing the indexing vector to keep track of the tissue of origin within the dataset.

Data filtering

Single cells are filtered to identify and potentially exclude from subsequent analysis errors in segmentation and cells lost through the imaging using morphological criteria based on cell-object segmented area (nuclear area and cytoplasmic area within a user-input range and nuclear object solidity above a user-input threshold) which are applied to all rounds for the cell object, and DAPI-based criteria which are applied to DAPI measurements for each round (nuclear measurements and ratio between nuclear and cytoplasmic measurements above user-input threshold). Filter information is allocated to a logical (0–1) structure ‘Filter’, and used to select cells to further analyze by indexing. Threshold selection is dataset dependent and performed by data inspection. Values used in each dataset are available with data analysis codes (Synapse.org, syn22300771).

Data normalization

Each channel distribution is normalized by probability density function centering and rescaling to center distributions of the log2 fluorescent signal at 0 and rescale the distribution widths to facilitate cross-channel comparisons. The data is first log-transformed (base 2). The standard normalization is performed using a 2-component Gaussian mixture model, each model capturing the negative and the positive cell population. If this model fails to approximate the channel distribution, two other strategies are attempted: i) a 3-component model is used assuming the components with the two highest means are the negative and positive distribution (i.e., discarding the lowest component) or ii) the user selects a percentage ‘x’ of assumed positive cells and a single Gaussian distribution fit is performed on the remainder of the data to capture the negative distribution. The single Gaussian fit is then used as the lower component in a 2-component model to estimate positive population distribution. The selected strategy is described (syn22300771).

The “add_coeff” is defined as the intersection of negative and positive distributions. The “mult_coeff” is defined as the difference between the mean of negative and positive distributions. The full distribution is normalized by subtracting the add_coeff and dividing by the mult_coeff. The normalization is performed on nuclear and cytoplasmic single-cell, single-channel distributions individually.

Individual analyses performed in selected datasets is as follows:

Cell type calling strategy

Cells from t-CyCIF are separated into lineages by cell-type markers based on the sign of the normalized value:

• epithelial cells, E-cadherin OR pan-cytokeratin positive;

• immune cells, CD45, CD3D, CD4, CD68, CD163, or CD8a positive;

• stromal cells, αSMA positive and negative for epithelial markers OR Vimentin positive and immune marker negative;

• others/not classifiable, negative for all the markers in above categories

Conflicts such as a cell called as more than one cell-type are resolved by comparing markers that triggered the cell-type calls and assigning cell type based on highest marker level. If markers are within 10% of each other, the cell is “not classifiable”.

Multivariate Proliferation Index (MPI) calculation

The Multivariate Proliferation Index, or MPI, is based on the normalized measurement of 5 markers: three proliferation markers (Ki-67, MCM2, PCNA) and two cell cycle arrest markers (p21, p27). The method avoids relying on single markers while separating cells expressing high level arrest markers (even if proliferation markers are expressed). The logic for the MPI determination is:

The determination of threshold values for proliferation and arrest is dataset dependent.

$$MPI:\text{=}\{\begin{array}{l}+1\text{if(}\sum \text{prolif}-\min (\text{prolif}))>{\text{thresh}}_{\text{prolif}}\\ -1\text{if}(\max (\text{arrest}))>{\text{thresh}}_{\text{arrest}}\\ 0\text{otherwise}\end{array}$$

However due to our marker normalization strategy the values were comparable between datasets (thresh_prolif = 0 and thresh_arrest ~ 0.25–0.75, tuned based on Ki-67 levels).

Clustering and t-SNE

Clustering is performed using k-means algorithm. Cluster arrangement is determined by hierarchical clustering of k-means clustering mean value per cluster (performed in MATLAB using “kmeans” and “clustergram”). t-SNE embedding was performed on a subset of cells with perplexity parameter set at 500.

Spatial Correlation Analysis

Spatial correlations C_xy(r) were computed as Pearson correlation between a cell of group X and its k^th nearest neighbor of group Y, for their respective variables x and y. A value of C_xy (r) was computed for each k up to 100, and distance r was assigned to each k as the average distance between k^th nearest neighbors. For the MPI spatial correlation cell groups X and Y were both epithelial/tumor cells, and variables x and y were logical, whether the cell belonged to the specified MPI category or not. For correlation between MPI categories and tumor microenvironment, group X was the epithelial/tumor cells and group Y was immune compartments. Variable x and y were logical, x = MPI category, y = subtype of immune cells. To calculate characteristic lengths l₁ and l₂, the C_xy data was fitted with a two exponential fit y = a₁*exp(−x/l₁) + a₂*exp(−x/l₂) by least-square fitting with all parameters constrained to be positive (MATLAB in-built function lsqcurvefit). Estimates derived from TMA cores were filtered for fits with residuals below 0.05 (as calculated by lsqcurvefit function) and for cores with >100 MPI+1 cells. Long range estimates were filtered for values below the core size (1.0mm for mesothelioma, 0.6mm for others).

Ripley’s L spatial aggregation analysis

Ripley’s K index was calculated using formula K(r) = (sum(D(D~=0)<r)/n)*(1/lambda), where D is calculated using rangesearch.m Matlab function, n is the number of cells, and lambda is overall tissue cell density. Ripleys’ L function is defined as L(r) = sqrt(K(r)/π)). Transformation to Ripley’s L allows for more direct interpretation in uniformly distributed samples L(r)-r = 0.

Upset plot

Upset plots are computed using the R-package available at https://caleydo.org/tools/upset/.

Pairwise cell cycle difference (ccD) and classical multidimensional scaling reduction (CMD)

ccD is calculated by taking the absolute value of the pairwise Pearson correlation between the cell cycle marker vector of normalized values of each cell. The CMD is performed with a MATLAB built-in function cmdscale. The ccD is reshaped to fit the requirements expected by the cmdscale algorithm, ccD’ = 0.5-ccD/2. The first two dimensions of the CMD scaling are plotted and used for further analysis.

Circular fit, cell cycle dynamics reconstruction, and cell cycle coherence summary metrics

For both simulation data and p-CyCIF/t-CyCIF data the same algorithm was used. CMD scaled two-dimensional data is fit by least-squares minimization to a circle. For each point in the data two parameters are calculated: i) distance to closest point of the circle (circle fit distance, CFD) and ii) angle of the point to the origin of the fitted circle. The angle is used to order cells in what is referred to as “cell cycle ordering”. Given the cyclical structure of the ordering, the origin (time 0) is arbitrary and set to separate M phase markers from early G1. Cell cycle distribution plots (Fig.4g, Fig.6g) are computed by aggregating cells from the ROI listed (5,000 cells max per ROI), running the ccD-CMD algorithm to order cells along the cell cycle, quantifying the histogram of cells belonging to each ROI, and normalizing the frequency to the cell number of the specific ROI.

Cell cycle coherence distance is the CFD detailed above. The angular distribution coefficient of variation is calculated by binning the angle measurements into 8 bins and calculating the proportion of cells/bin. The calculation is repeated by shifting the bin position by π/8 to ensure lack of positional bias in bin definition. We hence refer to this metric as the inter-octile angular variation (IOV). The IOV is the coefficient of variation of bin proportions (equal to 0 in a uniformly distributed population).

A comparison between ccD-CMD pseudotime cell cycle ordering and three time inference algorithms is detailed in Supplementary-Note1 and Extended-Data-Fig.5.

Outcome analysis

Outcome analysis was performed using Kaplan-Meyer estimation and logrank test. The analysis was computed in MATLAB using the MatSurv function⁸¹. Cutoffs were chosen based on cell line observations (IOV = 0.62, CFD = 42) or using the median value for Ki-67 cutoff. The CFD threshold for the mesothelioma cohort was lowered to 37 in order for the “non-canonical” category to have a minimum of 5 patients. Analysis was restricted to cases with >500 MPI+1 cells. The treatment received is listed in Supplementary-Tables6–7. Only patients that received chemotherapy were included.

Cell cycle modeling

The cell cycle was modeled in silico using a system of ordinary differential equations (ODEs) based on the model by Csikász-Nagy and Tyson⁸². A Python script utilizing Euler’s method was used to solve the ODEs. Measurement noise sampled from a Poisson distribution was introduced to reproduce background from microscopy experimental settings, to include both the shot noise and measurement fluctuations. For the “untreated” conditions, the ODEs, kinetic constants, and initial values were based on published parameters⁸², the only variation being lowering of the “maxmass” parameter to 1.8. The “G1 arrest” condition was simulated by setting values of the active CDK/cyclinD complexes to zero to model the effects of palbociclib.

Statistics & Reproducibility

Curve fitting was performed using MATLAB (except for linear fit in Extended-Data-Fig.1f,g which was performed in MS Excel). Statistical tests used are Pearson correlation, 2-sided t-test, 2-sided Kolmogorov–Smirnov (KS) and logrank as specified in figure legends (Fig.1g, 2g, 2i, 3h–i, 7a,b; Extended-Data-Fig.1f–i, 1k, 2f, 4b, 9b–c) performed with MATLAB built-in functions (no multiple hypothesis correction was used). Only samples with a minimum of 100 single cells (after quality control filtering) were included in analyses. Significance was defined as p-value<0.05. Information on sample size, number of independent repeats used, and statistics to summarize data is presented in Supplementary-Table1. Sample sizes were chosen to robustly exceed sample sizes from relevant literature on single cell imaging. When the distribution and variation of phenotypes observed were unknown, we used non-parametric hypothesis testing strategies. No data was excluded. Whenever data was filtered to subselect a population for a figure, the procedure is detailed in the text, figure legend or methods section. Sample randomization was not performed. Whenever visual analysis was performed (pathology scoring) the investigators performing the analysis were not involved in the data collection and were blinded to sample identity.

Extended Data

Extended Data Fig. 1: Multivariate Proliferation Index (MPI) in human cancer tissues.

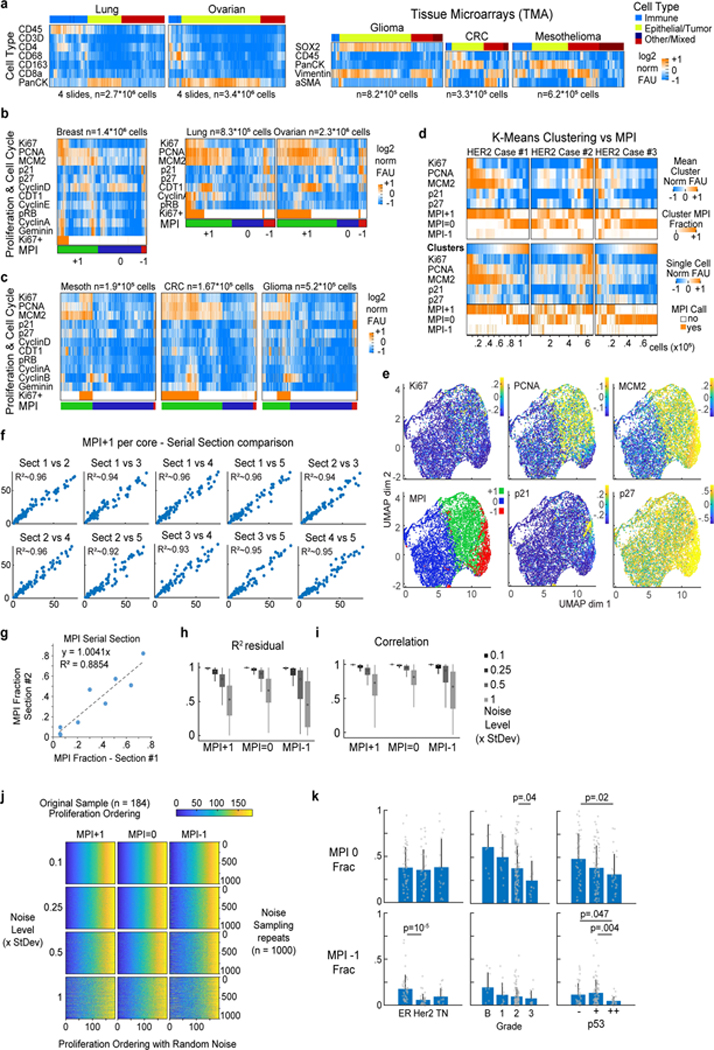
a. Clustered heat map of log2 normalized cell lineage marker signal intensities on a per-cell basis derived from CyCIF images of 4 whole slides of lung squamous cell carcinoma (SCC) and ovarian carcinoma, and tissue microarrays (TMAs) from glioma, colorectal carcinoma (CRC) and mesothelioma. b-c. Clustered heat map of single-cell signal intensities of cell cycle markers for epithelial/tumor cells in Fig. 1a (breast carcinoma) and panel a. Ki-67+ cells were identified by normalization using Gaussian mixture modeling with 2 components. Multivariate Proliferation Index (MPI) indicated: +1 (proliferative, green), 0 (non-proliferative, blue), or −1 (arrested, red). d. K-means clustering heat map of five MPI markers for epithelial/tumor cells of three HER2+ breast cancer samples (k = 20 clusters), and heat map of single-cell normalized log2 intensities. In both, the corresponding MPI category is depicted for comparison (k-mean clustering fraction of MPI category is depicted). e. UMAP plots for 180 samples of breast carcinomas from the Cooperative Human Tissue Network (CHTN) Stage II TMAs (#14–17) with proliferation markers mapped to color (MPI categories were not used as UMAP variables, n = 10,000 cells). f. MPI robustness comparison between five sets of serially cut tissue sections from Pantomics TMA BRC15010 and g. between two sets of serially cut tissue sections of the 3 breast HER2-positive cases from Fig. 1c,e. Each dot represents the fraction of MPI +1 cells in the two indicated tissue sections (linear least-square fit with fixed origin at y=x=0). h-j. Permutation testing of breast carcinomas from the CHTN Stage II TMAs (#14–17, n = 180 samples) with MPI calculations performed by adding increasing amounts of normally distributed noise (0.1x, 0.25x, 0.5x and 1x standard deviations of original marker distribution) to the five MPI cutoffs, repeated 1000 times using i. linear regression, i. correlation analysis (boxplots: median, 25–75^th percentile and min-max extremes from MatLab boxplot.m function), and j. intra-cohort ordering of MPI estimates. k. Comparison of MPI 0, and MPI −1 fractions in epithelial/tumor cells across different classifiers of breast cancer in Fig. 1g (n=142 samples, mean + SD, 2-sided KS p-values with 0.05 significance cutoff).

Extended Data Fig. 2: Multivariate Proliferation Index (MPI) short- and long-range correlations in human cancer tissues.

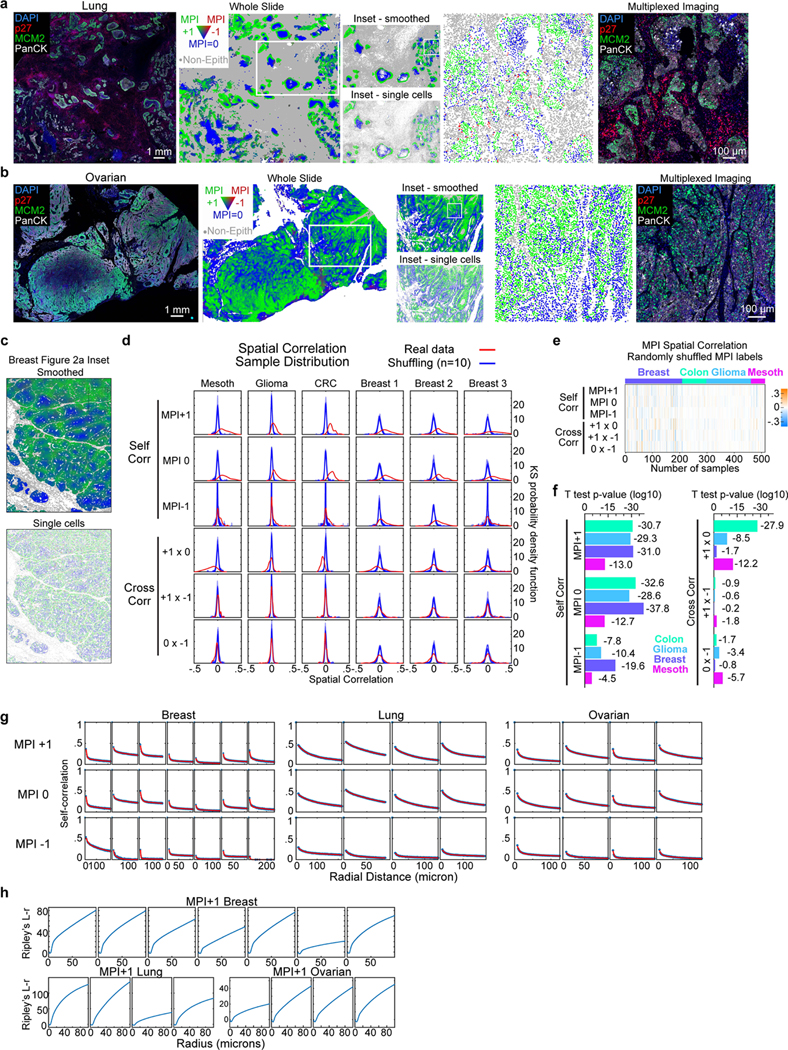
a-b. Composite CyCIF image from a. lung squamous cell carcinoma, and b. ovarian carcinoma (scale bar, 1mm) and corresponding image of long-range whole slide spatial maps of MPI categories (smoothed over 40 neighboring cells for visualization purposes only). Inset panel showing both smoothed and single-cell MPI calling in marked region of interest. Further inset panel of single-cell MPI calling and corresponding composite CyCIF image (scale bar, 100 μm; white = pan-cytokeratin, green = MCM2, red = p27, blue = DNA; example from 4 biological independent specimens). c. Spatial maps of MPI categories from inset 1 from Fig. 2a smoothed over 40 neighboring cells and non-smoothed (single-cell calling). d. Red density curve shows sample distribution of spatial correlations within and across (“self corr” and “cross corr”) MPI categories for mesothelioma, glioma, colorectal carcinoma (CRC) and three breast TMAs (n = 52, 163, 89, 69, 85, 57 samples respectively, k = 5^th neighbor approximation, KS density approximation). Blue density curve shows bootstrap distribution comparison obtained by randomly shuffling of MPI labels (10 independent shuffles). e. Heat map of spatial correlations within and across randomly shuffled MPI labels (“self corr” and “cross corr”, k = 5^th neighbor, n = 513 samples). f. 2-sided t-test p-values for red density curve distributions in panel d (log10 scale used for visualization purposes). g. Plots of spatial correlation from whole slides images of samples in Fig. 2d with two exponential fit for the three MPI categories. h. Ripley’s L-r function for MPI +1 across breast, lung, and ovarian tumors (whole slide images, Fig. 2d). Each column represents an individual and independent tissue.

Extended Data Fig. 3: Limits of cell cycle marker single cell distributions and multi-channel gating interpretation in tissues.

a. Representative single-channel cell cycle marker images from CyCIF imaging with E-cadherin from tissue in Fig. 3a (scale bar 100 μm, example from 3 biological independent specimens). b. Single-channel distributions and two-dimensional scatter plots of a subset of cell cycle markers from HER2 positive breast cancer case #2 in Fig. 1c,e (n = 1,000 epithelial/tumor cells, log2 signal per cell prior to normalization). c. Single channel distributions for cell lineage, proliferation, and cell cycle markers from three HER2+ breast cancer samples (KS density approximation) used in Fig. 1c,e. For proliferation and cell cycle markers only epithelial/tumor cells were used. d. Upset plot of three HER2+ breast cancer samples (n = 0.52 million cells) from Fig. 1 c, e showing frequency of cell cycle marker positivity and their combinations sorted by frequency.

Extended Data Fig. 4: Example of 27-plex CyCIF experiment with tumor sample and tonsil control tissues.

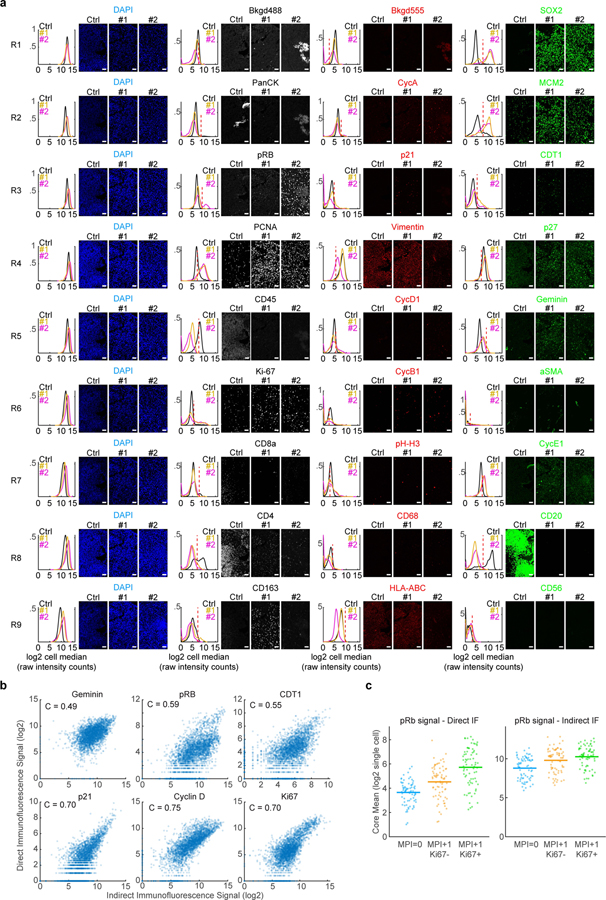
a. Example of positive and negative staining for all markers in CyCIF experiment through rounds of cyclic imaging. Three independent samples are shown: Ctrl is a non-malignant tonsil tissue sample (‘control’), #1 and #2 are glioma samples. Plots are single-cell kernel density estimation for patient samples from respective images (median per pixels within the cell area, log2 FAU, not normalized, black = tonsil, yellow = glioma sample #1, magenta = glioma sample #2, n = 4,278, 2,629, and 2,609 cells, respectively). Each row of images and data is a successive round of CyCIF acquired from the same tissue area (Rx is the x^th round of imaging). All images from antibody channels were linearly contrasted between 0 and 2000 fluorescence units for ease of comparison. Scale bar, 50 μm. Examples from tissue microarray containing 176 independent glioma specimens and 8 independent control specimens. b. Scatter plots of the single-cell correlation of the signal intensity of unconjugated antibodies to the indicated markers versus their fluorophore conjugated versions from 142 samples of tissue from 75 patients (Pantomics TMA BRC15010). Pearson correlation coefficients (C) are shown. All correlation had p-value < 10⁻¹⁷⁵. c. Plot of the phospho-Rb signal from MPI0, MPI +1/Ki-67−, and MPI +1/Ki-67+ cells from Pantomics TMA BRC15010 acquired using both conjugated (‘direct IF’) and unconjugated (‘indirect IF’) phospho-Rb antibodies (n=74 cores, Line is mean value).

Extended Data Fig. 5: Testing of ccD-CMD framework using cell cycle perturbation in vitro and cell cycle modeling in silico, and comparison of temporal inference methods.

a. Left, histograms of fluorescence single-cell log2 normalized signal by plate-based CyCIF (p-CyCIF) from untreated (blue) and 24h palbociclib 1μM treated (orange) MCF10A cells grown in culture (n = 10,000 cells per condition). Right, ccD-CMD plot. b. Heat map and time plot of single-cell signals ordered by ccD-CMD (normalized log2 FAU, n=10,000 cells moving mean over 200 cells). c. Traces from generalized model of mammalian cell cycle⁸¹. Top panels, no noise added. Middle panels, Gaussian measurement noise added (additive and multiplicative). Gray areas are the time frame used for plots in panels d. d. ccD-CMD plot of mathematical model results in shaded areas of panel c. Bottom panel, simulation switch to G1 arrest parameters (CDK/CyclinD complex set to 0) after one cell cycle. Color is the time variable in the mathematical model (n = 10,000 points). e-h. Comparison of time inference methods ccD-CMD, SCORPIUS, Palantir and Cyclum applied to e. synthetic data generated by the mathematical model in panel e. (n = 10,000 observations), f. HER2+ breast cancer tissue data from Fig. 3a–f., and g. MCF10A untreated cells from Fig. 3g. Left, two dimensional visualization output. Right, pseudotime ordering output (n = 5,000 cells, same cells used for all algorithms, normalized log2 FAU, moving mean over 200 cells). h. Comparison between two dimensional reduced space visualization from three time inference algorithms with data from HER2+ breast patient samples #1, 2, and 3 from Fig. 4b–d. i. Coefficient of variation of coherence metrics IOV and CFD in 5 tissues using increasing number of cells (n > 20,000 cells per tissue, CV calculated over 40 independent sub-samplings). j. Comparison of IOV and CFD when one or two markers are removed from ccD-CMD algorithm. Data from untreated MCF10A cells used in panel g. The green dot is the original representation. Orange, one marker removed. Blue, two markers removed. k. Comparison of IOV and CFD when MPI 0 and MPI −1 cells are added at increasing ratios. l. Examples of pseudotime ordering by ccD-CMD algorithm showing inferred CDT1 and Geminin across six tissues areas.

Extended Data Fig. 6: Orthogonal validation of changes in MPI and cell cycle coherence using cell cycle inhibition in vitro and in vivo.

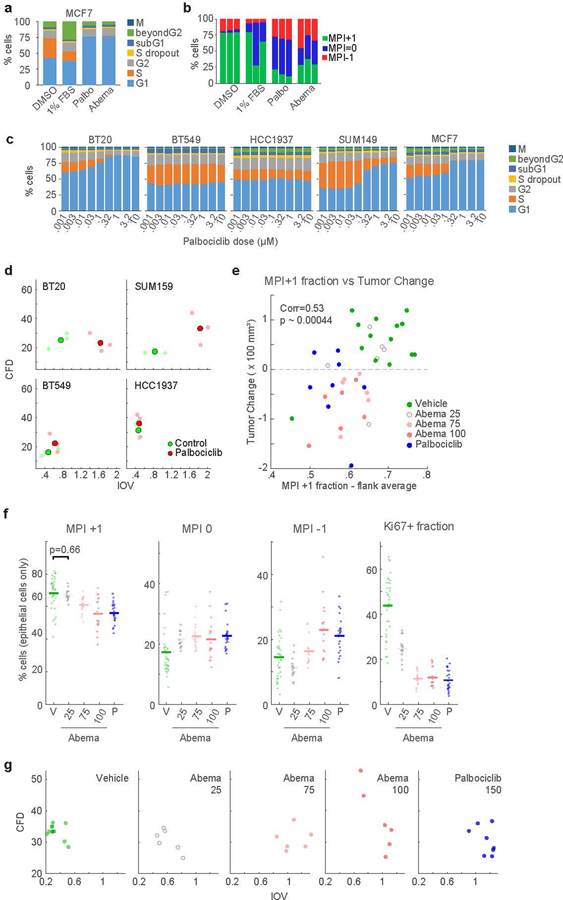
a-b. Stacked bar graphs showing a. cell cycle fractions using the dye drop method⁷⁶ and b. MPI frequencies by p-CyCIF for MCF-7 cells at baseline and in response indicated treatments for 24h c. Cell cycle fractions in five breast cancer cell lines showing differential response to treatment with increasing doses of Palbociclib dependent on the Rb status of the cell line. d. ccD-CMD plot from p-CyCIF from fixed untreated cells (Control), and cells exposed to 1 μM Palbociclib for 24h. Enlarged dot represents the average of 3 distinct biological replicates, n = 1000 cells each. e-g. t-CyCIF validation in MCF-7 xenografts in nude mice⁵⁴. Doses are in mg/kg. e. Scatter plot of change in tumor size and MPI +1 fraction. Vehicle, n = 14 tumors from 7 mice. Abemaciclib, n = 6 tumors from 3 mice per dose. Palbociclib, n = 8 tumors from 5 mice. Each dot represents an individual tumor (2-sided Pearson correlation p-value). f. MPI and Ki-67 fractions per TMA core (mean of n = 35, 15, 17, 18, and 24 total cores, 2-sided t-test p-value). g. ccD-CMD plots from individual MCF-7 xenografts tumors (4000 cells per mouse, n=12, 6, 6, 6, 8 mice).

Extended Data Fig. 7: Cell cycle dynamics from ccD-CMD from human cancer tissues.

a. Scatter plot of CFD versus IOV (for each ROI from Fig. 4f). b. K-means clustering of cell cycle markers from selected ROIs used in Fig. 4g (n = 3600 cells per ROI, k = 15 clusters). Left, single-cell clustering with ROI annotation (log2 normalized FAU). Middle, cluster median. Right, ROI composition for each cluster. c. Scanned image of hematoxylin and eosin (H&E) stained section from three HER2 positive breast tissues with pathology annotations. d. Composite CyCIF images of tissues from panel c (green CD45, red Vimentin, white E-Cadherin, scale bar 2mm). e. Inter-Octile Variation IOV, f. Circle Fit Distance (CFD), and g. MPI +1 fraction for each ROI noted in panel d.

Extended Data Fig. 8: HER2 expression and cell cycle dynamics in human breast cancer tissues and HER2 driven mouse model of breast cancer.

a. ccD-CMD plots for two HER2+ breast cancer tissue microarrays (TMA # 1 and #2) for increasing levels for HER2 protein. Single cells binned by normalized HER2 levels (n = 5,000 cells per bin were used). Right, ccD-CMD scatter plots of highest HER2 bin for both TMA1 and 2 with single marker normalized intensities mapped to color (n = 5,000 cells). b. ccD-CMD scatter plots of the single-cell data from MPI +1 cells from time course of HER2 induction and repression in GEMM with single marker normalized intensities mapped to color (n = 5,000 cells per plot, p27 was not used by the ccD-CMD algorithm). c. Mean +/− 25^th percentile of circle fit distance of cell cycle markers in tumor cells (in situ and invasive) from Fig. 5h (n = 5,000 cells per plot).

Extended Data Fig. 9: Association between with clinical outcome and cell proliferation metrics.

a. Scatter plots of CFD versus IOV from mesothelioma and glioblastoma sample cohorts (n = 22 and 32 patients, respectively). Colors represent binning into coherence groups according IOV and CFD metrics. b-c. Kaplan Meier estimation and logrank p-value of progression-free survival (PFS) for the two patient cohorts in Fig. 7. Patients were binned in b. three groups “coherent”, IOV^high “skewed” and IOV^low CFD^high “non-canonical” groups from panel a). or c. two groups based on the median Ki-67+ fraction.