Estimating sibling spillover effects with unobserved confounding using gain-scores

Abstract

Purpose

A growing area of research in epidemiology is the identification of health-related sibling spillover effects, or the effect of one individual’s exposure on their sibling’s outcome. The health within families may be inextricably confounded by unobserved factors, rendering identification of sibling spillovers challenging.

Methods

We demonstrate a gain-score regression method for identifying exposure-to-outcome spillover effects within sibling pairs in linear models. The method can identify the exposure-to-outcome spillover effect if only one sibling’s exposure affects the other’s outcome; and it identifies the difference between the spillover effects if both siblings’ exposures affect the others’ outcomes. The method fails with outcome-to-exposure spillover or outcome-to-outcome spillover. Analytic results, Monte Carlo simulations, and a brief application demonstrate the method and its limitations.

Results

We estimate the spillover effect of a child’s preterm birth on an older sibling’s literacy skills, measured by the Phonological Awareness Literacy Screening-Kindergarten test. We analyze 20,010 sibling pairs from a population-wide, Wisconsin-based (United States) birth cohort. Without covariate adjustment, we estimate that preterm birth modestly decreases an older sibling’s test score.

Conclusion

Gain-scores are a promising strategy for identifying exposure-to-outcome spillover effects in sibling pairs while controlling for sibling-invariant unobserved confounding.

INTRODUCTION

A sibling spillover effect (i.e., “interference,” “carryover effect”) is the effect of an individual’s exposure on their sibling’s outcome [1-3]. The past two decades of epidemiologic research witnessed a burgeoning interest in the role of family environments in childhood health, calling attention to the importance of spillovers within families [4-11]. Yet, sibling spillovers are largely unexamined in the epidemiologic literature, as most field-specific advancements in spillover identification have been restricted to infectious diseases [12-22]. With growing interest in the familial interdependence of health [5-11], the need for analytical tools to identify sibling spillovers is acute.

Unobserved confounding is particularly salient with sibling spillovers. Siblings often share family and social environments that affect their outcomes but remain unmeasured even in data-rich contexts [10]. Fixed effect (FE) designs that control for unobserved time-invariant confounding are immediately appealing [3, 23, 24], but there is little precedent for their use to identify sibling spillovers. Sjölander et al. (2016) investigated two-sibling FE models for identifying an individual’s exposure on their own outcome in the presence of spillover, noting that spillover may be identifiable [3]. Black et al.’s (2021) difference-in-differences method with three-sibling clusters measured a lower-bound estimate of the effect of a child’s disability on an older sibling’s academic performance [25].

In this paper, we demonstrate a method for identifying spillovers in sibling pairs with gain-scores (i.e., “change scores,” “difference scores”), a staple of FE estimation that removes shared confounding by differencing outcomes [26, 27]. Consistent with applied FE studies, we focus on linear models with homogenous effects [23, 24, 26, 27]. First, we briefly introduce causal directed acyclic graphs (DAGs), which illustrate our models. Second, we discuss various two-sibling models with one- or two-sided spillover and explain how and when gain-score methods identify spillover effects. Third, we illustrate our results with simulations. Fourth, we apply the method to identify the effect of a younger sibling's preterm birth on an older sibling's literacy test performance.

CAUSAL DIRECTED ACYCLIC GRAPHS

Causal DAGs are useful for explaining the identification of causal effects. We review necessary terminology for this exposition. Causal DAGs are diagrams consisting of nodes (variables) and directed edges (direct causal effects) that represent the assumed data-generating process (causal model) [28-33]. Paths are sequences of adjacent edges, regardless of the arrows’ directions. On causal paths between exposure and outcome, all arrows point from the exposure to the outcome. On non-causal paths between an exposure and an outcome, at least one arrow points away from the outcome. Causal paths “transmit” causal effects, whereas non-causal paths may transmit spurious associations. Colliders are variables that receive two inbound arrows on a path (a given variable may be a collider on one path but not on another). Pearl’s d-separation criterion determines which variables in data generated by the assumed DAG are conditionally or unconditionally independent: two variables are independent if all paths between them are closed; and a path is closed if it includes a conditioned noncollider variable, or if it includes an unconditioned collider variable [29, 30, 33]. Conversely, two variables may be associated if at least one path between them is open (d-connected); and a path is open if it is not closed.

Typically, health researchers attempt to identify causal effects by conditioning on observed variables through adjustment via regression analysis, matching, or inverse-probability weighting to close all non-causal paths between the exposure and outcome [29, 30, 33]. Unfortunately, open non-causal paths containing only unobserved intermediate variables cannot be closed by covariate adjustment. In multilevel analyses in which observations are clustered into groups (e.g., children in families), however, FE methods can sometimes identify causal effects by subtracting out certain types of group-level unobserved confounding [23-27]. Next, we describe several sibling spillover models with unobserved confounding and show when gain-score estimation can identify spillover effects.

METHOD FOR SIBLING SPILLOVER IDENTIFICATION

Model and assumptions

We present our baseline sibling spillover model and subsequently introduce variations on this model. For illustration, we discuss the spillover of a child’s early health shock on their sibling’s academic outcome. This example is purposefully generic but broadly applicable, drawing upon prior work of health-related spillover effects on academic performance [25] while motivating our empirical application.

Our baseline model is a linear two-sibling comparison design with one-sided spillover (Figure 1A). Subscript i = 1, …, N indicates family and subscript j = 1,2 indicates sibling. T_ij represents a binary or continuous exposure (e.g., the health shock), Y_ij represents a continuous outcome (e.g., academic performance), U_i represents unobserved family-level confounding (i.e., the FE), and D_i represents the gain-score, D_i = Y_i2 − Y_i1. Parameters include the spillover effect, θ (T_i1 → Y_i2), of sibling 1’s exposure on sibling 2’s outcome; the targeted effect, δ (T_ij → Y_ij), of an individual’s exposure on their own outcome; and unobserved family-level confounding effects χ (U_i → T_i1), γ (U_i → T_i2), and Ψ (U_i → Y_ij).

Figure 1.

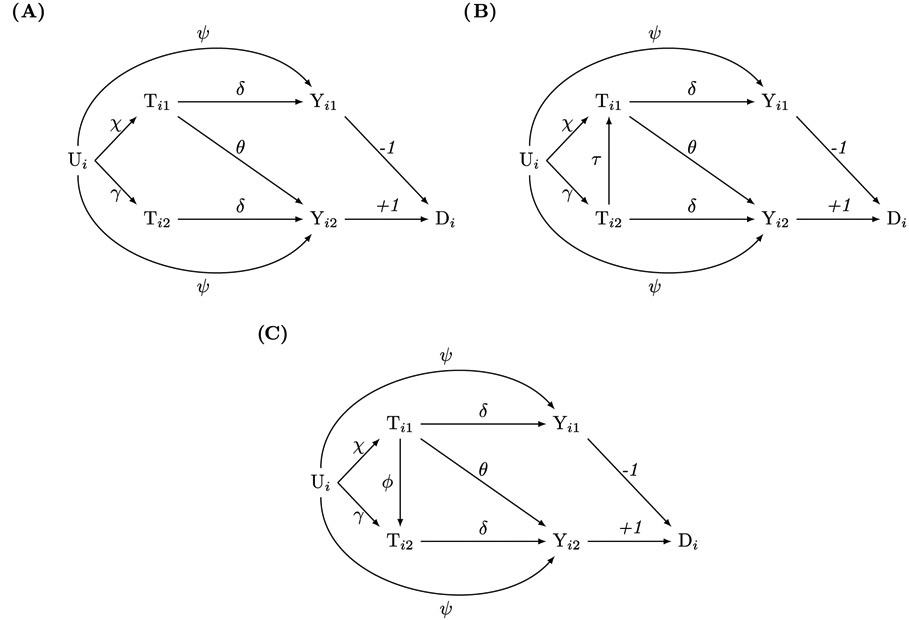
Causal directed acyclic graphs for linear data-generating models with one-sided exposure-to-outcome sibling spillover. Subscripts i and j denote family and sibling, respectively. T_ij is the exposure, Y_ij is the outcome, D_i is the gain-score, and U_i is an unobserved family-level confounder. Greek letters denote effects. (1A) does not have exposure-to-exposure spillover, whereas (1B) and (1C) have exposure-to-exposure spillovers. The gain-score method precisely identifies the spillover effect θ (T_i1 → Y_i2) in all three models.

All models embed several simplifying assumptions. First, targeted and unobserved family-level confounding effects on outcomes are sibling-invariant [23, 24]. Second, all effects are linear and homogenous. Third, spillovers exist within families but not between families (i.e., partial interference) [15, 34]. Aside from permitting partial interference, these assumptions align with conventional FE models [3, 23, 24, 26, 27].

Notably, our presentation abstracts from sibling-specific baseline covariates, C_ij. Covariates may be added to our baseline and subsequent models as long as controlling for C_ij in the gain-score regression does not induce new biases [35-38].

Gain-score estimation and identification of spillover effects

This subsection analyzes whether the gain-score estimator point-identifies spillover effects (i.e., recovers the spillover effect precisely) for nine different sibling spillover models. that differ by whether spillover is one- or two-sided and by whether additional spillovers are present.

Gain-score estimation

We investigate the ability of a gain-score estimator to identify exposure-to-outcome spillover effects. First, we regress the gain-score on both siblings’ exposures,

$$D_i=b_1{T}_{i1}+b_2{T}_{i2}+e_i,$$ (1)

where b₁ and b₂ are partial regression coefficients for T_i1 and T_i2, respectively, and e_i is the residual. We then sum the partial regression coefficients to compute a “spillover coefficient” (SC),

$$SC=b_1+b_2.$$ (2)

We will now interrogate whether the SC identifies causal spillover effects in each of several commonly assumed data generating processes in health research.

Settings with one-sided spillover

The object of interest (estimand) is the direct spillover effect, θ, of sibling 1’s health shock, T_i1, on sibling 2’s academic performance, Y_i2. Under the baseline model (Figure 1A), three open paths connect T_i1 and Y_i2. The first path, T_i1 → Y_i2, is the causal spillover effect of interest. The other two paths are non-causal paths that may transmit spurious association. The first non-causal path, T_i1 ← U_i → T_i2 → Y_i2, can be closed by adjusting for T_i2. However, the second non-causal path, T_i1 ← U_i → Y_i2, cannot be closed by covariate adjustment because it only contains the unobserved variable U_i.

Nonetheless, we can identify θ through gain-score regression. Under the assumptions of Figure 1A, it can be shown that b₁ = θ − δ and b₂ = δ, using elementary regression algebra. Therefore, the spillover coefficient equals SC = b₁ + b₂ = θ.

The intuition for this result is that first-differencing exactly offsets confounding biases involving U_i [26, 27], and that the SC corrects for the contamination of the spillover estimate in b₁. Specifically, the coefficient b₁ on T_i1 captures the association flowing along the two open paths from T_i1 to D_i. There are five paths from T_i1 to D_i (listed together with their corresponding path coefficients):

1. T_i1 ← U_i → T_i2 → Y_i2 → D_i (non-causal): δχγ

2. T_i1 ← U_i → Y_i1 → D_i (non-causal): −Ψχ

3. T_i1 ← U_i → Y_i2 → D_i (non-causal): Ψχ

4. T_i1 → Y_i1 → D_i (causal): −δ

5. T_i1 → Y_i2 → D_i (causal): θ

The first path is closed because the gain-score regression adjusts for T_i2. The second and third paths cancel each other out exactly. The fourth path transmits the negative of the targeted effect. The fifth path transmits the spillover effect. Hence, the regression coefficient b₁ = θ − δ identifies the difference between the spillover and targeted effect.

The coefficient b₂ on T_i2 captures the association flowing along the open paths from T_i2 and D_i. There are four paths from T_i2 to D_i:

1. T_i2 ← U_i → Y_i1 → D_i (non-causal): −δχγ

2. T_i2 ← U_i → Y_i1 → D_i (non-causal): −Ψγ

3. T_i2 ← U_i → Y_i2 → D_i (non-causal): Ψγ

4. T_i2 → Y_i2 → D_i (causal): δ

The first path is closed because the gain-score regression adjusts for T_i1; the second and third paths cancel each other out; and the fourth path captures the targeted effect. Thus, b₂ = δ identifies the targeted effect, and SC = b₁ + b₂ = θ identifies the causal spillover effect.

Many statistical software packages have functions for summing regression coefficients and obtaining standard errors. Examples include Stata’s lincom command, R’s contrast package, and SAS’s SCORE procedure [39-41].

The analysis is only slightly complicated in the presence of exposure-to-exposure spillover (T_ij → T_ij′)—for example, when one child’s serious illness increases their sibling’s risk of illness. When T_i2 → T_i1 (Figure 1B), the interpretation of the SC does not change. However, if T_i1 → T_i2 (Figure 1C), then the interpretation of SC = θ changes from representing the entire spillover effect of T_i1 on Y_i2 to capturing only the direct spillover effect, since the indirect component of the spillover effect that operates via the causal path T_i1 → T_i2 → Y_i2 is closed because the regression controls for T_i2. See the Appendix for details.

Settings with two-sided spillover

Analysts may also encounter scenarios with two-sided spillover. In our example, each siblings’ health shock could affect the other’s academic performance (T_i1 → Y_i2 and T_i2 → Y_i1). Reflecting this possibility, Figure 2A modifies the baseline model of Figure 1A to allow spillover T_i2 → Y_i1 with effect κ. The partial regression coefficients in the gain-score approach identify b₁ = θ − δ and b₂ = δ − κ, so that SC = b₁ + b₂ = θ − κ. Consequently, with two-sided exposure-to-outcome spillover, the SC does not identify the spillover effect of T_i1 on Y_i2 but instead the difference between the two exposure-to-outcome spillover effects. However, if the analyst can defend assumptions about one or more of the signs of the two spillover effects, then the SC remains informative even though it no longer point-identifies θ. Specifically, if κ > 0, the SC underestimates (i.e., gives a lower bound for) θ. By contrast, if κ < 0, then SC overestimates (gives an upper bound for) θ. One can make additional inferences about θ depending on the value of SC and the assumed sign of κ. For example, if SC > 0 and κ > 0, then θ > 0. Of note, a finding that SC = 0 is uninformative, because it is compatible with the possibility that the two spillover effects are equal (θ = κ ≠ 0) or that exposure-to-outcome spillovers are absent (θ = κ = 0).

Figure 2.

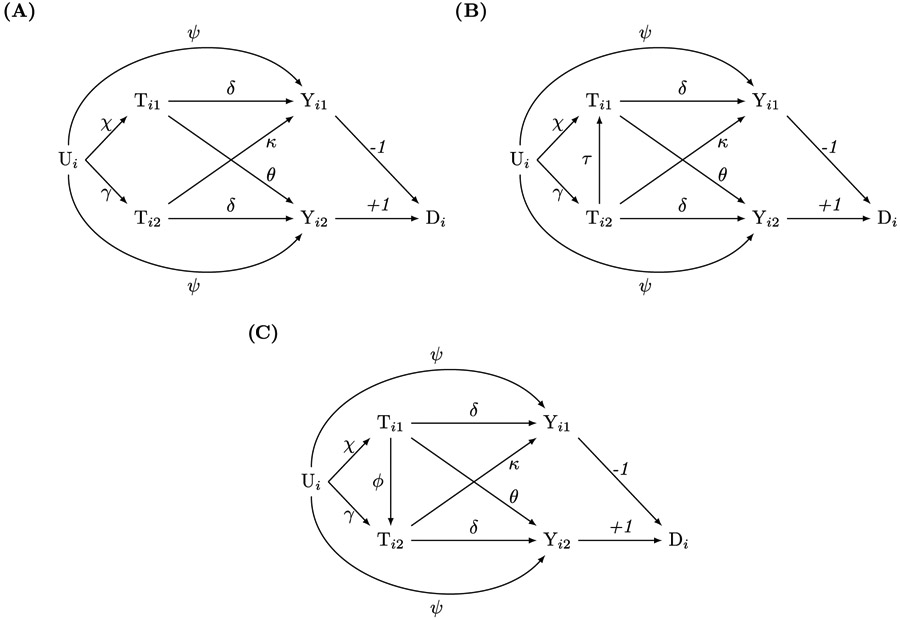
Causal directed acyclic graphs for linear data-generating models with two-sided exposure-to-outcome sibling spillover. Subscripts i and j denote family and sibling, respectively. T_ij is the exposure, Y_ij is the outcome, D_i is the gain-score, and U_i is an unobserved family-level confounder. Greek letters denote effects. (2A) does not have exposure-to-exposure spillover, whereas (2B) and (2C) have exposure-to-exposure spillover. The gain-score method identifies the differences between the spillover effects θ (T_i1 → Y_i2) and κ (T_i2 → Y_i1) in all three models.

If T_ij → T_ij′ in addition to two-sided spillover (Figures 2B-C), then SC identifies the difference between the direct parts of the siblings’ spillover effects that are not mediated by T_i1 or T_i2, respectively, i.e., SC will not consider the indirect spillover effects, T_ij → T_ij′ → Y_ij′. See the Appendix for details.

Settings with spillovers from outcomes

Analysts may also encounter settings with outcome-to-outcome spillover (Y_ij → Y_ij′) or outcome-to-exposure spillover (Y_ij → T_ij′). In our example, siblings’ academic outcomes may affect each other via outcome-to-outcome spillover. In contrast, an academic outcome causing a health shock is implausible, but outcome-to-exposure spillovers may be relevant elsewhere.

If one sibling’s outcome causes the other sibling’s exposure or outcome (Figure 3), then our gain-score approach does not identify spillovers or simple functions of spillovers. See the Appendix for details.

Figure 3.

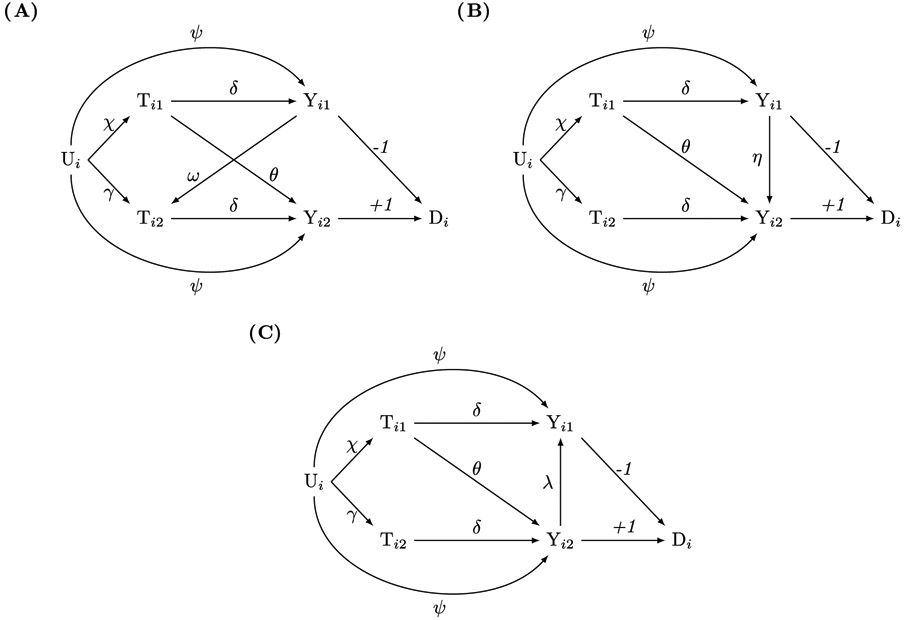
Causal directed acyclic graphs for linear data-generating models with one-sided exposure-to-outcome sibling spillover and spillover from outcomes. Subscripts i and j denote family and sibling, respectively. T_ij is the exposure, Y_ij is the outcome, D_i is the gain-score, and U_i is an unobserved family-level confounder. Greek letters denote effects. (3A) has outcome-to-exposure spillover, and (3B) and (3C) have outcome-to-outcome spillover. The gain-score method does not identify the spillover effect θ (T_i1 → Y_i2) in any of the three models.

SIMULATION

Nine Monte Carlo simulations [42]—one simulation for each model in Figures 1-3—demonstrated when the method identifies exposure-to-outcome spillover. Our simulation equations are¹:

$$U_i,v_{i1},v_{i2}\sim N(0,1)$$

$$T_{i1}=\{\begin{array}{c}0if\tau T_{i2}+\chi U_i\le 0.5\hfill \\ 1if\tau T_{i2}+\chi U_i>0.5\hfill \end{array}\phantom{\}}$$

$$T_{i2}=\{\begin{array}{c}0if\varphi T_{i1}+\omega Y_{i1}+\gamma U_i\le 0.2\hfill \\ 1if\varphi T_{i1}+\omega Y_{i1}+\gamma U_i>0.2\hfill \end{array}\phantom{\}}$$

$$Y_{i1}=\delta T_{i1}+\kappa T_{i2}+\lambda Y_{i2}+\psi U_i+v_{i1}$$

$$Y_{i2}=\delta T_{i2}+\theta T_{i1}+\eta Y_{i1}+\psi U_i+v_{i2}$$

$$D_i=Y_{i2}-Y_{i1}$$

We simulated each model with 1000 runs of 5000 observations each, where each observation represented a sibling pair (i.e., family). We set the following parameters at fixed values: θ = 0.5, δ = 1, ψ = 1, χ = 2, and γ = 3. Parameters that distinguish models—κ, τ, φ, ω, η, and λ—were set to zero in models where absent and were set to 0.3 in models where present. To avoid simultaneity, at least one parameter in each pair (τ, φ), (η, λ), and (κ, ω) was always set to zero. In each sample, we regressed the gain-score on siblings’ outcomes and computed the spillover coefficient according to equations (1) and (2). We conducted simulations in Stata Statistical Software: Release 16 [43]. Simulation code is in the Appendix.

Figure 4 displays the simulation results. The first three rows confirm that the spillover coefficient is unbiased in the three settings with one-sided exposure-to-outcome spillover of Figure 1, as the average of estimated spillover coefficient equals the known spillover effect, ${\widehat{SC}}_{Figure1}=0.5$ (empirical 95% CI: 0.42, 0.58). The subsequent three rows demonstrate that the spillover coefficient in the three models of Figure 2 with two-sided exposure-to-outcome spillover identifies the difference between the two spillovers, ${\widehat{SC}}_{Figure2}=0.5-0.3=0.2$ (empirical 95% CI: 0.12, 0.28). Since κ > 0, ${\widehat{SC}}_{Figure2}$ underestimates the spillover effect, θ. The final three simulations show that ${\widehat{SC}}_{Figure3}$ is biased in all models of Figure 3 with spillovers from outcomes. Size and direction of the biases are complicated functions of the coefficients in the data-generating model and can be large. The estimated ordinary least squares standard errors closely resemble the empirical standard errors for each model, indicating that the built-in standard errors in Stata’s lincom command are accurate [39].

Figure 4.

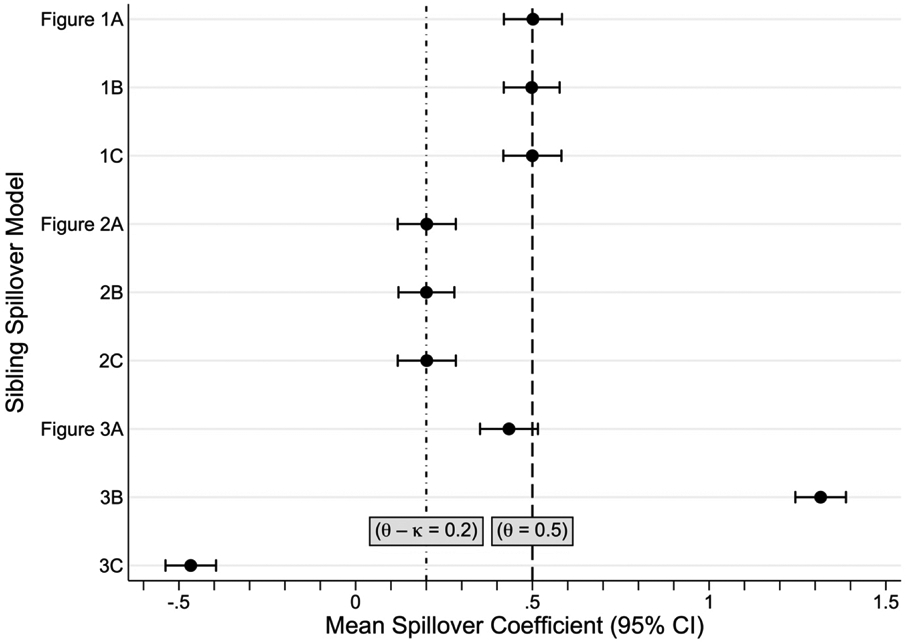
Results (average spillover coefficients and empirical 95% confidence intervals [CI]) from simulations of the nine sibling spillover models in Figures 1-3. Each simulation consisted of 1000 runs of 5000 observations, where each observation represented a sibling pair (i.e., family). Subscripts i and j indicate family and sibling, respectively. T_ij is the exposure and Y_ij is the outcome. The target quantity is the spillover effect (T_i1 → Y_i2), set to θ = 0.5 in all models. Other spillover effects include κ (T_i2 → Y_i1), τ (T_i2 → T_i1), φ (T_i1 → T_i2), ψ (Y_i1 → T_i2), η (Y_i1 → Y_i2), and λ (Y_i2 → Y_i1). Except for θ, all spillover parameters were set to zero except in the following cases: κ = 0.3 in Figures 2A-C; τ = 0.3 in Figures 1B and 2B; φ = 0.3 in Figures 1C and 2C; ω = 0.3 in Figure 3A; η = 0.3 in Figure 3B; and λ = 0.3 in Figure 3C. The spillover coefficient identifies (i.e., is unbiased) for θ in all models of one-sided spillover (Figure 1); identifies the difference between the two exposure-to-outcome spillover effects with two-sided spillover (Figure 2); and is biased in the presence of spillovers originating from outcomes (Figure 3).

EMPIRICAL APPLICATION

We applied the method to estimating the spillover effect of a child’s preterm birth (gestational age <37 weeks) on their older sibling’s literacy skills. This analysis builds upon evidence that short gestational age and other health shocks may harm children’s academic outcomes [25, 44, 45]. If a child is born preterm, parents may reallocate investments (time, financial, or otherwise) from older siblings to support the younger sibling's health, thereby inhibiting the older siblings' development, including early literacy.

For this application, we analysed Big Data for Little Kids (BD4LK), a longitudinal cohort of birth records for all live in-state resident deliveries in Wisconsin during 2007-2016 (N>660,000 deliveries) that links to multiple administrative data sources, including Medicaid data (2007-2016) and children’s Phonological Awareness Literacy Screening-Kindergarten (PALS-K) test scores from Wisconsin public schools (2012-2016 school years). BD4LK’s linking process is described elsewhere [45, 46]. PALS-K evaluates readiness for kindergarten-level literacy instruction on six domains (rhyme awareness; beginning sound awareness; alphabet knowledge; letter sounds; spelling; word concept) [46]. In Wisconsin, children must be five years-old at kindergarten enrolment to qualify for PALS-K testing [48]. Our analysis includes 20,010 sibling pairs (40,020 children) that were sequentially-born from different deliveries to the same biological mother and had non-missing English-language PALS-K test scores and covariates. The Appendix contains the full sampling description.

We estimate the following gain-score regression,

$$D_i=b_{1}PT{B}_{i1}+b_{2}PT{B}_{i2}+{\beta }_3{\mathit{C}}_{i2}+v_i$$

where D_i= PALSK_i2 – PALSK_i1 is the gain-score. Subscripts i = 1, … N and j = 1,2 indicate family and sibling, respectively, where j = 1 is the younger sibling. PTB_ij is a binary preterm birth indicator (1 if preterm; 0 otherwise), PALSK_ij is the continuous PALS-K score (0-102 points), and C_i2 is a vector of covariates measured at the older sibling’s delivery. Covariates include maternal age (years), maternal education (no high school diploma; high school diploma/equivalent; 1-3 years college; 4+ years college), and Medicaid delivery payment (no; yes).

We ran the regression twice, once with and once without covariates, and then computed the spillover coefficient, SC = b₁ + b₂. Assuming the one-sided spillover model of Figure 1A, SC from the regression without covariates identifies the effect of a younger sibling’s preterm birth on the older sibling’s PALS-K score. Additionally, b₂ identifies the effect of each sibling’s preterm birth on their own PALS-K score. We performed all analyses in Stata Statistical Software: Release 16 [43]. The University of Wisconsin-Madison minimal risk institutional review board approved our project.

Tables A.1 and A.2 summarize baseline characteristics of our sample (Appendix). Preterm birth incidence was slightly greater among older siblings relative to younger siblings (6.78% vs. 6.65%). On average, older siblings received slightly lower PALS-K scores (mean 63.58 points; SD 24.12 points) relative to younger siblings (mean 64.22 points; SD 23.83 points). Approximately 10% of observed families had discordant preterm birth exposures. In the regression without covariate adjustment, the older sibling's preterm birth coefficient was ${\widehat{b}}_2=\text{−}2.49$ points (95% CI −3.83, −1.15 points), the younger sibling's preterm birth coefficient was ${\widehat{b}}_1=0.38$ points (95% CI: −0.97, 1.73 points), and the resulting $\widehat{SC}$ was −2.11 points (95% CI: −3.82, −0.40 points) (Table 1). This indicates that a younger sibling’s preterm birth modestly harmed their older sibling’s PALS-K performance. Figure 5 displays these results graphically relative to the assumed data-generating model. However, covariate adjustment attenuated the $\widehat{SC}$ to −1.49 points (95% CI −3.21, 0.22 points).

Table 1.

Ordinary least squares regression of the difference in siblings’ PALS-K scores^a (points) on their preterm birth statuses (N = 20,010 sibling pairs)

	Unadjusted Regression Coefficient (95% CI)	Adjusted Regressionb Coefficient (95% CI)
Preterm birth (gestational age <37 weeks)
Older sibling	−2.49 (−3.83, −1.15)	−2.28 (−3.62, −0.94)
Younger sibling	0.38 (−0.97, 1.73)	0.79 (−0.57, 2.14)
Spillover coefficientc	−2.11 (−3.82, −0.40)	−1.49 (−3.21, 0.22)

^aThe difference in PALS-K scores equals the older sibling’s PALS-K Score minus the younger sibling’s PALS-K score.

^bCovariates include maternal age at delivery (years), maternal education at delivery (no high school diploma; high school diploma/equivalent; 1-3 years college; 4+ years college) and Medicaid delivery payment (no; yes), all of which were measured at the time of the older sibling’s delivery.

^cThe spillover coefficient is the sum of the partial regression coefficients for the older sibling’s preterm birth indicator and the younger sibling’s preterm birth indicator. Assuming one-sided spillover as in Figure 1A, this identifies the effect of a younger sibling’s preterm birth on the older sibling’s PALS-K score.

Abbreviations: ”CI” confidence interval; ”PALS-K” Phonological Awareness Literacy Screening-Kindergarten.

Figure 5.

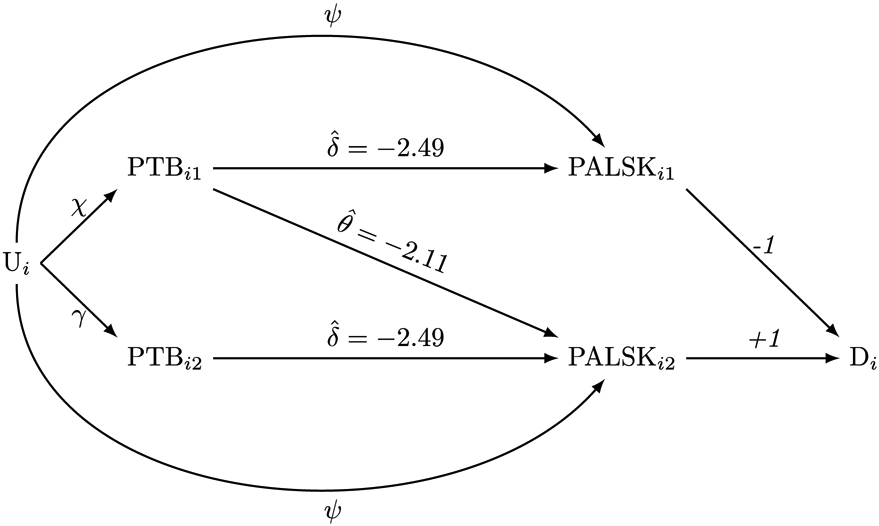
A directed acyclic graph of the relationship between siblings’ preterm birth (gestational age <37 weeks) and their score on the Phonological Awareness Literacy Assessment-Kindergarten test with overlaid estimates. Subscripts i and j denote family and sibling, respectively, where j = 1 is the younger sibling and j = 2 is the older sibling. PTB_ij is a preterm birth indicator, PALSK_ij the test score, D_i is a gain-score, and U_i is an unobserved confounder. Greek letters denote effects, and θ and δ are estimated using gain-score regression.

DISCUSSION

We described a simple gain-score approach for identifying spillovers in linear models of sibling pairs. This method can point-identify spillovers if only one sibling’s exposure affects the other’s outcome, and it can identify the difference in siblings’ spillovers in the presence of two-sided spillover. The method leverages the primary benefit of FE estimation: controlling for family-level, sibling-invariant, unobserved confounding. Whereas preceding epidemiologic research on spillover identification primarily considered infectious diseases, our work contributes to the growing literature on spillovers within families.

We acknowledge some limitations. First, we restricted our attention to linear models. This method does not necessarily apply to other settings, such as models with binary outcomes (see Sjölander et al. [2016] for binary outcomes in our Figure 1A [3]). Second, we accepted conventional FE assumptions, which include equal effects of the unobservables on siblings’ outcomes and a constant spillover effect that does not vary by characteristics, such as siblings’ age difference. Deviation from these assumptions may induce bias [3, 37, 38]. Third, we did not consider families of three or more siblings. Spillovers that originate from larger sibships may pose unique challenges that are unaddressed here—for example, whether one can identify the effect of a middle child's exposure on the youngest sibling's outcome if an eldest sibling's exposure affects all siblings' outcomes. Lastly, we did not investigate spillover in the presence of shared mediator or collider variables. Sjölander and Zetterqvist (2017) interrogated sibling comparison models with shared mediators and colliders, finding that such factors may induce bias [49].

Nonetheless, our paper lays groundwork for subsequent research. Specific avenues that advance this method include testing in nonlinear settings or settings with shared mediator variables, expanding models to allow three or more siblings, and developing tests for assessing bias from outcome-induced spillovers.

ABBREVIATIONS

BD4LK

Big Data for Little Kids

DAG

directed acyclic graph

FE

fixed effects

PALS-K

Phonological Literacy Awareness Screening-Kindergarten