Atomically sharp domain walls in an antiferromagnet

Abstract

The interest in understanding scaling limits of magnetic textures such as domain walls spans the entire field of magnetism from its physical fundamentals to applications in information technologies. Here, we explore antiferromagnetic CuMnAs in which imaging by x-ray photoemission reveals the presence of magnetic textures down to nanoscale, reaching the detection limit of this established microscopy in antiferromagnets. We achieve atomic resolution by using differential phase-contrast imaging within aberration-corrected scanning transmission electron microscopy. We identify abrupt domain walls in the antiferromagnetic film corresponding to the Néel order reversal between two neighboring atomic planes. Our work stimulates research of magnetic textures at the ultimate atomic scale and sheds light on electrical and ultrafast optical antiferromagnetic devices with magnetic field–insensitive neuromorphic functionalities.

Transmission electron microscopy reveals atomically sharp domain walls in a workhorse material of antiferromagnetic spintronics.

INTRODUCTION

Magnetic textures such as domain walls or vortices provide a basic test bed for our physical understanding of magnetic systems (1). From an applied perspective, when representing bits in information technologies, the texture dimensions determine the fundamental scaling limits for the data density (2). In common bulk magnets such as Fe or Co, a substantially larger exchange energy than the magnetic anisotropy energy results in typical domain wall widths that exceed interatomic distances by orders of magnitude. Nanometer-scale domain walls were observed in rare earth magnets with large magnetic anisotropies due to strongly relativistic heavy elements (3). Narrow domain walls were also detected in fragile low-temperature systems comprising a highly anisotropic monoatomic layer of a magnet deposited on a heavy-element substrate (4). Here, spin-polarized scanning tunneling microscopy (4–6) provided the means for high-resolution imaging of the studied surfaces. In our work, we explore the domain wall scaling limit in the bulk of antiferromagnetic CuMnAs. As a primary tool, we use aberration-corrected scanning transmission electron microscopy (STEM), which is bulk sensitive.

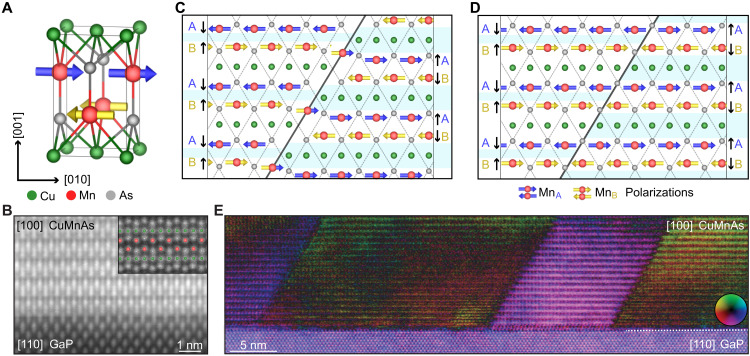
The tetragonal crystal of antiferromagnetic CuMnAs is composed of common light elements and has a correspondingly weak magnetic anisotropy of the Néel vector within the easy (001) plane (7, 8). The strong exchange energy leads to a transition to the antiferromagnetic order well above room temperature (7, 8). In Fig. 1A, we show a schematic of the CuMnAs unit cell. It has a specific symmetry in which the opposite magnetic Mn sublattices are not connected by a lattice translation, as they occupy crystallographically distinct noncentrosymmetric sites. Figure 1B shows an atomically resolved annular dark-field (Z-contrast) STEM image of the epitaxially grown single-crystal CuMnAs film on a lattice-matched GaP substrate.

Fig. 1. Crystal structure and atomically sharp domain walls in antiferromagnetic CuMnAs.

(A) Atomic model of the CuMnAs unit cell. (B) High-angle annular dark-field (HAADF)–STEM image of a [100] projection of the epitaxial CuMnAs film grown on lattice-matched GaP. (C and D) Schematics of the atomically sharp domain walls at an antiphase boundary defect and in an unperturbed area of the CuMnAs single crystal, respectively. Symbols A (blue) and B (yellow) label the upper and lower Mn sublattices from the unit cell in (A). Thin dashed lines highlight preserved As atom matrix. Black arrows represent Lorentz force direction at individual sublattices, which focuses the deflected beam into the areas with light blue overlay. (E) An overview DPC-STEM image of the atomically sharp domain walls in a CuMnAs film.

By using the differential phase-contrast (DPC)–STEM imaging technique (9–19), we identify atomically sharp domain walls in the antiferromagnetic CuMnAs epilayers. DPC-STEM produces an image that reflects the relative shifts observed on the convergent-beam electron diffraction disks of an atomic-size electron probe due to the material’s local electric and magnetic fields (9, 10) (for details on the DPC-STEM method, see Materials and Methods and section S1). A large field-of-view image of the antiferromagnetic CuMnAs film illustrating the sharp changes in the DPC-STEM contrast is shown in Fig. 1E. In the main body of the paper, which focuses on small field-of-view high-resolution imaging, we will associate the DPC-STEM signals with two types of abrupt Néel vector reversals, schematically illustrated in Fig. 1 (C and D): The first type occurs at a crystallographic antiphase boundary defect (Fig. 1C), while the second type forms in a part of the epilayer with no crystallographic perturbation detectable by STEM (Fig. 1D).

The paper is organized as follows: We start from an overview of magnetic imaging experiments in CuMnAs by the established x-ray magnetic linear dichroism photoemission electron microscopy (XMLD-PEEM). The range of scales of the antiferromagnetic textures in CuMnAs inferred from these measurements extends below the ≈10-nm detection limit of XMLD-PEEM, which directly motivated us to attempt the high-resolution DPC-STEM imaging. Next, we introduce our approach to the DPC-STEM measurement, which facilitates the imaging of sharp antiferromagnetic domain walls in CuMnAs, and then present the experimental results.

In the concluding outlook section, we discuss potential microscopic mechanisms that may make the atomically sharp domain walls stationary. The aim of the discussion is to provide initial guidelines for future research of static and dynamic properties of antiferromagnetic textures at the ultimate atomic scale.

RESULTS

XMLD-PEEM imaging

The common expectation based on the weak anisotropy and strong exchange energies in CuMnAs would imply a formation of wide domain walls. Early measurements in the antiferromagnetic tetragonal CuMnAs by synchrotron XMLD-PEEM identified 90° domain walls of ≈100-nm width (20). The experiments also demonstrated a reversible motion of these domain walls controlled by applied current pulses of opposite polarity. The electrical control was facilitated by a relativistic spin-orbit torque, owing to the specific crystallographic structure and antiferromagnetic ordering of CuMnAs (20, 21). Without an external stimulus, the walls can be stationary, although the microscopic pinning mechanism could not be identified by the available synchrotron x-ray absorption PEEM. In section S3 and fig. S2, we illustrate an analogous phenomenology of ≈100-nm-wide 180° domain walls in the CuMnAs films.

Studies of the CuMnAs epilayers also identified antiferromagnetic textures on unexpectedly small scales, whose quantitative determination is hindered by the ≈10-nm detection limit of the used synchrotron XMLD-PEEM (22, 23). In addition, here, while possible to control these nanotextures by external stimuli, the mechanism that makes them stationary has not been identified using the available microscopy techniques. Despite the unknown microscopic morphology and stabilizing mechanism, devices hosting these antiferromagnetic nanotextures led to experimental demonstrations of functionalities unprecedented in ferromagnets. These include insensitivity to extreme magnetic fields, unipolar electrical or optical switching with writing times scaled down from microseconds to a single femtosecond laser pulse, readout signals reaching giant magnetoresistance amplitudes, and reversible and reproducible analog switching and retention characteristics reminiscent of spiking neural network components (22).

In Fig. 2, we show images evidencing 180° Néel vector reversals on scales below the ≈10-nm detection limit of XMLD-PEEM in our CuMnAs epilayer (for details on the XMLD-PEEM method and detection limit in CuMnAs, see Materials and Methods, section S2, and fig. S1). The evidence follows from tracking the Néel vector reorientations along closed paths encompassing well-resolved biaxial domains separated by the ≈100-nm-wide 90° domain walls. With the x-ray polarization along one of the <110> magnetic easy axes of the biaxial CuMnAs, we observe a strong black and white contrast distinguishing micrometer-size domains with the Néel vector aligned with either the [110] axis or the $\left[1\overline{1}0\right]$ axis (Fig. 2, A to C). Here, we recall that the XMLD-PEEM contrast can only resolve Néel vectors aligned along different axes, while it is insensitive to the sign of the Néel vector. To identify the rotation angle of the Néel vector axis in the domain walls separating the [110]/$\left[1\overline{1}0\right]$ domains, we align the x-ray polarization along one of the <100> directions (Fig. 2, D to F). In these measurements, we image the ≈100-nm-wide 90° domain walls. The black and white contrast distinguishes between the mean axes of the Néel vector in the domain walls along either [100] or [010] directions. Because the observed ≈100-nm width of the domain walls significantly exceeds the ≈10-nm detection limit of our XMLD-PEEM measurements, we can exclude the presence of 270° domain walls. These would give a contrast inside the domain walls alternating between black, gray, and white, which is not observed in Fig. 2 (D to F).

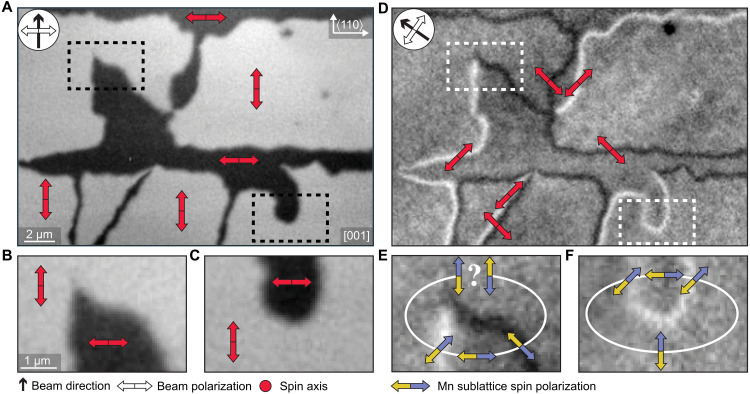
Fig. 2. The presence of sharp 180° domain walls inferred from XMLD-PEEM.

(A) XMLD-PEEM micrograph of the surface of the CuMnAs film. The compass indicates the direction of the x-ray beam, and the white double arrow indicates its polarization. Red double arrows indicate the spin axis of selected antiferromagnetic domains corresponding to the measured black/white contrast. (B and C) Zoom-ins on two regions selected from (A). (D) XMLD-PEEM micrograph corresponding to the area in (A) with the beam direction and polarization rotated by 45°. Red double arrows correspond to the mean angle of the spin axis in the micromagnetic domain walls. (E and F) Zoom-ins on the same regions as in (B) where the blue and yellow arrows indicate Mn_A and Mn_B sublattice moments, respectively, i.e., the orientation of the Néel vector. The Néel vector returns to its original orientation when closing a loop in (F). In contrast, the Néel vector appears to be reversed when completing the closed loop in (E), indicating that a 180° reversal had to occur an odd number of times along the loop and that the corresponding sharp domain wall is below the XMLD-PEEM detection limit.

The sharp contrasts for both x-ray polarizations allow us to track not only the Néel vector axis but also the vector itself, which makes a ±45° rotation whenever crossing from a domain to a 90° domain wall or vice versa. For example, starting from an arbitrary but fixed definition of the sign of the Néel vector in the bottom middle part of Fig. 2F, one can proceed along a closed loop intersecting two 90° domain walls. Because, in this case, the two domain walls have the same (white) contrast, the Néel vector returns to its original direction and sign when completing the loop. In Fig. 2E, the closed loop intersects two 90° domain walls of opposite contrast. This implies that the Néel vector flipped sign an odd number of times and that the width of the underlying sharp domain wall (walls) is below the ≈10-nm detection limit of XMLD-PEEM (for additional discussion of XMLD-PEEM imaging in CuMnAs, see section S3).

DPC-STEM imaging

Before presenting the DPC-STEM results, we first summarize the basic principles of our approach to the DPC-STEM measurement of the sharp domain walls in the CuMnAs antiferromagnet. Earlier, it has been established that a quantitative interpretation of the DPC-STEM data at subnanometer resolution is only feasible for thin lamellae and large collection angles (24, 25). Under these conditions, however, the magnetic component is a weak fraction of the total DPC-STEM signal, which has hindered the utility of the DPC-STEM technique for experimental imaging of the antiferromagnetic order. We reverse the approach by using thicker lamellae and smaller collection angles. It is guided by our density functional theory (DFT) Pauli multislice simulations of DPC-STEM in CuMnAs (for details see, section S4 and fig. S3). They indicate that, relative to the nonmagnetic contribution, the differences of DPC-STEM signals due to opposite sublattice moments in the two antiferromagnetic domains get gradually enhanced by dynamical diffraction effects, as the lamella thickness increases and the collection angle is reduced. Therefore, with our thicker lamellae and smaller collection angles, we trade the inevitable loss of quantitative interpretability of the spatial distribution of the DPC-STEM signal for a higher sensitivity to prominent qualitative features in the antiferromagnetic order. For the demonstration of the presence of the atomically sharp domain walls, which is the central aim of our work, the qualitative nature of our DPC-STEM measurements is sufficient. The special characteristics of the antiferromagnetic crystal structure of CuMnAs and of the studied domain walls are ideally suited for using the qualitative DPC-STEM imaging, as we detail in the following points:

1) According to the DFT calculations, Mn atoms in CuMnAs have a large magnetic moment of ±3.65-bohr magnetons. The moment is carried primarily by the 3d electrons that occupy only a fraction of the unit cell volume. The microscopically varying magnetic fields within the unit cell then have an amplitude on a 10-T scale (for more details on DFT calculations, see section S4). While ferromagnets can have similarly large amplitudes of the local magnetic fields, our antiferromagnetic system has a key qualitative advantage: The sign of the microscopic fields alternates between the opposite sublattices within the unit cell, and the alternation abruptly reverses between the opposite sides of the atomically sharp domain wall.

2) A necessary prerequisite of subnanometer-resolution DPC-STEM is to reach atomic-size electron beams. This requires active objective lenses that, in our measurements, generate a magnetic field of about 1.5 T aligned perpendicularly to the lamella. Unlike ferromagnets, this imposes no limitation for the imaging of our sharp antiferromagnetic domain walls, which are insensitive to magnetic fields (for more details, see section S1).

3) The atomically sharp magnetic domain walls make the abruptly changing magnetic contrast between the opposite domains observable down to nanoscale fields of view, which renders more gradually varying features less significant.

4) While the underlying crystal structure of the opposite antiferromagnetic domains is identical, the two antiferromagnetic domains cannot be transformed from one to the other by a simple translation in CuMnAs. This makes the DPC-STEM images of the opposite antiferromagnetic domains qualitatively distinct even without sub–unit cell resolution and despite the zero net magnetic moment integrated over the unit cell (cf. Fig. 1, A, C, and D).

5) The antiphase boundary defect in our films (Fig. 1C), with identical crystal structures on either side from this two-dimensional (2D) plane defect, imposes the formation of the atomically sharp antiferromagnetic domain wall at the defect. It can thus serve as an additional DPC-STEM contrast benchmark when searching for the sharp antiferromagnetic domain walls outside this defect. Here, we recall that the search for small-scale magnetic textures that are stationary but not fixed, e.g., to a permanent defect, has been directly prompted by the earlier XMLD-PEEM measurements of the control of the small-scale textures by external stimuli (22, 23).

We now proceed to the discussion of the STEM measurements performed on our relatively thick (50-nm) lamella samples fabricated from the CuMnAs epilayers. A representative high-angle annular dark-field (HAADF)–STEM image of an antiphase boundary defect in CuMnAs is shown in Fig. 3A. This crystallographic defect, identified in earlier structural STEM measurements (26), has a form of a lattice slip dislocation propagating along {011} planes and is a consequence of the epitaxial growth of CuMnAs on the III-V substrate. [In our experimental setup, we can detect the antiphase boundary defects along the $\left(0\overline{1}1\right)$ plane, as shown in Fig. 3A, and the (011) plane, as illustrated in fig. S16B.] The tetragonal CuMnAs lattice may start bonding to the substrate with either the lower or upper As plane (see Fig. 1A), corresponding to a change in the initial stacking of the Mn planes in the individual grains. As a result, ≈c/3 lattice-shift antiphase boundaries form when islands with different stacking coalesce during further growth. At the antiphase boundary, one of the Mn crystal sublattices (say Mn_A) closely aligns with the other Mn crystal sublattice (Mn_B). The antiphase boundary, therefore, acts as a source for the formation of an atomically sharp magnetic domain wall with Mn_A→ and Mn_B← on one side of the boundary and Mn_A← and Mn_B→ on the other side (see Fig. 1C). Simultaneously, the unperturbed nonmagnetic crystal structures on either side of the antiphase boundary are indistinguishable. In addition, the whole crystal structure is fixed by the matrix of As/P atoms, which extends from the GaP substrate to the CuMnAs layer (26), and is also preserved over the antiphase boundary and defines its angle, as illustrated in Fig. 1 (B and C). This makes the boundary an ideal object for detecting the magnetic configuration by DPC-STEM.

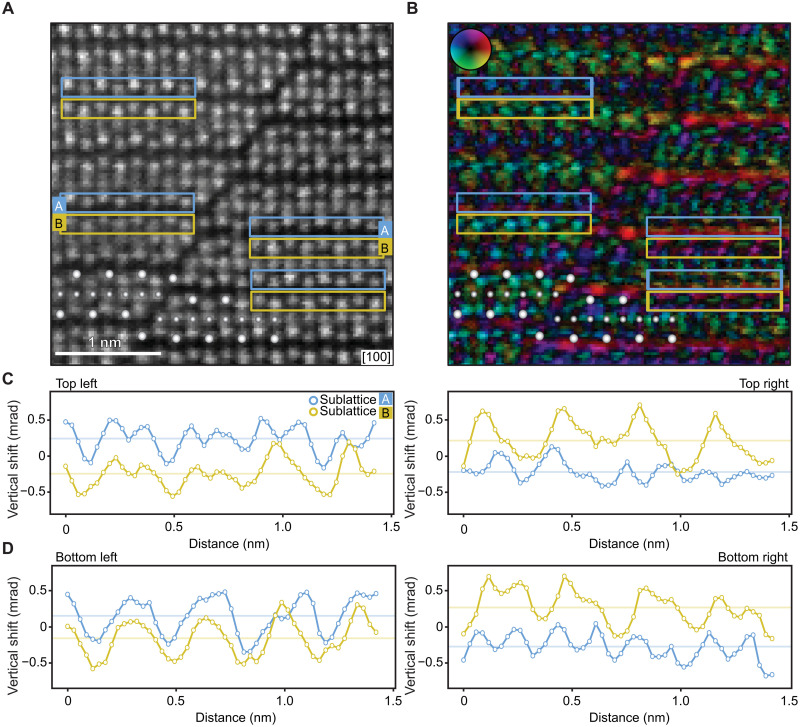
Fig. 3. DPC-STEM measurement of an atomically sharp domain wall at an antiphase boundary defect in CuMnAs.

(A) HAADF micrograph of a part of the CuMnAs epilayer containing an antiphase boundary defect. Large and small white spheres highlight Mn and Cu positions, respectively. Symbols A (blue) and B (yellow) label the upper and lower Mn sublattices. (B) DPC-STEM image of a corresponding area, reconstructed by calculating the shifts of the COM of the recorded ronchigrams for each pixel of the HAADF-STEM image. An average shift over the field of view is subtracted. The radius of the applied digital circular aperture mask is 9 mrad. (C) DPC-STEM horizontal line profiles from selected top areas on each side from the boundary corresponding, separately, to the crystal sublattice Mn_A (blue rectangles) and Mn_B (yellow rectangles). The line profiles show the vertical ([001]) component of the ronchigram COM shifts. The mutual shifts of the line profiles of the two sublattices are centered around 0. (D) Same as (C) for the selected bottom areas.

Figure 3B shows a high-resolution DPC-STEM image simultaneously acquired with the HAADF-STEM image in Fig. 3A. The DPC-STEM plot was reconstructed by calculating the shifts of the center of mass (COM) of the recorded convergent-beam electron diffraction patterns, also known as ronchigrams, by the pixelated detector for each pixel of the HAADF-STEM image (see Materials and Methods and section S1 for a detailed description of the method). To effectively reduce the collection angle, we applied a small (9-mrad radius) digital circular aperture mask on the recorded ronchigrams before extracting the COM shifts (see section S5 and fig. S4). The resulting DPC-STEM image in Fig. 3B shows a clear difference in contrast and intensity of the signal between the two sides of the antiphase boundary.

In Fig. 3 (C and D), we show DPC-STEM line profiles from selected areas on each side from the boundary corresponding, separately, to the crystal sublattice Mn_A (blue rectangles in Fig. 3A) and Mn_B (yellow rectangles in Fig. 3A). The line profiles are plotted as a function of the horizontal position, with each point corresponding to the shifts of the COM of masked ronchigrams integrated over the vertical dimension of the selected sub–unit cell area. In these line profiles, we plot the vertical ([001]) component of the shifts, which corresponds to the direction of the Lorentz force due to the sublattice magnetic Mn moments pointing in the (001) easy plane of antiferromagnetic CuMnAs. It also corresponds to the direction with a larger interatomic spacing in the CuMnAs lattice. We systematically observe that the direction of the shift from the crystal sublattice Mn_A relative to Mn_B reverses between the two sides from the antiphase boundary, consistent with the presence of the sharp antiferromagnetic domain wall.

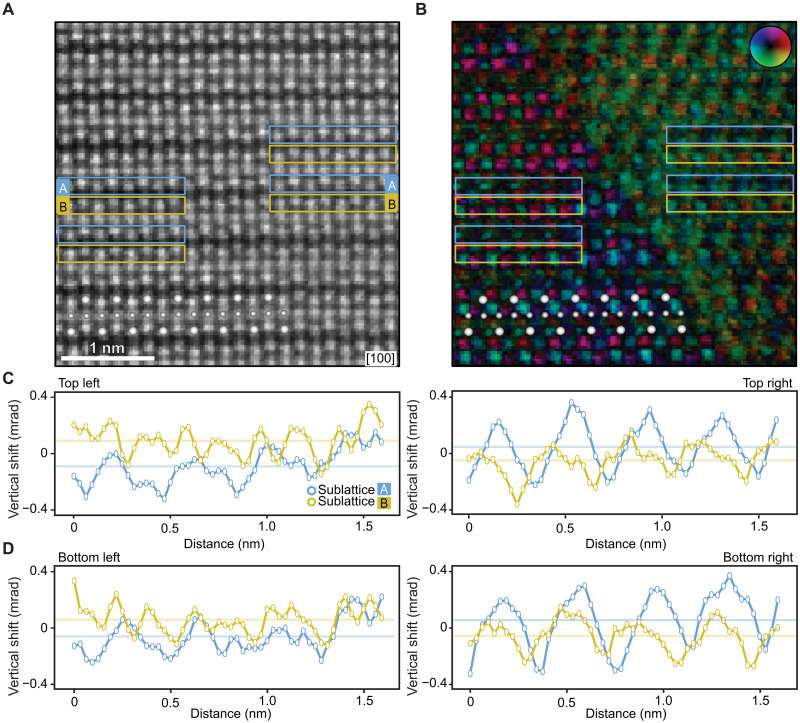
Figure 4 shows a representative measurement of an atomically sharp domain wall formed in a part of the antiferromagnetic CuMnAs single crystal with no detectable structural perturbation (cf. Fig. 1D). The absence of the antiphase boundary defect in the explored portion of the CuMnAs epilayer is confirmed by the HAADF-STEM measurement in Fig. 4A. The simultaneously acquired DPC-STEM image in Fig. 4B shows a distinct contrast between the two domains separated by an abrupt domain wall, analogous to Fig. 3B but now in the absence of the antiphase boundary defect (the domain wall in Fig. 4B is oriented along the (011) plane; examples of a domain wall along the $\left(0\overline{1}1\right)$ plane are shown in figs. S6C and S9A). Figure 4 (C and D) demonstrates the reversal between the two sides from the domain wall of the relative shifts of signals from the two crystal sublattices Mn_A and Mn_B, again analogous to Fig. 3 (C and D). We point out that the data presented in Fig. 4 were obtained using the same experimental procedure as in Fig. 3 (see section S5 and fig. S5).

Fig. 4. DPC-STEM measurement of an atomically sharp domain wall in a CuMnAs single crystal.

(A to D) Same as (A) to (D) in Fig. 3 for the domain wall in a part of the CuMnAs epilayer without a detectable crystal defect. The used experimental method, including the applied digital mask, is identical to Fig. 3.

The importance of applying the small digital circular mask in Figs. 3 and 4 for the high-resolution DPC-STEM imaging of the antiferromagnetic domain wall is illustrated in section S5 and figs. S4 to S6. The images show that the reversed direction of the relative shifts of the DPC-STEM signals from the crystal sublattices Mn_A and Mn_B in the opposite domains is unobservable without applying the small digital mask on the recorded ronchigrams for both the domain wall on the antiphase boundary defect and the domain wall in the unperturbed part of the CuMnAs crystal. On the other hand, again consistent with the qualitative expectation from the DPC-STEM simulations, the antiphase boundary crystal defect becomes more highlighted in these DPC-STEM images when reconstructed without applying the small digital mask, as seen in fig. S4 (for another example of a more pronounced contrast of crystal defects without applying the small mask, see fig. S12).

The sub–unit cell resolution achieved in Figs. 3 and 4 by applying the small digital mask and focusing on small fields of view provides a key evidence for associating the abrupt qualitative changes of the DPC-STEM signal across the sharp domain wall with the reversal of the antiferromagnetic order vector. However, the abrupt domain walls can be detected by DPC-STEM even without the high sub–unit cell resolution, owing to the lack of the translation symmetry connecting the opposite antiferromagnetic domain states in CuMnAs. In fig. S7, we show a zoomed-out version of fig. S5, which illustrates a clearly observable difference between the mean contrast in the opposite domains without applying the small digital mask. For a comparison, we also show in fig. S7 a lower-resolution, larger–field-of-view DPC-STEM image recorded by a four-quadrant detector (for more details on the method, see Materials and Methods). Again, without the sub–unit cell resolution, this DPC-STEM imaging allows us to identify the abrupt domain wall. The introductory Fig. 1E was obtained by the same lower-resolution four-quadrant DPC-STEM. The even larger field of view in Fig. 1E allows us to detect multiple sharp domain walls, which all abruptly terminate at the interface between the antiferromagnetic CuMnAs epilayer and the nonmagnetic GaP substrate, consistent with their magnetic origin.

All the DPC-STEM experimental results are in line with the qualitative guidelines for imaging the atomically sharp antiferromagnetic domain walls in CuMnAs, as provided by the Pauli multislice simulations and the points (1 to 5) listed at the beginning of this section. In the following section, we exclude possible structural artifacts by their systematic scrutiny.

Exclusion of structural artifacts

We start from considering strain variation effects (for details, see section S6). To address this point, we compare DPC-STEM images on CuMnAs/GaP and CuMnAs/GaAs samples. The former has a high-quality fully strained CuMnAs epilayer grown on a closely lattice-matched GaP substrate, resulting in a lateral mosaic block size in CuMnAs exceeding the ≈400-nm resolution limit of the used x-ray measurement (26). In the latter samples with a GaAs substrate, the partially relaxed CuMnAs epilayer is of a lower crystal quality with a ≈30-nm mosaic block size (26). The lattice mismatch between GaAs and CuMnAs leads to expected and clearly visible strain and distortion gradients on both sides of the epilayer/substrate interface, as illustrated in fig. S8. The images of CuMnAs/GaP are notably different (see Fig. 1E or fig. S8). The DPC-STEM contrast of the CuMnAs domains separated by the sharp domain walls stops abruptly at the interface, leaving the GaP substrate featureless. This rules out the strain artifact interpretation.

Additional simulations and measurements exclude the artifacts associated with local variations in material stoichiometry, lamella thickness, and crystal rotation (for details, see section S7). Our CuMnAs films are grown by molecular beam epitaxy at a rate of ∼8 A min⁻¹ under well-calibrated conditions (26). This means that sharp local changes in stoichiometry that would be large enough to affect the beam passing through the lamellae are unlikely to occur. We confirmed this by electron energy-loss spectroscopy (EELS) measurements shown in fig. S9. The EELS data also confirm the absence of an abrupt thickness variation across the antiferromagnetic domain wall. The exclusion of the thickness variation scenario is further underpinned by DPC-STEM simulations, which also rule out artifacts due to conceivable crystal rotations, as discussed in detail in section S7 and fig. S10.

Last, we inspect the possibility that the DPC contrast arises from CuMnAs crystals that initially had grown independently slightly shifted and that overlap on top of each other along the electron beam direction. Antiphase boundaries run within the epilayer along four degenerate angles corresponding to the {011} planes and are the only extended lattice defects observed in our STEM measurements of the high-quality CuMnAs/GaP epilayers. A crystal overlap in the layers can, therefore, be formed only by meeting of these defects when running along different {011} planes, as sketched in fig. S11.

An example of STEM images of the crystal overlap is shown in fig. S12A. A crystal overlap can be clearly identified by HAADF-STEM but is nearly invisible in the DPC-STEM when the images are processed with a small digital mask. This is an additional evidence that rules out that the DPC-STEM measurements of the domain walls shown in Figs. 3 and 4 with a small digital mask are arising from a crystal overlap artifact. Consistent with the structural nature of the crystal overlap, the defect becomes more clearly apparent without applying the small mask, as illustrated in fig. S12A. We again emphasize that this is an opposite trend than what is observed for the antiferromagnetic domain contrasts in figs. S4 to S6 and S12B.

A complementary evidence ruling out a crystal overlap artifact is that its crystallography would generate vertical intensity gradients in the STEM images on a ≈5-nm scale, as a result of the different angles of the antiphase boundaries forming the crystal overlap and as confirmed by our numerical simulations shown in fig. S13A. These gradients are, however, absent in the experimental DPC and HAADF images of the antiferromagnetic domains (see Fig. 1E and fig. S13B).

DISCUSSION

The atomically sharp domain walls on the antiphase boundary defects are an exceptional case in our high-quality single-crystal epilayers where we can experimentally identify the microscopic crystal origin of the pinning (or formation) of the antiferromagnetic domain wall. In the case of the atomically sharp domain walls detected by DPC-STEM in the part of the single crystal with no structural perturbation visible by STEM, the situation is more analogous to the XMLD-PEEM measurements of the larger-scale antiferromagnetic textures in CuMnAs, reviewed in the introductory part of the paper. While the DPC-STEM images identify stationary atomically sharp antiferromagnetic domain walls, the HAADF-STEM measurements of these high-quality single-crystal epilayers do not experimentally resolve the microscopic origin of the pinning. The aim of the following discussion/outlook paragraphs is thus to provide initial guidelines and motivation for future research of static and dynamic properties of these atomic-scale magnetic textures, which inevitably needs to start from the development of new experimental and theoretical approaches or techniques.

To enter the microscopic theory discussion, we have performed atomistic Heisenberg model simulations and first-principles DFT calculations of the energy of narrow domain walls of widths from ∼10 magnetic atoms down to an abrupt reversal between two neighboring atoms (for more details, see section S8). We compare the CuMnAs antiferromagnet with the conventional Fe ferromagnet. As shown in fig. S14, there is a good agreement in ferromagnetic Fe between the first-principles DFT calculations and the atomistic simulations, where, in both cases, the energy monotonously increases with decreasing the domain wall width. On the other hand, the atomistic simulations fail in antiferromagnetic CuMnAs, both on a quantitative and qualitative level, as shown in fig. S14. While the approximate atomistic simulations show an analogous trend to ferromagnets, the first-principles calculations reveal an oscillatory dependence of the energy on the domain wall width in CuMnAs, with a significant energy drop for the atomically sharp domain wall. Consistent with experiment, the first-principles DFT calculations also suggest that the domain wall angle, as shown in Fig. 1D and observed experimentally in Fig. 4, gives a significantly lower energy than higher angles or a vertical [001] orientation of the domain wall (for more details, see section S8 and fig. S15).

On the basis of the DFT calculations and additional DPC-STEM and scanning x-ray diffraction measurements, we now discuss two examples of possible pinning scenarios of the atomically sharp domain walls in the parts of the CuMnAs epilayer with no detectable defect by STEM. One candidate mechanism is that the propagation of the domain wall is inhibited in the vicinity of the antiphase boundary defect, which fixes a different antiferromagnetic domain wall at the defect position (for example, passing of the former free domain wall across the antiphase boundary would require erasing the latter fixed domain wall). Within the narrow available field of view, which still allows for the atomic resolution, we can identify a stationary domain wall in the unperturbed crystal neighboring the antiphase boundary domain wall. An example is illustrated in section S9.1 and fig. S16. The presence of a significant density of the antiphase boundary domain walls can then serve as an efficient nonlocal pinning mechanism of the domain walls within the unperturbed crystal. From STEM measurements, we infer that the mean lower bound of the separation of antiphase boundary defects in our CuMnAs film is on the ∼10-nm scale. Complementary scanning x-ray diffraction measurements, detailed in section S9.2 and fig. S17, determine that the upper bound of the mean distance between the antiphase boundary defects is less than 100 nm. This nonlocal pinning scenario is thus statistically relevant.

As a second possible mechanism, we discuss pinning on local defects. Among those, Mn vacancies have been earlier identified as low–formation energy defects whose average density in a 1 to 10% range can explain the experimental residual resistivity of CuMnAs (27). We have performed additional DFT calculations of the energy of the atomically sharp domain wall as a function of the distance from a plane of an excess density of the Mn vacancies. We obtained a narrow (few lattice constants) energy well above the numerical noise for the excess Mn-vacancy densities starting from a 10% scale. The depth of the energy well is larger than k_B × 500 K, i.e., consistent with a domain wall pinned at the excess Mn-vacancy plane at room temperature. In addition, we also recall that the atomically sharp domain walls prefer to align with a certain crystallographic plane, as seen in our experiment and consistent with our DFT theory (section S8 and fig. S15). A limited area of excess Mn vacancies within the domain wall plane can thus still efficiently prevent a parallel motion of the entire domain wall. We also note that other local defects can be considered, e.g., at the interfaces with the substrate or the capping layer.

To conclude, our results open the basic research front of atomically sharp magnetic domain walls. Illustrating the ultimate domain wall scaling limit in an antiferromagnet gives the field an opportunity to exploit the rich materials landscape of these abundant and diverse symmetry-type systems (28–34). Making the observation in CuMnAs has also immediate consequences for spintronic device physics and engineering. It sheds light on the microscopic mechanism of the recently observed quenching into high-resistive nanofragmented domain states in analog memory devices insensitive to extreme magnetic fields (22, 35), with potential in neuromorphic (36) and ultrafast optical applications (37). Combined with the earlier demonstrated electrical control of the domain wall motion in CuMnAs (20, 23, 38), it also opens the prospect of coding information in individual atomically sharp antiferromagnetic domain walls.

MATERIALS AND METHODS

Crystal growth

The description of the growth of CuMnAs thin films by molecular beam epitaxy on GaP and GaAs substrates and the detailed characterization and optimization of their properties are given in (26). Data shown in the main text are on optimized lattice-matched CuMnAs (50-nm) films on GaP substrate and are by measurements on CuMnAs (50 nm) on GaAs substrate.

X-ray PEEM

XMLD-PEEM and the x-ray absorption PEEM measurements were performed on beamline I06 at Diamond Light Source using linearly polarized x-rays at grazing incidence of 16° to the sample surface. Sensitivity to the antiferromagnetic spin axis was obtained from the asymmetry of images with the x-ray energies tuned to the Mn L₃ absorption edge (2p_3/2 → 3d transitions). Spatial contrast in the asymmetry images arises from the local variation of the angle of the spin axis with respect to the x-ray polarization vector E. Measurements in Fig. 2 were performed with E parallel to the <100> and <110> crystal axes, which are in-plane. The XMLD spectrum has a similar shape but opposite sign for both cases (39) so that dark and light areas correspond to perpendicular and parallel spin axis with respect to E for E parallel to <100>, and vice versa for E parallel to <110>. The sample environment in measurements in Fig. 2 of the main text was cooled to ≈100 K, which increases the XMLD contrast but does not significantly affect the size or shape of the magnetic domain pattern. Measurements in fig. S2 were performed with E parallel to <110> and at room temperature.

Scanning transmission electron microscopy

The prepared lamellae were investigated by three different high-resolution scanning transmission electron microscopes (TEMs). The aberration-corrected Nion UltraSTEM microscope operated at 100-kV acceleration voltage was used to acquire the images presented in Figs. 3 and 4 and figs. S4, S5, S7 (A and B), S12, and S13. The images were acquired using convergence semiangles of 25 or 18 mrad with a probe current of ≈58 pA. These images were acquired from regions of the lamellae with a thickness of around 50 nm. The DPC signal was recorded with a pixelated (also known as universal) detector Nion 2020 Ronchigram camera, equipped with a Hamamatsu ORCA ultralow noise scientific complementary metal-oxide semiconductor sensor with a 2048 × 2048 pixel display. The convergent-beam electron diffraction patterns had an average size of 80 × 80 pixels with an average pixel size of 1.2 mrad.

The Thermo Fisher Scientific (TFS) TEM Titan Themis 60-300 cubed microscope operated at 300-kV acceleration voltage was used to acquire images and EELS measurements presented in Fig. 1 (B and E) and figs. S7 (C and D), S8, S9, and S16. The STEM images were acquired with a convergence semiangle of 10 mrad and a probe current of ≈30 pA. The DPC images were recorded by a TFS four-quadrant DPC annular detector. For the DPC analysis, the TEM was aligned with a camera length of 580 mm (Fig. 1, B and E, and figs. S7, C and D, S8, and S16) and 460 mm (fig. S9), where the annular detector had the collection angle of 2.4 to 13.4 and 3 to 16.9 mrad, respectively. The sharp domain wall DPC contrast was observable for all studied lamella thicknesses of ≈50 to 150 nm.

The Jeol NEOARM microscope operated at 200-kV acceleration voltage was used to acquire images presented in fig. S6. The imaging was done using a 28-mrad convergence semiangle. The image was acquired from regions of the lamella with a thickness of around 50 nm. The DPC signal was recorded in a direct electron pixelated detector, binned to 132 × 132 pixels and using a pixel size of 1.5 mrad. For measurements on the Nion and Jeol microscopes, the lamellae were heated for 10 hours at 80°C under vacuum before loading the samples in the microscope columns.

Lamellae preparation

The as-grown samples were cleaved into 5 mm–by–5 mm chips and adjusted onto standard pin stubs by means of silver lacquer. The surface was coated with 10 to 15 nm of carbon using Leica ACE600. The STEM lamellae were then fabricated in FEI Helios 660 G3 FIB/SEM instrument following the commonly used protocol, using electron and ion beam–deposited tungsten as a protective cap. Final polishing was done at 2 kV and 25 pA. The resulting thickness varied from ≈50 to 150 nm in the regions of interest. The estimated thickness for the images in Figs. 3 and 4 is around 50 nm, as shown in fig. S9.

Data acquired by the pixelated and four-quadrant detectors

The 4D datasets acquired by the Nion and Jeol microscopes were reconstructed via modified scripts available in the open-source Nion Swift Python package (40). The raw datasets for each image consist of a HAADF image and a ronchigram recorded for each of its pixels. The DPC-STEM images represent individual shifts of the COM of the ronchigrams measured in each pixel. In the plots, an average COM shift over the field of view is subtracted. The digital circular aperture was applied as a mask on the ronchigrams before evaluating the COM shift. The four-quadrant detector DPC-STEM images were acquired using TFS software VELOX v.2.8 with a DPC plugin and are presented without further postprocessing.

Supplementary Materials

This PDF file includes:

Sections S1 to S9

Figs. S1 to S17

References