Abstract
Increasing the depth of mining leads to the location of the mine pit below the groundwater level. The entry of groundwater into the mining pit increases costs as well as reduces efficiency and the level of work safety. Prediction of the groundwater level is a useful tool for managing groundwater resources in the mining area. In this study, to predict the groundwater level, multilayer perceptron, cascade forward, radial basis function, and generalized regression neural network models were developed. Moreover, four optimization algorithms, including Bayesian regularization, Levenberg–Marquardt, resilient backpropagation, and scaled conjugate gradient, are used to improve the performance and prediction ability of the multilayer perception and cascade forward neural networks. More than 1377 data points including 12 spatial parameters divided into two categories of sediments and bedrock (longitude, latitude, hydraulic conductivity of sediments and bedrock, effective porosity of sediments and bedrock, the electrical resistivity of sediments and bedrock, depth of sediments, surface level, bedrock level, and fault), and besides, 6 temporal parameters are used (day, month, year, drainage, evaporation, and rainfall). Also, to determine the best models and combine them, 165 extra validation data points are used. After identifying the best models from the three candidate models with a lower average absolute relative error (AARE) value, the committee machine intelligence system (CMIS) model has been developed. The proposed CMIS model predicts groundwater level data with high accuracy with an AARE value of less than 0.11%. Sensitivity analysis indicates that the electrical resistivity of sediments had the highest effect on the groundwater level. Outliers’ estimation applying the Leverage approach suggested that only 2% of the data points could be doubtful. Eventually, the results of modeling and estimating groundwater level fluctuations with low error indicate the high accuracy of machine learning methods that can be a good alternative to numerical modeling methods such as MODFLOW.
1. Introduction
The reduction of surface mineral reserves has led to an increase in the depth of mining in open pit mining. Increasing the depth of mining leads to the location of the mine pit below the groundwater level.1 Due to the increased depth of mining, excavation may be done below the water table, which leads to the movement of water toward mining works. Excessive water entering the mining environment may delay the project or impede production, in addition to causing environmental and safety problems.2 The inflow of groundwater into the mining environment leads to increased equipment failure, destructive impact on the stability of the pit slope, increased use of explosives, unsafe working conditions, and lack of access to parts of the mining area. Therefore, to overcome these problems, it is necessary to develop an efficient dewatering system, while groundwater level prediction can contribute significantly to this design. Various numerical and modern methods can be used to model and predict groundwater fluctuations.
The numerical models are extensively used to simulate the quantity and quality of groundwater.3 Numerical modeling of groundwater by this model (i.e., MODFLOW) requires some input parameters; hence, preparing proper values for these parameters is a time-consuming and costly activity. In addition, the disadvantages of numerical methods include difficulties in representing irregular boundaries, nonoptimization for unstructured meshes, slow for large problems, and tendency to one-dimensional physics around edges.4,5 To control these limitations, soft computing techniques are a very valid option for predicting groundwater levels by providing results with high precision and less computational time.6 One of the advantages of soft computing techniques over numerical methods is the use of nonlinear algorithms for modeling and predicting the complex groundwater level behavior at various sites.7,8
To predict groundwater levels and the complexity of subsurface conditions, novel machine learning methods based on nonlinear dependence can be used without deep knowledge of basic physical parameters.9,10 In recent years, artificial intelligence methods have been widely used to predict water system variables due to their high ability to learn complex mathematical relationships between output and prediction variables.11−16 One of the most common machine learning algorithms used to predict the groundwater level is the artificial neural network (ANN).17−22 Multilayer perceptron (MLP), cascade forward (CF), radial basis function (RBF), general regression (GR), and committee machine intelligence system (CMIS) are the most widely used ANN methods based on their different architectures.23 used MLP to predict groundwater levels in Montgomery, Pennsylvania.24 modeled river flow using optimized CF and MLP in the Kelantan River in Malaysia.25 predicted trihalomethanes levels in tap water using RBF and gray relational analysis.26 have evaluated GR neural network models in simulating the groundwater contaminant transport.27 have implemented the supervised intelligence committee machine method to predict the reservoir water level variation for the design and operation of dams. Each of the models has its own characteristics, so it is possible to combine models that have acceptable errors with each other to use the characteristics of all these developed models for forecasting. In addition to different methods for modeling and predicting groundwater levels, different spatial and temporal data can affect groundwater levels.28 Most studies have used spatial or temporal parameters separately to predict groundwater levels using machine learning, but both spatial and temporal parameters affect groundwater levels.
The main purpose of this research is the use of powerful spatial and temporal data to model and predict groundwater level fluctuations using accurate machine learning methods as an alternative to numerical methods such as MODFLOW. For this purpose, 1542 data points including 12 spatial parameters and 6 temporal parameters were used. Out of which 1377 data points have been used to create different networks, and to evaluate the performance of these developed models, 165 extra validation data points have been used. Four MLP neural network models and four CF neural network models were then developed using four different optimized Bayesian regularization (BR), Levenberg–Marquardt (LM), resilient backpropagation (RB), and scaled conjugate gradient (SCG). Also, the RBF neural network and GR neural network methods have been used to model the groundwater level. After developing models, a CMIS is combined of three candidate models with the least error. The validity of the proposed CMIS is evaluated through statistical and graphical error analysis. The innovation of this research is the study of the powerful CMIS method as an alternative to numerical methods such as MODFLOW for groundwater level prediction. In addition, the relevancy factor of the data relative to the groundwater level as well as the outlier diagnosis has been identified.
The rest of this research is organized as follows: Section 2 provides information on the study area and the data used, in addition to the developed models and optimization techniques; Section 3 outlines the results and discussion of this research, and Section 4 presents the conclusions of this research.
2. Material and Methods
2.1. Experimental Data
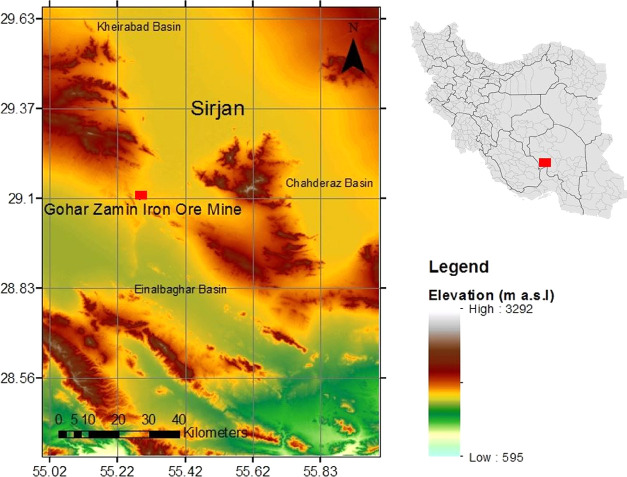
Gol Gohar iron ore deposit, one of the most pivot points of the mining industry in the Middle East, with six separate anomalies and a reservoir of about 1200 million tons, is located in an area of 10 km by 4 km. In anomaly no. 3 (Gohar Zamin iron ore mine), groundwater enters the pit, and also water permeates through the alluvium of the pit’s stairs. One of the probable factors of going groundwater inflow into the Gohar Zamin iron ore mine is the Kheyrabad plain with alluvial sediments situated in the northeast of the mine at a distance of 15 km (Figure 1). Around the Gohar Zamin iron ore mine, water pumping wells are located around anomaly no. 1, which is considered as a discharge area.
Figure 1.
Study area and location of the Gohar Zamin iron ore mine.
To estimate the spatial and temporal groundwater level as the target and output of the neural network, two sets of spatial and temporal data have been used as the input of the neural network. The input spatial data set includes five piezometer data around the Gohar Zamin iron ore mine. Besides, the input temporal data affecting the groundwater level in the period of March 21, 2019, to July 2, 2020. Because both sediments and bedrock affect the groundwater level, the spatial data input to the neural network is divided into two categories of bedrock and sediment parameters.
In Table 1, input spatial data to the neural network including latitude and longitude of piezometers, hydraulic conductivity of sediments and bedrock, effective porosity of sediments and bedrock, the electrical resistivity of sediments and bedrock, the piezometers surface level, bedrock height, depth of sediments, and the presence or absence of faults are shown. The input temporal data to the neural network include day, month, year, drainage volume, evaporation, and precipitation, which in Table 2, statistical explanation of these parameters are shown.
Table 1. Spatial Input Parameters of the Well Piezometer over the Gohar Zamin Iron Ore Mine.
| number of well piezometers | UTM:X (m) | UTM:Y (m) | hydraulic conductivity of sediments (m/day) | effective porosity of sediments | electrical resistivity of sediments (ohm m) | depth of sediments (m) | surface level (m) | hydraulic conductivity of bedrock (m/day) | effective porosity of bedrock | electrical resistivity of bedrock (ohm m) | bedrock level (m) | fault |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 333,513 | 3,219,470 | 200 | 15 | 14.9 | 130.55 | 1724.47 | 19 | 0.09 | 31.6 | 1590.37 | × |
| 2 | 332,489 | 3,219,947 | 187 | 20 | 29.4 | 180 | 1735.77 | 20 | 0.07 | 17.2 | 1645.77 | × |
| 3 | 332,149 | 3,220,733 | 150 | 18 | 55.8 | 212 | 1747.5 | 22 | 0.05 | 5.58 | 1641.5 | × |
| 4 | 332,861 | 3,221,499 | 160 | 14 | 9.69 | 139 | 1733.47 | 19 | 0.06 | 36.5 | 1663.97 | × |
| 5 | 334,438 | 3,220,764 | 315 | 10 | 22.3 | 141.65 | 1729.92 | 17 | 0.1 | 13.5 | 1659.1 | √ |
Table 2. Statistical Explanation of the Temporal Input Parameters.
| drainage (m3/day) | evaporation (m/day) | rainfall (m/day) | |
|---|---|---|---|
| mean | 9366 | 0.007 | 0.02 |
| median | 9183 | 0.006 | 0.006 |
| mode | 9504 | 0.004 | 0 |
| skewness | 0.119 | 0.257 | 1.37 |
| kurtosis | 0.245 | –1.345 | 0.862 |
| minimum | 0 | 0.002 | 0 |
| maximum | 17466 | 0.013 | 0.09 |
2.2. Models
2.2.1. MLP Neural Network
ANNs as a useful computational intelligence built on analogy with human information processing systems are widely used in distributed processing systems.29 Each ANN has two main elements as interconnections and processing elements. Interconnections, weights, make connections among neurons, while the processing elements, neurons or nodes, process information. Although the structures of the ANN are very varied, MLP is still one of the most dominant as well as the most extensive structure of the ANN.30,31 The MLP shown by Cybenko’s theorem (1989) is a universal function approximation used to create mathematical models using the regression analysis. With training on observation data, the network can learn specific features hidden in the collected data samples and even generalize what it has learned.32 MLP networks have a multilayered structure, and the first layer is the input data to the model, the last layer is the output data of the model, and the layers between the input and output are called hidden layers.19,33 The number of neurons in the input layer is the same as the input variables, the number of outputs is usually the same as the output parameter, and the hidden layers are responsible for the internal appearance of the relationship between the model inputs and the desired output.34,35 The value of each neuron in the hidden layer or output layer is the sum of each neuron in the previous layer multiplied in a particular weight for that neuron. This value then is summed with the bias and passed from an activation function. Figure 2 demonstrates the structure of the MLP neural network with two hidden layers implemented in this study.
Figure 2.
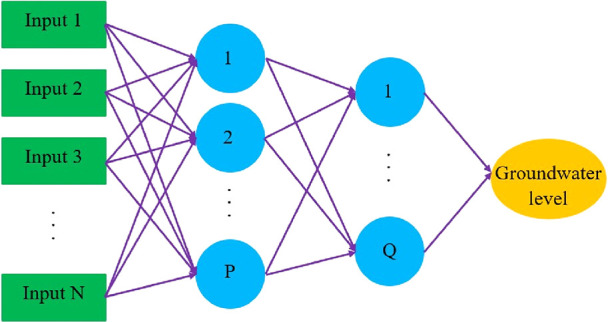
Schematic image of the MLP neural network structure.
The following is a summary of some of the common activation functions used for hidden and output layers.
| 1 |
| 2 |
| 3 |
| 4 |
The output of an MLP model with two hidden layers whose activation functions for these two layers are Logsig and Tansig, and Purlin activation function for the output layer are as follows36
| 5 |
where w1 and b1 are the weight matrixes and the bias vectors of the first hidden layers, w2 and b2 are the weight matrixes and the bias vectors of the second hidden layers, and w3 and b3 are the weight matrixes and the bias vectors of the output layers.
2.2.2. CF Neural Network
There is a direct relationship between the input and output in the perceptron connection, whereas in the feedforward neural network connection, there is an indirect relationship between the input and output, which is a hidden layer through a nonlinear activation function.37 If the connection form is combined in a multilayer network and perceptron, the network can be formed with a direct connection and the indirect connection between the input layer and the output layer.24 The network formed of this connection pattern is called the CF neural network, and the equations of this model can be written as follows
| 6 |
where fi is the
activation
function between the input layer and the output layer,  is the weight between the input layer and
the output layer, wb is the weight from
bias to output,
is the weight between the input layer and
the output layer, wb is the weight from
bias to output, 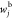 is the weight from bias to the hidden layer,
and fh is the activation function of each
neuron in the hidden layer. A schematic illustration of the CF neural
network architecture (with two hidden layers) and the interconnections
between the input and output parameters are illustrated in Figure 3.
is the weight from bias to the hidden layer,
and fh is the activation function of each
neuron in the hidden layer. A schematic illustration of the CF neural
network architecture (with two hidden layers) and the interconnections
between the input and output parameters are illustrated in Figure 3.
Figure 3.
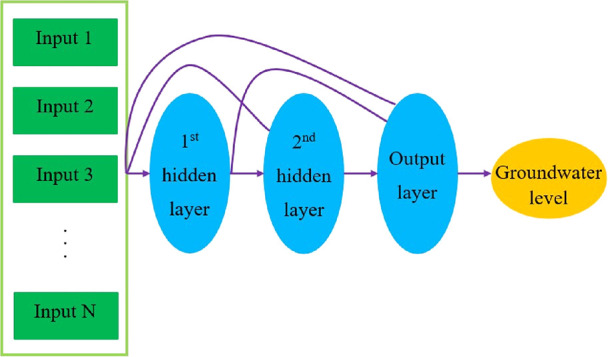
Architecture of the implemented CF neural network.
The optimization algorithm used for training has an influential impress on the efficiency of MLP and CF models, extremely in this research, and four important BR, Levenberg–Marquardt, RB, and SCG optimization algorithms have been used for optimization.
2.2.3. RBF Neural Network
The RBF neural network is one of the most powerful feedforward neural networks for solving regression problems using the performance approximation theory.38 Broomhead and Lowe,39 based on adaptive function interpolation, introduced an approach to local functional approximation. In general, an RBF neural network has a three-layer feedforward structure in which the input layer and the output layer are connected through a hidden layer. A schematic illustration of the RBF neural network architecture applied in this paper is shown in Figure 4.
Figure 4.
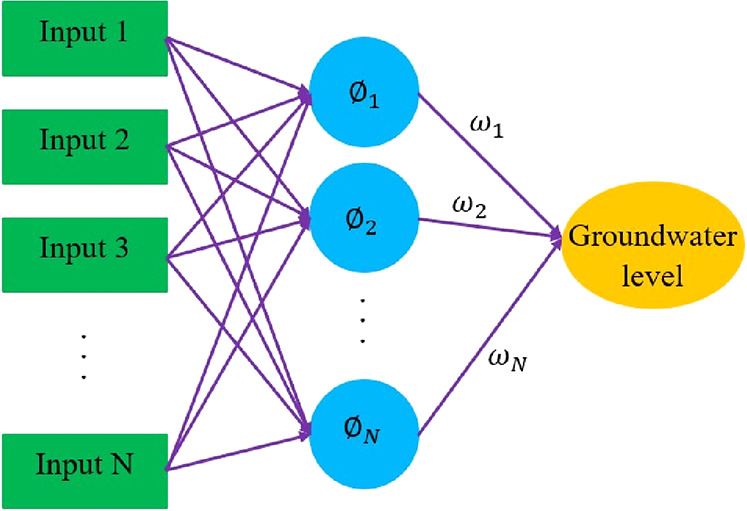
Implemented structure of the RBF neural network.
The principal part of the RBF neural network is the hidden layer, which transmits data from the input space to the hidden space with higher dimensions.36,40 Each point of the hidden layer with a particular radius is located at a given space, and in each neuron, the distance between the input vector and its center is calculated.41 Euclidean distance is used to measure the distance between centers and inputs, which is calculated from the following equation
| 7 |
For a model with 10 input variables, p = 10. To transfer the Euclidean distance from each neuron in the hidden layer to the output, a RBF has been used. The most common RBF is the Gaussian,42 which is obtained from the following interface
| 8 |
Due to its smoother and flexible behavior, the Gaussian function has been utilized as the activation function in this research. When x = cj, ϕ(r) is maximum, and as r increases, ϕ(r) decreases. When |r| → ∞· ϕ(r) → 0. σ is the spreading coefficient of the Gaussian function, which is defined experimentally.43 The model output is estimated from the following equation
| 9 |
where ω shows the connection weight, N is the number of neurons in the hidden layer, c denotes the center, and (∥x – c∥) is the Euclidean distance between the center of the radial function and the input data.44,45
2.2.4. Generalized Regression Neural Network
The GR neural network is a memory neural network that is a variation to the RBF neural network based on the statistical technique of kernel regression with a dynamic network structure with powerful nonlinear mapping and robustness (Specht 1991). GR has a high learning speed and is very useful for function approximation problems. For small sample data, the prediction effect is excellent, and also unstable data can be processed.26,46 GR does not have RBF accuracy but has a major advantage in classification and fit, especially when data accuracy is inappropriate. A GR model consists of four layers (input, pattern, summation, and output layer) as illustrated in Figure 5.47
Figure 5.
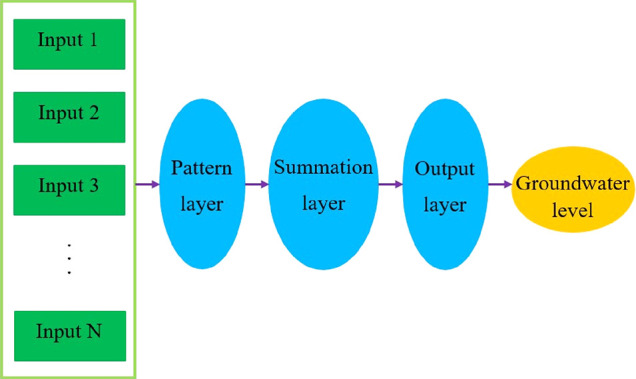
Schematic image of the GR neural network structure.
For the hidden layer RBF, the number of elements is equal to the number of training samples. The weight function of the hidden layer RBF is dist, which is used to determine the distance between the network input and the weight value IW11 of this layer and is calculated from the following equation
| 10 |
In the hidden layer, network product function netprod multiplies the threshold b1 and ∥dist∥ output to get net input n1. The net input n1 is passed to transfer function radbas. For the GR model, the Gaussian function is used as the transfer function, namely
| 11 |
In the above equation, σj is a smoothing factor, also called the spread parameter, which calculates the shape of RBF in the jth hidden layer.
The normalized weight product function is used as the weight function in the linear output layer, making the former layer’s output with the weight value IW21 in this layer as the weight output. The Purelin function is used as the transfer function for the output of the passed weight. The network output is calculated from the following equation
| 12 |
Due to the significant effect of the spread parameter on the model’s performance, only the optimal value of this parameter must be determined.48
2.2.5. Committee Machine Intelligent System
To achieve the objectives of the study, the best-developed models are chosen as candidates and other models are discarded.49 Under these circumstances, the cost incurred for the discarded models is wasted. For this purpose, intelligent models with their unique features are combined with each other and a committee machine is built.50,51 This CMIS was introduced by Nilsson in 1965; it is a kind of ANN and uses division and conquer to solve problems.
In the committee machine method, the models are combined to provide a more accurate solution.52 The linear combination method can be used using simple averaging or weighted averaging to combine the developed models.53 Because all models’ contribution in the simple averaging method is the same, a satisfactory answer is not obtained from this method because a more precise solution must contribute to the final model more.54 For this purpose, the solutions are combined based on their precision, and the sum of coefficients of linear composition is unity. In this research, added a bias term to the equation and an improved weighted average is used. In the final model, any model’s contribution corresponds to that model’s coefficient in the linear equation of the CMIS model.
2.3. Model Comparison
To determine the error related to the model output, various statistical measures can be used to compare the effectiveness of the developed models. The performance of the trained model is compared in terms of statistical measurement of precision. During this research, the average absolute relative error (AARE, %), average relative error (ARE, %), root mean square error (RMSE), and standard deviation (SD) are taken under consideration to check the efficiency of the models as predictive tools. The mentioned parameters are expressed as
| 13 |
| 14 |
| 15 |
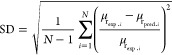 |
16 |
3. Results and Discussion
3.1. Model Development
In this research, 1542 data points of five piezometric wells have been used to model and predict the groundwater level. The data used are divided into spatial (sediments and bedrock) and temporal (March 21, 2019, to July 2, 2020). To apply the necessary complexity to intelligent machine learning methods, 12 spatial parameters (longitude, latitude, hydraulic conductivity of sediments, effective porosity of sediments, the electrical resistivity of sediments, depth of sediments, surface level, hydraulic conductivity of bedrock, effective porosity of bedrock, the electrical resistivity of bedrock, bedrock level, and fault) and 6 temporal parameters (day, month, year, drainage, evaporation, and rainfall) have been used, which have the greatest impact on the groundwater level. 1377 data points have been used to develop four MLP neural network models, four CF neural network models, one RBF neural network model, and one GR neural network model. MLP and CF models have been each optimized by Levenberg–Marquardt, BR, SCG, and RB methods. In all the mentioned models, 80% of the data were used for model training, and 20% of the data were used for model testing.55 The data are divided into testing and training sets using random distributions to prevent the local accumulation of data.
The number of hidden layers, the type of transmission function, and the number of neurons in each layer affects the efficiency of a developed model. Trial and error can be used to identify these parameters. In this research, two hidden layers were used for MLP and CF methods, and one hidden layer was used for RBF and GR neural network methods. Table 4 shows the function used and the best architecture in terms of the number of neurons for each model. Transfer functions are designed to correctly model the complex behavior of nonlinear input and output data sets. The architecture for the MLP model consists of four numbers, the first and last number being the number of inputs and outputs of the model, and the second and third numbers being the number of neurons in the first and second hidden layers. Because the efficiency of the MLP models is strongly influenced by the initial biases and weights, the training of ANNs with each optimizer using trial and error was executed more than 50 times with dissimilar initial biases and weights, and the most satisfactory results were chosen. The architecture for the CF model consists of five numbers, the first and last number being the number of inputs and outputs of the model, and the third and fourth numbers being the number of hidden layer neurons in the first and second. The second number is the number of neurons in the connection layer between the input and output. The architecture for the RBF model consists of three numbers, the first and last number being the number of inputs and outputs of the model and the second number being the number of maximum neurons in the hidden layers. RBF models consist of two key parameters: the number of neurons and the spread coefficient. To determine these two parameters, trial and error have been used. In this research, the number 5 for the coefficient of expansion and the number 30 for the number of neurons have been used. The GR neural network model, similar to the RBF model, has the spread coefficient parameter, which is 0.5 for this parameter by trial and error. To identify the optimal value for the coefficient of expansion and the number of neurons, the RBF model was implemented more than 100 times, and the best results were stored.
Table 4. Statistical Parameters and Information of All Developed Models for the Prediction of Groundwater Level Using 165 Extra Validation Data Points.
| models | ARE (%) | AARE (%) | SD | RMSE (m) | function used | best architecture |
|---|---|---|---|---|---|---|
| MLP-LM | –0.12983 | 0.16232 | 0.00177 | 2.77969 | Logsig-Purelin-Purelin | 18-12-8-1 |
| MLP-BR | –0.37058 | 0.37081 | 0.00396 | 6.20605 | Elliot2sig-Purelin-Purelin | 18-12-8-1 |
| MLP-SCG | –0.08426 | 0.20241 | 0.00230 | 3.60198 | Elliot2sig-Purelin-Purelin | 18-12-8-1 |
| MLP-RB | –0.30413 | 0.30413 | 0.00338 | 5.29602 | Elliot2sig-Purelin-Purelin | 18-12-8-1 |
| CF-LM | –0.55160 | 0.55160 | 0.00569 | 8.90091 | Elliot2sig-Purelin-Purelin | 18-6-20-12-1 |
| CF-BR | –0.08841 | 0.13097 | 0.00160 | 2.50210 | Tansig-Logsig-Purelin | 18-10-20-12-1 |
| CF-SCG | –0.14831 | 0.17299 | 0.00195 | 3.05459 | Tansig-Logsig-Purelin | 18-8-20-12-1 |
| CF-RB | 0.16633 | 0.18931 | 0.00217 | 3.40278 | Tansig-Logsig-Purelin | 18-8-11-7-1 |
| RBF | –0.12491 | 0.12945 | 0.00157 | 2.46439 | Gaussian | 18-30-1 |
| GR | –0.84633 | 0.84632 | 0.00873 | 13.6627 | Gaussian | |
| CMIS | –0.10723 | 0.11340 | 0.00141 | 2.22181 |
According to the statistical results in Table 3, a MLP neural network using the Levenberg–Marquardt (MLP-LM) optimizer with AARE (%), RMSE, and SD values of about 0.0175, 0.447, and 0.00027 is the most accurate method compared to other models. The low error of this method, both in the training and testing phase, indicates the acceptable fit of the developed model to the data. In addition, the small difference between the error of the training and testing phase shows the confirmation of the model developed for prediction. As shown in Table 3, the RBF model with AARE (%), RMSE, and SD values of about 0.0432, 0.934, and 0.00057 is less accurate than other models. Giving the same weight to each attribute is one of the disadvantages of this method and leads to the lack of high accuracy of this method compared to other methods. Based on the information in Table 3, the developed GR model has values of 0.0355, 0.00053, and 0.8633 for AARE (%), SD, and RMSE. The higher error rate of this model in the training and testing phase than other methods indicates that this method is underfitting. This problem can be smoothed out by increasing the number of input features. This model similar to RBF models requires less time (s) to run than other methods. RBF and GR methods are faster than the MLP and CF methods due to their monolayer. The results of Table 3 have been used to rank the proposed models based on having the highest accuracy
Table 3. Statistical Parameters of the Developed Models for the Prediction of Groundwater Level Using 1377 Data Points.
| ARE
(%) |
AARE
(%) |
SD |
RMSE
(m) |
T (s) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| statistical parameters | training data | test data | total | training data | test data | total | training data | test data | total | training data | test data | total | one iteration |
| MLP-LM | –0.00014 | 0.00077 | –0.00095 | 0.01678 | 0.01961 | 0.01751 | 0.00026 | 0.00028 | 0.00027 | 0.43486 | 0.46825 | 0.44701 | 39.8 |
| MLP-BR | –0.00054 | 0.00264 | –0.00059 | 0.01785 | 0.01663 | 0.01809 | 0.00029 | 0.00026 | 0.00029 | 0.47691 | 0.43057 | 0.48550 | 25.07 |
| MLP-SCG | 0.00013 | 0.00372 | –0.0001 | 0.03514 | 0.0389 | 0.03522 | 0.00052 | 0.00053 | 0.00051 | 0.85940 | 0.86466 | 0.84850 | 16.32 |
| MLP-RB | –0.00006 | 0.00265 | 0.00046 | 0.01872 | 0.02402 | 0.01992 | 0.00028 | 0.00037 | 0.00030 | 0.46062 | 0.60489 | 0.49080 | 14.36 |
| CF-LM | 0.00188 | 0.00609 | 0.00212 | 0.02053 | 0.02591 | 0.02123 | 0.00031 | 0.00040 | 0.00032 | 0.50853 | 0.65183 | 0.52822 | 15.5 |
| CF-BR | 0.00046 | –0.00052 | 0.00042 | 0.01741 | 0.02016 | 0.01791 | 0.00026 | 0.00029 | 0.00027 | 0.43614 | 0.48447 | 0.44753 | 16.41 |
| CF-SCG | –0.00017 | –0.00414 | –0.00076 | 0.03098 | 0.03671 | 0.03153 | 0.00045 | 0.00052 | 0.00045 | 0.73403 | 0.86044 | 0.74641 | 13.88 |
| CF-RB | –0.00001 | 0.00474 | 0.00083 | 0.02404 | 0.02384 | 0.02419 | 0.00036 | 0.00031 | 0.00036 | 0.59830 | 0.52017 | 0.59196 | 17.98 |
| RBF | 0.00006 | –0.0182 | –0.00266 | 0.04173 | 0.04892 | 0.04322 | 0.00055 | 0.00063 | 0.00057 | 0.90080 | 1.03346 | 0.93469 | 9.58 |
| GR | 0.00077 | 0.004 | 0.00035 | 0.0352 | 0.03805 | 0.03557 | 0.00052 | 0.00054 | 0.00053 | 0.85575 | 0.88188 | 0.86330 | 7.92 |
After developing different models using 1377 data points in the previous step, 165 extra validation data points have been used to identify the best models and their combination and to develop the proposed CMIS model. The statistical results of the developed models using 165 extra validation data points are shown in Table 4.
Out of 10 developed models, RBF, MLP-LM optimizer, and CF neural network using BR optimizer (CF-BR) have the lowest AARE (%) value. The high error of other models for predicting groundwater levels is due to overfitting. The close-to-reality predictions of these three methods reflect the high accuracy of the developed models. The three models developed with the highest accuracy are combined with a CMIS. To detect the optimal coefficients of this model, multiple linear regression is used, which is shown in the next equation
| 17 |
In the above equation, α1 to α4 are as follows
CMIS model proposed in this research is show in Figure 6.
Figure 6.
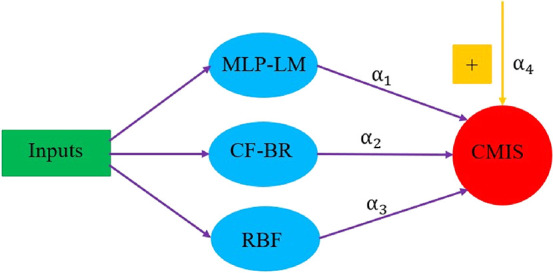
Architecture of the proposed CMIS model.
3.2. Evaluation of the Validity and Precision of the Developed Models
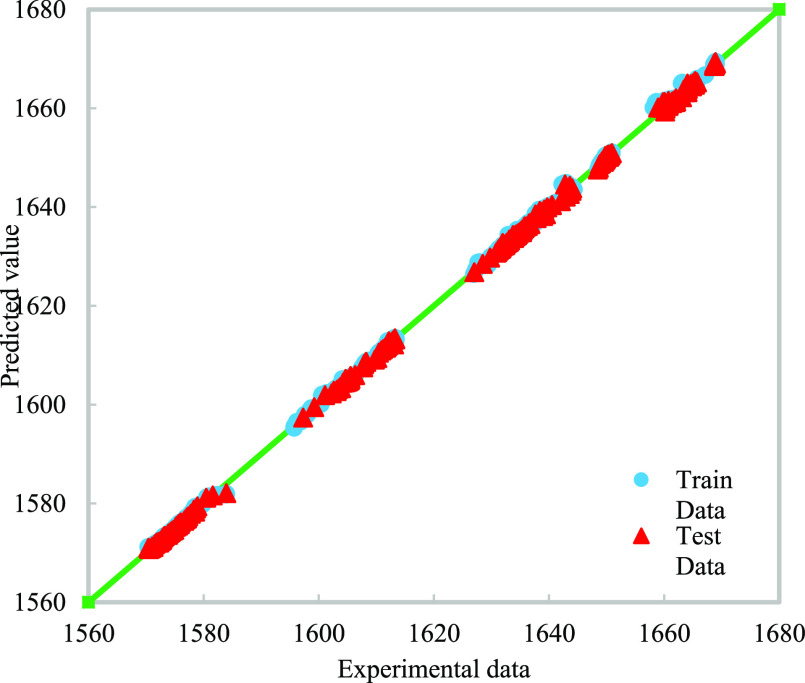
Statistical parameters such as AARE (%), ARE (%), RMSE, and SD for developed models are shown in Table 4. A model, such as RBF, which has the highest AARE value in Table 3, but here with one of the lowest error values, is one of the best models to predict, indicating accurate learning between the input and output relationships. Other models, such as the CF neural network using SCG optimizer, which do not have a good prediction of the groundwater level from extra validation data, due to overtraining and memorizing input–output rules or maybe stuck in local optimizations. AARE (%) and SD values of about 0.1134 and 2.2218 indicate that the proposed CMIS model is the most precise model for groundwater level forecasting among other developed models. A value of 0.00141 for SD indicates that the data of the developed model are close to the mean value, thus confirming the reliability of the developed model. To visually confirm the precision of the developed CMIS model using 1377 data points, the cross plot of the experimental data versus predicted relative groundwater level is plotted in Figure 7.
Figure 7.
Cross plot of the predicted relative groundwater level vs tentative relative groundwater level for test and train data using 1377 data points.
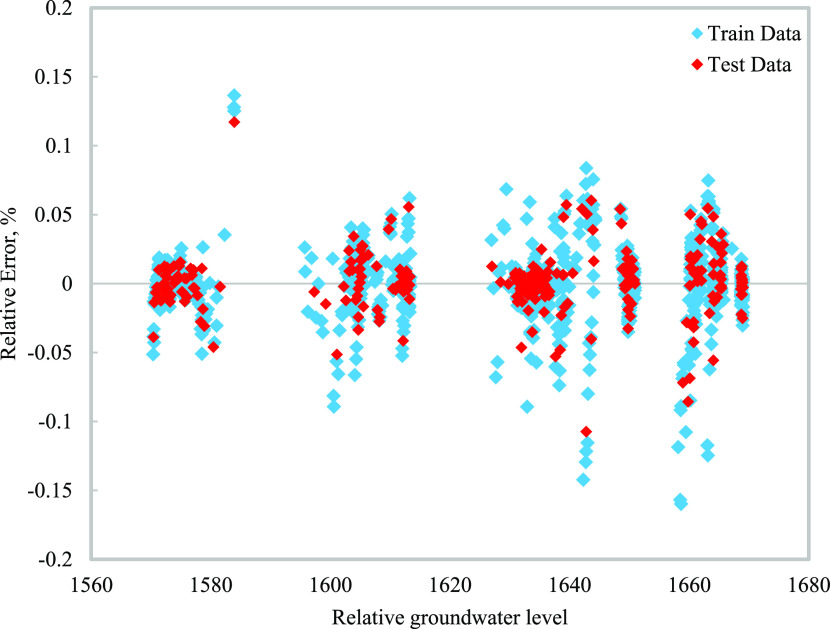
The high concentration of test and train data around the unit slope indicates the high accuracy of the CMIS model prediction. Predicted points of the groundwater level located in the range of 1580 (m) are related to well no. 3, located points in the range of 1600–1620 (m) are related to wells nos. 1 and 2, located points in the range of 1630–1650 (m) are related to well no. 5, and located points in the range of 1670 (m) are related to well no. 4. Figure 8 shows the relative error distribution curve for testing and training data set. In Figure 8, the maximum relative error of the predicted and experimental data values is 0.15%. Most of the data set points are located about the zero-error line for the tentative relative groundwater level. Most points below the 0.05% error confirm the acceptable stability between the experimental data and the CMIS model prediction.
Figure 8.
Relative error between the tentative and predicted relative groundwater level vs the tentative relative groundwater level for train and test data using 1377 data points.
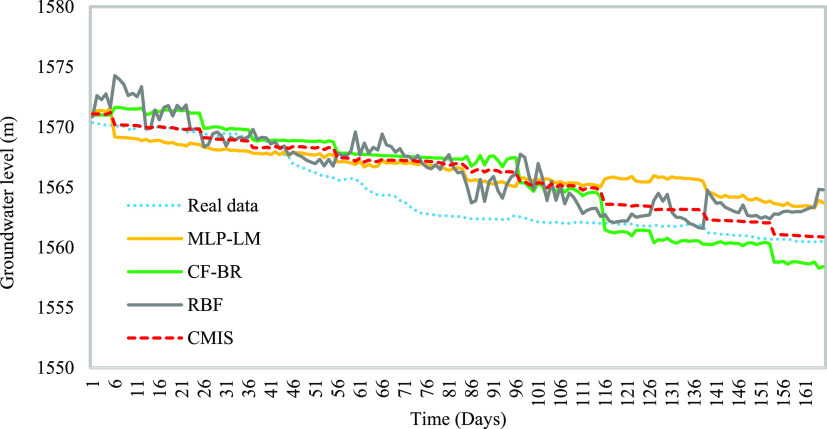
The actual groundwater level and groundwater level predicted for well no. 3 in the next 165 days by the developed models with the lowest AARE value are shown in Figure 9. Groundwater level fluctuations have reduced over this 165-day period, and all developed models have confirmed this correctly. The CMIS model has the highest accuracy for estimating the groundwater level throughout the time period in addition to significant smoothness.
Figure 9.
Prediction of the groundwater level for different models using 165 extra data points.
3.3. Sensitivity Analysis on Models’ Inputs
Sensitivity analysis is important from the perspective that uncertainty in model inputs affects uncertainty in the model output. Sensitivity analysis can be used to evaluate the correlation between model inputs and outputs, to search for errors in the model structure, and to simplify a developed model by removing its inputs that do not affect its output.56 To determine the effect of a model’s input parameter on its output, the reliable method of relevancy factor analysis can be used.57 The relevancy factor measures the effect of input parameter on the output and is denoted by r. The higher the r value, the greater the effect of the input on the output. The relevancy factor is calculated from the following equation
| 18 |
where Inpk.i shows the ith value, and Inpave.k is the average value of kth input, respectively (k represents the model inputs). μi and μave show the ith value and the average value of the predicted output.52Figure 10 shows the value of the relevancy factor. The obtained numbers show that spatial parameters have a more significant effect on the groundwater surface than temporal parameters. The most influential spatial parameters on the groundwater level are the electrical resistivity of sediments, depth of sediments, the electrical resistivity of bedrock, hydraulic conductivity of the bedrock, and effective porosity of sediments. Among the temporal parameters, drainage volume has the most significant impact on the groundwater level due to pumping wells in the pit mine’s southeastern region.
Figure 10.
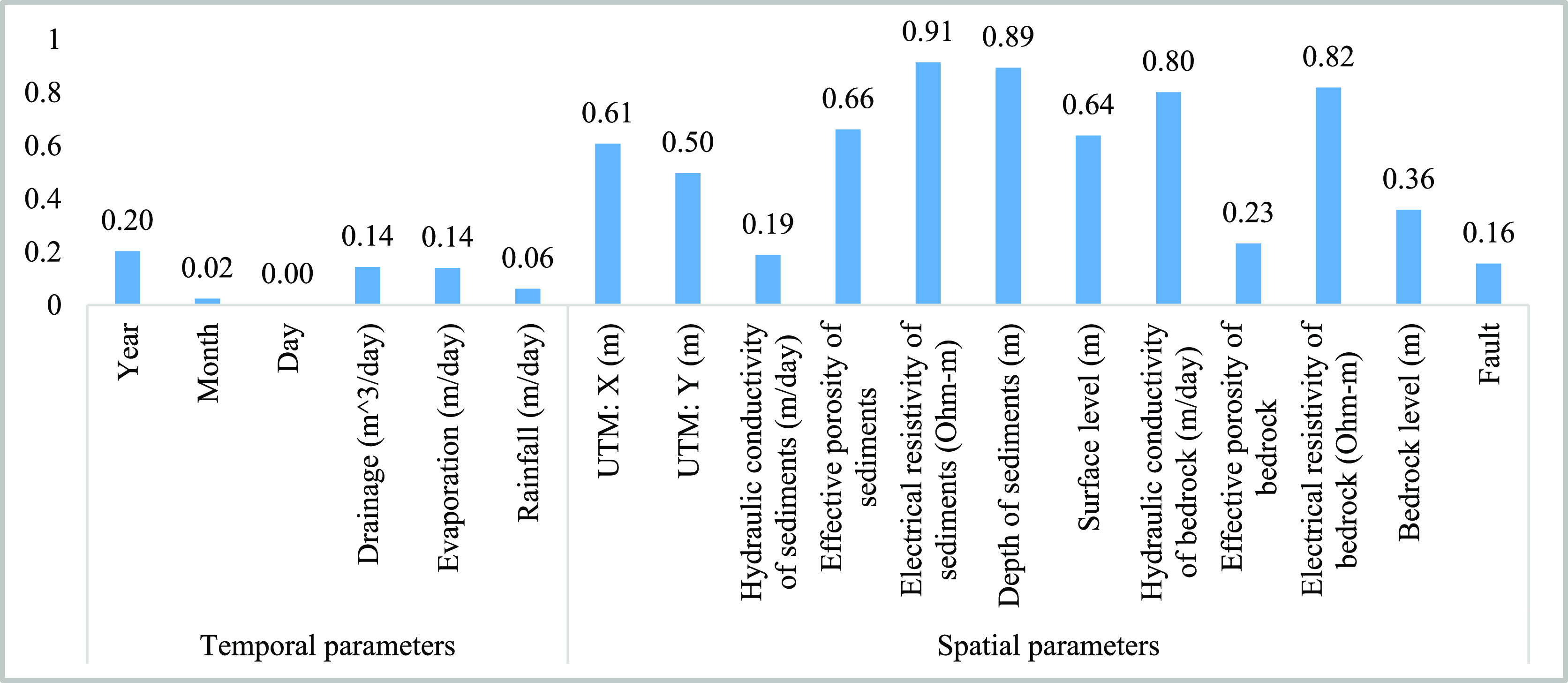
Relevancy factor for temporal and spatial parameters on the groundwater level.
3.4. Detailed Error Analysis
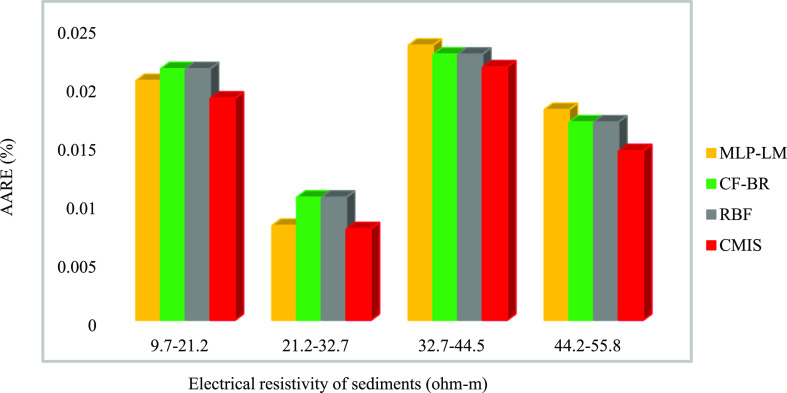
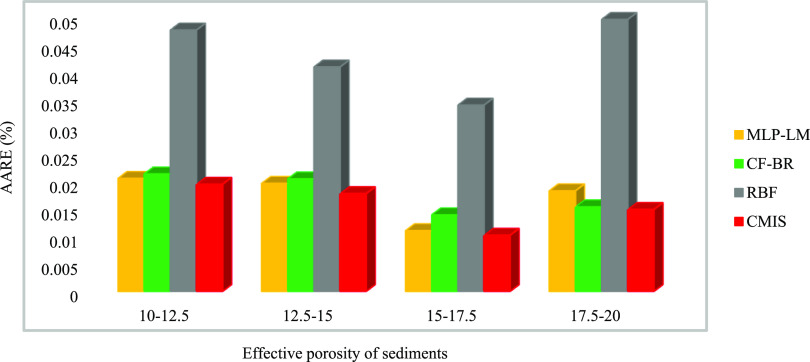
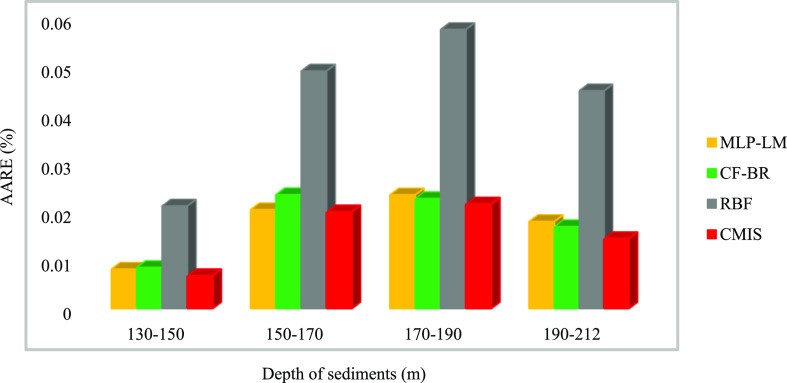
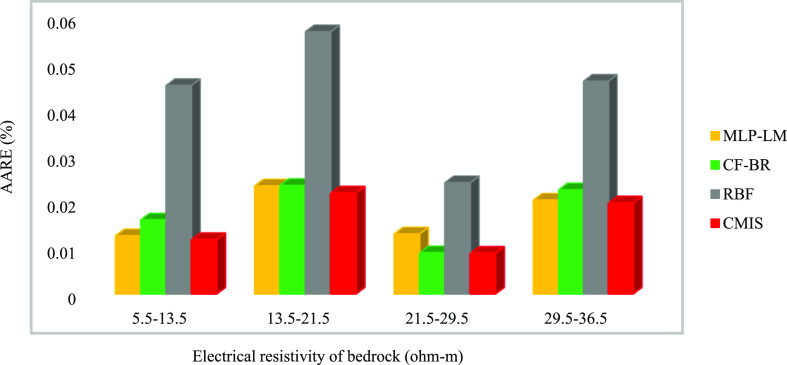
A detailed error analysis has been used to more compare the efficiency of the proposed CMIS model and other developed models for groundwater level prediction. The AARE (%) in Figures 11–15 is drawn as a function of the input parameters that have the most significant impact on the groundwater fluctuations. According to Figure 10, the highest relevancy is related to the electrical resistivity of sediments, depth of sediments, the electrical resistivity of bedrock, hydraulic conductivity of bedrock, and effective porosity of sediments. For this purpose, error analysis was performed by dividing the entire data into four groups to indicate the models’ precision in various ranges of crucial parameters.
Figure 11.
AARE (%) for the developed CMIS model and best models for different electrical resistivities of sediment ranges.
Figure 15.
AARE (%) for the developed CMIS model and best models for the effective porosity of sediments ranges.
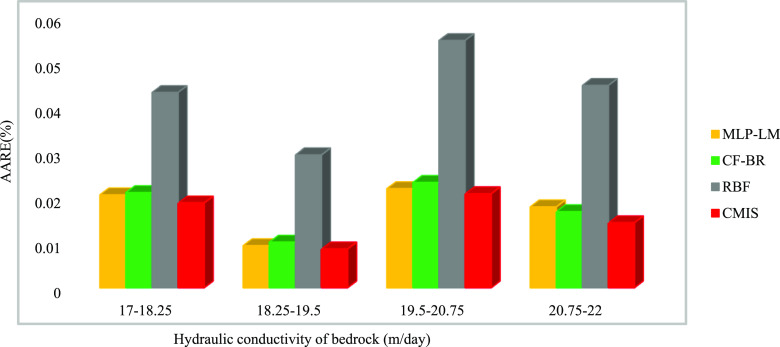
Figure 11 compares the AARE, % of dissimilar models in four ranges for the electrical resistivity of sediments. The maximum AARE value of 0.021% for the proposed CMIS model indicates its very high capability to predict the groundwater level in the whole range of electrical resistivity of sediments. As shown from this figure, all developed models for the range of 21–32 (ohm m) have a lower AARE (%) error than other values. Examination of the input data to developed models shows that this range is related to well no. 5.
Figure 12 clearly shows the lower AARE (%) of the CMIS model than all models in the four depth of sediment ranges. The lowest AARE (%) value is close to the surface in the range of 130–150 m and is related to wells no. 1 and 4.
Figure 12.
AARE (%) for the developed CMIS model and best models for the depth of sediment ranges.
Figure 13 presents the efficiency of the developed models over dissimilar ranges of the electrical resistivity of the bedrock. As can be easily seen, the CMIS model has the lowest AARE (%) in all four ranges. The lowest AARE value here is in the range of 21–30 (ohm m) and is related to well no. 1.
Figure 13.
AARE (%) for the developed CMIS model and best models for the electrical resistivity of bedrock ranges.
Figure 14 depicts the AARE of the developed models for dissimilar ranges of hydraulic conductivity of bedrock, and again, the proposed CMIS is more accurate than other models in all ranges. The minimum AARE (%) value is in the range of 18–19 (m/day) and this range is related to wells no. 1 and 4.
Figure 14.
AARE (%) for the developed CMIS model and best models for hydraulic conductivity of bedrock ranges.
The effect of porosity of sediments in Figure 15 in four ranges shows a low AARE (%) value for all models, mainly CMIS. In all ranges, the AARE values are close to each other models and below 0.05%. The lowest AARE (%) value is in the range of 15–17.5 and is related to well no. 1. Therefore, it can be concluded from Figures 8–12 that well no. 1 has the most accurate input data compared to other wells.
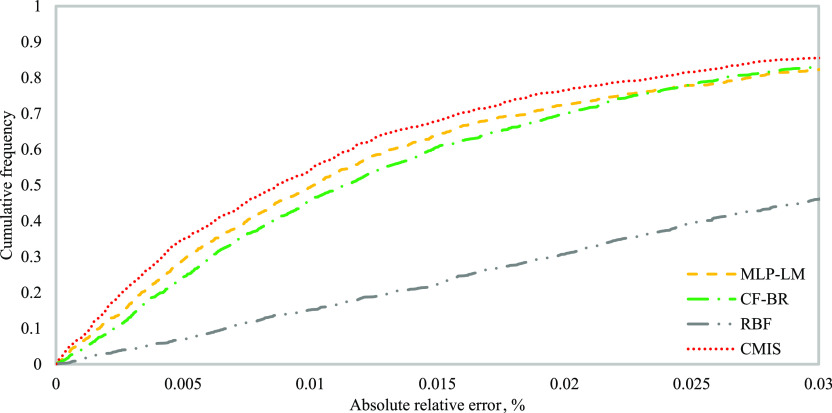
To better compare the models, the cumulative frequency of AARE for the developed CMIS model and all other models is shown in Figure 16 .58 According to this figure, about 85.5% of the groundwater level predicted by the developed CMIS model has an AARE, % of less than 0.03%. Other developed MLP neural networks using Levenberg–Marquardt optimizer, MLP neural networks using BR optimizer, and CF neural networks using BR optimizer models have 82.4, 83.1, and 82.9% errors. The results of this figure further indicate the success of the proposed CMIS method compared to other developed methods for groundwater level prediction.
Figure 16.
Cumulative frequency vs absolute relative error for all developed models.
3.5. Trend Analysis of the Developed Model
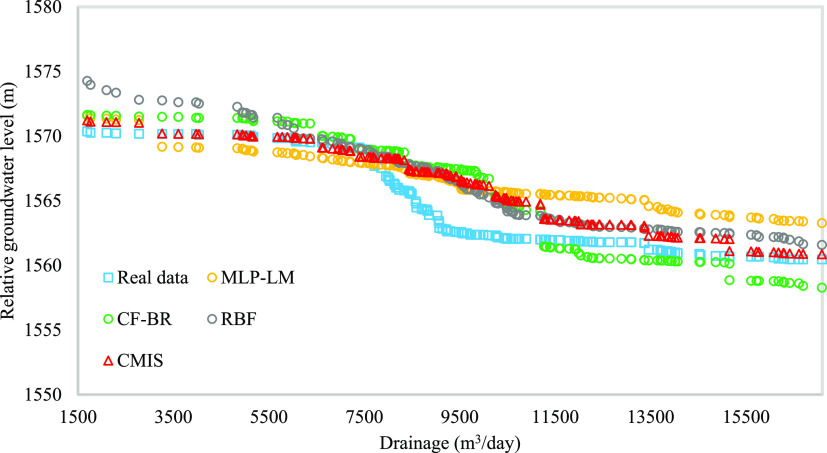
Trend analysis in a hydrogeological time series can be a practical tool to study groundwater level fluctuations.59 By examining the groundwater level predicted in Figure 9, significant changes are seen on days 40–110, indicating the pumping well in the southeastern part of the mine. For this reason, considering that the drainage time series is a parameter affecting the groundwater level, the physically expected trends of the groundwater level by changing the drainage is investigated by the models developed in Figure 17. As can be seen in this figure, the relative groundwater level decreases with the drainage increases. All developed models can record the expected trend with drainage changes. This figure also shows the accuracy of the proposed CMIS model compared to other methods.
Figure 17.
Comparing the relative variation with drainage for the proposed CMIS model and other developed models with real data.
3.6. Outlier Diagnosis and Applicability Domain of the Model
Outliers commonly appear in a comprehensive
set of experimental data and differ from the bulk of the data. Because
such a data set can affect the reliability and precision of experimental
models, thus finding this type of data set is essential in developing
models.60 One of the practical advantages
of this analysis is that by carefully examining the outlier data,
a good view of the model constraint can be provided, which may be
due to the ignoring of some justifiable effects. In this research,
the leverage approach has been used to determine and eliminate outliers,
including calculating the model deviation from the relevant experimental
data. The leverage values are diagonal elements of the projection
matrix 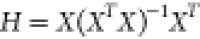 , where T denotes
the transpose
matrix operator and X is the matrix of explanatory
variables. The leverage values higher than a particular criterion
are known as high leverage points and are associated with uncertainties.
The following expression for calculating the leverage threshold (H*) have proposed by61
, where T denotes
the transpose
matrix operator and X is the matrix of explanatory
variables. The leverage values higher than a particular criterion
are known as high leverage points and are associated with uncertainties.
The following expression for calculating the leverage threshold (H*) have proposed by61
| 19 |
The computed model deviations are placed in a hat matrix and are called “standardized cross-validated residuals”.62 This parameter is obtained from the following expression
| 20 |
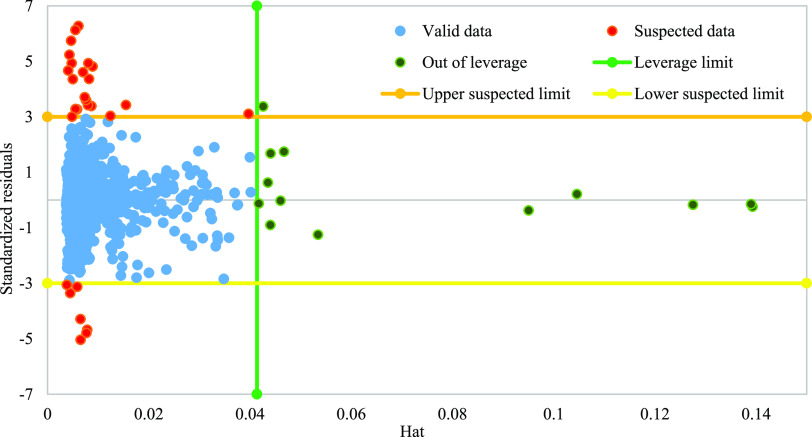
where hi is denoted for the ith leverage value, MSE stands the mean square of error, and ei is the error value associated with the ith record. William’s plot is plotted in Figure 18 for the resulting by the developed CMIS model for 1542 groundwater level predictions data. Due to the location of most of the predicted points in the feasibility domain of the proposed model (0 ≤ hat ≤ 0.0414 and −3 ≤ R ≤ 3), statistical validity and high reliability of the developed CMIS model are shown. About 2.65% of the points are outside the acceptable range of the model, which can be ignored due to the number of data points used in the model’s development. Points in the range of R < −3 or R > 3 are defined as “bad high leverage” regardless of their hat value compared to hat*.63 These data may be well predicted, but due to the difference with a large amount of data, but, are outside the acceptable range of the model.
Figure 18.
William’s plot for the resulting outputs by the proposed CMIS model.
4. Conclusions
In this research, the data of five piezometric wells, including 1542 data points around the Gohar Zamin iron ore mine located in Sirjan, Iran, have been used to predict the groundwater level fluctuations. 1377 spatial (sediment and bedrock) and temporal data points (276 days) have been used to develop 10 supervised learning models. These developed models have been used to predict the groundwater level of 165 extra validation data points. Three of the best models with the lowest AARE, % value have been combined in a single model, and the proposed CMIS model has been developed. The results of this research can be concluded:
-
1.
Almost all developed models with 1377 data points can model groundwater levels with acceptable AARE (%) values in the range of 0.017–0.043%.
-
2.
The running time (s) of different algorithms with similar conditions shows that GR and RBF algorithms are significantly faster due to these models’ monolayer.
-
3.
Developed models using 1377 data points to predict groundwater levels for 165 extra validation data points showed almost similar results, except that the RBF model has the lowest AARE (%). A lower AARE (%) value for the RBF model indicates an acceptable fit of the model to data and learning of the input–output relationships. Developed models can predict groundwater levels for these 165 extra validation data points with AARE values between 0.12 and 0.84%.
-
4.
The developed CMIS model has a better performance than all other models and can predict the groundwater level with an AARE (%) value of about 0.1134%. The proposed CMIS model, in addition to significant smoothness, predicts a downward trend in groundwater levels over the entire 165-day period.
-
5.
The electrical resistivity of sediments, depth of sediments, the electrical resistivity of bedrock, hydraulic conductivity of bedrock, and effective porosity of sediments of the 18 input parameters are the most influential input parameters on the groundwater level, respectively.
-
6.
Trend analysis for drainage parameters shows a decrease in the groundwater level with the increase in drainage due to pumping wells’ activity in the southeastern part of the mine.
-
7.
Based on the cumulative frequency results for the CMIS model, about 85.5% of the predicted groundwater level has an AARE less than 0.03%, which indicates the statistical validity of this method.
-
8.
Data that are out of the applicability domain of the proposed CMIS are about 2.65%, which indicates the high accuracy of this method.
Machine learning is one of the powerful tools for prediction. The high accuracy of machine learning methods, especially the proposed CMIS, can be an alternative to widely used numerical methods such as MODFLOW. It is suggested that for a more accurate prediction of the groundwater level, widely used methods for feature selection can be used.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c00536.
LM, BR, SCG, and RB algorithms (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Brawner C. O. Groundwater and coal mining. Min. Sci. Technol. 1986, 3, 187–198. 10.1016/s0167-9031(86)90331-2. [DOI] [Google Scholar]
- Singh R. N.; Atkins A. S. Analytical techniques for the estimation of mine water inflow. Int. J. Min. Eng. 1985, 3, 65–77. 10.1007/BF00881342. [DOI] [Google Scholar]
- Xu X.; Huang G.; Qu Z.; Pereira L. S. Using MODFLOW and GIS to Assess Changes in Groundwater Dynamics in Response to Water Saving Measures in Irrigation Districts of the Upper Yellow River Basin. Water Resour. Manag. 2011, 25, 2035–2059. 10.1007/s11269-011-9793-2. [DOI] [Google Scholar]
- Loredo C.; Roqueñí N.; Ordóñez A. Modelling flow and heat transfer in flooded mines for geothermal energy use: A review. Int. J. Coal Geol. 2016, 164, 115–122. 10.1016/j.coal.2016.04.013. [DOI] [Google Scholar]
- Zhang M.; Hu L.; Yao L.; Yin W. Numerical studies on the influences of the South-to-North Water Transfer Project on groundwater level changes in the Beijing Plain, China. Hydrol. Process. 2018, 32, 1858–1873. (acccessed 2021/06/09) 10.1002/hyp.13125. [DOI] [Google Scholar]
- Golestani Kermani S.; Sayari S.; Kisi O.; Zounemat-Kermani M. Comparing data driven models versus numerical models in simulation of waterfront advance in furrow irrigation. Irrig. Sci. 2019, 37, 547–560. 10.1007/s00271-019-00635-5. [DOI] [Google Scholar]
- Natarajan N.; Sudheer C. Groundwater level forecasting using soft computing techniques. Neural. Comput. Appl. 2020, 32, 7691–7708. 10.1007/s00521-019-04234-5. [DOI] [Google Scholar]
- Malakar P.; Mukherjee A.; Bhanja S. N.; Ray R. K.; Sarkar S.; Zahid A. Machine-learning-based regional-scale groundwater level prediction using GRACE. Hydrogeol. J. 2021, 29, 1027–1042. 10.1007/s10040-021-02306-2. [DOI] [Google Scholar]
- Parisouj P.; Mohebzadeh H.; Lee T. Employing Machine Learning Algorithms for Streamflow Prediction: A Case Study of Four River Basins with Different Climatic Zones in the United States. Water Resour. Manag. 2020, 34, 4113–4131. 10.1007/s11269-020-02659-5. [DOI] [Google Scholar]
- Tahmasebi P.; Sahimi M. Special issue on Machine Learning for Water Resources and Subsurface Systems. Adv. Water Resour. 2021, 149, 103851. 10.1016/j.advwatres.2021.103851. [DOI] [Google Scholar]
- Sahoo S.; Russo T. A.; Elliott J.; Foster I. Machine learning algorithms for modeling groundwater level changes in agricultural regions of the U.S. Water Resour. Res. 2017, 53, 3878–3895. (acccessed 2022/02/15) 10.1002/2016wr019933. [DOI] [Google Scholar]
- Leonard L. Using machine learning models to predict and choose meshes reordered by graph algorithms to improve execution times for hydrological modeling. Environ. Model. Software 2019, 119, 84–98. 10.1016/j.envsoft.2019.03.023. [DOI] [Google Scholar]
- Jang W. S.; Engel B.; Yeum C. M. Integrated environmental modeling for efficient aquifer vulnerability assessment using machine learning. Environ. Model. Software 2020, 124, 104602. 10.1016/j.envsoft.2019.104602. [DOI] [Google Scholar]
- Oppel H.; Schumann A. H. Machine learning based identification of dominant controls on runoff dynamics. Hydrol. Process. 2020, 34, 2450–2465. (acccessed 2021/06/09) 10.1002/hyp.13740. [DOI] [Google Scholar]
- Rahman A. T. M. S.; Hosono T.; Quilty J. M.; Das J.; Basak A. Multiscale groundwater level forecasting: Coupling new machine learning approaches with wavelet transforms. Adv. Water Resour. 2020, 141, 103595. 10.1016/j.advwatres.2020.103595. [DOI] [Google Scholar]
- Malakar P.; Mukherjee A.; Bhanja S. N.; Sarkar S.; Saha D.; Ray R. K. Deep Learning-Based Forecasting of Groundwater Level Trends in India: Implications for Crop Production and Drinking Water Supply. ACS ES&T Engg 2021, 1, 965–977. 10.1021/acsestengg.0c00238. [DOI] [Google Scholar]
- Nourani V.; Mogaddam A. A.; Nadiri A. O. An ANN-based model for spatiotemporal groundwater level forecasting. Hydrol. Process. 2008, 22, 5054–5066. (acccessed 2020/12/12) 10.1002/hyp.7129. [DOI] [Google Scholar]
- Trichakis I. C.; Nikolos I. K.; Karatzas G. P. Artificial Neural Network (ANN) Based Modeling for Karstic Groundwater Level Simulation. Water Resour. Manag. 2011, 25, 1143–1152. 10.1007/s11269-010-9628-6. [DOI] [Google Scholar]
- Banadkooki F. B.; Ehteram M.; Ahmed A. N.; Teo F. Y.; Fai C. M.; Afan H. A.; Sapitang M.; El-Shafie A. Enhancement of Groundwater-Level Prediction Using an Integrated Machine Learning Model Optimized by Whale Algorithm. Nat. Resour. Res. 2020, 29, 3233. 10.1007/s11053-020-09634-2. [DOI] [Google Scholar]
- Hussein E. A.; Thron C.; Ghaziasgar M.; Bagula A.; Vaccari M. Groundwater Prediction Using Machine-Learning Tools. Algorithms 2020, 13, 300. 10.3390/a13110300. [DOI] [Google Scholar]
- Cai H.; Shi H.; Liu S.; Babovic V. Impacts of regional characteristics on improving the accuracy of groundwater level prediction using machine learning: The case of central eastern continental United States. J. Hydrol. 2021, 37, 100930. 10.1016/j.ejrh.2021.100930. [DOI] [Google Scholar]
- Santos Finck J.; Correa Pedrollo O. Facing Losses of Telemetric Signal in Real Time Forecasting of Water Level using Artificial Neural Networks. Water Resour. Manag. 2021, 35, 1119. 10.1007/s11269-021-02782-x. [DOI] [Google Scholar]
- Kouziokas G. N.; Chatzigeorgiou A.; Perakis K. Multilayer Feed Forward Models in Groundwater Level Forecasting Using Meteorological Data in Public Management. Water Resour. Manag. 2018, 32, 5041–5052. 10.1007/s11269-018-2126-y. [DOI] [Google Scholar]
- Hayder G.; Solihin M. I.; Mustafa H. M. Modelling of River Flow Using Particle Swarm Optimized Cascade-Forward Neural Networks: A Case Study of Kelantan River in Malaysia. Appl. Sci. 2020, 10, 8670. 10.3390/app10238670. [DOI] [Google Scholar]
- Hong H.; Zhang Z.; Guo A.; Shen L.; Sun H.; Liang Y.; Wu F.; Lin H. Radial basis function artificial neural network (RBF ANN) as well as the hybrid method of RBF ANN and grey relational analysis able to well predict trihalomethanes levels in tap water. J. Hydrol. 2020, 591, 125574. 10.1016/j.jhydrol.2020.125574. [DOI] [Google Scholar]
- Pal J.; Chakrabarty D. Assessment of artificial neural network models based on the simulation of groundwater contaminant transport. Hydrogeol. J. 2020, 28, 2039–2055. 10.1007/s10040-020-02180-4. [DOI] [Google Scholar]
- Malekpour M. M.; Mohammad Rezapour Tabari M. Implementation of supervised intelligence committee machine method for monthly water level prediction. Arabian J. Geosci. 2020, 13, 1049. 10.1007/s12517-020-06034-x. [DOI] [Google Scholar]
- Rajaee T.; Ebrahimi H.; Nourani V. A review of the artificial intelligence methods in groundwater level modeling. J. Hydrol. 2019, 572, 336–351. 10.1016/j.jhydrol.2018.12.037. [DOI] [Google Scholar]
- Hebb D. O.The Organization Of Behavior: A Neuropsychological Theory, Chapman & Hall; JOHN WILEY, 1949. [Google Scholar]
- Savary M.; Johannet A.; Massei N.; Dupont J.-P.; Hauchard E. Karst-aquifer operational turbidity forecasting by neural networks and the role of complexity in designing the model: a case study of the Yport basin in Normandy (France). Hydrogeol. J. 2021, 29, 281–295. 10.1007/s10040-020-02277-w. [DOI] [Google Scholar]
- Cybenko G. Approximation by superpositions of a sigmoidal function. Math. Control, Signals, Syst. 1989, 2, 303–314. 10.1007/BF02551274. [DOI] [Google Scholar]
- Rostami A.; Hemmati-Sarapardeh A.; Shamshirband S. Rigorous prognostication of natural gas viscosity: Smart modeling and comparative study. Fuel 2018, 222, 766–778. 10.1016/j.fuel.2018.02.069. [DOI] [Google Scholar]
- Chiappini F. A.; Allegrini F.; Goicoechea H. C.; Olivieri A. C. Sensitivity for Multivariate Calibration Based on Multilayer Perceptron Artificial Neural Networks. Anal. Chem. 2020, 92, 12265–12272. 10.1021/acs.analchem.0c01863. [DOI] [PubMed] [Google Scholar]
- Hemmati-Sarapardeh A.; Ameli F.; Varamesh A.; Shamshirband S.; Mohammadi A. H.; Dabir B. Toward generalized models for estimating molecular weights and acentric factors of pure chemical compounds. Int. J. Hydrogen Energy 2018, 43, 2699–2717. 10.1016/j.ijhydene.2017.12.029. [DOI] [Google Scholar]
- Gamal H.; Abdelaal A.; Elkatatny S. Machine Learning Models for Equivalent Circulating Density Prediction from Drilling Data. ACS Omega 2021, 6, 27430–27442. 10.1021/acsomega.1c04363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemmati-Sarapardeh A.; Varamesh A.; Husein M. M.; Karan K. On the evaluation of the viscosity of nanofluid systems: Modeling and data assessment. Renew. Sustain. Energy Rev. 2018, 81, 313–329. 10.1016/j.rser.2017.07.049. [DOI] [Google Scholar]
- Fahlman S.; Lebiere C. The cascade-correlation learning architecture. Adv. Neural Inf. Process. Syst. 1990, 2, 524–532. [Google Scholar]
- Karkevandi-Talkhooncheh A.; Rostami A.; Hemmati-Sarapardeh A.; Ahmadi M.; Husein M. M.; Dabir B. Modeling minimum miscibility pressure during pure and impure CO2 flooding using hybrid of radial basis function neural network and evolutionary techniques. Fuel 2018, 220, 270–282. 10.1016/j.fuel.2018.01.101. [DOI] [Google Scholar]
- Broomhead D.; Lowe D.. Radial basis functions, multi-variable functional interpolation and adaptive networks; ROYAL SIGNALS AND RADAR ESTABLISHMENT MALVERN (UNITED KINGDOM), 1988. RSRE-MEMO-4148. [Google Scholar]
- Dashti A.; Amirkhani F.; Hamedi A.-S.; Mohammadi A. H. Evaluation of CO2 Absorption by Amino Acid Salt Aqueous Solution Using Hybrid Soft Computing Methods. ACS Omega 2021, 6, 12459–12469. 10.1021/acsomega.0c06158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang L.-C.; Chang F.-J.; Wang Y.-P. Auto-configuring radial basis function networks for chaotic time series and flood forecasting. Hydrol. Process. 2009, 23, 2450–2459. (acccessed 2021/06/09) 10.1002/hyp.7352. [DOI] [Google Scholar]
- Ying Z.; Wenxi L.; Haibo C.; Jiannan L. Comparison of three forecasting models for groundwater levels: A case study in the semiarid area of west Jilin Province, China. J. Water Supply: Res. Technol.--AQUA 2014, 63, 671–683. 10.2166/aqua.2014.023. [DOI] [Google Scholar]
- Meshram S. G.; Singh V. P.; Kisi O.; Karimi V.; Meshram C. Application of Artificial Neural Networks, Support Vector Machine and Multiple Model-ANN to Sediment Yield Prediction. Water Resour. Manag. 2020, 34, 4561–4575. 10.1007/s11269-020-02672-8. [DOI] [Google Scholar]
- Menad N. A.; Noureddine Z.; Hemmati-Sarapardeh A.; Shamshirband S. Modeling temperature-based oil-water relative permeability by integrating advanced intelligent models with grey wolf optimization: Application to thermal enhanced oil recovery processes. Fuel 2019, 242, 649–663. 10.1016/j.fuel.2019.01.047. [DOI] [Google Scholar]
- Specht D. F.A General Regression Neural Network; IEEE, 1991. (1045-9227 (Print)). [DOI] [PubMed] [Google Scholar]
- Kumar D.; Bhattacharjya R. K.. Forecasting Groundwater Fluctuation from GRACE Data Using GRNN. Soft Computing: Theories and Applications; Springer, 2020; pp 295–307. [Google Scholar]
- Tayfur G.; Aksoy H.; Eris E. Prediction of rainfall runoff-induced sediment load from bare land surfaces by generalized regression neural network and empirical model. Water Environ. J. 2020, 34, 66–76. (acccessed 2021/02/10) 10.1111/wej.12442. [DOI] [Google Scholar]
- Roshni T.; Jha M. K.; Drisya J. Neural network modeling for groundwater-level forecasting in coastal aquifers. Neural. Comput. Appl. 2020, 32, 12737. 10.1007/s00521-020-04722-z. [DOI] [Google Scholar]
- Rostami A.; Kalantari-Meybodi M.; Karimi M.; Tatar A.; Mohammadi A. H. Efficient estimation of hydrolyzed polyacrylamide (HPAM) solution viscosity for enhanced oil recovery process by polymer flooding. Oil Gas Sci. Technol. 2018, 73, 22. 10.2516/ogst/2018006. [DOI] [Google Scholar]
- Rostami A.; Baghban A.; Mohammadi A. H.; Hemmati-Sarapardeh A.; Habibzadeh S. Rigorous prognostication of permeability of heterogeneous carbonate oil reservoirs: Smart modeling and correlation development. Fuel 2019, 236, 110–123. 10.1016/j.fuel.2018.08.136. [DOI] [Google Scholar]
- Nilsson N.Learning Machines, 1965.
- Hemmati-Sarapardeh A.; Larestani A.; Nait Amar M.; Hajirezaie S.. Introduction. In Applications of Artificial Intelligence Techniques in the Petroleum Industry; Hemmati-Sarapardeh A., Larestani A., Nait Amar M., Hajirezaie S., Eds.; Gulf Professional Publishing, 2020; pp 1–22. [Google Scholar]
- Hashem S.; Schmeiser B.. Approximating a Function and its Derivatives Using MSE-Optimal Linear Combinations of Trained Feedforward Neural Networks. Proceedings of the Joint Conference on Neural Network, 1970.
- Perrone M. P.; Cooper L. N.. When Networks Disagree: Ensemble Methods for Hybrid Neural Networks. How We Learn; How We Remember: Toward an Understanding of Brain and Neural Systems,World Scientific Series in 20th Century Physics, 1995.
- Rostami A.; Baghban A. Application of a supervised learning machine for accurate prognostication of higher heating values of solid wastes. Energy Sources, Part A 2018, 40, 558–564. 10.1080/15567036.2017.1360967. [DOI] [Google Scholar]
- Rostami A.; Kamari A.; Panacharoensawad E.; Hashemi A. New empirical correlations for determination of Minimum Miscibility Pressure (MMP) during N2-contaminated lean gas flooding. J. Taiwan Inst. Chem. Eng. 2018, 91, 369–382. 10.1016/j.jtice.2018.05.048. [DOI] [Google Scholar]
- Mohammadi M.-R.; Hemmati-Sarapardeh A.; Schaffie M.; Husein M. M.; Karimian M.; Ranjbar M. On the evaluation of crude oil oxidation during thermogravimetry by generalised regression neural network and gene expression programming: application to thermal enhanced oil recovery. Combust. Theor. Model. 2021, 25, 1268–1295. 10.1080/13647830.2021.1975828. [DOI] [Google Scholar]
- Rostami A.; Arabloo M.; Esmaeilzadeh S.; Mohammadi A. H. On modeling of bitumen/n-tetradecane mixture viscosity: Application in solvent-assisted recovery method. Asia-Pac. J. Chem. Eng. 2018, 13, e2152(acccessed 2022/02/08) 10.1002/apj.2152. [DOI] [Google Scholar]
- Halder S.; Roy M. B.; Roy P. K. Analysis of groundwater level trend and groundwater drought using Standard Groundwater Level Index: a case study of an eastern river basin of West Bengal, India. SN Appl. Sci. 2020, 2, 507. 10.1007/s42452-020-2302-6. [DOI] [Google Scholar]
- Mahdaviara M.; Rostami A.; Keivanimehr F.; Shahbazi K. Accurate determination of permeability in carbonate reservoirs using Gaussian Process Regression. J. Pet. Sci. Eng. 2021, 196, 107807. 10.1016/j.petrol.2020.107807. [DOI] [Google Scholar]
- Hoaglin D. C.; Welsch R. E. The hat matrix in regression and ANOVA. Am. Statistician 1978, 32, 17–22. 10.1080/00031305.1978.10479237. [DOI] [Google Scholar]
- Rousseeuw P. J.; Leroy A. M.. Robust Regression and Outlier Detection; John Wiley & Sons, Inc., 1987. [Google Scholar]
- Hemmati-Sarapardeh A.; Ameli F.; Dabir B.; Ahmadi M.; Mohammadi A. H. On the evaluation of asphaltene precipitation titration data: Modeling and data assessment. Fluid Phase Equilib. 2016, 415, 88–100. 10.1016/j.fluid.2016.01.031. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.