Transporter networks can serve plant cells as nutrient sensors and mimic transceptor-like behavior

Summary

Sensing of external mineral nutrient concentrations is essential for plants to colonize environments with a large spectrum of nutrient availability. Here, we analyzed transporter networks in computational cell biology simulations to understand better the initial steps of this sensing process. The networks analyzed were capable of translating the information of changing external nutrient concentrations into cytosolic H⁺ and Ca²⁺ signals, two of the most ubiquitous cellular second messengers. The concept emerging from the computational simulations was confirmed in wet-lab experiments. We document in guard cells that alterations in the external KCl concentration were translated into cytosolic H⁺ and Ca²⁺ transients as predicted. We show that transporter networks do not only serve their primary task of transport, but can also take on the role of a receptor without requiring conformational changes of a transporter protein. Such transceptor-like phenomena may be quite common in plants.

Graphical abstract

Highlights

• •Nutrient sensing of plants was analyzed in computational cell biology simulations
• •Changes in external nutrient concentrations caused cytosolic H⁺ and Ca²⁺ signals
• •Nutrient transporter networks exhibit transceptor-like characteristics
• •Wet-lab experiments confirmed the conceptual predictions

Biological sciences; Mathematical biosciences; Plant biology; Plant physiology; Plant nutrition

Introduction

Plants are sessile organisms. For their autarchic lifestyle, they develop a large aerial surface that collects CO₂ and sunlight, and a large below-ground root surface that collects the additional resources needed for growth and development, especially water and mineral nutrients. Yet, plants often grow in soils that contain sub-optimal concentrations of the essential macronutrients nitrogen (N), phosphorus (P), potassium (K), and sulfur (S). To colonize environments with variable nutrient availability, plants sense mineral nutrient concentrations and adjust their transporter systems accordingly. Additionally, plants adapt their growth and development to the nutrient concentrations by, for example, fine-tuning root architecture, root hair density, as well as root and shoot growth ratios.

Plant cell nutrient-sensing process activates diverse signal transduction pathways that tune the transporter network and adjust growth properties to nutrient availability (Oldroyd and Leyser, 2020; Schachtman and Shin, 2007). At the cellular level, calcium signaling is at the core of the signaling network and has been associated to N, P, K, Mg, boron, and iron sensing (Kudla et al., 2018; Tang and Luan, 2017; Wilkins et al., 2016). In addition, H⁺ also plays an important role as another messenger in mineral nutrition (Martinière et al., 2018; Michard et al., 2017). On the one hand, H⁺ is directly involved in the transport processes mediated by the proton pump and a variety of co-transporters, such as K⁺/H⁺ and ${\text{NO}}_3^{-}$/2H⁺. On the other hand, H⁺ can also regulate the activity of ion transporters either through direct activation or inhibition, or indirectly by modulating cytoskeleton-associated targeting to the membrane. Although our understanding of how plants react to nutrient availability has strongly advanced, the perception of the external concentrations, i.e., the first step of this process, is not yet well understood.

Biological systems eventually confront variable external media and maintaining a constant internal environment indispensable for controlled cell biological reactions can appear challenging. To qualify and theorize the mechanisms involved, Walter Cannon (1932) coined the term homeostasis. In further examinations, studying the theoretical basis of how the animal central nervous system processes information to maintain homeostasis at the body level, W. Ross Ashby (1960) proposed the “homeostat” as a model of a state-dependent mechanism that produces adaptive behavior in an organism interacting with its environment. This model represented one of the earliest theories of self-organizing systems.

In a recent study, we investigated the fundamental bases of homeostatic conditions in plant cells (Dreyer, 2021). We demonstrated that a network of differently energized transporter types for the same nutrient, can adjust the actual cytosolic value to a target value. Such a network showed adaptable self-organizing properties and was named “homeostat” in analogy to Ashby’s model. By fine-tuning the transporter activities, the same intracellular steady-state conditions could be achieved for a broad range of external conditions. Interestingly, the flexibility in adjusting a cytosolic concentration was compromised by the establishment of energy-consuming nutrient cycles at the membrane (Britto et al., 2001; Britto and Kronzucker, 2006; Coskun et al., 2010, 2013; Munns et al., 2020; Rubio et al., 2020; Shabala et al., 2020) indicating a highly dynamic feature of the homeostats.

Here, we went one step further and investigated the behavior of homeostats under fluctuating external conditions using a computational cell biology approach. We propose that homeostats allow the cell to sense changes in the external nutrient concentrations. The model showed that changes in nutrient availability were initially translated into alterations in plasma membrane voltage and cytosolic pH. In combination with a simple Ca-homeostat, the voltage signal was further processed to a cytosolic Ca²⁺-signal. Importantly, H⁺ and Ca²⁺ signals are known to be essential starting points for the induction of a large variety of signaling events. Thus, in addition to their genuine role in transport, we predict that transporter networks could also operate as receptors and therefore mimic a transceptor-like behavior. This computational cell biology-derived hypothesis was challenged by wet-lab experiments with the guard cell model system using a dual-sensing Ca²⁺/H⁺ biosensor.

Results

To gain further insights into the dynamic features of transporter networks in plant membranes, we followed a synthetic computational cell biology approach in which we simulated in silico some selected cellular aspects of membrane transport processes. In the previous study mentioned above, we presented, among others, the computational representation of transporter networks involved in the establishment of potassium and anion homeostasis and we analyzed their steady-state properties (Dreyer, 2021). Here, we equipped a model plant cell with these anion and potassium homeostats and challenged the cell with varying external nutrient concentrations. Potassium (K⁺) was taken as a cationic macronutrient, while anions, A^–, generally represented mineral macronutrients such as nitrate (${\text{NO}}_3^{-}$), but also chloride (Cl⁻) and organic acids like malate which are important to balance charge and the osmotic pressure. For steady-state conditions it was sufficient and reasonable to clamp the cytosolic pH, but under the transient conditions studied here, some dynamic pH change was required. This dynamic component was introduced by a buffer reaction of the type: H⁺ + Buf^– ↔ HBuf, with a weak acid HBuf and its conjugate base Buf^–. The model was then closer to the actual cytosolic conditions where pH buffering is ensured by a complex network of biochemical reactions and exchange with endomembranes (Sze and Chanroj, 2018). As pointed out by Lars Wegner et al. (Wegner et al., 2021; Wegner and Shabala, 2020), H⁺ scavenging is mainly associated with malate decarboxylation catalyzed by malic enzyme, and via the GABA shunt of the tricarboxylic acid (TCA) cycle involving glutamate decarboxylation. We simulated different cellular buffer capacities by different starting values for [Buf^–] and [HBuf]. To facilitate understanding of the system, we first considered the case, in which only K⁺ transporters are active in the membrane, then the case of A^– transporters, and finally the combination of both.

Plasma membrane K-homeostat

At first, we focused on potassium (Britto et al., 2021; Chérel and Gaillard, 2019; Monder et al., 2021) by analyzing the K-homeostat in the plasma membrane and its interaction with the energizing proton pump (Figure 1A). The K-homeostat was composed of K⁺ channels, 1H⁺/1K⁺ symporters, and electroneutral 1H⁺/1K⁺ antiporters. We started the what-if computational simulations in a resting state in which stable values for the membrane voltage and the transmembrane K⁺ and H⁺ gradients have been established. As shown recently (Dreyer, 2021), steady-state values for the membrane voltage V, the Nernst equilibrium potentials for potassium, E_K, and for protons, E_H, depended on the activity of the different entities of the transporter network. Without limiting generality, we took for the presentation a physiological resting state with [K⁺]_cyt ≈ 100 mM, [K⁺]_apo ≈ 0.25 mM, [A^–]_cyt ≈ 50 mM, [A^–]_apo ≈ 0.25 mM, ΔpH ≈ 1.4, V ≈ −150 mV. Based on these initial conditions, in the following, the external K⁺/A^– concentrations were increased or decreased exemplarily by a factor of 1.5. Because the membrane was impermeable for the counter anion A^–, changes in its concentration had no effect on the system. In contrast, an increase of [K⁺]_apo (Figure 1B) induced an expected net influx of K⁺ which then resulted in an increase in [K⁺]_cyt. When the cytosolic pH was clamped to pH 7.2, the system evolved a steady state with the same V, E_K, and E_H values as before. The increased [K⁺]_apo was compensated by an increase in [K⁺]_cyt, whereby charge neutrality was maintained by an efflux of protons from the HBuf ↔ H⁺ + Buf^– reaction. However, when the proton buffering capacity of the cytosol was limited, the net K⁺ transport affected intracellular pH, which in turn affected H⁺-ATPase activity, the membrane voltage, and the energizing gradients of the K/H sym- and antiporters. As a consequence, different steady-state values for V, E_K, and E_H established that depended on the cellular buffer capacity (Figure 1B, different shading of the curves). To understand this phenomenon, we repeated the simulation with various sets of parameters. It turned out that the net K⁺ influx was always electrically compensated by a net H⁺ efflux irrespective of the activities of the different transporters of the K-homeostat. When this H⁺ efflux was fully compensated by the buffer (strong buffer), pH_cyt remained stable enabling a larger K⁺ influx (Figure 1D). However, when the net H⁺ efflux was only partially compensated by the buffer (weak buffer), [H⁺]_cyt decreased, which negatively affected the pump activity and the energy gradients driving net K⁺ uptake (Figure 1E).

Figure 1.

The plasma membrane K-homeostat under varying external [KA]

(A) The K-homeostat composed of K⁺ channels, H⁺/K⁺-symporters, and H⁺/K⁺-antiporters acts together with the H⁺-pump. The cytosolic proton concentration is controlled by a buffer reaction.

(B and C) Change of the apoplastic K⁺/A^– concentration. While the transporter network is in steady state, [KA]_apo is increased (B) or decreased (C) by a factor of 1.5 ([KA]_apo). In response, the cytosolic pH (pH_cyt), the cytosolic potassium concentration (K⁺_cyt), and the membrane voltage (V) settle to a new steady state, which depends on the buffer capacity of the cell. The stronger the buffer is, the more intense the line is. The time axes are the same in all cases. Values are not explicitly specified because each potential scale could be adjusted by multiplying transporter density or modifying cell size. The displayed results are obtained for one parameter set of the K-homeostat, but they are qualitatively representative for all possibilities.

(D–G) Graphical summary of the general effects of an increase (D and E) or decrease (F and G) of the apoplastic K⁺ concentration with a strong (D and F) or weak (E and G) cytosolic pH-buffer capacity.

A similar picture to the simulation of increasing [KA]_apo was obtained when decreasing the external concentrations (Figure 1C). While in the absence of anion transporters [A^–]_cyt remained stable, now, [K⁺]_cyt decreased in order to reestablish the original E_K. The net K⁺ efflux was electrically compensated by a net H⁺ influx. Depending on the buffering capacity, this net proton transport affected intracellular pH, H⁺-ATPase activity, the membrane voltage, and the energizing gradients of the K/H sym- and antiporters. When the cytosolic pH was strongly buffered, pH_cyt remained grossly stable enabling a larger K⁺ efflux (Figure 1F). In contrast, when the net H⁺ influx was only partially compensated (weak buffer), [H⁺]_cyt increased, which resulted in lower K⁺ release (Figure 1G). In summary, the general K-homeostat, in combination with the proton pump, mediated a 1K⁺:1H⁺ exchange until a new steady state was achieved. It therefore could serve as a sensor for changes in [K⁺]_apo. The external signal of a relative change in [K⁺]_apo was converted into a change in internal pH, the magnitude of which depended on the buffer capacity of the cell. Cells with a small buffer capacity reacted more sensitively than cells with a large capacity. Because regulation of cytosolic pH is coupled to cellular metabolism (Sakano, 2001), the change in the extracellular nutrient concentration sensed by the K-homeostat might thus directly influence cellular processes.

Plasma membrane anion/A-homeostat

In soil and the apoplast, K⁺ is neutralized by a varying mix of the anions Cl⁻, ${\text{NO}}_3^{-}$, and organic acids (mainly malate), for which there are also transporters in the plasma membrane. To include this anionic component, we ran computational simulations to monitor the consequences of changes in external K⁺/A^– concentrations in a model cell in which we implemented the anion-(A)-homeostat in the plasma membrane together with the energizing proton pump (Figure 2A). The A-homeostat was composed of anion channels and electrogenic proton/anion symporters. The activity of the transporters determined the steady-state values for the membrane voltage V, the Nernst equilibrium potential of the anion E_A, and the Nernst equilibrium potential of the protons E_H (Dreyer, 2021). Taking a similar method than for the K-homeostat analysis, we started the computation with appropriate parameters to set a physiological resting state. Then we increased or decreased the external K⁺/A^– concentrations exemplarily by a factor of 1.5. Note that the relative changes, rather than the absolute values were important in this context. Because the model membrane for the A-homeostat study was impermeable for K⁺, changes in the concentration of the latter had no effect on the system. In contrast, an increment of [A^–]_apo (Figure 2B) provoked a net influx of A^– and consequently a rise in [A^–]_cyt. With cytosolic pH held constant at pH 7.2, steady-state values of V, E_A, and E_H remained unchanged from resting state, indicating that the larger [A^–]_apo was compensated by an increased [A^–]_cyt. In contrast, with a limited cytosolic proton buffering capacity, the net A^– transport had an influence on intracellular pH due to the contribution of the H/A symporter. This fed back to the H⁺-ATPase activity, the membrane voltage, the driving force for symport, caused changes in the steady-state values for V, E_A, E_H, and therefore also for [A^–]_cyt and pH_cyt (Figure 2B, different shading of the curves). The repetition of the simulation with various parameter sets revealed that the net A^– influx was always electrically compensated by a net H⁺ influx regardless of the details of the A-homeostat. A full compensation of this H⁺ influx by the buffer (strong buffer) kept pH_cyt stable and provoked a larger A^– influx (Figure 2D). On the contrary, when the buffer only partially compensated the net H⁺ influx (weak buffer), the energy gradients driving the net A^– uptake were negatively affected resulting in lower A^– accumulation (Figure 2E).

Figure 2.

The plasma membrane A-homeostat under varying external [KA]

(A) The A-homeostat composed of A⁻ channels and H⁺/A⁻-symporters acts together with the H⁺-pump. The cytosolic proton concentration is controlled by a buffer reaction.

(B and C) Change of the apoplastic K⁺/A^– concentration. While the transporter network is in steady state, [KA]_apo is increased (B) or decreased (C) by a factor of 1.5 ([KA]_apo). In response, the cytosolic pH (pH_cyt), the cytosolic anion concentration (A^-_cyt), and the membrane voltage (V) settle to a new steady state, which depends on the buffer capacity of the cell. The stronger the buffer is, the more intense the line is. The time axes are the same in all cases. Values are not explicitly specified because each potential scale could be adjusted by multiplying transporter density or modifying cell size. However, the ticks indicate the same time intervals as in Figure 1. The displayed results are obtained for one parameter set of the A-homeostat, but they are qualitatively representative for all possibilities.

(D–G) Graphical summary of the general effects of an increase (D and E) or decrease (F and G) of the apoplastic A⁻ concentration with a strong (D and F) or weak (E and G) cytosolic pH-buffer capacity.

When [KA]_apo was decreased, the system reacted inversely (Figure 2C). A reduction of the external anion concentration induced a net A^– efflux and a decrease of [A^–]_cyt. The net A^– efflux was electrically compensated by a net H⁺ efflux. As a function of the buffer capacity, this net proton transport could differentially affect intracellular pH, H⁺-ATPase activity, the membrane voltage, and the energizing gradient of the H/A symporter. A strongly buffered pH stabilized pH_cyt and caused a larger A^– efflux (Figure 2F). In comparison, if the net H⁺ efflux was only partially compensated (weak buffer), [H⁺]_cyt decreased, which in turn caused a lower A^– release (Figure 2G). Thus, the combination of the general A-homeostat with the proton pump mediated a joined 1A^–:1H⁺ transport until a new steady condition was achieved. In case of a divalent anion, the stoichiometry would be 1A²⁻:2H⁺. This transporter network can therefore serve as a sensor for changes in the external anion concentration. As with the K-homeostat, the external signal was converted into an internal pH change, with cells with a small buffer capacity responding more sensitively than cells with a large capacity.

Combined K- and A-homeostats

Separate analyses of K- and A-homeostats showed that K⁺ transport occurred as a 1K⁺:1H⁺ antiport while anion transport as a 1A^–:1H⁺ symport. The resting state with [K⁺]_cyt ≈ 100 mM, [K⁺]_apo ≈ 0.25 mM, [A^–]_cyt ≈ 50 mM, [A^–]_apo ≈ 0.25 mM, ΔpH ≈ 1.4, V ≈ −150 mV, was set by the activities of the homeostats. Remarkably, in this exemplarily chosen physiological condition, the transporter activities of the K-homeostat were larger than those of the A-homeostat. As a consequence, equilibration was faster with the K-homeostat than it was with the A-homeostat. These individual features also influenced the characteristics of the combination of both homeostats (Figure 3A). In this third what-if scenario, we started with the same steady-state values as in the previous scenarios and then we changed the external [KA]_apo by a factor of 1.5. As in the cases before, an increase of [KA]_apo induced a net influx of K⁺ and anions which in turn resulted in rises of [K⁺]_cyt and [A^–]_cyt (Figure 3B). When the cytosolic pH was clamped to pH 7.2, [K⁺]_cyt and [A^–]_cyt increased by a factor of 1.5 and the system established a steady state with the same V, E_A, and E_H values as before. In this respect, the combination of the two homeostats behaved identically to the individual homeostats. The picture changed when the buffer capacity of the cytosol was limited. A weaker buffer introduced a new dynamic component. Whereas in the individual homeostats a reduced buffer capacity led to a less pronounced increase in cytosolic concentrations (Figures 1B and 2B), in the combined system, [K⁺]_cyt was less affected by this parameter and [A^–]_cyt showed an inverse behavior. In fact, [A^–]_cyt now increased by more than 1.5-fold, and the weaker the buffer capacity was, the greater the increase was (Figure 3B). This type of behavior was observed if at the beginning [K⁺]_cyt > [A^–]_cyt. When we inverted the starting conditions to [K⁺]_cyt < [A^–]_cyt, the roles of K⁺ and A^– flipped. In this case, [K⁺]_cyt increased by more than 1.5-fold while [A^–]_cyt maintained a larger increase than in the isolated homeostat (Figure S1). Thus, the smaller of both, [K⁺]_cyt or [A^–]_cyt, partially compensated the weaker role of the pH buffer. A very similar, although inverse, behavior was observed when decreasing [KA]_apo (Figure 3C). When the cytosolic pH was strongly buffered and [K⁺]_cyt and [A^–]_cyt decreased by a factor of 1.5, the system established a steady state with the same V, E_A, and E_H values as before. Thus, both [K⁺]_cyt and [A^–]_cyt declined 1.5-fold. In contrast, a weaker buffer capacity caused [K⁺]_cyt to decrease less and [A^–]_cyt to decrease more than by a factor of 1.5. Similar to the simulation outputs presented above, the roles of K⁺ and A^– were determined by the starting conditions. If [K⁺]_cyt < [A^–]_cyt, [A^–]_cyt decreased less and [K⁺]_cyt more than 1.5-fold. If both [K⁺]_cyt and [A^–]_cyt were equal, there was no dependency on the buffer capacity and both changed by a factor of 1.5 (Figure S2).

Figure 3.

Combination of plasma membrane K- and A-homeostat under varying external K⁺/A⁻

(A) Both, K- and A-homeostat act together with the H⁺-pump. The cytosolic proton concentration is controlled by a buffer reaction.

(B and C) Change of the apoplastic K⁺/A⁻ concentration. While the transporter network is in steady state, [KA]_apo is increased (B) or decreased (C) by a factor of 1.5 ([KA]_apo). In response, the cytosolic pH (pH_cyt), the cytosolic K⁺ and anion concentrations (K⁺_cyt, A^-_cyt), and the membrane voltage (V) settle to a new steady state, which depends on the buffer capacity of the cell. The stronger the buffer is, the more intense the line is.

(D) Integration of a Ca-homeostat into the transporter network of the plasma membrane. The simple Ca-homeostat is composed of a Ca²⁺ channel and a Ca²⁺ pump.

(E) Signal conversion at the plasma membrane. A change in the external K⁺/A⁻ concentration translates into a transient and permanent change of [H⁺]_cyt and [Ca²⁺]_cyt. The time axes are the same in all cases. Values are not explicitly specified because each potential scale could be adjusted by multiplying transporter density or modifying cell size. However, the ticks indicate the same time intervals as in Figure 1.

In any case, the change of the extracellular nutrient concentration caused transient and sometimes permanent changes in both the cytosolic proton concentration and the membrane voltage. V, in turn, controlled other transport processes susceptible to affect additional cellular parameters. To illustrate this concept, we included a simple Ca-homeostat into the system (Figure 3D). The combination of a Ca²⁺ channel, for instance an open OSCA, GLR-type or cyclic nucleotide-gated channel (Jarratt-Barnham et al., 2021; Michard et al., 2011; Ortiz-Ramírez et al., 2017; Thor et al., 2020), and a Ca²⁺ pump, was able to maintain a stable low [Ca²⁺]_cyt in resting conditions. Although this Ca-homeostat was fully independent of K⁺ and A^–, a change in [KA]_apo affected also [Ca²⁺]_cyt (Figure 3E). An increase of [KA]_apo caused a mostly transient decrease in [Ca²⁺]_cyt, while a decrease of [KA]_apo provoked a predominantly transient increase in [Ca²⁺]_cyt. The K-homeostat reacted to the changed [K⁺]_apo, while the A-homeostat sensed the changed [A^–]_apo. Both sensing mechanisms translated a varying external nutrient concentration into changes in V, which in turn caused an imbalance of the fluxes of the Ca-homeostat. As a final consequence, [H⁺]_cyt and [Ca²⁺]_cyt decreased upon an increase of [KA]_apo or increased upon a decrease of [KA]_apo. In conclusion, the three homeostats together allowed the cell to translate the external change of nutrient availability into two distinct internal [H⁺]_cyt and [Ca²⁺]_cyt signals. These transient signals may then trigger further downstream reactions, possibly synergistically and eventually depending on the signature of both signals.

The buffering role of the vacuole

Plant cells are obviously not as simple as considered in our theoretical work. They harbor also vacuoles as other potent buffer organelles. As demonstrated for K⁺ in barley root cells (Walker et al., 1996), storage in the vacuole allows stable cytosolic conditions on a long-term despite different external conditions. Nevertheless, this buffer system is inherently slow. Similar to the plasma membrane, the tonoplast is also the active site of proton pumps, channels, and proton-coupled transporters that shuttle K⁺ and counter-ions into or out of the vacuole. These transporters form homeostats as those described here in the plasma membrane (Dreyer, 2021). K⁺ transport across the vacuolar membrane occurs as a net 1K⁺:1H⁺ antiport, whereas transport of monovalent anions occurs as a net 1A^–:1H⁺ symport. Net fluxes of K⁺ and anions across the plasma membrane induced by varying [KA]_apo initially affect [K⁺]_cyt and [A^–]_cyt, which in a second step affect the fluxes across the vacuolar membrane. Sequestration of ions in the vacuole therefore buffers the cytosol and introduces additional dynamic components that can further shape the [H⁺]_cyt and [Ca²⁺]_cyt signatures. Despite these differences, the simplified models qualitatively describe the trends in dynamics and explain the basic principles of how information about altered external nutrient concentrations can be translated into second messenger signals.

Wet lab experimental proof of concept

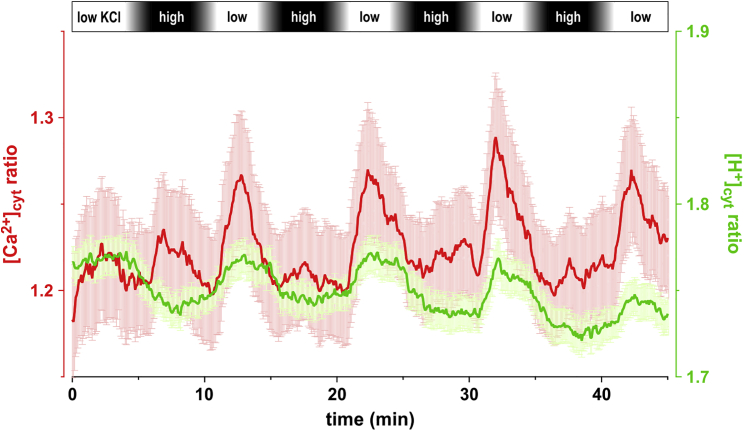
The computational cell biology experiments suggested that changes in the extracellular KA concentration can be translated into cytosolic pH and Ca²⁺ signals. To prove this concept in the plant context, we used epidermal strips of Nicotiana tabacum plants that stably expressed the genetically encoded fluorescence sensor CapHensor (Li et al., 2021). This tool allowed us to monitor the time course of [Ca²⁺]_cyt and [H⁺]_cyt in guard cells simultaneously during targeted changes of the external ionic conditions. Following a protocol to change and clamp cytosolic Ca²⁺ concentration (Allen et al., 2001; Cho et al., 2009), we alternatingly challenged the cells with high and low KCl-concentration buffers for ∼5 min each. It is worth to note that in contrast to previous Ca²⁺ clamp experiments, we kept the [Ca²⁺]_ext concentration constant at 1 mM when changing the KCl concentration. To avoid interfering effects to the guard cells caused by an osmotic imbalance when applying solutions with different concentrations of KCl, the osmolarities of the solutions were balanced with mannitol. In line with the computational results where [KCl]_apo was increased, application of the high KCl solution resulted in decreases in [Ca²⁺]_cyt and [H⁺]_cyt (Figure 4). In contrast, a switch to the low KCl solution triggered rapid transient [Ca²⁺]_cyt elevations and slowly increased [H⁺]_cyt. The experiments constitute a proof of principle of our conceptual proposition. Indeed, while guard cells express K⁺ and anion transporters with characteristics similar to the ones considered in our models, the effect of a change in K⁺ or A^– in the external media induced a response in terms of internal H⁺ and Ca²⁺ as qualitatively predicted by our computational simulations. In conclusion, a minimal set of ion transporters such as that used in our models is sufficient to explain complex homeostasis and signaling behaviors observed in plant cells.

Figure 4.

Varying external KCl concentrations induce changes in [Ca²⁺]_cyt and [H⁺]_cyt

Epidermal strips of N. tabacum plants stably expressing CapHensor allowed the simultaneous measurement of relative changes in [Ca²⁺]_cyt (red traces) and [H⁺]_cyt (green traces) in guard cells. Epidermal strips were placed in a bath chamber which was perfused with defined solutions. The bar at the top indicates the change between solutions containing low amount of KCl (white) and high amount of KCl (black). The intense red and green lines indicate the average of the simultaneous measurements at n = 30 different cells from several epidermal strips, while the shaded lines illustrate the standard errors (SEM).

Discussion

Mathematical modeling has proven very powerful in providing unprecedented insights into physiological mechanisms (Dale et al., 2021). Here, we continued our analyses of the properties of transport networks. The simulations presented are exemplary for a broad variety of biological realities. The aim of our study was not to computationally reconstruct a specific physiological state, but rather to highlight general features of transporter networks that remain hidden in common experimental studies.

Combined homeostats can mimic transceptor-like function

This study provides evidence that homeostats serve not only to transport the nutrient for which they are designed but also translate an external nutrient signal into internal H⁺ and Ca²⁺ signals. Such a dual function has been previously assigned to the nitrate transporter CHL1/NRT1.1 (Liu and Tsay, 2003; Liu et al., 1999) that has been proposed to serve also as a nitrate sensor in plants (Ho et al., 2009). This protein was therefore called a “transceptor”, i.e., a transporter with receptor function that senses very specifically the extracellular nitrate concentration and sets the cell toward the prevailing conditions (Gojon et al., 2011). The receptor properties were uncovered by investigating transporters with point mutations in the plant environment revealing that the mutants mimicked the effect of altered external nitrate conditions (Bouguyon et al., 2015; Ho et al., 2009). To date, it is unclear how the receptor mechanism of NRT1.1 works. Thus, it is not known whether NRT1.1 undergoes ligand-induced conformational changes that are recognized by downstream intracellular effectors, as required by the strict transceptor definition (Diallinas, 2017; Steyfkens et al., 2018; Thevelein and Voordeckers, 2009). Nevertheless, in the case of NRT1.1, [Ca²⁺]_cyt plays apparently an important role in transmitting the perceived signal to the cellular downstream pathways (Krouk, 2017; Wang et al., 2021). In the light of the computational cell biology analyses presented here, the apparent sensing phenomenon of NRT1.1 may now be seen from a different perspective. As demonstrated exemplarily, homeostats, i.e., the combination of different transporter types for the same ion/nutrient, are capable of sensing the environmental conditions. The involvement of proton-coupled transporters in such a homeostat links the sensing process to pH regulation and a Ca-homeostat in the plasma membrane renders membrane potential changes induced by the nutrient homeostat into changes in [Ca²⁺]_cyt. Thus, the combination of a nutrient homeostat and a Ca-homeostat can convert an extracellular nutrient signal into intracellular nutrient, [H⁺]_cyt and [Ca²⁺]_cyt signals that can be decoded by still not well understood intracellular signaling cascades. The apparent redundancy in sensing cations and anions might be deciphered by the different kinetics of the homeostats. In physiological conditions, the K-homeostat dominates the A-homeostat, which manifests in a slower answer toward changes in the anion concentration compared to changes in the cation concentration (Figure 3, but compare also Figures 1 and 2). The shape of both, [Ca²⁺]_cyt and [H⁺]_cyt, may therefore encode additional ion-specific information.

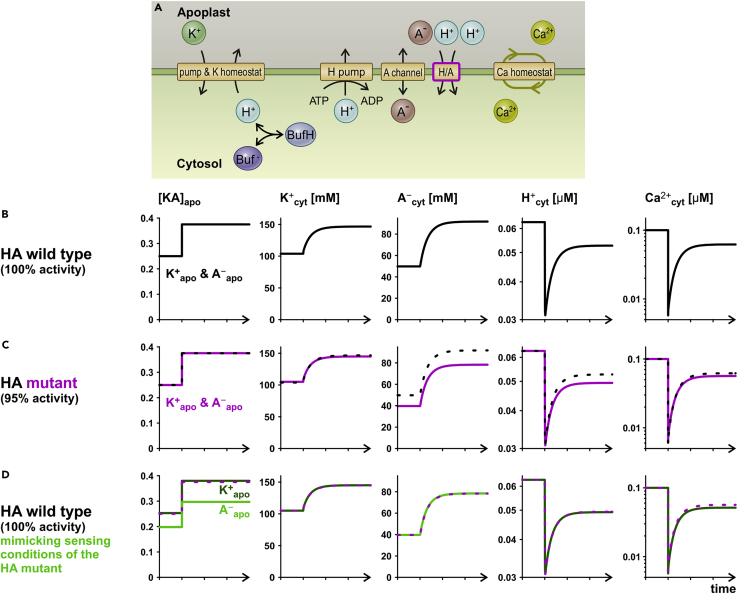
Mutations in one of the transporters of the network may cause slightly distorted signals, which could be interpreted by the cell as a different external nutrient concentration. To illustrate this, we conducted another computational what-if experiment (Figure 5), in which we compared three scenarios. In a first scenario, we challenged the combination of K-, A-, and Ca-homeostats (Figure 5A) exemplarily with [KA]_apo = 0.25 mM→0.375 mM (Figure 5B). For a second scenario, we created a mutant of the HA-transporter of the A-homeostat by reducing its activity by 5%. We let the cell equilibrate at [KA]_apo = 0.25 mM and thereafter applied again the [KA]_apo = 0.25 mM→0.375 mM regime (Figure 5C). Under this condition, in particular, the [A^–]_cyt and [H⁺]_cyt responses were significantly different from the wild-type situation. To determine what cellular misperceptions the mutation-induced changes might have led to, we again took the wild-type system and adjusted the [K⁺]_apo and [A^–]_apo conditions to reproduce the mutant signals (Figure 5D). In terms of K⁺, the mutated system was not much different from the wild type. However, due to the mutation in the HA-transporter, the cell was feigned to face an [A^–]_apo that was lower than the actual one. The similarities between the model scenario and the experimental observations on NRT1.1 clearly suggest that as part of a larger transporter network, the nitrate transporter could be entity of a receptor mechanism even without the need to undergo ligand-induced conformational changes. It should be emphasized that in the presented conceptual framework, the transporters would not be bona fide transceptors, but the homeostats as a network could mimic transceptor-like functions.

Figure 5.

Effect of a mutation in the HA-symporter on the nutrient-sensing process

(A) The combination of K-, A-, and Ca-homeostats was analyzed with and without changing the activity of the HA-transporter.

(B) Control condition with the wild-type system and apoplastic [KA]_apo = 0.25 mM → 0.375 mM concentrations. The curves of [K⁺]_cyt, [A^–]_cyt, [H⁺]_cyt, and [Ca²⁺]_cyt serve as reference for the following condition.

(C) The simulation of (B) was repeated using a system with a mutated HA transporter having 95% of its original activity. For comparison, data from (B) are shown as dotted black curves.

(D) The cytosolic conditions of simulation (C) were mimicked by using the wild-type system applying a different [A^–]_apo-regime. The data from (C) are shown as dotted purple curves.

Nutrient-sensing capacity may depend on cellular metabolism

An interesting finding of the simulations was that the cellular response to changing external nutrient concentrations depended on the buffer capacity of the cell. A strongly pH-buffered cytosol was less sensitive than a weakly buffered one. Plant cells maintain their cytosolic pH generally around 7 … 7.5 employing different mechanisms, such as H⁺ binding by buffering groups, H⁺ transport out of the cell or into the vacuole, and the so-called biochemical pH-stat, controlling the number of carboxyl residues, like malate, and thereby linking pH homeostasis to metabolism (Bethmann and Schönknecht, 2009; Felle, 2005; Kurkdjian and Guern, 1989; Mimura et al., 2000; Sakano, 2001). From an energetic point of view, our study further supports the notion that the proton buffering capacity is indeed another energy source for membrane transport (Wegner and Shabala, 2020). Furthermore, our work suggests that cellular metabolism may influence the sensitivity of the homeostats in its receptor-role, adding another level of complexity to the phenomenon presented.

Limitations of the study

The theoretical concept presented here is very basic and from a quantitative point of view far from any physiological reality. Several other contributors, such as the vacuole, influence the shape of the H⁺ and Ca²⁺ signals and introduce additional dynamic components. To evaluate in detail the impact of these additional contributors, more sophisticated models would be required that gradually increase in complexity.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental models: Organisms/strains
Nicotiana tabacum: 35S::CapHensor	Li et al., 2021	N/A
Software and algorithms
VCell Modeling & Analysis Software The Virtual Cell Model, “Dreyer_et_al_2022_iScience” by user “idreyer”, can be accessed within the VCell software (available at https://vcell.org).	Loew and Schaff, 2001; Schaff et al., 1997	https://vcell.org
Fiji/ImageJ	Schindelin et al., 2012	https://imagej.net/software/fiji
Igor Pro	Wavemetrics Inc.	https://www.wavemetrics.com

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact Ingo Dreyer (idreyer@utalca.cl).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Plants

In this study we used Nicotiana tabacum plants generated in a previous study (Li et al., 2021) that stably expressed the CapHensor under the 35S promotor. Plants were grown on soil with a day/night regime of 10 h/14 h, and a temperature of 22–24/20 to 22°C provided by a 30 klux white light (SON-T Agro 400 W; Philips).

Method details

Mathematical description of transporter activities

Plasma membrane H⁺-ATPase

The voltage-dependent current of the plasma membrane H⁺-ATPase that pumps with a 1 H⁺ : 1 ATP ratio (Blatt et al., 1990) was described with a mechanistic 6-state pump model (Dreyer, 2017; Reyer et al., 2020):

$$I_{pump}=I_{\mathit{max}}·i_p=I_{\mathit{max}}·\frac{{\left[H^{+}\right]}_{cyt}}{1.26nM+{\left[H^{+}\right]}_{cyt}}·\frac{1-e^{\frac{-F}{RT}\left(V-V_{0,pump}\right)}}{1+e^{\frac{-F}{RT}\left(V+135mV\right)}+e^{\frac{-F}{RT}\left(0.1·V+62.5mV\right)}}$$ (Equation 1)

Here, V is the membrane voltage at the plasma membrane, F the Faraday constant, R the gas constant and T the absolute temperature. I_max depends on the number of active pumps in the membrane and the apoplastic proton concentration, which was constant in the analyses in this study. $V_{0,pump}=E_H+{\tilde{V}}_0+{\tilde{V}}_1$ is the voltage at which the pump current is zero. It depends on the cytosolic and apoplastic proton concentrations (E_H) and on the cytosolic ATP, ADP, and Pi concentrations (${\tilde{V}}_0$), i.e., on the energy status of the cell (Rienmüller et al., 2012). In addition, the energy consumption of other transport processes can be taken into account (${\tilde{V}}_1$) resulting in a less negative setting of this parameter (Dreyer, 2021). For the simulations in this study we set V_0,pump = −200 mV. A different value would not change the results qualitatively.

H⁺ : K⁺ antiporter

Proton (J_H,KHa) and potassium (J_K,KHa) net efflux of a 1:1 H⁺-coupled K⁺/H⁺ antiporter were described as:

$$J_{H,KHa}=\frac{G_{KHa}}{e_0}·\left(E_K-E_H\right)$$ (Equation 2)

$$J_{K,KHa}=-\frac{G_{KHa}}{e_0}·\left(E_K-E_H\right)$$ (Equation 3)

where e₀ is the elementary charge, E_K the Nernst voltage for potassium and E_H the Nernst voltage for protons. G_KHa is the ‘membrane conductance’ of this transporter (unit pA/mV). Although it does not conduct electrical current, G_KHa was defined analogously to all other transporters. This trick has technical reasons to unify the equations.

H⁺ : K⁺ symporter

Proton (J_H,KHs) and potassium net flux (J_K,KHs) from the cell to the apoplast via a 1:1 H⁺-coupled K⁺/H⁺ symporter and the current-voltage relationship (I_KHs) were described as:

$$J_{H,KHs}=\frac{G_{KHs}}{e_0}·\left(2·V-E_H-E_K\right)$$ (Equation 4)

$$J_{K,KHs}=\frac{G_{KHs}}{e_0}·\left(2·V-E_H-E_K\right)$$ (Equation 5)

$$I_{KHs}=e_0·\left(J_{K,KHs}+J_{H,KHs}\right)=2·G_{KHs}·\left(2·V-E_H-E_K\right)$$ (Equation 6)

G_KHs is the membrane conductance of this transporter type (unit pA/mV).

K⁺ channel

Potassium net efflux (J_K,KC) and the current-voltage relationship (I_KC) of a potentially voltage-gated potassium channel was described as:

$$J_{K,KC}=\frac{G_{KC}}{e_0}·\left(V-E_K\right)$$ (Equation 7)

$$I_{KC}=e_0·J_{K,KC}=G_{KC}·\left(V-E_K\right)$$ (Equation 8)

with G_KC (unit pA/mV) being the membrane conductance for this channel. This factor may contain implicitly the voltage-dependence of the channel.

Anion channel

Anion net efflux (J_A,AC) and the current-voltage relationship (I_AC) of an anion channel were described as:

$$J_{A,AC}=-\frac{G_{AC}}{e_0}·\left(V-E_A\right)$$ (Equation 9)

$$I_{AC}=-e_0·J_{A,AC}=G_{AC}·\left(V-E_A\right)$$ (Equation 10)

with E_A being the Nernst voltage of the anion and G_AC (unit pA/mV) the membrane conductance for this channel type.

2H⁺ : 1 A⁻ symporter

Proton (J_H,HA) and anion (J_A,HA) net efflux and the current-voltage relationship (I_HA) of a 2:1 H⁺-coupled H⁺/A⁻ symporter were represented as:

$$J_{H,HA}=2·\frac{G_{HA}}{e_0}·\left(V-2·E_H+E_A\right)$$ (Equation 11)

$$J_{A,HA}=\frac{G_{HA}}{e_0}·\left(V-2·E_H+E_A\right)$$ (Equation 12)

$$I_{HA}=e_0·\left(J_{H,HA}-J_{A,HA}\right)=G_{HA}·\left(V-2·E_H+E_A\right)$$ (Equation 13)

where G_HA is the membrane conductance of this transporter type (unit pA/mV).

Ca²⁺ channel

Calcium net efflux (J_Ca,CaC) and the current-voltage relationship (I_CaC) of a calcium channel was described as:

$$J_{Ca,CaC}=\frac{G_{CaC}}{2e_0}·\left(V-E_{Ca}\right)$$ (Equation 14)

$$I_{CaC}=2e_0·J_{Ca,CaC}=G_{CaC}·\left(V-E_{Ca}\right)$$ (Equation 15)

with E_Ca being the Nernst voltage of calcium and G_CaC (unit pA/mV) the membrane conductance for this channel type. This parameter was several orders of magnitude smaller than G_KC, for instance.

Ca²⁺ pump

A simple description of an ATPase that pumps Ca²⁺ out of the cell is given by:

$$I_{Ca-pump}=2·I_{Ca}·\frac{1-e^{\frac{-F}{RT}\left(V-V_{0,Ca}\right)}}{1+e^{\frac{-F}{RT}\left(V-V_{0,Ca}\right)}}$$ (Equation 16)

Here, the maximum current I_Ca depends on the number of active pumps in the membrane. This parameter was 3-4 orders of magnitude smaller than I_max. $V_{0,Ca}$ is the voltage at which the pump current is zero. For the simulations in this study we set without limiting generality V_0,Ca = −200 mV.

pH conditions

In our simulations, we clamped the external pH to pH 5.8. Although there is growing evidence for the importance of pH_e in diverse physiological functions of plant cells (Tsai and Schmidt, 2021), we have not considered it as an additional parameter because the extracellular space has a much larger volume than the cytosol and therefore also a much larger buffer capacity (Martinière et al., 2018). The transmembrane proton fluxes affect therefore predominantly pH_cyt but not pH_e. In addition, we intended to synchronize the model with the experimental condition, in which pH_e has been buffered to pH5.8. In contrast, cytosolic pH was buffered in the simulations by the simple buffer reaction:

$$H^{+}+Bu{f}^{-}\rightleftarrows HBuf$$ (Equation 17)

$$\frac{d\left[H^{+}\right]}{dt}=\frac{d\left[Bu{f}^{-}\right]}{dt}=-\frac{d\left[HBuf\right]}{dt}=k_v·\left(\left[H^{+}\right]·\left[Bu{f}^{-}\right]-K_s·\left[HBuf\right]\right)$$ (Equation 18)

with pKs = 7.2. The reaction was chosen to be almost instantaneous (large k_v) compared to the transport reactions. To simulate different buffer capacities, the resting (starting) concentrations of [Buf⁻] = [HBuf] were varied between 10⁴ μM (weak buffer) and 10⁷ μM (strong buffer).

Dynamic system behavior

In the simulations of this study, the external conditions were kept constant. In contrast, the membrane voltage and the cytosolic concentrations were allowed to vary according to thermodynamic laws. The different fluxes and reactions changed the membrane voltage and the cytosolic concentrations according to:

$$\frac{dV}{dt}=-\frac{1}{C}·\left[I_{pump}+I_{KC}+I_{KHs}+I_{AC}+I_{HA}+I_{Ca-pump}+I_{CaC}\right]$$ (Equation 19)

$$\frac{d{\left[K^{+}\right]}_{cyt}}{dt}=\frac{-1}{Vol·N_A}·\left[J_{K,KC}+J_{K,KHs}+J_{K,KHa}\right]$$ (Equation 20)

$$\frac{d{\left[A^{-}\right]}_{cyt}}{dt}=\frac{-1}{Vol·N_A}·\left[J_{A,AC}+J_{A,HA}\right]$$ (Equation 21)

$$\frac{d{\left[H^{+}\right]}_{cyt}}{dt}=\frac{-1}{Vol·N_A}·\left[\frac{I_{pump}}{e_0}+J_{H,KHs}+J_{H,KHa}\right]-k_v·\left(\left[H^{+}\right]·\left[Bu{f}^{-}\right]-K_s·\left[HBuf\right]\right)$$ (Equation 22)

$$\frac{d{\left[C{a}^{2+}\right]}_{cyt}}{dt}=\frac{-1}{Vol·N_A}·\left[\frac{I_{Ca-pump}}{2e_0}+J_{Ca,CaC}\right]$$ (Equation 23)

with the membrane capacitance C, the cellular volume Vol, and the Avogadro constant N_A. The behavior of the network was mathematically simulated using Virtual Cell Modeling and Analysis Software developed by the National Resource for Cell Analysis and Modeling, University of Connecticut Health Center (Loew and Schaff, 2001; Schaff et al., 1997).

Live-cell Ca²⁺- and H⁺-Imaging

For live-cell imaging experiments we used guard cells in epidermal strips from Nicotiana tabacum plants that stably expressed the CapHensor under the 35S promotor. This system enabled the simultaneous ratiometric widefield imaging of cytosolic Ca²⁺ ([Ca²⁺]_cyt) and H⁺ ([H⁺]_cyt) as described previously (Li et al., 2021). Epidermal strips were recovered in standard solution composed of 1 mM CaCl₂, 1 mM KCl and 10 mM MES, pH 5.8 adjusted with Bis-tris propane (BTP). For the change in the external KCl concentration we used a low KCl solution (1 mM CaCl₂, 0.1 mM KCl, 100 mM mannitol, and 10 mM MES, pH 5.8 adjusted with BTP) and a high KCl solution (1 mM CaCl₂, 50.1 mM KCl, and 10 mM MES, pH 5.8 adjusted with BTP). All experiments were performed under permanent perfusion with a speed around 700 μL min⁻¹ while the volume of the medium within the recording chamber was about 800–1000 μL. Under a 40× objective, up to four tobacco guard cells per epidermal strip could be imaged at once and the time-course of fluorescence intensity was extracted and ratiometric [Ca²⁺]_cyt and [H⁺]_cyt were calculated in Fiji/ImageJ (Schindelin et al., 2012).

Quantification and statistical analysis

Data was processed and plotted with Igor Pro 5.02 (Wavemetrics Inc.). Traces are illustrated by mean ± standard errors (SEM). Statistical details of experiments can be found in the figure legends.

Published: April 15, 2022

Data and code availability

• •The Virtual Cell Model, “Dreyer_et_al_2022_iScience” by user “idreyer”, can be accessed within the VCell software (available at https://vcell.org).
• •Any additional information required to repeat the simulations and to reanalyze the data reported in this paper is available from the lead contact upon request.
• •All data reported in this paper will be shared by the lead contact upon request.