Summary
Group testing involves pooling individual specimens (e.g., blood, urine, swabs, etc.) and testing the pools for the presence of disease. When the proportion of diseased individuals is small, group testing can greatly reduce the number of tests needed to screen a population. Statistical research in group testing has traditionally focused on applications for a single disease. However, blood service organizations and large-scale disease surveillance programs are increasingly moving towards the use of multiplex assays, which measure multiple disease biomarkers at once. Tebbs and others (2013, Two-stage hierarchical group testing for multiple infections with application to the Infertility Prevention Project. Biometrics 69, 1064–1073) and Hou and others (2017, Hierarchical group testing for multiple infections. Biometrics 73, 656–665) were the first to examine hierarchical group testing case identification procedures for multiple diseases. In this article, we propose new non-hierarchical procedures which utilize two-dimensional arrays. We derive closed-form expressions for the expected number of tests per individual and classification accuracy probabilities and show that array testing can be more efficient than hierarchical procedures when screening individuals for multiple diseases at once. We illustrate the potential of using array testing in the detection of chlamydia and gonorrhea for a statewide screening program in Iowa. Finally, we describe an R/Shiny application that will help practitioners identify the best multiple-disease case identification algorithm.
Keywords: Case identification, Group testing, Infertility prevention project, Matrix pooling, Pooled testing, Screening
1. Introduction
When screening a population for low-prevalence diseases, testing specimens in pools can be far more cost efficient than testing specimens individually. Individuals in pools that test negatively can be classified as negative, and individuals in pools that test positively can be retested to determine which ones are positive. Testing pooled specimens, which is known as group testing, has a long history dating back to Dorfman (1943), who proposed it to screen United States military recruits for syphilis. Today, group testing is routinely used to screen blood and plasma donations for HIV, HBV, and HCV in the United States and in other developed nations (Mine and others, 2003; Seed and others, 2005; Vansteelandt and others, 2005; Schmidt and others, 2010; O’Brien and others, 2012; Stramer and others, 2013). Group testing also arises in screening and surveillance applications for other diseases, including West Nile virus (Busch and others, 2005), chlamydia and gonorrhea (Lewis and others, 2012), malaria (Wang and others, 2014), influenza (Edouard and others, 2015), and Zika virus (Saá and others, 2018).
There is a substantial literature on group testing case identification algorithms for a single disease, where the goal is to classify each individual as positive or negative. Such algorithms are generally described as being “hierarchical” or “non-hierarchical” in nature. A hierarchical algorithm uses master pools that are non-overlapping, and positive pools are resolved in stages by splitting each one into smaller non-overlapping subpools. Dorfman’s original proposal was to accomplish this in two stages; i.e., master pools are tested in the first stage and individuals (from positive pools) are tested in the second. When the disease prevalence is low, increasing the number of stages can further reduce the number of tests needed. For example, Pilcher and others (2005) use a three-stage algorithm for HIV testing in North Carolina with a master pool of size 90, nine second-stage subpools of size 10, and individual testing in the third stage. Sherlock and others (2007) describe how variations of this three-stage testing algorithm have been implemented in public health laboratories throughout the United States.
Array testing, also known as matrix pooling, is the most common type of non-hierarchical case identification algorithm. In (two-dimensional) array testing procedures, individual specimens are assigned to an array consisting of rows and columns. Row and column master pools are tested in the first stage, and individuals not classified as negative after the first stage are retested in the second. Phatarfod and Sudbury (1994) introduced array testing for disease screening purposes in the absence of testing error. Kim and others (2007) and Westreich and others (2008) offered comparisons of array testing and hierarchical algorithms for single diseases while allowing for imperfect assays. In other single-disease settings, Hudgens and Kim (2011) determined optimal configurations for square arrays, McMahan and others (2012) acknowledged individual covariate information, and Lendle and others (2012) accounted for correlated responses. Kim and Hudgens (2009) examined array testing in higher dimensions where, geometrically, one can envision that rows and columns are tested across multiple planes or hyperplanes. Martin and others (2013) implemented a three-dimensional version of this algorithm for HIV testing in New Jersey.
In this article, we extend the use of array testing to test for multiple diseases simultaneously. Our work is motivated by the development and increased use of “multiplex assays,” which detect multiple pathogens in a single application. These assays reduce the workload involved in screening a population for multiple diseases when compared with using singleplex (or one-disease) assays for each disease separately. Previous research merging group testing with multiplex assays has considered only hierarchical case identification algorithms. Tebbs and others (2013) characterized the performance of a two-stage algorithm for two diseases, motivated by current chlamydia and gonorrhea testing practices in Iowa. More recently, Hou and others (2017) developed a Markov chain framework to propose higher-stage hierarchical algorithms for multiple diseases. Here, the focus of our article is on group testing with multiplex assays carried out by using two-dimensional arrays. We demonstrate that this non-hierarchical design can be more efficient than hierarchical algorithms, a practically important finding for laboratories and high-volume testing centers that screen individuals for multiple diseases at once.
In Section 2, we define notation and restate the assumptions in Hou and others (2017), which are also used in this article. In Section 3, we describe how to derive closed-form expressions for the expected number of tests per individual and classification accuracy probabilities for two diseases in two-dimensional arrays. These expressions are complex when allowing for testing error, so we make extensive use of the supplementary material available at Biostatistics online. In Section 4, we provide a thorough comparison of array testing and the hierarchical algorithms in Tebbs and others (2013) and Hou and others (2017). In Section 5, we illustrate the potential benefit of using array testing when screening Iowa residents for chlamydia and gonorrhea simultaneously. In Section 6, we provide a summary discussion and describe our online resources that will help practitioners identify the best multiplex algorithm.
2. Notation and assumptions
Suppose individual specimens (e.g., blood, urine, swabs, etc.) are randomly assigned to the
cells of an 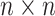 array, where
array, where
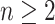 . In this article, we consider square
arrays for simplicity, although generalizing our derivations for rectangular arrays is
possible. To simplify the exposition, we assume the number of diseases is
. In this article, we consider square
arrays for simplicity, although generalizing our derivations for rectangular arrays is
possible. To simplify the exposition, we assume the number of diseases is
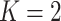 ; see Section 6 for a discussion on using
array testing for more than two diseases. Let
; see Section 6 for a discussion on using
array testing for more than two diseases. Let 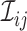 denote the
individual assigned to the
denote the
individual assigned to the 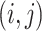 cell, for
cell, for  and
and
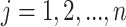 . In the first stage, rows are
tested producing
. In the first stage, rows are
tested producing 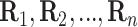 ,
where
,
where 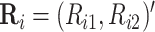 and
and
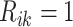 (
(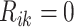 ) if the
) if the
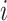 th row tests positively (negatively) for the
th row tests positively (negatively) for the
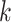 th disease,
th disease,  . Columns are
also tested in the first stage producing
. Columns are
also tested in the first stage producing 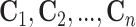 ,
where
,
where 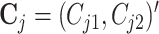 and
and
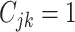 (
(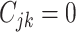 ) if the
) if the
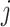 th column tests positively (negatively) for
the
th column tests positively (negatively) for
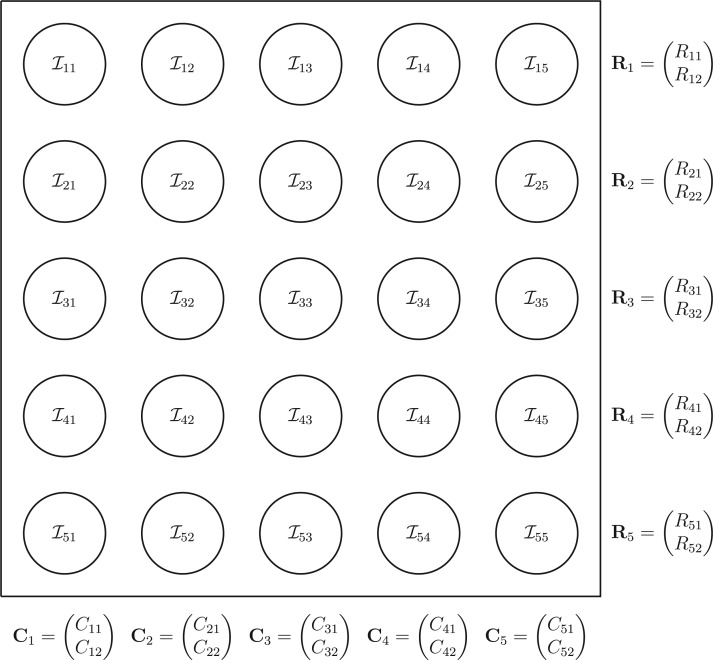
the 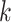 th disease. Figure 1 illustrates this notation for
th disease. Figure 1 illustrates this notation for 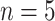 ; i.e., a
; i.e., a
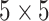 array. It is important to
emphasize that
array. It is important to
emphasize that 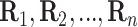 and
and 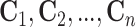 are the testing responses in the first stage; they could be incorrect because of inherent
assay error.
are the testing responses in the first stage; they could be incorrect because of inherent
assay error.
Fig. 1.
A 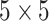 array for
array for
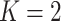 diseases. Row and column master pool
testing responses
diseases. Row and column master pool
testing responses 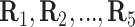 and
and 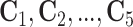 are observed in the first stage. The second stage involves retesting individuals
are observed in the first stage. The second stage involves retesting individuals
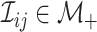 as
described in Section 2.
as
described in Section 2.
In the second stage, individual testing is used for those individuals not declared to be
negative after the first stage. If an assay is perfect, this collection of individuals is
easy to determine, that is, one need only to examine the intersections of positive rows and
columns. Otherwise, ambiguities may arise. For example, if the first row tests positively
for the first disease (i.e., 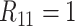 ) but all columns test negatively for
the first disease (i.e.,
) but all columns test negatively for
the first disease (i.e., 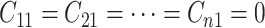 ), we assume
this is an ambiguity caused by assay error. To resolve this, we adopt the strategy in Kim and others (2007) and retest all
individuals in the first row. Following this convention for each disease separately (and
allowing for the analogous case when all rows test negatively), let
), we assume
this is an ambiguity caused by assay error. To resolve this, we adopt the strategy in Kim and others (2007) and retest all
individuals in the first row. Following this convention for each disease separately (and
allowing for the analogous case when all rows test negatively), let
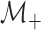 denote the collection who are
tested individually in the second stage. Mathematically, we can express
denote the collection who are
tested individually in the second stage. Mathematically, we can express
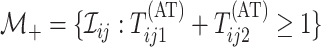 ,
where
,
where
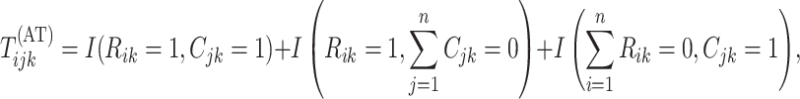 |
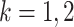 , and
, and 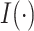 is the indicator
function. Individuals in the complement set
is the indicator
function. Individuals in the complement set 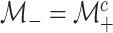 are not tested in the second stage and are declared to be negative for both diseases.
are not tested in the second stage and are declared to be negative for both diseases.
We now list five assumptions that are made for the remainder of this article. These assumptions are analogous to those in Hou and others (2017) for hierarchical algorithms and are used to derive operating characteristics in closed form.
Assumption 1
A discriminating multiplex assay is used to test both rows and columns in the first stage. Briefly, a multiplex assay is said to discriminate if upon application it provides a diagnosis for each disease separately. For example, a discriminating multiplex assay applied to the first row in Figure 1 produces both
and
. This same assay is also used to test individuals
in the second stage.
Assumption 2
Let
denote the true disease status of individual
. The
’s are independent and identically distributed random vectors with probability mass function
, where
and
.
Assumption 3
Let
and
denote the multiplex assay sensitivity and specificity for testing row and column master pools of size
, respectively, for the
th disease
. Let
and
denote the same multiplex assay accuracy probabilities for individual testing. We assume
,
,
, and
are known.
Assumption 4
We assume
and
for one disease do not depend on the true status of the other disease. The same assumption is made for
and
.
Assumption 5
Testing responses on rows, columns, and individuals are mutually independent, conditional on the true disease statuses of all individuals.
Several comments are in order. First, the widespread availability of discriminating multiplex assays for disease detection is discussed in Tebbs and others (2013) and Hou and others (2017). Multiplex assays best described as non-discriminating (i.e., assays that do not differentiate between diseases) are not considered in this article. In Assumption 3, we allow the sensitivity and specificity of the multiplex assay to be pool-size dependent as in Hou and others (2017). Pilot data on assay performance, which are typically available in the product literature published by manufacturers, can be used to elicit values for these accuracy probabilities; see also Section 6. Assumption 4 requires that an assay have adequate discriminating power to differentiate between diseases and that there is no interference in detection; see, for example, Ellington and others (2010) for a discussion of this issue with antibody-based multiplex assays. Finally, the conditional independence requirement in Assumption 5 is also common in the case identification literature for single diseases. This assumption means that misclassification can arise only because of errors in test implementation or other factors not related to true disease status.
3. Operating characteristics
We describe how to derive the expected number of tests per individual and classification
accuracy probabilities for array testing with 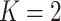 diseases. The derivations
are formidable when allowing for imperfect assays, so we highlight the salient starting
points herein and relegate specifics to the supplementary material available at Biostatistics
online. We also describe a modified version of the two-stage algorithm in Section 2 that
includes a preliminary test on the entire array.
diseases. The derivations
are formidable when allowing for imperfect assays, so we highlight the salient starting
points herein and relegate specifics to the supplementary material available at Biostatistics
online. We also describe a modified version of the two-stage algorithm in Section 2 that
includes a preliminary test on the entire array.
3.1. Efficiency
Henceforth, we denote the two-stage algorithm in Section 2 by AT. The first stage of AT
uses 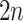 tests for the rows and columns.
Second-stage individual testing is used when the event
tests for the rows and columns.
Second-stage individual testing is used when the event 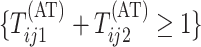 occurs. Therefore, the expected number of tests per individual, or
efficiency, for AT is given by
occurs. Therefore, the expected number of tests per individual, or
efficiency, for AT is given by
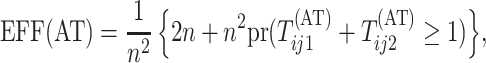 |
where 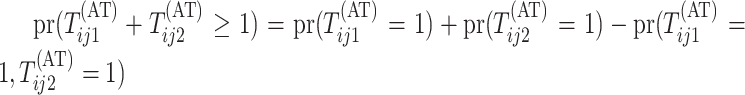 .
Calculating the marginal probability
.
Calculating the marginal probability 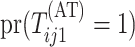 is
straightforward. By considering only the first disease, one can take Equation (9) in Kim and others (2007) and replace
is
straightforward. By considering only the first disease, one can take Equation (9) in Kim and others (2007) and replace
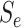 (
(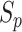 ) with
) with
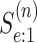 (
( )
and
)
and 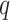 with
with 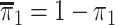 ,
where
,
where 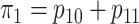 is the marginal
prevalence of the first disease. Calculating
is the marginal
prevalence of the first disease. Calculating 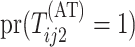 is
done similarly for the second disease by using
is
done similarly for the second disease by using 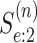 ,
,
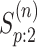 , and
, and
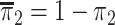 , where
, where
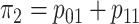 .
.
Calculating the joint probability 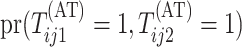 is difficult. Because array testing is generally preferred for low-prevalence diseases,
one might initially think to treat this probability as being negligible or at least to
approximate it under the assumption of no testing error, thereby creating a simple
approximation for EFF(AT). We concluded that both strategies would be unwise. Not only
does this lack verisimilitude (as few assays are perfect), but we have found that this
probability can be non-trivial even when the diseases are rare. By exploiting the symmetry
between rows and columns of the array, we can express
is difficult. Because array testing is generally preferred for low-prevalence diseases,
one might initially think to treat this probability as being negligible or at least to
approximate it under the assumption of no testing error, thereby creating a simple
approximation for EFF(AT). We concluded that both strategies would be unwise. Not only
does this lack verisimilitude (as few assays are perfect), but we have found that this
probability can be non-trivial even when the diseases are rare. By exploiting the symmetry
between rows and columns of the array, we can express  as the sum
as the sum
In the supplementary material available at Biostatistics online, we derive each of these probabilities. The derivations themselves are similar in spirit to those in the array testing literature for single diseases; see, e.g., Kim and others (2007). However, in the presence of testing error, these derivations are substantially more challenging and provide different answers when compared with the single-disease setting (e.g., when treating individuals as “disease free” or not).
3.2. Classification accuracy
As in Tebbs and others (2013) and
Hou and others (2017), we define
the pooling sensitivity 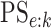 as the probability an
individual is classified as positive for the
as the probability an
individual is classified as positive for the 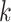 th disease,
th disease,
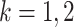 , given that the individual is truly
positive for the
, given that the individual is truly
positive for the 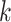 th disease. In two-dimensional array
testing,
th disease. In two-dimensional array
testing,
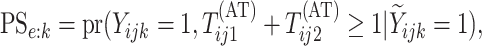 |
where 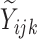 denotes the true
(binary) status of individual
denotes the true
(binary) status of individual 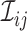 for disease
for disease
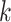 and
and 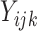 denotes the
corresponding individual testing response. The pooling specificity
denotes the
corresponding individual testing response. The pooling specificity
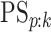 is defined analogously
for truly negative individuals being classified negatively; i.e.,
is defined analogously
for truly negative individuals being classified negatively; i.e.,
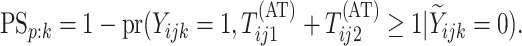 |
Using the inclusion-exclusion rule for conditional probabilities, we can write the
pooling sensitivity 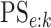 as
as
and, in the supplementary material available at Biostatistics online, we derive each of these probabilities. We also show the pooling specificity
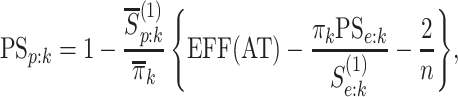 |
where 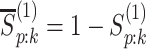 ,
,
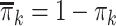 , and
, and
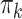 is the marginal prevalence of the
is the marginal prevalence of the
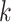 th disease.
th disease.
3.3. Adding a master array test
In array testing for a single disease, Kim and
others (2007) and Westreich
and others (2008) have demonstrated that a simple modification
to the two-stage procedure can further reduce the expected number of tests per individual
when the probability of disease is very small. The modification involves performing a
preliminary test on all specimens in the array; i.e., a test on all
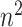 specimens in an
specimens in an 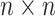 array. If this preliminary test is negative, all individuals in the array are declared to
be negative without further testing. Otherwise, one proceeds to test the rows and columns
as in the two-stage version.
array. If this preliminary test is negative, all individuals in the array are declared to
be negative without further testing. Otherwise, one proceeds to test the rows and columns
as in the two-stage version.
We adapt this three-stage algorithm for use with 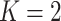 diseases, denoted
herein by ATM. In the first stage, let
diseases, denoted
herein by ATM. In the first stage, let 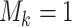 if the master array
tests positively for the
if the master array
tests positively for the 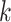 th disease,
th disease, 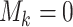 otherwise.
If the master array tests positively for either disease; i.e., if
otherwise.
If the master array tests positively for either disease; i.e., if
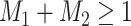 , then two-stage AT is used.
Mathematically, we can express the collection who are tested individually as
, then two-stage AT is used.
Mathematically, we can express the collection who are tested individually as
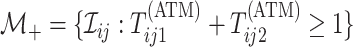 ,
where, for
,
where, for 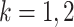 ,
,
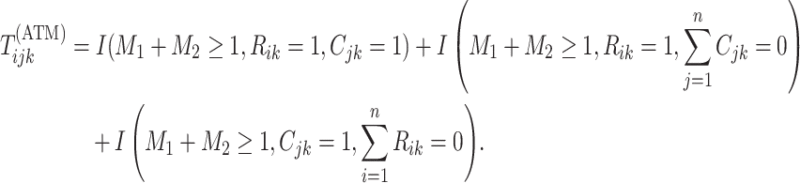 |
Therefore, the efficiency of ATM is given by
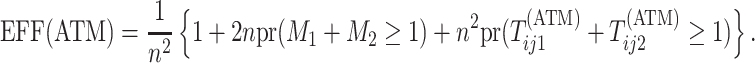 |
In the supplementary material
available at Biostatistics online, we derive EFF(ATM) in closed form as
well as the classification accuracy probabilities 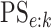 and
and
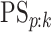 for ATM. These
derivations require a slight modification of Assumption 3 (see Section 2) where now known
values of
for ATM. These
derivations require a slight modification of Assumption 3 (see Section 2) where now known
values of 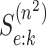 and
and
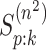 are elicited for the master
array. The conditional independence assumption (Assumption 5) is also broadened to include
the master array’s testing response.
are elicited for the master
array. The conditional independence assumption (Assumption 5) is also broadened to include
the master array’s testing response.
4. Comparisons
We compare our array-testing procedures to the hierarchical algorithms in Tebbs and others (2013) and Hou and others (2017). To examine
low-prevalence diseases where pooling would be useful, we consider values of
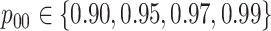 and
vary the remaining probabilities
and
vary the remaining probabilities 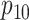 ,
, 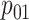 , and
, and
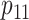 in two ways. First, we select these
probabilities so that the marginal disease probabilities
in two ways. First, we select these
probabilities so that the marginal disease probabilities 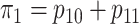 and
and
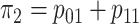 are equal. Second, we
investigate cases where the marginal probabilities are unequal; specifically, cases where
are equal. Second, we
investigate cases where the marginal probabilities are unequal; specifically, cases where
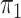 is approximately 4–5 times larger than
is approximately 4–5 times larger than
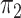 . To incorporate the possibility of
misclassification for each disease, we assume
. To incorporate the possibility of
misclassification for each disease, we assume 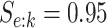 and
and
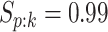 when testing all pools
(regardless of size) and all individuals. This might be reasonable when a multiplex assay
can be calibrated to perform similarly on both pooled and individual specimens; see Section
5. All of our array calculations of efficiency and classification accuracy are exact, based
on the derivations described in Section 3.
when testing all pools
(regardless of size) and all individuals. This might be reasonable when a multiplex assay
can be calibrated to perform similarly on both pooled and individual specimens; see Section
5. All of our array calculations of efficiency and classification accuracy are exact, based
on the derivations described in Section 3.
Because AT (ATM) is a two-stage (three-stage) procedure, our focus is on comparing (i) AT
with the two-stage procedure in Tebbs and
others (2013), denoted by H2, and (ii) ATM with the three-stage
procedure in Hou and others (2017),
denoted by H3. These comparisons are probably the most logical, as case identification
algorithms using the same number of stages have similar levels of complexity with regard to
implementation and similar turnaround times (Westreich
and others, 2008). All comparisons are made by using the optimal
versions of each algorithm in terms of efficiency. In other words, we identify and compare
the array and hierarchical procedures that minimize the expected number of tests per
individual. Note that we do invoke one constraint when selecting the optimal ATM algorithm;
namely, we do not consider arrays larger than 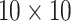 . This bounds the
number of individuals in the master array test at 100, a constraint also used in Kim and others (2007) and Kim and Hudgens (2009) for single diseases out of
concerns for dilution. Similar concerns can arise with multiplex assays; see Section 5.
. This bounds the
number of individuals in the master array test at 100, a constraint also used in Kim and others (2007) and Kim and Hudgens (2009) for single diseases out of
concerns for dilution. Similar concerns can arise with multiplex assays; see Section 5.
Efficiency comparisons for the eight configurations of 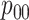 ,
,
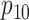 ,
,  , and
, and
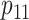 are shown in Table 1. Examining the two-stage designs, AT confers substantial gains in
efficiency when compared with H2. For example, in Case 2 where the marginal disease
probabilities are both 0.03, AT with
are shown in Table 1. Examining the two-stage designs, AT confers substantial gains in
efficiency when compared with H2. For example, in Case 2 where the marginal disease
probabilities are both 0.03, AT with 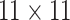 arrays is 20.6% more efficient
than the best two-stage hierarchical algorithm H2 (0.344 versus 0.433, respectively). This
and the other efficiency gains in Table 1, which
range from 9.1% to 41.1%, are practically significant for high-volume laboratories that
already use H2 for multiple diseases; as a two-stage procedure itself, AT is an attractive
alternative to further reduce testing costs without requiring additional resources. Moving
to the three-stage comparisons, ATM improves upon the best three-stage hierarchical
algorithm H3 in the
arrays is 20.6% more efficient
than the best two-stage hierarchical algorithm H2 (0.344 versus 0.433, respectively). This
and the other efficiency gains in Table 1, which
range from 9.1% to 41.1%, are practically significant for high-volume laboratories that
already use H2 for multiple diseases; as a two-stage procedure itself, AT is an attractive
alternative to further reduce testing costs without requiring additional resources. Moving
to the three-stage comparisons, ATM improves upon the best three-stage hierarchical
algorithm H3 in the 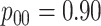 and
and 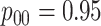 cases,
but not in the
cases,
but not in the 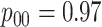 and
and 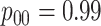 cases;
i.e., where one or both diseases are more rare. Note that our comparisons may penalize ATM
slightly in some cases because we do not consider arrays larger than
cases;
i.e., where one or both diseases are more rare. Note that our comparisons may penalize ATM
slightly in some cases because we do not consider arrays larger than
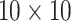 for ATM. Furthermore, it is
interesting to note that in each of the eight configurations, the best AT procedure is more
efficient than the best H3 procedure.
for ATM. Furthermore, it is
interesting to note that in each of the eight configurations, the best AT procedure is more
efficient than the best H3 procedure.
Table 1.
Efficiency of two- and three-stage algorithms with 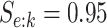 and
and
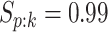 for testing all pools
(regardless of size) and individuals. H2 and H3 (hierarchical) algorithms are from Tebbs and others (2013) and Hou and others (2017), respectively.
Pool sizes are chosen to minimize the expected number of tests per individual. The
maximum allowable array size for ATM is
for testing all pools
(regardless of size) and individuals. H2 and H3 (hierarchical) algorithms are from Tebbs and others (2013) and Hou and others (2017), respectively.
Pool sizes are chosen to minimize the expected number of tests per individual. The
maximum allowable array size for ATM is 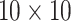 . For Cases
1–4, the marginal disease probabilities
. For Cases
1–4, the marginal disease probabilities 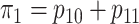 and
and
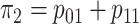 are equal. For Cases
5–8, the marginal disease probabilities are unequal
are equal. For Cases
5–8, the marginal disease probabilities are unequal
| Stages | Algorithm | Efficiency | Stages | Algorithm | Efficiency | ||||
|---|---|---|---|---|---|---|---|---|---|
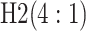
|
0.594 |
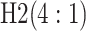
|
0.591 | ||||||
| Case 1 |
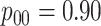

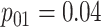
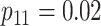
|
2 |
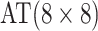
|
0.530 | Case 5 |
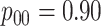
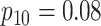
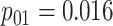
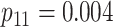
|
2 |
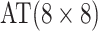
|
0.537 |
| 3 |
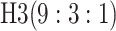
|
0.572 | 3 |
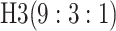
|
0.564 | ||||
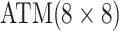
|
0.543 |
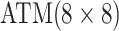
|
0.544 | ||||||
| 2 |
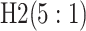
|
0.433 |
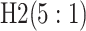
|
0.431 | |||||
| Case 2 |
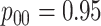
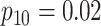
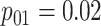
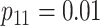
|
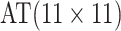
|
0.344 | Case 6 |
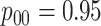
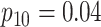
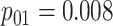

|
2 |
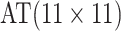
|
0.352 | |
| 3 |
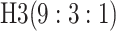
|
0.371 | 3 |
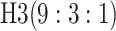
|
0.368 | ||||
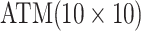
|
0.354 |
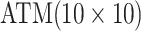
|
0.356 | ||||||

|
0.345 |
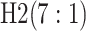
|
0.342 | ||||||
| Case 3 |
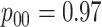
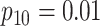
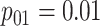
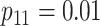
|
2 |
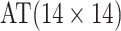
|
0.258 | Case 7 |
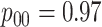
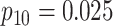
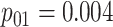
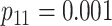
|
2 |
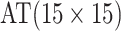
|
0.260 |
| 3 |
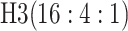
|
0.273 | 3 |
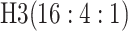
|
0.268 | ||||
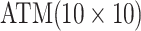
|
0.282 |
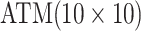
|
0.279 | ||||||
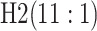
|
0.209 |
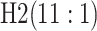
|
0.208 | ||||||
| Case 4 |
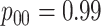
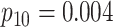
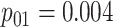
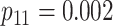
|
2 |
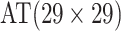
|
0.123 | Case 8 |
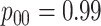
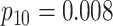
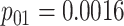
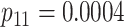
|
2 |
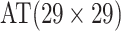
|
0.128 |
| 3 |
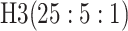
|
0.135 | 3 |
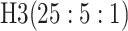
|
0.134 | ||||
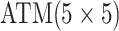
|
0.150 |
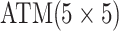
|
0.150 |
To complement the results in Table 1, we performed a
simulation study to assess the variability in the number of tests per individual for the
four algorithms H2, AT, H3, and ATM using the optimal configurations identified in Table 1. For each of the eight parameter configurations,
we generated the true disease statuses of 100 000 individuals, assigned the individuals to
master pools, and executed each algorithm while assuming 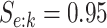 and
and
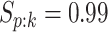 as before. This process was
repeated
as before. This process was
repeated 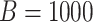 times for each parameter
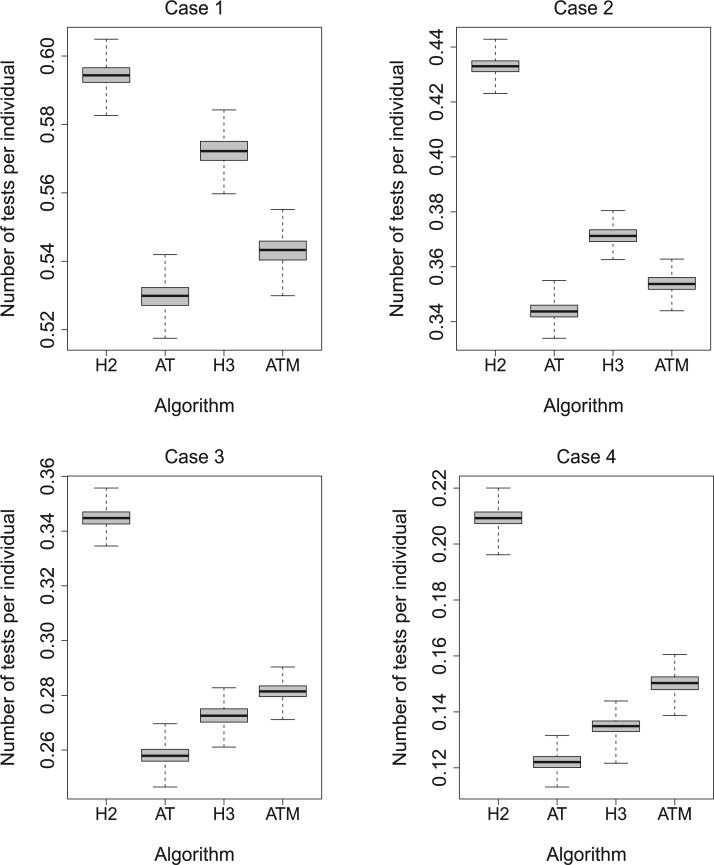
configuration. Figure 2 displays boxplots of the
resulting 1000 values of the number of tests per individual for Cases 1–4 in Table 1; the same boxplots for Cases 5–8 are shown in the
supplementary material available
at Biostatistics online. In all eight cases, there are only minor
differences in the variability in the number of tests per individual. Furthermore, among all
four procedures, the empirical distributions described by the boxplots tend to favor AT as
providing the smallest number of tests per individual.
times for each parameter
configuration. Figure 2 displays boxplots of the
resulting 1000 values of the number of tests per individual for Cases 1–4 in Table 1; the same boxplots for Cases 5–8 are shown in the
supplementary material available
at Biostatistics online. In all eight cases, there are only minor
differences in the variability in the number of tests per individual. Furthermore, among all
four procedures, the empirical distributions described by the boxplots tend to favor AT as
providing the smallest number of tests per individual.
Fig. 2.
Simulation study for Cases 1–4 in Table 1. Boxplots of the number of tests per
individual using 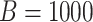 Monte Carlo data sets. Array and
hierarchical group sizes are the same as those in Table 1. The same figure for Cases 5–8
in Table 1 is in the supplementary
material available at Biostatistics online.
Monte Carlo data sets. Array and
hierarchical group sizes are the same as those in Table 1. The same figure for Cases 5–8
in Table 1 is in the supplementary
material available at Biostatistics online.
Finally, any comparison of competing case identification algorithms should examine
classification accuracy. In the supplementary material available at Biostatistics online, we
provide values of 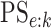 and
and
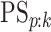 for each of the eight cases
in Table 1. We also include the pooling positive and
negative predictive values for each disease; i.e.,
for each of the eight cases
in Table 1. We also include the pooling positive and
negative predictive values for each disease; i.e.,
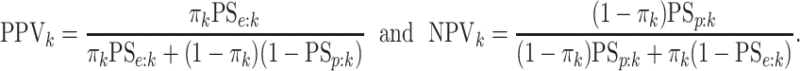 |
For the 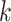 th disease,
th disease, 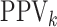 (
(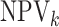 ) gives the probability an
individual is truly positive (negative) given that the algorithm has classified the
individual positively (negatively). Our calculations show that all four algorithms increase
specificity
) gives the probability an
individual is truly positive (negative) given that the algorithm has classified the
individual positively (negatively). Our calculations show that all four algorithms increase
specificity 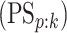 when compared with
individual testing and that their negative predictive values
when compared with
individual testing and that their negative predictive values 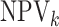 are
similar. Hierarchical algorithms are slightly preferred overall in terms of pooling
sensitivity. On the other hand, AT can provide higher values of
are
similar. Hierarchical algorithms are slightly preferred overall in terms of pooling
sensitivity. On the other hand, AT can provide higher values of 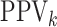 when compared with H2, most notably when
when compared with H2, most notably when 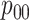 is larger.
is larger.
5. Application
Chlamydia (CT) and gonorrhea (NG) are two of the most common sexually transmitted diseases in the United States and elsewhere. In 2014, the Centers for Disease Control and Prevention (CDC) estimated that about 1.8 million new infections were reported in the United States (CDC, 2015). Untreated infections can lead to serious medical problems, including pelvic inflammatory disease, infertility, ectopic pregnancy, sterility, and an increased likelihood of acquiring or transmitting HIV (Papp and others, 2014; CDC, 2015). There is also a concern that certain strains of NG may soon become completely resistant to standard antibiotics used for treatment (Kirkcaldy and others, 2016). This has put new pressures on public health officials at statewide testing centers as they attempt to curtail the spread of both diseases.
Unfortunately, federal funds allocated to screen for CT/NG in the United States have declined in recent years, and this trend is expected to continue. The downward trend started in 2010 and coincided with the passage of the Affordable Care Act, which stipulated new requirements for private health insurance policies to cover CT/NG testing and other preventative services for young and “at-risk” women (JSI Research & Training Institute/Denver, 2013). This soon after lead to the discontinuation of the largest nationally funded CT/NG screening program in the United States, the Infertility Prevention Project, which since 1988 had provided financial support to public health laboratories in all 50 states. Dissolving the IPP has reduced the annual CT/NG testing budgets of these laboratories, leaving officials overseeing screening programs to become increasingly concerned about testing costs.
Given the current funding environment, pooling specimens emerges as an excellent option for statewide testing centers to reduce the cost of testing. The largest public health laboratory in Iowa, the State Hygienic Laboratory (SHL) in Coralville, already uses group testing with a multiplex CT/NG assay to accomplish this. Each year, the SHL receives thousands of individual specimens from STD clinics and family planning centers located throughout the state. Upon arrival at the laboratory, specimens are first cross-classified according to sex (female/male) and type (swab/urine). This quadfurcation of specimens is done primarily for two reasons. First, commercially available CT/NG multiplex assays exhibit different accuracy levels for individuals in these four strata (Gaydos and others, 2003, 2010; Cheng and others, 2011). Second, the populations of individuals represented by the specimens received at the SHL are substantially different for females and males. Males are more likely to be tested only when they exhibit symptoms of infection (e.g., painful urination/ejaculation, etc.), whereas most females are tested annually as part of routine health examinations.
The Iowa SHL uses the two-stage hierarchical procedure (H2) described in Tebbs and others (2013) to test female swab specimens in pools of size 4. All specimens from the other three strata (female urine, male swab, and male urine) are tested individually. In the hope of reducing testing costs further, our colleagues at the SHL are interested in the following questions:
Can AT, a comparable two-stage procedure, reduce the number of tests needed to diagnose female swab specimens for CT/NG?
Should the SHL pool specimens in the other three strata? If so, how does AT compare to hierarchical algorithms?
Using historical data from the SHL, we perform a feasibility study to investigate both questions.
Table 2 summarizes the diagnoses of 33 811 Iowa
residents during the 2013 calendar year. These diagnoses are cross-classified by sex and
specimen type, and estimates of 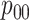 ,
, 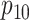 ,
,
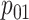 , and
, and 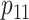 within each
sex/specimen type stratum are provided. The SHL uses the Gen-Probe Aptima Combo 2 Assay
(AC2A), a multiplex assay that utilizes nucleic acid amplification techniques to detect
ribosomal RNA from CT and/or NG. The values of
within each
sex/specimen type stratum are provided. The SHL uses the Gen-Probe Aptima Combo 2 Assay
(AC2A), a multiplex assay that utilizes nucleic acid amplification techniques to detect
ribosomal RNA from CT and/or NG. The values of 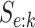 and
and
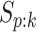 provided in Table 2 are taken from Gen-Probe’s product literature for the AC2A.
Specimens are carefully prepared by the lead technician at the SHL to ensure that testing
error rates are the same for pooled specimens and individual specimens, so we perform our
study under this assumption. The lab’s lead virologist estimates that each application of
the AC2A costs the laboratory $37 and requires 6 h to complete.
provided in Table 2 are taken from Gen-Probe’s product literature for the AC2A.
Specimens are carefully prepared by the lead technician at the SHL to ensure that testing
error rates are the same for pooled specimens and individual specimens, so we perform our
study under this assumption. The lab’s lead virologist estimates that each application of
the AC2A costs the laboratory $37 and requires 6 h to complete.
Table 2.
Iowa SHL data summary. CT/NG diagnoses for 33,811 individuals during 2013,
cross-classified by sex and specimen type. Stratum sample sizes
 are shown. Estimates of
are shown. Estimates of
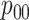 ,
, 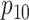 ,
,
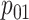 , and
, and 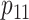 are
provided. The values of sensitivity and specificity are taken from the product
literature for the Aptima Combo 2 Assay (1 = CT; 2 = NG). The algorithms shown in the
last column minimize the expected number of tests per individual
are
provided. The values of sensitivity and specificity are taken from the product
literature for the Aptima Combo 2 Assay (1 = CT; 2 = NG). The algorithms shown in the
last column minimize the expected number of tests per individual
| Stratum | Count | CT/NG | Estimate | Sensitivity | Specificity | Algorithms | ||
|---|---|---|---|---|---|---|---|---|
| 18775 |
|
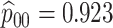
|
||||||
| Female Swab | 1442 |
|
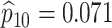
|
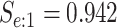
|
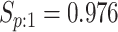
|
H2
|
||
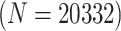
|
63 |
|
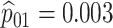
|
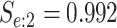
|
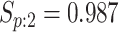
|
AT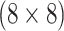
|
||
| 52 |
|
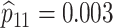
|
H3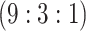
|
|||||
| 5438 |
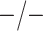
|
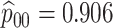
|
||||||
| Female Urine | 521 |
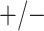
|
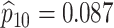
|
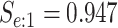
|
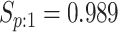
|
H2
|
||
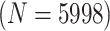
|
21 |
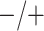
|
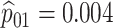
|
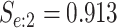
|
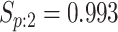
|
AT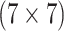
|
||
| 18 |
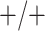
|
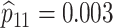
|
H3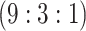
|
|||||
| 1050 |
|
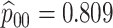
|
||||||
| Male Swab | 183 |
|
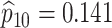
|
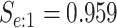
|
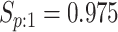
|
H2
|
||
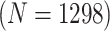
|
43 |
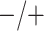
|
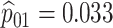
|
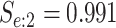
|
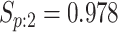
|
AT
|
||
| 22 |
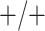
|
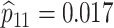
|
H3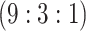
|
|||||
| 5137 |
|

|
||||||
| Male Urine | 919 |
|
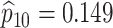
|
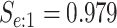
|
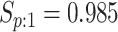
|
H2
|
||
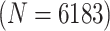
|
73 |
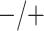
|
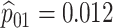
|
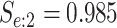
|
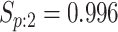
|
AT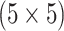
|
||
| 54 |
|
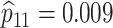
|
H3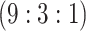
|
Our study is performed as follows. Using the 2013 estimates and common values of
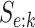 and
and 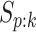 for pools
and individuals, we first determine the most efficient versions of H2, AT, and H3 for each
sex/specimen type stratum while assuming the master pool size is no larger than 10; see
Table 2. This constraint was invoked because the
pooling literature for CT/NG has not examined using pools larger than this; for this same
reason, we did not include ATM in this investigation. For each of the four strata, we then
simulate individual CT/NG diagnoses to emulate what would have occurred had these optimal
algorithms been used. For example, in the female/swab stratum, we simulate the true CT/NG
statuses of
for pools
and individuals, we first determine the most efficient versions of H2, AT, and H3 for each
sex/specimen type stratum while assuming the master pool size is no larger than 10; see
Table 2. This constraint was invoked because the
pooling literature for CT/NG has not examined using pools larger than this; for this same
reason, we did not include ATM in this investigation. For each of the four strata, we then
simulate individual CT/NG diagnoses to emulate what would have occurred had these optimal
algorithms been used. For example, in the female/swab stratum, we simulate the true CT/NG
statuses of 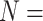 20 332 individuals based on the 2013
estimates, assign these individuals to optimally sized versions of H2, AT, and H3, and then
perform each algorithm. This same strategy is then implemented in the other three
sex/specimen type strata, and this is repeated
20 332 individuals based on the 2013
estimates, assign these individuals to optimally sized versions of H2, AT, and H3, and then
perform each algorithm. This same strategy is then implemented in the other three
sex/specimen type strata, and this is repeated 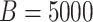 times in each stratum.
We used individual testing for those individuals that remained when a complete master
pool/array could not be formed. For example, in the female/swab stratum with
times in each stratum.
We used individual testing for those individuals that remained when a complete master
pool/array could not be formed. For example, in the female/swab stratum with
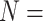 20 332 individuals, there were 5083 master
pools created for H2
20 332 individuals, there were 5083 master
pools created for H2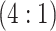 , 317 master arrays created for
AT
, 317 master arrays created for
AT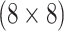 , and 2259 master pools created
for H3
, and 2259 master pools created
for H3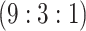 , admitting 0, 44, and 1 individual
tests, respectively.
, admitting 0, 44, and 1 individual
tests, respectively.
Table 3 shows the results. With the 5000 data sets
created in each sex/specimen type stratum, we calculate the mean and standard deviation of
the number of tests expended by H2, AT, and H3 to classify all individuals for CT and NG. We
also report estimates of the four accuracy probabilities (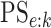 ,
,
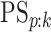 ,
, 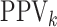 ,
and
,
and 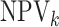 ) in each stratum for each
disease, which are calculated by comparing the true CT/NG statuses to the simulated
diagnoses in each data set and then averaging across them. Boxplots showing the
distributions of the number of tests are provided in the supplementary material available at
Biostatistics online. All operating characteristics in Table 3 are estimates calculated from our feasibility
study. Exact values of the efficiency and accuracy probabilities for H2, AT, and H3 (based
on the information in Table 2) are also provided in
the supplementary material
available at Biostatistics online. The estimates in Table 3 are very close to these exact values, although minor differences
arise occasionally for AT because we used individual testing for remainder arrays.
) in each stratum for each
disease, which are calculated by comparing the true CT/NG statuses to the simulated
diagnoses in each data set and then averaging across them. Boxplots showing the
distributions of the number of tests are provided in the supplementary material available at
Biostatistics online. All operating characteristics in Table 3 are estimates calculated from our feasibility
study. Exact values of the efficiency and accuracy probabilities for H2, AT, and H3 (based
on the information in Table 2) are also provided in
the supplementary material
available at Biostatistics online. The estimates in Table 3 are very close to these exact values, although minor differences
arise occasionally for AT because we used individual testing for remainder arrays.
Table 3.
Iowa SHL feasibility study results. Estimated operating characteristics for optimal
algorithms based on 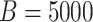 data sets in each sex/specimen
type stratum. The average (Mean) and standard deviation (SD) of the number of tests are
provided. Stratum sample sizes
data sets in each sex/specimen
type stratum. The average (Mean) and standard deviation (SD) of the number of tests are
provided. Stratum sample sizes 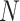 are shown. The estimated efficiency
(EFF) is the mean number of tests divided by
are shown. The estimated efficiency
(EFF) is the mean number of tests divided by 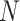 . Accuracy probabilities
(1 = CT; 2 = NG) are estimated by averaging over the 5000 data sets
. Accuracy probabilities
(1 = CT; 2 = NG) are estimated by averaging over the 5000 data sets
| Stratum | Algorithm | Mean (SD) | EFF |
|
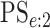
|
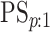
|

|
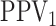
|
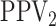
|
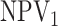
|
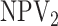
|
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|
H2
|
10907 (130) | 0.536 | 0.891 | 0.989 | 0.994 | 0.996 | 0.927 | 0.620 | 0.991 | 1.000 | ||
| Female Swab | AT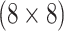
|
9930 (166) | 0.488 | 0.844 | 0.989 | 0.996 | 0.997 | 0.938 | 0.662 | 0.988 | 1.000 | |
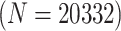
|
H3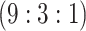
|
9815 (170) | 0.483 | 0.844 | 0.986 | 0.996 | 0.997 | 0.950 | 0.698 | 0.988 | 1.000 | |
H2
|
3429 (73) | 0.572 | 0.899 | 0.876 | 0.997 | 0.998 | 0.969 | 0.735 | 0.990 | 0.999 | ||
| Female Urine | AT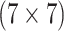
|
3253 (86) | 0.542 | 0.856 | 0.890 | 0.998 | 0.998 | 0.976 | 0.779 | 0.986 | 0.999 | |
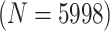
|
H3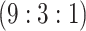
|
3223 (94) | 0.537 | 0.856 | 0.851 | 0.998 | 0.998 | 0.978 | 0.786 | 0.986 | 0.999 | |
H2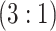
|
1058 (30) | 0.815 | 0.928 | 0.987 | 0.990 | 0.990 | 0.947 | 0.839 | 0.987 | 0.999 | ||
| Male Swab | AT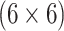
|
1044 (44) | 0.804 | 0.895 | 0.984 | 0.990 | 0.990 | 0.946 | 0.842 | 0.980 | 0.999 | |
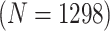
|
H3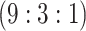
|
1110 (43) | 0.855 | 0.906 | 0.985 | 0.991 | 0.990 | 0.948 | 0.844 | 0.983 | 0.999 | |
H2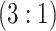
|
4726 (66) | 0.764 | 0.960 | 0.979 | 0.995 | 0.998 | 0.973 | 0.926 | 0.993 | 1.000 | ||
| Male Urine | AT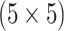
|
4796 (85) | 0.776 | 0.942 | 0.980 | 0.996 | 0.999 | 0.978 | 0.936 | 0.989 | 1.000 | |
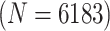
|
H3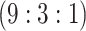
|
4942 (94) | 0.799 | 0.944 | 0.977 | 0.995 | 0.998 | 0.974 | 0.928 | 0.990 | 1.000 |
We now return to the questions posed by our colleagues. For the first question, our
investigation shows that switching from H2 to AT could be beneficial when screening female
swab specimens for CT/NG. The estimated efficiency for AT is 0.488 (see Table 3), which represents a 9.0% reduction in the
average number of tests per year when compared with H2 (EFF = 0.536). Assuming
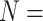 20,322 specimens are received per year, this
translates to an average reduction of 977 tests and an annual savings of $36 149. The
performance of AT is also comparable to H3, which is even slightly more efficient (EFF =
0.483). AT and H3 provide about the same variability in the number of tests expended and
similar levels of accuracy. Choosing between AT and H3 might involve a detailed examination
of each algorithm’s level of logistical complexity. For example, with each application of
the AC2A taking 6 h, H3 could increase the turnaround time from 12 h (for AT) to 18 h,
potentially delaying the laboratory in providing positive diagnoses by one working day. At
the same time, the most efficient version of AT requires a larger number of specimens to
pool (
20,322 specimens are received per year, this
translates to an average reduction of 977 tests and an annual savings of $36 149. The
performance of AT is also comparable to H3, which is even slightly more efficient (EFF =
0.483). AT and H3 provide about the same variability in the number of tests expended and
similar levels of accuracy. Choosing between AT and H3 might involve a detailed examination
of each algorithm’s level of logistical complexity. For example, with each application of
the AC2A taking 6 h, H3 could increase the turnaround time from 12 h (for AT) to 18 h,
potentially delaying the laboratory in providing positive diagnoses by one working day. At
the same time, the most efficient version of AT requires a larger number of specimens to
pool (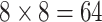 ) than H3, which may delay
testing all together if not enough specimens are received. These logistical issues aside,
the only reason to continue using H2 might be that it provides a slight improvement in
pooling sensitivity for CT.
) than H3, which may delay
testing all together if not enough specimens are received. These logistical issues aside,
the only reason to continue using H2 might be that it provides a slight improvement in
pooling sensitivity for CT.
For the second question, it is difficult to argue that pooling would not be useful when testing female urine specimens for CT/NG. The estimated efficiency of H2 is 0.572, which would provide an annual cost savings of $95 053 when compared with individual testing. AT and H3 can be even more efficient, reducing the average number of tests further by about 200 per year. Moving to the male strata, where the proportion of positives is larger, the benefits of pooling are obviously reduced but are probably still large enough to garner attention. For example, when screening male urine specimens for CT/NG, optimal versions of H2 and AT both reduce the average number of tests by about 1400 per year when compared with individual testing, which corresponds to over $50 000 in annual savings. On the other hand, individual testing might be preferred for male swab specimens due to the high prevalence in this stratum and also because the SHL receives far fewer specimens of this type each year.
6. Discussion
We have extended the utility of array testing to screening applications that use multiplex assays. For two diseases, we obtain closed-form expressions for the expected number of tests per individual and relevant classification accuracy probabilities. These expressions show that array testing can dramatically reduce the number of tests needed when compared with two-stage hierarchical algorithms and can compete well with hierarchical algorithms which use a larger number of stages. Our case study using CT/NG data in Iowa sheds light on questions posed by public-health officials and illustrates the cost-saving benefits of using array testing in practice.
On a recent visit to the SHL, our colleagues expressed concern about the future of CT/NG screening in the United States. This is due primarily to the fact that federal and state funds for screening are “plummeting” and the belief that CT/NG prevalence rates could rise as a result. It is our hope that the pooling algorithms described in this article and those in Tebbs and others (2013) and Hou and others (2017) will provide laboratories with viable options to reduce their testing costs for CT/NG screening purposes. To disseminate our work to potential stakeholders, we have created an R/Shiny application that performs efficiency and classification accuracy calculations for the algorithms in all three articles and determines the most efficient algorithm of each type. This resource should allow public health officials and lab technicians to quickly explore the potential benefits of CT/NG pooling and make informed decisions about which algorithm might be best to implement in their own laboratories.
We conclude with two remarks. First, an anonymous reviewer has pointed out that the
population-level parameters 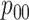 ,
, 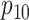 ,
,
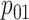 , and
, and 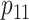 are rarely
known exactly, yet any evaluation of our algorithms in this article depends on them. Of
course, estimates of disease prevalence can be obtained from previous periods of testing
(e.g., the SHL has been testing Iowa residents for CT/NG in pools since 1999); however, even
good estimates are still subject to uncertainty. One possible way to address this issue
would be to perform efficiency and accuracy calculations for a range of disease prevalence
values (and possibly assay accuracy probabilities too) and select the optimal design based
on those identified in this range. Our R/Shiny application makes this approach feasible as
all calculations in this article (for
are rarely
known exactly, yet any evaluation of our algorithms in this article depends on them. Of
course, estimates of disease prevalence can be obtained from previous periods of testing
(e.g., the SHL has been testing Iowa residents for CT/NG in pools since 1999); however, even
good estimates are still subject to uncertainty. One possible way to address this issue
would be to perform efficiency and accuracy calculations for a range of disease prevalence
values (and possibly assay accuracy probabilities too) and select the optimal design based
on those identified in this range. Our R/Shiny application makes this approach feasible as
all calculations in this article (for 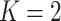 diseases) can be performed almost
instantly for arrays of reasonable size. Second, it is easy to envision how array testing
would work with a discriminating multiplex assay for three or more diseases. In fact, Stramer and others (2013) describe how
“triplex” nucleic acid test assays for the detection of HIV, HBV, and HCV have been
available since 2007 and summarize a feasibility study that evaluates a discriminating assay
of this type with pooled samples from blood donors in the United States. Deriving
closed-form expressions for the efficiency and classification accuracy probabilities for
diseases) can be performed almost
instantly for arrays of reasonable size. Second, it is easy to envision how array testing
would work with a discriminating multiplex assay for three or more diseases. In fact, Stramer and others (2013) describe how
“triplex” nucleic acid test assays for the detection of HIV, HBV, and HCV have been
available since 2007 and summarize a feasibility study that evaluates a discriminating assay
of this type with pooled samples from blood donors in the United States. Deriving
closed-form expressions for the efficiency and classification accuracy probabilities for
 diseases with AT (or ATM) becomes
nearly overwhelming even when
diseases with AT (or ATM) becomes
nearly overwhelming even when 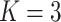 ; however, our R/Shiny application will
approximate these quantities by using simulation.
; however, our R/Shiny application will
approximate these quantities by using simulation.
7. Software
Software in the form of R code is available on GitHub (https://github.com/harrindy/multiplex).
Supplementary Material
Acknowledgments
The authors thank the Editors, the Associate Editor, and two anonymous referees for their help in improving this article. They also thank Jeffrey Benfer, Dr Lucy DesJardin, and Kristofer Eveland at the State Hygienic Laboratory (University of Iowa) and Dr Elizabeth Torrone at the Centers for Disease Control and Prevention. Conflict of Interest: None declared.
Funding
This research was supported by Grant R01 AI121351 from the National Institutes of Health.
References
- Busch, M., Caglioti, S., Robertson, E., McAuley, J., Tobler, L., Kamel, H., Linnen, J., Shyamala, V., Tomasulo, P. and Kleinman S. (2005). Screening the blood supply for West Nile virus RNA by nucleic acid amplification testing. New England Journal of Medicine 353, 460–467. [DOI] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention (2015). Sexually Transmitted Disease Surveillance 2014. Atlanta, GA: U.S. Department of Health and Human Services. www.cdc.gov. Accessed August 8, 2018. [Google Scholar]
- Cheng, A., Qian, Q. and Kirby, J. (2011). Evaluation of the Abbott RealTime CT/NG assay in comparison to the Roche Cobas Amplicor CT/NG Assay. Journal of Clinical Microbiology 49, 1294–1300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorfman, R. (1943). The detection of defective members of large populations. Annals of Mathematical Statistics 14, 436–440. [Google Scholar]
- Edouard, S., Prudent, E., Gautret, P., Memish, Z. and Raoult, D. (2015). Cost-effective pooling of DNA from nasopharyngeal swab samples for large-scale detection of bacteria by real-time PCR. Journal of Clinical Microbiology 52, 1002–1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellington, A., Kullo, I., Bailey, K. and Klee, G. (2010). Antibody-based protein multiplex platforms: technical and operational challenges. Clinical Chemistry 56, 186–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaydos, C., Cartwright, C., Colianinno, P., Welsch, J., Holden, J., Ho, S., Webb, E., Anderson, C., R., Zhang, L., Miller, T., Leckie, G., Abravaya, K. and Robinson, J. (2010). Performance of the Abbott RealTime CT/NG for detection of Chlamydia trachomatis and Neisseria gonorrhoeae. Journal of Clinical Microbiology 48, 3236–3243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaydos, C., Quinn, T., Willis, D., Weissfeld, A., Hook, E., Martin, D., Ferrero, D. and Schachter, J. (2003). Performance of the APTIMA combo 2 assay for detection of Chlamydia trachomatis and Neisseria gonorrhoeae in female urine and endocervical swab specimens. Journal of Clinical Microbiology 41, 304–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou, P., Tebbs, J., Bilder, C. and McMahan, C. (2017). Hierarchical group testing for multiple infections. Biometrics 73, 656–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudgens, M. and Kim, H. (2011). Optimal configuration of a square array group testing algorithm. Communications in Statistics: Theory and Methods 40, 436–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- JSI Research & Training Institute, Inc./Denver (2013). The future of Infertility Prevention Project health impact assessment: Policy implications and recommendations in light of passage of the Patient Protection and Affordable Care Act, July 25, 2012. www.nnptc.org. Accessed August 8, 2018.
- Kim, H. and Hudgens, M. (2009). Three-dimensional array-based group testing algorithms. Biometrics 65, 903–910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, H., Hudgens, M., Dreyfuss, J., Westreich, D. and Pilcher, C. (2007). Comparison of group testing algorithms for case identification in the presence of testing error. Biometrics 63, 1152–1163. [DOI] [PubMed] [Google Scholar]
- Kirkcaldy, R., Harvey, A., Papp, J., and others (2016). Neisseria gonorrhoeae antimicrobial susceptibility surveillance: The gonococcal isolate surveillance project, 27 sites, United States, 2014. Morbidity and Mortality Weekly Report 65. /www.cdc.gov. Accessed August 8, 2018. [DOI] [PubMed] [Google Scholar]
- Lendle, S., Hudgens, M. and Qaqish, B. (2012). Group testing for case identification with correlated responses. Biometrics 68, 532–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis, J., Lockary, V. and Kobic, S. (2012). Cost savings and increased efficiency using a stratified specimen pooling strategy for Chlamydia trachomatis and Neisseria gonorrhoeae. Sexually Transmitted Diseases 39, 46–48. [DOI] [PubMed] [Google Scholar]
- Martin, E., Salaru, G., Mohammed, D., Coombs, R., Paul, S. and Cadoff, E. (2013). Finding those at risk: acute HIV infection in Newark, NJ. Journal of Clinical Virology 58, 24–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMahan, C., Tebbs, J. and Bilder, C. (2012). Two-dimensional informative array testing. Biometrics 68, 793–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mine, H., Emura, H., Miyamoto, M., Tomono, T., Minegishi, K., Murokawa, H., Yamanaka, R., Yoshikawa, A. and Nishioka, K. (2003). High throughput screening of 16 million serologically negative blood donors for hepatitis B virus, hepatitis C virus, and human immunodeficiency virus type-1 by nucleic acid amplification testing with specific and sensitive multiplex reagent in Japan. Journal of Virological Methods 112, 145–151. [DOI] [PubMed] [Google Scholar]
- O’Brien, S., Yi, Q., Fan, W., Scalia, V., Fearon, M. and Allain, J. (2012). Current incidence and residual risk of HIV, HBV and HCV at Canadian Blood Services. Vox Sanguinis 103, 83–86. [DOI] [PubMed] [Google Scholar]
- Papp, J., Schachter, J., Gaydos, C. and Van Der Pol, B. (2014). Recommendations for the laboratory-based detection of Chlamydia trachomatis and Neisseria gonorrhoeae. Morbidity and Mortality Weekly Report 63. www.cdc.gov. Accessed August 8, 2018. [PMC free article] [PubMed] [Google Scholar]
- Phatarfod, R. and Sudbury, A. (1994). The use of a square array scheme in blood testing. Statistics in Medicine 13, 2337–2343. [DOI] [PubMed] [Google Scholar]
- Pilcher, C., Fiscus, S., Nguyen, T., Foust, E., Wolf, L., Williams, D., Ashby, R., O’Dowd, J., McPherson, J., Stalzer, B., Hightow, L., Miller, W., Eron, J., Cohen, M. and Leone, P. (2005). Detection of acute infections during HIV testing in North Carolina. New England Journal of Medicine 352, 1873–1883. [DOI] [PubMed] [Google Scholar]
- Saá, P., Proctor, M., Foster, G., Krysztof, D., Winton, C., Linnen, J., Gao, K., Brodsky, J., Limberger, R., Dodd, R. and Stramer, S. (2018). Investigational testing for Zika virus among US blood donors. New England Journal of Medicine 378, 1778–1788. [DOI] [PubMed] [Google Scholar]
- Schmidt, M., Pichl, L., Jork, C., Hourfar, M., Schottstedt, V., Wagner, F., Seifried, E., Muller, T., Bux, J. and Saldanha, J. (2010). Blood donor screening with cobas s 201/cobas TaqScreen MPX under routine conditions at German Red Cross institutes. Vox Sanguinis 98, 37–46. [DOI] [PubMed] [Google Scholar]
- Seed, C., Kiely, P. and Keller, A. (2005). Residual risk of transfusion transmitted human immunodeficiency virus, hepatitis B virus, hepatitis C virus, and human T lymphotrophic virus. Internal Medicine Journal 35, 592–598. [DOI] [PubMed] [Google Scholar]
- Sherlock, M., Zelota, N. and Klausner, J. (2007). Routine detection of acute HIV infection through RNA pooling: Survey of current practice in the United States. Sexually Transmitted Diseases 34, 314–316. [DOI] [PubMed] [Google Scholar]
- Stramer, S., Krysztof, D., Brodsky, J., Fickett, T., Reynolds, B., Dodd, R. and Kleinman, S. (2013). Comparative analysis of triplex nucleic acid test assays in United States blood donors. Transfusion 53, 2525–2537. [DOI] [PubMed] [Google Scholar]
- Tebbs, J., McMahan, C. and Bilder, C. (2013). Two-stage hierarchical group testing for multiple infections with application to the Infertility Prevention Project. Biometrics 69, 1064–1073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt, S., Goetghebeur, E., Thomas, I., Mathys, E. and Van Loock, F. (2005). On the viral safety of plasma pools and plasma derivatives. Journal of the Royal Statistical Society, Series A 168, 345–363. [Google Scholar]
- Wang, B., Han, S., Cho, C., Han, J., Cheng, Y., Lee, S., Galappaththy, G., Thimasarn, K., Soe, M., Oo, H., Kyaw, M. and Han, E. (2014). Comparison of microscopy, nested-PCR, and real-time-PCR assays using high throughput screening of pooled samples for diagnosis of malaria in asymptomatic carriers from areas of endemicity in Myanmar. Journal of Clinical Microbiology 52, 1838–1845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westreich, D., Hudgens, M., Fiscus, S. and Pilcher, C. (2008). Optimizing screening for acute human immunodeficiency virus infection with pooled nucleic acid amplification tests. Journal of Clinical Microbiology 46, 1785–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.