Abstract
The statistical associations between mutations, collectively known as linkage disequilibrium, encode important information about the evolutionary forces acting within a population. Yet in contrast to single-site analogues like the site frequency spectrum, our theoretical understanding of linkage disequilibrium remains limited. In particular, little is currently known about how mutations with different ages and fitness costs contribute to expected patterns of linkage disequilibrium, even in simple settings where recombination and genetic drift are the major evolutionary forces. Here, I introduce a forward-time framework for predicting linkage disequilibrium between pairs of neutral and deleterious mutations as a function of their present-day frequencies. I show that the dynamics of linkage disequilibrium become much simpler in the limit that mutations are rare, where they admit a simple heuristic picture based on the trajectories of the underlying lineages. I use this approach to derive analytical expressions for a family of frequency-weighted linkage disequilibrium statistics as a function of the recombination rate, the frequency scale, and the additive and epistatic fitness costs of the mutations. I find that the frequency scale can have a dramatic impact on the shapes of the resulting linkage disequilibrium curves, reflecting the broad range of time scales over which these correlations arise. I also show that the differences between neutral and deleterious linkage disequilibrium are not purely driven by differences in their mutation frequencies and can instead display qualitative features that are reminiscent of epistasis. I conclude by discussing the implications of these results for recent linkage disequilibrium measurements in bacteria. This forward-time approach may provide a useful framework for predicting linkage disequilibrium across a range of evolutionary scenarios.
Keywords: linkage disequilibrium, recombination, genetic drift, purifying selection, epistasis
The statistical associations between mutations, collectively known as linkage disequilibrium (LD), encode important information about past evolutionary forces. This article introduces a forward-time framework for predicting linkage disequilibrium between pairs of neutral or deleterious mutations as a function of their present-day frequencies. Good shows how these results can serve as a probe for estimating recombination rates and fitness costs in large cohorts and discusses the implications of these results for recent LD measurements in bacteria.
The statistical associations between mutations, collectively known as linkage disequilibrium (LD), play a central role in modern evolutionary genetics (Slatkin 2008). Correlations between mutations enable genome-wide association studies and related methods that map the genetic basis of diseases and other complex traits (Visscher et al. 2017). Genetic correlations are also important for evolutionary dynamics, since combinations of linked mutations provide the raw material on which natural selection and other evolutionary forces can act. As a result, contemporary patterns of LD encode crucial information about the historical processes of recombination (McVean et al. 2004; Rosen et al. 2015), natural selection (Sabeti et al. 2002; Garud et al. 2015), and demography (Li and Durbin 2011; Harris and Nielsen 2013; Ragsdale and Gravel 2019) that operate within a population. Yet while extensive theory has been developed for predicting marginal distributions of mutations (Kimura 1964; Sawyer and Hartl 1992; Polanski and Kimmel 2003; Coop and Ralph 2012; Neher and Hallatschek 2013; Kamm et al. 2017; Cvijović et al. 2018), higher-order correlations like LD remain poorly understood in comparison.
Many studies of LD have focused on pairwise correlations between mutations at different sites along a genome. These correlations are often summarized by the correlation coefficient,
| (1) |
where fAB is the fraction of individuals with mutations at both sites, and fA and fB are the marginal frequencies of the two mutations (Hill and Robertson 1968). The r2 statistic and related measures like (Lewontin 1964) quantify how the joint distribution of the two mutations differs from a null model in which the alleles are independently distributed across individuals. A celebrated theoretical result by Ohta and Kimura (1971) shows that, for a neutrally evolving population of constant size N, the frequency-weighted expectation of r2 is given by
| (2) |
where R is the recombination rate between the two sites, and is a weighting function that is normalized so that . The expression in Equation (2) approaches an constant in the limit of low recombination rates () and decays as when . Similar behavior also occurs for the unweighted expectation (McVean 2002), which shares the same scaling when (Song and Song 2007). As a result, the shape of this LD curve is frequently used to estimate rates of recombination, for example, by examining how genome-wide averages of LD decay as a function of the coordinate distance between sites (Chakravarti et al. 1984; Ansari and Didelot 2014; Lynch et al. 2014; Rosen et al. 2015; Garud et al. 2019).
While these classical results have been enormously influential for building intuition about LD, they suffer from several limitations that are increasingly important in modern genomic datasets. Chief among these is the absence of natural selection. While there has been some progress in predicting patterns of LD under particular selection scenarios (e.g. hitchhiking near a recent selective sweep; Kim and Nielsen 2004; Stephan et al. 2006; McVean 2007; Pfaffelhuber et al. 2008; Pokalyuk 2012), we currently lack analogous theoretical predictions for the empirically relevant case where a subset of the observed mutations are deleterious. This is a crucial limitation, since numerous studies have documented differences in the genome-wide patterns of LD between synonymous and nonsynonymous mutations (Sohail et al. 2017; Rosen et al. 2018; Arnold et al. 2020; Garcia and Lohmueller 2020) or for genic vs intergenic regions of the genome (Eberle et al. 2006), where purifying selection is thought to play an important role. Several recent studies have begun to explore these effects in computer simulations (Ragsdale and Gravel 2019; Arnold et al. 2020; Garcia and Lohmueller 2020). Yet without a corresponding analytical theory, it can be difficult to understand how these patterns depend on the underlying parameters of the model or to determine when more exotic forces like positive selection, epistasis, or ecological structure are necessary to fully explain the observed data.
A second and related limitation arises from the averaging scheme in Equation (2), which weights each pair of mutations by their joint heterozygosity, . This weighting tends to favor mutations with intermediate frequencies (e.g. ); these are often older variants that have been segregating for times comparable to the most recent common ancestor of the population (McVean 2002; Rogers 2014). Yet in practice, even a single population will typically harbor mutations across an enormous range of frequency scales, reflecting the broad range of timescales at which these mutations occurred (Cvijović et al. 2018). This broad range of frequencies is increasingly accessible in modern genomic datasets, where sample sizes can range from several hundred to several hundred thousand individuals (Shu and McCauley 2017; Allix-Béguec et al. 2018; Petit and Read 2018; Pasolli et al. 2019; Karczewski et al. 2020). Understanding how LD varies across these different frequency scales could therefore provide new information about the evolutionary processes that operate on different ancestral time scales, similar to existing approaches based on the single-site frequency spectrum (SFS) (Lawrie and Petrov 2014; Ragsdale et al. 2018). Such an approach could be particularly useful for probing aspects of the recombination process, which are difficult to observe from single-site statistics alone.
Yet at present, little is known about how different frequency and time scales contribute to the expected patterns of LD within a population. Previous theoretical work has explored how mutation frequencies constrain the possible values of statistics like r2, independent of the underlying evolutionary dynamics (Hedrick 1987; Lewontin 1988; VanLiere and Rosenberg 2008; Kang and Rosenberg 2019). However, few methods currently exist for predicting the quantitative values that are expected to emerge under a given evolutionary scenario. This limited frequency resolution is particularly problematic in the presence of natural selection, which is known to strongly influence the distribution of mutation frequencies. This makes it difficult to interpret the varying LD patterns that have been observed across different classes of selected sites in a variety of natural populations. Do the differences between synonymous and nonsynonymous LD arise purely due to differences in their mutation frequencies? Or are there residual signatures of selection that remain even after controlling for marginal mutation frequencies? What conclusions can we draw about the underlying selection and recombination processes when differences are observed for some frequency ranges but not others? The goal of this work is to develop the theoretical tools necessary to address these questions.
In the following sections, I present an analytical framework for predicting LD between pairs of neutral and deleterious mutations as a function of their present-day frequencies. I do so by generalizing the traditional weighted average in Equation (2), defining a family of weights that preferentially exclude mutations with frequencies . I show that the dynamics of LD become much simpler in the limit that mutations are rare (), where they can be analyzed using a forward-time branching process framework. I use this approach to derive analytical expressions for statistics like r2 as a function of the recombination rate, the frequency scale f0, and the additive and epistatic fitness costs of the two mutations. I find that the frequency scale f0 can have a dramatic impact on the shape of the weighted LD curve, reflecting the varying timescales over which these mutations persist within the population. I show how this scaling behavior can serve as a probe for estimating recombination rates and distributions of fitness effects in large cohorts, and I discuss the implications of these results for recent LD measurements in bacteria. This forward-time approach may provide a useful framework for predicting LD across a range of other evolutionary scenarios.
Model and results
Here we investigate the dynamics of LD between a pair of genomic loci in a population of constant size N. We assume that each locus accumulates mutations at rate μ per individual per generation, and we focus on the infinite sites limit where . The mutant and wildtype alleles at each locus are denoted by A/a and B/b, respectively. We assume that mutations at these loci reduce the fitness of wildtype individuals by an amount sA and sB, respectively, while the fitness of the double mutant is reduced by . The parameter ϵ allows us to account for epistatic interactions between the two mutations, while the additive limit is recovered when ϵ = 0. Since we envision eventual applications to bacteria, we will primarily focus on haploid genomes where we can neglect the further complications of dominance and ploidy. However, our main results will also apply to diploid organisms when mutations are semi-dominant (h = 1/2).
We assume that the two loci undergo recombination at rate R per individual per generation, producing double-mutant combinations from single mutants, and vice versa. These recombination events could be implemented through a variety of mechanisms, including crossover recombination, gene conversion, and homologous recombination of horizontally transferred DNA. In the context of our two-locus model, the differences between these mechanisms can be entirely absorbed in the definition of R, and will primarily influence how R scales as a function of the coordinate distance between the two loci. In simple cases, the scaling at short distances can often be captured by the linear relationship, , where r is a measure of the recombination rate per base pair. However, all of our results will be independent of the functional form of , provided that the distances are expressed in units of map length (R). We will revisit this point in more detail when we discuss applications to genomic data below.
These assumptions yield a standard two-locus model for the population frequencies of the four possible combinations (or haplotypes), fab, fAb, faB, and fAB, as well as the corresponding mutation (or allele) frequencies, and . In the diffusion limit (Ewens 2004), this model can be expressed as a coupled system of nonlinear stochastic differential equations,
| (3a) |
| (3b) |
| (3c) |
| (3d) |
where is the mean fitness reduction within the population,
| (3e) |
is the standard coefficient of LD, and are a collection of Brownian noise terms with a covariance structure that depends on (Good and Desai 2013). This Langevin formulation is formally equivalent to the diffusion limit of population genetics, which is more commonly expressed using the Fokker–Planck equation for the probability density, (Ewens 2004). In this case, we will see that the Langevin notation in Equation (3) will be slightly more convenient for our analytical calculations below. To streamline notation, we have also assumed that forward and reverse mutations occur at the same rate μ for both sites—this will not turn out to be a crucial distinction, since the mutation rates will largely cancel out when we focus on the infinite sites limit ().
Following previous work, our analysis will focus on measures of LD that are derived from different moments of D, fA, and fB. For example, the weighted average in Equation (2) is equivalent to the ratio of expectations,
| (4) |
where the angle brackets denote the expectation . This ratio of expectations is traditionally denoted by the symbol (Ohta and Kimura 1971). This quantity has the convenient property that it is independent of the mutation rate μ in the limit that , which eliminates the dependence on one of the parameters. In other words, primarily measures properties of the segregating mutations, rather than the target size for those mutations to occur. Here, we generalize this definition of to consider a family of weighted averages of the form
| (5) |
where f0 is a characteristic frequency scale. This is equivalent to choosing a weighting function,
| (6) |
in the weighted expectation , where the constant of proportionality is again chosen such that . The additional exponential factors in this weighting term act like a smeared out version of a step function, preferentially excluding contributions from mutations with frequencies much larger than f0. By scanning over different values of f0, this weighted version of allows us to quantify how LD varies over different frequency scales. This weighting scheme is reminiscent of the frequency thresholds that have previously been employed in empirical and computational studies of LD. From a qualitative perspective, the precise shape of the weighting function will turn out to be relatively unimportant—we argue below that any sufficiently sharp transition will produce qualitatively similar behavior for . However, the exponential function will turn out to have some particularly convenient properties that will be useful for our analytical calculations below.
In addition to , it will also be useful to consider more general weighted moments of D defined by
| (7) |
These moments will also be independent of μ in the infinite sites limit (), so that they also capture properties of the segregating mutations. We will be particularly interested in the k = 1 moment, which measures the degree to which mutations are in coupling linkage (AB/ab haplotypes) vs. repulsion linkage (Ab/aB haplotypes), as well as the k = 4 moment, which can be combined with to quantify fluctuations in D2.
Despite the simplicity of the two locus model in Equation (3), the resulting patterns of LD have been difficult to characterize theoretically. As in many population genetic problems, the major hurdles arise from nonlinearities in the , D, and terms in the stochastic differential equations, which typically require numerical approaches to make further progress. However, dramatic simplifications arise if we restrict our attention to frequency scales . In this case, the exponential weights in Equation (7) will be vanishingly small except in cases where fAB, , such that the vast majority of the population is comprised of wildtype individuals. Applying this approximation to the two-locus model in Equation (3), we obtain a nearly linear system of stochastic differential equations for the three mutant haplotypes,
| (8a) |
| (8b) |
| (8c) |
where the are independent Brownian noise terms with mean zero and variance one (Gardiner 1985). Note that there is some subtlety involved in this approximation, since our weighting scheme only places limits on the haplotype frequencies at the time of observation. Equation (8) requires the stronger assumption that for all previous times as well. This distinction will become important in our analysis below. When the approximations in Equation (8) hold, the only remaining nonlinearity enters through the term in D(t). This term is crucial for allowing double mutants to be produced from single mutants via recombination. However, in many cases of interest, the contribution from this term will turn out to be small, either because R itself is sufficiently small, or because D(t) is small (e.g. for sufficiently large R). This suggests that in many cases, we may be able to treat the nonlinearity in D(t) as a perturbative correction to the otherwise linear dynamics in Equation (8). Extensive theory has been developed for analyzing linear stochastic differential equations of this form, ranging from powerful heuristic approaches to exact analytical results (Desai and Fisher 2007; Fisher 2007; Weissman et al. 2009, 2010; Good 2016; Cvijović et al. 2018). The goal of the following sections is to flesh out this basic intuition and show how it can be used to obtain predictions for LD statistics like . We will begin by presenting a heuristic analysis of the problem, which will allow us to identify the key timescales and dynamical processes involved, and will be useful for building intuition for the formal analysis that follows. We will conclude by discussing potential applications of these results in the context of genomic data.
Heuristic analysis
We begin by presenting a heuristic analysis of the two-locus model, which focuses on the underlying lineage dynamics that contribute to LD statistics like . Roughly speaking, this heuristic analysis will be accurate to leading order in the logarithms of various quantities (e.g. mutation frequencies, recombination rates), while providing a more mechanistic picture of the underlying lineage dynamics that are involved. Readers who prefer a more formal treatment may find it useful to start with the Formal Analysis section below. Our heuristic approach is similar to the one developed by Weissman et al. (2010) to study the process of fitness valley crossing in sexual populations. A key difference in this work is that we are now more interested in understanding the steady-state frequency distributions of new mutations, rather than the transient process of valley crossing.
Single-locus dynamics
Before considering the full two-locus problem, it will be useful to briefly review the evolutionary dynamics that arise at a single genetic locus. We will focus on the infinite sites limit () where the population is almost always composed of wildtype individuals, and new mutations are introduced into the population at a total rate per generation. The vast majority of these lineages will drift to extinction without ever leaving more than a few descendants in the population. However, a lucky minority will survive for sufficiently long times that they can grow to reach observable frequencies. The dynamics of this process will strongly depend on the fitness cost s of the mutation. We consider both neutral (s = 0) and deleterious (s > 0) mutations below.
Neutral mutations
When s = 0, the frequency of a mutant lineage is only influenced by genetic drift. These dynamics take a particularly simple form when the mutation is sufficiently rare [], since the sublineages founded by different mutant individuals will evolve independently of each other. With probability , these individual mutant lineages will survive for at least generations and reach a characteristic size (Fisher 2007). More detailed calculations (Kendall 1948) show that the frequency of the surviving lineage is exponentially distributed around this characteristic size, so that
| (9) |
Most of this distribution is concentrated within an order of magnitude of the mean (), consistent with our notion of a “typical” value. However, there is also a small probability () that a surviving mutation will be observed at much lower frequencies (). This will become important in our discussion below.
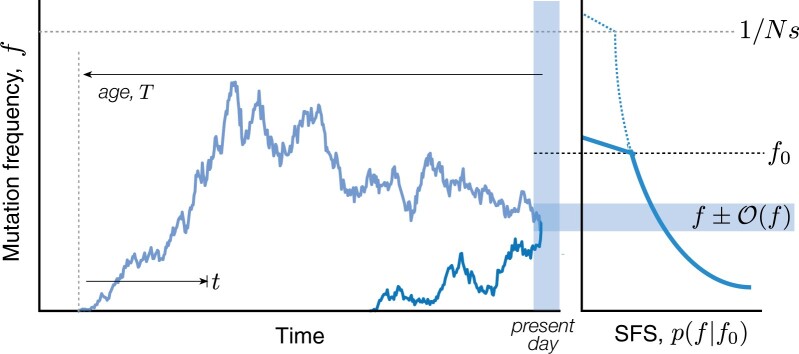
Essentially all of the results in this work will follow from repeated applications of these basic temporal dynamics. For example, the total probability of observing a mutation with a present-day frequency f can be calculated by summing Equation (9) over the possible times that the mutation could have originated in the past (Fig. 1). This allows us to recover the familiar neutral SFS,
| (10) |
Fig. 1.
Schematic illustration of mutation trajectories that contribute to the SFS. Left: Mutations arise at different times and drift to their present-day frequencies (shaded region). Dark and light blue lines show examples of present-day mutations with upward and downward trajectories, respectively. In both cases, deleterious mutations are prevented from growing much larger than the drift barrier, (gray dashed line). Right: The SFS is the sum of the probabilities of all mutation trajectories with a present-day frequency f. Each mutation can be characterized by its age T and historical trajectory f(t), with . When the frequency spectrum is dominated by upward trajectories, the effects of negative selection are similar to imposing a present-day frequency threshold f0 (black dashed line).
We can impose a maximum frequency threshold by inserting a unit step function, , so that
| (11) |
In contrast to the transient distribution in Equation (9)—which was concentrated around a typical frequency —the equilibrium SFS in Equation (11) is evenly distributed on a log scale, with equal contributions from all orders of magnitude between 0 and f0. Since there are many more orders of magnitude near 0 than near f0, this implies that most of the probability will be concentrated at extremely low frequencies—so much so that the distribution in Equation (11) is not even normalizable. However, these extremely rare mutations will only have a negligible influence on general moments of the form
| (12) |
which are dominated by mutations with frequencies of order when . Similarly, the total probability of observing a mutation with a frequency of order has a constant value,
| (13) |
where the integral denotes a sum over frequencies in the range . These integrated probabilities are insensitive to the divergence at low frequencies, and will play a crucial role in our analysis below.
Historical trajectories of mutations
Our LD analysis will also require information about the historical trajectories of mutations that are sampled at a given frequency in the present. We can analyze these trajectories using the same set of tools that we used to derive the SFS above. For example, the sum in Equation (10) suggests that the age T of a mutation with present-day frequency f (Fig. 1) will follow an inverse exponential distribution,
| (14) |
which has a peak at and a broad power law tail for . These different scallings suggest that it will be useful to consider the trajectories of mutations with ages and , respectively.
Mutations in the first category () will tend to have “upward trajectories” (Fig. 1) similar to the unconstrained dynamics in Equation (9). We can see this by considering the frequency of the mutation at some intermediate timepoint t (Fig. 1) and expressing the present-day frequency as a sum over the individual lineages that were founded at time t. The conditional distribution of f(t) then follows from Bayes rule,
| (15) |
where is the prior probability of transitioning from to f(t), and is the present-day frequency of the ith intermediate lineage. From our discussion above, each of these intermediate lineages has a probability of surviving until time T and growing to size . When , many independent lineages will survive to contribute to the present-day frequency , and f(t) will remain close to f by the central limit theorem. On the other hand, when , the typical size of a single surviving lineage () will already be comparable to the total present-day frequency (). This implies that the most likely way for the entire mutation to transition from f(t) to is for all but one of the intermediate lineages to go extinct. The total probability of this coarse-grained trajectory can therefore be approximated by
| (16) |
which reduces to
| (17) |
in the limit that . This conditional distribution has a typical frequency of order , similar to the unconditioned distribution in Equation (9). However, the historical trajectories have a much smaller probability of drifting to anomalously low frequencies at the intermediate timepoints (), since they have been conditioned on reaching much higher frequencies in the present ().
In contrast to these upward trajectories, older mutations () will tend to have “downward trajectories” similar to the one depicted in Fig. 1 (light blue line). These downward trajectories can be quantified using a similar lineage-based picture as above. The major difference is that there is now a broad range of intermediate timepoints () where the size of a single surviving lineage [] is much larger than the final frequency . In order to transition from f(t) to f, the sole surviving lineage must now also drift to an anomalously low frequency by the time of observation, while simultaneously avoiding extinction. Equation (9) shows that the probability of such an excursion is of order , so that the total probability of transitioning from f(t) to f is given by
| (18) |
The conditional distribution of f(t) then reduces to
| (19) |
which is valid in the limit that T and are both much larger than .
In contrast to the upward trajectories in Equation (17), the typical frequencies in Equation (19) now have a nonmonotonic dependence on the intermediate timepoint t,
| (20) |
These historical frequencies attain their maximum value near the middle of the trajectory () and decrease toward the present day. This motivates our “downward trajectory” naming scheme, since these older mutations will typically be decreasing in frequency at the time that they are sampled (Fig. 1). When , these historical frequencies can be much larger than any present-day frequency threshold f0, and can even reach a point where the rare mutation assumption starts to break down []. Fortunately, Equation (10) shows that these ancient mutations will have a negligible influence on the SFS, which is dominated by contributions from upward trajectories with .
However, downward trajectories can still play an important role in other evolutionary quantities, even when they provide a negligible contribution to the SFS itself. One of the simplest examples is the average age of a mutation with a present-day frequency f. Although the median age in Equation (14) occurs for —which provides the dominant contribution to the SFS—the tail in Equation (14) causes the average age to be dominated by increasingly older mutations with . This cannot continue indefinitely, however, since the historical sizes of these mutations will eventually become large enough that our rare mutation assumption will break down. For example, ancient mutations that drift to frequencies will eventually be more likely to fix than to drift back down to by the time of observation. We can account for this behavior in a crude way by truncating the integral in Equation (10) at a maximum age , which corresponds to a maximum historical frequency . This yields a finite value for the average age of a mutation as a function of its present-day frequency,
| (21) |
which matches the well-known result from Kimura and Ohta (1973) in the limit that . This same cutoff approximation will play a crucial role in analyzing the dynamics of LD below.
Deleterious mutations
Similar considerations apply for deleterious mutations (s > 0), except that natural selection will prevent them from growing much larger than a critical frequency, , above which natural selection starts to dominate over genetic drift (Fisher 2007; Good 2016). Conversely, genetic drift will continue to dominate over natural selection for frequencies , and the dynamics will resemble those derived for neutral mutations above. This suggests that we can approximate the deleterious SFS by adding an additional step function to the neutral result,
| (22) |
which enforces the condition that mutations will rarely be found above the “drift barrier,” .
The net effect of this new threshold will depend on the compound parameter , which captures the relative strength of selection on timescales of order . When , deleterious mutations are always sampled in their effectively neutral phase, and the SFS reduces to the neutral version in Equation (11). On the other hand, when , the frequency spectrum maintains a similar shape, but with an effective frequency threshold now set by the drift barrier . This implies that averages like will be dominated by frequencies of order , rather than the nominal frequency threshold f0.
To streamline notation, it will be useful to summarize this behavior by defining an effective fitness cost,
| (23) |
such that Equation (22) can be written in the compact form
| (24) |
or alternatively,
| (25) |
where the dependence on the underlying fitness cost s is completely encapsulated in the definition of . This notation emphasizes that the present-day frequencies of neutral and deleterious mutations will be essentially identical to each other, given an appropriate choice of .
However, this correspondence between neutral and deleterious mutations starts to break down when we consider the historical trajectories of these mutations at previous timepoints. The key difference is that natural selection will prevent deleterious mutations from growing much larger than at any point during their lifetime, and not only at the point of observation (Fig. 1). This distinction has a negligible impact on the upward trajectories that dominate , since their maximum sizes are by definition bounded by the present-day frequency f. However, the historical action of natural selection has a much stronger impact on the downward trajectories in Fig. 1, since it limits their peak frequencies to a maximum size of order . This frequency threshold implies a corresponding bound on the maximum age of a deleterious mutation of order , which alters the scaling of quantities like the average age of a rare mutation,
| (26) |
These differences will play an important role when we consider the dynamics of LD below.
Two-locus dynamics
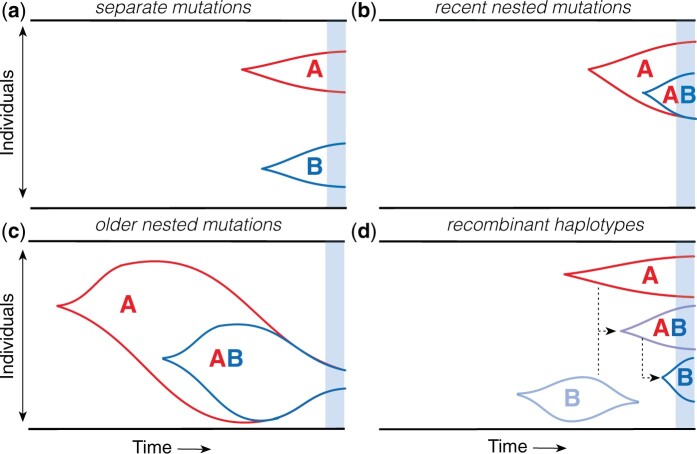
We are now in a position to analyze the joint behavior of a pair of genetic loci, which will allow us to develop a similar heuristic picture for the dynamics of LD. To do so, it will be useful to first consider the dynamics in the absence of recombination, when mutations at the two loci evolve in a completely asexual manner. LD is defined when both sites harbor segregating mutations at the same time (). In the weak mutation limit (), these variants must trace back to a single pair of mutation events at each of the two sites. There are only two different ways that these mutations can occur:
Separate mutations
In the simplest scenario, a mutation will first occur in the wildtype background at one of the two sites, and then a second mutation will arise in a different wildtype background while the first mutation is still segregating in the population (Fig. 2a). We refer to this scenario as the separate mutations case, since it involves only single-mutant haplotypes (), while the double mutant is absent (fAB = 0). At low mutation frequencies (), these single-mutant haplotypes will be approximately independent of each other, and can therefore be predicted from the single-locus dynamics described above. Equation (25) then shows that with probability
| (27a) |
the four haplotype frequencies will reach typical sizes of order
| (27b) |
where and are defined as in Equation (23) above. This coarse-grained sampling distribution allows us to quickly estimate the contribution to various moments, for example,
| (28) |
Fig. 2.
Schematic of different lineage dynamics that contribute to LD. a) Separate mutations: A and B mutations arise on independent wildtype backgrounds and are both still segregating at the time of observation (blue region). b) Recent nested mutations: a double mutant (AB) is produced by a single-mutant background (A) in the recent past, and both haplotypes are still segregating at the time of observation. c) Older nested mutations: a double mutant is produced by a larger single-mutant lineage in the distant past, but drifts back down to lower frequencies by the time of observation. d) Recombination produces double-mutant lineages from single-mutant lineages, and vice versa.
Nested mutations
In the alternative scenario, a mutation at the second locus can be produced by the original mutant lineage rather than the wildtype background (Fig. 2, b and c). We refer to this scenario as the nested mutations case, since it produces double-mutant haplotypes () without any single mutants at the other genetic locus (faB = 0). At low mutation frequencies (), we expect that these nested mutations will occur far less frequently than separate mutations, since the mutant lineage will produce mutations at a much lower rate . To understand these contributions, it is necessary to integrate over the historical frequencies of the Ab haplotype () at the various historical times T that the second mutation could have occurred. We can write this integral in the general form,
| (29) |
where denotes the equilibrium frequency distribution at the first site, and denotes the probability density of transitioning from the historical frequency to the present-day frequency fi in time T. Note that since represents the historical frequency of the Ab haplotype, it is not directly constrained by the present-day frequency threshold, , but is instead constrained indirectly through the dynamics in the term. This distinction will become important below.
To gain a more intuitive understanding of Equation (29), it will be useful to further distinguish between the contributions of relatively recent nested mutations () and those that arose in the distant past (), where is the double-mutant analogue of and in Equation (27b). For simplicity, we will restrict our attention to regimes where , such that the maximum lifetimes of the single mutants () are at least as long as the double mutants. This regime includes the traditional additive case (ϵ = 0), as well as cases with strong synergistic () and moderately antagonistic () epistasis, and will therefore capture much of the interesting behavior.
Recent nested mutations
When the age of the double mutant is of order , the characteristic dynamics will be dominated by upward trajectories, in which the double mutants reach their maximum frequency near the point of observation (Fig. 2b). Since , the historical frequency of the Ab haplotype cannot be much larger than , since it would otherwise be unlikely to drift back down to this threshold by the time of observation. This suggests that recent nested mutations will occur with a total probability
| (30a) |
and that the typical haplotype frequencies will be of order
| (30b) |
An analogous distribution exists for recent nested mutations that arise on an aB background. As expected, the total probability of these events is much smaller than the separate mutations case. However, the smaller probability is balanced by the larger typical values of that occur in this case, such that the total contribution to the corresponding moments,
| (31) |
is often of equal or larger magnitude than the separate mutations case in Equation (28) above.
Older nested mutations
In contrast, the characteristic dynamics of older mutations () will be dominated by downward trajectories that previously reached much higher frequencies in the distant past (Fig. 2c). We can analyze these trajectories using the same techniques that we used to study the average ages of neutral and deleterious mutations above. To streamline our notation, it will be useful to introduce a timescale for the maximum possible age of a double mutant,
| (32) |
which corresponds to a maximum historical size of order . This timescale depends on the true fitness cost sAB (rather than ) because the historical frequencies are not directly constrained by the present-day frequency threshold. When , this maximum age is located in the recent past (), which implies that there is a negligible chance of producing older nested mutations. In contrast, when , there will be a large range of timescales () where older nested mutations can arise.
These older double mutants will have a much smaller chance of surviving to the present while also maintaining a present-day frequency less than :
| (33) |
Similar constraints apply to the single-mutant trajectories that generate these double-mutant haplotypes. If the historical frequency is much larger than , the mutation is unlikely to drift back down to its present-day frequency threshold () by the time of observation. On the other hand, historical frequencies much smaller than are highly likely to go extinct before the present day (Fig. 2c), and will automatically satisfy the frequency threshold at the time of sampling. This suggests that historical frequencies will provide the dominant contribution to the total probability of this scenario. Combining these observations, we conclude that older nested mutations occur with a total probability
| (34a) |
and that the typical haplotype frequencies will be of order
| (34b) |
Note that the total probability of these events is still much smaller than the probability of arising on separate genetic backgrounds. However, the logarithmic factor ensures that this probability will be larger than the contribution from recent nested mutations whenever .
Estimating linkage disequilibrium
We now have all the ingredients necessary to calculate frequency-resolved LD statistics like in Equation (7). For the denominator, we note that the magnitude of is roughly the same regardless of whether the mutations occur on nested or separate backgrounds. However, since the separate backgrounds case is much more likely, this scenario will provide the dominant contribution to the average in the denominator, so that
| (35) |
In contrast, the numerator of will usually be dominated by the contributions from nested mutations, since the double-mutant frequency enters as a lower power in the LD coefficient . The precise form of this contribution will depend on the typical ages of the nested mutations, as described by Equations (27) and (30). By combining these results with the denominator term in Equation (35), we find that
| (36) |
which strongly depends on the magnitude of the scaled selection strength . In the absence of epistasis (ϵ = 0), Equation (36) shows that strongly deleterious mutations () will generally have lower LD than neutral mutations with comparable present-day frequencies () (Fig. 3). Equation (36) shows that the direction of this effect is similar to the effects of synergistic epistasis (). These differences between neutral and deleterious mutations are qualitatively different from the behavior we observed for the SFS in Equation (24), where fitness costs could be absorbed by a simple present-day frequency threshold (Fig. 1). Our lineage-based picture shows that these differences in LD primarily reflect the contributions of older nested mutations (Fig. 2c), which are sensitive to the effects of natural selection long before the time of sampling.
Fig. 3.
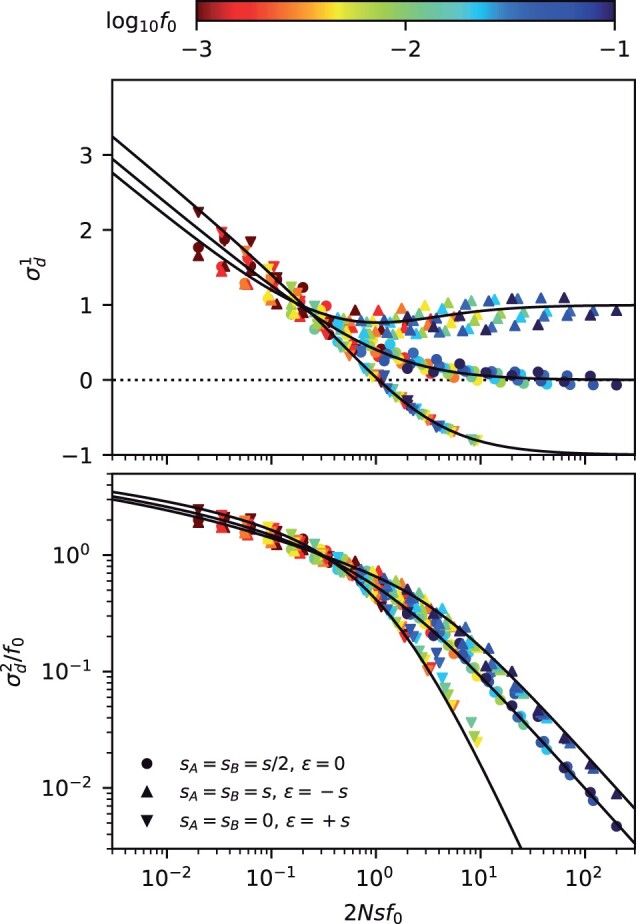
Frequency-resolved LD between deleterious mutations as a function of the scaled fitness cost of the double mutant. Top: the signed LD moment, , in Equation (7) is depicted for pairs of nonrecombining loci with additive (ϵ = 0), antagonistic (ϵ), and synergistic (ϵ) epistasis, which were chosen to have the same total cost for the double mutant (). Symbols denote the results of forward-time simulations (Appendix A) across a range of parameters with , and each symbol is colored by the corresponding value of f0. The solid lines shows the theoretical prediction from Equation (C8). Bottom: an analogous figure for the squared LD moment, , where solid lines show the theoretical predictions from Equation (C9). The “data collapse” in both panels indicates that frequency-weighted LD is primarily determined by the compound parameters and Nϵf0. Weak scaled fitness costs () lead to an excess of coupling linkage (), which qualitatively resembles the effects of antagonistic epistasis (ϵ).
An analogous argument can be used to calculate the first moment . We find that
| (37) |
which closely parallels the three regimes for in Equation (36). Once again, we observe a dramatic difference between neutral and deleterious mutations that cannot be captured by an effective frequency threshold . In this case, we see that the logarithmic behavior in the neutral limit is associated with an excess of coupling linkage (), which qualitatively resembles the effects of antagonistic epistasis (). These results emphasize the importance of older nested mutations in shaping contemporary patterns of LD among tightly linked loci.
Incorporating recombination
We can now ask how small amounts of recombination start to alter the basic picture described above. Recombination cannot change the rates at which separate or nested mutations are initially produced, but it can have a dramatic impact on their haplotype dynamics after they arise.
For example, in the nested mutations case, recombination will start to break up the AB haplotype at a per capita rate R, creating recombinant Ab and aB offspring (Fig. 2d). From the perspective of the fAB lineage, this loss of individuals through recombination will resemble an effective fitness cost, which can be absorbed in an effective selection coefficient for the double mutant,
| (38) |
When , this loss of individuals through recombination will have a negligible impact on fAB, but it will become the primary limiting factor on the lineage size when . For sufficiently low rates of recombination (evaluated self-consistently below), the recombinant offspring of AB lineages are unlikely to reach high enough frequencies to influence the LD coefficient . This suggests that we can approximate the future dynamics of the fAB lineage using the results for the asexual case above, but with Equation (38) replacing sAB.
Similarly, in the separate mutations scenario, recombination events between Ab and aB haplotypes will create recombinant AB haplotypes at a total rate per generation. In this case, the loss of individuals due to recombination is significantly smaller than for the AB lineages above, since the per capita rates of recombination for the single-mutant lineages are suppressed by additional factors of faB or fAb. However, these rare recombination events can still have a large effect on LD if they happen to seed a lucky AB lineage that drifts to observable frequencies. We can calculate the total probability of these events using a generalization of the approach that we used for nested mutations above.
In this recombinant scenario, the dominant contributions will come from relatively recent recombination events (), which reach their maximum typical size () near the time of observation (Fig. 2d). As above, the historical frequency of the Ab and aB haplotypes cannot be much larger than and at this timepoint, otherwise they would be unlikely to drift back down to these thresholds by the time of observation. This suggests that recombinant double mutant will occur with a total probability
| (39a) |
and that the haplotype frequencies will be of order
| (39b) |
Similar to the nested mutations case above, the total probability of the recombinant scenario is much smaller than the probability of the separate mutations case. However, as long as is much larger than —which will be true for all but the highest recombination rates—the smaller probability of this scenario will be counterbalanced by its significantly larger values of . By combining these results with our previous formulae for nested and separate mutations above, we can obtain an analogous set of predictions for the frequency-resolved LD statistics,
| (40a) |
and
| (40b) |
which are valid in the presence of recombination. For the special case of neutral mutations (), these results take on a particularly simple form:
| (41a) |
and
| (41b) |
These expressions constitute frequency-resolved analogues of the LD decay curves that are used to estimate recombination rates in genomic data (Fig. 4). In this case, we see that the behavior of the LD curves strongly depends on the compound parameter . When , we recover the well-known scaling of Equation (2), in which neither coupling or repulsion linkage is favored () (Ohta and Kimura 1971; Song and Song 2007). However, when , the frequency-weighted version of no longer saturates at a constant value, as in Equation (2), but instead displays a new logarithmic dependence similar to asexual case above. These quasi-asexual dynamics are accompanied by high levels of coupling linkage (), reflecting the important contributions of older nested mutations. Interestingly, our results show that the transition to this mutation-dominated regime can occur even for nominally high rates of recombination (), provided that the frequency scale f0 is chosen to be sufficiently small (). This highlights the utility of frequency-resolved LD statistics for probing the underlying timescales of recombination process—a topic that we will explore in more detail below.
Fig. 4.
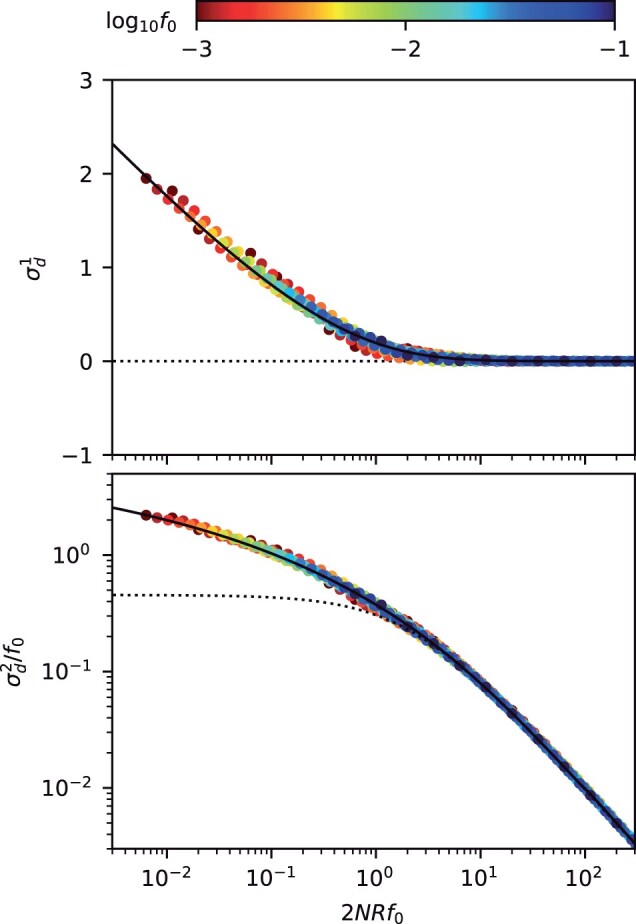
Frequency-resolved LD between neutral mutations as a function of the scaled recombination rate. An analogous version of Fig. 3, showing the first (top) and second (bottom) LD moments in Equation (7) for pairs of neutral mutations with a range of recombination rates, . As above, symbols denote the results of forward time simulations, and solid lines denote the theoretical predictions from Equations (D21) (top) and (D22) (bottom). Dashed lines show the classical predictions for the limit (Ohta and Kimura 1971). The “data collapse” in both panels indicates that frequency-weighted LD is primarily determined by compound parameter . Low scaled recombination rates () lead to an excess of coupling linkage (), which qualitatively resembles the effects of antagonistic epistasis (ϵ).
Transition to quasi-linkage equilibrium (QLE)
The results above assumed that double mutants provide the dominant contribution to when they reach their maximum typical frequencies. This will be a good approximation in the recombinant scenario provided that
| (42) |
which reduces to the simpler condition
| (43) |
for a pair of neutral mutations. At low frequencies (), this condition will generally be satisfied even for large recombination rates (), which are located deep into the recombination-dominated regions of the LD curves in Equation (41). This suggests that these previous expressions will be valid across a broad parameter range, which is sufficient to capture the transition from mutation-dominated to recombination-dominated behavior (). Nevertheless, for sites that are separated by sufficiently large coordinate distances , recombination rates may eventually grow large enough that , where our previous analysis starts to break down.
Fortunately, we can obtain a relatively complete picture of this transition by taking advantage of the large gap between and that emerges when , and restricting our attention to cases where . In this limit, the typical lifetimes of recombinant double mutants () are much shorter than the lifetimes of the single-mutant lineages that produce them (). This suggests that fAb and faB will be effectively “frozen” throughout the lifetime of an individual recombinant lineage, and that the production rate of these lineages will resemble a mutation process with an overall rate . When , recombinant fAB lineages will be produced only rarely, and can occasionally fluctuate to frequencies of order before they go extinct. This is sufficient to recover the familiar scaling,
| (44) |
that we observed in Equation (41).
On the other hand, when , many recombinant lineages will be produced every generation, and the total double-mutant frequency fAB will reach sizes much larger than . In this case, the double-mutant frequency will grow to the point where the production rate of new recombinants () is exactly balanced by their loss due to further recombination with the wildtype population (). This occurs when
| (45) |
which is equivalent to the condition that the A and B mutations are in linkage equilibrium (). In this way, we see that the regime can be identified with the traditional QLE regime of multilocus population genetics, in which the haplotype frequencies remain close to the typical values expected under linkage equilibrium. Genetic drift will still drive fluctuations around the average value in Equation (45), with a magnitude that is inversely proportional to the typical number of recombinant lineages that contribute to the total frequency:
| (46) |
Interestingly, this behavior leads to identical predictions for the two lowest order LD statistics, and , that we obtained in the limit above. However, as we will demonstrate below, the differences between these two regimes will become apparent when considering higher moments (or other properties of the joint haplotype distribution), due to the dramatic differences in the typical fluctuations of fAB. In this way, we see that low frequency mutations give rise to an entirely new regime of behavior (), in which previous notions of quasi-asexuality or quasi-linkage equilibrium do not apply. We will refer to this regime as the clonal recombinant regime, which reflects the fact that double mutants are primarily caused by rare recombinant lineages that drift to observable frequencies one-by-one. We will explore the consequences of these dynamics in more detail below.
Formal analysis
We now turn to a formal derivation of the heuristic results presented above. To implement our conditioning scheme for the maximum frequencies of the two mutations (), we will focus on the joint generating function of the unconditioned process,
| (47) |
such that the weighted moments follow from the identity
| (48) |
with . We can also define an effective conditional distribution using a similar weighting scheme,
| (49) |
such that the weighted moments can also be obtained directly from derivatives of . Thus, for this special choice of weighting function, the conditional moments can be straightforwardly calculated from solutions of the unconditioned generating function, . By differentiating Equation (47) with respect to time and applying the stochastic dynamics in Equation (8), we find that satisfies the partial differential equation,
| (50) |
with the initial condition , where we have defined a collection of scaled variables,
| (51) |
Here we have used the conventional symbols θ, ρ, and γi to define scaled rates of mutation, recombination, and selection, respectively. Note that in the latter two cases, we have defined these scaled variables to include an additional factor of f0 in order to match the key control parameters that we obtained in our heuristic analysis above. Motivated by these results, we will also restrict our attention to scenarios where , but where the scaled parameters ρ and γ can be either large or small compared to one. This will ensure that the maximum historical frequencies remain sufficiently small that the branching process approximation remains valid, while still capturing the full range of the qualitative behavior identified above.
Perturbation expansion for small f0
The partial differential equation in Equation (50) is difficult to solve in the general case. To make progress, we will focus on a perturbation expansion in the limit that θ and f0 are both small compared to one, using the series ansatz
| (52) |
with . The first few terms in this expansion are calculated in Appendix B. The first order contributions are simply a product of the corresponding single locus distributions,
| (53a) |
where we have defined
| (53b) |
The conditional distribution in Equation (49) then follows as
| (54) |
This distribution has a well-defined value even when , which shows how the frequency weighting in Equation (49) can eliminate the well-known divergence of the neutral branching process when . We also see that the resulting distributions are equivalent to the unconditioned frequency spectrum of a deleterious mutation with an effective selection coefficient , which has a well-known form,
| (55) |
This constitutes a quantitative version of the heuristic result in Equation (22), and confirms our previous intuition that the deleterious SFS can be mimicked by neutral mutations with an appropriate choice of f0.
By definition, these first order solutions do not provide any information about LD between the two loci, which only starts to enter at order . A more detailed calculation in Appendix B shows that these next order contributions can be written in the form
| (56a) |
where is a function that is independent of z, is a solution to the characteristic curve,
| (56b) |
with the initial condition , and and are defined by
| (57) |
Using this formal solution, the weighted moments then follow as
| (58) |
and
| (59a) |
where we have defined the functions
| (59b) |
and
| (59c) |
Substituting these moments into the definition of , we see that the leading order solution collapses onto a lower dimensional manifold,
| (60a) |
where is a dimensionless function that depends only on the scaled parameters γi and ρ:
| (60b) |
This solution is independent of the mutation rate, as expected, and depends on the frequency scale f0 only implicitly through the definitions of Σd, γi, and ρ. This is already an important constraint, as it implies that scenarios with different underlying values of f0, si, and r, but similar values of the scaled parameters γi and ρ, must necessarily have similar values of . Closed form expressions for are more difficult to obtain in the general case, due to the difficulty in solving the differential equation for for arbitrary parameter combinations. However, further analytical progress can still be made by examining the behavior of this equation in certain limits.
Nonrecombining loci
The simplest behavior occurs in the absence of recombination (ρ = 0), when the characteristic curve has an exact solution,
| (61) |
Substituting this expression into Equations (59c) and (60), we find that can be expressed as a definite integral,
| (62) |
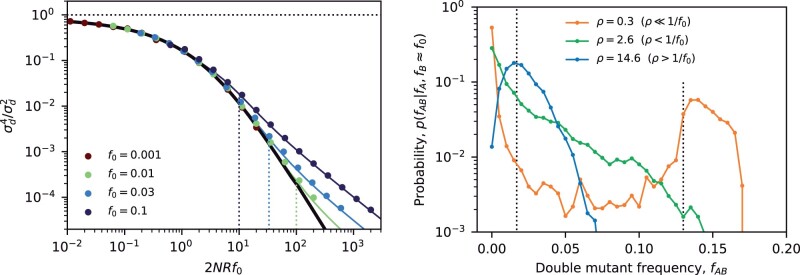
which is straightforward to evaluate numerically. Analogous integral expressions can be derived for the other moments, , as well as for the full conditional distribution, (see Appendix C). Asymptotic solutions of these integrals for small and large γAB show that they have same limiting behavior that we identified in our heuristic analysis above, while the numerical solutions accurately capture the quantitative behavior across the full range of intermediate parameter values (Fig. 3).
Neutral loci
Another important limit occurs for neutral mutations (), where the manifold in Equation (60) reduces to a single parameter curve, . This is already a useful prediction, since it implies that changes in R can be mimicked by changes in f0, and vice versa. However, the characteristic curve in Equation (56b) is now more difficult to solve than in the asexual case, due to the presence of the time-dependent terms, and . Physically, these terms represent the additional Ab and aB lineages that are created when the AB haplotype recombines with the wildtype background. Fortunately, an exact solution can still be obtained in this case using special functions, which is derived in Appendix D. After substituting this solution into Equation (59), we find that the scaling function can again be expressed as a definite integral,
| (63) |
where we have defined the function
| (64) |
and is the standard exponential integral function,
| (65) |
Analogous integral expressions for the moment and are presented in Appendix D. Once again, asymptotic evaluation of these integrals recovers the same and scaling observed in our earlier heuristic analysis for large and small ρ, respectively, while the numerical solutions accurately capture the quantitative behavior across the full range of ρ (Fig. 4). This full solution is often quite useful in practice, since the convergence to the asymptotic limits can be rather slow. In particular, we see that the corrections to the small ρ limit scale as , which implies that extremely small values of ρ (as low as ) are required to achieve good numerical accuracy. This leaves a broad intermediate regime () in which Equation (63) is critical for enabling quantitative comparisons with data.
Strong selection or recombination
The final limit we will consider is one in which at least one of scaled selection coefficients (γi) or the scaled recombination rate (ρ) is large compared to one. Physically, this approximation means that genetic drift is weak compared to the forces of selection and/or recombination. In this limit, it is possible to solve for the characteristic curve in Equation (56b) using a separation of timescales approach, treating the term as a perturbative correction. This perturbation expansion is outlined in Appendix E. We find that the first two moments are given by
| (66) |
which matches the asymptotic behavior in the nonrecombining (ρ = 0) and neutral () limits above. By comparing this result with the neutral version in Equation (63), we observe a quantitative confirmation of our heuristic prediction that LD is lower among deleterious mutations than among neutral mutations with identical present-day frequencies (). The most pronounced difference occurs for the first moment , where frequency-matched neutral mutations display an excess of coupling linkage () compared to the deleterious case (), which can be observed for recombination rates as large as (Fig. 5).
Fig. 5.
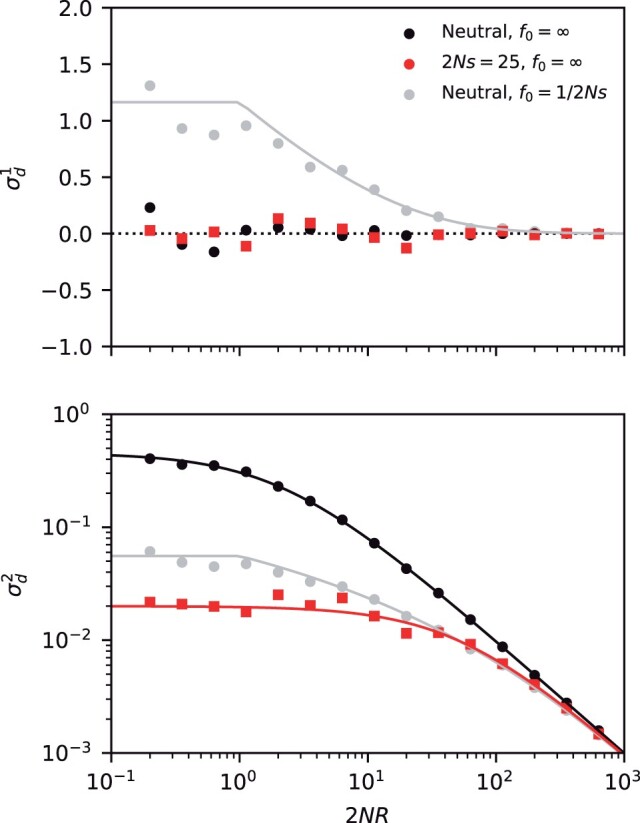
LD contains residual signatures of purifying selection after controlling for mutation frequencies. The top and bottom panels compare the first (top) and second (bottom) LD moments for a pair of neutral (black) and strongly deleterious mutations (red) across a range of recombination rates. Symbols denote the results of forward-time simulations, and the solid lines denote the theoretical predictions from Equation (2) (black) and Equation (66) (red). The gray symbols show frequency-weighted neutral mutations with the same present-day frequency spectrum as the deleterious mutations (). For small recombination rates, the neutral control group displays an excess of coupling linkage () driven by ancient nested mutations, which are suppressed in the deleterious case.
Transition to quasi-linkage equilibrium
The perturbation expansion in Equation (56) is valid to lowest order in , which means that it cannot capture the transition to the QLE regime that occurs when . Nevertheless, we can obtain an analogous set of predictions for this regime by returning to the underlying stochastic differential equations in Equation (8), and focusing on cases where and , but where is not necessarily small compared to one. In this limit, Equation (8) can be solved using a separation of timescales approach, in which fAB evolves on a fast timescale,
| (67) |
while fAb and faB are effectively fixed. These single-mutant frequencies then evolve on longer timescales according to the single-locus dynamics in Equation (54). In this approximation, the fast dynamics in Equation (67) approach an instantaneous equilibrium,
| (68) |
on a timescale of order , which is much shorter than the fluctuation timescales of fAb and faB in the limit that . This allows us to easily calculate various LD statistics from the conditional moments of Equation (68), by averaging over the single-locus distributions of fAb and faB in Equation (55). For the first few moments of , we find that
| (69) |
This confirms our heuristic result that the first two moments of are identical in the clonal recombinant and QLE regimes, while the higher moments start to diverge due to the differences in the statistical fluctuations of fAB. These differences can be observed by examining the ratio
| (70) |
which shifts from a rapid decay in the clonal recombinant regime to a shallower decay in the QLE regime, while saturating to a constant value when (Fig. 6, left).
Fig. 6.
Higher-order fluctuations reveal the transition to QLE. Left panel: an analogous version of the neutral collapse plot in Fig. 4 for the higher-order LD moment . Symbols denote the results of forward time simulations for a range of recombination rates, which are colored by the corresponding value of f0. The solid black line shows the prediction from the perturbation expansion in Equations (D22) and (D23), and the dashed lines indicate the position, , where the perturbation expansion is predicted to break down. The solid colored lines show the asymptotically matched predictions from Equation (F5), which capture the transition to the quasi-linkage equilibrium regime. Right panel: the conditional distribution of the double-mutant frequency for fixed values of the marginal mutation frequencies, . Colored lines show forward-time simulations for pairs of neutral mutations, in which the marginal frequencies of both mutations were observed in the range ; the double-mutant frequency was further downsampled to n = 200 individuals to enhance visualization. The dashed lines indicate the approximate positions of linkage equilibrium (; left) and perfect linkage (; right). Conditional distributions are shown for three different recombination rates, whose characteristic shapes illustrate the transition between the mutation-dominated (; orange), clonal recombinant (; green) and QLE (; blue) regimes.
The differences between these regimes are even easier to observe by examining the full conditional distribution of the double-mutant frequency, , at a fixed value of the marginal mutation frequencies, (Fig. 6, right). In the QLE regime, Equation (68) shows that the conditional distribution develops a peak around the linkage equilibrium value , while the clonal recombinant regime has a much broader distribution with a mode at fAB = 0 and an exponential cutoff at . These characteristic shapes are qualitatively distinct from the conditional distributions that are observed in the mutation-dominated regime (), which have a bimodal shape with one peak at fAB = 0 and a smaller peak at . This suggests that the shape of the conditional distribution might provide a particularly robust test for distinguishing between different rates of recombination. We will return to this topic in the Discussion when we discuss potential applications of our results to genomic data from bacteria.
Estimating frequency-resolved LD in finite samples
So far, our formal analysis has focused on predicting ensemble averages of various LD statistics at a single pair of genetic loci. To connect these results with empirical data, we will often want to estimate these ensemble averages in a slightly different way, by summing over many functionally similar pairs of genetic loci observed in a finite sample of n genomes. In these cases, we will not be able to observe the haplotype frequencies that enter into directly, but must instead infer them from the discrete counts, nAB, nAB, naB, and nab that are observed in our finite sample. We will assume that these haplotype counts are randomly sampled from the underlying population, so that they are multinomially distributed around the current haplotype frequencies:
| (71) |
In sufficiently large samples (), the haplotype counts will remain close to their expected values , and can be well-approximated by setting in Equation (7). However, for sufficiently low frequencies (), the additional uncertainty in fi will cause the naive estimator to be biased away from the true value of . Our heuristic results show that these low frequencies will generically dominate LD estimates—even in large samples—for sufficiently large values of NR or Nsi, or for sufficiently low choices of f0. Unbiased estimators of are therefore essential for extrapolating across the full range of frequency scales.
In this section, we will develop one particular class of estimators by generalizing an approach that we and others have previously used to estimate the unweighted version of in Equation (4) (Garud et al. 2019; Ragsdale and Gravel 2020). To extend this result to the frequency-resolved case, we will first take advantage of the fact that the multinomial distribution in Equation (71) reduces to a product of independent Poisson distributions,
| (72) |
in the limit that mutations are rare (). This joint distribution admits a general moment formula,
| (73) |
for arbitrary integers i, j, and k, and arbitrary real numbers x, y, and z. Thus, for the special choice
| (74) |
the conditional expectation reduces to
| (75) |
This motivates us to define the function,
| (76) |
whose total expectation—which now averages over sampling noise in addition to the underlying evolutionary stochasticity—satisfies the identity
| (77) |
Thus, we see that for this special choice of exponential weighting function, there is a simple relationship between the ensemble averages of haplotype frequencies and genome-wide averages over haplotype counts. Using this formula, it is a straightforward (though tedious) task to derive a corresponding set of estimators for , by expanding the fA and fB terms in Equation (7) and iteratively applying Equation (77). Expressions for the first few moments of are listed in Appendix G.
Applications to synonymous and nonsynonymous LD
LD curves are frequently calculated for pairs of synonymous or nonsynonymous mutations separated by similar coordinate distances (or ideally, by similar map lengths R). In these cases, the empirical estimators in the previous section converge to a weighted average,
| (78) |
where denotes the distribution of fitness costs of synonymous (i = S) or nonsynonymous (i = N) mutations, and denotes the corresponding distribution of epistatic interactions. In this way, any differences between the observed and curves can provide additional information about the differences in their underlying fitness costs.
To understand the consequences of the average in Equation (78), recall that our earlier analytical expressions showed that deleterious fitness costs generally lead to lower values of , where the magnitude of this effect depends on the relative values of R and f0. The additional factors that appear in the average in Equation (78) will further downweight the contributions of mutations with costs larger than . This shows that strongly deleterious mutations () will have a negligible impact in the numerator of Equation (78), as long as there is an appreciable fraction of mutations with smaller fitness costs. However, for the same reasons, these strongly deleterious mutations will also have a negligible impact on the denominator of Equation (78), which implies that they will have a negligible overall contribution to the site-averaged LD statistics and .
At the same time, we have seen that very weakly deleterious mutations () produce values that are nearly indistinguishable from neutral mutations, differing only by a slowly varying factor. These mutations contribute to the averages in and , but they cannot contribute to differences between the two quantities. Thus, in the absence of epistasis, we expect that the differences between synonymous and nonsynonymous LD will be driven by a narrow range of mutations with fitness costs , and will mainly be visible when .
On one hand, this sensitivity suggests that it might be possible to infer detailed information about by comparing and values across a range of frequency scales. On the other hand, our analytical expressions show that these marginal fitness costs will only lead to differences in , which will sensitively depend on the precise value of the integral in Equation (78). We leave a more detailed exploration of this dependence for future work. We also note that this limited resolution is no longer an issue in the presence of epistasis: strong synergistic epistasis between weakly selected mutations can produce large changes in if they are sufficiently common.
Discussion
Contemporary patterns of LD contain important information about the evolutionary forces at work within a population, which shape genetic variation over a vast range of length and time scales. Here, we have introduced a forward-time framework for predicting LD between pairs of neutral or deleterious mutations as a function of their present-day frequency scale f0. This additional dependence turned out to be more than a statistical curiosity, but instead enabled new insights into the dynamics of LD that had been difficult to obtain from existing methods (Ohta and Kimura 1971; McVean 2002; Song and Song 2007).
Our frequency-resolved approach shares some common features with existing moment-based approaches (Song and Song 2007; Good and Desai 2013; Ragsdale and Gravel 2019; Friedlander and Steinruecken 2021; Ragsdale 2021), which have developed recursion relations to calculate arbitrary higher-order moments of D, fA, and fB. These different moments also emphasize mutations with different frequencies, and can in principle be combined to single out particular frequency ranges as we have done above. For example, by Taylor expanding the exponential in Equation (7), our frequency-weighted statistic can be expressed as an infinite sum over the higher-order moments . By restricting our attention to rare mutations (), our present approach is able to sum up these infinite contributions analytically, without requiring the truncation schemes or moment closure approximations employed by previous methods. These benefits are particularly useful at the lowest frequency scales (), which are dominated by increasingly higher-order terms in the formal series expansion.
Our focus on rare mutations also allowed us to obtain a simple heuristic picture of LD that emphasizes the underlying dynamics of the lineages involved (Fig. 2). We saw that the frequency scale f0 can dramatically influence these dynamics, in a way that primarily depends on frequency-rescaled quantities like and . Our lineage-based picture highlighted the crucial importance of ancient nested mutations (Fig. 2c), which are substantially older than typical segregating variants, but which provide an increasingly large contribution to LD among tightly linked loci () with neutral or weakly deleterious fitness costs (). In these cases, we saw that ancient nested mutations will create an excess of coupling linkage () that qualitatively resembles the effects of antagonistic epistasis. This excess coupling linkage has previously been observed in computer simulations and in genomic data from diverse organisms (Sohail et al. 2017; Garcia and Lohmueller 2020; Sandler et al. 2020), where it has fueled an ongoing debate about the inference of epistasis from patterns of nonsynonymous and synonymous LD in a variety of species. Our analytical calculations suggest a potential mechanism for this counterintuitive behavior, and they demonstrate that this effect will generically arise even in the absence of admixture or other complex demographic scenarios.
Our results also allow us to answer a question we posed at the beginning of this work: do differences between synonymous and nonsynonymous LD curves primarily arise from differences in their underlying mutation frequencies? Our analytical results demonstrate that this is not the case: the key difference is that strongly deleterious mutations () can no longer sustain the ancient nested mutations in Fig. 2c, leading to lower levels of LD compared to neutral mutations with similar present-day frequencies (; Fig. 5). This shows that ordinary negative selection can generate differences between synonymous and nonsynonymous LD that qualitatively resemble the effects of negative epistasis. This could be an important potential confounder for efforts to infer negative epistasis by comparing levels of nonsynonymous and synonymous LD (Sohail et al. 2017; Sandler et al. 2020). However, we also saw that these strongly deleterious mutations can have a negligible impact on certain genome-wide averages like , due to their lower marginal frequencies. Thus, the quantitative magnitude of this effect can strongly depend on the underlying distribution of fitness effects as well as the averaging scheme employed. Moreover, while additive fitness costs can lead to lower relative values of LD, we also saw that they cannot produce negative values of on their own. This suggests that negative genome-wide values of signed LD may constitute a more robust indicator of negative epistasis than relative reductions in LD over synonymous sites.
More generally, our results provide a framework for leveraging the increasingly large sample sizes of modern genomic datasets to quantify the scaling behavior of LD across a range of underlying frequency scales. These scaling behaviors have a long history of application in other areas of statistical physics (Stanley 1999; Meshulam et al. 2019), and are commonly used in population genetics to infer evolutionary parameters from the shape of the single-SFS (Lawrie and Petrov 2014; Ragsdale et al. 2018). Our results provide a framework for extending this approach to multisite statistics like LD, potentially creating new opportunities to probe the underlying recombination process across a wide range of genomic length and time scales.
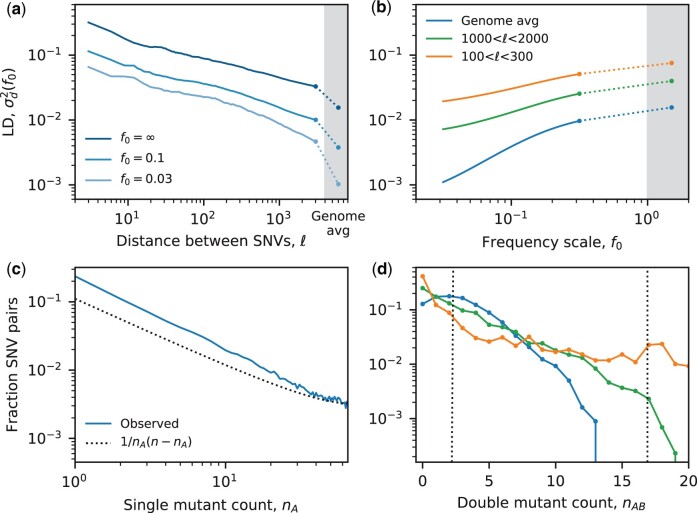
An example of this approach is illustrated in Fig. 7, which calculates frequency-resolved LD curves for 109 worldwide strains of the commensal human gut bacterium Eubacterium rectale (Appendix H). In a previous study, my collaborators and I used this dataset to infer the presence of widespread homologous recombination in the global population of E. rectale, by examining how the unweighted version of decays as a function of the coordinate distance (Garud et al. 2019). Our new frequency-resolved estimators now provide an analogous manifold of LD curves, , which allow us to examine the dynamics of LD across nearly two decades of frequency space (Fig. 7a and b). At a qualitative level, these empirical curves are similar to their theoretical counterparts in above Figs 4 and 5. While the precise mapping between coordinate distance and recombination rate is not known, we see that larger coordinate distances and smaller frequency scales both generally lead to lower values of (Fig. 7a), similar to the black and gray curves in Fig. 5b. However, the quantitative dependence on and f0 indicates dramatic departures from the simplest neutral null models analyzed in this work. In particular, the E. rectale data suggest that larger coordinate distances are more sensitive to reductions in f0 (Fig. 7, a and b), while our theoretical models predict the opposite trend (Fig. 5). Moreover, this unusual frequency dependence is observed even at the largest coordinate distances ( bp), where the overall reduction in might normally suggest convergence to the recombination-dominated regime (). This example shows how analytical predictions of frequency-resolved LD statistics can help identify deviations from our simple model that warrant future study, yet would be difficult to identify from intuition alone.
Fig. 7.
Frequency-resolved LD in the commensal human gut bacterium Eubacterium rectale. SNVs were obtained for a sample of n = 109 unrelated strains reconstructed from different human hosts (Garud et al. 2019) (Appendix H). a) Frequency-weighted LD () as a function of coordinate distance () between 4-fold degenerate synonymous SNVs in core genes. Solid lines were obtained by applying the unbiased estimator in Appendix G to all pairs of SNVs within 0.2 log units of , while the points depict genome-wide averages calculated from randomly sampled pairs of SNVs from widely separated genes. The two estimates are connected by a dashed line for visualization. b) Analogous curves as a function of the frequency scale f0. c) The single SFS, estimated from the fraction of SNV pairs in which the first mutation is observed with a given minor allele count, nA. d) The conditional distribution of the double-mutant frequency for fixed values of the marginal mutation frequencies, . Colored lines show the observed distributions for pairs of SNVs with marginal mutation frequencies in the range ; dashed lines indicate approximate positions of linkage equilibrium (; left) and perfect linkage (; right). The shapes of the three distributions are qualitatively similar to the mutation-dominated (; orange), clonal recombinant (; green) and quasi-linkage equilibrium (; blue) regimes predicted in Fig. 6.
In this case, the divergence between theory and data might have been anticipated, given that the marginal mutation frequencies in E. rectale already deviate from the dependence predicted under the simplest neutral null model (Fig. 7c). It is possible that the modest enrichment of rare mutations observed in the data could bias the relevant averages below the nominal value of f0, leading to somewhat stronger realized levels of linkage than would be expected under the simplest versions of our model. To reduce these potential uncertainties induced by the average in , it is also useful to quantify the same LD patterns in a different way, by examining the conditional distribution of the double-mutant frequency for a specific value of the marginal mutation frequencies, (Fig. 7d). When , the data display a clear transition between the three characteristic regimes identified in Fig. 6, with QLE emerging at the largest coordinate distances () and mutation-dominated behavior at shorter genetic distances (). On intermediate length scales (), the LD distribution transitions to an exponential shape expected in the clonal recombinant regime (), which provides a direct empirical demonstration of this qualitatively new behavior. The boundaries between these regimes provide an independent set of bounds on the corresponding recombination rates,
| (79) |
which no longer require extrapolation over multiple distance scales, or any associated assumptions about the shape of the curve. This example shows how the sampling distributions of different LD statistics can provide new insights into the dynamics of the underlying recombination process.
Of course, these empirical comparisons should be treated with a degree of caution, since our theoretical analysis focused on an extremely simple null model that lacks many of the complexities associated with real microbial populations. Our results suggest that it would be interesting to extend these approaches to account for other factors that might be relevant at short time scales, including time-varying population sizes, linked selection, and certain forms of spatial structure. We believe that our lineage-based framework will provide a useful starting point for predicting the dynamics of LD across these diverse evolutionary scenarios, which would allow us to better exploit the unique features of modern genomic datasets.
Data availability
Source code for forward-time simulations, data analysis, and figure generation are available at Github (https://github.com/bgoodlab/rare_ld). Polymorphism data from E. rectale were obtained from a previous study (Garud et al. 2019) and can be accessed using the accessions listed in that work. Postprocessed SNV data have been deposited in the GSA Figshare portal.
Supplemental material is available at figshare DOI: https://doi.org/10.25386/genetics.13369457
Acknowledgments
I thank Nandita Garud and Daniel Fisher for useful discussions during this project and Anastasia Lyulina, Zhiru Liu, Simon Gravel, and two anonymous reviewers for valuable feedback on the manuscript.
Funding
This work was supported in part by the Alfred P. Sloan Foundation (FG-2021-15708), a Terman Fellowship from Stanford University, and the Miller Institute for Basic Research in Science at the University of California, Berkeley.
Conflicts of interest
None declared.
Appendix A: Forward-time simulations
Forward-time simulations were used to compare our analytical predictions to the full two-locus model in Equation (3). These simulations used a discrete generation, Wright–Fisher sampling scheme, in which the number of individuals with each haplotype at generation t + 1 was drawn from a Poisson distribution with mean equal to the expected number of individuals predicted by Equation (3), given the haplotype frequencies at time t. To enhance computational efficiency for calculating LD statistics, our program only simulated timepoints in which both mutations were segregating in the population at the same time. This scheme was implemented by first drawing an initial (single-mutant) haplotype from the single-locus SFS (Sawyer and Hartl 1992),
| (A1) |
and then introducing a second mutation in a single individual from either the mutant or wildtype background with probability f or , respectively. The resulting population was then evolved until one of the mutations went extinct, and the process was restarted with a new pair of mutations. The frequencies of the four haplotypes were recorded every generations, and were used to generate the figures in the main text. The simulations in this work were performed with a population size of and a sampling interval of .
Appendix B: Perturbative solution of the generating function at small frequency scales
To obtain the perturbative solution of Equation (50) listed in Equation (59), it is be helpful to define a zeroth order differential operator,
| (B1) |
so that Equation (50) can be written as
| (B2) |
with all of the θ and f0 dependence is confined to the right-hand side. Substituting the series expansion in Equation (52) into this equation and grouping like terms, we find that the zeroth order solution is , as expected. The first order correction, which enters at , satisfies the equation
| (B3) |
which can be solved using the method of characteristics. To see this, we define a function
| (B4) |
where the characteristic curves and are given by
| (B5) |
Then satisfies a related differential equation,
| (B6) |
whose solution is given by
| (B7) |
The definition of in Equation (B4) then implies that
| (B8) |
which yields Equation (53) in the main text.
This same approach can be extended to higher orders of the series expansion Equation (52). At the next order (), we have
| (B9) |
which can again be solved by the method of characteristics. We define an analogous function,
| (B10) |
where the characteristic curves and are the same as above. Then satisfies
| (B11) |
and hence
| (B12) |
Note that this term is independent of z, which means that it cannot contribute to averages involving fAB.
The lowest order term in f0 is , since the term vanishes. At this order, we have
| (B13) |
where HA and HB are defined as above. The solution to this equation proceeds in a similar fashion as above. Let be defined by
| (B14) |
where the characteristic curve z is defined by
| (B15) |
Then, satisfies
| (B16) |
where and are defined by
| (B17) |
The solution for then follows as
| (B18) |
where is a function that is independent of z. Combining this expression with the and terms above yields the perturbative solution in Equation (56) in the main text. Thus, if we can find a solution for the characteristic curve in Equation (B15), then the leading order contributions to the generating function can be obtained by direct integration. We consider several such solutions in the Appendices below. To minimize confusion, we will use the notation in place of throughout the rest of this work, in order to emphasize the implicit dependence on the initial conditions , and .
Appendix C: Solution for nonrecombining loci
In the case of nonrecombining loci (ρ = 0), the characteristic curve in Equation (56b) reduces to a simple logistic equation, whose solution is given by
| (C1) |
This solution will also be valid for finite recombination rates, provided that . Substituting this solution into Equation (59), we find that the equilibrium generating function can be expressed as a definite integral,
| (C2) |
In this case, the integral can be evaluated using special functions,
| (C3) |
where is the hypergeometric function. This integral simplifies even further in the limit that , where we find that
| (C4) |
where is the polylogarithm function. For , the resulting distribution of fAB is approximately uniformly distributed up to a cutoff around , with . This is much broader than the standard single-locus prediction, and reflects the dominant contribution of ancient nested mutations that originated long before the time of sampling.
We can also use this same solution to evaluate various moments directly. To do so, it will be helpful to make use of the following identities:
| (C5) |
and
| (C6) |
for , such that
| (C7) |
Substituting these expressions into Equation (60), we obtain
| (C8) |
and
| (C9) |
Appendix D: Solution for neutral loci
In the limit where γA, γB, are all small compared to both 1 and ρ, we can obtain exact solutions for using special functions. Recall that since each of these scaled variables contains a factor of f0, this neutral regime can apply even when the nominal fitness costs are much larger than . When these conditions hold, the differential equation for the characteristic curve reduces to
| (D1) |
This equation is difficult to solve due to the presence of the time-dependent terms on the right-hand side, which vary over two different timescales and . Note, however, that moments like only depend on the value of this function in the special case that . Thus, for the purposes of computing , it will be sufficient to focus on the simpler equation
| (D2) |
which can be nondimensionalized using the transformation and , yielding
| (D3) |
The general solution to this equation is of the form
| (D4) |
or switching back to ,
| (D5) |
where we have defined
| (D6) |
and where the constant c(z) is chosen to satisfy the initial condition when ζ = 0:
| (D7) |
For our purposes, it will be useful to solve for . Solving for , we obtain
| (D8) |
which has derivatives
| (D9) |
It is then straightforward to compute derivatives of with respect to ϵ. For the first derivative, we find,
| (D10) |
Higher derivatives are facilitated by writing this as
| (D11) |
where we have defined
| (D12) |
| (D13) |
| (D14) |
The second, third, and fourth derivatives are therefore given by
| (D15) |
| (D16) |
| (D17) |
Evaluating at ϵ = 0, we have
| (D18) |
| (D19) |
| (D20) |
This yields
| (D21) |
| (D22) |
| (D23) |
where we have defined
| (D24) |
Appendix E: Solution for strong selection or recombination
We finally consider the regime where , which can occur either when any of γA, γB, or ρ are large compared to one. In this limit, we can obtain solutions via perturbation theory, treating the term as a small correction. We first rescale time , so that
| (E1) |
We can put this in a more compact form by defining , and , so that
| (E2) |
with initial condition . We can solve this equation using a perturbation expansion in ϵ, defining
| (E3) |
| (E4) |
with . At zeroth order, we have
| (E5) |
and hence
| (E6) |
For our purposes, it will suffice to continue this formal solution through second order in ϵ. At first order, we have
| (E7) |
and hence
| (E8) |
At second order, we have
| (E9) |
and hence
| (E10) |
Finally, at third order, we have
| (E11) |
and hence
| (E12) |
We can use these formal solutions to compute derivatives with respect to z:
| (E13) |
| (E14) |
| (E15) |
Note that all three expressions are independent of f(u) at lowest order. We can then use these expressions to calculate LD statistics:
| (E16) |
and
| (E17) |
and
| (E18) |
In the limit that , these expressions reduce to Equation (66) in the main text.
Appendix F: Transition to the quasi-linkage equilibrium regime
Using the quasi-stationary distribution in Equation (68) in the main text, it is straightforward to show that the first several conditional averages are given by
| (F1) |
| (F2) |
and
| (F3) |
in the limit that and . Averaging over the slowly evolving fAb and faB frequencies then yields the moments in Equation (69) in the main text. The ratio between the fourth and second moments then follows as
| (F4) |
To obtain a formula for η that works throughout the full range of NR and f0 values, we asymptotically match this expression with the corresponding formula from Equation (60), which yields
| (F5) |
where and are defined by Eqs. (D22) and (D23).
Appendix G: Estimating frequency-resolved LD in finite samples
As described in the main text, we can obtain unbiased finite-sample estimators for by expanding the D and terms in Equation (7) and applying the moment formula in Equation (77). To ensure a smooth mapping to the limit, it is useful to define a modified function,
| (G1) |
which satisfies a related moment formula
| (G2) |
in the limits that or . Carrying out this procedure for the first few moments, we obtain
| (G3a) |
| (G3b) |
and
| (G3c) |
which can be combined to obtain count-based formulae for and . One can then apply these estimators to genomic data by replacing the ensemble averages with appropriate sums over many functionally similar pairs of sites.
Appendix H: Applications to polymorphism data from E. rectale
The LD estimates in Fig. 7 were obtained from a sample of n = 109 E. rectale genomes that my collaborators and I analyzed in a previous study (Garud et al. 2019). In that work, we used a referenced-based approach to identify single-nucleotide variants (SNVs) in the intra-host populations of several common species of gut bacteria from a panel of sequenced fecal samples. We also identified samples in which the haplotype of the dominant strain of a given could be resolved with high confidence. This analysis yielded 159 “quasi-phaseable” E. rectale genomes, which we used to identify between-host SNVs in the global E. rectale population. After controlling for population structure, we identified a subset of n = 109 samples that were inferred to descend from the largest clade. These 109 genomes were used as the basis for the analysis in Fig. 7 in the present work. These calculations started from the same collection of SNVs identified in Garud et al. (2019), and focused specifically on the subset of SNVs that were located at 4-fold degenerate sites in core genes. Two-site haplotypes and coordinate distances were recorded for all pairs of SNVs located within four consecutive genes of each other on the E. rectale reference genome, and the A and B alleles were defined to coincide with the minority allele at each site. As a control, analogous two-site haplotypes were recorded for pairs of SNVs from a large number of randomly selected genes. The full collection of two-site haplotypes is provided in the Supplementary data. These counts were used as inputs for each of the calculations described in Fig. 7.
Literature cited
- Allix-Béguec C, Arandjelovic I, Bi L, Clifton D, Crook D, Fowler P, Gibertoni Cruz A, Hoosdally S, Hunt M, et al. Prediction of susceptibility to first-line tuberculosis drugs by DNA sequencing. N Engl J Med. 2018;379:1403–1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ansari MA, Didelot X.. Inference of the properties of the recombination process from whole bacterial genomes. Genetics. 2014;196(1):253–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold B, Sohail M, Wadsworth C, Corander J, Hanage WP, Sunyaev S, Grad YH.. Fine-scale haplotype structure reveals strong signatures of positive selection in a recombining bacterial pathogen. Mol Biol Evol. 2020;37(2):417–428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakravarti A, Buetow KH, Antonarakis S, Waber P, Boehm C, Kazazian H.. Nonuniform recombination within the human beta-globin gene cluster. Am J Hum Genet. 1984;36(6):1239–1258. [PMC free article] [PubMed] [Google Scholar]
- Coop G, Ralph P.. Patterns of neutral diversity under general models of selective sweeps. Genetics. 2012;192(1):205–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cvijović I, Good BH, Desai MM.. The effect of strong purifying selection on genetic diversity. Genetics. 2018;209(4):1235–1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desai MM, Fisher DS.. Beneficial mutation selection balance and the effect of genetic linkage on positive selection. Genetics. 2007;176(3):1759–1798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eberle MA, Rieder MJ, Kruglyak L, Nickerson DA.. Allele frequency matching between snps reveals an excess of linkage disequilibrium in genic regions of the human genome. PLoS Genet. 2006;2(9):e142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewens WJ. Mathematical Population Genetics. 2nd ed.New York: Springer-Verlag; 2004. [Google Scholar]
- Fisher DS. Evolutionary dynamics. In: Jean-Philippe Bouchaud MM, Dalibard J, editors. Complex Systems. Volume 85 of Les Houches. Amsterdam, The Netherlands: Elsevier; 2007. pp. 395–446. [Google Scholar]
- Friedlander E, Steinruecken M. A numerical framework for genetic hitchhiking in populations of variable size. bioRxiv 2021. [DOI] [PMC free article] [PubMed]
- Garcia JA, Lohmueller KE. Negative linkage disequilibrium between amino acid changing variants reveals interference among deleterious mutations in the human genome. PLoS Genet. 2021;17(7):e1009676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardiner C. Handbook of Stochastic Methods. New York: Springer; 1985. [Google Scholar]
- Garud NR, Good BH, Hallatschek O, Pollard KS.. Evolutionary dynamics of bacteria in the gut microbiome within and across hosts. PLoS Biol. 2019;17(1):e3000102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garud NR, Messer PW, Buzbas EO, Petrov DA.. Recent selective sweeps in North American Drosophila melanogaster show signatures of soft sweeps. PLoS Genet. 2015;11(2):e1005004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good BH. Molecular evolution in rapidly evolving populations [Ph.D. thesis]. [Cambridge (MA)]: Harvard University; 2016. [Google Scholar]
- Good BH, Desai MM.. Fluctuations in fitness distributions and the effects of weak linked selection on sequence evolution. Theor Popul Biol. 2013;85:86–102. [DOI] [PubMed] [Google Scholar]
- Harris K, Nielsen R.. Inferring demographic history from a spectrum of shared haplotype lengths. PLoS Genet. 2013;9(6):e1003521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedrick PW. Gametic disequilibrium measures: proceed with caution. Genetics. 1987;117(2):331–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill W, Robertson A.. Linkage disequilibrium in finite populations. Theor Appl Genet. 1968;38(6):226–231. [DOI] [PubMed] [Google Scholar]
- Kamm JA, Terhorst J, Song YS.. Efficient computation of the joint sample frequency spectra for multiple populations. J Comput Graph Stat. 2017;26(1):182–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang JT, Rosenberg NA.. Mathematical properties of linkage disequilibrium statistics defined by normalization of the coefficient d= pab–papb. Hum Hered. 2019;84(3):127–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karczewski KJ, Francioli LC, Tiao G, Cummings BB, Alföldi J, Wang Q, Collins RL, Laricchia KM, Ganna A, Birnbaum DP, et al. The mutational constraint spectrum quantified from variation in 141,456 humans. Nature. 2020;581(7809):434–443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kendall DG. On the generalized “birth-and-death” process. Ann Math Statist. 1948;19(1):1–15. [Google Scholar]
- Kim Y, Nielsen R.. Linkage disequilibrium as a signature of selective sweeps. Genetics. 2004;167(3):1513–1524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M. Diffusion models in population genetics. J Appl Prob. 1964;1(2):177–232. [Google Scholar]
- Kimura M, Ohta T.. The age of a neutral mutant persisting in a finite population. Genetics. 1973;75(1):199–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrie DS, Petrov DA.. Comparative population genomics: power and principles for the inference of functionality. Trends Genet. 2014;30(4):133–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewontin R. The interaction of selection and linkage. I. general considerations; heterotic models. Genetics. 1964;49(1):49–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewontin R. On measures of gametic disequilibrium. Genetics. 1988;120(3):849–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Durbin R.. Inference of human population history from individual whole-genome sequences. Nature. 2011;475(7357):493–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Xu S, Maruki T, Jiang X, Pfaffelhuber P, Haubold B.. Genome-wide linkage-disequilibrium profiles from single individuals. Genetics. 2014;198(1):269–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean G. The structure of linkage disequilibrium around a selective sweep. Genetics. 2007;175(3):1395–1406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean GA. A genealogical interpretation of linkage disequilibrium. Genetics. 2002;162(2):987–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean GA, Myers SR, Hunt S, Deloukas P, Bentley DR, Donnelly P.. The fine-scale structure of recombination rate variation in the human genome. Science. 2004;304(5670):581–584. [DOI] [PubMed] [Google Scholar]
- Meshulam L, Gauthier JL, Brody CD, Tank DW, Bialek W.. Coarse graining, fixed points, and scaling in a large population of neurons. Phys Rev Lett. 2019;123(17):178103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neher RA, Hallatschek O.. Genealogies in rapidly adapting populations. Proc Natl Acad Sci U S A. 2013;110(2):437–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohta T, Kimura M.. Linkage disequilibrium between two segregating nucleotide sites under the steady flux of mutations in a finite population. Genetics. 1971;68(4):571–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasolli E, Asnicar F, Manara S, Zolfo M, Karcher N, Armanini F, Beghini F, Manghi P, Tett A, Ghensi P, et al. Extensive unexplored human microbiome diversity revealed by over 150,000 genomes from metagenomes spanning age, geography, and lifestyle. Cell. 2019;176(3):649–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petit RA III, Read TD.. Staphylococcus aureus viewed from the perspective of 40,000+ genomes. PeerJ. 2018;6:e5261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfaffelhuber P, Lehnert A, Stephan W.. Linkage disequilibrium under genetic hitchhiking in finite populations. Genetics. 2008;179(1):527–537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pokalyuk C. The effect of recurrent mutation on the linkage disequilibrium under a selective sweep. J Math Biol. 2012;64(1–2):291–317. [DOI] [PubMed] [Google Scholar]
- Polanski A, Kimmel M.. New explicit expressions for relative frequencies of single-nucleotide polymorphisms with application to statistical inference on population growth. Genetics. 2003;165(1):427–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragsdale AP. Can we distinguish modes of selective interactions using linkage disequilibrium? bioRxiv 2021.
- Ragsdale AP, Gravel S.. Models of archaic admixture and recent history from two-locus statistics. PLoS Genet. 2019;15(6):e1008204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragsdale AP, Gravel S.. Unbiased estimation of linkage disequilibrium from unphased data. Mol Biol Evol. 2020;37(3):923–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragsdale AP, Moreau C, Gravel S.. Genomic inference using diffusion models and the allele frequency spectrum. Curr Opin Genet Dev. 2018;53:140–147. [DOI] [PubMed] [Google Scholar]
- Rogers AR. How population growth affects linkage disequilibrium. Genetics. 2014;197(4):1329–1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosen MJ, Davison M, Bhaya D, Fisher DS.. Fine-scale diversity and extensive recombination in a quasisexual bacterial population occupying a broad niche. Science. 2015;348(6238):1019–1023. [DOI] [PubMed] [Google Scholar]
- Rosen MJ, Davison M, Fisher DS, Bhaya D.. Probing the ecological and evolutionary history of a thermophilic cyanobacterial population via statistical properties of its microdiversity. PLoS One. 2018;13(11):e0205396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabeti PC, Reich DE, Higgins JM, Levine HZ, Richter DJ, Schaffner SF, Gabriel SB, Platko JV, Patterson NJ, McDonald GJ, et al. Detecting recent positive selection in the human genome from haplotype structure. Nature. 2002;419(6909):832–837. [DOI] [PubMed] [Google Scholar]
- Sandler G, Wright SI, Agrawal AF. Using patterns of signed linkage disequilibria to test for epistasis in flies and plants. Patterns and causes of signed linkage disequilibria in flies and plants. Mol Biol Evol. 2021;38(10):4310–4321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawyer SA, Hartl DL.. Population genetics of polymorphism and divergence. Genetics. 1992;132(4):1161–1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shu Y, McCauley J.. Gisaid: global initiative on sharing all influenza data - from vision to reality. Euro Surveill. 2017;22:30494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M. Linkage disequilibrium – understanding the evolutionary past and mapping the medical future. Nat Rev Genet. 2008;9(6):477–485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohail M, Vakhrusheva OA, Sul JH, Pulit SL, Francioli LC, van den Berg LH, Veldink JH, de Bakker PI, Bazykin GA, Kondrashov AS, et al. Negative selection in humans and fruit flies involves synergistic epistasis. Science. 2017;356(6337):539–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song YS, Song JS.. Analytic computation of the expectation of the linkage disequilibrium coefficient r2. Theor Popul Biol. 2007;71(1):49–60. [DOI] [PubMed] [Google Scholar]
- Stanley HE. Scaling, universality, and renormalization: three pillars of modern critical phenomena. Rev Mod Phys. 1999;71(2):S358–S366. [Google Scholar]
- Stephan W, Song YS, Langley CH.. The hitchhiking effect on linkage disequilibrium between linked neutral loci. Genetics. 2006;172(4):2647–2663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanLiere JM, Rosenberg NA.. Mathematical properties of the r2 measure of linkage disequilibrium. Theor Popul Biol. 2008;74(1):130–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Wray NR, Zhang Q, Sklar P, McCarthy MI, Brown MA, Yang J.. 10 years of gwas discovery: biology, function, and translation. Am J Hum Genet. 2017;101(1):5–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissman DB, Feldman MW, Fisher DS.. The rate of fitness-valley crossing in sexual populations. Genetics. 2010;186(4):1389–1410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissman DW, Desai MM, Fisher DS, Feldman MW.. The rate at which asexual populations cross fitness valleys. Theor Popul Biol. 2009;75(4):286–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Source code for forward-time simulations, data analysis, and figure generation are available at Github (https://github.com/bgoodlab/rare_ld). Polymorphism data from E. rectale were obtained from a previous study (Garud et al. 2019) and can be accessed using the accessions listed in that work. Postprocessed SNV data have been deposited in the GSA Figshare portal.
Supplemental material is available at figshare DOI: https://doi.org/10.25386/genetics.13369457