A Combined Interpolation and Weighted K-Nearest Neighbours Approach for the Imputation of Longitudinal ICU Laboratory Data

Abstract

The presence of missing data is a common problem that affects almost all clinical datasets. Since most available data mining and machine learning algorithms require complete datasets, accurately imputing (i.e. “filling in”) the missing data is an essential step. This paper presents a methodology for the missing data imputation of longitudinal clinical data based on the integration of linear interpolation and a weighted K-Nearest Neighbours (KNN) algorithm. The Maximal Information Coefficient (MIC) values among features are employed as weights for the distance computation in the KNN algorithm in order to integrate intra- and inter-patient information. An interpolation-based imputation approach was also employed and tested both independently and in combination with the KNN algorithm. The final imputation is carried out by applying the best performing method for each feature. The methodology was validated on a dataset of clinical laboratory test results of 13 commonly measured analytes of patients in an intensive care unit (ICU) setting. The performance results are compared with those of 3D-MICE, a state-of-the-art imputation method for cross-sectional and longitudinal patient data. This work was presented in the context of the 2019 ICHI Data Analytics Challenge on Missing data Imputation (DACMI).

Introduction

A typical issue when working with real-world datasets in the clinical as well as in other domains is the presence of missing values. This fact limits the use of many statistical methods and machine learning approaches, since most of these procedures are designed for complete data [20]. Furthermore, missing data can introduce potential bias in parameter estimation and weaken the generalisability of the results [2, 21]. For these reasons, a preliminary imputation step is often required.

Previous Work

Several methods for handling missing data are available to date [3]. The simplest approach is to consider only non-missing values in the analysis, by completely dropping all cases where at least one variable is missing (listwise deletion), or by only deleting cases having missing values in one of the variables being considered in the specific evaluated model (pairwise deletion). This causes loss of information, which in turn decreases statistical power and increases standard errors [14]. Simple statistical approaches, such as mean/median filling or value propagation (Last Observation Carried Backward or Next Observation Carried Forward), are often applied. These methods are fast and easily interpretable, but they can lead to low accuracy and biased estimates of the investigated associations [7].

More advanced methods which take into account the cross-sectional relationships among the data have been proposed. Regression approaches estimate missing values by regressing them from other related variables [22]. While deterministic regression limits the imputation to the exact prediction of the regression model, often producing an overestimation of the correlation among the variables, stochastic regression adds a random error term to the predicted value in order to recover a part of the data variability [17].

In [19], a non-parametric method based on a random forest, called missForest, was introduced. This method is based on the idea that a random forest intrinsically constitutes a multiple imputation scheme by averaging over many unpruned classification or regression trees, and can cope with categorical and continuous variables simultaneously. Multivariate imputation by chained equations (MICE) is another popular method of dealing with missing data [5]. This imputation procedure builds a conditional model for each variable to be imputed, with the other variables as possible predictors.

Since most imputation methods do not adequately handle longitudinal data (i.e. time series, a fundamental characteristic of clinical data), the 3D-MICE method has been recently introduced [12]. 3D-MICE imputes missing data based on both cross-sectional and longitudinal patient information by combining MICE with Gaussian process (GP) [9, 16] predictions. MICE is used to carry out cross-sectional imputation of the missing values, while a single-task GP is used to perform longitudinal imputation. The estimates obtained by the two methods are then combined by computing a variance-informed weighted average.

Aim of this Work

In the framework of the 2019 ICHI Data Analytics Challenge on Missing data Imputation (DACMI – http://www.ieee-ichi.org/challenge.html), an imputation task for longitudinal ICU laboratory test data was shared. This work describes the methodology we developed for the challenge, which is based on the combination of linear interpolation and a weighted K-Nearest Neighbours (KNN) procedure (briefly introduced in [6]). Both the methods were built up as intra-patient approaches, i.e. the values of the missing data are inferred by looking at the previous/following visits of the same patient. With the intent to integrate some inter-patient information in the KNN implementation, we first calculated the Maximal Information Coefficient (MIC) [18] values among pairs of features. Then, we used these values as weights when computing the distance between different time samples of the same patient. The MIC is a statistical measure that captures the strength of both linear and nonlinear relationships among analytes. First, we tested the linear interpolation and weighted KNN imputation approaches independently. Then, we combined them by selecting the best performing approach for each feature. The selected model was validated on an independent test set against 3D-MICE, i.e. the baseline proposed by the DACMI organisers. Our method demonstrated statistically significant improvements in 11 out of 13 analytes, with an average performance gain of 8.1%, as well as a considerably reduced computational time.

Materials and Methods

Dataset

The datasets [11] provided by the DACMI organisers to the challenge participants were derived from MIMIC-III [8, 10], a large real-world database containing de-identified information regarding the clinical care of patients who stayed within the intensive care units (ICU) at Beth Israel Deaconess Medical Centre. Both a training and a test set were provided in order to develop and validate the imputation methodology on two independent sets of data, each one consisting of inpatient test results for 13 analytes (laboratory tests): Chloride (PCL), Potassium (PK), Bicarbonate (PLCO2), Sodium (PNA), Hematocrit (HCT), Hemoglobin (HGB), Mean Cell Volume (MCV), Platelets (PLT), White Blood Cell count (WBC), Red blood cells Distribution Width (RDW), Blood Urea Nitrogen (PBUN), Creatinine (PCRE), and Glucose (PGLU). Each visit is composed of 13 analyte measurements and is identified by the time in minutes from the first visit (which is identified by timestamp 0). The training set consists of the test results of 8267 subjects for a total of 199 695 visits, while the test set consists of the test results of 8267 other subjects for a total of 199 936 visits.

A version of each dataset with randomly masked results was also provided by the challenge organisers in order to evaluate the performance of the developed imputation algorithms (see Tables 1 and 2); one result per analyte per patient-admission was randomly removed, i.e. each patient had 13 results masked across the various visits (time points), thus creating cases with known ground truth results. In this work, we imputed both natively missing and masked data together, and compared imputed with measured values for masked data elements to evaluate the performance of the imputation method.

Table 1.

Characteristics of the training set

Analyte	Units	Interquartile	Native missing	Missing rate after
		range	rate (%)	masking (%)
Chloride	mmol/L	100–108	1.18	5.32
Potassium	mmol/L	3.7–4.4	1.34	5.48
Bicarb.	mmol/L	22–28	1.39	5.53
Sodium	mmol/L	135–142	1.26	5.4
Hematocrit	%	26.8–32.7	12.51	16.65
Hemoglobin	g/dL	8.9–11	15.09	19.23
MCV	fL	86–94	15.23	19.37
Platelets	k/μ L	130–330	14.55	18.69
WBC count	k/μ L	7.1–14.1	14.8	18.94
RDW	%	14.5–17.4	15.34	19.48
BUN	mg/dL	16–43	0.74	4.88
Creatinine	mg/dL	0.7–1.9	0.7	4.84
Glucose	mg/dL	100–148	2.7	6.84

Table 2.

Characteristics of the test set

Analyte	Units	Interquartile	Native missing	Missing rate after
		range	rate (%)	masking (%)
Chloride	mmol/L	100–108	1.20	5.40
Potassium	mmol/L	3.7–4.4	1.28	5.48
Bicarb.	mmol/L	22–28	1.41	5.60
Sodium	mmol/L	136–142	1.26	5.45
Hematocrit	%	26.8–32.6	12.45	16.64
Hemoglobin	g/dL	8.9–11	14.93	19.13
MCV	fL	87–94	15.04	19.24
Platelets	k/μ L	133–332	14.42	18.62
WBC count	k/μ L	7.1–14.1	14.69	18.89
RDW	%	14.4–17.3	15.16	19.36
BUN	mg/dL	15–42	0.77	4.97
Creatinine	mg/dL	0.7–1.8	0.75	4.94
Glucose	mg/dL	100–147	2.63	6.83

Imputation Evaluation Metrics

The DACMI task required us to employ the normalised root-mean-square deviation (nRMSD) metric to evaluate the performance of the developed imputation methods and compare them with the performance of 3D-MICE. Let X_p,a,i be the test result prediction for analyte a of patient p at time i and let Y_p,a,i be the true measured value for that analyte. Also, let I_p,a,i be 1 if the value of analyte a for patient p at time i is missing, and 0 otherwise. The nRMSD of analyte a is calculated as:

$$\text{nRMSD}\left(a\right)=\sqrt{\frac{{\sum }_{p,i}{I}_{p,a,i}{\left(\frac{|X_{p,a,i}-Y_{p,a,i}|}{\max \left(Y_{p,a}\right)-\min \left(Y_{p,a}\right)}\right)}^2}{{\sum }_{p,i}{I}_{p,a,i}}}\mathrm{.}$$ 1

The nRMSD is frequently used to measure the differences between values predicted by a model and the ones observed [12]. The normalisation at the patient level facilitates the performance comparisons on analytes with different scales and dynamic ranges.

In order to better analyse and compare the distribution of the error, we also computed the normalised absolute error (nAE) of each imputed value. The nAE for analyte a of patient p at time i is given by:

$$\text{nAE}(p,a,i)=\frac{|X_{p,a,i}-Y_{p,a,i}|}{\max \left(Y_{p,a}\right)-\min \left(Y_{p,a}\right)}\mathrm{.}$$ 2

Analysing the nAE distribution for each analyte allows us to gain more insight on the quality of the imputation.

Linear Interpolation Imputation

We first implemented a simple imputation algorithm based on linear interpolation, described as follows. Given an analyte value to be imputed in a certain visit , we inspect the other visits from the same patient. If the missing data are located between known measurements, they are estimated by linear interpolation in the specific time points. Otherwise, if the missing data correspond to the first or last visits of a given patient, then, these values are imputed by simply carrying the next observation backward or the last observation forward. When the values of an analyte are missing in all the visits of a given patient, they are imputed with the corresponding average over the population.

Weighted K-Nearest Neighbours Imputation

We also implemented an intra-patient imputation procedure based on a weighted KNN algorithm, described as follows. Given a missing value in a patient visit, the algorithm uses the other visits from the same patient as neighbours. The KNN algorithm can be used for imputing missing data by finding the K neighbours closest to the observation with missing data, and then imputing them using the non-missing values from the neighbours [4]. The algorithm substitutes the missing data with plausible values that are close to the true ones. It is a similarity-based method that relies on distance metrics to determine the similarity among feature vectors. In this work, a weighted and normalised Euclidean distance metric was employed as a similarity measure.

In our implementation, the values of the 13 analytes are first normalised to the $\left[0,1\right]$ interval for each patient, in order to account for the differences among the analyte ranges. Let Y_p,a,i be the measured value for analyte a of patient p at time i, and let Y_p,a be the set of all known values for analyte a of patient p. The normalised value is given by:

$$n{Y}_{p,a,i}=\frac{Y_{p,a,i}-\min \left(Y_{p,a}\right)}{\max \left(Y_{p,a}\right)-\min \left(Y_{p,a}\right)}\mathrm{.}$$ 3

The missing data in a given patient visit are then imputed by selecting the most similar visits among the others from the same patient; once the distances to all the remaining visits of the current patient have been computed, the nearest K candidates are selected and the missing value is imputed using the average of the corresponding values in the K candidate visits, each weighted by the corresponding distance.

Maximal Information Coefficient

In order to exploit the inter-patient analyte dependencies, we integrated the cross-information over analytes in the KNN procedure by using the MIC. When trying to discover associations among pairs of variables, the statistic used to measure the dependence should exhibit two heuristic properties: generality and equitability [18]. Generality is the ability of a given statistic to capture a wide range of interesting associations, not limited to specific function types (such as linear, exponential, or periodic) or to functional relationships, provided that the sample size is sufficiently large. This property is essential because many important relationships are not well modelled by a specific function. Equitability, on the other hand, is the property of a given statistic to give similar scores to equally noisy relationships of different types. The MIC was shown to outperform several other methods in terms of generality and equitability, including mutual information estimation, distance correlation, Spearman’s rank correlation coefficient, principal curve-based methods, and maximal correlation [18].

The MIC measures the strength of the association (even if nonlinear) between two analytes in the $\left[0,1\right]$ range. High MIC values correspond to strongly associated variables, while low ones correspond to weak associations. The MIC uses binning in order to compute the mutual information of continuous random variables; the optimal number of bins that maximises the mutual information between variables is selected. We computed the MIC among all pairs of analytes on the whole dataset using the minerva R package v1.5.8 [1]. By using the MIC values as weights in the distance metric, we ensure that intra- and inter-patient information are integrated in the imputation procedure. A heatmap of the cross-sectional MIC among analytes on the training dataset is shown in Fig. 1.

Fig. 1.

Heatmap and dendrogram of the cross-sectional MIC among analytes computed on the training set

Distance Metric

For a given patient visit composed of the measurements of its 13 analytes $\mathbf{v}=\left(v_1,v_2,\dots ,v_{13}\right)$ with missing data to be imputed in index $i\in \{1,\dots ,13\}$, the algorithm computes the weighted Euclidean distance with the other visits of the current patient that do not have missing data in position i:

$$d(\mathbf{v},\mathbf{u})=\frac{\sqrt{{\sum }_{j\in N}{\text{MIC}}_{i,j}\cdot {\left(v_j-u_j\right)}^2}}{{\sum }_{j\in N}{\text{MIC}}_{i,j}},$$ 4

where N is the set of indices corresponding to non-missing values in both visits v and u, and MIC_i,j is the maximal information coefficient between analytes i and j computed on the whole dataset. By dividing the numerator in (4) by the quantity ${\sum }_{j\in N}{\text{MIC}}_{i,j}$, we are normalising the distance in order to account for other possible missing values (other than the one being currently imputed) and their importance. This favours candidate neighbouring visits that have many analytes highly associated with the one being currently imputed, and penalises candidate neighbouring visits that have missing values instead (a visit can have several missing values).

If a visit has multiple missing values to be imputed, the KNN procedure is repeated for each one of them separately, as the MIC weights (and consequently the distance values, see (4)) depend on the specific analyte being imputed. In our implementation, values previously imputed by the KNN are not used in distance computations and subsequent imputations. Again, if the values of an analyte for a given patient are missing in all his or her visits, the average over the population is used for the imputation of that analyte.

Selection of the Optimal K Parameter

To select the optimal number of neighbours K, we performed a 10-fold cross-validation (CV) at patient level on the training set. The 8267 subjects of the training dataset were randomly split into 10 disjoint folds. In turn, the visits of the subjects in a given fold were imputed using the MIC computed over the remaining 9 folds. In this framework, we tested different K values for the KNN algorithm, ranging from 1 to 15. The results are shown in Table 3: the best average nRMSD values were obtained for K ∈{3,4}.

Table 3.

Results of the 10-fold cross-validation procedure on the training set for the weighted KNN algorithm

Analyte	Number of selected neighbours
	K = 1	K = 2	K=3	K=4	K = 5	K = 6	K = 7	K = 8	K = 9	K = 10	K = 11	K = 12	K = 13	K = 14	K = 15
Chloride	0.2267	0.2028	0.1966	0.1977	0.2004	0.2038	0.2083	0.2124	0.2167	0.2210	0.2244	0.2275	0.2301	0.2323	0.2341
Potassium	0.2967	0.2633	0.2539	0.2507	0.2494	0.2492	0.2498	0.2507	0.2519	0.2530	0.2541	0.2549	0.2556	0.2562	0.2567
Bicarb.	0.2654	0.2376	0.2335	0.2328	0.2358	0.2380	0.2406	0.2434	0.2467	0.2497	0.2520	0.2540	0.2558	0.2576	0.2591
Sodium	0.2450	0.2199	0.2143	0.2132	0.2145	0.2171	0.2199	0.2230	0.2265	0.2292	0.2318	0.2341	0.2360	0.2377	0.2392
Hematocrit	0.1554	0.1438	0.1445	0.1497	0.1560	0.1630	0.1704	0.1782	0.1851	0.1903	0.1944	0.1977	0.2003	0.2025	0.2043
Hemoglobin	0.1540	0.1435	0.1453	0.1500	0.1568	0.1641	0.1716	0.1795	0.1863	0.1917	0.1960	0.1993	0.2021	0.2044	0.2063
MCV	0.3032	0.2710	0.2626	0.2607	0.2613	0.2630	0.2643	0.2662	0.2684	0.2704	0.2720	0.2734	0.2746	0.2757	0.2765
Platelets	0.2608	0.2334	0.2304	0.2328	0.2369	0.2423	0.2474	0.2526	0.2576	0.2617	0.2649	0.2677	0.2699	0.2718	0.2733
WBC counts	0.2772	0.2483	0.2430	0.2440	0.2471	0.2503	0.2536	0.2569	0.2597	0.2617	0.2635	0.2649	0.2661	0.2671	0.2679
RDW	0.2732	0.2435	0.2402	0.2418	0.2453	0.2493	0.2532	0.2575	0.2616	0.2646	0.2676	0.2702	0.2719	0.2734	0.2747
BUN	0.2563	0.2291	0.2231	0.2240	0.2269	0.2305	0.2334	0.2373	0.2409	0.2443	0.2477	0.2503	0.2528	0.2547	0.2563
Creatinine	0.2605	0.2353	0.2307	0.2294	0.2303	0.2330	0.2360	0.2393	0.2424	0.2453	0.2479	0.2500	0.2519	0.2535	0.2550
Glucose	0.3174	0.2820	0.2717	0.2672	0.2661	0.2654	0.2646	0.2648	0.2654	0.2657	0.2662	0.2666	0.2671	0.2675	0.2680
Average	0.2532	0.2272	0.2223	0.2226	0.2251	0.2284	0.2318	0.2355	0.2392	0.2422	0.2448	0.2470	0.2488	0.2503	0.2516

Best performances are highlighted in bold

Combined Imputation Method

The performances of the linear interpolation and weighted KNN imputation methods on the training set are reported in Table 4. We noticed that the interpolation-based imputation performed better than the KNN-based one in 7 out of 13 analytes, namely for Bicarbonate, MCV, Platelets, WBC count, RDW, BUN, and Creatinine. For this reason, we imputed these analytes using linear interpolation, and the remaining ones with the KNN-based approach.

Table 4.

Imputation performance comparison based on the nRMSE metric for each analyte and imputation method

Analyte	Training set						Test set
	Interp.	KNN	Selected	KNN+Interp.	Interp.+KNN	3D-MICE	Interp.+KNN	3D-MICE
		K = 3	method	K = 3	K = 3		K = 3
Chloride	0.2017	0.1966	KNN	0.1966 (1.6%)	0.1915 (4.1%)	0.1997	0.1921 (4.0%)	0.2000
Potassium	0.2590	0.2539	KNN	0.2539 (2.9%)	0.2505 (4.2%)	0.2614	0.2542 (3.4%)	0.2632
Bicarb.	0.2165	0.2335	Interp.	0.2165 (6.9%)	0.2165 (6.9%)	0.2326	0.2118 (8.5%)	0.2314
Sodium	0.2242	0.2143	KNN	0.2143 (− 0.3%)	0.2113 (1.1%)	0.2136	0.2085 (2.8%)	0.2145
Hematocrit	0.2248	0.1445	KNN	0.1445 (0.1%)	0.1434 (0.9%)	0.1447	0.1518 (-0.9%)	0.1505
Hemoglobin	0.2282	0.1453	KNN	0.1453 (− 1.7%)	0.1451 (− 1.5%)	0.1429	0.1485 (0.2%)	0.1488
MCV	0.2582	0.2626	Interp.	0.2582 (3.6%)	0.2582 (3.6%)	0.2679	0.2644 (2.5%)	0.2713
Platelets	0.1778	0.2304	Interp.	0.1778 (21.3%)	0.1778 (21.3%)	0.2260	0.1794 (21.8%)	0.2294
WBC counts	0.2183	0.2430	Interp.	0.2183 (14.6%)	0.2183 (14.6%)	0.2555	0.2198 (14.1%)	0.2560
RDW	0.2100	0.2402	Interp.	0.2100 (15.8%)	0.2100 (15.8%)	0.2493	0.2056 (16.4%)	0.2458
BUN	0.1521	0.2231	Interp.	0.1521 (17.7%)	0.1521 (17.7%)	0.1848	0.1546 (16.3%)	0.1846
Creatinine	0.2130	0.2307	Interp.	0.2130 (7.0%)	0.2130 (7.0%)	0.2291	0.2135 (8.7%)	0.2338
Glucose	0.2817	0.2717	KNN	0.2717 (1.9%)	0.2683 (3.1%)	0.2769	0.2677 (3.3%)	0.2769
Average	0.2204	0.2223	–	0.2055 (7.4%)	0.2043 (7.9%)	0.2219	0.2055 (8.1%)	0.2235

Best performances are highlighted in bold. The percentage of improvement over 3D-MICE is given in parentheses

The interpolation is run on each feature separately; thus, its results do not depend on the KNN step. On the other hand, the KNN could use the imputed values from the interpolation step during the distance computation. For this reason, we tested the imputation by combining the methods in both directions: by running the KNN first and the interpolation second (KNN+Interp.), and vice versa (Interp.+KNN). In the latter case, we tested a few values for K in cross-validation to confirm the optimality of the previously selected values: K = 3 was selected as the optimal value (the results are shown in Table 4).

Results

The developed imputation procedures were assessed on the training set using the nRMSD. The results in Table 4 show that the combined methods outperform 3D-MICE on 11–12 analytes out of 13. The average nRMSD values are equal to 0.2055 for KNN+Interp. K = 3 and 0.2043 for Interp.+KNN K = 3, which corresponds to an improvement of 7.4% and 7.9% respectively, compared with the baseline (0.2219).

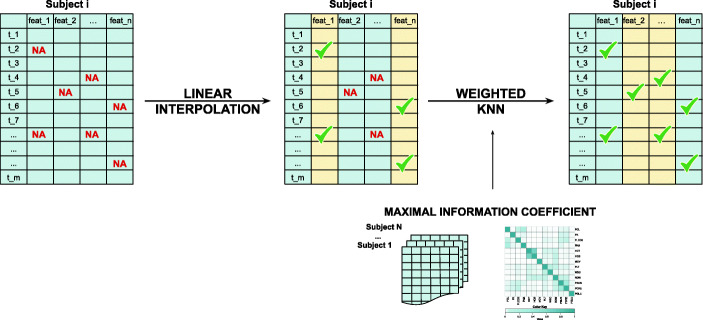
The best performing method Interp.+KNN was validated on the independent test set using the selected optimal K = 3 value, the MIC, and the population average values computed on the training set. Figure 2 schematically depicts the Interp.+KNN imputation procedure for a given subject. Performances are presented in the last two columns of Table 4. The average nRMSD value obtained for Interp.+KNN K = 3 on the test set, equal to 0.2055, is 8.1% lower than the 3D-MICE baseline (0.2235). Similarly to the training set, the combined method Interp.+KNN outperforms the baseline on average and on 12 out of 13 analytes, although reversing the sign of the improvement for the features Hematocrit and Hemoglobin.

Fig. 2.

Interp.+KNN imputation procedure. For each subject with missing values, 7 out of 13 analytes are first imputed with linear interpolation. The remaining missing values on the other analytes are then imputed with the KNN algorithm using the MIC values computed on the training set as weights for the distance metric

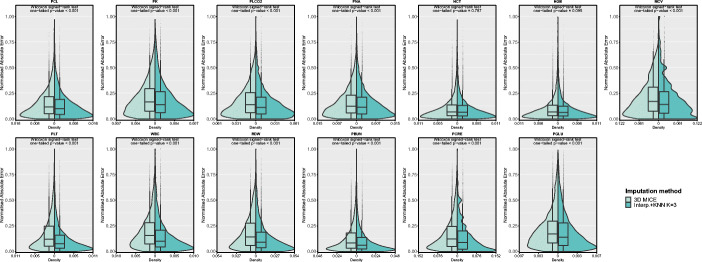
To assess the statistical significance of the improvement, we performed a one-tailed paired Wilcoxon signed-rank test on the nAEs obtained on the test set with 3D-MICE and Interp.+KNN for each analyte. Since the nRMSD can be directly derived from the nAE values (see (1) and (2)), the performed statistical tests can be used to assess the significance of the improvement in terms of both error measures. The test results in p values < 0.001 for 11 out of 13 analytes, while the features Hematocrit and Hemoglobin, whose p values are equal to 0.787 and 0.095 respectively, show no statistically significant improvement in terms of imputation error. This result is also confirmed by both the exiguous difference in the nRMSD values (less than 1% on the test set) obtained by our method compared with those of 3D-MICE for Hematocrit and Hemoglobin, and the reversal of the sign of the improvement on these analytes between training and test set. Figure 3 compares the nAE distributions, showing the shift to lower error values for the Interp.+KNN method with respect to the baseline.

Fig. 3.

Normalised absolute error distributions obtained with 3D-MICE and Interp.+KNN with K = 3 on the test set

Discussion

Both the interpolation-based and the KNN-based approaches always yield imputed values in the range of the existing data; more specifically, the intra-patient implementation preserves the analyte dynamic range of each patient.

The integration of the MIC in the weighted KNN approach adds some data-driven knowledge to the procedure. In the MIC computation (see Fig. 1), a few relationships that can be expected from the clinical literature emerge. Hematocrit and Hemoglobin, that present a normal ratio of 1:3 in healthy subjects and possibly altered values in the pathological ones [15], have the highest MIC value; similarly, the MIC value for Blood Urea Nitrogen and Creatinine is also high, being these analytes both referred to the renal function and with a normal ratio ranging from 10:1 to 20:1 [13]. It is interesting to observe how these pairs of features perform differently when this cross-sectional information is incorporated in the KNN imputation procedure, though they both have high MIC values. The weighted KNN outperforms the linear interpolation approach for Hematocrit and Hemoglobin, while falling behind for Blood Urea Nitrogen and Creatinine. This could be due to two possible reasons: (1) some analytes follow a linear trend in the intervals containing the missing values, or (2) the information included in the features themselves, exploited by the interpolation, is stronger than the cross-information. In the specific case of Blood Urea Nitrogen and Creatinine, the intra-feature information could be prevailing due to the low missingness rate (less than 5% after masking) which reinforces the latter hypothesis. The presence of specific patterns in the patients’ missing values is another fact that could promote the effectiveness of one method against the other. The absence of many analytes in one visit could decrease the effectiveness of the weighted KNN procedure while recurring missing measures of one specific analyte could penalise the interpolation-based approach.

In the KNN approach, the selection of a small K parameter ensures a good compromise between imputation performance and the need to preserve the original distribution of the data—a very important characteristic any imputation method should satisfy. Indeed, as a rule of thumb, it is advisable to limit the number of K neighbours, because of the risk of severely impairing the original variability of the data [4]. This matter requires particular care, since using the imputation accuracy (as measured for instance by the nRMSD) as the sole parameter selection criteria could lead to the choice of a large K value, while completely neglecting the data distortion aspect.

In general, with a KNN approach, the imputation precision is subject to the degree of dependencies the feature with missing data has with other features in the dataset; imputing features with little or no dependencies could lead to a lack of precision and could introduce spurious associations by considering dependencies where they do not exist [4]. In our approach, this risk is realistically mitigated by selecting the best performing method for each feature, the interpolations replaces the KNN approach on those analytes where the latter performs poorly.

It is worth noticing that the proposed algorithm is very time efficient. On a workstation with an Intel® Xeon® W3680 CPU (6 cores/12 threads @ 3.33GHz, 12MB L3 cache) and 24GB of DDR3 RAM, running Ubuntu Linux 16.04 LTS, our method can impute a whole dataset of 8267 subjects with roughly 200,000 visits in less than a minute; 3D-MICE requires several hours to impute the same dataset.

Conclusion

We introduce a novel algorithm that combines linear interpolation with weighted KNN for the imputation of longitudinal clinical laboratory test results across multiple visits of ICU patients. The KNN imputation integrates cross-sectional information by effectively using the MIC among analytes as weights for the distance metric. The proposed algorithm was shown to outperform 3D-MICE, a state-of the art method that combines MICE and GP-based imputation.

As future work, we plan to enhance the proposed methodology by refining the interpolation and weighted KNN steps, and by possibly adding new imputation strategies, thus expanding it into a full-fledged ensemble of imputation methods suitable to impute multiple types of clinical and laboratory data. Moreover, it would be very interesting to determine what thresholds of existing missing data and co-dependencies among features would begin to have an impact on the performance of the proposed approach. We also plan to run these experiments on additional real-world datasets.

The proposed imputation algorithm was implemented in R, and is freely available at: https://www.github.com/sebastiandaberdaku/PD_Impute.

Funding Information

This research has been partially supported by the University of Padova project C94I19001730001 “DECIPHER-ALS. Deconstruct and rebuild phenotypes: a multimodal approach toward personalised medicine in Amyotrophic Lateral Sclerosis” and by the Italian Ministry of Education, University and Research (MIUR) under the initiative “Departments of Excellence” (Law 232/2016).

Compliance with Ethical Standards

Conflict of Interest

The authors declare that they have no conflict of interest.