Describing Intersectional Health Outcomes

Abstract

Background:

Intersectionality theoretical frameworks have been increasingly incorporated into quantitative research. A range of methods have been applied to describing outcomes and disparities across large numbers of intersections of social identities or positions, with limited evaluation.

Methods:

Using data simulated to reflect plausible epidemiologic data scenarios, we evaluated methods for intercategorical intersectional analysis of continuous outcomes, including cross-classification, regression with interactions, multilevel analysis of individual heterogeneity (MAIHDA), and decision-tree methods (classification and regression trees [CART], conditional inference trees [CTree], random forest). The primary outcome was estimation accuracy of intersection-specific means. We applied each method to an illustrative example using National Health and Nutrition Examination Study (NHANES) systolic blood pressure data.

Results:

When studying high-dimensional intersections at smaller sample sizes, MAIHDA, CTree, and random forest produced more accurate estimates. In large samples, all methods performed similarly except CART, which produced less accurate estimates. For variable selection, CART performed poorly across sample sizes, although random forest performed best. The NHANES example demonstrated that different methods resulted in meaningful differences in systolic blood pressure estimates, highlighting the importance of selecting appropriate methods.

Conclusions:

This study evaluates some of a growing toolbox of methods for describing intersectional health outcomes and disparities. We identified more accurate methods for estimating outcomes for high-dimensional intersections across different sample sizes. As estimation is rarely the only objective for epidemiologists, we highlight different outputs each method creates, and suggest the sequential pairing of methods as a strategy for overcoming certain technical challenges.

Descriptive studies are integral to epidemiology, to identify health inequities and inform further study. Methods advances in recent decades have focused heavily on analytic epidemiology and causal modeling.^1,2 Methods for descriptive epidemiology have remained comparatively stagnant, often presented as “Table 1” means or percentages for a sample or population, or cross-tabulated across a small number of categories. An ongoing focus on health disparities—amplified by a need to assess larger numbers of intersections of social identities or positions and augmented by innovations in data analytic methods—suggests it is time to focus on advancing descriptive statistics, a foundational part of epidemiologic research.

TABLE 1.

Distributions of Variables in Data Generation Models 1 and 2

Variable	Analogous Social Position	Model 1: Categorical Inputs		Model 2: Mixed Inputs (Categorical And Continuous)
		Type	Distribution	Type	Distribution
X1	Income	Categorical	P(X1=0) = 0.25 P(X1=1) = 0.25 P(X1=2) = 0.25 P(X1=3) = 0.25	Continuous (split in quartiles to create intersections for estimation)	Mean = 0, Variance = 1
X2	Racialization (person of color, non-POC)	Binary	P(X2=1) = 0.2	Binary	P(X2=1) = 0.2
X3	Sex/gender (male, female)	Binary	P(X3=1) = 0.5	Binary	P(X3=1) = 0.5
X4	Education (completed postsecondary, did not complete)	Binary	P(X4=1 X3=0) = 0.4 P(X4=1 X3=1) = 0.7	Binary	P(X4=1 X3=0) = 0.4 P(X4=1 X3=1) = 0.7
X5	Immigrant status (immigrant, nonimmigrant)	Binary	P(X5=1) = 0.25	Binary	P(X5=1) = 0.25
X6	Age	Categorical	P(X6=0) = 0.33 P(X6=1) = 0.33 P(X6=2) = 0.33	Continuous (split in tertiles to create intersections for estimation)	Mean = 0, Variance = 1

Increasingly incorporated into quantitative health research,³ intersectionality is an analytic sensibility rooted in Black feminist theory that acknowledges that individuals’ locations at intersections of multiple social identities or positions (e.g., gender, race, class) result in unique lived experiences of privilege and oppression.^4,5 Six core tenets have been identified,⁶ and recognized as relevant for population health research⁷: social inequality, power, social context, relationality, complexity, and social justice. Intersectional understandings of relationality, social inequality, and power have the potential to transform descriptive statistical approaches in epidemiology, although all tenets may play roles in conceptualization and interpretation, and in shaping broader analytic research. Under intersectionality, the impact of social positions is not assumed to be independent; rather, the interplay of power embedded in social hierarchies results in each being shaped by the others, such that experiences (and health) at each intersection can be constituted in intersection-specific ways. This reflects the core idea of relationality or interconnectedness, specifically the relational idea of coformation, that coformed categories may no longer be divisible into their parts.⁸ Just as sociodemographic variables of interest in health equity research typically represent social positions bound up in historical and contextual power relations, their coformation is driven by social power. In quantitative research, intersectionality undercuts the often errant assumption that effects of social identities or positions are not coformed and can be added together to estimate an outcome (as in main effects regression). For instance, we cannot assume to understand the health of Black immigrant men by summing average population effects of being Black, an immigrant, and male.

Intercategorical intersectional research approaches focus on experiences and outcomes across intersections,⁹ and thus are particularly applicable to epidemiologic studies aiming to describe health and identify disparities, including at infrequently studied intersections.¹⁰ Although epidemiologic convention holds that heterogeneity of effects should be analyzed only with prior evidence or justification, intersectionality provides a theoretical rationale for switching this default, avoiding assumptions of homogeneity by estimating outcomes across intersections. Although the original convention is rooted in concerns regarding hypothesis testing and inflated total type 1 error, our primary objective is, instead, valid outcome estimates for coformed intersectional population groups. Intersectional models lead to different outcome estimates compared with nonintersectional models that assume effects are purely additive.¹¹

When applying an intersectional framework to descriptive studies, there are alternative approaches for data analysis beyond conventional methods of regression with interaction terms or simple cross-classification (reporting intersection-specific unadjusted means). A systematic review of methods in quantitative intersectionality research identified multilevel analysis of individual heterogeneity and discriminatory accuracy (MAIHDA) and decision trees as novel methods used to assess health across high-dimensional intersections formed from more than two or three social identities/positions.³ Although new, MAIHDA has been suggested as the “gold standard” for this purpose.^12,13 Nonparametric decision-tree methods use covariates to create groups with similar outcomes by partitioning data according to a set of decision rules. They do not provide standard errors for group estimates, an inherit limitation for epidemiologic analyses. However, they allow many covariates and any level of interaction without prior specification, and can be used for variable selection, to identify a set of covariates best suited to predict an outcome.

This study evaluates three statistical and three decision-tree methods for estimating health outcomes across a large number of intersections: regression with interaction terms, cross-classification, MAIHDA, classification and regression trees (CART), conditional inference trees (CTree), and random forest. This evaluation focuses on descriptive, noncausal analyses with continuous outcomes. These methods, while not unique to intersectionality analyses, are able to independently estimate mean outcomes for coformed intersections. We first present a simulation study evaluating estimation accuracy of intersection-specific outcome means for all methods, and performance in variable selection for decision-tree methods. We then present an application of each method using National Health and Nutrition Examination Survey (NHANES) 2015 to 2018 data on systolic blood pressure (SBP). Although there has been debate on whether all intersections are of sufficient value for study,^10,14 our study will assume interest in estimating outcomes for all intersections formed across a set of social positions, as is common practice in intersectional analyses using population data. Notably, although our focus is intersectionality and health inequities, the results may also be useful in other epidemiologic contexts where outcome heterogeneity is assessed.

SIMULATION STUDY

Simulation Methods

Simulation Process

We chose variable and sample size characteristics to reflect published research studying high-dimensional intersections.^11,12,15 In data generation model 1, all input variables were categorical; model 2 included categorical and continuous variables (distributions of input variables are provided in Table 1). Formulas to generate the continuous outcome Y were as follows:

Model 1 (Categorical inputs):

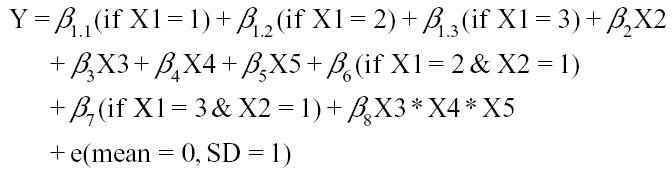
Model 2 (Mixed inputs):

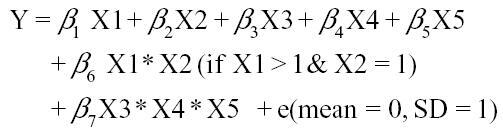
X1 and X6 were both multicategorical or continuous in model 1 and model 2, respectively, and all other variables were binary. We simulated each model over 1,000 replications for four sample sizes (N = 2,000, 5,000, 50,000, 200,000). For each replication, effect sizes for X1 to X5 were selected from a truncated normal distribution (SD = 1) between 0.06 and 1.94, or –0.06 and –1.94. We determined minimum effect size by a power analysis (see eAppendix 1; http://links.lww.com/EDE/B901 for details). X6 had no effect on the outcome.

Each simulated model resulted in 192 intersections, (4*2*2*2*2*3 = 192), for which outcome Y was estimated by each method. Analyses were conducted using R software version 3.6.1 (R Foundation for Statistical Computing, Vienna, Austria).¹⁶ Full simulation code is available online (https://github.com/m-mahendran/methods_for_intersectionality_simulation).

Description of Methods

Conventional Statistical Approaches

For a nonintersectional comparison, we included a main effects linear regression with variables X1 to X6. Cross-classification was the descriptive approach of taking the outcome mean for each intersection, with no statistical adjustments. The correctly specified regression model included all main effects and only the interactions from the true model, X1*X2 and X3*X4*X5 (including lower-level terms X3*X4, X4*X5, and X3*X5). This demonstrates a best-case nonrealistic scenario, where relevant interaction terms are known a priori. In contrast, the saturated regression model included all possible interaction terms. We emphasize that we included interaction terms to improve intersection-specific estimation rather than to identify statistically significant interactions.

MAIHDA

The MAIHDA working model can be represented as

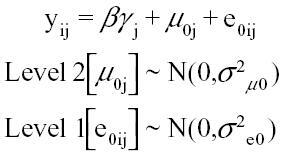
where i is each individual in intersection j, γ_j represents a vector of the intercept and main effect predictors, and β is a vector of the parameter values.¹² Fixed effects are assigned to each social position, with no interaction terms, and random intercepts for each intersection (μ_0j). The term (e_0ij) is for individual-level error. All individuals in the same intersection were assigned the same random intercept, and the same fixed effects (variables X1 to X6). Published applications use Bayesian models with uninformative priors. Due to computational power and time restraints in running 1,000 simulations for multiple scenarios, this simulation used frequentist analysis. A brief simulation in eAppendix1; http://links.lww.com/EDE/B901 demonstrates that Bayesian and frequentist models yield similar results, given the use of uninformative priors. Analysis was conducted using the R-package “lme4.”¹⁷

Decision trees

For CART, the variable used to split the data is selected by a predetermined criterion (here, reducing the sum of squares).¹⁸ Tenfold cross-validation was performed to select the complexity parameter with minimal cross-validation error. CTree selects covariates using univariate regression models, and then finds a variable split with the strongest association with the outcome, using an alpha of 0.05. For both methods, this process is repeated iteratively for each resulting subgroup, until a predetermined stopping criterion is satisfied. Default minimum node size was 20. For random forest, multiple decision trees are built from bootstrapped subsamples and aggregated to create predictions. The splitting criterion was response variance (node impurity), with a threshold improvement value of 0.05. Models were built with 500 trees, tuned using the parameter mtry by a step factor of 1, and the default minimum node size was 5. The variable importance measure, which assesses variables for their quantitative relevance to the outcome, was based on reductions in impurity. Analyses for CART, CTree, and random forest were respectively run using R-packages “rpart”,¹⁹ “partykit”,²⁰ and “tuneRanger”²¹ (selected for its quick implementation and built-in tuning function).

Outcomes

Primary Objective: Evaluation of Intersection-Specific Estimation Accuracy

Ground truth was defined as the outcome mean within each intersection. Accuracy was then evaluated by mean squared error (MSE),

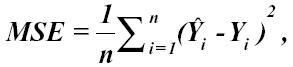
where n was 192 (reflecting the 192 intersections), 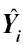was the estimated mean for intersection i, and 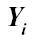was the true population mean for intersection i, taken from the data generation formulas. As cross-classification and MAIHDA cannot produce estimates for intersections with no respondents, MSE calculations for these methods excluded up to 13 intersections at N = 2,000, and up to 3 at N = 5,000. Note that accuracy was calculated at the population level (for each intersection), rather than the individual level, so that each intersection was equally weighted. In the context of intersectionality and health equity, this emphasized methodologic fairness by avoiding default prioritation of accuracy for numerically larger intersections, as multiply marginalized intersections are often less populated.

Secondary Objective: Identification of Individual Social Identity/Position Variable Relevance

We define variable selection for descriptive intersectional research as a tool to refine a set of social positions to include in analysis, by identifying the variables most quantitatively relevant to the outcome, a goal that differs from hypothesis testing. For CART and CTree, we assessed variable selection by the percentage of simulation replicates where each variable was used as a splitting variable. An ideal method would split on X1 to X5 100% of the time, and never on X6, to correctly identify the presence or absence of their simulated effects. We also presented the mean number of leaves or subgroups in the tree. We assessed variable selection for random forest using the average variable importance measure, as models produce no single splitting pattern; ideally X6 would have the lowest mean variable importance measure values. Variable selection was not assessed for single-level regression and MAIHDA, as they do not produce singular measures of variable relevance.

Simulation Results

Estimation Accuracy

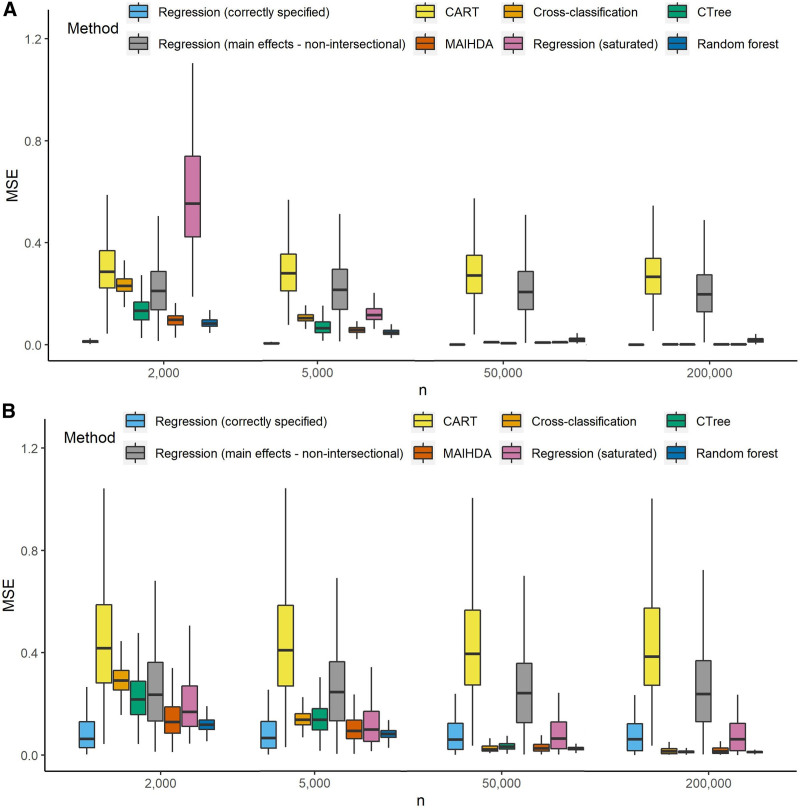
Accuracy is summarized in Figure 1, via. boxplots presenting the distribution of the estimation MSE over 1,000 simulations. Nonintersectional main effects regression had poorer estimation accuracy compared with the majority of the intersectional methods, especially at larger sample sizes. Among intersectional methods, for smaller sample sizes, the least accurate estimators were CART, regression (saturated model), and cross-classification, and the best performers were MAIHDA, correctly specified regression, and random forest. At larger sample sizes, CART had the highest estimation error, although all other intersectional methods produced an MSE near zero. One exception is that for models with mixed inputs at N ≥ 50,000, the single-level regression methods performed slightly worse than other non-CART intersectional methods.

FIGURE 1.

A,B, Boxplots of the MSE of intersection estimations for four different sample sizes (graph excludes outliers): (A) Categorical inputs and (B) Mixed inputs. Methods include three single-level regression models, the MAIHDA, cross-classification, and three tree-based methods: CART, CTree, and random forest. CART, classification and regression trees; CTree, conditional inference trees; MAIHDA, multilevel analysis of individual heterogeneity and discriminatory accuracy; MSE, mean squared error.

Individual Social Identity/Position Variable Relevance

Variable selection results are presented in Table 2 for CART and CTree, and Table 3 for random forest. CART split less frequently on X1 to X5 than CTree, but CTree was more likely to split on X6 than CART, this increasing with increasing sample size. Although CTree split on all relevant variables the majority of the time at N = 2,000, the number of leaves indicated that not all relevant subgroups were identified. For variables X1 to X5 there were 64 possible unique subgroups, and CTree identified an average of only 24 at N = 2,000. For random forest, X6 consistently had the lowest variable importance measure in the categorical inputs scenario. However, for the mixed inputs model at N = 2,000, variables X2 to X6 had similar importance values; which variable was least important was difficult to distinguish.

TABLE 2.

CART and CTree Splitting Percentages (% of Replications Variable Is Split on in Tree) and Average Number of Leaves

		CART				CTree
		N = 2,000	N = 5,000	N = 50,000	N = 200,000	N = 2,000	N = 5,000	N = 50,000	N = 200,000
Categorical inputs	×1 (%)	96.3	96.2	96.7	96.7	100	100	100	100
	×2 (%)	55.4	53.5	51.1	50.3	98.6	100	100	100
	×3 (%)	79.5	79.2	76.3	77.5	99.3	100	100	100
	×4 (%)	81.9	79.7	77	78.1	99.4	99.9	100	100
	×5 (%)	78.3	77.9	73.2	74.2	99.4	100	100	100
	×6 (%)	0	0	0	0	41.8	64.1	91	94.5
	Average leaves (2.5th, 97.5th percentile)	9 (5, 13)	9 (5, 13)	8 (4, 12)	9 (5, 13)	24 (12, 36)	34 (19, 49)	56 (39,68)	62 (50,70)
Mixed inputs	×1 (%)	93	92.5	91.3	92.3	99.6	99.9	100	100
	×2 (%)	56	54	49.7	52.8	98.2	99.7	100	100
	×3 (%)	66.5	67.7	63.5	64.4	96.4	99.7	100	100
	×4 (%)	67.5	69.8	64.3	62.7	98.3	99.6	100	100
	×5 (%)	56.9	57.2	54.6	53.3	98	99.9	100	100
	×6 (%)	0	0	0	0	34.6	55	92.5	98.8
	Average leaves (2.5th, 97.5th percentile)	10 (5, 14)	10 (5, 14)	9 (5, 14)	10 (5, 14)	34 (12, 59)	56 (19, 95)	162 (47, 276)	279 (88, 449)

CART indicates classification and regression tree; CTree, conditional inference tree.

TABLE 3.

Average VIM From Random Forests Fitted to Categorical and Mixed Input Models at N = 2,000 and N = 200,000

		N = 2,000	N = 200,000
Categorical inputs	×1	616	57,416
	×2	231	19,919
	×3	651	65,800
	×4	698	64,650
	×5	339	31,567
	×6	72	85
Mixed inputs	×1	2,731	239,953
	×2	308	31.906
	×3	642	63,981
	×4	635	63,664
	×5	325	32,870
	×6	552	9,558

VIM indicates variable importance measures.

EXAMPLE NHANES ANALYSIS—SYSTOLIC BLOOD PRESSURE

As an illustrative example of how results differ across methods, we present a descriptive analysis using 2015–2018 NHANES data to identify health disparities in SBP, an important risk factor for cardiovascular disease.²² Differences in SBP across US population groups are well documented,²³ allowing comparison between results and expectations. Our example also demonstrates how methods can be used sequentially for data-driven variable selection and intersection estimation. In practice, intersectional approaches would incorporate existing theoretical or community knowledge into variable selection, and applications of such a data-driven sequential approach may be limited. Our evaluation will focus on methods performance, but our discussion will elaborate on balancing quantitative methods with theoretical considerations.

Example Analysis Methods

Data

NHANES uses a complex multistage probability sample of the US population.²⁴ Ethical review was not required as data are publicly available. SBP (mm Hg) was calculated by averaging up to three measures. Eight social position variables were used to potentially form the intersections (Table 4). After removal of missing data, sample size was N = 9,124.

TABLE 4.

NHANES VIM Results for CART, CTree, and Random Forest

	CART	CTree		Random Forest
	Splitting Variable (Yes/No)	Splitting Variable (Yes/No)	Impurity-based VIM	Permutation-based VIM	Permutation-based VIM, P value
Age (20–39, 40–59, 60+ years)	Yes	Yes	477,183.3	111.4	0.010
Gender (male, female)	Yes	Yes	38,325.7	10.5	0.010
Race/ethnicity (Hispanic, non-Hispanic White, Black, Asian, other)	No	Yes	52,847.6	13.6	0.020
Education (high-school education or less, at least some college education)	No	Yes	25,974.0	4.4	0.010
Marital status (married, not married)	No	Yes	16,299.8	2.2	0.010
Health insurance (insured, not insured)	No	Yes	14,982.7	3.5	0.010
Immigrant (born in the United States, immigrant)	No	Yes	12,195.0	6.0	0.792
Income (above federal poverty line, below)	No	No	12,368.3	1.5	0.188

CART indicates results for classification and regression trees; CTree, conditional inference trees; VIM, variable importance measure.

Analysis Methods

We first used the three decision-tree methods for variable selection. For random forest, in addition to the impurity-based variable importance measures, we calculated permutation-based variable importance measures and importance p values,²⁵ to provide a more interpretable measure for decision-making. For the purposes of our analysis, we then selected the four variables with the highest impurity-based variable importance measure to form intersections. We applied each method (excluding correctly specified regression as ground truth is unknown) to estimate mean SBP for each intersection. Method-specific outputs are provided in eAppendix 2; http://links.lww.com/EDE/B901.

Example Analysis Results

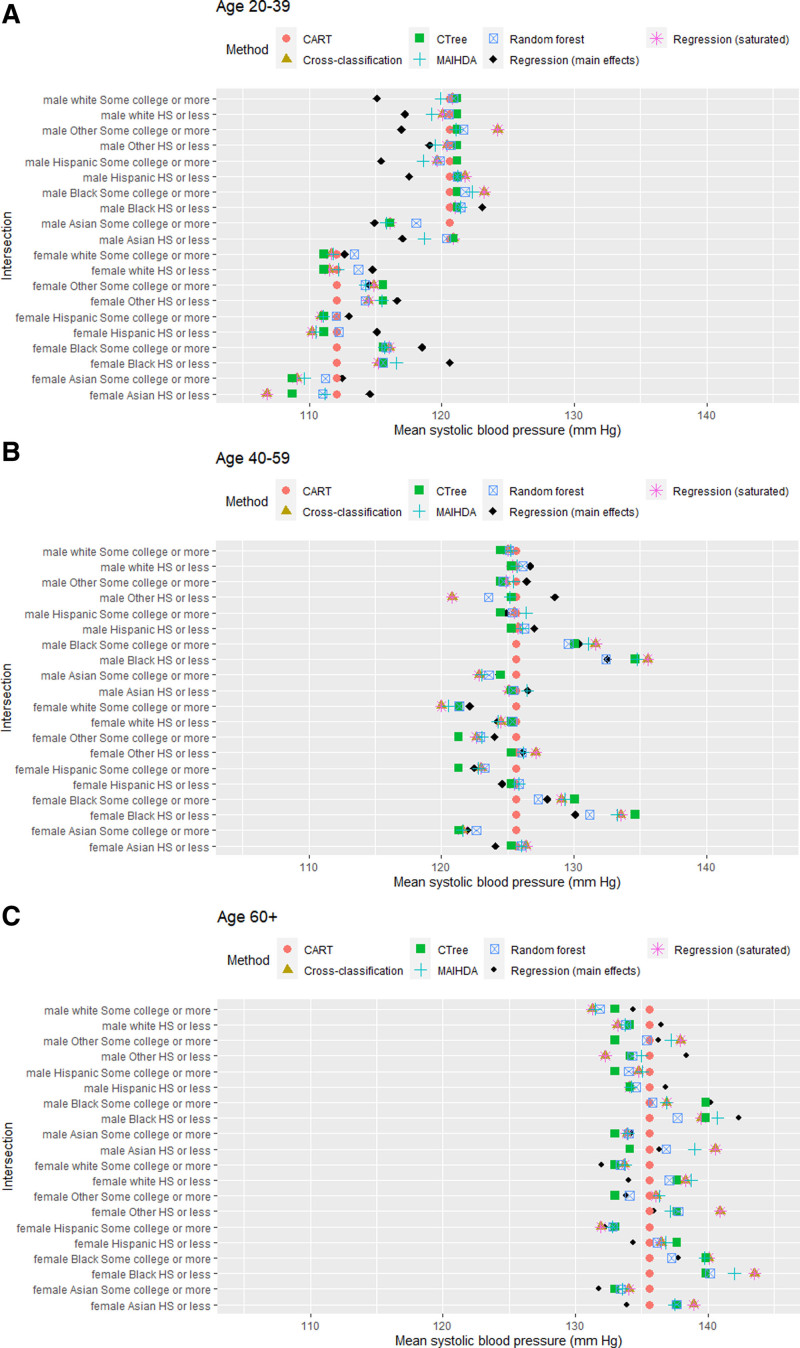
Variable selection results are summarized in Table 4. Similar to our simulation, CART was a more conservative estimator of variable relevance than CTree. We then used age, race, gender, and education to form 60 intersections.

Results in Figure 2A–C present the estimated unweighted mean SBP for each of the 60 intersections, by each method. Although effects were similar between some intersections, for other intersections the main effects analysis under- or overestimated effects compared with the intersectional methods. Outcome estimates also varied across intersectional methods. For example, for Black adults age 40–59 with a high-school education or less, choice in method resulted in an approximately 10 mm Hg difference in predicted SBP, a clinically significant difference.²² For cross-classification, MAIHDA, random forest, and regression, the highest SBP group was consistent: Black females age 60+ with a high-school education or less.

FIGURE 2.

A–C, Estimated mean systolic blood pressure (mm Hg) by intersection. Methods include two single-level regression models, MAIHDA, cross-classification, and three tree-based methods: CART, CTree, and random forest. CART, classification and regression trees; CTree, conditional inference trees; MAIHDA, multilevel analysis of individual heterogeneity and discriminatory accuracy.

CART analysis resulted in four final subgroups split by age and gender, although CTree produced 15 subgroups split by all four variables. For CART the highest SBP subgroup was all participants age 60+, and for CTree all Black participants age 60+. Because decision trees can create subgroups by splitting continuous variables, we present in eAppendix 2; http://links.lww.com/EDE/B901 CART and CTree models using a continuous rather than categorical age variable, with final subgroups increasing to five for CART, and 26 for CTree.

DISCUSSION

This study aims to support the adoption of intersectionality frameworks in descriptive epidemiologic research by assessing method performance for descriptive intercategorical intersectionality across large numbers of intersections. We present our resulting recommendations (Table 5) with several caveats: (1) Recommendations regard estimation performance, not which methods best match other intersectional objectives. (2) Although our use of methods aimed to follow common conventions, different parameters or options may change results sufficiently to alter recommendations. (3) “Variable relevance” refers to quantitative rather than social relevance. Finally, (4) Limitations regarding “small” sample sizes will apply less strictly when studying fewer intersections. Our simulation intentionally pushed limits to assess performance; we do not endorse some analyses, for example, a saturated regression model assessing 192 intersections at N = 2,000 (for a mean intersection size of 10.4), as reasonable expectations. Our NHANES analysis demonstrated a more realistic example assessing outcomes for 60 intersections at N = 9,000.

TABLE 5.

Recommendations for Methods When Assessing Continuous Outcomes

	Recommended Uses	Recommended With Potential Alterations	Not Generally Recommended	Not Applicable
Cross-classification	Estimation at large-sample sizesa		Estimation at small sample sizesa	Variable selection
Regression (saturated model)	Estimation at large-sample sizesa		Estimation at small sample sizesa	Variable selection (partial information)
MAIHDAb	Estimation at all sizes			Variable selection (partial information)
CARTc			Estimation at all sample sizes Variable selection
CTreed	Estimation at all sample sizes		Variable selection (may be improved with cross-validation for alpha)
Random forest	Estimation at all sample sizes	Variable selection: with adjusted VIMe

^aDefining sample size as “large” or “small” is relative to the number of intersections of interest. In our scenario with 192 intersections of interest, we considered smaller sample sizes to be N = 2,000 to 5,000 and larger sample sizes as N = 50,000 and greater. A smaller number of intersections under study would allow for smaller sample sizes.

^bMultilevel analysis of individual heterogeneity and discriminatory accuracy.

^cClassification and regression trees.

^dConditional inference trees.

^eVariable importance measure.

Although analytic aims vary, intersectionality researchers generally want accurate intersection-specific outcome estimates, with disaggregation of data where substantial heterogeneity exists. The nonintersectional main effects approach was a misspecified model, resulting in inaccurate intersection-specific estimates and no improvement with increasing sample size. All intersectional methods evaluated other than CART were suitable for large-sample estimation. At smaller sample sizes, random forest, MAIHDA, and CTree were more accurate estimators compared with conventional saturated regression or cross-classification. As an ensemble method, random forest is more stable and less prone to overfitting than regression or single-tree methods.^26–28 MAIHDA has weighted residuals to reduce effects of outliers within small intersections.¹² Note that main effects must remain in MAIHDA fitted models, even if not interpreted, to maintain the full effect of these weighted residuals.²⁹ Finally, saturated regression models performed slightly worse for the continuous inputs model, due to the nonlinear interaction in our data generation process which was unspecified in the fitted models. When exploring intersectional effects, nonlinear effects are not often considered in regression models, but could for example be incorporated using generalized additive models.³⁰

Although CART has been the most frequently applied decision-tree method in intersectionality research,³¹ it performed poorly across all sample sizes; its lack of improvement with increasing sample size has been previously noted.³² CART’s splitting criterion prematurely limits tree depth, and resulting estimates represent averages for still-heterogenous groups, thus not meeting the objective of identifying all intersections with prominent differences. In comparison, the CTree model will continue splitting, creating more accurate final estimates.

In our simulation, CART underidentified relevant variables during variable selection, while CTree had a high false-positive rate. Tuning CTree with the alpha parameter may reduce false positives by creating a higher significance threshold for splitting. For random forest, the variable importance measure was difficult to interpret for low values. A potential solution would be an adjusted variable importance measure,²⁵ which creates interpretable P values and adjusts for a known bias favoring continuous variables.³³ The NHANES analysis demonstrated how the quantitative variable selection process produces results similar to expected findings, such as the prominence of age, gender, and race as major predictors of SBP.²³

Importantly, purely data-driven variable selection risks creating intersections that are not socially relevant as intervention points or equity stratifiers. Variable selection in practice will often be based in theoretical knowledge of how structures of social power may affect outcomes. If a priori relevance of intersections is unclear, data-driven variable selection techniques can optionally support exploration of potential unknown heterogeneities or provide decision support in paring down infeasibly long lists of potential variables. For such uses, decision trees create a variable selection process that accounts for possible interaction effects between variables.

As decision trees lack variance estimation—a major limitation for estimation of population-level outcomes—a two-step process of variable selection followed by estimation using regression, cross-classification, or MAIHDA allows for the creation of outputs that typical epidemiologic research favors. As illustrated in our NHANES analysis, one could use random forest for data-driven identification of important variables to be encoded in a subsequent MAIHDA analysis. Alternately, one could use CTree to identify potential interactions to fit in a regression model within a sample too small to power a saturated-model regression. A limitation of two-step processes is that final variance estimates will not account for the selection process, and further work may be needed to incorporate methods of postselection inference.³⁴

A general consideration in the uses we describe is that focus on group means—the “tyranny of averages”—risks stigmatizing particular groups by classifying them as “high risk” while ignoring within-group heterogeneity.³⁵ In the simulation study, analyses included all explanatory variables. In real-word analyses, there would be unmodeled individual- and structural-level effects impacting the outcome. MAIHDA analyses produce measures of discriminatory accuracy, the percent of outcome variation due to the intersections.³⁶ For example, the final 60 intersections in the NHANES analysis produced a discriminatory accuracy of 22.06% (calculations in eAppendix 3; http://links.lww.com/EDE/B901), indicating substantial within-intersection variation. Calculations of intersectional discriminatory accuracy can be used in non-MAIHDA analyses as well to highlight heterogeneity of experiences within intersections and contextualize final results.

We note other capabilities and outputs of the selected methods in Table 6. For example, while single-level regression and MAIHDA produce no variable relevance measures, large effects of a variable in lower-order or interaction terms (in saturated regression) or in main effects or random intercepts (in MAIHDA) may suggest a variable as relevant. Effect estimates from the two methods do have different interpretations^37,38; however, these differences do not impact the utility of either method for estimation of intersection-level outcomes. Methods may have pragmatic as well as theoretical limitations. For example, decision-tree methods are data-adaptive and not theory-based; trees may oversplit, especially on continuous variables, and create subgroups that are too granular, or do not meaningfully map onto communities. Additional work is required to evaluate outputs in Table 6 for their theoretical match with intersectionality frameworks. We present in eAppendix 3; http://links.lww.com/EDE/B901 additional readings related to MAIHDA and decision trees.

TABLE 6.

Summary of Method Outputs and Capabilities

	Regression (Saturated Model)	Cross-Classification	MAIHDAa	CARTb	CTreec	Random Forest
Outcome estimation by intersection	X	X	X	X	X	X
Variance estimates for intersections	X	X	X
Effect size estimates comparing outcome across intersections	X	d	X
Identification of social identity/position variables relevant to the outcomef	e		e	X	X	X
Identification of social identity/position category subgroups relevant to the outcomef	e		e	X	X
Identification of interactions of social identity/position variables relevant to the outcomec	X			X	X
Ability to use continuous social identity/position variables without prior categorization	X			X	X	X
Visual subgroup identification through tree diagrams				X	X
Ability to control for confounding	X		X	X	X	X

^aMultilevel analysis of individual heterogeneity and discriminatory accuracy.

^bClassification and regression trees.

^cConditional inference trees.

^dCan be estimated using a linear regression

^eNo singular measure is produced that indicates overall relevance, but there is some information contained (see Discussion).

^fRelevance is variably defined and quantified.

Interpretation of final intersection-specific estimates should call on additional tenets of intersectionality such as social context. Intersectional positions reflect numerous contextual and structural factors, such as discrimination and healthcare accessibility, and interpretations should remain rooted in structural and interindividual concepts of social power. Moreover, critical consideration of how results may be affected by measurement or sampling biases is required. Although large population datasets offer an accessible way to map health disparities, the provided measures of social positions may not match a researcher’s question. Our NHANES analysis used measures that were not truly mutually exclusive (e.g., Black race and Hispanic ethnicity), or did not address multidimensionality (e.g., sex and gender), potentially limiting interpretability and utility. Finally, as our conceptualization of estimation in this study was for descriptive analysis, we did not address confounding. The regression-based and decision-tree methods can accommodate confounders,³⁹ but causal approaches are beyond the scope of this study.

We have focused on estimation rather than hypothesis testing. Intersectionality scholars have made clear that intersectionality in research is an approach, rather than a testable hypothesis.⁴⁰ Unlike additive models, methods that can incorporate interaction effects (i.e., some methods in this study) can more accurately produce estimates for intersections. Testing for a large number of interactions introduces the risk of identifying spurious interactions, which is a secondary reason our recommendations focus on accuracy of intersection-specific estimation, rather than statistical interaction. Accurately identifying intersectional population groups with favorable and unfavorable health outcomes is important to targeted research and policy and to identifying areas where existing single-identity or -position approaches to public health or healthcare access may produce inequity, and this is true regardless of whether or not those levels can be attributed to statistical interaction.

As simulation results are partially a result of the data generating process, results for continuous outcomes do not necessarily hold for binary or categorical outcomes, requiring further evaluation. We additionally welcome alternative ways of applying these methods that may improve performance, such as use of penalized regression methods to incorporate higher order terms and improve estimation accuracy.⁴¹ This study is not meant to limit the methods deemed suitable for intersectional research, but to act as a starting point for researchers searching for a more varied toolchest of quantitative methods.

We note that methods themselves do not make a study intersectional. Similarly, the approach presented is only one specific application of intersectionality. Methods in this study can incorporate intersectionality in other ways, for example, by including process-related variables such as discrimination to understand driving factors producing inequities. We urge researchers to be attentive to the core tenets of intersectionality in structuring research questions, choosing variables, interpreting results in the context of social power, and engaging with communities.^6,7,40 We consider this a starting point in a process of comparative evaluation of quantitative methods across a much broader range of intersectional research questions and data scenarios, including descriptive studies with categorical outcomes, consideration of match between theory and methods, causal intersectional methods, and greater attention to sampling, measurement, and research process, all to ultimately advance health equity through research.

ACKNOWLEDGMENTS

The authors wish to thank Yayuan Zhu for input into the design of this project and for comments on drafts, and Charlene Ronquillo, Paul Wesson, and Prerna Thaker for their valuable comments on an earlier version of this article.