Impaired expected value computations coupled with overreliance on stimulus-response learning in schizophrenia

Abstract

Background:

While many have emphasized impaired reward prediction error (RPE) signaling in schizophrenia, multiple studies suggest that some decision-making deficits may arise from overreliance on stimulus-response systems together with a compromised ability to represent expected value. Guided by computational frameworks, we formulated and tested two scenarios in which maladaptive representations of expected value should be most evident, thereby delineating conditions that may evoke decision-making impairments in schizophrenia.

Methods:

In a modified reinforcement learning paradigm, 42 medicated people with schizophrenia (PSZ) and 36 healthy volunteers learned to select the most frequently rewarded option in a 75-25 pair: once when presented with more deterministic (90-10) and once when presented with more probabilistic (60-40) pairs. Novel and old combinations of choice options were presented in a subsequent transfer phase. Computational modeling was employed to elucidate contributions from stimulus-response systems (“actor-critic”) and expected value (“Q-learning”).

Results:

PSZ showed robust performance impairments with increasing value difference between two competing options, which strongly correlated with decreased contributions from expected value-based (“Q-learning”) learning. Moreover, a subtle yet consistent contextual choice bias for the “probabilistic” 75 option was present in PSZ, which could be accounted for by a context-dependent RPE in the “actor-critic”.

Conclusions:

We provide evidence that decision-making impairments in schizophrenia increase monotonically with demands placed on expected value computations. A contextual choice bias is consistent with overreliance on stimulus-response learning, which may signify a deficit secondary to the maladaptive representation of expected value. These results shed new light on conditions under which decision-making impairments may arise.

Introduction

Reinforcement learning (RL) and decision-making impairments are a recurrent phenomenon in people with schizophrenia (PSZ) and are thought to play a key role in abnormal belief formation (1) and motivational deficits (2). While many have emphasized an impairment in stimulus-response learning (3–5), multiple studies suggest that some of these deficits may in fact arise from overreliance on stimulus-response learning together with a compromised ability to represent the prospective value of an action or choice (i.e. expected value) (e.g. (6, 7), for overview see Waltz & Gold (2)). However, such conclusions have typically been based on inferences, rather than experimental designs intended to reveal such effects. We therefore formulated and tested two hitherto unexplored scenarios motivated by the posited computations under which deficits in the representation of expected value should be most evident.

Optimal decision-making relies on a pas de deux between a flexible and precise representation of expected reward values, supported by orbitofrontal cortex (OFC) (8–10), which is complemented by a gradual build-up of stimulus-response associations, credited to dopaminergic teaching signals (reward prediction errors; RPEs) that project to striatum (11, 12). Previous work has demonstrated that maladaptive representations of expected value, rather than diminished stimulus-response learning per se, is one consistent feature of RL deficits in PSZ (13–16).

Findings of impaired representations of expected value in PSZ have often relied on computational models of learning and decision-making. In RL computational frameworks, it is thought that “Q-learning” and “actor-critic” models capture expected value and stimulus-response learning, respectively. In Q-learning (17), the RPE (the difference between expectation and outcome) directly updates the expected value of a choice option - similar to the representation of a reward value by OFC (18, 19) – and response tendencies are driven by large action values. In contrast, in the actor-critic framework (20), RPEs signaled by the critic – who observes outcomes - update its state value (e.g. being presented with a certain choice pair), rather than updating the value of each choice option separately. Importantly, the critic’s RPE additionally updates the actor’s response tendency for the chosen option. Thus, the actor develops response tendencies for choices associated with more positive (better than expected) than negative (worse than expected) RPEs signaled by the critic, and not on the basis of an exact estimate of reward value. It is thought that the slow build-up of the actor’s response tendencies, on the basis of an accumulation of RPEs, reflect DA-mediated changes in synaptic weights in basal ganglia (21–23). Crucially, because the RPE fulfills different roles in these two computational frameworks (that is, updating reward value directly versus modifying stimulus-response weights), it follows that, by definition, reward value is more precisely represented in the Q-learning than actor-critic frameworks. In one study, we showed that a computational modeling parameter that captured the balance between Q-learning versus actor-critic-type learning was tilted in favor of the latter in PSZ, suggesting relative underutilization of expected value and, perhaps secondarily, overreliance on stimulus-response learning (6). To date, however, little is known about the conditions under which deficits in the computation of expected value should be most observable.

We therefore sought to test two predictions of our theoretical account, which emphasizes maladaptive representation of expected value (Q-learning) in PSZ:

1. Counter-intuitively, and in contrast to many situations where PSZ may be most impaired at high levels of difficulty, our model based on less precise representations of reward value (decreased Q-learning) predicts that PSZ should suffer the largest decision-making deficits for the easiest value discriminations: that is, when the value difference between two competing options increases.

2. Secondly, if the relative contribution of actor-critic type learning is greater in PSZ - because of a decrease in Q-learning - then one might observe biases in action selection among choice options that have identical reinforcement probabilities, based on differences in critic RPEs. In the actor-critic architecture, RPEs are evaluated relative to the overall reward rate of the context. Thus, rewards in contexts with low reward rates elicit larger RPEs than those presented in more deterministic contexts. Therefore, a second diagnostic prediction is that PSZ should elicit observable context-dependent choice biases, even among items with identical reinforcement histories.

In the current study, we test these two hypothesized consequences of deficits in the representation of expected value using a modified RL paradigm. Participants were presented with two pairs of stimuli with identical reward value; one pair was presented in a “reward-rich” context (where the other pair had a higher reward rate), while the other pair was presented in a “reward-poor context” (where the other pair had a lower reward rate). Afterwards, participants were presented with old and novel combinations of choice options. We exploited the wide range in reward value to test our hypothesis relating to performance deficits as a function of the value difference between two competing options. Pairs with identical reward value in different contexts allowed us to address hypotheses relating to a contextual choice bias that should be present to the degree that individuals rely on actor-critic type learning.

To accomplish these aims, we used a previously-validated hybrid computational model that estimates one’s tendency to use Q-learning versus actor-critic along a parametric continuum (6). As observed previously (6), we expected PSZ to rely less on Q-learning than actor-critic, resulting in the aforementioned deficits.

Methods and Materials

Sample

We recruited 44 participants with a Diagnostic and Statistical Manual of Mental Disorders, Version IV (DSM-IV) diagnosis of schizophrenia or schizoaffective disorder (PSZ) and 36 healthy volunteers (HV). Two PSZ were excluded; one participant was mistakenly administered an old version of the task, while another participant consistently performed far below chance, leaving a sample of 42 PSZPSZ were recruited through clinics at the Maryland Psychiatric Research Center. HV were recruited were recruited by advertisements posted on the Internet (Craigslist) and via notices on bulletin boards in local libraries and businesses. A diagnosis of schizophrenia or schizoaffective disorder in PSZ, as well as the absence of a clinical disorder in HV, was confirmed using the SCID-I (24). The absence of an Axis II personality disorder in HV was confirmed using the SIDP-R (25). 37 PSZ were diagnosed with schizophrenia; five PSZ were diagnosed with a schizoaffective disorder. Co-morbid disorders included obsessive-compulsive disorder (n=1), anxiety disorder (n=1), and a cannabis dependence disorder (in remission, n=1). All PSZ were on a stable antipsychotic medication regimen. No changes in medication dose/type were made in the four weeks leading up to study participation. Major exclusion criteria included: pregnancy, current illegal drug use, substance dependence (in past year), a neurological disorder, and/or medical condition affecting study participation. All participants provided written informed consent.

The study was approved by the Institutional Review Board of the University of Maryland SOM.

Clinical ratings

The avolition-apathy and asociality-anhedonia (AA) subscales of the Scale for the Assessment of Negative Symptoms (SANS; (26)) and positive symptom subscale of the Brief Psychiatric Rating Scale (BPRS) (27) were used as measures of negative and positive symptoms, respectively. Please see the supplemental text for details on these scales, as well as other sociodemographic and clinical variables.

Reinforcement Learning Paradigm

Participants completed an RL paradigm consisting of a 320-trial learning phase and 112-trial transfer phase.

Learning Phase

Participants were presented with pairs of stimuli and were asked to select one using their left (left choice) or right (right choice) index finger, after which they received positive (+$.05) or neutral ($0.00) feedback (Figure 1). The learning phase consisted of two 160-trial blocks in which four pairs were presented per block. In one block, two pairs were presented that rewarded optimal choices 90% of the time (and no reward on the remaining 10% of trials), together with two pairs that rewarded optimal choices 75% of the time (no reward 25%). In the other block, two pairs were presented that rewarded optimal choices 75% of the time (no reward 25%), together with two pairs that rewarded optimal choices 60% of the time (no reward 40%) (Figure 1). Feedback contingencies for the suboptimal choice were the mirror image of the optimal choice. Trial presentation was pseudo-randomized within each block and block order was counterbalanced among participants, as were block theme (butterfly or bird stimuli), option-probability pairing, and option-position pairing (left/right side of screen). Note that two out of four 75-25 pairs always comprised bird-themed stimuli, and the other two pairs butterfly-themed stimuli (Figure 1).

Figure 1.

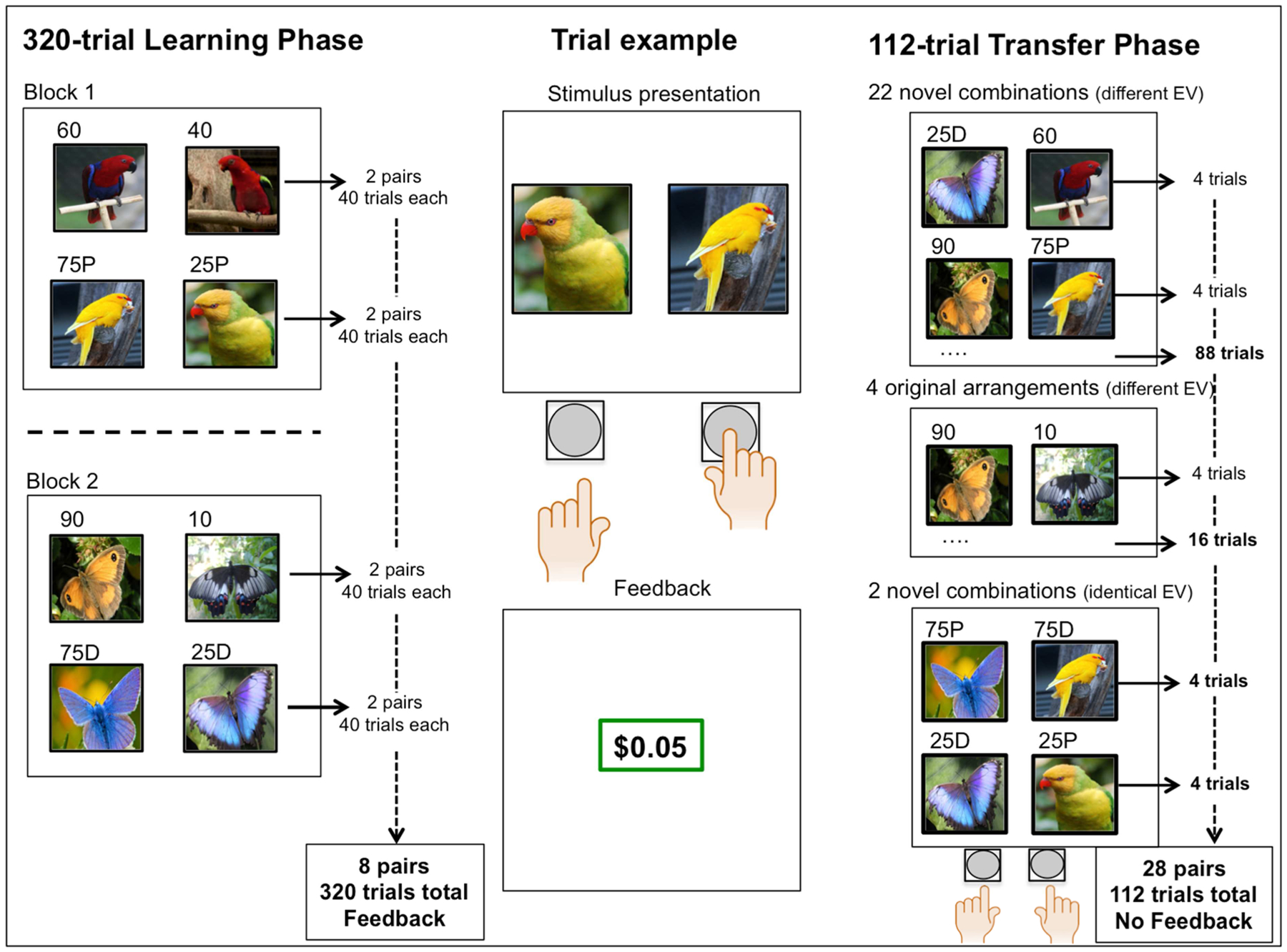
Schematic of the reinforcement learning paradigm

By combining 75-25 pairs with more deterministic (90-10) and probabilistic (60-40) pairs in separate blocks, we aimed to investigate context-dependent RL, meaning that perceived choice value (here, 75-25 pairs) might be dependent on contextual reward rate (the average reward rate of optimal choice options within a block). Henceforth, we will refer to 75-25 pairs that were presented together with 90-10 pairs as “75-25D” (“D” for the more deterministic context) and 75-25 pairs that were presented with 60-40 pairs as “75-25P” (“P” for the more probabilistic context).

Transfer Phase

The 112-trial transfer phase served two purposes: I) to assess the ability to compare choice options using their reward value, and, II) a formal test of a contextual choice bias.

Every possible combination of two choice options (new and original combinations) was presented and the participant was instructed to “select the option that was rewarded most often” (Figure 1). To prevent further learning, no feedback was delivered. Combining all possible choice options yielded twenty-eight combinations with non-identical expected value; twenty-two novel combinations (e.g. 90-60 or 75D-10) and four original combinations (90-10, 75-25D, 75-25P, 60-40). In addition, we produced two novel combinations with identical expected value; 75P-75D and 25P-25D. Table S1 provides an overview of all twenty-eight transfer pairs.

Note that there were two pairs of each contingency in the learning phase, with the exception of 75-25 pairs, of which there four. Thus, although every unique combination of choice options was presented only once in the transfer phase, there were always four presentations of each expected value combination (as an example; with two 90-10 pairs from the learning phase one can generate four unique 90-10 combinations in the transfer phase).

Computational model

In an attempt to relate deficits in expected value and a contextual choice bias to latent variables, we used a previously-validated hybrid model allowing for combined influences of Q-learning (action selection as a function of expected reward value) and actor-critic (basal ganglia dependent stimulus-response learning) frameworks on decision-making (6). This model was compared to a basic actor-critic and Q-learning model. The hybrid model had the best trade-off between model complexity, fit, and posterior predictive simulations, and contained six free parameters: a critic learning rate (αc), actor learning rate (α_a), Q learning rate (α_q), inverse temperature (β), mixing (m), and undirected noise (ε) parameter, which were estimated for every subject via maximum likelihood optimization. The supplemental text and Figure S1 contain a detailed description of the model and selection procedure, including the use of context (i.e. block) dependent state values for the critic and an ε-softmax choice function. After fitting the hybrid model to the learning phase data, the final action weights of all eight original pairs were used to simulate transfer phase performance for all pairs (n(simulations)=250 for every participant).

Statistical analyses

Performance on both pairs of each probability level (90-10, 75-25D, 75-25P, 60-40) was averaged. Next, learning phase trials were divided into four bins of 10 trials for each probability level. A 2×4×4 repeated-measures ANOVA using group status (predictor) and probability level (4 levels) and trial-bin (bins; 4 levels) as dependent variables was run to test for a group-by-condition-by-time interaction. Group-by-time and group-by-condition interactions were also investigated. Greenhouse-Geisser sphericity-corrected values were reported when assumptions were violated.

Transfer phase accuracy was averaged across all four presentations of every unique (n=28) combination of expected values and compared using two-sample t-tests. Transfer phase pairs were next ranked on their value difference (see Table S1 for details regarding trial combinations). A logistic regression analysis with value difference (left-right option) as predictor and correct choice (left vs. right button) as dependent variable was conducted to test the hypothesis that PSZ show impaired performance with increasing value difference. Individual value difference slopes were compared in a two-sample t-test.

Context-dependent learning was investigated using a two-sample t-test, as well as a one-sample t-test to compare preference for either option against chance. As a direct measure of context-dependent learning, we focused on trials where 75P was coupled with 75D. As an indirect measure of context-dependent learning, average performance on all trials where 75P and 75D stimuli were presented with any other option (excluding the 25 stimulus that they were originally partnered with) was compared in a 2×2 group-by-pair ANOVA. Table S1 provides a detailed overview of transfer phase trials that were used for this analysis. Significance thresholds for performance data were set to p<.05.

Correlation analyses between model parameters, clinical, and psychometric variables were carried out using Pearson’s r, Spearman’s ρ and subgroup splits (the latter two when distributions were skewed). Significance thresholds for correlation/subgroup split analyses were Bonferroni-corrected for the number of parameters in the model (p_{Bonferroni-corrected}=.05 = p_uncorrected=.008).

Results

Demographics

Participant groups were matched on most demographics. However, PSZ did have a lower IQ-score than HV, as well as poorer MATRICS performance (Table 1).

Table 1.

Demographics

		HV (n=36)	PSZ (n=42)	t/X2	p
Age		42.81 (8.86)	44.60 (8.26)	−.92	.36
Gender [F, M]		[12, 24]	[13, 29]	.05	.82
Race
African American, Caucasian, Other		[11,24,1]	[13,25,4]	2.74	.60
Education level (years)		14.86 (1.99)	12.69 (2.20)	4.49	<.001
Maternal education level		13.60 (2.19)	13.46 (2.51)	.25	.80
Paternal education level		13.29 (3.05)	13.89 (4.20)	−.70	.48
WASI-II IQ score		114.86 (10.59)	98.10 (14.89)	5.76	<.001
MATRICS Domains
Processing Speed		54.66 (9.47)	35.12 (11.57)	7.99	<.001
Attention/Vigilance		51.77 (11.47)	41.45 (12.44)	3.75	<.001
Working Memory		54.23 (10.16)	38.02 (11.13)	6.62	<.001
Verbal Learning		50.11 (10.58)	36.69 (8.10)	6.30	<.001
Visual Learning		45.46 (11.23)	35.02 (13.49)	3.64	<.001
Reasoning		53.84 (9.99)	43.02 (9.64)	4.82	<.001
Social Cognition		50.91 (8.93)	36.83 (11.12)	6.04	<.001
Antipsychotic Medication
Total Chlorpromazine		-	332.36 (424.21)	-	-
Total Haloperidol		-	6.88 (9.10)	-	-
Clinical Ratings
BPRS Positive (sum)		-	9.30 (5.37)	-	-
SANS AA/RF (sum)		-	17.00 (7.73)	-	-
SANS AFB/Alog (sum)		-	10.67 (7.89)	-	-

^*MATRICS ratings and IQ score missing for 1 HV

^*M Education missing for 1 HV and 5 PSZ

^*P Education missing for 1 HV and 4 PSZ

^*CPZ/Haldol missing for 1 PSZ

Learning Phase performance

We observed a group*probability interaction (F_3,228=4.39, p=.005), such that HV outperformed PSZ in the 90-10 (p=.002), 75-25D (p=.007), 75-25P (p=.04), but not 60-40 (p=.63), probability condition (Figure 2A). Group*probability*time (F_9,684=.98, p=.46) and group*time (F_3,228=.62, p=.60) interactions were not significant. Performance on 60-40 trials in bin 4 was significantly above chance for both groups (HV: t₃₅=2.88, p=.007; SZ: t₄₁=2,64, p=.01). See Figure S2 for individual data points for each probability level.

Figure 2. Learning and transfer phase performance.

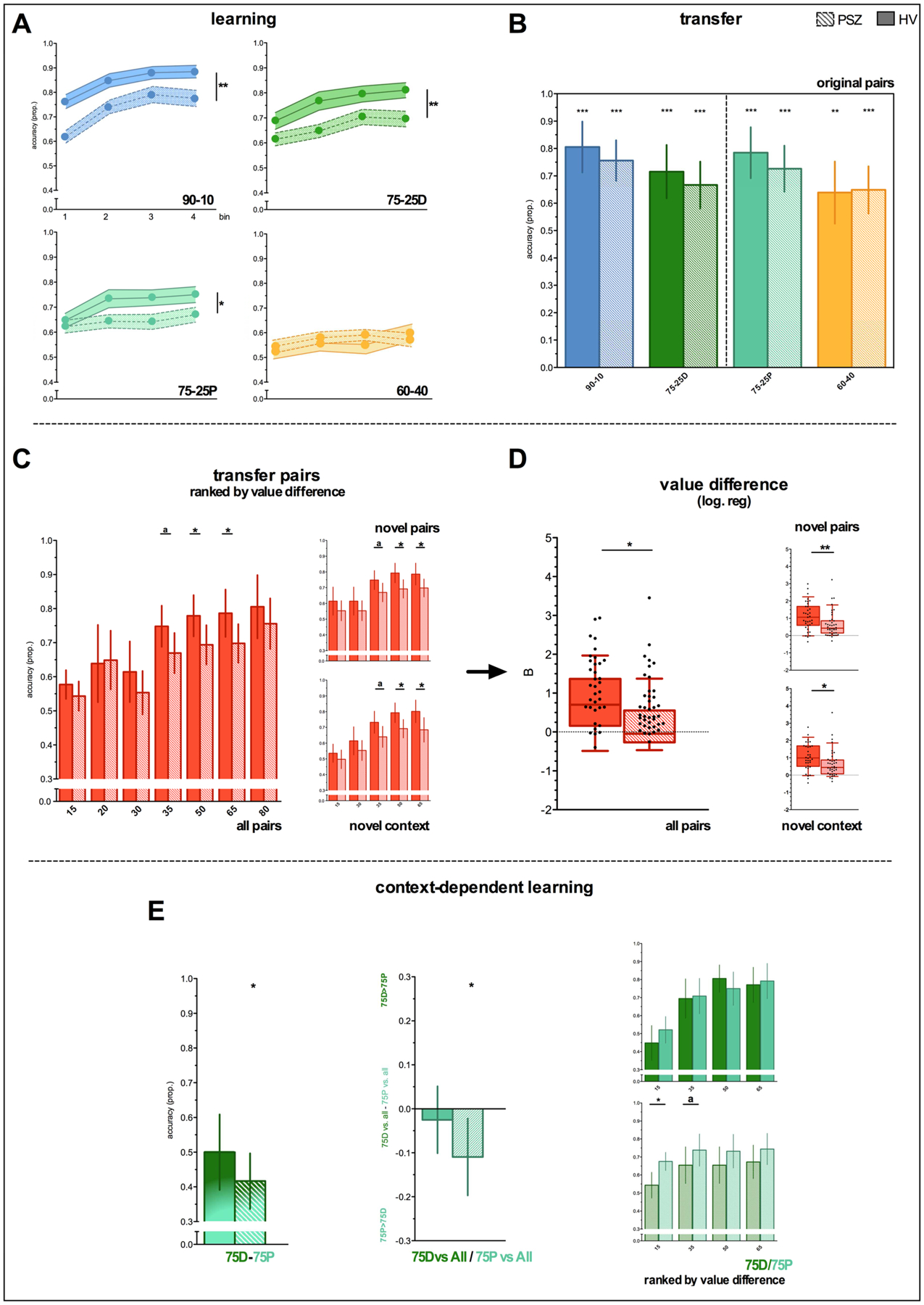
Solid bars represent HV; bars with diagonal lines represent PSZ. *= p<.05, ** = p<.01, *** = p<.001, a = trend (p = .06–.09). Error bars represent 95% CI, except for learning phase data, where bars represent SEM. Asterisks above error bars represent significant preference against chance; asterisks above solid horizontal line represent between- or within-group differences. Panel E, center: “75D vs. All/75 vs. All” = performance on 75D/P trials versus all choice options of non-identical value. Panel E, right: separate plots for 75D and 75P versus other choice options broken down by their value difference (x-axis).

Transfer Phase performance

Despite poorer learning accuracy in PSZ there were no group differences in transfer accuracy for 90-10, 75-25D, 75-25P or 60-40 pairings (all p>.39; Figure 2B), with accuracy above chance on all pairs.

Smaller performance improvements with increasing value difference in PSZ

Accuracy on all novel pairs is shown in Figure S3. When all combinations of reward contingencies were considered, accuracy on trials with a value difference of 35 (t₇₆=3.55, p=.06), 50 (t₇₆=4.26, p=.04), and 60 (t₇₆=4.08, p=.05) were (trend-wise) greater in HV compared to PSZ (Figure 2C). This was also true when using only novel pairs or only pairs consisting of one choice option from each context (Figure 2C). To formally test the presence of a greater accuracy deficit with increasing value difference, we compared individual slopes from a logistic regression predicting accuracy as a function of value difference. Using all pairs (t₇₄=5.84, p=.02), novel pairs (t₇₄=6.99, p=.01), and novel context pairs (t₇₃=6.05, p=.02), the slope for HV was always greater than PSZ (these results could not be used in 2–4 participants due to limited choice variability; Figure 2D). This all suggests that PSZ, compared to HV, improved less as the value difference between two competing stimuli increased, thereby confirming our initial hypothesis.

Context influences perceived choice value in PSZ, but not HV

A direct comparison of 75D-75P performance revealed no significant group difference (t₇₆=1.61, p=.21) (Figure 2E). PSZ (one sample t-test against chance: t₄₁=−2.10, p=.04), but not HV (t₃₅=0.01, p=.99), did however show a significant preference for 75P over 75D. The more indirect group*pair interaction for 75P and 75D performance vs. other options showed similar numerical patterns but was not significant (t_1,67=2.11, p=.15). Nevertheless, PSZ (t₄₁=−2.52, p=.015), but not HV (t₃₅=−.67, p=.51), more often selected 75P than 75D when paired with another option (Figure 2E). The direct and indirect measure of context-sensitivity correlated in PSZ (Pearson’s r= −.53, p<.001). Taken together, these results provide subtle yet consistent evidence that context may impact perceived choice value in PSZ, but not HV. To formally test whether the trial-by-trial pattern of choices can be explained by context-dependent value learning, we next turn to computational modeling results.

Computational modeling

Model Parameters

Hybrid model parameters for HV and PSZ are shown in Figure 3A and summarized in Table 2. The average mixing (m) parameter was greater than .5 in PSZ and HV, suggesting that both groups made more use of Q-learning compared to actor-critic type learning. Importantly, as predicted, the m parameter was significantly greater in HV than PSZ (Table 2). This result points to a decrease in Q-learning and a relative increase in actor-critic type learning in PSZ compared to HV. In addition, the undirected noise (ε) parameter was greater in PSZ than HV (Table 2). See Table S2 for individual parameter estimates.

Figure 3. Hybrid model parameters and simulated data.

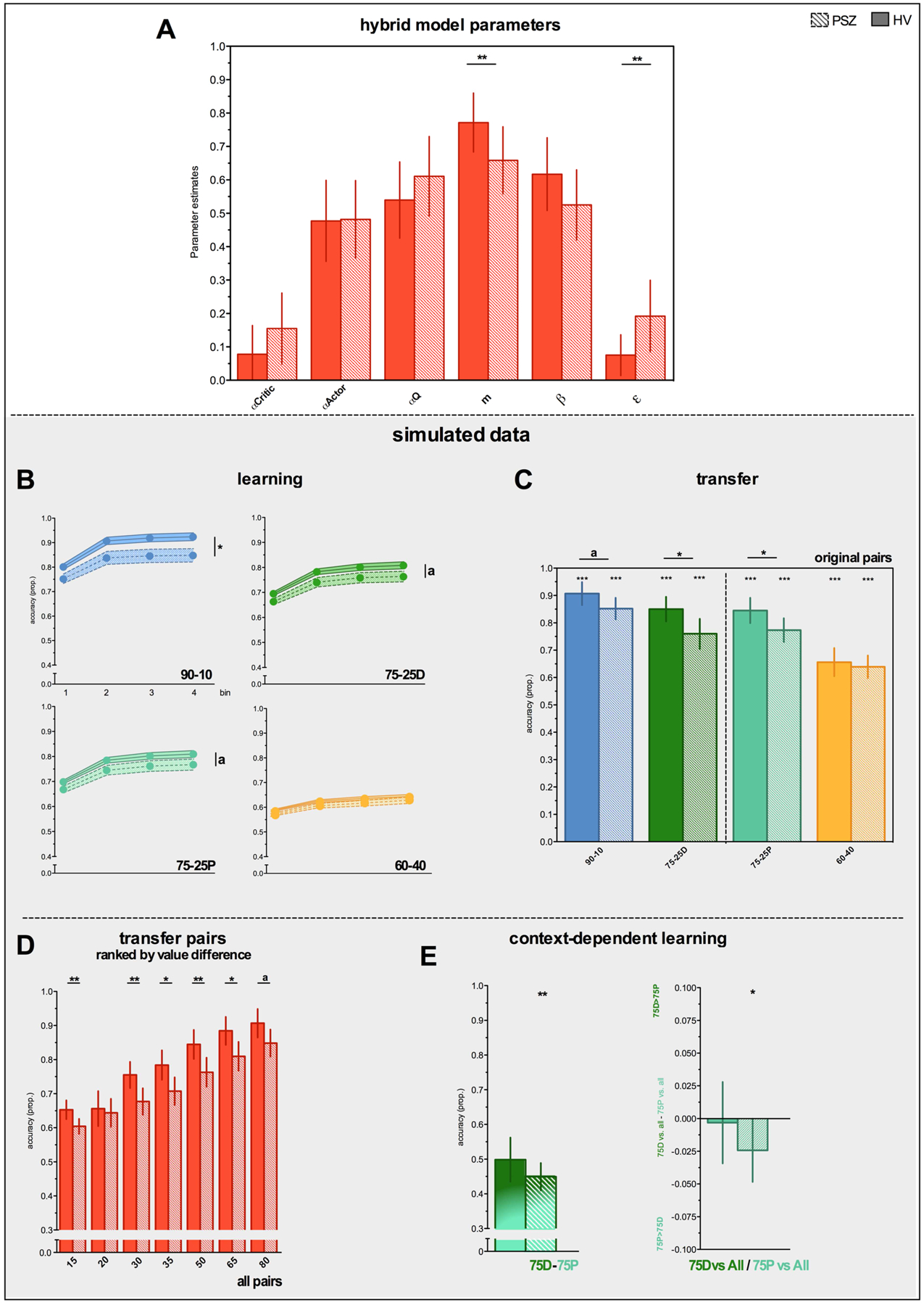
n(simulations)=250, simulated with ε of 50%

Table 2.

Hybrid model parameters per participant group

	HV (n=36)	PSZ (n=42)	t	p
Critic learning rate (αc)	.08 (.24)	.16 (.31)	1.40	.17
Actor learning rate (αa)	.46 (.35)	.50 (.34)	.47	.64
Q learning rate (αq)	.54 (.34)	.59 (.34)	.69	.50
Mixing parameter (m)	.78 (.25)	.61 (.33)	2.51	.01
Inverse temperature (β)	.61 (.32)	.52 (.32)	1.30	.20
Undirected noise (ε)	.09 (.20)	.27 (.38)	2.52	.01

Hybrid Model Simulations – Learning Phase

True to the actual learning phase data, model simulations revealed numerically greater performance in HV relative to PSZ for 90-10, 75-25D, 75-25P (but not 60-40) contingencies, which became (trend-)significant when increasing the number of simulations (n(simulations) = 1000 shown in Figure 3B).

Hybrid Model Simulations – Transfer Phase

Given the low number of transfer phase trials for every combination (n=4) and because the amount of undirected noise may be greater during learning compared to transfer phase performance, we set ε to 50% of the original value during transfer phase simulations. All findings remained when simulating transfer data with ε set to 100% (Figure S4).

Simulated group differences in transfer phase accuracy on 90-10 (t₇₆=1.93 p=.06), 75-25D (t₇₆=2.53 p=.01), 75-25P (t₇₆=2.30 p=.02), and 60-40 (t₇₆=.52 p=.60) pairs were subtle (Figure 3C), as was the case in the original data, yet (trend) significant for some pairs, owing to the number of simulations (Figure 3C; n(simulations) for all transfer data = 250). Importantly, simulated data from the hybrid model predicted numerically greater performance deficits in PSZ with increasing value difference (Figure 3D).

Hybrid Model Simulations – Context-dependent learning

The direct and indirect context effects in PSZ were both present in the simulated data (Figure 3E): that is, I) a preference for 75P over 75D (t₄₀=2.59, p=.01) and II) better performance when 75P was paired with other choice options, compared to when 75D was paired with other choice options (t₃₉=2.03, p=.05). One outlier in the PSZ sample with high values overall/difference scores was removed from the simulated data; excluding this subject from the actual data did not change the results.

Evidence that model parameters capture task performance

The m (Spearman’s ϱ=−.67, p<.001) and ε (Spearman’s ϱ=.38, p<.001) parameter significantly correlated with the slope of the value difference effect in the entire sample, suggesting that decreased reliance on Q-learning and greater undirected noise were associated with smaller performance improvements with increasing value difference (Figure 4A/B).

Figure 4.

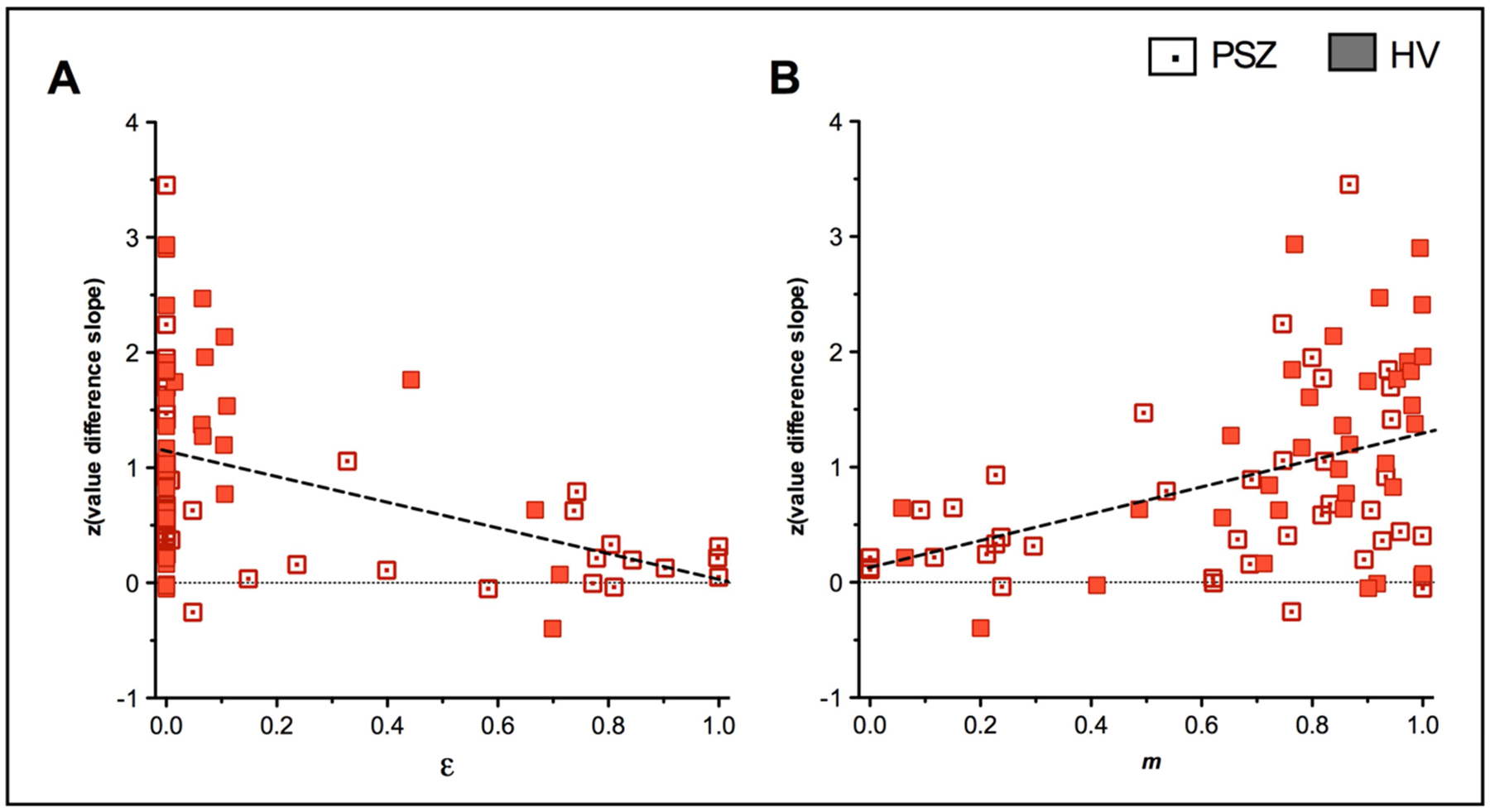
Significant correlations between model parameters and task performance

Next, we focused on the α_c parameter, which can produce the context effect within the actor-critic model. To demonstrate this, m and ε were both fixed to 0 and the direct and indirect context effect were simulated. This analysis removes contributions from Q-learning and undirected noise, while all other parameters were set to their original values. In PSZ, α_c correlated with the size of the simulated direct (Spearman’s ϱ=−.42, p<.005) and indirect (Spearman’s ϱ r=.47, p<.001) context effect. This confirms our intuition that varying levels of critic learning rate are sufficient to account for the context effect. Moreover, when simulating data using individual m and ε parameters, α_c-weighted [α_c*(1-m) – i.e. the degree to which αc could have produced a context effect] also significantly correlated with the simulated indirect context effect (Pearson’s r=.34, p=.02), while the correlation with the simulated (Pearson’s r=−.28, p=.07) and actual (Pearson’s r=−.13, p=.41) direct context effect was in the expected direction but not significant. This provides evidence that greater α_c values can account for a context-dependent choice bias, although this also crucially depends on the degree to which participants rely on Q-learning and the amount of undirected noise.

Associations with clinical and demographic variables

Parameter estimates for low (avo−) and high (avo+) motivational deficit subgroups (median AA sum score = 17; 19 avo−; 23 avo+) are shown in Table S3 and Figure S5. Avo+ compared to avo− showed a selective increase in α_c (t₄₀=2.84, p_{Bonferroni-corrected}=.04); the same trend was observed for avo+ vs. HV (t₅₇=2.54, p_{Bonferroni-corrected}=.06). Given that α_c strongly correlated with measures of context-dependent RL and in light of the lower m parameter in PSZ relative to HV, these results suggest that avo+ were more sensitive to context-dependent RL if they relied strongly on actor-critic type learning.

Focusing on model parameters that could explain group differences in task performance, m (HV low vs. high IQ: t₃₃=1.37, p_uncorrected=.18; PSZ low vs. high IQ: t₄₂=1.04, p_uncorrected=.31) and α_c (HV low vs. high IQ: t₃₃=.50, p_uncorrected=.62; PSZ low vs. high IQ: t₄₂=1.40, p_uncorrected=.18) were not associated with IQ. In PSZ (low vs. high IQ: t₄₂=2.56, p_{Bonferroni-corrected}=.09), but not in HV (low vs. high IQ: t₃₃=.49, p_uncorrected=.63), there was a trend of a lower IQ being associated with more undirected noise (i.e. greater ε).

Finally, m, ε and α_c were not associated with haloperidol equivalents (all p_uncorrected>.71) or age (p_uncorrected>.32). SANS AA sum scores were not associated with model fit (Spearman’s ϱ=−.003, p_uncorrected=.98).

Follow-up analyses in a subsample of participants that performed particularly well are reported in the supplemental text.

Discussion

Using theory-based predictions, our primary aim was to investigate two hypothesized RL and decision-making deficits that could result from a relative underutilization of expected value. As predicted, PSZ showed robust performance impairments as the difference in reward value between two choice options increased. Moreover, we observed a subtle yet consistent contextual choice bias that was not present in HV: when presented with two options of identical reward value (75D and 75P), or when these options were paired with options of other reward value, PSZ preferred the 75 option from the more probabilistic context (75P).

Performance deficits amplified at greater levels of value difference are diagnostic of a change in the choice function rather than a general learning impairment, which would typically manifest in the opposite manner: that is, worse performance for more difficult judgments. These results are particularly noteworthy because they further corroborate the notion that some learning and decision-making deficits in PSZ are associated with a highly selective deficit in the representation of expected value. A more general learning impairment, potentially via altered DA-dependent stimulus-response learning (1, 3, 5), would predict performance impairments with increasing levels of difficulty. We have previously observed a hint for performance deficits at greater levels of value difference in other RL tasks (6, 28), suggesting that this is a recurrent impairment in PSZ. Our computational model provides evidence that such impairments stem from a decrease in action value (Q-) learning (via the m parameter) and a greater relative contribution from actor-critic type learning. Importantly, these results conceptually replicate our previous work for the first time, in which we showed a decreased contribution of Q-learning during a gain-seeking/loss-avoidance task (6). In the current study, performance impairments were also in part related to increased undirected noise (ε), which accounts for non-deterministic choices even in the face of strong evidence. We have observed this in previous reinforcement learning studies (15), and, in the current study was mostly associated with inter-individual differences in IQ.

Which mechanisms could underlie a selective impairment in the representation of expected value? Decreased learning from gains, as opposed to intact loss-avoidance, has been identified as one potential mechanism (6, 14, 29, 30). In this study, impaired performance on more deterministic pairs, associated with more gains than neutral outcomes, but spared performance on 60-40 trials, where learning occurs almost equally from gains and neutral outcomes, provides circumstantial evidence for this notion. One improvement compared to previous paradigms is that, here, we focused on reward value instead of contrasting valence conditions, which is a direct test of expected value deficits. The current results show for the first time that a diminished role of expected value in driving choices can lead to suboptimal behavior in a dose-response fashion; that is, performance impairments increase monotonically with increased demands placed on expected value computations. This work further strengthens the claim that deficits in the representation of expected value are a central feature of learning and decision-making impairments in PSZ, and here we reveal when these deficits should be most evident.

The relationship between the value difference effect and Q-learning fits well with previous neuroimaging studies. Work from our group has identified attenuated expected value signals in insula and anterior cingulate, regions that encode (state-dependent) expected value (31, 32), in PSZ with motivational deficits (5, 14). Ventromedial and orbitofrontal prefrontal cortex dysfunction, consistently involved in tracking reward value (8, 9, 33), has also been linked to learning and decision-making deficits in schizophrenia (34, 35). Thus, a diminished role for expected value in decision-making, demonstrated by the value difference effect and confirmed by our computational model, are suggestive of impairments in a range of cortical areas that encode reward value.

We have argued that underutilization of expected value and a relative increase in reliance on stimulus-response learning can also enhance the effect of context on stimulus valuation, leading to a unique prediction in which preferences can arise among choice options with identical reinforcement probabilities. For this hypothesis we found subtle but consistent evidence only in PSZ, but not HV, which could selectively be accounted for by a context-dependent state-value RPE (via α_c). Interestingly, the magnitude of this context parameter was greater in individuals with high motivational deficits. Given that there was no association between motivational deficits and the mixing parameter (nor between the mixing and context parameter), this result implies that a context-dependent choice bias in PSZ with motivational deficits can only be observed to the degree that they rely on actor-critic type learning. This may suggest that increased sensitivity to context and impairments in Q-learning may be differentially sensitive to symptom severity and patient status, respectively.

Although the effect of contextual reward availability on decision-making was subtle in PSZ, these findings are noteworthy. Klein et al (36) revealed that learning the value of one stimulus relative to another can lead to sub-optimal decision-making. In their study, a relative RPE signal was specifically encoded by the striatum. Despite clear differences between the task design of Klein et al. (36) and the current study, most notably pair-wise vs. block-wise context effects, their work does provide evidence for the notion that the effect of context on perceived stimulus value seems to be encoded specifically by brain regions typically associated with RPE signaling.

Related to this point, we observed intact learning on 60-40 trials in PSZ (also see Waltz et al. (28)), which improved gradually and relies on slow accumulation of RPEs (18). Subtle evidence for a context effect, a relative increase in the contribution of actor-critic-type learning, and adequate learning on 60-40 trials are consistent with relatively intact striatal function in our medicated sample. These findings align well with intact striatal RPE signaling in medicated PSZ (37) as well as normalization of reward signals following treatment with antipsychotics (38).

It is interesting to speculate on how impairments in stimulus-response learning and expected value may change with illness phase or medication status. In non-medicated and/or first episode patients, abnormal RPE signals in among other striatum and midbrain have been reported (4, 39, 40), while a recent study did not observe differences in striatal RPE signals between HV and chronic, medicated, PSZ (37). Additionally, there exists some evidence that deficits in expected value can be observed in both first episode patients (16), in addition to chronic PSZ (6, 29, 41). In the absence of correlations between antipsychotic dose and Q-learning, this work may suggest that deficits in the representation of expected value exist across the psychosis spectrum, while impaired stimulus-response learning may be especially pronounced in the early phase of the illness, and perhaps rescued by antipsychotic medication. While disentangling illness phase from medication effects is an arduous task, such studies may ultimately provide much-needed insights into symptom mechanisms across the psychosis spectrum.

To summarize, this work provides specific evidence that decision-making impairments in PSZ increase monotonically with demands placed on expected value computations. A greater influence of stimulus-response learning as a result of underutilization of expected value may produce additional violations of optimal decision-making policies, such as a contextual or relative choice bias. This work provides a novel source of evidence suggesting a diminished role of expected value in guiding optimal decisions in PSZ and sheds light on the conditions that facilitate such impairments.

Limitations

Some limitations warrant discussion. While we were able to replicate our previous finding of decreased Q-learning/relative increase in actor-critic learning in PSZ (6), the mixing parameter was not associated with symptom ratings. Previous studies investigating RL deficits in PSZ have reported mixed results regarding relationships to negative symptoms (6, 16, 29). Compared to our previous study (6), here we used a wide range of choice pairs and a comprehensive transfer phase. Greater demands placed on expected value computations may have increased sensitivity to detect group differences, as opposed to differences in HV and PSZ with high motivational deficits only. Moreover, the use of a context-dependent learning rate for the critic, which was associated with motivational deficits, may have explained some of the variance that would have otherwise been captured by other model parameters. While multiple factors may explain the absence of an association between the mixing parameter and motivational deficit severity, the current study results still provides evidence for the notion that expected value deficits are an essential part of schizophrenia.

It should also be noted that an alternative account of the current findings is that PSZ may rely less on model-based strategies (42). Both Q- and model-based learning make identical predictions for this task: that is, Q-learning predicts improved performance at greater levels of value difference via action-value learning, while model-based strategies predict improved performance when action-outcome sequences are better understood. Importantly, this alternative explanation does not change the interpretation of increased reliance on model-free stimulus-response learning in PSZ.