Utility of linear mixed effects models for event-related potential research with infants and children

Abstract

Event-related potentials (ERPs) are advantageous for investigating cognitive development. However, their application in infants/children is challenging given children’s difficulty in sitting through the multiple trials required in an ERP task. Thus, a large problem in developmental ERP research is high subject exclusion due to too few analyzable trials. Common analytic approaches (that involve averaging trials within subjects and excluding subjects with too few trials, as in ANOVA and linear regression) work around this problem, but do not mitigate it. Moreover, these practices can lead to inaccuracies in measuring neural signals. The greater the subject exclusion, the more problematic inaccuracies can be. We review recent developmental ERP studies to illustrate the prevalence of these issues. Critically, we demonstrate an alternative approach to ERP analysis—linear mixed effects (LME) modeling—which offers unique utility in developmental ERP research. We demonstrate with simulated and real ERP data from preschool children that commonly employed ANOVAs yield biased results that become more biased as subject exclusion increases. In contrast, LME models yield accurate, unbiased results even when subjects have low trial-counts, and are better able to detect real condition differences. We include tutorials and example code to facilitate LME analyses in future ERP research.

Highlights

• •Linear Mixed Effects models (LMEs) have advantages for event-related potential analyses.
• •For infant/child ERPs especially, LME is superior to traditional ANOVA models.
• •In simulated ERP data, ANOVAs returned biased results, but LME was unbiased.
• •In real, child ERP data, LME detected condition differences where ANOVA did not.
• •Tutorial and sample codes given to guide use of LMEs in future research.

1. Introduction

Event-related potentials (ERPs) extracted from the electroencephalogram (EEG) are commonly used to examine brain activity in infants and young children. ERPs have advantages for assessing cognitive development across infancy, childhood, and adulthood compared to eye-tracking and behavioral methods. However, there are also challenges to their application in infants and young children who have difficulty being still and attentive for the multiple trials required in an ERP task. Thus, a large problem in developmental ERP research is the high rates of subject exclusion due to low numbers of analyzable trials. Current approaches to ERP analysis work around this problem, but do not mitigate it, and moreover, can lead to inaccuracies in measuring neural signals. The greater the subject exclusion, the more problematic these inaccuracies can be. In this paper, we demonstrate an alternative approach to ERP analysis: linear mixed effects (LME) modeling (also referred to as multilevel models, random-effects models, or hierarchical linear models). These models are becoming increasingly common in adult ERP research (Frömer et al., 2018, Volpert-Esmond et al., 2021), but offer unique utility in developmental ERP data despite remaining an uncommon analysis method. As we demonstrate with both simulated and real ERP data, the LME framework addresses problems that arise from high subject exclusion, and provides a more accurate assessment of the real underlying neural signals in ERP data.

1.1. The advantages of ERPs in studying cognitive development

The ERP method is useful for studying cognitive development, and has advantages over other common methods such as eye-tracking and behavioral tasks. Unlike behavioral tasks and eye-tracking which capture only distal measures of cognition (e.g., downstream responses resulting from combinations of prior cognitive and motor processes), ERPs afford a proximal measure of cognition by directly measuring the underlying changes in neural activity as they occur essentially in real time (Sur and Sinha, 2009). Behavioral measures can be more challenging to interpret: eye-gaze and behavioral responses can conflict (e.g., Cuevas and Bell, 2010), and it can be difficult to find comparable tasks across wide age ranges (e.g., infants, children, adults) in which cognitive and behavioral task demands vary to accommodate subjects’ discrepant capabilities. In contrast, ERP designs can use similar or identical stimuli across a wide range of ages to examine neural specificity across development (Clawson et al., 2017, Guy et al., 2016, Halit et al., 2003, Leppänen et al., 2007, Taylor et al., 1999).

ERPs are the time-locked EEG activity corresponding to a cognitive, motor, or sensory event, and constitute waveforms that capture a pattern of event-related brain activity. These event-related waveforms emerge when the neural activity over multiple trials (i.e., multiple presentations of an event) is averaged together to reveal the neural activity that is common across trial presentations, with the ‘noise’ or non-event-related activity ‘averaged out’ (see Fig. 1). ERPs offer a powerful approach to study development of cognitive and perceptual processes, especially given many ERP tasks do not require a subject response, and can thus reveal cognition and development in preverbal infants and young children for whom overt responses are difficult or impossible. Indeed, meaningful and distinct patterns of neural activity (i.e., ‘components’) are revealed in the ERP that are detectable and comparable across the lifespan, and that reflect cognitive processes (see e.g., Clawson et al., 2017; Guy et al., 2016; Halit et al., 2003; Leppänen et al., 2007; Taylor et al., 1999).

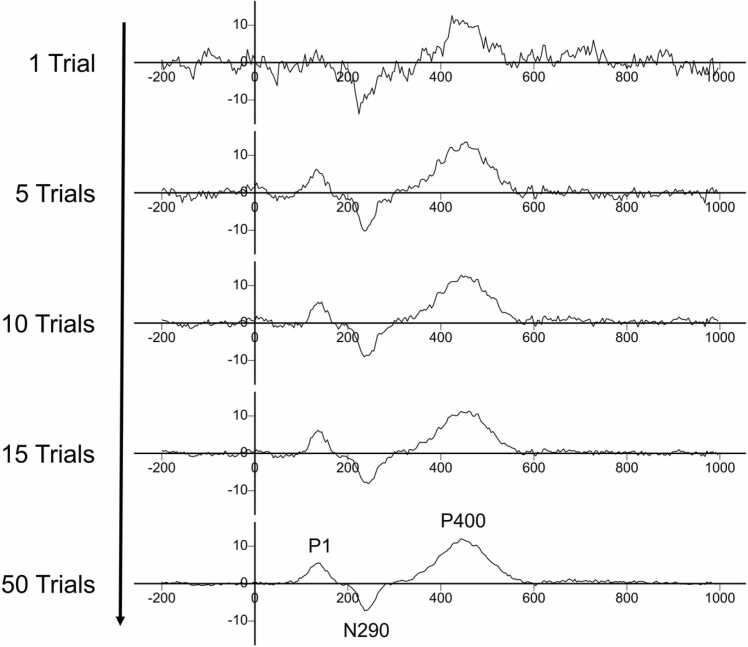
Fig. 1.

Example of how single ERP trials are averaged within a condition to reveal a mean-averaged ERP waveform. As more trials are averaged together, noise from single trials are ‘averaged-out’ in order to measure latency-to-peak and amplitude of ERP components (e.g., P1, N290, P400).

1.2. Challenges with ERP analyses especially for developmental studies: problems with casewise deletion and mean averaging

Despite its many advantages, there are also challenges to ERP research, especially with infants and children. These challenges arise in part from the difficulty of getting subjects to sit still enough and for long enough to yield the many trials required to reveal the ERP. A common way that researchers analyze ERP data is to first average voltages across many trials per subject, and then mean average across subjects to reveal a grand-average ERP (which can then be analyzed for group or condition effects). In a process of casewise deletion (also referred to as complete-case analysis and listwise deletion), researchers exclude subjects with few artifact-free trials from mean averaging because of concerns that these subjects have ERPs with a low signal-to-noise ratio.

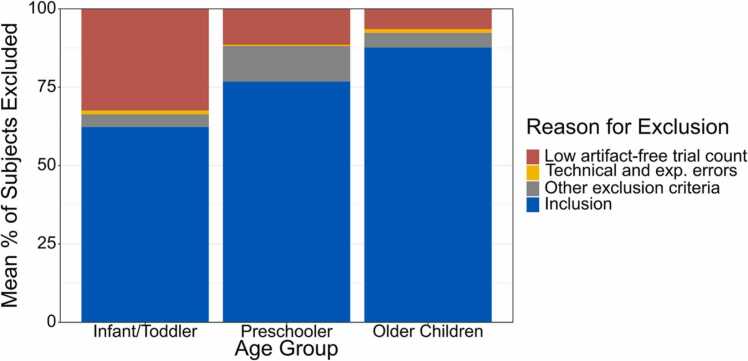
High casewise deletion of subjects with too few trials is especially prevalent in developmental studies. This higher rate of subject exclusion exists in part because ERP tasks designed for infants and children have fewer trials to begin with in order to accommodate the young subjects’ shorter attention spans and faster rates of fatigue. Additionally, infants and children have greater difficulty sitting still and attending to each trial, and thus more trials are flagged for removal in pre-processing due to excessive movement or inattention. To illustrate this high subject exclusion that increases as the target population decreases in age, we conducted a review of 122 ERP studies published in the journal Developmental Cognitive Neuroscience from January 2011 to April 2021 (see Appendix A for the literature review procedures). The review revealed that, across studies (N = 53)1 that used a trial-rejection threshold and required a minimum of 10 trials/condition for subject inclusion (representing the most common threshold in our literature review), on average, 32.44% of infants and toddlers (0- to 35-months-old), 11.45% of preschoolers (3- to 5-years-old), and 6.49% of older children (6- to 13-years-old) who participated in the study were excluded from analyses (see Fig. 2). These results highlight the problem of high data loss due to high casewise deletion in mean averaging approaches.

Fig. 2.

Stacked bar plot of the mean percent of excluded subjects in studies requiring at least 10 trials/condition for ERP analysis (N = 53)¹, representing the most common threshold used in our literature review (see Appendix A). All studies were published in the journal Developmental Cognitive Neuroscience from January 2011 to April 2021. Infant/Toddlers = 0- to 35-month-olds; Preschoolers = 3- to 5-year-olds; Older Children = 6- to 13-year-olds.

Both casewise deletion and mean averaging can cause problems for ERP analyses. As we outline in sections below, these practices can lead to issues such as arbitrarily determining exclusion criteria, inefficient data collection, decreased power to detect condition or group differences, and an incomplete interpretation of ERP results. Most problematic for developmental research, these problems are often exacerbated in studies that exclude a large number of subjects due to low trial count.

1.2.1. Problems with casewise deletion: casewise deletion decreases power, represents large sunk costs, and its determination is arbitrary

Given that ERPs extracted from fewer trials have reduced signal-to-noise ratios, researchers commonly exclude subjects who have too few artifact-free trials in a condition through casewise deletion. But the cutoff point for ‘too few trials’ is arbitrarily set by researchers. A common cutoff is to exclude subjects with fewer than 10–15 trials. In our review of developmental ERP studies noted above, 48 studies reported a trial cutoff. Of these studies, a 10–15 trial cutoff was the most common cutoff used across each age group (52% of infant/toddler studies, 37.50% of preschooler studies, and 31.25% of older children studies employed a trial cutoff within this range, see Appendix Table A.2). Although some research has examined how different trial cutoff points affect ERP data quality, this research has used adult populations to determine the number of trials sufficient to eliminate random error in the mean-averaged ERP (Boudewyn et al., 2018, Luck, 2014). These heuristics may be inappropriate for child ERPs, which are noisier than adult ERPs (Hämmerer et al., 2013). This higher noise in child data is reflected in thresholds for rejecting noisy trials. For example, common simple voltage thresholds for preschool ERP studies are between ± 150 to ± 250 µV (Carver et al., 2003, Cicchetti and Curtis, 2005, D’Hondt et al., 2017, Decety et al., 2018, Taylor et al., 1999, Webb et al., 2006); whereas many adult studies use a stricter simple voltage threshold of ± 40 to ± 100 µV (Brusini et al., 2016, Duta et al., 2012, Huang et al., 2019, Sanders and Zobel, 2012, Shephard et al., 2014). However, the relation between trials and noise in developmental ERPs is not clear given that infants and children also have a higher signal-to-noise ratio due to thinner skulls than adults (see Roche-Labarbe et al., 2008). Thus, there may be different factors for children versus adults that influence the number of ERP trials necessary to obtain a clean ERP signal.

In part to address this issue, researchers have recently developed alternative methods of assessing single-subject ERP data quality (e.g., subject-level reliability, Clayson et al., 2021; standardized measurement error, Luck et al., 2021) to provide researchers with more objective and quantitative approaches to identifying subjects who should be excluded. These alternative methods may result in fewer subject exclusions (e.g., subjects with few trials may still be retained if their ERP is assessed as ‘high quality’ by one of these alternative metrics). However, any amount of casewise deletion, regardless of how exclusion is determined, impacts power to detect a significant effect in the sample. Power is a function of sample size, effect size and variability; thus, with all other factors held constant, decreased sample size decreases power to detect differences across groups or across conditions (Jones et al., 2003, Little et al., 2016). Moreover, collecting clean developmental ERP data is time intensive and costly. Even before an experiment begins, time and funds have been spent recruiting and scheduling families, and laboratories often hire paid research staff to run experimental sessions with infants and children given that researchers must have extensive training to maximize infant/child task compliance. Thus, any subject excluded from analyses represents a large sunk cost.

1.2.2. Problems with mean averaging: possible errors in interpretation of results (Simpson’s Paradox)

Statistical analyses commonly applied to ERP data to determine condition differences or relations among behavioral variables include regression and analysis of variance (ANOVA, i.e., regression with categorical predictors). In our literature review, 90.16% of studies examining ERPs in children used one or more regression/ANOVA analyses, representing the most common analysis in the review (see Appendix Table A.1). However, when performing these analyses over mean-averaged ERPs, the results may offer an incomplete picture of neural phenomena, particularly when there are different within- and between-subjects effects (see Fig. 3). This problem is known as Simpson’s Paradox (Simpson, 1951, Snijders and Bosker, 2012). ERP data are susceptible to Simpson’s Paradox because although there may be both within- and between-subjects effects, mean averaging only captures between-subjects patterns. Within-subjects variability describes different patterns that subjects show within their ERP trials. For example, subjects can have varying slopes of reduced mean amplitude across trials. Between-subjects variability includes behavioral characteristics of subjects that influence their ERP. For example, ERPs may be influenced by subjects’ age (e.g., N290 amplitude becomes sensitive to face stimulus orientation in older infants, de Haan et al., 2002; Halit et al., 2003), temperament (Bar-Haim et al., 2003, Lahat et al., 2014), or other behavioral characteristics. Both linear regression and ANOVA require mean averaging ERPs within-subjects, which make examining within-subjects variability challenging or impossible given that the within-subjects variability is collapsed. Alternatives (such as binning behavioral responses to create categories of within-subjects variability) can result in errors in inference. Specifically, when researchers dichotomize continuous variables (e.g., anxiety levels), there are Type II errors in models with a single predictor and Type I errors when there are multiple predictors (Irwin and McClelland, 2003, Krueger and Tian, 2004, Maxwell and Delaney, 1993). Further, dichotomizing ordinal data results in biased parameter estimates (Sankey and Weissfeld, 1998).

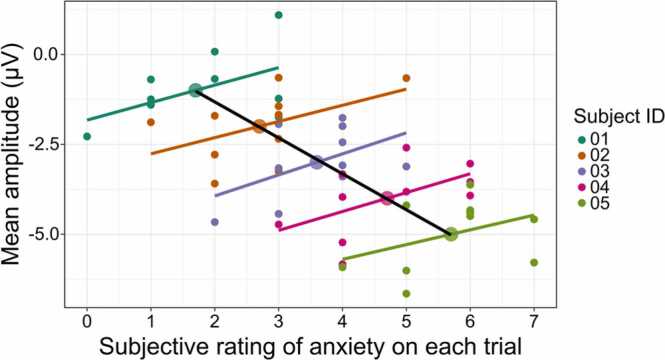
Fig. 3.

Illustration of Simpson’s Paradox, in which there are different within-subjects effects (shown here by colored lines indicating individual subjects’ regression lines) and between-subjects effects (shown here by the black regression line). Figure was created in the R package ‘correlation’ (Version 0.6.1; Makowski et al., 2020).

Ignoring the within-subjects variability that exists in ERP data when using standard linear regression models can result in only describing part of the ERP component’s characteristics (whereas LMEs can describe the complete within- and between-subjects effects). To illustrate issues arising when only between-subjects effects are modeled, consider an example in which subjects are shown a series of images and asked to rate them across each trial (e.g., rating subjective anxiety on a series of International Affective Picture System images, Lang et al., 2008). In this hypothetical study, the within-subjects variability illustrates that higher anxiety on individual trials is related to less negative ERP amplitude. However, at the between-subjects level, higher anxiety is related to more negative ERP amplitude (see Fig. 3). Using mean averaging in a standard linear regression framework would reveal the negative between-subjects relation, but not the positive within-subjects relation, which best characterizes the relation between subjects’ anxiety and their ERP amplitude. Thus, as illustrated in this example, the interpretation of data and conclusions researchers draw from mean-averaged data can suggest the opposite effect of what occurs at the within-subjects level.

1.2.3. Problems with using casewise deletion in ordinary least squares: violation of missingness assumptions can lead to grand-mean ERPs that are biased or incorrect

Also problematic, the use of casewise deletion (used in common ERP analyses such as linear regression and ANOVA) can lead to grand-mean ERPs that are biased or incorrect. These biases occur when missingness assumptions for casewise deletion are violated, as is often the case in ERP research and in developmental ERP studies in particular. We first describe the types of missing data that may occur in ERP studies using examples. We then clarify why some types of missing data result in biased grand-mean ERPs when using casewise deletion, but remain unbiased in LME (which uses maximum likelihood instead of casewise deletion).

Rubin and colleagues (Little and Rubin, 2002, Rubin, 1976) have described three mechanisms of missing data, and these mechanisms and solutions have been expanded upon (Baraldi and Enders, 2010, Graham, 2009). These types of missingness are: (1) missing completely at random (MCAR), (2) missing not at random (MNAR), and (3) missing at random (MAR). Importantly, missing mechanisms describe a specific dataset being used in a model or analysis, and are not characteristics of a complete dataset itself (Baraldi and Enders, 2010). Therefore, within a larger dataset and depending on which variables are included in the model, there may be independent analyses that meet assumptions for MCAR, MAR, and MNAR (Nakagawa and Freckleton, 2008). As we describe in sections below, while both MNAR and MAR violate assumptions of casewise deletion, LME in contrast remains unbiased when data are MAR. Additionally, while MNAR is problematic for both casewise deletion and LME models, LME allows for the inclusion of other variables that can make LME analyses more likely to meet MAR assumptions.

1.2.3.1. Types of missing data

MCAR occurs when the probability of missing data on a given target measure (e.g., trial-level mean amplitude) is not related to other measured variables (e.g., age), not related to unmeasured variables (e.g., other constructs that may be relevant but that were not assessed in a given study, e.g., prenatal exposure to medication), and also not related to the missing values of the target measure itself (i.e., the hypothetical values of the variable that would have been observed if they were not missing) (Rubin, 1976, Little et al., 2016). For example, MCAR can emerge from a child moving away during a longitudinal experiment, experimenter error, or equipment failure during the experiment. These examples describe MCAR because the data that would have been observed (e.g., if the equipment did not fail) are not related to any variable, either measured or unmeasured. That is, the missingness is ‘completely random’. If data are MCAR, the dataset will not violate missing assumptions of casewise deletion (used in ANOVA and linear regression) or LME, and parameter estimates of analyses remain unbiased.

MNAR occurs when the probability of missing data on a target measure is related to unmeasured variables and related to the missing values of the target measure itself (Nakagawa and Freckleton, 2011). For example, there may be greater missing ERP data for infants with behaviorally inhibited temperaments who fuss more during the experiment and therefore have greater missing trials (de Haan et al., 2004). Thus, if temperament was not measured by the researcher and the target ERP component of interest is modulated by temperament, data will be MNAR. That is, the probability of missing ERP data is not random (it is related to temperament), and the ERP data observed is biased due to greater missingness in behaviorally inhibited children in the sample. When data are MNAR, missingness assumptions of both casewise deletion and LME are violated.

MAR occurs when the probability of missing data can be predicted completely by measured variables, and thus after accounting for these sources of missingness, the remaining missing data are random (Snijders and Bosker, 2012, Graham, 2009). In this way, data can be MAR if missingness is (1) related to other observed measures, and any remaining missingness is random (Baraldi and Enders, 2010), or (2) related to unobserved measures that are not related to the missing values of the target measure itself (Higgins et al., 2008). For example, if researchers collect information on subject temperament, then the missing data that is more likely to occur in behaviorally inhibited infants (e.g., due to more frequent fussing) can be modeled and accounted for in analyses, resulting in unbiased ERP data despite greater missing trials for behaviorally inhibited infants in the sample. Likewise, if temperament was not measured, but was unrelated to the ERP component of interest, then the reduced trial count for behaviorally inhibited infants in the sample would still not systematically bias the ERP data that were observed, because temperament did not modulate this specific component of interest. When data are MAR, missingness assumptions are met for LME, but not for casewise deletion (used in ANOVA and linear regression).

1.2.3.2. Casewise deletion in ordinary least squares is more vulnerable to violations of missingness compared to LME

Understanding the mechanism of missing data that best describes a researcher’s analysis is critical, because as we summarized above, casewise deletion is only appropriate in ordinary least squares models (e.g., ANOVA, linear regression) when data are MCAR (Baraldi and Enders, 2010). In contrast, LME, which we present in greater detail below, is appropriate when data are either MCAR or MAR.

In addition, LME can account for trial-level reasons for missingness, therefore making data more likely to fall under MAR assumptions versus MNAR. Specifically, given MNAR can occur when missing data on a target measure are predicted by an unmeasured variable, LME can incorporate ‘auxiliary’ variables, or variables that are not of interest themselves but that likely relate to missingness. As noted above, by definition, MAR occurs when the probability of missing data can be predicted completely by measured variables. Thus, when an auxiliary variable is included in LME, missing data within a target variable can be accounted for, at both within- and between-subjects levels, enabling the variable to meet MAR assumptions. In contrast, if auxiliary variables are added to ANOVA or regression models, missingness will only be accounted for at the between-subjects level (because the mean averaging in these analyses obscures within-subjects effects). As a particularly salient example, trial presentation number is frequently related to missing data in developmental ERP studies, because infants and children are fussier toward the end of the recording and therefore end the session early or have larger artifacts (due to motion) on later trials that ultimately get excluded from analyses. Trial presentation number is a within-subjects variable and thus can be accounted for in LME, making the analysis MAR and meeting assumptions. In contrast, neither regression nor ANOVA can account for this within-subjects effect, and missingness assumptions will be violated for these analyses, biasing results (see also Section 1.3.1 for further discussion of this example).

As we demonstrate in both simulated (Section 3) and real ERP data (Section 4), when missingness assumptions in ordinary least squares methods are violated (as is common in ERP research), casewise deletion biases parameter estimates (Baraldi and Enders, 2010, Little et al., 2016, Roth, 1994), and can lead researchers to believe that mean amplitude is higher or lower than it truly is at the population level. Further, given that there is greater bias at higher levels of casewise deletion (Little et al., 2016), infant ERP research—which has the highest levels of casewise deletion (see Fig. 2)—is particularly vulnerable to biased parameter estimates.

1.3. LME as an alternative approach to grand-mean averaging and casewise deletion

We have described several issues arising from the use of casewise deletion and mean averaging in ERP research that can weaken studies’ power, lead to incomplete conclusions about the relation between neural signals and cognitive processes, and bias results from statistical analyses. Here, we discuss in greater detail an alternative approach to mean averaging subjects’ ERP waveforms using linear mixed effects models (LME), which does not involve casewise deletion and can handle missing data that are either MCAR or MAR.

LME can be used to answer research questions about both within- and between-subjects effects, and therefore can be used for most existing developmental ERP studies, including studies examining condition differences, group differences and individual differences. Thus, LME has wide-ranging utility to answer many of the developmental questions that concern research in developmental neuroscience. Importantly, as we discuss in the sections below, the LME approach provides more accurate estimates of effects in statistical analyses, allows researchers to include all subjects (even those who only contribute one trial), and can be easily incorporated into existing ERP data processing pipelines. Despite the usefulness and flexibility of LMEs for developmental ERP research, only 4.92% of studies in our Developmental Cognitive Neuroscience review have utilized this valuable approach.

1.3.1. LME provides more accurate estimates of effects by modeling both random and fixed effects, at both between- and within-subjects levels

Given that LMEs can model both within- and between-subjects effects, they can better model variability that arises from effects that are not of interest themselves but that may bias an effect-of-interest (so-called ‘nuisance’ variables). The capability to model a broad array of nuisance variables allows for better isolation of an effect-of-interest. LMEs are further advantageous because they can model not only fixed effects (that are modeled in ordinary least squares), but also random effects, thereby accounting for even more sources of nuisance variability to further isolate an effect of interest.

Random effects are assumed to be sampled randomly from the population and are typically not of interest themselves (DeBruine and Barr, 2021). However, if random effects are included in a model, it can account for more sampling variability, and thus more accurately estimate a fixed effect of interest. ERP data contains several sources of variability that can be modeled as random effects. Thus, LMEs can be especially advantageous when used in ERP research. For example, the specific electrode channels of interest for a given ERP component, stimulus-level characteristics, and even the subjects themselves can be modeled as random effects. Including these random effects helps account for this extra variability and better isolate the target effect of ERP component amplitude. To illustrate, in an ERP experiment wherein subjects view emotions (e.g., happy, fearful, and angry emotion conditions) that are expressed across different actors, the ERP amplitude might be modulated by random stimulus-level characteristics of the actors themselves (such as hair color, face shape). Including ‘actor’ as a random effect in the model accounts for this stimulus-level variability and thus enables more accurate estimation of the effect-of-interest (i.e., the ERP amplitude modulated by emotion) (see Section 2.2 for further discussion of this example and for additional examples of random effects).

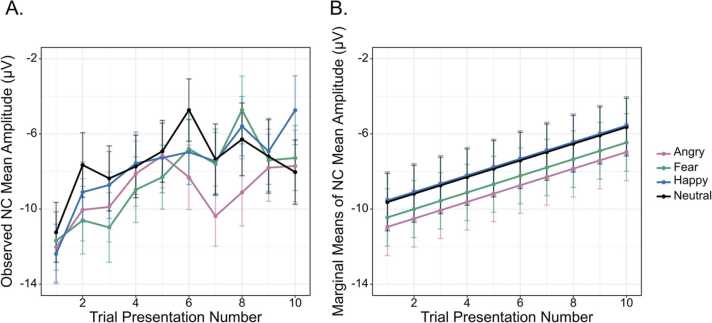
Including fixed effects in models also enables more accurate estimation of effects of interest. Fixed effects are assumed to be non-random, related to the target variable of interest, and consistent across samples from the population. Between-subjects fixed effects are modeled in ordinary least squares analyses, but because LME can also model within-subjects fixed effects, LME is again advantageous in its ability to model more nuisance variables. In particular, unlike ordinary least squares, LME can model fixed effects at the trial level, which is especially advantageous for developmental ERP studies. To illustrate, some ERP components show an amplitude ‘decay’ (habituation) over repeated trials (e.g., the Negative Central or NC; Borgström et al., 2016; Friedrich and Friederici, 2017; Junge et al., 2012; Karrer et al., 1998; Nikkel and Karrer, 1994; Reynolds and Richards, 2019; Snyder et al., 2010; Wiebe et al., 2006; but see also Quinn et al., 2006, Quinn et al., 2010; Snyder et al., 2002). In ordinary least squares that cannot model trial-level variability, early trials will be mean averaged with later trials. This practice is not problematic in and of itself, however, in developmental ERP studies in which infants and young children often ‘fuss out’ early, there are commonly more missing trials toward the end of the experiment. Thus, if the trial-level amplitude decay is not modeled (e.g., by including trial presentation number as a within-subjects fixed effect), then results will be biased toward the mean amplitude from earlier trial presentations and artificially inflated. Modeling amplitude decay when it occurs within this pattern of missing data is particularly important when comparing mean amplitude across different age groups. For example, if results show that preschool children have greater mean ERP amplitude compared to adolescents, this ‘age effect’ could be driven at least in part by the bias in the preschool sample wherein the proportion of high-amplitude trials from the beginning of the experiment may be over-represented (because more preschoolers ended the task early).

In sum, LMEs can importantly model both fixed and random effects, at both between- and within-subjects levels. Thus, LMEs have the capability to account for a broad array of nuisance variables and more accurately estimate the effect of interest. These functions make LMEs especially advantageous when used to analyze developmental ERP data in which random effects (e.g., of stimulus-level characteristics) may obscure condition-level fixed effects of interest, and in which within-subjects fixed effects (e.g., at the trial-level) can bias estimates of ERP amplitude—a bias that can disproportionately affect infant and child samples.

1.3.2. LME does not require casewise deletion, and produces unbiased estimates regardless of whether missingness is random (MAR) or completely random (MCAR)

LME does not require casewise deletion, and instead uses maximum likelihood estimation to account for missing data. Maximum likelihood as a means to handle missing data in developmental ERP experiments has several benefits. It allows researchers to analyze all artifact-free data from subjects, even from those who would have otherwise been removed due to too few analyzable trials. Further, maximum likelihood estimation produces unbiased estimates regardless of whether data are MCAR or MAR; whereas casewise deletion only produces unbiased estimates when data are MCAR (Baraldi and Enders, 2010, Little et al., 2016). Given that ERP studies commonly have data that are MAR, LME and its use of maximum likelihood is advantageous: LME produces unbiased estimates where mean averaging and casewise deletion does not (as we demonstrate in Section 3).

1.3.3. LMEs use partial pooling to enable inclusion of all usable trials

As previously discussed, for ordinary least squares analyses with developmental ERP data, high numbers of subjects are casewise deleted because of not enough usable artifact-free trials to contribute to a subject average. In contrast, LMEs can include all available artifact-free trials, even if children have more data in one condition than another, and even if children have only one artifact-free ERP trial. LMEs account for different numbers of trials being contributed by different subjects through partial pooling of the model’s variance.

Specifically, LMEs partially pool the within-subjects and between-subjects variance in the model (also referred to as “shrinkage”, Gelman and Hill, 2007). Partial pooling combines the group-level effect (e.g., the average effect for all subjects) and the subject-level effect, and therefore subjects’ individual effect estimates are drawn toward the group estimate. The number of trials that subjects contribute to the group mean dictates the extent to which subjects’ estimates are pulled toward the group mean. In addition, subjects with fewer trials (who have a less reliable estimate of their mean amplitude) are weighted less in the mean than subjects with a high trial count. Therefore, subjects with even just a single artifact-free ERP trial (who otherwise would be casewise deleted before mean averaging) are included in analyses, and subjects with fewer trials will have less weight in the group mean than a subject with more usable trials. Retaining as many subjects as possible for ERP analysis helps increase power to detect effects, and is particularly valuable for developmental studies given the large sunk cost of testing infants and young children. It also sidesteps the issue of using an arbitrary trial cut-off for exclusion with casewise deletion.

In contrast, in a model with complete pooling of variance, trial-level data are fit without a categorical predictor of subject, and all trials would be treated as part of a single ‘group’ or subject, which ignores within-subjects variability (e.g., a subject may have higher or lower amplitude than the rest of subjects). ANOVA assumes that all conditions or groups are sampled from a population with the same variance, and calculates a single pooled standard deviation (i.e., all conditions have the same standard deviation value). In a model with no pooling, the regression model would be fit individually to each subject. However, fitting a model to each individual subject overfits data (Gelman and Hill, 2007). Therefore, partial pooling in LME has the advantage of including subjects who have few artifact-free ERP trials, but also gives these subjects less weight in the sample mean to account for their less precise estimate of amplitude (due to few trials).

2. Comparing LME and linear regression

In the sections that follow, we describe how LME is an extension of regression, and demonstrate how data that would typically be analyzed in a mean-averaged regression or ANOVA (which both use ordinary least squares estimation) can be analyzed in an LME framework. We begin by reviewing linear regression, and then illustrate how this formula is modified in LME.

ERP data have a hierarchical structure in which trials are “nested” within subjects, and trials within one subject are more similar to each other than trials from another subject. Statistical models need to account for this nested structure in which the value of one trial is influenced or dependent upon other trials. In linear regression, this nesting is accounted for by mean averaging to produce a single mean amplitude value per condition per subject. However, in LME this nesting is accounted for by modeling within-subjects variability (at the trial level) and including random effects for subjects (e.g., subjects can differ in their intercepts or grand mean across all conditions; and in their slopes or their effect across conditions).

2.1. Linear regression

Eq. (1): Linear regression can be represented as:

y_j = β₀ + β₁x_1j + β₂x_2j + Ɛ_j

β₀ represents the intercept, and β₁, β₂ represent the slope of fixed effects.

j represents subject-level estimates.

Ɛ_j represents error residuals where Ɛ_j ~N(0,σ²).

For example, the following model describes the influence of condition on mean amplitude while controlling for age:

Mean amplitude = β₀ + β₁Condition + β₂Age + Ɛ

where β₀ is the intercept (mean amplitude across all conditions when Age = 0), β₁ and β₂ are fixed effects, meaning that the coefficients do not vary (i.e., are non-random), and Ɛ is residual variance. In linear regression, the relation between mean amplitude and Condition, and mean amplitude and Age, is the same for every subject.

2.2. Linear mixed effects model (LME)

In contrast to linear regression which only models between-subjects variability of ERPs, LMEs model variability at both the within-subjects (also called ‘level 1’) and between-subjects (also called ‘level 2’) levels. We present LME models using the two-level notation style from Raudenbush and Bryk (2002). Data dependence is accounted for by random effects, or effects that are assumed to be sampled from a population (for further description see Section 1.3.1 above). In ERP studies, some common examples of random effects are variability in trial amplitude that is a function of subject (e.g., trials within a subject are similar to each other) or a feature of stimulus (e.g., trials in which the same actor expresses different emotions have a similar amplitude across subjects). We illustrate a simplified LME model (see Eq. (2) below) with the most universal random effect of ‘Subject’ to account for each subject having ERPs more similar to themselves than to another subject. This model also includes one level 2 fixed effect (called ‘Predictor’). Thus, this simplified LME model includes a fixed effect of a level 2 Predictor, and one random effect (a random intercept for Subject). Note that this ‘Predictor’ slot is highly flexible. For example, in an LME model examining condition differences (e.g., a model similar to ANOVA), the Predictor could be a fixed effect of condition; whereas in an LME model examining individual differences (e.g., a model similar to linear regression), the Predictor could be any continuous variable of interest (e.g., age, executive function). We describe and interpret a more complex model with both level 1 and level 2 fixed effects in Section 3.

Eq. (2).

Level 1 (within-subjects): y_ij = β_0j + Ɛ_ij.

i represents trial-level estimates.

j represents subject-level estimates.

Level 2 (between-subjects):

β_0j = γ₀₀ + γ₀₁Predictor_j + u_0j.

γ₀₀ = Grand mean intercept across the sample.

γ₀₁ = Predictor’s mean across the sample.

u_0j = Each Subject’s increment to the grand mean.

The level 2 model illustrates that each subject has a unique intercept, and all subjects share a single slope of Predictor (e.g., a fixed effect of condition or the slope of an individual differences predictor) within the model.

The assumptions of a linear mixed effects model analysis are similar to linear regression; they include linearity, normal distribution of residuals, and homoscedasticity. The first assumption, linearity, states that the independent variables must be linearly related to the outcome variables. A dataset’s linearity can be visually inspected by plotting the model’s residuals with the observed outcome variable. The second assumption, normal distribution of residuals, states that the residuals of the dependent variable should follow a normal distribution and not be skewed. For datasets with samples between 3 and 5000 (Royston, 1995), the model’s residuals can be tested with the Shapiro-Wilk test of normality. Datasets with sample sizes greater than 5000 require using visual inspection of the model’s residuals. If this assumption is violated, then the fixed effects or outcome variable can be transformed to a different scale, such as a log scale (e.g., reaction time is frequently log-transformed to meet the assumption of normal distributions of residuals). The third assumption, homoscedasticity (i.e., homogeneity of variance) states that each group (e.g., younger vs. older age group) should have a similar distribution of values. This assumption can be tested using the Levene's test for homogeneity of variance. Note that these three assumptions must also be met in order to use regression analysis but linear mixed effects models do not require independence of datapoints, which is an additional assumption of linear regression.

3. LME and ANOVA comparison in simulated ERP data

To demonstrate how and when regression and ANOVA biases ERP results, we conducted simulations wherein the population parameters of ERPs were specified and therefore known. These simulations enabled systematic evaluation of the extent to which the use of casewise deletion in mean averaging biased parameter estimates compared to the alternative LME approach. We measured bias in both estimated marginal mean amplitudes (e.g., condition mean for one predictor averaged over presentation number) and standard deviations such that greater bias was evident when (1) estimated marginal mean amplitudes were more different from the population mean, and (2) had larger standard deviations. We examined bias in 3 separate simulations in which we systematically varied the type of missingness to approximate the different characteristics of real ERP data in existing studies, and to illustrate the capabilities of LME versus casewise deletion in ANOVA to handle these missingness patterns. Specifically, we simulated: (1) greater missing data for later trials and for younger subjects (missingness at both within- and between-subjects levels), (2) greater missing data for later trials with a uniform distribution across subject ages (missingness at within-subjects level only), and (3) a uniform distribution of missing trials across stimulus presentation number and subject ages (i.e., MCAR). For each of these three sets of simulations, we also systematically varied the number of subjects who would be casewise deleted due to too few artifact-free trials (10 trials/condition) in an ANOVA framework. These subjects were included in LME analyses. Therefore, the percentage of casewise deleted subjects was varied to create different amounts of casewise deletion that matched common percentages revealed in our review of developmental ERP studies (i.e., 0%, 6%, 11%, 32%; see Appendix Table A.3). In this way, simulations were used to determine how different percentages of casewise deletion bias measurements of ERP amplitude and increase standard deviation in estimates.

We simulated the Negative Central (NC) ERP component from a hypothetical experiment in which subjects in two groups (e.g., ‘younger group’ and ‘older group’) passively viewed still images of actors expressing emotions in two conditions (e.g., emotion A ‘happy’; emotion B ‘angry’). NC is a commonly elicited component to face processing in developmental ERP research with infants, and children (Dennis et al., 2009, Leppänen et al., 2007, Todd et al., 2008, Xie et al., 2019; for a review, see de Haan, 2001). To best approximate real ERP studies, we built the simulated data based on characteristics of real NC ERP data in existing developmental research. That is, we drew from the literature to determine population mean NC amplitude (Leppänen et al., 2007, Smith et al., 2020), age differences in NC mean amplitude (Di Lorenzo et al., 2020), and NC amplitude decay across trials (Borgström et al., 2016). We also modeled fixed and random effects commonly found in real ERP data such as condition differences and subject-level variability.

3.1. Methods

3.1.1. Data simulation

Data were simulated in MATLAB (Version 2019a; MATLAB, 2019) using the SEREEGA toolbox (Version 1.1.0; Krol et al., 2018) for a hypothetical ERP experiment presenting two emotional face conditions: A and B. SEREEGA is a toolbox designed to simulate realistic ERP data using a neural source (e.g., coordinates of neural sources from prior fMRI and source-localization ERP research), and allows researchers to induce noise in the simulated ERP waveform to model noise in single-trial ERP data. For the present study, we generated single-trial Negative Central (NC) mean amplitude values using the prefrontal ICA component cluster reported in Reynolds and Richards (2005) and the Atlas 1 (0–2 years old) lead field from the Pediatric Head Atlas (Version 1.1; Song et al., 2013).

Simulated data for each condition were drawn from a normal distribution with a mean of − 10 and − 12 μV, respectively, and a standard deviation of 5 μV. These mean and standard deviation values were chosen based on those reported in previous infant NC studies (Leppänen et al., 2007, Smith et al., 2020).

Each emotional face condition was displayed by 5 different ‘actors’ with 10 presentations each (total of 50 trials/condition). A within-subjects fixed effect of presentation number was simulated in order to model the ‘decay’ phenomena that ERP components reduce in amplitude in response to a repeated stimulus. Based on values reported in Borgström and colleagues (2016), the amplitude for a specific emotion and actor was reduced by 1.5 μV for each successive presentation. This amplitude decay or habituation has been documented in the NC component by several other studies (Friedrich and Friederici, 2017, Junge et al., 2012, Karrer et al., 1998, Nikkel and Karrer, 1994, Reynolds and Richards, 2019, Snyder et al., 2010, Wiebe et al., 2006). Given age-related changes in NC reported by Di Lorenzo and colleagues (2020), a categorical fixed effect of age (younger group vs. older group) was assigned, in which 2 μV were subtracted from each trial-level amplitude value for subjects in the ‘older’ group and were added to each trial-level amplitude to the ‘younger’ group. In each simulation sample, there were random intercepts for each actor and for each subject. Within each sample, the random intercept for each actor was drawn from a normal distribution with means [− 10, − 5, 0, 5, 10 μV] and a standard deviation of 5 μV. Within each sample, the random intercept for each subject was drawn from a normal distribution with a mean of 0 μV and a standard deviation of 10 μV. Finally, trial-level noise in EEG data was simulated using pink Gaussian noise (Doyle and Evans, 2018). For more information, see Appendix B which includes the full simulation methods, a link to a GitHub containing the MATLAB and R code for reproducing the simulation results, and an example simulated datafile.

The simulated datasets met the LME assumptions discussed above: linearity, normal distribution of residuals, homoscedasticy. That is, the effects of emotion condition, presentation number, age, subject, and actor were linearly related to the outcome variable (NC mean amplitude). The distribution of residuals for the LME model (see Eq. (3) below) was confirmed for each sample using the Shapiro-Wilk test and a low number of samples did not have normal residuals (8.5% of samples with p < .05). Finally, the variance across each condition (e.g., emotion A and emotion B) was simulated using the same standard deviation values in order to be comparable. Levene’s test for homogeneity of variance was conducted for each sample and identified only a few samples that did not meet this assumption (3.9% of samples with p < .05). In addition to the LME assumptions, the intraclass correlation coefficients (ICC) for subject in the simulated datasets ranged from .23 to .70, which indicates nested data and the appropriate application of LME analysis (Aarts et al., 2014, Aitkin and Longford, 1986, McCoach and Adelson, 2010, Musca et al., 2011).

3.1.2. Inducing missing data patterns in the simulated datasets

As stated above in Section 1.2.3, an assumption of casewise deletion is that data are missing completely at random (MCAR). However, in ERP designs, particularly with young children, it is more likely that data will be missing at random (MAR) in that the probability of missingness for within- and between-subjects effects can be predicted by measured variables. Missing data are often related to measured variables in developmental ERP studies because subjects often differ in age, temperament (de Haan et al., 2004), or other characteristics that can be correlated with the probability of missing data. For example, there are commonly fewer artifact-free trials in younger subjects compared to older ones. Moreover, there are commonly fewer artifact-free trials occurring at the end of the experiment, resulting in relations between missing data and trial presentation number. Thus, to best approximate real ERP data, we systematically varied patterns of missingness following common patterns in existing studies. Specifically, in Missingness Pattern #1, we induced more missing data for ‘younger’ than ‘older’ subjects, and more missing trials toward the end of the experiment. That is, of children assigned to have fewer than 10 trials in one or both conditions, 70% were in the ‘younger’ group and 30% were in the ‘older’ group. Additionally, of the trials assigned to be removed, 70% were from trials 6–10 and 30% were from trials 1–5. In Missingness Pattern #2, we induced more missing data in trials toward the end of the experiment (of the trials removed, 70% were from trials 6–10 and 30% were from trials 1–5) across both age groups. These two patterns of missingness were compared to Missingness Pattern #3, in which data were MCAR—which is likely uncommon in actual data (Raghunathan, 2004). In Missingness Pattern #3, missing trials were drawn uniformly from both age groups (50% from ‘younger’ and 50% from ‘older’), and from all trial numbers (each trial number was equally likely to be missing). The aim of these simulations was to illustrate different biases that commonly occur in developmental ERP data, and that result in violations of missingness assumptions when using casewise deletion in ordinary least squares. These biases increase as levels of casewise deletion increase, but are absent in LME models in which missingness assumptions are met. Because LME is able to account for trial-level missingness (e.g., by modeling trial presentation number), Missingness Patterns #1 and #2 would meet MAR assumptions for LME. In contrast, these same patterns would fall under MNAR in ANOVA because after mean averaging trials within subjects, ANOVA is unable to account for the trial-level missingness.

Given that mean amplitude was less negative over repeated trials (i.e., for the simulated negative component, mean amplitude reduced over the course of the experiment), we expected that removing more trials from presentation numbers 6–10 (which had less negative amplitudes) would downward bias parameter estimates extracted from ANOVA compared to the population mean in both Missingness Patterns #1 and #2. Additionally, given that younger children had less negative mean amplitudes, we expected that removing more young children would further downward bias marginal mean estimates in Missingness Pattern #1 in which there were both more later trials removed and more younger children removed. In contrast, we expected Missingness Pattern #3 (MCAR for both trial number and subject ages) to produce unbiased parameter estimates for both LME and ANOVA because missing trials were not systematically correlated with measured variables, which is a criteria for the appropriate employment of casewise deletion.

Simulated datasets (N = 1000) were generated using the parameters discussed in Section 3.1.1. For each dataset, missing trials were removed following Missingness Pattern #1, #2 or #3. For each Missingness Pattern, the proportion of subjects assigned to have fewer than 10 trials per condition in one or both emotion conditions were assigned to be either 0% (trial-level data were assigned to be missing, but no subjects had fewer than 10 trials/condition), 6% (missing trial-level data were induced so that 6% of subjects had fewer than 10 trials/condition in at least one emotion condition), 11%, and 32%. These percentages were taken to match the percentages common in our review of developmental ERP studies (see Section 1.2 and Appendix Table A.3). In line with common developmental ERP practices, subjects with fewer than 10 trials per condition were casewise deleted and thus removed from the ANOVA analyses. In contrast, no subjects were removed from LME analyses, and therefore the LME analysis included subjects who had fewer than 10 trials in any condition. In the sections that follow, we refer to the different percentages of subjects with fewer than 10 trials in one or more conditions as ‘percentages of casewise deleted subjects’ when emphasizing results from ANOVAs, and as ‘percentages of low trial-count subjects’ when emphasizing results from LME. In addition, a ‘population model’ in both ANOVA and LME frameworks were fit to each of the 1000 datasets, and in this model zero trials were missing. We expected that at the population model with zero trials removed, ANOVA and LME would produce identical NC mean estimates. Given that casewise deletion is only appropriate when data are MCAR, in our simulations in which data were not MCAR, we expected increasing bias in ANOVA at greater percentages of casewise deletion; whereas LME would remain unbiased at all percentages of low trial-count subjects.

3.1.3. Analysis models

Two models were used to analyze the simulated dataset in R (Version 3.6.1; R Core Team, 2019): a two-way repeated measures ANOVA examining emotion condition and age as factors, and an LME model with fixed effects of emotion condition, presentation number, and age (see Eq. 3). The ANOVA model was fitted using the afex package (Version 0.28–1; Singmann et al., 2021) and the LME model was fitted using the lme4 package (Version 1.1–25; Bates et al., 2015). P-values were calculated using the lmerTest package (Version 3.1–3; Kuznetsova et al., 2017). The ANOVA was designed to reflect traditional ERP analyses, as ANOVA/regression appeared in 90.16% percent of developmental ERP studies we reviewed (see Appendix Table A.1). In ANOVA models, subjects with a low ERP trial count are casewise deleted and the remaining data are averaged within subjects for each condition. In comparison, the LME model was fit to data at the trial level after induced missingness, and all subjects were included in this analysis. Restricted maximum likelihood estimation was used to fit all LME models because it produces less biased random variance components, and is recommended for fitting the final model (Zuur et al., 2009). These two models were fit to each of the 1000 simulated datasets to examine whether simulated mean amplitude estimates were accurate (i.e., matched the population values assigned) in LME and ANOVA. A small percentage of LME models did not converge with the random effects structure in Eq. (3), and these datasets were not included in analyses (see Appendix Table B.2).

Eq. (3): LME model for simulated datasets.

Level 1 (within-subjects): MeanAmplitude_ij = β_0j + β_1jEmotion_ij + β_2jPresentationNumber_ij + Ɛ_ij.

Level 2 (between-subjects):

β_0j = γ₀₀ + γ₀₁Age_j (coefficient of the fixed effect of Age) + u_0j + v_0a.

β_1j = γ₁₀ (coefficient of the fixed effect of Emotion).

β_2j = γ₂₀ (coefficient of the fixed effect of Presentation Number).

i represents trial-level estimates.

j represents subject-level estimates.

γ represents mean estimates for predictors.

u represents Subject-level deviation from the grand mean (i.e., random intercept for Subject).

v represents Actor-level deviation from the grand mean (i.e., random intercept for Actor [a]).

For each simulated dataset, the marginal means (averaged over age) for emotion A and emotion B were extracted from the ANOVA and LME models (Appendix Table B.3 and Table B.7) using the emmeans package (Version 1.5.3; Lenth, 2021). For the LME model only, the estimated marginal means were specified at presentation number 5.5 (i.e., the average presentation number simulated in the dataset), in order for the values to be comparable to the averaged dataset used for the ANOVA model. Therefore, the population parameter for emotion A corresponds to − 3.25 μV and the population parameter for emotion B corresponds to − 5.25 μV.

The two models’ marginal means were then assessed with two measures. First, we examined root mean squared error (RMSE) of each model’s mean estimate’s divergence from the population mean. RMSE values are in the same unit of measurement and therefore correspond to how many μV of bias and variance were in the sample. Lower RMSE values are associated with models that are less biased and more precise. Second, we examined percent relative bias, which assesses the degree (as a percentage) that model’s parameter estimates differ from the population value (Enders et al., 2020). Based on previous simulation literature, less than 10% bias is an acceptable value (Enders et al., 2020, Finch et al., 1997, Kaplan, 1988). These procedures were repeated for 1000 simulated datasets. We report the estimated marginal means, RMSE, and percent relative bias in line with reports from other research with simulated data (Demirtas and Doganay, 2012, Enders et al., 2020, Lee and Carlin, 2017, Schielzeth et al., 2020). All reported results below correspond to emotion A (see also Appendix Tables B.3–B.6). Similar results for emotion B are reported in Appendix Tables B.7–B.10.

3.2. Results

When no missing trials were removed (the population model), ANOVA and LME had identical marginal means and standard deviations, illustrating that these models are identical in modeling mean estimates (see Fig. 4, far left panel in all rows). In contrast, LME and ANOVA results differed substantially when data were missing, as demonstrated in sections below.

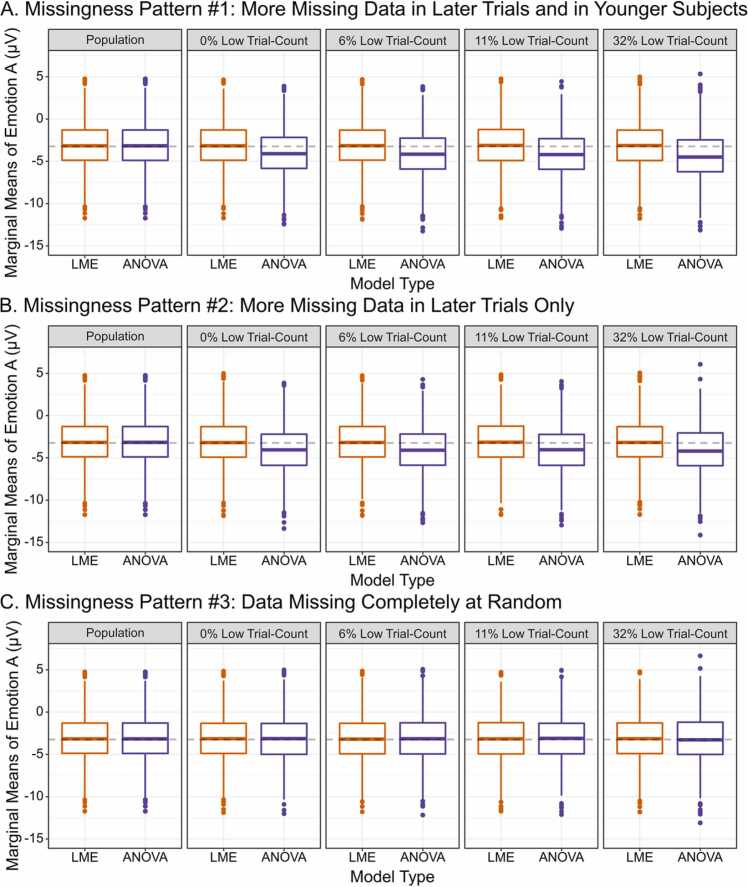
Fig. 4.

Marginal means of emotion A were extracted for 1000 simulated datasets. The population parameter of emotion A (averaged over age and presentation number) is indicated by the dashed line at − 3.25 μV. Means were estimated from datasets in which no trials were removed (Population), all subjects were assigned to have 10 or more trials (0% Low Trial-Count), and at varying percentages of low trial-count subjects taken from the Developmental Cognitive Neuroscience literature review. Percentages of low trial-count subjects represent the average percentage of casewise deletion in older children (6%), preschoolers (11%), and infants/toddlers (32%). Marginal means were extracted from each of the three patterns of missingness. For Missingness Pattern #3, missing trials were uniformly drawn from early and late trials and older and younger children.

3.2.1. Missingness pattern #1: more missing data in later trials and in younger subjects

More missing data induced for both later trials and younger subjects resulted in biased (more negative) ANOVA mean estimates compared to LME, even when no subjects were casewise deleted (see Fig. 4, and Appendix Fig. B.1 for similar results with emotion B). As the percentage of casewise deletion increased, the ANOVA marginal means became even more negatively biased. In contrast, the LME provided unbiased means at all percentages of low trial-count subjects. Further the error variance (i.e., standard deviation) of the ANOVA marginal means increased with greater percentages of casewise deletions, but LME error variance was unchanged.

To quantify the increasing negative bias in the ANOVA and assess its significance, we examined the ANOVA model’s RMSE and relative bias values. The increase in the ANOVA model’s error variance contributed to a greater RMSE value at all percentages of casewise deletion (0%−32%). Furthermore, the ANOVA model’s RMSE increased with greater percentages of casewise deletion (reported in Appendix Tables B.4 and B.8). In comparison, the LME model’s RMSE value remained low at all percentages of low trial-count subjects. Similarly for relative bias, the ANOVA model’s bias values were greater than the acceptable 10% threshold at every percentage of casewise deletion, and increased as percentages increased (reported in Appendix Tables B.5 and B.9). In comparison, the LME model’s relative bias remained below the 10% relative bias threshold and remained comparable at all percentages of low trial-count subjects. Paired t-tests with a Bonferroni correction of α = 0.003 indicated that the relative bias values for the LME and ANOVA significantly differed starting at 0% (see Appendix Tables B.6 and B.10).

These results illustrate the advantages of LME over ANOVA: there were clear detrimental effects of using ANOVA when data were missing for both within- and between-subjects effects, even when no subjects were casewise deleted, and the ANOVA’s biases increased with greater percentages of casewise deletion. Specifically, when an increasing number of later trials were removed, earlier trials that showed a greater negative amplitude were reflected in the marginal mean, and this decreasing amplitude over presentation number was not accounted for in the ANOVA. Further, when an increasing number of younger subjects were casewise deleted, this further biased the ANOVA model’s marginal means to reflect the mean amplitude of older subjects, who had more negative amplitudes. In contrast, by accounting for random effects (subject and actor) and including data from all subjects, LME remained unbiased even when data were missing for both within- and between-subjects effects.

3.2.2. Missingness pattern #2: more missing data in later trials only

More missing data for trials presented later in the experiment (reflecting greater missingness for a within-subjects effect and simulating a more ideal ERP data collection result) still resulted in biased (more negative) ANOVA mean estimates compared to LME. Comparable to results from Missingness Pattern #1, the ANOVA model’s marginal means were negatively biased from the population marginal means at all percentages of casewise deletion, as quantified by relative bias values that were greater than 10%. In addition, the ANOVA model’s marginal means had greater error variance and RMSE values that increased with greater percentages of casewise deletion. In contrast, the LME models’ marginal means were not biased, and all relative bias values were below the 10% threshold. As with Missingness Pattern #1, paired t-tests indicated that the relative bias values significantly differed between the LME and ANOVA models at all percentages of missing data examined (0–32%, Appendix Tables B.6 and B.10).

There were also small improvements in the ANOVA model’s results compared to those from Missingness Pattern #1. Specifically, the marginal means extracted from this ANOVA model with greater missing data for later trials only did not increase in bias at greater percentages of casewise deletion—the relative bias remained at approximately 25% (in contrast to the increasing bias at greater proportions of deletion in Missingness Pattern #1). In addition, the ANOVA model’s RMSE values at 6%, 11% and 32% casewise deletion were lower compared to the RMSE values from Missingness Pattern #1. Thus, compared to missing data for within- and between-subjects effects (e.g., both trial number and age), missingness in only the within-subjects effect (e.g., only trial number) was slightly less detrimental for the ANOVA model, but LME was still clearly advantageous, again producing unbiased and robust results at all percentages of low trial-count subjects.

3.2.3. Missingness pattern #3: data missing completely at random

In contrast to the prior two missingness patterns, when MCAR was induced for both between- and within-subjects effects (simulating an ideal, though less likely, ERP data collection result), the ANOVA and LME models performed more comparably. The ANOVA and LME marginal means only differed by 0.04 μV or less at every percentage of missingness examined (0%, 6%, 11%, and 32%). The relative bias values for both models were below 10% and did not significantly differ at any percentage of casewise deletion/low trial-count subjects.

However, even in this more ideal simulation, the ANOVA model’s error variance and RMSE values still increased with greater percentages of casewise deletion, demonstrating that the ANOVA model is associated with less precise estimates even when assumptions of MCAR are met. In contrast, and in line with the prior two patterns of missingness, LME performed similarly at all percentages of low trial-count subjects. Therefore, although the marginal means did not differ between the ANOVA and LME when data were MCAR, the error around marginal means was still increased for ANOVA, illustrating a continued disadvantage of the ANOVA model compared to LME.

3.3. Discussion of simulation results

Overall, analysis of the simulated data illustrates the limitations of ANOVA models in modeling the true population mean amplitude in a dataset, and the clear advantages of the LME model at realistic amounts of low trial counts (i.e., as reflected in our literature review, see Fig. 2 and Appendix A). In the simulated data, following parameters of real NC ERP data (Borgström et al., 2016, Di Lorenzo et al., 2020, Leppänen et al., 2007, Smith et al., 2020), younger subjects had less negative amplitude compared to older subjects, and trials presented later in the experiment had less negative amplitude compared to earlier trials. We then simulated common patterns of missingness such that there were fewer artifact-free trials in younger subjects (missingness between-subjects), and fewer artifact-free trials occurring at the end of the experiment (missingness within-subjects). ANOVA results were biased by the following mechanisms: 1) ANOVA was unable to account for the within-subjects mean amplitude habituation over repeated trials (because data were mean averaged), 2) Casewise deletion resulted in fewer included subjects, and 3) Casewise deletion was inappropriately implemented in Missingness Patterns #1 and #2 because data were not MCAR. Thus, the ANOVA yielded estimates that were negatively biased compared to the population mean that were most evident when there was missing data for both within- and between-subjects effects. Moreover, these biases increased at greater percentages of casewise deletion. Even in the simulation of ideal missingness—when data were missing completely at random across trial number and subject age (which is less likely in developmental ERP data collection)—the ANOVA still resulted in greater error in mean estimates compared to LME. In contrast, the LME model accounted for missing data using maximum likelihood, retained all subjects for analysis—even subjects assigned to have low trial counts—and moreover accounted for the decrease in amplitude over repeated trials through a fixed effect of trial number. The LME models thus yielded unbiased parameter estimates (that accurately captured the population mean) at all percentages of low trial-count subjects, in all three patterns of missingness. These results highlight two advantages of LME: 1) Casewise deletion is not needed to improve model performance or to extract the true population mean amplitude in a dataset, and 2) LME models can extract unbiased mean estimates even with missing data corresponding to 32% casewise deletion (approximating the highest percentage of casewise deletion observed in our review of developmental ERP studies).

4. LME and ANOVA comparison in real ERP data from preschool children

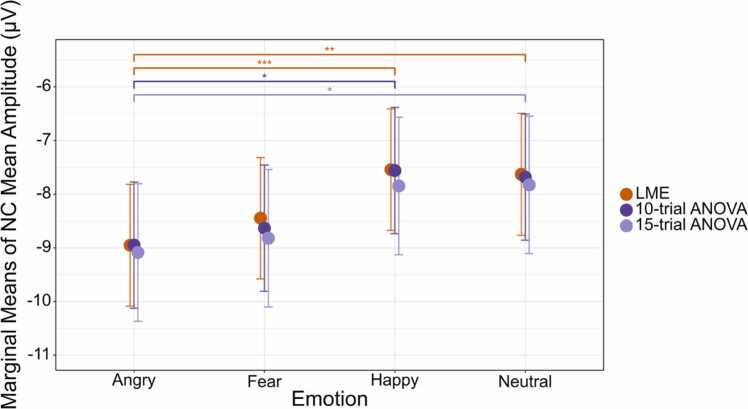
In addition to simulated data, we also use real developmental ERP data to demonstrate the advantages of LME over traditional ANOVA approaches that employ casewise deletion and mean averaging. Paralleling the simulation, in this real dataset, we examined amplitude of the NC ERP component in typically developing 3- to 6-year-old children who passively viewed faces depicting different emotional expressions (e. g., happy, angry, fearful, neutral). As discussed above, the NC is an emotion-sensitive ERP component that can be elicited by emotional face stimuli (Grossmann et al., 2007, Leppänen et al., 2007). NC amplitude is maximal at central electrodes from approximately 300 to 600 ms in both infants and preschool children (Dennis et al., 2009, Todd et al., 2008, Xie et al., 2019), and commonly differs when viewing angry faces versus happy faces (Cicchetti and Curtis, 2005, Grossmann et al., 2007, Xie et al., 2019).

Similar to the approach taken with the simulated data, we analyze these real NC data using both traditional ANOVAs with casewise deletion, and compare these results to LME analyses that utilized the whole sample of subjects and employed restricted maximum likelihood estimation to account for missing trial-level data.

4.1. Methods

4.1.1. Subjects

A diverse sample of typically developing children (N = 44) was tested in a laboratory setting for a one-time visit when children were 3- to 6-years-old. Subjects were recruited from a database of families willing to participate in research, and compensated for their time with a toy, a photo of the child wearing the EEG cap, and a $5 giftcard. The Institutional Review Board approved all methods and procedures used in this study, and all parents gave informed consent prior to participation. Six subjects were excluded from the final sample: Five were excluded due to technical issues and one due to refusal to wear the EEG cap. Thus, the final sample for analysis was 38 preschool children (16 males, 22 females, M_age = 59.92 months, SD = 6.85). Demographics for the final sample were representative of the community from which they were recruited: 26 were Caucasian (19% Latinx, Chicanx or Hispanic), 5 were multi-racial (80% Latinx, Chicanx or Hispanic), 2 were African or African American (not Latinx, Chicanx or Hispanic), 3 were Asian or Asian-American (not Latinx, Chicanx or Hispanic), 1 subject did not report race, and was Latinx, Chicanx or Hispanic, and 1 subject did not report race or ethnicity. The median educational attainment of the child’s mother was a four-year college degree (N = 14); 16 mothers had a graduate degree, 5 had an Associate’s or technical degree, 2 had a high school diploma or equivalent and 1 did not report educational attainment. The median educational attainment of the child’s father was a four-year college degree (N = 14); 12 fathers had a graduate degree, 1 had an Associate’s or technical degree, 9 had a high school diploma or equivalent and 2 did not report educational attainment. Median family income was $100,000 and greater (N = 18); 9 families earned $75-$99k, 5 earned $50–74k, 2 earned $35–49k, 1 earned less than $16k and 3 did not report income.

4.1.2. Measures

Stimuli for the ERP task paralleled common developmental ERP tasks designed to study the NC and other face- and emotion-sensitive ERP components (e.g., Xie et al., 2019). Face stimuli consisted of female faces expressing the following 6 emotions: happiness, anger, fear, neutral (no emotion), as well as two reduced intensity images—40% fear, and 40% anger—achieved by morphing the neutral and emotional exemplars until final images included 40% of the emotional expression and 60% of the neutral expression. Face stimuli were taken from the NimStim set of emotional faces (Tottenham et al., 2009). There were four face sets consisting of African American actors, East Asian actors, and two sets of Caucasian actors. Children saw the face set that best matched their own race as reported by their parent. Caucasian face sets were counterbalanced across Caucasian subjects, and represent the majority of stimuli used in the present study (81.58%). The face sets consisted of unique actors that each displayed all emotional expressions: There were five unique East Asian actors, four unique African American actors, and nine unique Caucasian actors distributed across the two Caucasian face sets with one actor repeated across both sets. Within each face set, subjects saw each actor express each of the 6 emotions 10 times (except where one actor was presented 20 times across each emotion in the African American set) for a total of 300 trials in the experiment. Faces were presented in a semi-randomized order via E-Prime (Version 3.0; Psychology Software Tools, 2016) such that the same emotion was not presented twice in a row. Faces were presented for 1000 ms and were preceded by a fixation cross for 800–1400 ms (see Fig. 5). ERPs were time-locked to the onset of the face stimulus. The ERP experiment lasted approximately 25 min, and children took a short break between each of the 20 blocks of 15 trials during which they placed a stamp on a colorful piece of paper, rested their eyes, or wiggled their fingers and shoulders briefly. For the present study, we examine NC amplitude across each of the 100% emotion categories (happiness, anger, fear, and neutral) for a maximum trial count of 200 trials across the experiment (see experimental design in Fig. 6). In our sample, trial counts per subject per emotion condition were not statistically different, F(3,111) = 1.62, p = .189, and data met assumptions of sphericity, p's > .168. The average number of trials in each condition was M = 27.24, SD = 11.60 for happy faces; M = 26.61, SD = 11.71 for angry faces; M = 27.05, SD = 10.50 for fearful faces; and M = 25.68, SD = 10.21 for neutral faces.

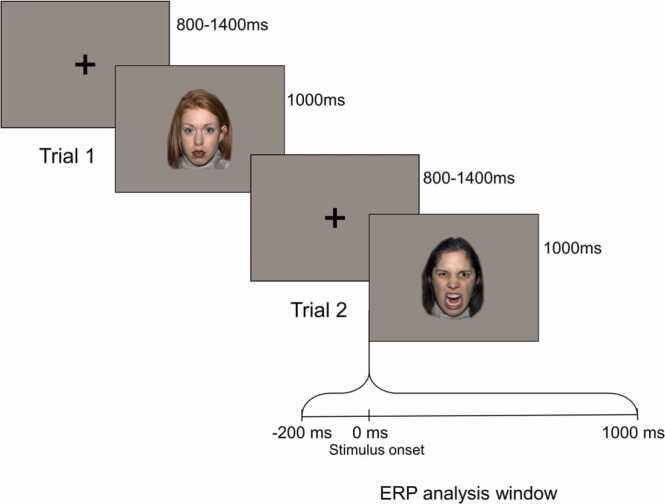
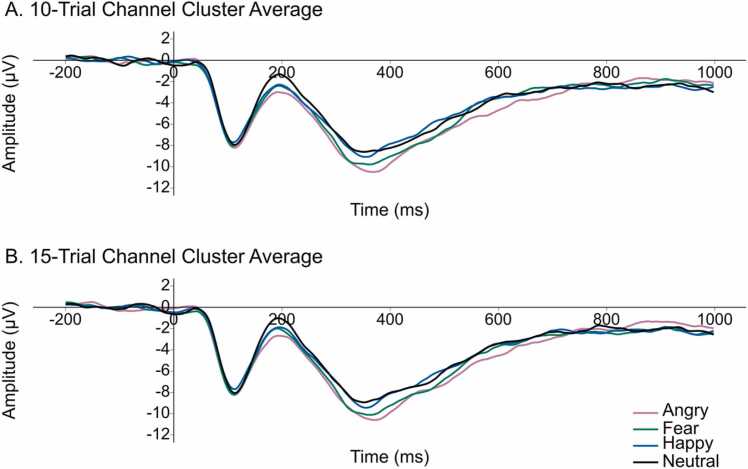
Fig. 5.

ERP experimental design illustrating inter-trial interval, stimulus duration, and ERP extraction window. Before each trial, a fixation cross was presented for a random interval between 800 and 1400 ms. A neutral, happy, angry or fearful face was presented for 1000 ms in a random order and the same emotion was not presented for two consecutive trials. ERPs were baseline corrected using the mean amplitude from − 200–0 ms, in which 0 ms is time-locked to stimulus onset. ERPs were analyzed from 0 to 1000 ms post stimulus onset.

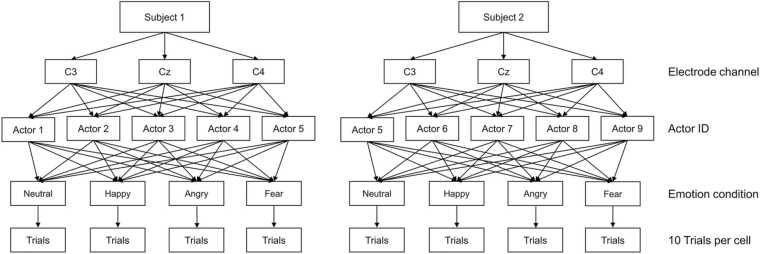
Fig. 6.

ERP experimental design shown for two example subjects (Subject 1 and 2). Data were analyzed from 3 electrode channels corresponding to the NC ERP component. In the present study’s final data set, there were 18 unique actors displaying emotions in 4 conditions. Electrode channel and emotion were fully-crossed within the study design (i.e., all subjects saw all emotions and had usable data from each electrode), and actor was partially-crossed (i.e., subjects in the same race condition saw the same set of actors, and subjects in other race conditions saw different actors).

4.1.3. Set-up to facilitate trial-level analysis with LME

To facilitate analysis using LME, each individual trial presented to a given subject was tagged with a unique event marker code, applied at the time of data collection. In the present study, event markers were inserted via stimulus presentation software (E-Prime Version 3.0; Psychology Software Tools, 2016) corresponding to emotion condition and a unique actor code. After data collection, event markers were replaced with a five-digit code indicating the emotion condition (first digit), actor (second and third digits), and presentation number (fourth and fifth digits). For example, the first presentation of Caucasian actor 1 expressing ‘happy’ corresponds to the five-digit code 60101; whereas the second presentation of the same actor and condition corresponds to code 60102 (see Appendix C). The EEG files were processed in EEGLAB (Version 2019_0; Delorme and Makeig, 2004) and ERPLAB (Version 8.01; Lopez-Calderon and Luck, 2014; see Section 4.1.4), and epochs were extracted at the trial-level using ERPLAB’s BINLISTER function. See Appendix C and D for further details on how to create trial-level event marker codes. These appendices also include the GitHub link to our laboratory’s MATLAB and R code for a tutorial ERP LME analysis pipeline.

4.1.4. ERP data processing

Electroencephalographic (EEG) data were recorded continuously throughout the ERP experiment using a BrainVision Recorder (Version 1.21.0303; Brain Products GmbH, Gilching, Germany), actiCHamp (2020c) amplifier (actiCHamp, Brain Products GmbH, Gilching, Germany), and a 64-channel montage High Precision fabric actiCAP snap (2020b) cap (actiCAP snap, Brain Products GmbH, Gilching, Germany) that positioned actiCAP slim electrodes in line with the 10–20 International system (actiCAP slim (2020a), Brain Products GmbH, Gilching, Germany). Data were recorded bandpass filtered from 0 to 140 Hz, referenced online to Cz, and digitized at 500 Hz sampling rate.

Data were analyzed offline in the MATLAB (Version 2019a; MATLAB, 2019) toolboxes EEGLAB (Version 2019_0; Delorme and Makeig, 2004) and ERPLAB (Version 8.01; Lopez-Calderon and Luck, 2014). Continuous EEG was bandpass filtered using a Butterworth filter 12 dB/octave from 0.1 to 30 Hz in line with prior research (Batty and Taylor, 2006, Cicchetti and Curtis, 2005). Data were then visually inspected to identify areas of egregious artifact due to excessive motion/noise: noisy segments were rejected, noisy channels were flagged for interpolation (mean channels interpolated = 0.26, SD = 0.72) using spherical spline. This practice is recommended (Debener et al., 2010, Debnath et al., 2020) to improve the accuracy of subsequent Independent Components Analysis (ICA) to identify blinks. ICA was then performed in EEGLAB to identify blink components. A component resembling a blink (according to characteristics outlined in Debener et al., 2010) was identified in 92% of subjects and removed before epoching. Trials were epoched from − 200 to 1000 ms to constitute a 1000 ms post-stimulus epoch with 200 ms baseline, in line with prior studies examining face- and emotion-sensitive components with similar study designs in infants and children (Cicchetti and Curtis, 2005, de Haan et al., 2004, Hoehl and Striano, 2010). In ERPLAB (Version 8.01; Lopez-Calderon and Luck, 2014) via automated processing, epochs were rejected if they contained an artifact in which any single channel exceeded − 120–120 µV (Batty and Taylor, 2006) or in which sample-to-sample µV exceeded 100 µV (Kungl et al., 2017, Todd et al., 2008), in line with prior preschool ERP research pre-processing parameters. After epoching and artifact rejection, subjects contributed an average of 26.64 trials/condition (SD = 10.63 trials).

Mean amplitude was extracted in each remaining artifact-free epoch. We extracted mean amplitude rather than peak because it provides an unbiased amplitude estimate (Luck, 2014). In comparison, peak amplitude can be biased by noise, and may overestimate the true amplitude value (Clayson et al., 2013, Luck, 2014). In mean-averaged analyses, the probability of a Type 1 error increases when comparing the peak amplitude between conditions with different trial numbers (and subsequently different noise levels, Luck, 2014). This increased error rate may affect developmental ERP research in particular, given that children’s data are noisy and may have an unequal number of trials across conditions.

NC mean amplitude was extracted from the following channels based on previous ERP research with infants and children (Dennis et al., 2009, Stahl et al., 2010, Xie et al., 2019): C3, Cz, and C4. The time window for extracting mean amplitude was taken as 300–500 ms, in line with prior studies examining the NC (Quadrelli et al., 2019, Todd et al., 2008). To confirm that this extraction window was appropriate for our sample, the grand average waveform, collapsed across all conditions so as to avoid the possibility of visualizing any condition effects, was visually inspected to verify that the time window symmetrically captured the negative deflection characteristic of the NC. Each subject’s condition-averaged waveforms were then examined to verify that the time window reasonably captured the NC across the entirety of the sample.

4.2. Data analysis plan

We examined whether NC mean amplitude was modulated by emotion condition in our sample of typically developing preschoolers. Based on previous research (Moulson et al., 2009, Grossmann et al., 2007, Xie et al., 2019; but see also Dennis et al., 2009, Todd et al., 2008), we expected that NC would be modulated by emotion. To compare LME to traditional ANOVA approaches commonly employed in developmental ERP research, we examined emotion effects across three models: a linear mixed effects model and two repeated measures ANOVA models.

The linear mixed effects model analyzed trial-level data at each electrode site from all subjects who contributed any number of clean trials, which included several fixed effects: the main effect of interest (emotion) and two control variables (electrode and trial presentation number), in addition to two random intercepts (subject and actor). Electrode was included as a fixed effect due to the low number of levels (3: C3, Cz, and C4) based on recommendations from previous literature (Volpert-Esmond et al., 2021). As with the simulation analysis, LME models were fit with restricted maximum likelihood (REML) to calculate less biased random variance components. REML has been recommended for testing fixed effects for small sample sizes (Snijders and Bosker, 2012). Although centering is generally recommended in LMEs (see Raudenbush and Bryk, 2002), data were not centered in order for model coefficients to remain comparable to the ANOVA models, and all models’ coefficients are in µV. Data were analyzed in R (Version 3.6.1; R Core Team, 2019) using the lme4 package (Version 1.1–25; Bates et al., 2015) and p-values were calculated using the lmerTest package (Version 3.1–3; Kuznetsova et al., 2017).

Results from two repeated measures ANOVAs were compared to results from LME. The ANOVAs were conducted in R using the afex package (Version 0.28–1; Singmann et al., 2021). Assumptions of sphericity were met in all samples and therefore p-values were not Greenhouse-Geisser corrected. The two ANOVAs differed in the criteria used to determine casewise deletion of subjects. Specifically, two common methods of casewise deletion were examined: deleting subjects with fewer than 10 trials in any one condition, and a more stringent criterion of deleting subjects with fewer than 15 trials in any one condition. These exclusion criteria represent the lower and upper limit of the most common trial-count cutoffs used in developmental ERP studies, as revealed in our review (see Appendix A).

After testing for an omnibus effect of emotion in each of these three models, pairwise comparisons of marginal means for both LME and ANOVA were conducted using the emmeans package (Version 1.5.3; Lenth, 2021), and p-values were adjusted using the Sidak correction (Sidak, 1967) for 6 pairwise emotion comparisons. Based on results with the simulated data, we hypothesized that the LME would return different effects of emotion condition compared to the ANOVAs.

4.3. LME analyses

4.3.1. LME model

We aimed to include the maximal number of random effects that would converge, in line with LME recommendations in the field (Barr et al., 2013, Brauer and Curtin, 2018). Our attempted maximal model was a 2-level random slope model in which the outcome was NC mean amplitude at the trial level; fixed effects were emotion, presentation number, and electrode; a random intercept for subject; random by-subject slopes for emotion and presentation number; a random intercept for actor; and random by-actor slopes for emotion and presentation number. The maximal model did not converge and was thus simplified based on recommendations from Brauer and Curtin (2018) in which we incrementally removed random effects until the model would converge. The final model was a 2-level random intercept model in which the outcome was NC mean amplitude at the trial level; fixed effects were emotion, presentation number, and electrode; and random intercepts were subject and actor (see Eq. 4). We report the full model selection process and accompanying R script in Appendix D.6. The LME assumptions of linearity and a normal distribution of residuals for the final model were confirmed based on visual inspection, and homogeneity of variance was confirmed with a Levene’s test (p = .745). A normal distribution of residuals was confirmed with visual inspection, and not a Shapiro-Wilk test, because the number of samples exceeded 5000 (Royston, 1995).

Eq. (4): LME model for preschooler dataset.

Level 1 (within-subjects): MeanAmplitude_ij = β_0j + β_1jEmotion_ij + β_2jElectrode_ij + β_3jPresentationNumber_ij + Ɛ_ij.

Level 2 (between-subjects):

β_0j = γ₀₀ + u_0j + v_0a.

β_1j = γ₁₀ (coefficient of the fixed effect of Emotion).

β_2j = γ₂₀ (coefficient of the fixed effect of Electrode).

β_3j = γ₃₀ (coefficient of the fixed effect of Presentation Number).

i represents trial-level estimates.

j represents subject-level estimates.

γ represents mean estimates for predictors.

u represents Subject-level deviation from the grand mean (i.e., random intercept for Subject).

v represents Actor-level deviation from the grand mean (i.e., random intercept for Actor [a]).

4.3.2. LME results

The LME model revealed a significant effect of presentation number, in which later trials showed less negative NC amplitude (β = 0.44, SE = 0.04, p < .001), see Fig. 7. This effect is in line with previous literature demonstrating a habituation effect in the NC (Borgström et al., 2016, Reynolds and Richards, 2019), and highlights the importance of controlling for trial presentation number in analyses. In addition, the LME model revealed a significant effect of electrode. Pairwise comparisons with Sidak-corrected p-values for 3 pairwise electrode comparisons indicated that Cz had a significantly more negative NC amplitude than C3 (t(12097) = −4.21, p < .001) and C4 (t(12097) = −3.19, p = .004). As discussed in Section 4.2, electrode was included as a nuisance fixed effect due to its low number of levels (3) so we do not further interpret this significance.

Fig. 7.

The observed means of NC mean amplitude over repeated trial presentations (A, left). The marginal means of NC mean amplitude estimated by the LME model over repeated trial presentations (B, right). Error bars represent 95% confidence intervals. Trial repetitions for one actor in the African American condition presented 20 times are not plotted, but were estimated in the model.

The LME revealed an effect of emotion condition, which was detected through model comparison of the full model, and a model that did not include a fixed effect of emotion (but did include all other predictors: presentation number and electrode, and random intercepts for subject and actor). Comparison of these two models revealed that including a fixed effect of emotion significantly improved model fit, and therefore that there were differences between the emotions’ means, χ²(3, N = 12,150) = 18.58, p < .001. Pairwise comparisons revealed significantly more negative NC amplitude for Angry versus Neutral faces, t(12114) = −3.41, p = .004, and more negative amplitude for Angry versus Happy faces, t(12115) = −3.69, p = .001. All other pairwise emotion comparisons were not significant (t’s > −2.38, p’s > .100).

Therefore, despite noise in single-trial waveforms (see Fig. 8 for an example of single-trial data from one subject), the LME model was able to detect significant differences across conditions and account for error variability through random effects.

Fig. 8.

Example single-trial waveforms for one subject in the dataset. For a single trial in a given condition, ERP data are noisy. However, LME is able to account for noise in single-trial data because it models the condition means and accounts for ‘nuisance’ variables that cause related trials to be more similar to each other.

4.4. ANOVA analyses

4.4.1. ANOVA models

To examine whether NC mean amplitude differed across the three electrodes analyzed, we first tested for an interaction between electrode and emotion in a two-way repeated measures ANOVA where predictors were emotion and electrode, and the outcome variable was NC mean amplitude. There was not a significant interaction between electrode and emotion at either the 10-trial threshold, F(6,204) = 0.67, p = .673, nor at the 15-trial threshold, F(6,162) = 2.05, p = .062. Therefore, cluster-level data (averaged across 3 electrodes) was averaged within each emotion at the subject-level, as is common in ERP analyses (see Fig. 9 for grand-mean averaged ERP waveforms). Unlike in the LME model, ANOVA does not model the effects of presentation number or actor because data are averaged over the entirety of the experiment within condition (across all actors) and within subject. Therefore, the final ANOVA model was a one-way repeated measures ANOVA.

Fig. 9.

Grand-mean average ERP waveforms for subjects with at least 10 trials/condition (N = 35, A, top) and at least 15 trials/condition (N = 28, B, bottom). Waveforms were collapsed across channels of interest (Cz, C3, and C4).

4.4.2. ANOVA results

The one-way repeated measures ANOVA was conducted on each of the two subsets of data (10-trial casewise deletion, N = 35; and 15-trial casewise deletion, N = 28). In these ANOVAs, the outcome variable was NC mean amplitude averaged over the three electrode sites (C3, Cz, and C4) to form an NC ‘cluster’, and emotion was a within-subjects predictor. Shapiro-Wilk tests of both models confirmed the residuals were normally distributed, p’s > .246, and Levene’s test showed that homogeneity of variance was met, p’s > .750. Grand-mean averaged waveforms are visible in Fig. 9.

Similar to the LME results, both ANOVAs revealed an omnibus significant effect of emotion: ANOVA on data with minimum 10 trials/condition cutoff, F(3,102) = 4.20, p = .008; ANOVA on data with minimum 15 trials/condition cutoff, F(3,81) = 3.92, p = .011. However, follow-up comparisons revealed that each ANOVA only yielded a single significant pairwise condition effect (compared to the two significant condition effects yielded with LME). Further, these ANOVA condition effects were different depending on which trial cutoff was used: For the 10-trial cutoff data, NC amplitude was more negative for Angry versus Happy faces, t(102) = −2.92, p = .026; whereas for the 15-trial cutoff data, NC amplitude was more negative for Angry versus Neutral faces t(81) = −2.70, p = .050.

4.5. Comparison of LME and ANOVA models

The LME and ANOVA models differed in several ways: the observations modeled, the inclusion of presentation number and random effects, and the sample size. Specifically, LME modeled trial-level data extracted at the electrode-level, whereas the ANOVA modeled mean-averaged data across electrode sites extracted at the ‘cluster’-level. The LME model included a fixed effect of presentation number to account for amplitude decay over repeated presentations, whereas data in the ANOVA was averaged across the repeated presentations and across actors used in the four stimuli conditions. The LME model accounted for nesting of the trial-level data through two random intercepts: subject and actor. ANOVA accounted for nested data through mean averaging trials within subjects. Finally, given that LME analyzes trial-level data, all subjects (N = 38) were included in analyses, compared to the 10-trial casewise deletion ANOVA (N = 35) and to the 15-trial casewise deletion ANOVA (N = 28). Therefore, ANOVAs had a smaller sample size compared to LME due to casewise deletion of subjects with too few trials in each emotion condition.

Each of these three models detected a significant omnibus effect of emotion on NC mean amplitude. However, whereas the LME was able to detect significantly greater (more negative) amplitude between Angry and both Happy and Neutral, the ANOVA models each only detected one of these significant effects. Moreover, different effects were detected across the two ANOVA models.

The marginal means across these three models differed slightly (see Fig. 10), in which the ANOVA means were more negative across conditions compared to the LME model. As discussed in simulation results in Section 3, this may be because of greater missing data toward the end of the experiment (when children are fussier and have fewer clean trials) resulting in over-representation of the early presented trials which have more negative amplitudes. The ANOVAs cannot account for this effect of trial presentation and thus yielded more negative means. In addition to accounting for trial presentation order, the LME model was also able to account for other nuisance variables such as individual differences across subjects (e.g., some children have generally higher or lower amplitude EEG), actor (e.g., where a more salient actor, such as an actor with red hair, has similar amplitude across subjects), and electrode site (e.g., where Cz amplitude is similar across subjects because of scalp location). These advantages to LME were illustrated through better sensitivity to detect significant differences in NC mean amplitude compared to ANOVA.

Fig. 10.

Marginal means compared across the three models: LME, repeated measures ANOVA at 10 trials/condition casewise deletion, and repeated measures ANOVA at 15 trials/condition casewise deletion. Error bars represent 95% confidence intervals.

4.6. Discussion of real ERP data from preschool children

Both LME and the ANOVAs revealed a significant effect of emotion. However, for the ANOVAs, the estimated marginal means analysis did not consistently identify the significant differences between both Angry and Happy, and Angry and Neutral, which were each revealed in the LME analysis. This reduced efficacy of the ANOVA was expected given that casewise deletion reduces the sample size, therefore lowering the power to detect a significant effect across conditions. The discrepant results from the two ANOVAs also illustrate the problem of arbitrary trial-count cutoffs for casewise deletion. Specifically, researchers’ decisions to set a 10 or 15 trial/condition minimum is arbitrary. In our dataset, setting a 10 versus a 15 trial/condition threshold resulted in (1) the inability to detect both condition differences in the sample, and (2) different effects detected across these two cutoffs. As these results illustrate, the arbitrary selection of a given cutoff for casewise deletion may be associated with Type II error – accepting the null hypothesis when there is a significant effect in the population.

This example dataset demonstrates how LME addresses issues in mean-averaging analyses and casewise deletion, using real developmental ERP data. Specifically, arbitrary trial-number thresholds for ERP data can result in ‘researcher degrees of freedom’ (Gelman and Loken, 2013) in choosing which threshold to use, and therefore which condition difference to report. In contrast, LME may have been better able to detect all significant condition differences due to increased power by including all subjects, or by accounting for error in subject, actor, and electrode variability, which the ANOVA models were unable to account for. These results from real preschool ERP data support findings in simulated data previously presented in Section 3, and demonstrate the utility of applying LME models to developmental ERP data.

5. Challenges and limitations to LME

LME resolves issues in traditional grand-mean averaging in ANOVA, including issues relating to casewise deleting subjects resulting in loss of power and biased mean amplitude estimates, as well as issues of violating missingness assumptions when trial-level missingness is predicted by a measured variable (i.e., MAR). However, implementing LME in ERP designs requires careful thought when planning the experimental design, fitting the LME model, and in reporting results and plotting ERPs. We break down issues that may arise during planning, fitting models, and reporting results, and present challenges and suggestions for researchers to consider.

5.1. Considerations when planning an ERP experiment

While not necessarily a challenge to LME, there are prerequisites in planning an ERP experimental design in order to fit LME models. Specifically, the researcher must insert event markers during ERP data collection that indicate which stimulus is presented (as outlined in Section 4.1.3; see also tutorial on creating unique event markers and accompanying code for LME analysis in Appendix D. For an example spreadsheet with text descriptions for each numeric value, see LME_EventMarkerMappingKey.xlsx in https://github.com/basclab/LME_MixedEffectsERPTutorial/blob/main/LMETutorialScripts). Event markers should indicate both the trial type and which specific stimulus was presented (e.g., actor, emotion, presentation number). In addition to facilitating LME analyses, an added benefit to inserting trial-specific markers is that they allow the researcher to identify and remove specific stimuli or trials that present as systematic outliers in post-processing.

An additional issue in planning an ERP experiment using LME is in determining the required sample size to reach adequate power. Currently, there is a lack of convenient power analysis software to determine sample size (e.g., G*Power, Faul et al., 2007) for LME. However, in planning ERP experiments where data will be analyzed with LME, the available simulation code can be used to calculate power and required sample size before running an ERP experiment (see Appendix B for link to GitHub with simulation code and additional resources). Specifically, code can be adapted with the estimated number of trials each subject will complete in order to estimate the parameter coefficients of the experimental conditions (e.g., expected mean amplitude across conditions). Power can then be calculated by examining in how many simulations the effect of interest was observed.

In addition, Baraldi and Enders (2010) recommend that researchers include auxiliary variables (described in Section 1.2.3). These additional variables allow researchers to examine mechanisms of missing data and give researchers greater confidence that their model’s data are likely MAR. For example, trial presentation number (in which more trials are missing toward the end of the experiment), age (in which younger children have less usable trials), executive function (in which children with greater inhibitory control can sit still for longer and have more usable trials), and temperament (in which children with more agreeable temperaments can tolerate longer experiments and yield more usable trials) are a few examples of auxiliary variables that developmental ERP researchers may want to collect in order to examine missing data patterns. In addition, infant researchers may want to collect data on the infant’s last feeding time or hours slept in the previous day. These additional variables allow for a more comprehensive examination of missing data patterns and can give researchers more confidence that their data are likely MAR and thus meets missingness assumptions of LME.

Currently, there are limitations to LME in analyzing difference waves (e.g., as done in regression or correlational analyses with behavioral predictors). Typically, difference waves are calculated by subtracting the subject-level mean amplitude of a baseline condition (e.g., a neutral face) from the subject-level mean amplitude of a condition of interest (e.g., a happy face). For LME analyses, specific trials would need to be paired in order to calculate trial-level difference values. It is not straightforward how trials should be paired for this model. Some potential workarounds would be pairing the same trial presentation number to account for amplitude decay after repeated trials, but high numbers of missing trials would make this approach challenging. A second approach may be to run permutations in which trials are randomly paired. In sum, more research is needed to document a reliable approach to modeling difference waves using LME.

Finally, LMEs may currently only be appropriate to fit to single-trial mean amplitude, and not to single-trial latency. Peak latency is susceptible to noise at the single-trial level (e.g., high frequency noise). As such, extracting a subject’s peak latencies from each single trial and then taking the average of these values does not result in the same value as the peak latency of the subject’s mean-averaged waveform. An exploratory analysis in our laboratory examined latency-to-peak ERP amplitude in the N170 to explore whether the advantages of LME over ANOVA for mean amplitude data were also evident in latency data. In line with the amplitude results, LME detected condition differences in N170 latency that were not captured by 10- and 15-trial casewise deletion ANOVAs. Thus, it is possible that LME can be used to examine single-trial peak latency for earlier-peaking ERP components, but using LMEs to model latency is under-explored, and requires further systematic investigation. In contrast to single-trial latency, LMEs are appropriate to model mean amplitude, and to compare across ANOVA and LME, because the subject’s averaged waveform across all trials has the same mean amplitude as the average of their single-trial mean amplitude.

5.2. Challenges in fitting LME models to ERP data

Once ERP data are collected, there are several considerations in fitting a model to best test a hypothesis. These considerations include centering variables and using effects coding to correctly interpret LME output, specifying the random effects structure, and how to handle non-convergence issues in fitting models.

In our examples in 3, 4 above, we chose not to center ERP amplitude in order to extract coefficients that would be comparable across the LME and ANOVA models. However, centering variables in LME is generally advised (Raudenbush and Bryk, 2002), and is particularly useful for interpreting interactions (Brauer and Curtin, 2018). There are several ways to center data before fitting LME models, and researchers should carefully select which reference group (e.g., grand-mean, within-clusters) to center on depending on their research question and design (Bliese et al., 2018, Snijders and Bosker, 2012, Volpert-Esmond et al., 2021). Centering is frequently done on predictors (e.g., behavioral responses associated with each trial), but can also be done on outcome variables (e.g., mean amplitude). Centering involves subtracting a value from each individual trial-level datapoint, and maintains the scale of the original data (e.g., when centering amplitude, centered data are still in µV). Centering should be done after any exclusions (e.g., some ERP studies exclude left handed subjects [e.g., Kayser et al., 1997; Kutas and Hillyard, 1980], and therefore these subjects who were not included in the final sample should also not be included in calculating the mean on which data are centered).

The most common examples of centering are grand-mean centering (GMC; which is often used to examine between-subjects effects), and centering on the individual’s mean (also referred to as centering within clusters, CWC, which is often used to examine the within-subjects effects). GMC can be done on level 2 predictors (e.g., the subject-level in our examples in 3, 4). In GMC of a predictor (e.g., age), the mean age of all subjects is calculated and then subtracted from each single subject’s age. Therefore, coefficients describe how variables influence deviation from the grand mean in relation to the “averaged” subject (Nezlek, 2012, Snijders and Bosker, 2012).

CWC is done on level 1 predictors (e.g., the trial level in our examples in 3, 4), and is recommended when researchers have a theory about a variable’s relative effect within-subjects influencing the outcome variable (Snijders and Bosker, 2012), although other scholars advocate to always CWC level 1 predictors (Brauer and Curtin, 2018, Raudenbush and Bryk, 2002) and a few advocate to never center level 1 predictors (Antonakis et al., 2021). Examples of level 1 predictors are presentation number (e.g., in 3, 4) or behavioral responses (e.g., certainty levels, reaction time) associated with each trial. Parameter estimates after CWC describe within-subjects variability, and therefore resulting centered data reflect relatively higher or lower levels of the predictor for each subject. For example, CWC of transformed reaction times (RT) when emotional expressions are repeated versus novel (e.g., in a design such as Naumann et al., 2020) would be done by averaging RT within each subject and subtracting the average RT from each subject’s single-trial data. Therefore, data for each subject is representative of relatively slower or faster RT trials compared to that subject’s mean RT. In general, either CWC or GMC may be appropriate depending on your research question (for further guidance see Antonakis et al., 2021; Enders and Tofighi, 2007; Raudenbush and Bryk, 2002, Chapter 5; Snijders and Bosker, 2012; for an ERP-specific discussion see Volpert-Esmond et al., 2021).

Comparisons of categorical predictors (e.g., emotion condition, gender) can be examined through pairwise comparisons of the LME model (as conducted in 3, 4) or through applying contrasts (e.g., effects coding also known as sum contrasts; and treatment coding also known as dummy coding) to the categorical predictor before fitting the model. R defaults to using treatment coding for factors (R Core Team, 2019). In treatment coding of a binary categorical predictor, one factor level (assigned 0) is the reference group that the other is compared to (assigned 1). When using treatment coding, β’s represent the difference between the reference group’s mean and the other group’s mean (Baayen, 2012). In contrast, when using effects coding for a binary categorical predictor, the factors are assigned as − 1 and 1, or factors can be assigned as − 0.5 and 0.5 in order to extract the same slope as in dummy coding (Schad et al., 2020). In effects coding, β’s represent the difference between each group’s mean and the grand mean of the predictor (i.e., the mean across both levels) (see Schad et al., 2020 for further discussion on applying contrasts in LME). Therefore, contrasts should be applied prior to fitting the final model given that they influence coefficients and thus interpretation of LMEs.

Identification of the appropriate model for a given ERP dataset requires careful consideration of the random effects structure. For example, there can be model misspecification if sources of random variance are not accounted for (e.g., if a random effect in the model is ‘left out’). For example, in our dataset we included a random intercept of actor, but alternatively we may have left out this random intercept from the model, or we could have included a random intercept of actor race only, which would not be able to account for variance that may stem from other stimulus features (e.g., hair color, hair style). These alternative models would be a poorer fit to the variance in our dataset and therefore may influence LME results and subsequent interpretation. Therefore, there can be issues in model misspecification if a random effect is not included in the model, because the model will not contain information about the relation between trial-level factors and error (Nezlek, 2012). Volpert-Esmond and colleagues (2021) recommend that random effects should have 5 or more levels, and therefore nuisance variables with fewer levels (e.g., electrode in Section 4) should be included as control variables as fixed effects. Researchers should thoughtfully consider which variables should be included in their random effects structure.

Lastly, it is possible that when fitting an LME model to one’s data, the model may not converge (i.e., find a solution of coefficients that best explain the dataset). This lack of convergence can happen more often when attempting to fit particularly complex models, when there are especially low trial counts, and/or when there are a small number of subjects. Thus, developmental ERP researchers may be more likely to encounter problems with model convergence given they are limited by the number of artifact-free ERP trials they are able to collect, and by the time and cost of collecting more subjects. Barr and colleagues (2013) recommend fitting the maximal number of random effects in LME models (e.g., a maximum number of random intercepts and random slopes in the model) (but see also Matuschek et al., 2017 for alternative recommendations). However, in designs with low numbers of trials or subjects, or in cases where data are not very nested within groups (e.g., low ICCs for trials within subjects), fitting a maximal random effects structure may not converge. Maximal models may not converge because the model is estimating many parameters (e.g., all fixed effects, all random effects, all covariances of the random effects within each level, variances of residuals) (Brauer and Curtin, 2018).

Including fixed effect interaction terms in an LME may also pose problems for model convergence because it compounds how many parameters the model has to estimate (e.g., a fixed effect interaction between categorical predictors in a 2x2 design would then result in 1 more fixed effect (the interaction) and an additional random slope for the interaction term to be estimated in order to fit the maximal model, as described in Brauer and Curtin, 2018). This issue is compounded in more complex designs (e.g., 2x2x2 design). The addition of interaction terms thus results in even higher numbers of parameters for the model to estimate across fixed and random effects, thus increasing the likelihood that the model may not converge.

In the case that a model does converge but has a singular fit (in which there is a singular covariance matrix for one or more random effects), coefficients should not be interpreted and the model should be simplified. If a model does not converge, researchers should first center and/or rescale data and increase the iterations that the model will run before simplifying the model (Barr et al., 2013, Brauer and Curtin, 2018). If the model still does not converge, researchers can calculate the ICC within different random effects and remove the random effect with the lowest ICC until the model converges (Garson, 2013). An example of the progression from the ideal maximal model to the final model that would converge for analyses in Section 4 is provided in Appendix D.6. See also Barr et al. (2013) and Bates et al. (2018), and Brauer and Curtin (2018) for further suggestions on model simplification.

5.3. Challenges in reporting results from LME models

Once an LME model has been fit, there may be several challenges in reporting results, particularly given that ERP researchers are accustomed to seeing results presented in an ANOVA or regression framework. For example, there are multiple methods of calculating degrees of freedom in an LME, including Satterthwaite and Kenward-Roger. Simulation results suggest that both Satterthwaite and Kenward-Roger produce acceptable Type I error rates (approximately .05), even with samples as small as 12 subjects (Luke, 2017). In our results in 3, 4, we use the Satterthwaite approximation, which can be implemented easily in R using mode = "satterthwaite", and has been recommended for fitting LMEs to ERP data (Volpert-Esmond et al., 2021).

There can be challenges in reporting effect size for LMEs, which can be problematic given that many journals now require effect size estimates to improve the field’s best practices. There is not a consensus in the LME literature about how to calculate effect size. However, as an alternative to conventional effect size estimates (e.g., R² in linear regression), some scholars suggest using standardized β’s as a measure of the effect. Effect size is a standardized estimate of the relation between variables, so standardized β’s will indicate how much variance is explained by a predictor (Ferron et al., 2008, Snijders and Bosker, 2012).

Finally, for visualizing the results of an LME analysis, we recommend plotting the LME model’s estimated marginal means for the fixed effects of interest. For example, in our NC preschooler analysis reported in Section 4, we plot the marginal means of NC mean amplitude over repeated trial presentations (see Fig. 7B) and for each emotion condition (see Fig. 10; see also additional examples in: Berry et al., 2019; Brush et al., 2018; Rodríguez-Gómez et al., 2020; and Volpert-Esmond et al., 2018). To further visualize the effect and facilitate comparison with previous ERP studies, we also recommend plotting the grand-mean waveform averaged across all subjects (i.e., without casewise deletion). Finally, if a model includes random slopes (e.g., if the slope of presentation number varied across subjects), each subject’s random intercept and slope for presentation number could be plotted to visualize between-subjects variability in the effect of trial number. For an example of a random slope visualization, we recommend Volpert-Esmond and colleagues (2021).

6. Conclusion

The present study illustrates the utility of linear mixed effects (LME) models over ordinary least squares models (e.g., linear regression, ANOVA) to analyze ERP data. The use of casewise deletion and mean averaging in ordinary least squares models can decrease power, bias estimates of amplitude when data are not missing completely at random (e.g., systematically missing toward the end of an experiment due to fussiness/fatigue of infants and children), and result in incomplete interpretation of results when within- and between-subjects effects differ. In contrast, LME provides a more accurate estimate of effects through modeling both the effect of interest and random sampling variability, does not implement casewise deletion, and provides unbiased estimates even when the probability of missing data is dependent on a measured variable.

We demonstrated these advantages in simulated and real ERP data. Our simulation results demonstrated that ANOVA models had greater error than LME in estimating mean amplitude, and were biased when there were more missing data from the end of the experiment and in younger subjects. The advantages of the LME models over ANOVAs with casewise deletion were also evident in real ERP data from typically developing preschool children: the LME model detected two significant effects across emotion conditions, whereas ANOVAs following casewise deletion only detected one effect, and the effect detected was different depending on which trial cutoff exclusion criteria were used.

We demonstrated advantages of the LME in analyzing NC ERP amplitude from a common emotion-perception paradigm, but LMEs can be used to analyze any ERP component in studies that examine other condition differences, that compare samples, and that analyze individual differences. We include tutorials and example code in appendices to help researchers employ these methods in future ERP studies.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material

.

Data Availability

All simulation scripts, tutorial scripts, and an example dataset are available at https://github.com/basclab/LME_MixedEffectsERPTutorial.