A Review of Imputation Strategies for Isobaric Labeling-Based Shotgun Proteomics

Abstract

The throughput efficiency and increased depth of coverage provided by isobaric-labeled proteomics measurements have led to increased usage of these techniques. However, the structure of missing data is different than unlabeled studies, which prompts the need for this review to compare the efficacy of nine imputation methods on large isobaric-labeled proteomics data sets to guide researchers on the appropriateness of various imputation methods. Imputation methods were evaluated by accuracy, statistical hypothesis test inference, and run time. In general, expectation maximization and random forest imputation methods yielded the best performance, and constant-based methods consistently performed poorly across all data set sizes and percentages of missing values. For data sets with small sample sizes and higher percentages of missing data, results indicate that statistical inference with no imputation may be preferable. On the basis of the findings in this review, there are core imputation methods that perform better for isobaric-labeled proteomics data, but great care and consideration as to whether imputation is the optimal strategy should be given for data sets comprised of a small number of samples.

Graphical Abstract

INTRODUCTION

High-resolution mass spectrometry coupled with liquid chromatography (LC-MS) has become a primary technology for measuring global protein profiles in a biological system.^1–3 Isobaric-labeled proteomics, using tandem mass tags (TMT)⁴ and isobaric tags for relative and absolute quantitation (iTRAQ),⁵ allows for the multiplexing or simultaneous quantitation of multiple samples through the use of channels. Hereafter, a multiplex experiment with samples quantitated at the same time will be referred to as a plex. TMT and iTRAQ provide increased multiplexing capacity, high depth of coverage, and accurate quantitation compared to label-free approaches.⁶ Thus, many researchers, particularly those dealing with large cohorts of samples, are generating data in this manner rather than using the label-free approach. For example, the Clinical Proteomic Tumor Analysis Consortium (CPTAC) has generated numerous proteomics data sets using isobaric-labeled proteomics.^7–9

In the case of both label-free (LC-MS) and isobaric-labeled proteomics, each peptide is identified (or not) in the context of each sample processed through the experiment, and thus the peptides identified from sample to sample will differ. A peptide may be missing from one or more samples due to a variety of underlying mechanisms, which adds significant complexity to proteomics data. There are multiple characteristics associated with the peptide and instrumentation that modify the probability of confidently identifying a peptide.^10,11 A peptide may be missing at random (MAR), i.e., missing due to reasons independent of the abundance value itself. For example, a peptide may not be correctly identified due to biological factors or to noise associated with the measurements on the instrument. Alternatively, a peptide may be missing due to factors dependent on the abundance value of the peptide, i.e., not missing at random (NMAR). For example, the peptide abundance may be below the limit-of-detection of the instrument, or poor ionization or other factors could occur and affect identification. The combination of MAR and NMAR missing data mechanisms can result in 20–50% of the possible identifications being unobserved.^12,13 Several studies have indicated that missing values in large-scale omics data can hinder downstream analyses; for instance, this missing information, at the peptide and protein level, can reduce the power of the downstream statistical analyses, and can prevent the full, complete, and accurate extraction of quantitative and functional information.^14,15. Thus, to utilize many statistical, machine learning, and systems biology methods, one must (1) discard data for any peptide or protein with a missing value, (2) remove samples with any missing values, or (3) impute missing values. Because of the volume of missing data for proteomics experiments, ignoring missing values (options 1 and 2) can dramatically reduce the size and completeness of the data and limit the researchers’ ability to make meaningful biological inference. Thus, understanding differences in performance of imputation methods for proteomics data is important to improve the quality of downstream analyses reliant on complete data.

In the case of label-free proteomics, a number of reviews and comparisons of existing imputation methods are available.^12,16 For labeled proteomics data, the missing data structure is different than for unlabeled studies. Specifically, as seen in Figure 1, using representative examples of labeled and label-free data from CPTAC, the relationships between the fraction of missing data and log₂ peptide abundance (before normalization to reference pool for isobaric labeled data) are similar (Figure 1A,B), but the labeled data shows a clear pattern where either all the peptides are quantified or not quantified within a single 4-plex experiment (Figure 1C,D). Despite the usage and availability of labeled proteomics data, very little guidance currently exists as to whether imputation methods applied to unlabeled data, or to other omics data, work similarly for labeled proteomics data. To date, most of the existing evaluations are for a small number of methods developed for microarray data applied to labeled clinical proteomics data.¹⁷ This review compares and contrasts nine imputation methods, as well as the effect of not imputing, applied to two large isobaric-labeled proteomics data sets with adequate size and scale for a comprehensive comparison.

Figure 1.

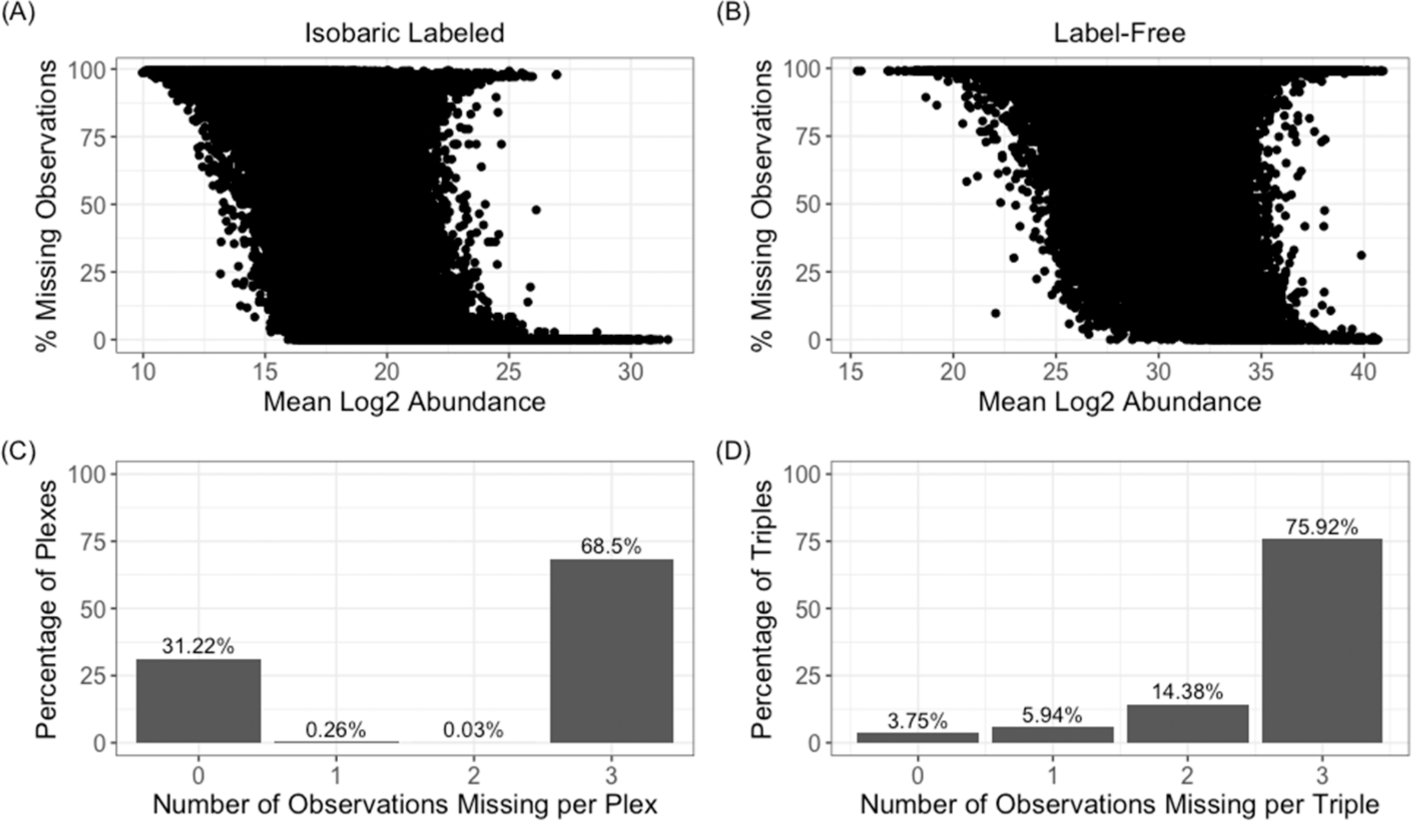
Evaluation of the missing data for the labeled CPTAC data set shows (A) a marginal negative correlation between the mean log₂ abundance (before normalization to the reference pool) and the percentage of missing data and (C) that within a 4-plex experiment that the majority of peptides are either all present or all absent for the three nonreference samples. For a similar unlabeled CPTAC data set it is observed that (B) there is a similar negative correlation between log₂ abundance (before normalization) and missing data, but for (D) sampling of data in a 4-plex manner yields varying probabilities across the number that will be present or absent.

IMPUTATION METHODS

Numerous imputation methods have been developed and discussed throughout ‘omics literature in recent decades.^16,18–22 In this review nine distinct imputation methods, described below in terms of imputing peptide values, were evaluated. All methods were available from open-source R packages or easily coded by hand and were implemented in R²³ version 3.6.0. Table 1 gives a brief description of all imputation methods evaluated, the R package used to implement the method, references for the method, and any parameters specified outside of the default values. Several algorithms were amendable to tuning the parameters, such as the number of principal components (PCs) used. Here, the number of PCs to be used by the principal component analysis (PCA) methods was estimated based on the number of components which accounted for a majority of the variance in the data. Other parameters are much more difficult to optimize and were left at the recommended value of the software. The utility of an algorithm is also associated with the time it takes to generate the results and thus the computational time for each imputation method was recorded.

Table 1.

Statistical Approaches to Impute Missing Intensity Values

method	description	R package	method reference	R parameters
BPCA	the posterior distribution of the model parameters and the missing values are estimated using a variational Bayes algorithm	pcaMethods24 (Bioconductor)	Oba et al.25	nPcs = 3 method = “bpca”
EM	expectation maximization: the observed data are used to estimate missing data via penalized likelihood expectation maximization	PEMM26 v 1.0 (CRAN)	Chen et al.27	phi = 0
IRMI	iterative robust model-based imputation: each peptide with missing values is iteratively used as a response variable in linear regression while the remaining peptides are used as explanatory variables	VIM28 v.5.1.0 (CRAN)	Templ et al.29
kNN	k-nearest neighbors: values are imputed using a weighted average intensity of k most similar peptides	VIM28 v.5.1.0 (CRAN)	Kowarik et al.28	k = 5
LLS	local least-squares: the missing values are imputed based on linear locally weighted least-squares regression	imputation30 v 2.0.1 leveraging locfit31 v 1.5–9.1 (Github)	Loader32
MEAN	mean replacement: missing values are filled in with the mean observed value for the respective peptide
MICE	multivariate imputation by chained equations: multiple imputation method that replaces missing values by predictive mean matching	mice33 v 3.8.0 (CRAN)	Little34	m = 5
PCA	principal component analysis: runs PCA, imputes the missing values with the regularized reconstruction formulas and repeats until convergence	missMDA35 v 1.16.0 (CRAN)	Josse et al.36	ncp = 3
RF	random forest: nonparametric method to impute missing values using a random forest trained on the observed parts of the data set, repeated iteratively until convergence	MissForest37 v 1.4 (CRAN)	Stekhoven et al.38	ntree = 100

SINGLE-VALUE APPROACH

The most straightforward imputation approaches are methods which replace missing values with a constant value or random draw from a distribution. One of the most common methods with proteomics data is to replace all missing values across a peptide with a constant. Because replacement methods have been shown to perform poorly in imputing label-free proteomics¹² data, only one simple replacement method, which replaced missing values with the mean of observed intensity values for the respective peptide (MEAN), was evaluated. The method of replacing missing values with half of the minimum observed value for a peptide was also evaluated, but results are not presented, because the performance of this method was orders of magnitude below the other approaches in the context of measurement error.

LOCAL SIMILARITY APPROACHES

The local least-squares (LLS) and k-nearest neighbor (kNN) methods impute missing values for each peptide by identifying similar peptides and using their expression values for estimation of missing values.

The kNN algorithm calculates pairwise peptide similarities and imputes missing values for a peptide based on a distance weighted regression of the k most similar peptides.²⁸ By default, the VIM package uses the five most similar peptides.

The LLS method estimates missing values for a peptide as a linear combination of the most similar peptides, based on correlation of pairwise peptide intensity profiles. The optimal number of similar peptides used is estimated by the algorithm.

GLOBAL-STRUCTURE APPROACHES

The expectation maximization (EM), Bayesian principal component analysis (BPCA), principal component analysis (PCA), and iterative robust model-based imputation (IRMI) methods attempt to leverage the global structure of the entire data set to impute missing values. In particular, EM, BPCA, and PCA apply dimension reduction techniques to form a reduced set of features that capture a majority of the variability in the data and use the reduced set of features to reconstruct the missing values; IRMI uses multivariate regression to iteratively update the missing values.

The EM imputation method is implemented as a penalized EM algorithm (PEMM), which assumes the data set follows a multivariate Gaussian distribution. Gaussian parameters and missing values are then estimated in an iterative manner, until convergence is reached, using a maximum penalized likelihood function, where peptides unrelated to the peptide of interest have minimal or no weight in the estimation of the missing values.²⁷

The BPCA and PCA methods take similar approaches to imputation by using PCA to reduce the dimension of the original data set and represent data values as a linear regression with the principal components as explanatory variables. Both methods perform estimation in an iterative manner until convergence is reached, and both require the specification of the number of principal components that should be used. The two methods differ in the estimation of model parameters. BPCA uses a Bayesian principal component regression model and the simultaneous estimation of the regression parameters and missing values is done using a variational Bayes algorithm.²⁵ PCA uses a regularized principal component regression model and EM to estimate parameters and missing values.³⁶ In both cases, R reduced the data down to the first three principal components.

The iterative robust model-based imputation (IRMI) method imputes missing values for each peptide iteratively. It first uses a naïve single-valueimputationandthenforeach peptide it uses a robust MM-estimated³⁹ regression model with all other peptides used as explanatory variables to update the imputed values.²⁹ This process is repeated for all peptides across the data set until convergence.

ENSEMBLE APPROACHES

Much like the local similarity approaches, the random forest (RF) imputation and multivariate imputation by chained equations (MICE) method both use algorithms to identify peptides or samples to use in calculating imputed values. However, these approaches differ from the local similarity approaches by imputing based on multiple sets, or ensembles, of similar peptides or samples.

RF imputation is based on the RF regression machine learning technique. RF regression models consist of trees which find optimal breakpoints of explanatory variables to predict the outcome; these trees are built on different splits of the data, and trees are combined to form a RF which aggregates trees’ results to make predictions. The RF imputation method estimates missing values using a RF trained on the observed parts of the data set with a single peptide as the response variable. This process is repeated iteratively across peptides until imputed values stabilize.³⁸

MICE is a multiple imputation method, meaning more than one realization of the imputed value is drawn for each missing value. Multiple imputation is often favored over single imputation methods as the resulting imputations can produce unbiased estimates and estimate uncertainty when done well. MICE uses the predictive mean matching technique^34,40 to replace missing values. For each missing entry, MICE identifies a small set of candidate samples from all complete cases that have predicted values closest to the predicted value for the missing entry. One sample’s value is then randomly drawn from the candidates and is used to replace the missing value. The assumption is that the distribution of the missing value is the same as the observed data of the candidate donors. By default, the mice package generates five imputation realizations. For the most benefit to be gained from multiple imputation, downstream analysis methods would be modified to account for the multiple imputed data sets, which currently is not a standard approach for proteomics data and thus beyond the scope of this review. To maintain comparability with other data sets, the results of the imputed values were averaged for each missing observation after MICE was implemented, which is similar to how it would be implemented in a standard proteomics analysis pipeline. However, it should be noted that the results may be skewed by this averaging of the imputed data.

DATA

The following evaluations of imputation methods were conducted using two isobaric labeled data sets. The first data set consists of proteomics data for a large collection of ovarian tumor samples analyzed using iTRAQ instrumentation. The second data set is a large set of human iPSC cell lines from male and female donors with data analyzed using TMT instrumentation. In both cases, data was available at the peptide- and protein-level. Additionally, a complementary label-free data set associated with CPTAC was used to compare properties of missing data between label-free and labeled proteomics data.

CPTAC DATA

Labeled Data

A global labeled proteomics data set for 84 TCGA ovarian cancer tumor samples was utilized. Its size allowed for down-selection to the subset of complete data and simultaneous evaluation of various parameters associated with the data that may affect imputation accuracy, such as the number of samples (i.e., number of plexes) and proportions of data missing for various subsets. These data were generated by the CPTAC at the Pacific Northwest National Laboratory (PNNL), a CPTAC Proteome Characterization Center (PCC), using iTRAQ instrumentation and protein quantification methods. Data are publicly available on the CPTAC data portal (https://cptac-data-portal.georgetown.edu/cptac/s/S020), and a detailed description of data generation is given elsewhere.⁴¹ Data were generated using a 4-plex iTRAQ, each consisting of three TCGA samples and one common internal reference sample for a total of 28 plexes. All data preprocessing was done in R²³ with the pmartR package.⁴² Normalization to the reference sample was computed as the ratio of each sample’s peptide abundances to the respective reference sample’s peptide abundances calculated within each plex. A total of 247 141 peptides mapping to 41 751 unique proteins were observed across all plexes. At the peptide-level, abundances were missing for 68.57% of values. Peptide-level data were log₂ transformed, filtered to remove peptides not present in at least 50% of samples, and then normalized using a global median correction. Hereafter, we refer to this as the Base Data Set. Postimputation, the data was quantified to the protein-level using a median reference-based approach.⁴³ This resulted in a final data set consisting of 15 601 proteins with normalized log₂ abundance values across 28 plexes (84 samples).

Label-Free Data

Prior to TMT labeling of the aforementioned TCGA ovarian samples, all digested samples were analyzed by 1D LC-MS/MS to verify sample quality and content. The MS/MS data were preprocessed with DeconMSn⁴⁴ and DtaRefinery⁴⁵ for recalibration of parent ion m/z. The calibrated spectra were processed with MS-GF+ (v9881),⁴⁶ matching against the RefSeq human protein sequence database, release version 37 (https://www.ncbi.nlm.nih.gov/assembly/GCF_000001405.13/), combined with 15 common contaminant proteins. The search included partially tryptic peptides and was carried out using dynamic methionine oxidation and static cysteine alkylation modifications. Area under the curve intensities for identified peptides were extracted using MASIC software,⁴⁷ and appended to MSGF results. Peptide intensities were summed up to the protein level as described previously.⁴⁸ Data were not normalized since this data set was only used to evaluate patterns of missing values.

IPSC CELL DATA

A global labeled proteomics data set for 189 iPSC cell line samples was utilized. Data were generated from a previous study¹³ and the data set after peptide identification was downloaded from the PRIDE repository.⁴⁹ A detaile description of data generation and peptide identification and quantitation is given elsewhere.¹³ In short, data were generated using a TMT-10 where each plex consisted of nine samples and one internal reference sample. A total of 21 plexes for which donor sex information was available were downloaded. Data preprocessing was done with the pmartR package⁴² in R.²³ Reverse hit peptides and potential contaminants were first removed from the data. Normalization to the reference sample was computed as the ratio of each’s peptid abundances to the respective reference sample’s peptide abundances calculated within each plex. A total of 181 389 peptides mapping to 10 495 unique proteins were observed across all plexes. Peptide-level data were log₂ transformed and then normalized using a global median correction, and data were quantified to the protein-level using a median reference-based approach.⁴³

IMPUTATION EFFICACY WITH SIMULATED MISSING DATA

The CPTAC labeled and label-free data were compared to illustrate differences in missing data patterns between label-free and labeled proteomics data. The relationship of missing data to the peptide abundance has been evaluated previously in the context of label-free data and found a moderate negative correlation on two data sets of −0.51 and −0.40.¹² A similar correlative relationship was observed here, with both the labeled and label-free CPTAC data of −0.45 and −0.20, respectively (Figure 1A,B). However, subsequent analysis of the pattern of the missing data shows that in the majority of peptides they are either all present or all absent within a plex 99.7% of the time (Figure 1C) across all plex and peptide combinations. A random selection of subsets of samples of the same size as a 4-plex from the unlabeled CPTAC data shows a clearly different pattern where 79.7% fit the same complete absence or presence criteria (Figure 1D), with a much smaller proportion being observed in all samples. Thus, we observe a similar overall relationship between peptide abundance and missing data, but, for the pattern of missing data, the peptides tend to be observed in a structured way for isobaric labeled data and less so for label-free.

The CPTAC isobaric labeled data was used as the basis to generate data for which ground truth would be known. The size of this data set, both in terms of number of samples and peptides, was large enough to allow for the identification of subsets of proteins (after quantitating to the protein level) and plexes with no missing data such that all values are known. Missingness was then introduced into the data at varying levels, reflecting the two core parameters: (1) the likelihood a peptide has missing data based on its abundance, and (2) the likelihood that values are missing from 1, 2, 3, or 4 of the labeled channels within a 4-plex experiment. For the first parameter, this simulation utilizes the relationship between peptide abundance and the likelihood of having missing data to sample appropriately peptides that would have missing data. Figure 2 gives the distribution used to perform this sampling based on log₂ intensity bins and median proportion of missing data. The probability of a peptide being selected was proportional to the median proportion of missing data for the peptide’s respective log₂ intensity bin derived from Figure 1. Once a peptide is selected, the number of samples for which the value is set to missing within a 4-plex is sampled proportional to that observed in the full data set as shown in Figure 1C. Finally, it has been shown that it is optimal to impute data at the peptide level before quantitating to the protein level.¹⁶ Thus, imputation methods were implemented at the peptide level and evaluated in the context of imputation accuracy as well as the effects of imputation on statistical analyses and the correctness of conclusions drawn at the protein level.

Figure 2.

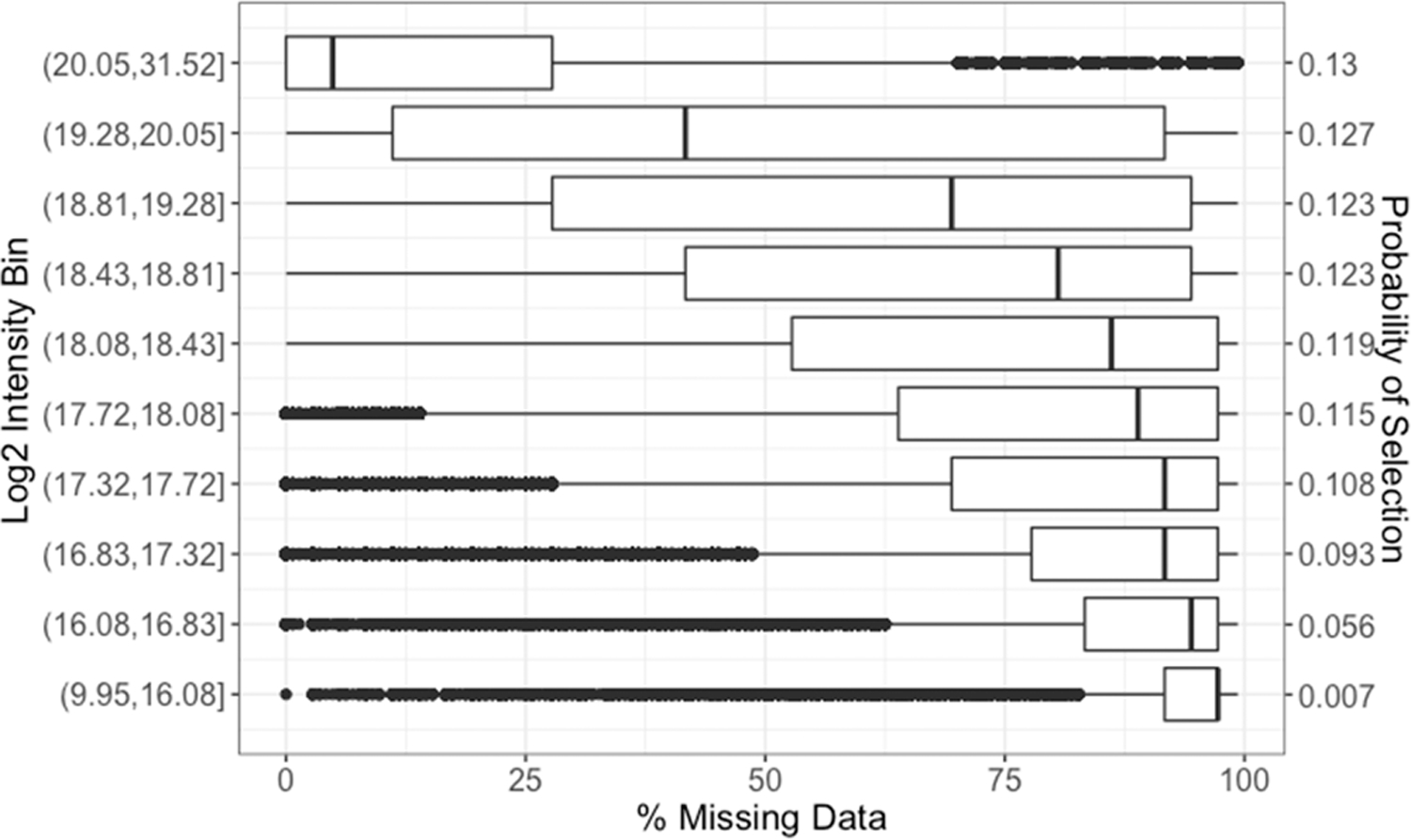
Proportion of missing data across peptides belonging to each log₂ intensity bin based on mean log₂ intensity, and the resulting discrete likelihood distribution of the probability that a peptide will have missing data based on its measured log₂ abundance and median proportion of missing data across all peptides in a respective bin.

EVALUATION DATA

The data used for evaluation is formulated from the Base Data Set to allow assessment of how the imputation methods perform under various numbers of plexes (samples) and amounts of missing data. Missing data is introduced, as described below, to mimic the manner in which labeled data goes missing. Let i represent the number of iTRAQ plexes sampled from the Base Data Set. Data consisting of i = 2, 3, 4, 5, 10, 15, 20, and 25 plexes were evaluated. This range of plexes was selected to reflect data sets with small to large sample sizes (n = 6 to n = 75). Let m denote the percentage of missing data introduced. Percentages m = 20, 30, 40, and 50 were considered. This range of percentages of missing data was chosen based on those noted in a previous study¹³ detailing percentages of missing data for varying numbers of plexes. One hundred simulated data sets were generated using the following steps for each combination of i and m:

1. Randomly select i iTRAQ plexes, corresponding to 3*i samples, and subset the Base Data Set to these samples to form the Reduced Data Set.

2. Filter the Reduced Data Set to peptides with no missing values for the selected samples.

   • If the number of proteins mapping to the peptides in the resulting Reduced Data Set is greater than 5000, randomly sample 5000 proteins and use their associated peptides to from the Reduced Complete Data Set where d_sj(k) is the peptide abundance for the j-th peptide of the k-th plex, where s = 1, 2, and 3 for each measured sample in the iTRAQ plex. The number of proteins was limited to 5000 to ensure reasonable computation time and a size representative of a normal plasma proteomics data set.
3. From the Reduced Complete Data Set, randomly select a peptide j, with selection probability distribution in Figure 2, and a single iTRAQ plex k to replace with missing values.

   • Randomly sample, using the distribution shown in Figure 1C, the number of samples for which the peptide’s abundances should go missing.
   • Replace abundance values for those samples with NA values.
   • If this step results in all values for the selected peptide being NA across the full Reduced Complete Data Set, do not replace values.

4. Repeat Step 3 until the observed percentage of missing data is greater than or equal to m; the final data set with the inserted missing values denoted as Missing Complete Data Set.

On the basis of the 8 sample sizes (number of plexes sampled) and 4 missing data percentages, the replication of this process yielded 3200 simulated data sets for evaluation by each imputation methodology, which allows for statistical comparisons to be made between imputation methodologies. Imputation was done at the peptide level and then quantitated to the protein level, as described previously. Additional evaluation of the properties of the 3200 simulated data sets were done to ensure the simulation process generated data with similar characteristics to the Base Data Set, and results of these evaluations can be found in the Supporting Information. Figure S1 shows the correlation between mean log₂ peptide abundance and percentage of missing data distributions for each number of plexes, and Figure S2 shows the median proportion of peptides making up each simulated data set for each intensity bin and each plex.

PERFORMANCE EVALUATION METHODS

For every Reduced Complete Data Set, data was quantitated to the protein level as described previously and the true value of each missing protein abundance is known, thus performance of imputation methods were first evaluated by comparison of the imputed values to the true known values. A common method for evaluation of imputation approaches is to calculate a metric of the distance between the imputed and true values. For each Missing Complete Data Set generated, the root mean-squared error (RMSE), a common method for estimating variance and bias, was used as a metric of deviation of the imputed values from the true values, at the protein level, in the corresponding Reduced Complete Data Set. The RMSE formula is given as

$$\mathrm{RMSE}=\sqrt{\frac{1}{NP}\sum _{s=1}^N\sum _{j=1}^P(d_{sj}-d_{sj}^{*})2}$$ (1)

where d_sj and $d_{sj}^{*}$ represent the true and imputed log protein abundances, respectively, for sample s and protein j.

The most common downstream analyses performed on proteomics data are univariate statistics to identify proteins that are significantly changing based on groups of interest, also referred to as differential analyses. While it is important for imputation methods to fill in missing abundances with low bias and variance, it is also important to consider the implications of an imputation method’s application to downstream statistical analyses. Thus, differential abundance tests were conducted and used to evaluate imputation methods. Samples were divided into two groups according to residual tumor disease size; specifically, samples with 0–10 mm residual tumor disease were compared to samples with all other residual tumor disease sizes. Only 74 of the 84 total TCGA samples had a residual tumor disease size denoted, thus analysis was limited to these samples (0–10 mm: 44 samples, >10 mm: 30 samples). The subset of samples with unavailable meta information resulted in the number of testable proteins to be between 4005 and 4912 depending on the number of samples. Welch’s t test,⁵⁰ which does not assume equal variances, was conducted in R using the pmartR package,⁴² and within a data set adjusted p-values were calculated using a Benjamini-Hochberg multiple comparison adjustment.⁵¹

For each Reduced Complete Data Set, Welch’s t test was performed on every protein. The adjusted p-values were considered ground truth for comparison to the results generated from imputed data sets. Proteins with an adjusted p-value less than or equal to 0.05 and greater than 0.05 were denoted as positives (P) and negatives (N), respectively. For each Missing Complete Data Set, the adjusted p-values were compared back to known p-values from the Reduced Complete Data Set and the number of true positives (TP) were computed along with the true positive rate (TPR = TP/P) based on a significance threshold established by a 5% false discovery rate (FDR). Additionally, the false positive rate (FPR) was calculated (FPR = FP/N).

For a given Missing Complete Data Set, the RMSE and TPR were calculated using only protein abundance values or proteins, respectively, which were impacted by imputation. Specifically, protein abundances or proteins, for RMSE and TPR, respectively, that were a result of complete peptide observations were not factored into these evaluation metrics.

The computational time of a given imputation method was evaluated as an additional performance metric. All imputation methods were implemented using a computer with a 2.1 GHz 16-core AMDD Interlagos processor with 64 GB of 1600 MHz memory.

CLASSIFICATION ON REAL EXPERIMENTAL DATA

The CPTAC and iPSC cell data sets were utilized in evaluating the performance of imputation methods in a classification setting. The two data sets were collected on real samples, thus estimates of the actual values of any missing data are not available. Again, imputation was performed at the peptide level before quantitating to the protein level. Imputation methods were evaluated based on the effect the imputation method had on the classification of sample types.

DATA SETS

The CPTAC labeled proteomics data as observed, i.e., no introduction of simulated missing values, was utilized. The aforementioned residual tumor size groups (0–10 mm and >10 mm) were used as the outcome of interest. The data was subset to the 74 TCGA samples for which a residual tumor disease size was denoted, resulting in 44 samples with a tumor residual size between 0 and 10 mm and 30 samples with a tumor residual size greater than 10 mm. For the iPSC cell data, the sex of the donor was used as the outcome of interest. There were 95 female and 94 male donors who made up the 189 samples.

When fitting classification models to high-dimensional data, a common approach is to perform dimension reduction to attain a small number of latent variables and perform classification with the latent variables used as predictor variables rather than the original variables. For each data set, each imputation method was applied, and based on the imputed complete data, traditional PCA was performed to reduce the dimension of the data. The number of principal components that explained 80% of the variance were retained for each of the imputation methods. This step reduced the set of possible explanatory variables from thousands of explanatory variables (proteins) down to tens of explanatory variables (latent variable) which were uncorrelated.

PERFORMANCE EVALUTION METHODS

A linear discriminant analysis (LDA) classifier⁵² was fit to the data, and 5-fold cross-validation was performed and applied to each imputed data set. The classification accuracy was calculated as the number of samples predicted correctly divided by the total number of samples. Classification accuracy was calculated using the standard 0.5 probability threshold. The area under the curve (AUC) of the receiver operating characteristic (ROC) curve⁵³ was also calculated to evaluate performance for all possible thresholds. Cross-validation was repeated 100 times for each imputed data set to get an estimate of the uncertainty in the classification metrics.

RANK METRICS

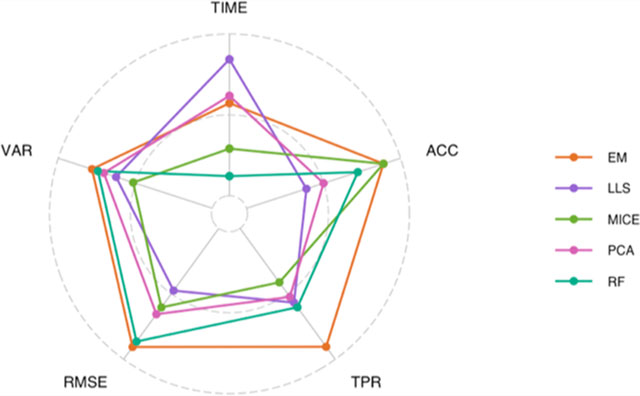
A summary evaluation of the rank of each imputation method was done across five metrics: mean of RMSE values (RMSE), variance of RMSE values (VAR), mean computational time (TIME), mean differential analysis TPR values (TPR), and the mean classification accuracy (ACC). The rank of each imputation method was calculated for each combination of number of plexes and percent missing data for RMSE, VAR, TIME, and TPR, and the mean rank over all data set sizes and missingness were then computed for each imputation method. The mean rank over cross-validation repetitions, (ACC), for each imputation method and data set (i.e., CPTAC and iPSC) was calculated and then averaged over the two data sets.

RESULTS AND DISCUSSION

Imputation Efficacy with Simulated Missing Data

Imputation methods were evaluated based on the similarity of the imputed values to the known abundance metrics, as well as the implications of the imputation on univariate statistics. These were all evaluated on the 3200 Missing Complete Data Sets. Each data set was restricted to a maximum of 5000 proteins per data set to ensure all algorithms would complete within a month. Several algorithms, such as the RF, requires hours of run-time for just one simulated data set, and therefore for the purposes of analyzing thousands of simulated data sets, this number was selected to be representative of a typical plasma proteomics data set. However, when more plexes are included in a data set the percentage of missing data increases and this restricts the number of proteins which can be included in a Reduced Complete Data Set and the resulting Missing Complete Data Set. The number of proteins mapping to the peptides for a given Missing Complete Data Sets was more than 4000 across all simulations.

Imputation Root Mean Square Error.

For each imputation method, the mean RMSE was computed for each of the Missing Complete Data Sets. Boxplots showing the full distribution of RMSE values by number of plexes and percentage missing are given in Figure S3 of the Supporting Information. These results are summarized in Figure 3 for all levels of missing data and a subset of plex sizes, 2, 3, 10, and 15, respectively. Heatmaps of the mean RMSE for all levels of iTRAQ plexes are given in Figure S4 in the Supporting Information. In general, for each imputation method, besides the MEAN method, the mean RMSE decreases as the number of plexes in the data set increases, indicating that these imputation algorithms perform better when there is more information to leverage. The mean RMSE for the MEAN algorithm tends to decrease minimally, compared to other methods, as the number of plexes in the data increases. This is expected as MEAN attempts to leverage less structural information about the data and only focuses within a protein, thus the amount of additional information gained is minimal compared to other methods. Additionally, for each imputation method, besides IRMI, the mean RMSE tends to increase as the percentage of missing data increases and the number of plexes is held constant, further confirming that less information in the data leads to poorer performance for an imputation method. IRMI shows the opposite RMSE trend in all cases except for data sets consisting of 2 iTRAQ plexes. IRMI implements a multivariate regression using all other proteins as explanatory variables. The decrease in RMSE as the percentage of missing data increases may be due to more values in proteins being initialized using the median value, thus placing more weight on more informative proteins (i.e., those with very few missing values). As seen in Figure 3(D) this indicates that IRMI requires a large data set size to equal the performance of methods such as the EM, PCA, or RF approaches. The kNN approach also suffers dramatically at lower sample sizes without as many samples to infer the imputed values from.

Figure 3.

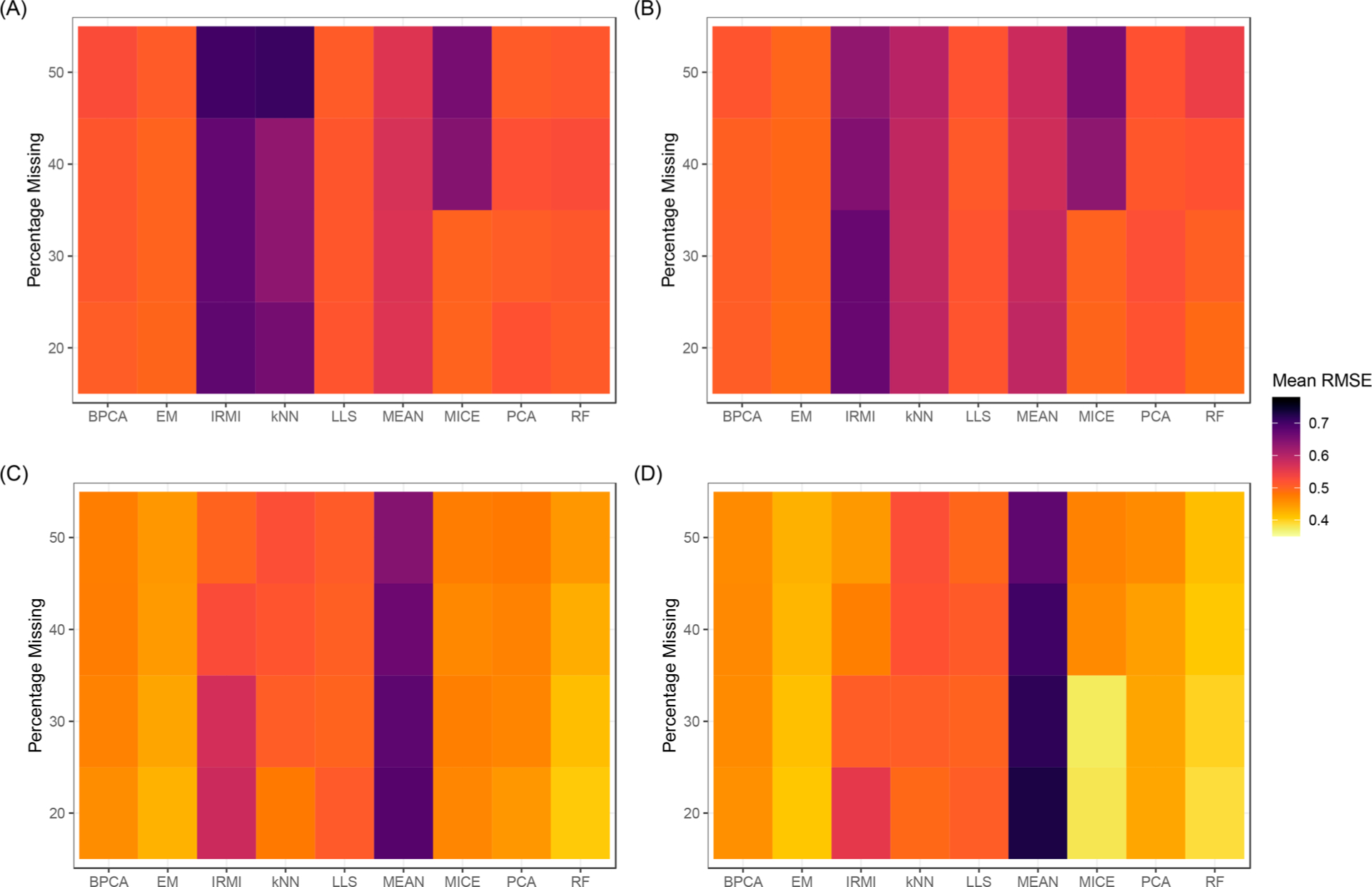
Heatmaps of the mean RMSE value, across 100 data sets, for each imputation method and varying levels of missing data. Data sets consisting of 2, 3, 10, and 15 iTRAQ plexes (6, 9, 30, and 45 samples) are given in panels (A), (B), (C), and (D), respectively.

The RMSE values in Figure 3 can be used to rank each imputation method for levels of the number of iTRAQ plexes (i.e., sample sizes) for each of the levels of missing data. As seen in Figure S5, MEAN performs consistently poor and never ranks better than 6 out of the nine imputation methods. IRMI also ranks toward the bottom for small sample sizes but improves to the top 3 or 4 methods for data sets with 20 or more iTRAQ plexes (60 or more samples) and at least 30% of observations missing. The kNN approach also is extremely variable for small sample sizes (i.e., 2 and 3 iTRAQ plexes). MICE performs considerably better in cases where 30% or less of the data is missing and is among the top performing methods for larger data sets with 15 or more iTRAQ plexes and the lower levels of missing data. EM is consistently in the top two imputation methods across all percentages of missing data and number of plexes. RF outperforms all other methods when data consists of at least 10 iTRAQ plexes; however, the method does not perform nearly as well when data sets consist of a small number of samples and higher levels of missing data. Figure S6 in the Supporting Information shows the standard deviation of RMSE values for a given number of plexes and percentage of missing values. MEAN, IRMI, and kNN are consistently the most variable in their performance in the context of the RMSE to the known values.

Statistical Testing.

The impact that imputed values have on downstream statistical analysis and inference is also an important consideration. Data sets consisting of 2 plexes are excluded from differential abundance (i.e., t test) analyses, as random sampling of the larger CPTAC data and small sample sizes in the Reduced Complete Data Sets result in poor statistical power and too few significant proteins for meaningful evaluation. Additionally, statistical tests without imputation of missing values (i.e., “None” imputation method) were not conducted for data sets comprised of 3 iTRAQ plexes, as there was rarely enough data to conduct t test analyses when data were missing for a protein. Figure 4 shows the distribution of TPR values at a standard FDR of 5% for the differential abundance analysis for each level of missing data and select levels of the number of iTRAQ plexes. Overall, the imputation adds considerable variability such at the accuracy drops considerably, even in the case of large data sets. The missing data also appears to reduce the statistical power that ignoring it also does not improve the ability to correctly classify the differential proteins. In general, the TPR values at an FDR of 5% increase as the number of plexes increase reflecting the increase in statistical power when more samples are added. When there is a small number of plexes, 5 and below, most of the imputation methods result in similar TPR values; however, as the amount of data increases the EM and RF approaches pull ahead followed by PCA. IRMI again shows it can work well under the scenario of a large data set and large amounts of missing data.

Figure 4.

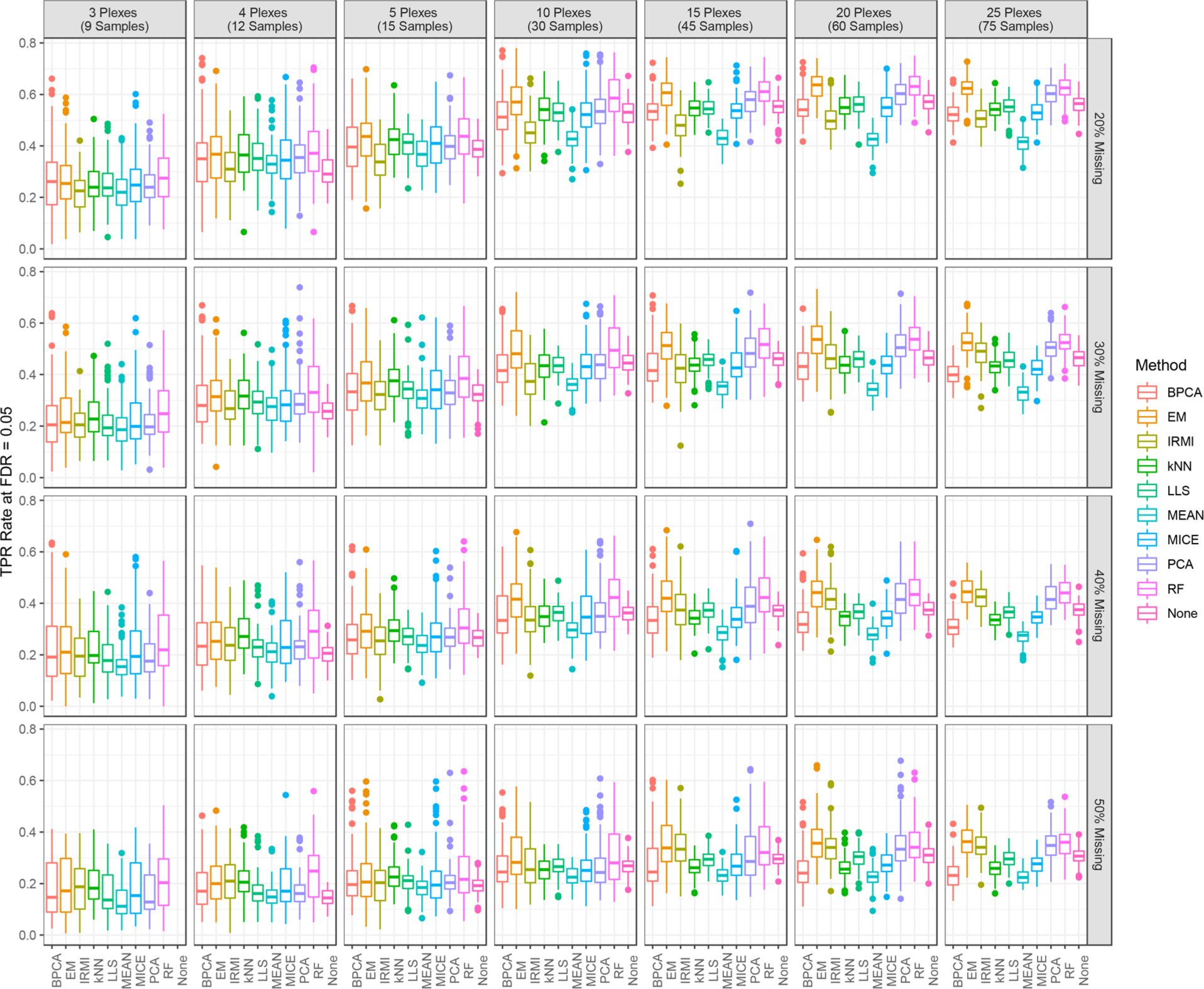
TPR at 5% FDR for each imputation method by percentage of missing data and for select levels of number of iTRAQ plexes.

Similar results for the FPR are shown in Figure S7 in the Supporting Information. Overall, the performance trends of different imputation methods are similar to those seen for the TPR results. The RF imputation method had one of the highest FPRs for data sets comprised of very few samples. Additionally, the MEAN method consistently had the highest FPR across data sets with more than 3 plexes for all levels of missing data. Finally, it is worth noting that tests conducted based on data which was not imputed (None) consistently had one of the lowest FPRs across all data set sizes and levels of missing data.

Additional Metrics.

The percentage of missing data had very little effect on computational time, given data sets of the same size. Table 2 gives the mean computational run time, in minutes, for each imputation method for each level of number of iTRAQ plexes in the data. RF had the highest mean computational times across all data set sizes ranging from 4.42 min to 2.7 h. IRMI, MICE and kNN had mean run times greater than an hour for the largest data set sizes. All other imputation methods had mean computational times less than a few minutes for all data sets.

Table 2.

Mean Run Time, in Minutes, for Each Imputation Method by Data Set Size

	BPCA	EM	IRMI	kNN	LLS	MEAN	MICE	PCA	RF
2 plexes (6 samples)	0.005	0.06	1.30	1.29	0.003	0.001	1.15	0.08	4.42
3 plexes (9 samples)	0.005	0.07	2.37	2.36	0.004	0.001	3.42	0.14	13.10
4 plexes (12 samples)	0.006	0.09	3.84	3.81	0.005	0.002	8.66	0.17	17.37
5 plexes (15 samples)	0.006	0.11	5.57	5.50	0.006	0.002	13.01	0.20	21.00
10 plexes (30 samples)	0.009	0.33	19.40	19.13	0.011	0.003	46.83	0.35	62.78
15 plexes (45 samples)	0.013	0.72	37.93	37.30	0.015	0.003	67.23	0.51	99.37
20 plexes (60 samples)	0.017	1.52	56.58	55.73	0.019	0.004	120.82	0.63	132.05
25 plexes (75 samples)	0.022	2.72	76.62	75.79	0.022	0.004	200.78	0.68	163.48

CLASSIFICATION ON REAL EXPERIMENTAL DATA

Most machine learning approaches require complete data sets with no missing values, thus impact that imputed values have on downstream classification models and inference is also an important consideration. Figure 5 shows the cross-validation classification accuracy distributions, over the 100 repetitions of 5-fold cross-validation, for each imputation method and the two data sets evaluated. The vertical, dashed lines mark accuracy by random chance, and the dotted lines mark accuracy achieved by prediction of the majority class for all samples. In general, the performance of the classification models was higher for the iPSC cell data set than the CPTAC tumor data set. In the iPSC analysis, there are two clear groups of imputation methods; IRMI, kNN, and LLS perform only marginally better than expected by random chance. It is noteworthy that these three methods all attempt to leverage local similarity within data sets and have much poorer predictive ability on the iPSC data set. The MICE algorithm also attempts to identify and leverage locally similar peptides; however, this method differs from IRMI, kNN, and LLS in that it identifies similar sets based on predictive performance rather than regression-based approaches. Their poor performance, on both the iPSC and CPTAC data sets, suggests that either dimension reduction via PCA of the imputed data resulting these methods is muting potential signal in the features, or the imputation strategies are muting signal that was found in the data for other imputation strategies. On the iPSC data set, all other methods, including the MEAN imputation strategy, perform well with cross-validation accuracies in the 0.8 to 0.9 range. The EM and MICE methods rank as the top two imputation methods for this data set. The CPTAC data set was much more challenging than iPSC for classification. The EM and RF methods outperform the other imputation methods with median accuracies higher than other methods by ~0.10. Both IRMI and kNN had median accuracies less than what is expected by random chance or majority class prediction. Figure S5 in Supporting Information gives the analogous results for the cross-validated AUC under the ROC curve. The figure shows that the general pattern in performance holds regardless of where the classification threshold is set. However, unsurprisingly, there appears to be much more heterogeneity across human tissue samples for CPTAC data set than the iPSC data set. In the instance where much more heterogeneity exists, the gap between the performance of IRMI, kNN, and LLS and other methods closes considerably.

Figure 5.

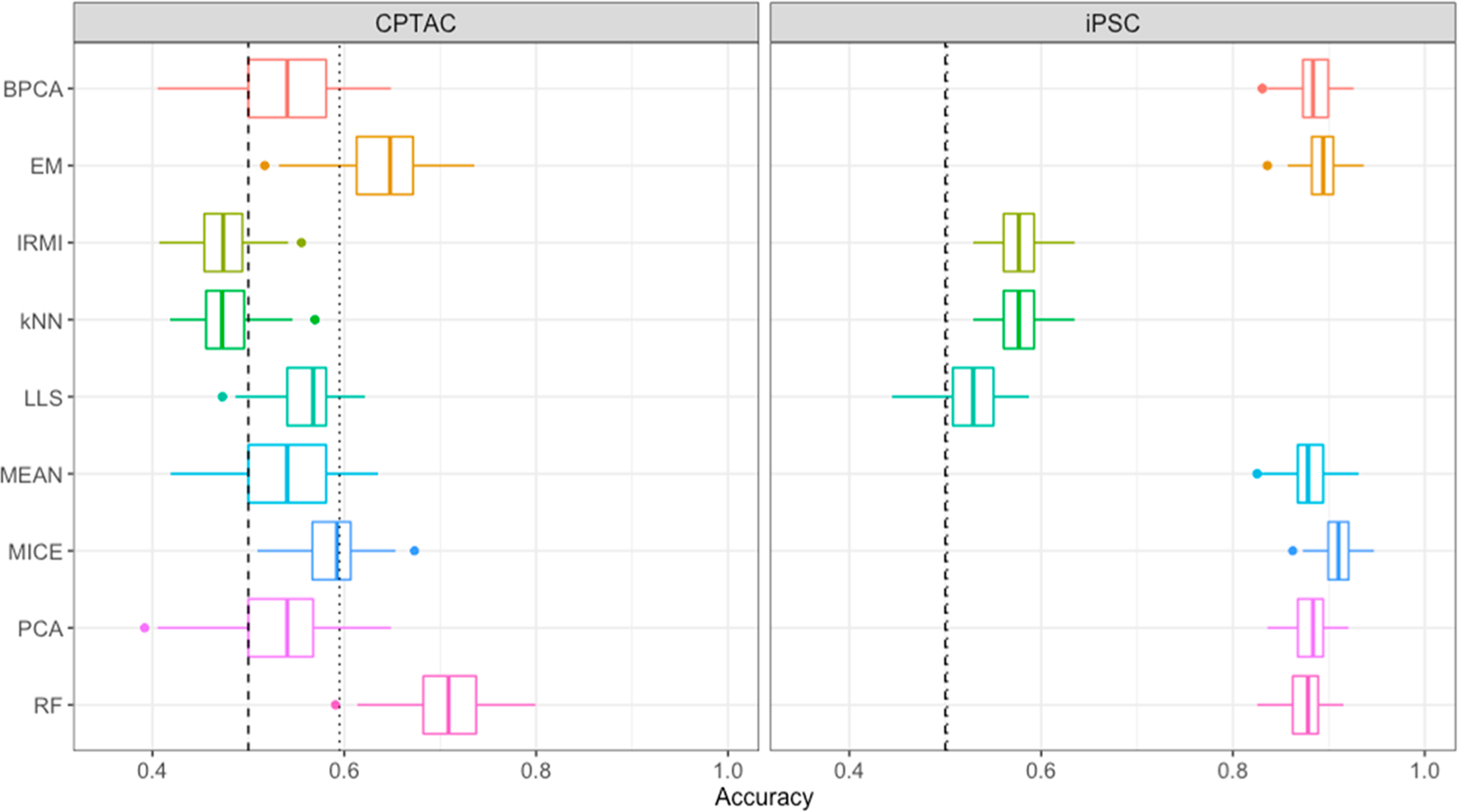
Cross-validated classification accuracy distributions, over 100 repetitions of 5-fold cross-validation, for each imputation method by data set.

CONCLUSIONS

There are numerous considerations when selecting an imputation method for labeled proteomics data, which include the quality of the imputed values as well as implementation factors. Here, evaluation of each imputation method was done across five metrics: RMSE, VAR, TIME, TPR, and ACC. To provide guidance on the selection of an imputation approach for labeled-free data Figure 6 gives the mean rank, across all levels of missing data and number of plexes, for all of the imputation methods for each metric. Values on the outer circle correspond to the best ranking method, and values on the inner circle correspond to the worst ranking method. In general, the EM imputation method as applied in PEMM performs among the best of all methods in all metrics, other than computational time. The RF approach was also often at the top of performance metrics, but requires large amounts of computational time, often on the order of hours. The MICE multiple imputation method performed in the middle of the pack for most applications, but in practice one should consider taking full advantage of the multiple imputations to potentially improve performance. Local similarity approaches based on regression strategy for identification of similar features tended to perform poorly in general, with the exception of IRMI which showed the ability to perform differential analyses well with a large number of samples, even in the presence of high levels of missing data. Largely these results agree with prior evaluation of imputation on label-free data,¹² although several of the ensemble approaches were not available and local similarity approaches did slightly better. Thus, these results in combination with Figure 1 suggest that although the missing data at the plex level appears quite different between the two proteomics methods the macro structure is similar.

Figure 6.

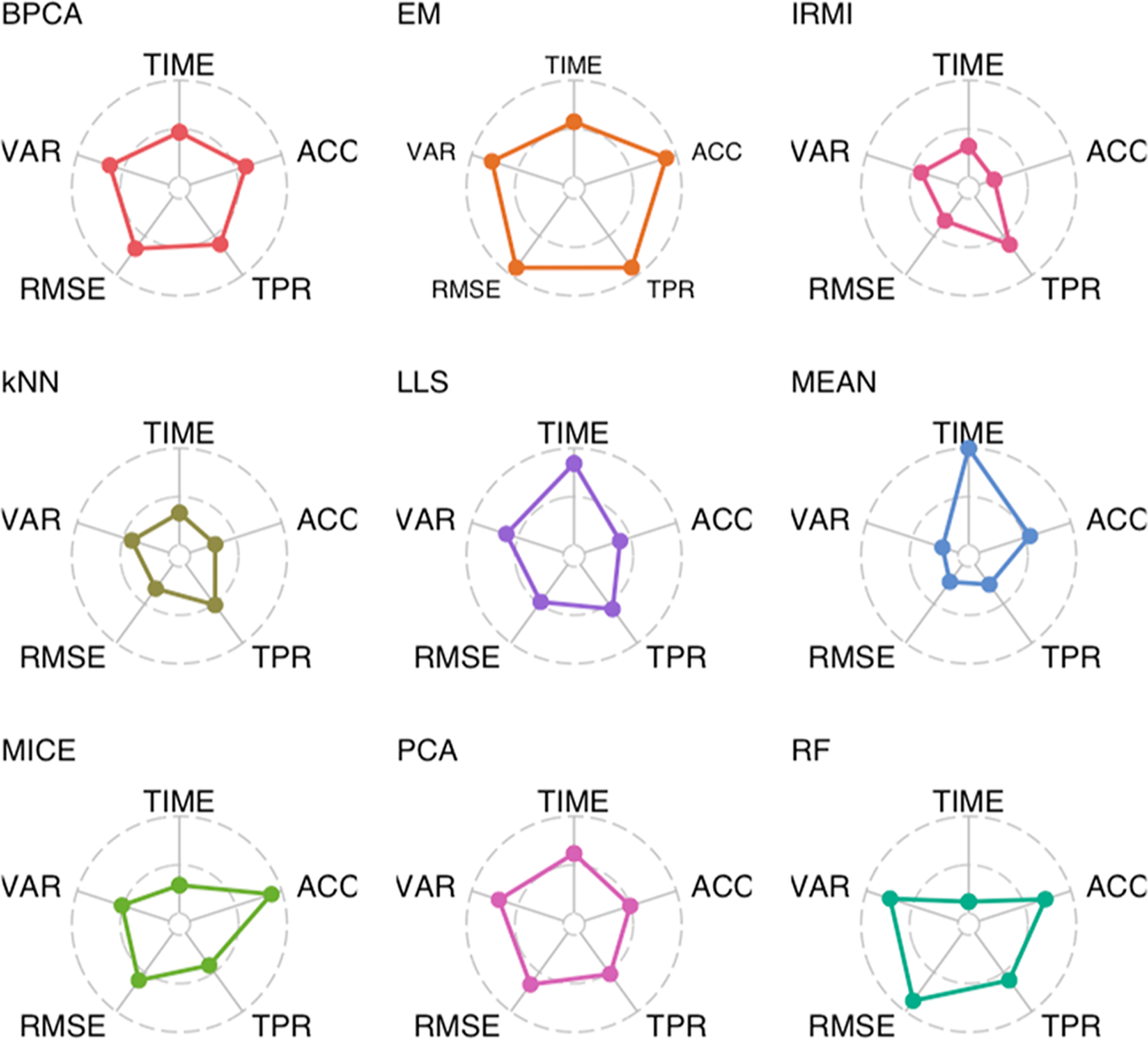
Radar plots giving the mean rank of each imputation method, across all levels of the number of plexes and percentage of missing data, for five performance metrics. Values on the outer circle and inner circle correspond to the best and worst performing imputation methods, respectively.

It is important to note that the imputation methods implemented here were done so using default parameter choices as suggested by their respective R packages. These parameter values may be more or less appropriate depending on the data set, and care should be taken in specifying and investigating appropriate parameter values. Additionally, many of the methods presented here can be implemented in multiple ways. For example, the PCA method as implemented uses expectation maximization algorithm; however, the method may also be applied using a regularized regression approach. As mentioned previously the implementation of MICE averaged the multiple imputations and this approach may perform differently if statistics and classification are performed for each imputed data set and then combined post hoc. Thus, each of the imputation methods discussed in this manuscript do not ubiquitously represent every implementation or variant of the respective method and performance may vary depending on the implementation. Finally, the classification analyses done here utilized all proteins regardless of the amount of missing data. In this case, dimension reduction was used to reduce the set of predictor variables considerably and the effect of any single protein will be diminished. If classification is performed using imputed data with feature selection rather than a method like PCA dimension reduction, careful consideration should be given to the amount of missing data that is tolerable. In this case, a protein with nearly all imputed values could be retained and weighted considerably, if no filtering is done on the data before the classification model is fit.

Although no single imputation method is best in all cases of scale and missing data, there are a few that stand out based on the implementations performed in this review. The EM method performs well and the most consistently across the three evaluations based on the difference from ground truth within the simulation, identification of differentially expressed proteins based on statistics, and classification. It also is relatively quick, and thus if a researcher does not have the experience to evaluate multiple imputation methods, this is a generally good choice and should return reasonable imputed values for downstream analysis goals. The RF approach is very similar in overall results, although at an increased computational cost, which is likely not a major disadvantage for the imputation of a single data set and therefore would also be a good choice without taking the data set characteristics into account. Beyond the top two there are four additional methods that are worth considering by a user and three that in general will not perform well in most cases. The three that we do not recommend area MEAN, kNN, and LLS, which were generally at the bottom in terms of all five metrics and under most circumstances would not be an optimal choice for a researcher. The remaining four are more challenging and would require thought and investigation by the researcher as their method of choice. Both of the dimension-reduction approaches, BPCA and PPCA, performed quite well in terms of the RMSE, but this did not lead to strong performance in terms of accuracy from standard statistics (Figure 4) or classification (Figure 5). The last two approaches, MICE and IRMI, appear to work very well under specific data set criteria. Thus, if a researcher has a data set with less than 30% missing data and a smaller sample size (e.g., less than 15) this approach works quite well in all aspects of our evaluation. The method of IRMI works well in the opposite scenario, if the data set is larger than 15 samples and has a lot of missing data. Finally, even with the best performing imputation methods the TPR of downstream statistical analyses was often relatively low for the CPTAC data, which is very heterogeneous, even for the largest data sets. This highlights the need for careful consideration in the experimental design process to minimize the impact of missing values on proteomics data analyses, in addition to choosing an appropriate imputation method.

As noted previously, imputation of missing data is not a simple task in the field of proteomics, and as the findings show, different imputation approaches work well not only under different data set sizes, but also with different scales of missingness and different analyses. Not all of the methods that performed best, for example, in terms of RMSE were able to also see similar results for either the statistical analysis of the data or classification. Therefore, as seen in Figure 6, there are some methods that are likely to perform the best out-of-the-box, but researchers should work to evaluate the performance of multiple methods on their data sets prior to the selection of an approach.