Torsional Stiffness of Extended and Plectonemic DNA

Abstract

DNA torsional elastic properties play a crucial role in DNA structure, topology, and the regulation of motor protein progression. However, direct measurements of these parameters are experimentally challenging. Here, we present a constant-extension method integrated into an angular optical trap to directly measure torque during DNA supercoiling. We measured the twist persistence length of extended DNA to be 22 nm under an extremely low force (~ 0.02 pN) and the twist persistence length of plectonemic DNA to be 24 nm. In addition, we implemented a rigorous data analysis scheme that bridged our measurements with existing theoretical models of DNA torsional behavior. This comprehensive set of torsional parameters demonstrates that at least 20% of DNA supercoiling is partitioned into twist for both extended DNA and plectonemic DNA. This work provides a new experimental methodology, as well as an analytical and interpretational framework, which will enable, expand, and enhance future studies of DNA torsional properties.

DNA elastic properties are vital to fundamental processes including transcription, replication, and DNA repair and recombination. The inherent double-stranded helical nature of DNA dictates that as a motor protein progresses along DNA, it must also generate DNA supercoiling[1–3]. Resulting supercoiling may buckle the DNA to form plectonemes, denature the DNA into other structures[4,5], or dissociate bound proteins[6,7]. In turn, this DNA torsional stress may slow or stall the progression of motor proteins, leading to regulation of the aforementioned processes[8–10]. Thus, the torsional stiffness of DNA not only impacts the topology and structure of DNA, but also determines the resistance that a motor protein encounters while moving against DNA supercoiling.

The torsional stiffness of the B-form of DNA is characterized by two parameters[11]: effective twist persistence length C_eff of extended DNA and twist persistence length P of plectonemic DNA. Both C_eff and P measure how much twist is introduced when turns are added to DNA and thus reflect the energetic cost to supercoil DNA (Supplemental Material[12]). For an extended DNA molecule much longer than its bending persistence length, C_eff is expected to be force-dependent[13,14]: C_eff(F). At low forces, DNA thermal fluctuations create writhe, lowering the energy to supercoil DNA, reducing the amount of twist, and thus softening the DNA torsional stiffness. As force increases, thermal fluctuations are suppressed so that supercoiling can only be partitioned to twist, with C_eff(F) plateauing to the intrinsic twist persistence length C: C_eff(F) ≤ C. Thus $\frac{C_{eff}}{C}$ provides a measure of the supercoiling partition into twist instead of writhe. In contrast, plectonemic DNA has zero extension, i.e., a zero end-to-end distance, and its twist persistence length P should be independent of force[11]. A comprehensive description of the torsional properties of DNA requires determination of C_eff(F) and P.

In the past two decades, measurements of DNA torsional stiffness have become possible using single-molecule mechanical manipulation techniques[15–23]. Nonetheless, direct torque measurements are experimentally challenging, hampering full examination of DNA torsional stiffness. In particular, measurements of C_eff under very low forces have not been demonstrated. The low force limit is of particular importance, as DNA is thought to be subjected to near-zero forces in vivo during many cellular functions. Furthermore, no experimental approach has been able to directly measure P, which characterizes the torsional properties of plectonemic DNA.

In this work, we present a new method, the constant-extension method, to enable the determination of these parameters via direct torque measurements using an AOT. An AOT can simultaneously measure the torque, angle, force, and position of a trapped birefringent particle such as a nanofabricated quartz cylinder[16,24,25] and is ideally suited for studying the torsional properties of DNA[16–18,26–28] (Supplemental Material[12]; Fig. S1). The constant-extension method makes torsional measurements with a DNA molecule held under a constant extension, as opposed to under a constant force [17,18,29]. Although the constant-force method is effective at measuring C_eff when F ≥ 0.2 pN[30], measurements at much smaller forces are challenging as the measured force may contain an unknown offset (Supplemental Material[12]), which is relatively small for large forces but significant for forces approaching zero. To circumvent this limitation, the constant-extension method utilizes the AOT’s ability to accurately determine the absolute DNA extension[30,31] and the well-established force-extension relation for DNA under no torsion[32,33] (Supplemental Material[12]; Fig. S2) to identify the force offset at zero turns and remove it for all measured forces at non-zero turns.

To illustrate the utility of the constant-extension method in measuring the twist persistence length of DNA under extremely low forces, we compare measurements using the constant-force method under higher forces (Fig. 1a) and the constant-extension method at much lower forces (Fig. 1b). For both types of experiments, a DNA molecule of 12.7 kilobase pairs (kbp) was torsionally constrained between the surface of a coverslip and the bottom of a nanofabricated quartz cylinder held in an AOT.

FIG. 1.

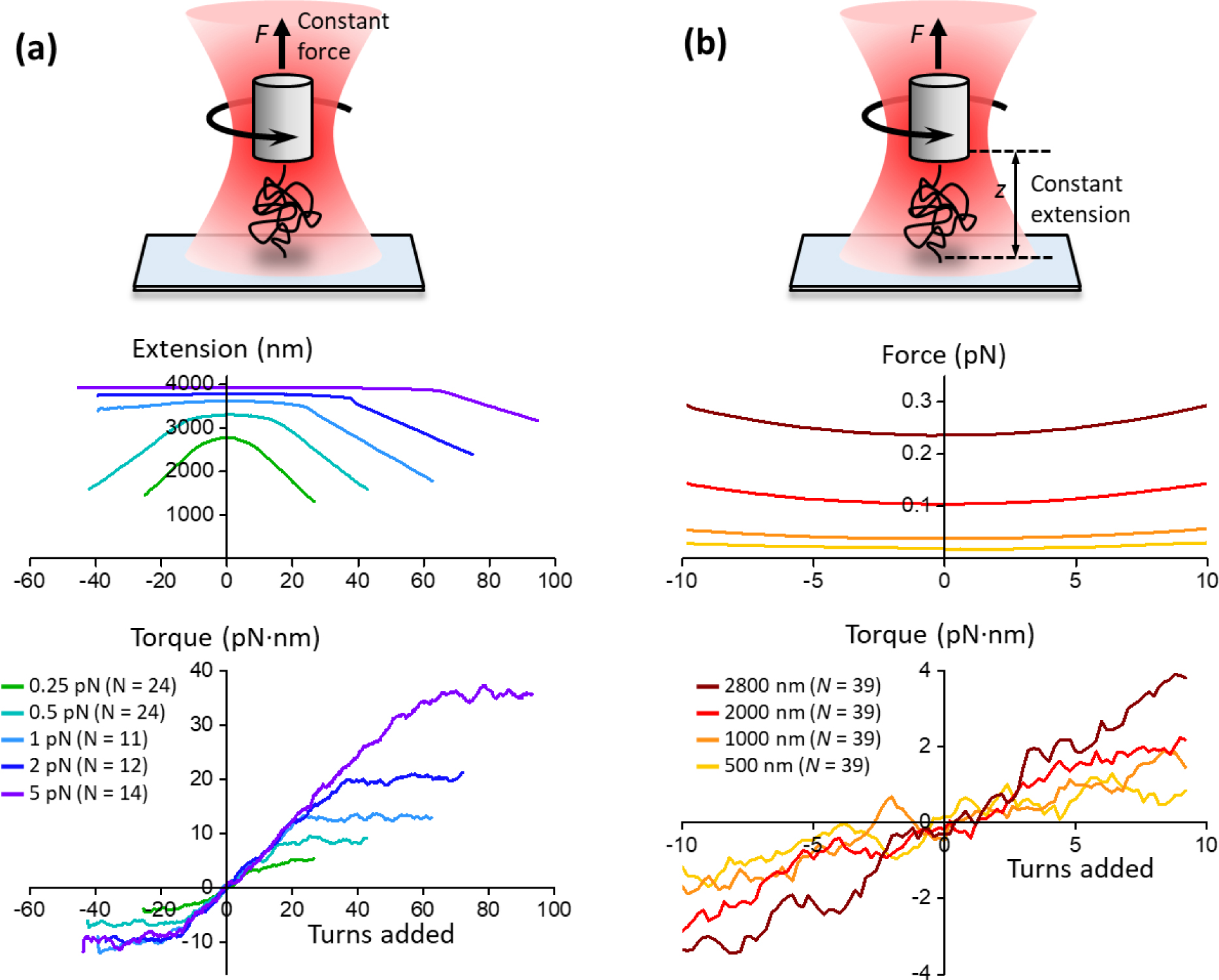
Torque measurements by an AOT during DNA supercoiling using either the constant-force or the constant-extension method. In both methods, a DNA molecule was torsionally constrained between a coverslip surface and a nanofabricated quartz cylinder held in the AOT. For each experimental condition, the number of traces (N) is also indicated. (a) Constant-force method. As turns were introduced to DNA with the force in the DNA held constant, the DNA extension and torque were simultaneously measured. (b) Constant-extension method. As turns were introduced to DNA with the DNA extension held constant, the force and torque on the DNA were simultaneously measured. Notably, the force on the DNA in constant-extension experiments can be much lower than the smallest attainable force in previous constant-force measurements.

For the constant-force measurements (Fig. 1a), the force in the DNA was clamped by a feedback loop that modulated the coverslip height to maintain a constant force on the cylinder at a constant laser power. As expected, prior to DNA buckling/denaturation, DNA extension remained nearly constant, and the torque in DNA increased with turns, consistent with previous findings[17,18,28]. To determine C_eff at a given force, the slope of the torque-turns relation before buckling/denaturation was determined and then converted to the twist persistence length C_eff (Supplemental Material[12]).

We implemented the constant-extension method by modulation of the coverslip height to maintain a constant distance between the cylinder and coverslip (Fig. 1b). As turns were introduced by the AOT at a specified DNA extension, the resulting torque was directly measured. The force was simultaneously measured and corrected for the small force offset. As shown in Fig. 1b, when turns were added, the force increased only slightly between −10 and +10 turns. However, the torque increased nearly linearly in this range, which corresponds to a range prior to DNA buckling[34] (Supplemental Material[12]; Fig. S3). Thus, the twist persistence length C_eff at a specific force was determined using the slope of the torque signal over this range. Note that the smallest extension used (500 nm) corresponded to only 1/9^th of the DNA contour length or ~ 0.02 pN.

Fig. 2 summarizes the measurements of C_eff over a broad force range using the constant-force method at higher forces and the constant-extension method at lower forces. As a check, values of C_eff at ~ 0.25 pN obtained from both methods show good agreement. Results from repeating these measurements with another DNA template with difference sequence (Fig. S4; Supplemental Material[12]) are in full agreement with those shown in Fig. 1 and Fig. 2 and indicates that C_eff(F) is rather insensitive to DNA sequence. In addition, C_eff(F) values measured using the constant-force method are comparable to those of previous studies at similar forces[8,9,17,22,28].

FIG. 2.

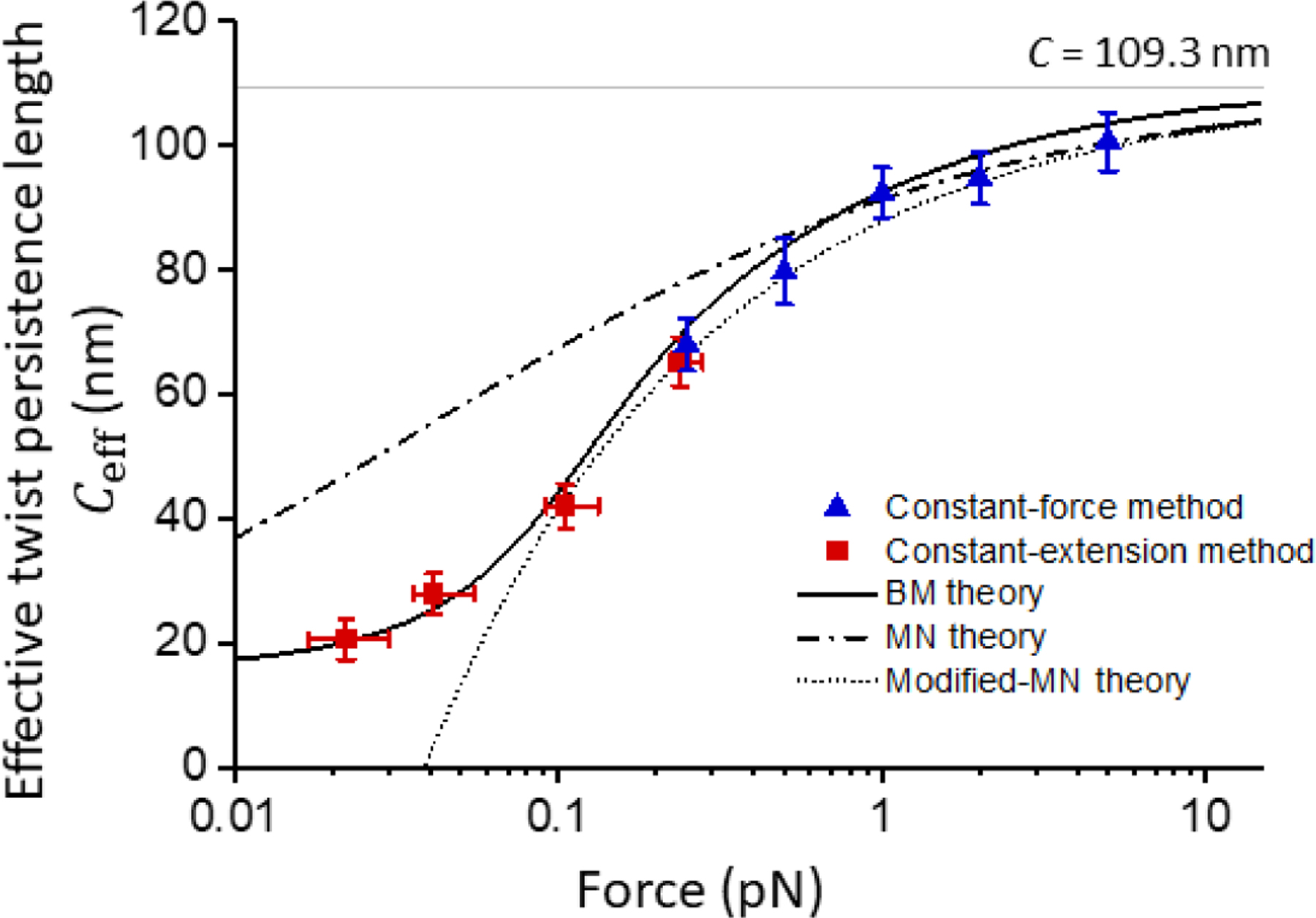
The effective twist persistence length C_eff of extended DNA versus force F. Data are from constant-force (blue symbols, Fig. 1a) and constant-extension (red symbols, Fig. 1b) experiments. The vertical error bars represent the SEM of the slope obtained from fitting individual traces. For each constant-extension condition, the force value indicated is the mean force of the fitting range in Fig. 1a, the error bars represent the minimum and maximum force in the same range. Also shown are predictions from Bouchiat-Mézard (BM) model, Moroz-Nelson (MN) model, and modified Moroz-Nelson (modified-MN) model. C = 109.3 nm is indicated as the gray solid line.

Previously, several models have been formulated to describe the torsional properties of DNA prior to buckling/denaturation. The most commonly employed model is the Moroz and Nelson (MN) model[13,14], which provides a convenient analytical expression:$C_{\text{eff}}{(F)}^{-1}=C^{-1}+{\left(4A\sqrt{\frac{AF}{k_{\text{B}}T}}\right)}^{-1}$, where A is the bending persistence length of DNA. Marko also introduced a modification to the MN model (referred to as the modified-MN model here)[11]:$C_{\text{eff}}(F)=C\left(1-\frac{C}{4A}\sqrt{\frac{k_{B}T}{AF}}\right)$. Since both the MN and modified-MN models require that DNA be subjected to a substantial force, they are only suited to the high force regime and are not expected to be valid in the low force regime. Thus we fit our high force (F ≥ 1 pN) data using the MN model with A = 43 nm measured under our experimental conditions (Supplemental Material[12])[35] and obtained C = 109 nm. This value of C is similar to those obtained previously via single-molecule methods[17,19,22,36]. We then used this C and plotted the modified-MN model for comparison. As expected, both the MN and modified-MN models agree well with measurements at high forces but deviate from measurements at low forces, (Fig. 2).

On the other hand, the model formulated by Bouchiat and Mézard (BM) should apply to both the low and high force regimes[37,38]. However, the BM model does not provide any analytical expression for C_eff(F) and thus has frequently been overlooked for comparison with experimentally measured C_eff(F). To make the BM model more accessible, we provide a detailed explanation of the numerical calculation of C_eff(F) by finding the ground-state energy of a Schrödinger equation of a quantum symmetric top problem (Supplemental Material[12]). In addition, we have verified our numerical implementation (Figs. S2; S5) and investigated the sensitivity of the model to various model parameters (Fig. S6). To evaluate whether the BM model can predict our measurements, we plotted the prediction of the BM model using the values of A and C from above (Fig. 2). We found that the BM model shows excellent agreement with measurements throughout the entire force range in this work. Furthermore, the BM model predicts a non-zero torsional modulus even at near zero force: C_eff(F → 0) = 16 nm k_BT, which is close to our measured C_eff at the lowest force.

To determine twist persistence length P of plectonemic DNA, we measured the torque-turns relation when a DNA molecule was held under a constant extension of 500 nm as turns were introduced to buckle DNA into a plectonemic state (Fig. 3a). The 500 nm extension, which is much smaller than the DNA contour length of 4300 nm, was chosen to minimize any contributions from the extended DNA region to the measurements and to limit potential interactions of DNA with the surfaces of the cylinder and coverslip that could exist at smaller extensions. In contrast to experiments in Fig. 1b that investigated pre-buckled DNA, this experiment instead focused on post-buckled DNA by introducing a large number of turns.

FIG. 3.

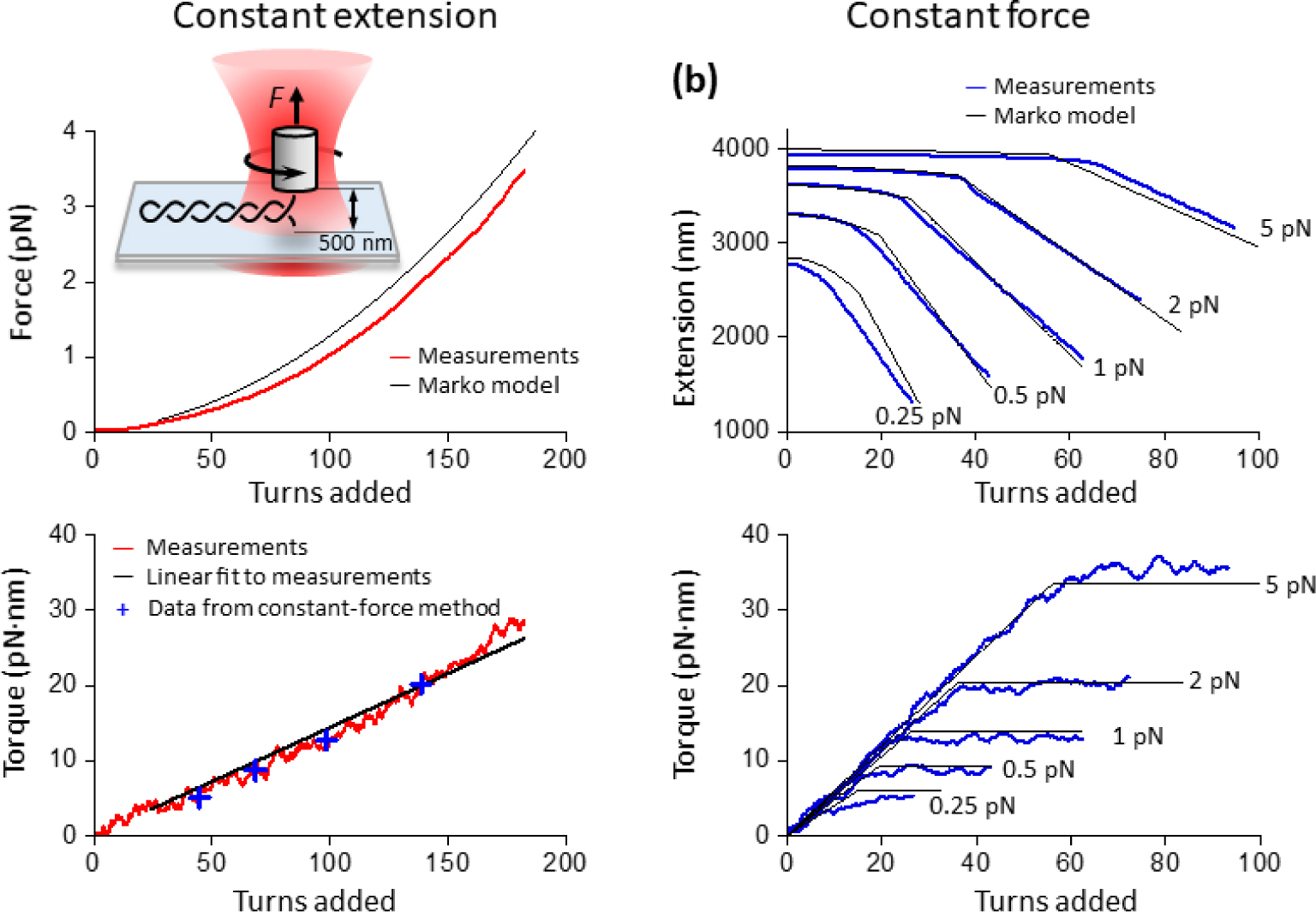
Direct measurement of the twist persistence length P of plectonemic DNA and theoretical predictions of DNA buckling transition. (a) Direct measurement of the torsional twist persistence length P of plectonemic DNA, compared with the Marko model. The DNA was torsionally anchored between a coverslip surface and a nanofabricated quartz cylinder under a constant extension of 500 nm. Both force (top) and torque (bottom) were simultaneously measured as a function of turns (red curves). P was determined by the slope of a linear fit to the torque-turns relation (bottom panel, black line) between +24 turns and +190 turns. The linear fit yields P = 24 ± 0.3 nm. For comparison, the torque measured from constant-force experiments in Fig. 1a (blue crosses) under the same conditions are shown. For the force versus turns relation, the grey solid line shows the Marko model prediction. (b) Marko model predictions of the DNA buckling transition at constant force. Data are from Fig. 1a (blue curves), and predictions from the Marko model (black curves) using A = 43 nm, C = 109 nm, and P = 24 nm.

As shown in Fig. 3a, DNA was expected to buckle to form plectonemic DNA after >24 turns were added (Supplemental Material[12]; Fig. S3). Continued addition of turns further extruded the plectonemic DNA, resulting in increases in both the torque and force in DNA. The torque increased nearly linearly as turns were added. We performed a linear fit to the torque-turns relation, and based on the slope of this fit, we determined P = 24 nm. This parameter was previously indirectly estimated (21–27 nm[11]), but our measurement represents a direct experimental determination. We estimated the errors introduced by the presence of the extended DNA region by finding upper and lower bounds bracketing the measured torque (Supplemental Material[12]; Fig. S7). We show that these two bounds tightly envelope the measured torque, suggesting that the extended DNA region contribution is essentially negligible. We also found that the corresponding force-turns relation is nearly perfectly quadratic (Fig. S8).

We subsequently used the measured C_eff(F) and P for theoretical predictions of the torsional properties of the DNA buckling transition. While the BM model is excellent at predicting DNA torsional properties prior to buckling, it may not be accurate near buckling and post-buckling[39–41]. However, Marko formulated a model for DNA buckling, treating it as a phase transition problem[11]. This formulation allows predictions of the extension-turns relation and the torque-turns relation, but the Marko model requires C_eff(F). For F ≥ 0.3 pN, the modified-MN model and the BM model give similar C_eff(F) (see Fig. 2), and we used the modified-MN model for simplicity. In addition, the Marko model requires an expression for the stretching energy, and while an analytical expression is frequently used[11], it is only accurate at high forces. To improve the predictive power of the Marko model at lower forces, the accurate form of the stretching energy[42] was used (Supplemental Material[12]; Figs. S2 and S3).

Fig. 3a (top panel) shows a comparison of this Marko model implementation with force directly measured from the constant-extension experiment. The predicted force-turns relation is also nearly perfectly quadratic (Fig. S8), though somewhat greater than the measured force. Fig. 3b shows a comparison of the predictions with measurements from the constant-force experiments. There is excellent agreement between the Marko model and the data with forces between 0.5–5 pN, but the model deviates substantially from the data taken at 0.25 pN. This deviation may suggest some limitations of the Marko model within the low force regime.

Previously, it was proposed that anharmonicity in the torsional energy of plectonemic DNA may contribute significantly to the torsional behavior of buckled DNA[43,44]. However, we found that after incorporating the anharmonicity terms, the predictions of the Marko model became less optimal for the constant-extension data and did not change substantially for the constant-force data (Supplemental Material[12]; Fig. S9).

In this work, we directly measured the twist persistence length C_eff (F) of extended DNA to be 22 nm at a force (~ 0.02 pN), an order of magnitude lower than previously attainable. Prior to this work, DNA torsional modulus at this force limit was unclear due to experimental challenges and a lack of a clear theoretical understanding. Consequently, there has been the frequent presumption that as the force on DNA approaches zero, C_eff also decreases to zero, suggesting that work is no longer required to twist DNA. Our measurements clearly show that C_eff does not decrease to zero and instead approaches a finite value. In addition, we have directly measured the twist persistence length P of plectonemic DNA to be 24 nm, which is close to C_eff at the extremely low force limit. This comprehensive description of the torsional stiffness of B-form DNA shows that at least ~ 20% (C_eff/C or P/C) of DNA supercoiling is partitioned into twist for both extended DNA and plectonemic DNA. By placing a minimum value on the torsional modulus of DNA, this work demonstrates that supercoiling always represents an obstacle for motor progression.

By integrating direct torque measurements with an in-depth analysis of three prior theoretical models, we have provided a rigorous understanding of DNA supercoiling and the buckling transition. Our constant-extension method has allowed determination of the torsional parameters of DNA that were previously unattainable. Although this work focuses on torsional studies of B-form of DNA, the constant-extension method should be broadly applicable to many other studies of DNA torsional mechanics. We anticipate that the constant-extension method, together with the data analysis scheme and interpretation techniques developed for this work, will provide new avenues to explore and resolve various DNA phases in the complex DNA phase diagram.