A workflow for the joint modeling of longitudinal and event data in the development of therapeutics: Tools, statistical methods, and diagnostics

Abstract

Clinical trials investigate treatment endpoints that usually include measurements of pharmacodynamic and efficacy biomarkers in early‐phase studies and patient‐reported outcomes as well as event risks or rates in late‐phase studies. In recent years, a systematic trend in clinical trial data analytics and modeling has been observed, where retrospective data are integrated into a quantitative framework to prospectively support analyses of interim data and design of ongoing and future studies of novel therapeutics. Joint modeling is an advanced statistical methodology that allows for the investigation of clinical trial outcomes by quantifying the association between baseline and/or longitudinal biomarkers and event risk. Using an exemplar data set from non‐small cell lung cancer studies, we propose and test a workflow for joint modeling. It allows a modeling scientist to comprehensively explore the data, build survival models, investigate goodness‐of‐fit, and subsequently perform outcome predictions using interim biomarker data from an ongoing study. The workflow illustrates a full process, from data exploration to predictive simulations, for selected multivariate linear and nonlinear mixed‐effects models and software tools in an integrative and exhaustive manner.

INTRODUCTION

Clinical trials are a gold standard in the development of novel therapeutics. Through clinical studies, information and data are generated and may be integrated on a continuous basis, thereby improving our understanding of disease pathology and progression, pharmacologic intervention, trial design, and, ultimately, personalized medicine. ¹ , ²

Clinical outcomes may be assessed based on a number of criteria. ³ In earlier stages of development, longitudinal biomarkers may be measured according to a defined schedule, allowing for the investigation of patient response trends and to determine whether a biomarker reaches a target value. In later phases of clinical studies and often in addition to longitudinal biomarkers, it is common to assess endpoints such as time‐to‐event data or event rates. Depending on the disease or indication, outcomes may encompass overall survival (OS) or progression‐free survival (in oncology), exacerbation risk and/or rates (e.g., chronic obstructive pulmonary disease [COPD], asthma), relapse rates (e.g., multiple sclerosis), myocardial infarction, stroke, or other cardiovascular events (e.g., cardiovascular diseases, chronic kidney disease [CKD]), and so on. ³

Intuitively, one may expect that baseline and/or longitudinal biomarkers are correlated to some degree with observed event outcomes. For example, the forced expiratory volume in 1 s is associated with exacerbation risk in COPD ⁴ ; the sum of the longest diameters of target lesions (SLD) is associated with risk of death in non‐small cell lung cancer (NSCLC). ⁵ The association between biomarker and time‐to‐event data has also been identified and studied in multiple analyses of various diseases, including heart failure, CKD, diabetes, Alzheimer's disease, infectious diseases, colorectal and prostate cancers, and so on. ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³  These analyses have investigated the association of biomarkers and time‐to‐event data via joint models (JMs). ¹⁴ JMs represent an extended class of parametric survival models, which are based on proportional hazards models and are able to integrate both baseline values and dynamics of longitudinal covariates. JMs may ultimately be used to address essential questions in the assessment and prediction of clinical trial outcomes, including investigation and prediction of longitudinal biomarker trends, biomarker association with an event risk, individual survival predictions, and unbiased estimation for both biomarker and time‐to‐event outcomes. ³ , ⁶ , ¹⁴

In this tutorial, we focus on technical aspects of a modeling workflow for a common class of JMs that incorporate noninformative right censoring and proportional hazards survival submodels. Right censoring is a specific property of time‐to‐event data and is frequently encountered in clinical trials. An event of interest does not necessarily occur for all subjects during the trial observation period, and the time to that event, if an event occurs at all, will vary among trial subjects. A censoring event occurs when a subject leaves the study for a specific reason. Depending on the dropout nature, censoring could be classified as informative or noninformative. ¹⁴ Informative censoring assumes that the censoring event is directly related to the subject's disease progression, whereas noninformative censoring assumes the censoring is independent from the subject's condition and therefore from the event of interest. The noninformative hypothesis is commonly used for survival modeling in clinical trials. ⁶ , ¹⁰ , ¹⁴

The JMs described in this tutorial may be developed using various software tools integrating linear and nonlinear mixed‐effects (LME and NLME, respectively) approaches to handle longitudinal data.

This modeling workflow seamlessly integrates multiple steps, including data exploration, survival model selection, and qualification (goodness‐of‐fit and parameter interpretation) using training data and subsequent model validation against interim external data accumulated up to a certain timepoint (Figure 1). Such a workflow can be applied by a data analyst or modeling scientist who, upon collecting retrospective information and data from completed clinical trials, aims at predicting outcomes of another clinical study, for which only interim data are available.

FIGURE 1.

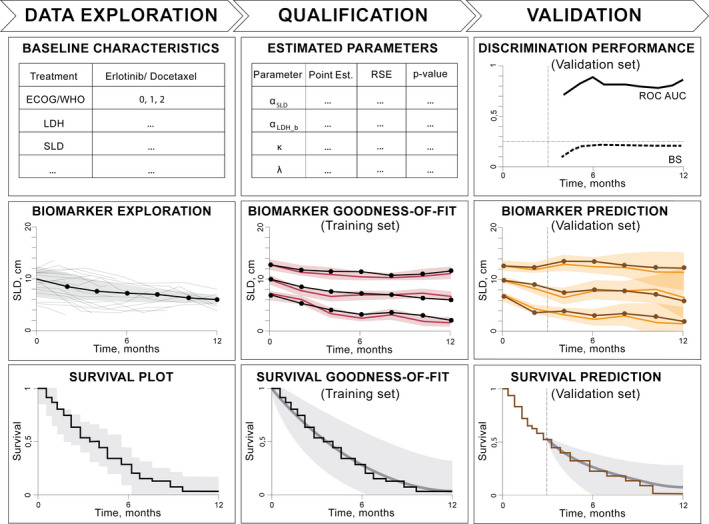
Schematic representation illustrating the steps required for a joint modeling analysis. Left to right: data exploration involves plotting biomarker and survival data as well as study baseline characteristics. Qualification of survival models is performed against a training data set to obtain model parameters, visual predictive checks for biomarkers, and survival goodness‐of‐fit plots. Validation of a joint model is completed by using the previously estimated model parameters to perform a survival discrimination analysis by means of ROC‐AUC and BS as well as simulate biomarker trends and make survival predictions against interim validation data. BS, Brier score; ECOG, Eastern Cooperative Oncology Group score; LDH, lactate dehydrogenase; ROC‐AUC, area under the receiver operating characteristic curve; SLD, sum of the longest diameters of target lesions; WHO, World Health Organization score.

Using particular NSCLC data sets, ¹⁵ , ¹⁶ we implemented and tested the JM workflow to investigate the association between selected biomarkers and OS and to quantify the incremental benefit that is gained using longitudinal biomarker data versus baseline biomarker only.

STRUCTURE OF JMS

Biomarker and event data may be described using various regression models. ¹⁷ , ¹⁸ LME and NLME models are typically developed to characterize longitudinal biomarkers:

$$\left\{\begin{array}{c}{y}_i\left(t\right)=X_i\left(t\right)\beta +Z_i\left(t\right)b_i+{\epsilon }_i\left(t\right),\\ b_i\sim N\left(0,D\right),\\ {\epsilon }_i\sim N\left(0,{\sigma }^2{I}_{n_i}\right),\end{array}\right.$$ (1)

Equation (1) represents a linear model, where X_i and Z_i are known design matrices for, respectively, fixed‐effects regression coefficients β and random‐effects coefficients b_i , with i representing the patient index, where I_ni denotes the n_i ‐dimensional identity matrix. ¹⁴ Random effects are assumed to follow a multivariate normal distribution (because multiple biomarkers and model parameters may be considered) with a mean vector of 0 and a variance–covariance matrix D and are also assumed to be independent from the error terms ε_i , that is, cov(b_i , ε_i ) = 0. Further details on univariate and multivariate model structures for longitudinal biomarkers and their interpretation may be taken from the literature. ¹⁴ , ¹⁹

Proper selection of model structure and subsequent qualification of LME and NLME models may provide the modeler with biomarker trends in the population under study as well as information on random effects and residual error as typically performed in pharmacometric research. ²⁰ Similarly to previous analyses, one may use predetermined NLME models defined in the form of explicit/empirical functions or using ordinary differential equations (ODEs). ¹⁷ However, for many biomarkers, such information may not be available, and additional research would be required to identify an adequate model.

Time‐to‐event data may be analyzed using survival models, which are defined by a hazard function ¹⁴ :

$$\begin{array}{c}{h}_i\left(t\right)=\underset{dt\to 0}{\mathrm{\text{lim}}}\frac{\mathrm{\text{Pr}}(t\le T_i^{\ast }<t+dt|T_i^{\ast }\ge t)}{\mathit{dt}},t>0\hfill \end{array}$$ (2)

Equation (2) describes the instantaneous risk of an event in the time interval [t, t + dt], provided survival up to time t. Given this definition, h_i(t) is also referred to as the instantaneous risk function. $T_i^{\ast }$ denotes the true time of events for the patient of interest. The hazard function defined previously can be used to derive individual survival probabilities according to the following equation ¹⁴ :

$$S_i\left(t\right)=\exp \left\{‐H_i\left(t\right)\right\}=\exp \left\{‐{\int }_0^t{h}_i\left(s\right)ds\right\}$$ (3)

The survival function (whether it represents actual survival, or progression, exacerbations, relapses, etc., depending on the disease and indication under study) can be expressed by means of a cumulative hazard function H_i(t) that describes the accumulated risk up to time t. Function H_i(t) can also be interpreted as the expected number of events to be observed up to time t. Individual survival functions S_i(t) can be further used to estimate the survival of the overall population and may be compared with a nonparametric survival estimator by means of a Kaplan‐Meier (KM) curve.

JMs may be used to associate baseline (w_i ) and longitudinal covariates (represented by the individual biomarker time course: $m_i(t)=X_i(t)\beta +Z_i(t)b_i$ from Equation (1) with event risk from Equation (2). For such proportional hazards models, h_i (t) may be formulated as follows:

$$h_i\left(t\right)=h_0\left(t\right)\ast \exp \left\{{\alpha }_b{w}_i+\alpha m_i\left(t\right)\right\},$$ (4)

In Equation (4), α_b represents the association parameters for the baseline biomarkers (as typically implemented in Cox models), and $\alpha$ is the association parameter for the longitudinal biomarker. Equation (4) is formulated for one baseline and one longitudinal biomarker. For multivariate models, each of the considered biomarkers should have α_b or α assigned depending on a biomarker type.

If biomarkers are considered at baseline only, then Cox proportional hazards models can be used and h₀(t) is not specified because the Cox model parameter optimization is handled using partial log‐likelihood function. However, in JMs with longitudinal biomarkers, h₀(t) should be specified in either way (i.e., piecewise constant function, splines, a Weibull distribution). ¹⁴ , ²¹ Parameters of a JM can be identified using the principle of maximum likelihood based on the following formulation for the logarithmic joint conditional likelihood function ¹⁴ , ²² :

$$l_i\left(\theta \right)=\log \int \left\{\prod _j^{n_i}p(y_{\mathit{ij}}|b_i;\theta )\right\}\left\{h{(T_i|b_i;\theta )}^{{\delta }_i}{S}_i(T_i|b_i;\theta )\right\}p\left(b_i;\theta \right)d{b}_i,$$

where:

$$\begin{array}{c}{S}_i(t|b_i;\theta )=\exp \left(‐{\int }_0^t{h}_0\left(s;\theta \right)\exp \left\{{\alpha }_b{w}_i+\alpha m_i\left(s\right)\right\}ds\right)\hfill \end{array}$$ (5)

In Equation (5), δ_i is an event indicator (i.e., assumes a value of 1 for an event and of 0 for censoring from the study), T_i is the observed event time or censoring time (T_i  = min( $T_i^{\ast }$, C_i), where C_i is the censoring time and θ denotes the full vector of model parameters). Averaged S_i (t) represents the marginal survival for the entire patient cohort and can be compared with KM estimates of OS. ¹⁴

Other approaches that incorporate a sequential analysis of biomarkers and time‐to‐event data (including extended Cox models that handle time‐varying biomarkers) have also been investigated in the literature. However, such analyses may require methodological improvements to address the potential bias presented in parameter estimates. ¹⁴ , ²¹ , ²³

OVERVIEW OF SELECTED TOOLS FOR JOINT MODELING

There is a wide variety of statistical software tools available for JM development and assessment—see Table 1 for a nonexhaustive list. Each JM software comes with specific sets of options as well as data set format requirements. For example, if a simple univariate analysis is targeted in the JM package ²⁴ in R, then only one longitudinal biomarker may be considered, whereas the other available biomarkers can only be accounted at baseline levels. Beyond this limitation, the JM package provides a comprehensive set of options, such as predefined functions for model qualification/diagnostics (embedded in the JM object in the R environment) and validation/simulation (available via predict() and survfitJM() functions), and it is computationally fast.

TABLE 1.

Joint modeling tools, their features, diagnostics, and simulation capabilities

	JM package	JMbayes package	rstanarm package	NONMEM	Monolix	Stan
LME models	Yes	Yes	Yes	Yes	Yes	Yes
NLME models	No	No	No	Yes	Yes	Yes
Multivariate models	No	Yes	Yes	Yes	Yes	Yes
Biomarker and survival predictions	Available	Limited	Limited	Available	Available	Available

Abbreviations: LME, linear mixed effects; NLME, nonlinear mixed effects.

If models with multiple longitudinal biomarkers are considered, the JMbayes and rstanarm software packages, ²⁵ , ²⁶ which provide Bayesian inference for biomarker characterization, can be used. However, in these multivariate JM packages, the advanced diagnostics for longitudinal biomarkers are less convenient to handle, and the embedded features for biomarker/survival simulations have limited functionality. Also, these packages require similar measurement times for all considered longitudinal biomarkers (often it is not the case in actual clinical data sets). Moreover, all of these packages (JM, JMbayes and rstanarm) reach limitations when it comes to the description of biomarker dynamics because only linear functions for biomarker description may be used. Thus, if the dynamics of biomarkers need to be investigated with more mechanistic models, these R‐based LME packages may not represent ideal choices. Nevertheless, with some data sets, linear models, for example, based on splines, may adequately characterize biomarker dynamics. ⁴

NLME models have become a standard in quantitative clinical pharmacology for longitudinal biomarker analysis. ²⁷ These models represent a natural choice to describe these biomarkers and to associate their dynamics with event risk in a JM framework. For such advanced nonlinear JMs, the widely known NONMEM and Monolix pharmacometric software tools may be used. ²⁸ , ²⁹ , ³⁰ NLME JMs can also be implemented in Stan software, with even more advanced options including user‐defined likelihood function formulation. ⁵ , ⁶ , ³¹ , ³²

In this tutorial, and for illustrative purposes, we implemented a JM workflow using the following set of modeling tools: JM v1.4–8 and JMbayes v0.8–85 packages for LME JMs, and Monolix 2020R1 for NLME JMs. All R‐based packages were tested in the R 4.0.2 environment. ³³

CASE STUDY: DATA DESCRIPTION AND EXPLORATION

Data from subsets of control arms from two NSCLC clinical studies, NCT00312377 ¹⁶ and NCT00364351, ¹⁵ were taken from the Project Data Sphere repository. ³⁴ In both subsets, patient data had been deidentified and did not include data from Chinese patients. Biomarker and OS data from the NCT00312377 study were used for model qualification (training data set); data from the NCT00364351 study were used for external model validation (validation data set), according to the workflow illustrated in Figure 1.

The treatments administered to these subjects with advanced NSCLC were as follows: chemotherapy (docetaxel) in the training data set and targeted therapy (erlotinib) in the validation data set. To build a JM framework, we focused on prognostic biomarkers, which may potentially provide information on survival outcomes regardless of treatment type. Interestingly, patient baseline characteristics across the two selected data sets matched rather well, including the percentage of patients with mutations in the epidermal growth factor receptor—see Table S1.

For simplicity, we limited the number of investigated biomarkers to two: tumor size and levels of lactate dehydrogenase (LDH). ³⁵ , ³⁶ Tumor size was represented by SLD, measured according to the Response Evaluation Criteria in Solid Tumors 1.1. ³⁷ LDH was selected as a biomarker because it is a measure linked to the magnitude of tumor metabolic activities. Data for both selected biomarkers were available at baseline as well as longitudinal measurements, with a sampling schedule defined in Table S1. Exploratory plots of the selected biomarkers as well as OS data are shown in Figure 2.

FIGURE 2.

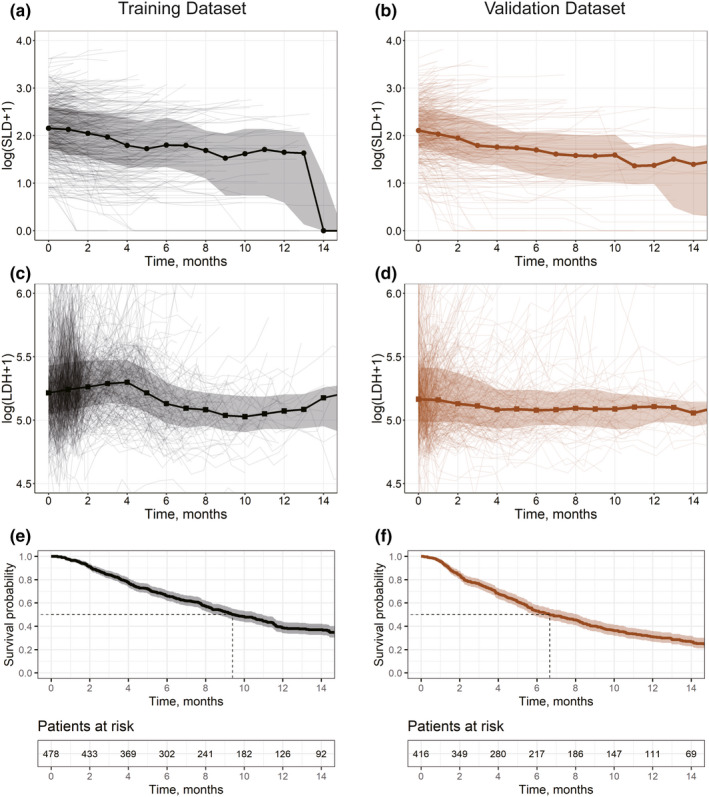
Exploration plots for training (black, left) and validation (brown, right) data sets. (a–d) Spaghetti plots for log‐transformed biomarkers showing mean values (solid lines; circles, SLD; squares, LDH) and interquartile range (shaded area). (e–f) Survival plots showing experimental Kaplan‐Meier curves (solid lines) and 95% confidence interval (shaded area). LDH, lactate dehydrogenase; SLD, sum of the longest diameters of target lesions

When examining these data sets across the two chosen clinical studies, likeness in trends can be observed for SLD, whereas differences in both LDH and OS were noted. Given the similarity in patients’ baseline characteristics across the two studies, the apparently different patterns in longitudinal LDH and OS may be caused by the administered therapies. The observed trends in biomarker dynamics may also be dependent on the study design, measurement schedule, and patient censoring, whereas at longer times, only surviving patients with smaller tumor sizes and lower LDH levels typically remain in the study.

With the exploratory plots at hand (Figure 2), we next describe the subsequent steps in the data processing and JM model qualification and validation illustrated schematically in Figure 1. Specifically, there we represent the analysis and diagnostics for the association of baseline and longitudinal biomarkers with OS. For more details on the JM workflow and its description, see the Supplementary Materials, Figure S1.

DATA SET PREPARATION

A standard vertical data set can be prepared for Monolix ³⁸ , ³⁹ , ⁴⁰ as described in the Supplementary Materials, Section 1.1. The data frame may be saved as a comma‐separated values (CSV) file to develop and test models via the graphical user interface or may be kept as an object in the R environment, if lixoftConnectors/RsSimulx packages are used to control Monolix. ⁴¹

The R‐based LME tools used in this tutorial require a data set format that is common for conventional analyses of longitudinal data (in nlme ⁴² or lme4 ⁴³ packages) and time‐to‐event data (in survival ⁴⁴ package) in R. All data can be incorporated into a single data frame. We provide suggestions on data set structuring for JM/JMbayes in the Supplementary Materials, Sections 1.2 and 1.3.

An actual view of the formatted data, ready for further analyses in JM/JMbayes and Monolix, is provided in the Supplementary Materials, Figure S2.

Different biomarker data transformations may be considered for optimal model convergence (e.g., log₂, log₁₀, square root). ¹⁴ In the present data set and because of the high dynamic ranges observed (Figure 2), SLD and LDH data were log‐transformed into ln(SLD+1) and ln(LDH+1).

SURVIVAL MODEL BUILDING

In survival modeling, the point estimates of parameters obtained in the model outputs should be studied. The size of the parameter association with OS can be assessed using the hazard ratio (HR) value, which is calculated as exp(α_b) from Equation (4) for baseline or as exp(α) for longitudinal biomarkers. A covariate increase by one unit would result in an instantaneous hazard change by a corresponding HR value. ¹⁴ Thus, in addition to providing statistical significance for a biomarker (a p value of <0.05 should be taken ¹⁴ ), HR provides the inference for clinical significance similarly to a conventional pharmacometric analysis. ⁴⁵

In some cases, a particular pattern in biomarker dynamics may not have a profound effect on time‐to‐event outcomes, although these statistically significant biomarkers may be associated with an improved quality of life, patient‐reported outcomes, or other aspects related to disease burden. ⁴ There may also be situations when biomarker measurement noise is high and/or data sampling is too sparse (e.g., biomarkers of interest are measured only at baseline and at the end of a study), so that the actual trends cannot be properly captured, and model qualification cannot be performed adequately.

Cox proportional hazards models for baseline biomarkers

An initial and simple step in the analysis of association between biomarkers and a time‐to‐event endpoint may include selection and testing of relevant baseline biomarkers via semiparametric Cox proportional hazards models that are conventionally used in clinical study analysis and offer fast parameter optimization. ⁴⁶ For further survival analysis involving JMs, these initially identified statistically significant biomarkers may be investigated longitudinally by means of fully parametric JMs.

Cox proportional hazards models may be developed and tested using survival package in R via the coxph() function ⁴⁴ and with the following syntax:

COX <‐ coxph(Surv(EVENT_TIME,EVENT) ~ SLDb + LDHb, data = jmdata.id, x = TRUE)

As seen from the model code, we investigated the importance of two baseline biomarker candidates, SLD and LDH. The optimal model should incorporate both statistical significance of the tested biomarkers (via a p value assessment for the association parameters) and the lowest value for a chosen penalized likelihood statistical criterion (i.e., Akaike information criterion [AIC]), which describes the relative goodness‐of‐fit of the tested models against the training data set. We considered the following three survival models: univariate Cox SLD, univariate Cox LDH, and multivariate Cox SLD+LDH, represented in the aforementioned code and hereafter referred to as “COX.” The outputs of these tests (Table S2) suggest that the multivariate COX model should be selected for further research.

In terms of parameter estimates in the survival models developed here, it should be noted that the size of the biomarker effects (i.e., the estimates of the association parameters) may change when additional baseline or longitudinal covariates are introduced into the model. Therefore, the summary effect on event risk may get spread over a broad range of the chosen statistically significant biomarkers. In particular, it can be noticed from Table S2 that in univariate Cox models, the value of SLD and LDH association parameters have smaller magnitude than in the multivariate model. In further data analysis, one may also include and test additional biomarkers for their association with OS, for example, smoking status, Eastern Cooperative Oncology Group (ECOG) score, and so on. ⁵

Following the analysis of baseline SLD and LDH, we next investigate the association of longitudinal biomarker trends with OS in the training data set (Figure 1).

Linear JMs

As mentioned previously, various tools may be used for JM development. An easy way to investigate longitudinal biomarkers and event risk is to develop linear univariate or multivariate JMs using the JM/JMbayes packages in R. ¹⁴ The codes for the tested LME JMs are available in the Supplementary Materials, Section 2.1.

In these models, the dynamics of longitudinal biomarkers are described using natural spline functions. ¹⁴ The knot position of the splines may be updated or additional covariates may be introduced to further optimize the description of biomarkers, depending on the available measurement frequency.

The survival submodels for univariate JMs ¹⁴ (JM SLD and JM LDH for longitudinal SLD and longitudinal LDH, respectively) were developed in the JM package using a Weibull formulation for the baseline hazard. To reach the optimal model convergence for a multivariate SLD and LDH model (JM SLD+LDH), the model was built in the JMbayes package using a spline representation of the baseline hazard.

Nonlinear JMs

Advanced JMs can be developed and tested with NLME models for biomarkers. A full representative Monolix model code is provided in the Supplementary Materials, Section 2.2. In this analysis, we considered biexponential functions to describe SLD and LDH dynamics ⁵ , ¹⁷ using the following ODE formulation:

$$\begin{array}{c}\begin{array}{cc}\hfill \frac{\mathit{dDegr}}{\mathit{dt}}=& ‐d\ast Degr\hfill \\ \hfill \frac{\mathit{dGrowth}}{\mathit{dt}}=& g\ast Growth\hfill \\ \hfill Biom=& Bio{m}_b(Degr+Growth‐1)\hfill \\ \hfill \ln Biom=& \ln (Biom+1),\hfill \end{array}\hfill \end{array}$$ (6)

where $d$ and $g$ are parameters representing rate constants of biomarker dynamics, and ${\mathit{Biom}}_b$ is the estimated baseline value for a biomarker. Equation (6) represents a longitudinal submodel for either of the chosen biomarkers: SLD or LDH. These models can also be formulated by means of explicit nonlinear functions. A set of nonlinear models similar to the one for LME tools has been built in Monolix (JM SLD, JM LDH, and JM SLD+LDH). Univariate models may be generated by removing relevant longitudinal biomarker sections (either for SLD or LDH) from the model code and considering this biomarker at baseline only. ⁴⁷

For these NLME JMs, the hazard function embeds the Weibull formulation of the baseline hazard, and it can be represented as follows:

$$\begin{array}{c}{h}_i\left(t\right)=\frac{k}{\lambda }\ast {\left(\frac{t}{\lambda }\right)}^{k‐1}\ast e^{\left({\alpha }_j\ast \log Bio{m}_{\mathit{ij}}+BaseCov\right),}\hfill \end{array}$$ (7)

where parameters k and λ define the shape of the Weibull baseline hazard function, and α_j is the association parameter for the jth longitudinal biomarker (either SLD or LDH). There are no random effects added to k, λ, and α_j . ¹⁴ In Monolix survival models, a special parameter BaseCov is used to introduce baseline covariates (its fixed‐effect value should be set to 0, and random effects should be turned off). ²⁹ , ⁴⁷ The baseline covariates of interest should be associated with this BaseCov parameter; thus, the respective association coefficients will reflect the values of α_b in Equation (4). Finally, in univariate JMs, if SLD is considered as longitudinal, then LDH is taken at baseline only and vice versa.

Monolix incorporates a set of embedded tools to check for optimal model convergence. Typically, for successful model convergence and usability toward advanced diagnostics and predictions, one should pay attention to the available recommendations. ³⁰ , ⁴⁸ , ⁴⁹ , ⁵⁰ , ⁵¹ More details are provided in the Supplementary Materials, Section 2.3.

MODEL DIAGNOSTICS

Detailed summaries of univariate and multivariate JMs for the selected LME and NLME tools are provided in the Supplementary Materials, Table S3. The association parameters for baseline and longitudinal biomarkers and OS are provided in Table 2. These results suggest a similarity in biomarker association with OS in the training data set across the same JMs developed with different tools.

TABLE 2.

Association parameters for all tested joint models

	R‐based tools			Monolix tools
Model type	JM SLD	JM LDH	JM SLD+LDH	JM SLD	JM LDH	JM SLD+LDH
αSLD	0.77 (13.3)	0.53 (20.5)	0.7778 (12.9 )	0.85 (7.41)	0.54 (6.06)	0.75 (7.35)
αLDH	0.44 (29.7)	0.75 (14.8)	0.4581 (22.1)	0.38 (13.0)	0.78 (3.57)	0.60 (7.85)
k	1.31 a	1.34 a	N/A b	1.28 (2.3)	1.26 (2.2)	1.26 (1.82)
λ	6520 a	14,300 a	N/A b	8380 (15.9)	28,100 (22.6)	19,300 (16.4)

Values in bold font indicates the association parameters for longitudinal biomarkers tested in the models. Values are provided as point estimates (%RSE).

Abbreviations: JM, joint model; LDH, lactate dehydrogenase; SLD, sum of the longest diameters of target lesions.

^a Derived from JM summary (see Supplementary Materials, Table S3).

^b Because Weibull baseline hazard parametrization is not available (N/A) in JMbayes, splines were used instead.

Advanced graphical diagnostics of the developed JMs include various plots to efficiently assess the goodness‐of‐fit for the biomarker and time‐to‐event data description (Figure 3). These graphical diagnostics can be generated in R environment for both LME tools and Monolix in a similar manner—see the Supplementary Materials, Section 3.

FIGURE 3.

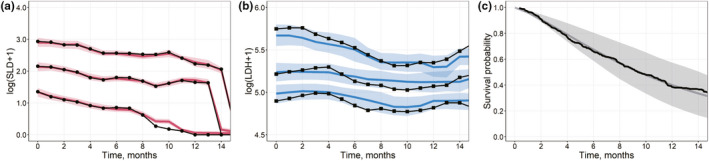
(a, b) Visual predictive check plots for the training data set (Qualification Step). Model results obtained using a multivariate nonlinear biexponential joint model in Monolix. Solid black lines represent aggregated log‐transformed biomarker data from the training data set (circles, SLD; squares, LDH). Solid colored lines represent 10%, 50%, and 90% quantiles of averaged individual predictions (red, SLD; blue, LDH). Prediction intervals for each quantile are computed with a 95% confidence interval (shaded area). (c) Survival plot shows experimental Kaplan‐Meier curve (solid black) from the training data set and the mean model prediction (solid gray) with the interquartile range (shaded area). LDH, lactate dehydrogenase; SLD, sum of the longest diameters of target lesions

Individual predictions of biomarker trends and S_i(t) in Monolix were retrieved by performing a sampling from the conditional distribution of individual biomarker submodel parameters using a Markov Chain Monte Carlo (MCMC) procedure (50 simulated parameters per patient) that may be controlled in the Monolix graphical user interface or using the lixoftConnectors/RsSimulx tools in R. ¹⁴ , ⁵²

Visual predictive checks (VPCs) provide further information on how well a model describes or predicts longitudinal data. The observed data were represented with medians and 10% and 90% quantiles of observations using a moving average of a fixed length (e.g., 30 days). Biomarker trend predictions were obtained only for timepoints corresponding to actual observations. Similarly to the observed data, the predicted values were drawn using a moving average: solid lines represented 10%, 50%, and 90% quantiles of averaged individual predictions. Prediction intervals for each quantile were computed with a 95% confidence interval. VPCs were plotted against the training data, thus describing the goodness of fit.

Patient survival plots (middle column, bottom graph in Figure 1) represent an important step in the model qualification assessment. They illustrate the alignment of the survival function from a qualified JM and actual KM estimates for the training data. Per timepoint, the mean value of the sampled individual survival probability (see Equation 5) is further averaged across all subjects to derive the predicted marginal survival. The range over the predicted marginal survival represents the 25th and 75th percentiles of the aggregated individual survival predictions. For JMs developed in Monolix, the individual survival function S_i(t) was manually coded in R, according to Equation (5), subsequently aggregated, and taken as an output from the RsSimulx script (see the Supplementary Materials, Section 3.1).

Similarly, these plots may be generated in R when using LME JM tools (see Figure S3). However, graphical diagnostics for multivariate JMs in JMbayes are limited. Thus, VPC plots for SLD and LDH as well as patient survival plots for the training data were generated for univariate models (JM SLD and JM LDH) handled within the JM package.

Finally, comparable goodness‐of‐fit (Figure 3 and S3) as well as parameter estimates (Table 2) were obtained for LME and NLME models against the training data. Upon achieving successful model convergence and adequate diagnostics, we considered further model applicability to predict biomarker dynamics as well as survival and perform discrimination analyses against the interim validation data. These steps are schematically described in Figure 1 (right column).

EXTERNAL VALIDATION

A validation procedure usually necessitates an analysis of model performance against an external data set—data that were not used in the earlier model qualification. As stated previously and represented in Figure 1, we performed such an analysis against an interim validation data set with biomarker and survival data known for the first 3 months of observation.

In Monolix, individual predictions of biomarker trends and patient survival were obtained via sampling from the conditional distribution of random effects, whereas the rest of the model parameters were fixed at their estimated values obtained during qualification. In LME JMs, these parameters were sampled from the posterior parameter distribution obtained from the qualification procedure. ¹⁴ We further performed survival discrimination assessment for all generated LME and NLME JMs, thus comparing model predictions against actual survival outcomes in the validation study.

Survival discrimination performance is typically analyzed using the well‐established metrics of area under the receiver operating characteristic curve (ROC‐AUC) and BS (Brier score). ⁵³ , ⁵⁴ ROC‐AUC values range from 0 to 1, with a higher value representing higher discrimination performance, whereas a value of 0.5 would signify no discrimination ability. BS represents a mean square error of individual survival probability predictions, and its values range from 0 to 1, with lower values representing higher precision. ⁵

Both ROC‐AUC and BS were calculated for survival predictions S_i(t) obtained at specific timepoints of interest (e.g., at different months following the longitudinal data cutoff in the validation study). Models with higher discrimination performance may potentially be further used to adequately stratify patient subgroups. Although this additional step is not described in the present tutorial, it has been detailed in a previously published JM analysis. ⁵

The chosen data cutoff of 3 months in the validation data set represents an early biomarker assessment in selected NSCLC studies. It provides enough data to perform predictions of biomarker dynamics given the sample measurement frequency in the considered studies, combined with an appropriate JM structure (especially for NLME multivariate JMs—see Figure 5). However, depending on the clinical studies and data, a different cutoff time may be tested to identify the optimal amount of interim longitudinal data that would allow for adequate biomarker predictions and efficient survival discrimination. ⁵

FIGURE 5.

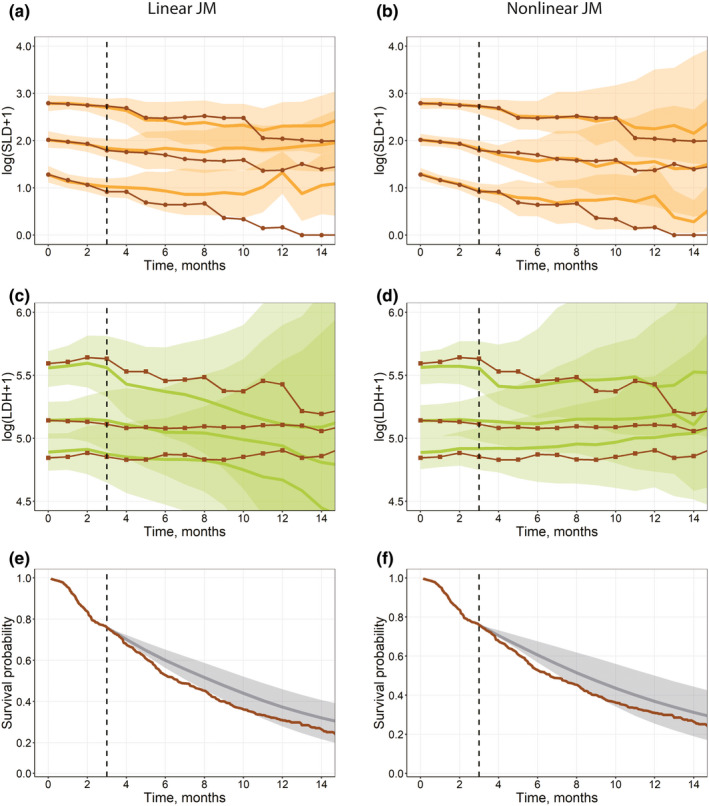
(a–d) Visual predictive check plots for the interim validation data set (Validation step), based on univariate linear joint models in JM (a, c) and a multivariate nonlinear biexponential joint model in Monolix (b, d). Solid black lines represent aggregated log‐transformed biomarker data from the validation data set (circles, SLD; squares, LDH). Solid colored lines represent 10%, 50%, and 90% quantiles of averaged individual predictions (orange, SLD; green, LDH). Prediction intervals for each quantile are computed with a 95% confidence interval (shaded area). (e–f) Survival plot shows the experimental Kaplan‐Meier curve (solid brown) from the validation data set and the mean model prediction (solid gray) with the interquartile range (shaded area) for a multivariate linear joint model in JMbayes (e) and a multivariate nonlinear biexponential joint model in Monolix (f). LDH, lactate dehydrogenase; SLD, sum of the longest diameters of target lesions

ROC‐AUC and BS can be calculated in a unified manner for model predictions generated using LME and NLME JM tools, as shown in the Supplementary Materials, Section 4. Implemented ROC‐AUC and BS calculations are adapted to right‐censored data using the inverse probability of censoring weighting. ⁵⁵ , ⁵⁶ Both ROC‐AUC and BS were calculated using the means of sampled individual survival predictions without considering the uncertainty in model parameters and random effects. Also, the JM package includes embedded functions for ROC‐AUC and BS calculations. ¹⁴ Outputs of the discrimination analysis are presented in Figure 4.

FIGURE 4.

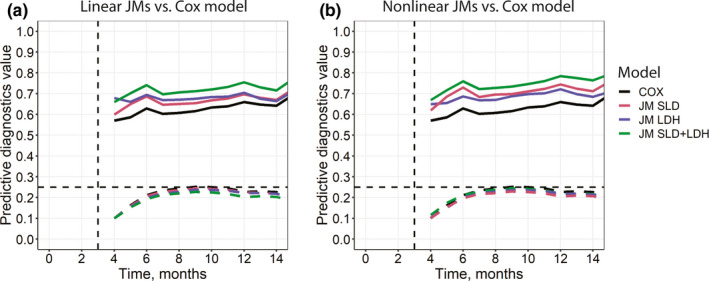
Area under the receiver operating characteristic curve (solid line) and Brier score (dashed line) diagnostics for the interim validation data set based on the selected survival models. (a) Linear models in JM/JMbayes packages. (b) Nonlinear models in Monolix. Both plots feature the same COX model, which was qualified using the coxph() function in R (see the Supplementary Materials, Section 4.2, Table S2 and “Cox Proportional Hazards Models for Baseline Biomarkers” section in the main text). COX, conventional semiparametric survival model; JM, joint model; LDH, lactate dehydrogenase; SLD, sum of the longest diameters of target lesions

The conventional semiparametric survival model (COX), which incorporated only baseline biomarker values, was a poor performer in these diagnostics, whereas the multivariate JMs in JMbayes and Monolix performed well, indicating that longitudinal trajectories of SLD and LDH biomarkers were important to achieve higher survival discrimination for the validation data. If further discrimination performance gain was sought, one may want to identify and add other baseline or longitudinal covariates deemed important to the augmented multivariate JMs. Interestingly, a higher number of significant baseline covariates in a conventional Cox proportional hazards model may result in a similar or higher discrimination performance versus JMs with a smaller number of longitudinal and baseline biomarkers (data not shown). However, such baseline biomarker models would not allow for making inference for biomarker dynamics that may carry clinical importance or may even be foreseen as study endpoints. For all the univariate and multivariate survival models considered in this tutorial, an assessment should be performed to determine whether a biomarker's association parameter p value is below 0.05 (information usually available in the model summaries—refer to Table S3). Likewise, a relevant statistical criterion representing the goodness‐of‐fit and incorporating parameter count penalization (i.e., AIC) should be evaluated to compare the models and combat overparameterization. ⁵⁷ , ⁵⁸

To provide VPCs and patient survival prediction diagnostics (Figure 1, right column) using the selected LME and NLME JM tools, a set of functions and scripts such as those used in the model qualification steps were applied (see the Supplementary Materials, Sections 3 and 5). For LME JMs, which were implemented in the JM and JMbayes packages, the predict() and survfitJM() functions were used to obtain predictions of individual longitudinal trends and individual survival S_i(t) for the validation data. These functions represent outcomes of the sampling from subject‐specific conditional probabilities of individual random effects and corresponding survival or biomarker predictions ¹⁴ obtained from previously qualified JMs.

In Monolix, predictions of longitudinal biomarker trajectories and individual survival S_i(t) were generated in the lixoftConnectors/RsSimulx packages (see the Supplementary Materials, Section 5.1). The estimated population parameters from previously qualified JMs were fixed and used for individual parameter sampling in a MCMC procedure ⁵² against the interim validation data set.

For validation VPC plots, longitudinal biomarker predictions and S_i(t) were simulated only for those patients who survived (event or censoring times for these patients should exceed the selected cutoff of 3 months), at timepoints for which further experimental observations were available. The other features of the validation figures were the same as in the qualification step. VPCs and patient survival prediction plots were similarly generated for LME and NLME tools (Figure 5).

Within the tested JM tools, comparable diagnostic performance for OS predictions were achieved using the JM/JMbayes packages and Monolix. However, Monolix provided improved predictions of longitudinal biomarker trends. In the initial section of the present tutorial, we mentioned possible limitations of LME JMs, owing to the longer term behavior of the longitudinal submodels. Splines may cause nonmeaningful trends in the areas with few observations or extrapolation areas (in case of the validation data set, beyond the 3‐month cutoff interval). Although these LME models provided an adequate goodness of fit versus NLME models in Monolix (e.g., compare Figure S3 and Figure 3) for the training data, the capability of LME JMs to adequately predict the longer term longitudinal biomarker dynamics for the validation data was limited (Figure 5).

We considered standard spline models in the JM/JMBayes packages and biexponential models in Monolix. Additional research may be required to determine whether these models are fully optimal compared with those that can be generated using customized knot positions for splines or using various empirical or mechanistic NLME biomarker submodels in Monolix. One option may also be to identify and introduce significant covariates for the longitudinal submodels of JMs (i.e., the biomarker trend may depend on patient's baseline characteristics, disease status, external conditions, chosen therapy, etc.). However, one needs to consider that these advanced JMs may require substantial computational times.

CONCLUSIONS

In this tutorial, we proposed and implemented a unified workflow for joint modeling to perform a comprehensive analysis of multiple longitudinal biomarkers and a time‐to‐event endpoint. The workflow incorporates an initial data exploration phase, steps in performing JM building and qualification using a training data set, as well as testing against an external data set for model validation. It has been implemented in R‐based LME tools and in more advanced NLME tools such as Monolix. These tools allow one to comprehensively assess information and data previously collected through clinical trials to predict the outcomes of another trial based on its interim data.

The outcomes of the analysis suggest that for the considered NSCLC data sets, nonlinear multivariate JMs in Monolix provide the highest performance in predicting longitudinal biomarker trends and survival discrimination. Moreover, advanced NLME joint modeling tools such as NONMEM, Monolix, or Stan may further overcome actual study data limitations with respect to the clinical development process. When multiple biomarkers are being evaluated in patients it often happens that both the measurement schedule and the duration of observations vary across biomarkers, hence the biomarker data are not aligned in time. For the sake of simplicity, in this tutorial, we considered a scenario whereby all interim biomarker data were collected up to the same cutoff in time. However, the approach we delineated may also be applied to an analysis that includes multiple biomarkers that have different observation times.

JMs are emerging as a data analytics methodology, which may provide a link between advanced mechanistic biomarker submodels (which may include quantitative systems pharmacology submodels) and time‐to‐event data to perform state‐of‐the‐art clinical trial simulations. Joint modeling, in effect, represents a powerful methodology in pharmacometric analyses, supported by efficient tools, to characterize the dynamic behavior of biomarkers and its association with clinical trial outcomes.

CONFLICT OF INTEREST

Kirill Zhudenkov, Sergey Gavrilov, Alina Sofronova, Oleg Stepanov, Nataliya Kudryashova, and Kirill Peskov are employees of M&S Decisions, LLC. Kirill Peskov is also affiliated with the Sechenov First Moscow State Medical University. Gabriel Helmlinger is an employee of Obsidian Therapeutics.

Supporting information

Supplementary Material

Figure S1

Figure S2

Figure S3

Table S1

Table S2

Table S3

Zhudenkov K, Gavrilov S, Sofronova A, et al. A workflow for the joint modeling of longitudinal and event data in the development of therapeutics: Tools, statistical methods, and diagnostics. CPT Pharmacometrics Syst Pharmacol. 2022;11:425‐437. doi: 10.1002/psp4.12763