Abstract
Compared to all-atom molecular dynamics (AA-MD) simulations, coarse-grained (CG) MD simulations can significantly reduce calculation costs. However, existing CG-MD methods are unsuitable for sampling structures that depart significantly from the initial structure without any biased force. In this study, we developed a new adaptive CG elastic network model (ENM), in which the dynamic cross-correlation coefficient based on short-time AA-MD of at most ns order is considered. By applying Bayesian optimization to search for a suitable parameter among the vast parameter space of adaptive CG-ENM, we succeeded in reducing the searching cost to approximately 10% of those for random sampling and exhaustive sampling. To evaluate the performance of adaptive CG-ENM, we applied the new methodology to adenylate kinase (ADK) and glutamine binding protein (GBP) in the apo state. The results showed that the structural ensembles explored by adaptive CG-ENM could be considerably more diverse than those by conventional ENMs with enhanced sampling such as temperature replica exchange MD and long-time AA-MD of 1 μs. In particular, some of the structures sampled by adaptive ENM are relatively close to the holo-type structures of ADK and GBP. Furthermore, as a challenging task, to demonstrate the advantages of the CG model with lower calculation cost, we applied our new methodology to a larger biomolecule, integrin (αV) in the inactive state. Then, we sampled various structural ensembles, including extended structures that are apparently different from inactive ones.
Introduction
To elucidate the dynamic behavior of conformational changes in biomolecules, it is important to understand their mechanisms of function to facilitate applications in drug discovery and medical treatment. Experimental and in silico simulation approaches have been used to investigate the functional mechanisms. However, even with the development of experimental technologies related to structural analysis such as X-ray crystallography, electron cryomicroscopy, and nuclear magnetic resonance, tracking a series of in-solution behaviors remains challenging.1 With simulations, calculation costs can be prohibitive. Concretely, even utilizing the specialized high-speed supercomputer ANTON,2 all-atom molecular dynamics (AA-MD) simulations cannot calculate the entire process of spontaneous large-scale structural changes in macromolecules, such as the lever-arm motion of the myosin motor,3 which ranges from milliseconds to seconds, within a realistic calculation time. Alternatively, coarse-grained (CG) MD simulation techniques4−6 such as the elastic network model (ENM) of Tirion7 and an off-lattice Go model such as AICG,8−10 in which only the degrees of freedom of the Cα atom for each residue are considered, can reproduce the dynamics of biomolecules with lower calculation costs. By applying the multiple-basin11 and domain motion-enhanced (DoME)12 potential, in which experimental structures prior to (initial) and following (target) conformational change are used as references, CG-MD has succeeded in reproducing the large-scale conformational changes between the initial and target structures of macromolecules such as the transporter AcrB.13 However, under the condition that only the initial structure is given, CG-MD retains the critical limitation of being unable to efficiently explore target structures that are structurally distant from the initial conformation. In particular, the structures sampled by conventional CG-ENM tend to be trapped or localized around the initial and reference structures.7,14,15
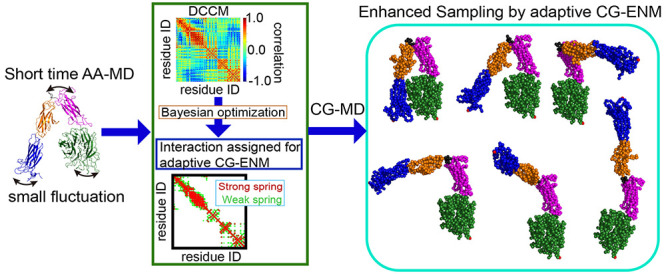
To overcome these problems, in this study, we developed a new adaptive CG-ENM that can effectively explore the target structure and sample various structural ensembles based on the initial structure without using any structural information of the target. The basic concept behind our method is that an appropriate assignment of interactions with different strengths between residue pairs, which constitute the building blocks of an ENM, will enable wider sampling while maintaining the overall structure. In this study, we attempt to determine the appropriate weights for this adaptive elastic network from the dynamic cross-correlation coefficient map (DCCM)16,17 based on the results of a short AA-MD starting from a given initial structure. One of the limitations of this strategy is the existence of numerous candidates for the weights of the adaptive network, rendering it difficult to determine the appropriate parameters. Therefore, this study introduces a parameter search based on Bayesian optimization (BO)18−20 to search efficiently for suitable parameter candidates for structural sampling. As a result, we searched for a suitable parameter set for adaptive ENM by applying BO yielding drastically reduced exploring cost, being approximately 10% of the cost required by random sampling (RS).
To evaluate the performance of adaptive ENM, we applied our methodology to the apo-state structure of two kinds of proteins, adenylate kinase (ADK)21 and glutamine binding protein (GBP),22 that also have other structural states as a holo state. The results reveal that the structural ensembles sampled by adaptive CG-ENM are considerably more diverse than those sampled by the temperature replica exchange MD (TREMD)23 of conventional CG-ENM and those sampled by conventional AA-MD for 1 μs order. In particular, some of the structures sampled by adaptive CG-ENM resemble the target holo-type structure.
Finally, as a challenging task, to demonstrate the advantages of the CG model with lower calculation cost, we applied our new methodology to a larger biomolecule, integrin (αV), in a V-shaped inactive state.24 After efficiently exploring a suitable parameter set with BO, we successfully sampled various structural ensembles, including V-shape bent and extended structures, assumed to be similar to one in the active state. However, the whole x-ray crystal structure in an active state remains unresolved.24
Materials and Methods
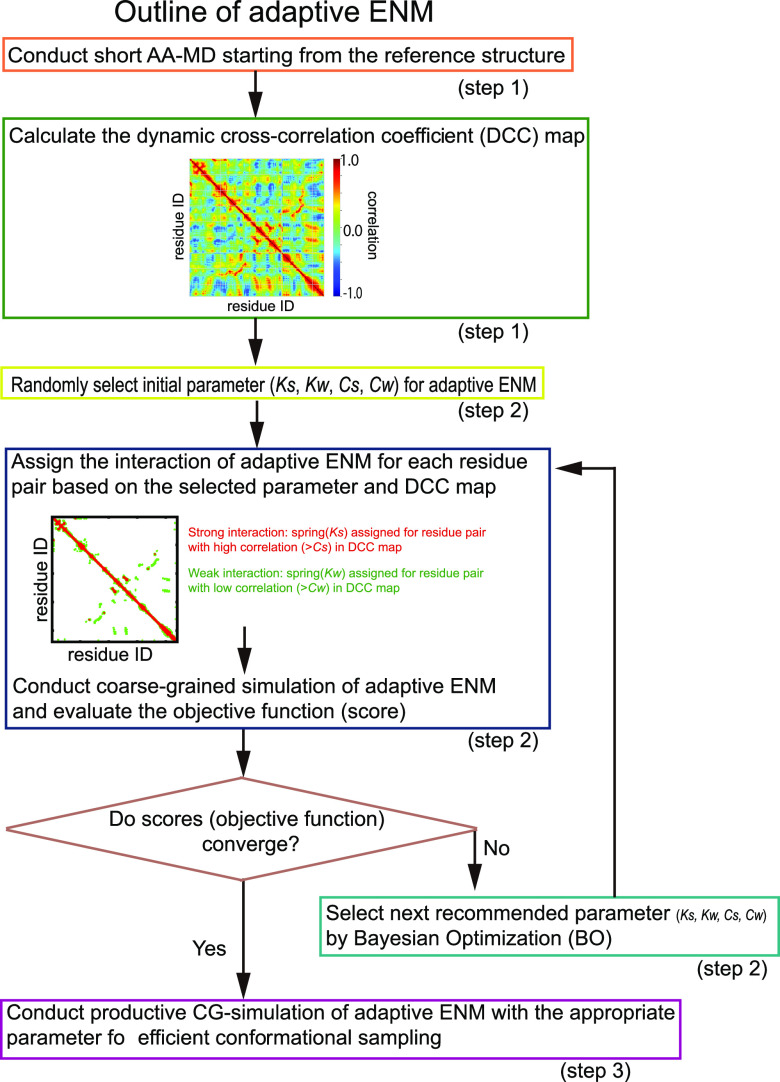
Our new adaptive CG-ENM can be achieved according to the flowchart shown in Figure 1 and consists of three main steps as follows. In step 1, short-time AA-MD starting from the initial structure with the evaluation of DCCM for each residue pair is conducted to capture the dynamic domains25 composed of the rigid and flexible domains in the protein easily. In step 2, the suitable parameter set for adaptive CG-ENM is efficiently searched by BO to enhance the fluctuation of flexible parts and the variety of sampled structural ensembles while maintaining an average Q-score higher than 0.8, which indicates that the protein system is significantly stable (see Supporting Information S1 for a detailed explanation of the Q-score). In step 3, productive simulation using adaptive CG-ENM under suitable parameters is performed for efficient and broader conformational sampling.
Figure 1.
Flowchart of adaptive CG-ENM for efficient conformational sampling. Conformational sampling of the new adaptive CG-ENM comprised three steps: (1) evaluation of the DCCM based on short-time AA-MD, (2) efficient exploration of a suitable parameter set using BO, and (3) broader conformational sampling via productive CG-MD simulations.
Conducting Short-Time AA-MD Simulations and Calculating DCC Maps
Short-time AA-MD simulations of nanosecond order should be conducted as the first step in adaptive CG-ENM. In this study, we chose the apo-state structures registered in PDB as initial structures for ADK21 and GBP22 (IDs 4AKE (Figure 2A) and 1WDN (Figure 2B), respectively) and the inactive-state structure in PDB as the initial structure for integrin. Starting from PDB structures in the apo state and in the inactive state, we applied GROMACS (version4.6.5)26 with the AMBER ff99SB-ILDN force field27 incorporating energy minimization and equilibrated AA-MD to conduct five productive AA-MD simulations at the NPT ensemble (temperature, 298 K; pressure, 1 atm) for nanosecond order (maximum, 50 ns), with the coordinate frames saved every 2 ps. The details of the AA-MD simulation protocol are provided in Supporting Information S2. Using five equilibrium AA-MD trajectories in the NPT ensemble, a dynamic cross-correlation coefficient map (DCCM),16 representing the correlation of fluctuation between all residue pairs, was calculated. The dynamic cross-correlation coefficient for the residue pair between i and j is defined by the following equation
| 1 |
where r⃗i is the coordinate of residue i and ⟨r⃗i⟩ is the time-averaged coordinate after all frames sampled by MD are aligned to the reference (initial PDB structure). Thus, Cij indicates the correlation of the deviation vectors from the mean structure. In this work, concretely, the five short AA-MD trajectories were concatenated to provide a single Cij value for each residue pair. The probability distributions of root-mean-square displacement (RMSD) vs initial structure for five short AA-MD trajectories quite resemble each other and are significantly narrower than the broader ensemble sampled by adaptive CG-ENM (as seen in Figure S1). The DCCM is expected to extract the dynamic domains that constitute the regions of rigid and flexible domains in the target biomolecule.
Figure 2.
Reference structures of the two proteins and DCCM (cij) for corresponding systems. (A and B) Initial structures for ADK and GBP for the apo state registered in PDB, respectively. Experimentally suggested domains are shown in different colors: NMP (orange), LID (blue), and core (magenta) for ADK; small (magenta) and large (orange) for GBP. (C and D) Color map of DCC in the plane of all residue pairs evaluated based on the short AA-MD trajectories for ADK and GBP, respectively. The higher (lower) correlation cij for residue pairs i–j is reflected by the color in DCCM being closer to red (blue), whereas a color close to green indicates almost no pair correlation (cij ∼ 0).
Construction of New Adaptive CG-ENM and Efficient Exploration of Suitable Parameter Sets by BO
The force field for our new adaptive CG-ENM is expressed by the following equation, which is similar that for ordinary Tirion-type CG-ENM7
| 2 |
where Kij (kcal/(mol Å2)) and rij (Å) are the spring constant and the distance between the ith and jth residue pair in a given structure and rij0 is the distance in the reference (initial PDB) structure for the corresponding pair. Whereas the spring Kij in ordinary Tirion-type CG-ENM is constant (Kij = KT = 10) in the default parameters of CafeMol version3.2 as described in Supporting Information S3, the spring Kij in adaptive CG-ENM is set according to the value of DCC for the corresponding pair as follows
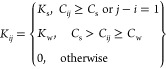 |
3 |
where strong interaction, Ks, is assigned for residue pairs with higher correlation (>cs) and weak interaction, Kw, is assigned for those with weaker correlation (>cw), whereas no spring is applied to residue pairs whose DCC value cij is lower than cw. This may potentially lead to the realization of a broader range of structural sampling compared with that from ordinal Tirion-type CG-ENM, in which only static information of the reference PDB is considered by the distance threshold = 6.5 Å for the native contact pair. A detailed explanation of the native contact pair of the Tirion-type ENM is provided in Supporting Information S3. In ordinal Tirion-type CG-ENM, by taking account of only static information of the reference structure, the strong-constant spring is assigned for the native contact residue pair even with significantly weaker interaction. So, specifically, it is assumed that ordinal Tirion CG-ENM may seldom reproduce the dissociation process of two adjacent domains in the reference structure even if the interaction of the boundary area between corresponding two domains was quite weak. By contrast, in our adaptive CG-ENM, either weak or no springs are assigned for residue pairs if these DCC values, reflecting the interaction strength of corresponding pairs suitably, are lower. Therefore, it is expected that adaptive CG-ENM has the potential to generate a broader conformational sampling such as interdomain motion compared with ordinal Tirion CG-ENM.
Depending on the parameter set related to the spring constants (Ks > Kw) and dynamic cross-correlation thresholds (1 ≥ Cs > Cw ≥ 0), the adaptive CG-ENM may qualitatively exhibit various sampling behaviors. We aim to search efficiently and determine a suitable parameter set with adaptive CG-ENM to realize many varieties of structural ensembles, including structures distant from the reference, while stably preserving the structure within each domain of the system. In this study, we focus on the wide range of four-dimensional parameter space defined by Ks, Kw = 1, 2, ..., 10 and Cs, Cw = 0.1, 0.2, ..., 1.0, under the conditions of Ks > Kw and Cs > Cw. Because the combination number within the defined parameter space (Ks, Kw, Cs, Cw) is significantly large (2025 in total), we applied the BO method,18 a representative machine learning technique, to efficiently explore the suitable parameter set and reduce the search cost.
At the initial stage of BO, we randomly chose a parameter set (Ks, Kw, Cs, Cw). As the target function FBO for BO, we adopted the measurement defined by the following equation
| 4 |
where ⟨Q⟩ is the time-averaged Q-score28 (based on the initial structure), which stands for domain stability (see Supporting Information S1 for a detailed explanation of the Q-score), χ(x) is a step function (χ(x) = 1 for x > 0, otherwise 0), and Var[RMSD], which indicates the variety of sampled structures, is the time variance of the root-mean-square displacement (RMSD) between the sampled structure and reference structure. We set the Q-score threshold as q0 = 0.8, which is a relatively high value. Therefore, it is expected that the parameter set that realizes a higher target function would enable the exploration of various structures while maintaining a stable domain structure.
The target function FBO for each parameter set selected by BO is evaluated using a trajectory of adaptive CG-MD simulations for 107 steps at each corresponding parameter set (see Supporting Information S4 for details regarding CG-MD simulations with underdamped Langevin dynamics). To search for a better parameter set that realizes a higher target function FBO, CG simulation and BO based on its trajectory were sequentially executed until the target function converged.
In this research, COMBO/PHYSBO,29 a publicly available program, was used to implement BO.
Broader Conformational Sampling via Productive CG-MD Simulation of Adaptive ENM with the Appropriate Parameter Set
In step 3 of the adaptive CG-ENM, a productive CG-MD simulation with an appropriate parameter set tuned by BO is conducted for broader conformational sampling. In this study, for ADK and GBP, a productive simulation by adaptive CG-MD with the respective parameters (Ks, Kw, Cs, Cw) = (8.0, 7.0, 0.8, 0.6) and (10.0, 8.0, 0.8, 0.6) searched by BO was conducted for 107 steps using underdamped Langevin dynamics at T = 300 K and dt = 0.2. To analyze the sampled structure ensemble, as shown in Sampling Performance of New Adaptive CG-ENM and Comparison with Conventional CG-ENM and AA-MD section, 5000 structures taken every 2000 steps from one trajectory were used. Furthermore, to compare the sampling performance of adaptive CG-ENM with that of other sampling methods, we prepared the structural ensembles using conventional long-time AA-MD for 1 μs and the ensemble of conventional CG-ENM with default parameters sampled by the enhanced sampling algorithm (TREMD), the simulation protocols for which are presented in Supporting Information S2, S3, and S5.
Results and Discussion
First, we show that the structural domains, which are consistent with experimentally suggested domains to some extent, could be revealed from DCCM evaluated using short-time AA-MD simulations of at most nanosecond order for the targets (ADK and GBP). Then, we discuss the various parameter dependencies of adaptive CG-ENM and the significant improvement of the parameter searching efficiency obtained by applying BO. Subsequently, we demonstrate that the performance of structural exploration by adaptive CG-ENM with an appropriate parameter set explored by BO is significantly better than those of long-time AA-MD and original CG-ENM with TREMD, which is a typical enhanced sampling method. Finally, as a challenging task, to demonstrate the advantages of the CG model with lower calculation cost, we applied our new methodology to a larger biomolecule, integrin (αV), in an inactive state.
Evaluation of DCCM Based on Short-Time AA-MD Simulations
Using the short-time AA-MD trajectories for at most nanosecond order, we evaluated DCCM for all residue pairs of ADK (Figure 2C) and GBP (Figure 2D). Experimentally, ADK and GBP are suggested to be composed of three and two domains, respectively: NMP-binding (residue ID: 30–59), LID (residue ID: 122–159), and core (all of the other residues) domains for ADK21 and small (residue ID: 90–180) and large (all the other residues) globular domains for GBP.22 In Figure 2A,B, each domain for ADK and GBP in the apo state is shown in a different color. From Figure 2C,D, it can be observed that the regions (clusters) with high correlation values in the DCC map correspond well to each domain region experimentally suggested in both protein systems. This indicates that the analysis of DCC based on short-time AA-MD for at most nanosecond order succeeds in appropriately discriminating between the rigid and flexible domains of the target proteins.
In the case of GBP, several DCC maps were also evaluated by varying the time length of the all-atom MD trajectories used for the analysis of DCC from 0.01 × 5 to 50 ns × 5. From Figure S2, DCCMs appear to converge sufficiently at used-time lengths longer than 1.5 ns × 5. The similarity (correlation coefficient) between DCCM for 1.5 ns × 5 shown in Figure 2D and that for 50 ns × 5 shown in Figure S2 (H) is significantly high (approximately 0.82). Therefore, we conclude that the short-time AA-MD for at most nanosecond order is sufficient to capture the information related to the domain and structural fluctuations.
Parameter Dependence of Adaptive CG-ENM
Depending on the parameter set (Ks, Kw, Cs, Cw), the adaptive CG-ENM is expected to exhibit various sampling behaviors. For the adaptive CG-ENM of ADK and GBP with two extreme cases, (Cs, Cw) = (0.2, 0.1) and (1.0, 0.9), we investigated the colored map of the assigned interaction strengths Kij in the residue pair plane and the time evolution of RMSD from the initial structure and Q-score, as shown in Figures S3 and S4, respectively. From panels A and D of these figures, we can observe that for progressively smaller Cs and Cw values, more springs are densely applied, and the system increasingly stabilizes (Q-score ∼ 1) and tends to be more strongly trapped around the reference structure (RMSD ∼0). Conversely, as shown in panels B and E, with larger Cs and Cw values the assigned spring density decreases significantly, with the entire system structure appearing to become unstable and ultimately almost unfolding (Q-score < 0.5). Adaptive CG-ENM with the moderate parameter set (Cs, Cw) = (0.8, 0.6) appears to enable various structural samplings with higher RMSD variance while stably preserving the structure within each domain of the system (Q-score > 0.8), as shown in panels C and F of Figures S3 and S4.
We also checked the contour plot FBO score, consisting of the mean of the Q-score and the variance of RMSD, on the two types of two-dimensional planes defined by (Cs, Cw) and (Ks, Kw) under limited conditions in which either (Ks, Kw) or (Cs, Cw) is fixed at a specific value. Figure S5A (ADK) and Figure S6A (GBP) show that a higher FBO tends to be realized in the localized region on the (Cs, Cw) plane, whereas no systematic and clear dependence of FBO is observed on the (Ks, Kw) plane (Figures S5 and S6, panel B). Therefore, the application of BO is essential to optimize the FBO score efficiently, which exhibits complicated parameter (Ks, Kw, Cs, Cw) dependence.
Efficient Exploration of the Suitable Parameter Set for Adaptive CG-ENM by Applying BO
For step 2 of the new adaptive CG-ENM (Figure 1), it is necessary to search efficiently for a suitable parameter set (Ks, Kw, Cs, Cw) from a wider parameter space. Because exploring a suitable parameter set with a simple exhaustive search algorithm and RS is computationally expensive and impractical, we applied the BO algorithm to reduce the search cost. To realize a broader structural ensemble by adaptive CG-ENM, it is necessary that many structural varieties that are distant from the initial structure should be frequently sampled and explored while preserving the stability of the entire structure, including each rigid domain, to some extent. For this purpose, as a target function FBO of BO, we adopted a score composed of the time average of the Q-score and the variance of RMSD, as described in the Materials and Methods section. In this study, starting from randomly selected initial parameter set by applying the BO algorithm, suitable parameter sets of adaptive CG-MD, (Ks, Kw,Cs, Cw) = (8.0, 7.0, 0.8, 0.6) and (10.0, 8.0, 0.8, 0.6), for ADK and GBP are selected, respectively.
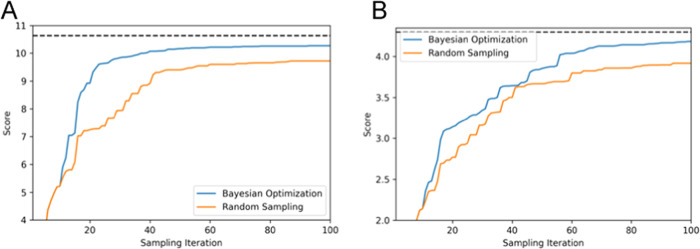
To accurately evaluate the performance of the parameter searching methods, such as RS and BO, we repeated 30 trials using randomly selected initial parameter sets and averaged the score ⟨FBO⟩. Figure 3 shows the sampling iteration number dependence of the averaged score over 30 trials. For both ADK (A) and GBP (B), compared with the score obtained by RS, the score ⟨FBO⟩ by BO appeared to reach 90% of the optimal value smoothly and to converge before the sampling iteration number reached a maximum of 50–100. Within a small iteration number (approximately 100), the converged score produced by BO tended to be significantly higher than that by RS.
Figure 3.
Sampling iteration number dependence of the averaged score ⟨FBO⟩ in exploring suitable parameter sets by Bayesian optimization (BO) and random sampling (RS). (A) Result for ADK and (B) result for GBP. In each panel, the blue and orange lines correspond to the average score by BO and RS, respectively. The dashed line indicates the optimum value of score FBO: 10.63 for ADK (A) and 4.30 for GBP (B).
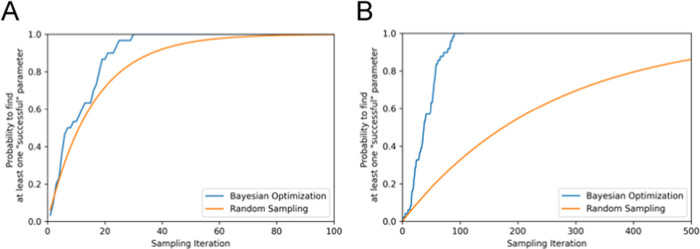
As shown in Figure 4, we also investigated the probability of finding at least one “successful” parameter, where the frequency of CG sampling structures with RMSD values from the target holo structure below a certain threshold is finite. In this study, as target structures for ADK and GBP, we chose the experimentally resolved PDB structures in the holo state (PDB-ID = 2ECK and 1GGG), as shown in Figures 5C and 6C, respectively. We set 5.0 and 4.5 Å as thresholds of the successful parameter related to the RMSD value, being smaller than 85% of the RMSD value between the initial (apo) and target (holo) structure: 7.2 and 5.3 Å for ADK and GBP, respectively. With ADK, at least one successful parameter could be found through 55 sampling iteration times, representing 1/37 and 1/5 of the search cost using exhaustive search and RS. In the case of GBP, a parameter could be found following 89 iterations, affording a reduction to 1/23 of the exhaustive search and 1/8 of RS cost. For both proteins, the successful parameter could be identified within a maximum of 100 times by applying BO, representing <10% of the calculation cost of the exhaustive search method.
Figure 4.
Sampling iteration number dependence of the probability to find at least one successful parameter. (A) Result for ADK and (B) result for GBP. In each panel, the blue and orange lines correspond to the probability afforded by BO and RS, respectively.
Figure 5.

Comparison of the new adaptive ENM with conventional ENM and AA-MD for ADK. (A) Comparison of structural ensembles sampled by adaptive ENM, conventional ENM, and AA-MD (50 ns and 1 μs) in the PCA plane, of which PC1 and PC2 axes are defined by the ensemble using adaptive CG-MD. Sampling points for adaptive ENM, ENM(TREMD), and AA-MD (50 ns and 1 μs) are colored green, magenta, blue, and orange, respectively. In particular, green gradation for sampling points of adaptive ENM depends on the Q-score (holo). Reference (apo) and target (holo) structures are colored light green (square) and red (triangle), respectively. (B) Time evolution of RMSD vs target: holo, Q-score (apo), Q-score (holo), and Rg for adaptive ENM, conventional ENM, and AA-MD (50 ns and 1 μs). The red dashed line for RMSD represents the certain threshold of RMSD for a successful parameter; i.e., 5.0 Å, whereas the green and red dashed lines for Rg correspond to Rg for apo and holo states, i.e., 19.5 and 16.3 Å, respectively. (C) structural comparison between initial (apo state as the reference), target (X-ray structure for the holo state), and representative structures sampled by adaptive CG-ENM (S1–S5). The sampling point for each structure (S1–S5) is shown in panels (A) and (B) for adaptive ENM using a black “x”. RMSD and Q-score based on holo and Rg values are added to each snapshot.
Figure 6.
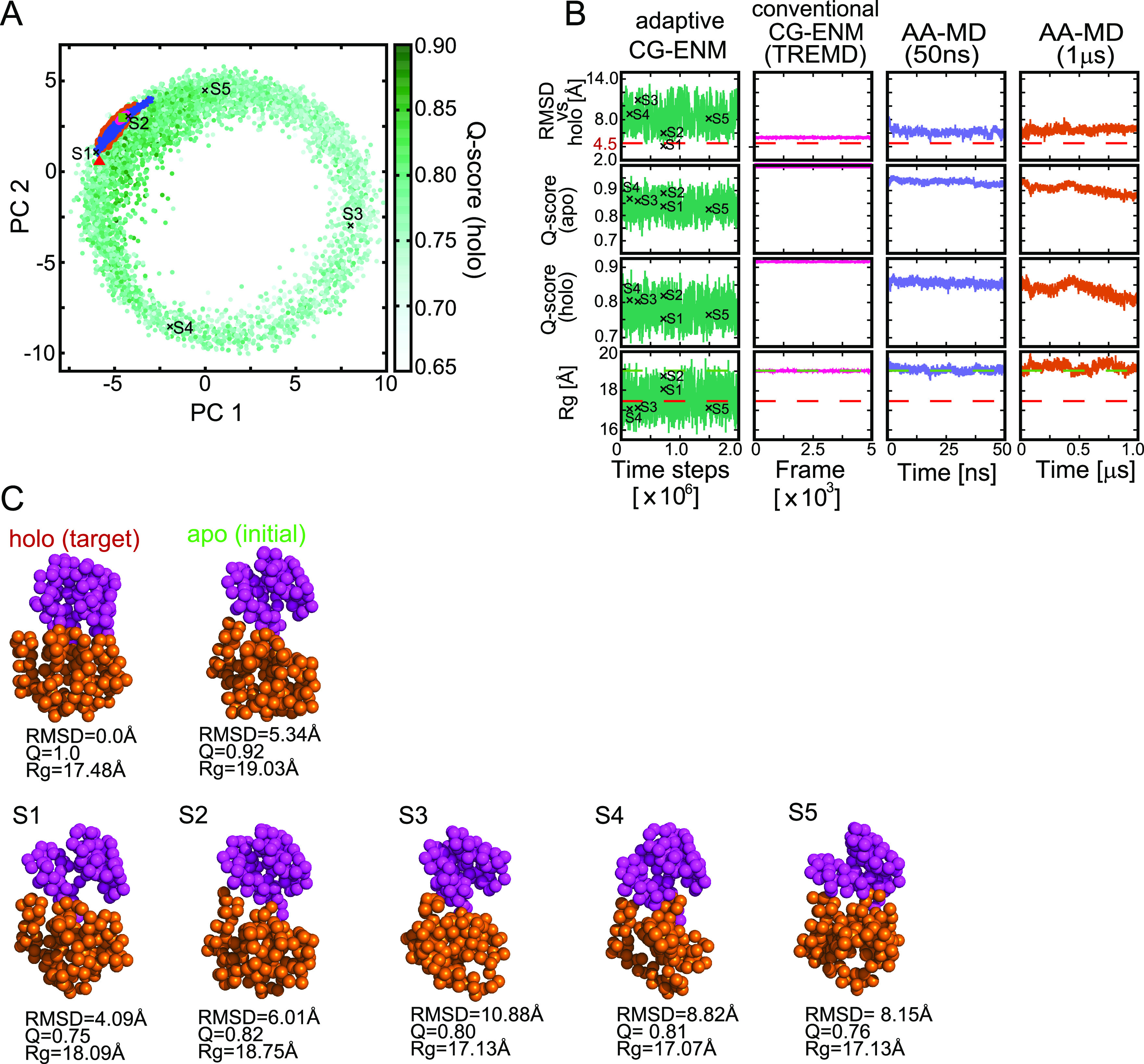
Comparison of the new adaptive ENM with conventional ENM and AA-MD for GBP. (A) Comparison of structural ensembles sampled by adaptive ENM, conventional ENM, and AA-MD (50 ns and 1 μs) in the PCA plane, of which the PC1 and PC2 axes are defined by the ensemble via adaptive CG-MD. Sampling points for adaptive ENM, ENM(TREMD), AA-MD (50 ns and 1 μs) are colored green, magenta, blue, and orange, respectively. In particular, green gradation for sampling points of adaptive ENM depends on the Q-score (holo). Reference (apo) and target (holo) structures are colored light green (square) and red (triangle), respectively. (B) Time (frame) dependence of RMSD vs target structure, Q-score (apo), Q-score (holo), and Rg for adaptive ENM, conventional ENM, and AA-MD (50 ns and 1 μs). The red dashed line for RMSD represents the certain threshold of RMSD for a successful parameter; i.e., 4.5 Å, whereas the green and red dashed lines for Rg correspond to Rg for apo and holo states, i.e., 19.0 and 17.5 Å, respectively. (C) Structural comparison between initial (apo state as the reference), target (X-ray structure for the holo state), and representative structures sampled by adaptive CG-ENM (S1–S5). Sampling points for each structure (S1–S5) are shown in panels (A) and (B) for adaptive ENM using a black x. RMSD and Q-score based on holo and Rg values are added to each snapshot.
To investigate convergence (speed) of the score under the same condition for Figure 3, we also checked the sampling iteration number “i” dependence of the averaged improvement of score: ⟨FBO(i) – FBO⟩ over 30 trials, as shown in Figure S7. Whereas the value of FBO seems to improve sometimes even around iteration numbers 60–100, the most part of the score improves significantly in the first half of 100 iteration numbers: the improvement of score ⟨FBO(i) – FBO⟩ in the first half of 100 iterations tends to be quite higher than the corresponding one in the last half of 100 iterations frequently, as seen in Figure S7. The quite similar qualitative tendency could also be confirmed in sampling iteration number (i) dependence of the raw improvement of score FBO(i) – FBO for each 30 trial of the BO procedure, as shown in Figure S8. Therefore, this suggests that through the BO procedure, the target score tends to converge sufficiently in approximately 100 iterations.
For ADK, the sampling iteration number dependence of the probability of finding a successful parameter by BO appears to be relatively similar to the dependence of the probability by RS. This tendency occurs for ADK because the number of successful parameters that meet the condition related to the RMSD threshold, 5.0 Å in all combinations of parameter space, is significantly larger (204/2025) than the corresponding number (80/2025) for GBP. Therefore, if the RMSD threshold for the success parameter is reduced in ADK, the probability of finding the success parameter will decrease significantly from 204/2025 and the difference of search efficiency between BO and RS is expected to become more significant.
Here, it should be emphasized that it is assumed to be generally difficult to determine the best score uniquely for broader and better sampling because there may be multiple criteria and various measurements to indicate sampling goodness quantitatively. In this research, as one of the candidates for sampling performance measurement, we adopted (presented) a score function FBO, which is defined by eq 4, to aim for broader sampling while ensuring that the domain structure remains as stable as possible. In some cases, there may be some parameter sets with higher score FBO; however, we assume that these are all good parameters in the sense that they satisfy (achieve) the original purpose qualitatively and sufficiently.
In this study, we demonstrated that the efficiency of the parameter search can be improved drastically by applying BO compared with RS and exhaustive search methods. However, some calculations are still required for BO. In the future, by applying adaptive ENM to various proteins and constructing a machine learning predictor based on accumulated data, an appropriate parameter range for target proteins is expected to be predicted without any exploration cost.
Sampling Performance of New Adaptive CG-ENM and Comparison with Conventional CG-ENM and AA-MD
From Figure 5A, it can be seen that the structural ensemble sampled by adaptive CG-ENM (gradated green according to the Q-score based on the holo structure) for ADK is sufficiently broader than the ensemble of ENM by TREMD (magenta) and those by conventional AA-MD for 50 ns (blue) and 1 μs (orange) in the PCA plane, where the vector of PC12 is defined by the ensemble of structures sampled by adaptive CG-ENM. The structures sampled by other methods (AA-MD and conventional CG-ENM by TREMD) are projected onto the plane defined by the PC12 vector originating from the ensemble of adaptive CG-ENM. To compare the variety of ensembles quantitatively, we evaluated the surface area of the bounding box for each ensemble in the PCA plane using convex-hull algorithms,30 as shown in Table 1. The surface area for adaptive CG-ENM is significantly larger than that for conventional CG-ENM by TREMD and that for conventional AA-MD of 1 μs. Notably, the significance of structure diversity sampled by adaptive CG-ENM does not depend on how the PCA axis is placed, as shown in Table S1. From Figure 5B for the panel of adaptive CG-ENM, we can confirm that the broader structural ensemble, including structures that are distant from the initial state, is explored while stably preserving the entire structure (i.e., the time average of the Q-score (apo) is significantly higher than 0.8). Furthermore, adaptive CG-ENM succeeds in sampling structures that are close to the target structure in the holo state, where the RMSD value is <5.0 Å, as shown in Figure 5B. The RMSD value of the structure closest to the holo structure sampled by adaptive CG-ENM is 3.8 Å, which is significantly smaller than the RMSD between the initial (apo) and target (holo) structures. From Figure 5C, we can confirm that many varieties of structures, including not only apolike and hololike structures (S2 and S1) but also fully extended structures such as S3 and S4, were sampled broadly.
Table 1. Surface Area of the Bounding Box for Structural Ensemble Points Explored by Each Model in the PC12 Plane Defined by the Eigenvector of Adaptive CG-ENMa.
| adaptive CG-ENM | conventional CG-ENM by TREMD | AA-MD (50 ns) | AA-MD (1 μs) | |
|---|---|---|---|---|
| ADK | 1.00 | 3.18 × 10–3 | 5.26 × 10–2 | 7.79 × 10–2 |
| GBP | 1.00 | 3.76 × 10–4 | 1.11 × 10–2 | 1.04 × 10–2 |
The surface areas of the bounding boxes for AA-MD and conventional CG-ENM by TREMD are normalized by that of adaptive CG-ENM.
A similar qualitative tendency related to the structural exploration performance of adaptive CG-ENM could also be confirmed in other protein systems, such as GBP, as shown in Figure 6 and Table 1: the structural ensemble sampled by adaptive ENM is significantly broader than that obtained by other methods. In particular, adaptive CG-ENM for GBP succeeds in sampling frequently structures that are close to the target structure in the holo state, where the RMSD value is <4.5 Å, as shown in Figure 6B. (The RMSD value of the structure closest to the holo sampled by adaptive CG-ENM was 4.0 Å.) The results suggest that adaptive CG-ENM for relatively small globular protein may enhance the diversity of structural sampling compared with other methods such as AA-MD and conventional CG-ENM with TREMD.
Even with other suitable parameter sets (Ks, Kw, Cs, Cw) = (7.0, 5.0, 0.9, 0.6) and (8.0, 6.0, 0.7, 0.6) tuned by BO for ADK and GBP with other initial conditions, the variety of sampled structural ensembles explored by adaptive CG-ENM is robustly richer than those by conventional CG-ENM by TREMD and conventional AA-MD of 1 μs, as shown in Figure S9. Furthermore, the significance of the diversity of structures explored by adaptive CG-ENM is retained even when compared with conventional CG-ENM, in which the spring constant is weakened by 0.1-fold of the default value, as shown in Figure S10.
With reference to panel B of Figures 5 and 6, it should be noted that with adaptive CG-ENM, the broader structural ensemble, which results in various RMSD and Rg values, can be realized not by “just” breaking contact interaction between arbitrary residue pairs but by preserving Q-score high appropriately; the Q-score (apo and holo) with adaptive CG-ENM seems to be not so inferior to the one obtained with AA-MD (1 μs). This suggests that when sampled with adaptive CG-ENM, intradomain structures remain reliable and are similar to the corresponding domains in apo and holo.
From Figures 5A, 6A, S11, and S12, we can extract a rough tendency related to the distribution of sampled structures by adaptive CG-ENM for ADK and GBP; in the region closer to apo and holo, such as representative models S1 and S2, the values of Q-holo and Q-apo tend to be higher. By contrast, in the larger PC1 area where model S3 exits, RMSD vs holo becomes higher. Especially, ADK forms an extended structure, like model S3 in the higher PC1 area where Rg also becomes higher. The potential energy of the system seems to be distributed almost uniformly and has no evident dependence on the location in the PC1–2 plane.
In addition, the detailed structure of model S1 with smaller RMSD vs target (holo) sampled by adaptive CG-ENM was investigated for ADK and GBP (Figures S13 and S14, respectively). Concretely, the probability distributions of the Cα pairwise distance (panel A) and Cα distance matrix (panel B) for all residue pairs were investigated for model S1, apo, and holo. The results showed that in the case of ADK, both the probability distribution and the distance matrix for S1 were significantly closer to the ones for target holo than the ones for apo, whereas in GBP, both the probability distribution and the distance matrix for model S1, holo, and apo were quite similar to each other with similar high correlation coefficients (Table S2). In the case of GBP, by focusing on a limited distance matrix with only ligand-binding-pocket residues (residues colored in red in panel C of Figure S14) as shown in panel-D of Figure S14, the binding pocket structure of S1 seems to be significantly similar to holo than apo; correlation coefficient is 0.85 between S1 and apo, and 0.90 between S1 vs holo (here, the ligand-binding-pocket residue is defined as a residue in which a heavy atom is present at a distance <6.5 Å from the ligand (glutamate) in GBP of the holo state). From the snapshot for model S1, apo, and holo in panel C of Figures S13 and S14, we can confirm that the Cα distances for S1 (20.0 and 9.6 Å) between representative residue pairs 40–149 for ADK and 50–118 for GBP are more similar to the corresponding distances for holo (20.3 and 7.5 Å) than the ones for apo (39.8 and 18.7 Å).
For representative structures S1–S5, we also investigated the probability distributions of the Cα pairwise distance for the entire system (panel A) and for each intradomain, core, LID, and NMP domains for ADK (panel B in Figure S15), and large and small domain for GBP (panel B in Figure S16). From panel A in the figures, it can be confirmed that there was no significant difference of distribution between the entire S1–S5 of GBP, whereas distributions for the entire S1–S5 of ADK were different from each other, reflecting the difference in global topology. On the other hand, from panel B in the figures, the Cα pairwise distributions for sampled structures S1–S5, especially for small distance (<5 Å), appeared to be quite similar to ones for reference (apo) and target (holo) structures regardless of the domain. This means that the realistic and reliable intradomain local structure, which is similar to apo and holo, is held stably even in a broader structure ensemble with adaptive CG-ENM. In addition, from the probability distribution of the intradomain within a distance <8–10 Å, it can be seen that the local structure of the small domain in GBP and those of NMB and LID domains in ADK were also maintained in the almost same way as apo and holo structures, whereas the distributions for other intradomains showed model dependence. This suggests that the structural diversity of S1–S5 is due to localized changes in the specific domain such as the core domain in the case of ADK and the large domain in the case of GBP.
The adaptive CG-ENM sampling for ADK and GBP provides significantly large doughnut-shaped ensemble plots in the PC1–PC2 plane, as seen in panel A of Figures 5 and 6. To comprehend the origin of this shape, we constructed the average structure “AV” using structure ensembles with adaptive CG-ENM. Furthermore, we modeled the neighborhood structures (V1, V2, V3, V4) by adding small perturbations along either of the eigenvector for PC1 or PC2 to average structure: AV. In the PC1–PC2 plane, the coordinates of AV and the perturbated structures {V1, V2, V3, V4} are at {(0, 0), (−1, 0), (1, 0), (0, −1), (0, 1)} for ADK and {(0, 0), (−0.5, 0), (2, 0), (0, −2), (0, 0.5)} for GBP. These modeled structures, {AV, V1, V2, V3, V4}, seem to be located in the central cavity region of a donut-shaped ensemble on the PC1–PC2 plane, as seen in panel A of Figure S17 for ADK and Figure S18 for GBP. From panel D of Figure S17 and panel E of Figure S18, it can be seen that the part of the LID domain for ADK and the small domain of GBP in the modeled structures (AV and V1–V4) are significantly condensed and shrunk. Owing to these partial condensations of the domain structure, the energies of AV and V1–V4 for ADK and GBP are much higher than the ones for whole sampled structures by adaptive CG-ENM and its representative structures S1–S4, as seen in panels B and C of Figures S17 and S18, respectively. Therefore, it is assumed that the energetically higher condensed structures such as AV and V1–V4 near the center of the cavity region could not be spontaneously sampled by adaptive CG-ENM and result in a donut-shaped ensemble in the PC1–PC2 plane.
We also compared adaptive CG-ENM with another two sampling methodologies that can realize modeling hololike structure from apo conformation.31,32 A detailed discussion related to the comparison of sampling performance with other sampling methods is provided in Supporting Information S6.
Application of the New Adaptive CG-ENM to Larger Protein System Integrin αV
Our main motivation to develop the new adaptive CG-ENM was that conducting AA-MD simulations for larger proteins is highly expensive. Therefore, to demonstrate the advantages of the adaptive CG-ENM, we applied our new methodology to a larger biomolecule, the extracellular segment of integrin αV, with a size of 927 residues except for gap regions (the residue size of αV is about 5 times larger than the size of ADK and GBP). As shown in Figure 7A, the V-shape bent structure of integrin αV in the inactive state has been resolved by X-ray crystal structural analysis (PDB-ID = 1JV2);24 integrin αV is mainly composed of five domains: β-propeller (residue ID: 1–438), thigh domain (residue ID: 439–592), linker (residue ID: 593–601), calf-1 domain (residue ID: 602–738), and calf-2 domain (all other residues).
Figure 7.
Reference structures of larger protein integrin αV for the inactive state registered in PDB and DCCM (cij). (A) Experimentally suggested domains are shown in different colors: β-propeller, green; thigh, magenta; linker, gray; calf-1, orange; and calf-2, blue. (B) Colored DCCM in the plane of all residue pairs evaluated based on the short AA-MD trajectories for integrin in the inactive state.
First, using the short-time AA-MD trajectory that is generated by concatenating five trajectories of production AA-MD for 1.5 ns with different initial velocities, we evaluated a DCCM for all residue pairs of integrin αV in the active state (Figure 7B) (see the detailed procedure of AA-MD for integrin in Supporting Information S7). From Figure 7B, it can be observed that the regions with high correlation values in the DCCM correspond well to each domain region experimentally suggested in integrin. This indicates that the DCC analysis based on short-time AA-MD for at most nanosecond order succeeds in appropriately extracting the domain structure even for a larger system such as integrin.
Second, by applying the BO algorithm with a target function FBO as mentioned in the Materials and Methods section, we identified a suitable parameter set (Ks, Kw, Cs, Cw) = (7.0, 1.0, 1.0, 0.8) from a wider parameter space, the combination number of which is 2025. For the larger system (integrin), to accurately evaluate the performance of the parameter searching methods, such as RS and BO, we also conducted investigations similar to ones for ADK and GBP; we repeated 30 trials using randomly selected initial parameter sets and averaged the score ⟨FBO⟩. Figure 8 shows the sampling iteration number dependence of the averaged score over 30 trials. Even for the larger system, integrin, compared with the score obtained by RS, the score ⟨FBO⟩ by BO appeared to smoothly converge before the number of sampling iterations reached a maximum of 50–100. Within a small iteration number (approximately 100), the converged score produced by BO tended to be significantly higher than that produced by RS.
Figure 8.
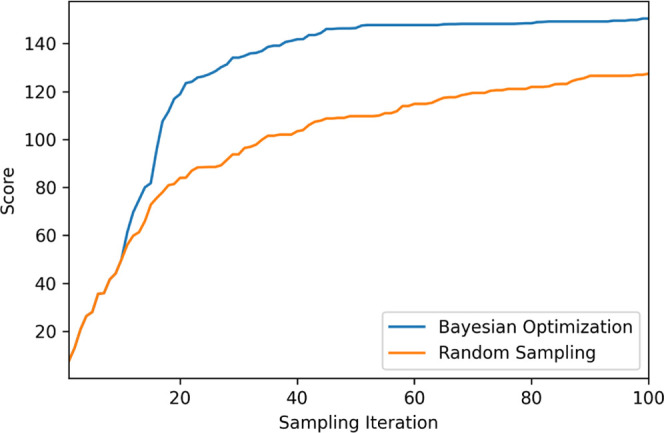
Sampling iteration number dependence of the averaged score ⟨FBO⟩ in exploring suitable parameter sets by Bayesian optimization (BO) and random sampling (RS) for integrin αV. The blue and orange lines correspond to the average scores by BO and RS, respectively.
Third, a productive simulation using adaptive CG-ENM under a suitable parameter set (Ks, Kw, Cs, Cw) = (7.0, 1.0, 1.0, 0.8) was performed to demonstrate the sampling performance of our new methodology. From Figures 9A and S21, it can be seen that the structural ensemble sampled by adaptive CG-ENM (green) for integrin is sufficiently broader than the ensemble of ENM by TREMD (magenta) and those by conventional AA-MD for 50 ns (blue) in the PCA plane, where the vector of PC12 is defined by the ensemble of structures sampled by adaptive CG-ENM. To compare the variety of ensembles quantitatively, we evaluated the surface area of the bounding box for each ensemble in the PCA plane, as shown in Table 2. The surface area for adaptive CG-ENM was significantly larger than that for conventional CG-ENM by TREMD and that for conventional AA-MD. From Figure 9B for the panel of adaptive CG-ENM, it can be confirmed that the broader structural ensemble, including structures that are distant from the initial state, with various RMSDs, angles (between two vectors that represent the direction of the long axis of the thigh domain by γ571 – γ470 and calf-1 domain by γ619 – γ602, where the subscript of the coordinate vector represents the residue ID), and Rg values, is explored while stably preserving the entire structure (the Q-score is significantly higher than 0.9). From Figure 9C, we can confirm that many varieties of structures, including not only reference-like (S7) but also fully extended structures such as S1–S3 with an angle of around 180°, were sampled broadly. This suggests that by implementing adaptive CG-ENM, efficient and broader conformational sampling could be realized even for significantly larger systems like integrin.
Figure 9.
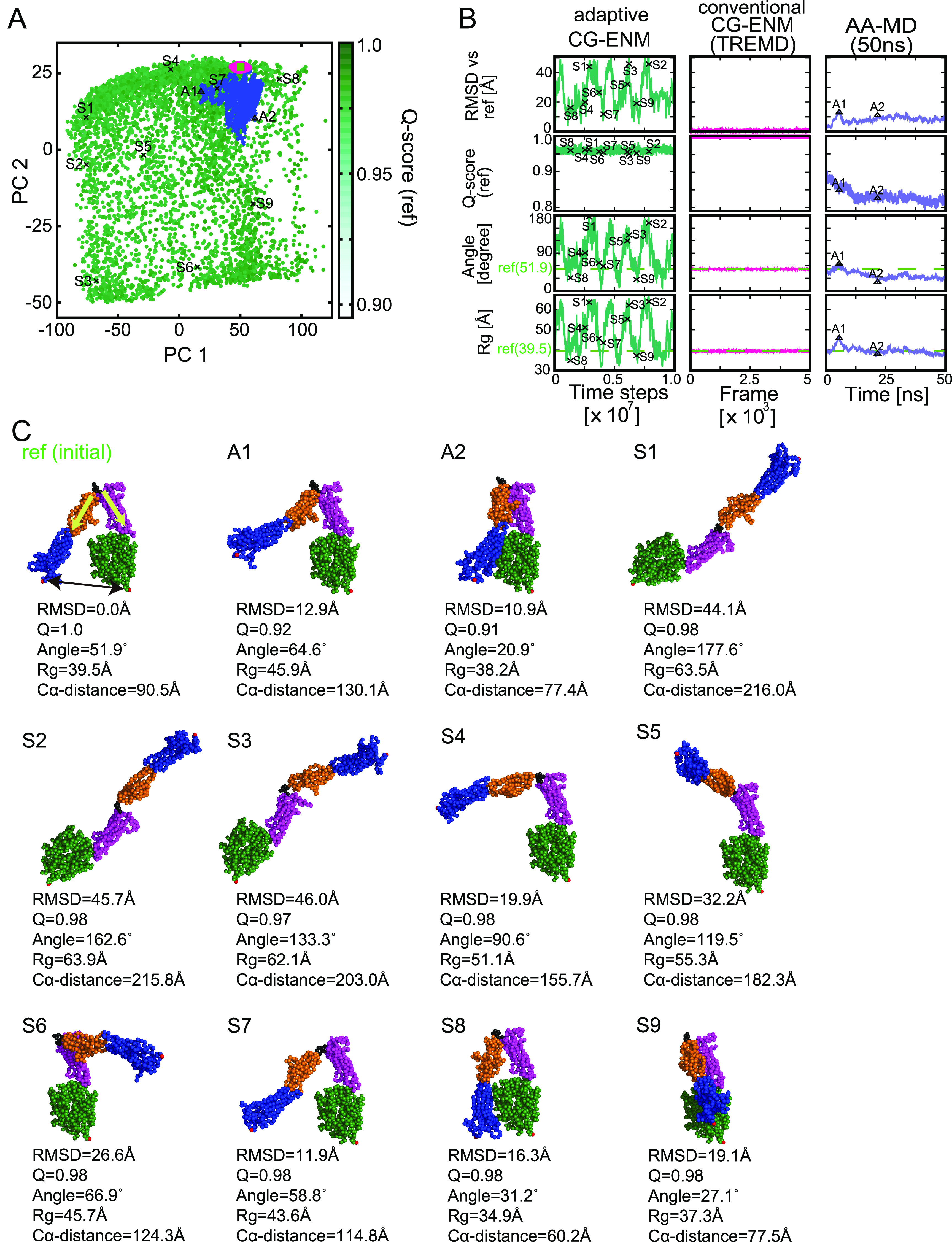
Comparison of the new adaptive ENM with conventional ENM and AA-MD for integrin αV. (A) Comparison of structural ensembles sampled by adaptive ENM, conventional ENM, and AA-MD (50 ns) in the PCA plane, of which PC1 and PC2 axes are defined by the ensemble using adaptive CG-MD. Sampling points for adaptive ENM, ENM(TREMD), and AA-MD (50 ns) are colored green, magenta, and blue, respectively. In particular, green gradation for sampling points of adaptive ENM depends on the Q-score (ref). Reference structures in the inactive state are colored light green (square). (B) Time evolution of RMSD vs reference (ref), Q-score (ref), angle (between two vectors that represent the direction of the long axis of the thigh domain by γ571 – γ470 and calf-1 domain by γ619 – γ602), and Rg for adaptive ENM, conventional ENM, and AA-MD (50 ns). The green dashed lines for angle and Rg correspond to ones for the reference structure, i.e., 51.9° and 39.5 Å, respectively. (C) Structural comparison between initial (inactive state as reference) and representative structures sampled by AA-MD (A1 and A2) and adaptive CG-ENM (S1–S9). The sampling point for each structure (S1–S9, A1–A2) is shown in panels (A) and (B) for adaptive ENM and AA-MD using a black x and triangle. The Cα distance between two residues, 82–764, is depicted by a black arrow in the S1 snapshot, whereas two vectors (γ571 – γ470 and γ619 – γ602) for the angle of V-shape integrin are depicted by yellow arrows.
Table 2. Surface Area of the Bounding Box for Structural Ensemble Points of Integrin Explored by Each Model in the PC12 Plane Defined by the Eigenvector of Adaptive CG-ENMa.
| adaptive CG-ENM | conventional CG-ENM by TREMD | AA-MD (50 ns) | |
|---|---|---|---|
| integrin | 1.00 | 1.65 × 10–3 | 5.60 × 10–2 |
The surface areas of the bounding boxes for AA-MD and conventional CG-ENM by TREMD are normalized by that of adaptive CG-ENM.
Potential and Limitations of Adaptive CG-ENM
Here, we mention the prospect of achieving a wider sampling with adaptive CG-ENM by assigning interactions (spring) according to the value of DCCM based on short-time AA-MD trajectories. Generally, in the biomolecule, the flexible region such as the loop and hinge and the boundary region between interdomains tend to have weak interactions and are likely to dissociate sometimes. However, by only conventional AA-MD, it is difficult to sample the entire process starting from the dissociation of interdomains to large-scale relative motion of multiple domains or hingelike motion because the characteristic time of the corresponding process is assumed to be longer than several microseconds to milliseconds. On the other hand, even with short AA-MD of the order of nanoseconds, the significant difference of DCC between the rigid intradomain, which is stabilized by strong interactions, and interdomain boundary with potential dissociation due to weaker interaction is expected to be sufficiently detected, because DCCM could reflect the localized fluctuation between residues. Therefore, by either weakening or cutting the spring (interaction) between the interdomain boundary with lower DCC based on short-time AA-MD, broader sampling is expected to be enhanced, which includes interdomain dissociation and large-scale motion, the time scale of which may be more than several microseconds to milliseconds.
The type of AA-MD force field may influence the sampling performance of adaptive CG-ENM. For example, the AMBER94 force field tends to stabilize α helix more easily than other force fields.33 Therefore, if by AA-MD with the AMBER94 force field, a stable helix was formed in the hinge, which is the important key region for large-scale structural changes, DCC for the corresponding region may be overestimated due to its rigidity of α helix. In this case, it may be difficult for adaptive CG-ENM simulations to reproduce large-scale conformational changes because a stronger spring would be assigned to residue pairs within the key area in adaptive CG-ENM owing to higher DCC. However, because the time scale of AA-MD for evaluation of DCCM is quite short (at most nanosecond order), the stable α helix is assumed to be seldom formed. Therefore, it is expected that the influence of the type of AA-MD force filed on sampling efficiency will not be so critical for broader sampling with adaptive CG-ENM.
Conclusions
To explore various structures, including those distant from the initial structure extant without any biased force, we developed a new adaptive CG-ENM, in which the interaction strength is assigned depending on DCCM based on the short-time AA-MD trajectory starting from the initial structure. To evaluate the performance of adaptive CG-ENM, we applied the new methodology to ADK and GBP in the apo state. We found that nanosecond-order AA-MD trajectories were sufficient to reveal and discriminate between the rigid and flexible domains of protein systems such as ADK and GBP through DCCM-based analysis. By applying the BO algorithm to search for a suitable parameter set among the vast parameter space of adaptive CG-ENM, we succeeded in reducing the searching cost to approximately 10% of that required by RS and exhaustive sampling. Furthermore, the structural ensembles explored by adaptive CG-ENM could be considerably more diverse than those by long-time AA-MD of 1 μs and by conventional ENM even with enhanced sampling via TREMD. In particular, some of the structures sampled by adaptive ENM did not significantly differ from the target structure in the holo state of ADK and GBP. Finally, as a challenging task, to demonstrate the advantages of the CG model with lower calculation cost, we applied our new methodology to a larger biomolecule, integrin (αV) in the V-shape inactive state. After efficiently exploring suitable parameter set with BO, we sampled various structural ensembles, including not only V-shape bent structures but also extended structures.
In this study, in several structures sampled by adaptive CG-ENM, there is a rare probability that the distance between Cα residues will be <3.8 Å. If AA models were reconstructed based on this sampled CG model, an atomistic collision may occur locally. Therefore, in the future, it will be necessary to develop a refined adaptive CG-ENM model that will prohibit sampling the structures with local collision much as possible by applying the excluded volume interaction to Cα residues. To reduce the probability of atomistic collision in sampled structures, it is also conceivable to increase the threshold related to the Q-score, q0 = 0.8, as high as possible. In future work, by applying software for reconstruction of the AA model, such as PD2ca2main34 and SCWRL4,35 to the explored structures provided by adaptive CG-ENM, it is expected that some reconstructed structures could inform and contribute to practical experiments such as the prediction of an unresolved metastable state.
Acknowledgments
This research was supported by MEXT (Ministry of Education, Culture, Sports, Science and Technology in Japan) through the “Program for Promoting Researches on the Supercomputer Fugaku” (Application of Molecular Dynamics Simulation to Precision Medicine Using Big Data Integration System for Drug Discovery, JPMXP1020200201) and used computational resources of the supercomputer Fugaku provided by RIKEN Center for Computational Science (Project IDs: hp200129, hp210172) and Camphor2 of CRAY XC40 provided by Kyoto University through the High-Performance Computing Infrastructure System Research Project (Project IDs: hp200053 and hp210126). This work was also supported by JSPS KAKENHI (Grant number 19K06535). We would like to thank Dr. Shoji Takada for useful discussions.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.1c01074.
Additional methods including the Q-score: contact fraction of native contact pairs, all-atom molecular dynamics (AA-MD) simulation, conventional coarse-grained (CG)-ENM, CG-MD simulation with underdamped Langevin dynamics, temperature replica exchange MD (TREMD) of conventional CG-ENM, comparison with two enhanced sampling methodologies, detailed information related to the AA-MD procedure for integrin αV in the inactive state, and data related to model performance and application (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Kermani A. A. A Guide to Membrane Protein X-ray Crystallography. FEBS J. 2021, 288, 5788–5804. 10.1111/febs.15676. [DOI] [PubMed] [Google Scholar]
- Shaw D. E.; Deneroff M. M.; Dror R. O.; Kuskin J. S.; Larson R. H.; Salmon J. K.; Young C.; Batson B.; Bowers K. J.; Chao J. C.; Eastwood M. P.; Gagliardo J.; Grossman J. P.; Ho C. R.; Ierardi D. J.; Kolossváry I.; Klepeis J. L.; Layman T.; McLeavey C.; Moraes M. A.; Mueller R.; Priest E. C.; Shan Y.; Spengler J.; Theobald M.; Towles B.; Wang S. C. Anton, a Special-Purpose Machine for Molecular Dynamics Simulation. Commun. ACM 2008, 51, 91–97. 10.1145/1364782.1364802. [DOI] [Google Scholar]
- Fujita K.; Iwaki M.; Iwane A. H.; Marcucci L.; Yanagida T. Switching of Myosin-V Motion between the Lever-Arm Swing and Brownian Search-and-Catch. Nat. Commun. 2012, 3, 956 10.1038/ncomms1934. [DOI] [PubMed] [Google Scholar]
- Kenzaki H.; Koga N.; Hori N.; Kanada R.; Li W.; Okazaki K.; Yao X.-Q.; Takada S. CafeMol: A Coarse-Grained Biomolecular Simulator for Simulating Proteins at Work. J. Chem. Theory Comput. 2011, 7, 1979–1989. 10.1021/ct2001045. [DOI] [PubMed] [Google Scholar]
- Clementi C.; Nymeyer H.; Onuchic J. N. Topological and Energetic Factors: What Determines the Structural Details of the Transition State Ensemble and “En-Route” Intermediates for Protein Folding? An Investigation for Small Globular Proteins. J. Mol. Biol. 2000, 298, 937–953. 10.1006/jmbi.2000.3693. [DOI] [PubMed] [Google Scholar]
- Takada S.; Kanada R.; Tan C.; Terakawa T.; Li W.; Kenzaki H. Modeling Structural Dynamics of Biomolecular Complexes by Coarse-Grained Molecular Simulations. Acc. Chem. Res. 2015, 48, 3026–3035. 10.1021/acs.accounts.5b00338. [DOI] [PubMed] [Google Scholar]
- Tirion M. M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett. 1996, 77, 1905 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
- Li W.; Wolynes P. G.; Takada S. Frustration, Specific Sequence Dependence, and Nonlinearity in Large-Amplitude Fluctuations of Allosteric Proteins. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 3504–3509. 10.1073/pnas.1018983108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W.; Terakawa T.; Wang W.; Takada S. Energy Landscape and Multiroute Folding of Topologically Complex Proteins Adenylate Kinase and 2ouf-Knot. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 17789–17794. 10.1073/pnas.1201807109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W.; Wang W.; Takada S. Energy Landscape Views for Interplays among Folding, Binding, and Allostery of Calmodulin Domains. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, 10550–10555. 10.1073/pnas.1402768111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okazaki K. -i.; Koga N.; Takada S.; Onuchic J. N.; Wolynes P. G. Multiple-Basin Energy Landscapes for Large-Amplitude Conformational Motions of Proteins: Structure-Based Molecular Dynamics Simulations. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 11844–11849. 10.1073/pnas.0604375103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi C.; Matsunaga Y.; Koike R.; Ota M.; Sugita Y. Domain Motion Enhanced (DoME) Model for Efficient Conformational Sampling of Multidomain Proteins. J. Phys. Chem. B 2015, 119, 14584–14593. 10.1021/acs.jpcb.5b07668. [DOI] [PubMed] [Google Scholar]
- Yao X.-Q.; Kimura N.; Murakami S.; Takada S. Drug Uptake Pathways of Multidrug Transporter AcrB Studied by Molecular Simulations and Site-Directed Mutagenesis Experiments. J. Am. Chem. Soc. 2013, 135, 7474–7485. 10.1021/ja310548h. [DOI] [PubMed] [Google Scholar]
- Zheng W.; Doniach S. A Comparative Study of Motor-Protein Motions by Using a Simple Elastic-Network Model. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 13253–13258. 10.1073/pnas.2235686100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moritsugu K.; Smith J. C. REACH Coarse-Grained Biomolecular Simulation: Transferability between Different Protein Structural Classes. Biophys. J. 2008, 95, 1639–1648. 10.1529/biophysj.108.131714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCammon J. A. Protein Dynamics. Rep. Prog. Phys. 1984, 47, 1–46. 10.1088/0034-4885/47/1/001. [DOI] [Google Scholar]
- Kasahara K.; Fukuda I.; Nakamura H. A Novel Approach of Dynamic Cross Correlation Analysis on Molecular Dynamics Simulations and Its Application to Ets1 Dimer–DNA Complex. PLoS One 2014, 9, e112419 10.1371/journal.pone.0112419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahriari B.; Swersky K.; Wang Z.; Adams R. P.; de Freitas N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. 10.1109/JPROC.2015.2494218. [DOI] [Google Scholar]
- Ueno T.; Rhone T. D.; Hou Z.; Mizoguchi T.; Tsuda K. COMBO: An Efficient Bayesian Optimization Library for Materials Science. Mater. Discovery 2016, 4, 18–21. 10.1016/j.md.2016.04.001. [DOI] [Google Scholar]
- Terayama K.; Tsuda K.; Tamura R. Efficient Recommendation Tool of Materials by an Executable File Based on Machine Learning. Jpn. J. Appl. Phys. 2019, 58, 098001 10.7567/1347-4065/ab349b. [DOI] [Google Scholar]
- Müller C.; Schlauderer G.; Reinstein J.; Schulz G. Adenylate Kinase Motions during Catalysis: An Energetic Counterweight Balancing Substrate Binding. Structure 1996, 4, 147–156. 10.1016/S0969-2126(96)00018-4. [DOI] [PubMed] [Google Scholar]
- Sun Y.-J.; Rose J.; Wang B.-C.; Hsiao C.-D. The Structure of Glutamine-Binding Protein Complexed with Glutamine at 1.94 Å Resolution: Comparisons with Other Amino Acid Binding Proteins. J. Mol. Biol. 1998, 278, 219–229. 10.1006/jmbi.1998.1675. [DOI] [PubMed] [Google Scholar]
- Sugita Y.; Okamoto Y. Replica-Exchange Molecular Dynamics Method for Protein Folding. Chem. Phys. Lett. 1999, 314, 141–151. 10.1016/S0009-2614(99)01123-9. [DOI] [Google Scholar]
- Xiong J.-P.; Stehle T.; Diefenbach B.; Zhang R.; Dunker R.; Scott D. L.; Joachimiak A.; Goodman S. L.; Arnaout M. A. Crystal Structure of the Extracellular Segment of Integrin AVβ3. Science 2001, 294, 339–345. 10.1126/science.1064535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi G.; Lee R.; Hayward S. A Comprehensive and Non-Redundant Database of Protein Domain Movements. Bioinformatics 2005, 21, 2832–2838. 10.1093/bioinformatics/bti420. [DOI] [PubMed] [Google Scholar]
- Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- Lindorff-Larsen K.; Piana S.; Palmo K.; Maragakis P.; Klepeis J. L.; Dror R. O.; Shaw D. E. Improved Side-Chain Torsion Potentials for the Amber Ff99SB Protein Force Field. Proteins 2010, 78, 1950–1958. 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. B.; Hummer G.; Eaton W. A. Native Contacts Determine Protein Folding Mechanisms in Atomistic Simulations. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 17874–17879. 10.1073/pnas.1311599110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Motoyama Y.; Tamura R.; Yoshimi K.; Terayama K.; Ueno T.; Tsuda K.. Bayesian Optimization Package: PHYSBO. 2021, arXiv:2110.07900. arXiv.org e-Print archive. https://arxiv.org/abs/2110.07900.
- Barber C. B.; Dobkin D. P.; Huhdanpaa H. The Quickhull Algorithm for Convex Hulls. ACM Trans. Math. Software 1996, 22, 469–483. 10.1145/235815.235821. [DOI] [Google Scholar]
- Seeliger D.; de Groot B. L. Conformational Transitions upon Ligand Binding: Holo-Structure Prediction from Apo Conformations. PLoS Comput. Biol. 2010, 6, e1000634 10.1371/journal.pcbi.1000634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dokainish H. M.; Sugita Y. Exploring Large Domain Motions in Proteins Using Atomistic Molecular Dynamics with Enhanced Conformational Sampling. Int. J. Mol. Sci. 2021, 22, 270 10.3390/ijms22010270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoda T.; Sugita Y.; Okamoto Y. Comparisons of Force Fields for Proteins by Generalized-Ensemble Simulations. Chem. Phys. Lett. 2004, 386, 460–467. 10.1016/j.cplett.2004.01.078. [DOI] [Google Scholar]
- Moore B. L.; Kelley L. A.; Barber J.; Murray J. W.; MacDonald J. T. High-Quality Protein Backbone Reconstruction from Alpha Carbons Using Gaussian Mixture Models. J. Comput. Chem. 2013, 34, 1881–1889. 10.1002/jcc.23330. [DOI] [PubMed] [Google Scholar]
- Krivov G. G.; Shapovalov M. V.; Dunbrack R. L. Improved Prediction of Protein Side-Chain Conformations with SCWRL4. Proteins 2009, 77, 778–795. 10.1002/prot.22488. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.