Abstract
Growing experimental evidence indicates that topological defects could serve as organizing centers in the morphogenesis of tissues. Here, we provide a quantitative explanation for this phenomenon, rooted in the buckling theory of deformable active polar liquid crystals. Using a combination of linear stability analysis and computational fluid dynamics, we demonstrate that active layers, such as confined cell monolayers, are unstable to the formation of protrusions in the presence of disclinations. The instability originates from an interplay between the focusing of the elastic forces, mediated by defects, and the renormalization of the system’s surface tension by the active flow. The posttransitional regime is also characterized by several complex morphodynamical processes, such as oscillatory deformations, droplet nucleation, and active turbulence. Our findings offer an explanation of recent observations on tissue morphogenesis and shed light on the dynamics of active surfaces in general.
Far from being mere imperfections, topological defects can help tissues develop features such as tentacles and protrusions.
INTRODUCTION
The development of multicellular organisms crucially hinges on internal and external mechanical cues, which are transduced by the mechanosensing machinery of cells to give rise to system-wide spatiotemporal rearrangements and, eventually, to the formation of early embryonic features (1, 2). These processes comprise a vast spectrum of active and passive forces, whose regulation relies not only on the molecular repertoire of tissue-forming cells but also on their shape, motility, and local organization. In the past decade, the conceptual framework of active matter (3)—namely, materials whose building blocks can autonomously move and perform mechanical work—has enormously contributed to classify the arsenal of physical mechanisms behind force generation and collective migration in both eukaryotes and prokaryotes. However, how these physical mechanisms can be harnessed to achieve biological functionality remains a major open question at the crossroads between developmental biology and mechanics (4–7).
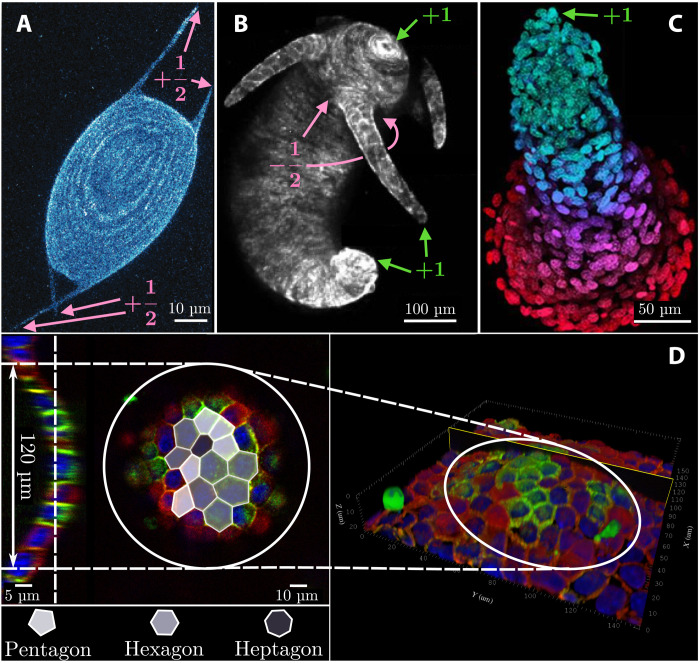
One of the most fascinating hypotheses in this respect revolves around the possibility that multicellular systems could take advantage of topological mechanisms to create the conditions, in terms of reproducibility and robustness, for the origin and maintenance of life. In particular, defects have recently been identified by several in vitro studies as potential candidates for the role of “topological morphogens” in various biomimetic systems and model organisms. Keber et al. (8), for instance, demonstrated that protocells, consisting of a single layer of microtubule-kinesin active nematic liquid crystal enclosed in a lipid vesicle and powered by adenosine triphosphate, relieve the mechanical stress, originating from the presence of four topologically required +1/2 disclinations, by growing persistent tubular protrusions (Fig. 1A). More recently, the same mechanism has been invoked in experimental (9–12) and theoretical (4, 13, 14) studies to explain the growth and regeneration of tentacles in Hydra (Fig. 1B). The accumulation of extensile stresses in proximity of integer and semi-integer disclinations has also been proposed by Saw et al. (15) as a strategy to achieve cell apoptosis and extrusion in epithelial layers [see also (16, 17) for recent supporting evidence from simulations] and, more recently, by Guillamat et al. (18) as a route to the formation of multicellular protrusions in confined myoblasts (Fig. 1C). Long before the importance of defects for the development of nonplanar features in tissues had been recognized, blister-like hemicysts—also known as “domes”—were already routinely observed in many epithelial cell cultures derived from renal cell lines [see, e.g., (6, 19, 20)]. An example of a dome, obtained from a monolayer of epithelial Madin-Darby Canine Kidney (MDCK) cells, was reproduced here and is shown in Fig. 1D (see also movies S1 and S2 and fig. S1). The central region of this dome, where the curvature is larger than elsewhere, features a multitude of topological defects (i.e., five- and seven-sided cells) with net positive topological charge: i.e., ∑i ∈ dome(6 − ci) > 0, with ci the number of sides of the ith cell. That is, the system exhibits an excess of positive disclinations (i.e., five-sided cells) where its curvature is maximal. This observation (see sections S1 and S2 for further experimental evidence) suggests the possibility that, similar to the other examples illustrated above, the formation of cellular domes could be facilitated by topological defects in combination with other system-specific mechanism, such as the injection of fluid under the cell layer, which results in a focal detachment (21, 22).
Fig. 1. Examples of morphogenic events in the presence of topological defects.
(A) Active nematic protocell consisting of a monolayer of microtubules and kinesin enclosed in a lipid vesicle. The four topologically required +1/2 defects deform the lipid envelope, thereby creating tubular protrusions [adapted from (8)]. (B) Example of Hydra featuring +1 disclinations in proximity of the mouth, the foot, and the tip of each tentacle and two −1/2 defects at the base of each tentacle [adapted from (11)]. (C) Multicellular protrusion in layers of collectively migrating myoblasts, featuring a +1 disclination at the tip [adapted from (18)]. (D) Example of a dome obtained from an initially flat monolayer of cultured MDCK GII cells. The central region of the dome, where the curvature is larger than elsewhere, hosts several topological defects (i.e., five- and seven-sided cells), with a net positive topological charge. On the left-hand side, a cross section and a top view of the dome with a superimposed tessellation are shown (red, F-actin; green, E-cadherin; blue, nuclei).
Whereas these experimental studies have now convincingly shown the existence of a correlation between topological defects and certain morphogenic events, a clear theoretical picture of the mechanical nature of this behavior is still missing. Here, we address this conceptual deficit. Using a combination of classical differential geometry, linear stability analysis, and computational fluid dynamics, we demonstrate that confined active layers, here modeled as active polar liquid crystals, are unstable to the formation of protrusions in the presence of a +1 disclination. In extensile systems with positive flow alignment, the instability originates from an interplay between the focusing of elastic forces, mediated by the defect, and a renormalization of the system’s surface tension by the active flow, arising in response to the perpetual injection of active stress under confinement. In the posttransitional phase, such competition leads to additional dynamical regimes, which includes oscillatory deformations, the nucleation of droplets, and a turbulent state with proliferating protrusions. By contrast, in contractile systems, the same phenomenon stabilizes the flat configuration, thus preventing the formation of protrusions.
A precise account of all the examples of defect-mediated morphogenesis illustrated in Introduction requires, in principle, a great deal of biophysical details and a case-by-case approach. However, their very diversity suggests the existence of a general underlying mechanism. Our goal is to identify and rationalize this mechanism in the simplest possible setting, thus making it amenable for an in-depth analytical description.
RESULTS
The model
Our model layer consists of a thin film of active polar or nematic liquid crystal, whose midsurface ℳ is spanned by the unit normal n and the pair of orthogonal tangent vectors gi, with i = 1,2, and gij = gi · gj the associated metric tensor. The mean and Gaussian curvatures are denoted by H and K, respectively [see Fig. 2A and, e.g., (23)]. The local average orientation of the cells is described by the unit vector p = pigi, with ∣p∣2 = pipi = 1. The system free energy is given by
| (1) |
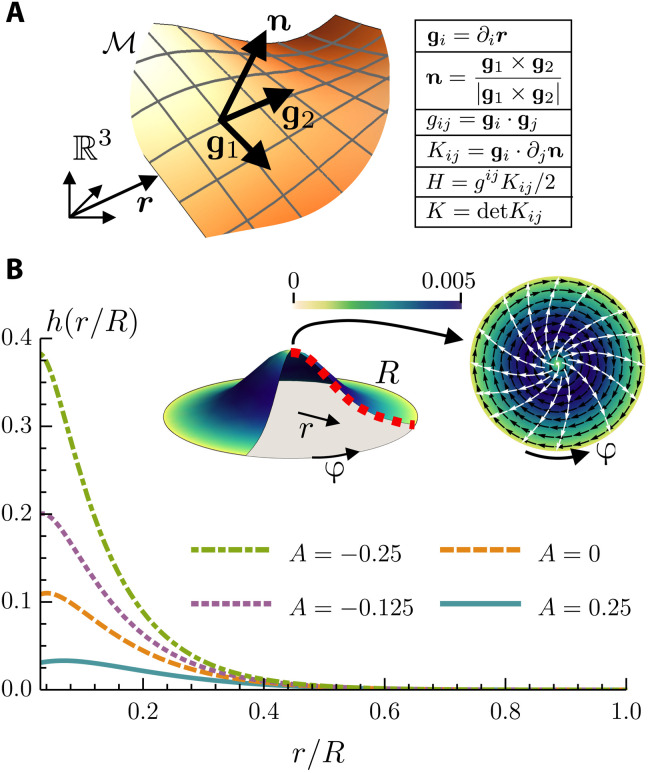
Fig. 2. Post-buckling geometry of layer.
(A) Sketch of the midsurface ℳ embedded in ℝ3. In the table, the cross and the dot refer to the vector and scalar product, respectively, with respect to the Euclidean metric of ℝ3. In the figure and throughout the article, bold letters indicate ℝ3 vectors, and Latin indices indicate surface coordinates on ℳ. The coordinate system on ℳ is denoted by {g, n}, and it defines the metric gij and the curvature tensor Kij of the surface, hence the mean curvature H and Gaussian curvature K. (B) In the top middle, a sketch of the buckled surface with a +1 defect at the center. The disk on the top right is a view from the top. The black arrows are the azimuthal velocity field, the color scale is its magnitude, and the white arrows are the director field. In addition, we solved Eqs. 2 and 3 numerically to plot the height profile h(r/R) of the surface for different values of the active number . Comparing the active with the passive (A = 0) case, we see how an extensile activity (A < 0) favors the buckling, while a contractile one activity inhibits it. The values of the constants used are the following: γ = 0.012, Γ = 1, λ = 1.1, κF = 0.02, κB = 0.01, and η = 5/3.
The first three terms on the right-hand side of Eq. 1 account for the energetic cost of deformations of the midsurface, where γ is the surface tension, κB is the bending rigidity, and κG is the Gaussian splay modulus (24). The last term, on the other hand, is the Frank free energy (25) expressing the compliance of the system to a local distortion of the cellular polarization, with ∇i denoting covariant differentiation and κF denoting the rotational stiffness in the one-elastic-constant approximation.
The steady state that we aim at describing comprises a dense population of cells freely translating and rotating along a stationary midsurface ℳ. The former requirements amount to the following set of hydrodynamic equations for p and the momentum density ρv = ρvigi on the tangent plane (26–29)
| (2a) |
| (2b) |
The total cellular mass M = ∫ dA ρ is assumed to be constant in time, although the number of cells could, in principle, fluctuate as a consequence of cell division and apoptosis. Thus ρ = const and ∇ivi = 0. This assumption is justified by the fact that, in cellular systems, the speed v of migrating cells is orders of magnitude lower than the speed of sound cs. Because the typical magnitude of density fluctuations is δρ ∼ Ma2, with Ma = v/cs the Mach number, this implies, to first approximation, δρ ≈ 0. The three terms on the right-hand side of Eq. 2a correspond, respectively, to the hydrodynamic stress tensor —where Ph is the pressure, η is the shear viscosity, and uij = (∇ivj + ∇jvi)/2 is the strain-rate tensor—the active stress and the force per unit length , originating from the distortion induced by defects and Gaussian curvature and driving the so-called elastic “backflow” (30). The latter can be derived from expressing the polarization gradients in terms of the geometric potential χ, subject to the Poisson equation ∇2χ = K − ρd, where ρd is the topological charge density (29, 31–33). Explicitly, (see the Supplementary Materials). Thus, at equilibrium, ρd ∼ K, so that defects place themselves in regions of like-sign Gaussian curvature to minimize the elastic free energy (33). Last, the active stress tensor embodies the contribution of the force dipoles autonomously generated by the cells and, following a standard construction, can be expressed as (3, 34–37). The phenomenological constant α quantifies the magnitude of the cellular forces and is positive (negative) for contractile (extensile) systems.
Equation 2b governs the rotational dynamics of the cells, which, in turn, is dictated by the coupling with the local flow field, expressed by the first two terms on the right-hand side of the equation, with λ the flow alignment parameter and ωij = (∇ivj − ∇jvi)/2 the vorticity tensor. The last term is the molecular field hi = − δF/δpi = κF∇2pi, which drives the system toward the ground state of the free energy, with Γ−1 the rotational viscosity [see, e.g., (25)].
Last, the stationarity of the midsurface ℳ requires the net force acting along the normal direction n to vanish, hence
| (3) |
where Kij is the curvature tensor (see Fig. 2A). The normal forces per unit length and on the left-hand side of Eq. 3 are found from minimizing the free energy F (see the Supplementary Materials) and are given by and (29, 38–41). We stress that Eq. 3 reduces to the Helfrich shape equation, , in the limit α = κF = 0 (23, 38), and to the van Kármán equation, , in the limit α = κB = 0 (42, 43).
Stability of defective active layers: Topology, geometry, and morphogenesis
In this section, we investigate how topological defects and activity conspire to render an initially flat layer unstable to the growth of protrusions. While Eqs. 2a, 2b, and 3 hold for arbitrary conformations of the midsurface ℳ, here, we consider the simpler case of an axisymmetric surface and a liquid crystal with polar symmetry, where the local polarization and velocity fields depend solely on the distance r ≤ R from the symmetry axis, with R the radius of the layer: i.e., p = p(r) and v = v(r). Under this assumption, the polarization field inevitably features a +1 topological defect at the center of the system. Thus, taking ρd = 2πδ(r), with δ( · ) a delta function on ℳ, and setting χ = 0 at r = R without loss of generality, the geometric potential can readily be found to be χ = − log (r/R).
To make progress, we parameterize the midsurface ℳ in a Monge patch, so that the position r = r(r, φ) of a generic point is given by r = rgr + hez, with ez a unit vector in the z direction and h = h(r) the height. Following a standard approach of membrane physics [see, e.g., (23)], we then assume that ∣∇h∣≪1, so that one can ignore terms of order 𝒪(∣∇h∣2) and higher in Eqs. 2 and 3. Under such a small gradient approximation, gij ≈ δij, H ≈ −∇2h/2, K ≈ 0, and Eq. 2 reduce to their flat counterpart. Moreover, axial symmetry and incompressibility yield vr = 0, so that v = 1/r vφgφ with vφ = vφ(r) and p = cos ϵ gr + 1/r sin ϵ gφ with ϵ a constant and (r, φ) polar coordinates on the h = 0 plane. Solving Eq. 2b, we find ϵ = ± arccos (−1/λ)/2 under the assumption that ∣λ∣ > 1. Similarly, neglecting unimportant inertial terms (44) and solving Eq. 2a for no-slip boundary conditions gives, after standard algebraic manipulations [see, e.g., (45–47)]
| (4a) |
| (4b) |
consistent with a classic result by Kruse et al. (45). It is worth stressing that, by virtue of Eq. 4b, the pressure nominally diverges at the origin, where the +1 defect is located. Similar to other divergences stemming from the continuous description of defects, however, this one too can be regularized by introducing the coherence length ℓc, setting the short length scale cutoff at which the continuous theory breaks down, because the magnitude of the polarization field, here assumed to be constant, drops in proximity of a defect. Thus, ℓc ≤ r ≤ R. Last, replacing Eq. 4 in Eq. 3 gives a stability condition for the flat conformation of the midsurface ℳ in the form of a fourth-order linear partial differential equation with position-dependent coefficients
| (5) |
where γeff = γ − Ph and κeff = κF + αr2/(2λ) are the effective surface tension and Frank’s elastic constant, respectively, which include the renormalization resulting from the active flow. Note that the velocity field does not enter Eq. 5 explicitly, as the term Kijuij vanishes identically. Moreover, ℳ is clamped at the boundary such that h and all its derivatives vanish at r = R. We stress that the assumption of rotational symmetry restricts us to the low-activity regime. Upon increasing the activity, the system would eventually enter a turbulent regime, thereby losing its spatial symmetry. Evidently, this regime cannot be captured by our solution.
Now, to gain insight into the stability of the system with respect to the formation of protrusions, we separately consider three limit cases, namely, (i) κB = 0 and α = 0, (ii) κB = 0 and α ≠ 0, and (iii) κB ≠ 0 and α ≠ 0. From a physical perspective, the first two cases correspond to layers of passive and active subunits, respectively, whose elastic stiffness is sufficiently small to be considered negligible, but where surface tension penalizes an increase in the area. The vanishing bending modulus, in particular, renders highly curved features, such as kinks or cusps, energetically acceptable. The first scenario has been considered by Frank and Kardar (48) and corresponds to the case of a passive liquid-crystalline disk-like interface plagued by a +1 disclination in the center. In this case, Eq. 5 can be integrated exactly, to give
| (6) |
with . Because of our boundary conditions for h, this equation admits a nontrivial solution only if . Even Eq. 3 is exactly integrable in this case, and ℳ is found to be a parabolic pseudosphere—namely, a surface of constant negative Gaussian curvature—whose height and mean curvature diverge as r → 0 (48). Similarly, in the second scenario, Eq. 5 reduces to Eq. 6, but with Rc given by the solution of the transcendental equation . As in the previous case, we find that there is a nontrivial solution only if R > Rc, thus the flat conformation becomes unstable to the growth of protrusions when the radius R of the active layer exceeds the critical radius
| (7) |
Equivalently, for fixed R values, Eq. 7 provides a threshold in ∣α∣, above which the layer becomes unstable to buckling. Note that, for λ > 1, the activity reduces (increases) the effective surface tension in the presence of contractile (extensile) stresses and vice versa for negative λ [see also (41)]. Conversely, if γ ≤ α/(2λ), then Eq. 7 has no nontrivial solutions, and the flat solution is always stable.
Last, in the third and most generic scenario, Eq. 5 cannot be reduced to Eq. 6, and one cannot find a stability criterion as simple as that expressed by Eq. 7. However, as for the passive instability discussed in (48), we expect the bending stiffness κB to merely renormalize Frank’s elastic constant κF. In addition, a finite bending rigidity makes cusps, kinks, and other singularities characterized by a diverging curvature energetically prohibitive; hence, we expect the tip of the protrusion to become increasingly smooth with increasing κB. To substantiate the latter statement, we have lifted the small gradient approximation and numerically integrated Eqs. 2 and 3 on an axisymmetric surface. The equations do not decouple in this limit; therefore, it is not possible to condense them in a single equation for the height h. However, one finds from the incompressibility equation and with p = 1/g cos ϵ gr + 1/r sin ϵ gφ, where , that v = 1/r vφgφ, and the angle ϵ as well as the pressure Ph are left unchanged. The remaining fields, vφ and h, can be numerically computed, and h is shown in Fig. 2B for different values of activity. Note that the solutions found for vφ are essentially identical to the analytical solutions obtained using the small gradient expansion.
In summary, the presence of a +1 defect renders the planar configuration of an active polar layer unstable to buckling. The instability arises from the fact that the defect introduces an angular deficit in the orientation of the polarization field that a like-sign Gaussian curvature can compensate, thereby mitigating the distortion sourced by the defect (33). Despite having a passive origin, this instability is affected by the hydrodynamic flow fueled by the layer’s extensile or contractile activity. This flow changes the later pressure acting on an arbitrary fluid patch, resulting in an additional compression (for extensile activity) or stretching (for contractile activity) of the layer, which, in turn, inevitably interferes with how the layer itself deforms out of plane, thus making the system respectively more or less probe to buckling.
Buckling, oscillatory regime, and droplet nucleation
The interplay between defect-mediated stress focusing and the elasticity of the active layer, illustrated in the previous section, is a notable example of how the interplay between the topology of the polarization field and the geometry of the flow cooperatively render an initially flat layer unstable to the growth of protrusions. In this section, we look at the evolution of the instability to unveil how topological defects influence the morphology of the protrusion in the post-buckling scenario. To this end, we numerically simulate an active polar layer, whose thickness ξ is comparable in magnitude with the coherence length ℓc, which, in turn, represents the shortest length scale in our continuum description. The active layer is sandwiched between two Newtonian fluids, whose relative concentration is described by the phase field ϕ = ϕ(r) (49, 50). In the limit ξ → 0, the simulated interface can be factually interpreted as the midsurface ℳ of “The model” section (13, 51). A description of the model is provided in Materials and Methods and the Supplementary Materials. We numerically integrate the three-dimensional (3D) hydrodynamic equations of this diffuse interface model in a cylindrical container with homeotropic boundary conditions along the base, so that the equilibrium configuration in the absence of activity is stationary and characterized by a +1 disclination at the center of the disk. The interface is slightly deformed at the defect position to accommodate the tendency of the liquid crystal to escape in the normal direction. Outside the defect core ℓc, the interface is flat, in agreement with our analytical prediction in “Stability of defective active layers: Topology, geometry, and morphogenesis” section, since, in the absence of activity, we have buckling only in a disk of radius . In the following, we will restrict our analysis to extensile systems as we find that contractile ones do inhibit a buckling instability, in agreement with what is predicted by our analytical argument. The main control parameters that we varied in our numerical experiments are (i) the dimensionless activity and (ii) the reduced surface tension Σ = γℓc/κF.
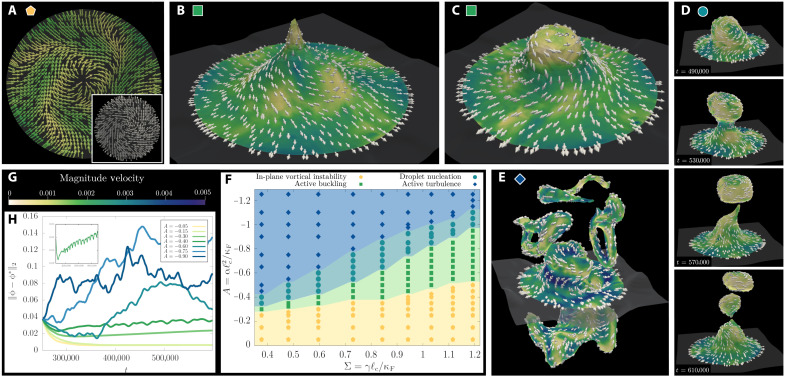
As the dimensionless activity A is increased, four different regimes are encountered. At small A values, the surface is flat, whereas the polarization evolves into a spiral configuration coupled to a vortex flow (Fig. 3A), in agreement with our prediction in “Stability of defective active layers: Topology, geometry, and morphogenesis” section and (45). As activity is further increased, the interface undergoes a buckling instability (light green squares in Fig. 3F), which results in the development of a protrusion, featuring a +1 defect at the tip. Thanks to our computational approach, we notice that once the instability is set by the previously described competition between defect-mediated stress focusing and elasticity, the development of nonplanar features is further facilitated by the lengthening of the vortical flow field out of plane, a process called vortex stretching, which occurs in 3D fluids as the result of conservation of angular momentum (52). The transition line between the flat and buckled configurations in the phase diagram of Fig. 3F shows a linear behavior in the A − Σ plane, consistent with the analytical criterion expressed by Eq. 7.
Fig. 3. Dynamical regimes in active layers.
(A to E) Defect-mediated buckling and activity-driven shape deformations of an active polar layer obtained from numerical simulations (see “Buckling, oscillatory regime, and droplet nucleation” section). The corresponding phase diagram is shown in (F). In all simulations, we fix the dimensionless surface tension Σ = 0.6 and vary the dimensionless activity A. The white vectors mark the polarization field, while the color code in (G) refers to the local magnitude of the flow. At small activity (yellow pentagon in the phase diagram), we find a vortical flow structure, and the interface is flat outside the defect core. This is illustrated in (A), where A = − 0.2 and the inset shows the spiral pattern in the polarization field. Beyond the threshold of the buckling instability (green squares), the layer attains a funnel-like profile with the topological defect at the end of the hollow; this is shown in (B). At slightly higher activity, just below the transition to the region of droplet production (A = − 0.4), we find that the interface begins to oscillates between this funnel-like state and the configuration shown in (C). Next, in (D), we show snapshots taken at different times during the process of droplet nucleation at A = − 0.55 (cyan circles). Last, in (E), we show a chaotic configuration of the layer in the active turbulent regime (A = − 1.0, blue diamonds). (H) The time evolution of the normalized distance in the L2 space between the simulated profile of the phase field ϕ and the equilibrium one, ϕ* = tanh (z/ξ), with ξ the equilibrium interface width between the two isotropic fluids and z the coordinate in the direction normal to the interface. The inset on the top left in (H) refers to the case at A = − 0.4 and shows the periodic oscillations between the configurations of (B) and (C) for A = − 0.4 in terms of the normalized L2 distance.
The competition between active and elastic stresses may eventually give rise to large perturbations around the stationary cuspidal profile, with the surface oscillating from the singular configuration with negative curvature of Fig. 3B to the smooth configuration of Fig. 3C. The dynamic of the oscillations can be captured by measuring the temporal evolution of the distance of the simulated interface from the flat configuration, shown in Fig. 3H, and its inset for the case at A = −0.4 and Σ = 0.6 (see also movie S3). The frequency of the oscillation linearly increases with ∣α∣ along the transition line, which can be rationalized either by dimensional analysis or from the balance of nonequilibrium stresses and viscous ones. This oscillatory instability lies at the heart of another notable behavior, which is observed when activity is further increased. In this case, the surface’s entropic elasticity is no longer able to counteract the active stresses fueling the growth of the protrusion (top panels in Fig. 3D and movie S4). This results in a steady increase of the passive stresses along the protrusion, which eventually results in the breaking of the interface and the consequent nucleation of a droplet (bottom panels in Fig. 3D and movie S4). The emulsified droplets are therefore enclosed in a thin active polar shell, which separates the interior of the droplet from the outer Newtonian fluid. For each droplet, the polarization field develops two boojums (i.e., +1 defects) as required by the Gauss-Bonnet theorem.
In the limit of very large activity (blue diamonds in Fig. 3F), the dynamics becomes fully chaotic, a regime which is known as active turbulence in the literature (26, 44, 53, 54). The active layer is characterized by the proliferation of many amorphous protrusions (see Fig. 3E and movie S5), which elongate under the straining effect of bending deformations in the polarization pattern. A similar chaotic state is also observed for very large contractile activity.
Last, we stress that the results in “Stability of defective active layers: Topology, geometry, and morphogenesis” section are quantitatively unchanged by the frictional interaction between active layer and the surrounding Newtonian fluid, which the diffused interface model summarized in this section naturally accounts for. This can be understood by the fact that, at low Reynolds number, such an interaction gives rise to a damping force ff = − ζv, with ζ a drag coefficient, in the active layer (55). This, in turn, introduces an additional length scale, i.e., , reflecting the competition between viscous (i.e., momentum conserving) and frictional dissipation. That is, for distances smaller than ℓf, friction does not produce substantial effects, and momentum is approximately conserved as in the absence of friction. By contrast, at distances larger than ℓf, frictional dissipation takes over, and the momentum density decays exponentially. Because the defect-mediated buckling transition discussed here is highly localized around the defect core, friction will not produce any substantial change, unless the coefficient is unrealistically large.
DISCUSSION
Here, we elucidated how the interplay between topology, geometry, and hydrodynamics enables the development of nonplanar features in active liquid crystals, as recently observed in experiments on biological and biomimetic systems and, more prominently, in eukaryotic cell layers (Fig. 1) (9–12). Whereas the amount of biochemical detail necessary for a thorough account of all aspects of this phenomenon often results in a complex tangle that hinders fundamental understanding, here, we followed a more generic approach, by focusing on the dynamics at the mesoscopic scale and retaining only the orientational and elastic degrees of freedom that all realizations of defect-mediated morphogenesis have in common.
By looking at an axisymmetric surface plagued in the center by a +1 disclination, we analytically demonstrated that defective active layers with liquid crystalline order are unstable to out-of-plane deformations and obtained a stability criterion in terms of system size, orientational stiffness, surface tension, and active stresses. This mechanism allows defects to serve as topological morphogenes for the formation of nonplanar features, such as domes and protrusion. Such an instability originates from the competition between the focusing of the elastic forces, mediated by defects, and the renormalization of the system’s surface tension by the active flow. Upon modeling the cell layer as a diffuse active polar interface and turning to computational fluid dynamics, we further investigated the posttransitional regime and constructed an exhaustive phase diagram. At low activity, we recover the results of our analytical approach. Upon increasing the activity, we first find a regime where the layer oscillates periodically between two different buckled states and then a regime where the high activity breaks up the interface leading to continuous droplet nucleation. Last, at very high activity, we see a turbulent regime, which is characterized by the chaotic proliferation of protrusions.
Whereas undoubtedly simplified with respect to the seemingly endless complexity of living matter, our study contributes to shed light on how developing organisms can take advantage of topology to achieve biological organization from physical mechanisms, with potential application to various biomechanical processes such as morphogenesis, embryogenesis, cancerogenesis, and vesicle formation. As mentioned in Introduction, +1 disclinations are not the only type of defect encountered in morphogenesis. Nematic (i.e., ±1/2; see Fig. 1, A and B) and, in general, p-atic defects (e.g., ±1/6; see Fig. 1D), are also equally common; we plan to investigate these additional defect types in the future. Last, while there are several experiments observing the role defects play in the formation of protrusions, we are not aware of any study investigating the other regimes, particularly droplet nucleation. Naturally, the question occurs whether these other regimes also play a role in biological systems.
MATERIALS AND METHODS
Experimental setup
Parental MDCK GII cells (provided by M. Gloerich, Universitair Medisch Centrum Utrecht) were grown on noncoated coverslips until tissue buckling. F-actin, E-cadherin, and nuclei were stained on fixed samples. Samples were imaged at high resolution on a spinning disk confocal microscopy setup. Cell boundaries were identified from a maximum intensity projection of a z-stack of the top part of the dome. Fiji software was used for the orthogonal view. 3D reconstructions were done by Imaris Viewer 9.7.0, and z directions were corrected for spherical aberration and axial distortion (56). See the Supplementary Materials for details.
Numerical simulations
The dynamical fields of the model used for simulations are the incompressible flow field v = v(r, t) (∇ · v = 0) and the polarization field P = P(r, t), which is confined at the interface between two isotropic fluids, whose relative concentration is encoded in the scalar phase field ϕ = ϕ(r, t). Note that, in this section, P and v are 3D vectors, and ∇ now denotes differentiation in ℝ3. The equilibrium is defined by a generalized Landau–de Gennes functional (49, 50)
| (8) |
where the constants a and kϕ are model parameters related to the surface tension and the width of the interface by and , respectively. To confine the polar liquid crystal at the ϕ interface, the parameter ψ = ψ(∇ϕ) is chosen to be a function of ∇ϕ, such that ψ = − 1 if ∣∇ϕ∣ is larger than a suitable threshold and 0 otherwise. In addition, the coupling between P and ∇ϕ ensures tangential anchoring of the liquid crystal for β > 0, so that the polarization field actually lays on the interface. The bulk constant A0 fixes the coherence length of the liquid crystal , which controls how fast the order parameter P drops to zero from its equilibrium value ∣P∣ = 1 in proximity of a topological defect. Note that, in the limit of vanishing interfacial width, ξ → 0, such a phase field model, can be mapped on the analytical model of “The model” section [see, e.g., (13, 51)]. The dynamics of the system is governed by the following set of partial differential equations
| (9a) |
| (9b) |
| (9c) |
Equation 9a is the Navier-Stokes equation, which rules the hydrodynamics of the system in the full 3D space. Here, the stress tensor has been divided in a passive and an active part. The former includes, in turn, three terms: a hydrodynamic, an elastic, and a phase field contribution σp = σh + σe + σi, whose explicit expressions are given by
Here, Ph is the hydrodynamic pressure, η is the shear viscosity, λ is the flow alignment parameter, and Γ−1 is the rotational viscosity. f denotes the free energy density, such that ℱ = ∫ dVf, h = −δℱ/δP is the molecular field, and u = [(∇v) + (∇v)T]/2 and ω = [(∇v) − (∇v)T]/2 are the strain rate and vorticity tensor, respectively. The 3D active stress tensor σa is given by
| (10) |
Last, Eq. 9b is the Ericksen-Leslie equation for the polarization field P in 3D, whereas the dynamics of the concentration field is governed by the advection-diffusion equation, Eq. 9c, with μ the mobility parameter.
The dynamical equations have been integrated by means of a hybrid lattice Boltzmann (LB) method (57), where the hydrodynamics is solved through a predictor-corrector LB algorithm, while the dynamics of the order parameter has been treated with a finite difference approach, implementing a first-order upwind scheme and fourth-order accurate stencil for the computation of spacial derivatives. The hydrodynamics was integrated in a cylindrical geometry with radius R = 32ℓc under soft homeotropic boundary conditions for the polarization field, while the concentration field satisfies neutral wetting boundary conditions at the top and bottom walls, respectively, where ϕ = ± 1. The system is initialized with ϕ = 1 (ϕ = − 1) in the top (bottom) half of the system and the polarization field in an aster configuration at the interface in the center of the system and 0 otherwise.
The numerical code has been parallelized by means of message passing interface (MPI) by dividing the computational domain in slices and by implementing the ghost-cell method to compute derivatives on the boundary of the computational subdomains. Runs have been performed using 64 CPUs on a computational box size of 96 by 96 by 256 for at least 106 LB iterations (corresponding to ∼35 days of CPU time on Intel Xeon 8160 processors). A mapping between simulation and physical units is provided in the Supplementary Materials.
Acknowledgments
J.E. and L.G. acknowledge M. Gloerich, UMC Utrecht, for providing us the MDCK cells. L.A.H. thanks J. A. Santiago for helpful discussions.
Funding: This work is supported by the Netherlands Organization for Scientific Research (NWO/OCW), as part of the Vidi scheme (L.A.H. and L.G.), and by the European Union via the ERC-CoG grant HexaTissue (L.N.C. and L.G.). Part of this work was carried out on the Dutch National e-Infrastructure with the support of SURF through the grant 2021.028 for computational time (L.A.H., L.N.C., and L.G.).
Author contributions: L.A.H., L.N.C., and L.G. designed and performed the research, analyzed the data, and wrote the paper. L.A.H. and L.G. developed the analytical model. L.N.C. performed the simulations. J.E. performed the MDCK GII experiments and analysis.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Data are available at Zenodo (DOI: 10.5281/zenodo.6240881).
Supplementary Materials
This PDF file includes:
Sections S1 to S6
Figs. S1 and S2
Table S1
Other Supplementary Material for this manuscript includes the following:
Movies S1 to S5
REFERENCES AND NOTES
- 1.Conte V., Ulrich F., Baum B., Muñoz J., Veldhuis J., Brodland W., Miodownik M., A biomechanical analysis of ventral furrow formation in the drosophila melanogaster embryo. PLOS ONE 7, e34473 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nelson C. M., On buckling morphogenesis. J. Biomech. Eng. 138, 021005 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Marchetti M. C., Joanny J. F., Ramaswamy S., Liverpool T. B., Prost J., Rao M., Simha R. A., Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013). [Google Scholar]
- 4.Metselaar L., Yeomans J. M., Doostmohammadi A., Topology and morphology of self-deforming active shells. Phys. Rev. Lett. 123, 208001 (2019). [DOI] [PubMed] [Google Scholar]
- 5.Mietke A., Jülicher F., Sbalzarini I. F., Self-organized shape dynamics of active surfaces. Proc. Natl. Acad. Sci. U.S.A. 116, 29–34 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wyatt T. P. J., Fouchard J., Lisica A., Khalilgharibi N., Baum B., Recho P., Kabla A. J., Charras G. T., Actomyosin controls planarity and folding of epithelia in response to compression. Nat. Mater. 19, 109–117 (2020). [DOI] [PubMed] [Google Scholar]
- 7.S. C. Al-Izzi, R. G. Morris, Active flows and deformable surfaces in development. arXiv:2103.12264 (2021). [DOI] [PubMed]
- 8.Keber F. C., Loiseau E., Sanchez T., DeCamp S. J., Giomi L., Bowick M. J., Marchetti M. C., Dogic Z., Bausch A. R., Topology and dynamics of active nematic vesicles. Science 345, 1135–1139 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Livshits A., Shani-Zerbib L., Maroudas-Sacks Y., Braun E., Keren K., Structural inheritance of the actin cytoskeletal organization determines the body axis in regenerating hydra. Cell Rep. 18, 1410–1421 (2017). [DOI] [PubMed] [Google Scholar]
- 10.Braun E., Keren K., Hydra regeneration: Closing the loop with mechanical processes in morphogenesis. Bioessays 40, 1700204 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Maroudas-Sacks Y., Garion L., Shani-Zerbib L., Livshits A., Braun E., Keren K., Topological defects in the nematic order of actin fibres as organization centres of Hydra morphogenesis. Nat. Phys. 17, 251–259 (2021). [Google Scholar]
- 12.Livshits A., Garion L., Maroudas-Sacks Y., Shani-Zerbib L., Keren K., Braun E., Plasticity of body axis polarity in Hydra regeneration under constraints. bioRxiv 2021.02.04.429818 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ruske L. J., Yeomans J. M., Morphology of active deformable 3D droplets. Phys. Rev. X 11, 021001 (2021). [Google Scholar]
- 14.F. Vafa, L. Mahadevan, Active nematic defects and epithelial morphogenesis. arXiv:2105.01067 (2021). [DOI] [PubMed]
- 15.Saw T. B., Doostmohammadi A., Nier V., Kocgozlu L., Thampi S., Toyama Y., Marcq P., Lim C. T., Yeomans J. M., Ladoux B., Topological defects in epithelia govern cell death and extrusion. Nature 544, 212–216 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Loewe B., Chiang M., Marenduzzo D., Marchetti M. C., Solid-liquid transition of deformable and overlapping active particles. Phys. Rev. Lett. 125, 038003 (2020). [DOI] [PubMed] [Google Scholar]
- 17.S. Monfared, G. Ravichandran, J. E. Andrade, A. Doostmohammadi, Mechanics of live cell elimination. arXiv:2108.07657 (2021).
- 18.Guillamat P., Blanch-Mercader C., Kruse K., Roux A., Integer topological defects organize stresses driving tissue morphogenesis. bioRxiv 2020.06.02.129262 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Popowicz P., Kurzyca J., Popowicz S., “Dome-curve”—three size classes of domes of MDCK epithelial monolayer. Exp. Pathol. 29, 147–151 (1986). [DOI] [PubMed] [Google Scholar]
- 20.Arslan F. N., Eckert J., Schmidt T., Heisenberg C.-P., Holding it together: When cadherin meets cadherin. Biophys. J. 120, 4182–4192 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cereijido M., Robbins E., Dolan W., Rotunno C., Sabatini D., Polarized monolayers formed by epithelial cells on a permeable and translucent support. J. Cell Biol. 77, 853–880 (1978). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Latorre E., Kale S., Casares L., Gómez-González M., Uroz M., Valon L., Nair R. V., Garreta E., Montserrat N., del Campo A., Ladoux B., Arroyo M., Trepat X., Active superelasticity in three-dimensional epithelia of controlled shape. Nature 563, 203–208 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Deserno M., Fluid lipid membranes: From differential geometry to curvature stresses. Chem. Phys. Lipids 185, 11–45 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Helfrich W., Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforsch. C 28, 693–703 (1973). [DOI] [PubMed] [Google Scholar]
- 25.P. M. Chaikin, T. C. Lubensky, Principles of Condensed Matter Physics (Cambridge Univ. Press, 1995). [Google Scholar]
- 26.Giomi L., Geometry and topology of turbulence in active nematics. Phys. Rev. X 5, 031003 (2015). [Google Scholar]
- 27.Pearce D. J. G., Ellis P. W., Fernandez-Nieves A., Giomi L., Geometrical control of active turbulence in curved topographies. Phys. Rev. Lett. 122, 168002 (2019). [DOI] [PubMed] [Google Scholar]
- 28.Mietke A., Jemseena V., Kumar K. V., Sbalzarini I. F., Jülicher F., Minimal model of cellular symmetry breaking. Phys. Rev. Lett. 123, 188101 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Santiago J. A., Stresses in curved nematic membranes. Phys. Rev. E 97, 052706 (2018). [DOI] [PubMed] [Google Scholar]
- 30.Tóth G., Denniston C., Yeomans J. M., Hydrodynamics of topological defects in nematic liquid crystals. Phys. Rev. Lett. 88, 105504 (2002). [DOI] [PubMed] [Google Scholar]
- 31.Bowick M. J., Nelson D. R., Travesset A., Interacting topological defects on frozen topographies. Phys. Rev. B 62, 8738–8751 (2000). [Google Scholar]
- 32.Giomi L., Bowick M., Crystalline order on Riemannian manifolds with variable Gaussian curvature and boundary. Phys. Rev. B 76, 054106 (2007). [Google Scholar]
- 33.Bowick M. J., Giomi L., Two-dimensional matter: Order, curvature and defects. Adv. Phys. 58, 449–563 (2009). [Google Scholar]
- 34.Pedley T. J., Kessler J. O., Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24, 313–358 (1992). [Google Scholar]
- 35.Aditi Simha R., Ramaswamy S., Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys. Rev. Lett. 89, 058101 (2002). [DOI] [PubMed] [Google Scholar]
- 36.Asano Y., Jiménez-Dalmaroni A., Liverpool T. B., Marchetti M. C., Giomi L., Kiger A., Duke T., Baum B., Pak3 inhibits local actin filament formation to regulate global cell polarity. HFSP J. 3, 194–203 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.You Z., Pearce D. J. G., Sengupta A., Giomi L., Geometry and mechanics of microdomains in growing Bacterial colonies. Phys. Rev. X 8, 031065 (2018). [Google Scholar]
- 38.Capovilla R., Guven J., Stresses in lipid membranes. J. Phys. A Math. Gen. 35, 6233–6247 (2002). [Google Scholar]
- 39.Capovilla R., Guven J., Stress and geometry of lipid vesicles. J. Phys. Condens. Matter 16, S2187 (2004). [Google Scholar]
- 40.Guven J., Laplace pressure as a surface stress in fluid vesicles. J. Phys. A 39, 3771–3785 (2006). [Google Scholar]
- 41.Salbreux G., Jülicher F., Mechanics of active surfaces. Phys. Rev. E 96, 032404 (2017). [DOI] [PubMed] [Google Scholar]
- 42.L. D. Landau, E. M. Lifshitz, Theory of Elasticity (Pergamon Press, 1970). [Google Scholar]
- 43.Seung H. S., Nelson D. R., Defects in flexible membranes with crystalline order. Phys. Rev. A 38, 1005–1018 (1988). [DOI] [PubMed] [Google Scholar]
- 44.Carenza L., Biferale L., Gonnella G., Cascade or not cascade? Energy transfer and elastic effects in active nematics. EPL 132, 44003 (2020). [Google Scholar]
- 45.Kruse K., Joanny J. F., Jülicher F., Prost J., Sekimoto K., Asters, vortices, rotating spirals in active gels of polar filaments. Phys. Rev. Lett. 92, 078101 (2004). [DOI] [PubMed] [Google Scholar]
- 46.Giomi L., Bowick M. J., Mishra P., Sknepnek R., Marchetti M. C., Defect dynamics in active nematics. Philos. Trans. R. Soc. A 372, 20130365 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hoffmann L. A., Schakenraad K., Merks R. M. H., Giomi L., Chiral stresses in nematic cell monolayers. Soft Matter 16, 764–774 (2020). [DOI] [PubMed] [Google Scholar]
- 48.Frank J. R., Kardar M., Defects in nematic membranes can buckle into pseudospheres. Phys. Rev. E 77, 041705 (2008). [DOI] [PubMed] [Google Scholar]
- 49.Carenza L. N., Gonnella G., Marenduzzo D., Negro G., Rotation and propulsion in 3D active chiral droplets. Proc. Natl. Acad. Sci. U.S.A. 116, 22065 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Carenza L., Gonnella G., Marenduzzo D., Negro G., Chaotic and periodical dynamics of active chiral droplets. Phys. A 559, 125025 (2020). [Google Scholar]
- 51.Liu C., Shen J., A phase field model for the mixture of two incompressible fluids and its approximation by a Fourier-spectral method. Phys. D 179, 211–228 (2003). [Google Scholar]
- 52.P. G. Drazin, Cambridge Texts in Applied Mathematics, in Nonlinear Systems (Cambridge Univ. Press, 1992). [Google Scholar]
- 53.Alert R., Joanny J.-F., Casademunt J., Universal scaling of active nematic turbulence. Nat. Phys. 6, 682–688 (2020). [Google Scholar]
- 54.Carenza L. N., Biferale L., Gonnella G., Multiscale control of active emulsion dynamics. Phys. Rev. Fluids 5, 011302 (2020). [Google Scholar]
- 55.Stone H. A., Ajdari A., Hydrodynamics of particles embedded in a flat surfactant layer overlying a subphase of finite depth. J. Fluid Mech. 369, 151–173 (1998). [Google Scholar]
- 56.Diel E. E., Lichtman J. W., Richardson D. S., Tutorial: Avoiding and correcting sample-induced spherical aberration artifacts in 3D fluorescence microscopy. Nat. Protoc. 15, 2773–2784 (2020). [DOI] [PubMed] [Google Scholar]
- 57.Carenza L. N., Gonnella G., Lamura A., Negro G., Tiribocchi A., Lattice Boltzmann methods and active fluids. Eur. Phys. J. E 42, 81 (2019). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Sections S1 to S6
Figs. S1 and S2
Table S1
Movies S1 to S5