Development and Validation of Fluorinated, Aromatic Amino Acid Parameters for Use with the AMBER ff15ipq Protein Force Field

Abstract

We developed force field parameters for fluorinated, aromatic amino acids enabling molecular dynamics (MD) simulations of fluorinated proteins. These parameters are tailored to the AMBER ff15ipq protein force field and enable the modeling of 4, 5, 6, and 7F-tryptophan, 3F- and 3,5F-tyrosine, and 4F- or 4-CF₃-phenylalanine. The parameters include 181 unique atomic charges derived using the implicitly polarized charge (IPolQ) scheme in the presence of SPC/E_b explicit water molecules and 9 unique bond, angle, or torsion terms. Our simulations of benchmark peptides and proteins maintain expected conformational propensities on the μs time scale. In addition, we have developed an open-source Python program to calculate fluorine relaxation rates from MD simulations. The extracted relaxation rates from protein simulations are in good agreement with experimental values determined by ¹⁹F NMR. Collectively, our results illustrate the power and robustness of the IPolQ lineage of force fields for modeling the structure and dynamics of fluorine-containing proteins at the atomic level.

I. Introduction

While NMR spectroscopy using the ¹⁹F nucleus is emerging as a powerful tool for measuring various structural and dynamical properties of fluorine-labeled biomolecules,¹ the availability of force fields for modeling the corresponding conformational dynamics at the atomic level has been limited. To address this unmet need, we have expanded upon the standard amino acids available in the AMBER ff15ipq protein force field² and present a comprehensive set of parameters for the most commonly used, fluorinated, aromatic amino acids in ¹⁹F NMR experiments. Coupled with GPU-accelerated molecular dynamics (MD) simulations,^3,4 we can now begin to effectively integrate the results from ¹⁹F NMR experiments with atomistic MD simulations.

The fluorine nucleus has several features that render it a particularly useful NMR probe. Specifically, ¹⁹F is a 100% naturally abundant isotope with a high gyromagnetic ratio, which makes it almost as sensitive as ¹H. Importantly, ¹⁹F chemical shifts span a very large range and are exquisitely responsive to the local chemical and electronic environment around the atom.⁵⁻⁷ Fluorine is absent from virtually all naturally occurring biomolecules. Therefore, studies of fluorinated biopolymers can be carried out in any routine buffer system or environment without interference from background signals.⁸ In general, only one or a handful of fluorine atoms are introduced into a biopolymer, overcoming the common handicap of spectral overlap in proton spectra that necessitated uniform labeling with ¹³C and ¹⁵N, in conjunction with three-dimensional (3D) and four-dimensional (4D) heteronuclear spectroscopy, for resonance assignments in bioNMR. These desirable properties have propelled ¹⁹F NMR-based studies of biomolecular systems forward, such as investigations of thermodynamics⁹ and kinetics,¹⁰ protein structure and dynamics,¹¹⁻¹³ or protein–protein and protein–ligand interactions.¹⁴⁻¹⁹ Efforts are also ongoing toward ¹⁹F NMR method development, including relaxation optimization approaches^20,21 to extend applicability to larger systems and to exploit ¹⁹F paramagnetic relaxation enhancement to determine long distances up to 35 Å.²²¹⁹F NMR is particularly useful in the pharmaceutical arena, guiding fragment-based screening²³ and drug discovery/design.²⁴ Finally, a more recent and exciting direction is the movement of ¹⁹F NMR into a physiological environment, measuring spectra of fluorinated proteins directly in Escherichia coli,²⁵Xenopus laevis oocytes,²⁶ and mammalian cells.²⁷

Naturally, ¹⁹F NMR of proteins is not a panacea and has shortcomings and limitations. The 1.47 Å van der Waals radius of the fluorine atom lies between those of hydrogen (1.2 Å) and oxygen (1.52 Å). Therefore, fluorine is frequently substituted for hydrogens, hydroxyl groups, or carbonyl oxygens. While such substitutions are often only weakly perturbing, with little to no effect on a protein’s structure and biological activity,^5,9,12,13 this is not necessarily the case and needs to be verified for each system under study.²⁸ Compared to more traditional NMR probes (¹H, ¹⁵N, ¹³C), introducing a highly electronegative fluorine atom changes electronic surroundings and thereby local interactions, especially if the substituted H or OH was involved in hydrogen bonding. In addition, although resonance overlap is avoided, having only a few probes available, compared to thousands with traditional ¹H, ¹⁵N, ¹³C labeling, limits the information content and several samples may need to be prepared where single fluorinated amino acids are judiciously placed to probe different parts of the biomolecule. MD simulations can help bridge this gap in information content at the all-atom level.

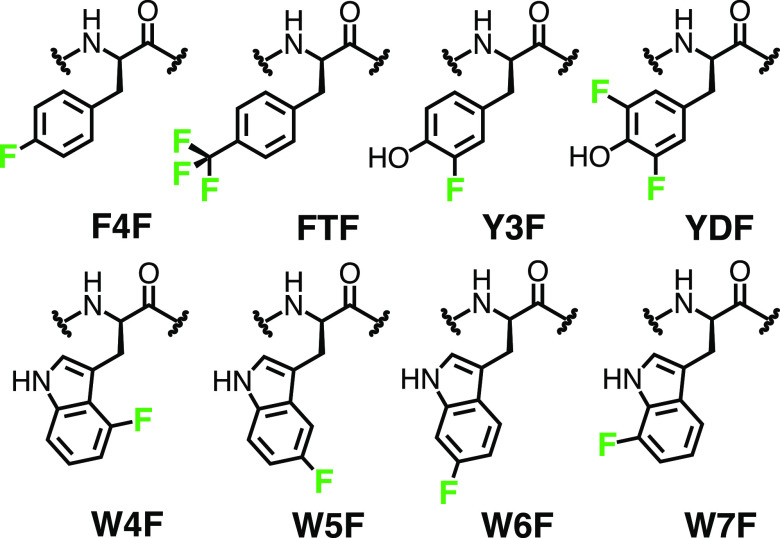
Here, we have developed new force field parameters for eight commonly used fluorinated, aromatic amino acids, facilitating more accurate atomic-level simulations of ¹⁹F NMR observables. As indicated in Figure 1, our study focuses on 4, 5, 6, and 7-fluoro-tryptophan (W4F, W5F, W6F, W7F); 3, and 3,5-fluoro-tyrosine (Y3F, YDF); as well as 4-fluoro- and 4-trifluoromethyl-phenylalanine (F4F, FTF). These fluorinated derivatives of tryptophan, tyrosine, and phenylalanine were selected because they are readily available and can be easily incorporated into proteins for ¹⁹F NMR.²⁹⁻³² Our parameters are intended for use with the AMBER ff15ipq force field and were derived using a general workflow that has been used previously for deriving new classes of noncanonical residues.³³ Consistent with the ff15ipq force field, we derived implicitly polarized atomic charges in the presence of explicit solvent. The implicit polarization of atomic charges has been demonstrated to be essential for modeling condensed-phase electrostatics by fixed-charge force fields^2,34–that is, when polarizable force fields that employ Drude oscillators³⁵ or inducible multipoles³⁶ are not feasible. Furthermore, application of the ff15ipq force field with the intended SPC/E_b water model yields more accurate rotational diffusion times of proteins, enabling direct calculation of NMR observables.^2,37,38 Using the GPU-accelerated AMBER MD engine,^39,40 we have extensively validated our force field parameters by simulating both peptides and proteins that include each of the eight fluorinated amino acids, yielding over 47 μs of aggregate simulation time. Our parameters maintain expected conformational propensities of both fluorinated peptide- and protein-based systems on the μs time scale, and our relaxation rates from simulation agree with those from ¹⁹F NMR experiments.

Figure 1.

Eight commonly used fluorinated, aromatic amino acids with their respective three-letter identifier codes. The fluorine atom is highlighted in green.

Until now, parameters for the full set of fluorinated, aromatic amino acids listed above for the AMBER ff15ipq protein force field have not been available, although recently, parameters for over 400 nonstandard amino acids were added to the CHARMM36 protein and CHARMM general force fields,⁴¹ including some for several fluorinated amino acids. The CHARMM parameters were derived by isolating only the side-chain atoms of the amino acid of interest and optimizing select water interactions based on quantum mechanical (QM) calculations at either the MP2/6-31G(d) or the HF/6-31G(d) level of theory. However, CHARMM parameters are not available for 7-fluoro-tryptophan and 4-fluoro-phenylalanine. In addition, parameters for apolar, nonaromatic, fluorinated amino acids are available for use with the AMBER ff14SB force field, which selectively optimized fluorine specific Lennard-Jones parameters and derived atomic charges at the RHF/6-31G* level of theory.^42,43 Also, for use with the ff14SB force field, a set of unnatural phenylalanine and tyrosine derivatives was parameterized, which included 3,5-fluoro-tyrosine.⁴⁴ Atomic charges for these parameters were based on electrostatic potential calculations of a blocked dipeptide at the HF/6-31G* level of theory. Other efforts to develop parameters for simulating fluorinated proteins have been primarily ad hoc and single-use cases.⁴⁵⁻⁴⁷

II. AMBER ff15ipq Force Field

Parameters for the eight different fluorinated amino acids were developed for use with the AMBER ff15ipq protein force field, the latest version of the implicitly polarized charge (ipq) force field lineage.^2,48 These parameters are also compatible with the ff15ipq-m force field for protein mimetics.³³ Ipq force fields feature implicitly polarized atomic charges, with each charge optimized to reproduce the mean-field electron density of the molecule in explicit solvent.⁴⁹ Notably, the ff15ipq force field is parameterized using the three-point, explicit SPC/E_b (extended simple point charge) water model,⁵⁰ which reproduces the experimental rotational diffusion of proteins and can therefore yield reasonable dynamical observables such as those measured by NMR without the computational burden associated with four-point water model alternatives.

The original motivation behind the ff15ipq force field was to obtain more accurate propensities for salt-bridge formation, which is a common limitation of most contemporary fixed-charge force fields.³⁴ The final ff15ipq implementation was a complete rederivation of its predecessor,⁴⁸ including a greatly expanded torsion and angle parameter set, atomic charges derived at the MP2/cc-pVTZ level in explicit solvent, and adjustments to atomic radii for polar hydrogens. The ff15ipq force field reproduces the experimental probabilities of salt-bridge formation while maintaining the secondary structure of stably folded and disordered systems on the μs time scale and faithfully predicts J-coupling constants for a penta-alanine peptide as well as NMR relaxation rates for protein systems.²

Additional developments involved a modification of methyl side-chain rotational barriers that help to accurately predict methyl relaxation rates,^38,51,52 as well as an expanded force field (ff15ipq-m) for modeling four classes of artificial backbone units, including D- and Cα-methylated amino acids, β-amino acids, and two cyclic β residues.³³ These developments are implemented in both the AMBER^39,40,53 and open-source OpenMM⁵⁴ GPU-accelerated biomolecular simulation software packages and are accessible to other such packages through the ParmEd program⁵⁵ for format conversion.

Our new parameters for the eight fluorinated, aromatic amino acids were derived using a workflow designed to be consistent with the parent ff15ipq derivation process. As done for the ff15ipq-m force field, one minor difference pertained to the generation of blocked dipeptide conformations for both the charge and bonded parameter derivation: to increase and safeguard conformational diversity, we progressively restrained the backbone torsions at evenly spaced intervals before energy minimizing each restrained conformation.³³ In the parent ff15ipq force field, conformations were generated using high-temperature MD simulations.²

III. Methods

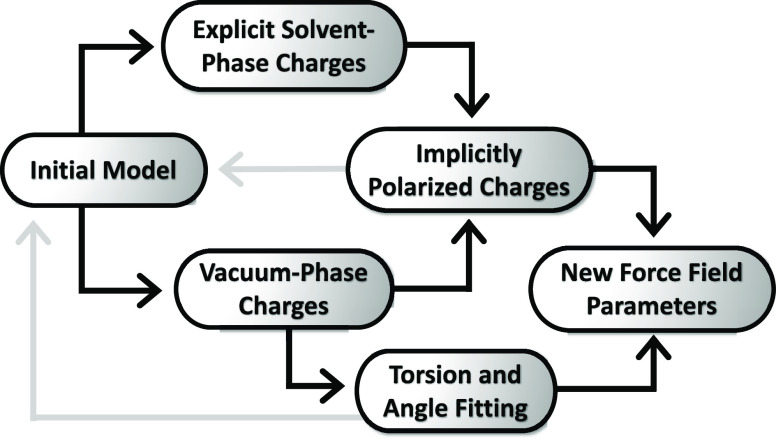
The general workflow for developing ff15ipq force field parameters is outlined on Figure 2. Throughout this workflow, Lennard-Jones parameters for all atoms, including fluorine, were taken from the parent ff15ipq force field.

Figure 2.

Workflow for developing ff15ipq force field parameters. Starting from a model consisting of multiple coordinate and topology files, the IPolQ charge derivation protocol is used to fit atomic charges from electrostatic potential calculations in both vacuum and explicit solvent phases. These charges are averaged, implicitly modeling solvent polarization effects. The vacuum-phase charges are used to fit bonded parameter terms to the vacuum-phase QM targets and used iteratively with the implicitly polarized charges, as indicated by the gray arrows, to generate a new initial model until the parameters are self-consistent.

III.I. Derivation of IPolQ Atomic Charges

For each fluorinated residue, IPolQ atomic charges were derived using a four-step iterative procedure until convergence was reached:

• 1.Generate a set of conformations. Each type of fluorinated amino acid was flanked with acetyl (Ace) and N-methylamide (Nme) N- and C-terminal capping groups, and the resulting molecule was named “dipeptide.” The 20 dipeptide conformations were generated by progressively restraining the backbone Φ/Ψ torsion angles within −180° to 180° using a force constant of 32 kcal/mol. Aside from the backbone dihedral angles, no other restraints were applied for generating the initial set of dipeptide conformations. Only for the first iteration, the initial set of atomic charges was derived using the AM1-BCC charge method.⁵⁶ Each restrained conformation was then subjected to energy minimization and solvated using a truncated octahedral box of SPC/E_B water molecules with at least a 12 Å clearance between the solute and the edge of the box. After another round of energy minimization, each solvated system underwent a two-stage equilibration, which included a 10 kcal/(mol Ų) positional restraint on the entire dipeptide. In the first stage, 20 ps of dynamics were carried out at constant temperature (25 °C) and volume. In the second stage, 100 ps of dynamics were carried out at constant temperature (25 °C) and pressure (1 atm). A final 500 ps simulation was performed at constant temperature (25 °C) and volume during which the solute remained fixed, and the solvent coordinates were used to generate a distribution of point charges that represent the solvent reaction field potential. This distribution consisted of an inner cloud of point charges based on the coordinates of the solvent molecules within 5 Å of the solute and three outer shells of point charges that reproduce contributions to the solvent reaction field potential from the periodic system beyond 5 Å.
• 2.Calculate the electrostatic potential of each conformation in vacuum and in explicit solvent. Two sets of QM electrostatic potential calculations were carried out for each dipeptide conformation at the MP2/cc-pVTZ⁵⁷⁻⁶⁰ level of theory using the ORCA 4.2.0⁶¹ software package. The first set of QM calculations was in vacuum and the other set included the solvent reaction field potential to represent the surrounding explicit solvent molecules.
• 3.Fit the average electrostatic potential over all conformations to atomic charges, both in vacuum and in explicit solvent. All eight aromatic fluorinated amino acids were fit together using the fitq module of the mdgx program,⁵³ with atomic charges of the Ace and Nme capping groups fixed to net neutral values during the process.
• 4.Average the vacuum-phase and solvent-phase point charges to obtain implicitly polarized atomic charges. This averaged charge set was used as the starting point for the next iteration of charge generation and fitting as described above.

The above procedure was repeated four times to reach convergence of the partial atomic charge values within 10% of the previous iteration’s values.

III.II. Generation and Fitting of the Bonded Parameter Dataset

Bonded parameters were derived using an iterative, multistep procedure: (i) 1000 conformations of each fluorinated dipeptide were generated in vacuum, taking trial torsion and angle parameters from the parent ff15ipq force field, if available, or otherwise from the general amber force field 2 (GAFF2).⁶² Atomic charges were obtained from the vacuum-phase set of converged point charges as described above. Each conformation was generated by progressively restraining backbone Φ and Ψ torsion angles of the dipeptide between −180° and 180° using a force constant of 32 kcal/mol. After energy minimization Φ and Ψ distributions of the conformation set were evaluated to ensure extensive sampling of the configurational space. (ii) For each conformation, the quantum mechanical (QM) single-point energy was calculated at the MP2/cc-pVTZ level of theory, along with the molecular mechanical (MM) energy. Linear least-squares fitting for the entire set of bond, angle, and torsion parameters was carried out using mdgx.⁶³ (iii) Force field bonded parameters such as torsional barrier heights, angle equilibria, angle stiffness, bond length equilibria, and bond stiffness were adjusted to minimize the error between the QM and MM energies. Using the updated parameter set, the second round of conformer generation and QM energy calculations was carried out in the absence of restraints to prevent becoming trapped in local minima. This new set of conformations excluded redundant conformations, as defined by those with MM energies that differ by <0.01 kcal/mol. Another round of fitting was then performed using both sets of conformations and their respective energies to obtain the final parameter set for each iteration. Steps (i–iii) were repeated until the root-mean-square error (RMSE) between the QM and MM energies was less than 1% from the previous iteration.

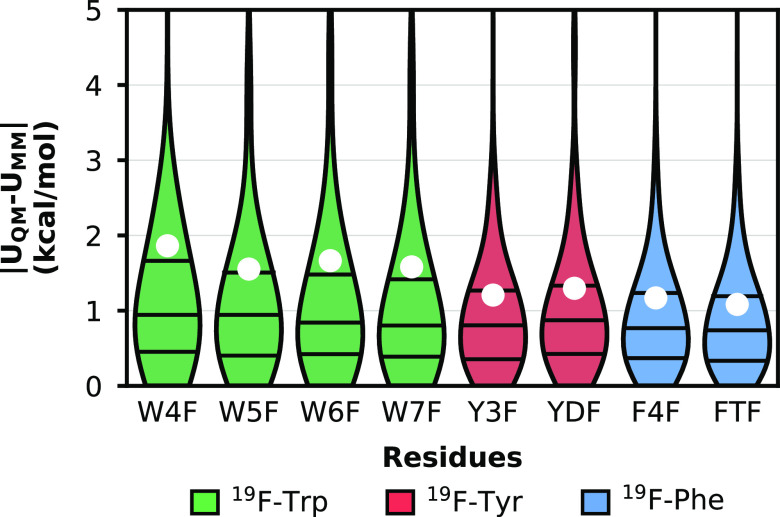
The accuracy of the molecular mechanical energies (U_MM) produced using the optimized parameters for each fluorinated dipeptide was assessed by comparing them to the respective QM energies (U_QM) for all generated conformations (Figure 3). During each iteration of the above fitting procedure, optimization of the bonded parameters was monitored by the RMSE, which reached final values of 1.08–1.86 kcal/mol for all eight residues. On average, these errors are slightly higher than those of the nonfluorinated tryptophan (0.89 kcal/mol), tyrosine (0.87 kcal/mol), and phenylalanine (0.93 kcal/mol) counterparts from the ff15ipq force field² for canonical residues. The difference in RMSE of the fluorinated residue from the canonical counterpart may be due to fewer parameters in the fitting procedure and/or the presence of electronegative fluorine atom(s).

Figure 3.

Distributions of residuals between quantum mechanical (U_QM) energies and molecular mechanical (U_MM) energies for the eight fluorinated Ace-Xaa-Nme dipeptides, where Xaa is the fluorinated residue of interest. The 25th, 50th, and 75th percentiles are represented by horizontal lines, and root-mean-square-error values are represented by white filled circles. Each dataset is colored according to the original residue type indicated in the legend.

III.III. Preparation of Validation Systems

Models of fluorinated and canonical peptides were built using Avogadro⁶⁴ and tleap.⁶³ To generate the 4, 5, 6, and 7F-Trp-modified protein systems, the atomic coordinates of cyclophilin A [CypA; Protein Data Bank⁶⁵ (PDB) ID: 3K0N]⁶⁶ were modified using Chimera,⁶⁷ with fluorine atoms substituted individually for hydrogens in Trp121 at the respectively numbered positions on the indole ring. All C–F bonds were initially modeled using a 1.42 Å bond length. Each system was solvated in a truncated octahedral box of explicit SPC/E_b⁵⁰ water molecules with a 10 Å clearance between the solute and the edge of the box for the peptides and a 12 Å clearance for the proteins. All systems with unpaired charges were neutralized by adding Na⁺ or Cl^– ions, treated with Joung and Cheatham ion parameters.⁶⁸ Protonation states for ionizable residues were adjusted to represent the major species present at pH 6.5 to match the experimental NMR conditions.⁶⁹

III.IV. Umbrella Sampling of Fluorinated and Canonical Peptides

To validate the conformational preferences of each fluorinated residue, umbrella sampling simulations were carried out for systems that consisted of a fluorinated amino acid (Xaa) flanked on either side by an alanine and the Ace and NMe capping groups at the N- and C-terminal ends, respectively. These molecules (Ace-Ala-Xaa-Ala-NMe) are named tetrapeptides thereafter. Ramachandran plots were generated for each tetrapeptide by calculating the potential of mean force as a function of the Φ and Ψ torsion angles of the fluorinated residue. Prior to umbrella sampling, each tetrapeptide was solvated and equilibrated as described above for unrestrained simulations, differing only in the duration of the final equilibration stage, which was 100 ps instead of 1 ns. Each window was then subjected to a 200 ps incrementally restrained equilibration prior to a 2 ns restrained simulation at constant temperature (25 °C) and pressure (1 atm). The Φ and Ψ torsions of the central residue were restrained using a harmonic penalty function with a force constant of 8 kcal/(mol rad²) for each window with 10° intervals about each torsion angle. This restraint scheme resulted in a series of 1296 windows for each set of two torsions, cumulating into 22.8 μs of aggregate simulation time for the eight fluorinated residue classes and 10,368 windows. From each set of 1296 windows, the unbiased potential of mean force was reconstructed using the weighted histogram analysis method (WHAM).⁷⁰⁻⁷²

III.V. MD Simulations of Fluorinated and Wild-Type CypA

Simulations of the 4, 5, 6, 7F-Trp fluorinated and the wild-type CypA proteins were carried out using the GPU-accelerated pmemd module of the AMBER 18 software package,^39,40,53 ff15ipq force field,² and our new fluorinated amino acid parameters. Each system was initially subjected to energy minimization followed by a three-stage equilibration. In the first stage, a 20 ps simulation was carried out at constant volume and temperature (25 °C) in the presence of solute heavy-atom positional restraints using a harmonic potential with a force constant of 1 kcal/(mol Ų). In the second stage, a 1 ns simulation was carried out at constant temperature (25 °C) and pressure (1 atm) using the same harmonic positional restraints. Finally, an unrestrained 1 ns simulation was carried out before performing a 1 μs production simulation with both constant temperature (25 °C) and pressure (1 atm). Five production simulations were run for each CypA protein, yielding 25 μs of aggregate simulation time.

Temperatures were maintained using a Langevin thermostat with a frictional constant of 1 ps^–1, while pressure was maintained using a Monte Carlo barostat with 100 fs between system volume changes. Van der Waals and short-range electrostatic interactions were truncated at 10 Å, while long-range electrostatic interactions were calculated using the particle mesh Ewald method.⁷³ To enable a 2 fs time step, all CH and NH bonds were constrained to their equilibrium values using the SHAKE algorithm.⁷⁴ Coordinates were saved every ps and analysis was performed in CPPTRAJ.⁷⁵

III.VI. Backbone Conformations of Fluorinated Amino Acids in the PDB

A “ligand expo” search⁷⁶ was carried out to determine whether each fluorinated amino acid of interest was present in PDB deposited structures. The corresponding three-letter identifiers in the PDB were as follows: 4FW, FTR, FT6, F7W, PFF, 55I, YOF, and F2Y, which are equivalent to the following identifiers in the current study: W4F, W5F, W6F, W7F, F4F, FTF, Y3F, and YDF (Figure 1), respectively. Each identifier was associated with at least one structure and was used to construct a query for structures that included the fluorinated residue as a part of a polymer chain, avoiding fluorinated ligand molecules. For structures determined by X-ray crystallography, only those with a resolution ≤ 2.5 Å were included, resulting in a total of 56 structures with at least one fluorinated residue each (Table S2). The backbone Φ and Ψ torsion angles were then calculated using a custom Python script, omitting the torsion angles belonging to fluorinated C-terminal and N-terminal residues.

III.VII. Calculation of ¹⁹F NMR Relaxation Rates

¹⁹F longitudinal (R₁) and transverse relaxation rates (R₂) were calculated from MD simulations for each of the four ¹⁹F-Trp CypA protein systems using eqs 1–4.^5,77R₁ and R₂ values for these fluorinated CypA protein variants have been previously determined experimentally using ¹⁹F NMR.⁶⁹ Both types of relaxation rates are affected by dipole–dipole (DD) interactions and chemical shift anisotropy (CSA). The influence of DD interactions is described by eqs 1 and 2

1

2

where γ is the gyromagnetic ratio of fluorine or hydrogen, ℏ is the reduced Plank’s constant, ω is the Larmor frequency of fluorine or hydrogen, and τ_c is the rotational correlation time.

For each frame in the MD simulations, the distances between each hydrogen and the fluorine atoms within a 3 Å radius around the fluorine were calculated (r_FH) and used in eqs 1 and 2 to calculate the relaxation rate contribution to fluorine from each nearby hydrogen. These contributions were summed to account for the influence of all surrounding hydrogen dipoles.

The influence of CSA effects is described by eqs 3 and 4

3

4

where δ_σ is the reduced anisotropy and η is the asymmetry parameter, as described in Haeberlen⁷⁸ convention by the following equations

5

6

7

8

The final relaxation rate values were then calculated as the sum of the individual DD and CSA-based components.

These equations assume the following approximations: (i) protein tumbles isotropically with the rotational correlation time remaining constant, and the fluorinated side-chain motion is governed by the same overall protein rotational correlation time; (ii) fluorine–hydrogen distances close to the F atom remain constant and can be described by a single value; (iii) cross-correlation interactions⁷⁹ are not accounted for, even though a 10–25% cross-term contribution to the total R₂ relaxation rate may be possible;⁶⁹ and (iv) the effects of chemical exchange on R₂ are neither considered nor expected to affect the fluorine on the tryptophan indole ring.

For all CypA variants, a single rotational correlation time (τ_c) of 8.2 ns⁸⁰ was used, along with the ¹⁹F CSA values from solid-state magic angle spinning (MAS) NMR experiments for 4, 5, 6, or 7-fluoro-tryptophans⁸¹ (Table S4) to calculate δ_σ and η. To sample a representative ensemble, only the last 800 ns of each trajectory, from each independent 1 μs production simulation, was used. All fluorine relaxation calculations were carried out using a custom-made and open-source Python program (https://github.com/chonglab-pitt/fluorelax).

IV. Results and Discussion

Our parameters for the eight fluorinated aromatic amino acids were derived using the IPolQ workflow (Figure 2). Briefly, a set of conformations for a capped dipeptide with the fluorinated residue of interest was generated, and electrostatic potentials of each conformation were calculated quantum mechanically, both in vacuum and in the presence of an explicit solvent. The resulting set of vacuum and solvent-phase atomic charges were then optimized to reproduce the respective electrostatic potential calculations, before being averaged to obtain an implicitly polarized charge set. Along with van der Waals interactions, these atomic charges estimate the nonbonded contributions of the force field. With the vacuum-optimized charges, the bonded terms of the force field, such as bond angles and dihedrals, were fit to minimize the error between the molecular mechanical and the quantum mechanical energies of each conformation. Both the atomic partial charges and the bonded parameter derivation steps were repeated until they were self-consistent. To validate our force field parameters, we initially carried out peptide simulations to explore the changes in the conformational free-energy landscape of each fluorinated residue. We then performed protein-based simulations of 4, 5, 6, and 7F-Trp-substituted cyclophilin A (CypA) and compared our simulation results with those of the native CypA protein. Finally, we calculated NMR relaxation rates from our MD simulation data of CypA and compared these rates to the respective, experimentally determined ¹⁹F relaxation rates from NMR.

IV.I. Conformational Preferences of Individual Fluorinated Residues

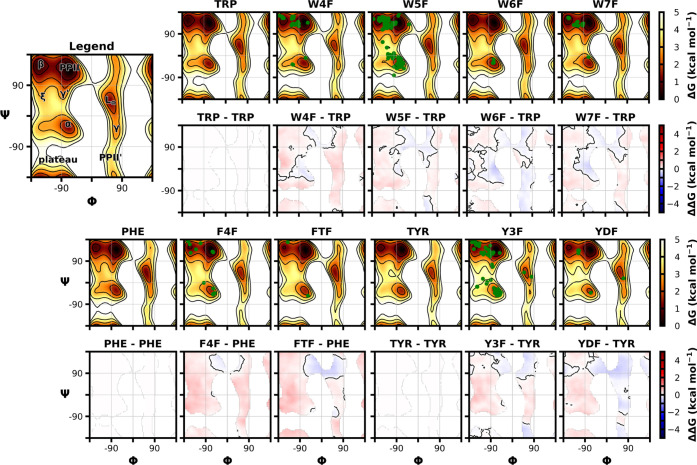
Backbone conformational preferences for the blocked tetrapeptide systems (Ace-Ala-Xaa-Ala-Nme) were assessed using umbrella sampling simulations in which the central residue (Xaa) backbone dihedrals were progressively restrained (Figure 4). In umbrella sampling, a chosen reaction coordinate is initially divided into a series of windows or sections and a harmonic restraint is applied. In our case, this coordinate was the backbone Φ and Ψ dihedrals of the central residue. We choose 10° intervals from −180° to 180° using a force constant of 8 kcal/(mol rad²) to ensure that the reaction coordinate remained within the center of the window during MD simulations (see Methods Section III.V). A series of histograms along the reaction coordinate was generated, and because these distributions were overlapping, our umbrella sampling parameters were determined to be exhaustive and allowed for the corresponding unbiased, free-energy landscape to be recovered using WHAM.⁷⁰⁻⁷² Umbrella sampling was carried out for the fluorinated tetrapeptides as well as their nonfluorinated counterparts (Trp, Tyr, Phe), as depicted in the relative free-energy difference plots (Figure 4). In addition, we compared our simulation results to the experimentally observed conformations for each fluorinated variant extracted from 56 protein structures deposited in the PDB.

Figure 4.

Free-energy profiles for the central residue of tetrapeptides as a function of backbone Φ and Ψ torsions about the central residue, as well as the difference in free energy relative to the canonical nonfluorinated residue containing tetrapeptide. Each system is an Ace-Ala-Xaa-Ala-NMe peptide that underwent umbrella sampling simulations with subsequent application of WHAM. The green-filled circles represent the backbone torsion angles observed for crystal structures that contain the relevant fluorinated residue in their protein structure.

Our results show that most free-energy barriers between different secondary structures were either unperturbed or only slightly increased for the fluorinated residues relative to their nonfluorinated counterparts, indicating less favorable sampling of that region. An exception is the area between the polyproline II (Φ ≈ −70°, Ψ ≈ 140°) and left-handed α helical (Φ ≈ 60°, Ψ ≈ 40°) regions, which were more favorably sampled in all cases for fluorinated residues. For tyrosine and phenylalanine variants, we saw this favorable sampling amplified with more fluorine atoms present in the rings, such as with tyrosine possessing one or two fluorine atoms and phenylalanine with a single fluorine or the trimethyl fluorine group. For tryptophan, our resulting energy landscapes produced a similar trend, except that the α helical (Φ ≈ −70°, Ψ ≈ −20°) and γ′ (Φ ≈ −80°, Ψ ≈ 60°) regions were more favorably sampled, with fluorination at the 6-position of the indole ring exhibiting the largest difference. All dihedral angles of fluorinated residues remained consistent with those experimentally observed in structures deposited in the PDB. The backbone Φ and Ψ torsion angle energies for fluorine-containing peptides are very similar to nonfluorinated peptides, with DDG values ranging from −0.63 to 0.64 kcal/mol for the tryptophan variants, −0.55 to 0.65 kcal/mol for the tyrosine variants, and −0.53 to 0.88 kcal/mol for the phenylalanine variants (Table S3). The average ΔΔG of our nonfluorinated versus fluorinated peptides are all close to zero, further supporting our conclusion that only minimal perturbations are induced upon fluorine substitution. The only exception is for 4-fluoro-phenylalanine, for which an average ΔΔG value of 0.273 ± 0.186 kcal/mol was observed. Overall, these findings are consistent with previous studies where fluorinated tryptophan,^13,82 tyrosine,⁸³ and phenylalanine⁹ substitutions introduced minimal to no differences in the global protein structure or the local dihedral angles around the fluorinated residue.

IV.II. Simulations of Fluorinated Cyclophilin A

To evaluate our force field parameters in the context of a protein, we carried out multiple μs time scale simulations for each of four variants of cyclophilin A (CypA), a 18.3 kDa peptidyl–prolyl isomerase that is a known host factor for HIV-1 infection.⁸⁴ The variants are singly fluorinated at four different indole ring positions of Trp121, which is close to the active site of the protein. These fluorinated variants of CypA have been studied previously⁶⁹ and serve as useful benchmark proteins for our simulation studies.

Our data show that both wild-type and the fluorinated CypA variants all remained stable over the course of multiple μs time scale simulations (Figure 5), and only small deviations are noted. For the wild-type CypA simulations, the average backbone RMSD value is 1.37 ± 0.37 Å (average ± one standard deviation), while the fluorinated Trp121 CypA variants exhibited average backbone RMSD values of 1.28 ± 0.23 Å (W4F CypA), 1.22 ± 0.27 Å (W5F CypA), 1.35 ± 0.31 Å (W6F CypA), and 1.21 ± 0.20 Å, (W7F CypA). RMSD values for each individual 1 μs simulation as a function of simulation time are shown in Figure S2.

Figure 5.

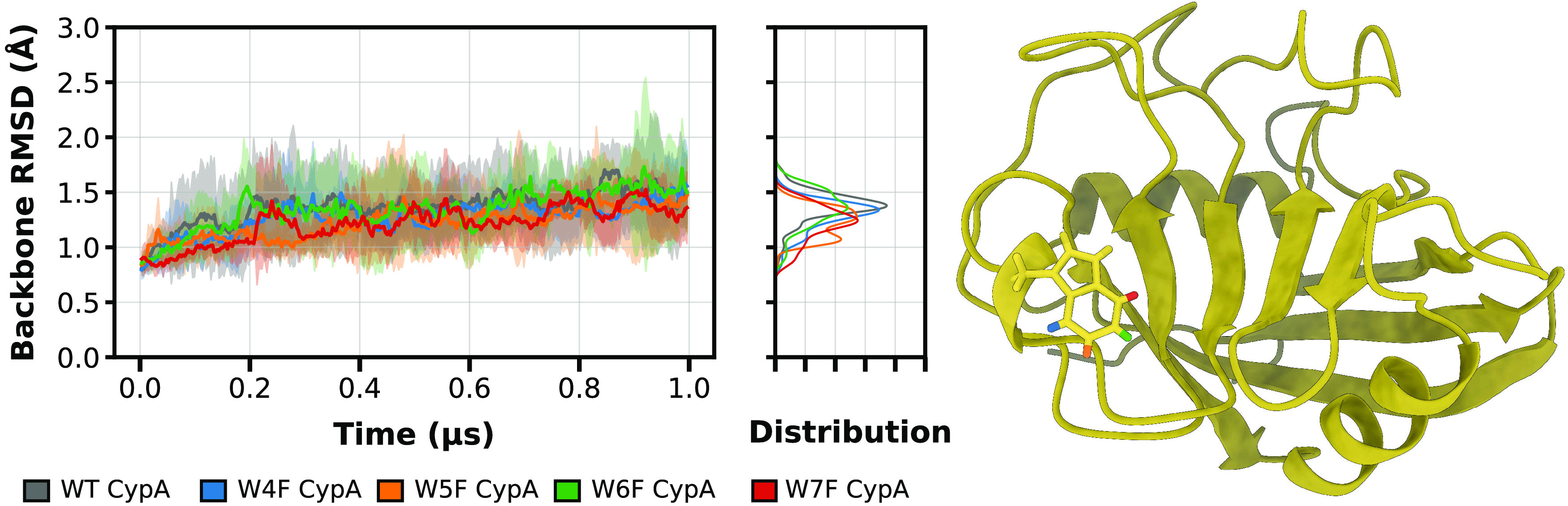
Average backbone RMSD values from the experimental X-ray structure (PDB: 3K0N)⁶⁶ coordinates for native and fluorinated CypA proteins as a function of simulation time. Data shown is based on five independent 1 μs replicates, with one standard deviation of each time point shown in transparent coloration. The distribution of RMSD values is depicted in the middle panel, and the protein structure being simulated is depicted on the right with individual fluorine positions on the TRP121 indole ring colored according to the legend.

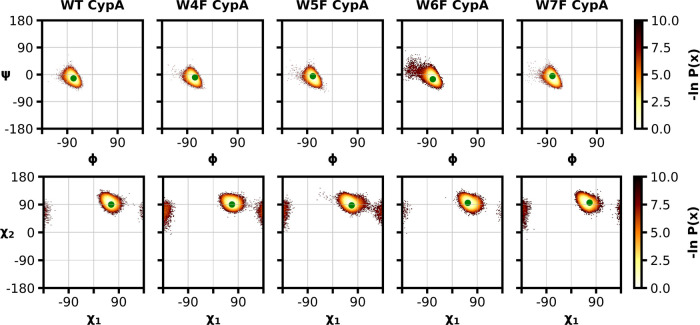
In addition to backbone RMSD values, we also assessed the dihedral angle propensities of our aggregate simulation data by generating Ramachandran (Φ and Ψ) and Janin (χ₁ and χ₂) plots. All dihedral probabilities for the fluorinated CypA proteins remained within the same distribution as that of wild-type CypA (Figure 6). Only for W6F, a slightly larger range of conformational sampling around the α helical region in the Ramachandran plot and a slightly restricted conformational sampling distribution in the Janin plots was noted. These findings are similar to those with our peptide systems, where the W6F substitution also indicated a change in a sampling of the free-energy landscape near the α helical region, compared to the other fluorinated tryptophan moieties (Figure 4).

Figure 6.

Ramachandran (Φ and Ψ) and Janin (χ₁ and χ₂) plots for an aggregate simulation time of 5 μs for fluorinated or native CypA proteins. The green-filled circles indicate the original dihedral angle in either the native CypA crystal structure⁶⁶ or the fluorinated CypA crystal structures at the respective 4, 5, 6, or 7 positions of the indole ring (unpublished data).

When evaluating the backbone RMSD and secondary structure predictions on a per-residue basis (Figure S4), excellent stability was maintained throughout multiple simulation replicates. However, a sharp increase in RMSD and corresponding change in secondary structure was noted between residues 146–153 and 102–107 during a fraction of both the wild-type and fluorinated CypA simulations. We isolated the characteristics of these increases in RMSD and found that they were largely driven by compensatory peptide-plane flips, which occur when changes in |Ψ_i| + |Φ_i+1| are large, while changes in |Ψ_i + Φ_i+1| are comparatively small.⁸⁵ We accessed the per-residue level torsion angles of each trajectory (Figure S5) and found that residues 146–153 are a part of a loop that undergoes a hinge motion that is associated with a peptide-plane flip of residues 149 and 150. Furthermore, residues 102–107 are a part of a β turn that becomes twisted throughout our simulations and is compensated by peptide-plane flips of residues 103/104 and 107/108 (Figure S6).

IV.III. ¹⁹F Relaxation of CypA

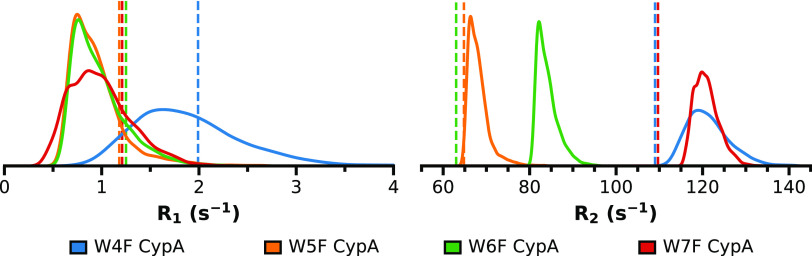
In addition to structural properties, we also evaluated whether longitudinal and transverse fluorine NMR relaxation rates would be accessible from our aggregate CypA simulation data. NMR relaxation rates function as useful probes to study dynamics and depend on the properties of a nucleus, modulated by its local environment. Fluorine relaxation is governed by both dipole–dipole interactions with neighboring proton spins as well as chemical shift anisotropy (CSA).⁵ While dipole–dipole interactions and CSA affect both the longitudinal (R₁) and transverse (R₂) relaxation rates of the fluorine nucleus, dipole–dipole-based contributions dominate R₁ and CSA dominates R₂.

In a first approximation, we calculated R₁ and R₂ from our aggregate CypA simulation data using an overall rotational correlation time τ_c of 8.2 ns⁸⁰ (Methods Section III.VII). For each frame of the MD ensemble, we estimated the dipole–dipole-based relaxation contributions from each hydrogen atom within 3 Å of the fluorine atom. The CSA-based relaxation contributions used previously measured chemical shift tensors from solid-state NMR⁸⁴ (Table S4) and were kept constant for each frame of the MD ensemble. We compared these calculated rates to the measured experimental rates⁶⁹ (Figure 7). Overall, our calculated relaxation rates from aggregate MD simulation data are in good agreement with the experimental values. The average calculated longitudinal rates are systematically somewhat smaller than the experimental values, although within a reasonable error (Table S5). W4F CypA exhibited a somewhat larger R₁ value (∼2 s^–1) than all others, which are similar and grouped around 1 s^–1. The calculated transverse relaxation rates are in good agreement with experimental values for all CypA variants, except for W6F. They can be grouped into two sets comprising W5F and W6F CypA with R₂ values around 60–80 s^–1, and W4F and W7F CypA with R₂ values around 110–120 s^–1. Overall, the calculated relaxation values follow the same trends and agree well with the experimental ¹⁹F NMR relaxation rates.

Figure 7.

Fluorine longitudinal (R₁) and transverse (R₂) NMR relaxation rate distributions extracted from the final 80% of the 5 μs of aggregate MD simulation data for each fluorinated CypA variant. Experimental relaxation rates⁶⁹ (Table S5) are shown as dashed vertical lines.

At this juncture, it should be pointed out that our methodology for calculating relaxation rates from MD simulation data includes several key assumptions. In particular, our calculations assume that (i) the tryptophan side chain essentially moves like the overall protein, i.e., it does not exhibit internal motions in addition to the overall molecular tumbling of the protein (ii) only hydrogens within a radius of 3 Å around the fluorine atom contribute to the relaxation rate, and (iii) any contribution from dipole–dipole and CSA cross-correlated relaxation⁷⁹ is unaccounted for, since they may only contribute 10–25% to the total R₂ relaxation rate.⁶⁹ Furthermore, the experimental relaxation rates are extracted using single exponential fitting of the signal intensity decays, although multiexponential fitting may more accurately capture cross-correlation-induced relaxation.^69,77,86 Despite these differences between the simulation and experiment, as well as their respective assumptions, the simulation-based calculated rates agree surprisingly well with the experimental relaxation rates. In the future, more complex methods^52,87 for fluorine relaxation rate calculations from MD simulations can be tested, which will help to dissect which components predominantly affect relaxation decay rates.

V. Conclusions

We have reported the development and validation of force field parameters for a set of eight fluorinated, aromatic amino acids that are commonly used for ¹⁹F NMR, for use with the AMBER ff15ipq protein force field. Our parameters include 181 implicitly polarized atomic charges and 9 unique bonded terms for 4, 5, 6, and 7-fluoro-tryptophan; 3, and 3,5-fluoro-tyrosine; as well as 4-fluoro- and 4-trifluoromethyl-phenylalanine. We validated that our new parameters maintain the expected conformational propensities of the fluorinated amino acids consistent with both the respective canonical residues and previously characterized experimental X-ray structure-derived propensities extracted from structures deposited in the PDB. Fluorinated amino acid-containing proteins, such as CypA, maintain the overall globular protein fold over multiple μs time scale simulations and extracted ¹⁹F NMR relaxation rates are in good agreement with the corresponding experimental rates.

Overall, our results demonstrate the robustness of the “sweeping optimization” approach using the mdgx program of AMBERTools20 distribution⁶³ and the power of the IPolQ lineage of AMBER force fields for modeling fluorinated proteins. Our workflow is readily applicable to other residue classes³³ and can be easily expanded to include other fluorinated amino acids, if so desired. On the practical side, our force field parameters have numerous potential implications, particularly for use with complementary ¹⁹F NMR studies and when considering structural ensembles. Since ¹⁹F NMR data can be used to guide MD simulations and vice versa, our parameters will aid in deriving an integrated, all-atom view of any fluorinated protein. Our parameters extend the macromolecular chemical space available to the AMBER ff15ipq force field and bridge the gap between the computation and experiment for the collaborative study of fluorinated proteins at the atomic level.

Similar to the IPolQ methodology, the Force Balance approach and the corresponding AMBER-FB15 force field⁸⁸ perform sweeping optimization of hundreds of parameters simultaneously and include nonlinear optimization methods, which can incorporate alternative datasets, such as in vitro experiments, directly into the parameter optimization process. The FB15 force field has also recently been expanded to include parameters for phosphorylated amino acids,⁸⁹ but at this time, it does not have parameters for halogenated residues such as the fluorinated amino acids presented in this work. In contrast to the IPolQ workflow, which is fully physics-based, the burgeoning development of machine learning-based force fields⁹⁰ is promising but is heavily dependent on the training dataset being used. Thus, while physics-based approaches are more generalizable, deep learning methods can be more specialized for specific atoms or dependent on dataset properties. The goal of such machine learning-based approaches is to narrow the gap between the efficiency of classical models and the accuracy of ab initio methods, by training a machine learning model to predict molecular potential energies, usually using quantum mechanical datasets. Examples of these approaches include the ANAKIN-ME^91,92 neural network potential and the OrbNet⁹³ method, which, once fully trained, can accurately predict the energetic properties of organic molecules within chemical accuracy of ab initio density functional theory calculations but at a fraction of the computational cost. In the future, machine learning-based methods may be readily paired with the IPolQ method to further enhance the efficiency of the parameter fitting and optimization process.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.2c00255.

• Atom types for fluorinated amino acids and further analysis of CypA simulations: individual RMSD plots, carbonyl to backbone distances, secondary structure, per-residue RMSD, and per-residue backbone dihedral angles; tables include individual force field bonded parameters, PDB identifier codes for each fluorinated amino acid, relative free-energy differences between blocked tetrapeptides, CSA tensors used for relaxation calculations, and comparison of average relaxation rates to experimental values (PDF)

The authors declare the following competing financial interest(s): L.T.C. is a current member of the Scientific Advisory Board of OpenEye Scientific and an Open Science Fellow with Roivant Sciences.

Notes

Input files, analysis scripts, and the force field parameter files are available from https://github.com/chonglab-pitt/ff15ipq-19F. The Python program for fluorine relaxation calculations is open source and available from https://github.com/chonglab-pitt/fluorelax.