Estimation of Older Adult Mortality from Information Distorted by Age Misreporting

Abstract

Testing theories about human senescence and longevity demands accurate information on older adult mortality. With some exceptions, this is available for most countries in North America, Western Europe and some in Eastern Europe and Asia, but rare in low to middle income countries where the raw data are distorted by defective completeness and systematic age misreporting. For this reason these populations are frequently excluded from empirical tests of mortality and longevity theories thus limiting their reach as they only reflect a small and selected human mortality experience. In this paper we formulate an integrated method to compute estimates of older adult mortality when vital registration and population counts are defective due to inaccurate coverage and/or systematic age misreporting. The procedure is validated with a simulation study that identifies a strategy to compute adjustments that, under some assumptions, performs quite well. While the paper focuses on countries of Latin America and the Caribbean region (LAC), the method is quite general and, with additional information and some model reformulation, could be applied to other populations with similar problems.

1. Background

Empirical testing of theories about the nature of human mortality, senescence and longevity requires accurate information on older adult mortality. This information is available for countries in North America, Western Europe and some in Eastern Europe and Asia, but is rare in low to middle income countries. As a result, empirical tests are incomplete as they reflect only a reduced and selected human mortality experience. Our goal is to describe and illustrate a method to compute adjusted estimates of older adult mortality when vital registration and population counts are subject to errors of completeness and systematic age misreporting. In this paper we use the term ‘adult’ to refer to the population aged 5 and older, ‘older adult’ to populations older than 45, and ‘children’ to populations younger than age 5.

We emphasize at the outset that we are not advertising the proposed technique as a cure-all tool. It is designed to work under some conditions that may be satisfied by some, not all populations. As all techniques of this sort, it is vulnerable to violation of assumptions and should not be applied mechanically without an assessment of consistency between assumptions and observed data.

We assume the investigator has data consisting of yearly deaths and population census counts by sex and single year age groups. These data may be subject to two types of errors. First, death and population censuses counts are defective leading to estimates of mortality rates distorted by errors of ‘relative completeness’, e.g. the ratio of the observed to the true mortality rates. Second, age reporting of populations and deaths counts is deficient and may lead to inaccurate estimates of mortality rates. A well-known class of age reporting errors is age heaping (Myers 1940; Shryock et al. 1971; Gupta 1975). If left uncorrected, it can produce irregular life table functions but, in general, will not lead to systematic biases of statistics that rely on cumulative functions. Furthermore, age heaping is readily detectable and there are well-known and widely accepted adjustment procedures, including redistribution algorithms, smoothing, and high order polynomial fitting of cumulative age distributions. (Sprague 1880; Shryock et al. 1971; McNeil 1977; Camarda et al. 2008).

A second, more insidious, type of error consists of systematic over or under age reporting. If left uncorrected it can impart biases to all estimates of life table parameters. Unlike age heaping, these errors are rarely visible to the naked eye, are difficult to detect with certainty, and cannot be readily adjusted with anything resembling a widely accepted technique (Coale and Kisker 1986; Dechter and Preston 1991; Condran et al. 1991; Preston et al. 1999, 2003).

The method we propose integrates adjustments for defective completeness and identification and correction of systematic age misreporting. Although we only focus on the experience of Latin American Countries (LAC) during 1950–2010, the procedure could be generalized to other populations if and when additional information about conditions producing the observed data is available. We hasten to emphasize that throughout we only address the problem of older adult age misreporting, e.g at ages over 45. While in some demographic contexts, this type of error may also be common at younger ages, this does not appear to be the case in populations in LAC.

The paper is in seven sections. In section 2 we briefly review direction and magnitudes of errors induced by defective vital statistics (death counts) and census enumerations (population counts) in LAC. Section 3 introduces a model of age misreporting that will be used throughout. Section 4 proposes a technique to identify and adjust for age misreporting and section 5 describes a step-bystep procedure integrating adjustment for death underregistration and systematic age misreporting. Section 6 is a detailed empirical illustration. The last section summarizes and highlights advantages and limitations of the integrated procedure.

2. Defective measurement of adult mortality

The post-1950 mortality data in LAC and in most low- to middle-income countries is limited by defective coverage and adult age misreporting. By and large, observed death counts are a variable fraction of the ‘true’ number of deaths as they exclude events that, for a number of reasons, are recorded with delays or never recorded. Since census counts are also distorted by errors of coverage, mortality rates computed with raw data may contain smaller net errors than would be induced by defective vital registration alone. In general, however, the observed mortality rates underestimate true mortality levels.

Another important domain of errors is systematic age over(under) reporting of older adult population counts. Census population counts in LAC are, almost without exception, distorted by older adult age overstatement, particularly at ages 45 and older (Ortega and Garcia 1985; Dechter and Preston 1991; Grushka 1996; Del Popolo 2000).In most cases, systematic age overreporting will lead to underestimates of mortality rates at older adult ages. Indeed, when the (true) age distribution of a population is roughly exponential —as it is always the case in stable and quasi-stable populations—systematic age overstatement of populations induces downward biases in mortality rates at older ages. These biases are not offset when there is an equal propensity to overstate ages at death. The reason these two type of errors do not, as a rule, offset each other is that while both the adult mortality rates and adult population age distribution are roughly exponential, one slopes upwards (mortality rates) whereas the other slopes downwards (population age distribution). Matters are made only worse when, as is almost always the case, the rate of decrease of population by age (natural rate of increase in a stable population) is an order of magnitude lower than the rate of increase of (the log of) adult mortality rates (rate of senescence or Gompertz slope). The consequence is that, unless the propensity to overestimate ages at death is much higher than the propensity to overestimate ages of population, observed mortality rates of older adults will be biased downwards. If left uncorrected, estimates of life expectancy and of the rate of acceleration of the force of mortality at older ages will contain downward biases. Furthermore, as the quality of vital registration and census enumeration improves over time the magnitude of these biases decreases and will induce distortions of the time trajectory of older adult mortality levels and age patterns.

Unlike errors associated with age heaping, distortions caused by systematic age misreporting are harder to diagnose and more difficult to correct. As we show below, adjustments require knowledge of two functions that are generally unknown: (a) the conditional (on age) propensity of individuals to exaggerate (reduce) their true age and (b) the conditional (on age) distribution of the difference between the correct and declared ages. The information needed to estimate these two functions is generally unavailable and, in countries with deficient population and vital records, it is either inexistent or not ready to use.

To solve this problem we propose a model of age misreporting and a technique requiring minimal information to adjust observed adult mortality rates. In its current formulation the technique is applicable to populations whose patterns of age misreporting resemble those found in some LAC countries. While the logic of the method we propose is quite general and could be easily adapted to other populations, a number of considerations need to be kept in mind. First, there are precious few instances in which the researcher has access to at least two independent sources of age declaration, one of which is considered to be “correct” (this excludes the frequent case of a census and a post-enumeration survey). This means that it is difficult to decide ex ante the nature of the age misreporting pattern in the second data source. Second, as we show later, one does not need to know the exact level or seriousness of age misreporting, only its age pattern. This may be a escape route from the problem identified before. However, if the determinants of the levels of age misreporting exert influences on the age patterns, the assumption of independence between the two on which the method proposed rests, will be violated. The problem is that we know very little about the nature of these determinants. The only ones we have some control over are associated with observable individual profiles, namely, age, gender, race or ethnic group. Much less, if anything, is known about cultural or institutional determinants, such as regimes of schooling admission and graduation regimes, regulations regarding military conscription, eligibility rules for health care, unemployment benefits or pensions, all of which operate as checks on the accuracy of individuals’ ages, much as it does the individuals’ levels of education. In sum, applications of the technique to populations with no documentation confirming the nature (not the level) of systematic (not age heaping) age misreporting, should be carried out with caution.

3. A model of systematic adult age misreporting

3.1. Definitions

We begin with a few definitions. Let ${\theta }_x^o$ be the average probability that individuals aged x overstate their age and ${\theta }_x^u$ the average probability that they understate their age. Then $\left(1-{\theta }_x^o-{\theta }_x^u\right)$ is the probability of an accurate age statement at age x. Individuals who over(under) state their age do so by choosing, not always randomly, the age declared in the census. This age could be n > 0 years removed from the true age. As we show below, it suffices to let n range between 1 and 10+ since the number of individuals who over(understate) their age by more than ten years in LAC populations is exceedingly small. Let ${\rho }_x^o(n)$ be the average conditional probability that individuals aged x who overstate ages will do so by n years. An analogous definition applies to the probabilities of age understatement, ${\rho }_x^u$ (n) with ${\sum }_n{\rho }_n^u\left(n\right)={\sum }_n{\rho }_x^o\left(n\right)$ = 1. To compute the population observed at age y, $P_y^o$, we consider the true population count at that age, $P_y^T$, and apply the conditional probabilities defined above to get: or, using a more compact matrix notation:

$$P_y^o=P_y^T\left(1-{\theta }_y^O-{\theta }_y^u\right)+\sum _{n=10}^{n=1}{P}_{y-n}^T{\rho }_{y-n}^o(n){\theta }_{y-n}^o+\sum _{n=10}^{n=1}{P}_{y+n}^T{\rho }_{y+n}^u(n){\theta }_{y+n}^u.$$ (3.1)

or, using a more compact matrix notation:

$${\prod }^o=\mathrm{\Theta }{\prod }^T$$ (3.2)

where ${\prod }^o$ is the (101×1) vector of observed single age population counts at ages 0 to 100, Π^T is the (101×1) vector of true population counts at those ages, and Θ is a 101×101 square matrix of transition probabilities, e.g. the probabilities of ‘migrating’ (via age misreporting) into or out of single year age-groups. The diagonal of Θ contains the probabilities of correctly declaring ages, $\left(1-{\theta }_y^o-{\theta }_y^u\right)$. Entries in the off-diagonal cells pertaining to the yth row and columns y+1,y+2,...,y+10 are the quantities ${\rho }_{y+1}^u(1){\theta }_{y+1}^u,\dots ,{\rho }_{y+10}^u(10){\theta }_{y+10}^u$. Entries in the off-diagonal cells pertaining to the yth row and columns y−1,y−2,...,y−10 are the quantities ${\rho }_{y-1}^o(1){\theta }_{y-1}^o,\dots ,{\rho }_{y-10}^o(10){\theta }_{y-10}^o$. It is possible to retrieve the vector of true population counts by pre-multiplying the previous expression by the inverse of Θ⁻¹, that is

$${\Theta }^{-1}{\prod }^o={\prod }^T.$$ (3.3)

This operation requires full knowledge of the matrix Θ and we only have superficial information about its nature in LAC countries or anywhere else for that matter (but see (Bhat 1990) for an illustration of observed patterns of age misreporting in India). To circumvent this problem we will adopt shortcuts that lead to an estimable and invertible matrix of transition probabilities.

3.2. What do we know about Θ? Patterns of systematic adult age misreporting in population counts

Although there is an extensive literature on systematic adult age misreporting in population counts in low to middle income countries (Mazess and Forman 1979; Bhat 1987, 1990; Coale and Li 1991; Dechter and Preston 1991; Grushka 1996; Del Popolo 2000), high income countries (Coale and Kisker 1986; Condran et al. 1991; Elo and Preston 1994; Preston et al. 1999, 2003) and in US migrant populations groups (Hispanic or Hispanic origins) (Rosenwaike and Preston 1984; Spencer 1984), we know very little about the nature of Θ. Systematic age overstatement has also been invoked to explain the so-called Black-White mortality crossover (Elo and Preston 1994) and the Hispanic paradox of lower mortality in the US (Palloni and Arias 2004).

Partial information on Θ comes from studies involving record linkages (Elo and Preston 1994; Preston et al. 1996; Rosenwaike and Preston 1984; Rosenwaike 1987), post enumeration surveys (Ortega and Garcia 1985), and comparisons of two independent data sources that should produce the same outcomes (Bhat 1990). However, in all these studies the information on population counts is either aggregated in five-year age groups or applies to populations with levels of education higher than those in LAC countries. Lack of age detail is problematic since computation of conditional probabilities in coarse age groups rests on approximations that, if violated, are generally harmful to the accuracy of estimates. Using a transition matrix appropriate for a population with higher or lower levels of literacy than the target one may lead to distortions because age misreporting is associated with a population’s literacy level. In the section that follows we propose an estimate of Θ suitable for LAC populations.

3.3. Estimation of a standard pattern of older adult age misreporting

To estimate Θ we employ an unusual study launched in 2002 by the Central American Center for Population at the University of Costa Rica. This study was designed to assess the quality of information of death registration and the accuracy of the 2000 census counts for an older adult population.One of the components of this study was a linkage of a sample of individual census records with national voting registers, a database that contains information from birth certificates. A stratified sample of census records consisting of 7,426 individuals aged 55 and older in the census were matched to the voting registers. This represents about .81 of the total (observed) sample of census records originally sampled. Observations in the data set are classified by nationality, age (reported and from birth records), sex and education.

To estimate entries of the matrix Θ from this dataset we proceed in two steps:

1. Estimation of probabilities of age over and understatement at ages x, ${\theta }_x^o(V)$ and ${\theta }_x^u(V)$ (V is a vector of individual characteristics): We first estimate a logistic model to predict age misreporting, an event that affected a total of 2,894 individuals (40 percent) of whom 1,992 overreported and 902 underreported. We create a 1/0 binary variable whose value is set to 1 when there is either over or under statement and zero otherwise. To be useful in general applications, the vector V only includes covariates universally available in a population census, namely, age and sex. Since the effects of sex and quadratic age had statistically insignificant effects, the final model we adopt includes true ages as the only predictor. Because by design the sample only includes individuals aged 55 and above, it excludes individuals who reported ages younger than 55. As a consequence, the probabilities of age misreporting and, in particular, age understatement, will be underestimated if the true age falls (approximately) in the neighborhood of ages 55 to 59. To minimize the size of this bias we estimate models using a sample restricted to those who are 60 and older. This reduces the effective sample size from 7,246 to 6,290 of whom 1,786 overreported and 789 under reported. Table 1 displays estimated parameters for over and under stating ages using the weighted sample.

2. Estimation of conditional probabilities of over(under) stating ages by n years, ${\rho }_x^o(n)$ and ${\rho }_x^u(n)$: We estimate a (conditional) multinomial model with 9 categories for n = 1,2...,10+ that includes (true) continuous age as independent variable. The model is conditional on over (under) reporting ages and includes only age as an independent variable. Since the magnitude of age effects is quite small in 6 out of 8 contrasts in models of overstatement and in 5 out of 8 contrasts in models of understatement, we will utilize null models for the conditional probability that the declared age exaggerates (or reduces) the true age by n years. This model summarizes the average pattern of over (under) reporting ages in the population 60 and older. The values of the predicted probabilities of over and understating the true age by n years are in Table 2.

3. Extensions: The quantities estimated above reflect mostly errors in the population 60 and above, partially among those older than 55, and more marginally among those aged 45–49. Although empirical evidence for LAC and other populations suggests that systematic age misreporting (but not age heaping) becomes significant at ages over 55–59, we will include probabilities of misreporting (over and understatement) for ages 45–59. We estimate these using predicted values from the logistic model. This extrapolation is justified on the grounds that the fit of the model is very good and the conditional distribution of years of age misreporting is age invariant.

Table 1:

Estimated parameters of best logistic models for age misreporting.

Variable	Overreporting Coeff(se)	Underreporting Coeff(se)
True age1	0.014(0.0036)	0.002(0.0040)
Constant	−2.127(0.271)	−1.846(0.297)
N	7,402	7,402

¹Models estimated in a sample of 6,290 individuals reported to be older than 60, excluding ambiguous cases a foreign citizens.

Note: All models estimated using sampling weights from the strati ed sample; Coeff corresponds to coefficients andse to standard errors.

Table 2:

Average (conditional) probabilities¹ of age misreporting by n years.

N	Overstating	Understating	Difference
1	0.621	0.510	0.111
2	0.191	0.128	0.063
3	0.079	0.091	−0.012
4	0.040	0.052	−0.012
5	0.023	0.041	−0.018
6	0.015	0.035	−0.020
7	0.009	0.028	−0.019
8	0.007	0.026	−0.019
9	0.005	0.013	−0.008
10+	0.009	0.060	−0.051

¹Predicted values computed from a null multinomial logistic model with 10 categories, from a model estimated in subsample of 1,786 individuals. All models estimated using sampling weights from the stratified sample. Figures may not add up to 1 due to rounding errors.

Although it is now possible to compute an estimate of the target mobility matrix, $\widehat{\mathrm{\Theta }}$, its application to populations other that those similar to Costa Rica may be hard to justify if, as empirical evidence suggests, the severity of age misstatement is a function of a population’s literacy levels.

A less constraining assumption is that while the magnitude or severity is different and may depend on population characteristics, including education levels, the age pattern of age misreporting is similar across countries (irrespective of population education levels). This could be captured by shifting the probabilities of over (under) stating ages by some constant, say ${\varphi }^o$ and ${\varphi }^u$ for over and understatement respectively.

Although this is a reasonable strategy, it generates a new problem, namely, a unique solution for equation (3.2) may not exist since different combinations of ${\varphi }^o$ and ${\varphi }^u$ could yield identical results.To circumvent this difficulty we propose to use an age pattern of probabilities of net age overstatement defined as ${\phi }_x^S={\theta }_x^o-{\theta }_x^u$.

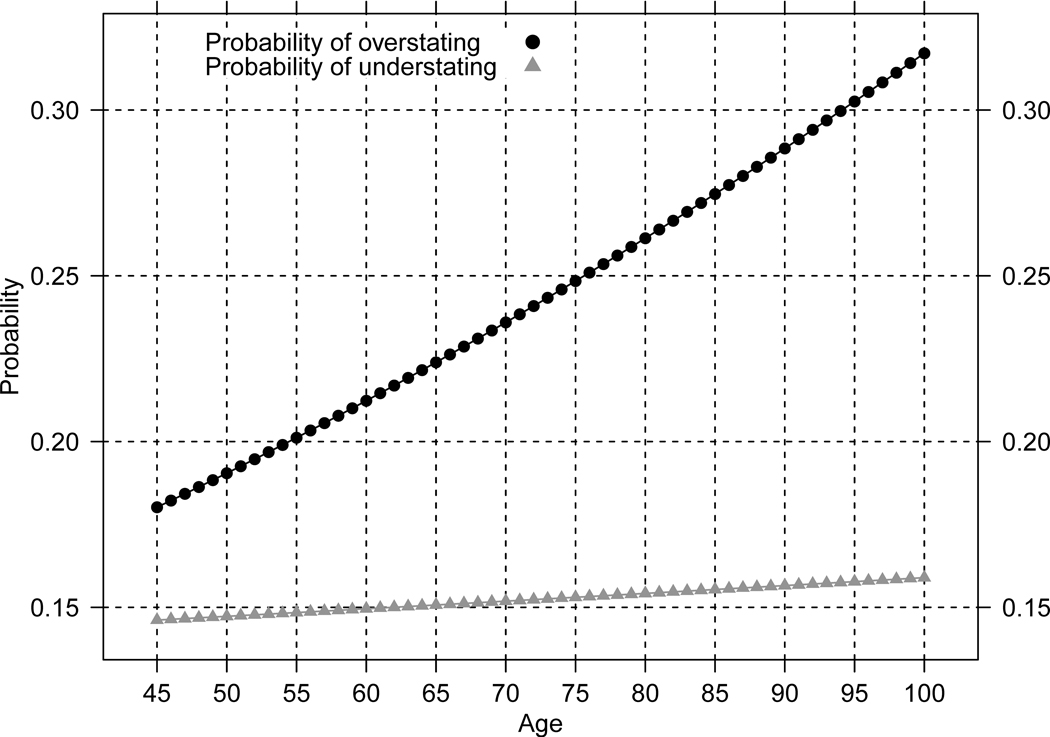
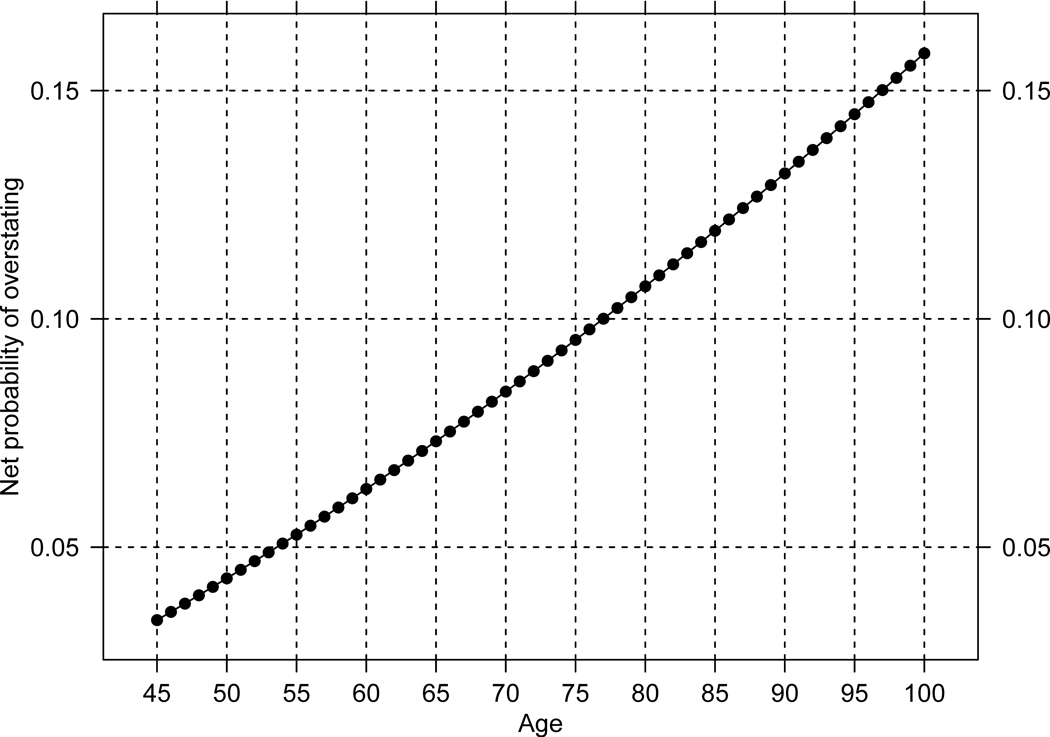
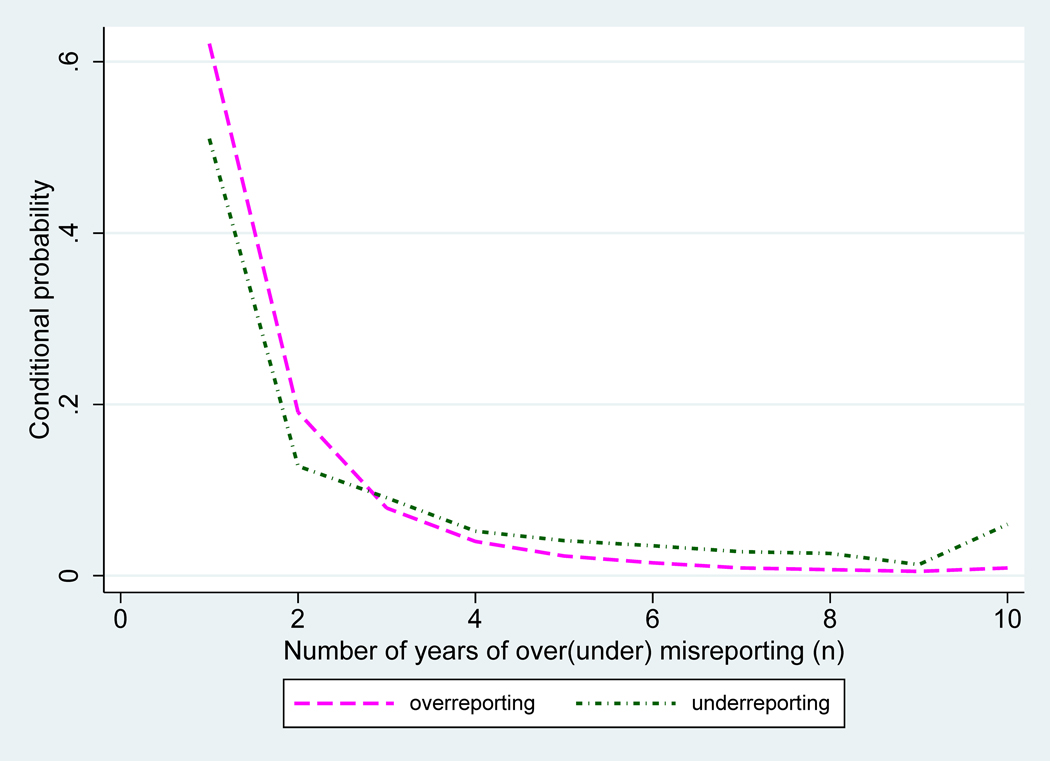
Two conditions must be met before the age pattern of net age misreporting can be useful. First, at all ages older than 45 the probabilities of age overstatement must be larger than the probabilities of age understatement. Second, the conditional distribution of n, the integer number of years by which individuals exaggerate (diminish) their true age, follows a similar pattern among those who over and understate ages. Figure 1 displays predicted (from the logit model) probabilities of over and understating ages by age, $\widehat{{\theta }_x^o}$ and ${\widehat{\theta }}_x^u$, Figure 2 displays the differences ${\phi }_x^S={\theta }_x^o-{\theta }_x^u$ or net overstatement, and Figure 3 shows predicted conditional probabilities of over and under stating ages by n years. These figures confirm that the first condition is always satisfied whereas the second condition is very closely met in these data as the differences in the conditional probabilities of under and overstating age by n years are trifle.

Figure 1.

Predicted probabilities of over- and understating age, by age: Costa Rica 2000

Source: Estimates using a logit model with data from matching study of Costa Rica 2000 Population Census and voting registers (Central American Center for Population at the University of Costa Rica).

Figure 2.

Predicted probabilities of net overstating age, by age: Costa Rica 2000. Source: As for Figure 1.

Figure 3.

Conditional probabilities of over- and understating age by n years, by age: Costa Rica 2000

Source: Estimates using a multinomial logit model with data from matching study of Costa Rica 2000 Population Census and voting registers (Central American Center for Population at the University of Costa Rica).

Jointly, the set of age-specific probabilities of net overstatement (Table 1) and associated conditional probabilities of overstating by n years (column 1 in Table 2), constitute what we will refer to as a standard pattern of age net overstatement. The introduction of this standard pattern simplifies the off-diagonal cells of a redefined matrix of net age overstatement, ${\widehat{\mathrm{\Theta }}}^s$, as all entries for age understatement become zeros. Under conditions described below, identification is possible and a unique solution for ${\varphi }^{no}$, a parameter measuring the magnitude of net overstatement relative to the standard pattern, is possible.

The formulation we propose defines observed patterns of net age overstatement as constant multiples of the standard pattern. Although this simplifies description, it should be borne in mind that the standard pattern is a set of probabilities, all bounded by 1 and, therefore, permissible values for the constant must be bounded above and below. Simple logit transform can resolve this.

3.4. Systematic misreporting of adult ages at death

Up to this point we focused solely on age misreporting in population counts. Although we know much less about about misreporting of ages at death, there is evidence suggesting that it also takes place (Rosenwaike1987; Coale and Li 1991). A handful of studies based on record linkages show that misreporting of ages at death does occur and is also dominated by age overstatement (Rosenwaike and Preston 1984). Additional empirical evidence originates in applications of techniques that detect footprints of overstatement of ages at death in a number of low and high income countries(see below). If so, it may be possible to estimate a transition matrix just like Θ but specialized to death counts. The information required is the following: (a) reported ages at death, (b) accurate dates of death, (c) accurate birth dates. To our knowledge, there are no examples of a data set that combines all three sources of information in LAC nor is there an empirical estimate of the associated transition matrix.

To circumvent this roadblock we rely on the following “identity”: there is a standard pattern of age net overstatement of death counts identical to the standard pattern of age net overstatement of population counts and, in addition, the level or magnitude of misreporting could be different in death and population counts. Although, as we show below, this leads to a simple solution of the problem, the assumption is quite strong and requires at least crude tests to assess its accuracy. We pursue these later in the paper.

We can now compactly define the final model of age misreporting in a set of two equations with two unknown parameters:

$${\prod }^o={\varphi }^{no}{\widehat{\mathrm{\Theta }}}^s{\prod }^T$$ (3.4)

$${\Delta }^o={\lambda }^{no}{\widehat{\mathrm{\Theta }}}^s{\Delta }^T$$ (3.5)

where Π^T and Π^o are the true and observed population age distributions, ${\varphi }^{no}$ is the level of net population age overstatement relative to the standard pattern embedded in ${\widehat{\mathrm{\Theta }}}^s$, Δ^T and Δ^o are the true and observed age distributions of death counts, and ${\lambda }^{no}$ is the level of net death age overstatement relative to the standard pattern embedded in ${\widehat{\mathrm{\Theta }}}^s$.

In closed populations equations (3.4) and (3.5) are naturally related and it is unlikely that solving for the two unknowns, one equation at time and, as shown in Appendix A, this will always lead to under-identification of ${\varphi }^{no}$ and ${\lambda }^{no}$. A brief proof of lack of identification is in Appendix A. In sections 4.2 we propose a strategy that leads to a satisfactory treatment of the problem.

4. Identification and estimation of errors due to systematic age misreporting

We first describe tools to identify the existence and nature of age misreporting in empirical data. We then combine these tools with the model in (3.4) and (3.5) to estimate the two unknown parameters of age misreporting from observed data. Finally, we describe a step-by step adjustment procedure.

4.1. Identification of systematic age misreporting

A key component of our analysis is the detection and identification of patterns of age misstatement in the population and death counts. The model discussed before suggests that distortions associated with age misreporting in population and death counts is more complex than those involving faulty completeness. Similarly, and unlike the case of age heaping, detecting the problem is difficult and, in the absence of overt and striking regularities, is likely to remain unnoticed.

There are two strategies to identify the existence of systematic age over(under) statement in either population or death counts. The first one requires external data sources with correct dates of birth (or ages) that can be compared to age-specific population (death) counts. These types of record linkages using multiple sources are costly and require resolution of complicated confidentiality issues.

A second strategy is much less data demanding, considerably less expensive, and simple to apply. However, it can only detect but not correct age misreporting and provides only a handful of clues about its nature. The procedure was first proposed by Preston and colleagues (Rosenwaike and Preston1984; Bhat 1990; Elo and Preston 1994; Grushka1996) and has been applied in countries of North America, Western Europe and in Latin America (Condran et al. 1991; Dechter and Preston 1991; Grushka 1996; Del Popolo 2000; Palloni and Pinto 2004). In a nutshell, the method consists of comparing cumulative population counts in a census in year t₁ to the expected cumulative population counts in a second population census in year t₂. The computation of expected quantities requires both an initial census opening the intercensal interval, a second census counts at time t₂ closing the intercensal interval, and age specific deaths counts in the intercensal period spanning an interval of k = (t₂ − t₁ + 1) years. The ratio of observed to expected population is an indicator of age misstatement:

$$cm{R}_{x,\left[t_1,t_2\right]}^o=\frac{cm{P}_{x+k,t_2}^o/cm{P}_{x,t_1}^o}{1-\left(cm{D}_{x,\left[t_1,t_2\right]}^o/cm{P}_{x,t_1}^o\right)}$$ (4.1)

where $cm{P}_{x,t_1}^o$ and $cm{P}_{x+k,t_2}^o$ are cumulative populations above ages x and x+k in the first and second census, respectively, and $cm{D}_{x,\left[t_1,t_2\right]}^o$ is the cumulative (intercensal) number of deaths after age x experienced by the cohort aged x in the first census. This expression is a simple contrast between two different estimators of the same underlying unobserved parameter, namely, the cumulative survival ratio: the denominator uses the complement of the observed ratio of (cumulative) intercensal deaths to the (cumulative) population in the first census, whereas the numerator expresses the same parameter as a survival ratio computed from the cumulative counts in two successive population censuses.

The behavior of this index can be summarized as follows:

1. When there are no errors, the values of the two estimates of the cumulative survival ratios will be identical and the index will be exactly 1;

2. When there is systematic age overstatement of population counts ONLY, the index will be less than 1 and will slope downward with age;

3. When there is systematic age overstatement of death counts ONLY, the index will be larger than 1 and will slope upwards with age;

4. When there is systematic age overstatement of BOTH population and death counts, the index will be generally larger than 1 and, with some exceptions, will slope upwards with age (but much less so than in case (3) above).

Appendix B contains an informal algebraic justification of the expected behavior of the index under the conditions specified above.

The foregoing description suggests that the observed sequence of values cmR_x,[t1,t2] provides partial indication, albeit not completely unambiguous, about the nature and levels of systematic age misreporting in any particular case. Before venturing too far, however, three notes of caution are needed. First, empirical patterns of age overstatement of deaths and populations could offset each other and produce ratios close to 1. That is, it is possible (but unlikely) that in scenario (4) the ratios cmR_x,[t1,t2] are 1 at all ages even though there is net age overstatement in population and death counts. Because of this possibility, diagnostics based on the observed value of cmR_x,[t1,t2] alone can only detect consistency (including error consistency) rather than accuracy of age declaration in population and death counts (Dechter and Preston 1991).

Second, throughout we assumed that there is perfect coverage of both population and death counts and that the sequence cmR_x,[t1,t2] could only be distorted by age misreporting. This is an unrealistic assumption, at least in LAC countries. In Appendix B we show that, under conditions of defective census and death registration coverage, the values of the sequence cmR_x,[t1,t2] will also depend on C_t1, C_t2 and CD_[t1,t2], the completeness of the first and second census, and the average completeness of intercensal death registration, respectively. The quantities C_t1, C_t2 and CD_[t1,t2] are the ratio of the observed to the true counts in the first and second census and death respectively. Following standard practice, we assume that completeness of population and death registration are age invariant. In the evaluation study described later we identify procedures that are robust to violations of this assumption. This result justifies following standard practice throughout. As shown in Appendix B, the intrusion of C_t1, C_t2 and CD_[t1,t₂] in the expression for cmR_x,[t1,t₂] makes it impossible to separate the influence of age overstatement and of defective completeness. Lack of completeness will generate values of the index that are far away from 1 even if there is no age misreporting at all. As a consequence, the observed values of cmR_x,[t1,t2] cannot be used to infer patterns of age misreporting unless population and death counts are first suitably adjusted for defective completeness. Well-known adjustment techniques for completeness of population and death counts are identified and evaluated in Appendix C and D.

Third, like defective completeness, intercensal migration flows will distort the sequence of values cmR_x,[t1,t2] even in the absence of errors in population and death counts or age distributions. If migration is known to have taken place, the observed ratios must be adjusted for age specific migration counts.

The technique to estimate the unknown parameters described below assumes that values of cmR_x,[t1,t2] have been computed with data adjusted for defective completeness and migration.

4.2. Estimation of levels (severity) of age misreporting

Is it possible to use the adjusted- for- completeness sequence of values cmR_x,[t1,t2] to retrieve the two unknown parameters, ${\lambda }^{no}$ and ${\varphi }^{no}$? Under some conditions, a handful of solutions are possible. These depend on regularities discovered in an exploration of the effects of systematic age misreporting in simulated populations described below.

4.2.1. Simulated populations

To assess the effects of age misreporting we generated a very large number of simulated populations (N = 63,720) and their trajectories during a 100 year time span. The assessment we describe in this paper uses only one intercensal interval, roughly corresponding to 1970–80. This large set includes a broad range of stable and non-stable populations, population and death counts with defective completeness, and population and death age distributions distorted by patterns of age misreporting described before.

Below we use the simulated populations to investigate the behavior of the sequence of values cmR_x,[t1,t2]. In particular, we examine the relation between adjusted values of cmR_x,[t1,t2] and the pair of unknown parameters for levels of age misreporting of deaths and population.

4.2.2. An important regularity in the simulated populations

Given its nature, it should be intuitively clear that the adjusted (for completeness and migration) sequence of values cmR_x,[t1,t2] must be closely related to age and the magnitude of net age overstatement, namely, ${\lambda }^{no}$ and 𝜙^no. Less intuitive is the nature of such a relation. It came as a surprise to us that a very simple linear model captures the relation in the simulated population. The model is as follows:

$${\left(cm{R}_{ix,\left[t_1{,t}_2\right]}\right)}^{-1}={\alpha }_{0x}+{\alpha }_{1x}{\lambda }_i^{no}+{\alpha }_{2x}{\varphi }_i^{no}$$ (4.2)

where i is an index for the simulated population, x ≥ 45 refers to age and, importantly, the values of cmR_ix,[t1,t2] are distorted only by age misreporting, not by defective completeness.

In this model the independent “variables” are the values of the levels of age misreporting λ_i^no and 𝜙_i^no in the ith population whereas α_0x, α_1x and α_2x are parameters estimable from the simulated data. Table 3 displays estimates of coefficients for the independent variables λ_i^no and 𝜙_i^no from these simulated population. The table shows that the fit of the model is very good and, importantly, that the estimated values of the constant of the model is always close to 1, as it should be when the parameters λ_i^no and 𝜙_i^no drift to 0. The range of feasible values of the parameters of interest is in the closed interval ∼ [0,3]. Values outside this range produce implausible death and population age distributions (See Appendix C).

Table 3:

Regression model relating index of age misstatement and parameters of age misreporting.

Age	α0	α1	α2	R2
45	0,99750	−0,02605	−0,00351	0,9996
46	0,99874	−0,01187	−0,00426	0,9996
47	0,99925	−0,00599	−0,00490	0,9996
48	0,99954	−0,00278	−0,00555	0,9996
49	0,99973	−0,00062	−0,00623	0,9996
50	0,99988	0,00104	−0,00699	0,9997
51	1,00002	0,00245	−0,00785	0,9997
52	1,00015	0,00377	−0,00886	0,9997
53	1,00028	0,00505	−0,01004	0,9996
54	1,00043	0,00636	−0,01140	0,9996
55	1,00059	0,00772	−0,01299	0,9995
56	1,00077	0,00918	−0,01483	0,9995
57	1,00100	0,01090	−0,01698	0,9994
58	1,00130	0,01293	−0,01951	0,9993
59	1,00169	0,01537	−0,02252	0,9992
60	1,00219	0,01830	−0,02612	0,9991
61	1,00283	0,02173	−0,03033	0,9990
62	1,00365	0,02575	−0,03526	0,9989
63	1,00472	0,03058	−0,04117	0,9987
64	1,00612	0,03647	−0,04836	0,9985
65	1,00797	0,04371	−0,05717	0,9983
66	1,01040	0,05240	−0,06776	0,9980
67	1,01360	0,06275	−0,08046	0,9977
68	1,01791	0,07543	−0,09610	0,9974
69	1,02375	0,09123	−0,11566	0,9969
70	1,03163	0,11114	−0,14036	0,9965
71	1,04227	0,13588	−0,17126	0,9959
72	1,05678	0,16619	−0,20957	0,9953
73	1,07669	0,20367	−0,25758	0,9945
74	1,10412	0,25015	−0,31805	0,9936
75	1,14202	0,30774	−0,39439	0,9926

How can the above finding help us to estimate the unknown parameters ${\lambda }^{no}$ and 𝜙^no? If the population observed by the investigator is a member of the simulated set, the observed sequence of values (cmR_ix)⁻¹ must obey equation (4.2). Thus, knowing what the values of α_0x, α_1x, and α_2x are (in the simulated populations) suffices to identify the unknown parameters that generate the sequence cmR_x,[t1,t2]. This requires to simply “invert” the relation represented by (4.2) as follows: for any observed population we define the vector of values [cmR_x,[t1,t2]]⁻¹ for all x > 45 as the ‘dependent variable’ and the corresponding vectors containing the values of the coefficients for ages x > 45 in Table 3 as the “independent variables”. We then estimate a regression equation using as many observed values of [cmR_x,[t1,t2]] as there are single year age groups in the observed data. The estimated regression coefficients will be unbiased estimates of the pair of unknown parameters (${\lambda }^{no}$, 𝜙^no) in the set of simulated populations. It follows, that they will also be unbiased estimates of the same parameters in the observed population as long as this belongs to the simulated set.

Table 4 displays results of the inverse procedure applied to the simulated populations with a limited combination of values of the unknown parameters. The first two columns of the table display estimates of the parameters ${\lambda }^{no}$, 𝜙^no whereas the third and fourth columns display the actual values of these parameters in the simulated data. The last column of the table displays the values of R². The table shows that, given the vector of values {cmR_x=45, …, ₁₀₀} from the simulated populations and the vectors of parameters {α_1x=45, …_,100} and {α_2x=45 …_.,100} extracted from Table 3 and used as independent variables, there is a best (in mean squared error sense) solution for the unknown parameters of model (4.2). The model (4.2) is ‘best’ in the sense that interaction terms or higher order moments of the independent variables do not reduce the mean squared error by a statistically significant amount. A comparison of ‘true’ (first and third columns) and estimated parameters (second and fourth columns) reveals satisfactory concordance. If one of the unknown parameters is close to 0 (the simulated data contains no age overreporting) the inverse technique could produce a negative estimate for that parameter. But even so, it will always generate an accurate estimate for the other parameter as long as it is different from zero. A negative estimate is thus a tell-tale sign that the unknown parameter is too close to its lowest boundary (e.g no systematic age overstatement) and adjustments should only be a function of the other unknown parameter.

Table 4:

Results of inverse method to recover parameters of age misreporting.

run	${\varphi }^{no}$	${\widehat{\varphi }}^{no}$	${\lambda }^{no}$	${\widehat{\lambda }}^{no}$	$R^2$
1	0.000	0.061	0.350	0.370	1.000
2	0.000	0.002	0.700	0.685	1.000
3	0.000	−0.059	1.050	0.999	1.000
4	0.000	−0.118	1.400	1.313	1.000
5	0.000	−0.178	1.750	1.628	1.000
6	0.000	−0.238	2.100	1.942	1.000
7	0.000	−0.298	2.450	2.256	1.000
8	0.000	−0.358	2.800	2.571	1.000
9	0.350	0.393	0.700	0.727	1.000
10	0.350	0.392	1.050	1.078	1.000
11	0.350	0.391	1.400	1.429	1.000
12	0.350	0.390	1.750	1.780	1.000
13	0.350	0.388	2.100	2.130	1.000
14	0.350	0.387	2.450	2.481	1.000
15	0.350	0.386	2.800	2.832	1.000
16	0.700	0.710	1.050	1.067	1.000
17	0.700	0.755	1.400	1.445	1.000
18	0.700	0.801	1.750	1.823	1.000
19	0.700	0.846	2.100	2.201	1.000
20	0.700	0.892	2.450	2.579	1.000
21	0.700	0.938	2.800	2.957	1.000
22	1.050	1.013	1.400	1.393	1.000
23	1.050	1.096	1.750	1.791	1.000
24	1.050	1.179	2.100	2.189	1.000
25	1.050	1.262	2.450	2.587	1.000
26	1.050	1.345	2.800	2.985	1.000
27	1.400	1.303	1.750	1.704	1.000
28	1.400	1.416	2.100	2.117	1.000
29	1.400	1.530	2.450	2.530	1.000
30	1.400	1.643	2.800	2.943	1.000
31	1.750	1.582	2.100	2.004	0.999
32	1.750	1.720	2.450	2.427	1.000
33	1.750	1.859	2.800	2.851	1.000
34	2.100	1.851	2.450	2.292	0.999
35	2.100	2.009	2.800	2.723	1.000
36	2.450	2.110	2.800	2.569	0.998

4.2.3. Alternative regression estimates

Although the simple regression procedure outlined above may work well in most cases, it is desirable to deploy other methods to generate a range of estimates of the unknown parameters and to reveal, at least informally, the uncertainty associated with adjustments. To accomplish this, we propose two different strategies.

1. Constrained regressions. The very large set of simulated populations include values of parameters ${\lambda }^{no}$, ^no within a range, ∼ [0,3]. Thus, an obvious strategy is to estimate a regression model constraining the estimates to be within this permissible parameter space only. It is, of course, important to verify that the regression fits the data well. In addition, the constrained estimates should be approximately equal to the unconstrained ones. Significant differences may be an indication of violation of some of the assumptions.

2. Optimal regression. We could define a countable set of possible combinations of values of the unknown parameters ${\lambda }^{no}$, ${\varphi }^{no}$ within the permissible range. Each pair will generate a set of predicted values for the elements of the vector cmR_x,[t1,t2]. The mean (median) absolute difference between these predicted vectors and a vector of 1’s is a measure of errors associated with the combination of parameters ${\lambda }^{no}$, 𝜙^no that generated the predicted vector. One could then choose the combination that minimizes the mean (median) absolute difference between the two vectors. It may be the case that there are multiple pairs of estimates that perform well and distinguishing among them could be difficult. If so, a plausible strategy is to construct adjusted life tables with each of the competing pairs of estimates. In a subsequent step one reevaluates their performance in light of the consistency of the adjusted life tables with other known life tables for the same population in different periods.

4.2.4. Important checks

All three regression methods described above should only be applied if the data passes two basic checks. The first is that the sequence of values cmR_x,[t1,t2] must be free of errors associated with defective completeness. To ensure that this is the case the observed sequence must be adjusted for defective completeness. The adjusted values of the sequence are computed as follows

$$\left(ADJcm{R}_{x,\left[t_1,t_2\right]}\right)=\frac{\left(C_{t_2}/C_{t_1}\right)\ast \left(cm{P}_{x+k,t_2}^o/cm{P}_{x,t_1}^o\right)}{1-\left(.5\ast \left(C_{t_1}+C_{t_2}\right)/C{D}_{\left[t_1,t_2\right]}\right)\ast \left(1/\left(\left(C_{t_1}/C_{t_2}\right)+1\right)\right)\ast \left(cm{D}_{x,\left[t_1,t_2\right]}^o/cm{P}_{x,t_1}^o\right)}$$ (4.3)

an expression that includes the observed data and the estimated adjustment factors for completeness.

The second check must ensure that the sequence of adjusted values is well-behaved. By this we mean that it must contain only positive values and there should be no sharp discontinuities. Negative values and sharp discontinuities can be caused by inappropriate adjustments for relative completeness of death registration and/or violation of some or all of the assumptions supporting the use of the standard of age misreporting. But they can also be a consequence of erratic behavior of very low counts of population and deaths at extreme ages. In this case, it is advisable to trim the age groups included in the regression equation.

4.2.5. A regression-free solution

A regression-free approach yields a more general solution. It can be implemented by first constructing the matrix ${\widehat{\mathrm{\Theta }}}^s$ using the standard patterns of age misreporting. With this matrix it is possible to compute partially adjusted vectors of populations in both censuses and intercensal deaths. These adjusted vectors are associated with a unique sequence of values cmR_x,[t1,t2] that corresponds to what would be observed if the pattern of age misreporting is well identified and the true parameters ${\varphi }^{no}$ and ${\lambda }^{no}$ were equal to 1. One can then search for alternative values for the pair of unknown parameters and repeat the computations. In each case, a new sequence of values cmR_x,[t1,t2] will be generated. Each of these sequences is associated with a measure of error, namely, the mean (median) absolute deviation from 1. One can then choose the pair of estimates that generates a sequence with minimal mean (or median) absolute deviation from 1 as the best possible estimates for the observed data. As in the case of an optimal regression, multiple pairs may perform well and the investigator may need exogenous criteria to choose among competing pair of parameter estimates.

5. An integrated procedure to remove distortions due to adult age misreporting

As argued before, a condition for the application of the above technique is that the sequence of values cmR_x,[t1,t2] be adjusted for defective deaths and populations counts. Choosing a suitable procedure to do this, however, is complicated because there are multiple candidate methods to choose from, each with its own idiosyncracies, advantages, and shortcomings. To establish solid grounds for selecting an optimal adjustment method, we use the simulated populations and evaluate the performance of several techniques (see Appendices C and D). This evaluation study suggests the following strategy to compute final adjustments for age misreporting:

1. In the absence of exogenous information about the difference in completeness between the two census, obtain estimates of relative completeness of the two census enumerations. Brass (Brass 1979b, a) proposed a couple of procedures to estimate these quantities, one resting on the assumption of stability and another applicable to more general populations. To our knowledge, Hill(Hill and Choi 2004; Hill et al. 2009) suggested the use Brass’s method to adjust intercensal rates of growth rate before using methods to estimate defective dearth registration (see (ii) below). We will refer to this adjustment as the Brass-Hill method.

2. Use the estimate of relative completeness obtained in the first step to correct the rates of intercensal growth and then apply one of the variants of Bennett and Horiuchi (1981) technique to estimate relative completeness of death registration;

   At this point one can choose one of the following two options (or both)

3. a Use results from (i) and (ii) to compute an adjusted sequence of values cmR_x,[t1,t2] and apply the inverse technique in one of its three variants, unconstrained, constrained and optimal, to retrieve estimates of the unknown parameters ${\lambda }^{no}$, ${\varphi }^{no}$. or, alternatively, iii.a iii.b Use the regression-free approach to obtain best estimates of the unknown parameters;

4. Compute the matrix of age misreporting, ${\widehat{\text{Θ}}}^S$ and its inverse. Use these matrices and the estimates of levels of age misreporting for the unknown parameters, ${\lambda }^{no}$ and ${\varphi }^{no}$, obtained in step (iii.a) and/or (iii.b). Finally, use expressions (3.4) and (3.5) and the observed vectors of population and deaths, Π^o and Δ^o, to compute adjusted populations and intercensal deaths counts.

5. Calculate mid-intercensal period mortality rates and adjust then for defective completeness;

6. Compute an intercensal life table, centered in mid-period, with the adjusted intercensal mortality rates.

Needless to say, application of the integrated procedure requires a preliminary investigation to assess if the assumptions on which it rests are indeed satisfied. To support this assessment, Appendix E contains a sensitivity analysis with a partial evaluation of errors induced by departures from the assumptions about patterns of age misreporting in population and death counts.

6. Empirical illustration

We apply the integrated procedure to data for Guatemala in the intercensal period 1981–1994. Despite much recent progress, the country’s death registration and census counts are still defective and offer good testing grounds for the technique as estimates of relative completeness of death registration in Guatemala after 1950 range between .75 and .91.

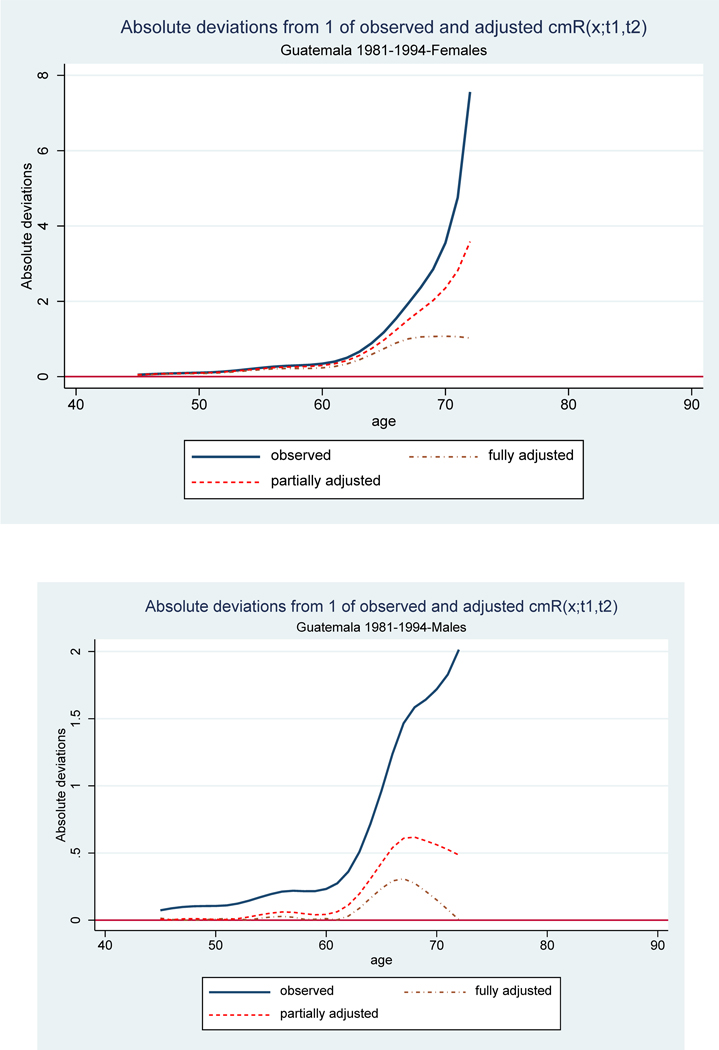
Figure 4 displays plots of deviations of observed, partially, and fully adjusted sequences cmR_{x,[1981,1994]} from 1. The observed sequences reflect the impact of both defective completeness and age misreporting. They exhibit the expected upward slope caused by systematic age overstatement of both population and deaths. Large values of the sequence (and even sharp discontinuities leading to negative values) at very old ages are not uncommon and may not always be a sign of unusually large age overstatement. It could also be an artifact of random fluctuations of small counts at these ages and/or a result of inappropriate adjustments for defective census or vital registration coverage. The median values of absolute deviations are .30 for females and .21 for males.

Figure 4.

Absolute deviations of observed, partially, and fully adjusted values of cmRx,[1981,1994] from vector of ones, by sex: Guatemala 1981–94. Source: Authors’ calculations. Data and code available at https://gitlab.com/csic-echo/lambda-pop

To remove errors due to defective completeness we estimate completeness of the first census relative to the second, C₁₉₈₁/C₁₉₉₄, 1.03 for males and .98 for females, and relative completeness of death registration, CD_[1981,1994]/(.5 ∗ (C₁₉₈₁ + C₁₉₉₄), .90 and .89 for males and females. We multiply the observed values of the function cmR_{x,[1981,1994]} by the correction factor (see equation 4.3) and obtain the sequence of partially adjusted values plotted in the figure. As shown in the figure, adjustment for defective completeness significantly improves the behavior of the sequences, particularly among males but less so among females. The maximum deviation for males drops from about 2 to .5. Among females the reduction is from 7.5 to about 3.5. The median values are .27 and .056 for females and males respectively.

To adjust for age misreporting we choose the regression-free method. To do so, we identify the pair of values for ${\lambda }^{no}$ and ${\varphi }^{no}$ that, when used jointly with the adjustment for defective completeness, yields a best fitting sequence cmR_{x,[1981,1994]}, e.g. one that minimizes absolute deviations from a vector of 1’s. These best estimates of ${\lambda }^{no}$, ${\varphi }^{no}$ are in the range (0,.5) and (2–2.5) for females and (0-.5) and (1.5–2) for males. The parameters ${\lambda }^{no}$ and ${\varphi }^{no}$ are real numbers and can attain an uncountable number of values in the permissible range. To short-circuit the search of the optimal pair we looped through all 36 possible combinations of discrete values 0, .5, 1, 1.5, 2.0 and 2.5. Thus, strictly speaking the solution we present here only identifies a range of values within which the “true” values are contained.

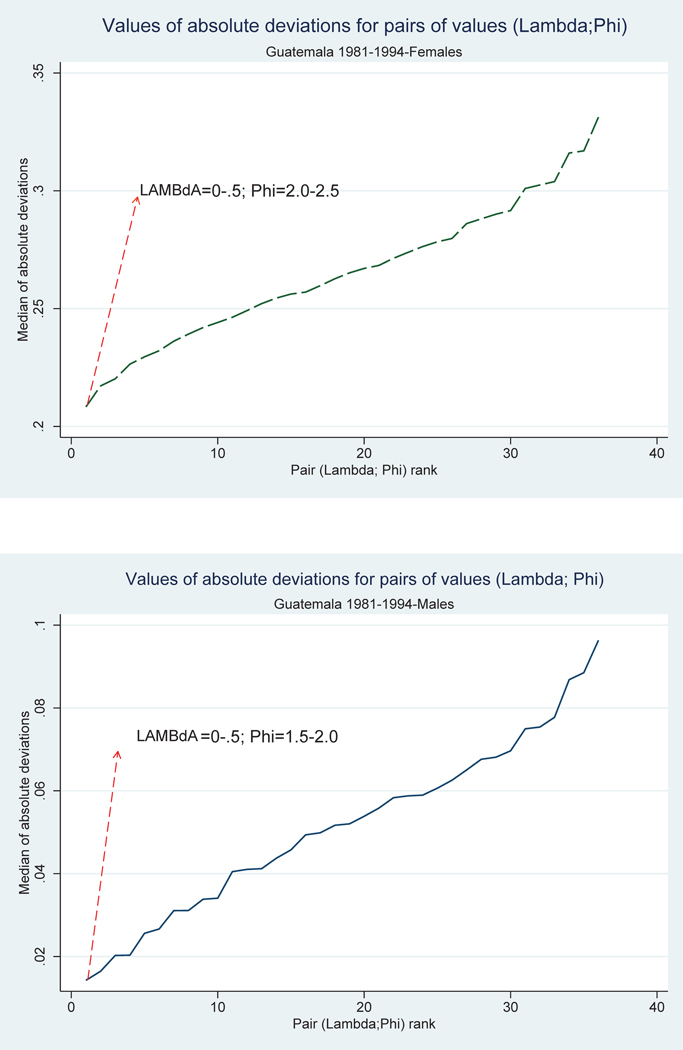
Figure 5 plots the median values of deviations of the fully adjusted sequences. The figure plots the median deviations of the fully adjusted sequences for each of the 36 pairs of parameters values. Before plotting, we rank the absolute deviations in ascending order so that the lowest value to the left of the graph is associated with the pair of optimal parameter estimates. In contrast, the highest value is associated with the worst performer pair. The scale of the x-axis is arbitrarily set to the natural numbers reflecting the rank order of the absolute deviations. In the case of females, for example, the minimum median value of absolute deviations from 1 was generated by estimates of ${\lambda }^{no}$ in the range (0-.5) and estimates of ${\varphi }^{no}$ in the range (2.0–2.5).

Figure 5.

Median of deviations of fully adjusted values of cmRx, [1981,1994] from vector of ones for 36 pairs of unknown parameters, by sex: Guatemala 1981–94 Note: Absolute deviations are ranked in ascending order from left to right. Source: As for Figure 4.

Ideally, the fully adjusted values of the sequence cmR_{x,[1981,1994]} should be equal to or very close to 1. The smallest medians of absolute deviations of fully adjusted values from a vector of 1’s plotted in the figure are .014 and .21 for males and females. They represent 7 and 70 percent of the male and female observed values, respectively, and 26 and 78 percent of the partially adjusted values. Although improvements are substantial, we live in an imperfect world and the fully adjusted values for females are less satisfactory than for males. In both cases these sequences are devoid of discontinuities, considerably flatter and closer to 1 than the observed ones but, as revealed by the values attained by absolute deviations, the adjustments are less satisfactory at the oldest ages. This could be an indication of mismatches between the assumed and underlying patterns of age reporting or imperfect adjustment for completeness of census and death registration.

In a final step, we use the inverse of the (male and female) estimated matrices ${\widehat{\mathrm{\Theta }}}^s$, estimates of the two level parameters and compute adjusted (for age misreporting) vectors of age-specific population and intercensal death counts. We then calculate adjusted (for defective coverage and age misreporting) age specific intercensal mortality rates, and an adjusted life tables centered in middle of the intercensal interval. Table 5 displays observed, partially and fully adjusted values of life expectancy at ages 5 and 60. Partially adjusted values only reflect adjustment for relative completeness and ignore age misreporting. The relative differences between observed and partially adjusted life expectancy at age 5, on one hand, and observed and fully adjusted values, on the other, are as follows: for life expectancy at age 5 they are about 3.7 percent and 4.1 percent for males and 2.8 percent and 3.9 percent for females. For life expectancy at age 60 the contrasts are sharper: differences for females are 6.3 percent and 12 percent very similar to those for males, 6.1 percent and 12 percent.

Table 5:

Observed and adjusted life expectancy at ages 5 and 60: Guatemala, 1981–1994.

		Observed and adjusted life expectancy1
Population	Age	Observed	Adjusted
			Partially2	Fully3
Males
	5	60.06	58.3	57.73
	60	17.11	16.12	15.24
Females
	5	65.13	63.37	62.7
	60	18.51	17.41	16.54

¹Relative completeness of first to second census: Males=1.0256; Females=0.984; Relative completeness of death registration: Males=0.899; Females=0.888. Severity of age misreporting: Males: ${\lambda }^{no}$ value set to middle of range (0-.5); ${\varphi }^{no}$ value set to middle of range (1.5–2); Females: ${\lambda }^{no}$ value set to middle of range (0–.5) and ${\varphi }^{no}$ value set to middle of range (2–2.5).

²Adjusted for completeness only.

³Adjusted for completeness and age misreporting.

7. Summary and discussion

The method proposed here combines corrections for completeness of censuses and death registration coverage with adjustments that remove effects of age misreporting in population censuses and death registration. Results from the evaluation study suggest that, under some assumptions, the proposed strategy is quite accurate and applies to a broad set of conditions frequently encountered in populations with defective censuses and vital statistics.

The logic of the technique is quite general and could be adapted to populations that exhibit patterns of age misreporting different from the standard adopted here. However, any adaptation demands that the age pattern in the observed population be known to the investigator and that suitable modifications are introduced before applying the adapted version of the technique

In cases in which the standard age pattern of age misreporting is consistent with the one adopted here, proper application of the technique requires that the observed population belongs to the large set of simulated populations. For this to be the case several conditions must be satisfied. The first condition is that the age pattern of age misreporting be a simple transform of the Costa Rican standard. This implies that (a) probabilities of net overstatement increase linearly (approximately) with age and (b) the conditional distribution of n, the number of years of overstatement be approximated by a negative binomial (or similar) density function.

The second condition is that the age patterns of older adult age misreporting of death counts be identical to the age pattern of age misreporting of population counts. The technique could be made more general and powerful if future research exploits record linkages to assess patterns of age misreporting of death counts. In the absence of this type of data, we proposed a handful of tests that detect severe departures from the assumption (see Appendix E).

The third condition is that the population is either closed to migration or that population counts are adjusted for migration. If the vector of values cmR_x,[t1,t2] is accurately adjusted for defective completeness but not for migration, it will confound the effects of age misstatement with those of migration.

A useful application of the technique demands that the investigator ascertains if and to what an extent the observed data depart from any of the above assumptions. Mild departures may cause no damage whereas large departures will almost surely produce anomalous results that can be taken as a sign that application of the technique is unwarranted.

A final note is needed regarding the relation between adjustments for age heaping and adjustments for systematic age overeporting. Throughout we ignored age heaping. As emphasized in the text, systematic age misreporting is a different problem and has different implications than those of age heaping. Because it depends in accumulated quantities, the integrated technique minimizes the effects of age heaping and the resulting adjustments smooth out some of its impacts. If there are visible signs of age heaping, one could first smooth out the age distribution using a number of available procedures (assuming that the one chosen is adequate for the observed population) and then adjust for systematic age overstatement. Doing the reverse could violate some the assumptions of the method.

In summary, the integrated procedure can handle a limited set of populations with a particular profile of defective statistics. It is not a grand solution to problems created by all classes of errors in population and death counts. It is, however, quite flexible and, with additional information, could be modified and applied to populations that do not fit the error profile for which it is originally designed.