Asymmetric autoregressive models: statistical aspects and a financial application under COVID-19 pandemic

Abstract

In the present study, we provide a motivating example with a financial application under COVID-19 pandemic to investigate autoregressive (AR) modeling and its diagnostics based on asymmetric distributions. The objectives of this work are: (i) to formulate asymmetric AR models and their estimation and diagnostics; (ii) to assess the performance of the parameters estimators and of the local influence technique for these models; and (iii) to provide a tool to show how data following an asymmetric distribution under an AR structure should be analyzed. We take the advantages of the stochastic representation of the skew-normal distribution to estimate the parameters of the corresponding AR model efficiently with the expectation-maximization algorithm. Diagnostic analytics are conducted by using the local influence technique with four perturbation schemes. By employing Monte Carlo simulations, we evaluate the statistical behavior of the corresponding estimators and of the local influence technique. An illustration with financial data updated until 2020, analyzed using the methodology introduced in the present work, is presented as an example of effective applications, from where it is possible to explain atypical cases from the COVID-19 pandemic.

1. A motivating example from financial return data

The COVID-19 virus pandemic has affected people beyond the propagation of the disease itself. The virus has spread throughout the world and has caused problems of various kinds. For example, this pandemic has produced the largest global recession in history, with more than a third of the world's population blocked in their personal, social and work activities. In particular, global stock markets fell on 24 February 2020 due to a significant increase in the number of COVID-19 cases outside of China. On 28 February 2020, stock markets around the world posted their biggest declines in a single week since the 2008 financial crisis. Global stock markets crashed in March 2020, with several percent declines in the major world indexes.

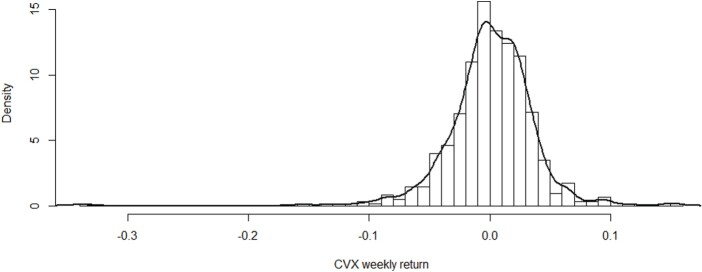
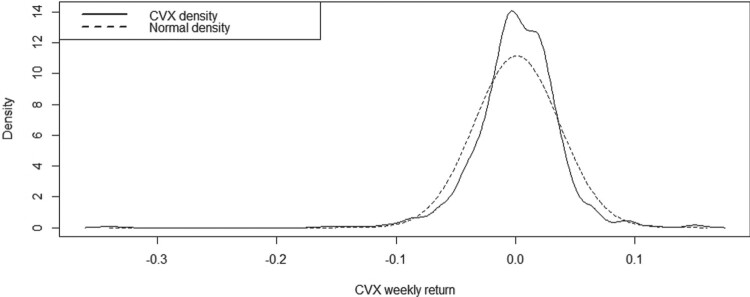
As the pandemic spreads, various world events have been postponed or canceled. While the monetary impact on the travel and commerce industry has yet to be estimated, it is likely to be in the billions and growing. The motivation for our investigation comes from a study of Chevron shares (hereinafter referred to as CVX weekly financial return data), which were collected from 2 January 2009 to 31 December 2020, obtained from Yahoo Finance. A statistical summary of the weekly financial returns is presented in Table 1, which includes quantiles, median, mean, standard deviation (SD), coefficients of skewness and kurtosis, standard error (SE) and lower/upper confidence limits (LCL/UCL). From this summary, we identify an asymmetrical behavior for the distribution of the data, a high level of kurtosis, and the need to count with a distribution with support on all the real line of numbers. The t-test for the skewness used in [47] is conducted. The t-statistic is valued at −14.8493 with an associated p-value less than 0.0001 so that we reject at 1% of significance the null of symmetry to confirm that the weekly returns are skew distributed. Figures 1 and 2 display the histogram and a plot of density estimation with the normal distribution of the CVX weekly returns. Note that the fit with the normal distribution is clearly inadequate. For example, the skewed generalized t distribution derived in [46] may be suitable for these data. The special and limiting cases of this distribution include twelve alternative distributions [15].

Table 1.

Basic statistics of CVX weekly return data.

Sample size	Minimum	Maximum	1st quartile	3rd quartile	Mean	Median
627	$-$0.3398	0.1544	$-$0.0155	0.0214	0.0010	0.0021
SE (Mean)	LCL (Mean)	UCL (Mean)	Variance	SD	Skewness	Kurtosis
0.0014	$-$0.0018	0.0038	0.0012	0.0358	$-$1.4526	14.2925

Figure 1.

Histogram of CVX weekly return data.

Figure 2.

Density of CVX weekly return data.

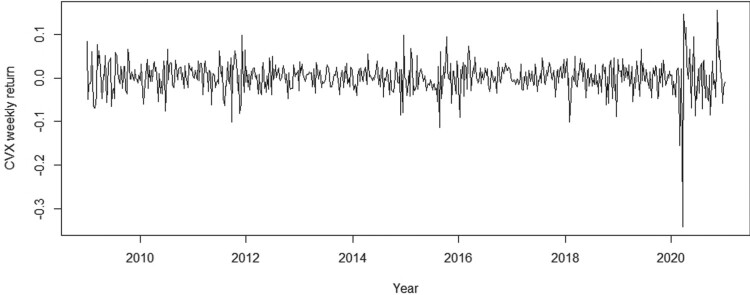
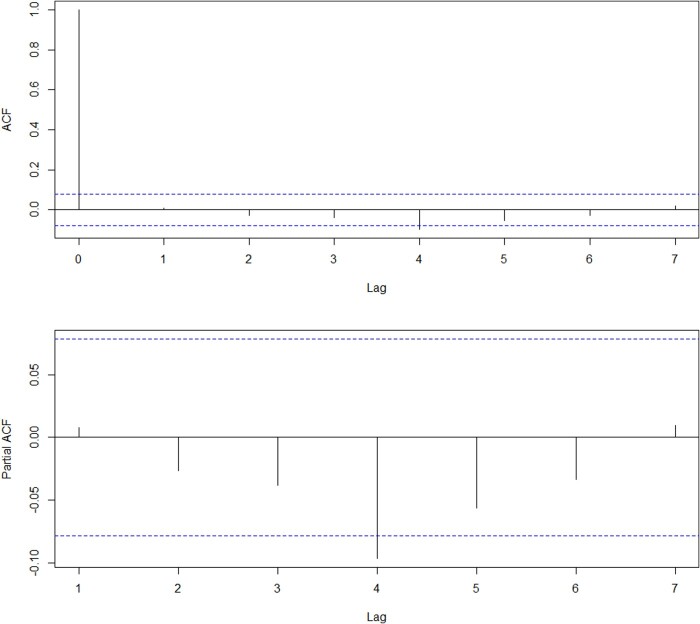
Figure 3 shows the CVX weekly return data (a total of 627 observations). We perform an augmented Dickey-Fuller (ADF) unit root test, with lags = 12, to detect a possible nonstationarity in these data. The value of the ADF statistic is −8.3518 and its associated p-value is less than $0.01$. Therefore, we reject the null hypothesis at 1% of significance and then the data are identified to be stationary. Furthermore, we perform a Box-Ljung test on the CVX weekly return data, with lags = 12, to detect whether the data are a white noise series or not. The value of the chi-square statistic is 27.891 and its associated p-value is 0.0057. Therefore, we reject the null hypothesis at 1% and the data are not a white noise series. In addition, note that the autocorrelation function (ACF) and partial autocorrelation function (PACF) in Figure 4 on the CVX weekly returns indicate that an AR(4) model may be suitable to describe these data, which is verified formally below.

Figure 3.

CVX weekly financial return data.

Figure 4.

ACF and PACF of CVX weekly return data.

First, the order of the AR model is established by assuming the data are generated from an AR $\left(p\right)$ model stated by

$$\begin{array}{rl}{Y}_t& ={\mathrm{\text{β}}}_1{y}_{t-1}+{\mathrm{\text{β}}}_2{y}_{t-2}+\cdots +{\mathrm{\text{β}}}_j{y}_{t-j}+\cdots +{\mathrm{\text{β}}}_p{y}_{t-p}+u_t\\ & =\sum _{j=1}^p{\mathrm{\text{β}}}_j{y}_{t-j},+u_t,j=1,\dots ,p;t=p+1,\dots ,T.\end{array}$$ (1)

For the model defined in (1), let ${\widehat{\mathrm{\text{β}}}}_j$ be the ordinary least squares (OLS) estimate of ${\mathrm{\text{β}}}_j$. Then, the corresponding residual is defined as

$${\hat{u}}_t=y_t-{\widehat{\mathrm{\text{β}}}}_1{y}_{t-1}-{\widehat{\mathrm{\text{β}}}}_2{y}_{t-2}-\cdots -{\widehat{\mathrm{\text{β}}}}_p{y}_{t-p},$$

and the estimated variance for the AR(p) model is expressed as

$${\hat{\sigma }}_p^2=\frac{1}{T-2p-1}\sum _{t=p+1}^T{\hat{u}}_t^2.$$

We obtain the jth and $(j-1)$th equations from (1) to test

$${\mathrm{H}}_0:{\mathrm{\text{β}}}_j=0\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{u}\mathrm{s}{\mathrm{H}}_1:{\mathrm{\text{β}}}_j\ne 0,$$

that is, we test the AR(j) model versus the AR(j−1) model, for $j=1,\dots ,p$. The associated test statistic is defined as

$$M\left(j\right)=-(T-j-2.5)\log \left(\frac{{{\hat{\sigma }}_j}^2}{{{\hat{\sigma }}_{j-1}}^2}\right).$$ (2)

In our case, $M\left(j\right)$ stated in (2) is asymptotically chi-square distributed with one degree of freedom, that is, $M\left(j\right)\sim {\chi }^2\left(1\right)$. We calculate $M\left(j\right)$ by (2), for $j=1,\dots ,8$, and present the results in Table 2. As the 95th percentile of the chi-square distribution with one degree of freedom is 3.84, that is, ${\chi }_{0.95}^2\left(1\right)=3.84$, from Table 2, we select the order p of the autoregressive (AR) model to be p = 4.

Table 2.

Test statistic $M\left(j\right)$, for $j=1,\dots ,8$, of CVX weekly return data.

Order	1	2	3	4	5	6	7	8
$M\left(j\right)$	1.9580	1.5453	1.0800	3.8679	0.0246	1.3333	1.9480	3.2800

In summary, the CVX weekly financial return data are AR of order p, stationary, and asymmetrically distributed. Thus, this example serves as motivation to formulate an AR(4) model based on an asymmetrical distribution of the data with support on the real numbers (negative and positive) and a high level of kurtosis. Of course, diagnostic analytics should be conducted after fitting the model to evaluate the effect of observations concentrated at the tails of the distribution. Therefore, an AR(4) model based on the skew-normal distribution is a suitable structure to describe these time series data.

2. Introduction

AR models are an important tool when analyzing data with dependence over time. These models have been applied to diverse areas and the reader interested is referred to [4,27] for time series modeling and applications. Standard time series models, including AR structures, assume that their errors are independently, identically and normally distributed [21,28,51]. This assumption is often problematic and questioned in many practical situations.

As an alternative to normality, skew distributions may be more appropriate, for example, as it occurs with economic and financial data; see Section 1. In order to deal with such data, skew-normal distributions and their properties, modeling and features have been studied by a number of authors [2,5,10,11,32,48,50]. Particularly, the skew-normal distribution was used in [6] for describing asset pricing issues with stock return data.

AR models with skew-normal errors have been considered in [41], but the expectation-maximization algorithm was not utilized to do an efficient procedure for the parameter estimation when the maximum likelihood method was employed. The expectation-maximization algorithm is a powerful iterative technique for the maximum likelihood estimation with incomplete data [35]. AR models based on finite scale-mixtures of skew-normal distributions were derived in [32] using the expectation-maximization algorithm to estimate the corresponding parameters. Recently, skew-normal and skew-Student-t distributions were considered in [48] instead of symmetric distributions for regression models with AR errors. Note that the model proposed in [48] corresponds to skew-normal regression models with AR errors, which is different from a skew-normal AR (SNAR) regression model.

Diagnostic analytics should be conducted after fitting a model [22,26,45]. A diagnostic method, mainly due to the less intensive computational work, is the local influence technique, which has been widely used [9,33]. This technique allows us to identify observations that, under small perturbations in the model or in the data, may cause disproportionate changes in the maximum likelihood estimates of the model parameters, affecting the quality and inference of its fitting [21,28]. Because the local influence technique is based on the likelihood function of the observed data, when the expectation-maximization algorithm is employed to estimate the model parameters, it is possible to consider this algorithm using the Q-displacement function [52]. Diagnostic analytics has been employed in diverse regression and time series models. Among others, a number of authors [5,18,24,25,30,42–44] investigated the local influence of linear or non-linear regression models under non-normal distributional assumptions. In a framework of time series data, diagnostics in conditionally heteroskedastic time series models under elliptical distributions were studied in [21]; influence diagnostics in AR models under normality were derived in [51]; and influence diagnostics in a vector AR model also under normality was conducted in [28]. Diagnostics in the non-linear model with scale mixtures of skew-normal distributions and AR errors was analyzed in [5]. Diagnostic analytics for the SNAR model was developed in [29].

The objectives of this work are: (i) to formulate asymmetric AR models and their estimation and diagnostics; (ii) to assess the performance of the parameters estimators and of the local influence technique for these models; and (iii) to provide a tool to show how data following an asymmetric distribution under an AR structure must be analyzed. By using Monte Carlo simulations, we evaluate the behavior of the corresponding estimators, and of the local influence technique. An illustration with weekly financial return data are analyzed using the methodology presented in this work as an example of effective applications. We use the matrix differential calculus [31] to establish the results used in our data analysis. We implement the maximum likelihood method with the expectation-maximization algorithm to estimate the SNAR model parameters, whereas the local influence technique with four perturbation schemes is utilized for the diagnostic analytics.

After providing a motivating example from finance in times of COVID-19 pandemic and the introduction with historical background, the reminder of this paper is organized in the following manner. Section 3 introduces the SNAR model, including properties of the skew-normal distribution, as well as the estimation method, and the associated expectation-maximization algorithm. In Section 4, we derive local influence diagnostics and obtain the normal curvatures under different perturbations, that is, the case-weight, data, variance parameter and skewness parameter schemes. In Section 5, two simulation studies related to performance of the maximum likelihood estimators and of the diagnostic techniques are presented. In Section 6, we retake the motivating example presented in Section 1 now involving the SNAR model and its diagnostics to show its potential applications. Our concluding remarks and future research are addressed in Section 7. Supplementary material with mathematical results is provided on the website of the journal which can be accessed at https://doi.org/10.1080/02664763.2021.1913103.

3. A skew-normal autoregressive model

In this section, we provide details of the skew-normal distribution and of the SNAR model. Hence, the maximum likelihood estimation of model parameters is derived by means of the expectation-maximization algorithm.

3.1. Model formulation

Let Y follow a skew-normal distribution with location ( $\mu \in \mathbb{R}$), scale ( $\sigma >0$) and skewness ( $\lambda \in \mathbb{R}$) parameters. In this case, the notation $Y\sim \mathrm{S}\mathrm{N}(\mu ,{\sigma }^2,\lambda )$ is used and its density function is stated as

$$f\left(y\right)=\frac{2}{\sigma }\varphi \left(\frac{y-\mu }{\sigma }\right)\mathrm{\Phi }\left(\lambda \left(\frac{y-\mu }{\sigma }\right)\right),y\in \mathbb{R},$$ (3)

with ϕ and Φ being the density and cumulative distribution function (from here on distribution function) of the standard normal distribution, respectively. Note that if $\lambda =0$, then the density of Y defined in (3) reduces to the normal density.

The skew-normal distribution has interesting properties, some of which are employed here and presented next. If $Y\sim \mathrm{S}\mathrm{N}(\mu ,{\sigma }^2,\lambda )$, then $\mathrm{E}\left(Y\right)=\mu +\sigma \delta \sqrt{2/\pi }$ and $\mathrm{V}\mathrm{a}\mathrm{r}\left(Y\right)={\sigma }^2-\left(2/\pi \right){\sigma }^2{\delta }^2$, with $\delta =\lambda /\sqrt{1+{\lambda }^2}$. Further, Y may be represented stochastically as

$$Y=\mu +\sigma \delta H+\sigma \sqrt{(1-{\delta }^2)}{H}_1,$$ (4)

with $H=|H_0|$ and both $H_0,H_1$ being independent normal distributed. Note that

$$Y|H=h\sim \mathrm{N}\left(\mu +\frac{\lambda \sigma }{\sqrt{1+{\lambda }^2}}h,\frac{{\sigma }^2}{1+{\lambda }^2}\right),$$ (5)

where $H\sim \mathrm{H}\mathrm{N}(0,1)$, that is, H follows the half normal distribution.

Let the random variable $Y_t$ be modeled by a stationary AR(p) process expressed as

$$Y_t={\mathrm{\text{β}}}_1{y}_{t-1}+\cdots +{\mathrm{\text{β}}}_j{y}_{t-j}+\cdots +{\mathrm{\text{β}}}_p{y}_{t-p}+u_t,j=1,\dots ,p;t=p+1,\dots ,T,$$ (6)

with $Y_t$ being a time series, and $y_1,\dots ,y_p$ being the p initial values for $Y_t$ ${\mathrm{\text{β}}}_j$ being a regression parameter, for $j=1,\dots ,p$; and $u_t$ being the model error which has a skew-normal distribution, that is, $u_t\sim \mathrm{S}\mathrm{N}(0,{\sigma }^2,\lambda )$, where ${\sigma }^2$ and λ are the scale and skewness parameters, respectively. For convenience purposes, the SNAR(p) model defined in (6) may be represented as

$$Y_t={\mathit{x}}_t^{\mathrm{\top }}\mathrm{\text{β}}+u_t,t=p+1,\dots ,T,$$ (7)

where ${\mathit{x}}_t=(y_{t-1},\dots ,y_{t-p}{)}^{\mathrm{\top }}$ is a $p\times 1$ vector, $\mathrm{\text{β}}={({\mathrm{\text{β}}}_1,\dots ,{\mathrm{\text{β}}}_p)}^{\mathrm{\top }}$ is a $p\times 1$ regression coefficient vector, and $\mathit{\theta }=(\mathrm{\text{β}},{\sigma }^2,\lambda {)}^{\mathrm{\top }}$ is the $(p+2)\times 1$ vector of SNAR(p) parameters.

3.2. Estimation and expectation-maximization algorithm

The maximum likelihood estimate of the parameter $\mathit{\theta }$ can be obtained by maximizing the corresponding log-likelihood function. The maximum likelihood estimates of the SNAR(p) model parameters may be obtained by differentiating the log-likelihood function with respect to the mentioned parameters, generating the associated score vector. This vector must be equated to zero being the solution the maximum likelihood estimates. However, such equations do not have closed-form and then they need to be solved numerically to maximize the associated log-likelihood function. Subsequently, a non-linear optimization method is needed [17]. We use the expectation-maximization algorithm to facilitate this estimation.

Next, we estimate the parameters of the SNAR model with the maximum likelihood method. We detail below the steps to implement the expectation-maximization algorithm and to efficiently obtain the corresponding estimates. We use the notation ${\mathit{Y}}_c,{\mathit{Y}}_o,{\mathit{Y}}_m$ for the random vectors associated with ${\mathit{y}}_c,{\mathit{y}}_o,{\mathit{y}}_m$, respectively, where ${\mathit{y}}_c=({\mathit{y}}_o,{\mathit{y}}_m{)}^{\mathrm{\top }}$ is the complete data set, ${\mathit{y}}_o$ is the observed data set and ${\mathit{y}}_m$ is the missing data set. Consider ${\mathit{\theta }}^{\left(0\right)}$ as an initial estimate and then ${\mathit{\theta }}^{\left(1\right)},{\mathit{\theta }}^{\left(2\right)},\dots$ can be obtained iterating the two steps of the expectation(E)-maximization(M) algorithm defined as follows.

E-step: Calculate the conditional expectation of the log-likelihood function ${\ell }_c(\mathit{\theta },{\mathit{Y}}_c)$ given ${\mathit{Y}}_o={\mathit{y}}_o$, named as the Q function, and evaluate it at the previous value $\mathit{\theta }={\mathit{\theta }}^{\left(k\right)}$, that is, $Q\left(\mathit{\theta }\right){|}_{\mathit{\theta }={\mathit{\theta }}^{\left(k\right)}}=\mathrm{E}\left[{\ell }_c\right(\mathit{\theta },{\mathit{Y}}_c)|{\mathit{Y}}_o={\mathit{y}}_o]{|}_{\mathit{\theta }={\mathit{\theta }}^{\left(k\right)}}$, for $k=0,1,\dots$

M-step: Maximize $Q\left(\mathit{\theta }\right){|}_{\mathit{\theta }={\mathit{\theta }}^{\left(k\right)}}$ at ${\mathit{\theta }}^{(k+1)}$, that is, ${\hat{\mathit{\theta }}}^{(k+1)}=\arg \underset{\mathit{\theta }}{max}Q\left(\mathit{\theta }\right){|}_{\mathit{\theta }={\mathit{\theta }}^{\left(k\right)}}$, for $k=1,2,\dots$

Since the expectation-maximization algorithm is an iterative procedure, then the function $Q\left(\mathit{\theta }\right)$ to be maximized must be evaluated at a previous value to the $(k+1)$th iteration of $\mathit{\theta }$, inducting the notation $Q\left(\mathit{\theta }\right){|}_{\mathit{\theta }={\mathit{\theta }}^{\left(k\right)}}$. The expectation-maximization algorithm must be iterated until reaching convergence, for example, when

$$|{\hat{\mathit{\theta }}}^{(k+1)}-{\hat{\mathit{\theta }}}^{\left(k\right)}|<{10}^{-5},$$

with ${\hat{\mathit{\theta }}}^{(k+1)}$ being the current maximum likelihood estimate of $\mathit{\theta }$ and ${\hat{\mathit{\theta }}}^{\left(k\right)}$ its previous estimate; see details in [35, pp. 21–23].

Note that, in some cases, the expectation-maximization algorithm does not admit an analytical solution in its E-step or M-step. Hence, it becomes necessary to use iterative methods for the computation of the expectation or maximization. For variants of the expectation-maximization algorithm based on approximations of its E-step or M-step, which preserve its convergence properties, see [33]. Based on the model for $Y_t$ defined in (7), the properties of the skew-normal distribution established in (4) and (5), that is,

$$\begin{array}{rl}Y|H=h& \sim \mathrm{N}(\mu +h\lambda \sigma /\sqrt{1+{\lambda }^2},{\sigma }^2/(1+{\lambda }^2\left)\right),\\ H& \sim \mathrm{H}\mathrm{N}(0,1),\end{array}$$

and considering ${\mathit{y}}_o=(y_{p+1},\dots y_T{)}^{\mathrm{\top }}$, ${\mathit{y}}_m=(h_{p+1},\dots h_T{)}^{\mathrm{\top }}$, ${\mathit{y}}_c=({\mathit{y}}_o,{\mathit{y}}_m{)}^{\mathrm{\top }}$ as the observed, missing and complete data sets, respectively, we get the complete-data log-likelihood function for $\mathit{\theta }=(\mathrm{\text{β}},{\sigma }^2,\lambda {)}^{\mathrm{\top }}$ stated as

$${\ell }_c(\mathit{\theta },{\mathit{y}}_c)=\sum _{t=p+1}^T\left(-\frac{1}{2}\log \left({\sigma }^2\right)+\frac{1}{2}\log \left(1+{\lambda }^2\right)-\frac{1+{\lambda }^2}{2{\sigma }^2}{\left(y_t-{\mathit{x}}_t^{\mathrm{\top }}\mathrm{\text{β}}-\frac{\lambda \sigma }{\sqrt{1+{\lambda }^2}}{h}_t\right)}^2\right).$$ (8)

Therefore, for the E-step of the expectation-maximization algorithm, given the current estimate ${\hat{\mathit{\theta }}}^{\left(k\right)}$ and based on (9), we can calculate the Q function as

$$\begin{array}{rl}Q\left(\mathit{\theta }\right){|}_{\mathit{\theta }={\hat{\mathit{\theta }}}^{\left(k\right)}}& =\mathrm{E}\left[{\ell }_c\right(\mathit{\theta },{\mathit{Y}}_c)|{\mathit{Y}}_o={\mathit{y}}_o]{|}_{\mathit{\theta }={\hat{\mathit{\theta }}}^{\left(k\right)}}\\ & =-\frac{(T-p)}{2}\log \left({\sigma }^2\right)+\frac{T-p}{2}\log (1+{\lambda }^2)\\ & -\frac{(1+{\lambda }^2)}{2}{\sum _{t=p+1}^{\mathrm{\top }}\left(\frac{y_t-{\mathit{x}}_t^{\mathrm{\top }}\mathrm{\text{β}}}{\sigma }-\frac{\lambda }{\sqrt{1+{\lambda }^2}}{\hat{c}}_t\right)}^2-\frac{{\lambda }^2}{2}\sum _{t=p+1}^{\mathrm{\top }}({\hat{c}}_t^2-{\left({\hat{c}}_t\right)}^2),\end{array}$$ (9)

with

$$\begin{array}{rl}{\hat{c}}_t& =\mathrm{E}\left(H_t|{\mathit{Y}}_o={\mathit{y}}_o\right){|}_{\mathit{\theta }={\hat{\mathit{\theta }}}^{\left(k\right)}}={\tau }_1+\frac{\varphi \left({\tau }_1/{\tau }_2\right)}{\mathrm{\Phi }\left({\tau }_1/{\tau }_2\right)}{\tau }_2,\\ {\hat{c}}_t^2& =\mathrm{E}\left(H_t^2|{\mathit{Y}}_o={\mathit{y}}_o\right){|}_{\mathit{\theta }={\hat{\mathit{\theta }}}^{\left(k\right)}}={\tau }_1^2+{\tau }_2^2+\frac{\varphi \left({\tau }_1/{\tau }_2\right)}{\mathrm{\Phi }\left({\tau }_1/{\tau }_2\right)}{\tau }_1{\tau }_2,\\ {\tau }_1& =\frac{{\hat{\lambda }}^{\left(k\right)}}{{\hat{\sigma }}^{\left(k\right)}\left(1+({\hat{\lambda }}^{\left(k\right)}{)}^2\right){)}^{1/2}}(y_t-{\mathit{x}}_t{\widehat{\mathrm{\text{β}}}}^{\left(k\right)}),\\ {\tau }_2& =\frac{1}{(1+({\hat{\lambda }}^{\left(k\right)}{)}^2{)}^{1/2}}.\end{array}$$

Note that ${\hat{c}}_t^2$ is different from $({\hat{c}}_t{)}^2$. For M-step, we update ${\hat{\mathit{\theta }}}^{\left(k\right)}$ by the Newton–Raphson iteration as

$$\dot{Q}\left({\hat{\mathit{\theta }}}^{(k+1)}\right)=\dot{Q}\left({\hat{\mathit{\theta }}}^{\left(k\right)}\right)+\ddot{Q}\left({\hat{\mathit{\theta }}}^{\left(k\right)}\right)({\hat{\mathit{\theta }}}^{(k+1)}-{\hat{\mathit{\theta }}}^{\left(k\right)})+o(|{\hat{\mathit{\theta }}}^{(k+1)}-{\hat{\mathit{\theta }}}^{\left(k\right)}|),$$ (10)

with $\dot{Q}$ denoting the gradient vector, $\ddot{Q}$ being the Hessian matrix, and o standing for the higher order terms in the Taylor expansion. As $({\hat{\mathit{\theta }}}^{(k+1)}-{\hat{\mathit{\theta }}}^{\left(k\right)})\to 0$, the $(k+1)$th estimate of $\mathit{\theta }$ may be stated by

$${\hat{\mathit{\theta }}}^{(k+1)}={\hat{\mathit{\theta }}}^{\left(k\right)}-{\ddot{Q}\left({\hat{\mathit{\theta }}}^{\left(k\right)}\right)}^{-1}\dot{Q}\left({\hat{\mathit{\theta }}}^{\left(k\right)}\right),$$

with $\dot{Q}$ and $\ddot{Q}$ being defined in (10). Under wild conditions and based on an initial value ${\hat{\mathit{\theta }}}^{\left(0\right)}$, the sequence ${\hat{\mathit{\theta }}}^{\left(k\right)}$ obtained from the expectation-maximization algorithm converges to the maximum likelihood estimate $\hat{\mathit{\theta }}$. Note that a suitable initial value ${\hat{\mathit{\theta }}}^{\left(0\right)}$ is important and difficult to find in numerical computation. Thus, we can consider ${\hat{\mathit{\theta }}}^{\left(0\right)}=({\widehat{\mathrm{\text{β}}}}^{\left(0\right)},{\hat{\sigma }}^{2^{\left(0\right)}},{\hat{\lambda }}^{\left(0\right)})$ assuming ${\widehat{\mathrm{\text{β}}}}^{\left(0\right)}$ as the OLS estimate and so ${\hat{\sigma }}^{2^{\left(0\right)}}$ and ${\hat{\lambda }}^{\left(0\right)}$ may be calculated as $\hat{\mathit{\theta }}=(\widehat{\mathrm{\text{β}}},{\hat{\sigma }}^2,\hat{\lambda })$ until $|{\hat{\mathit{\theta }}}^{(k+1)}-{\hat{\mathit{\theta }}}^{\left(k\right)}|<{10}^{-5}$. We employ the matrix differential calculus [31] to establish algebraic results related to the Hessian matrix, which are provided as supplementary material onto the website of the journal which can be accessed at https://doi.org/10.1080/02664763.2021.1913103.

4. Diagnostics in the skew-normal autoregressive model

In this section, we derive local influence diagnostics and obtain the normal curvatures under four perturbations, that is, the case-weight, data, variance parameter and skewness parameter schemes.

4.1. The local influence technique

Let $\ell \left(\mathit{\theta }\right)$ be the log-likelihood function for the model defined in (6), with $\mathit{\theta }$ being a $(p+2)\times 1$ vector of unknown parameters and its maximum likelihood estimate being $\hat{\mathit{\theta }}$. In addition, let $\mathit{\omega }=({\omega }_1,\dots ,{\omega }_q{)}^{\mathrm{\top }}$ be a $q\times 1$ vector of perturbations of a some open subset of ${\mathbb{R}}^q$ and let ${\mathit{\omega }}_0$ be a $q\times 1$ non-perturbation vector, with q being a suitable dimension and ${\mathit{\omega }}_0=(0,\dots ,0)$ or ${\mathit{\omega }}_0=(1,\dots ,1)$. Hence, $\ell \left(\mathit{\theta }\right)$ and $\ell \left(\mathit{\theta }|\mathit{\omega }\right)$ represent the log-likelihood functions of the postulated and perturbed models, respectively. Note that $\ell \left(\mathit{\theta }\right)=\ell \left(\mathit{\theta }|{\mathit{\omega }}_0\right)$. We suppose that $\ell \left(\mathit{\theta }|\mathit{\omega }\right)$ is twice continuously differentiable in a vicinity of $(\hat{\mathit{\theta }},{\mathit{\omega }}_0)$. We are interested in comparing $\hat{\mathit{\theta }}$ and ${\hat{\mathit{\theta }}}_{\mathit{\omega }}$ using the local influence technique, which investigates the degree of inference affected by those changes in the corresponding perturbations. The likelihood displacement (LD) to assess the influence of the perturbation $\mathit{\omega }$ is defined as [9]

$$\mathrm{L}\mathrm{D}\left(\mathit{\omega }\right)=2\left(\ell \right(\hat{\mathit{\theta }})-\ell ({\hat{\mathit{\theta }}}_{\mathit{\omega }}\left)\right).$$

Note that large values of $\mathrm{L}\mathrm{D}\left(\mathit{\omega }\right)$ provide evidence that $\hat{\mathit{\theta }}$ and ${\hat{\mathit{\theta }}}_{\mathit{\omega }}$ are considerably different with respect to the contours of the non-perturbed log-likelihood function $\ell \left(\mathit{\theta }\right)$. This is based on analyzing the local behavior of $\mathrm{L}\mathrm{D}\left(\mathit{\omega }\right)$ and the normal curvature $C_{\mathit{l}}\left(\mathit{\theta }\right)$ in a unit-length vector $\mathit{l}$, with $||\mathit{l}||=1$. The normal curvature employed to evaluate the local influence of the perturbation vector at $\mathit{\omega }={\mathit{\omega }}_0$ is stated by [9]

$$C_{\mathit{l}}\left(\mathit{\theta }\right)=2|{\mathit{l}}^{\mathrm{\top }}\ddot{F}\mathit{l}|=2|{\mathit{l}}^{\mathrm{\top }}\left({\mathbf{\Delta }}^{\mathrm{\top }}{\ddot{\mathit{\ell }}}^{-1}\mathbf{\Delta }\right)\mathit{l}|,$$

with $\ddot{F}={\mathrm{\partial }}^2\ell \left(\mathit{\theta }|\mathit{\omega }\right)/\mathrm{\partial }\mathit{\omega }\mathrm{\partial }{\mathit{\omega }}^{\mathrm{\top }}$, $\mathbf{\Delta }={\mathrm{\partial }}^2\ell \left(\mathit{\theta }|\mathit{\omega }\right)/\mathrm{\partial }\mathit{\theta }\mathrm{\partial }{\mathit{\omega }}^{\mathrm{\top }},\ddot{\mathit{\ell }}={\mathrm{\partial }}^2\ell \left(\mathit{\theta }\right)/\mathrm{\partial }\mathit{\theta }\mathrm{\partial }{\mathit{\theta }}^{\mathrm{\top }},\mathit{l}$ being a $q\times 1$ vector of unit length, $-\ddot{\mathit{\ell }}$ being the $(p+2)\times (p+2)$ observed information matrix for the underlying model, $\mathbf{\Delta }$ being the $(p+2)\times q$ perturbation matrix for the perturbed model, and $-\ddot{\mathit{\ell }},\mathbf{\Delta }$ being evaluated at $\mathit{\theta }=\hat{\mathit{\theta }}$ and $\mathit{\omega }={\mathit{\omega }}_0$. The suggestion is to make the local influence diagnostic analytics by finding the maximum curvature $C_{max}=\underset{||\mathit{l}||=1}{max}{C}_l$, with $C_{max}$ corresponding to the largest absolute eigenvalue ${\lambda }_{max}$ and its associated eigenvector ${\mathit{l}}_{max}$ of the matrix $\ddot{F}={\mathbf{\Delta }}^{\mathrm{\top }}{\ddot{\mathit{\ell }}}^{-1}\mathbf{\Delta }$. If the absolute value of the $i$th element of ${\mathit{l}}_{max}$ is the largest, then the $i$th observation in the data may be the most influential potentially. To examine the magnitude of influence, it is useful to have a benchmark value for $C_{max}$ and for the elements of ${\mathit{l}}_{max}$ [24,28,37].

4.2. Local influence assessment in the SNAR model

Next, we conduct a local influence diagnostic analytics for the SNAR(p) model. Due to the complexity of the skew-normal distribution, we obtain the maximum likelihood estimates based on the expectation-maximization algorithm. As suggested in [11,37], the Q function and Q displacement function may be used to replace the log-likelihood function and likelihood displacement, respectively, in the local influence method to assess the effect of the perturbation. Thus, the normal curvature should be changed to be

$$C_{\mathit{l}}\left(\mathit{\theta }\right)=2|{\mathit{l}}^{\mathrm{\top }}\ddot{F}\mathit{l}|=2|l^{\mathrm{\top }}\left({\mathbf{\Delta }}^{\mathrm{\top }}{\ddot{Q}}^{-1}\mathbf{\Delta }\right)l|,$$

with $\ddot{F}={\mathrm{\partial }}^{2}Q\left(\mathit{\theta }|\mathit{\omega }\right)/\mathrm{\partial }\mathit{\omega }\mathrm{\partial }{\mathit{\omega }}^{\mathrm{\top }},\mathbf{\Delta }={\mathrm{\partial }}^{2}Q\left(\mathit{\theta }|\mathit{\omega }\right)/\mathrm{\partial }\mathit{\theta }\mathrm{\partial }{\mathit{\omega }}^{\mathrm{\top }}$, and $\ddot{Q}={\mathrm{\partial }}^{2}Q\left(\mathit{\theta }\right)/\mathrm{\partial }\mathit{\theta }\mathrm{\partial }{\mathit{\theta }}^{\mathrm{\top }}$, with $\mathit{l}$ being a $q\times 1$ vector of unit length, and $\ddot{F},\ddot{Q}$ and $\mathbf{\Delta }$ being $q\times q,(p+2)\times (p+2)$ and $(p+2)\times q$ matrices, respectively. In addition, $\ddot{Q}$ and $\mathbf{\Delta }$ need to be evaluated at $\mathit{\theta }=\hat{\mathit{\theta }}$ and $\mathit{\omega }={\mathit{\omega }}_0$.

We use $C_t=C_{{\mathit{l}}_t}\left(\mathit{\theta }\right)$ to examine the total local influence, where ${\mathit{l}}_t$ is a $q\times 1$ unit-length vector with one at the tth position and zeros elsewhere. We denote $S=-{\mathbf{\Delta }}^{\mathrm{\top }}{\ddot{Q}}^{-1}\mathbf{\Delta }$. Since $C_{\mathit{l}}\left(\mathit{\theta }\right)$ is not invariant under a uniform change of scale, the conformal normal curvature $B_{\mathit{l}}\left(\mathit{\theta }\right)=C_{\mathit{l}}\left(\mathit{\theta }\right)/\left(2\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(S\right)\right)$ was proposed in [37]. An interesting property of the conformal normal curvature is that for any unit-length direction $\mathit{l}$, $0\le B_{\mathit{l}}\left(\mathit{\theta }\right)\le 1$ is obtained, which allows comparison of curvatures among different models.

Note that the tth observation is potentially influential [37] if $N(0{)}_t=B_{l_t}$ is greater than the benchmark $1/q+c^{\ast }S\left(N\right(0\left)\right)$, with $S\left(N\right(0\left)\right)$ being the sample SE of $N(0{)}_k$, for $k=1,\dots ,q$, and $c^{\ast }$ is a constant value. Depending on the specific application, $c^{\ast }$ may be taken to be a suitably selected positive value. The forms given in Subsection 4.2 are used to obtain our normal curvature results under the four perturbations, namely the case-weight, data, variance parameter and skewness parameter schemes. The matrices $\ddot{Q}$ and $\mathbf{\Delta }$ need to be established for each scheme. We employ the matrix differential calculus [31] to establish these algebraic results, which are provided as supplementary material onto the website of the journal which can be accessed at https://doi.org/10.1080/02664763.2021.1913103.

5. Monte Carlo simulations

In this section, two simulation studies related to performance of the maximum likelihood estimators and of the diagnostic techniques are presented.

5.1. Study I

Next, we conduct a simulation study to illustrate the performance of our results given in Section 4. We take p = 1, 2, 3, 4 in the SNAR $\left(p\right)$ model. The sample sizes are taken as n = 250, 500, 1000. The true values of the parameters are taken as ${\sigma }^2=1$ and $\lambda =-0.20,-0.15,-0.10,-0.05,0.1$. From Tables 3 and 4, we see that our proposal is proven to be valid. The mean values of the parameter estimates are close to the true values, so as the medians. Our estimated results of the error variance are satisfactory, and the mean squared errors (MSEs) and SEs of the estimators are also very small. The skewness is not reported here, as well as the other parameters, but their estimates are satisfactory.

Table 3.

Empirical mean, median, SE, SD, LCL and UCL for the indicated values of n, λ (negative) and SNAR model parameters with simulated data.

		n = 250				n = 500				n = 1000
		SNAR(1)	SNAR(2)	SNAR(3)	SNAR(4)	SNAR(1)	SNAR(2)	SNAR(3)	SNAR(4)	SNAR(1)	SNAR(2)	SNAR(3)	SNAR(4)
${\varphi }_1$	True value	0.7	1.2	1.2	1.2	0.7	1.2	1.2	1.2	0.7	1.2	1.2	1.2
	Mean	0.699615	1.198326	1.213548	1.200235	0.698168	1.199453	1.213583	1.194775	0.69886	1.199512	1.213028	1.196481
	Median	0.700765	1.1989	1.2127	1.2024	0.6988	1.19995	1.2155	1.19435	0.699925	1.20025	1.2146	1.1969
	SE (mean)	0.002322	0.002083	0.002679	0.002843	0.001554	0.001488	0.001859	0.002051	0.001096	0.001054	0.001311	0.001428
	SD	0.03671	0.032928	0.04236	0.04496	0.034755	0.033281	0.041571	0.045863	0.034671	0.033315	0.041462	0.045151
	LCL (mean)	0.695042	1.194224	1.208271	1.194634	0.695114	1.196529	1.20993	1.190745	0.696709	1.197445	1.210455	1.19368
	UCL (mean)	0.704188	1.202428	1.218824	1.205835	0.701222	1.202377	1.217235	1.198805	0.701012	1.201579	1.215601	1.199283
${\varphi }_2$	True value	–	$-$0.7	$-$0.7	$-$0.7	–	$-$0.7	$-$0.7	$-$0.7	–	$-$0.7	$-$0.7	$-$0.7
	Mean	–	$-$0.69775	$-$0.70746	$-$0.7051	–	$-$0.69979	$-$0.70653	$-$0.69861	–	$-$0.69895	$-$0.7058	$-$0.69989
	Median	–	$-$0.69962	$-$0.71058	$-$0.70333	–	$-$0.70102	$-$0.70822	$-$0.69693	–	$-$0.7009	$-$0.70752	$-$0.69955
	SE (mean)	–	0.002081	0.003723	0.004271	–	0.001492	0.002612	0.003114	–	0.001035	0.001872	0.00215
	SD	–	0.032898	0.058872	0.067529	–	0.033372	0.058415	0.069637	–	0.032721	0.059192	0.067987
	LCL (mean)	–	$-$0.70184	$-$0.71479	$-$0.71351	–	−0.70272	−0.71166	−0.70473	–	−0.70098	−0.70948	−0.70411
	UCL (mean)	–	$-$0.69365	$-$0.70013	$-$0.69668	–	$-$0.69685	$-$0.7014	$-$0.69249	–	$-$0.69692	$-$0.70213	$-$0.69568
${\varphi }_3$	True value	–	–	0.3	0.3	–	–	0.3	0.3	–	–	0.3	0.3
	Mean	–	–	0.315807	0.303356	–	–	0.314438	0.297795	–	–	0.313783	0.299921
	Median	–	–	0.314665	0.310225	–	–	0.313535	0.298625	–	–	0.313285	0.301375
	SE (Mean)	–	–	0.002738	0.004257	–	–	0.001815	0.00305	–	–	0.001343	0.00212
	SD	–	–	0.043287	0.067311	–	–	0.04059	0.068199	–	–	0.042484	0.067036
	LCL (mean)	–	–	0.310415	0.294972	–	–	0.310872	0.291802	–	–	0.311147	0.295761
	UCL (mean)	–	–	0.321199	0.311741	–	–	0.318005	0.303787	–	–	0.31642	0.30408
${\varphi }_4$	True value	–	–	–	0.1	–	–	–	0.1	–	–	–	0.1
	Mean	–	–	–	0.092073	–	–	–	0.094778	–	–	–	0.092742
	Median	–	–	–	0.087778	–	–	–	0.09487	–	–	–	0.091923
	SE (mean)	–	–	–	0.00276	–	–	–	0.001907	–	–	–	0.001365
	SD	–	–	–	0.043637	–	–	–	0.042643	–	–	–	0.043178
	LCL (mean)	–	–	–	0.086638	–	–	–	0.091032	–	–	–	0.090063
	UCL (mean)	–	–	–	0.097509	–	–	–	0.098525	–	–	–	0.095422
σ	True value	1	1	1	1	1	1	1	1	1	1	1	1
	Mean	0.996724	0.957133	0.995972	0.993711	0.998946	0.95831	0.993768	0.994974	0.997188	0.961357	0.99203	0.992205
	Median	0.983695	0.957005	0.91776	0.99086	0.984435	0.95706	0.921825	0.98631	0.98663	0.962865	0.92203	0.986255
	SE (mean)	0.00691	0.003752	0.003562	0.004166	0.005794	0.002725	0.002538	0.003573	0.003678	0.002016	0.001811	0.002348
	SD	0.109252	0.059324	0.056327	0.065878	0.129558	0.060922	0.056746	0.0799	0.116302	0.063755	0.057266	0.074242
	LCL (mean)	0.983115	0.949743	0.988955	0.985505	0.987562	0.952957	0.988692	0.987953	0.989971	0.957401	0.988476	0.987598
	UCL (mean)	1.010333	0.964523	1.022988	1.001917	1.010329	0.963663	0.998844	1.001994	1.004405	0.965314	0.995584	0.996812
λ	True value	−0.1	−0.2	−0.15	−0.05	−0.1	−0.2	−0.15	−0.05	−0.1	−0.2	−0.15	−0.05
	Mean	−0.10255	−0.19768	−0.14649	−0.05109	−0.10439	−0.19926	−0.14716	−0.05493	−0.1004	−0.19903	−0.14841	−0.05039
	Median	−0.08814	−0.19579	−0.15483	−0.03529	−0.09185	−0.1993	−0.15698	−0.0336	−0.09214	−0.20017	−0.15622	−0.03282
	SE (mean)	0.008548	0.006831	0.003232	0.005423	0.006292	0.004599	0.002337	0.00455	0.004016	0.003163	0.001678	0.002827
	SD	0.135153	0.10801	0.051104	0.085748	0.1407	0.102829	0.052261	0.101746	0.126994	0.100037	0.053062	0.089388
	LCL (mean)	−0.11939	−0.21114	−0.15286	−0.06177	−0.11675	−0.20829	−0.15175	−0.06387	−0.10828	−0.20524	−0.1517	−0.05593
	UCL (mean)	−0.08572	−0.18423	−0.14013	−0.04041	−0.09202	−0.19022	−0.14256	−0.04599	−0.09252	−0.19282	−0.14512	−0.04484

Table 4.

Mean, median, SE, SD, LCL and UCL for the indicated values of of n, λ (positive) and SNAR model parameters with simulated data.

		n = 250				n = 500				n = 1000
		SNAR(1)	SNAR(2)	SNAR(3)	SNAR(4)	SNAR(1)	SNAR(2)	SNAR(3)	SNAR(4)	SNAR(1)	SNAR(2)	SNAR(3)	SNAR(4)
${\varphi }_1$	True value	0.7	1.2	1.2	1.2	0.7	1.2	1.2	1.2	0.7	1.2	1.2	1.2
	Mean	0.692618	1.198974	1.19857	1.208956	0.695559	1.196588	1.198086	1.207733	0.698298	1.1966	1.197522	1.207338
	Median	0.692915	1.19735	1.19915	1.20535	0.696935	1.1972	1.1984	1.20565	0.698915	1.1982	1.1979	1.20765
	SE (mean)	0.002225	0.002157	0.002397	0.002846	0.001588	0.001526	0.001829	0.002004	0.001011	0.001	0.001372	0.001296
	SD	0.035182	0.034111	0.037893	0.045007	0.0355	0.034112	0.040895	0.044814	0.031964	0.03161	0.04339	0.028973
	LCL (mean)	0.688235	1.194725	1.19385	1.203349	0.69244	1.193591	1.194493	1.203796	0.696315	1.194638	1.19483	1.204793
	UCL (mean)	0.697	1.203223	1.20329	1.214562	0.698679	1.199586	1.20168	1.211671	0.700282	1.198561	1.200215	1.209884
${\varphi }_2$	True value	–	−0.7	−0.7	−0.7	–	−0.7	−0.7	−0.7	–	−0.7	−0.7	−0.7
	Mean	–	−0.699214	−0.69611	−0.699159	–	−0.69561	−0.69804	−0.6994	–	−0.69445	−0.69781	−0.69967
	Median	–	−0.702075	−0.69665	−0.69302	–	−0.69799	−0.70007	−0.69311	–	−0.69552	−0.69777	−0.69838
	SE (mean)	–	0.00215	0.003511	0.004262	–	0.001498	0.002562	0.003127	–	0.001074	0.001929	0.002087
	SD	–	0.033989	0.055512	0.067384	–	0.033501	0.057282	0.06992	–	0.033951	0.060986	0.046671
	LCL (mean)	–	−0.703448	−0.70302	−0.707552	–	−0.69855	−0.70307	−0.70554	–	−0.69656	−0.70159	−0.70377
	UCL (mean)	–	−0.694981	−0.6892	−0.690765	–	−0.69266	−0.69301	−0.69325	–	−0.69234	−0.69402	−0.69557
${\varphi }_3$	True value	–	–	0.3	0.3	–	–	0.3	0.3	–	–	0.3	0.3
	Mean	–	–	0.297855	0.301047	–	–	0.299663	0.30205	–	–	0.297801	0.302723
	Median	–	–	0.29946	0.30205	–	–	0.30182	0.30178	–	–	0.29839	0.299475
	SE (mean)	–	–	0.002516	0.004073	–	–	0.001862	0.003042	–	–	0.001333	0.002182
	SD	–	–	0.039786	0.064392	–	–	0.041632	0.068029	–	–	0.042166	0.048793
	LCL (mean)	–	–	0.292899	0.293026	–	–	0.296005	0.296073	–	–	0.295184	0.298435
	UCL (mean)	–	–	0.30281	0.309068	–	–	0.303321	0.308027	–	–	0.300418	0.30701
${\varphi }_4$	True value	–	–	–	0.1	–	–	–	0.1	–	–	–	0.1
	Mean	–	–	–	0.106186	–	–	–	0.105439	–	–	–	0.106076
	Median	–	–	–	0.102115	–	–	–	0.103755	–	–	–	0.105655
	SE (mean)	–	–	–	0.002776	–	–	–	0.001939	–	–	–	0.001431
	SD	–	–	–	0.043889	–	–	–	0.043352	–	–	–	0.031992
	LCL (mean)	–	–	–	0.100719	–	–	–	0.10163	–	–	–	0.103265
	UCL (mean)	–	–	–	0.111653	–	–	–	0.109248	–	–	–	0.108887
σ	True value	1	1	1	1	1	1	1	1	1	1	1	1
	Mean	0.985395	1.003628	0.985879	0.937454	0.990282	1.002746	0.993314	0.937351	0.989842	1.003633	0.987593	0.942468
	Median	0.692915	0.99222	0.984615	0.93369	0.983755	0.989735	0.987605	0.9345	0.9839	0.99258	0.982775	0.94311
	SE (mean)	0.004569	0.007706	0.005048	0.003976	0.003716	0.005158	0.005645	0.002701	0.002468	0.004019	0.003103	0.00186
	SD	0.072247	0.12184	0.079815	0.06287	0.083096	0.115347	0.126235	0.060385	0.078034	0.127082	0.098112	0.041585
	LCL (mean)	976396	0.988451	0.975937	0.929623	0.982981	0.992611	0.982222	0.932045	0.984999	0.995746	0.981505	0.938814
	UCL (mean)	0.994395	1.018805	0.995821	0.945285	0.997583	1.012881	1.004406	0.942657	0.994684	1.011519	0.993682	0.946121
λ	True value	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1
	Mean	0.094806	0.080006	0.099247	0.108235	0.095823	0.088792	0.099446	0.108506	0.091764	0.073248	0.097862	0.105891
	Median	0.093934	0.080007	0.098328	0.11324	0.094276	0.075158	0.095509	0.11184	0.094247	0.065461	0.099616	0.10657
	SE (mean)	0.005012	0.011274	0.00646	0.002136	0.004316	0.008102	0.005555	0.001304	0.002372	0.00554	0.003101	0.000557
	SD	0.07924	0.178255	0.102143	0.033776	0.0965	0.181157	0.124223	0.02916	0.075003	0.175177	0.098078	0.012449
	LCL (mean)	0.084935	0.057802	0.086524	0.104028	0.087344	0.072875	0.088532	0.105944	0.08711	0.062378	0.091776	0.104797
	UCL (mean)	0.104676	0.10221	0.111971	0.112442	0.104302	0.104709	0.110361	0.111068	0.096418	0.084119	0.103949	0.106985

5.2. Study II

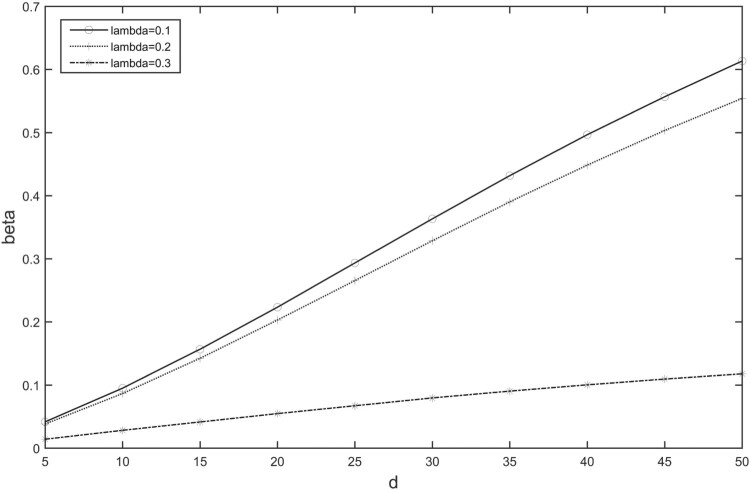
By using Section 3, consider an SNAR(1) model stated as $Y_t=\mathrm{\text{β}}{y}_{t-1}+u_t$, with $u_t\sim \mathrm{S}\mathrm{N}(0,{\sigma }^2,\lambda )$ $\mathrm{\text{β}}=0.12$, ${\sigma }^2=0.003$, $\lambda =0.1$, and T = 400 observations being generated. The performance of the maximum likelihood estimators in presence of five perturbed cases is evaluated with $\lambda =0.1,0.2,0.3$. The value $y_t$ is perturbed by ${y_t}^{\ast }=y_t+\mathrm{\text{β}}{y}_{t-1}d$, with t = 200, 201, 202, 203, 204 and $d=5,10,\dots ,50$ to obtain atypical observations. Then, the maximum likelihood estimate of β is obtained by fitting perturbed and non-perturbed data sets with the SNAR(1) model and $\lambda =0.1,0.2,0.3$. Hence, the relative changes of the estimates are calculated as $\mathrm{R}\mathrm{C}=|\left({\widehat{\mathrm{\text{β}}}}_{\left(i\right)}^{\ast }-\widehat{\mathrm{\text{β}}}\right)/\widehat{\mathrm{\text{β}}}|,$ with ${\widehat{\mathrm{\text{β}}}}_{\left(i\right)}^{\ast }$ being the estimate of β under the perturbed data and $\widehat{\mathrm{\text{β}}}$ is the estimate of β under the non-perturbed data. The good performance of the influence diagnostic techniques is observed in Figure 5.

Figure 5.

Relative change of estimated β against d with simulated data.

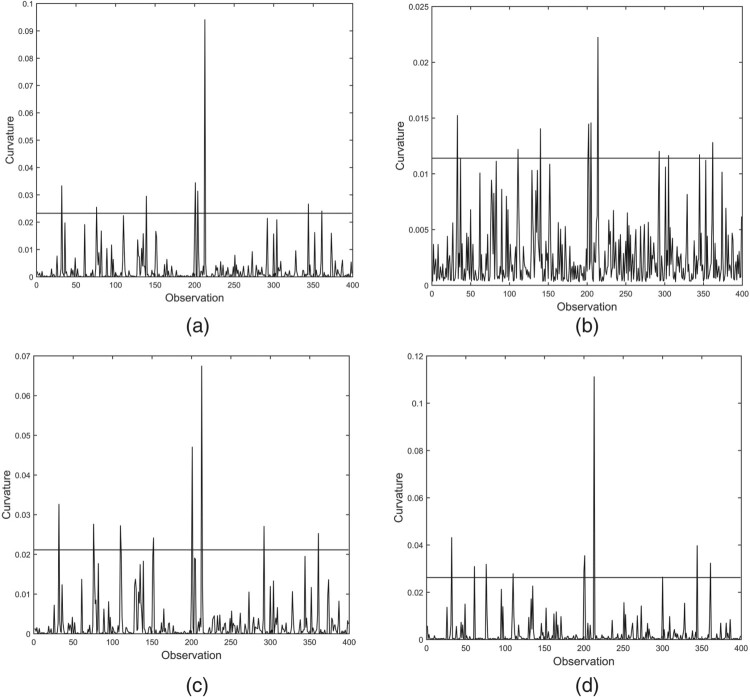
Next, a numerical simulation is conducted to evaluate the performance of our methodology. Skew-normal and normal distributions are compared as follows: (i) simulated data $(\lambda =0.1)$ with $y_t$ being perturbed by ${y_t}^{\ast }=y_t+\mathrm{\text{β}}{y}_{t-1}d$ are used, for d = 5 and t = 200, 201, 202, 203, 204, and then an AR(1) model is fitted under normality to the data by $Y_t=0.1549y_{t-1}+u_t$, with $u_t\sim \mathrm{N}(0,0.0151);$ (ii) a local influence diagnostic analytics is conducted under the normal distribution using the diagnostic results stated in [28]; and (iii) the local influence results for the normal distribution in (ii) are compared. In Figure 6, 24 influence observations are detected under the skew-normal distribution. These results are summarized in Table 5.

Figure 6.

Diagnostics for perturbations of case-weight (a), data (b), variance (c) and skewness (d) with $\lambda =0.1$ and d = 5 using simulated data.

Table 5.

Local influence results for normal and skew-normal models with simulated data.

ID	Index under the normal model	Index under the skew-normal model	Observed value
1	33	33	−0.334
2	34	34	0.030
3	–	62	−0.271
4	77	77	−0.260
5	111	111	−0.297
6	112	112	−0.225
7	140	140	0.319
8	141	141	0.089
9	–	153	−0.175
10	–	201	−0.269
11	202	202	−0.326
12	203	203	−0.090
13	205	205	0.328
14	206	206	−0.124
15	214	214	−0.406
16	215	215	−0.159
17	293	293	0.296
18	294	294	−0.012
19	–	301	−0.278
20	306	306	0.043
21	345	345	−0.293
22	346	346	−0.092
23	362	362	−0.307
24	363	363	−0.048

Note that 24 potentially influential observations are identified by the local influence technique using the skew-normal distribution, whereas twenty potentially influential values are identified under normality. The potentially influential cases #62, #153, #201 and #301 for the skew-normal model have a value less than zero. Therefore, if λ of the skew-normal distribution is greater than zero, it is easier to find potentially influential values less than zero due to the difference in patterns between the skew-normal and normal distributions. This says us that the diagnostic results under the skew-normal distribution established in Section 4 work well.

6. A motivating example from finance (continued)

In this section, we retake the motivating example presented in Section 1 now involving the SNAR model and its diagnostics to show its potential applications. We use the returns from 2 January 2009 to 13 November 2020 to train our model. Then, the remaining data are used to test the trained model with the predicted values.

6.1. Estimation under the SNAR model

The estimate of the parameter $\hat{\mathit{\theta }}$ obtained with the expectation-maximization algorithm detailed in Section 4 is

$$({\widehat{\mathrm{\text{β}}}}_1,{\widehat{\mathrm{\text{β}}}}_2,{\widehat{\mathrm{\text{β}}}}_3,{\widehat{\mathrm{\text{β}}}}_4,{\hat{\sigma }}^2,\hat{\lambda })=(-0.0179,-0.0474,-0.0415,-0.0944,0.0013,-0.0111).$$

The values of the Akaike (AIC), Bayesian (BIC) and Hannan-Quinn (HQC) information criteria for the SNAR model are −2.9306; 23.7151 and −3.7545, respectively. As the estimated ${\mathrm{\text{β}}}_1$, ${\mathrm{\text{β}}}_2$, ${\mathrm{\text{β}}}_3$ and ${\mathrm{\text{β}}}_4$ in absolute value are all less than one, the CVX time series is assumed to be stationary for the AR(4) model, which coincides with what was concluded by the ADF test. The estimated λ is negative, as suggested by the empirical density shown in Figure 2, and significantly different from zero, as confirmed by the Tsay test ( $p-\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}<0.0001$). Therefore, we have more evidence that the returns are skew distributed and not symmetrically. The corresponding approximate estimated SEs for all the estimators of model parameters are calculated in the usual manner and they allowed us to detect reasonable significance levels in some cases. In addition, the SNAR(4) model is better than the AR(4) model in terms of predictions. Then, we obtain as predictive model the SNAR(4) structure trained as

$${\hat{y}}_t=-0.0179y_{t-1}-0.0474y_{t-2}-0.0415y_{t-3}-{0.0944}_{t-4},$$

with $\hat{\mu }=0$, ${\hat{\sigma }}^2=0.0013$, and $\hat{\lambda }=-0.0111$. A stationary financial series has economic implications. Among them, we can assume that their returns are characteristic of a constant mean function over time and its covariance function depends only on the lag and not on the moment time.

6.2. Diagnostics under the SNAR model

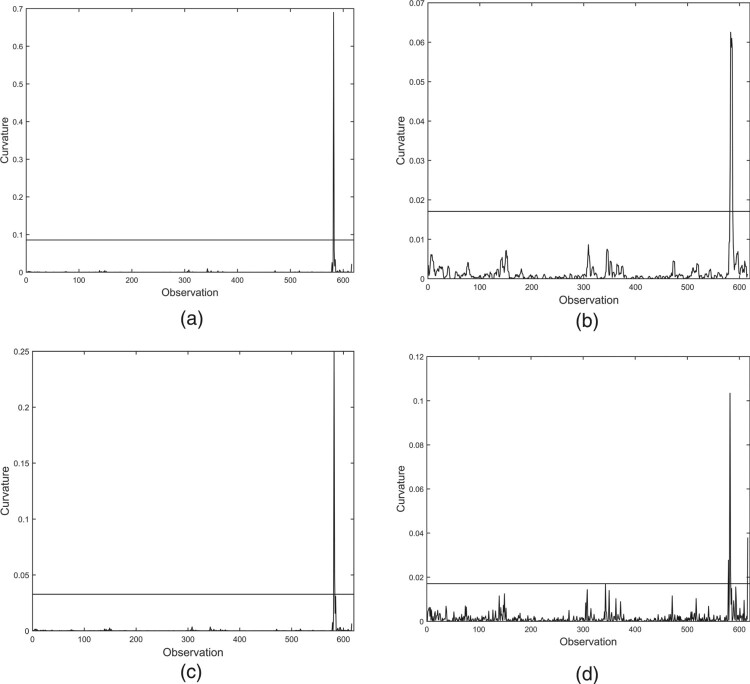
Next, we conduct local influence diagnostic analytics for the SNAR(4) model. In this case, the benchmark $1/616+3$ $S\left(N\right(i\left)\right)$ is considered, for i = 1, 2, 3, 4, with the values of 0.0855, 0.0171, 0.0327 and 0.0171 for the perturbation schemes of case-weight, data, variance parameter and skewness parameter, respectively. In Figure 7, the straight line is the benchmark establishing whether a case is potentially influential or not. Firstly, we identify case #586 to be potentially influential. The other potential influential cases can be masked by case #586. Similar to a step-wise diagnostic technique [42], a second round of identification of influential cases is carried out. Then, the value of case #586 is replaced by the average of its two neighbors (cases #585 and #587) to obtain a new time series. Subsequently, an AR model is refitted as in the first round. For the new time series, the SNAR(4) model parameters are once again estimated with the expectation-maximization-algorithm. Hence, the new SNAR(4) model is given by

$${\hat{y}}_t=-0.00130y_{t-1}+0.0079y_{t-2}-0.0679y_{t-3}-0.0980y_{t-4},$$

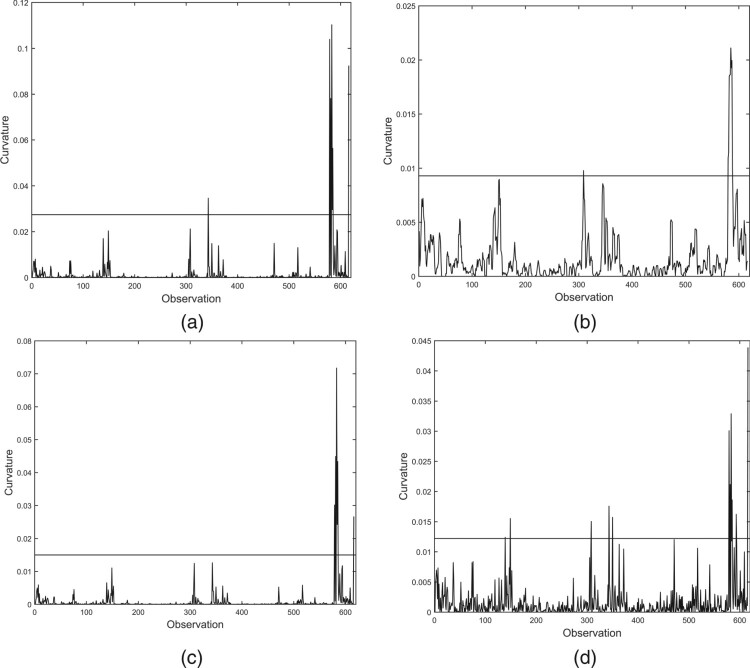
with $\hat{\mu }=0$, ${\hat{\sigma }}^2=0.0011$, $\hat{\lambda }=-0.0114$. The AIC, BIC and HQC values are $-2.9866,23.6591$ and $-3.8106$, respectively. Since the absolute values of ${\widehat{\mathrm{\text{β}}}}_1,{\widehat{\mathrm{\text{β}}}}_2$, ${\widehat{\mathrm{\text{β}}}}_3$, and ${\widehat{\mathrm{\text{β}}}}_4$ are all less than one, the CVX time series is assumed to be stationary with the SNAR(4) model and then we carry out a new influential analytics. Now, the benchmarks are 0.0274, 0.0093, 0.0150 and 0.0122 for the perturbation schemes of case-weight, data, variance parameter and skewness parameter, respectively. Now, 27 influence observations are identified in Figure 8; see Table 6, where * denotes that the cases is detected via the assigned perturbation scheme. Note that the points reported in Table 6 are a number of historical events. Many of these points are related to events around the COVID-19 pandemic in 2020. For example, on 9 March 2020 (Monday), international oil prices plummeted by $30\mathrm{\%}$, which was the biggest one-day drop since 1991. On the same day, US stock market opened four minutes, and the S&P 500 index plummeted by $7\mathrm{\%}$, triggering the first level circuit breaker mechanism. On 12 March 2020, as the S&P 500 index fell by 7.02%, the market was triggered to stop trading for 15 minutes. This was the second time that the circuit breaker mechanism had been triggered since Monday in the week, and the third time in the US stock history. On 17 March 2020, steep falls as markets opened triggered another automatic halt to trading. Before 9 March 2020, such halts, known as circuit breakers, had not been used in more than two decades. But the sell-off continued after the 15 minute suspension, with the Dow losing nearly 3000 points or 12.9%, its worst percentage drop since 1987. We see that such findings showcase the effectiveness of our procedures in identifying potentially influential observations to improve modeling outcomes.

Figure 7.

Diagnostics for the perturbations of case-weight (a), data (b), variance (c) and skewness (d) in the SNAR(4) model – first round – with CVX weekly return data.

Figure 8.

Diagnostics for the perturbations of case-weight (a), data (b), variance (c) and skewness (d) in the SNAR(4) model – second round – with CVX weekly return data.

Table 6.

Summary of the curvature-based diagnostic analytics with CVX weekly return data based on the SNAR(4) model.

Case	Date	CVX return	Case-weight	Data	Variance	Skewness
#143	23 November 2011	−10.15%				*
#153	2 December 2011	9.70%				*
#343	19 December 2014	9.80%		*		*
#347	21 August 2015	−11.41%	*			*
#354	9 October 2015	9.38%				*
#583	28 February 2020	−15.52%	*		*	*
#584	6 March 2020	2.10%		*
#585	13 March 2020	−13.34%	*	*	*
#586	20 March 2020	−33.98%	*	*	*	*
#587	27 March 2020	14.68%	*	*	*	*
#588	3 April 2020	8.80%	*	*	*
#589	9 April 2020	11.55%	*	*	*	*
#590	17 April 2020	3.34%		*
#597	5 May 2020	9.47%				*
#620	13 November 2020	15.44%	*	*	*	*

We make the predictions by the new SNAR(4) model and the traditional AR(4) model, presenting their comparisons in Table 7. The MSE of the predicted values by the two models are 0.001730 and 0.000965, respectively. Note from the results that the predictions made after removing the potentially influential cases are better than those made by using the original data.

Table 7.

Predicted results by the AR(4) and SNAR(4) models with CVX weekly return data.

Date	CVX returns	AR(4)	SNAR(4)
20 November 2020	0.0473	0.0223	0.0105
27 November 2020	0.0623	0.0223	0.0311
4 December 2020	0.0213	0.0386	0.0167
11 December 2020	−0.0089	−0.0164	−0.0033
18 December 2020	−0.0586	0.0102	−0.0095
24 December 2020	−0.0216	−0.0645	−0.0466
31 December 2020	−0.0104	0.0440	0.0262

7. Concluding remarks and future research

In this study, we have used a motivating example with a financial application under COVID-19 pandemic to investigate autoregressive modeling based on the skew-normal distribution. We have taken advantage of the stochastic representation of the skew-normal distribution to estimate the parameters of the corresponding autoregressive model efficiently with the expectation-maximization algorithm. In addition, we have researched the local (rather than global) influence diagnostics in the skew-normal autoregressive model to detect potentially influential observations under four perturbations: case-weight, data, variance parameter, and skewness parameter schemes. We have conducted two Monte Carlo simulation studies to evaluate the statistical performance of the corresponding estimators, and to obtain approximate benchmark values for determining potentially influential cases. We have applied this model to analyze weekly financial return data of Chevron under COVID-19 pandemic. In general, the results have shown that:

1. The parameter estimators for the skew-normal autoregressive model have produced suitable values of empirical bias and mean squared error with very close results to the true values used in the Monte Carlo simulations.

2. Approximate benchmark measures for determining potentially influential cases for diagnostics in the skew-normal autoregressive model have performed well.

3. Many of the potentially influential points are related to events around the COVID-19 pandemic, which we have detected with the Chevron times series data using the skew-normal autoregressive model.

Therefore, the findings outlined in this paper suggest that our formulation, estimation and local influence approach in the skew-normal autoregressive model effectively identifies potentially influential observations and improves the fit of the model. The numerical results have shown the good performance of the methodology presented in this paper. Thus, it may be a valuable addition to the tool-kit of econometrist, applied statisticians and data scientists.

The following aspects are open problems for skew-normal autoregressive models and they may be considered for future research:

1. It is known that certain financial, environmental and other data follow heavy-tailed distributions [23,36]. In the case that extremal observations are involved in the data, where heavy-tailed as well as skewed characteristics are present, the use of heavy-tailed distributions, for example, the Student-t distribution, may be considered to replace the normality assumption in the skew-normal autoregressive model.

2. Locally influential cases could not be globally influential cases. Thus, relevant studies on techniques to detect global influential cases for the skew-normal and skew-t autoregressive models need to be conducted [45].

3. A number of studies [3,8] have shown that understanding the behavior of volatility in financial time series data has important economic implications. We suggest that the volatility of Chevron returns and other data are analyzed by using models from the autoregressive conditional heteroskedasticity families.

4. The procedure of data-influence analytics is very useful for identifying a set of the particular observations termed influential potentially. However, this set may include other type of particular observations that are those so-called outliers. These outliers are those that are not well fitted by the model and their detection is based commonly on the residual analysis. Therefore, developing a methodology that allows us to identify outliers detected in a data set using different types of residuals is of interest for future study about quality of fit and predictive capability of the model [49].

5. Multivariate extensions and to spatial dependence case are also of interest [1,39].

6. Incorporation of temporal, spatial, functional, and quantile regression structures in the modeling, as well as errors-in-variables, and partial least squares regression, should be studied [7,13,14,16,19,20,34,38,40].

The derivation of diagnostic techniques to detect potentially influential cases are needed and constitute an important tool to be used in all statistical modeling [7,12,29]. Therefore, the methodology used in this investigation promotes new challenges and offers an open door to explore other theoretical and numerical issues. Research on these and other issues are in progress and their findings will be reported in future articles.

Funding Statement

The research of Y. Liu was supported by the Natural Science Foundation of China [grant number 11271259]. The research of V. Leiva was partially supported by the National Agency for Research and Development (ANID) of the Chilean government [grant number FONDECYT 1200525].

Disclosure statement

No potential conflict of interest was reported by the authors.