Functional additive models for optimizing individualized treatment rules

Summary:

A novel functional additive model is proposed which is uniquely modified and constrained to model nonlinear interactions between a treatment indicator and a potentially large number of functional and/or scalar pretreatment covariates. The primary motivation for this approach is to optimize individualized treatment rules based on data from a randomized clinical trial. We generalize functional additive regression models by incorporating treatment-specific components into additive effect components. A structural constraint is imposed on the treatment-specific components in order to provide a class of additive models with main effects and interaction effects that are orthogonal to each other. If primary interest is in the interaction between treatment and the covariates, as is generally the case when optimizing individualized treatment rules, we can thereby circumvent the need to estimate the main effects of the covariates, obviating the need to specify their form and thus avoiding the issue of model misspecification. The methods are illustrated with data from a depression clinical trial with electroencephalogram functional data as patients’ pretreatment covariates.

1. Introduction

We propose a flexible functional regression approach to optimizing individualized treatment decision rules (ITRs) where the treatment has to be chosen to optimize the expected treatment outcome. We focus on the situation in which a potentially large number of patient characteristics is available as pretreatment functional and/or scalar covariates. Recent advances in biomedical imaging and high-throughput gene expression technology produce massive amounts of data on individual patients, opening up the possibility of tailoring treatments to the biosignatures of individual patients from individual-specific data (McKeague and Qian, 2014). Notably, some randomized clinical trials (e.g., Trivedi et al., 2016) are designed to discover biosignatures that characterize patient heterogeneity in treatment responses from vast amounts of patient pretreatment characteristics. In this paper, we focus on some specific types of high-dimensional pretreatment patient characteristics observed in the form of curves or images, for instance, electroencephalogram (EEG) measurements. Such data can be viewed as functional (e.g., Ramsay and Silverman, 1997) and are becoming increasingly prevalent in modern randomized clinical trials (RCTs) as pretreatment covariates.

Much work has been carried out to develop methods for optimizing ITRs using data from RCTs. Regression-based methodologies are intended to optimize ITRs by estimating treatment-specific response (e.g., Qian and Murphy, 2011; Lu et al., 2011; Tian et al., 2014; Shi et al., 2016; Jeng et al., 2018) while attempting to maintain robustness with respect to model misspecification. Machine learning approaches for optimizing ITRs are often framed as a classification problem (e.g., Zhang et al., 2012; Zhao et al., 2019), including outcome weighted learning (e.g., Zhao et al., 2012, 2015; Song et al., 2015) based on support vector machines, tree-based classification (e.g., Laber and Zhao, 2015) and adaptive boosting (Kang et al., 2014), among others. However, to date there has been relatively little research on ITRs that directly utilize pretreatment functional covariates. McKeague and Qian (2014) proposed methods for optimizing ITRs that depend upon a single pretreatment functional covariate. Ciarleglio et al. (2016) considered a flexible regression for a single functional covariate. Focusing on a single covariate, Laber and Staicu (2018) considered sparse, noisy and irregularly spaced functional data, treating patient longitudinal information as a sparse functional covariate. Ciarleglio et al. (2015) proposed a method that allows for multiple functional/scalar covariates, which was then extended to incorporate a simultaneous covariate selection for ITRs in Ciarleglio et al. (2018). However, both of these approaches are limited to a stringent linear model assumption on the treatment-by-covariates interaction effects that limits flexibility in optimizing ITRs and to two treatment conditions.

In this paper, we allow for nonlinear interactions between the treatment and multiple pretreatment functional covariates on the outcome and also for more than two treatment conditions. We incorporate a simultaneous covariate selection for ITRs through an L¹ regularization to deal with a large number of functional and/or scalar covariates. In a review by Morris (2015) on functional regression, the functional additive regression of Fan et al. (2015) and the functional generalized additive model of McLean et al. (2014) are two popular approaches to functional additive regression. In this paper, we base our method on the functional additive regression model of Fan et al. (2015) that utilizes one-dimensional data-driven functional indices and the associated additive link functions. In Ciarleglio et al. (2016), nonlinear effects are presented with the functional additive regression of McLean et al. (2014), for a single covariate. However, the approach of McLean et al. (2014) requires more parameters for estimation and is based on an L² penalty rather than on L¹ penalties, which is less suitable in the context of many functional covariates and when sparsity is desired. In this paper, we develop a flexible approach to optimizing ITRs that can easily impose structural constraints in modeling nonlinear heterogenous treatment effects with functional and/or scalar pretreatment covariates.

2. Constrained functional additive models

Let $Y^{(a)}\in ℝ$ be the potential outcome under treatment A = a (a = 1, …, L). We consider a set of p functional-valued pretreatment covariates X = (X₁, …, X_p), and q scalar-valued pretreatment covariates $Z=\left(Z_1,\dots ,Z_q\right)\in {ℝ}^q$. These pretreatment covariates (X, Z) are considered as potential biomarkers for optimizing ITRs. We will assume that each functional covariate X_j is a square integrable random function, defined on a compact interval, say, [0, 1], without loss of generality. The L available treatment options are assigned with associated randomization probabilities (π₁, …, π_L), such that ${\sum }_{a=1}^L{\pi }_a=1$, π_a > 0, independent of (X, Z) (see Section A.17 of Supporting Information for a dependent case).

In this context we focus on optimizing ITRs based on $(X,Z)\in \mathcal{X}$. Without loss of generality, we assume that a larger value of the outcome Y^(a) is better. The goal is then (for a single decision point) to find an optimal ITR $\mathcal{D}:\mathcal{X}\mapsto \{1,\dots ,L\}$, such that the treatment assignment $A=\mathcal{D}(X,Z)$ maximizes the expected treatment outcome, the so-called value (V) function (Murphy, 2005), $V(\mathcal{D})≔E\left[Y^{(\mathcal{D})}\right]$. Under the standard causal inference assumptions in the Supporting Information Section A.16, $V(\mathcal{D})=E[E[Y\mid X,Z,A=\mathcal{D}(X,Z)]]$, and the optimal ITR ${\mathcal{D}}^{opt}$, that maximizes $V(\mathcal{D})$, satisfies: ${\mathcal{D}}^{opt}(X,Z)=\text{arg}{\text{max}}_{a\in \{1,\dots ,L\}}E\left[Y\mid X,Z,A=a\right]$ (Qian and Murphy, 2011). In particular, ${\mathcal{D}}^{opt}$ does not depend on the “main” effect of the covariates (X, Z) and depends only on the (X, Z)-by-A interaction effect (Qian and Murphy, 2011) in the mean response function E[Y|X, Z, A]. However, if this mean response model inadequately represents the interaction effect, the associated ITR may perform poorly.

Thus, we will focus on modeling possibly nonlinear (X, Z)-by-A interaction effects, while allowing for an unspecified main effect of (X, Z). We base the model on the functional additive model (FAM) of Fan et al. (2015) allowing for nonlinear (X, Z)-by-A interactions:

$$E[Y\mid X,Z,A]=\underset{(X,Z)“\text{main}”\text{effect}}{\underbrace{\mu (X,Z)}}+\underset{(X,Z)\text{-by-}A\text{interaction}\text{effect}}{\underbrace{\sum _{j=1}^p{g}_j\left(\langle X_j,{\beta }_j\rangle ,A\right)+\sum _{k=1}^q{h}_k\left(Z_k,A\right)}}.$$ (1)

In model (1), the treatment a-specific (with a ∈ {1, …, L}) component functions {g_j(·, a), j = 1, …, p} ∪ {h_k(·, a), k = 1, …, q} are unspecified smooth one-dimensional (1-D) functions. Specifically, each function X_j appears as a 1-D projection $\langle X_j,{\beta }_j\rangle ≔{\int }_0^1{X}_j(s){\beta }_j(s)ds$, via the standard L² inner product with a coefficient function β_j ∈ Θ, where Θ is the space of square integrable functions over [0, 1], restricted, without loss of generality, to a unit L² norm. (This is to ensure model identifiability; due to the unspecified nature of the functions β_j and g_j, β_j is only identifiable up to multiplications by nonzero constants.) The form of the function μ in (1) is left unspecified. For model (1), we assume an additive noise, Y = E[Y|X, Z, A] + ϵ, where $ϵ\in ℝ$ is a zero-mean noise with finite variance.

In model (1), to separate the nonparametric (X, Z) “main” effect from the additive (X, Z)-by-A interaction effect components, and to obtain an identifiable representation, we will constrain the p + q component functions {g_j, j = 1, …, p}∪{h_k, k = 1, …, q} associated with the (X, Z)-by-A interaction effect to satisfy the following identifiability conditions:

$$\begin{gathered} E\left[g_j\left(\langle X_j,{\beta }_j\rangle ,A\right)\mid X_j\right]=0\hspace{1em}\left(\forall {\beta }_j\in \Theta \right)\hspace{1em}(j=1,\dots ,p)\hspace{1em}\text{and} \\ E\left[h_k\left(Z_k,A\right)\mid Z_k\right]=0\hspace{1em}(k=1,\dots ,q) \end{gathered}$$ (2)

(almost surely), where the expectation is taken with respect to the distribution of A given X_j (or Z_k). Condition (2) implies $E\left[{\sum }_{j=1}^p{g}_j\left(\langle X_j,{\beta }_j\rangle ,A\right)+{\sum }_{k=1}^q{h}_k\left(Z_k,A\right)\mid X,Z\right]=0$ (almost surely), which makes not only representation (1) identifiable, but also the two effect components in model (1) orthogonal to each other. We call model (1) subject to the constraint (2), a constrained functional additive model (CFAM), which is the main model of the paper.

Notation 1:

For a fixed β, let us denote the L² space of component functions, g(·,·), over the random variables (〈X, β〉, A) as: ${\mathcal{H}}^{(\beta )}=\{g\mid E[g(\langle X,\beta \rangle ,A)]=0,\Vert g\Vert <\infty \}$, with the norm $\Vert g\Vert =\sqrt{E\left[g^2(\langle X,\beta \rangle ,A)\right]}$, where the expectation is taken with respect to the joint distribution of (〈X, β〉, A) and the inner product of the space defined as 〈g, g′〉 = E[g(〈X, β〉, A)g′(〈X, β〉, A)]. Similarly, let us denote the L² space of component functions, h(·,·), over (Z, A) as: $\mathcal{H}=\{h\mid E[h(Z,A)]=0,\Vert h\Vert <\infty \}$ with the norm $\Vert h\Vert =\sqrt{E\left[h^2(Z,A)\right]}$, where the expectation is with respect to the distribution of (Z, A), and similarly defined inner product. Without loss of generality, we suppress the treatment-specific intercepts in model (1), by removing the treatment a-specific means from Y, and assume E[Y|A = a] = 0 (a = 1, …, L), i.e., the main effect of A is 0 (see Supporting Information Section A.15 for the model with the treatment-specific intercepts).

Under the formulation (1) subject to the constraint (2), the “true” (i.e., optimal) functions, denoted as $\left\{g_j^{*},j=1,\dots ,p\right\}\cup \left\{{\beta }_j^{*},j=1,\dots ,p\right\}\cup \left\{h_k^{*},k=1,\dots ,q\right\}$ that constitute the (X, Z)-by-A interaction effect, can be viewed as the solution to the constrained optimization:

$$\begin{array}{lll}\left\{g_j^{*},{\beta }_j^{*},h_k^{*}\right\}\hspace{1em}=\hfill & \underset{g_j\in {\mathcal{H}}_j^{\left({\beta }_j\right)},{\beta }_j\in \Theta ,h_k\in {\mathcal{H}}_k}{\text{argmin}}\hfill & E{\left\{Y-\sum _{j=1}^p{g}_j\left(\langle X_j,{\beta }_j\rangle ,A\right)-\sum _{k=1}^q{h}_k\left(Z_k,A\right)\right\}}^2,\hfill \\ \hfill & \text{subject}\text{to}\hfill & E\left[g_j\left(\langle X_j,{\beta }_j\rangle ,A\right)\mid X_j\right]=0\hspace{1em}\forall {\beta }_j\in \Theta \hspace{1em}(j=1,\dots ,p)\hspace{1em}\text{and}\hfill \\ \hfill & \hfill & E\left[h_k\left(Z_k,A\right)\mid Z_k\right]=0\hspace{1em}(k=1,\dots ,q).\hfill \end{array}$$ (3)

Specifically, representation (3) does not involve the “main” effect functional μ, due to the orthogonal representation (1) implied by (2) (see Section A.1 of Supporting Information for additional detail). If μ in (1) is a complicated functional subject to model misspecification, exploiting the representation on the right-hand side of (3) for $\left\{g_j^{*},j=1,\dots ,p\right\}\cup \left\{{\beta }_j^{*},j=1,\dots ,p\right\}\cup \left\{h_k^{*},k=1,\dots ,q\right\}$ on the left-hand side is particularly appealing, as it provides a means of estimating the interaction terms without having to specify μ, thereby avoiding any issue of possible model misspecification for μ. The function μ can also be specified similar to (3) and estimated separately (see Section A.11 of Supporting Information), due to orthogonality in model (1). In particular, estimators of {$g_j^{*}$, ${\beta }_j^{*}$, $h_k^{*}$} based on optimization (3) can be improved in terms of efficiency if Y in (3) is replaced by a “residualized” response $Y-\widehat{\mu }(X,Z)$, where $\widehat{\mu }$ is some estimate of μ (see also Section A.11 of Supporting Information). However, for simplicity, we will focus on the representation (3) with the “unresidualized” Y.

Under model (1), the potential treatment effect-modifiers among {X_j, j = 1, …, p} ∪ {Z_k, k = 1, …, q} appear in the model only through the (X, Z)-by-A interaction effect terms in (1). Ravikumar et al. (2009) proposed a sparse additive model (SAM) for relevant covariate selection in a high-dimensional additive regression. As in SAM, to deal with a large p + q and to achieve treatment effect-modifying variable selection, under the often reasonable assumption that most covariates are inconsequential as treatment effect-modifiers, we impose sparsity on the set of component functions {g_j, j = 1, …, p} ∪ {h_k, k = 1, …, q} of CFAM (1). This sparsity structure on the set of component functions can be usefully incorporated into the optimization-based representation (3) of {$g_j^{*}$, ${\beta }_j^{*}$, $h_k^{*}$}:

$$\begin{array}{lll}\left\{g_j^{*},{\beta }_j^{*},h_k^{*}\right\}=\hfill & \underset{g_j\in {\mathcal{H}}_j^{\left({\beta }_j\right)},{\beta }_j\in \Theta ,h_k\in {\mathcal{H}}_k}{\text{argmin}}\hfill & E{\left\{Y-\sum _{j=1}^p{g}_j\left(\langle X_j,{\beta }_j\rangle ,A\right)-\sum _{k=1}^q{h}_k\left(Z_k,A\right)\right\}}^2+\lambda \left\{\sum _{j=1}^p\Vert g_j\Vert +\sum _{k=1}^q\Vert h_k\Vert \right\},\hfill \\ \hfill & \text{subject}\text{to}\hfill & E\left[g_j\left(\langle X_j,{\beta }_j\rangle ,A\right)\mid X_j\right]=0\hspace{1em}\forall {\beta }_j\in \Theta \hspace{1em}(j=1,\dots ,p)\hspace{1em}\text{and}\hfill \\ \hfill & \hfill & E\left[h_k\left(Z_k,A\right)\mid Z_k\right]=0\hspace{1em}(k=1,\dots ,q),\hfill \end{array}$$ (4)

for some sparsity-inducing parameter λ ⩾ 0. In (4), the component ${\sum }_{j=1}^p\Vert g_j\Vert +{\sum }_{k=1}^q\Vert h_k\Vert$ behaves like an L¹ ball across different functional components {g_j, j = 1, …, p; h_k, k = 1, …, q} to encourage functional sparsity. For example, a relatively large value of λ in (4) will result in many components to be exactly zero, thereby enforcing sparsity on the set of functions {$g_j^{*}$, $h_k^{*}$} on the left-hand side of (4). Specifically, equation (4) can help model selection when dealing with potentially many functional/scalar pretreatment covariates. Potentially, separate sparsity tuning parameters λ_j and ${\check{\lambda }}_k$ (for X_j and Z_k) can be employed in (4). However, we restrict our attention to the case of a single sparsity tuning parameter that treats all X_j and Z_k on the equal footing for treatment effect modifier selection.

3. Estimation

We first consider a population characterization of the algorithm for solving (4) in Section 3.1 and then a sample counterpart of the population algorithm in Section 3.2.

3.1. Population algorithm

For a set of fixed coefficient functions {β_j, j = 1, …, p}, the minimizing component function $g_j\in {\mathcal{H}}_j^{\left({\beta }_j\right)}$ (and $h_k\in {\mathcal{H}}_k$) for each j (and each k) of the constrained objective function of (4) has a component-wise closed-form expression, as indicated below.

Theorem 1:

Given λ ⩾ 0 and a set of fixed single-index coefficient functions {β_j, j = 1, …, p}, the minimizing component function $g_j\in {\mathcal{H}}_j^{\left({\beta }_j\right)}$ of the constrained objective function of (4) satisfies:

$$g_j\left(\langle X_j,{\beta }_j\rangle ,A\right)={\left[1-\frac{\lambda }{\Vert P_j\Vert }\right]}_{+}{P}_j\left(\langle X_j,{\beta }_j\rangle ,A\right)\hspace{1em}\left(\mathit{\text{almost}}\mathit{\text{surely}}\right),$$ (5)

where the function $P_j\in {\mathcal{H}}_j^{\left({\beta }_j\right)}$:

$$P_j\left(\langle X_j,{\beta }_j\rangle ,A\right)≔E\left[R_j\mid \langle X_j,{\beta }_j\rangle ,A\right]-E\left[R_j\mid \langle X_j,{\beta }_j\rangle \right],$$ (6)

in which

$$R_j=Y-\sum _{j^{\prime }\ne j}{g}_{j^{\prime }}\left(\langle X_{j^{\prime }},{\beta }_{j^{\prime }}\rangle ,A\right)-\sum _{k=1}^q{h}_k\left(Z_k,A\right)$$ (7)

represents the jth (functional covariate’s) partial residual; similarly, the minimizing component function $h_k\in {\mathcal{H}}_k$ of the constrained objective function of (4) satisfies:

$$h_k\left(Z_k,A\right)={\left[1-\frac{\lambda }{\Vert {\check{P}}_k\Vert }\right]}_{+}{\check{P}}_k\left(Z_k,A\right)\hspace{1em}\left(\mathit{\text{almost}}\mathit{\text{surely}}\right),$$ (8)

where the function ${\check{P}}_k\in {\mathcal{H}}_k$:

$${\check{P}}_k\left(Z_k,A\right)≔E\left[{\check{R}}_k\mid Z_k,A\right]-E\left[{\check{R}}_k\mid Z_k\right],$$ (9)

and

$${\check{R}}_k=Y-\sum _{j=1}^p{g}_j\left(\langle X_j,{\beta }_j\rangle ,A\right)-\sum _{k^{\prime }\ne k}{h}_{k^{\prime }}\left(Z_{k^{\prime }},A\right)$$ (10)

represents the kth (scalar covariate’s) partial residual. (In (5) and (8), [u]₊ = max(0, u) represents the positive part of u.)

The proof of Theorem 1 is in Section A.2 of Supporting Information. Given a sparsity tuning parameter λ ⩾ 0, optimization (4) can be split into two iterative steps (Fan et al., 2014, 2015). First (Step 1), for a set of fixed single-indices 〈X_j, β_j〉 (j = 1, …, p), the component functions {g_j, j = 1, …, p} ∪ {h_k, k = 1, …, q} of the model can be found by a coordinate descent procedure that fixes {g_j′; j′ ≠ j} ∪ {h_k, k = 1, …, q} and obtains g_j by equation (5) (and that fixes {g_j, j = 1, …, p} ∪ {h_k′; k′ ≠ k} and obtains h_k by equation (8)), and then iterates through all j and k until convergence. This step (Step 1) amounts to fitting a SAM (Ravikumar et al., 2009) subject to the constraint (2). Second (Step 2), for a set of fixed component functions {g_j, j = 1, …, p} ∪ {h_k, k = 1, …, q}, the jth single-index coefficient function β_j ∈ Θ can be optimized by solving, for each j ∈ {1, …, p} separately:

$$\underset{{\beta }_j\in \Theta }{\text{minimize}}E{\left\{R_j-g_j\left(\langle X_j,{\beta }_j\rangle ,A\right)\right\}}^2(j=1,\dots ,p),$$ (11)

where the jth partial residual R_j is defined in (7). These two steps can be iterated until convergence to obtain a population solution {$g_j^{*}$, ${\beta }_j^{*}$, $h_k^{*}$} on the left-hand side of (4).

To obtain a sample version of the population solution, we can insert sample estimates into the population algorithm, as in standard backfitting in estimating generalized additive models (Hastie and Tibshirani, 1999), which we describe in the next subsection.

3.2. Sample version of the population algorithm

To simplify the exposition, we only describe the optimization of g_j(〈X_j, β_j〉, A) (j = 1, …, p) associated with the functional covariates X_j (j = 1, …, p). The components h_k(Z_k, A) (k = 1, …, q) associated with the scalar covariates Z_k (k = 1, …, q) in (4) are optimized in the same way, except that we do not need to perform Step 2 of the alternating optimization procedure; i.e., when optimizing h_k(Z_k, A) (k = 1, …, q), we only perform Step 1.

3.2.1. Step 1.

First, we consider a sample version of Step 1 of the population algorithm. Suppose we are given a set of estimates $\left\{{\widehat{\beta }}_j,j=1,\dots ,p\right\}$ and the data-version of the jth partial residual R_j in (7): ${\widehat{R}}_{ij}=Y_i-{\sum }_{j^{\prime }\ne j}{\widehat{g}}_{j^{\prime }}\left(\langle X_{i{j}^{\prime }},{\widehat{\beta }}_{j^{\prime }}\rangle ,A_i\right)-{\sum }_{k=1}^q{\widehat{h}}_k\left(Z_{ik},A_i\right)(i=1,\dots ,n)$, where ${\widehat{g}}_{j^{\prime }}$ represents a current estimate for g_j′ and ${\widehat{h}}_k$ that for h_k. For each j, we update the component function g_j in (5) in two steps: first, estimate the function P_j in (6); second, plug the estimate of P_j into ${\left[1-\frac{\lambda }{\Vert P_j\Vert }\right]}_{+}$ in (5), to obtain the soft-thresholded estimate ${\widehat{g}}_j$.

Although any linear smoothers can be utilized to obtain estimators $\left\{{\widehat{g}}_j,j=1,\dots ,p\right\}$ (see Section A.3 of Supporting Information), we shall focus on regression spline-type estimators, which are simple and computationally efficient to implement. For each j and ${\beta }_j={\widehat{\beta }}_j$, we will represent the component function $g_j\in {\mathcal{H}}_j^{\left({\widehat{\beta }}_j\right)}$ on the right-hand side of (4) as:

$$g_j\left(\langle X_j,{\widehat{\beta }}_j\rangle ,a\right)={\Psi }_j{\left(\langle X_j,{\widehat{\beta }}_j\rangle \right)}^{\top }{\theta }_{j,a}\hspace{1em}(a=1,\dots ,L)$$ (12)

for some prespecified d_j-dimensional basis Ψ_j(·) (e.g., cubic B-spline basis with d_j−4 interior knots, evenly placed over the range (scaled to, say, [0, 1]) of the observed values of $\langle X_j,{\widehat{\beta }}_j\rangle$) and a set of unknown treatment a-specific basis coefficients ${\left\{{\theta }_{j,a}\in {ℝ}^{d_j}\right\}}_{a\in \{1,\dots ,L\}}$. Based on representation (12) of $g_j\in {\mathcal{H}}_j^{\left({\widehat{\beta }}_j\right)}$ for fixed ${\widehat{\beta }}_j$, the constraint E[g_j(〈X_j, β_j〉, A)|X_j] = 0 in (4) on g_j, for fixed ${\beta }_j={\widehat{\beta }}_j$, can be simplified to: $E\left[{\theta }_{j,A}\right]={\sum }_{a=1}^L{\pi }_a{\theta }_{j,a}=0$. If we fix ${\beta }_j={\widehat{\beta }}_j$, the constraint in (4) on the function g_j can then be succinctly written in matrix form:

$${\pi }^{(j)}{\theta }_j=0,$$ (13)

where ${\theta }_j≔{\left({\theta }_{j,1}^{\top },{\theta }_{j,2}^{\top },\dots ,{\theta }_{j,L}^{\top }\right)}^{\top }\in {ℝ}^{d_{j}L}$ is the vectorized version of the basis coefficients {θ_{j, a}}_{a∈{1, …, L}}, and the d_j × d_jL matrix ${\pi }^{(j)}≔\left({\pi }_1{I}_{d_j};{\pi }_2{I}_{d_j};\dots ;{\pi }_L{I}_{d_j}\right)$ where $I_{d_j}$ is the d_j × d_j identity matrix.

The details provided in Section A.4 of Supporting Information (where constraint (13) is incorporated in the estimation) yield an estimate of the treatment a-specific function g_j(·,a) (a = 1, …, L) that appears in model (1):

$${\widehat{g}}_j(\cdot ,a)={\Psi }_j{(\cdot )}^{\top }{\widehat{\theta }}_{j,a}\hspace{1em}(a=1,\dots ,L)\hspace{1em}(j=1,\dots ,p)$$ (14)

estimated within the class of functions (12), for a given tuning parameter λ ⩾ 0, resulting in the estimates of the component functions $\left\{{\widehat{g}}_j,j=1,\dots ,p\right\}\cup \left\{{\widehat{h}}_k,k=1,\dots ,q\right\}$; this completes Step 1 of the alternating optimization procedure.

3.2.2. Step 2.

We now consider a sample version of Step 2 of the population algorithm that optimizes the coefficient functions {β_j, j = 1, …, p} on the right-hand side of (4), for a fixed set of the component function estimates $\left\{{\widehat{g}}_j,j=1,\dots ,p\right\}\cup \left\{{\widehat{h}}_k,k=1,\dots ,q\right\}$ provided by Step 1. As an empirical approximation to (11), we consider

$$\underset{{\beta }_j\in \Theta }{\text{minimize}}\sum _{i=1}^n{\left\{{\widehat{R}}_{ij}-{\widehat{g}}_j\left(\langle X_{ij},{\beta }_j\rangle ,A_i\right)\right\}}^2\hspace{1em}(j=1,\dots ,p),$$ (15)

where ${\widehat{R}}_{ij}$ is given from the previous Step 1 at convergence. For this alternating step, solving (15) for β_j can be approximately achieved based on a first-order Taylor series approximation of the term ${\widehat{g}}_j\left(\langle X_{ij},{\beta }_j\rangle ,A_i\right)$ at the current estimate of β_j, which we denote as ${\widehat{\beta }}_j^{(c)}\in \Theta$:

$$\begin{gathered} \sum _{i=1}^n{\left\{{\widehat{R}}_{ij}-{\widehat{g}}_j\left(\langle X_{ij},{\beta }_j\rangle ,A_i\right)\right\}}^2\approx \sum _{i=1}^n{\left\{{\widehat{R}}_{ij}-{\widehat{g}}_j\left(\langle X_{ij},{\widehat{\beta }}_j^{(c)}\rangle ,A_i\right)-{\dot{\widehat{g}}}_j\left(\langle X_{ij},{\widehat{\beta }}_j^{(c)}\rangle ,A_i\right)\langle X_{ij},{\beta }_j-{\widehat{\beta }}_j^{(c)}\rangle \right\}}^2 \\ =\sum _{i=1}^n{\left\{{\widehat{R}}_{ij}^{*}-\langle X_{ij}^{*},{\beta }_j\rangle \right\}}^2, \end{gathered}$$ (16)

where the “modified” residuals ${\widehat{R}}_{ij}^{*}$ and the “modified” covariates $X_{ij}^{*}$ are defined as:

$$\begin{array}{ll}{\widehat{R}}_{ij}^{*}={\widehat{R}}_{ij}-{\widehat{g}}_j\left(\langle X_{ij},{\widehat{\beta }}_j^{(c)}\rangle ,A_i\right)+{\dot{\widehat{g}}}_j\left(\langle X_{ij},{\widehat{\beta }}_j^{(c)}\rangle ,A_i\right)\langle X_{ij},{\widehat{\beta }}_j^{(c)}\rangle \hfill & (i=1,\dots ,n),\hfill \\ X_{ij}^{*}={\dot{\widehat{g}}}_j\left(\langle X_{ij},{\widehat{\beta }}_j^{(c)}\rangle ,A_i\right)X_{ij}\hfill & (i=1,\dots ,n),\hfill \end{array}$$ (17)

in which each ${\dot{\widehat{g}}}_j(\cdot ,a)$ denotes the first derivative of ${\widehat{g}}_j(\cdot ,a)$ in (14) given from Step 1. We can perform a functional linear regression (e.g., Cardot et al., 2003) with scalar response ${\widehat{R}}_{ij}^{*}$ and (functional) covariate $X_{ij}^{*}$ to minimize the right-hand side of (16) over β_j ∈ Θ. Specifically, we represent the smooth coefficient function β_j in (16) by a prespecified and normalized m_j-dimensional B-spline basis $B_j(s)={\left(b_{j1}(s),\dots ,b_{j{m}_j}(s)\right)}^{\top }\in {ℝ}^{m_j}$, where m_j depends only on the sample size n (Fan et al., 2015):

$${\beta }_j(s)=\sum _{r=1}^{m_j}{b}_{jr}(s){\gamma }_{jr}\hspace{1em}s\in [0,1],$$ (18)

with an unknown basis coefficient vector ${\gamma }_j={\left({\gamma }_{j1},{\gamma }_{j2},\dots ,{\gamma }_{j{m}_j}\right)}^{\top }\in {ℝ}^{m_j}$. Suppose the functional covariate X_ij(s) (i = 1, …, n) is discretized at points $\left\{s_l:0=s_0<s_1<s_2<\dots <s_{r_j}=1\right\}$, with the distance between two adjacent discretization points denoted as Δ_l. Based on the approximation $\langle X_{ij},{\widehat{\beta }}_j^{(c)}\rangle \approx {\sum }_{l=1}^{r_j}{\Delta }_l{X}_{ij}\left(s_l\right){\widehat{\beta }}_j^{(c)}\left(s_l\right)$, we approximate ${\widehat{R}}_{ij}^{*}$ and $X_{ij}^{*}$ in (17). Let $\Delta X_j^{*}$ be the n × r_j matrix whose ith (i = 1, …, n) row is the length-r_j vector ${\left({\Delta }_1{X}_{ij}^{*}\left(s_1\right),\dots ,{\Delta }_{r_j}{X}_{ij}^{*}\left(s_{r_j}\right)\right)}^{\top }$, corresponding to the ith subject’s $X_{ij}^{*}(s)$ evaluated at the discretization points $\left\{s_1,\dots ,s_{r_j}\right\}$ where each evaluation is multiplied by the corresponding Δ_l. Let B_j be the r_j × m_j matrix whose lth (l = 1, …, r_j) row is the length-m_j vector ${\left(b_{j1}\left(s_l\right),b_{j2}\left(s_l\right),\dots ,b_{j{m}_j}\left(s_l\right)\right)}^{\top }$, corresponding to the vector of basis in (18) evaluated at s_l. Given β_j(s) in (18) discretized at $\left\{s_1,\dots ,s_{r_j}\right\}$, we can represent the right-hand side of (16) as:

$${\Vert {\widehat{R}}_j^{*}-U_j^{*}{\gamma }_j\Vert }^2,$$ (19)

where ${\widehat{R}}_j^{*}≔{\left({\widehat{R}}_{1j}^{*},\dots ,{\widehat{R}}_{nj}^{*}\right)}^{\top }\in {ℝ}^n$ and $U_j^{*}≔\mathit{\text{Δ}}{X}_j^{*}{B}_j\in {ℝ}^n\times {ℝ}^{m_j}$. Minimizing (19) over ${\gamma }_j\in {ℝ}^{m_j}$ for each j separately (j = 1, …, p) provides estimates {${\widehat{\beta }}_j$, j = 1, …, p} of the coefficient functions under (18). Here, the minimizer ${\widehat{\gamma }}_j$ for (19) is scaled to $\Vert {\widehat{\gamma }}_j\Vert =1$, so that the resulting ${\widehat{\beta }}_j(s)={\sum }_{r=1}^{m_j}{b}_{jr}(s){\widehat{\gamma }}_{jr}\hspace{1em}(s\in [0,1])$ satisfies the identifiability constraint ${\widehat{\beta }}_j\in \Theta$. This completes Step 2 of the alternating optimization procedure.

3.2.3. Initialization and convergence criterion.

At the initial iteration, we need some estimates {${\widehat{\beta }}_j$, j = 1, …, p} of the single-index coefficient functions to initialize the single-indices {$u_j=\langle {\widehat{\beta }}_j,X_j\rangle$, j = 1, …, p}, in order to perform Step 1 (i.e., the coordinate-descent procedure) of the estimation procedure described in Section 3.2.1. At the initial iteration, we take ${\widehat{\beta }}_j(s)=1(s\in [0,1])$, i.e., we take $u_j={\int }_0^1{X}_j(s)ds(j=1,\dots ,p)$, which corresponds to the common practice of taking a naïve scalar summary of each functional covariate. The proposed algorithm alternating between Step 1 and Step 2 terminates when the estimates {${\widehat{\beta }}_j$, j = 1, …, p} converge. To be specific, the algorithm terminates when ${\text{max}}_{j=1,\dots ,p,r=1,\dots ,m_j}\Vert \left({\widehat{\gamma }}_{jr}-{\widehat{\gamma }}_{jr}^{(c)}\right)/{\widehat{\gamma }}_{jr}\Vert$ is less than a prespecified convergence tolerance; here, ${\widehat{\gamma }}_{jr}^{(c)}$ represents the current estimate for γ_jr in (18) at the beginning of Step 1, and ${\widehat{\gamma }}_{jr}$ is the updated estimate at the end of Step 2. The proposed computational procedure is summarized as Algorithm 1 in Section A.6 (with discussion on computational time and convergence provided in Sections A.7 and A.9) of Supporting Information. The sparsity tuning parameter λ ⩾ 0 can be chosen to minimize an estimate of the expected squared error of the models over a dense grid of λ’s, estimated, for example, by a 10-fold cross-validation.

4. Simulation study

4.1. ITR estimation performance

In this section, we assess the optimal ITR estimation performance of the proposed method based on simulations. We generate n independent copies of p functional-valued covariates X_i = (X_i1, X_i2, …, X_ip) (i = 1, …, n), where we use a 4-dimensional Fourier basis, $\Phi (s)=(\sqrt{2}\text{sin}(2\pi s)$, $\sqrt{2}\text{cos}(2\pi s)$, $\sqrt{2}\text{sin}(4\pi s)$, $\sqrt{2}\text{cos}(4\pi s){)}^{\top }\in {ℝ}^4(s\in [0,1])$, and random coefficients ${\tilde{x}}_{ij}\in {ℝ}^4$, each independently following $\mathcal{N}\left(0,I_4\right)$, to form the functions $X_{ij}(s)=\Phi {(s)}^{\top }{\tilde{x}}_{ij}$ (i = 1, …, n; j = 1, …, p). Then these covariates are evaluated at 50 equally spaced points ${\left\{s_l\right\}}_{l=1}^{50}$ between 0 and 1. We also generate n independent copies of q scalar covariates $Z_i={\left(Z_{i1},\dots ,Z_{iq}\right)}^{\top }\in {ℝ}^q(i=1,\dots ,n)$, based on the multivariate normal distribution with each component having mean 0 and variance 1, with correlations between the components corr(Z_ij, Z_ik) = 0.5^|j−k|. We generate the outcomes Y_i(i = 1, …, n) from:

$$Y_i={ϵ}_i+\delta \left\{\sum _{j=1}^8\text{sin}\left(\langle {\eta }_j,X_{ij}\rangle \right)+\sum _{k=1}^8\text{sin}\left(Z_{ik}\right)\right\}+4\left(A_i-1.5\right)\left[\text{sin}\left(\langle {\beta }_1,X_{i1}\rangle \right)-\text{sin}\left(\langle {\beta }_2,X_{i2}\rangle \right)+\text{cos}\left(Z_{i1}\right)-\text{cos}\left(Z_{i2}\right)+\xi \left\{\text{cos}\left(\langle X_{i1},X_{i2}\rangle \right)+\text{sin}\left(Z_{i1}{Z}_{i2}\right)\right\}\right],$$ (20)

where the treatments A_i ∈ {1, 2} are generated with equal probability, independently of (X_i, Z_i) and ${ϵ}_i~\mathcal{N}\left(0,{0.5}^2\right)$. In (20), there are only four “signal” covariates (X_i1, X_i2, Z_i1 and Z_i2) influencing the effect of A_i on Y_i (i.e., 4 treatment effect-modifiers). The other p + q − 4 covariates are “noise” covariates not critical in optimizing ITRs. We set p = q = 20, therefore we consider a total of 40 pretreatment covariates in this example. In (20), we set the single-index coefficient functions, β₁ and β₂, to be: β₁(s) = Φ(s)^⊤ (0.5, 0.5, 0.5, 0.5) and β₂(s) = Φ(s)^⊤ (0.5, −0.5, 0.5, −0.5), respectively (see Figure 2). We set the coefficient functions η_j (j = 1, …, 8) associated with the X_j “main” effect to be: ${\eta }_j(s)=\Phi {(s)}^{\top }{\tilde{\eta }}_j$, with each ${\tilde{\eta }}_j\in {ℝ}^4(j=1,\dots ,8)$ following $\mathcal{N}\left(0,I_4\right)$ and then rescaled to a unit L² norm $\Vert {\tilde{\eta }}_j\Vert =1$. The data model (20) is indexed by a pair (δ, ξ). The parameter δ ∈ {1, 2} controls the contribution of the (X, Z) main effect component, $\delta \left\{{\sum }_{j=1}^8\text{sin}\left(\langle {\eta }_j,X_{ij}\rangle \right)+{\sum }_{k=1}^8\text{sin}\left(Z_{ik}\right)\right\}$, to the variance of Y, in which δ = 1 corresponds to a relatively moderate (X, Z) main effect (about 4 times greater than the interaction effect when ξ = 0) and δ = 2 corresponds to a relatively large (X, Z) main effect (about 16 times greater than the interaction effect when ξ = 0). In (20), the parameter ξ ∈ {0, 1} determines whether the A-by-(X, Z) interaction effect component has an additive structure (ξ = 0) of the specified form (1) or whether it deviates from an additive structure (ξ = 1). In the case of ξ = 0, the proposed CFAM (1) is correctly specified, whereas, for the case of ξ = 1, it is misspecified. For each simulation replication, we consider the following four approaches to estimating ${\mathcal{D}}^{opt}$:

1. The proposed approach (4) estimated via Algorithm 1 in Supporting Information Section A.6, where the dimensions of the cubic B-spline basis for {g_j, h_k, β_j} are set at d_j = d_k = m_j = 4 + (2n)^1/5 (rounded to the closest integer) following the conditions of Corollary 3 of Fan et al. (2015). The sparsity tuning parameter λ > 0 is chosen to minimize 10-fold cross-validated prediction error of the fitted models.

2. The functional linear regression approach of Ciarleglio et al. (2018),

   $$\underset{{\beta }_j\in L^2[0,1],{\alpha }_k\in ℝ}{\text{minimize}}E{\left\{Y-\sum _{j=1}^p\langle {\beta }_j,X_j\rangle (A-1.5)-\sum _{k=1}^q{\alpha }_k{Z}_k(A-1.5)\right\}}^2+\lambda \left\{\sum _{j=1}^p\left(\Vert {\beta }_j\Vert +{\rho }_j{\gamma }_j^{\top }{S}_j{\gamma }_j\right)+\sum _{k=1}^q\left|{\alpha }_k\right|\text{)}\right\},$$

   which tends to yield a sparse set {β_j} ∪ {α_k}, estimated based on representation (18) for β_j with m_j = 10 and an associated m_j × m_j P-spline penalty matrix (S_j) that ensures appropriate smoothness. The tuning parameters λ > 0 and ρ = ρ_j > 0 (j = 1, …, p) are chosen to minimize a 10-fold cross-validated prediction error (Ciarleglio et al., 2018). Since the component functions {g_j, h_k} associated with Ciarleglio et al. (2018) are restricted to be linear (i.e., we restrict them to g_j(〈β_j, X_j〉, A) = 〈β_j, X_j〉(A − 1.5) and h_k (Z_k, A) = α_kZ_k(A − 1.5)) corresponding to a special case of CFAM, we call the model of Ciarleglio et al. (2018), a CFAM with linear component functions (CFAM-lin) for the notational simplicity.

3. The outcome weighted learning (OWL; Zhao et al., 2012) method based on a linear kernel (OWL-lin), implemented in the R-package DTRlearn. Since there is no currently available OWL method that deals with functional covariates, we compute a scalar summary of each functional covariate, i.e., ${\overline{X}}_j={\int }_0^1{X}_j(s)ds\in ℝ$, and use ${\overline{X}}_j$ along with the other scalar covariates Z_k as inputs to the augmented (residualized) OWL procedure. To improve its efficiency, we employ the augmented OWL approach of Liu et al. (2018), which amounts to pre-fitting a linear model for μ in (1) via Lasso (Tibshirani, 1996) and residualizing the response Y. The tuning parameter κ in Zhao et al. (2012) is chosen from the grid of (0.25, 0.5, 1, 2, 4) (the default setting of DTRlearn) based on a 10-fold cross-validation.

4. The same approach as in 3 but based on a Gaussian radial basis function kernel (OWL-Gauss) in place of a linear kernel. The inverse bandwidth parameter ${\sigma }_n^2$ in Zhao et al. (2012) is chosen from the grid of (0.01, 0.02, 0.04, …, 0.64, 1.28) and κ is chosen from the grid of (0.25, 0.5, 1, 2, 4), based on a 10-fold cross-validation.

Figure 2.

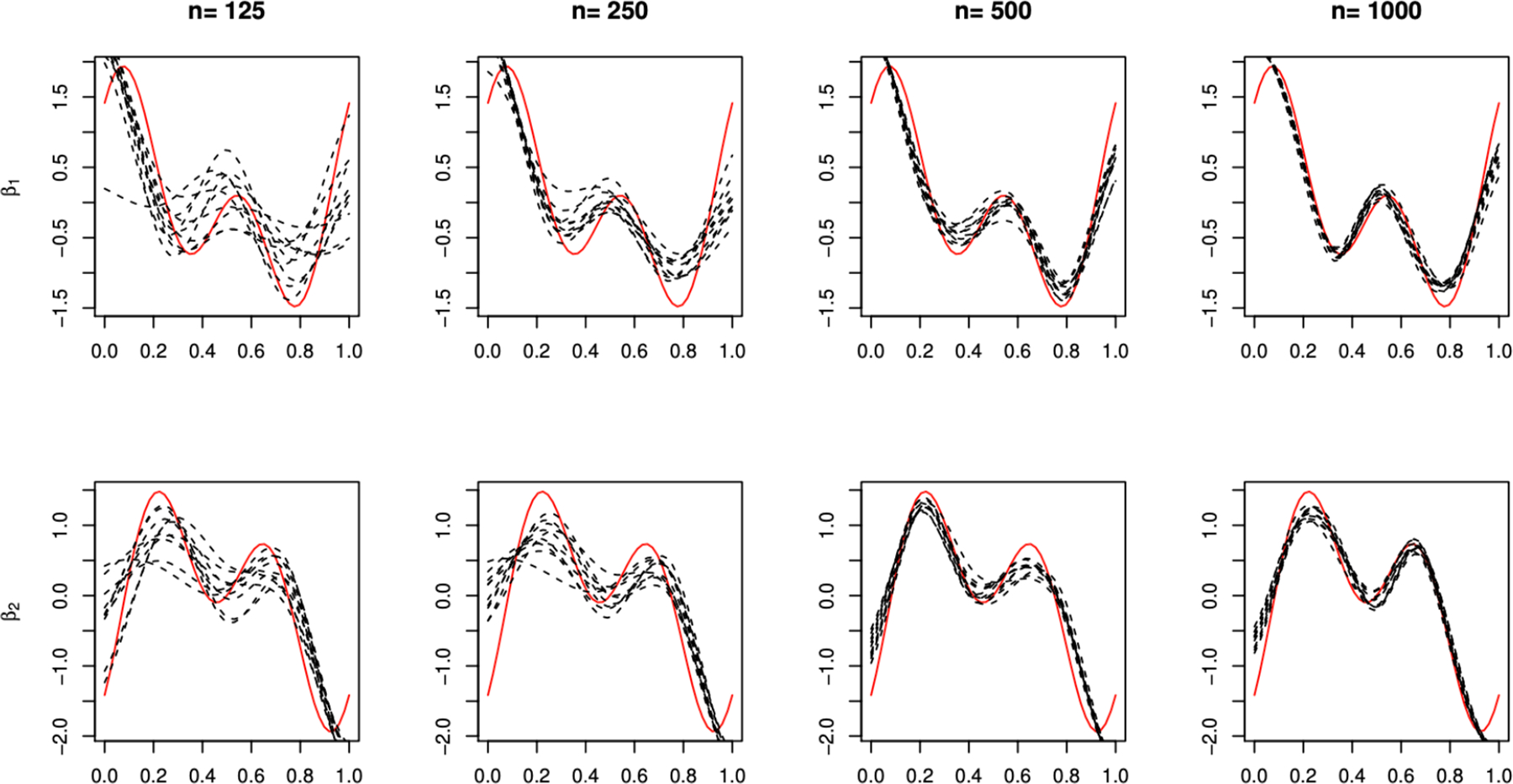
An illustration of typical 10 CFAM sample estimates ${\widehat{\beta }}_j(s)$ (black dashed curves) for the parameters β_j(s) (the red solid curves), for j = 1 and 2 in the top and bottom panels, respectively, with a varying training sample size n ∈ {125, 250, 500, 1000} for the case of δ = 1.

Throughout the paper, for CFAM and CFAM-lin, we fit the (X, Z) “main” effect on Y based on the (misspecified) linear model with the naïve scalar averages of X_j, i.e., ${\overline{X}}_j$, along with Z_k, fitted via Lasso with 10-fold cross-validation for the sparsity parameter and utilize the “residualized” response $Y-\widehat{\mu }(X,Z)$. For each simulation run, we estimate ${\mathcal{D}}^{opt}$ from each of the above four methods based on a training set (of size n ∈ {250, 500}), and to evaluate these methods, we compute the value $V\left({\widehat{\mathcal{D}}}^{opt}\right)=E\left[E\left[Y\mid X,Z,A={\widehat{\mathcal{D}}}^{opt}(X,Z)\right]\right]$ of each estimate ${\widehat{\mathcal{D}}}^{opt}$, based on a Monte Carlo approximation using a separate random sample of size 10³. Since we know the true data generating model in simulation studies, the optimal ${\mathcal{D}}^{opt}$ can be determined for each simulation run. Given each estimate ${\widehat{\mathcal{D}}}^{opt}$ of ${\mathcal{D}}^{opt}$, we report $V\left({\widehat{\mathcal{D}}}^{opt}\right)-V\left({\mathcal{D}}^{opt}\right)$, as the performance measure of ${\widehat{\mathcal{D}}}^{opt}$. A larger (i.e., less negative) value of the measure indicates better performance.

In Figure 1, we present boxplots, obtained from 200 simulation runs, of the normalized values $V\left({\widehat{\mathcal{D}}}^{opt}\right)$ (normalized by the optimal values $V\left({\mathcal{D}}^{opt}\right)$) of the decision rules ${\widehat{\mathcal{D}}}^{opt}$ based on the four approaches, for each combination of n ∈ {250, 500}, ξ ∈ {0, 1} (corresponding to correctly-specified or mis-specified CFAM interaction models, respectively) and δ ∈ {1, 2} (corresponding to moderate or large main effects, respectively). The results in Figure 1 indicate that the proposed method (CFAM) outperforms all other approaches. In particular, if the sample size is relatively large (n = 500), for a correctly-specified CFAM (ξ = 0), the method gives a close-to-optimal performance with respect to ${\mathcal{D}}^{opt}$. With nonlinearities present in the underlying model (20), CFAM-lin is outperformed by CFAM that utilizes the flexible component functions g_j(·, a) and h_k(·,a), although it substantially outperforms the OWL-based approaches.

Figure 1.

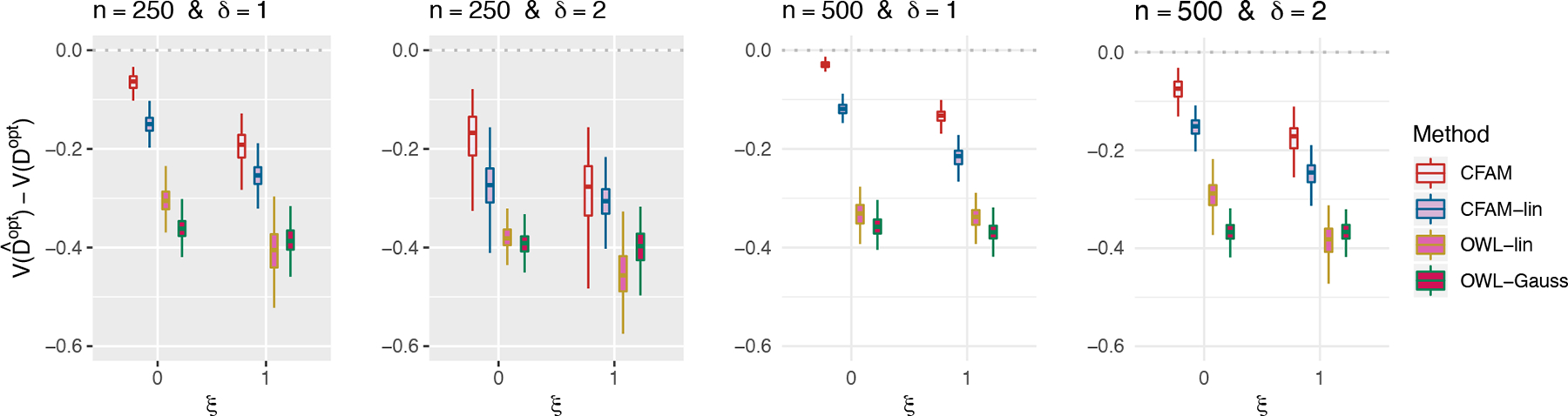
Boxplots obtained from 200 Monte Carlo simulations comparing 4 approaches to estimating ${\mathcal{D}}^{opt}$, given each scenario indexed by ξ ∈ {0, 1}, δ ∈ {1, 2} and n ∈ {250, 500}. The dotted horizontal line represents the optimal value corresponding to ${\mathcal{D}}^{opt}$.

In Section A.12 of Supporting Information, we have also considered a set of similar experiments under a “linear” A-by-(X, Z) interaction effect, in which CFAM-lin outperforms CFAM, but by a relatively small amount, whereas if the underlying model deviates from the exact linear structure and n = 500, CFAM tends to outperform CFAM-lin. This suggests that, in the absence of prior knowledge about the form of the interaction effect, the more flexible CFAM that accommodates nonlinear treatment effect-modifications can be set as a default approach over CFAM-lin for optimizing ITRs. The estimated values of the OWL methods using linear and Gaussian kernels, respectively, are similar to each other; however, since the current OWL methods do not directly deal with the functional pretreatment covariates, both are outperformed by CFAM, even when CFAM is incorrectly specified (i.e., when ξ = 1). When the (X, Z) “main” effect dominates the A-by-(X, Z) interaction effect (i.e., when δ = 2), although the increased magnitude of this nuisance effect dampens the performance of all approaches to estimating ${\mathcal{D}}^{opt}$, the proposed approach outperforms all other methods.

In Table S.1 of Supporting Information Section A.10, we additionally illustrate the estimation performance for model parameters β₁ and β₂ (and g₁, g₂, h₁ and h₂) when ξ = 0 (i.e., when CFAM is correctly specified) with varying δ ∈ {1, 2} and n ∈ {250, 500, 1000}, with respect to the root squared error $\text{RSE}\left({\beta }_j\right)=\sqrt{\int {\left({\widehat{\beta }}_j(s)-{\beta }_j(s)\right)}^{2}ds}$ (j = 1, 2) (similarly for RSE(g_j) and RSE(h_k)). In Figure 2, we display typical CFAM estimates ${\widehat{\beta }}_j$ of β_j from 10 random samples, for each sample size n (for the case of δ = 1). With sample size increasing, the estimators ${\widehat{\beta }}_j$ get close to the true coefficient functions β_j. (Similar results are provided for g_j and h_k in Table S.1 of Supporting Information.)

4.2. Treatment effect-modifier variable selection performance

In this subsection, we will report simulation results for the treatment effect-modifier selection among {X_j, j = 1, …, p}∪{Z_k, k = 1, …, q}. The complexity of the (X, Z)-by-A interaction terms of CFAM (1) can be summarized in terms of the size (cardinality) of the index set of {g_j, j = 1, …, p} ∪ {h_k, k = 1, …, q} that are not identically zero, each of which can be either correctly or incorrectly estimated to be equal to zero. As in Section 4.1, we generate 200 datasets based on (20), with varying ξ ∈ {0, 1}, δ ∈ {1, 2} and sample size n ∈ {50, 100, 200, …, 700, 800} and p = q = 20, i.e., we consider a total of p + q = 40 potential treatment effect-modifiers, among which there are only 4 “true” treatment effect-modifiers.

Figure 3 summarizes the results of the treatment effect-modifier covariate selection performance with respect to the true/false positive rates (the top/bottom panels, respectively), comparing the proposed CFAM and the CFAM-lin of Ciarleglio et al. (2018). The results are reported as the averages (and ±1 standard deviations) across the 200 simulated datasets, for each simulation scenario. Figure 3 illustrates that the proportion of correct selection out of the 4 true treatment effect-modifiers (i.e., the “true positive” rate; the top gray panels) of CFAM (the red solid curves) tends to 1, as n increases from n = 50 to n = 800, whereas the proportion of incorrect selection (i.e., the “false positive” rate; the bottom white panels) out of the 36 irrelevant “noise” covariates tends to 0; these proportions tend to either 1 or 0 quickly for moderate main effect (δ = 1) scenarios compared to large main effect (δ = 2) scenarios. On the other hand, the proportion of correct selections for CFAM-lin (the blue dotted curves), even with a large n, tends to be only around 0.55, due to the stringent linear model assumption on the from of the (X, Z)-by-A interaction effect. Figure 3 appears in color in the electronic version of this article, and any mention of color refers to that version.

Figure 3.

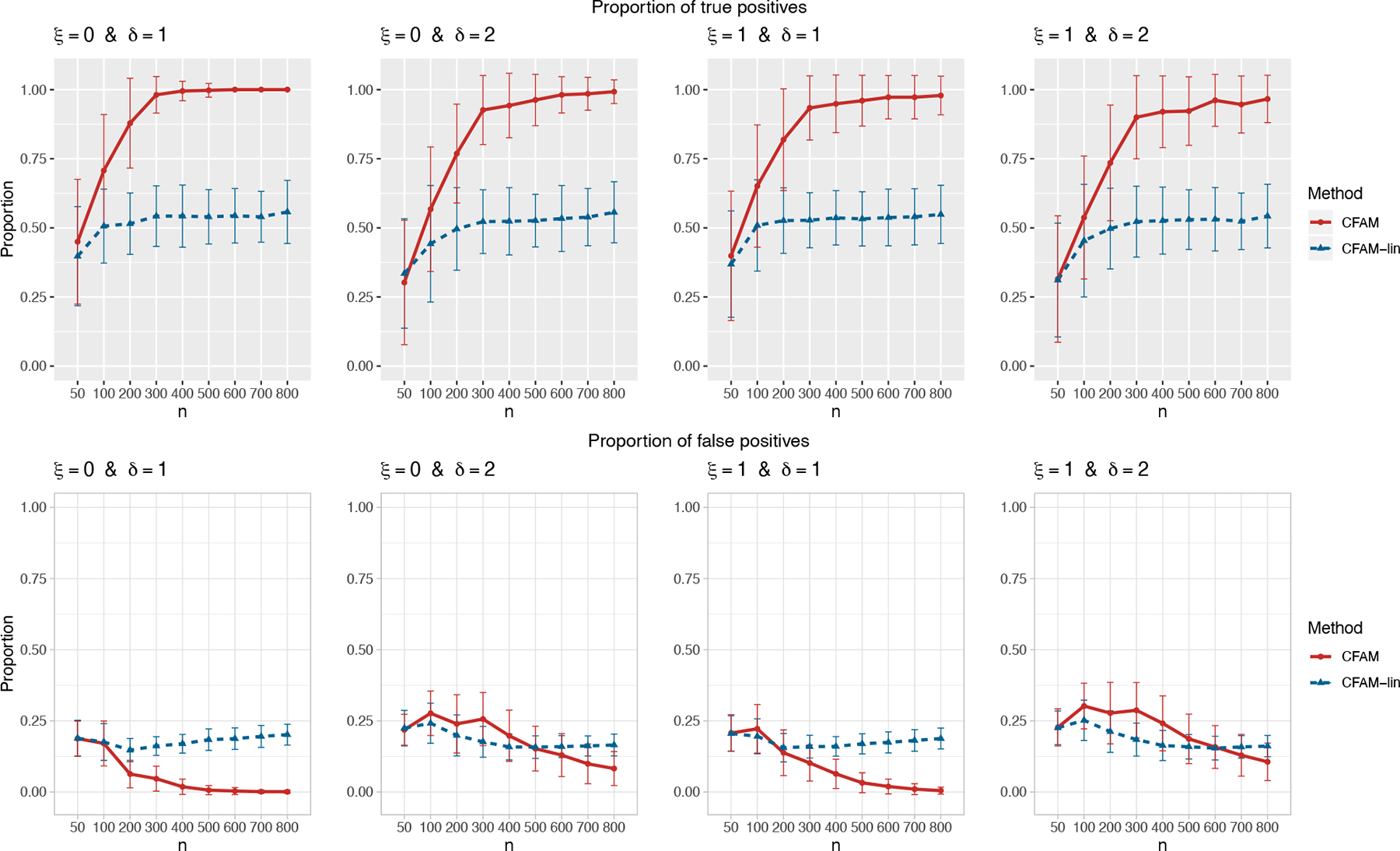
The proportion of the relevant covariates (i.e., the treatment effect-modifiers) correctly selected (the “true positives”; the top gray panels), and the “noise” covariates incorrectly selected (the “false positives”; the bottom white panels), respectively (and ±1 standard deviation), with a varying sample size n ∈ {50, 100, 200, …, 800}, for each combination of ξ ∈ {0, 1} and δ ∈ {1, 2}.

5. Application

In this section, we illustrate the utility of CFAM for optimizing ITRs, using data from an RCT (Trivedi et al., 2016) comparing an antidepressant and placebo for treating major depressive disorder. The study collected various scalar and functional patient characteristics at baseline, including electroencephalogram (EEG) data. Study participants were randomized to either placebo (A = 1) or an antidepressant (sertraline) (A = 2). Subjects were monitored for 8 weeks after initiation of treatment. The primary endpoint of interest was the Hamilton Rating Scale for Depression (HRSD) score at week 8. The outcome Y was taken to be the improvement in symptoms severity from baseline to week 8 taken as the difference: week 0 HRSD score - week 8 HRSD score (larger values of the outcome Y are considered desirable).

There were n = 180 subjects. We considered p = 19 pretreatment functional covariates consisting of the current source density (CSD) amplitude spectrum curves over the Alpha frequency range (observed while the participants’ eyes were open), measured from a subset of EEG channels from a total of 72 EEG electrodes which gives a fairly good spatial coverage of the scalp. The locations for these 19 electrodes are indicated in the top panel of Figure 4. The Alpha frequency band (8 to 12 Hz) considered as a potential biomarker of antidepressant response (e.g., Wade and Iosifescu, 2016) was scaled to [0, 1], hence each of the functional covariates X = (X₁(s), …, X₁₉(s)) was defined on the interval [0, 1]. We also considered q = 5 baseline scalar covariates consisting of the week 0 HRSD score (Z₁), sex (Z₂), age at evaluation (Z₃), word fluency (Z₄) and Flanker accuracy (Z₅) cognitive test scores, which were identified as predictors of differential treatment response in a previous study (Park et al., 2020). In this dataset, 49% of the subjects were randomized to the sertraline (A = 2). The average outcomes Y for the sertraline and placebo groups were 7.41 and 6.29, respectively. The means (and standard deviations) of Z₁, Z₃, Z₄ and Z₅ were 18.59 (4.44), 37.7 (13.57), 38 (11.42) and 0.19 (0.11), respectively, and 67% of the subjects were female.

Figure 4.

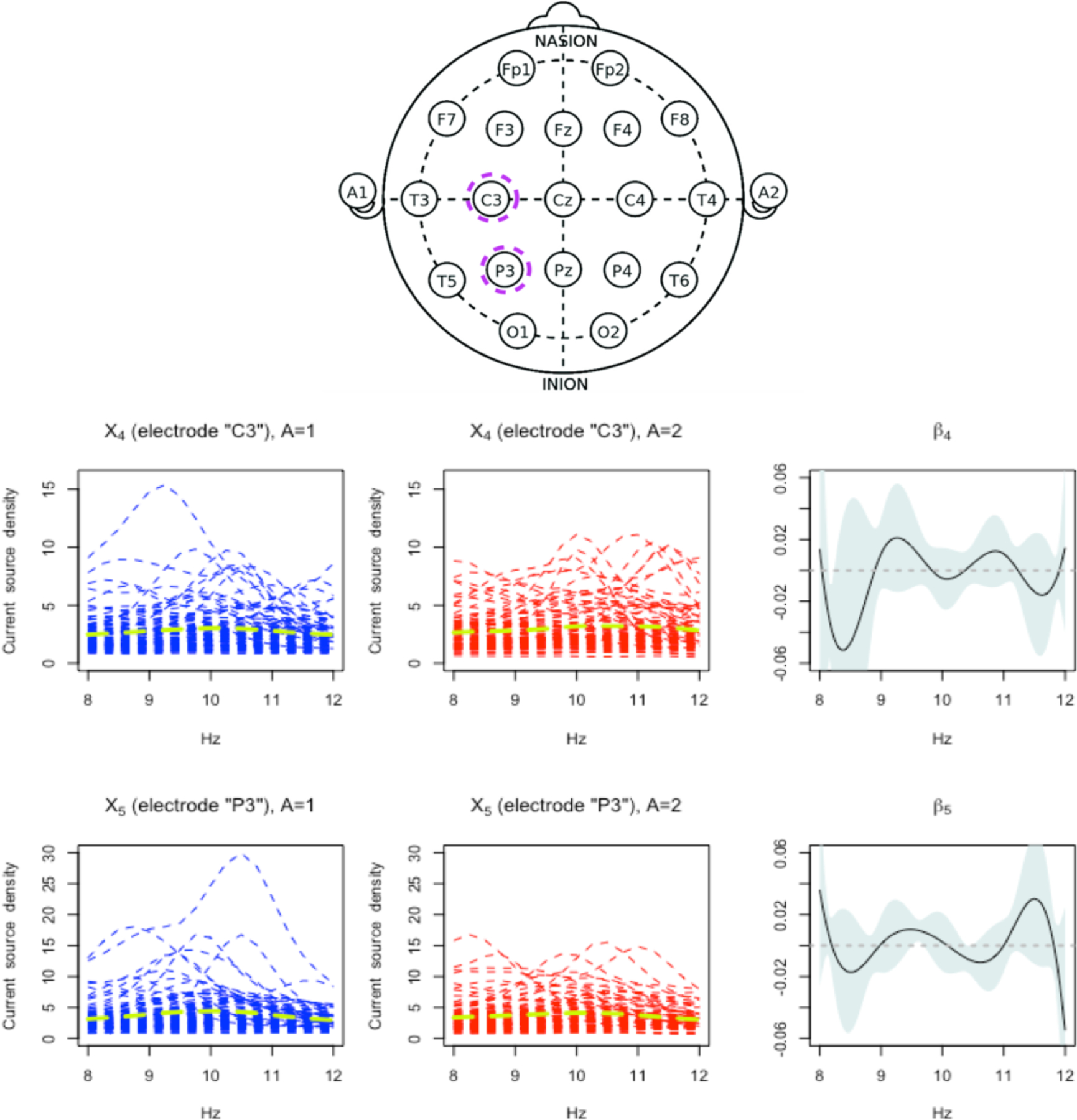
Top row: The locations for the 19 electrode channels (“A1” and “A2” were not used). Those 2 electrodes (“C3” and “P3”) highlighted in dashed violet circles are the selected electrodes from the proposed approach. Bottom rows: First two columns: observed current source density (CSD) curves from the selected electrodes X₄ (“C3”) and X₅ (“P3”) (each electrode corresponds to each row), over the Alpha band (8 to 12 Hz), for the placebo A = 1 arm (in the first column) and the active drug A = 2 arm (in the second column), measured before treatment. The arm-specific mean functions are overlaid as dashed green curves. Third column: the estimated single-index coefficient functions (β₄ and β₅) for the selected channels X₄ and X₅ (with the associated 95% confidence bands, conditioning on the jth partial residual and ${\widehat{g}}_j$).

The proposed CFAM approach (4) selected two functional covariates: “C3” (X₄) and “P3” (X₅) (the selected electrodes are indicated by the dashed circles in the top panel of Figure 4), and a scalar covariate: “Flanker accuracy test” (Z₅). In the left two columns of Figure 4, we display the treatment arm-specific CSD curves for the selected two functional covariates, X₄(s) and X₅(s) (measured before treatment), from the 180 subjects. In the third column of Figure 4, we display the associated coefficient function estimates, ${\widehat{\beta }}_4(s)$ and ${\widehat{\beta }}_5(s)$. The coefficient function β_j(s), discretized at $\left\{s_1,s_2,\dots ,s_{r_j}\right\}$, is represented by $B_j{\widehat{\gamma }}_j\in {ℝ}^{r_j}$ in (19), whose variance estimate, $B_j\widehat{V}{B}_j^{\top }$, is used to construct a 95% point-wise normal approximated confidence band in Figure 4, where $\widehat{V}$ represents the covariance of the length-m_j vector ${\widehat{\gamma }}_j$, i.e., the minimizer of (19) scaled to unit norm (see Section A.8 of Supporting Information for discussion on this confidence band).

In this example, the coefficient functions ${\widehat{\beta }}_j(s)$ summarizing the X_j(s) lead to data-driven indices $u_j=\langle {\widehat{\beta }}_j,X_j\rangle \in ℝ$ that are linked to differential treatment response via two estimated nonzero component functions, ${\widehat{g}}_j\left(u_j,A\right)$ (j = 4, 5; i.e., for X₄ and X₅), displayed in the left two panels on the top row of Figure 5. Roughly put, the placebo (A = 1) effect tends to slightly increase with the index u_j (j = 4, 5), whereas the sertraline (A = 2) effect slightly decreases with the index. In the third column of Figure 4, β₄ puts a bulk of its negative weight on lower frequencies (8 to 9 Hz), meaning that patients whose CSD values are small in those frequency regions would have large values of 〈β₄, X₄〉, over the values which the placebo effects are predicted to be relatively strong, in comparison to the sertraline effects. In the third panel on the top row of Figure 5, the estimated component function ${\widehat{h}}_5\left(Z_5,A\right)$ associated with the selected scalar covariate Z₅ is displayed, where the placebo (A = 1) effect tends to increase with Z₅.

Figure 5.

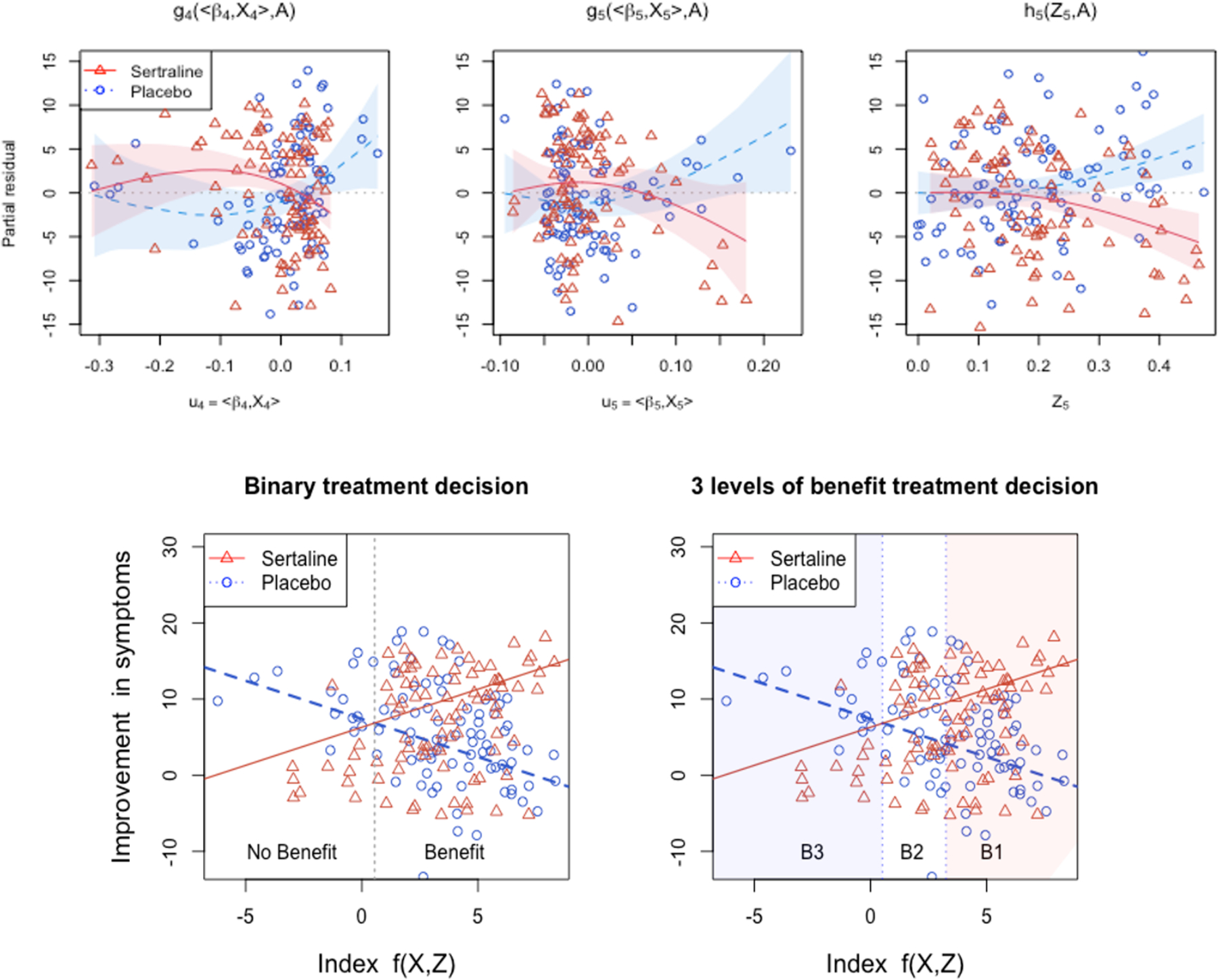
Top row: The scatter plots of the (jth; j = 4, 5) (and kth; k = 5) partial residual vs. the estimated functional indices u₄ = 〈X₄, β₄〉 and u₅ = 〈X₅, β₅〉 (and Z₅), respectively, for the placebo A = 1 (blue circles) and sertraline A = 2 (red triangles) treated individuals. The estimated nonzero treatment-specific component functions g₄(u₄, A), g₅(u₅, A) and h₅(Z₅, A) are overlaid separately for the A = 1 (placebo; blue dotted curve) condition and the A = 2 (sertraline; red solid curve) condition (with the associated 95% confidence bands, given the partial residuals and ${\widehat{\beta }}_j$). Bottom row: The scatter plots of the observed treatment-specific response Y vs. the “index” f(X, Z) = g₄(〈X₄, β₄〉, 2) + g₅(〈X₅, β₅〉, 2) + h₅(Z₅, 2), with possible two-group recommendation grouping (in the left panel; the cut-point was the crossing point= 0.56 between the two treatment-specific expected responses) and possible three-group recommendation grouping (in the right panel; the cut-point for B2 and B1 was 3.15, which gives the difference(= 7.42) in the two treatment-specific expected responses larger than the expected marginal response under sertraline(= 7.41); note that this cut-point choice was just for an illustration of the idea of the benefit stratification).

In model (1), without loss of generality, the treatment-specific intercept was suppressed. Let τ_a (a = 1, 2) represent the treatment a-specific intercept, so that τ₂ − τ₁ represents the marginal treatment effect (comparing a = 2 with a = 1). For the most common situation of binary treatment conditions (i.e., L = 2), let us define a 1-dimensional index $f(X,Z)≔{\sum }_{j=1}^p{g}_j\left(\langle X_j,{\beta }_j\rangle ,a=2\right)+{\sum }_{k=1}^q{h}_k\left(Z_k,a=2\right)$ that parameterizes the treatment effect “contrast” according to (1), $E[Y\mid X,Z,A=2]-E[Y\mid X,Z,A=1]={\tau }_2-{\tau }_1+f(X,Z)\frac{1}{{\pi }_1}$, as a linear function (see Supporting Information Section A.15 for this parametrization). The index f(X, Z) provides a continuous gradient of the benefit from one treatment to another. The bottom row of Figure 5 displays the observed treatment-specific outcome Y^(a) vs. this combined index f(X, Z). In those panels, the treatment benefit (comparing a = 2 vs a = 1) corresponds to the contrast between the solid and dotted lines, and the benefit increases monotonically with this combined index: an index greater than the crossing point (group “Benefit”) indicates that the patient is expected to benefit from Sertraline, and an index smaller than the crossing point (group “No Benefit”) indicates that the patient is expected to benefit from placebo. Given this monotone relationship between the treatment benefit and the continuous index f(X, Z), a more refined decision using three or more groups (e.g., benefit level groups “B1”, “B2” and “B3”, specified in the right panel, where the associated cut-points were determined based on the treatment-specific expected responses) than a simple binary recommendation can be also considered when recommending treatments to patients, that can help triage of patients according to the expected benefit by the treatment.

To evaluate the ITR performance of the four different approaches described in Section 4, we randomly split the data into a training set and a testing set (of size $\tilde{n}$) with a ratio of 5 : 1, replicated 500 times, each time estimating an ITR ${\widehat{\mathcal{D}}}^{opt}$ based on the training set, and its “value” $V\left({\widehat{\mathcal{D}}}^{opt}\right)=E\left[E\left[Y\mid X,Z,A={\widehat{\mathcal{D}}}^{opt}(X,Z)\right]\right]$, by an inverse probability weighted estimator (Murphy, 2005) $\widehat{V}\left({\widehat{\mathcal{D}}}^{opt}\right)={\sum }_{i=1}^{\tilde{n}}{Y}_i{I}_{\left(A_i={\widehat{\mathcal{D}}}^{opt}\left(X_i,Z_i\right)\right)}/{\sum }_{i=1}^{\tilde{n}}{I}_{\left(A_i={\widehat{\mathcal{D}}}^{opt}\left(X_i,Z_i\right)\right)}$, computed based on with the testing set (of size $\tilde{n}$). For comparison, we also include two naïve rules: treating all patients with placebo (“All PBO”) and treating all patients with the active drug (“All DRUG”), each regardless of the individual patient’s characteristics (X, Z). The resulting boxplots obtained from the 500 random splits are illustrated in Figure 6.

Figure 6.

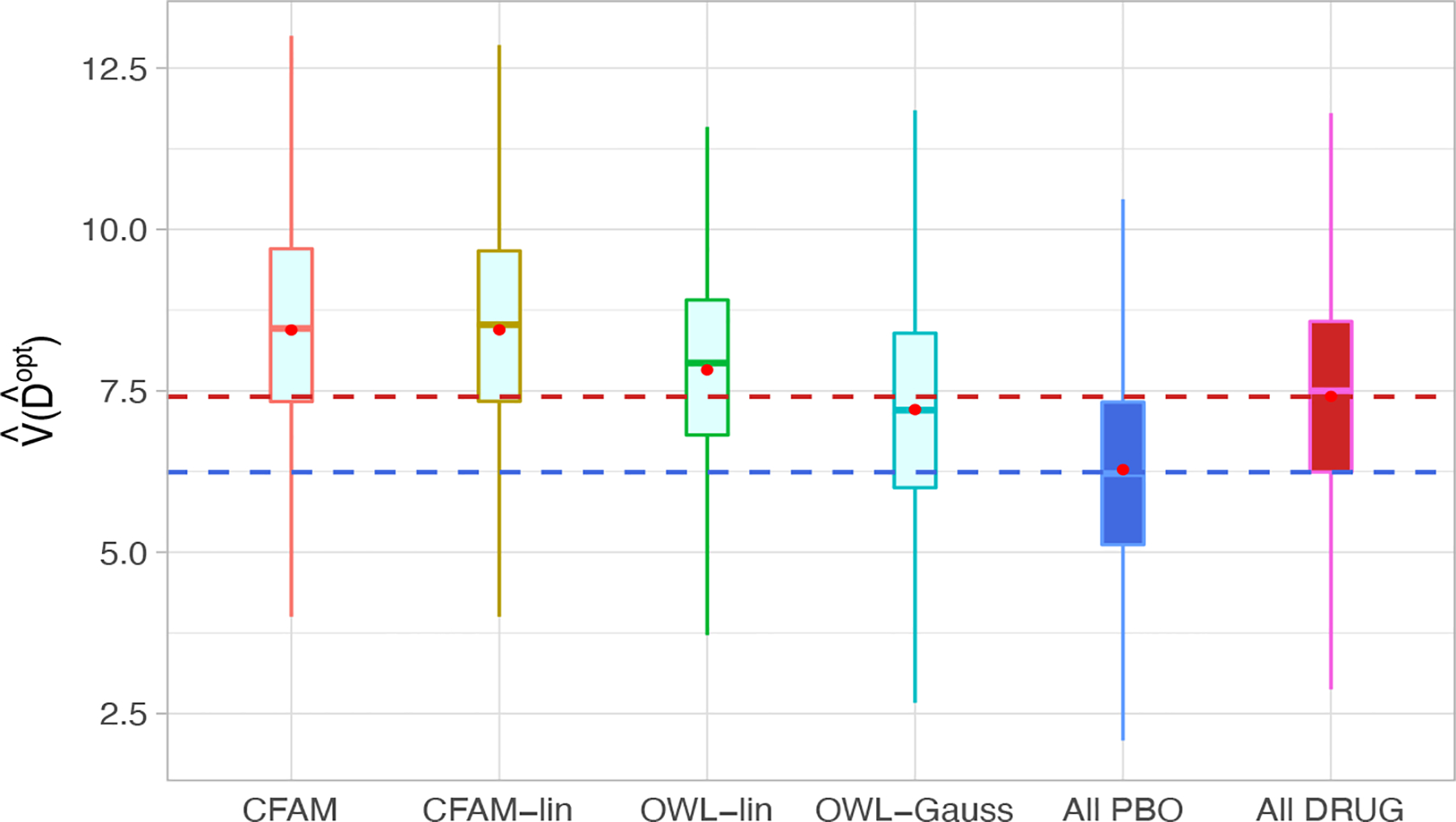
Boxplots of the estimated values of the treatment rules ${\widehat{\mathcal{D}}}^{opt}$ estimated from 6 approaches, obtained from 500 randomly split testing sets. Higher values are preferred.

The results in Figure 6 demonstrate that CFAM and CFAM-lin perform at a similar level, showing a clear advantage over the both OWL-lin and OWL-Gauss, suggesting that regression utilizing the functional nature of the EEG measurements, that targets the treatment-by-functional covariates interaction effects is well-suited in this example. Specifically, in Figure 6, the superiority of CFAM (or CFAM-lin) over the policy of treating everyone with the drug (All DRUG) was of similar magnitude of the superiority of All DRUG over All PBOs. This suggests that accounting for patient characteristics can help treatment decisions. The estimated model parameters (β_j, g_j, h_k) for CFAM-lin are provided in Section A.13 of Supporting Information (see also for the proportion of agreement of the recommended treatments from the four ITR approaches considered). In this example, the estimated nonlinear treatment effect-modification is rather modest, as can be observed from the first row of Figures 5. As a result, the performances of CFAM and CFAM-lin are comparable to each other. However, as demonstrated in Section 4, the more flexible CFAM can be employed as a default approach over CFAM-lin, allowing for potentially important nonlinearities when modeling treatment effect-modification.

6. Discussion

We have developed a functional additive regression approach specifically focused on extracting possibly nonlinear pertinent interaction effects between treatment and multiple functional/scalar covariates, which is of paramount importance in developing effective ITRs for precision medicine. This is accomplished by imposing appropriate structural constraints, performing treatment effect-modifier selection and extracting one-dimensional functional indices. The estimation approach utilizes an efficient coordinate-descent for the component functions and a functional linear model estimation procedure for the coefficient functions. The proposed functional regression for ITRs extends existing methods by incorporating possibly nonlinear treatment-by-functional covariates interactions. Encouraged by our simulation results and the application, future work will investigate the asymptotic properties of the method related to variable selection and estimation consistency. The main theoretical challenge is in that the working model associated with the proposed estimation criterion is misspecified (see Supporting Information Section A.18 for discussion). Another important direction is the development of a Bayesian framework for the model accounting for the posterior uncertainty in β_j g_j, h_k and the unmodeled noise variance in predicting the individualized treatment benefit using the index f(X, Z), and making inference on the (X, Z)-by-A interactions.

The proposed method is not directly applicable to the functional covariates irregularly or sparsely sampled or observed with non-negligible error, and an initial step to de-noise and re-construct the underlying curves is required, as is done in Goldsmith et al. (2011) using the principal component decomposition of the observed functions (see Supporting Information Section A.14 for discussion) in such cases.

The proposed approach to optimizing ITRs can also accommodate data from observational studies, under condition Y^(a) ⊥ A given additive measurable functions of 〈X_j, β_j〉(j = 1, …, p) and Z (see Supporting Information Section A.16 for discussion). For more general cases, with treatment propensity information available, we can reparametrize model (1) and accommodate the treatment propensities in the estimation (see Supporting Information Section A.17).

Data Availability Statement

The data that support the findings of this paper are available from the corresponding author upon reasonable request.