Abstract
Natural vibrations and resonances are intrinsic features of protein structures and enable differentiation of one structure from another. These nanoscale features are important to help to understand the dynamics of a protein molecule and identify the effects of small sequence or other geometric alterations that may not cause significant visible structural changes, such as point mutations associated with disease or drug design. Although normal mode analysis provides a powerful way to accurately extract the natural frequencies of a protein, it must meet several critical conditions, including availability of high-resolution structures, availability of good chemical force fields and memory-intensive large-scale computing resources. Here, we study the natural frequency of over 100 000 known protein molecular structures from the Protein Data Bank and use this dataset to carefully investigate the correlation between their structural features and these natural frequencies by using a machine learning model composed of a Feedforward Neural Network made of four hidden layers that predicts the natural frequencies in excellent agreement with full-atomistic normal mode calculations, but is significantly more computationally efficient. In addition to the computational advance, we demonstrate that this model can be used to directly obtain the natural frequencies by merely using five structural features of protein molecules as predictor variables, including the largest and smallest diameter, and the ratio of amino acid residues with alpha-helix, beta strand and 3–10 helix domains. These structural features can be either experimentally or computationally obtained, and do not require a full-atomistic model of a protein of interest. This method is helpful in predicting the absorption and resonance functions of an unknown protein molecule without solving its full atomic structure.
Natural vibrations and resonances are intrinsic features of protein structures and can be learnt from existing structures.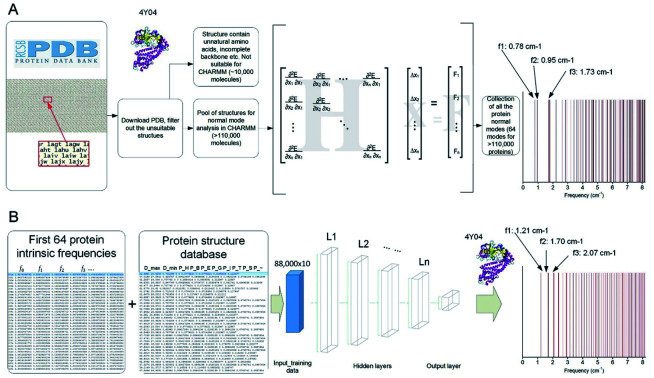
Introduction
Protein molecules constitute the basic biopolymers that are found in many different forms in the body of living creatures. A protein molecule is usually composed of one or several polypeptide chains that wind together to form a certain folded three-dimensional (3D) protein structure.1–5 The formation of protein structure is typically a spontaneous self-folding process, driven by the interaction inside or between the building blocks of the polypeptide chains, known as amino acids.6,7 There are strong interactions, such as the covalent bonds between the three atoms (N–Cα–C) of the backbone and its interactions with the functional groups at the side chains. There are also weak interactions, such as charge interactions, van der Waals interactions and the hydrogen bonding that often exist between any atoms, accounting for the attraction and repulsion forces between amino acids and chains. The combination of different interactions, coupled with the complex 3D irregular structures, makes the dynamics of the protein molecule much more complicate than its constituting bonds, angles or dihedral angles.8–11 However, many evidences resulting from structural biology and computational modeling show that there is no intrinsic difference between the vibration of a protein molecule and the vibration of a large-scale structure such as a building12 responding to external forces, especially for the low-frequency range, which does not involve the charge distribution in the atomic electronic states for optical excitation.6,11 It is reasonable to believe that the protein's hierarchical structure and the interaction among amino acids affects its vibration, which in turn can also be useful to determine the structure changes or effects.11 Indeed, it has been shown in earlier literature that the mutation of a single amino acid residue can bring about a significant change in the frequencies of the vibrational modes, indicating that the nature of the low-frequency motions can be unexpectedly sensitive to the specific local geometry.6,11
The recent evolution of experimental techniques makes molecular-scale high-temporal resolution imaging feasible,13 making it more possible to monitor the dynamical behavior of nanostructures. However, up to date, the most advanced imaging technique provides atomic and microsecond resolutions, which is only able to capture the dynamic behavior of 106 Hz, or equivalent as 0.00003 cm−1, which is five orders of magnitude smaller than the frequency of the first vibration mode of most protein structures.14 One way to obtain the vibrational modes of a protein through computational analysis is normal mode analysis (NMA),8,14 which is a computationally intensive process and it requires the atomistic structure of the protein and the force field that defines all the interatomic interactions.
The key steps in this process include building the Hessian matrix, a 3N × 3N square matrix composed of second-order partial derivatives of the potential energy function with the coordinates of atom in all the three dimensions, and computing the eigenvector and eigenvalue of this matrix. For large protein structures, the time and memory requirement for NMA can be huge. For example, a membrane protein that has more than 1000 amino acids requires more than 3.6 GB memory for simply loading the Hessian matrix, making computing more difficult for larger protein structures. Moreover, the method can only be applied to proteins with known high-resolution 3D structure (which must be obtained either from experiments, e.g. by using Nuclear Magnetic Resonance, X-ray Diffraction or Cryo-electron microscopy or could be obtained from a computational simulation of protein folding15,16). However, neither of the two strategies are cost and time efficient, and often require significant computational resources.
Artificial intelligence (AI), enabled by machine learning (ML) techniques, has demonstrated its advantage in solving sophisticated scientific problems that involve multiple physics-based interactions that are hard to directly model or non-polynomial problems that require extremely large computational power that cannot be solved by brute force methods.17 It now provides a novel feasible way of solving such problems by utilizing efficient algorithms to searching a high-dimensional parameter space for optimal solutions. In several recent materials-focused studies, such a data-driven material modeling for optimized mechanics of mechanical properties of materials, it has shown a unique and powerful role.18–21 Moreover, it shows a breakthrough capability to optimize the multiscale and multiparadigm architecture of materials for high sensitivity to environmental factors, as needed in sensors, electronics and for multi-purpose material applications.22
Here we use a dataset of the structural features and the first 64 normal modes of more than 100 000 protein molecular structures to train and test a machine-learning model that is capable of predicting the frequency spectrum of any protein. This computational model will be helpful that allows to directly obtain a protein's frequency spectrum without knowing the high-resolution 3D structure nor solving for its eigenvalues.
Results and discussion
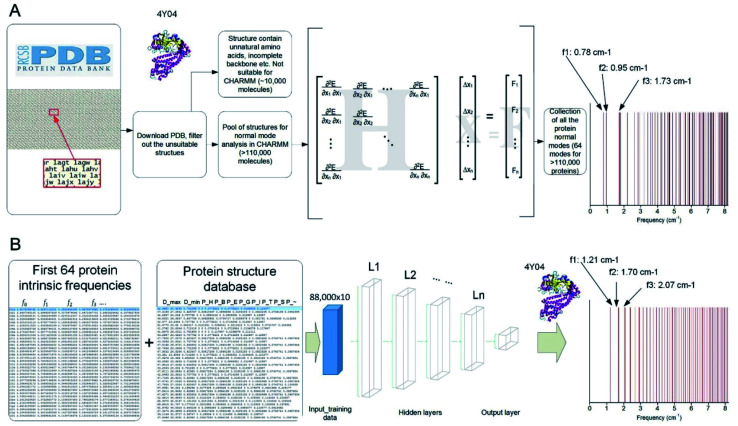
We developed a parallel code to extract the vibrational feature of 110 511 protein structures available in the Protein Data Bank by applying NMA on each of them,8 which is used to compute all the normal modes as the most general motion of a protein structure, as well as the natural frequency that corresponds to each of the modes.23 The collection of the all the discrete natural frequencies, as shown in Fig. 1A, defines the locations of all the peaks of a mechanical spectrum where the mechanical resonance of the structure gets more significant than other frequencies. The key process and the content of code to compute the molecular-based vibrational data from a full-chemistry model are given in a former paper.23 Besides the frequency spectrum, any possible vibration of a protein structure, such as a thermal fluctuation in a certain temperature, can be given by a superposition of its normal modes.24 The modes are normal in the sense that each mode is orthogonal to all the other modes, suggesting that the mode cannot be expressed by other modes, that is to say, that an excitation of one mode will never cause motion of a different mode.
Fig. 1. Overview of the method to run massive in-parallel NMA to obtain the natural frequency spectrum of over 110 000 protein structures present in the Protein Data Bank (PDB) (A) and use the result to train (with 80% of the dataset) and test (with the rest 20% of the dataset) a machine learning model by FNN to predict the frequency spectrum directly by using several structural features (B).
Here we hypothesize that the frequency spectrum, which is defined by the chemistry and the folded structure of a protein, provides a unique fingerprint to identify a protein from others. Such a feature has been applied in infrared and Raman spectroscopy to identify the content of small chemical groups. Combining these experiments with the library of the frequency spectrum of proteins may enable to identify a protein only if it has a high-resolution structure deposited in the Protein Data Bank. However, the Protein Data Bank only includes a tiny portion of proteins, with most of them only known for their sequence and functions (such as the 147 413 762 protein sequences given in https://www.uniprot.org25) but not for high-resolution protein structures.
Indeed, it is difficult to identify the complex structure of a protein, which requires advanced tools including Nuclear Magnetic Resonance, X-ray Diffraction or Cryo-electron microscopy, as well as protein crystal samples. Hence, the ML technique provides a great opportunity to obtain the frequency spectrum of a protein without experimentally solving for its folded 3D structure. To achieve that, we develop an ML model and train it based on a randomly selected portion (80%) of the NMA calculation results as the first 64 natural frequencies of all the protein structures in the Protein Data Bank.23 This training set is integrated with another table that summarizes 10 structural features of each protein molecule, including the largest diameter (Dmax, measured as the largest distance between the two infinite parallel sheets that clamp the molecule), the smallest diameter (Dmin, measured as the smallest distance between the two infinite parallel sheets that clamp the molecule) and the ratio of all the secondary structures given by DSSP (pH: content of alpha helix; pB: content of residue in isolated beta-bridge; pE: content of beta-strand; pG: content of 3–10 helix; pI: content of pi-helix; pT: content of turn; pS: content of bend and p∼: content of unstructured parts).
We train the ML model to predict the natural frequencies from the 10 structural features. For the sack of simplicity, we introduce a fitting function for the first 64 natural frequencies fi (f0…63) given as
| fi_fit = biM | 1 |
Which gives the natural frequency fi_fit for the (i + 1) mode (i starts from 0) where b = f0 for the value of base frequency, M is the power of the function that defines the increment trend of the natural frequencies for larger modes. We also quantitatively compute the standard error of the fitted value for each protein structure by
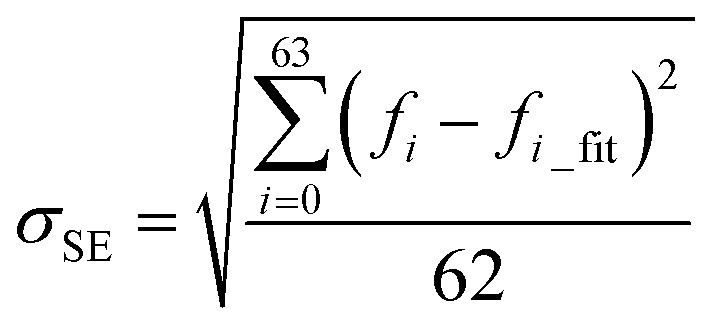 |
2 |
It has been shown that all the 64 frequencies of each of the protein structures can be fitted by eqn (1) to obtain its [b, M] value for the structure, and the frequencies of over 99% of the protein structure get interpreted with a small standard error σSE < 1 cm−1.23
By using eqn (1), we train the ML model to predict the value of b and M instead of predicting each of the 64 natural frequencies. The ML is implemented in TensorFlow in Python.26,27 We start by using the 10 structural features as predictor variables and using the b and M value as the target variables. We use a Feedforward Neuron Network (FNN) with Rectified Linear Unit (ReLU) activation function to read in the training data (80% randomly selected data, ∼88 000 records) with a batch size of 10 000 records and develop this data-driven model by minimize the standard error between the predicted and measured [b, M] values by using an Adam optimizer.28,29 This FNN ML model is realized via four hidden layers with 40, 20, 10 and 5 neurons included for each of the layer and a final output layer to evaluate the outcome, as shown in Fig. 1B. We use the remaining 20% data for validation. We run the training for 100 000 epochs, with each of which represents one complete presentation of the training data to be learned by the machine, to ensure there is no further improvement for the optimization. We have tried to increase the number of layers to 10 layers and the width of each layer to 60 neurons and find the increment of depth and width do not improve the standard errors for training and validation, so we keep using this ML architecture for our study.
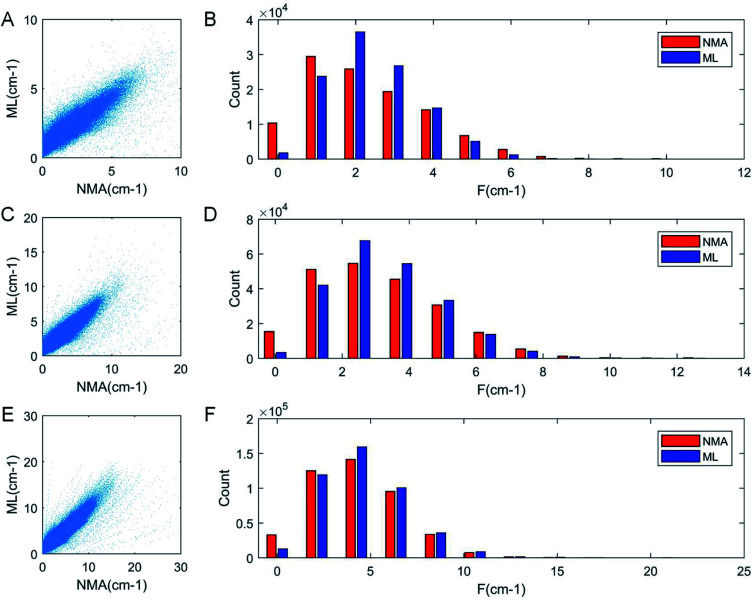
As a result of the validation, we obtain the predicted [b, M] of the protein structures within the validation dataset. Using the values, we compute each of the natural frequencies as fi_ML = biM and compare with their measurement result, with the comparison outcome summarized in Fig. 2. The comparison between the frequencies of the first 5 modes, 10 modes, and 20 modes are given in Fig. 2A, C and E, respectively, with each point (fi_NMA, fi_ML) plotted in the figure. It is shown that the ML prediction and the NMA data have a very strong correlation and most data point concentrated along the line fi_NMA = fi_ML, suggesting the overall good predicting result. Similar to eqn (2), the different between the two dataset is quantified by using the standard error as 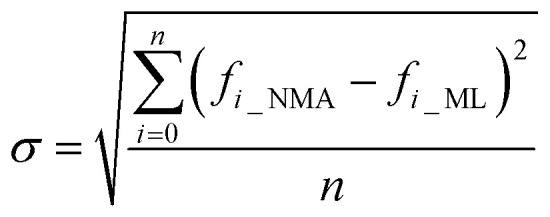 , where n is the total number of data points in the plot. We find the standard error of computing the first 5, 10 and 20 modes is 0.836, 0.860 and 1.256 cm−1, respectively. The standard error increases for having more modes as the natural frequency increase for higher modes. The prediction error σ = 1.256 cm−1 is still considered relatively low because the mean value and standard deviation of the natural frequency of the 20th mode of all the protein structures is 6.96 ± 3.50 cm−1. The histograms of the predicted frequencies, as given in Fig. 2B, D and F for the first 5, 10 and 20 modes, respectively, show a different trend as the more modes yields statistically better agreement between the prediction and measurement, suggesting the larger prediction error comes merely from the nature of the larger data value for higher modes. Moreover, it is interesting to see that the distribution of the frequencies is log-normal all the time, suggesting that the relatively low frequencies (corresponding to the peak of the log-normal distribution) correspond to more normal modes and also account more for mechanical resonance and energy absorption, because of the equipartition principle,24 which states that each normal mode takes equal kinetic energy for free vibration.
, where n is the total number of data points in the plot. We find the standard error of computing the first 5, 10 and 20 modes is 0.836, 0.860 and 1.256 cm−1, respectively. The standard error increases for having more modes as the natural frequency increase for higher modes. The prediction error σ = 1.256 cm−1 is still considered relatively low because the mean value and standard deviation of the natural frequency of the 20th mode of all the protein structures is 6.96 ± 3.50 cm−1. The histograms of the predicted frequencies, as given in Fig. 2B, D and F for the first 5, 10 and 20 modes, respectively, show a different trend as the more modes yields statistically better agreement between the prediction and measurement, suggesting the larger prediction error comes merely from the nature of the larger data value for higher modes. Moreover, it is interesting to see that the distribution of the frequencies is log-normal all the time, suggesting that the relatively low frequencies (corresponding to the peak of the log-normal distribution) correspond to more normal modes and also account more for mechanical resonance and energy absorption, because of the equipartition principle,24 which states that each normal mode takes equal kinetic energy for free vibration.
Fig. 2. Comparison of the frequencies predicted by ML and directly obtained from NMA that corresponds to the first 5 (A), 10 (C) and 20 modes (E) of all the protein structures for testing (22 000 structures), with the histogram of the ML and NMA results summarized by bars of different colors in (B), (D) and (F) respectively. It is consistently shown that for low-frequency modes, the distribution has a log-normal shape, with a center peak, that corresponds to most normal modes, concentrates at a low-frequency region.
The result is important because it demonstrates that the ML model is able to directly predict the natural frequencies of a protein structure, instead of using the high-resolution 3D structure and NMA calculation or dynamic simulations. The ML model is validated by the testing data and can be applied to any protein molecule with unknown 3D structure but knowing the few structural features. For example, the minimum and maximum diameters can be measured by dynamic light scattering (DLS), and the secondary structure ratio can be extracted from Fourier Transform Infrared (FTIR) spectroscopy and these experiments are much easier than solving the 3D structure of a protein. It thus provides a convenient way of predicting the spectrum of natural frequencies of a protein. However, many of the eight secondary structures that are defined for FTIR are much less clear than what is defined for the full atomistic protein structures by the Dictionary of Protein Secondary Structure (DSSP),30 as what is used for the predictor variables. For instance, helix and beta sheet structures are usually better defined than other coiled or random structures for FTIR.31
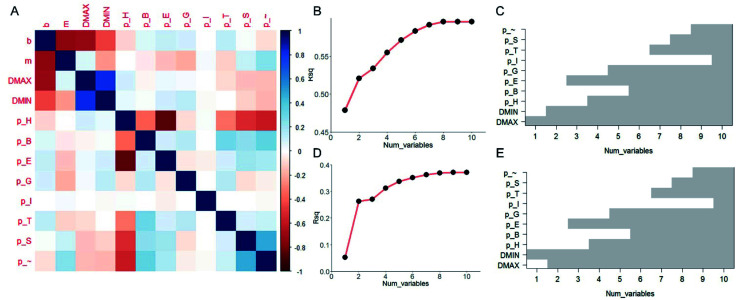
It is useful to understand the contribution of each of the ten predictor variables and find out which are more essential than the others in prediction. Although FNN provides a convenient way of predicting the [b, M] from [Dmax, Dmin, pH, pB, pE, pT, pI, pG, pS, p∼], the relationship among each target variable and the predictor variables are highly nonlinear and difficult to quantify. We thus take the linear model and compute the pairwise correlation function between the twelve variables by using all the data records, as shown in Fig. 3A. As expected, not all of the predictor variables correlate much to [b, M]. b correlates more to [Dmax, Dmin, pH] than others while m correlates more to [Dmin, pE, pG] than others. Using the linear model,32 we increase the number of predictor variables nvar from 1 to 10 and for each nvar we test all the possible subsets of predictor variables for C10nvar times of tests. In total, we perform C101 + C102 + C103 + … + C1010 = 210 = 1024 tests in total. For each nvar, we select the best subsets for predicting b (Fig. 3B and C) and M (Fig. 3D and E) values with maximum coefficient of determination (rsq) value, which has value between 0 and 1 and measures the percentage of the response variable variation that is explained by a linear model. It is shown in Fig. 3B and D that the contribution of a unit increment in nvar keeps decrease for larger nvar value in predicting b and M, respectively. Actually, for nvar > 5, the further increment of nvar has only a small effect. Moreover, by running these 1024 tests, we manage to obtain the best subsets for each nvar value, as shown in Fig. 3C and E for b and M, respectively. It is shown that if we are only accessible to one predictor variable, Dmax and Dmin will be the most predictive for b, M, respectively. By using five predictor variables, the combination of [Dmax, Dmin, pH, pE, pG] will be the most predictive.
Fig. 3. Results by linear analysis. (A) Visualization of the correlation matrix between pairs out of the twelve variables, including two target variables [b, M] and ten predictor variables [Dmax, Dmin, pH, pB, pE, pT, pI, pG, pS, p∼], computed by using all the ∼110 000 data records. We study the number of predictor variables from 1 to 10 by testing all the possible subsets of predictor variables with 1024 tests in total and present the best subsets that yield the highest coefficient of determination (rsq) value for explaining b (B) and M (D) values. The best subsets are presented in (C) and (E) for b and M values, respectively by the gray column, which shows for a certain number of predictor variables (1 to 10), which variables are included in the best subset that yields the highest rsq value.
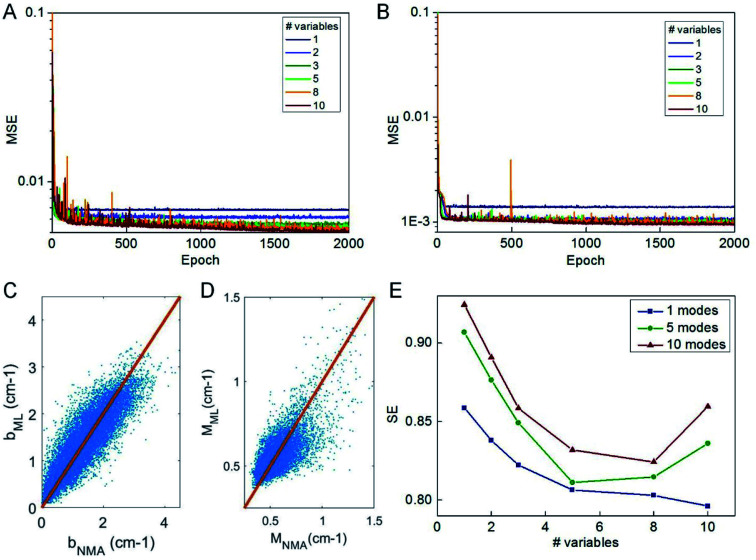
We use the knowledge obtained from a linear model to reduce the number of predictor variables of our ML model. We test nvar from 1 to 10 and the types of predictor variables are selected according to their importance as given in Fig. 3C. We use the selected predictor variables to train the ML model based on the selected columns of the training data by using the same learning architecture and compute the mean-square error of the testing data during the optimization process, as given in Fig. 4A and B. It is shown that 2000 epochs are enough to yield overall converged mean-square error and nvar > 5 does not yield a significant difference from nvar = 5, as what is predicted by the linear model. It is also shown that for nvar = 5, the ML predicted [b, M] values well agree with the measured [b, M] value of the testing data, as shown in Fig. 4C and D, respectively. The high correlation coefficient (0.88 for b and 0.78 for M) and low standard error (0.35 cm−1 for b and 0.084 for M) can be computed from Fig. 4C and D, which support the accuracy of the prediction. In addition to the comparison of the fitting parameters, we can expand the predicted [b, M] values back to fi_ML for each of the protein structure within the testing dataset and compute the standard error σ with fi_NMA as given in Fig. 4E. It is shown that nvar = 5 has an advantage in reaching small σ value for several different comparisons, including comparing of f1per se, as well as from f1 to f5 and from f1 to f10.
Fig. 4. Performance of ML train by a different number of predictor variables. The MSE computed during the training of predicting b (A) and M (B) values by using the number of predictor variables from 1 to 10 with the FNN model. The comparison between the ML predicted b (C) and M value (D) by using the five predictor variables, [Dmax, Dmin, pH, pE, pG], as suggested by the linear model, with the NMA result for the 22 000 structures for testing. (E) The standard error (SE) for comparison of the frequencies predicted by ML (trained by the five predictor variables) and directly obtained from NMA that corresponds to the first 1, 5 and 10 modes of all the protein structures for testing.
For any protein sequences, recent progress in folding algorithms makes it possible to accurately predict their 3D atomic structures.33,34 Combining with classical force fields, these structures yields a Hessian matrix that is often too big to solve for their eigenvalues by NMA. The method proposed here provides an efficient way to obtain the eigenvalues without NMA. Thus, it can combined with the recent innovative method of solving eigenvectors from eigenvalues35 and provide all the normal frequencies and normal modes of a protein. We can use the information to predict the dynamic behavior of a protein. For example, for any protein, we obtain the ith normal modes as a {xi,yi,zi} normal frequency fi. By using the equipartition theorem, we can compute that each mode has the equal kinetic energy parts as (3/2)NkBT/M for the first M modes of a protein structure under the temperature of T, where N is the total number of atoms and kB is the Boltzmann constant. Because each of the normal modes are normal to the other modes, the velocity distribution for atom j in mode i is vij and should yield
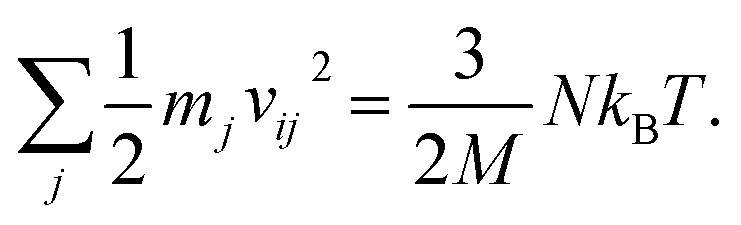 |
3 |
Considering the atomic velocity is also given by the magnitude of the particle vibration as 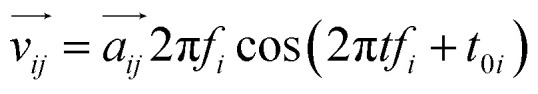 , and the magnitude of vibration
, and the magnitude of vibration 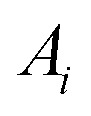 is given by the
is given by the 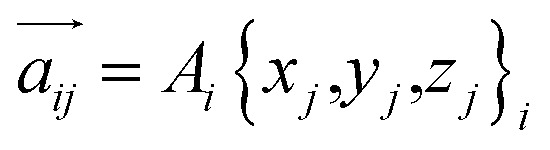 as {xj,yj,zj}i the ith normal mode on atom j. Putting these relations to eqn (3), we obtain the magnitude of vibration as
as {xj,yj,zj}i the ith normal mode on atom j. Putting these relations to eqn (3), we obtain the magnitude of vibration as
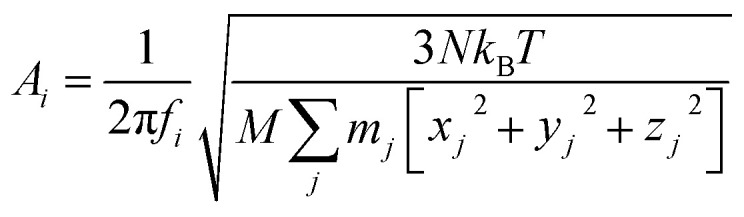 |
4 |
This equation can be used to calculate the thermal vibration of the protein structure without running molecular dynamics simulations. With the coordinate of each atom given by a function of time t
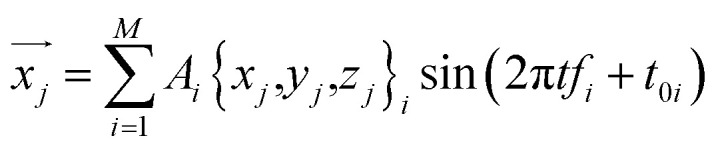 |
5 |
For example, we focus on the protein structure with PDB ID 1FH1 and perform this superposition analysis by using the predicted normal frequencies and obtain its thermal vibration spectrum at 300 K as given in ESI Video 1.†
Discussion
The collection of the natural frequencies of a protein gives the location of all the peaks of the mechanical spectrum where the mechanical resonance of the structure gets more significant than other frequencies, which represents an important fingerprint to identify the protein. Although NMA provides an accurate way to measure all the natural frequencies, it is considered as a very expensive process because of the difficulty in obtaining the high-resolution atomic structure and the time and resource to solve the eigenvalues of the elastic matrix. Here, we demonstrate that ML can be used to directly obtain the natural frequencies without using the atomic structures or solving the eigenvalues, but by merely using several structural features that can be easily obtained. We use a linear model to reduce the number of predictor variables and find that five variables including the largest and smallest diameter, the ratio of amino acid with alpha-helix, beta strand and 3–10 helix domains36 can be used to predict the natural frequencies with a small standard error.
The selection of the initial structural features, including diameter and secondary structure ratios is more intuitive than fully rational. The reasons are the availability of experimental measurements (DLS, FTIR, etc.) and their consistency with in silico measurements of atomic protein structures. It forms the fundamental basis of training an ML model with the computational data, which provides the only feasible way of generating massive data records for training and validation. Using linear models, we have successfully reduced the number of predictor variables to five. It is possible that there can be other structure features that can better predict the natural frequencies but the features are not included. Considering the automatic generation of the database and rational analysis based on ML and linear models, as long as these features can be extracted from the high-resolution protein structures, this ML model can be easily updated by considering other geometric features beyond the current ones.
The method proposed here can serve as a useful and computationally efficient approach to predict the absorption and resonance functions of the protein molecule with unknown structure and sequence. It can be useful in categorizing the dynamic function of unknown proteins according to their structural features. This method, combined with the recently evolved techniques that allow prediction of protein structure from its sequence,15,16 could facilitate predicting the natural frequencies of all the known protein sequences (such as sequences presented in the UniProt,25 with 99.9% of them not included in the Protein Data Bank), which may be a useful resource to identify protein type according to its frequency spectrum.
Looking ahead, our new method could also be applied to predict the vibrational features of other nanoscale objects such as nanoparticles. It may also be used to extract other material properties besides vibrational spectra, and as such, be broadly applied in a materials-by-design approach where geometric features are identified to achieve certain material properties. Other applications may include material sonification methods, to offer a rapid method to create audible representation of proteins in musical form.23
Methods
Normal model analysis
At the foundation of the method, we build a full database of the first 70 normal modes of each of 110 511 natural protein structures composed of only standard amino acids out of the full list of more than 130 000 structures that are currently available in the Protein Data Bank. We developed a bash script that allows integrating multiple open source software with the CHARMM c37b1 program to automatically download, clean and analyze each of the protein molecular structure. The details of the bash script are given in our earlier paper.23
We use a Block Normal Mode (BNM) method8,37 in CHARMM for normal mode analysis on each of the protein structure. BNM projects the full atomic hessian matrix into a subspace spanned by the eigenvectors of blocks, as each block is defined by an amino acid. We save the first 70 modes with lowest frequencies, ordered from lower to higher frequency, of each protein molecule.
The first 6 modes always have zero eigenvalue and zero frequency because they correspond to the rigid-body movement and rotation of the molecule. The higher order modes 7 and onwards, i.e. the last 64 normal modes amongst the 70 generated, describe the molecular deformation. We hence only use the frequency value of the last 64 modes out of these 70 ones. These frequency values are denoted in sequence as f0, f1, f2, … f63.
Linear model analysis
We use R to study the number of predictor variables from 1 to 10 by testing all the possible subsets of predictor variables with 1024 tests in total and present the best subsets that yield the highest coefficient of determination value for explaining b and M values. We share the links to the database and R code of this work.
Feedforward neural network
The machine learning model is implemented in TensorFlow in Python. We use a Feedforward Neuron Network (FNN) with Rectified Linear Unit (ReLU) activation function to read in the training data (80% randomly selected data, ∼88 000 records) with a batch size of 10 000 records and develop this data-driven model by minimize the standard error between the predicted and measured [b, M] values by using an Adam optimizer. This FNN ML model is realized via four hidden layers with 40, 20, 10 and 5 neurons included for each of the layer and a final output layer to evaluate the outcome. We use the remaining 20% data for validation. We run the training for 100 000 epochs, with each of which represents one complete presentation of the training data to be learned by the machine, to ensure there is no further improvement for the optimization. We share the database and python codes of this ML model as ESI.†
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
This research was supported by ONR (grant #N00014-16-1-2333) and NIH U01 EB014976. Additional support from the Army Research Office (ARO) 73793EG is acknowledged.
Electronic supplementary information (ESI) available: File 1: database used for linear model: combine_name_freq2param_max_min_ss.dat; File 2: R code for linear model: R_code; File 3: database used for ML model: combine_freq2param_max_min_ss.dat; File 4: Python code for predicting b value: predict_f0.py; File 5: Python code for predicting m value: predict_power.py; Video 1: the dynamics of protein 1FH1 by using both superposition and MD simulations: Equipartition theorem.mp4. See DOI: 10.1039/c9ra04186a
References
- Berman H. M. Westbrook J. Feng Z. Gilliland G. Bhat T. N. Weissig H. Shindyalov I. N. Bourne P. E. The Protein Data Bank. Nucleic Acids Res. 2000;28(1):235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazaridis T. Karplus M. “New View” of Protein Folding Reconciled with the Old through Multiple Unfolding Simulations. Science. 1997;278(5345):1928–1931. doi: 10.1126/science.278.5345.1928. [DOI] [PubMed] [Google Scholar]
- Paci E. Karplus M. Unfolding Proteins by External Forces and Temperature: The Importance of Topology and Energetics. Proc. Natl. Acad. Sci. U. S. A. 2000;97(12):6521–6526. doi: 10.1073/pnas.100124597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin Z. Kreplak L. Buehler M. J. Hierarchical Structure Controls Nanomechanical Properties of Vimentin Intermediate Filaments. PLoS One. 2009;4(10) doi: 10.1371/journal.pone.0007294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buehler M. J. and Cranford S. W., Biomateriomics, Springer, Netherlands, 2012 [Google Scholar]
- Rischel C. Spiedel D. Ridge J. P. Jones M. R. Breton J. Lambry J. C. Martin J. L. Vos M. H. Low Frequency Vibrational Modes in Proteins: Changes Induced by Point-Mutations in the Protein-Cofactor Matrix of Bacterial Reaction Centers. Proc. Natl. Acad. Sci. U. S. A. 1998;95(21):12306–12311. doi: 10.1073/pnas.95.21.12306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ackbarow T. Chen X. Keten S. Buehler M. J. H. Multiple Energy Barriers, and Robustness Govern the Fracture Mechanics of -Helical and Beta-Sheet Protein Domains. Proc. Natl. Acad. Sci. U. S. A. 2007;104(42):16410–16415. doi: 10.1073/pnas.0705759104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tama F. Gadea F. X. Marques O. Sanejouand Y. H. Building-Block Approach for Determining Low-Frequency Normal Modes of Macromolecules. Proteins. 2000;41(1):1–7. doi: 10.1002/1097-0134(20001001)41:1<1::aid-prot10>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
- Xu Z. P. Paparcone R. Buehler M. J. Alzheimer's A Beta(1-40) Amyloid Fibrils Feature Size-Dependent Mechanical Properties. Biophys. J. 2010;98(10):2053–2062. doi: 10.1016/j.bpj.2009.12.4317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karplus M. Kuriyan J. Molecular Dynamics and Protein Function. Proc. Natl. Acad. Sci. U. S. A. 2005;102(19):6679–6685. doi: 10.1073/pnas.0408930102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodrigues C. H. M. Pires D. E. V. Ascher D. B. DynaMut: Predicting the Impact of Mutations on Protein Conformation, Flexibility and Stability. Nucleic Acids Res. 2018;46:W350–W355. doi: 10.1093/nar/gky300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H. Büyüköztürk O. Probabilistic Updating of Building Models Using Incomplete Modal Data. Mech. Syst. Signal Process. 2016;75:27–40. doi: 10.1016/j.ymssp.2015.12.024. [DOI] [Google Scholar]
- Wang S. S. Qin Z. Jung G. S. Martin-Martinez F. J. Zhang K. Buehler M. J. Warner J. H. Atomically Sharp Crack Tips in Monolayer MoS2 and Their Enhanced Toughness by Vacancy Defects. ACS Nano. 2016;10(11):9831–9839. doi: 10.1021/acsnano.6b05435. [DOI] [PubMed] [Google Scholar]
- Go N. Noguti T. Nishikawa T. Dynamics of a Small Globular Protein in Terms of Low-Frequency Vibrational Modes. Proc. Natl. Acad. Sci. U. S. A. 1983;80(12):3696–3700. doi: 10.1073/pnas.80.12.3696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper S. Khatib F. Treuille A. Barbero J. Lee J. Beenen M. Leaver-Fay A. Baker D. Popović Z. Players F. Predicting Protein Structures with a Multiplayer Online Game. Nature. 2010;466:756–760. doi: 10.1038/nature09304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conchúir S. Barlow K. A. Pache R. A. Ollikainen N. Kundert K. O'Meara M. J. Smith C. A. Kortemme T. A Web Resource for Standardized Benchmark Datasets, Metrics, and Rosetta Protocols for Macromolecular Modeling and Design. PLoS One. 2015;10(9):e0130433. doi: 10.1371/journal.pone.0130433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silver D. Huang A. Maddison C. J. Guez A. Sifre L. van den Driessche G. Schrittwieser J. Antonoglou I. Panneershelvam V. Lanctot M. et al., Mastering the Game of Go with Deep Neural Networks and Tree Search. Nature. 2016;529:484–489. doi: 10.1038/nature16961. [DOI] [PubMed] [Google Scholar]
- Gu G. X. Chen C. T. Richmond D. J. Buehler M. J. Bioinspired Hierarchical Composite Design Using Machine Learning: Simulation, Additive Manufacturing, and Experiment. Mater. Horiz. 2018;5(5):939–945. doi: 10.1039/c8mh00653a. [DOI] [Google Scholar]
- Hanakata P. Z. Cubuk E. D. Campbell D. K. Park H. S. Accelerated Search and Design of Stretchable Graphene Kirigami Using Machine Learning. Phys. Rev. Lett. 2018;121:255304. doi: 10.1103/physrevlett.121.255304. [DOI] [PubMed] [Google Scholar]
- Gu G. X. Chen C. T. Buehler M. J. De Novo Composite Design Based on Machine Learning Algorithm. Extreme Mechanics Letters. 2018;18:19–28. doi: 10.1016/j.eml.2017.10.001. [DOI] [Google Scholar]
- Yu C. H. Qin Z. Martin-Martinez F. Buehler M. J. A Self-Consistent Sonification Method to Translate Amino Acid Sequences into Musical Compositions and Application in Protein Design Using AI. ACS Nano. 2019;13:7471–7482. doi: 10.1021/acsnano.9b02180. [DOI] [PubMed] [Google Scholar]
- Popova M. Isayev O. Tropsha A. Deep Reinforcement Learning for de Novo Drug Design. Sci. Adv. 2018;4(7):eaap7885. doi: 10.1126/sciadv.aap7885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin Z. Buehler M. J. Analysis of the Vibrational and Sound Spectrum of over 100,000 Protein Structures and Application in Sonification. Extreme Mechanics Letters. 2019:100460. doi: 10.1016/j.eml.2019.100460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greiner W., Rischke D., Neise L. and Stöcker H., Thermodynamics and Statistical Mechanics; Classical Theoretical Physics, Springer, New York, 2000 [Google Scholar]
- Consortium UniProt T. U. A Worldwide Hub of Protein Knowledge. Nucleic Acids Res. 2019;47(D1):D506–D515. doi: 10.1093/nar/gky1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abadi M., Barham P., Chen J., Chen Z., Davis A., Dean J., Devin M. and Ghemawat S., et al., TensorFlow: A System for Large-Scale Machine Learning, Proceedings of the 12th USENIX conference on Operating Systems Design and Implementation, USENIX Association, Savannah, GA, USA, 2016, pp. 265–283 [Google Scholar]
- Rossum G. Van. and Drake F. L., Python Tutorial, Technical Report CS-R9526, 1995, 10.1016/j.abb.2004.09.015 [DOI] [Google Scholar]
- Schmidhuber J. Deep Learning in Neural Networks: An Overview. Neural Network. 2015;61:85–117. doi: 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
- Nair V. and Hinton G., Rectified Linear Units Improve Restricted Boltzmann Machines, in Proceedings of the 27th International Conference on Machine Learning, 2010 [Google Scholar]
- Kabsch W. Sander C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-bonded and Geometrical Features. Biopolymers. 1983;22(12):2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- Yang H. Yang S. Kong J. Dong A. Yu S. Obtaining Information about Protein Secondary Structures in Aqueous Solution Using Fourier Transform IR Spectroscopy. Nat. Protoc. 2015;10(3):382–396. doi: 10.1038/nprot.2015.024. [DOI] [PubMed] [Google Scholar]
- R Developement Core Team, R: A Language and Environment for Statistical Computing, 2008
- Qin Z. Wu L. Sun H. Huo S. Ma T. Lim E. Chen P. Y. Marelli B. Buehler M. J. Artificial Intelligence Method to Design and Fold Alpha-Helical Structural Proteins from the Primary Amino Acid Sequence. Extreme Mechanics Letters. 2020;36:100652. [Google Scholar]
- Senior A. W. Evans R. Jumper J. Kirkpatrick J. Sifre L. Green T. Qin C. Žídek A. Nelson A. W. R. Bridgland A. et al., Improved Protein Structure Prediction Using Potentials from Deep Learning. Nature. 2020;577(7792):706–710. doi: 10.1038/s41586-019-1923-7. [DOI] [PubMed] [Google Scholar]
- Denton P. B., Parke S. J., Tao T. and Zhang X.Eigenvectors from Eigenvalues: A Survey of a Basic Identity in Linear Algebra, 2019, arXiv e-prints, arXiv:1908.03795 [Google Scholar]
- Silva R. A. Yasui S. C. Kubelka J. Formaggio F. Crisma M. Toniolo C. Keiderling T. A. Discriminating 310- from α-Helices: Vibrational and Electronic CD and IR Absorption Study of Related Aib-Containing Oligopeptides. Biopolymers. 2002;65(4):229–243. doi: 10.1002/bip.10241. [DOI] [PubMed] [Google Scholar]
- Ruiz L. Xia W. J. Meng Z. X. Keten S. A Coarse-Grained Model for the Mechanical Behavior of Multi-Layer Graphene. Carbon. 2015;82:103–115. doi: 10.1016/j.carbon.2014.10.040. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.