A stacked approach for chained equations multiple imputation incorporating the substantive model

Summary:

Multiple imputation by chained equations (MICE) has emerged as a popular approach for handling missing data. A central challenge for applying MICE is determining how to incorporate outcome information into covariate imputation models, particularly for complicated outcomes. Often, we have a particular analysis model in mind, and we would like to ensure congeniality between the imputation and analysis models.

We propose a novel strategy for directly incorporating the analysis model into the handling of missing data. In our proposed approach, multiple imputations of missing covariates are obtained without using outcome information. We then utilize the strategy of imputation stacking, where multiple imputations are stacked on top of each other to create a large dataset. The analysis model is then incorporated through weights. Instead of applying Rubin’s combining rules, we obtain parameter estimates by fitting a weighted version of the analysis model on the stacked dataset. We propose a novel estimator for obtaining standard errors for this stacked and weighted analysis. Our estimator is based on the observed data information principle in Louis (1982) and can be applied for analyzing stacked multiple imputations more generally. Our approach for analyzing stacked multiple imputations is the first method that can be easily applied (using R package StackImpute) for a wide variety of standard analysis models and missing data settings.

1. Introduction

Missing data is a common problem in modern observational data analysis, and the handling and treatment of these missing data can often have a large impact on statistical inference (Little and Rubin, 2002). In response, a suite of statistical methods has been developed to tackle the various challenges that arise. In particular, a statistical strategy called multiple imputation has emerged as a popular and attractive approach for handling missing data in a wide variety of settings. For multiple imputation, we use statistical models to draw multiple versions of the missing data, resulting in M complete datasets. Then, the desired analysis is applied to each complete dataset separately and combined across datasets using Rubin’s combining rules (Little and Rubin, 2002). The central challenge of multiple imputation is specifying the statistical models or distributions used to obtain the draws of the missing data.

Traditional multiple imputation strategies involve filling in values for the missing data by drawing from distributions obtained from an assumed joint distribution for all the variables of interest. Rather than specifying a joint model, an alternative strategy called multiple imputation by chained equations (MICE) involves specifying conditional distributions for each variable with missingness directly (Raghunathan, 2001; Van Buuren et al., 2006). These imputation distributions can be very flexible (e.g. random forests), or they can be based on standard regression models. Generally, these imputation models will not correspond to a valid joint distribution. Compared to imputation using a valid joint distribution, MICE has fewer theoretical guarantees (Liu et al., 2013; Hughes et al., 2014). However, MICE is often easy to implement and understand, and it can accommodate complicated variable relationships such as bounds, nonlinearity, and interactions. Software development has made MICE readily accessible to analysts, leading MICE to become an essential tool in the statistical toolbox for handling missing data.

With easy-to-use software at an analyst’s fingertips, it can become tempting to throw MICE at any missing data problem without careful thought about the imputation distributions. Suppose our ultimate goal is to model the relationship between some outcome, Y, and covariates X. Suppose we have missingness in X and possibly also in Y. Literature suggests that we should somehow incorporate information in Y into the distributions used to impute missing values in X (Moons et al., 2006). A particularly tricky problem arises when Y is complicated. Y may be a longitudinal or survival-type outcome, or the relationship between Y and X may be involve interactions. Incorporating complicated Y into imputation models for X can be challenging and can potentially have a large impact in terms of bias in downstream analyses (Beesley et al., 2016).

Bartlett et al. (2014) proposes a strategy called SMC-FCS (substantive model compatible fully conditional specification) that uses the assumed Y|X relationship directly to incorporate Y into the imputation distributions. In particular, missing covariate X_p is imputed from a distribution proportional to the outcome model f(Y|X) multiplied by an assumed relationship between X_p and the other covariates, X_−p. An advantage of this approach over traditional MICE is that the assumed relationship between Y and X used for imputation is consistent with the assumed relationship in the analysis model, called congeniality (Meng, 1994). A lack of congeniality can sometimes produce bias in the downstream estimation of standard errors by Rubin’s rules (Robins and Wang, 2000). Additionally, this imputation strategy can substantially simplify the task of incorporating Y into the imputation of missing X. However, the resulting imputation distribution is often known only up to proportionality, and more advanced methods such as rejection sampling or Metropolis-Hastings methods must often be used to obtain imputed values for each X_p. Stata and R packages titled smcfcs exist for implementing SMC-FCS in certain outcome modeling settings, but this method can require additional work to implement in general (Bartlett and Morris, 2015).

In this paper, we propose a novel strategy for incorporating the outcome model structure into the imputation pipeline that maintains the advantages of the method in Bartlett et al. (2014) but is more easily implemented, particularly for complicated or non-standard Y|X. We utilize the strategy of imputation stacking, where multiple imputations of the missing data are stacked on top of each other to create a large dataset (Robins and Wang, 2000; Van Buuren, 2018). In our proposed approach, multiple imputations of missing X are obtained using imputation distributions that do not involve the outcome Y. While this approach will generally result in bias for standard multiple imputation, our method attains valid parameter estimates by augmenting the stacked dataset with weights defined using the Y|X model structure. We then estimate parameters in the analysis model by fitting a weighted model for Y|X on the stacked dataset. This strategy allows imputation and data analysis to be easily performed by separate analysts without concerns about uncongeniality between the imputation and analysis models and the potential negative impact on inference. Additionally, this imputation stacking strategy is particularly useful in settings where we want to impose restrictions across imputed datasets such as when variable selection is of primary interest (Wood et al., 2008). This work is the first to propose a statistical strategy for chained equations imputation that (1) directly incorporates the outcome model structure and (2) involves imputation from standard models such as regression models.

While imputation stacking can produce valid parameter estimates when the imputation models are well-specified, additional work is needed to obtain valid standard error estimates (Robins and Wang, 2000; Van Buuren, 2018). Robins and Wang (2000) and Kim (2011) provide strategies for estimating standard errors using stacked, imputed data. As we will discuss later on, both approaches have substantial limitations that may reduce their usage in practice. Wood et al. (2008) proposes an approach for estimating standard errors that is easy to implement but weakly justified in settings where missingness is not completely random. In this paper, we develop an alternative strategy for estimating standard errors for data analysis using stacked multiple imputations, and this estimator can be applied in general imputation settings. Our approach for estimating standard errors based on stacked multiple imputations is the first proposed method that can be easily and routinely applied for a wide variety of standard analysis models and missing data settings. We have developed an accompanying R package StackImpute that will allow the proposed estimation to be easily implemented for many popular regression models including generalized linear models and Cox proportional hazards models. Table 1 provides a breakdown of the advantages and disadvantages of the proposed approach relative to existing methods.

Table 1:

Summary of some existing and proposed imputation and data analysis strategies. Proposed methods highlighted in gray.

	Standard MICE	Bartlett et al. (2014)	Stacked, 1/M weighted	Stacked, f(Y|X) weighted
Covariate Imputation	f(Xp|X−p, Y), specified as regression model	f(Xp|X−p, Y)∝ f(Y|X)f(Xp|X−p), where f(Xp|X−p) is a regression model	Often, same as MICE. Could also apply other imputation methods.	f(Xp|X−p), specified as regression model
Point Estimation	Fit model to each imputed dataset separately	Fit model to each imputed dataset separately	Fit single weighted model to stacked imputations.*	Fit single weighted model to stacked imputations. Weights ∝f(Y|X)
Standard Errors	Rubin’s rules	Rubin’s rules	Previously, unclear how to estimate.** We propose new approach in Eq. 3.	We propose new approach in Eq. 3.
Comments	↳ Easy to implement ↳ Tricky to specify imputation regressions	↳ Limited outcome models supported by current software ↳ Easy to implement for supported models ↳ Outcome model built into imputation	↳ Inherits properties of imputation approach chosen ↳ Different data analysis ↳ Proposed new standard errors	↳ Imputation ignores Y. Easy to implement. ↳ Imputation and analysis separated. Easy to compare outcome models.
R Packages	mice	smcfcs	mice, StackImpute †	mice, StackImpute †

^*Tall stack corresponds to stack of M imputed datasets, with complete cases listed M times. All rows given weight 1/M. Short stack corresponds to stack with complete cases listed only once. Imputed rows given weight 1/M and complete cases given weight 1.

^**Sandwich estimator applied to weighted, stacked data known to under-estimate standard errors. Wood et al. (2008) proposed largely untested ad hoc correction method for stacked analysis standard errors. Bootstrap methods for estimating standard errors are computationally expensive.

^†R package for estimating standard errors using Eq. 3. Development version available at https://github.com/lbeesleyBIOSTAT/StackImpute. Can be implemented for additional outcome models using custom software. See Web Appendix Section 3 for details.

In Section 2 of this paper, we detail our proposed imputation algorithm and its theoretical motivation. In Section 3, we provide a strategy for estimating standard errors. In Section 4, we demonstrate the potential of our proposed method through a simulation study. In Section 5, we apply this imputation approach to handle missing data in a study of overall survival and time to recurrence for patients with head and neck cancer. In Section 6, we present a discussion.

2. Imputation Strategy

Suppose we are interested in the relationship between outcome Y and covariate variables represented by matrix X. We will assume for now that Y is fully observed, and we will extend to the setting with missing Y later on. Let binary R_i indicate whether subject i is a complete case (all X_i observed), where i = 1, …, n. Let $X_i^{(mis)}$ and $X_i^{(obs)}$ correspond to the missing and observed entries in X_i respectively. We will assume that observations are independent across i, although our results can be extended to settings with correlation across i. Additionally, we will assume that the data are missing at random (MAR) as defined in Little and Rubin (2002), where missingness may depend only on fully-observed variables. We suppose our interest is in parameter θ corresponding to the assumed distribution for Y|X.

Multiple imputation strategies attempt to draw multiple potential values for $X_i^{(mis)}$ from the posterior predictive distribution $f\left(X_i^{(mis)}\mid X_i^{(obs)},Y_i\right)$ as follows:

$$f\left(X_i^{(mis)}\mid X_i^{(obs)},Y_i\right)\propto f\left(Y_i\mid X_i\right)f\left(X_i^{(mis)}\mid X_i^{(obs)}\right).$$ (Eq. 1)

Obtaining a draw from Eq. 1 directly can be difficult, since the distribution is only known up to proportionality. Usual MICE imputation would attempt to approximate a draw from Eq. 1 by drawing missing covariates from a series of simpler distributions. An alternative strategy for approximating a draw from Eq. 1 is via importance sampling as discussed in Little and Rubin (2002) and Tanner (1993), where we first draw multiple times from $f\left(X_i^{(mis)}\mid X_i^{(obs)}\right)$. Note that this distribution does not condition on Y. Then, we choose a single imputation of $X_i^{(mis)}$ from these draws using a multinomial distribution where we select the j^th draw with probability proportional to f(Y_i|X_ij) and where X_ij corresponds to the j^th draw of $X_i^{(mis)}$. Inference for either approach could then proceed by constructing multiple imputed datasets, fitting the model of interest to each dataset, and combining inference across imputed datasets using Rubin’s combining rules (Little and Rubin, 2002). This approach can work well, but it can involve taking many, many draws from $f\left(X_i^{(mis)}\mid X_i^{(obs)}\right)$, which can increase the computational burden.

2.1. Proposed imputation strategy

Rather than taking multiple draws from $f\left(X_i^{(mis)}\mid X_i^{(obs)}\right)$ to obtain a single imputation from Eq. 1, we propose using all those draws as our multiple imputations and weighting them proportional to f(Y_i|X_i) in the final analysis, where weights are scaled to sum to 1 across imputations. Weights, therefore, are defined across imputed datasets rather than within imputed datasets. In order to make inference about θ, we perform the steps detailed below and shown in Figure 1. We provide example R code for implementation in Web Appendix 3, and we provide a detailed theoretical justification for this approach in Web Appendix 4. Table 1 provides a comparison of the proposed approach with existing methods.

Figure 1:

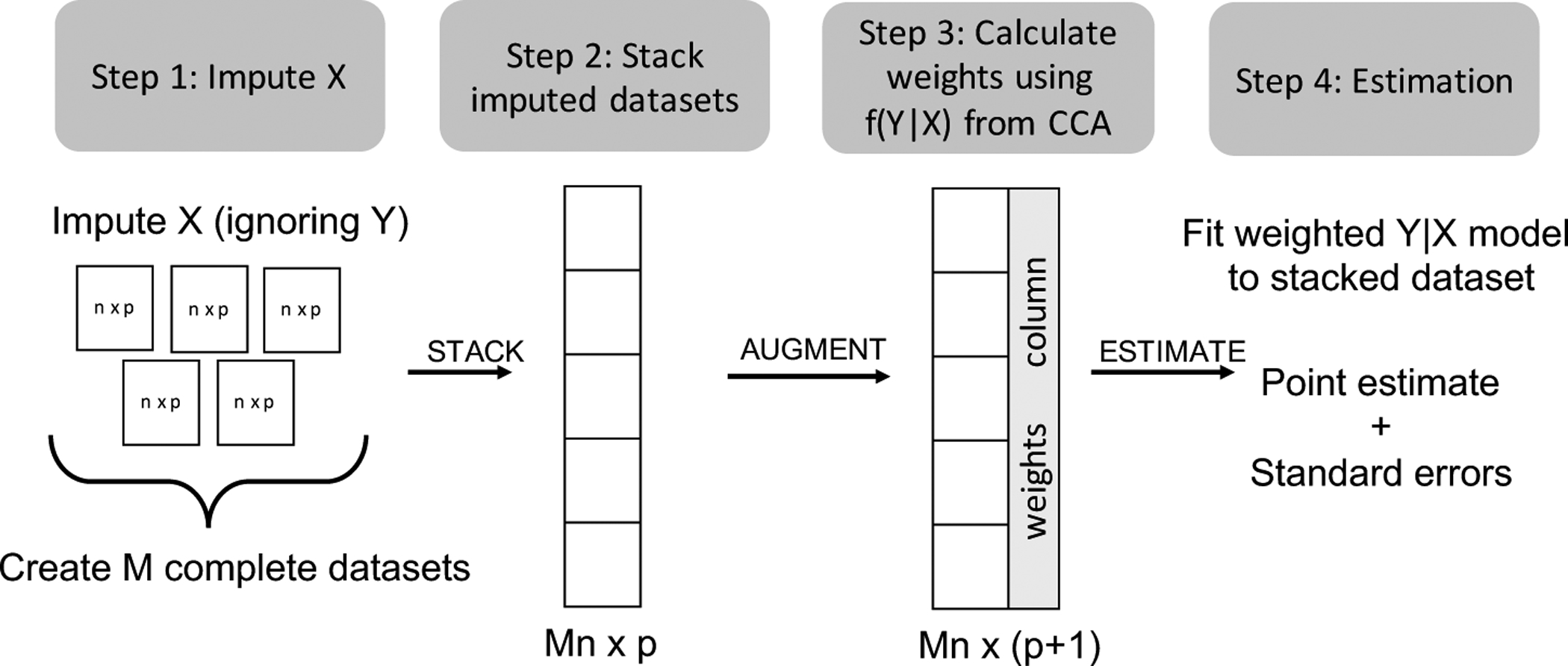
Diagram of Proposed Covariate Imputation Strategy*^†

*CCA = complete case analysis.

^† Missing Y, if any, can be imputed separately from f(Y|X) fixing imputed X from Step 1.

• Step 1: Impute missingness in covariates ignoring Y

In this step, we obtain the multiple imputations of X_i from an assumed distribution for $f\left(X_i^{(mis)}\mid X_i^{(obs)}\right)$, which in practice can be implemented using MICE by specifying regression models for each covariate with missingness given the other covariates but not including the outcome. An additional complication arises when we also have missingness in Y. In this case, we can proceed as above to obtain imputations of X ignoring Y and then impute missing values of Y from f(Y|X) for each imputed dataset. See Web Appendix 4.4 for details.

• Step 2: Stack imputations

We obtain a stacked version of the data, where each of the M imputed datasets of size n × p are stacked on top of each other to form a Mn × p dataset, called the “tall stack.” An alternative stacking strategy is to include subjects with fully-observed data only once in the stacked dataset. If n₁ is the number of subjects with fully-observed data, this will result in a stacked dataset with n₁ + (n − n₁)M rows, called the “short stack.” In settings where n or M is large, this may be a more memory- and computationally-efficient stacking strategy and should have no impact on resulting inference for appropriately defined weights.

• Step 3: Assign weights

In the existing point estimation strategy using stacked multiple imputations (see Table 1), we augment the stacked dataset with weights defined for each row as 1 divided by the number of times that subject appears in the stacked dataset. In our modified imputation stacking approach, we augment the stacked dataset with a weight column, where weights are defined to be proportional to f(Y_i|X_i). In practice, this may be hard to calculate, since it involves integrating out the corresponding parameter. Instead, we replace f(Y_i|X_i) with $f\left(Y_i\mid X_i;{\widehat{\theta }}_{cc}\right)$ where ${\widehat{\theta }}_{cc}$ is the estimated θ obtained from complete case analysis (CCA) for Y|X (fit Y|X to data from subjects without any missingness). We define weights using complete case data following logic in Section 2.2 and Web Appendix 4. For the row corresponding to the m^th imputation for the i^th subject and corresponding imputation X_im, assign weight

$$w_{im}=\frac{f\left(Y_i\mid X_{im};{\widehat{\theta }}_{cc}\right)}{{\sum }_{j=1}^{M}f\left(Y_i\mid X_{ij};{\widehat{\theta }}_{cc}\right)}.$$

If we define the stack using the short stack method, define the weight to be 1 for all subjects with fully-observed data. Weights for fully-observed subjects should be set to 1/M for the tall stack method. An alternative weighting strategy is to define weights as $w_{im}=\frac{f\left(Y_i\mid X_{im};{\theta }_{cc}^m\right)}{{\sum }_{j=1}^{M}f\left(Y_i\mid X_{ij};{\theta }_{cc}^j\right)}$ where ${\theta }_{cc}^j$ is a draw of the complete-case θ rather than the MLE. In simulations (not shown), we saw little difference between the two approaches, but the difference will likely be larger for smaller complete case samples. We use point estimates of θ_cc in our simulations in Section 4.

• Step 4: Estimate θ

Estimate θ by fitting a weighted model for Y|X to the stacked dataset with weights w. We describe how to estimate corresponding standard errors in Section 3.

2.2. Missingness dependent on Y

Now, we consider the particular case where missingness is MAR dependent on Y. In this case, the proposed imputation strategy ignoring Y induces a missing not at random (MNAR) mechanism when missingness is expressed only as a function of X (Little and Rubin, 2002). Therefore, additional thought is needed to assess whether it is appropriate to impute missing X using the proposed approach when missingness depends explicitly on Y. Let R_i represent the random variable indicating missingness, where the observed R_i is the data realization of R_i. Under MAR dependent on Y,

$$f\left(Y_i\mid X_i,R_i=1\right)\ne f\left(Y_i\mid X_i\right)\text{\hspace{0.17em}and\hspace{0.17em}}f\left(X_i^{(mis)}\mid X_i^{(obs)},R_i=1\right)\ne f\left(X_i^{(mis)}\mid X_i^{(obs)}\right).$$

Complete case analysis will produce biased results for the parameters related to f(Y_i|X_i) and $f\left(X_i^{(mis)}\mid X_i^{(obs)}\right)$ when missingness depends on Y. However, we have that

$$f\left(X_i^{(mis)}\mid X_i^{(obs)},Y_i\right)=f\left(X_i^{(mis)}\mid X_i^{(obs)},Y_i,R_i=1\right)\propto f\left(\left(,Y_i\mid X_i,R_i=1,\right)\right)f\left(\left(,X_i^{(mis)}\mid X_i^{(obs)},R_i=1,\right)\right).$$ (Eq. 2)

We can obtain a draw from $f\left(X_i^{(mis)}\mid X_i^{(obs)},Y_i\right)$ by first drawing missing X from $f\left(X_i^{(mis)}\mid X_i^{(obs)},R_i=1\right)$ and then weighting these draws proportional to f(Y_i|X_i, R_i = 1). We can apply complete case analysis (using realization R of R) to estimate parameters related to the distributions for Y|X, R = 1 and X^(mis)|X^(obs), R = 1. Suppose we can assume that the structure of the conditional and unconditional distributions in Eq. 2 and Eq. 1 respectively are approximately the same. For example, if Y|X is a linear regression, suppose Y|X, R = 1 approximately follows a linear regression with different parameter values. Under this assumption, we can also apply the strategy in Figure 1 to obtain approximate draws from $f\left(X_i^{(mis)}\mid X_i^{(obs)},Y_i\right)$, allowing us to handle MAR missingness related to Y using the same strategy as before.

In summary, we can use the method in Figure 1 to obtain essentially unbiased estimates of the outcome model parameters under MAR dependent on Y even though we have bias in (1) the estimated weights f(Y_i|X_i) from Step 3 and (2) the parameter draws performed within the covariate imputation in Step 1. Ultimately, these biases in the individual stages of imputation and weighting wash out in the final proposed data analysis. Additional commentary can be found in Supplementary Section 4.

In order to apply the method in Figure 1 under MAR dependent on Y, we assume imputation is performed by drawing parameters using the overall complete case data, but this is not how parameters are often drawn within the MICE imputation algorithm. Instead, the algorithm usually draws parameters for imputation of a given covariate X_p using data from subjects with X_p fully observed, treating the most recent sampled values of X_−p as observed. This difference in how parameters are drawn results in a potential for residual bias in estimating outcome model parameters downstream, but we expect this bias to be generally small (see Supplementary Section 5.2 for more information).

3. Estimating Standard Errors

A major drawback of the stacked imputation approach in general is the difficulty in estimating standard errors. Conventional estimators such as sandwich estimators only account for the so-called “within-imputation” variation, ignoring the “between-imputation” variation (Wood et al., 2008). Wood et al. (2008) proposed a strategy for scaling up the standard errors obtained from fitting a model to the stacked data. Standard errors associated with covariate X_p are obtained by fitting a model for Y|X and weighting each row of the stacked data by $\frac{1-f_p}{M}$, where f_p is the fraction of missing information in X_p. The fraction of missing information f_p is roughly estimated as the proportion of subjects with missing values for X_p. This strategy requires the model of interest to be re-fit multiple times to obtain standard errors for each X_p. Alternatively, we can obtain similar standard errors by post-multiplying the variance associated with covariate X_p by $\frac{M}{1-f_p}$ after fitting a single regression model weighted by 1/M. This approach from Wood et al. (2008) is motivated under MCAR missingness and simple to implement, but its ability to estimate standard errors in other missingness settings is unclear.

Yang and Kim (2016) and Kim (2011) developed a stacked imputation strategy in the survey sampling context called fractional multiple imputation. Estimation proceeds using an iterative algorithm in which we define weights as a function of the analysis/imputation methods and survey weights, estimate parameters of interest, re-estimate weights, etc. Standard errors are then estimated using a jackknife-type approach. This estimator can be complicated and computationally expensive to estimate, and the lack of available software for general parametric fractional imputation severely limits its ability to be used in practice.

Another strategy in the literature for estimating standard errors for stacked multiple imputation was developed in Robins and Wang (2000) and more recently applied in Hughes et al. (2016). This estimator requires score and information matrices for both the imputation and analysis models. Additionally, the estimator itself can be complicated to conceptualize and compute, and no standard software exists to make such calculations routine. This approach also requires that the imputation models are standard parametric models from which we can obtain score and information matrices, which excludes many popular non-parametric imputation strategies such as random forests or predictive mean matching. Given the complexity that serves as a barrier to general use of this estimator, we chose not to implement the methods in Robins and Wang (2000) and Kim (2011) in our simulations later on.

We propose an alternative strategy for estimating standard errors that, like the method in Robins and Wang (2000), involves the score and information matrices from the outcome model. Unlike Robins and Wang (2000), however, we do not require information about the imputation distributions. Our proposed estimator can be applied (1) when multiple imputations are obtained using existing imputation methods (e.g. MICE, joint modeling, SMC-FCS) and then stacked or (2) when we apply our modified imputation and weighting approach in Figure 1. Like standard errors from Rubin’s rules (but unlike Robins and Wang (2000)), our estimator is not guaranteed to have good performance when imputation and analysis models are uncongenial.

In obtaining an estimator, we use the complete information principle discussed in Louis (1982), namely I_obs(θ) = I_com(θ) − I_mis(θ), where I_obs is the observed data information matrix (the target), I_com is the expected complete data information matrix given the observed data, and I_mis is the expected missing information given the observed data. While I_obs can be difficult to estimate directly, I_com and I_mis may be more readily estimated. First, we will assume data are independent across values of i. Let $J_{com}^i$ correspond to the complete data Fisher information matrix contribution for subject i, and let $U_{com}^i$ be the corresponding score matrix contribution for subject i. See Web Appendix 2 for an example. Wei and Tanner (1990) proposed a Monte Carlo version of the estimator developed in Louis (1982) that involves averaging the estimated I_com and I_mis across multiple imputations of the data. Using a similar strategy, we propose a generalization of the estimator in Louis (1982) that allows for individual and imputation-specific weights, w_im, and involves averaging across multiple imputations. With imputation as in Figure 1, w_im corresponds to the augmented weight in Step 3. When applying standard imputation strategies that incorporate Y (e.g. MICE, joint modeling, SMC-FCS), we can define w_im for each i as the number of times that subject appears in the stacked dataset (M for tall stack, 1 for short stack). Let X_im denote the m^th imputation of X_i. For subjects with fully-observed X_i, define X_im = X_i. As shown in Web Appendix 1, we can express

$$\begin{gathered} I_{obs}(\widehat{\theta })\approx \sum _i{E}_{\widehat{\theta }}\left[J_{com}^i\left(X_i,Y_i\right)\mid X_i^{obs},Y_i\right]-\sum _{i}Va{r}_{\widehat{\theta }}\left[U_{com}^i\left(X_i,Y_i\right)\mid X_i^{obs},Y_i\right] \\ \approx \sum _i\sum _m{w}_{im}{J}_{com}^i\left(X_{im},Y_i\right)-\sum _i\sum _m{w}_{im}{\left[U_{com}^i\left(X_{im},Y_i\right)-{\overline{U}}_{com}^k\right]}^{\otimes 2} \end{gathered}$$ (Eq. 3)

where ${\overline{U}}_{com}^k={\sum }_j{w}_{kj}{U}_{com}^k\left(X_{kj},Y_k\right)$ and where $\widehat{\theta }$ is the point estimate obtained from fitting the weighted model for Y|X on the stacked data. The first element in the above equation is the weighted complete data information matrix for the outcome model evaluated using the stacked dataset. The second term is the weighted variance of $U_{com}^i$ summed over subjects. Given the equations for the complete data score and information matrix for an individual under the outcome model, these quantities can be easily calculated using the stacked data. We have developed an accompanying R package StackImpute that provides functions for calculating these standard errors for several common regression models including generalized linear models and Cox proportional hazards models.

4. Simulations

In this section, we provide results from a simulation study exploring the performance of the proposed imputation strategy and corresponding standard error estimator in terms of bias, coverage, and empirical variances of point estimates. This simulation study is broken up into four scenarios: (1) Gaussian Y with missingness in a single covariate, (2) binary Y with missingness in two covariates, (3) Gaussian Y with missingness in a single covariate and interactions in the outcome model, and (4) censored survival-type Y with missingness in a single covariate. We consider four different missingness mechanisms: MCAR, MAR dependent on X, MAR dependent on Y, and MAR dependent on both X and Y.

4.1. Simulation set-up

In all four scenarios, we generated 500 simulated datasets of 2000 subjects each. Simulations then proceeded as follows:

Scenario 1: Gaussian Y|X₁, X₂ with missingness in X₂ We generate covariates X₁ and X₂ from a multivariate normal distribution with mean 0, Var(X₁) = 0.49, Var(X₂) = 0.09, and covariance of 0.12. We then generated Y|X₁, X₂ ~ N(0.53X₁+1.25X₂, 0.55). Roughly 50% missingness was generated in X₂ under the model logit(P(X₂ observed|X₁, Y)) = ϕ₀ + ϕ₁X₁ + ϕ₂Y with values ϕ = {0, 0, 0}, (0, 1, 0), (0, 0, 1), (0, 1, −1)}. These values of ϕ correspond to MCAR, MAR dependent on X₁, MAR dependent on Y, and MAR dependent on X₁ and Y respectively.

Scenario 2: Binary Y|X₁, X₂, X₃ with missingness in X₂, X₃ We generate covariates X₁, X₂, and X₃ from a multivariate normal distribution with mean 0, unit variances, and pairwise covariance of 0.3. We then generated binary Y using the relation logit(P(Y = 1|X₁, X₂, X₃)) = 0.5+0.5X₁+0.5X₂+0.5X₃. Missingness in X₂ was generated using the model from Scenario 1 with ϕ = {(0.5, 0, 0), (0.5, 1, 0), (0.5, 0,1), (0.5, 1, −1)} and independent of X₃. We then induced 30% MCAR missingness for X₃. This resulted in roughly 40% of subjects having complete data.

Scenario 3: Gaussian Y|X₁, X₂, X₁ × X₂ with missingness in X₂ We generate covariates X₁ and X₂ from a multivariate normal distribution with mean 0, Var(X₁) = 0.81, Var(X₂) = 1.21, and covariance of 0.59. We then generated Y|X₁, X₂ ~ N(0 + X₁ + X₂ + X₁ × X₂, 1). We generate missingness in X₂ as in Scenario 1.

Scenario 4: Exponential T|X₁, X₂ with missingness in X₂ and uniform censoring We generate covariates X₁ and X₂ from a multivariate normal distribution with mean 0, Var(X₁) = 1, Var(X₂) = 1, and covariance of 0.5. We then generated T|X₁, X₂ to have an exponential distribution with scale parameter $e^{0.5X_1+0.5X_2}$. Uniform(0.2, 3) censoring was then imposed on T. Roughly 50% missingness was generated in X₂ under the model logit(P(X₂ observed|X₁, Y)) = ϕ₀ + ϕ₁X₁ + ϕ₂δ with values ϕ = {(0, 0, 0), (0, 1, 0), (−0.7, 0, 1), (−0.7, 1, −1)} where δ corresponds to the event/censoring indicator and is a part of Y. Missingness dependent on δ could be induced by missingness related to unobserved variable U related to the outcome.

Once the data were simulated, we performed multiple imputation of the missing values of X using methods described in Table 1 to obtain M = 50 multiple imputations. We then analyzed the results fitting the correct outcome model either using Rubin’s combining rules or the proposed stacking method. In analyzing stacked data, standard errors were estimated using various strategies including the standard sandwich estimator from the R package sandwich, the method in Wood et al. (2008), and our estimator in Eq. 3. In Scenario 4, stacked analysis weights were defined based on a Cox model fit to the complete case data. From this fit, we obtained the Breslow estimator for the cumulative baseline hazard and defined a piecewise constant baseline hazard that integrated to produce the estimated cumulative baseline hazard. Weights proportional to f(Y|X; θ) could then be calculated. In Scenario 3, we considered MICE imputation with Y incorporated into the imputation model through a main effect only or through main effects and an interaction with X₁.

4.2. Simulation results

Table 2 shows the average estimated bias of outcome model parameters across 500 simulated datasets. Complete case analysis shows substantial bias in Scenarios 1, 3, and 4 whenever missingness depends on Y. In Scenario 3, where the true outcome model included interactions, inclusion of interactions in the covariate imputation models did not reduce bias in estimating outcome model parameters. In Scenario 2, complete case analysis is biased only when missingness depends on both Y and covariate values, following well-known properties of logistic regression under case-control sampling (Scott and Wild, 1986). MICE with Y in the imputation model resulted in correctly-specified imputation models in Scenario 1 only. Evidence of resulting bias can be see for Scenario 3 and, to a lesser extent, Scenario 4. Similar bias is not seen in Scenario 2. In all scenarios, imputation using SMC-FCS as in Bartlett et al. (2014) tends to produce little bias since imputation was performed using the “correct” distributions. Similarly, the proposed analysis based on stacking MICE imputations obtained without Y and then weighting rows by f(Y|X) produced little bias across simulation scenarios. When these same imputations (obtained without Y) were analyzed using Rubin’s rules, bias resulted in all scenarios. These simulations demonstrate the ability of the proposed imputation and f(Y|X) weighting strategy to produce unbiased point estimates comparable to those obtained using the method in Bartlett et al. (2014).

Table 2:

Bias of outcome model parameters under various imputation strategies and outcome model settings. Results across 500 simulations are presented. Biases greater than 0.05 are shaded. In all settings, X₁ was fully-observed and X₂ and possibly X₃ were imputed. All biases were multiplied by 100.

	Bias × 100 in effect of X1				Bias × 100 in effect of X2
Missingness:†	MCAR	X 1	Y	X1, Y	MCAR	X 1	Y	X1, Y
	Scenario 1: Linear Regression
Full Data	0.02	0.01	0.14	0.28	−0.05	−0.15	−0.17	−0.20
Complete Case	−0.03	−0.05	−5.18	5.29	−0.16	0.18	−13.11	−13.59
MICE with Y*
↳ Rubin’s rules	0.08	0.03	0.28	0.36	−0.41	0.02	−0.75	−0.30
↳ Stacked, 1/M weighted	0.11	0.07	0.32	0.39	−0.53	−0.12	−0.88	−0.41
MICE without Y*
↳ Rubin’s rules	16.1	16.1	18.48	18.0	−62.6	−62.3	−69.09	−69.4
↳ Stacked, f(Y|X) weighted	0.32	0.27	0.60	0.66	−1.36	−0.88	−1.85	−1.46
Bartlett et al. (2014) ⋈	0.14	0.11	0.47	0.47	−0.61	−0.21	−1.38	−0.72
	Scenario 2: Logistic Regression
Full Data	0.34	−0.03	0.09	0.13	0.24	−0.09	0.22	0.12
Complete Case	0.75	0.37	−0.12	21.0	0.18	−0.09	0.56	0.32
MICE with Y
↳ Rubin’s rules	0.35	−0.08	0.05	−0.07	−0.17	−0.60	0.17	−0.53
↳ Stacked, 1/M weighted	0.35	−0.08	0.04	−0.09	−0.26	−0.73	0.10	−0.72
MICE without Y
↳ Rubin’s rules	5.85	5.87	5.01	6.49	−18.49	−20.8	−14.5	−26.6
↳ Stacked, f(Y|X) weighted	0.49	0.11	0.13	0.30	−0.25	−0.61	0.12	−0.43
Bartlett et al. (2014)	0.42	0.05	0.09	0.08	0.12	−0.31	0.30	−0.19
	Scenario 3: Linear Regression with Interaction
Full Data	0.10	0.10	0.29	−0.22	−0.14	−0.04	−0.30	0.26
Complete Case	0.21	−0.10	−8.97	−0.58	−0.36	−0.09	−9.90	−14.88
MICE with Y
↳ Rubin’s rules	−2.12	−13.9	−4.73	−7.99	−12.28	13.14	−1.35	−3.97
↳ Stacked, 1/M weighted	−2.07	−13.95	−4.70	−7.82	−12.40	13.11	−1.38	−4.29
MICE with Y + interaction*	−2.75	18.93	−10.05	−17.52	−10.28	21.35	5.93	−10.14
MICE without Y
↳ Rubin’s rules	36.8	24.13	16.84	81.70	−50.20	−32.75	−35.32	−70.16
↳ Stacked, f(Y|X) weighted	0.05	0.05	−1.22	−1.24	−0.10	−0.08	− 1.37	0.01
Bartlett et al. (2014)	0.38	0.19	0.35	0.40	−0.49	−0.22	−0.50	0.16
	Scenario 4: Cox Proportional Hazards Regression
Full Data	0.12	0.04	−0.07	0.21	0.18	0.10	−0.01	0.15
Complete Case	0.12	0.07	−5.69	−9.07	0.07	0.26	−5.29	−4.31
MICE with Y
↳ Rubin’s rules	−1.62	−1.65	−2.04	−1.83	−4.18	0.37	−3.42	0.94
↳ Stacked, 1/M weighted	−1.61	−1.59	−2.02	−1.75	−4.30	0.27	−3.54	0.83
MICE without Y
↳ Rubin’s rules	0.48	1.58	0.95	2.59	−27.2	−25.02	−29.69	−27.47
↳ Stacked, f(Y|X) weighted	0.15	0.56	−0.18	0.91	−0.30	−2.43	−1.26	−2.47
Bartlett et al. (2014)	0.15	−0.05	−0.08	0.12	0.03	0.25	0.11	0.22

^†Missingness is MCAR or MAR dependent on the fully-observed terms listed.

^*MICE either including or excluding Y from the linear regression imputation models. An interaction between Y and X₁ was included in one setting for Scenario 3. MICE with Y for Scenario 4 followed recommendations in White and Royston (2009). Unless otherwise specified, MICE imputations were analyzed using Rubin’s rules.

^⋈X_p imputed from distribution proportional to f(Y|X)f(X_p|X_−p) using R package smcfcs. Then, apply Rubin’s rules.

Table 3 shows the relative empirical variance of point estimates (compared to analysis of the full data) across 500 simulated datasets. Empirical variances were calculated as the sample variance of the point estimates across 500 simulated datasets. Stacking of MICE imputations ignoring Y and then weighting by f(Y|X) produces similar empirical variances to the SMC-FCS method from Bartlett et al. (2014). When the MICE imputation model is correctly specified as a function of Y as in Scenario 1, methods explicitly incorporating the outcome model structure (Bartlett et al. (2014) method and MICE without Y with subsequent stacking and f(Y|X) weighting) produce similar results to standard MICE with Y analysis. Empirical variances for SMC-FCS can be higher or lower than those seen with MICE when the chained equations regressions are misspecified as a function of Y (Scenarios 2–4).

Table 3:

Relative empirical variance of outcome model parameters under various imputation strategies and outcome model settings (relative to full data without missingness). Results across 500 simulations are presented. In all settings, X₁ was fully-observed and X₂ and possibly X₃ were imputed.

	Relative variance for effect of X1				Relative variance for effect of X2
Missingness:†	MCAR	X 1	Y	X1, Y	MCAR	X 1	Y	X1, Y
	Scenario 1: Linear Regression
Full Data	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Complete Case	2.06	2.07	1.87	1.85	1.88	2.09	1.75	1.73
MICE with Y*
↳ Rubin’s rules	1.35	1.37	1.45	1.31	1.70	1.85	1.98	1.90
↳ Stacked, 1/M weighted	1.35	1.37	1.45	1.31	1.70	1.85	1.97	1.90
MICE without Y*
↳ Rubin’s rules	0.86	0.87	0.85	0.86	0.55	0.54	0.48	0.48
↳ Stacked, f(Y|X) weighted	1.34	1.37	1.45	1.31	1.69	1.83	1.95	1.89
Bartlett et al. (2014) ⋈	1.39	1.45	1.50	1.33	1.74	1.95	2.07	1.99
	Scenario 2: Logistic Regression
Full Data	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Complete Case	2.52	2.29	2.02	4.08	2.36	2.46	2.15	3.66
MICE with Y
↳ Rubin’s rules	1.08	1.08	1.04	1.13	1.64	1.64	1.45	2.35
↳ Stacked, 1/M weighted	1.08	1.07	1.04	1.12	1.63	1.63	1.45	2.33
MICE without Y*
↳ Rubin’s rules	0.93	0.95	0.92	0.94	0.54	0.45	0.60	0.43
↳ Stacked, f(Y|X) weighted	1.09	1.08	1.03	1.14	1.78	1.82	1.55	2.77
Bartlett et al. (2014)	1.09	1.09	1.05	1.14	1.73	1.74	1.52	2.58
	Scenario 3: Linear Regression with Interaction
Full Data	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Complete Case	2.14	2.13	1.78	2.37	2.11	2.04	1.83	2.50
MICE with Y
↳ Rubin’s rules	2.85	2.12	1.34	5.20	3.16	3.35	1.62	4.02
↳ Stacked, 1/M weighted	2.85	2.12	1.34	5.21	3.16	3.35	1.62	4.05
MICE with Y + interaction*	2.92	2.45	1.81	4.40	4.96	4.51	2.79	5.81
MICE without Y
↳ Rubin’s rules	2.25	1.69	1.16	4.54	1.03	0.77	0.86	0.85
↳ Stacked, f(Y|X) weighted	1.50	1.40	1.26	2.07	1.74	1.71	1.60	2.06
Bartlett et al. (2014)	1.52	1.46	1.29	2.07	1.75	1.60	1.55	1.99
	Scenario 4: Cox Proportional Hazards Regression
Full Data	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Complete Case	1.85	2.20	1.64	2.05	2.13	1.81	2.12	1.79
MICE with Y
↳ Rubin’s rules	1.06	1.13	1.02	1.17	1.62	1.57	2.02	1.95
↳ Stacked, 1/M weighted	1.07	1.24	1.02	1.17	1.62	1.64	2.01	1.94
MICE without Y
↳ Rubin’s rules	0.97	1.01	0.95	0.99	0.42	0.42	0.45	0.44
↳ Stacked, f(Y|X) weighted	1.14	1.21	1.08	1.17	1.91	1.61	2.18	1.81
Bartlett et al. (2014)	1.15	1.27	1.11	1.19	2.02	1.83	2.39	2.01

^†Missingness is MCAR or MAR dependent on the fully-observed terms listed.

^*MICE either including or excluding Y from the linear regression imputation models. An interaction between Y and X₁ was included in one setting for Scenario 3. MICE with Y for Scenario 4 followed recommendations in White and Royston (2009). Unless otherwise specified, MICE imputations were analyzed using Rubin’s rules.

^⋈X_p imputed from distribution proportional to f(Y|X)f(X_p|X_−p) using R package smcfcs. Then, apply Rubin’s rules.

Figure 2 shows the average estimated standard errors and the 95% confidence interval coverage rates for different variance estimation strategies based on stacked data analysis. These are also compared to Rubin’s rules-based standard errors for imputations based on the Bartlett et al. (2014) and standard MICE with Y methods. The sandwich estimator applied to the stacked and weighted data tends to strongly under-estimate variance. This is because this estimator accounts for “within-imputation” variation but does not appropriately address “between-imputation” variation. The method in Wood et al. (2008) is an improvement over the sandwich estimator, but this estimator can result in sub-optimal coverage even in the MCAR setting. The Wood et al. (2008) method produced overly-conservative standard errors for imputed covariates. The proposed estimation strategy was applied in two cases: (1) covariates imputed using MICE with Y and then stacking and weighting by 1/M and (2) covariates imputed using MICE without Y and then stacking and weighting by f(Y|X). In Case 1, estimated standard errors behaved similarly to Rubin’s rules-based estimates for MICE with Y imputations. In Case 2, the proposed strategy produced nominal coverage and standard error estimates near those obtained using the Bartlett et al. (2014) method, here viewed as a gold standard. In the proposed algorithm, weights were obtained using parameter estimates from a complete case fit for f(Y|X) rather than parameter draws. Although not shown, drawing the corresponding parameter when defining weights produced very similar results.

Figure 2:

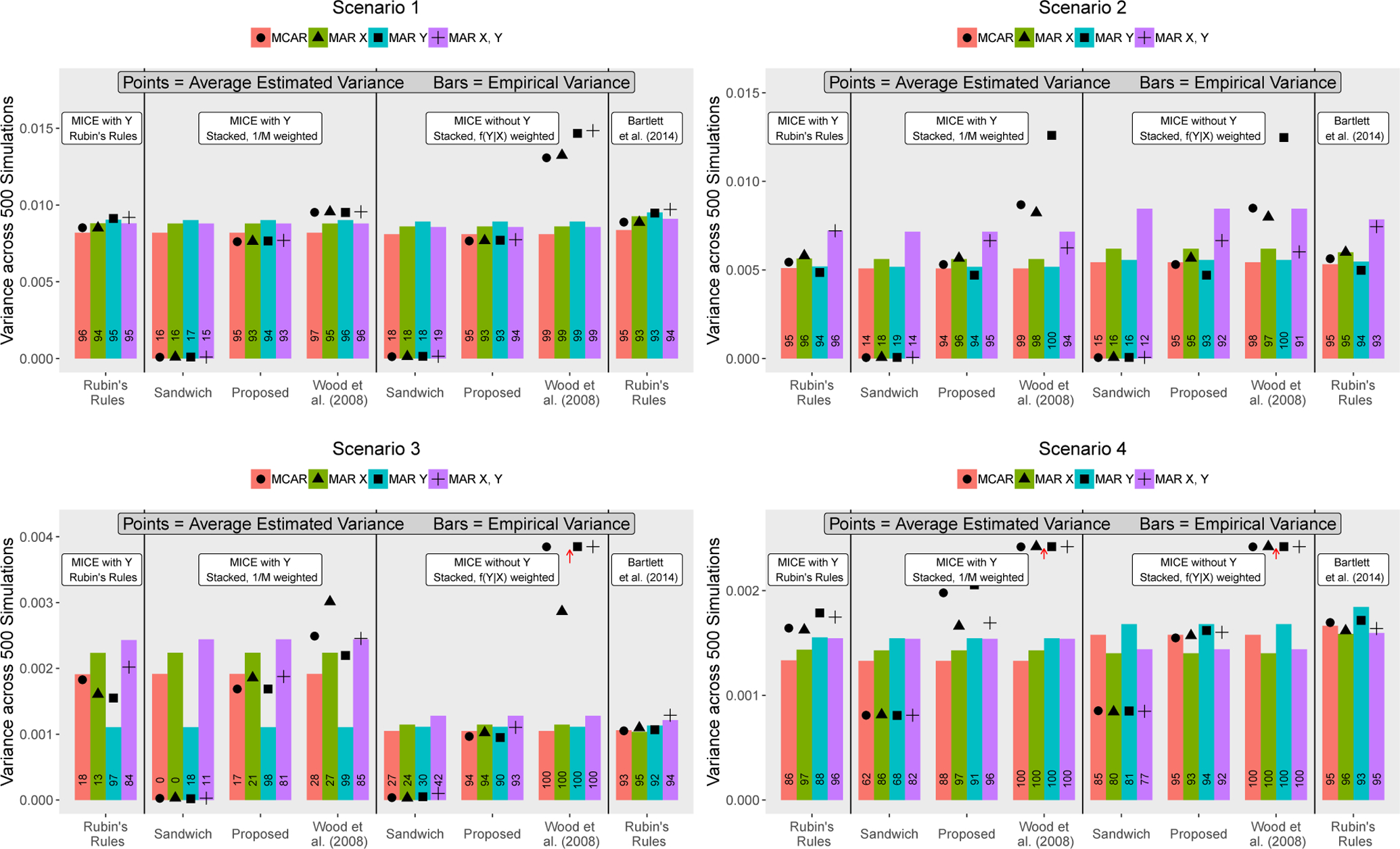
Empirical and average estimated variances (bars and points respectively) for X₂ parameter across 500 simulated datasets for various data analysis strategies and simulation settings. Coverage of 95% confidence intervals is printed along each bar.* ^†

* White boxes correspond to four different point estimation strategies considered. Both stacked approaches rely on standard MICE imputations (with or without including Y). For the two stacked approaches, three different methods were applied to estimate standard errors: (1) Huber-White sandwich estimation (Freedman, 2006) (2) the proposed method in Eq. 3, and (3) the method from Wood et al. (2008). For Scenario 3, MICE with Y corresponds to imputation without interactions.

^† Some estimated variances were very large and were truncated, denoted by the red arrows. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

5. Illustrative example: head and neck cancer survival

In this section, we illustrate the proposed methods for handling covariate missingness when we have a time-to-event outcome. In particular, we consider data from a study of 1226 patients treated for head and neck cancer at The University of Michigan. After initial treatment, consenting patients were followed for cancer recurrence and death. Smoking status (none, former, never), ACE27 comorbidities (none, mild, moderate, severe), HPV (human papillomavirus) status (positive, negative), age, cancer site (hypopharynx, larynx, oral cavity, oropharynx), and T stage (T0, T1, T2, T3) were recorded at baseline for the majority of patients, but T stage and HPV status were missing for roughly 30% and 45% of patients respectively. Small amounts of missingness were also present in smoking status and comorbidities. Additional study details can be found in Duffy et al. (2008) and Peterson et al. (2016).

We explore the impact of different imputation strategies on Cox proportional hazards model fits for overall survival and time to cancer recurrence. We note that a Cox proportional hazards mixture cure model would be more appropriate for time to cancer recurrence for head and neck cancer, but we will explore a standard Cox model fit for simplicity (Beesley et al., 2016). For each outcome model, our observed outcome can be written as Y = (T, δ), where T is the event or censoring time for a given outcome event, and δ is the corresponding event/censoring indicator. We are interested in imputing missing values in X (particularly, HPV status and T stage) using chained equations and somehow incorporating information in Y.

Several methods exist in the literature for imputing missing covariates with time-to-event outcomes. Van Buuren et al. (1999) suggests imputing missing values in X_p using a regression model with X_−p and log(T) as predictors, where X_−p represents the covariates in X excluding X_p. White and Royston (2009) proposes imputation using predictors X_−p, δ, and H₀(T) as predictors, where H₀(T) is an estimate of the cumulative baseline hazard for the event of interest. In practice, White and Royston (2009) suggests using the Nelson-Aalen estimate of the marginal cumulative hazard for imputation. We compared these imputation strategies to MICE imputation that entirely ignores the outcome variables T and δ. Imputation of HPV status assumed a logistic regression model structure, and imputation of all other variables assumed a multinomial regression. We then fit the outcome models of interest to each of the imputed datasets and obtained a single set of parameter estimates and standard errors for each model using Rubin’s combining rules (Little and Rubin, 2002).

Using imputations that were generated ignoring Y = (T, δ), we applied our proposed stacking and weighting strategy in Figure 1, where we weighted each row proportional to $f\left(T_i,{\delta }_i\mid X_i\right)={\left[{\lambda }_0\left(T_i\right)e^{\theta X_i}\right]}^{{\delta }_i}{e}^{-{\Lambda }_0\left(T_i\right)e^{\theta X_i}}$ where λ₀(t) and Λ₀(t) are the baseline and cumulative baseline hazard functions respectively. These were obtained by fitting a Cox proportional hazards model to the complete case data. From there, we obtained the Breslow estimator for Λ₀(t) and defined λ₀(t) to be piecewise constant so that it integrated to Λ₀(t). Standard errors for the stacked analyses were estimated using the method in Eq. 3.

Figure 3 presents the resulting estimated HPV status log-hazard ratio from Cox regressions for overall survival and time to recurrence outcomes adjusting for other patient-related factors. In both cases, imputation was performed using the overall survival outcome, so we might treat the time-to-recurrence analysis as a secondary analysis applied to previously imputed data, where the imputation and analyses models are not congenial. For the overall survival outcome, the proposed methods produced HPV status confidence intervals very near those obtained using Rubin’s rules and MICE imputation using H(t) as in White and Royston (2009). However, the stacked imputation method produces a larger hazard ratio estimate for the time to recurrence outcome compared to all other methods. This difference may be because, unlike the other methods, our proposed method incorporates the assumed time-to-recurrence model structure into the imputation and, therefore, does not suffer from uncongeniality.

Figure 3:

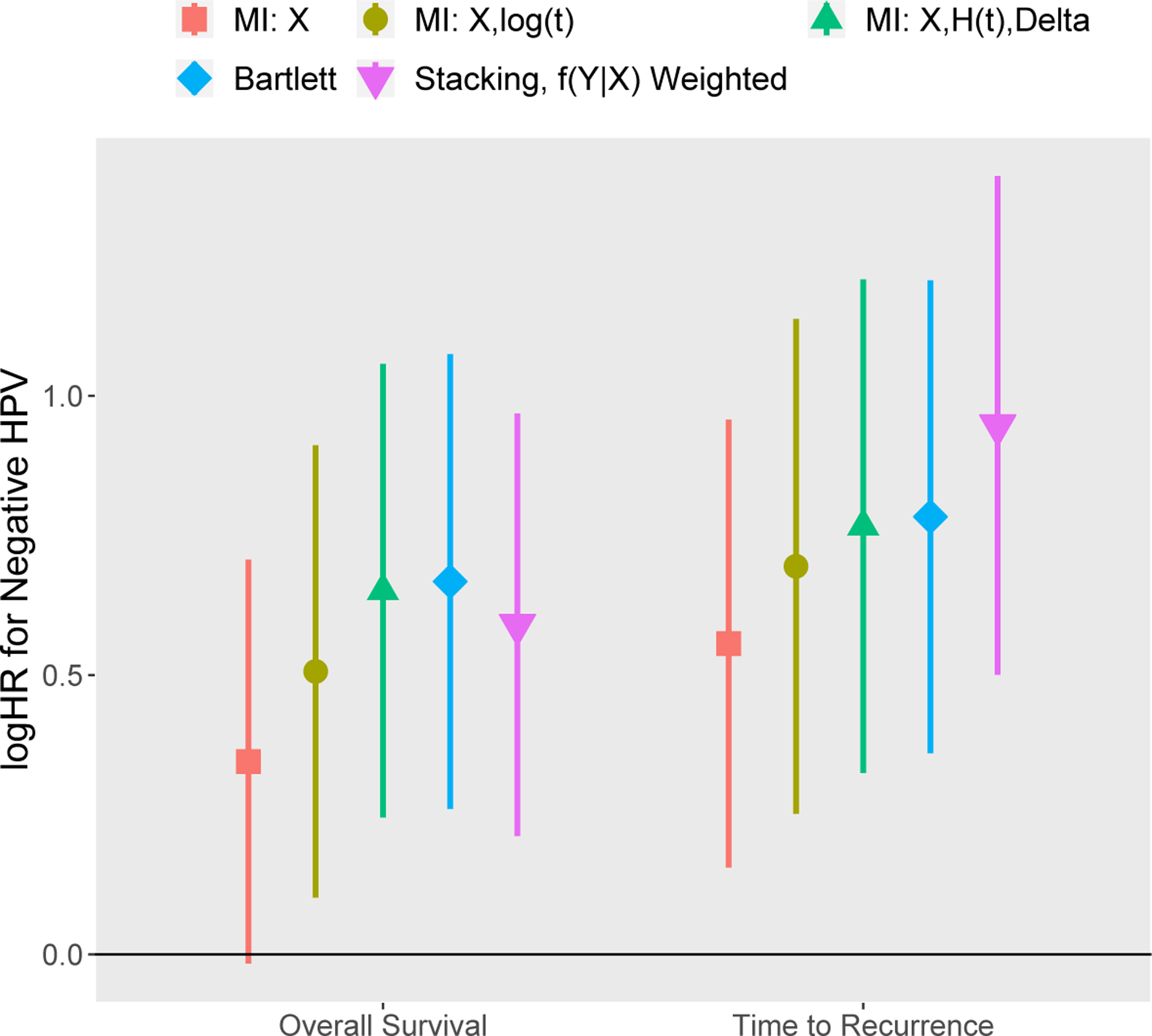
HPV log-hazard ratio from Cox modeling of overall survival and time to recurrence using imputed head and neck cancer data*

* Five imputation strategies are considered: (1) MICE based only on X, (2) MICE based on X and the log of the event/censoring time, (3) MICE based on X, the event indicator Delta, and the Nelson-Aalen estimate of the cumulative hazard H(t), (4) method of Bartlett et al. (2014), and (5) proposed strategy, where covariates are imputed ignoring the outcome and analysis involves stacking the imputations and weighting by f(Y|X). Imputation for strategies (2)-(4) use the overall survival outcome. For all methods, we present log-hazards ratios associated with HPV status from a Cox regression model for (A) overall survival and (B) time to recurrence based on the imputed data. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

6. Discussion

Multiple imputation using chained equations (MICE) is a popular and attractive approach for handling missing data in a variety of settings. A substantial challenge, however, is determining how to properly incorporate complicated outcome Y into imputation models for missing covariates X, since the way in which the outcome is incorporated can have substantial impact on downstream analysis (Beesley et al., 2016). Bartlett et al. (2014) developed an imputation strategy that directly uses the target analysis model structure (e.g. f(Y|X) to impute missing covariate values. This approach is appealing since it ensures that the imputation and analysis models are compatible with respect to the assumed relationship between Y and X. However, the approach in Bartlett et al. (2014) can often be challenging to apply in many practical data analysis strategies, since the imputation distributions may only be known up to proportionality. Existing R and Stata software implements the Bartlett et al. (2014) method for many standard regression modeling settings (e.g. Weibull, linear, and logistic regressions). However, implementation of this method for unsupported models requires custom software and may involve more advanced sampling methods (e.g. rejection sampling, Metropolis Hastings algorithms) that require tuning, making this approach challenging to apply for routine imputation.

In this paper, we propose a novel imputation and data analysis strategy that involves (1) imputing missing covariates ignoring the outcome Y, (2) stacking the multiple imputations to form a single dataset, (3) augmenting the dataset with weights based on the assumed analysis model structure, f(Y|X), and (4) analyzing the weighted, stacked data using a novel estimator for standard errors. This imputation strategy avoids the problem of incorporating Y into covariate imputation models entirely, but it still can produce valid estimates for the analysis model parameters through the use of weights. Additionally, the covariate imputation and outcome modeling steps are separated in this data analysis pipeline, allowing these steps to be implemented independently by different analysts. This is particularly useful when the outcome model includes interactions, polynomial terms, or takes a complicated form, and it facilitates comparison of multiple competing outcome models without concerns about uncongeniality with covariate imputation models. The proposed method also inherits the flexibility of chained equations imputation model specification in terms of incorporating bounds, auxiliary variables, or complex models such as random forests into the imputation procedure.

A limitation of data analysis based on stacked multiple imputations in general is the lack of convenient estimators for corresponding standard errors. In this paper, we develop a novel approach for estimating standard errors for stacked multiple imputations in Eq. 3. This estimator can be applied in our particular substantive model compatible imputation strategy, but it can also be applied for general data analysis of multiply imputed data as an alternative to Rubin’s rules. An advantage of the proposed data analysis approach over separate analysis of the imputed datasets as in Rubin’s rules is that we can easily impose restrictions in model estimates across multiple imputations such as in analyses with variable selection (Wood et al., 2008). A disadvantage of our approach is that is requires calculation of the score and information matrices for a given parametric model. However, these can be easily calculated using existing software in R for many popular parametric models. Our proposed estimator can be easily implemented for several analysis models (e.g. generalized linear models, Cox proportional hazards models) using our R package StackImpute. Additional work is needed to extend this estimator to the setting with penalized likelihood estimation, particularly when the penalty function is not differentiable.

Data Availability

Data from illustrative example are not shared due to third-party data sharing restrictions and to protect patient privacy.