Abstract
Transition-metal-doped boron nanoclusters exhibit interesting structures and bonding. Inspired by the experimentally discovered inverse sandwich D6h Ta2B6 and spherical trihedral D3h La3B18− and based on extensive first-principles theory calculations, we predict herein the structural transition from perfect di-metal-doped inverse sandwich D7h Ta2B7+ (1) and D8h Ta2B8 (2) to tri-metal-doped spherical trihedral D3h Ta3B12− (3). As the smallest metallo-borospherene reported to date, Ta3B12− (3) contains three octa-coordinate Ta atoms as integral parts of the cage surface coordinated in three equivalent η8-B8 rings which share two eclipsed equilateral B3 triangles on the top and bottom interconnected by three B2 units on the waist. Detailed orbital and bonding analyses indicate that both Ta2B7+ (1) and Ta2B8 (2) possess σ + π dual aromaticity, while Ta3B12− (3) is σ + π + δ triply aromatic in nature. The IR, Raman, and UV-vis or photoelectron spectra of the concerned species are computationally simulated to facilitate their future spectroscopic characterizations.
Structural transition from inverse sandwich Ta2B7+ (1) and Ta2B8 (2) with σ + π dual aromaticity to the smallest metallo-borospherene D3h Ta3B12− (3) which is σ + π + δ triply aromatic in nature.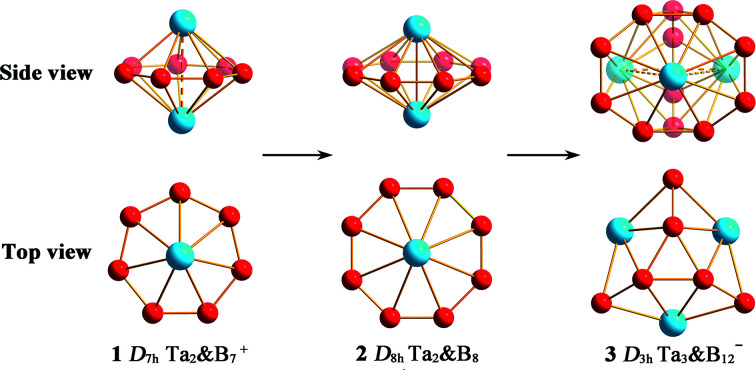
1. Introduction
Boron exhibits strong propensity to form multicentre-two-electron bonds (mc-2e bonds) in both polyhedral molecules and bulk allotropes due to its prototypical electron-deficiency.1–4 Joint photoelectron (PE) spectroscopy experimental and first-principles theory investigations in the past two decades have unveiled a rich landscape for Bn−/0 boron nanoclusters from planar or quasi-planar structures (n = 3–38, 41–42) to cage-like borospherenes (n = 39, 40).3–7 Cage-like D2d B40−/0 are the first borospherenes discovered in 2014,5 while C3/C2 B39− are the first axially chiral borospherenes confirmed in experiments as the global minima (GM) of the Bn− monoanions.6 These discoveries mark the onset of borospherene chemistry parallel to fullerene chemistry. The borospherene family has been systematically expanded by our group at first-principles theory levels to the cage-like Bnq series in different charge states (n = 36–42, q = n–40) which all possess twelve delocalized π bonds on the surface and follow the universal σ + π double delocalization bonding pattern.5–10 Sea-shell-like C2 B28−/0 and Cs B29− were later observed as minor isomers of the monoanions in PES experiments11,12 and sea-shell-like Cs B29+, C2 B31+, C2 B32, C2 B34, C2 B35+, and cage-like Cs B39+ have also been predicted recently in theory.13–16
Transition-metal (TM)-doping induces dramatic structural changes and leads to earlier planar → tubular → spherical structural transitions in boron clusters due to effective TM–B coordination interactions, as evidenced by the experimentally observed pyramidal C8v Ta©B8−,17Cs Ta©B9−,18 and perfect planar D10h Ta©B10− which has the highest coordination number of CN = 10 in planar species19 and the theoretically predicted half-sandwich TaB12−.20 A family of transition-metal-centred double-ring tubular boron complexes in staggered motifs were recently observed in experiments, including D8d Co@B16−,21D9d Rh@B18−,22 and Cs Ta@B20−,23 with Cs Ta@B20− (B2–[Ta@B18]−) behaving like a tubular molecular rotor at 900 K facilitated by prototypical multicentre fluxional bonds (FBs) which form and break constantly.24 A series of perfect di-metal-doped inverse sandwich complexes have also been observed in PE experiments, including D6h Ta2B6−/0,25D8h La2B8, and D8h Pr2B8.26 Our group recently reported the smallest core-shell-like tubular molecular rotor C2h La2[B2@B18] which contains a B2 core rotating inside a B18 tube almost freely.27 The first experimentally observed tri-metal-doped inverse triple-decker C2v La3B14− exhibits a tilted La–B8–La–B8–La triple-decker structure with two conjoined η8-B8 rings sharing a B–B unit on one edge.28 With increasing cluster size, the first perfect spherical trihedral metallo-borospherenes D3h Ln3B18− (Ln = La, Tb) were very recently discovered in a joint PE experimental and first-principles theory investigation.29 These metallo-borospherenes represent a new class of unusual geometry with tunable magnetic or catalytic properties, with three deca-coordinate Ln centres as integral parts of the cage surface coordinated in three equivalent η10-B10 decagons which share two eclipsed triangular B6 units interconnected by three B2 units. Metallo-borospherenes were previously proposed in theory for MB40 (M = Be, Mg) and NinB40 (n = 1–4) which contain hepta-coordinate metal centres on the cage surface of B40, with the corresponding metallo-borophenes with hepta-coordinate metal centres as precursors.30,31 However, it remains unknown at current stage what is the possible smallest size of metallo-borospherenes and if such coordination-stabilized metallo-borospherenes can be characterized in experiments.
Based on extensive first-principles theory calculations, we predict in this work the possibility of the perfect di-TM-doped inverse sandwich D7h Ta2B7+ (1) and D8h Ta2B8 (2) and, more importantly, the smallest tri-TM-doped cage-like metallo-borospherene D3h Ta3B12− (3) which contains three octa-coordinate Ta centres as integral parts of the cage surface coordinated in three equivalent η8-B8 octagons that share two equilateral B3 triangles interconnected by three B2 units. Detailed analyses indicate that both Ta2B7+ (1) and Ta2B8 (2) are σ + π dually aromatic in nature, while Ta3B12− (3) is the first transition-metal-doped boron complex reported to date with σ + π + δ triple aromaticity.
2. Theoretical procedure
Extensive global minimum (GM) searches were performed on Ta2B7+, Ta2B8, and Ta3B12− using the Tsinghua Global Minimum (TGMin) package32,33 based on a constraint Basin-Hopping algorithm,34 with more than 2000 singlet or triplet stationary points explored for each cluster at PBE/DZVP level.35 Low-lying isomers were then fully optimized at the PBE0 (36) level with the 6-311+G* basis set37 for B and Stuttgart relativistic small-core pseudopotential38,39 for Ta using the Gaussian 16 program suite,40 with vibrational frequencies checked to make sure that all isomers reported are true minima. The 15 lowest-lying isomers were subsequently fully re-optimized at both PBE0 and BP86 (ref. 41 and 42) levels with the basis sets of aug-cc-pVTZ for B43,44 and Stuttgart+2f1g for Ta. Relative energies for the four lowest-lying isomers were further refined using the more accurate coupled cluster method with triple excitations CCSD(T)45–47 implemented in Gaussian 16 with the same basis sets. Natural bonding orbital (NBO) analyses were performed using the NBO 6.0 program48 and detailed bonding analyses carried out utilizing the adaptive natural density partitioning (AdNDP) approach.49,50 Molecular dynamics (MD) simulations were performed on Ta2B7+ (1), Ta2B8 (2), and Ta3B12− (3) for 30 ps using the CP2K software suite at different temperatures.51 The anisotropy of the current-induced density (ACID) analysis52 was realized using the ACID code, with the ring-current maps generated using POV-Ray 3.7.53 The iso-chemical shielding surfaces (ICSSs)54,55 were generated with the Multiwfn 3.7 code.56 The UV-vis and PES spectra were simulated using the time-dependent TD-DFT-PBE0 approach.57
3. Results and discussions
3.1. Structures and stabilities
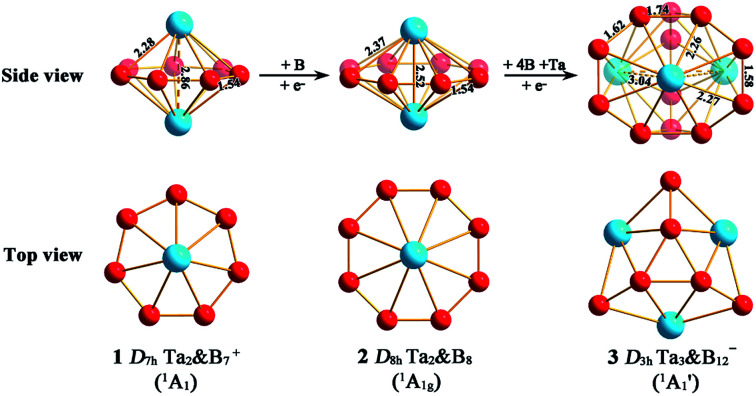
We start from Ta2B7+, the smallest di-metal-doped Ta–B complex concerned in this work. Extensive GM searches indicate that inverse sandwich D7h Ta2B7+ (1, 1A1) is the deep-lying GM of the monocation which lies 1.58 eV lower than the second lowest-lying isomer C2v Ta2B7+ (1A1) at CCSD(T) level (Fig. S1†), with the large HOMO–LUMO gap of ΔEgap = 3.77 eV at PBE0. The monocation contains a perfect B7 ring sandwiched between two Ta atoms along the C7 molecular axis at the two ends (similar to the experimentally observed inverse sandwich D6h Ta2B6 which has a perfect B6 ring sandwiched between two Ta atoms24), with the B–B bond length of rB–B = 1.54 Å, Ta–B distance of rTa–B = 2.28 Å, and Ta–Ta distance of rTa–Ta = 2.86 Å (which is obviously larger than the proposed Ta–Ta single bond length of 2.46 Å58). With one more B atom added in, the perfect inverse sandwich D8h Ta2B8 (2,1A1g) is achieved which is the deep-lying GM of the neutral lying 0.62 eV lower in energy than the second lowest-lying isomer Cs Ta2B8 (1A′) at CCSD(T) (Fig. S2†). It encompasses a perfect B8 ring sandwiched between two Ta atoms along the C8 molecular axis at the two ends, with the HOMO–LUMO gap of ΔEgap = 2.15 eV at PBE0. With a B8 octagon as the ligand, the Ta–Ta distance in Ta2B8 (2) is effectively shortened to rTa–Ta = 2.52 Å which is close to the proposed average Ta–Ta single bond length.58 The highly stable inverse sandwich Ta2B7+ (1) and Ta2B8 (2) may serve as building blocks to form tri-metal-doped Ta–B complexes, similar to the situation in the experimentally observed triple-decker C2v La3B14− (28) and spherical trihedral D3h La3B18−.29
Following the direction, we obtained the lowest-lying C2v Ta3B10+ (1A1) for Ta3B10+, Cs Ta3B11− (1A′) for Ta3B11−, and Cs Ta3B11− (2A′) for Ta3B11− which all possess incomplete spherical-trihedral structures with one edge broken (Fig. S3†). The smallest perfect spherical trihedron was achieved at D3h Ta3B12− (3, 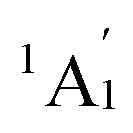 ) which, as the GM of the monoanion, lies 0.24 eV lower than the second lowest-lying C2v Ta3B12− (1A1) and 1.06 eV lower than the third lowest-lying Cs Ta3B12− (1A′) (which both belong to metallo-borospherenes) at the most reliable CCSD(T) level (Fig. S4†). As shown in Fig. 1, Ta3B12− (3) contains three equivalent octa-coordinate Ta centres as integral parts of the cage surface coordinated in three equivalent η8-B8 rings which share two eclipsed equilateral B3 triangles at the top and bottom interconnected by three B2 units on the waist. It has the calculated B–B bond lengths of rB–B = 1.58–1.74 Å, Ta–B coordination distances of rTa–B = 2.26–2.27 Å, and elongated Ta–Ta distances of rTa–Ta = 3.04 Å, respectively, with the large HOMO(e′′)–LOMO(e′) gap of ΔEgap = 2.50 eV at PBE0 which is comparable with the corresponding value of 2.70 eV calculated for the experimentally observed D3h La3B18− (29) at the same theoretical level. Ta3B12− (3) can be constructed from Ta2B8 (2) by adding one B4 edge (
B–B–B–B
) perpendicular to the B8 ring in the front and one Ta atom coordinated to the newly formed B8 ring, forming three interconnected Ta2B8 inverse sandwiches around the C3 main molecular axis (Fig. 1). In comparison with D3h Ln3B18− (Ln = La, Tb) which possess a perfect cage-like D3h B18 ligand with three equivalent η10-B10 decagons sharing two eclipsed B6 triangles at the top and bottom interconnected by three B2 units on the waist,29 Ta3B12− (3) has a perfect cage-like D3h B12 ligand with three equivalent η8-B8 octagons sharing two eclipsed B3 triangles at the top and bottom interconnected by three B2 units on the waist. Ta3B12− (3) has the same symmetry (D3h) as Ln3B18−, but smaller in size with six less B atoms in the ligand. Such a structural change can be understood based on the fact that Ta ([Xe]5d36s2) has a smaller atomic radius (1.46 Å) than that (1.83 Å) of La ([Xe]5d16s2),59 but possesses two more 5d valence electrons than the latter. The Ta centres appear to have the right atomic radii and electronic configurations to match the D3h B12 ligand both electronically and geometrically. Ta3B12− (3) is therefore the smallest metallo-borospherene reported to date. Perfect spherical trihedral D3h Nb3B12− and D3h V3B12− also appear to be true minima of the systems at both PBE0 and BP86 levels (Fig. S5†), with the HOMO–LUMO gaps of ΔEgap = 2.59 and 2.67 eV at PBE0, respectively.
) which, as the GM of the monoanion, lies 0.24 eV lower than the second lowest-lying C2v Ta3B12− (1A1) and 1.06 eV lower than the third lowest-lying Cs Ta3B12− (1A′) (which both belong to metallo-borospherenes) at the most reliable CCSD(T) level (Fig. S4†). As shown in Fig. 1, Ta3B12− (3) contains three equivalent octa-coordinate Ta centres as integral parts of the cage surface coordinated in three equivalent η8-B8 rings which share two eclipsed equilateral B3 triangles at the top and bottom interconnected by three B2 units on the waist. It has the calculated B–B bond lengths of rB–B = 1.58–1.74 Å, Ta–B coordination distances of rTa–B = 2.26–2.27 Å, and elongated Ta–Ta distances of rTa–Ta = 3.04 Å, respectively, with the large HOMO(e′′)–LOMO(e′) gap of ΔEgap = 2.50 eV at PBE0 which is comparable with the corresponding value of 2.70 eV calculated for the experimentally observed D3h La3B18− (29) at the same theoretical level. Ta3B12− (3) can be constructed from Ta2B8 (2) by adding one B4 edge (
B–B–B–B
) perpendicular to the B8 ring in the front and one Ta atom coordinated to the newly formed B8 ring, forming three interconnected Ta2B8 inverse sandwiches around the C3 main molecular axis (Fig. 1). In comparison with D3h Ln3B18− (Ln = La, Tb) which possess a perfect cage-like D3h B18 ligand with three equivalent η10-B10 decagons sharing two eclipsed B6 triangles at the top and bottom interconnected by three B2 units on the waist,29 Ta3B12− (3) has a perfect cage-like D3h B12 ligand with three equivalent η8-B8 octagons sharing two eclipsed B3 triangles at the top and bottom interconnected by three B2 units on the waist. Ta3B12− (3) has the same symmetry (D3h) as Ln3B18−, but smaller in size with six less B atoms in the ligand. Such a structural change can be understood based on the fact that Ta ([Xe]5d36s2) has a smaller atomic radius (1.46 Å) than that (1.83 Å) of La ([Xe]5d16s2),59 but possesses two more 5d valence electrons than the latter. The Ta centres appear to have the right atomic radii and electronic configurations to match the D3h B12 ligand both electronically and geometrically. Ta3B12− (3) is therefore the smallest metallo-borospherene reported to date. Perfect spherical trihedral D3h Nb3B12− and D3h V3B12− also appear to be true minima of the systems at both PBE0 and BP86 levels (Fig. S5†), with the HOMO–LUMO gaps of ΔEgap = 2.59 and 2.67 eV at PBE0, respectively.
Fig. 1. Optimized structures of D7h Ta2B7+ (1), D8h Ta2B8 (2), and D3h Ta3B12− (3) at PBE0//B/aug-cc-pVTZ/Ta/Stuttgart+2f1g level, with bond lengths indicated in Å.
Extensive MD simulations (Fig. S6†) indicate that Ta2B7+ (1), Ta2B8 (2), and Ta3B12− (3) are dynamically stable at 1200 K, 700 K, and 1200 K, with the small calculated average root-mean-square-deviations of RMSD = 0.11, 0.10, and 0.11 Å and maximum bond length deviations of MAXD = 0.27, 0.24, and 0.29 Å, respectively. No high-lying isomers were observed during the MD simulation. Ta–B complexes with larger HOMO–LUMO energy gaps appear to be dynamically more stable than the ones with narrower energy gaps.
3.2. Natural orbital and bonding analyses
The high stabilities of these high-symmetry complexes originate from their unique electronic structures and bonding patterns. Detailed natural bonding orbital (NBO) analyses show that the Ta centres in Ta2B7+ (1), Ta2B8 (2), and Ta3B12− (3) possess the electronic configurations of Ta [Xe]6s0.215d3.46, Ta [Xe]6s0.225d3.64, and Ta [Xe]6s0.245d3.72, natural atomic charges of qTa = +1.34|e|, +1.12|e| and +1.01|e|, and total Wiberg bond indexes of WBITa = 4.85, 4.80, and 5.07, respectively, indicating that each Ta centre in these complexes donates its 6s2 electrons almost completely to the Bn ligand (n = 7, 8, 12), while, in return, accepts roughly one electron in its partially filled 5d orbitals from the Bn ligands via p → d back-donations. The formations of effective Ta–B coordination interactions in 1–3 are strongly supported by the calculated Ta–B bond orders of WBITa–B = 0.59, 0.40, and 0.50–0.53 (Ta–B interactions within TaB7 or TaB8 pyramids) which appear to be systematically higher than the typical Cr–C coordination bond orders of WBICr–C = 0.34 in D6h Cr(C6H6)2. As mentioned above, a Ta centre in Ta3B12− (3) has the total bond order of WBITa = 5.07 which is also obviously higher than the corresponding value of WBICr = 4.12 calculated for Cr in D6h Cr(C6H6)2.
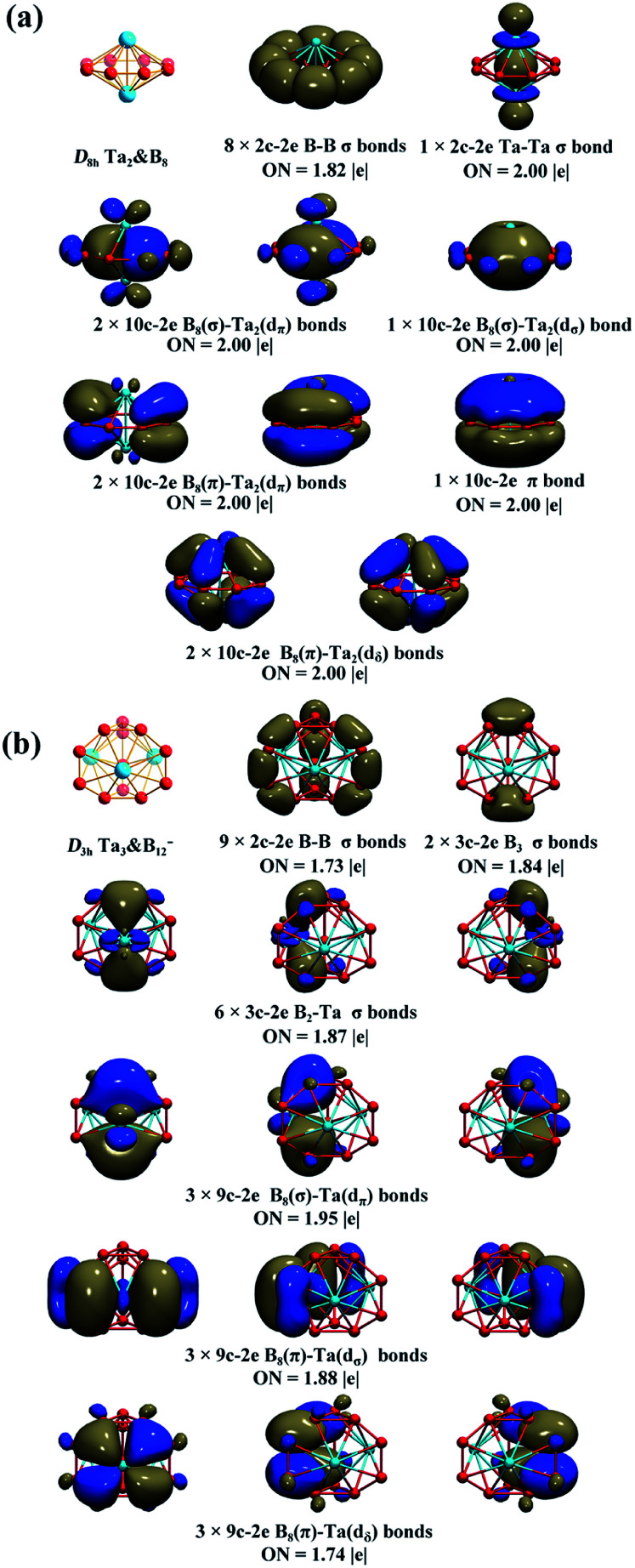
Detailed AdNDP bonding analyses unveil both the localized and delocalized bonds of the concerned systems. As shown in Fig. 2a, Ta2B8 (2) possesses 8 2c–2e B–B σ bonds on the periphery of the η8-B8 ligand with the occupation numbers of ON = 1.82|e| and 1 2c–2e Ta–Ta σ bond between the two Ta centres with ON = 2.00|e| in the first row. The remaining 16 valence electrons form 8 totally delocalized 10c–2e coordination bonds between the η8-B8 ligand and two Ta coordination centres with ON = 2.00|e|, including 3 10c–2e σ bonds in the second row, 3 10c–2e π bonds in the third row, and 2 10c–2e (p–d) δ bonding interactions in the fourth row. Both the delocalized 6e σ-system and delocalized 6e π-system match the 4n + 2 aromatic rule (n = 1) and together they render σ + π dual aromaticity to Ta2B8 (2). Similarly, both the experimentally observed D6h Ta2B6 (ref. 25) and D7h Ta2B7+ (1) are σ + π doubly aromatic in nature, as clearly indicated in their canonical molecular orbitals (CMOs) depicted in Fig. S7.†
Fig. 2. AdNDP bonding patterns of (a) D8h Ta2B8 (2) and (b) D3h Ta3B12− (3), with the occupation numbers (ON) indicated.
The AdNDP bonding pattern of spherical trihedral Ta3B12− (3) (Fig. 2b) exhibits certain similarity with that of the inverse sandwich Ta2B8 (2), but it is more complex and intriguing. Ta3B12− (3) possesses 9 localized 2c–2e σ B–B bonds in the three B2 units and between the B2 units and the six apexes of the two B3 triangles and 2 equivalent 3c–2e σ bonds on the two B3 triangles at the top and bottom in the first row and 6 equivalent 3c–2e B2–Ta σ bonds between the three Ta atoms and the two B3 triangles at the top and bottom in the second row. The remaining 18 valence electrons form 9 delocalized 9c–2e bonds evenly distributed on three equivalent C2v TaB8 octagonal pyramids (which are similar to the experimentally observed C8v TaB8− octagonal pyramid17) around the C3 main molecular axis, including 3 equivalent 9c–2e B8(σ)–Ta(dπ) bonds in the third row, 3 equivalent 9c–2e B8(π)–Ta(dσ) bonds in the fourth row, and 3 equivalent B8(π)–Ta(dδ) bonds in the fifth row. Each Ta&B8 octagonal pyramid thus possesses 1 9c–2e B8(σ)–Ta(dπ) bond, 1 9c–2e B8(π)–Ta(dσ) bond, and 1 B8(π)–Ta(dδ) bond. Overall, the Ta3&B12− (3) spherical trihedron has 3 equivalent (d–p)σ bonds, 3 equivalent (d–p)π bonds, and 3 equivalent (d–p)δ bonds evenly distributed on three equivalent Ta&B8 octagonal pyramids around the C3 molecular axis, forming one delocalized 6e σ-system, one delocalized 6e π-system, and one delocalized 6e δ-system on the cage surface each matching the 4n + 2 rule (n = 1) independently. Such a delocalized bonding pattern renders σ + π + δ triple aromaticity to the smallest metallo-borospherene of Ta3B12− (3) which is a highly stable D3h spherical trihedron with 18 delocalized electrons evenly distributed on the cage surface.60
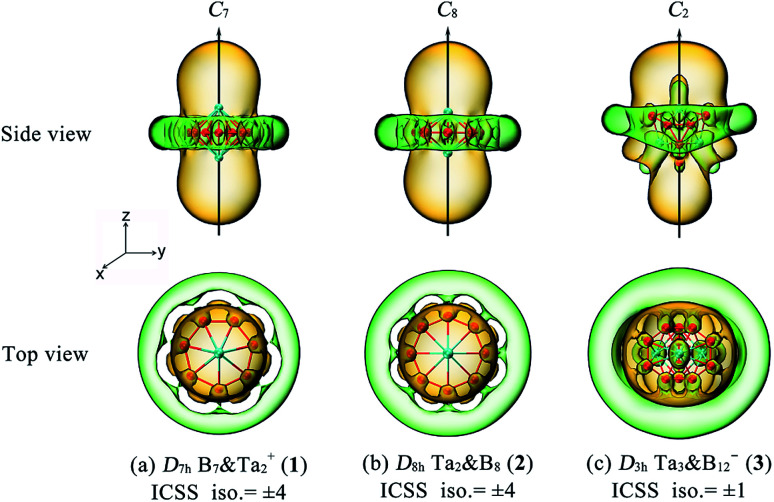
The aromatic nature of Ta2B7+ (1), Ta2B8 (2), and Ta3B12− (3) is further evidenced by their calculated nucleus-independent chemical shift (NICS) values of NICS = −110.5, −101.9, and −86.6 ppm at the geometrical centres, respectively. Based on the calculated NICS-ZZ components, Fig. 3 plots their iso-chemical-shielding surfaces54,55 with Z-axis parallel to the designated C7, C8, or C2 molecular axes to illuminate the chemical shielding around the TaB7 or TaB8 pyramids in these complexes. Obviously, the space inside the spherical trihedron surrounded by the delocalized Ta–Bn coordination bonds in horizontal direction or within about 1.0 Å above the Ta centres in vertical direction belong to chemical shielding regions (highlighted in yellow) with negative NICS-ZZ values, indicating that the aromatic contribution mainly comes from Ta(5d)–B(2p) coordination interactions between the Ta centres and Bn ligands around them (n = 7 or 8), while the chemical de-shielding areas (highlighted in green) with positive NICS values are located outside the Bn ring in horizontal direction. The ICSSs of these complexes appear to be analogous to that of the prototypical aromatic benzene.54–56
Fig. 3. Calculated iso-chemical shielding surfaces (ICSSs) of (a) Ta2B7+ (1), (b) Ta2B8 (2), and (c) Ta3B12− (3), with the corresponding NICS-ZZ components indicated. The C7 axis of Ta2B7+ (1), C8 axis of Ta2B8 (2), and C2 axis of Ta3B12− (3) are designated as z axis in vertical direction to compare the shielding effects around the TaBn pyramids (n = 7, 8). Yellow regions stand for chemical shielding areas, while green areas represent chemical de-shielding areas.
Fig. S8† depicts the corresponding ring current maps of Ta2B7+ (1), Ta2B8 (2), and Ta3B12− (3). Consistent magnetic responses occur in 1, 2, and 3 in an external magnetic field in the vertical direction parallel to the assigned molecular axes, irrespective of the electron type, similar to the situations in both benzene52,53 and double-ring tubular B20 (61) which are known to possess typical planar or tubular aromaticity. Such diatropic ring currents well support the aromatic nature of these Ta-doped boron complexes.
3.3. Simulated IR, Raman, and PE spectra of Ta3B12− (3)
We computationally simulate the IR, Raman, and UV-vis or PES spectra of Ta2B7+ (1), Ta2B8 (2), and Ta3B12− (3) at PBE0 level to facilitate their future spectral characterizations. PE measurements and infrared photodissociation (IR-PD) spectra in combination with first-principles theory calculations have proven to be powerful approaches in characterizing novel clusters in gas phases.3–7,17–28,62 As shown in Fig. 4, the high-symmetry Ta3B12− (3) exhibits relatively simple IR and Raman spectral patterns, with the major IR active peaks at 507 (e′), 559 (e′), 668 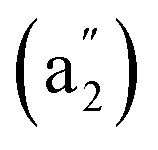 , and 881 (e′) cm−1 (Fig. 4a) and main Raman spectral features at 209
, and 881 (e′) cm−1 (Fig. 4a) and main Raman spectral features at 209 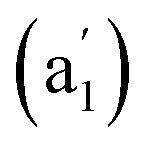 , 881 (e′), 998 (e′′), and 1201
, 881 (e′), 998 (e′′), and 1201 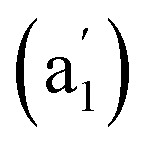 cm−1 (Fig. 4b), respectively. The first Raman active symmetrical vibrational mode
cm−1 (Fig. 4b), respectively. The first Raman active symmetrical vibrational mode 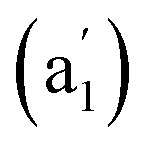 at 209 cm−1 corresponds to typical “radial breathing mode” (RBM) of the metallo-borospherene which may be used to characterize the hollow structures of single-walled boron nanoclusters in experiments.63
at 209 cm−1 corresponds to typical “radial breathing mode” (RBM) of the metallo-borospherene which may be used to characterize the hollow structures of single-walled boron nanoclusters in experiments.63
Fig. 4. Simulated (a) IR, (b) Raman, and (c) PES spectra of D3h Ta3B12− (3) at PBE0//B/aug-cc-pVTZ/Ta/Stuttgart+2f1g level.
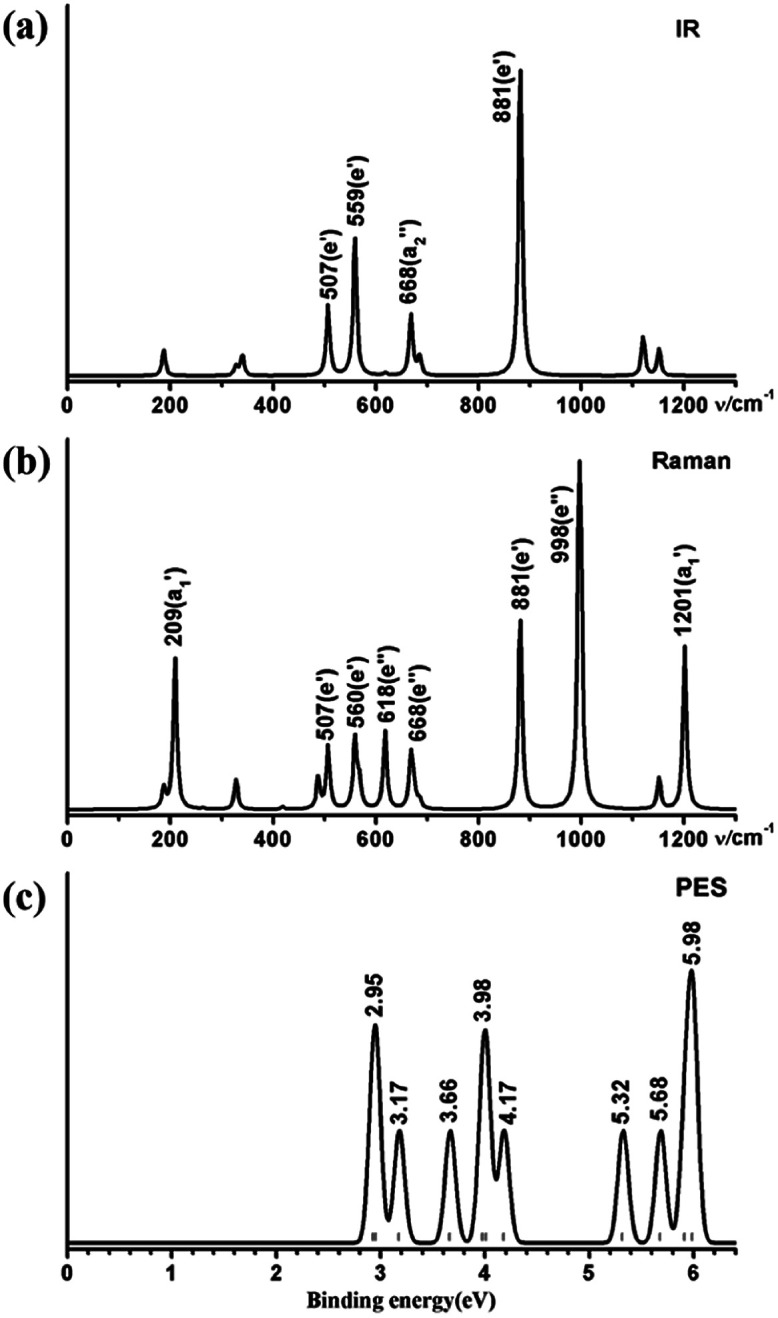
The calculated PE spectrum of Ta3B12− (3) in Fig. 4c exhibits major spectral features at 2.95 (2E′′), 3.17  , 3.66
, 3.66 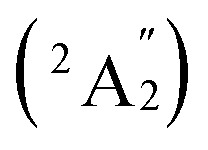 , 3.98 (2E′), 4.17
, 3.98 (2E′), 4.17 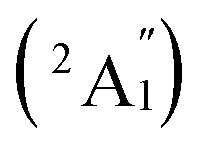 , 5.32 (2E′), 5.68 (2E′), and 5.98
, 5.32 (2E′), 5.68 (2E′), and 5.98 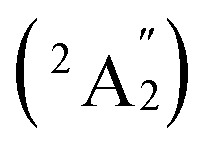 , respectively, corresponding to vertical electronic transitions from the ground state of the anion
, respectively, corresponding to vertical electronic transitions from the ground state of the anion 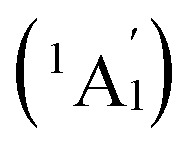 to the excited states of the neutral at the ground-state geometry of the anion. The open-shell neutral Ta3B12 has a slightly distorted C2v Ta3B12 (2A2) ground-state structure due to Jahn–Teller effect, with the calculated electron affinity of EA = 2.87 eV. The simulated IR, Raman, and UV-vis spectra of Ta2B7+ (1) and Ta2B8 (2) are depicted in Fig. S9.†
to the excited states of the neutral at the ground-state geometry of the anion. The open-shell neutral Ta3B12 has a slightly distorted C2v Ta3B12 (2A2) ground-state structure due to Jahn–Teller effect, with the calculated electron affinity of EA = 2.87 eV. The simulated IR, Raman, and UV-vis spectra of Ta2B7+ (1) and Ta2B8 (2) are depicted in Fig. S9.†
4. Conclusions
Extensive first-principles theory calculations performed in this work indicate a structural transition from perfect inverse sandwich D7h Ta2B7+ (1) and D8h Ta2B8 (2) to the smallest metallo-borospherene D3h Ta3B12− (3). As the first transition-metal-doped boron complex reported to date with σ + π + δ triple aromaticity, Ta3B12− (3) possesses three octa-coordinate Ta centres as integral parts of the cage surface coordinated in three equivalent η8-B8 octagons. The results obtained in this work suggest that a large family of coordination-stabilized multi-TM-doped TMmBn metallo-borospherenes with tunable magnetic and electronic properties may exist in experiments in which the transition metal dopants and Bn ligands match both geometrically and electronically.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
The work was supported by the National Natural Science Foundation of China (21720102006 and 21973057 to S.-D. Li).
Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05570k
Notes and references
- Lipscomb W. N. Science. 1977;196:1047. doi: 10.1126/science.196.4294.1047. [DOI] [PubMed] [Google Scholar]
- Cotton F. A., Wilkinson G., Murillo C. A., and Bochmann M., Advanced Inorganic Chemistry, Wiley, New York, 6th edn, 1999 [Google Scholar]
- Wang L. S. Int. Rev. Phys. Chem. 2016;35:69. [Google Scholar]
- Jian T. Chen X. N. Li S. D. Boldyrev A. I. Li J. Wang L. S. Chem. Soc. Rev. 2019;48:3550. doi: 10.1039/C9CS00233B. [DOI] [PubMed] [Google Scholar]
- Zhai H. J. Zhao Y. F. Li W. L. Chen Q. Bai H. Hu H. S. Piazza Z. A. Tian W. J. Lu H. G. Wu Y. B. Mu Y. W. Wei G. F. Liu Z. P. Li J. Li S. D. Wang L. S. Nat. Chem. 2014;6:727. doi: 10.1038/nchem.1999. [DOI] [PubMed] [Google Scholar]
- Chen Q. Li W. L. Zhao Y. F. Zhang S. Y. Hu H. S. Bai H. Li H. R. Tian W. J. Lu H. G. Zhai H. J. Li S. D. Li J. Wang L. S. ACS Nano. 2015;9:754. doi: 10.1021/nn506262c. [DOI] [PubMed] [Google Scholar]
- Chen Q. Zhang S. Y. Bai H. Tian W. J. Gao T. Li H. R. Miao C. Q. Mu Y. W. Lu H. G. Zhai H. J. Li S. D. Angew. Chem., Int. Ed. 2015;54:8160. doi: 10.1002/anie.201501588. [DOI] [PubMed] [Google Scholar]
- Chen Q. Li H. R. Miao C. Q. Wang Y. J. Lu H. G. Mu Y. W. Ren G. M. Zhai H. J. Li S. D. Phys. Chem. Chem. Phys. 2016;18:11610. doi: 10.1039/C5CP06169E. [DOI] [PubMed] [Google Scholar]
- Tian W. J. Chen Q. Li H. R. Yan M. Mu Y. W. Lu H. G. Zhai H. J. Li S. D. Phys. Chem. Chem. Phys. 2016;18:9922. doi: 10.1039/C6CP01279E. [DOI] [PubMed] [Google Scholar]
- Chen Q. Li H. R. Tian W. J. Lu H. G. Zhai H. J. Li S. D. Phys. Chem. Chem. Phys. 2016;18:14186. doi: 10.1039/C6CP02369J. [DOI] [PubMed] [Google Scholar]
- Wang Y. J. Zhao Y. F. Li W. L. Jian T. Chen Q. You X. R. Ou T. Zhao X. Y. Zhai H. J. Li S. D. Li J. Wang L. S. J. Chem. Phys. 2016;144:064307. doi: 10.1063/1.4941380. [DOI] [PubMed] [Google Scholar]
- Li H. R. Jian T. Li W. L. Miao C. Q. Wang Y. J. Chen Q. Luo X. M. Wang K. Zhai H. J. Li S. D. Wang L. S. Phys. Chem. Chem. Phys. 2016;18:29147. doi: 10.1039/C6CP05420J. [DOI] [PubMed] [Google Scholar]
- Pei L. Li H. R. Yan M. Chen Q. Mu Y. W. Lu H. G. Wu Y. B. Li S. D. Phys. Chem. Chem. Phys. 2018;20:15330. doi: 10.1039/C8CP01078A. [DOI] [PubMed] [Google Scholar]
- Pei L. Yan M. Zhao X. Y. Mu Y. W. Lu H. G. Wu Y. B. Li S. D. RSC Adv. 2020;10:10129. doi: 10.1039/D0RA01087A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H. Chen Q. Li H. R. Zhao X. Y. Tian X. X. Mu Y. W. Lu H. G. Li S. D. Phys. Chem. Chem. Phys. 2018;20:15344. doi: 10.1039/C8CP01769G. [DOI] [PubMed] [Google Scholar]
- Zhao X. Y. Chen Q. Li H. R. Mu Y. W. Lu H. G. Li S. D. Phys. Chem. Chem. Phys. 2017;19:10998. doi: 10.1039/C7CP00725F. [DOI] [PubMed] [Google Scholar]
- Li W. L. Ivanov A. S. Federič J. Romanescu C. Černušák I. Boldyrev A. I. Wang L. S. J. Chem. Phys. 2013;139:104312. doi: 10.1063/1.4820401. [DOI] [PubMed] [Google Scholar]
- Romanescu C. Galeev T. R. Li W. L. Boldyrev A. I. Wang L. S. J. Chem. Phys. 2013;138:134315. doi: 10.1063/1.4798935. [DOI] [PubMed] [Google Scholar]
- Galeev T. R. Romanescu C. Li W. L. Wang L. S. Boldyrev A. I. Angew. Chem., Int. Ed. 2012;51:2101. doi: 10.1002/anie.201107880. [DOI] [PubMed] [Google Scholar]
- Chen B. L. Sun W. G. Kuang X. Y. Lu C. Xia X. X. Shi H. X. Maroulis G. Inorg. Chem. 2018;57:343. doi: 10.1021/acs.inorgchem.7b02585. [DOI] [PubMed] [Google Scholar]
- Popov I. A. Jian T. Lopez G. V. Boldyrev A. I. Wang L. S. Nat. Commun. 2015;6:8654. doi: 10.1038/ncomms9654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jian T. Li W. L. Chen X. Chen T. T. Lopez G. V. Li J. Wang L. S. Chem. Sci. 2016;7:7020. doi: 10.1039/C6SC02623K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W. L. Jian T. Chen X. Li H. R. Chen T. T. Luo X. M. Li S. D. Li J. Wang L. S. Chem. Commun. 2017;53:1587. doi: 10.1039/C6CC09570D. [DOI] [PubMed] [Google Scholar]
- Yan M. Li H. R. Zhao X. Y. Lu X. Q. Mu Y. W. Lu H. G. Li S. D. J. Comput. Chem. 2019;40:966. doi: 10.1002/jcc.25728. [DOI] [PubMed] [Google Scholar]
- Li W. L. Xie L. Jian T. Romanescu C. Huang X. Wang L. S. Angew. Chem. 2014;126:1312. doi: 10.1002/ange.201309469. [DOI] [PubMed] [Google Scholar]
- Li W. L. Chen T. T. Xing D. H. Chen X. Li J. Wang L. S. Proc. Natl. Acad. Sci. U. S. A. 2018;115:E6972. doi: 10.1073/pnas.1806476115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu X. Q. Chen Q. Tian X. X. Mu Y. W. Lu H. G. Li S. D. Nanoscale. 2019;11:21311. doi: 10.1039/C9NR07284E. [DOI] [PubMed] [Google Scholar]
- Chen T. T. Li W. L. Chen W. J. Li J. Wang L. S. Chem. Commun. 2019;55:7864. doi: 10.1039/C9CC03807H. [DOI] [PubMed] [Google Scholar]
- Chen T. T. Li W. L. Chen W. J. Yu X. H. Dong X. R. Li J. Wang L. S. Nat. Commun. 2020;11:2766. doi: 10.1038/s41467-020-16532-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai H. Chen Q. Zhai H. J. Li S. D. Angew. Chem., Int. Ed. 2015;54:941. doi: 10.1002/anie.201408738. [DOI] [PubMed] [Google Scholar]
- Li H. R. Tian X. X. Luo X. M. Yan M. Mu Y. W. Lu H. G. Li S. D. Sci. Rep. 2017;7:5701. doi: 10.1038/s41598-017-06039-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y. F. Chen X. Li J. Nano Res. 2017;10:3407. doi: 10.1007/s12274-017-1553-z. [DOI] [Google Scholar]
- Chen X. Zhao Y. F. Wang L. S. Li J. Comput. Theor. Chem. 2017;1107:57. doi: 10.1016/j.comptc.2016.12.028. [DOI] [Google Scholar]
- Wales D. J. Doye J. P. J. Phys. Chem. A. 1997;101:5111. doi: 10.1021/jp970984n. [DOI] [Google Scholar]
- Perdew J. P. Burke K. Ernzerhof M. Phys. Rev. Lett. 1996;77:3865. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Adamo C. Barone V. J. Chem. Phys. 1999;110:6158. doi: 10.1063/1.478522. [DOI] [Google Scholar]
- Feller D. J. Comput. Chem. 1996;17:1571. doi: 10.1002/(SICI)1096-987X(199610)17:13<1571::AID-JCC9>3.0.CO;2-P. [DOI] [Google Scholar]
- Andrae D. Häußermann U. Dolg M. Stoll H. Preuß H. Theor. Chim. Acta. 1990;77:123. doi: 10.1007/BF01114537. [DOI] [Google Scholar]
- Martin J. M. L. Sundermann A. J. Chem. Phys. 2001;114:3408. doi: 10.1063/1.1337864. [DOI] [Google Scholar]
- Frisch M. J., et al., Gaussian 16, Revision A.03, Gaussian Inc., Wallingford, CT, 2016 [Google Scholar]
- Becke A. D. Phys. Rev. A: At., Mol., Opt. Phys. 1988;38:3098. doi: 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Phys. Rev. B: Condens. Matter Mater. Phys. 1986;33:8822. doi: 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]
- Dunning Jr T. H. J. Chem. Phys. 1989;90:1007. doi: 10.1063/1.456153. [DOI] [Google Scholar]
- Kendall R. A. Dunning Jr T. H. Harrison R. J. J. Chem. Phys. 1992;96:6796. doi: 10.1063/1.462569. [DOI] [Google Scholar]
- Čížek J. Adv. Chem. Phys. 1969;14:35. [Google Scholar]
- Purvis G. D. Bartlett R. J. J. Chem. Phys. 1982;76:1910. doi: 10.1063/1.443164. [DOI] [Google Scholar]
- Raghavachari K. Trucks G. W. Pople J. A. Head-Gordon M. Chem. Phys. Lett. 1989;157:479. doi: 10.1016/S0009-2614(89)87395-6. [DOI] [Google Scholar]
- Glendening P. E. D., Badenhoop J. K., Reed A. E., Carpenter J. E., Bohmann J. A., Morales C. M., Landis C. R. and Weinhold F., NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013 [Google Scholar]
- Zubarev D. Y. Boldyrev A. I. Phys. Chem. Chem. Phys. 2008;10:5207. doi: 10.1039/B804083D. [DOI] [PubMed] [Google Scholar]
- Tkachenko N. V. Boldyrev A. I. Phys. Chem. Chem. Phys. 2019;21:9590. doi: 10.1039/C9CP00379G. [DOI] [PubMed] [Google Scholar]
- VandeVondele J. Krack M. Mohamed F. Parrinello M. Chassaing T. Hutter J. Comput. Phys. Commun. 2005;167:103. doi: 10.1016/j.cpc.2004.12.014. [DOI] [Google Scholar]
- Geuenich D. Hess K. Köhler F. Herges R. Chem. Rev. 2005;105:3758. doi: 10.1021/cr0300901. [DOI] [PubMed] [Google Scholar]
- Povray, Persistence of vision raytracer, POV-Ray 3.7, http://www.povray.org/
- Klod S. Kleinpeter E. J. Chem. Soc., Perkin Trans. 2. 2001;2:1893. [Google Scholar]
- Kleinpeter E. Klod S. Koch A. J. Mol. Struct. 2007;811:45. doi: 10.1016/j.theochem.2007.02.049. [DOI] [Google Scholar]
- Lu T. Chen F. W. J. Comput. Chem. 2012;33:580. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- Bauernschmitt R. Ahlrichs R. Chem. Phys. Lett. 1996;256:454. doi: 10.1016/0009-2614(96)00440-X. [DOI] [Google Scholar]
- Pyykkö P. Atsumi M. Chem.–Eur. J. 2009;15:186. doi: 10.1002/chem.200800987. [DOI] [PubMed] [Google Scholar]
- Dean J. A., Lange's Hand book of Chemistry, McGraw-Hill Book Co., 1999, Table 4.6 [Google Scholar]
- Tlahuice-Flores A. Muñoz-Castro A. Int. J. Quantum Chem. 2019;119:e25756. doi: 10.1002/qua.25756. [DOI] [Google Scholar]
- Johansson M. P. J. Phys. Chem. C. 2009;113:524. doi: 10.1021/jp8087918. [DOI] [Google Scholar]
- Wang G. J. Zhou M. F. Goettel J. T. Schrobilgen G. J. Su J. Li J. Schlöder T. Riedel S. Nature. 2014;514:475. doi: 10.1038/nature13795. [DOI] [PubMed] [Google Scholar]
- Ciuparu D. Klie R. F. Zhu Y. Pfefferle A. L. J. Phys. Chem. B. 2004;108:3967. doi: 10.1021/jp049301b. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.