Spin-triplet superconductivity from excitonic effect in doped insulators

Significance

We present a mechanism for unconventional superconductivity in doped band insulators, where short-ranged pairing interaction arises from Coulomb repulsion due to virtual interband or excitonic processes. Remarkably, electron pairing is found upon infinitesimal doping, giving rise to Bose–Einstein condensate (BEC)–Bardeen–Cooper–Schrieffer (BCS) crossover at low density. Our theory explains puzzling behaviors of superconductivity and predicts spin-triplet pairing in electron-doped ZrNCl and WTe₂.

Abstract

Despite being of fundamental importance and potential interest for topological quantum computing, spin-triplet superconductors remain rare in solid state materials after decades of research. In this work, we present a three-particle mechanism for spin-triplet superconductivity in multiband systems, where an effective attraction between doped electrons is produced from the Coulomb repulsion via a virtual interband transition involving a third electron [V. Crépel, L. Fu, Sci. Adv. 7, eabh2233 (2021)]. Our theory is analytically controlled by an interband hybridization parameter and explicitly demonstrated in doped band insulators with the example of an extended Hubbard model. Our theory of exciton-mediated pairing reveals how, as a matter of principle, a two-particle bound state can arise from the strong electron repulsion upon doping, opening a viable path to Bose–Einstein condensate (BEC)–Bardeen–Cooper–Schrieffer (BCS) physics in solid state systems. In light of this theory, we propose that recently discovered dilute superconductors such as ZrNCl, WTe₂, and moiré materials can be spin-triplet and compare the expected consequences of our theory with experimental data.

Spin-triplet superconductors display a plethora of unconventional phenomena, including multicomponent order parameter, fractional vortices (1, 2), Majorana fermions (3), and topological boundary modes (4, 5). Further interest in spin-triplet superconductors is fueled by their prospect as a material platform for topological qubits (6–9). However, triplet superconductors are rare to find. Inspired by superfluid helium-3 (10), the search for triplet pairing has traditionally been focused on nearly ferromagnetic metals, such as Sr₂RuO₄ (11), UPt₃ (12), and UTe₂ (13, 14). In recent years, anisotropic spin-triplet pairing has also been discovered in superconducting doped topological insulators such as Cu_xBi₂Se₃ (15–18), where strong spin-orbit coupling plays an important role (19–22). While significant progress has been made, the pairing symmetry and pairing mechanism of these superconducting materials are not yet completely understood.

In this work, we introduce an electronic mechanism for spin-triplet superconductivity in doped insulators, where the pairing of doped electrons arises from interband electronic effects. By developing a controlled hybridization expansion, we show that an attractive interaction between two conduction electrons arises from virtual interband transition, as illustrated in Fig. 1A. Since this mechanism involves two electrons forming the pair and a third one undergoing a virtual interband transition, we dub it “three-particle mechanism” for superconductivity (23). Equivalently, we may view that the pairing of doped electrons is assisted by virtual excitons.

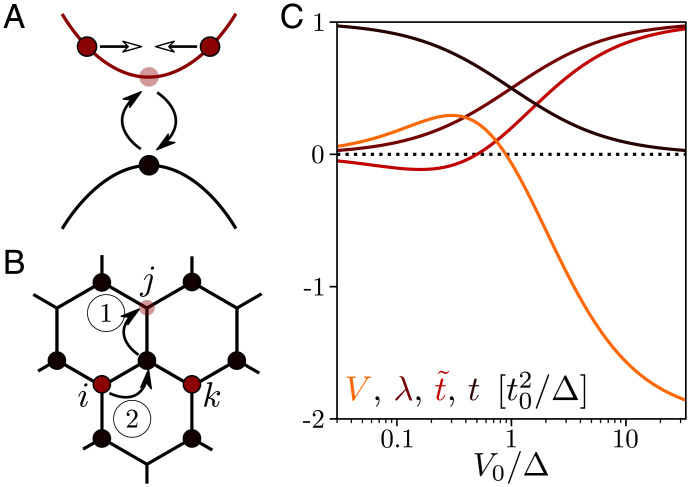
Fig. 1.

(A) Virtual interband transitions involving three electrons in the upper band mediate an effective pairing interaction between conduction electrons. (B) Second-order process of ${\mathcal{H}}_f$ corresponding to correlated hopping. Doubly occupied orbitals forming the band insulator are shown as black dots, and doped electrons are shown in red. (C) The hopping and interaction amplitudes of ${\mathcal{H}}_f$ as a function of the original lattice parameters $V_0/\mathrm{\Delta }$ for $U_B=4V_0$.

The idea of excitons as a replacement of phonon to mediate superconductivity has a long history (24–27). However, experimental evidence of exciton-mediated superconductivity remains elusive. A major challenge is that most proposals rely on metal layers on a separate excitonic medium, which often result in weak coupling between conduction electrons and virtual excitons. Moreover, theoretical works on this subject have only considered s-wave pairing, which is usually disfavored in electron systems with strong repulsive interaction. Last but not the least, the large energy scale of intermediate states involving interband excitations means that the induced interaction is nonretarded, in contrast to phonon-mediated pairing. Thus, new theoretical methods are needed to tackle the problem of superconductivity from repulsive interaction in multiband systems.

Our work solves the above problems and challenges. We study multiband systems that naturally host both excitons and conduction electrons, interacting strongly with each other by electrostatic forces. Using a two-band Hubbard model as an example, we show with exact solutions that virtual interband effects lead to spin-triplet pairing of two doped electrons in a band insulator. The spin-triplet electron pair naturally avoids the large Coulomb repulsion at short distance.

Since our hybridization expansion method is nonperturbative in the interaction strength, we obtain an asymptotically exact theory of strong-coupling superconductivity at low doping, without distractions from other competing states and without requiring any bosonic glue. Our theory provides a mechanism whereby superconductivity arises upon infinitesimal doping of a band insulator. It predicts a direct transition from a band insulator to a superconductor without single-particle gap closing and a Bose–Einstein condensate (BEC)–Bardeen–Cooper–Schrieffer (BCS) crossover as a function of doping concentration.

Our theory sheds light on unconventional superconductivity behaviors in doped band insulators. We shall focus on two materials: electron-doped ZrNCl and WTe₂, which both superconduct at very low doping. Remarkably, a BEC–BCS crossover has recently been observed in two-dimensional ZrNCl (28). In monolayer WTe₂, a direct insulator–superconductor transition was found under electrostatic gating (29, 30). We will compare our theoretical predictions of spin-triplet superconductivity with the experimental data on these dilute superconductors. In particular, we highlight the observed increase of T_c in WTe₂ under a small in-plane magnetic field as a strong evidence for spin-triplet superconductivity.

Illustrative Model

To illustrate the interband electronic mechanism for superconductivity, we consider a two-band Hubbard model on the honeycomb lattice with staggered potential on A/B sites and extended interactions. The Hamiltonian takes the form

$$\begin{array}{l}\mathcal{H}=-t_0{\displaystyle \sum _{\langle r,r\prime \rangle ,\sigma }(c_{r,\sigma }^{†}{c}_{r\prime ,\sigma }+hc)}+\frac{{\mathrm{\Delta }}_0}{2}\left[{\displaystyle \sum _{r\in B}{n}_r}-{\displaystyle \sum _{r\in A}{n}_r}\right]\\ +U_A{\displaystyle \sum _{r\in A}{n}_{r\uparrow }}{n}_{r\downarrow }+U_B{\displaystyle \sum _{r\in B}{n}_{r\uparrow }}{n}_{r\downarrow }+V_0{\displaystyle \sum _{\langle r,r\prime \rangle }{n}_r}{n}_{r\prime },\end{array}$$ [1]

where ${\mathrm{\Delta }}_0$ is the staggered sublattice potential, U_A and U_B are on-site interactions, and V₀ is the nearest-neighbor repulsion. We consider this two-band model at or slightly above the filling of n = 2 electrons per unit cell.

To controllably describe the effects of interband processes on doped charges, we will consider situations where the two sublattices or bands are weakly coupled. This is realized in the following two regimes, developed in Kinetic Energy Expansion and Interaction Expansion, respectively:

• •When $t_0=0$, the lower and upper bands of our model are formed by A and B sublattice states, respectively. A small tunneling amplitude $t_0\ll {\mathrm{\Delta }}_0$ induces weak hybridization between these sublattices/bands, which we treat as a perturbation to derive an effective model for doped electrons.
• •When interactions are small compared to the single particle band gap ${\mathrm{\Delta }}_0$, the two bands also weakly hybridize. This regime, often studied with standard many-body perturbation theory, extends our results to a wider and potentially more experimentally relevant range of parameters.

In both regimes, the same essential physics—attractive interaction induced by virtual interband processes, sketched in Fig. 1A—is at play, as highlighted by the consistency between the kinetic and interaction-based perturbative methods in their overlapping domain of validity $(t_0,V_0)\ll {\mathrm{\Delta }}_0$.

Kinetic Energy Expansion

Effective Dynamics of Charge Carriers.

For $\mathrm{\Delta }\equiv {\mathrm{\Delta }}_0-U_A+3V_0>0$ and $t_0=0$, the ground state of Eq. 1 at n = 2 is an insulator with all A sites doubly occupied and all B sites empty. This state remains insulating upon increasing t₀ while keeping $t_0\ll \mathrm{\Delta }$. In particular, it is adiabatically connected to the noninteracting band insulator obtained for $U_A=U_B=V_0=0$ if $t_0\ll {\mathrm{\Delta }}_0$. In this section, our goal is to extend the method pioneered in ref. 23 to our spinful model and to obtain an effective Hamiltonian ${\mathcal{H}}_f$ describing the dynamics of doped charges above the n = 2 insulating state, assuming $t_0\ll \mathrm{\Delta }$.

When $t_0=0$, the Pauli exclusion principle forces the $x\equiv n-2$ doped electrons to live on the B triangular lattice. It also prohibits direct tunneling onto doubly occupied A sites, such that ${\mathcal{H}}_f$ is composed of second-order tunneling processes, whose first step necessarily creates a hole on an A site (Fig. 1B). To account for all such processes, we perform a Schrieffer–Wolff transformation that integrates out high-energy degrees of freedom (31). This procedure, detailed in SI Appendix, section 1, gives

$$\begin{array}{l}{\mathcal{H}}_f=\hspace{0.17em}t{\displaystyle \sum _{\langle i,j\rangle ,\sigma }(f_{j,\sigma }^{†}{f}_{i,\sigma }+hc)}+U{\displaystyle \sum _i{n}_{i,\uparrow }}{n}_{i,\downarrow }+V{\displaystyle \sum _{\langle i,j\rangle }{n}_i}{n}_j\\ +\frac{\tilde{t}}{2}{\displaystyle \sum _{\langle i,j\rangle ,\sigma }(f_{j,\sigma }^{†}{f}_{i,\sigma }+hc)(n_i+n_j)}\\ +\lambda {\displaystyle \sum _{\mathit{ijk}\in △,\sigma }\left[f_{j,\sigma }^{†}{n}_k{f}_{i,\sigma }+P_{\mathit{ijk}}\right]},\end{array}$$ [2]

where the fermion operators f_i describe doped electrons on the triangular B lattice. Besides single-particle hopping (t), on-site, and nearest-neighbor interaction ($U,V$), this effective Hamiltonian contains two types of correlated hopping terms: In the first type, an electron hops between i and j when one of the two sites is already occupied by another electron of the opposite spin ($\tilde{t}$) or when their common neighbor k is occupied (λ). The second type—hereafter referred to as λ-hopping—acts on upper triangles $(\mathit{ijk}\in △)$ of the B lattice. Finally, P_ijk denotes all possible permutations of the vertices ijk. Our derivation also yields three-body interactions (SI Appendix, section 1), which we momentarily discard since their effect is negligible in the low-density limit.

The density–density interaction and correlated hopping terms between doped electrons arise because the bare interactions ($U_A,U_B,V_0$) affect the energy of intermediate excitonic states. For example, in the process leading to λ-hopping, shown in Fig. 1B, the presence of a charge at site k in the upper triangle ijk decreases the energy of the intermediate state in the electron tunneling event $f_{j,\sigma }^{†}{f}_{i,\sigma }$ from $\mathrm{\Delta }+V_0$ to Δ (32). The hopping amplitude accordingly increases from t to $t+\lambda$, with

$$t=\frac{t_0^2}{\mathrm{\Delta }+V_0},\hspace{1em}\lambda =\frac{t_0^2}{\mathrm{\Delta }}-\frac{t_0^2}{\mathrm{\Delta }+V_0}.$$ [3]

Similar considerations yield the other coefficients of ${\mathcal{H}}_f$ (SI Appendix, section 1) and give $(\tilde{t},V)\propto t_0^2/\mathrm{\Delta }$ and $U\simeq U_B$ when $U_B\gg t_0^2/\mathrm{\Delta }$. These parameters are plotted in Fig. 1C. The bandwidth $W=9t$ largely dominates the interactions scales $\tilde{t},\lambda ,V$ when $V_0\le \mathrm{\Delta }$, while the interaction dominate in the opposite regime $V_0\ge \mathrm{\Delta }$.

${\mathcal{H}}_f$ is exact up to second order in the hybridization parameter $t_0/\mathrm{\Delta }$ that governs the perturbative Schrieffer–Wolff transformation, holds at all dopings, and features interactions between doped electrons that are instantaneous on the time scale set by their kinetic energy t. Our derivation can be straightforwardly extended to account for longer-range hopping between B orbitals, allowing us to describe materials with a bandwidth larger than W, in which case doped electrons may be weakly interacting even for $V_0\ge \mathrm{\Delta }$. The effects of longer-range interactions can also be included in Schrieffer–Wolf transformation, as described in ref. 23.

It is important to note that our hybridization expansion only requires the dimensionless ratio $t_0/\mathrm{\Delta }$ to be small, which allows both the band gap ${\mathrm{\Delta }}_0$ and the hopping amplitude t₀ to be large. In such case, the bandwidth and interaction energies, which are on the order of $t_0^2/\mathrm{\Delta }$ (assuming $V_0\sim \mathrm{\Delta }$), can still be large in absolute unit.

Two-Particle Bound State.

Remarkably, ${\mathcal{H}}_f$ features an attractive interaction between conduction electrons forming a spin-triplet state. This effective attraction surprisingly emerges in the purely repulsive Hubbard model in Eq. 1 due to λ-hopping as it lowers the energy of two electrons on adjacent sites compared to the case when they are far apart.

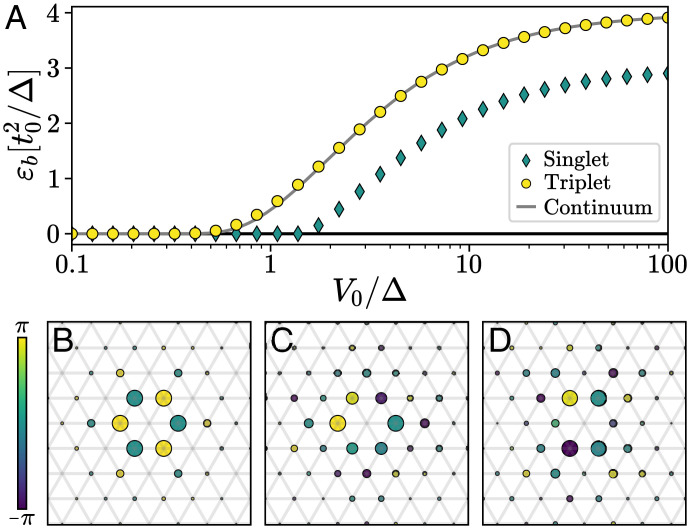
To demonstrate pairing, we consider the analog of Cooper’s problem in a doped band insulator and solve Eq. 2 for two doped electrons (SI Appendix, section 2). Bound state are signaled by a positive energy ${\epsilon }_b=6t-E_2$, with E₂ being the two-electron ground state energy, that we show in Fig. 2A as a function of the original model parameters $U_B,\mathrm{\Delta }$ and V₀. Bound pairs are found in the spin-triplet channel in a very large parameter range and in the spin-singlet channel for sufficiently large values of $V_0/\mathrm{\Delta }$. Their binding energy reach a maximum when $V_0\gg \mathrm{\Delta }$ and are equal to $V-2\lambda$ (triplet) and $V-\lambda$ (singlet), as can be checked by a straightforward diagonalization of the interacting part of ${\mathcal{H}}_f$ on a single triangle.

Fig. 2.

(A) Binding energy of spin singlet (diamonds) and triplet (circle) pairs, obtained by solving the lattice two-electron problem for $t_0/\mathrm{\Delta }=0.1$ and $U_B=3V_0$. The lowest two-particle bound state has spin-1, and its energy is perfectly captured by the effective continuum model in Eq. 8 (gray line). We also show the (B) triplet and (C and D) degenerate singlet bound state wave functions as a function of the relative distance between the two doped charges, with $V_0=2\mathrm{\Delta }$. The radius and color of the circles indicate the amplitude and phase, respectively, of the wave function on each site.

In Fig. 2 B–D, we represent these bound states as a function of the relative position between the two particles. The spin-triplet wave function exhibits f-wave symmetry; i.e., it is symmetric under threefold rotation and changes sign under any reflection flipping one of the primitive vectors ${\mathbf{a}}_j$. In contrast, the spin-singlet bound state is twofold degenerate and shows d-wave symmetry.

Let us emphasize that pairing occurs at infinitesimal carrier doping in a band insulator with purely repulsive interactions. Notably, electron pairing from repulsion can be established in a simple system, without any connection to resonating valence bond or quantum spin liquid.

Our pairing mechanism relies on short-range repulsion (such as V₀ between adjacent A and B sites) that couples itinerant electrons in the conduction band with core electrons in the filled band. Such interband effects produce attractive pairing interaction, as we have rigorously demonstrated above. We further show in SI Appendix, section 2, that the formation of two-particle bound state is stable against the longer-range part of the Coulomb repulsion (which directly couples conduction electrons). Note that in our theory, the attractive pairing interaction from interband effects is nonperturbative in V₀ and can reach sizable values, especially for large t (23, 33). This property protects electron pairing against direct longer-range repulsion. Moreover, at finite doping concentration, the Coulomb potential is dynamically screened by free carriers and effectively becomes short-ranged. Thanks to the beneficial effect of dynamical screening, our interband electronic mechanism for superconductivity can also work at finite doping, even when a two-particle bound state does not exist.

Binding in the Dilute Limit.

The existence of spin-triplet bound states is suggestive of superconductivity at finite doping. To understand its emergence beyond the microscopic details of ${\mathcal{H}}_f$ on the lattice scale, we now derive an effective continuum theory that captures the long-wavelength behavior of this liquid. Naturally, the latter can only be derived at sufficiently small doping concentrations $x\ll 1$, where electrons primarily occupy states near the two degenerate minima of the single-particle dispersion ${\epsilon }_{\mathbf{k}}=2t{\displaystyle {\sum }_{j=1}^3\cos }(\mathbf{k}·{\mathbf{a}}_j)$, located at the corners K and $K\prime$ of the Brillouin zone. This continuum description remains valid so long as the size of two-particle bound states is large compared to the lattice constant or, equivalently, their binding energy is small compared to the single particle bandwidth. This condition is satisfied in the parameter range $V_0<\mathrm{\Delta }$, which we consider below (Fig. 2).

We now derive an effective continuum theory that captures the long-wavelength behavior of this two-valley electron liquid. Retaining fermionic modes $f_{\sigma }(\tau K+\mathbf{k})\equiv {\psi }_{\sigma \tau }(\mathbf{k}),\hspace{0.17em}\sigma \in \{\uparrow ,\downarrow \}$, close to either of the valleys $\tau \in \{K,K\prime \}$, we derive the effective continuum description of the lattice model ${\mathcal{H}}_f$

$$\tilde{\mathcal{H}}={\tilde{\mathcal{H}}}_0+{\tilde{\mathcal{H}}}_i,\hspace{1em}{\tilde{H}}_0={\displaystyle \int \text{d}}x{\displaystyle \sum _{\sigma \tau }{\psi }_{\sigma \tau }^{†}}\left[\frac{-{\nabla }^2}{2m}\right]{\psi }_{\sigma \tau },$$ [4]

with $m=2/(3t{a}^2)$ the effective mass at K and $K\prime$. ${\tilde{\mathcal{H}}}_i$ consists of three symmetry-allowed contact interactions:

$${\tilde{\mathcal{H}}}_i={\displaystyle \int \text{d}}x\hspace{0.17em}{g}_0({\rho }_{K\uparrow }{\rho }_{K\downarrow }+{\rho }_{K\prime \uparrow }{\rho }_{K\prime \downarrow })+g_1{\rho }_K{\rho }_{K\prime }+g_2{\mathbf{s}}_K·{\mathbf{s}}_{K\prime },$$ [5]

where ${\rho }_{\tau }={\psi }_{\alpha ,\tau }^{†}{\psi }_{\alpha ,\tau }$ and ${\mathbf{s}}_{\tau }={\psi }_{\alpha ,\tau }^{†}{\mathit{\sigma }}_{\alpha \beta }{\psi }_{\beta ,\tau }$ denote the density and spin, respectively, at valley τ.

The coupling constants g₀ and g₁ correspond to intravalley and intervalley repulsion, respectively, while g₂ describes intervalley exchange interactions. They are related to the original microscopic lattice model Eq. 2 by (SI Appendix, section 3)

$$g_0=(U+6V-6\lambda -6\tilde{t})/\mathcal{A}>0,$$ [6a]

$$g_1=(U+15V-24\lambda -6\tilde{t})/(2\mathcal{A})>0,$$ [6b]

$$g_2=-2(U-3V+12\lambda -6\tilde{t})/\mathcal{A}<0,$$ [6c]

with $\mathcal{A}=\sqrt{3}/a^2$ the Brillouin zone area. The most remarkable feature of these interactions is the emergence of ferromagnetic intervalley exchange interaction ($g_2<0$), which can be intuitively understood as Hund’s rules applied to the valley degree of freedom.

This ferromagnetic intervalley coupling predicts the existence of spin-triplet valley-singlet bound states in the s-wave channel when

$$g=g_1+g_2/4=9(V-2\lambda )/\mathcal{A}<0.$$ [7]

These valley-singlet bound states correspond to the f-wave electron pairs obtained on the lattice (Fig. 2) as they are invariant under threefold rotation ${\psi }_K\to e^{i2\pi /3}{\psi }_K,{\psi }_{K\prime }\to e^{-i2\pi /3}{\psi }_{K\prime }$ but change sign under reflections exchanging the two valleys ${\psi }_K\leftrightarrow {\psi }_{K\prime }$. Their binding energy is given by (34)

$${\epsilon }_b=\mathrm{\Lambda }/\left[\exp \left(\frac{4\pi }{m\left|g\right|}\right)-1\right],$$ [8]

with Λ a UV energy cutoff. As shown in Fig. 2B, this formula almost perfectly reproduces our solution of the two-body problem on the lattice with no fitting parameter since $\mathrm{\Lambda }=2\pi t/\sqrt{3}$ is fixed by the requirement ${\epsilon }_b(V_0\gg \mathrm{\Delta })=2\lambda -V{|}_{V_0\gg \mathrm{\Delta }}$. This proves the validity of our derivation and the predictive power of the continuum theory Eq. 5 for the microscopic lattice model.

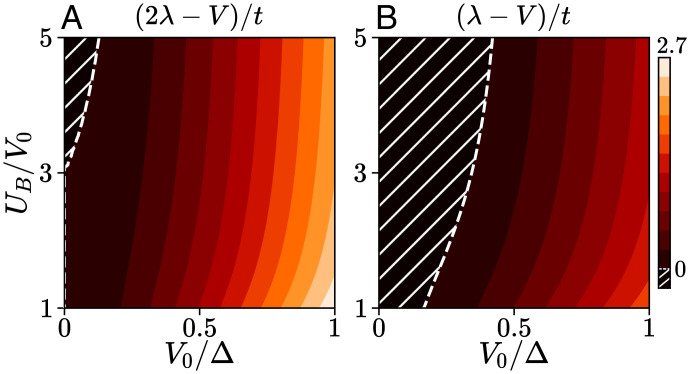
From a broader perspective, the spin-triplet/valley-singlet pairs obtained within the continuum model arise when the intervalley ferromagnetic exchange interaction g₀ (valley Hund’s rule) becomes sufficiently large to overcome the bare repulsion g₁. Both g₀ and g₁ are effective interactions for doped electrons that arise from the short-range repulsion via interband polarization. The condition g  <  0 provides an analytical criterion for when this happens as a function of the original lattice parameters ${\mathrm{\Delta }}_0,U_A,U_B$ and V₀. Using Eq. 3, we observe that this criterion is satisfied in a wide parameter window, which is shown in Fig. 3A. Note that in the presence of on-site repulsion $U_B\ne 0$, pairing occurs only when the nearest-neighbor repulsion V₀ exceeds a critical value that depends on U_B and Δ. To capture such effect, it is thus essential that our theory of exciton-mediated pairing is nonperturbative in interaction strength.

Fig. 3.

(A) The coupling strength in the spin-triplet f-wave channel $\propto (2\lambda -V)/t$ is positive for most lattice parameters, heralding attractive interactions and superconductivity. (B) Idem for the subleading d-wave channel with coupling strength $\propto (\lambda -V)/t$. Hatched regions locate effective repulsive interaction in each channels.

Within our continuum approach, d-wave bound pairs only arise if we include higher-order terms in the small $\left|\mathbf{k}a\right|$ expansion of the interaction near the K and $K\prime$ valleys. This subleading behavior explains why these bound states have lower binding energy than the spin-triplet pairs (Fig. 2). We can nevertheless extend our analytical criterion to identify the regime in which d-wave bound states exist. This happens when the coupling constant $V-\lambda$ is negative and is depicted in Fig. 3B.

T_c versus Doping.

At finite density, the spin-triplet valley-singlet pairing leads to a superconducting state with a vector order parameter (10)

$$\mathbf{d}=\langle {\psi }_{K,\alpha }{[\mathit{\sigma }(i{\sigma }_y)]}_{\alpha ,\beta }{\psi }_{K\prime ,\beta }\rangle .$$ [9]

This state is fully gapped and isotropic; i.e., the order parameter d is constant around each of the two valleys (Fig. 4A). This property is unusual for triplet superconductors, where the antisymmetry of the Cooper pair wave function implies $\mathbf{d}(\mathbf{k})=-\mathbf{d}(-\mathbf{k})$. For a singly connected Fermi surface centered at $\mathbf{k}=0$, the condition necessarily requires strong variations of the d vector over the Fermi surface, as exemplified in the A and B phases of ³He. In stark contrast, in our case the presence of two disconnected Fermi surfaces centered around K and $K\prime$ enables intervalley spin-triplet pairing with a constant and opposite d vector over the Fermi surface of each valley.

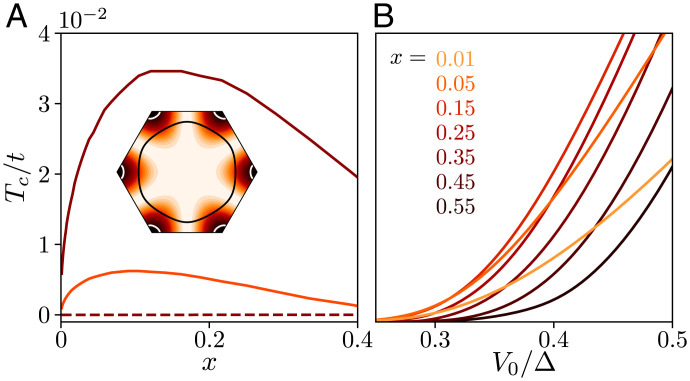
Fig. 4.

(A) Critical temperature T_c as a function of x in the f-wave (solid line) and d-wave (dashed line) channels. We fix $U_B=3V_0$ and use $V_0=\mathrm{\Delta }/3$ (orange) and $V_0=4\mathrm{\Delta }/9$ (red), for which the d-wave effective interaction is repulsive and attractive, respectively. (Inset) $|\mathbf{d}(\mathbf{k}){|}^2$, which is fully gapped on the Fermi surface for x = 0.1 (white line) and nodal for x  >  0.5 (black line). (B) T_c as a function of the bare interaction parameter $V_0/\mathrm{\Delta }$.

Another important feature of our theory is the nonretarded pairing interaction, which spreads over the entire bandwidth of doped charges. This sharply contrasts with electron–phonon superconductors, where the attractive interaction is cut off by the Debye energy and thus limited to the vicinity of the Fermi surface. The absence of energy cutoff changes the expression of the superconducting critical temperature T_c and zero temperature triplet superconducting gap ${\mathrm{\Delta }}_t=\left|\mathbf{d}\right|$. We find that they both strongly depend on the carrier density x, despite the constant density of states (35, 36)

$${\mathrm{\Delta }}_t=\sqrt{2{\epsilon }_F{\epsilon }_b},$$ [10a]

$$k_B{T}_c=\frac{e^{\gamma }{\mathrm{\Delta }}_t}{\pi }\propto \sqrt{xW}\exp \left(-\frac{4\pi }{m\left|g\right|}\right),$$ [10b]

with ${\epsilon }_F\propto x$ the noninteracting Fermi energy of doped charges.

In two dimensions, the above mean-field estimate of the critical temperature, determined as the point where the superconducting order parameter vanishes, overestimates the true BKT transition temperature $T_{\text{BKT}}$ of the superconductor, where phase fluctuations make the superfluid phase quasi–long-range ordered (assuming that triplet d vector is pinned by weak spin-orbit coupling). Nevertheless, T_c provides a good estimate of the $T_{\text{BKT}}$ as long as the binding energy remains smaller than the Fermi energy ${\epsilon }_b<{\epsilon }_F$, referred to as BCS limit (37). In the opposite limit ${\epsilon }_F<{\epsilon }_b$, BEC limit, more accurate estimates of $T_{\text{BKT}}$ are necessary (37). One important consequence of the presence of pairing at infinitesimal doping in our model is the emergence of a BEC–BCS crossover as a function of density.

Let us now restrict our attention to the BCS limit, i.e., for high doping concentrations, where lattice effects become important. This can be done efficiently by restricting our attention to $V_0<\mathrm{\Delta }$ where the binding energy is small and the BCS limit is already reached for densities $x\sim 1\%$. In that region, we need to perform mean-field calculations directly on the lattice model in Eq. 2 (as detailed in SI Appendix, section 4). In agreement with earlier results, these calculations show that the spin-triplet f-wave pairing channel is the leading instability in our model. The mean-field order parameter takes the form

$${\mathbf{d}}_{\mathbf{k}}=\mathbf{d}{\displaystyle \sum _j\sin }(\mathbf{k}·{\mathbf{a}}_j)\equiv s_{\mathbf{k}}\mathbf{d}.$$ [11]

Its dependence on the crystal momentum, shown in Fig. 3A, is determined by the form of interactions. The overall amplitude of d is obtained from the spin-triplet f-wave gap equation

$$\frac{3}{2\lambda -V}={\displaystyle \int \frac{{\text{d}}^2\mathbf{k}}{\mathcal{A}}}\frac{s_{\mathbf{k}}^2}{E_{\mathbf{k}}}\tanh \left(\frac{E_{\mathbf{k}}}{2k_{B}T}\right),$$ [12]

which always has a solution in the pairing region identified by Eq. 7 (Fig. 3A). Here the quasi-particle energy spectrum $E_{\mathbf{k}}=\sqrt{{({\epsilon }_{\mathbf{k}}-\mu )}^2+|{\mathbf{d}}_{\mathbf{k}}{|}^2}$, with μ the chemical potential, remains gapped at the Fermi level throughout the transition from the band insulator to the spin-triplet superconductor (recall that $\left|{\mathbf{d}}_{\mathbf{K}}\right|=\left|{\mathbf{d}}_{\mathbf{K}\prime }\right|\ne 0$).

In Fig. 4, we show the critical temperature T_c extracted from Eq. 12 as a function of x and $V_0/\mathrm{\Delta }$. At small doping, the f-wave pairing vector $\left|{\mathbf{d}}_{\mathbf{k}}\right|$ is nearly constant around K, and $K\prime$. T_c sharply rises with $\sqrt{x}$ dependence, in agreement with the continuum prediction in Eq. 8. As doping increases, the Fermi surface approaches the $\mathrm{\Gamma }-M$ lines, where the order parameter ${\mathbf{d}}_{\mathbf{k}}\propto s_{\mathbf{k}}$ vanishes. Its small amplitude close to these lines leads to a reduction of T_c for x  >  0.15, as can be seen in Fig. 4.

In summary, we observe a nonmonotonous behavior of T_c as a function of doping (Fig. 4), with an initial increase following a $\sqrt{x}$ dependence expected from the effective continuum theory and a subsequent decrease related to the reduction of the order parameter near the $\mathrm{\Gamma }-M$ line. At low doping, the Fermi surface is made of two pockets encircling the K and $K\prime$ points. Around these two points, the order parameter $\overrightarrow{d}$ has a constant direction and results in a full superconducting gap. Importantly, this f-wave spin-triplet state is robust against intra-valley scattering by a smooth disorder potential, while intervalley scattering by atomic impurities is detrimental. Unlike superfluid He-3, this spin-triplet superconducting state is adiabatically connected to the BEC regime and therefore is nontopological (38).

Subleading d-Wave Pairing.

We saw that an effective attraction in the d-wave channel also appears for sufficiently large interactions V₀. The effective strength of that attraction is, however, weaker than g (Fig. 3) and yields bound states with smaller binding energies (Fig. 2). As a result, we have up to now considered the case of f-wave superconducting order parameter.

In the dilute limit, the f-wave order parameter leads to a full superconducting gap on two disconnected Fermi surfaces around $\pm K$. In contrast, the two d-wave order parameters produce nodal lines crossing the K and $K\prime$ points, leading to point nodes on the Fermi surface for any real combination of $d_{x^2-y^2}$ and d_xy order parameters as shown in SI Appendix, section 4. To highlight the subleading nature of d-wave pairing, we have also computed the critical temperature obtained by solving the linearized gap equation assuming f- or d-wave symmetry. Our results, depicted in Fig. 4A for $U_B=3V_0$ and $V_0=4\mathrm{\Delta }/9$, show the clear dominance of f-wave paired state in our model.

When $x\ge 0.5$, the Fermi surface becomes a singly connected pocket around Γ. Then, the f-wave order parameter produces nodes and the T_c obtained from Eq. 12 become negligibly small (Fig. 4B). While the d-wave order parameter is still subleading in this regime, other studies based on weak interaction expansions show that it can become dominant if additional terms are added to the Hamiltonian (39, 40). For instance, a next-nearest neighbor $V_2>0$ automatically penalizes the f-wave B – B next-nearest neighbor pairing but can be accommodated by a d-wave superconducting state which features A – B nearest neighbor pairing. Similarly, when the sublattice potential ${\mathrm{\Delta }}_0$ decreases, doped charges start to populate A sites, which may again favor a nearest neighbor d-wave order. Both effects are further enhanced near Van Hove doping, where d-wave states are provably more stable than f-wave order in the limit ${\mathrm{\Delta }}_0=0$ (41).

Interaction Expansion

In this section, we show that the three-particle mechanism for superconductivity described in Kinetic Energy Expansion is not restricted to the ionic limit $t_0\ll \mathrm{\Delta }$ but extends at any value of the tunneling parameter. To preserve analytical control of interband effects, we work in the small interaction limit, such that interband hybridization remains small. In this regime, we find evidence of attractive interaction between conduction electrons using a similar method to that in Kinetic Energy Expansion. We follow the methodology of Kinetic Energy Expansion; i.e., we first derive an effective model for doped electrons with a unitary transformation and then study the obtained model for small doping concentrations.

Unitary Transformation.

We start from the Hamiltonian Eq. 1 written in momentum space as $\mathcal{H}={\mathcal{H}}_0+\mathcal{V}$ with

$${\mathcal{H}}_0={\displaystyle \sum _1{\epsilon }_1}{c}_1^{†}{c}_1,\hspace{1em}\mathcal{V}=\frac{1}{N_s}{\displaystyle \sum _{1234}{V}_{43}^{21}}{\delta }_{43}^{21}{c}_4^{†}{c}_3^{†}{c}_2{c}_1,$$ [13]

where we have used a generalized index $i=({\mathbf{k}}_i,b_i,{\sigma }_i)$ gathering the momentum ${\mathbf{k}}_i$, band $b_i=\pm$, and spin σ_i labels. Our goal is to derive an effective Hamiltonian for the upper band assuming the lower one fully filled. We do so by eliminating the direct interband mixing interaction terms in the Hamiltonian with the help of a unitary transformation.

This transformation is carried out explicitly in SI Appendix, section 5, where we find the leading corrections to the dispersion relation ε and the scattering vertex V. The former is akin to the Hartree–Fock correction of standard many-body perturbation theory:

$$\begin{array}{l}\delta {\epsilon }_{\mathbf{k},+}=\frac{1}{N_s}{\displaystyle \sum _{\mathbf{q},\sigma }\left[V_{(\mathbf{q},-,\sigma )(\mathbf{k},+,\uparrow )}^{(\mathbf{k},+,\uparrow )(\mathbf{q},-,\sigma )}+V_{(\mathbf{k},+,\uparrow )(\mathbf{q},-,\sigma )}^{(\mathbf{q},-,\sigma )(\mathbf{k},+,\uparrow )}\right]}\\ -\frac{1}{N_s}{\displaystyle \sum _{\mathbf{q}}\left[V_{(\mathbf{k},+,\uparrow )(\mathbf{q},-,\uparrow )}^{(\mathbf{k},+,\uparrow )(\mathbf{q},-,\uparrow )}+V_{(\mathbf{q},-,\uparrow )(\mathbf{k},+,\uparrow )}^{(\mathbf{q},-,\uparrow )(\mathbf{k},+,\uparrow )}\right]},\end{array}$$ [14]

where we have used the spin-independence of V and choose ↑ as a preferred spin index. This small correction does not change the position of the band minima, which remain degenerate at the K and $K\prime$ points. Expanding around these minima in the limit $t_0\ll {\mathrm{\Delta }}_0$ gives ${(\epsilon +\delta \epsilon )}_{\tau K+\mathbf{k},+}\simeq |\mathbf{k}{|}^2/(2m^{*})$ with

$$\frac{1}{m^{*}}=\frac{3t_0^2{a}^2}{2{\mathrm{\Delta }}_0^2}\left[{\mathrm{\Delta }}_0+U_A-4V_0\right],$$ [15]

which agrees with the result of Eq. 4 obtained with the kinetic expansion provided interactions are small compared to ${\mathrm{\Delta }}_0$. This offers an important consistency test between the two methods in their overlapping regimes of validity.

Attraction in Dilute Limit.

The expressions for the corrections to the scattering vertex $\delta V$ being quite involved (SI Appendix, section 5), we simply support here the emergence of attractive interactions in the f-wave scattering channel by computing the effective interaction strength in the spin-triplet valley-singlet channel, i.e., between equal-spin electrons living in opposite valleys. Writing $\tilde{V}=V+\delta V$, this coefficient can be expressed as

$$\begin{array}{ll}{U}_0=\hfill & {\tilde{V}}_{(K+)(K\prime +)}^{(K\prime +)(K+)}+{\tilde{V}}_{(K\prime +)(K+)}^{(K+)(K\prime +)}\hfill \\ \hfill & -{\tilde{V}}_{(K+)(K\prime +)}^{(K+)(K\prime +)}-{\tilde{V}}_{(K\prime +)(K+)}^{(K\prime +)(K+)},\hfill \end{array}$$ [16]

where all spin component are equal. This coefficient greatly simplifies as the Bloch states at the K and $K\prime$ point in the upper band are localized on B sites, ${\mathrm{\Psi }}_{K/K\prime ,+}^A=0$. Using this simplification, we end up with

$$U_0=\frac{12t_0^2{V}_0(U_B-3V_0)}{N_s}{\displaystyle \sum _{\mathbf{q}}\frac{|f(\mathbf{q}){|}^2}{{(2{\epsilon }_{\mathbf{q},+})}^3}},$$ [17]

which also agrees with the our results of Kinetic Energy Expansion in the limit where both methods are analytically controlled (SI Appendix, section 5). The presence of an effective attraction $U_0<0$ in the f-wave channel when $U_B<3V_0$ proves that the results of Fig. 3 hold for nonperturbative tunneling amplitudes t₀.

Complementary to the strong-coupling expansion for ionic insulators (Kinetic Energy Expansion), the interaction expansion described here is based on the band picture and can also apply to band insulators where the conduction band’s width is larger than the band gap. This generalization extends the list of potential material realization of the excitonic-driven superconductivity via our three-particle mechanism.

Application to Dilute Superconductors

Let us recapitulate our results so far. Using the specific model in Eq. 1 as an example, we have demonstrated a general mechanism of spin-triplet superconductivity in doped band insulators with strong repulsive interaction. Focusing on the low-density regime, we have derived a universal continuum model for the two-valley Fermi liquid. When either tunneling or interactions are small compared to the n = 2 insulator gap, we have shown that virtual interband transitions can produce a sufficiently strong intervalley ferromagnetic interaction that leads to spin-triplet pairing. A remarkable consequence of our theory is that spin-triplet superconductivity occurs at infinitesimal doping, with a sharp increase $T_c\sim \sqrt{x}$. Based on this theory, we hereby propose that the recently discovered dilute superconductors ZrNCl and WTe₂ are spin-triplet. We also highlight the plausible realization of our model in some moiré materials.

ZrNCl.

ZrNCl shares many common features with our toy model in Eq. 1. At the single-particle level, it is a band insulator with a large gap $\mathrm{\Delta }\sim 2.5$ eV (42, 43), where a single band with quadratic minima at the K and $K\prime$ points is relevant to describe the physics at low carrier density (44, 45). Upon electron doping through Li-intercalation Li${}_{\alpha }$ZrNCl, two-dimensional superconductivity arises in the ZrN planes (46, 47), even for extremely small dopant concentrations $\alpha =0.0038$ (28). Note that the stoichiometric concentration of lithium α differs from the number of doped charges per unit cells x by a factor of 2, $x=2\alpha$ since each unit cell features two Zr atoms.

The observed critical temperatures, ranging from 11.5 to $19\hspace{0.17em}\text{K}$, are hard to explain within the standard electron–phonon mechanism, which makes ZrNCl an unconventional superconductor. A compelling argument against the phonon mechanism of pairing is the simultaneous enhancement of T_c (48) and reduction of electron–phonon interactions, probed by Raman scattering (49), when α decreases from 0.2 to 0.05.

We now highlight that our theory consistently captures the available experimental results on the superconducting state in ZrNCl (50) and propose that this material be regarded as a legitimate candidate for spin-triplet pairing.

First, we find pairing at infinitesimal doping above the band insulator and predict a smooth crossover from a BEC of pairs to a BCS regime as the Fermi energy increases (23), which has recently been observed in extremely high quality ZrNCl samples (28). On the BCS side of this crossover, we expect a gap to critical temperature ratio $2\mathrm{\Delta }/k_B{T}_c>3.5$ (37, 51, 52). This is because the induced pairing interaction in Eq. 2 is instantaneous on the time scale of the inverse bandwidth, so that all carriers in the narrow band contribute to the superconducting gap. This contrasts with phonon-mediated retarded attractions, which only spread over a Debye width near the Fermi level and lead the universal ratio of 3.5. The gap to T_c ratio measured ZrNCl is two to five times larger than the BCS value (28, 53), a sign of strong coupling superconductivity and nonretarded pairing interactions which are well captured by our model.

Second, our theory accounts for the typical critical temperatures observed in ZrNCl. Using the DFT results for the lattice constant $a=3.663\hspace{0.17em}\AA$ and the effective mass at the K point $m=0.580m_e$ (54, 55), we estimate $t\sim 0.65\hspace{0.17em}\text{eV}$. With the parameters $U_B=3V_0=\mathrm{\Delta }$ of Fig. 4 for the sake of concreteness, we obtain a critical temperature $T_c\sim 0.002t\simeq 17.5\hspace{0.17em}\text{K}$ for $\alpha =16\%$ doping, which lies close to the experimentally measured value.

Finally, our theory also successfully captures the nonmonotonic dependence of T_c on doping observed in ref. 28. The original increase of T_c follows from the BEC/BCS physics described earlier. Specific heat measurements point toward a change from an almost isotropic to a highly anisotropic order parameter upon increasing the doping level (56, 57) from $\alpha =5\%\to 20\%$ (48). This is consistent with an f-wave superconducting order, where the reduction of T_c is caused by the reduction of the gap near $\mathrm{\Gamma }-M$ lines due to the form factor s_q (shown in Fig. 4A). The unconventional pairing symmetry is further substantiated by the lack of coherence peak in the NMR signal of ref. 58.

The spin-triplet property of ZrNCl could be experimentally probed using tunneling spectroscopy under an in-plane magnetic field. In such conditions, spin-singlet superconductors are known to exhibit a linear splitting of their Bogoliubov modes $E_{\sigma }(k)=\sqrt{{\epsilon }_k^2+|{\mathrm{\Delta }}_s{|}^2}+\sigma {\mu }_{B}B$ with μ_B the Bohr magneton and Δ_s the singlet order parameter at T = 0 and B = 0 (59). In the triplet case, the d vector can align perpendicular to the magnetic field to produce equal-spin electron pairs even at $B\ne 0$ (60). In this case, the Zeeman term simply shifts the chemical potential of spin-up and spin-down electrons. Provided that the Zeeman energy is much smaller than the Fermi energy, the triplet superconducting gap at zero temperature is little affected, even at high fields exceeding the Pauli limit. This behavior can be used to test the triplet nature of ZrNCl in future experiments.

WTe₂.

Monolayer WTe₂ is a topological insulator with spin-helical edge states (61–65). Recently, two independent groups discovered a transition from insulating to superconducting state in monolayer WTe₂ under electron doping via electrostatic gating (29, 30). Another separate work observed superconductivity in epitaxial thin film of WTe₂ (66). The origin of superconductivity and the nature of the superconducting state are unknown and have attracted considerable interest (67, 68).

Our picture is that superconductivity in electron doped WTe₂ is driven by excitonic effects and exhibits spin-triplet pairing. Indeed, a recent experiment on insulating WTe₂ reported evidence of strong excitonic effects which significantly enhance the single-particle gap (69). While the electronic structure of WTe₂ is far more complicated than our model used to illustrate the exciton pairing mechanism, they both feature two valleys in the conduction band. Therefore, electron doped WTe₂ at low density is a two-valley Fermi liquid described by our continuum theory in Eq. 5. If excitons in WTe₂ mediate strong enough intervalley ferromagnetic exchange, our theory predicts the emergence of a spin-triplet superconducting state.

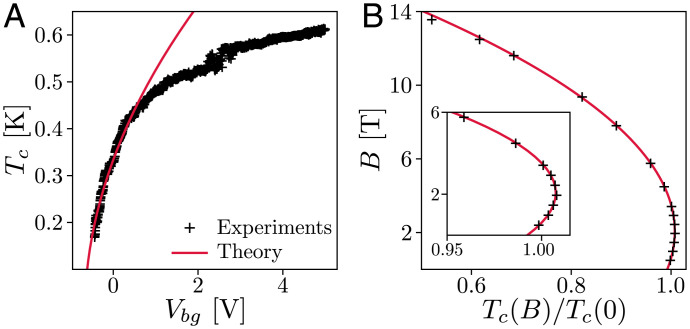
This motivates a thorough comparison between the expected consequences of spin-triplet superconductivity to experimental findings on WTe₂. First, differential resistance measurements (29) show that upon doping, an insulating resistance peak transforms directly into to a superconducting resistance dip, consistent with our picture of an insulator–superconductor transition. The experimentally observed sharp increase of T_c with doping (29) agrees remarkably well with the prediction $T_c\sim \sqrt{x}$ in the low-density regime, as shown in Fig. 5. Another prediction of our theory is that the single-particle gap does not close across the doping-induced insulator–superconductor transition, which can be tested in future tunneling measurements.

Fig. 5.

The doping dependence of T_c, measured in ref. 29, is well captured by our low-density prediction in Eq. 10. (B) Perfect agreement is found between the critical temperature measured in ref. 66 under an in-plane magnetic field B and the prediction in Eq. 19.

The scenario of spin-triplet superconductivity in WTe₂ is supported by the observation of an in-plane critical field much larger than the Pauli limit in both monolayers and thin films (29, 30, 66). The most significant experimental evidence of spin-triplet superconductivity is the initial increase of T_c upon application of an in-plane magnetic field (29, 66). This behavior is incompatible with s-wave superconductivity [even after considering the effect of spin-orbit interaction (68, 70)]. On the contrary, the enhancement of T_c by magnetic field follows naturally from our equal-spin triplet superconducting state in two-valley systems. This can be seen with the Landau free energy:

$$F=\alpha (\mathbf{d}·{\mathbf{d}}^{*})+\mu \mathbf{B}·(i\mathbf{d}\times {\mathbf{d}}^{*})+\eta |\mathbf{B}·\mathbf{d}{|}^2+\chi B^2(\mathbf{d}·{\mathbf{d}}^{*}),$$ [18]

with $\alpha =\kappa (T-T_c(B=0))$ and $\kappa ,\mu ,\eta ,\chi >0$ near T_c. Importantly, the magnetic field B results in a linear Zeeman shift for pairs of total spin $\mathbf{S}=i(\mathbf{d}\times {\mathbf{d}}^{*})$. The η term describes the preferred equal-spin pairing with $\mathbf{d}\perp \mathbf{B}$; i.e., the spins are aligned or antialigned with the field. The last term accounts for orbital effect of the in-plane B field, which causes pair breaking.

From the Landau free energy, we obtain

$$\mathrm{\Delta }{T}_c^B=\mu B-\chi B^2,$$ [19]

with $\mathrm{\Delta }{T}_c^B=T_c(B)-T_c(0)$. Due to the Zeeman effect on triplet pairs, T_c increases linearly with B at small field. This nonanalytic dependence on B is a consequence of the degeneracy of triplet superconducting states associated with spin degrees of freedom at zero field. At such large B, orbital effect dominates and reduces T_c. As shown in Fig. 5, the above theoretical curve $T_c(B)$ fits excellently with experimental data.

The presence of spin-orbit coupling in WTe₂ is expected to lift the degeneracy between different triplet states. Due to a plane mirror symmetry perpendicular to the a crystallographic axis, an additional term $F_{\text{SOC}}=2\gamma |d_x{|}^2$ is allowed after including the spin-orbit effect. If $\mathbf{B}\parallel b$, the linear increase of T_c is rounded off by γ according to

$$\mathrm{\Delta }{T}_c^B=\sqrt{{(\mu B)}^2+{\gamma }^2}-|\gamma |-\chi B^2.$$ [20]

For small spin-orbit coupling $\gamma <{\mu }^2/2\chi$, the Zeeman term dominates, which still enables the enhancement of T_c for $\mathbf{d}\propto {(\mathrm{\Delta }{T}_c^B+\chi B^2,0,i\mu B)}^T$. For larger γ, $T_c(B)$ decreases monotonously with field. When $\mathbf{B}\parallel a$, we should distinguish two cases. First, if $\gamma >0$, both spin-orbit and magnetic field favor the vector $\mathbf{d}\propto {(0,1,i)}^T$, and we recover Eq. 19. Then for $\gamma <0$, the original spin degeneracy is fully lifted, and we observe a competition between two different triplet states with $\mathbf{d}\parallel a$ and $\mathbf{d}\perp a$ favored at low and high field, respectively. This leads to

$$\mathrm{\Delta }{T}_c^B=\{\begin{array}{ll}-(\eta +\chi )B^2\hfill & \text{if:} B<B^{*}\hfill \\ \mu B-\left|\gamma \right|-\chi B^2\hfill & \text{if:} B>B^{*}\hfill \end{array},$$ [21]

which exhibits a kink at $B^{*}\simeq \left|\gamma \right|/\mu$ where the system undergo a first-order phase transition. We hope more measurements of T_c as a function of both in-plane magnetic field strength and direction can be performed to establish the highly unusual behavior predicted by Eqs. 19 and 21, which we regard as unambiguous evidence for triplet superconductivity.

Moiré Materials.

Moiré materials based on transition metal dichalcogenides and graphene provide a promising platform for faithfully realizing our extended Hubbard model on the honeycomb lattice with a tunable charge transfer gap ${\mathrm{\Delta }}_0$. Indeed, in these two-dimensional heterostructures, the long-range part of Coulomb interaction can be screened by nearby metallic gates. Since the distance to gates can be comparable to the moiré lattice constant, the screened interaction mainly consists of on-site and nearest-neighbor repulsion as captured in our model. For example, the MX and XM stacking regions in twisted homobilayer MoS₂ correspond to the A and B sites of the honeycomb lattice, and the sublattice potential difference ${\mathrm{\Delta }}_0$ can be controlled by the displacement field (71). Similarly, low-energy moiré bands in twisted WSe₂, WSe₂/WS₂, and ABC trilayer graphene–hBN heterostructures are well described by honeycomb tight-binding model with a sublattice potential (72, 73).

In SI Appendix, section 2, we estimate that the effective attraction exposed in our manuscript continues to hold if $\mathrm{ϵ}a>85\hspace{0.17em}\mathrm{\AA }$, with ϵ the effective dielectric constant accounting for the presence of the nearby gate and a the moiré lattice constant. This condition is easily satisfied in typical moiré materials, which makes our superconductivity mechanism applicable.

Interestingly, recent experiments on twisted bilayer graphene, twisted trilayer graphene, and ABC trilayer graphene–hBN heterostructure all show that superconductivity essentially appears immediately upon doping insulating states. It seems to us that this behavior necessarily implies the existence of bound state for two doped electrons. Our theory of exciton-mediated pairing reveals how, as a matter of principle, two-particle bound state can arise from the strong electron repulsion, opening a path to BCS–BEC physics in a variety of solid state systems.

Data Availability

All study data are included in the article and/or SI Appendix.