BIDIMENSIONAL LINKED MATRIX FACTORIZATION FOR PAN-OMICS PAN-CANCER ANALYSIS

Abstract

Several modern applications require the integration of multiple large data matrices that have shared rows and/or columns. For example, cancer studies that integrate multiple omics platforms across multiple types of cancer, pan-omics pan-cancer analysis, have extended our knowledge of molecular heterogeneity beyond what was observed in single tumor and single platform studies. However, these studies have been limited by available statistical methodology. We propose a flexible approach to the simultaneous factorization and decomposition of variation across such bidimensionally linked matrices, BIDIFAC+. BIDIFAC+ decomposes variation into a series of low-rank components that may be shared across any number of row sets (e.g., omics platforms) or column sets (e.g., cancer types). This builds on a growing literature for the factorization and decomposition of linked matrices which has primarily focused on multiple matrices that are linked in one dimension (rows or columns) only. Our objective function extends nuclear norm penalization, is motivated by random matrix theory, gives a unique decomposition under relatively mild conditions, and can be shown to give the mode of a Bayesian posterior distribution. We apply BIDIFAC+ to pan-omics pan-cancer data from TCGA, identifying shared and specific modes of variability across four different omics platforms and 29 different cancer types.

1. Introduction.

Data collection and curation for the Cancer Genome Atlas (TCGA) program, completed in 2018, provide a unique and valuable public resource for comprehensive studies of molecular profiles across several types of cancer (Hutter and Zenklusen (2018)). The database includes information from several molecular platforms for over 10,000 tumor samples from individuals representing 33 types of cancer. The molecular platforms capture signal at different omics levels (e.g., the genome, epigenome, transcriptome, and proteome) which are biologically related and can each influence the behavior of the tumor. Thus, when studying molecular signals in cancer, it is often necessary to consider data from multiple omics sources at once. This and other applications have motivated a very active research area in statistical methods for multiomics integration.

A common task in multiomics applications is to jointly characterize the molecular heterogeneity of the samples. Several multiomics methods have been developed for this purpose which can be broadly categorized by: (1) clustering methods that identify molecularly distinct subtypes of the samples (Huo and Tseng (2017), Lock and Dunson (2013), Gabasova, Reid and Wernisch (2017)), (2) factorization methods that identify continuous lower-dimensional patterns of molecular variability (Lock et al. (2013), Argelaguet et al. (2018), Gaynanova and Li (2019)), or methods that combine aspects of (1) and (2) (Shen, Wang and Mo (2013), Mo et al. (2018), Hellton and Thoresen (2016)). These extend classical approaches, such as: (1) k-means clustering and (2) principal components analysis, to the multiomics context, allowing the exploration of heterogeneity that is shared across the different omics sources while accounting for their differences.

Several multiomics analyses have been performed on the TCGA data, including flagship publications for each type of cancer (e.g., see Network et al. (2012, 2014), Verhaak et al. (2010)). These have revealed striking molecular heterogeneity within each classical type of cancer which is often clinically relevant. However, restricting an analysis to a particular type of cancer sacrifices power to detect important genomic changes that are present across more than one cancer type. In 2013, TCGA began the Pan-Cancer Analysis Project, motivated by the observation that “cancers of disparate organs reveal many shared features, and, conversely, cancers from the same organ are often quite distinct” (Weinstein et al. (2013)). Subsequently, several pan-cancer studies have identified important shared molecular alterations for somatic mutations (Kandoth et al. (2013)), copy number (Zack et al. (2013)), mRNA (Hoadley et al. (2014)), and protein abundance (Akbani et al. (2014)). However, a multiomics analysis found that pan-cancer molecular heterogeneity is largely dominated by cell-of-origin and other factors that define the classical cancer types (Hoadley et al. (2018)).

In this study we do not focus on baseline molecular differences between the cancer types. Rather, we focus on whether patterns of variability within each cancer type are shared across cancer types, that is, whether multiomic molecular profiles that drive heterogeneity in one type of cancer also drive heterogeneity in other cancers. Systematic investigations of heterogeneity in a pan-omics and pan-cancer context are presently limited by a lack of principled and computationally feasible statistical approaches for the comprehensive analysis of such data. In particular, the data take the form of bidimensionally linked matrices, that is, multiple large matrices that may share row sets (here, defined by the omics platforms) or column sets (here, defined by the cancer types); this is illustrated in Figure 1, and the formal framework is described in Section 2. Such bidimensional integration problems are increasingly encountered in practice, particularly for biomedical applications that involve multiple omics platforms and multiple sample cohorts that may correspond to different studies, demographic strata, species, diseases, or disease subtypes.

Fig. 1.

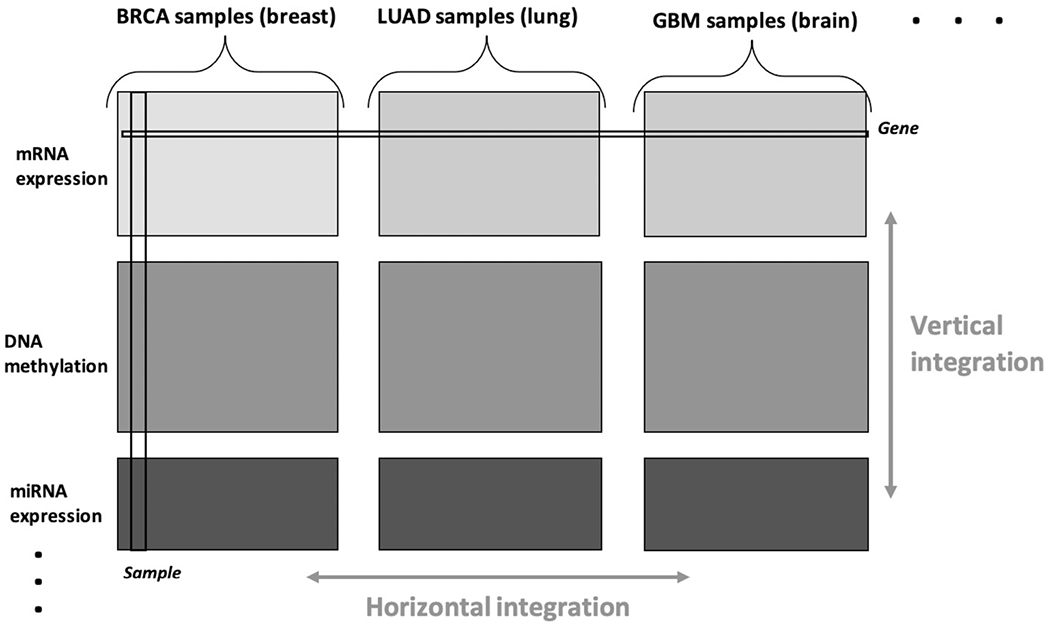
Bidimensional integration of pan-omics pan-cancer data.

In this article we propose a flexible approach to the simultaneous factorization and decomposition of variation across bidimensionally linked matrices, BIDIFAC+. Our approach builds on a growing literature for the factorization and decomposition of linked matrices, which we review in Section 3. However, previous methods have focused on multiple matrices that are linked in just one dimension (rows or columns) or assume that shared signals must be present across all row sets or column sets. This is limiting for pan-cancer analysis and other applications, where we expect patterns of variation that are shared across some, but not necessarily all, cancer types and omics platforms. With this motivation our proposed approach decomposes variation into a series of low-rank components that may be shared across any number of row sets (e.g., omics platforms) or column sets (e.g., cancer types). We develop a new approach to model selection and new estimating algorithms to accommodate this more flexible decomposition. We establish theoretical results, most notably, concerning the uniqueness of the decomposition without orthogonality constraints which are entirely new for linked matrix decompositions. Moreover, we show how BIDIFAC+ can improve the estimation of underlying structures over existing methods, even in the more familiar context for which matrices are linked in just one dimension.

2. Formal framework and notation.

Here, we introduce our framework and notation for pan-omics pan-cancer data. Let X_ij : M_i × N_j denote the data matrix for omics data source i and sample set (i.e., cancer type) j for j = 1, … , J and i = 1, … , I. Columns of X_ij represent samples, and rows represent variables (e.g., genes, miRNAs, proteins). The sample sets of size N = [N₁, … , N_J] are consistent across each omics source, and the features measured for each omics source M = [M₁, … , M_I] are consistent across sample sets. As illustrated in Figure 1, the collection of available data can be represented as a single data matrix X.. : M × N, where M = M₁ + … + M_I and N = N₁ + … + N_J by horizontally and vertically concatenating its constituent blocks,

$$\begin{array}{cc}X\mathbf{..}=\left[\begin{array}{cccc}{X}_{11}& X_{12}& \cdots & X_{1J}\\ ⋮& ⋮& \cdots & ⋮\\ X_{I1}& X_{I2}& \cdots & X_{IJ}\end{array}\right]& \text{where}{\mathbf{X}}_{ij}\mathrm{are}{M}_i\times N_j.\end{array}$$ (1)

Similarly, X_i. defines the concatenation of omics source i across cancer types, and X._j defines the concatenation of cancer type j across omics sources,

$$X_i\mathbf{.}=\left[X_{i1}\cdots X_{iJ}\right],X{\mathbf{.}}_j={\left[X_{1j}^{\prime }\cdots X_{Ij}^{\text{'}}\right]}^{\prime }.$$

The notation X_ij[·, n] defines the nth column of matrix ij, X_ij[m, ·] defines the mth row, and X_ij[m, n] defines the entry in row m and column n. In our context, the entries are all quantitative, continuous measurements; missing data are addressed in Section 9.

We will investigate shared or unique patterns of systematic variability (i.e., heterogeneity) among the constituent data blocks. We are not interested in baseline differences between the different omics platforms or sample sets, and after routine preprocessing the data will be centered so that the mean of the entries within each data block, X_ij, is 0. Moreover, to resolve the disparate scale of the data blocks, each block will be scaled to have comparable variability, as described in Section 6.1.

In what follows, ‖A‖_F denotes the Frobenius norm for any given matrix so that $\parallel A{\parallel }_F^2$ is the sum of squared entries in A. The operator ‖A‖_∗ denotes the nuclear norm of A which is given by the sum of the singular values in A; that is, if A : M × N has ordered singular values D[1, 1], D[2, 2], … , then ${\parallel A\parallel }_{\ast }={\sum }_{r=1}^{\min (M,N)}D[r,r].$

3. Existing integrative factorization methods.

There is now an extensive literature on the integrative factorization and decomposition of multiple linked datasets that share a common dimension. Much of this methodology is motivated by multiomics integration, that is, vertical integration of multiple matrices {X₁₁, X₂₁, … , X_I1} with shared columns in the setting of Section 2. For example, the Joint and Individual Variation Explained (JIVE) method (Lock et al. (2013), O’Connell and Lock (2016)) decomposes variation into joint components that are shared among multiple omics platforms and individual components that only explain substantial variability in one platform. This distinction not only simplifies interpretation but also improves accuracy in recovering underlying signals. Accuracy improves because structured individual variation can interfere with finding important joint signal, just as joint structure can obscure important signal that is individual to a data source. The factorized JIVE decomposition is

$$X_{i1}=U_i{V}^T+U_i^{\ast }{V}_i^T+E_i\text{for}i=1,\dots ,I.$$ (2)

Joint structure is represented by the common score matrix V : N₁ × R which summarize patterns in the samples that explain variability across multiple omics platforms. The loading matrices U_i : M_i × R indicate how these joint scores are expressed in the rows (variables) of platform i. The score matrices V_i : N₁ × R_i summarize sample patterns specific to platform i with loadings ${\mathbf{\text{U}}}_i^{*}$. Model (2) can be equivalently represented as a sum of low-rank matrices

$$X{\mathbf{.}}_1=S{\mathbf{.}}^{(0)}+\sum _{i=1}^I{S}_{\mathbf{.}}^{(i)}+E\mathbf{.},$$ (3)

where ${\mathbf{\text{S}}}_{\mathbf{\text{.}}}^{\left(0\right)}=\mathbf{\text{U}}{\mathbf{\text{.V}}}^T$ is of rank R and ${\mathbf{\text{S}}}_{\mathbf{\text{.}}}^{\left(i\right)}=[{\mathbf{\text{S}}}_1^{\left(i\right)\prime }\cdots {\mathbf{\text{S}}}_I^{\left(i\right)\prime }]\prime$ is the matrix of rank R_i, given by the individual structure for platform i and zeros elsewhere,

$$S_{i^{\prime }}^{(i)}=\{\begin{array}{ll}{\mathbf{0}}_{M_{i^{\prime }}\times N}& \text{if}{i}^{\prime }\ne i,\\ {\mathbf{\text{U}}}_{i^{\prime }}^{*}{\mathbf{\text{V}}}_i^T& \text{if}{i}^{\prime }=i.\end{array}$$

Several other methods result in a factorized decomposition similar to that in (2) and (3), including approaches that allow for different distributional assumptions on the constituent matrices (Li and Gaynanova (2018), Zhu, Li and Lock (2020)), nonnegative factorization (Yang and Michailidis (2016)), and the incorporation of covariates (Li and Jung (2017)). The Structural Learning and Integrative Decomposition (SLIDE) method (Gaynanova and Li (2019)) allows for a more flexible decomposition in which some components are only partially shared across a subset of the constituent data matrices. SLIDE extends model (3) to the more general decomposition

$$X{\mathbf{.}}_1=\sum _{k=1}^K{S}_{\mathbf{.}}^{(k)}+E\mathbf{.},$$ (4)

where $S_{\mathbf{.}}^{(k)}=[S_1^{(k)\prime }\cdots S_I^{(k)\prime }]\prime$ is a low-rank matrix with nonzero values for some subset of the sources that is identified by a binary matrix R : I × K and

$$S_i^{(i)}=\{\begin{array}{ll}{\mathbf{0}}_{M_i\times N}& \text{if}\mathbf{\text{R}}\left[i,k\right]=0,\\ {\mathbf{\text{U}}}_i^{\left(k\right)}{\mathbf{\text{V}}}^{\left(k\right)T}& \text{if}\mathbf{\text{R}}\left[i,k\right]=1.\end{array}$$

Here, V^(k) gives scores that explain variability for only those patterns for the omics sources identified by R[·, k].

The BIDIFAC approach (Park and Lock (2020)) is designed for the decomposition of bidimensionally linked matrices as in (1). Its low-rank factorization can be viewed as an extension of that for JIVE, decomposing variation into structure that is shared globally (G), across rows (Row), across columns (Col), or individual to the constituent matrices (Ind). Following (3) for JIVE and (4) for SLIDE, its full decomposition can be expressed as

$$X\mathbf{..}=S_{\mathbf{..}}^{(\text{G})}+\sum _{i=1}^I{S}_{\mathbf{..}}^{(i,\text{Row})}+\sum _{j=1}^J{S}_{\mathbf{..}}^{(j,\text{Col})}+\sum _{i=1}^I\sum _{j=1}^J{S}_{\mathbf{..}}^{(i,j,\text{Ind})}+E\mathbf{..},$$ (5)

where $S_{ij}^{(\text{G})}=U_i^{(\text{G})}{V}_j^{(\text{G})T}$,

$$\begin{array}{cc}{S}_{i^{\prime }{j}^{\prime }}^{(i,\text{Row})}=\{\begin{array}{ll}{\mathbf{0}}_{M_i\times N_j}& \text{if}{i}^{\prime }\ne i,\\ {\mathbf{\text{U}}}_i^{\left(i,\text{Row}\right)}{\mathbf{\text{V}}}_{{}^j}^{\left(i,\text{Row}\right)T}& \text{if}{i}^{\prime }=i,\end{array}& S_{i^{\prime }{j}^{\prime }}^{(j,\text{Col})}=\{\begin{array}{ll}{\mathbf{0}}_{M_i\times N_j}& \text{if}{j}^{\prime }\ne j,\\ {\mathbf{\text{U}}}_i^{\left(j,\text{Col}\right)}{\mathbf{\text{V}}}_{{}^j}^{\left(j,\text{Col}\right)T}& \text{if}{j}^{\prime }=j,\end{array}\end{array}$$

and

$$S_{i^{\prime }{j}^{\prime }}^{(i,j\text{Ind})}=\{\begin{array}{ll}{\mathbf{0}}_{M_i\times N_j}& \text{if}{i}^{\prime }\ne i\text{or}{j}^{\prime }\ne j,\\ {\mathbf{\text{U}}}_i^{\left(i,j,\text{Ind}\right)}{\mathbf{\text{V}}}_j^{\left(i,j,\text{Ind}\right)T}& \text{if}{i}^{\prime }=i\text{and}{j}^{\prime }=j.\end{array}$$

4. Proposed model.

We consider a flexible factorization of bidimensionally linked data that combines aspects of the BIDIFAC and SLIDE models. Our full decomposition can be expressed as

$$X\mathbf{..}=\sum _{k=1}^K{S}_{\mathbf{..}}^{(k)}+E\mathbf{..},$$ (6)

where

$$S_{\mathbf{..}}^{(k)}=\left[\begin{array}{llll}{S}_{11}^{(k)}& S_{12}^{(k)}& \dots & S_{1J}^{(k)}\\ ⋮& ⋮& \dots & ⋮\\ S_{I1}^{(k)}& S_{I2}^{(k)}& \cdots & S_{IJ}^{(k)}\end{array}\right]$$

and the presence of each ${\mathbf{S}}_{ij}^{\left(k\right)}$ is determined by a binary matrix of row indicators R : I × K and column indicators C : J × K,

$$S_{ij}^{(k)}=\{\begin{array}{ll}{0}_{M_i\times N_j}& \text{if}R[i,k]=0\text{or}C[j,k]=0,\\ U_i^{(k)}{V}_j^{(k)T}& \text{if}R[i,k]=1\text{and}C[j,k]=1.\end{array}$$

Each ${\mathbf{S}}_{\mathbf{..}}^{\left(k\right)}$ gives a low-rank module that explains variability within the omics platforms identified by R[·, k] and the cancer types identified by C[·, k]. By requiring R[i, k] = 1 and C[j, k] = 1, the module is nonzero on a contiguous submatrix. There are, in total, (2^I − 1)(2^J − 1) such submatrices, so by default we set K = (2^I − 1)(2^J − 1) and let R and C enumerate all possible modules (see Appendix A (Lock, Park and Hoadley (2022))). The SLIDE decomposition (4) is a special case when J = 1 or I = 1 (i.e., unidimensional integration); the BIDIFAC model (5) is a special case where each column of R and C contains either entirely 1’s (i.e., all rows or columns included) or just one 1 (i.e., just one row set or column set included). In practice, if the row and column set for a structural module is not included, it may be subsumed into a larger module or broken into separate smaller modules. The matrix E.. is an error matrix whose entries are assumed to be sub-Gaussian with mean 0 and variance 1 after scaling (see Section 6.1).

Let the rank of each module be rank $({\mathbf{S}}_{\mathbf{..}}^{\left(k\right)})=R_k$ so that the dimensions of the nonzero components of the factorization are ${\mathbf{\text{U}}}_i^{\left(k\right)}:M_i\times R_k$ and ${\mathbf{\text{V}}}_j^{\left(k\right)}:N_j\times R_k$. The rth component of the kth module gives a (potentially multiomic) molecular profile $\{{\mathbf{\text{U}}}_i^{\left(k\right)}[\mathbf{·},r]:\mathbf{R}[i,k]=1\}$ that explains variability within those cancer types, defined by C[·, k] with corresponding sample scores $\{{\mathbf{\text{V}}}_j^{\left(k\right)}[r,\mathbf{·}]:\mathbf{C}[j,k]=1\}$.

5. Objective function.

To estimate model (6), we minimize a least squares criterion with a structured nuclear norm penalty,

$$\underset{{\{S_{\mathbf{..}}^{(k)}\}}_{k=1}^K}{\mathrm{argmin}}\frac{1}{2}{\Vert X\mathbf{..}-\sum _{k=1}^K{S}_{\mathbf{..}}^{(k)}\Vert }_F^2+\sum _{k=1}^K{\lambda }_k{\Vert S_{\mathbf{..}}^{(k)}\Vert }_{\ast }$$ (7)

subject to ${\mathbf{\text{S}}}_{ij}^{\left(k\right)}={\mathbf{0}}_{M_i\times N_j}$ if R[i, k] = 0 or C[j, k] = 0. The choice of the penalty parameters ${\left\{{\lambda }_k\right\}}_{k=1}^K$ is critical and must satisfy the conditions of Proposition 1 to allow for nonzero estimation of each module.

Proposition 1.

Under objective (7), the following are necessary to allow for each ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{\left(k\right)}$ to be nonzero:

1. If for $k\prime \ne k$ the rows and columns of module k′ are contained within those for module $k,R[i,k]-R\left[i,k^{\prime }\right]\ge 0\forall i$ and $\mathbf{C}[j,k]-C\left[j,k^{\prime }\right]\ge 0\forall j$, then ${\lambda }_k>{\lambda }_{k^{\prime }}$.

2. If ${\mathcal{I}}_k\subset \{1,\dots ,k-1,k+1,\dots ,K\}$ is any subset of modules that together cover the rows and columns of module $k,{\sum }_{j\in {\mathcal{I}}_k}R[\mathbf{·},j]=r\cdot R[\mathbf{·},k]$ and ${\sum }_{j\in {\mathcal{I}}_k}\mathbf{\text{C}}[\mathbf{·},j]=c\cdot \mathbf{\text{C}}[\mathbf{·},k]$ for positive integers r and c, then ${\lambda }_k<{\sum }_{j\in {\mathcal{I}}_k}{\lambda }_j$.

We determine the λ_k’s by random matrix theory, motivated by two well-known results for a single matrix that we repeat here in Propositions 2 and 3.

Proposition 2 (Mazumder, Hastie and Tibshirani (2010)).

Let UDV^T be the SVD of a matrix X. The approximation A that minimizes

$$\frac{1}{2}{\parallel X-A\parallel }_F^2+\lambda {\parallel A\parallel }_{*}$$ (8)

is $\mathbf{\text{A}}=\mathbf{\text{U}}\widetilde{\mathbf{\text{D}}}{\mathbf{\text{V}}}^T$, where $\widetilde{\mathbf{\text{D}}}$ is diagonal with entries $\widetilde{\mathbf{\text{D}}}\left[r,r\right]=\max \left(\mathbf{\text{D}}\left[r,r\right]-\lambda ,0\right)$.

Proposition 3 (Rudelson and Vershynin (2010)).

Let D[1, 1] be the largest singular value of a matrix E : M × N of independent entries with mean 0, variance σ², and finite fourth moment. Then, $D[1,1]\approx \sigma (\sqrt{M}+\sqrt{N})$ as M, N → ∞, and if the entries of E are Gaussian $\mathbb{E}(D[1,1])\le \sigma (\sqrt{M}+\sqrt{N})$ for any M, N.

Fixing $\lambda =\sigma (\sqrt{M}+\sqrt{N})$ is a reasonable choice for the matrix approximation task in (8), because it keeps only those components r whose signal is greater than that expected for independent error by Proposition 3: $\mathbf{\text{D}}\left[r,r\right]>\sigma (\sqrt{M}+\sqrt{N})$ (Shabalin and Nobel (2013)). For our context, σ = 1 after normalizing, as discussed in Section 6.1, and thus we set ${\lambda }_k=\sqrt{R[\mathbf{·},k]\cdot M}+\sqrt{C[\mathbf{·},k]\cdot N}$, where R[·, k] · M × C[·, k] · N gives the dimensions of the nonzero submatrix for ${\mathbf{\text{S}}}_{\mathbf{..}}^{\left(k\right)}$,

$$R[\mathbf{·},k]\cdot M=\sum _{i=1}^I{M}_{i}R[i,k]\text{and}C[\mathbf{·},k]\cdot N=\sum _{j=1}^J{N}_{j}C[j,k].$$

Our choice of λ_k is motivated to distinguish signal from noise in module ${\mathbf{\text{S}}}_{\mathbf{..}}^{\left(k\right)}$, conditional on the other modules. Moreover, it is guaranteed to satisfy the necessary conditions in Proposition 1, which we establish in Proposition 4.

Proposition 4.

Setting ${\lambda }_k=\sqrt{R[\mathbf{·},k]\cdot M}+\sqrt{C[\mathbf{·},k]\cdot N}$ in (7) satisfies the necessary conditions of Proposition 1.

A similarly motivated choice of penalty weights is used in the BIDIFAC method which solves an equivalent objective under the restricted scenario where the columns of R and C are fixed and contain either entirely 1’s (i.e., all rows or columns included) or just one 1 (i.e., just one row set or column set included). Thus, we call our more flexible approach BIDIFAC+.

It is often infeasible to explicitly consider each of the K = (2^I − 1)(2^J − 1) possible modules in (7), and the solution is often sparse, with ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{\left(k\right)}=\mathbf{0}$ for several k. Thus, in practice, we also optimize over the row and column sets R and C for some smaller number of modules $\tilde{K}\ll K$ ,

$$\underset{R,C,{\{S_{\mathbf{..}}^{\left(k\right)}\}}_{k=1}^{\tilde{K}}}{\mathrm{argmin}}\frac{1}{2}{\Vert X\mathbf{..}-\sum _{k=1}^{\tilde{K}}{S}_{\mathbf{..}}^{(k)}\Vert }_F^2+\sum _{k=1}^{\tilde{K}}(\sqrt{M\cdot R[\mathbf{·},k]}+\sqrt{N\cdot C[\mathbf{·},k]}){\Vert S_{\mathbf{..}}^{(k)}\Vert }_{\ast }.$$ (9)

Note that if $\tilde{K}$ is greater than the number of nonzero modules, then the solution to (9) is equivalent to the solution to (7) in which R and C are fixed and enumerate all possible modules. If $\tilde{K}$ is not greater than the number of nonzero modules, then the solution to (9) can still be informative, as the set of $\tilde{K}$ modules that together give the best structural approximation via (7). In this case it helps to order the estimated modules by variance explained; if the $\tilde{K}$ th module still explains substantial variance, consider increasing $\tilde{K}$. Moreover, we suggest assessing the sensitivity of results to different values of $\tilde{K}$.

6. Estimation.

6.1. Scaling.

We center each dataset X_ij to have mean 0 and scale each dataset to have residual variance var(E_ij) of approximately 1. Such scaling requires an estimate of the residual variance for each dataset. By default, we use the median absolute deviation estimator ${\widehat{\sigma }}_{\text{MAD}}^2$ of Gavish and Donoho (2017), which is motivated by random-matrix theory under the assumption that X_ij is composed of low-rank structure and mean 0 independent noise of variance σ². We estimate ${\widehat{\sigma }}_{\text{MAD}}^2$ for the unscaled data ${\mathbf{\text{X}}}_{ij}^{\text{unscaled}}$ and set ${\mathbf{\text{X}}}_{ij}={\mathbf{\text{X}}}_{ij}^{\text{unscaled}}/{\widehat{\sigma }}_{\text{MAD}}$. An alternative approach is to scale each dataset to have overall variance 1, var(X_ij) = 1, which is more conservative because $\mathrm{var}\left(\mathbf{\text{E}}\mathbf{..}\right)\le \mathrm{var}\left({\mathbf{\text{X}}}_{ij}\right)$; thus, this approach results in relatively larger λ_k in the objective function and leads to sparser overall ranks. Yet another approach is to normalize each data block to have unit Frobenius norm, as in Lock et al. (2013). However, our default choice of penalty parameters λ_k in Section 5 is theoretically motivated by the assumption that residual variances are the same across the different data blocks.

6.2. Optimization algorithm: Fixed modules.

We estimate across all modules k = 1, … , K, simultaneously, by iteratively optimizing the objectives in Section 5. First, assume the row and column inclusions for each module, defined by R and C, are fixed, as in objective (7). To estimate ${\mathbf{\text{S}}}_{\mathbf{..}}^{\left(k\right)}$, given the other modules ${\{{\mathbf{\text{S}}}_{\mathbf{..}}^{(k^{\prime })}\}}_{k^{\prime }\ne k}$, we can apply the soft-singular value estimator in Proposition 2 to the residuals on the submatrix, defined by R[·, k] and C[·, k]. The iterative estimation algorithm proceeds as follows:

1. Initialize ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}=0_{M\times N}$ for k = 1, … , K .

2. For k = 1, … , K :

   1. Compute the residual matrix $X_{\mathbf{..}}^{(k)}=X\mathbf{..}-{\sum }_{k^{\prime }\ne k}{\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{\left(k^{\prime }\right)}$.

   2. Set $X_{ij}^{(k)}=0_{M_i\times N_j}$ where R[i, k] = 0 or C[j, k] = 0.

   3. Compute the SVD of $X_{\mathbf{..}}^{(k)},X_{\mathbf{..}}^{(k)}=U_{\mathbf{.}}^{(k)}{D}^{(k)}{V}_{\mathbf{.}}^{(k)}$.

   4. Update ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}=U_{\mathbf{.}}^{(k)}{\widehat{\mathbf{\text{D}}}}^{(k)}{V}_{\mathbf{.}}^{(k)}$ where $\widehat{D}\left[r,r\right]=\max \left(\mathbf{\text{D}}\left[r,r\right]-{\lambda }_k,0\right)$ for r = 1, 2, … .

3. Repeat step 2. until convergence of the objective function (9).

Step 2(d) minimizes the objective (7) for ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}$, given ${\{{\mathbf{\text{S}}}_{\mathbf{..}}^{(k^{\prime })}\}}_{k^{\prime }\ne k}$, by Proposition 2. In this way we iteratively optimize (7) over the K modules ${\{{\mathbf{\text{S}}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K$ until convergence.

6.3. Optimization algorithm: Dynamic modules.

If the row and column inclusions R and C are not predetermined, we incorporate additional substeps to estimate the nonzero submatrix, defined by R[·, k] and C[·, k], for each module to optimize (9). We use a dual forward-selection procedure to iteratively determine the optimal row-set R[·, k] with columns C[·, k] fixed, and the column-set C[·, k] with rows R[·, k] fixed, until convergence prior to estimating each ${\mathbf{\text{S}}}_{\mathbf{..}}^{(k)}$. The iterative estimation algorithm proceeds as follows:

1. Initialize ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}={\mathbf{0}}_{M\times N}$ for k = 1, … , K.

2. Initialize $\widehat{\mathbf{\text{C}}}\left[j,k\right]=1$ for j = 1, … , J.

3. For k = 1, … , K:

   1. Compute the residual matrix ${\mathbf{\text{X}}}_{\mathbf{..}}^{\left(k\right)}={\mathbf{\text{X}}}_{\mathbf{..}}-{\sum }_{k^{\prime }\ne k}{\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k^{\prime })}$

   2. Update $\widehat{\mathbf{\text{R}}}\left[\mathbf{·},k\right]$ and $\widehat{\mathbf{\text{C}}}\left[\mathbf{·},k\right]$, as follows:

      1. With $\widehat{\mathbf{\text{C}}}\left[\mathbf{·},k\right]$ fixed, update $\widehat{\mathbf{\text{R}}}\left[\mathbf{·},k\right]$ by forward selection, beginning with $\widehat{\mathbf{\text{R}}}\left[\mathbf{·},k\right]=\mathbf{0}$ and iteratively adding rows $i(\widehat{\mathbf{\text{R}}}\left[i,k\right]=1)$ to minimize the objective (9).

      2. With $\widehat{\mathbf{\text{R}}}\left[\mathbf{·},k\right]$ fixed, update $\widehat{\mathbf{\text{C}}}\left[\mathbf{·},k\right]$ by forward selection, beginning with $\widehat{\mathbf{\text{C}}}\left[\mathbf{·},k\right]=0$ and iteratively adding columns $j(\widehat{\mathbf{\text{C}}}\left[i,k\right]=1)$ to minimize the objective (9).

      3. Repeat steps i. and ii. until convergence of the chosen row and column sets $\widehat{\mathbf{\text{C}}}\left[\mathbf{·},k\right]$ and $\widehat{\text{R}}\left[\mathbf{·},k\right]$.

   3. Set ${\mathbf{\text{X}}}_{ij}^{\left(k\right)}={\mathbf{0}}_{M_i\times N_j}$, where $\widehat{\mathbf{\text{R}}}\left[i,k\right]=0$ or $\widehat{\mathbf{\text{C}}}\left[j,k\right]=0$.

   4. Compute the SVD of $X_{\mathbf{..}}^{(k)},X_{\mathbf{..}}^{(k)}=U_{\mathbf{.}}^{(k)}{D}^{(k)}{V}_{\mathbf{.}}^{(k)}$.

   5. Update ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}=U_{\mathbf{.}}^{(k)}{\widehat{\mathbf{\text{D}}}}^{(k)}{V}_{\mathbf{.}}^{(k)}$, where $\widehat{\mathbf{\text{D}}}\left[r,r\right]=\max \left(\mathbf{\text{D}}\left[r,r\right]-{\lambda }_k,0\right)$ for r = 1, 2, … .

4. Repeat step 3. until convergence of the objective function.

For the steps in 3b), objective (9) can be efficiently computed using the singular values for the residual submatrix, given by $\widehat{\mathbf{\text{R}}}\left[\mathbf{·},k\right]$ and $\widehat{\mathbf{\text{C}}}\left[\mathbf{·},k\right]$, without reestimating ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}$ completely at each substep.

6.4. Convergence and tempered regularization.

The algorithms in Sections 6.2 and 6.3 both monotonically decrease the objective function at each substep, and thus both converge to a coordinatewise optimum. For (7) the objective function and solution space are both convex, and the algorithm with fixed modules tends to converge to a global optimum, as observed for the BIDIFAC method Park and Lock (2020). However, the stepwise updating of R and C in Section 6.3 can get stuck at coordinatewise optima, analogous to stepwise variable selection in a predictive model. In practice, we find that the convergence of the algorithm improves substantially if the initial iterations use a high nuclear norm penalty that gradually decreases to the desired level of penalization. Thus, in our implementation for the first iteration the penalties are set to ${\tilde{\lambda }}_k=\alpha {\lambda }_k$ for k = 1, … , K and some α > 1. The penalties then gradually decrease over each subsequent iteration of the algorithm before reaching the desired level of regularization (α = 1).

7. Uniqueness.

Here, we consider the uniqueness of the decomposition in (4) under the objective (7). To account for permutation invariance of the K modules, throughout this section we assume that R and C are fixed and that they enumerate all of the K = (2^I − 1)(2^J − 1) possible modules. Note that the solution may still be sparse, with ${\mathbf{\text{S}}}_{\mathbf{..}}^{(k)}=\mathbf{0}$ for some or most of the modules. Without loss of generality, we fix R and C, as in Supplementary Material Appendix A (Lock, Park and Hoadley (2022)). Then, let ${\mathbb{S}}_{\widehat{X}}$ be the set of possible decompositions that yield a given approximation $\widehat{\mathbf{\text{X}}}\mathbf{..}$,

$${\mathbb{S}}_{\widehat{X}}=\left\{{\{S_{\mathbf{.}}^{(k)}\}}_{k=1}^K\mid \widehat{X}\mathbf{..}=\sum _{k=1}^K{S}_{\mathbf{..}}^{(k)}\right\}.$$

If either I > 1 or J > 1, then the cardinality of ${\mathbb{S}}_{\widehat{X}}$ is infinite; that is, there are an infinite number of ways to decompose $\widehat{\mathbf{\text{X}}}\mathbf{..}$. Thus, model (4) is clearly not identifiable, in general, even in the no-noise case E.. = 0. However, optimizing the structured nuclear norm penalty in (7) may uniquely identify the decomposition; let f_pen(·) give this penalty,

$$f_{\text{pen}}({\{S_{\mathbf{..}}^{(k)}\}}_{k=1}^K)=\sum _{k=1}^K(\sqrt{R[\mathbf{·},k]\cdot M}+\sqrt{C[\mathbf{·},k]\cdot N}){\Vert S_{\mathbf{..}}^{(k)}\Vert }_{\ast }.$$

Proposition 5 gives an equivalence of the left and right singular vectors for any two decompositions that minimize f_pen(·).

Proposition 5.

Take two decompositions ${\{{\widehat{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K\in {\mathbb{S}}_{\widehat{X}}$, and ${\{{\tilde{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K\in {\mathbb{S}}_{\widehat{X}}$, and assume that both minimize the structured nuclear norm penalty,

$$f_{\text{pen}}({\{{\widehat{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K)=f_{\text{pen}}({\{{\tilde{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K)=\underset{{\mathbb{S}}_{\widehat{X}}}{\min }{f}_{\text{pen}}({\{S_{\mathbf{..}}^{(k)}\}}_{k=1}^K).$$

Then, ${\widehat{S}}_{\mathbf{..}}^{(k)}=U_{\mathbf{.}}^{(k)}\widehat{D}{V}_{\mathbf{.}}^{(k)T}$ and ${\widehat{S}}_{\mathbf{..}}^{(k)}=U_{\mathbf{.}}^{(k)}{\tilde{D}}^{(k)}{V}_{\mathbf{.}}^{(k)T}$, where $U_{\mathbf{.}}^{(k)}:M\times R_k$ and $V_{\mathbf{.}}^{(k)}:N\times R_k$ have orthonormal columns and ${\widehat{\mathbf{\text{D}}}}^{\left(k\right)}$ and ${\widetilde{\mathbf{\text{D}}}}^{\left(k\right)}$ are diagonal.

The proof of Proposition 5 uses two novel lemmas (see Supplementary Material Appendix B (Lock, Park and Hoadley (2022))): one establishing that ${\widehat{S}}_{\mathbf{..}}^{(k)}$ and ${\tilde{S}}_{\mathbf{..}}^{(k)}$ must be additive in the nuclear norm, ${\Vert {\widehat{S}}_{\mathbf{..}}^{(k)}+{\tilde{S}}_{\mathbf{..}}^{(k)}\Vert }_{*}={\Vert {\widehat{S}}_{\mathbf{..}}^{(k)}\Vert }_{\ast }+{\Vert {\tilde{S}}_{\mathbf{..}}^{(k)}\Vert }_{\ast }$ and a general result establishing that any two matrices that are additive in the nuclear norm must have the equivalence in Proposition 5.

Proposition 5 implies that left or right singular vectors of ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}({\widehat{\mathbf{\text{D}}}}^{\left(k\right)}\left[r,r\right]>0)$ are either shared with ${\widehat{S}}_{\mathbf{..}}^{(k)}(\text{if}{\widetilde{\mathbf{\text{D}}}}^{\left(k\right)}\left[r,r\right]>0)$ or orthogonal to ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}(\text{if}{\widetilde{\mathbf{\text{D}}}}^{\left(k\right)}\left[r,r\right]=0)$. For uniqueness, one must establish that ${\widehat{\mathbf{\text{D}}}}^{\left(k\right)}\left[r,r\right]={\widetilde{\mathbf{\text{D}}}}^{\left(k\right)}\left[r,r\right]$ for all k and r. Theorem 1 gives sufficient conditions for uniqueness of the decomposition.

Theorem 1.

Consider ${\{{\widehat{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K\in {\mathbb{S}}_{\widehat{X}}$, and let $U_{\mathbf{.}}^{(k)}{\widehat{D}}^{(k)}{\mathbf{\text{V}}}_{\mathbf{.}}^{(k)T}$ give the SVD of ${\widehat{S}}_{\mathbf{..}}^{(k)}$ for k = 1, … , K. The following three properties uniquely identify ${\{{\widehat{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K$:

1. ${\{{\widehat{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K$ minimizes $f_{\text{pen}}(\cdot )over{\mathbb{S}}_{\widehat{X}}$,

2. $\{{\widehat{\mathbf{\text{U}}}}_i^{(k)}[\mathbf{·},r]:R[i,k]=1and{\widehat{\mathbf{\text{D}}}}^{(k)}[r,r]>0\}$ are linearly independent for i = 1, … I,

3. $\{{\widehat{\mathbf{\text{V}}}}_j^{(k)}[\mathbf{·},r]:C[j,k]=1and{\widehat{\mathbf{\text{D}}}}^{(k)}[r,r]>0\}$ are linearly independent for j = 1, … , J.

The linear independence conditions (2. and 3.) are, in general, not sufficient, and several related integrative factorization methods, such as JIVE (Lock et al. (2013)) and SLIDE (Gaynanova and Li (2019)), achieve identifiability via stronger orthogonality conditions across the terms of the decomposition. Theorem 1 implies that orthogonality is not necessary under the penalty f_pen(·). Conditions 2 and 3 are straightforward to verify for any ${\{{\widehat{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K$, and they will generally hold whenever the ranks in the estimated factorization are small relative to the dimensions ${\{M_i\}}_{i=1}^I$ and ${\{N_j\}}_{j=1}^J$. Moreover, the conditions of Theorem 1 are only sufficient for uniqueness; there may be cases for which the minimizer of f_pen(·) is unique and the terms of its decomposition are not linearly independent. Theorem 1 implies uniqueness of the BIDIFAC decomposition (Park and Lock (2020)) under linear independence as a special case which is a novel result.

8. Bayesian interpretation.

Express the BIDIFAC+ model (6) in factorized form

$$X\mathbf{..}=\sum _{k=1}^K{U}_{.}^{(k)}{V}_{.}^{(k)T}+E\mathbf{..},$$ (10)

where

$$U_{\mathbf{.}}^{{(k)}^{\prime }}={[U_1^{{(k)}^{\prime }}\cdots U_I^{{(k)}^{\prime }}]}^{\prime }\text{with}{U}_i^{(k)}=M_1\times R_k\text{and}{U}_i^{(k)}=0_{M_1\times R_k}\text{if}R[i,k]=1$$ (11)

for all i and k, and

$${\mathbf{\text{V}}}_{\mathbf{.}}^{(k)}=[{\mathbf{\text{V}}}_1^{(k)}\cdots {\mathbf{\text{V}}}_J^{(k)}]\mathrm{with}{\mathbf{\text{V}}}_i^{(k)}=N_j\times R_k\text{and}{\mathbf{\text{V}}}_i^{(k)}=0_{N_j\times R_k}\text{if}\mathbf{\text{C}}[j,k]=1$$ (12)

for all j and k. The structured nuclear norm objective (7) can also be represented by L₂ penalties on the factorization components ${\mathbf{\text{U}}}_{\mathbf{.}}^{(k)}$ and ${\mathbf{\text{V}}}_{\mathbf{.}}^{(k)}$. We formally state this equivalence in Proposition 6 which extends analogous results for a single matrix (Mazumder, Hastie and Tibshirani (2010)) and for the BIDIFAC framework (Park and Lock (2020)).

Proposition 6.

Fix R and C. Let ${\{{\widehat{U}}_{·}^{(k)}\}}_{k=1}^K$ and ${\{{\widehat{V}}_{\mathbf{.}}^{(k)}\}}_{k=1}^K$ minimize

$${\Vert X\mathbf{..}-\sum _{k=1}^K{U}_{\mathbf{.}}^{(k)},V_{\mathbf{.}}^{(k)}\Vert }_F^2+\sum _{k=1}^K{\lambda }_k({\Vert U_{\mathbf{.}}^{(k)}\Vert }_F^2+{\Vert V_{\mathbf{.}}^{(k)}\Vert }_F^2)$$ (13)

with the restrictions (11) and (12). Then, ${\{{\widehat{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K$ solves (7), where ${\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}={\widehat{\mathbf{\text{U}}}}_{\mathbf{.}}^{(k)}{\widehat{\mathbf{\text{V}}}}_{\mathbf{.}}^{(k)T}$ for k = 1,…, K.

From (13), it is apparent that our objective gives the mode of a Bayesian posterior with normal priors on the errors and the factorization components, as stated in Proposition 7.

Proposition 7.

Let the entries of E.. be independent Normal(0, 1), the entries of $U_i^{(k)}$ be independent Normal(0, τ²) if R[i, k] = 1, and the entries of ${\mathbf{\text{V}}}_j^{(k)}$ be independent Normal $(0,{\tau }_k^2)$ if C[j, k] = 1, where ${\tau }_k^2=1/{\lambda }_k$. Then, (13) is proportional to the log of the joint likelihood

$$p(X\mathbf{..},{\{U_{\mathbf{.}}^{(k)}\}}_{k=1}^K,{\{V_{\mathbf{.}}^{(k)}\}}_{k=1}^K\mid R,C).$$

9. Missing data imputation.

The probabilistic formulation of the objective, described in Section 8, motivates a modified expectation-maximization (EM)-algorithm approach to impute missing data. Let $\mathcal{M}$ index observations in the full dataset X.. that are unobserved: $\mathcal{M}=\{(m,n):X\mathbf{..}[m,n]\text{is missing}\}$. Our iterative algorithm for missing data imputation proceeds as follows:

1. Initialize $\widehat{\mathbf{\text{X}}}\mathbf{..}$ by

   $$\widehat{X\mathbf{..}}[m,n]=\{\begin{array}{ll}X\mathbf{..}[m,n]& \text{if}(m,n)\notin \mathcal{M},\\ 0& \text{if}(m,n)\in \mathcal{M}.\end{array}$$

2. M-step: Estimate ${\{{\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K$ by optimizing (7) for $\widehat{\mathbf{\text{X}}}\mathbf{..}$.

3. E-step: Update $\widehat{\mathbf{\text{X}}}\mathbf{..}$ by $\widehat{\mathbf{\text{X}}}\mathbf{..}\left[m,n\right]={\sum }_{k=1}^K{\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{(k)}\left[m,n\right]$.

4. Repeat steps 2 and 3 until convergence.

Analogous approaches to imputation for other low-rank factorization techniques have been proposed (Kurucz, Benczúr and Csalogány (2007), O’Connell and Lock (2019), Park and Lock (2020), Mazumder, Hastie and Tibshirani (2010)). Due to centering, initializing missing data to 0 in step 1 is equivalent to starting with mean imputation which is used by other SVD-based imputation approaches (Mazumder, Hastie and Tibshirani (2010), Kurucz, Benczúr and Csalogány (2007)); however, in practice, random initializations can also be used. The M-step maximizes the joint density for the model in Proposition 7, where ${\widehat{S}}_{\mathbf{..}}^{(k)}={\widehat{U}}_{\mathbf{.}}^{(k)}{\widehat{V}}_{\mathbf{.}}^{(k)T}$ for k = 1, … , K. The E-step updates the log joint density with its conditional expectation over $\{X\mathbf{..}[m,n]:(m,n)\in \mathcal{M}\}$ by an argument analogous to that in Zhang et al. (2005). Thus, the approach is an EM-algorithm for maximum a posteriori imputation under the model in Section 8, and it is also a direct block coordinate descent of objective (7) over ${\{S_{\mathbf{..}}^{(k)}\}}_{k=1}^K$ and $\{X\mathbf{..}[m,n]:(m,n)\in \mathcal{M}\}$. Crucially, for our context the method can be used to impute data that may be missing from an entire column or an entire row of each X_ij or, in certain cases, can even be used to impute an entire matrix X_ij, based on joint structure.

10. Application to TCGA data.

10.1. Data acquisition and preprocessing.

Our data were curated for the TCGA Pan-Cancer Project and were used for the pan-cancer clustering analysis described in Hoadley et al. (2018). We used data from four (I = 4) omics sources: (1) batch-corrected RNA-Seq data capturing (mRNA) expression for 20, 531 genes, (2) batch-corrected miRNA-Seq data capturing expression for 743 miRNAs, (3) between-platform normalized data from the Illumina 27K and 450K platforms capturing DNA methylation levels for 22,601 CpG sites, and (4) batch-corrected reverse-phase protein array data capturing abundance for 198 proteins. These data are available for download at https://gdc.cancer.gov/about-data/publications/PanCan-CellOfOrigin [accessed 11/19/2019]. We consider data for N = 6973 tumor samples from different individuals with all four omics sources available; these tumor samples represent J = 29 different cancer types, listed in Table 1.

Table 1.

TCGA acronyms for the 29 different cancer types considered

Acronym	Cancer type	Acronym	Cancer type
ACC	Adrenocortical carcinoma	BLCA	Bladder urothelial carcinoma
BRCA	Breast invasive carcinoma	CESC	Cervical carcinoma
CHOL	Cholangiocarcinoma	CORE	Colorectal adenocarcinoma
DLBC	Diffuse large B-cell lymphoma	ESCA	Esophageal carcinoma
HNSC	Head/neck squamous cell	KICH	Kidney chromophobe
KIRC	Kidney renal clear cell	KIRP	Kidney renal papillary cell
LGG	Brain lower grade glioma	LIHC	Liver hepatocellular carcinoma
LUAD	Lung adenocarcinoma	LUSC	Lung squamous cell carcinoma
MESO	Mesothelioma	OV	Ovarian cancer
PAAD	Pancreatic adenocarcinoma	PCPG	Pheochromocytoma and paraganglioma
PRAD	Prostate adenocarcinoma	SARC	Sarcoma
SKCM	Skin cutaneous melanoma	STAD	Stomach adenocarcinoma
TGCT	Testicular germ cell tumors	THCA	Thyroid carcinoma
THYM	Thymoma	UCEC	Uterine corpus endometrial carcinoma
UCS	Uterine carcinosarcoma

We log-transformed the counts for the RNA-Seq and miRNA-Seq sources. To remove baseline differences between cancer types, we center each data source to have mean 0 across all rows for each cancer type,

$$\text{mean}\left(X_{ij}[m,\mathbf{·}]\right)=0\text{for all}i,j,m.$$

We filter to the 1000 genes and the 1000 methylation CpG probes that have the highest standard deviation after centering, leaving M₁ = 1000 genes, M₂ = 743 miRNAs, M₃ = 1000 CpGs, and M₄ = 198 proteins. Lastly, to account for differences in scale we standardize so that each variable has standard deviation 1,

$$\text{SD}\left(X_i\mathbf{.}[m,\mathbf{·}]\right)=1\text{for all}i,m.$$

This is a conservative alternative to scaling by an estimate of the noise variance, as mentioned in Section 6.1.

10.2. Factorization results.

We apply the BIDIFAC+ method to the complete-case data with I = 4 omics sources and J = 29 cancer types. We simultaneously estimate a maximum of K = 50 low-rank modules; all modules are nonzero, but the variation explained by the smaller modules are negligible. Figure 2 gives the total variance explained by each module, ${\Vert {\widehat{\mathbf{\text{S}}}}_{\mathbf{..}}^{\left(k\right)}\Vert }_F^2$, for k = 1, … , 50 in decreasing order. The top 15 modules, ordered by total variance, explained are given in Table 2, and all 50 modules are given in the Supplementary Material Spreadsheet S1 (Lock, Park and Hoadley (2022)). The first module explains global variation, with all cancer types and all omics sources included. Other modules that explain substantial variability across all or almost all cancer types are specific to each omics source: miRNA (Module 2), methylation (Module 3), gene expression (Module 5), and Protein (Module 8).

Fig. 2.

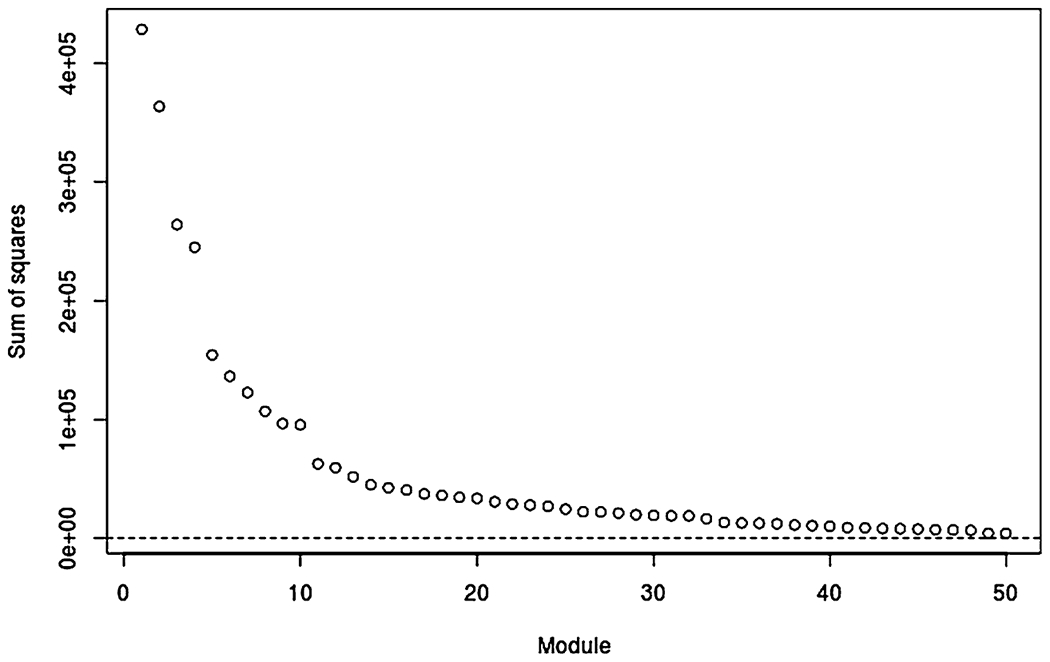
Total sum of squared entries in each of the 50 modules, ordered from largest to smallest.

Table 2.

Cancer types and sources for the first 15 modules, ordered by variation explained

Module	Rank	Cancer types	Omics sources
1	37	All cancers	mRNA miRNA Meth Protein
2	25	All cancers	miRNA
3	22	BLCA BRCA CESC CHOL CORE DLBC ESCA HNSC LIHC LUAD LUSC OV PAAD PRAD SKCM STAD TGCT UCEC UCS	Meth
4	10	ACC BLCA CHOL CORE DLBC ESCA HNSC KICH KIRC KIRP LGG LIHC LUAD LUSC MESO PAAD PCPG SARC SKCM STAD THCA THYM	mRNA Meth
5	24	All cancers	mRNA
6	17	BRCA	mRNA miRNA Meth Protein
7	15	LGG	mRNA miRNA Protein
8	20	All cancers *but* LGG	Protein
9	15	THCA	mRNA miRNA Protein
10	20	All cancers *but* LGG and TGCT	miRNA
11	15	CHOL KIRC KIRP LIHC	mRNA miRNA Meth Protein
12	34	LGG	Meth
13	20	BLCA CESC CORE ESCA HNSC LUSC SARC STAD	mRNA miRNA Meth Protein
14	8	KICH KIRC KIRP	mRNA miRNA Protein
15	21	BLCA BRCA CESC CHOL ESCA HNSC LUAD LUSC PAAD PRAD SKCM STAD TGCT UCEC UCS	mRNA miRNA

The module that explains the fourth most variation (Module 4) identifies structure in the genes and DNA methylation that explains variation in 22 of the 29 cancer types; we focus on this module as an illustrative example. The cancer types *not* included in Module 4 are BRCA (breast), CESC (cervical), OV (ovarian), PRAD (prostate), TGCT (testicular), UCEC (uterine endometrial), and UCS (uterine). Interestingly, all tumor types that were excluded were cancers specific to either males or females (or heavily skewed in BRCA); while cancer types included have both sexes. Figure 3 shows that Module 4 is indeed dominated by a single component that corresponds to molecular differences between the sexes. The gene loadings for this component are negligible, except for those on the Y chromosome and two genes on the X chromosome that are responsible for X-inactivation in females, XIST and TSIX; the methylation loadings are negligible, except for those in the X chromosome. These results are an intuitive illustration of the method, revealing a multiomic molecular signal that explains heterogeneity in some cancer types, but not all cancer types (only those that have both males and females).

Fig. 3.

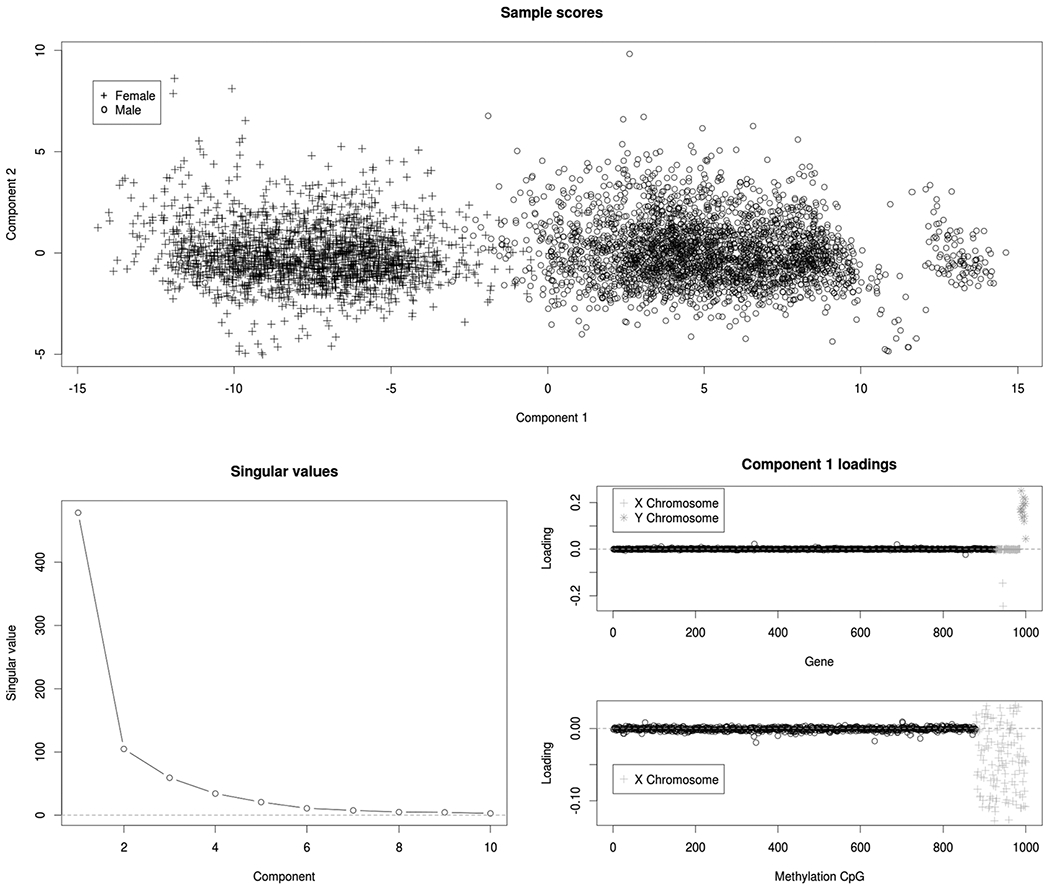
For Module 4: Sample scores for the first two components (top), scree plot of singular values (bottom left), and loadings on genes and methylation CpGs (bottom right) for the first component. This module includes 22 cancer types with samples from both sexes, and it is dominated by molecular signals that distinguish males from females.

The module that explains the sixth most variation (Module 6) identifies structure across all four omics sources that explains variation in the breast cancer (BRCA) samples only. Figure 4 shows that the first two components in this module are driven primarily by distinctions between the PAM50 molecular subtypes for BRCA (Network et al. (2012)). Thus, our analysis suggests that molecular signals that distinguish these subtypes are present across all four omics sources, but that these signals do not explain substantial variation within any other type of cancer considered.

Fig. 4.

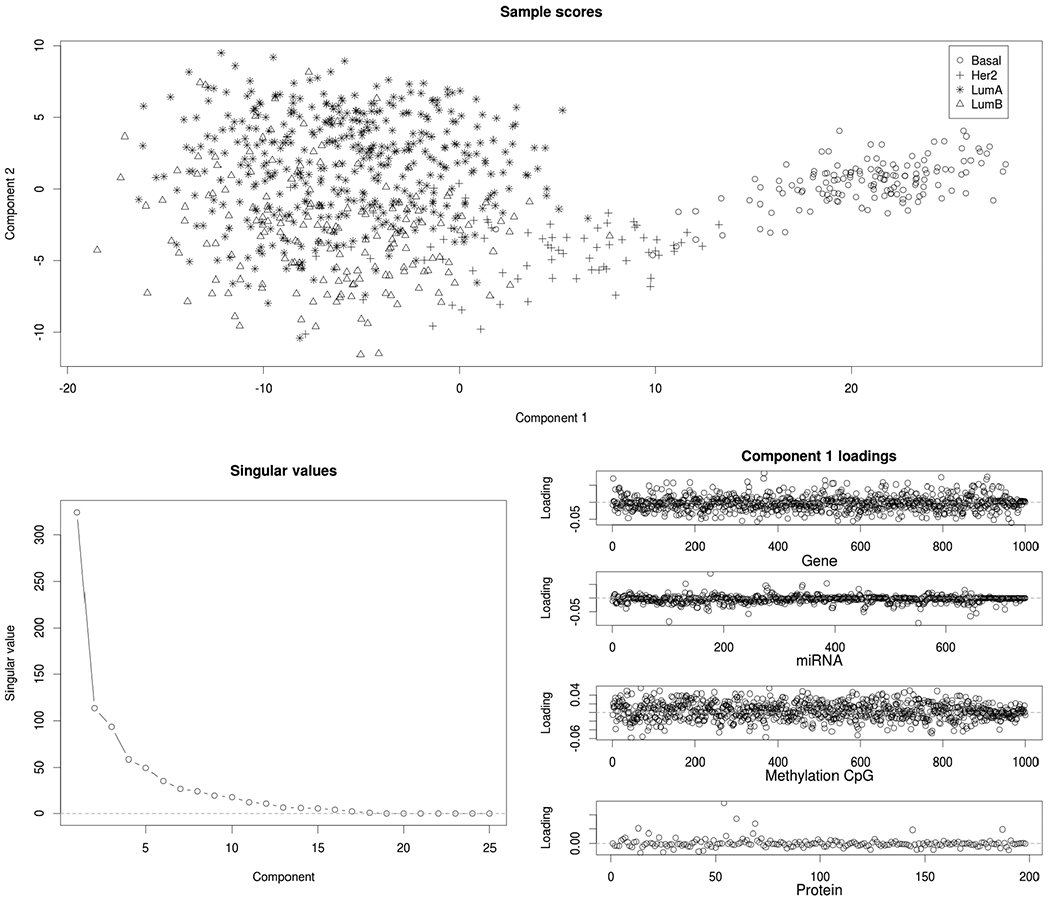
For Module 6: Sample scores for the first two components (top), scree plot of singular values (bottom left), and loadings for all four omics platforms (bottom right). This module includes only breast (BRCA) tumor samples, and it is dominated by molecular signals that distinguish the PAM50 subtypes (Bsasal, Her2, LumA, and LumB).

Several other modules explain variability in just one type of type of cancer, including LGG (Module 7: mRNA, miRNA and Protein), THCA (Module 9), UCEC (Module 16), and PRAD (Modules 18 and 19). Module 12, which is specific to LGG methylation, reveals distinct clustering by mutation status of the IDH genes (see Figure 5). IDH mutations have been shown to lead to a distinct CpG-island hypermethylated phenotype (Noushmehr et al. (2010)). Other modules explain variability in multiple cancer types that share similarities regarding their origin or histology. For example, Module 14 explains variability within the three kidney cancers (KICH, KIRC, and KIRP), and digestive and gastrointestinal cancers (CORE, ESCA, PAAD, STAD) are represented in Modules 25 (methylation) and 28 (mRNA).

Fig. 5.

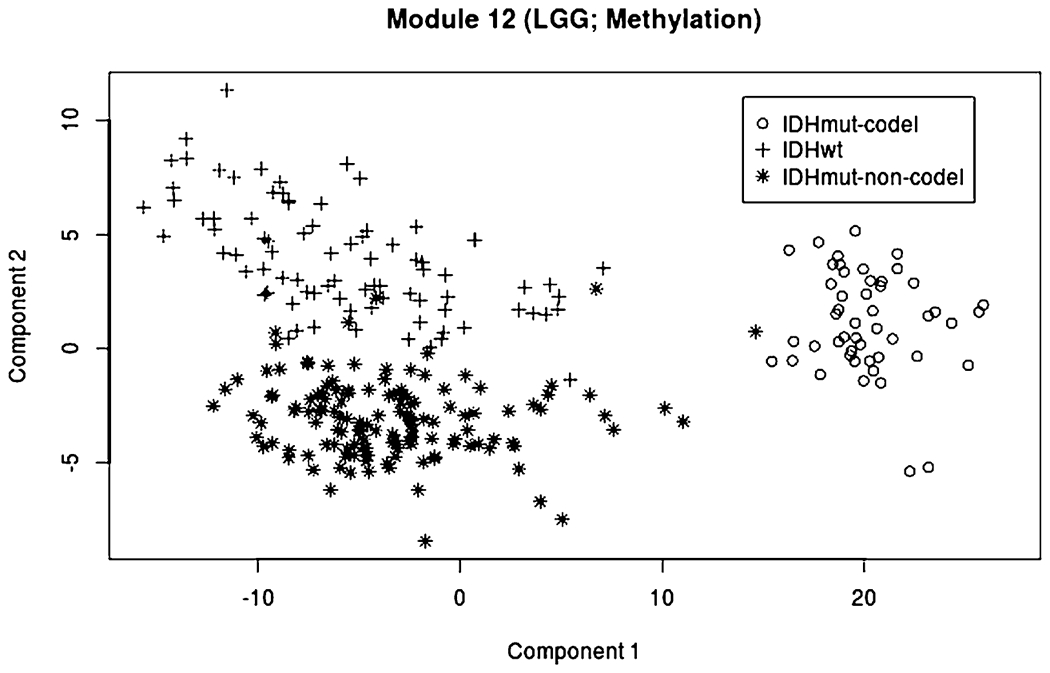
Scores for the first two components of Module 12 (LGG, methylation), with symbols and colors showing separation by IDH mutation status (wild-type, IDH mutant, and IDH mutant with codeletion).

To assess sensitivity of the results to the maximum number of modules $\tilde{K}=50$, we also performed the decomposition with $\tilde{K}=25$, 30, 35, 40, or 45. The resulting decompositions share several similarities. Nine of the 15 modules in Table 2 have a precise match in each of the six decompositions (Modules 1, 2, 4, 5, 6, 7, 9, 12, 14). Entrywise correlations for the terms $S_{\mathbf{..}}^{(k)}$ between matched modules ranged from r = 0.88 to r = 0.99. Other modules had slight variations to the cancer types and omics sources included. The modules for different $\tilde{K}$ are provided as separate tabs in Supplementary Material Spreadsheet S1 (Lock, Park and Hoadley (2022)). The overall structural approximations ${\sum }_{k=1}^{\tilde{K}}{\mathbf{\text{S}}}_{\mathbf{..}}^{\left(k\right)}$ were very similar across decompositions, with entrywise correlations all greater than r = 0.99.

10.3. Missing data imputation.

To assess the accuracy of missing data imputation using BIDIFAC+, we hold out observed entries, rows, and columns of each dataset in the pan-omics pan-cancer and impute them using the approach in Section 9. We randomly set 100 columns (samples) to missing for each of the four omic platforms, and we randomly set 100 rows (features) to missing for each of the 29 cancer types. We then randomly set 5000 of the values remaining in the joint matrix X.. to missing. We impute missing values using BIDIFAC+, as described in Section 9, and, for comparison, we use an analogous approach to imputation using four other low-rank factorizations: (1) soft-threshold (nuclear norm) SVD of the joint matrix X.., (2) soft-threshold SVD of each matrix X_ij, separately, (3) hard-threshold SVD (SVD approximation using the first R singular values) of X.., (4) hard-threshold SVD of each X_ij separately. For the soft-thresholding SVD methods, the penalty factor is estimated by random matrix theory, as in Section 5. For the hard-thresholding methods the ranks are determined by cross-validation by minimizing imputation error on an additional held-out cohort of the same size.

We consider the imputation error under the different methods, broken down by: (1) observed values, (2) values that are missing but have the rest of their row and column present (entrywise missing), (3) values that are missing their entire row, (4) values that are missing their entire column, and (5) values that are missing both their row and their column. For a given set of values $\mathcal{M}$, we compute the relative squared error as

$$\text{RSE}=\frac{{\sum }_{(m,n)\in \mathcal{M}}{(X\mathbf{..}[m,n]-\widehat{X}\mathbf{..}[m,n])}^2}{{\sum }_{(m,n)\in \mathcal{M}}X\mathbf{..}{[m,n]}^2},$$

where $\widehat{\mathbf{\text{X}}}\mathbf{..}$ is the structural approximation resulting from the given method. Table 3 gives the RSE for each method and for each missing condition. Imputation by BIDIFAC+ outperforms the other methods for each type of missingness, illustrating the advantages of decomposing joint and individual structures. The hard-thresholding approaches have much less error for the observed data than for the missing data, due to overfitting of the signal.

Table 3.

Imputation RSE under different approaches and different types of missingness

Method	Observed	Entrywise	Row	Column	Both
BIDIFAC+	0.510	0.558	0.670	0.807	0.881
Soft-SVD (joint)	0.531	0.621	0.678	0.834	0.894
Soft-SVD (separate)	0.564	0.610	1.000	1.000	1.000
Hard-SVD (joint)	0.431	0.559	0.829	0.908	1.200
Hard-SVD (separate)	0.344	0.581	1.000	1.000	1.000

11. Simulation studies.

11.1. Vertically linked simulations.

We conduct a simulation study to assess the accuracy of the BIDIFAC+ decomposition in the context of vertical integration, where there is a single shared column set (J = 1). For all scenarios we simulate data according to model (4), wherein the entries of the residual noise E.. are generated independently from a Normal(0, 1) distribution and the entries of each ${\mathbf{\text{U}}}_i^{\left(k\right)}$ and V^(k) are generated independently from a Normal (0, σ²) distribution.

We first consider a scenario with I = 3 matrices, each of dimension 100 × 100 (N = 100 and M₁ = M₂ = M₃ = 100), with low-rank modules that are shared jointly, shared across each pair of matrices and individual to each matrix,

$$R=\left[\begin{array}{lllllll}1& 1& 1& 0& 1& 0& 0\\ 1& 1& 0& 1& 0& 1& 0\\ 1& 0& 1& 1& 0& 0& 1\end{array}\right].$$ (14)

We consider a “low-rank” and a “high-rank” condition across three different signal-to-noise levels. For the low-rank condition, each of the seven modules has rank R = 1; for the high-rank condition, each module has rank R = 5. The variance of the factorized signal component, σ² is set to be $\sqrt{1/2}$, 1 or $\sqrt{10}$ so that the signal-to-noise ratio (s2n) of each components is 1/2, 1, or 10, respectively.

For each condition we apply four approaches to uncover the underlying decomposition:

1. BIDIFAC+, with R given by (14), as in the true generative model,

2. BIDIFAC+, with R estimated,

3. SLIDE, with R and the true ranks of each module (R = 1 or R = 5) provided,

4. SLIDE, with R and the ranks of each module estimated via the default cross-validation scheme.

We use SLIDE as the basis of comparison with BIDIFAC+, because it is the only other method that is designed to recover each term in the decomposition and it generally outperforms other vertically linked decomposition methods (Gaynanova and Li (2019), Park and Lock (2020)). For each case we compute the mean relative squared error (RSE) in recovering each module of the decomposition:

$$\text{RSE}=\frac{1}{K}\sum _{k=1}^K\frac{{\Vert S_{\mathbf{..}}^{(k)}-{\widehat{S}}_{\mathbf{..}}^{(k)}\Vert }_F^2}{{\Vert S_{\mathbf{..}}^{(k)}\Vert }_F^2}.$$ (15)

The mean RSE for each condition and under each approach is shown in Table 4, broken down by the global module, pairwise modules, and individual modules. BIDIFAC+ generally outperforms or performs similarly to SLIDE, even when the true ranks are used for the SLIDE implementation (the ranks are never fixed for BIDIFAC+). An exception is when the ranks and s2n ratio are small (rank = 1, s2n = 0.5), where BIDIFAC+ tends to overshrink the signal. BIDIFAC+ performs particularly well, relative to SLIDE, when the rank is large and s2n is high. One likely reason for this improvement is that the SLIDE model necessarily restricts the factorized components ${\mathbf{\text{U}}}_i^{\left(k\right)}$ and ${\mathbf{\text{V}}}^{\left(k\right)}$ to be mutually orthogonal, whereas BIDIFAC+ has no such constraint. This restriction can be limiting when decomposing generated signals that are independent but not orthogonal (Park and Lock (2020)). Moreover, when estimating the ranks, the SLIDE model can drastically underperform relative to using the true ranks. The results for BIDIFAC+, when fixing the true modules R vs. estimating R, are nearly identical; because all possible modules are present for this scenario, the two approaches are very similar despite subtle differences in the algorithms.

Table 4.

Comparison of BIDFAC+ and SLIDE signal decomposition RSE (I = 3 sources)

		BIDIFAC+		SLIDE
Scenario	Structure	True R	Estimated R	True ranks	Estimated ranks
Rank = 1, s2n = 0.5	Global	0.130	0.130	0.120	0.120
	Pairwise	0.157	0.156	0.103	0.103
	Individual	0.197	0.197	0.118	0.118
Rank = 1, s2n = 1	Global	0.060	0.060	0.084	0.084
	Pairwise	0.068	0.068	0.053	0.053
	Individual	0.070	0.070	0.048	0.048
Rank = 1, s2n = 0	Global	0.010	0.010	0.035	3.65
	Pairwise	0.005	0.005	0.027	1.00
	Individual	0.008	0.008	0.037	0.689
Rank = 5, s2n = 0.5	Global	0.270	0.270	0.276	0.869
	Pairwise	0.268	0.268	0.263	0.460
	Individual	0.329	0.329	0.306	0.317
Rank = 5, s2n = 1	Global	0.123	0.123	0.232	1.320
	Pairwise	0.121	0.121	0.189	0.674
	Individual	0.148	0.148	0.241	0.485
Rank = 5, s2n = 10	Global	0.080	0.080	0.233	2.36
	Pairwise	0.060	0.060	0.189	0.917
	Individual	0.089	0.089	0.249	0.703

We consider another scenario with a larger number of matrices (I = 10), each of dimension 100 × 100 (N = 100, M₁ = ⋯ = M₁₀ = 100) and sparsely distributed modules. We generate 10 low rank modules out of 2¹⁰ − 1 = 1023 possibilities that are present on (1) X₁₁ only, (2) X₁₁ and X₂₁, (3) X₁₁, X₂₁, and X₃₁, etc. We again consider low-rank (R = 1) and high-rank (R = 5) scenarios for all modules, and three signal-to-noise levels 0.5, 1, and 10. The resulting mean RSE (15) over all modules, for each approach, is shown in Table 5. Here, BIDIFAC+ with fixed true R generally performs better than estimating R; however, these gains are modest for most scenarios, suggesting the BIDIFAC+ generally does a good job of identifying which of the 1023 possible modules are nonzero.

Table 5.

Comparison of BIDFAC+ and SLIDE signal decomposition RSE (I = 10 sources)

		BIDIFAC+		SLIDE
Ranks	s2n	True R	Estimated R	True ranks	Estimated ranks
1	0.5	0.150	0.150	0.116	0.116
1	1	0.076	0.078	0.105	0.105
1	10	0.032	0.025	0.060	0.060
5	0.5	0.297	0.320	0.402	0.685
5	1	0.177	0.189	0.324	0.603
5	10	0.167	0.245	0.347	0.347

11.2. Missing data simulation.

Here, we assess the performance of missing data imputation for a 3 × 3 grid of matrices (I = J = 3) with X_ij : 100 × 100 for each i, j. Data X.. are generated as in model (6), with one fully shared module (R[·, 1] = C[·, 1] = [1, 1, 1]) and modules specific to each of the 9 matrices (R[·, 1] = C[·, 1] = [1, 0, 0], etc.). All modules have rank 5. The entries of residual noise are generated independently from a Normal(0, 1) distribution, and the entries of each ${\mathbf{\text{U}}}_i^{\left(k\right)}$ and ${\mathbf{\text{V}}}_i^{\left(k\right)}$ are generated independently from a Normal $(0,{\sigma }_k^2)$ distribution. We consider different levels of the joint signal strength ${\sigma }_j^2:={\sigma }_1^2$ and the matrix-specific (i.e., individual) signal strength ${\sigma }_i^2:={\sigma }_2^2=\cdots ={\sigma }_{10}^2$. We further consider scenarios with different kinds of missingness: (1) 1/9 of the entries in X.. missing at random, (2) 1/9 of the columns in each X_ij entirely missing at random, and (3) one of the nine datasets X_ij entirely missing.

For each scenario we impute missing values using the same approaches used in Section 10.3. For hard SVD imputation we use the true rank of the underlying structure. We consider three versions of BIDIFAC+ imputation: (1) initializing by setting missing values to 0, (2) initializing by generating missing values randomly from a N(0,1) distribution, and (3) initializing at 0 and fixing the modules R and C to match the data generation (i.e., one fully shared module and one module specific to each matrix). The resulting RSEs for the missing signal,

$$\text{RSE}=\frac{{\sum }_{(m,n)\in \mathcal{M}}{({\sum }_{k=1}^{10}{S}_{\mathbf{..}}^{(k)}[m,n]-\widehat{X}\mathbf{..}[m,n])}^2}{{\sum }_{(m,n)\in \mathcal{M}}{({\sum }_{k=1}^{10}{S}_{\mathbf{..}}^{(k)}[m,n])}^2},$$

are shown in Table 6, averaged over 100 replications. Imputation by BIDIFAC+ is flexible and performs relatively well across the different scenarios. As expected, the accuracy of columnwise and blockwise imputation depends strongly on the relative strength of the joint signal. Initializing missing values to 0 or randomly generated values gave very similar results, suggesting that either approach is reasonable in practice. BIDIFAC+ using the true R and C is comparable to estimating R and C across most scenarios. An exception is for block-missing data (i.e., missing an entire X_ij); in this context, there is some ambiguity on whether shared signals, defined by $\widehat{\mathbf{\text{R}}}$ and $\widehat{\mathbf{\text{C}}}$, include the missing block, and so the performance with the true R and C is slightly better. Also, as for other blocks, values for the missing block are imputed under the assumption of error variance 1 and mean 0; in practice, they cannot be transformed back to their original measurement scale without prior knowledge of the mean and error variance.

Table 6.

Imputation RSE under different approaches, for different types of missingness and joint and individual signal strengths (${\sigma }_j^2$ and ${\sigma }_i^2$, respectively)

	Entry missing			Column missing			Block missing
Joint signal $({\sigma }_j^2)$	$\sqrt{10}$	1	1	$\sqrt{10}$	1	1	$\sqrt{10}$	1	1
Individual signal $({\sigma }_i^2)$	1	1	$\sqrt{10}$	1	1	$\sqrt{10}$	1	1	$\sqrt{10}$
BIDIFAC+	0.01	0.06	0.01	0.11	0.56	0.93	0.16	0.57	0.94
BIDIFAC+ (random init)	0.01	0.06	0.01	0.11	0.56	0.93	0.16	0.57	0.94
BIDIFAC+ (true R, C)	0.01	0.06	0.01	0.10	0.55	0.92	0.10	0.52	0.93
Soft-SVD (joint)	0.03	0.15	0.04	0.11	0.58	0.94	0.10	0.53	0.93
Soft-SVD (separate)	0.02	0.09	0.02	1.00	1.00	1.00	1.00	1.00	1.00
Hard-SVD (joint)	0.01	0.06	0.01	0.99	2.02	0.99	1.26	2.15	1.04
Hard-SVD (separate)	0.01	0.03	0.01	1.00	1.00	1.00	1.00	1.00	1.00

11.3. Application-motivated simulation.

Here, we assess the recovery of the underlying structure and the accuracy of the decomposition into shared components for a bidimensionally linked scenario that reflects our motivating application in Section 10. We generate data by taking the estimated decomposition from Section 10.2 and adding independent noise to it. That is, we simulate

$$\tilde{X}\mathbf{..}=\sum _{k=1}^{50}\alpha {\widehat{S}}_{\mathbf{..}}^{(k)}+\tilde{E}\mathbf{..},$$

where ${\{{\widehat{S}}_{\mathbf{..}}^{(k)}\}}_{k=1}^K$ is the estimated decomposition from Section 10.2, the entries of $\tilde{E}\mathbf{..}$ are independent Normal(0, 1), and α > 0 is a parameter that controls the total signal-to-noise ratio. We consider three total signal-to-noise ratios, defined by

$$\text{s}2\text{n}=\mathrm{var}\left(\sum _{k=1}^{50}\alpha {\widehat{S}}_{\mathbf{..}}^{(k)}\right)/\mathrm{var}(\tilde{E})=\mathrm{var}\left(\sum _{k=1}^{50}\alpha {\widehat{S}}_{\mathbf{..}}^{(k)}\right),$$

s2n = 0.2, 0.5, and 5. The scenario with s2n = 0.5 corresponds most closely to the real data, for which the ratio of the estimated signal variance over the residual variance is 0.552. For each scenario we estimate the underlying decomposition using BIDIFAC+ with the true R and C fixed, and using BIDIFAC+ with estimated modules $\widetilde{\mathbf{\text{R}}}$ and $\widetilde{\mathbf{\text{C}}}$ and $\tilde{K}=50$. In each case we compute the RSE as follows:

$$\text{RSE}=\frac{1}{50}\sum _{k=1}^{50}\frac{{\Vert {\tilde{S}}_{\mathbf{..}}^{(k)}-\alpha {\widehat{S}}_{\mathbf{..}}^{(k)}\Vert }_F^2}{{\Vert \alpha S_{\mathbf{..}}^{(k)}\Vert }_F^2}.$$ (16)

When computing RSE, we permute the 50 modules so that $\tilde{R}[\mathbf{·},k]=R[\mathbf{·},k]$ and $\tilde{C}[\mathbf{·},k]=C[\mathbf{·},k]$, wherever possible, and set ${\tilde{S}}_{\mathbf{..}}^{(k)}=0$ if $\tilde{R}[\mathbf{·},k]\ne R[\mathbf{·},k]$ and $\tilde{C}[\mathbf{·},k]\ne C[\mathbf{·},k]$. We also compute the relative overall signal recovery (ROSR) as

$$\text{ROSR}=\frac{{\Vert {\sum }_{k=1}^K{\widehat{S}}_{\mathbf{..}}^{(k)}-{\sum }_{k=1}^K\alpha {\widehat{S}}_{\mathbf{..}}^{(k)}\Vert }_F^2}{{\Vert {\sum }_{k=1}^K\alpha S_{\mathbf{..}}^{(k)}\Vert }_F^2}.$$ (17)

The results are shown in Table 7 and demonstrate that the underlying decomposition is recovered reasonably well in most scenarios. However, the RSE for estimated modules is often substantially more than the RSE using the true modules, as the row and column sets defining the modules can be estimated incorrectly. Moreover, the overall signal recovery error (ROSR) is, generally, substantially less than the mean error in recovering each module (RSE), demonstrating how the decomposition can be estimated incorrectly, even if the overall signal is estimated with high accuracy.

Table 7.

Relative squared error of the decomposition (RSE) and relative overall signal recovery (ROSR) using BIDIFAC+ with known modules (R and C) and estimated modules ($\widehat{\mathbf{\text{R}}}$ and $\widehat{\mathbf{\text{C}}}$)

s2n	RSE(R, C)	RSE $(\widetilde{\mathbf{\text{R}}},\widetilde{\mathbf{\text{C}}})$	ROSR (R, C)	ROSR $(\widetilde{\mathbf{\text{R}}},\widetilde{\mathbf{\text{C}}})$
0.2	0.356	0.531	0.170	0.189
0.5	0.242	0.386	0.131	0.143
5	0.128	0.346	0.012	0.026

12. Discussion.

The successful integration of multiple large sources of data is a pivotal challenge for many modern analysis tasks. While several approaches have been developed, they largely do not apply to the context of bidimensionally linked matrices. BIDIFAC+ is a flexible approach for dimension reduction and decomposition of shared structures among bidimensionally linked matrices which is competitive with alternative methods that integrate over a single dimension (rows or columns). Here, we have focused primarily on the accuracy of the estimated decomposition and exploratory analysis of the results. BIDIFAC+ may also be used for other tasks, such as missing data imputation or as a dimension reduction step preceding statistical modeling (e.g., as in principal components regression). For these other tasks it is desirable to model statistical uncertainty and fully Bayesian extensions that capture the full posterior distribution about the mode in Section 8 are potentially very useful. Moreover, while we have explored the uniqueness of the decomposition under BIDFAC+, it is worthwhile to establish conditions that are both necessary and sufficient for its identifiability.

An implicit assumption of the BIDIFAC+ framework is that shared structures are present over complete submatrices. However, it is conceivable that structured variation may take other partially shared forms. For example, a pattern of variation in DNA methylation may exist across several cancer types but only regulate gene expression in some of those cancer types. Allowing for such shared structures, which do not exist over a complete submatrix, is an interesting direction of future work for which the separable form of the objective (13) may be useful. Moreover, the approach may be extended to account for different layers of granularity in the row and column sets; for example, it would be interesting to also identify shared and specific patterns of variability among known subtypes within each cancer type. We select penalty terms by random matrix theory which requires assumptions of independent error and homogenous variance; an alternative strategy is to use the imputation accuracy of held-out data as a metric for parameter selection.

Computing time for BIDIFAC+ can range from < five minutes for each simulation in Sections 11.1 and 11.2 to ≈ 24 hours until convergence for the pan-omics pan-cancer application in Section 10 and the accompanying simulation in Section 11.3. Thus, computational feasibility must be considered carefully or larger scale problems.

Our application to pan-omics pan-cancer data from TCGA revealed molecular patterns that explain variability across all or almost all types of cancer, both across omics platforms and within each omics platform. However, it also revealed patterns several instances in which patterns are specific to one or a small subset of cancers, and these often show sharp distinctions of previously known molecular subtypes (e.g., for BRCA and LGG). Interestingly, BRCA was the only tumor type that showed up with all four platforms in a module. Together, they strongly separated the Basal-like molecular subtype from other subtypes of breast cancer. This mirrors the analysis of individual data types in Network et al. (2012). The LGG data also split by both histological groups and mutation status, based on BIDFAC+, even though both were not included in the analysis. Module 7 included mRNA, miRNA, and protein and was predominantly driven by codeletion of 1p/19q which is predominantly observed in oligodendrogliomas and is associated with better overall survival. This mirrors the previous TCGA work that showed that the LGG could be predominately split by 1p/19q deletion, IHD1 status (Module 12, for methylation) or TP53 mutation status (Network (2015)). An important insight provided by BIDIFAC+ is that these molecular distinctions are specific to BRCA and LGG, respectively, suggesting that similar phenomena do not account for heterogeneity within other types of cancers. Other modules that are broadly shared across cancer types have potential to reveal relevant molecular signal that are undetectable within a single cancer type, especially those with smaller sample sizes. Beyond exploratory visualization, to systematically investigate the clinical relevance of the underlying modules one can cluster their structure to identify novel subtypes analogous to the approach described in Hellton and Thoresen (2016). Furthermore, one can use the results in a predictive model for a clinical outcome, analogous to the approach described in Kaplan and Lock (2017). We are currently pursuing the use of BIDIFAC+ results for these tasks.

Availability.

A GitHub repository for BIDIFAC+ is available at https://github.com/lockEF/bidifac, and R code for all analyses presented herein is provided in a supplemental zipped folder.