Molecular paradigms for biological mechanosensing

Abstract

Many proteins in living cells are subject to mechanical forces, which can be generated internally by molecular machines, or externally, e.g. by pressure gradients. In general, these forces fall in the piconewton range, which is similar in magnitude to forces experience by a molecule due to thermal fluctuations. While we would naively expect such moderate forces to produce only minimal changes, a wide variety of ‘mechanosensing’ proteins have evolved with functions that are responsive to forces in this regime. The goal of this review is to provide a physical chemistry perspective on protein-based molecular mechanosensing paradigms used in living systems, and how these paradigms can be being explored using novel computational methods.

Graphical Abstract

Overview

We are accustomed to experiencing mechanical forces on the macroscopic scale, the regime that we learn about in high school physics. Yet, at the same time that we might be pushing a child’s stroller, or blowing up a balloon for their birthday, analogous processes are simultaneously occurring throughout our bodies at the nanometer scale.

Pico-scale forces applied to nano-scale structures underlie a cells’ abilities to transport material, replicate, move, divide, grow, and heal. These processes are accomplished through the active physical deformation of multiple cellular materials including covalent biopolymers (DNA, RNA, collagen, etc), noncovalent cytoskeletal polymers (e.g. actin, microtubules), and cellular barriers (e.g. plasma membrane, bacterial cell wall). Many of these structures are central to the ways in which a cell interacts with its mechanical environment.

Given that so many sub-cellular objects are subject to mechanical perturbation, it is natural that mechanisms have evolved to sense and respond to force. In this perspective, we will describe a range of protein ‘mechanosensors,’ and explore what is and is not known about the various mechanisms by which their activity changes in response to mechanical forces. It would be impossible to review this vast area in a short perspective article, and so here we will describe a few key examples that illustrate the diversity of possible mechanisms of biomolecular mechanosensation, focusing on a few unifying themes. In particular, we will describe how proteins adapt their behavior to approximately constant piconewton-scale mechanical forces, and explain why the robustness of their behavior is surprising from a physical chemistry perspective.

General considerations

Thermal environment

A molecule in solution is constantly subjected to random forces due to thermal fluctuations. Physical chemists are familiar with the energy scale associated with these fluctuations, k_BT, with k_B being Boltzmann’s constant and T the temperature—or perhaps more conveniently, RT, with R being the ideal gas constant ~8.314 kJ/(mol K). As a rule of thumb, most biology and biochemistry experiments are performed at temperatures within 5% of ambient (~300K), where this energy scale is ~ 2.5 kJ/mol or ~ 0.60 kcal/mol.¹

Yet physical chemists are less likely to be familiar with the scale of thermal forces. To gain intuition into this question, we may express the energy scale associated with thermal fluctuations in units of force times distance: k_BT ~ 4.1pN nm. In other words, molecular machines that generate piconewtons of force must compete with thermal fluctuations of comparable magnitude in order to produce displacements of ~ 1nm, which is the relevant length scale for most proteins.¹ Within a cell, activity may contribute to correlated fluctuations which are more complex than those which give rise to Brownian motion, but we still expect these environmental forces to be of a similar magnitude.² Any mechanosensing protein must be robust to random force but able to convert a particular directed force into some kind of biochemical signal.

Linear response

In many cases, we would like to understand how a molecular mechanosensor responds to a constant applied force. This could be the result of time-averaging over the discrete action of many molecular motors, or because the environment of the protein is under constant tension as in a strained membrane or cytoskeletal structure. We are interested in how the conformational ensemble of a molecule changes in response to this constant force. At constant temperature, the probability of seeing a system in a specific configuration X is given by the Boltzmann distribution,

$$P(\mathit{X})=\frac{e^{-\beta U(\mathit{X})}}{\int d\mathit{X}{e}^{-\beta U(\mathit{X})}},$$ (1)

where β = (k_BT)⁻¹, and U(X) describes the potential energy of the entire system.^3,4

The effect of adding an external force F to the system is to “tilt” the energy landscape of the system in the direction of the pulling force, such that

$$P(\mathit{X},\mathit{F})=\frac{e^{-\beta U(\mathit{X})+\beta \mathit{F}\cdot \mathit{Q}(\mathit{X})}}{\int d\mathit{X}{e}^{-\beta U(\mathit{X})+\beta \mathit{F}\cdot \mathit{Q}(\mathit{X})}}.$$ (2)

Q(X) is a vector to which the force is applied (Fig. 1). If F and Q are parallel or antiparallel, F · Q(X) can be replaced by the magnitude ±FQ. This formula also applies if Q is a list of different positions/distances to which forces F are applied.

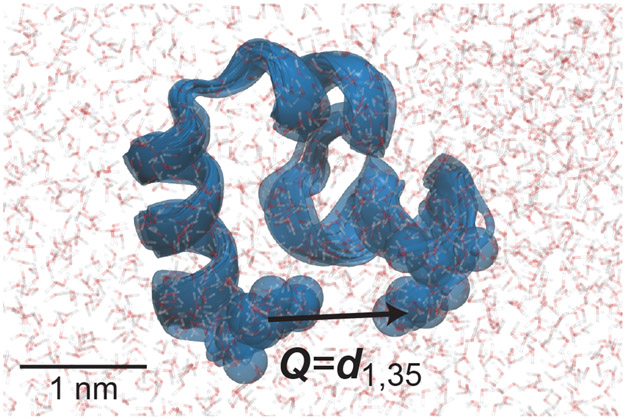
Figure 1:

HP35 (villin headpiece, PDB 1YRF) in water. Transparent protein shows five structures from 50 ns of MD simulation at 300K (see SI), illustrating the size of fluctuations produced by thermal forces. An arrow illustrates an example vector Q upon which a force might be applied, in this case between the C_α atoms at the N- to C- termini. Motion of beads highlighting these C_αs show thermal fluctuations in Q of ~0.2 nm, which is 20% of the average distance.

The value of any observable A(X) with applied force F (e.g. the radius of gyration of the protein) can be computed from this probability density by ensemble averaging: ³

$$\langle A{\rangle }_F=\int d\mathit{X}A(\mathit{X})P(\mathit{X},\mathit{F}).$$ (3)

The response of A to the force F is the change after applying force: ⟨δA⟩_F ≡ ⟨A⟩_F − ⟨A⟩₀.

We have asserted that piconewton forces are “small,” but how can we make that statement more precise? We show in the supporting information (SI) that for small forces,

$$\langle \delta \mathit{Q}{\rangle }_F=\beta \mathit{F}{\sigma }_Q^2,$$ (4)

where ${\sigma }_Q^2=\langle \delta \mathit{Q}\delta \mathit{Q}{\rangle }_0$ is the equilibrium variance of coordinate Q at zero force. This is the linear response regime, where the change in coordinate Q is directly proportional to (and in the same direction as) F. Statistical mechanical principles tell us that such a regime always exists for a sufficiently small applied force.⁶ The response is larger if the force is applied along a “floppy” direction in the protein.^a

What forces actually produce a linear response, where Eq. 4 is satisfied? We propose a rule-of-thumb that a force is in the linear response regime if it only changes the magnitude of Q relative to its equilibrium standard deviation by <10%, i.e.

$$0.1>\frac{\langle \delta Q{\rangle }_F}{{\sigma }_Q}=\beta F{\sigma }_Q\Rightarrow F<\frac{0.41\text{pNnm}}{{\sigma }_Q}$$ (5)

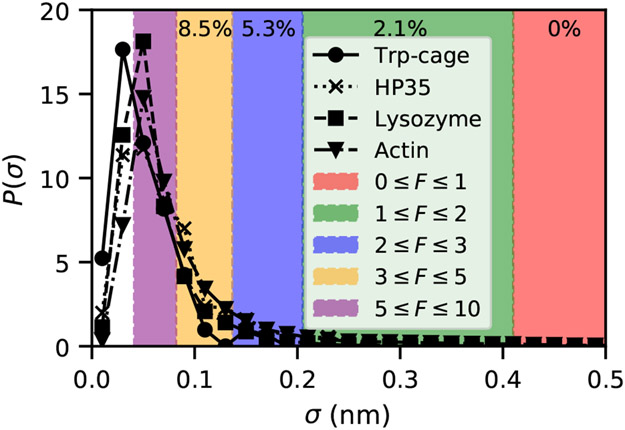
Therefore, whether a force is in the linear response regime also depends on how floppy the pulling coordinate is. In Fig. 2 we show what this regime looks like for four folded proteins. For these proteins, pulling on any pair of residues with forces < 1 pN satisfy the linear response bound in Eq. 5. Forces of < 5 pN are in the linear response regime for pulling on ≳ 85% of possible residue pairs in all four cases.

Figure 2:

Distribution of standard deviations of inter-residue distances over 50 ns of MD for four different protein systems. Actin data is from Ref. 5 and simulation details for other systems are described in the SI. Colored regions show for which forces linear-response along a particular residue-residue distance would be violated, according to Eq. 5. Percentages at the top reflect the fraction of distances in HP35 where linear response would be violated by a force in the colored regime.

The effect of constant force on kinetics and thermodynamics

Our qualitative understanding of the effects of force on molecular activity comes from considering systems that are well represented by two discrete states separated by a barrier along some reaction coordinate (e.g. folded/unfolded, open/closed) (Fig. 3). If a force is applied along this coordinate, it has the effect of “tilting” the energy landscape. For this one-dimensional problem U(Q, F) = U(Q) − FQ, where U is the potential energy and the negative sign defines a positive F as “pulling,” stabilizing larger Q. This tilt in the energy landscape has two important types of consequences:

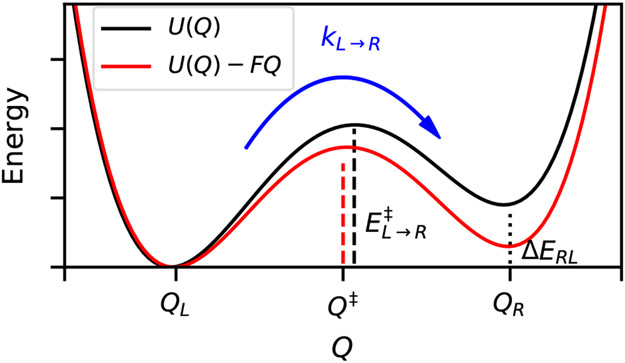
Figure 3:

Original potential U(Q) shows two states (Left, Right) separated by a barrier, which decreases when a force is applied. The rate constant k_L→R depends exponentially on the height of the barrier (vertical dashed line), which is the difference in energy between Q^‡ and Q_L. For small forces, the positions of Q_L, Q_R, and Q^‡ do not move much, but it is evident here that this force shifts the position of the transition state. In addition to the barrier, the applied force also decreases the energy difference between the two states, ΔE_RL.

1. It changes the equilibrium constant (K_eq). K_eq is the ratio of the probabilities of being in state right (R) versus state left (L), as shown in Fig. 3, K_eq = P(R)/P(L).³ As shown in the SI, to first approximation this results in K_eq = e^{−β(U(Q_R)−U(Q_L))} = e^−βΔE_RL. When force is applied, K_eq(F) = e^{−β(U(Q_R)−FQ_R−U(Q_L)+FQ_L)}. Therefore, force produces an exponential change K_eq(F) = K_eq(F = 0)e^{βF(Q_R−Q_L)}. Our sign convention is consistent—with Q_R > Q_L, positive F increases K_eq, favoring state R.

2. It changes the transition rates between the two states. The rate constant for crossing a sufficiently high barrier will follow Arrhenius kinetics, with k = Ae^−βE‡, where E^‡ is the energy of the barrier to be crossed, e.g. $E_{L\to R}^{‡}=U(Q^{‡})-U(Q_L)$.^3,6 Making the assumption that the force does not strongly affect the shape or location of the barrier, this implies k(F)/k(F = 0) = e^{−β(E‡(F)−E‡(0))} = e^{−β(U(Q‡,F)−U(Q_L,F)−E‡(0))} = e^{βF(Q‡−Q_L)}. That is, the rate constant for switching from L to R also scales exponentially with applied force.

This simple approach was applied to the case of cell adhesion proteins by Bell,⁷ with the two states being bound and unbound states of cell surface proteins. Bell’s Law for the unbinding rate constant is precisely the exponential kinetic relationship just described. A key question in the molecular biophysics community is to what molecules and to what extent this simple theoretical formulation (or more accurate extended versions thereof^8-10) applies. Bell’s Law requires assumptions to derive even when the pulling force occurs exactly along a one-dimensional reaction coordinate; hence as stated in Ref. 8, “uncritical use can lead to significant errors in the estimated intrinsic lifetime and the distance to the transition state.” In real situations, we should expect deviations except at very small forces, but it is not known a priori at what force this breakdown should occur; we will address this explicitly below.

Molecular mechanosensing paradigms

Mechanical Allostery

One conceptually simple form of molecular mechanotransduction is a single protein where the function or activity in one region is sensitive to mechanical forces applied to a different region. This concept is analogous to chemical allostery, where binding of a ligand in one location on a protein shifts its conformational ensemble such that binding or enzymatic activity in another region is altered.¹¹ An excellent example of allosteric mechanochemical coupling is the FimH system, discussed below.¹² This mechanical definition of allostery has been exploited both in the study of proteins, and in the design of programmable mechanical networks.^11,13,14

For mechanical allostery, we would like to know by which paths a mechanical signal is propagated from one side of a protein to another. This is equivalent to asking how some distances in the protein change when we perturb some other distances in the protein, which could be done by applying a force to the atoms in that region. For this, we need to compute the response of a quantity Q′ to a force applied along Q (e.g., see Fig. 4). For small forces, we can derive a formula analogous to Eq. 5, except the variance of quantity Q is replaced by the equilibrium covariance of Q and Q′ (see SI),

$$\langle \delta {\mathit{Q}}^{\prime }{\rangle }_F=\beta \langle \delta {\mathit{Q}}^{\prime }(\mathit{X})\delta \mathit{Q}(\mathit{X}){\rangle }_0\mathit{F}\equiv \beta \text{Cov}({\mathit{Q}}^{\prime },\mathit{Q})\mathit{F}$$ (6)

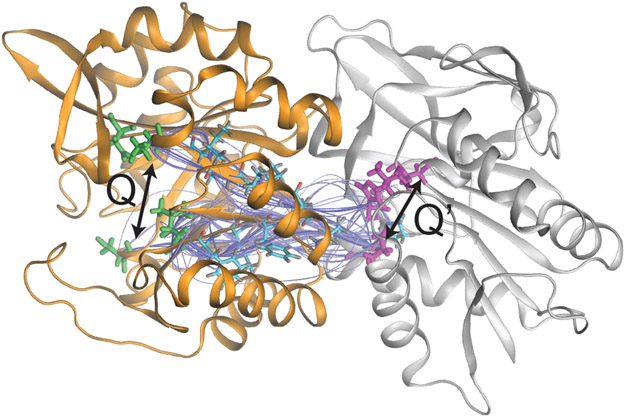
Figure 4:

Example of chemical allostery. The 100 shortest allosteric pathways from the residues at the end of the Q arrows to the residues indicated by the Q′ arrow for the protein IGPS, adapted from Ref. 15. In IGPS, binding a ligand near the highlighted residues in the orange/left domain accelerates catalysis of a chemical reaction in the white/right domain at the highlighted region by ~5000 fold.¹⁵

The covariance matrix of residue displacements is proportional to the inverse of the Hessian of an elastic network model, representing Gaussian fluctuations about the free energy minimum of the protein structure.¹⁵ Previous studies have exploited this connection to determine the importance of particular intermediate residues in propagating changes from one side of the protein to another during chemical allostery^15-17 (Fig. 4).

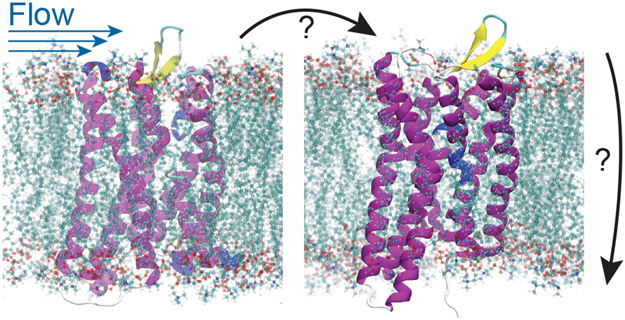
Mechanical allostery could play an important role in biological signaling processes. Here, a mechanical perturbation to a membrane protein on the outside of a cell would result in a change in activity of that protein on the inside of the cell. An example we are particularly interested in is the G-protein coupled receptor (GPCR) known as GPR68, which was recently shown to regulate flow through blood vessels by changing its activity in response to shear stress.¹⁸ This mechanical stimulus presumably changes the affinity of the receptor’s intracellular domain for a G-protein, in analogy with how typical GPCRs bind a ligand to modulate their G-protein binding affinity.

We estimate the in vivo shear forces applied in Ref. 18 to be in the piconewton regime, as with the other cases considered in this perspective. However, we do not know in this case how shear forces on a membrane protein perturb the structure as compared to a mechanical force applied at a particular point, or the role of the membrane drag in this process. One approach to this problem could be to follow Ref. 19, which demonstrated using Lattice Boltzmann MD that unfolding pathways can be quite different for flow induced forces versus mechanical pulling.

Stretch-activated Channels

Stretch-activated transmembrane channels constitute another important paradigm for molecular mechanosensation. These channels, which open in response to increases in membrane tension, were first discovered in muscle cells.²⁰ This is distinct from flow-activated membrane proteins, because these so-called stretch activated channels tend to open when radially symmetric force is imposed when the membrane itself is stretched.

The discovery of prokaryotic stretch-activated channels, however, provided what is now our best-understood model system for this class of mechanosensor.²¹ In bacteria, the only known physiological function of stretch-activated channels is to protect cells from exploding in response to hypoosmotic shocks (acute reduction of extracellular osmolarity), which cause an increase in the intracellular turgor pressure. Historically, it is believed that stretch-activated channels protect cells by releasing cytosolic solutes upon activation, thereby preventing or reversing increases in turgor.^22-24 However, this mechanism has not been carefully tested in vivo; another model proposes that the channels act as “slack” within the membrane, and reduce membrane tension upon cell swelling by contributing extra area to the membrane.^25-27 In principle, these mechanisms are not mutually exclusive.

Most bacterial species possesses multiple genes that encode distinct stretch-activated channels (e.g., E. coli has 6, B. subtilis has 4); these are classified based on their electrical conductance as measured in in vitro patch-clamp experiments.^21,23 In these experiments, micropipettes loaded with electrolyte solution are used to remove patches of membrane from cells, and then to apply constant hydrostatic pressure resulting in a constant tension within the membrane. Simultaneously, an electrode within the micropipette is used to apply a voltage and to measure the resulting electric current. Under tension, channels open and close stochastically; therefore, channels can be characterized by the threshold membrane tension at which channels are open 50% of the time as well as their conductance. Interestingly, these two variables are correlated: higher conductance channels typically have higher threshold tensions.^23,28

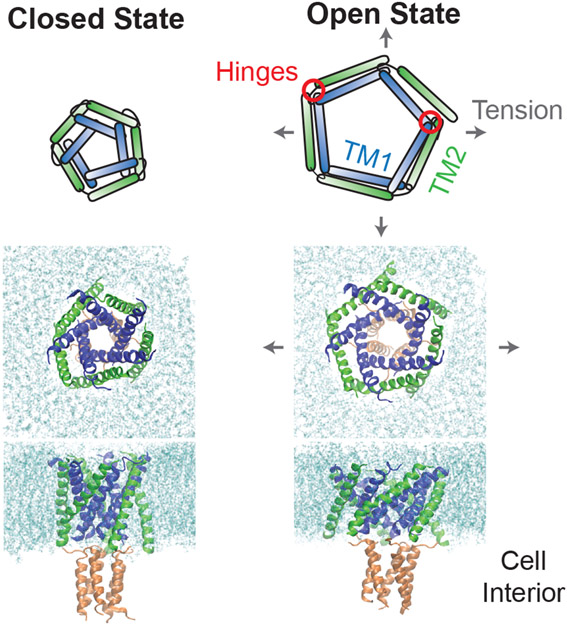
Structural and computational studies have revealed multiple distinct mechanisms of channel activation at the molecular level (Fig. 6).^29-31,33-38 The best understood mechanism is perhaps that exhibited by MscL, the channel with both the highest threshold tension and conductance. This channel is formed by a homopentamer of individual MscL polypeptide subunits (≈ 15 kDa per subunit). Each subunit has two transmembrane α-helices (called TM1 and TM2) connected by a short extracellular loop. When the subunits pentamerize into a channel, the hydrophobic TM1 domains form the surface of the channel pore, while the TM2 domains form the outer surface of the channel that interacts with phospholipids. The prevailing model for channel activation is that tension in the membrane applies an outward radial force to the TM2 domains, which are initially oriented roughly perpendicular to the membrane surface. Each TM2 domain transduces this force to its respective TM1 domain through a distributed “hinge” comprised of a interface of residues between the two TM domains near the extracellular loop. Each TM1 domain is also connected to a TM1 domain from a neighboring subunit via a second “hinge” near the cytosolic surface of the membrane, providing an additional constraint for global conformational change of the channel. The net results of this system are that (1) TM1 and TM2 domains rotate with respect to each other, and (2) both domains tilt toward the plane of the membrane, increasing the component of their length within this plane, which increases the radius of the channel. The opening of MscL is thus often compared to that of an iris since twisting of the channel couples to widening of its pore. ³³

Figure 6:

(Top) Schematic of MscL’s opening mechanism described in the main text.^29,30 (Middle and Bottom) Preliminary MD simulations of MscL opening following exactly the protocol of Ref. 31, applied to a B. subtilis homology model generated with the swiss-model server.³² An osmotic pressure imbalance between the cellular interior and exterior results in a lateral stretching of the bacterial membrane. The tension on the lipids is transferred to the protein, causing a rearrangement and flattening of the transmembrane domains, and the opening of a pore sufficient for conductance.

Interestingly, the next largest channel class, MscS, uses a completely different molecular mechanism of force transduction that, in essence, relies on a series of “levers” rather than a series of “hinges”, demonstrating the richness of investigating stretch-activated channels as models of molecular mechanosensors.^35,39,40

Despite intense investigation into stretch-activated channels, key questions remain with respect to the molecular mechanism of activation and physiology:

1. What triggers activation in vivo? All studies of channel activation have been performed in vitro or in silico. There is currently no reporter for activation that allows us to monitor opening in real-time within living cells. Such a reporter is sorely needed since recent single-cell data challenges the conventional paradigm for channel function formed from patch-clamp experiments.²⁶

2. Why are there so many channel orthologues? Bacteria encode multiple stretch-activated channels with different activation characteristics, which historically been interpreted as an indication of hierarchical channel activation that can be precisely tuned to hypoosmotic shock magnitude. However, the various channels have different gating mechanisms, which may indicate that they respond to fundamentally different forms of stimuli (e.g. membrane tension, loading rate, membrane bending) and serve distinct physiological function in addition to protection from hypoosmotic shock.

3. Why are there so many copies of each channel? Channels are typically expressed in large copy numbers (< 1000) even though it is predicted that only a few channels would be sufficient to protect cells from rupture.⁴¹ This discrepancy may again underlie new roles for channels or new mechanisms by which they protect cells from hypoosmotic shocks, including mechanisms by which direct interaction between channels plays a role in the gating mechanism.⁴²

Our current interest is deciphering the molecular mechanisms of stretch-activated channel activation and exploring the alternative physiological roles that different stretch-activated channel classes may serve. To achieve this, novel experimental and computational techniques need to be developed and applied to match the complexity of this system at the single-cell and cell population levels. In addition, the framework developed in the context of bacterial mechanosensation can be directly applied to the understanding of more complicated systems like the mechanosensitive nucleocyto-plasmic shuttling process in Eukaryotes, which depends on cell’s substrate stiffness, cellular deformation, and increasing membrane tension to regulate the intracellular concentration of the transcriptional activator YAP.⁴³

Peptide tension sensors

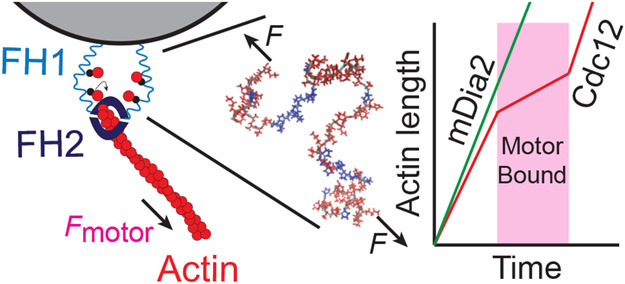
The deformation of a molecule at small force is proportional to the force applied (Eq. 4), which means that it acts as a linear spring, with spring constant $k_{B}T∕{\sigma }_Q^2$. This suggests that disordered peptides or protein regions could be important in some mechanosensing processes, since they can be easily deformed using small forces. Several years ago, we helped show that this is a key mechanism in the regulation of actin polymerization by a yeast protein called formin Cdc12.⁴⁴ Formins have a donut shaped domain that attaches to the growing end of an actin filament, and floppy ‘arms’ of over 100 amino acids that contain actin binding domains, which are believed to increase the local concentration of actin near the growing filament end (Fig. 7).

Figure 7:

Schematic of experiments demonstrating formin mechanoinhibition through a disordered domain. The formin FH2 domain binds and accelerates polymerization of actin (red circles) by binding free actin monomers with its disordered FH1 domain (center, actin binding domains in blue). In Ref. 44, formin is anchored to a bead through the FH1 domains, and the length of fluorescently labeled actin is observed as a function of time. When fission yeast formin Cdc12 is used, polymerization rate decreases in the presence of myosin pulling, but not when the FH1 domains are swapped with those from mamallian formin mDia2.⁴⁴

In in vitro experiments where the formin arms are anchored to a micron sized bead, we observed a three-fold decrease in actin polymerization rate by the formin when the filament is pulled on myosin. In this setup, the force produced by the motor as it walks along actin was dictated by the drag of the bead in solution; due to the low viscosity environment of the experiments, we estimated the forces to be < 1 pN, and hence suspected that these arm domains were the source of mechanosensitivity.⁴⁴ Interestingly, when these arms were swapped out for sequences from a mammalian formin, the mechanoinhibition disappeared⁴⁴ (Fig. 7). We still do not know what it is about the precise peptide sequence of the formin arms that confers mechanosensitivity (is it the stiffness of the molecule, the position of the actin binding domains, or something yet to be implicated?). Further studies aimed to address these questions using atomistic and coarse-grained molecular dynamics are ongoing.

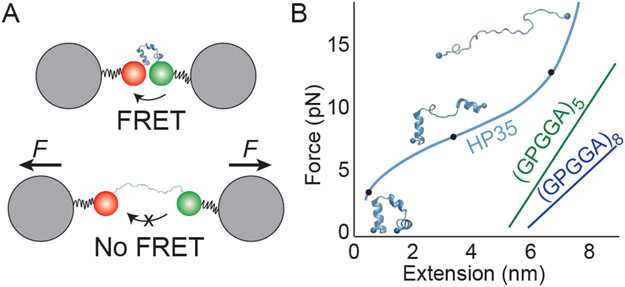
Scientists have taken advantage of this same paradigm of stretchable peptides to design in vivo methods for measuring force. The idea is to develop a “molecular ruler” using a peptide, where the length of the peptide can be measured and then converted to an applied force through a set of calibration experiments^45-47 (Fig. 8A). Peptide length in vivo can be estimated by expressing a pair of fluorescent proteins on the ends of the peptide that undergo fluorescence resonance energy transfer (FRET); here, a donor fluorophore absorbs and emits light when the peptide is stretched, but the excitation transfers to the acceptor fluorophore before emitting when the peptide is unstretched. FRET efficiency is sensitive to distance, and hence serves as a ruler.^45-47 Calibration experiments involve stretching the peptide using known forces with optical tweezers and simultaneously measuring the FRET signal, so that force can be inferred from FRET data in in vivo experiments^45-47 (Fig. 8B).

Figure 8:

(A) Schematic of a FRET-based tension sensor calibration experiment. Energy transfers from donor to acceptor dye on the end of a mechanosensitive protein when the ends are near each other. The length at a given force applied by optical tweezers can be correlated with the FRET efficiency. (B) Sketch of measured force-extension curves (to scale) for tension sensors HP35⁴⁹ and spider-silk peptides (GPGGA)_N.⁴⁶ Structures show possible configurations of HP35 commensurate with marked point on the force-extension curve taken from our preliminary MD simulations. The structure of the silk peptides under force in these experiments is not well understood.⁴⁶

As pointed out in Ref. 45, a crucial property for a tension sensor to be used in vivo is that the peptides cannot show any hysteresis, which means measurements of a quantity of interest are independent of the peptide’s history—otherwise we could not say that length and force have a one-to-one correspondence. While linear response theory only predicts spring-like behavior at small force, certain peptides have been identified that have linear force-extension behavior up to higher forces; this behavior is surprising, and suggests some degree of structure as we expect extended peptide chains to follow a wormlike-chain behavior.^46,48 One example are tension sensors based on Flagelliform silk peptides (GPGGA)_N, which show this elastic behavior and have an effective spring constant which decreases as N is increased⁴⁶ (Fig. 8B). This “tension sensor module” with N = 5 (TS-mod) was used to measure the force distributions in focal adhesion complexes consisting of integrin, vinculin, and actin.⁴⁶

In addition to these more extended peptides, compact folded proteins have also been exploited as tension sensors. The 35 residue villin headpiece (HP35) (Fig. 1), whose folding behavior has been extensively studied in the past,^50,51 also exhibits a linear-force extension relationship over a certain force range of 6 to 8 pN. HP35 has been used as a tension sensor to study the force on talin in focal adhesions, and those studies suggest that the force is shifting the folding/unfolding equilibrium of the protein.^47,49 If so, the linear regime observed in behavior at intermediate forces may come from the linear shift in free energy between folded and unfolded states derived above, rather than an elastic deformation of the structure.

For in vivo experiments, it is important to match the range of force sensitivity to the scale of forces involved in a given molecular process. So far, the force sensitivity of FRET-based tension sensors and the lack of hysteresis has been determined empirically. In order to design optimal tension-sensing peptides, we are currently working to predict these properties and the mechanism of force response using MD simulations.

Force sensitive binding kinetics

All of the previous molecular mechanisms of mechanosensing can be thought of in terms of thermodynamics, as a direct of a shift in conformational ensemble of the protein. As described in General Considerations, we can also think about the change in kinetics due to force as an alternative method of mechanosensing.

There are many force sensitive ‘bonds’ in cells which are formed by non-covalent protein-protein interactions. Many of these bonds are found at focal adhesions or in cell-cell junctions. In modeling cellular adhesion, Bell famously included an exponential decrease in bond lifetime with with force.⁷ This is an example of a slip bond, where a ligand unbinds faster with increasing force, and as derived above, it is what we would expect for an unbinding reaction that is well described by a single barrier along a one-dimensional reaction coordinate (Fig. 9).

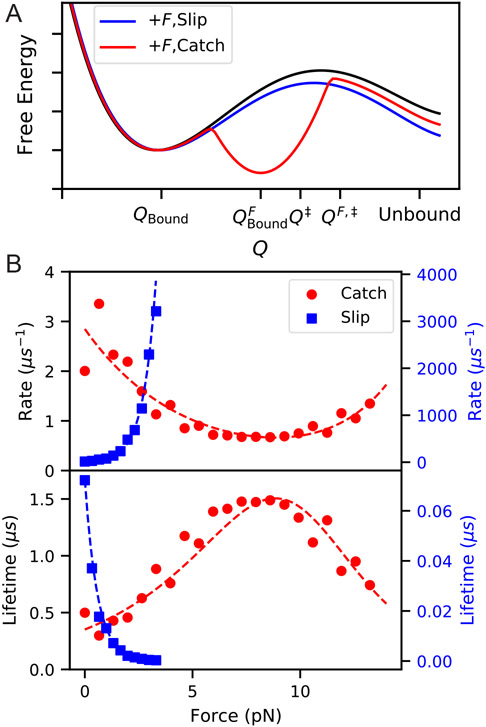
Figure 9:

(A) Schematic of a free energy landscape for an unbinding reaction (black), which with applied force F behaves as either a slip bond (blue) or catch bond (red). For models of a catch bond projected into a 1D reaction coordinate Q, we imagine that application of force creates a new stable minimum which in turn has a higher barrier for transition to the same unbound state. (B) Illustration of catch and slip bond kinetics computed by preliminary MD simulations using infrequent metadynamics⁵² on 2D potentials in pesmd.⁵³ The slip bond potential is a simple double well aligned with the x-axis, with force applied along the x-axis. The catch-bond potential is a modification of the titled double-well potential from Ref. 10, with a third local minimum added in such that the third state becomes the most stable at intermediate force. Dashed lines show fits to Bell’s law for slip-bonds and the two-pathway model for catch bonds.⁵⁴

Because proteins have many degrees of freedom and can sample many different states during an unbinding process, we should not assume that the reaction is well described by a 1D coordinate.¹⁰ A multitude of biologically important protein-ligand complexes have been shown to have more complicated unbinding behavior under applied force, and in fact some exhibit what is known as catch bond behavior, where the bond lifetime actually increases over some force range⁵⁵ (Fig. 9).

Substantial theoretical work has gone into describing possible mechanisms for catch bonds, and there are at least four general explanations for how they could arise.^36,55-58 In order for the bond lifetime to become higher, the effective barrier to unbinding must increase, and hence the force must produce some change in the transition state. This could be because the applied force directly disfavors the transition state of the zero-force unbinding reaction. Alternatively, the force could shift the conformational ensemble of the protein or the position of the ligand (directly or allosterically) such that this shifted lowest free-energy state has a higher barrier to unbinding through a new transition state (Figure. 9).

Catch bond behavior has been observed in many protein-ligand systems, including FimH/mannose, P-selectin/PSGL-1, vinculin/F-actin, and kinetochore/microtubules,.^12,59-65 The two-pathway, allosteric, and sliding-rebinding models have been used to describe the kinetics of these systems.^56,58,65 Despite many theoretical models for these processes, substantial work remains to describe the precise molecular details that would give rise to the different catch bonding mechanisms.

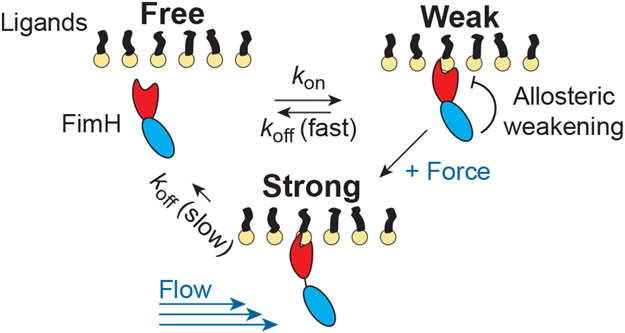
An example catch bonding system whose molecular mechanism has been studied in detail is the bacterial adhesin FimH.^59,66 Bacterial cells attach to surfaces via pili which consist of thousands of proteins.^12,59 It has been shown that FimH, which is at the tip of these pili, forms a catch bond with mannose sugars attached to glycoproteins on the surface of human epithelial cells.^12,59 FimH consists of two domains which are essential for catch bond behavior to arise.^12,59 Without applied force, one domain allosterically inhibits binding of mannose by the other domain; however, when force is applied, the domains separate and affinity for mannose increases by 100,000 fold (Fig. 10).^59,66 This mechanism allows E. coli to adhere strongly in the human urinary tract in the presence of fluid flow.⁵⁹

Figure 10:

Schematic of FimH catch bond mechanism. FimH transitions from a weakly bound to a strongly bound state when shear forces cause separation of its two domains.⁵⁹

While some MD simulation work has been performed to help detail possible molecular mechanisms of catch bonding such as the one just described for FimH, to our knowledge, equilibrium catch bonding kinetics have not been observed in atomistic MD simulations to date. Our efforts to do so will be described in the next section.

Probing mechanosensing with molecular dynamics simulations

Molecular dynamics (MD) simulations provide a powerful tool for probing the molecular details of biomolecular processes. In essence, MD simulations iteratively solve Newton’s equations of motions, using special modifications to the equations of motion to sample at constant temperature or constant temperature and pressure rather than constant energy.^4,67 A major limitation of an atomistic MD simulation is that we need to use very small time intervals, usually 2 femtoseconds, to simulate our model accurately.⁴ With modern high performance computing resources, this typically limits our simulations to system sizes up to hundreds of thousands of atoms (including solvent) for up to a few microseconds. One issue that arises from this is the “sampling problem,” which is that we likely will not observe all biologically relevant conformations within this time, and they will not occur with their proper Boltzmann statistical frequencies; hence, averages computed from these data can be wrong.^4,53 Many mechanosensing processes will also take longer to observe than the amount of time we can directly simulate. There are two general solutions to the sampling problem—(1) we can use a lower resolution coarse-grained model, which allows us to effectively study larger systems for longer times with less fidelity, or (2) we can use enhanced sampling techniques to accelerate conformational sampling in a controlled way.⁶⁷

Early work using MD to study the effect of force on proteins focused on mechanical unfolding of proteins e.g. titin and fibronectin. This gave rise to the method now known as ‘steered molecular dynamics’ (SMD).⁶⁸ In SMD, typically a harmonic bias is applied to a collective variable of interest, and the center of that harmonic bias (Q₀) is moved over time, perhaps with a linear speed.

$$V_{bias}(\mathit{Q})=\frac{1}{2}k(\mathit{Q}(\mathit{X}(t))-{\mathit{Q}}_0(t){)}^2$$ (7)

Either this collective variable can be a distance across the protein, or it can be the distance of a particular atom to a fixed position in space, as long as another atom in the protein is held rigid. The setup of SMD was meant to mimic the experimental techniques used to unfold proteins, where optical traps or Atomic Force Microscopy was used to apply pulling forces directly to the protein (through tethering molecules).⁶⁸

SMD can be applied in more abstract contexts than the ones which directly mimic single molecule experiments, for example, SMD has recently been applied on a protein-ligand coordination number variable, in order to produce a local tension to observe opening of the MscL channel.³¹ SMD has also been fruitfully applied to study mechanochemistry of small molecule reactions involving changes in covalent bonding.⁶⁹

SMD itself is a non-equilibrium technique, although it was quickly proposed that equilibrium free-energies can be obtained using non-equilibrium reweighting such as via the Jarzynski equality,⁷⁰ and that kinetic predictions can be made as well.⁸ While SMD has been a useful tool for studying protein unfolding and some other force dependent properties, it generally requires moving the center of the bias at rates that are far faster than experiment in order to observe events within an accessible simulation time; this in turn produces extremely high and unrealistic forces for biological systems.⁶⁸

The mechanosensing mechanisms we are interested in studying using MD techniques occur at much smaller and effectively constant forces. Hence we propose studying these molecular paradigms for mechanosensing by employing equilibrium techniques to sample from Eq. 2. We are currently successfully employing a number of the standard enhanced sampling techniques to sample conformational changes under applied force, including Metadynamics, Parallel Tempering, Umbrella Sampling, and TAMD/d-AFED as implemented in the PLUMED enhanced sampling library.^4,53,71 In addition, we recently developed the Infinite Switch Simulated Tempering in Force (FISST) method, which concurrently samples a range of forces within a single simulation and actually uses that applied force to overcome sampling barriers.⁷²

To study catch bonds and unbinding rates of protein-ligand interactions under small applied force, we believe it should also be possible to use a number of techniques that have been developed to compute protein-ligand unbinding rates in the context of small molecule drugs. One technique we are currently using to do this is called Infrequent Metadynamics. Infrequent metadynamics is based on earlier ideas from Voter,^73,74 and works by slowly and infrequently adding energy biases to explored positions until an unbinding event is observed. Using simple arguments from chemical kinetics, an ‘acceleration factor’ can be computed from the applied bias to say what the escape time would have been without the bias. If this rescaled time is averaged over many events, then the lifetime of the bound state can be predicted. This method assumes that transitions are rare and the coordinate(s) being biased are a good representation of the full transition path,⁵² which may not be true. Nevertheless, if the underlying assumptions hold for a particular case with and without force, we can in theory use this method to predict equilibrium unbinding kinetics under force. An alternative approach to computing unbinding rates is the Weighted Ensemble MD method (WE),^75,76 which has a different set of underlying assumptions. Here, a set of unbiased trajectories are run, and those which move closer to a target state are cloned; the statistical weights of these trajectories are computed over time until an escape event occurs; the probability of observing that trajectory is used to reweight the observed escape time.^75,76

Outlook

Within biological systems, a wide range of molecular motifs have evolved to confer mechanosensing abilities. Scientists have exploited some of the biological motifs in order to design their own mechanosensors, and even novel bio-inspired mechanoresponsive materials. Here we have only just scratched the surface of the known mechanosensitive functional motifs. For example, a whole class of indirect mechanosensing mechanisms have been neglected, where a protein confers mechanosensitivity due to its ability to bind stressed structures within the cell, rather than responding to forces applied directly to it. This paradigm seems to be particularly prevalent in the actin cytoskeleton, where a number of actin binding proteins modulate their affinity based on the mechanical state of filaments.^77-81

In our work, we seek to determine the molecular mechanism of action for systems such as those described above using computational techniques. While we do not believe that MD simulations are perfectly accurate, we believe that careful use of MD simulations in conjunction with enhanced sampling techniques can point us towards experimentally verifiable predictions of how proteins really respond to small mechanical forces, and how those mechanisms are excited even in the presence of the complex fluctuating mechanical environment of the cell.

Figure 5:

Schematic of GPR68 activation by flow. Structures shown are homology models derived from inactive (left) and active (right) μ–opiod GPCR structures (4DKL, and 5C1M, respectively).

Biographies

David Gomez studied physics at the Universidad de los Andes in Colombia. He then moved to the Max Planck Institute of Colloids and Interfaces in Potsdam in Germany, where he obtained his Ph.D. in 2016 under the supervision of Stefan Klumpp. In Potsdam, his work focused on the effects of molecular crowding in enzymatic reactions, gene expression, and protein folding. After a two-year postdoc at the University of Tel Aviv under Yair Shokef and Ayelet Lesman, he relocated in 2020 to New York City to pursue a second postdoc at NYU under the supervision of Glen Hocky and Enrique Rojas. His current research interest is resolving the mechanisms of mechanosensitive channel gating in bacteria at the single-cell level.

Yuvraj Singh received his B.A. with honors from Rutgers University Camden in 2018, majoring in Chemistry and Mathematics. There he worked with Luca Larini (Physics), using enhanced sampling molecular dynamics to study Tau aggregation in Alzheimer’s and other neurodegenerative diseases. Yuvraj started his Ph.D. in Chemistry at NYU in 2018, where he is developing and applying enhanced sampling techniques to study peptides under mechanical forces

Willmor Pena Ccoa studied chemistry and computer science at Iona College in New York where he explored hydrogen gas storage and water permeation through lipid bilayers via MD simulations. He joined the Information Technology department as an administrator and was an adjunct faculty in computer science. In 2018 Willmor started his Ph.D. in the Hocky group at NYU as a graduate student in Chemistry. He is applying computational techniques to determine unbinding rates for mechanosensitive protein-ligand interactions.

Enrique Rojas majored in physics and mathematics at the University of Pennsylvania before pursuing his Ph.D. at Harvard University in physics. At Harvard, he investigated the mechanical mechanisms of polar cell growth in plants, fungi and protists in the lab of Jacques Dumais. After completing his Ph.D., he spent 7 months teaching medical physics and chemistry at the Patan Academy of Health Sciences, a medical school in Nepal. He then did postdoctoral research in the labs of K.C. Huang and Julie Theriot at Stanford University, investigating the mechanical mechanisms of bacterial cell growth and division. During his postdoc, he also spent one year performing field research in Bangladesh, investigating the microbial ecology underlying cholera epidemics. He then joined the NYU Biology Department as an Assistant Professor, where his lab investigates how microbial cells sense, generate, control, and use mechanical forces in order to execute important physiological functions, and how these forces are integrated with biochemical systems that also control physiology.

Glen Hocky did undergraduate studies at the University of Chicago, where he majored in Mathematics and Chemistry. There he worked with Tobin Sosnick and Karl Freed on protein folding and protein structure prediction. He then moved to Columbia University, where he worked with David Reichman, and used simple computational models to probe the origin of the glass transition and anomalous dynamics in supercooled liquids. He returned to the University of Chicago as a Kadanoff-Rice and then NIH NRSA Postdoctoral Fellow, where this time he worked with Aaron Dinner and Gregory Voth. His postdoctoral research focused on atomistic, coarse-grained, and theoretical studies of the actin cytoskeleton, as well as computational methods development. He then bounced back to New York City for a second time in 2018 to join the Department of Chemistry at NYU as an Assistant Professor. A major emphasis in his group is the topic of this perspective article. He also enjoys ongoing projects related to soft matter physics and self-assembly of colloidal particles.