Voltage-Gated Intrinsic Conductances Shape the Input-Output Relationship of Cortical Neurons in Behaving Primate V1

SUMMARY

Neurons are input-output (I/O) devices—they receive synaptic inputs from other neurons, integrate those inputs with their intrinsic properties, and generate action potentials as outputs. To understand this fundamental process, we studied the interaction between synaptic inputs and intrinsic properties using whole-cell recordings from V1 neurons of awake, fixating macaque monkeys. Our measurements during spontaneous activity and visual stimulation reveal an intrinsic voltage-gated conductance that profoundly alters the integrative properties and visual responses of cortical neurons. This voltage-gated conductance increases neuronal gain and selectivity with subthreshold depolarization and linearizes the relationship between synaptic input and neural output. This intrinsic conductance is found in layer 2/3 V1 neurons of awake macaques, anesthetized mice, and acute brain slices. These results demonstrate that intrinsic conductances play an essential role in shaping the I/O relationship of cortical neurons and must be taken into account in future models of cortical computations.

In Brief

Li et al. used whole-cell recording to reveal a large and unexpected voltage-gated intrinsic conductance that dramatically alters the integrative properties of primate V1 neurons. Therefore, a standard computational model of sensory neurons that incorporates linear integration of synaptic inputs followed by a threshold nonlinearity requires revision.

INTRODUCTION

Primary visual cortex (V1) has long been a model area for studying cortical computation. The visual responses of V1 neurons and their synaptic inputs from the visual thalamus have been described in quantitative detail and reveal a striking set of visual computations that result in the emergence of binocularity, orientation selectivity, and motion selectivity (Alonso et al., 2001; Hubel and Wiesel, 1962, 1977). These emergent features reflect a computation that is being performed by the cortical circuitry and have most often been studied with a focus on the functional identity of the synaptic inputs that converge on neurons (Ferster and Miller, 2000; Priebe and Ferster, 2012). Computational models for the emergence of selectivity in visual cortex most often incorporate a two-stage process in which the synaptic inputs are integrated linearly within a neuron and are then passed through a simple (static) threshold nonlinearity (Anderson et al., 2000b; Carandini et al., 1999; Heeger, 1993; Priebe and Ferster, 2008).

Neurons are complex devices, however, with elaborate dendritic trees and numerous voltage-dependent intrinsic conductances. For example, we know that intrinsic conductances, subthreshold to action potential generation, shape how auditory inputs are integrated for sound localization (Mathews et al., 2010), control the spontaneous activity of cerebellar Purkinje cells (Raman and Bean, 1997), and generate resonant properties in pyramidal cells (Hu et al., 2002; Narayanan and Johnston, 2007). Intrinsic conductances may therefore play key roles in sculpting the selectivity of neurons.

Although these in vitro recordings demonstrate that intrinsic conductances may play an important role in neuronal computations, less is known about their role in behaving animals, though it is clear that dendritic nonlinearities contribute to sensitivity and selectivity in mice (Labarrera et al., 2018; Smith et al., 2013; Takahashi et al., 2016). Previous records from anesthetized animals have been equivocal regarding the impact of subthreshold intrinsic conductances. Some have failed to reveal strong nonlinear responses that would reflect the influence of voltage-gated conductances (Monier et al., 2003, 2008; Paré et al., 1998). Others have reported that input resistance declines (Paré et al., 1998) or increases (Waters and Helmchen, 2006) during spontaneous depolarizations. We have recently developed a technique to perform whole-cell recordings from V1 of awake, behaving macaque monkeys that allows access to the subthreshold intrinsic properties of cortical neurons while taking advantage of the exquisite behavioral paradigms developed with these animals (Tan et al., 2014). Our resistance and membrane potential measurements made during spontaneous activity and visual stimulation demonstrate the presence of a powerful, subthreshold, voltage-gated conductance that changes the integrative properties of cortical neurons. We couple these novel observations with a computational model that demonstrates how this intrinsic conductance sculpts the orientation selectivity of individual V1 neurons. By increasing neuronal input resistance during subthreshold depolarization, this intrinsic conductance increases neuronal gain and sharpens output tuning. It also acts to linearize the otherwise intrinsically nonlinear (saturating) relationship between synaptic input and membrane potential. Overall, our results demonstrate that intrinsic conductances play an essential role in shaping the input-output relationship of cortical neurons and must be taken into account in future models of cortical computations.

RESULTS

The Relationship between Input Resistance and Membrane Potential

The primary goal of our study was to shed light on how synaptic inputs combine with the intrinsic properties of neurons to generate the responses of neurons in visual cortex of awake, behaving primates. To gain access to the intrinsic properties of neurons, we used whole-cell recordings in trained macaques providing us precise control over the state of the animal and the sensory input to visual cortex. Previous studies in anesthetized animals and in vitro studies revealed the presence of a voltage-gated increase in input resistance as neurons become depolarized (Routh et al., 2017; B. Scholl et al., 2012, Soc. Neurosci., conference; Spruston and Johnston, 1992; Waters and Helmchen, 2006). Motivated by these observations, we set out to measure how input resistance covaries with spontaneous fluctuations in membrane potential while macaques fixate on a small central fixation spot on a uniform gray screen. Fluctuations of membrane potential occur in the absence of visual stimuli while animals fixate (Figure 1A). To access neuronal input resistance during these spontaneous changes in membrane potential, we measured the voltage response of neurons using brief injections of negative current (Figure 1B). We fitted the response to current injections using a sum of two exponentials, where the first component corresponds to the electrode resistance and the second to the input resistance (Figures 1C and S1; related to Figure 1; see STAR Methods). Mean resistance measures varied across our sample population (210 ± 76 MΩ; n = 32), consistent with previous in vivo measurements in the cat, rat, and mouse (Anderson et al., 2000a; Monieret al., 2003, 2008; Tan et al., 2004, 2011; Tan and Wehr, 2009) but higher than those reported in rodent barrel cortex (Margrie et al., 2002; Moore and Nelson, 1998; Waters and Helmchen, 2006).

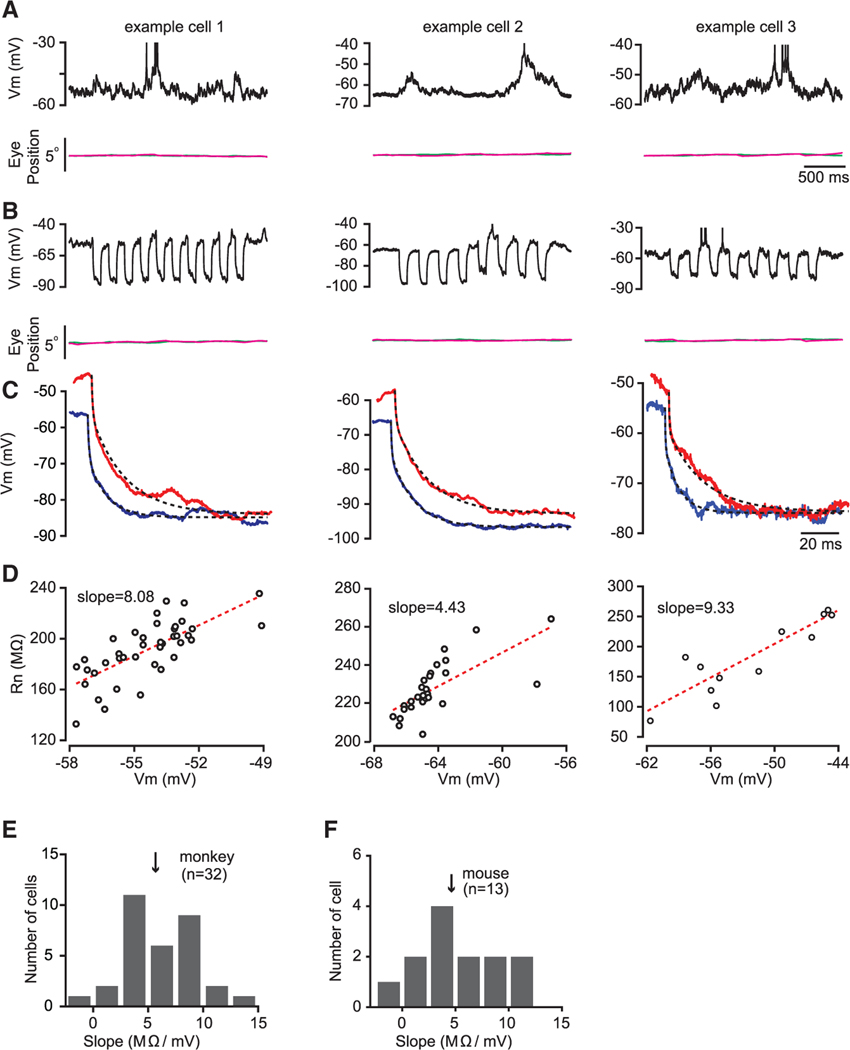
Figure 1. Input Resistance Changes with Membrane Potential during Spontaneous Activity.

(A) Membrane potential fluctuation for three example cells in V1 of behaving macaque in a fixation task. Top: membrane potential in single trials is shown. Bottom: horizontal (magenta) and vertical (green) eye traces are shown. The short horizontal bar indicates timescale.

(B) Input resistance measurements for these three example cells were obtained by injecting negative current pulses. The duration of these current pulses was 100 ms with a 150-ms interval (top). Bottom: eye traces are shown.

(C) Estimation of input resistance by fitting changes in membrane potential with a sum of two exponentials functions (see STAR Methods for details) for the three example cells. Dashed lines represent double exponentials used to fit the data.

(D) A positive relationship between input resistance (Rn) and membrane potential (Vm) for the three example cells. Each dot represents a current injection pulse. Only injection pulses that fell within the 3-mV inclusion criteria (see STAR Methods) were included in the analysis. Red dashed lines represent linear regressions.

(E) Histograms of the Rn-Vm slopes for a population of cells from two behaving macaques. The arrow indicates the median slope.

(F) Histograms of the Rn-Vm slopes for a population of V1 cells from anesthetized mice.

If the main source of variations in membrane potential during spontaneous activity was the change in the number of active excitatory synaptic inputs, we would have expected the input resistance to decrease as the cell was depolarized (due to the increase in excitatory drive). We found, however, a systematic dependence of input resistance on the membrane potential of the neuron in the opposite direction: during spontaneous depolarizations, we found that input resistance was larger than during hyperpolarizations (Figure 1D; each point is an individual Rm measurement). Although individual neurons were characterized by distinct relationships between membrane potential and input resistance (Figure 1D), this relationship was positive: more depolarized membrane potentials were associated with increases in input resistance. We quantified this dependence by measuring the slope of the relationship between membrane potential and resistance across 32 neurons in the fixating macaque and found that the median slope of the relationship was high, near 5 MΩ/mV (Figure 1E). That is, a spontaneous increase of subthreshold membrane potential by 10 mV had a large impact on the integrative properties of neurons, increasing input resistance by 50 MΩ on average.

We next asked whether this link between membrane potential and input resistance was particular to the primate V1 or whether this is a more general property of neurons in V1 layers 2/3. We therefore made recordings from mouse V1 neurons in spontaneous conditions and found a similar trend: the median dependence of input resistance on membrane potential was near 5 MΩ/mV and was characterized by a similar distribution (Figures 1F and S2; related to Figure 1). Note that this relationship between membrane potential and resistance is similar to that found in vitro in layer 2/3 of mouse prefrontal cortex (Routh et al., 2017).

There are at least two possible explanations for the positive relation between input resistance and spontaneous fluctuations in membrane voltage. First, membrane resistance may increase as the cell becomes more depolarized, because intrinsic voltage-gated channels close as the cell depolarizes. Such intrinsic conductance will then have the effect of magnifying the ongoing excitatory input due the increase in input resistance. Such intrinsic channels are known to exist in cortical cells and have been ascribed to inward rectifying K⁺ channels (Nisenbaum and Wilson, 1995) as well as the non-selective cation HCN chan- nels (Magee, 1999; Stuart and Spruston, 1998). In addition, persistent sodium channels are also voltage gated and could lead to an apParént increase in input resistance with depolariza-tion (Bennett et al., 2000). All of these intrinsic channels have the property that they alter the resistance of the cell with membrane potential such that resistance is larger for more depolarized membrane potential. Alternatively, if the main source of varia-tions in membrane potential during spontaneous activity is fluc-tuations in the inhibitory input, membrane resistance may in-crease as the cell becomes more depolarized from the decrease in inhibitory conductance.

To determine whether intrinsic voltage-gated channels could play a role in the changes in resistance we observe, we systematically varied the membrane potential of neurons using constant current injection and then made slope resistance measurements (ΔV/ΔI at different membrane potentials) with brief negative current pulses (Figure 2A). If the main source of the positive relation between membrane potential and input resistance during spontaneous activity is an intrinsic conductance, changing resting membrane potential with a constant current injection should have a similar positive effect on input resistance.

Figure 2. Rn-Vm Relationship during Constant Current Injection.

(A) Input resistance measurements when Vm baseline was manipulated by injecting constant currents to an example V1 neuron in behaving monkeys (top) and an example V1 neuron in anesthetized mice (bottom). Colors indicate different level of constant current injections. Similar to Figure 1, Rn was obtained by fitting the changes in Vm in response to brief negative current pulses with a double-exponent function.

(B) Input The relationship between Rn and Vm forthe example macaque cell (top) and the example mouse cell (bottom) in (A). Each dot represents mean values of Rn and Vm at a constant current level, which is indicated by color bars (right). Percentage changes in Rn are given in the ordinate scale on the right. Error bars represent ± SEM.

(C) Input Histograms of the slope for cells in behaving monkey (top) and anesthetized mice (bottom). Gray bars represent data from current-clamp recording and black bars from voltage-clamp recording. Arrows represent median slopes.

As in the case of spontaneous membrane potential fluctuations, a systematic relationship between input resistance and membrane potential was observed when the resting potential of neurons was altered by constant current injection, providing direct evidence for the existence of an intrinsic conductance. To quantify the degree of this change, we measured the slope of the relationship between resting membrane potential and input resistance (Figure 2B). This relationship was systematically positive across all the neurons we have examined in both the primate and the rodent, suggesting that voltage-gated intrinsic channels were closing as the neuron became depolarized during spontaneous activity (Figure 2C; macaque slope mean ± standard deviation = 4.42 ± 1.58, n = 9, significantly different from 0, t test, p < 0.001; mouse slope mean ± standard deviation slope = 3.06 ± 2.14, n = 13, significantly different from 0, t test, p < 0.001). Current injection allowed us to control membrane potential directly, whereas our original observations relied on spontaneous fluctuations of membrane potential within a smaller range (Figure 1). These two methods yielded similar relationships between membrane potential and resistance in the same neurons (macaque: slope mean ± standard deviation = 5.29 ± 3.87 mV, not significantly different from current injection data, Kolmogorov-Smirnov test; mouse: slope mean ± standard deviation = 5.20 ± 3.82, not significantly different from current injection data, Kolmogorov-Smirnov test). To estimate the proportion of the voltage-dependent input resistance to the voltage-independent membrane resistance, we compared the input resistance at the most hyperpolarized membrane potentials (mean Vm = −84.2 ± 3.2 mV) and depolarized membrane potentials (mean Vm = −51.8 ± 2.9 mV). Input resistance doubled (geometric mean = 2.04) across this range in macaque neurons, indicating that voltage-dependent channels comprise at least 50% of those responsible for input resistance over this span of membrane potentials. To better control membrane potential, we also performed recordings in voltage clamp mode for a subset of the neurons in mice. The same positive relationship between holding voltage and input resistance was evident in these records (mean slope = 3.42 ± 2.12 [n = 10]; Figures 2C, bottom, and S3; related to Figure 2).

Our estimates of input resistance have been derived from the responses to short pulses of current or voltage at different membrane potentials. These are therefore estimates of the slope resistance of the cell at a given Vm. The assumption, however, is that these short current steps will not dramatically alter the input resistance during the step. An alternative method to estimate the input resistance is to measure the voltage-current relationship using steady holding current and the resulting membrane potential and then computing the V-I relationship from these values (i.e., the chord resistance; see Figures S4A and S4B; related to Figure 2). Because the input resistance depends on voltage, we used an exponential to fit the voltage-current relationship and estimated the holding resistance for each membrane potential (see STAR Methods). We compared resistance estimates based on pulses (Figure S4C; related to Figure 2) to those based on holding current for each cell at the different steady current injection amplitudes (Figure S4D; related to Figure 2) and found that these estimates are similar, both displaying large changes in resistance with membrane potential. Slope and chord resistance were highly correlated in individual neurons (median R² = 0.96), demonstrating that measurements from steps or from steady current injection yielded similar changes in resistance with voltage.

Finally, to further demonstrate that these resistance changes were due to the intrinsic properties of neurons, we made recordings using broad-spectrum channel blockers cesium and QX-314 from anesthetized mice. These channel blockers resulted in a reverse of the dependence of resistance on membrane potential during spontaneous activity: spontaneous depolarizations were coupled with declines in input resistance instead of increases, reflecting a blockage of the voltage-gated conductance (Figure S5; related to Figure 2).

Our in vivo records suggested that input resistance in layer 2/3 cortical cells declined as the subthreshold membrane potential increased due to intrinsic properties rather than to spontaneous synaptic input. If this were true, we should be able to recapitulate these changes in vitro, where synaptic conductances are negligible. To determine whether input resistance changes also occur with membrane potential in vitro, we made acute brain slices from layer 2/3 of V1 in adult mice. We employed the same paradigm used in vivo in which membrane potential was systematically varied with steady current injection, and short pulses of current were injected to measure input resistance (Figure 3A). As with our in vivo records, input resistance systematically increased as cells are depolarized, and this relationship had a similar slope as that found in vivo (4.6 ± 0.4 MΩ/mV).

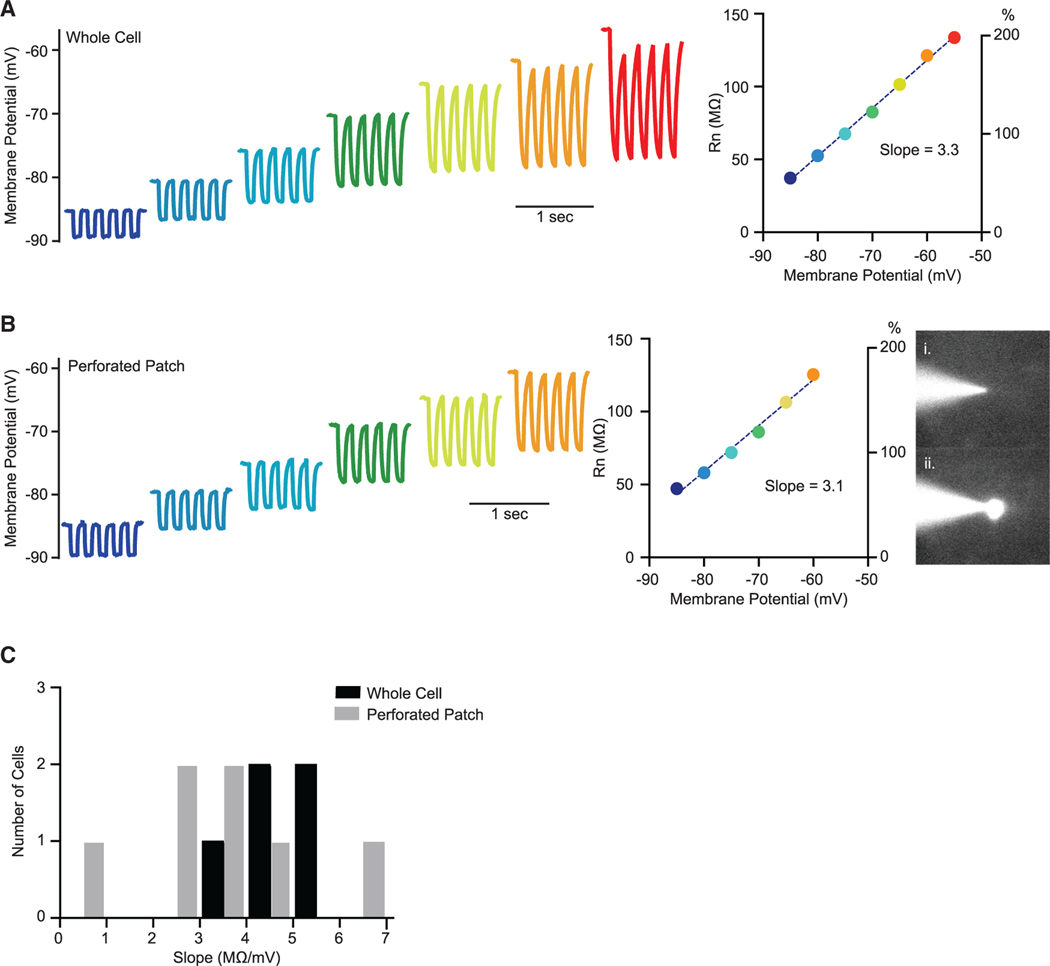
Figure 3. Dependence of Input Resistance on Membrane Potential In Vitro.

(A) Representative traces from an in vitro whole-cell recording (left) and corresponding input resistance (Rn) measurements across the range of membrane voltages (right). The Rn/Vm slope in this cell was 3.3 MΩ/mV.

(B) Representative traces from a perforated patch recording (left) with corresponding input resistance (Rn) measurements that revealed a Rn/Vm slope of 3.1 (middle). Perforated patches were observed with OGB-1 in the pipette, and recordings were terminated upon evidence of break-in: (i) patch pipette during a perforated patch recording and (ii) same patch pipette after break-in.

(C) Histograms forthe Rm/Vm slopes in whole-cell recordings (black) and perforated patch recordings (gray). Mean slope values are 4.6 ± 0.4 for whole cell and 3.0 ± 0.7 for perforated patches.

The subthreshold voltage-dependent resistance changes observed here in vivo and in vitro stand in contrast to the diverse results from previous records that have demonstrated both input resistance declines (Paré et al., 1998) and increases (Waters and Helmchen, 2006) with membrane potential depolarization. There are many experimental differences between the present records and previous ones, but one of these differences is methodological, as patch electrodes were used in this study and sharp electrodes were used in other studies. A potential problem with whole-cell recordings is that the internal concentrations of ions may change during recordings as the contents of the internal solution in the patch pipette diffuse into the cell. Using our in vitro paradigm, however, we were also able to use the perforated patch technique to gain electrical access to the cells without dialyzing the cell (Rae et al., 1991; Spruston and Johnston, 1992). We made perforated patch recordings by including amphotericin B and Oregon Green Bapta 1 in the patch solution (see STAR Methods). After gaining a gigaohm seal, the amphotericin acts to make small holes in the membrane, affording electrical access to the neuron. Using this technique, we uncovered a similar degree of resistance change as membrane potential was shifted (Figures 3B and 3C), demonstrating that the voltage-gated resistance change was not due to the dialysis of the cell by the wholecell technique. Although we did gain electrical access to neurons using amphotericin B, we were concerned that our access to the cell might be due to larger transmembrane holes than those provided by the antibiotic. As a control for this, we therefore monitored OGB1 fluorescence while performing the experiments. For the periods in which our access was only due to amphotericin, OGB1 should stay in the pipette and not perfuse the cell. This was indeed the case for our recordings (Figure 3B). Once we acquired our data, however, we gained whole-cell access to the neuron, resulting in OGB1 perfusion and the appearance of fluorescence in the cell body (Figure 3Bii). In sum, these in vitro experiments demonstrate that the voltage-gated intrinsic mechanisms were not an artifact of the internal solution of our pipettes and were instead due to intrinsic voltage-gated mechanisms in the neuron.

Visually Evoked Shifts in Membrane Potential and Resistance

Our records thus far demonstrate that voltage-gated intrinsic mechanisms exist that act to increase input resistance with depolarizing membrane potentials. We next sought to understand how this intrinsic mechanism might shape the sensitivity of V1 neurons to visual input by coupling visual stimulation and current injection.

What is the expected relationship between visual response and membrane potential? First, consider a case in which membrane potential only depends on synaptic inputs and a static leak conductance. The currents that result from both excitatory and inhibitory synaptic inputs depend on the resting potential of the neuron. When membrane potential is hyperpolarized near the reversal potential of inhibition, for example, the driving force for inhibitory current is small so little current is passed through inhibitory synapses relative to when membrane potential is depolarized and the driving force for inhibition is large. The opposite effect exists for excitation: when resting membrane potential is hyperpolarized, the driving force for excitation is large, evoking large currents, relative to when the neuron is depolarized. Apart from shunting effects, at hyperpolarized membrane potentials, inhibitory inputs should have a relatively weak effect, whereas excitatory inputs have a strong effect. The response to a visual stimulus, in terms of a change in membrane potential, should therefore be larger when a neuron is more hyperpolarized than when depolarized. To make this intuition more concrete, we constructed a simple single-compartment model based on the membrane equation and simulated the responses of the model neuron to a fixed mixture of excitatory and inhibitory inputs while adjusting membrane potential with holding current (see STAR Methods). For the same synaptic drive, the amplitude of the response from rest systematically varied with resting Vm such that hyperpolarized resting potentials led to large membrane potential changes, whereas depolarized resting potentials led to smaller membrane potential changes (Figure 4A). One concern might be that this behavior reflects the particular synaptic drive we employed in this model. For the model, we used excitation and inhibition that modulated in time at the same phase (Figure S6A; related to Figure 4). Using excitatory and inhibitory inputs that modulated out of phase resulted in a similar pattern of predictions in that the amplitude of response was larger for more hyperpolarized resting potentials than depolarized potentials (Figure S6B; related to Figure 4). This observation also did not depend on the presence of inhibition, though inhibition can certainly amplify the effects of resting membrane potential on the evoked responses (Figure S6C; related to Figure 4).

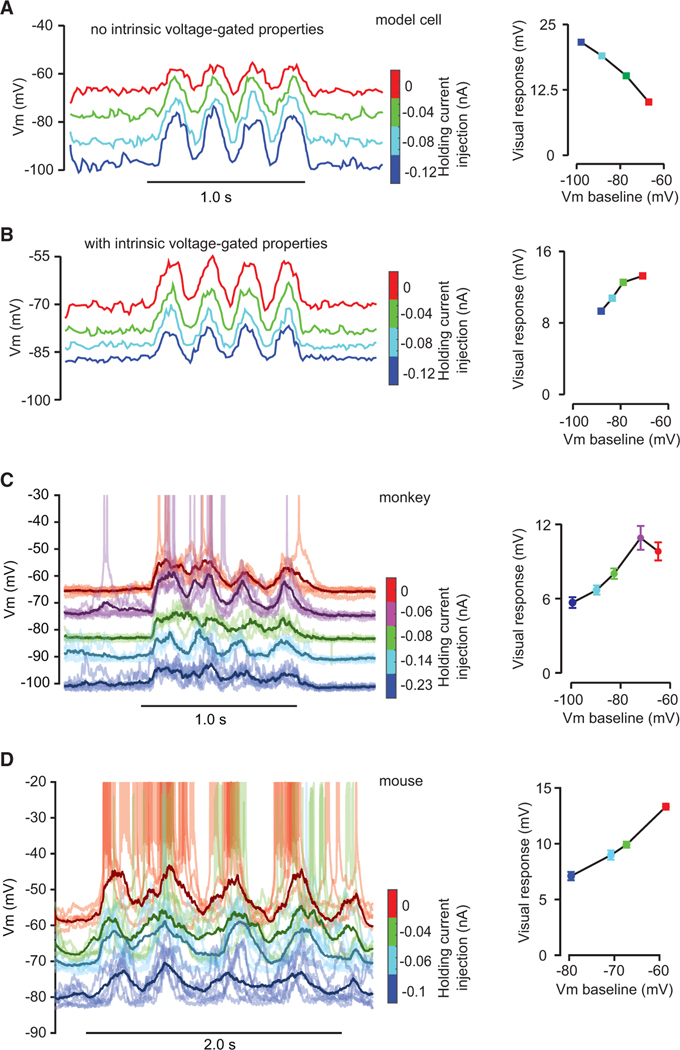
Figure 4. Visual Responses at Different Vm Baseline Levels during Constant Current Injection.

(A and B) Simulated responses for a model neuron without (A) and with (B) intrinsic voltage-gated properties at different Vm baseline levels. The horizontal bar indicates stimulus onset and duration (left), which includes four cycles of a drifting sine-wave grating in a trial (4 Hz). The color bars indicate constant current injection levels (middle). Responses (right) are mean values of the peak across trials and cycles of visual stimulus.

(C and D) Measured visual responses of example V1 cells from behaving macaque (C) and anesthetized mouse (D). Symbols are similar to (A) and (B). Error bars indicate ± SEM.

The presence of a voltage-gated intrinsic conductance changed the relationship between visual response and membrane potential: the voltage-gated intrinsic conductance led to an increase in input resistance with depolarization increasing the gain of the neuron as it was depolarized (Figure 4B). Therefore, a voltage-gated intrinsic conductance could fundamentally alter the relationship between baseline activity and sensory-evoked responses.

As predicted by the model with a voltage-gated intrinsic conductance, we found that visually evoked responses increased in amplitude during current-evoked depolarization in behaving macaque V1. We systematically adjusted the holding current that we injected into neurons and measured the responses evoked by the presentation of a drifting grating at the preferred orientation (Figures 4C and 4D). The amplitude of the evoked membrane potential responses systematically increased with cell depolarization. Although this trend occurred for most of the resting potentials we used, when the cell was depolarized such that many action potentials were evoked, the amplitude of the evoked response began to decline (Figures 4C, rightward point, and S7; related to Figure 4). This was likely due to the effects of the Na⁺ and K⁺ currents involved with action potential generation. In sum, the increased evoked response with membrane potential was consistent with the presence of a voltage-gated intrinsic conductance that decreased as the neuron depolarized.

We have demonstrated that, during spontaneous activity, the resistance of neurons increased with depolarization. We next examined how depolarizations evoked by visual stimulation impact the integrative properties of V1 neurons. Neurons in V1 are orientation selective and exhibit nonlinear response components, such as an attenuation in response to a central stimulus when a surround stimulus is presented, even though the surround stimulus by itself produces no response (Cavanaugh et al., 2002a, 2002b; Knierim and van Essen, 1992; Smith et al., 2006). To determine how synaptic and intrinsic conductances interact during visual stimulation, we measured the responses to small- and large-oriented gratings while injecting pulses of current to measure the overall cell resistance (Figures 5Aand 5B). During visual stimulation with the small and large stimuli, we observed a systematic decline in the resistance of the cell (Figures 5B and 5C). Input resistance was highest in the absence of stimulation and lowest for the small grating, which often evoked the largest response (Figure 5C).

Figure 5. Changes in Input Resistance with Visual Stimulus Size.

(A) Visual responses to large-size (top middle) and small-size (top right) stimuli for an example cell in behaving macaque V1. Neural signals to the blank control are shown on the top left column. The magenta and green curves on the bottom are corresponding horizontal and vertical eye traces. Black and red dashed vertical lines represent onsets of the fixation point (FP) and visual stimuli.

(B) Rn measurements for the blank and the large and small stimuli for the same example cell in (A). Each trial includes 8 negative injection pulses. Both the duration and interval between each negative pulse were 100 ms.

(C) Rn for the blank and the large and small stimuli with (open circles) and without (solid circles) voltage-gated intrinsic properties for three example cells. To estimate Rn without intrinsic properties, we subtracted intrinsic-induced Rn that equals the product of Vm and the mean slope in Figure 2C from the measured Rn. Error bars indicate ± SEM.

(D) Scatterplots of Rn for the blank, large, and small stimuli with and without intrinsic properties for a population of cells (n = 13). Red dashed lines indicate the equality diagonal.

These membrane potential and resistance measurements stand in contrast to our findings during spontaneous activity. Visually evoked responses were characterized by declines in resistance with increased depolarization, not increases in resistance. The voltage-gated resistance changes we described increased as the neuron became more depolarized, whereas visual stimulation increases synaptic inputs, which opens channels and depolarizes the neuron. The measures of cell resistance we made stem from a combination of increases in synaptic conductance and decreases in intrinsic conductances. To separate the contribution of the voltage-dependent intrinsic conductance from the synaptic conductances, we removed the intrinsic conductance changes using the estimates for its voltage dependence (Figure 2) and replotted the underlying resistance change that was due to the synaptic input (Figure 5C, “synaptic”). This separation reveals that the overall changes in synaptic input were stronger than revealed by the original membrane resistance estimates. Across our sample population, we found that the small stimulus evoked a change in the synaptic resistance of 47.85 ± 26.92 MΩ, whereas the total resistance change, including both the synaptic and voltage-gated intrinsic conductance, was much weaker, 32.76 ± 17.61 MΩ (p = 0.002; Wilcoxon signed rank test). During visual stimulation, synaptic channels open while voltage-gated intrinsic channels close. Input resistance measurements do not distinguish between these two properties, leading to an underestimate of the degree that synaptic channels open in response to visual stimulation.

Note that the total resistance that we observed for large stimuli was larger than for small stimuli—suggesting a reduced synaptic input instead of an increased amount of input due to surround inhibition (Levitt and Lund, 1997; Sceniak et al., 2002; 196.80 ± 93.52 MΩ relative to 169.85 ± 99.65 MΩ; p = 0.003; Wilcoxon signed rank test). These data suggest that surround suppression was not due to an increase in inhibitory input but instead a decline in the overall input that the neuron receives (Figure 5D). Note that resistance measurements for the small and large stimuli are consistent with recent findings from cat and mouse (Adesnik, 2017; Haider et al., 2010; Ozeki et al., 2009; Satoetal., 2016), demonstrating that the decline in response to large stimuli—surround suppression—is not consistent with a model in which large stimuli increase synaptic inhibition in V1. Such an increase in inhibitory input would lead to a decline in resistance for large stimuli, whereas we observed an increase in resistance.

The Impact of Voltage-Gated Input Resistance Changes on Selectivity

We have demonstrated that intrinsic conductances counteract resistance changes due to synaptic input and alter the effects of driving force. To explore how the intrinsic conductance shapes the firing properties of neurons, we returned to our simple computational model. The model allows us to evaluate the impact of the intrinsic conductance on membrane potential and firing rate because we can add or remove the conductance in our model. To ensure that our model recapitulates the membrane potential fluctuations we observed in behaving macaque, we used the individual trial-by-trial responses of recorded neurons as a basis for Poisson synaptic inputs from excitatory and inhibitory neurons (see STAR Methods). Employing a combination of both the recorded Vm and dVm/dt as synaptic drive to our simple model resulted in Vm responses that were remarkably similar to those that we measured (Figures 6A and 6B). By stimulating the model neuron using all of the visual conditions and repeats from our experimental data, we were able to extract how synaptic conductance and the intrinsic conductance varied with mean membrane potential (Figure 6C). As synaptic conductance increased, the mean membrane potential also increased. In concert with that change in membrane potential, the intrinsic conductance closes, mitigating some of the effects of the synaptic conductance change. In this way, the voltage-gated intrinsic channels were acting to compensate for the large changes in input resistance caused by synaptic input. Note, however, that this compensation is not complete. That is, the intrinsic channels in our model were not able to fully counteract the conductance changes due to synaptic input during visual stimulation.

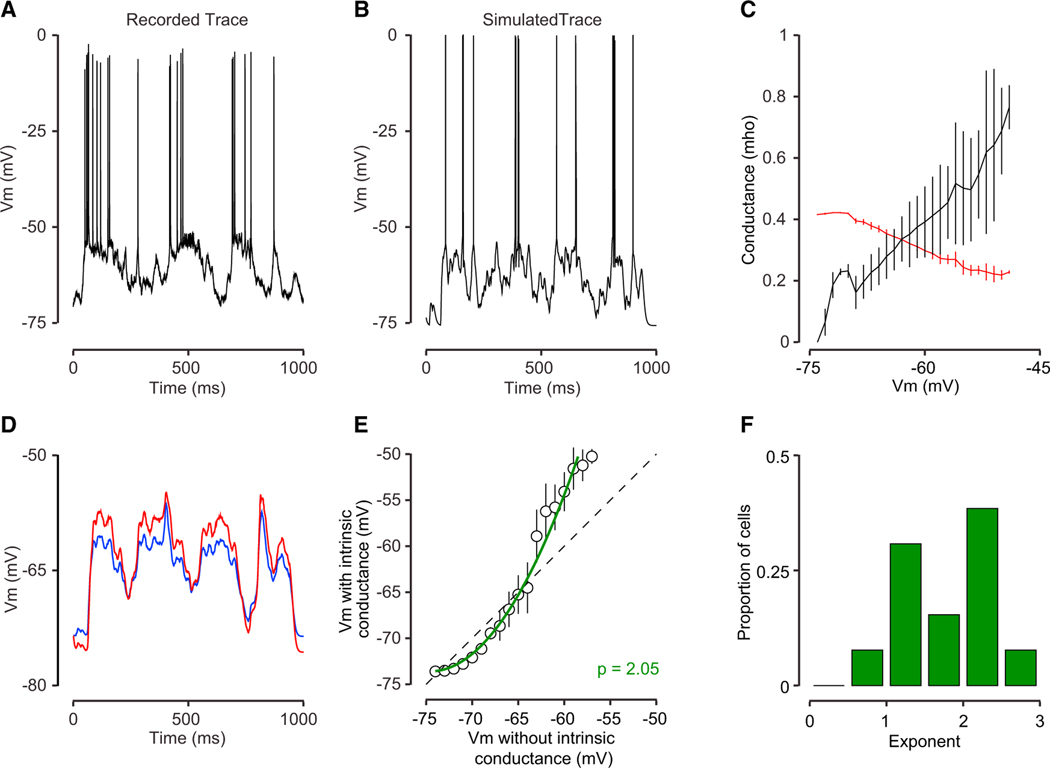
Figure 6. Modeling the Responses of Primate V1 Neurons with Voltage-Gated Conductances.

(A) A single-trial membrane potential response to a grating presented at the preferred orientation from macaque monkey V1.

(B) A model of that trial’s response.

(C) The relationship between the model membrane potential and conductances in the simulations. The conductance forthe intrinsic channel (red) declined with depolarization although synaptic conductance increased with depolarization (black).

(D) Membrane potential traces for a model with the intrinsic channel (red) and without the intrinsic conductance (blue) for the same synaptic input.

(E) Average Vm for the model with the voltage-gated conductance is plotted relative to the Vm for the model without the voltage-gated conductance for the example cell. The green line indicates a power law fit between Vm in the two models.

(F) The distribution of the fit exponent across neurons in our population of primate neurons.

The effects of the intrinsic channel in this model not only shaped the overall input resistance but also the membrane potential itself. We used our simulation to compare the membrane potential responses with and without the intrinsic conductance using identical synaptic inputs (but making sure that the average input resistance was matched; Figure 6C). We found that the intrinsic conductance made systematic alterations in the membrane potential, enhancing large deflections in the time course of the membrane potential of the visual response (Figure 6D). To quantify these intrinsic channel-dependent distortions in membrane potential trajectory, we plotted the membrane potential with and without the intrinsic conductance across all trials. This relationship was characterized by an expansive nonlinearity (Figure 6E). That is, the intrinsic conductance had the effect of reducing responses for conditions that had weak synaptic input and expansively increasing responses for conditions that generated larger depolarizations. We fit the relationship between membrane potentials with and without the intrinsic conductance, elicited by the same synaptic conductances, with a power-law nonlinearity (see STAR Methods). The exponent of the power law was significantly larger than 1 across our sample population, demonstrating the expansive impact of the intrinsic conductance (Figure 6F; mean p = 1.8).

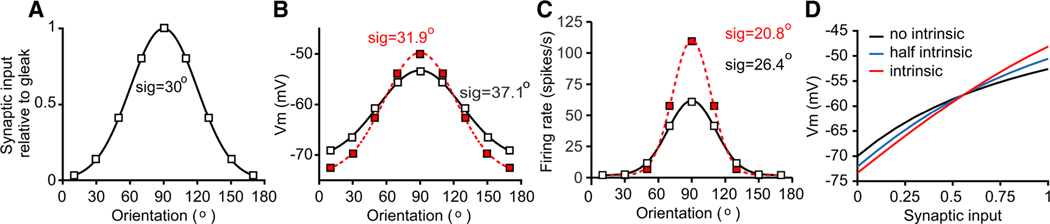
The systematic distortions in membrane potential are reminiscent of the nonlinearity observed when comparing membrane potential and firing rate (Anderson et al., 2000b; Carandini and Ferster, 2000; Hansel and van Vreeswijk, 2002; Miller and Troyer, 2002). The threshold expansive nonlinearity has the effect of enhancing selectivity and distinguishing functional cell classes. We hypothesized that the intrinsic conductance described here might play a similar role, that is, by increasing the dynamic range of cells it would sculpt the orientation selectivity of cortical neurons at a subthreshold level. To measure the impact of the intrinsic channel on selectivity, we compared the orientation selectivity of conductance-based models that either included the intrinsic voltage-gated conductance or did not. We first computed the steady-state membrane potential that resulted in a model that lacked the intrinsic conductance. Due to the effect of driving force (Figure 4A), the transformation of input conductance to membrane potential was compressive, resulting in a broader membrane potential selectivity than the input selectivity (Figures 7A and 7B, black points). If we included the intrinsic conductance, however, the membrane potential responses that emerged had a similar selectivity to those that are observed in the input (Figures 7A and 7B, red points). This difference in subthreshold tuning was magnified by the threshold nonlinearity, leading to a sharpening of the spike rate selectivity by 20% (Figure 7C).

Figure 7. Effects of Voltage-Gated Intrinsic Properties on Orientation Selectivity of a Model V1 Neuron.

(A) Orientation tuning of synaptic input to a model cell In V1. The tuning width (sigma) of the synaptic input is set at 30°. The maximum synaptic input strength relative to the leak conductance is set at 1.0.

(B and C) Orientation tuning of Vm (B) and spiking (C) activity with (black open squares) and without (red filled squares) intrinsic properties.

(D) Changes in Vm with increasing strength of both excitatory and inhibitory synaptic inputs both in the absence of the intrinsic conductance (black) and with increasing proportions of the voltage-gated conductance relative to the leak conductance.

In our simple model, without voltage-gated intrinsic channels, the relationship between synaptic input and membrane potential was compressive, weakening the differences between distinct synaptic inputs (Figure 7D, black). The intrinsic channel, when used in similar amounts as those we measured in real cells, acted to linearize the relationship between changes in synaptic input and changes in membrane potential (Figure 6D, red line). The overall impact of the intrinsic conductance depends on how strong it is relative to the leak conductance, because reducing the relative amount of the voltage-gated intrinsic component only partially overcame the saturating nonlinearity between input and membrane potential (Figure 7D, blue). The degree of the expression of this intrinsic conductance therefore significantly modulates the transformation of inputs into membrane potential and, consequentially, action potentials.

DISCUSSION

Using novel experimental measurements and a simple computational model, we have provided evidence for an intrinsic voltage-gated conductance in layer 2/3 V1 cells of awake macaques, anesthetized mice, and acute mouse brain slices. We found that this voltage-gated conductance significantly modulated the input resistance of neurons, altering how inputs were converted into membrane potential responses. This voltage-gated conductance follows the profile of anomalous rectification, closing as the neuron become more depolarized.

The presence of this intrinsic conductance led us to predict that the visual response of V1 neurons would be significantly impacted by the baseline membrane potential, which is evident in our recordings (Figure 4). Nonetheless, it is also apparent that visual stimuli evoked large changes in input resistance, causing an overall decline in input resistance. We found that this decline existed both for small-diameter stimuli, which evoked large responses and large resistance declines, and for large stimuli, which evoked weaker responses and smaller resistance changes, indicating a dominance of visually evoked synaptic input over the voltage-gated intrinsic channel.

What role does this intrinsic conductance play in transforming inputs to outputs? We hypothesized that there might be at least two properties of this conductance that could alter the processing of visual information. First, as excitatory synaptic inputs increase onto a neuron, the input resistance of the cell declines, which acts to shunt other inputs. By closing intrinsic channels as the neuron depolarizes, the cell counteracts this shunting process (Wilson, 1992). Although we have demonstrated that the conductance does counteract this shunt, it did so in an incomplete fashion. That is, when we delivered the preferred stimulus, the synaptic drive dominated the intrinsic changes and led to an overall decline in input resistance (Figure 5C). Second, because the intrinsic conductance acts to boost inputs as the cell becomes more depolarized, it acts as a subthreshold expansive nonlinearity, increasing the dynamic range of the neurons and sharpening tuning. This effect is similar to the expansive nonlinearity that exists between membrane potential and spike rate, which is thought to be a key component to enhance the selectivity of neurons (Carandini and Ferster, 2000; Priebe and Ferster, 2008). The intrinsic conductance counteracts nonlinearities that exist in the membrane equation and helps to linearize the relationship between inputs and membrane potential. The inclusion of the voltage-gated conductance in the model had a large impact on the overall output spiking of neurons, increasing orientation selectivity by 20%.

Neurons acted in distinct manners during spontaneous and visually evoked conditions. During spontaneous activity, membrane potential depolarization led to a systematic increase in input resistance (i.e., positive correlation between Vm and Rn). In contrast, during visually evoked activity, membrane potential depolarization led to a systematic decrease in input resistance (i.e., negative correlation between Vm and Rn). This difference indicates that there is a different tone of inputs that impinge on neurons during spontaneous and evoked responses. In particular, the intrinsic conductance was dominant during spontaneous activity although the synaptic drive dominated during visually evoked activity. These data therefore reveal the different modes that the visual cortex functions: spontaneous fluctuations are driven by weak changes in input strength (Waters and Helmchen, 2006) although visually driven fluctuations are driven by large changes in inputs strength (Tan et al., 2014), even for similar membrane potential fluctuations.

We have interpreted the voltage-dependent changes in input resistance as being related to a closure of intrinsic channels. An alternative interpretation, however, is that these changes are instead due to opening of slowly inactivating voltage-gated sodium (or calcium) channels. When membrane potential is depolarized by steady current, the opening of sodium channels could boost that shift in membrane potential, leading to the appearance of an increased membrane resistance (Fernandez et al., 2015). Although a persistent sodium conductance may indeed contribute to these changes in input resistance, there are three reasons we suspect that it does not play a dominant role. First, sodium channels inactivate overtime. When membrane potential was adjusted with steady current injection, neurons were held at those values for long periods, over periods of minutes, ample time for the sodium channel to inactivate. Second, increases in membrane potential by steady current injection did not result in a sag that would be characteristic of a large sodium conductance playing a role (data not shown). Finally, the activation range of sodium currents is more depolarized (>−60 mV) than the majority of our measurements, and yet we find changes in input resistance over large ranges in membrane potential. These three reasons suggest that the opening of sodium channels was unlikely to play the primary role in the changes in input resistance we observed, but some contribution cannot be ruled out (Wilson, 2005). Further experiments are required to dissect the set of voltage-gated conductances that contribute to the nonlinear responses we observed in visual cortex (Figure 4).

Our results demonstrating that input resistance increases with membrane potential depolarization during spontaneous activity contrast with measurements made from the cat and ferret neocortex during UP and DOWN states (Destexhe et al., 2003; Haider et al., 2006; Paré et al., 1998). These studies showed that input resistance declines when neurons shift to the UP state, which has been interpreted as evidence that synaptic drive increases during those epochs. Neurons in awake primate V1 do not exhibit UP and DOWN states, so a direct comparison to these studies is difficult (Paré et al., 1998). We interpret our observed increases in input resistance during spontaneous depolarization as the combination of two factors: a decline in resistance caused by an increase in synaptic input and an increase in resistance caused by the closing of one or more intrinsic channels. Indeed, using broad-spectrum channel blockers cesium and QX-314 inverted this relationship, and more depolarized potentials were associated with declines in cell resistance (Figure S5; related to Figure 2). Our records were from the superficial layers of primate and rodent V1, whereas previous measurements may be from deeper layers, which we have not examined (Paré et al., 1998). In addition, there is another demonstration that input resistance increases with spontaneous depolarization in the superficial layers of anesthetized rodent S1, which arrived at a similar interpretation as our work (Waters and Helmchen, 2006). In sum, the differences in how membrane potential is linked to membrane resistance may reflect distinct membrane potential dynamics, depending on which cells are recorded, the area of cortex studied, or the species used.

Our results are consistent with the idea that there are voltage-gated ion channels that counteract the changes in resistance induced by changes in synaptic input. Such an anomalous current has been previously described in muscles (Fatt and Katz, 1951), invertebrate neurons (Kandel and Tauc, 1966), dopaminergic neurons in the striatum (Wilson and Kawaguchi, 1996), and rat S1 (Waters and Helmchen, 2006). These reports all describe an unexpected increase in membrane resistance during depolarization. Here, we demonstrate that this increase occurred during spontaneous activity but that, during visually evoked responses, the voltage-gated conductance counteracted and partially mitigated the shunts that are induced by strong synaptic stimulation. Nonetheless, the presence of the intrinsic channel(s) acts to modulate how synaptic inputs are converted into membrane potential responses. Some of the channels that may be involved in this process are G-protein coupled and/or sensitive to second messengers, suggesting that this transformation could be dynamically adjusted using neuromodulatory systems, and may be one way to change the gain of inputs during overall changes in network state or attention.

Neurons exhibit complex characteristics that make them naturally behave in a nonlinear fashion. These characteristics include voltage-gated channels, nonlinear dendritic processes, spike threshold, and calcium currents. Even the simple membrane equation itself yields a nonlinear relationship between input strength and membrane potential response (Figure 7). We hypothesize that at least some of the complexity of neurons, including the voltage-gated anomalous rectifying conductance we have described, acts to counteract or shape these nonlinearities, thus allowing neurons to exhibit membrane potential responses proportional to their inputs.

STAR★METHODS

Detailed methods are provided in the online version of this paper and include the following:

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Nicholas Priebe, nicholas@mail.utexas.edu

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Experiments were performed in adult, behaving rhesus macaques, in adult, anesthetized C57/Bl6J mice, and in an in vitro brain slice preparation from adult C57/BL6J mice. All procedures were approved by the University of Texas Institutional Animal Care and Use Committee and conformed to National Institutes of Health standards.

METHOD DETAILS

Behavioral task and visual stimuli for behaving monkeys

Three adult male macaque monkeys were trained to perform a visual fixation task. Each trial began when a fixation spot was displayed at the center of a monitor in front of the monkey. The size of the fixation spot is 0.1°, and the monkey had to shift gaze to the fixation point and maintain fixation within a small window (less than 2° full width) for at least 1,500 ms to receive a reward. While the monkey was maintaining fixation, a drifting sinusoidal grating was presented at the preferred orientation for 1,000 ms. Receptive field position for neurons in the recording chamber were predetermined by a voltage sensitive dye imaging (VSDI) experiment (Yang et al., 2007). Visual stimuli of drifting sinusoidal grating were presented on a gamma-corrected 21-inch color display (Sony Trinitron GDM-F520) at a fixed mean luminance of 30 cd/m². The display subtended 20.5° x 15.4° at a viewing distance of 108 cm and had a pixel resolution of 1024 × 768, 30-bit color depth and a refresh rate of 100 Hz. Visual stimuli were generated by using a custom-designed software. Behavioral measurements and data acquisition were controlled by a PC running a software package for neurophysiological recordings from alert animals (Reflective Computing). Eye positions were monitored with an infrared eye-tracker (EyeLink).

Whole cell recordings in behaving monkeys

The whole-cell recording procedures were described in details in our previous work (Tan et al., 2014). Recording chambers were located on the dorsal portion of V1, with the anterior portion of the chamber reaching close to the lunate sulcus and the border between V1 and V2. The cortex in our cranial windows represents stimuli that are approximately 2.5°−5° away from the fovea in the lower quadrant of the contralateral hemifield. Intracellular records of Vm were obtained with blind in vivo whole-cell recordings. To increase recording stability, we filled the recording chamber with 2%−4% agarose in artificial cerebrospinal fluid (CSF). To minimize the damage to the brain, we stopped advancing the electrodes when it reached about 1300 Mm in the brain, therefore our intracellular recording were primarily from layer 2/3 in V1. As a reference electrode, a silver chloride wire was inserted into the agarose. The potential of the CSF was assumed to be uniform and equal to that of the reference electrode. Pipettes (6–12 MΩ) were pulled from borosilicate glass capillaries (KG-33, 1.2mm outer diameter, 0.70mm inner diameter; King Precision Glass) on a P-2000 micropipette puller (Sutter Instruments). Patch pipettes were filled with (in mM) 135 potassium gluconate, 4 NaCl, 0.5 EGTA, 2 MgATP, 10 phosphocreatine disodium, 10 HEPES, pH adjusted to 7.3 with KOH (Sigma-Aldrich). Whole-cell current-clamp recordings were performed with an Axoclamp 2B Microelectrode Amplifier (Molecular Devices).

Physiological procedures in anesthetized mice

Physiological procedures for mouse recordings were based on those previously described (Tan etal., 2011). All our experiments were conducted with adult C57BL/6 mice (age 5–10 wk). For surgery, mice were sedated with an intraperitoneal injection of chlorprothixene (5 mg/kg) and then anesthetized with urethane (1.0 g/kg). Brain edema was prevented by intraperitoneal injection of 20 mg/kg dexamethasone. Animals were warmed with a thermostatically controlled heat lamp to maintain body temperature at 37° C. A tracheotomy was performed. The head was placed in a mouse adaptor (Stoelting), and a craniotomy and duratomy were performed over visual cortex. Mouse eyes were kept moist with a thin layer of silicone oil. Current-clamp and voltage-clamp whole-cell recording were conducted in the binocular zone of V1 (Gordon and Stryker, 1996). Visual stimuli were generated by a Macintosh computer (Apple) using the Psychophysics Toolbox for MATLAB (MathWorks) and presented on a Sony video monitor (GDM-F520) placed 25 cm from the animal’s eyes. The video monitors had a refresh rate of 100 Hz and a spatial resolution of 1024 × 768 pixels, which subtended 40 × 30 cm (77° × 62°). The video monitor had a mean luminance of 40 cd/cm2. Drifting grating stimuli were presented to the contralateral eye with the duration of 2 s, size of 20°, spatial frequency of 0.03 cpd, contrast of 100%, and temporal frequency of 2 Hz.

In vitro physiology procedures

Brain slices from layer 2/3 of V1 in adult mice were prepared in a similar manner as in Routh et al. (2017). Slices were submerged in a heated chamber (32–34°C) that was continuously perfused at 1–2 mL/min with a bubbled aCSF solution consisting of (in mM): 125 NaCl, 3 KCl, 1.25 NaH₂PO₄, 25 NaHCO₃,12.5 dextrose, 2 CaCl₂, 1 MgCl₂, and 3 sodium pyruvate. Layer 2/3 cells were visualized using a Zeiss Axioskop 2 microscope fitted with DIC optics, or a two-photon laser scanning microscope (Leica SP5-RS) using Dodt contrast. Patch pipettes (3–6 MΠ) were pulled from borosilicate glass of 1.65 mm outer diameter (World Precision Instruments), using a Flaming/Brown micropipette puller (model P-97, Sutter Instruments), and wrapped with parafilm to minimize pipette capacitance. For whole cell recordings pipettes were filled with a solution containing (in mM): 120 K-gluconate, 16 KCl, 10 HEPES, 8 NaCl, 7 K₂-phosphocreatine, 0.3 Na-GTP, and 4 Mg-ATP (pH to 7.3 with KOH). For perforated patch recordings, pipette tips were first filled with a drug-free solution consisting of (in mM): 130 K-gluconate, 7 KCl, 1 NaCl, 4 MgCl₂, and 10 HEPES (pH to 7.3 with KOH, and sucrose added to an osmolarity of 300 mOsM). Then pipettes were backfilled with the same solution, with the addition of 120–240 ug/ml Amphotericin B (Sigma Aldrich) and 100 μM Oregon green 488 bapta-1 (Thermo Fisher). Perforated patches were made by obtaining 1–5 GΩ seals, and membrane perforation was allowed to progress for 15–20 minutes before recordings were performed. Whole cell and perforated patch current clamp recordings were made with a Dagan BVC-700 amplifier and custom-written software in IgorPro or a Multiclamp 700B amplifier with Axograph acquisition software. Pipette capacitance was compensated for, and the bridge was balanced for each recording. Whole cell recordings were included only if Rs was under 20 MΩ. Perforated patch recordings had Rs in the range of 30–50 MΩ and were visualized with OGB-1 throughout the experiment to ensure break-in didn’t occur. In all slice experiments, a holding current was used to set Vm at different membrane potentials, from −85 mV to −60 mV, in increments of 5 mV. We waited at least 30 s after changing the membrane potential to begin collecting current step data. Membrane voltage responses to −100 pA current steps were recorded at each Vm, and input resistance, Rm, was calculated as the average ΔVm/I_injected at each holding potential.

Input resistance (Rn) measurements

We employed two methods to estimate input resistance. Details of Rn measurements using current pulses have been described in previous studies (Anderson et al., 2000a; Tan et al., 2014). In brief, to measure Rn, negative current pulses (100 to 200 pA) were injected into the cell. Although we neutralized the capacitance and resistance of the electrodes before patching a cell, the electrode resistance Re increased dramatically when a neuron was obtained. The total resistance for a patch in whole-cell recording consists of two components, Rn and Re. Therefore, the value of Re must be properly removed to obtain an accurate estimation of Rn. All bridge balance was performed offline. We estimated Rn from membrane potential (Vm) responses to the hyperpolarizing current pulses by fitting Vm signal with a sum of two exponential functions:

$$V(t)=I_{inj}\left[R_n\left(1-e^{\frac{-t}{{\tau }_m}}\right)+R_e\left(1-e^{\frac{-t}{{\tau }_e}}\right)\right]$$ (Equation 1)

where V is the voltage response, t is time, I_inj is injected current, Rn is input resistance, ${\tau }_m$ is membrane time constant, Re is electrode resistance, and ${\tau }_e$ is electrode time constant.

The second method we employed to estimate input resistance was to measure the mean membrane potential for different steady holding current levels, after bridge balancing (Figure S4, Related to Figure 2). We then fit current-voltage relationship using a simple exponential:

$$V(I)=a{e}^{\frac{I}{\tau }}+b$$ (Equation 2)

Using this fit we could estimate the input resistance and its dependence on membrane potential.

Data analysis

Membrane potential recordings in V1 exhibit large fluctuations which could disrupt our ability to accurately measure Rm. We estimated membrane resistance based on changes in membrane potential by injecting negative current pulses. Therefore, the measurement of membrane resistance would be significantly underestimated or overestimated if there is a large fluctuation in membrane potential during current injection. In our experiment, a standard current injection is composed of a 100-ms negative pulse following by a 150-ms recovery interval. To assure that the membrane potential does not fluctuate greatly during the Rm measurement we constrained our analysis to those measurements in which the membrane potential level at the onset of a current injection and 150 ms after the current injection differed by less than 3 mV. Our results do not depend on this choice (Figure S1, Related to Figure 1).

Model simulations

We constructed single compartment models in MATLAB (Mathworks) based on the membrane equation that included terms for excitation, inhibition, a leak conductance and a voltage-gated subthreshold conductance:

$$C\frac{d{V}_m}{dt}=g_E\left(V_e-V_m\right)+g_I\left(V_i-V_m\right)+g_{leak}\left(V_{rest}-V_m\right)+g_{ir}\left(V_m\right)\left(V_{ir}-V_m\right)$$ (Equation 3)

where C is the cell capacitance, V_m is the cell membrane potential, g_E, g_i, g_leak and g_ir are the maximal conductances for excitation, inhibition, leak and the voltage-gated conductance. For those simulations that lacked the voltage-gated conductance, g_ir was set to 0. The time courses for g_E and g_I are modeled as a difference of exponentials:

$$g(t)=\overline{g}\sum (e^{\frac{-\left(t-t_j\right)}{{\tau }^{fall}}})-(e^{\frac{-\left(t-t_j\right)}{{\tau }^{rise}}})$$ (Equation 4)

where ${\tau }^{fall}$ and ${\tau }^{rise}$ shape the synaptic dynamics following a presynaptic action potential at time t_j (Troyer et al., 1998). V_e, V_i, and V_ir were set to 0, −70 and −75 mV, whereas V_rest was set to the resting potential of recorded neurons from macaque V1 (between −75 and −60 mV). For simulations that lacked a voltage-gated conductance the leak conductance (gl) was set to the inverse of Rm measured from rest. When both the voltage-gated conductance and the leak conductance were included in simulations the gl and gir were set so that each contributed equally to the resistance at rest. We used the extracted positive relationship between Rm and Vm to model the voltage dependence of g_ir.

For the simulations shown in Figure 4, 300 excitatory and inhibitory presynaptic neurons with a time-varying Poisson responses served as inputs. The time course of the changes in excitatory and inhibitory rate were either governed by sinusoids that in phase, out of phase or with inhibition that only exhibited a mean increase in input (Figure S6, Related to Figure 4). For a subset of simulations, action potentials were included using an integrate-and-fire mechanism(Troyer et al., 1998; Troyer and Miller, 1997) with a spike threshold of −52.5 mV and a reset after 1.5 ms to −57.5 mV (Figure 6). To simulate membrane responses with similar dynamics as those in our records, we generated inhomogeneous Poisson spike trains that reflected a combination of the mean evoked membrane potential and the first derivative of the recorded membrane potential. For these simulations the V_rest and R_m were constrained by our records for each neuron. Comparisons between simulations with and without voltage-gated conductance were made by comparing the responses to the exact same synaptic inputs.

A power-law was used to fit the relationship between membrane potential with and without the intrinsic conductance (Figure 6E). The power-law was defined as:

$$V_{int}\left(V_{ni}\right)=a{\lfloor V_{ni}-V_{th}\rfloor }_{+}^p$$ (Equation 5)

where V_int is the membrane potential with the intrinsic conductance, V_ni is the membrane potential in the absence of the intrinsic conductance, a is a gain parameter, V_th is a threshold parameter and p is the exponent.

Finally, we examined the impact of an intrinsic channel on stimulus selectivity using Equation 3 with exctiatory and inhibitory inputs of equivalent orientation selectiivty (sigma = 30 degrees, Figure 7A) and extracting the steady state voltage (Figure 7B) wth and without the intrinsic channel. We modeled the transformation to spiking activity using a power law (Figure 7C):

$$Fr\left(V_m\right)=a{\lfloor V-V_{th}\rfloor }_{+}^p$$ (Equation 6)

QUANTIFICATION AND STATISTICAL ANALYSIS

Membrane potential recordings in V1 exhibit large fluctuations which could disrupt our ability to accurately measure Rn. We estimated membrane resistance based on changes in membrane potential by injecting negative current pulses. Therefore, the measurement of membrane resistance would be significantly underestimated or overestimated if there is a large fluctuation in membrane potential during current injection. In our experiment, a standard current injection is composed of a 100-ms negative pulse following by a 150-ms recovery interval. To assure that the membrane potential does not fluctuate greatly during the Rm measurement we constrained our analysis to those measurements in which the membrane potential level at the onset of a current injection and 150 ms after the current injection differed by less than 3 mV. Our results do not depend on this choice (Figure S1, Related to Figure 1). An alternative method to estimate input resistance is to measure membrane potential to steady current injection and to quantify the slope of the relationship between current injection and membrane potential (Figure S4, Related to Figure 2). We compared these two methods of measuring input resistance and found that they were comparable (median R² was 0.96).

DATA AND CODE AVAILABILITY

The datasets supporting the current study have not been deposited in a public repository but are available from the Lead Contact on request.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Cesium methanesulfonate	Sigma	C1426
Potassium d-gluconate	Sigma	G4500
Lidocaine N-ethyl bromide	Sigma	L57S3
Oregon Green 488 BAPTA-1	Thermo/Fisher	06S06
Amphotericin B	Sigma	Y0000005
Experimental Models: Organisms/Strains
Mouse C57BL/6J	Jackson Labs	000664
Software and Algorithms
MATLAB 2015	Mathworks	N/A
Igor Pro	Wavemetrics	N/A

Highlights.

• Neurons in behaving macaque V1 exhibit a large voltage-gated intrinsic conductance

• This conductance leads to an increase in membrane resistance with depolarization

• This mechanism increases neuronal gain and selectivity to subthreshold depolarization

• This nonlinearity should be incorporated into future models of cortical computations