Flow stability for dynamic community detection

Abstract

Many systems exhibit complex temporal dynamics due to the presence of different processes taking place simultaneously. An important task in these systems is to extract a simplified view of their time-dependent network of interactions. Community detection in temporal networks usually relies on aggregation over time windows or consider sequences of different stationary epochs. For dynamics-based methods, attempts to generalize static-network methodologies also face the fundamental difficulty that a stationary state of the dynamics does not always exist. Here, we derive a method based on a dynamical process evolving on the temporal network. Our method allows dynamics that do not reach a steady state and uncovers two sets of communities for a given time interval that accounts for the ordering of edges in forward and backward time. We show that our method provides a natural way to disentangle the different dynamical scales present in a system with synthetic and real-world examples.

The flow stability method extracts simplified descriptions of complex time-resolved datasets at different dynamical scales.

INTRODUCTION

Interactions in complex systems typically result from a multitude of temporal processes such as adaptation, cascading behavior, or cyclical patterns that all take place simultaneously but often at different spatial and temporal scales (1). The concept of temporal networks (2, 3, 4, 5) is used to study these time-dependent networks. The fundamental constituent of temporal networks are events, instead of edges in the case of static networks, that represent interactions between two nodes of a graph, delimited in time, and usually take the form of a quadruplet (u, v, s_i, e_i), where u is the source node, v is the target node, s_i is the starting time of event i, and e_i is its ending time. Nodes of a network may represent, for example, individuals, companies, neurons, genes, or words, while events represent their relations that may refer to social interactions, economic transactions, activity correlation, regulation, or co-occurrence, depending on the context. Several representations of temporal networks exist, each associated to different algorithms and methods, for example, as a sequence of static graphs representing time windows over which the activity is aggregated (6), as contact sequences when events are instantaneous in continuous time, or as interval graphs (7) or link streams (8,9) in continuous time with events that may have a duration. The study of the dynamics and structure of time-dependent networks has attracted many contributions from several fields such as sociology (10, 11, 12), computer science (8, 13, 14, 15, 16, 17), epidemiology (18, 19), mathematics, and network science (6, 20, 21, 22, 23, 24, 25) (references are not exhaustive).

Community detection in networks is the task of extracting a simplified view of a network’s structure and is fundamental to understanding the functioning of the systems that they represent (26). Loosely speaking, a community is a relatively dense subgraph, and it may be called a module or a cluster depending on the field of application. Within a temporal setting, Rossetti and Cazabet (27) classify dynamic community detection methods on the basis of how the dynamic communities that they find depend on time in three categories ranked in increasing degree of their temporal smoothness: (i) instant optimal, when the community structure at time t depends only on the topology of the network at that time [e.g., (23, 13)]; (ii) temporal trade-off, when the community structure at time t depends on the topology of the network at t and on the past topology or past community structure [e.g., (14, 15)]; and (iii) cross-time, when the community structure at time t depends on the entire network evolution [e.g., (24, 25, 17)].

Critically, most methods aggregate the temporal dimension over a sequence of time windows, transforming the network in a sequence of static networks defined on a discrete time grid, hence losing the precise ordering of the edge activations within each slice. This is necessary as these approaches rely on a static concept of communities, i.e., defined as a group of nodes that are more densely connected with each other than with the rest of the network, and to be meaningful in a temporal context, the notion of density of connections necessarily implies connections considered over some time interval. They then either apply standard community detection algorithms for static networks to each aggregated time slice and follow the evolution of the communities across time slices with special algorithms (15, 28, 29) or consider each slice as a layer of a multilayer network and apply a community detection method to the entire multilayer network [e.g., (6, 30)], hence defining communities over extended periods of time. Methods based on an underlying dynamical process (31, 32), taking place on each slice (33, 34) or on the entire multilayer network (6, 30), consider a process decoupled from the intrinsic time of the system under study to guarantee its stationarity. Statistical approaches have also been developed; for example, Peixoto and Rosvall (20) have generalized the framework of stochastic block model inference to a dynamical framework by including a Markov chain in the inferred model. Their generative model approach takes into account continuous-time Markov chain and can capture the ordering of events; however, it requires that the Markov chains describing the system must be stationary on different epochs.

Here, we propose a novel method that considers random walks (RWs) evolving on the network and restricted by the activation times of the edges. We consider the similarity of diffusion patterns over a given time interval as a way to cluster nodes together without recurring to temporal aggregation and while only considering time-respecting paths. This approach generalizes the notion of cluster density used in static methods, such as Markov stability (32), to the temporal case. We derive quality functions that allow one to find partitions that best cluster the flow of random walkers and that do not need to be evaluated using the stationary state of the diffusion process. This is necessary as the existence of such a state is not guaranteed when considering a process evolving with the temporal network.

We show that the temporal evolution of networks leads to potentially asymmetrical relations between vertices that can be captured by using two network partitions for a given time interval: the forward partition and the backward partition that cluster nodes from the point of view of the beginning and end of the time interval, respectively. We leverage the novel possibility of our method to be used with nonstationary realizations of a diffusion process to find dynamic communities relating the temporal influence between a small group of nodes and the entire network. We also show that our method allows one to reveal different dynamical scales present in temporal networks by using an RW process evolving with the network and varying its rate of diffusion. When compared to methods that necessitate aggregating the network evolution in several static time windows, we find that our method can capture dynamical scales existing at rates that are lost in the aggregation procedure. Our framework generalizes the concept of Markov stability (32, 35) and dynamical embeddings (36) to the case of temporal networks without having to be evaluated at stationarity.

RESULTS

Temporal flow stability

We consider the general case of a temporal network with a set of N vertices V, a set of M events E, and two sets of M not necessarily distinct starting and ending times, T^s and T^e. Here, the term event is used to represent the generalization of edges to the temporal case (4). Event i can be written as a tuple $e_i=(u, v, t_i^s, t_i^e)$ where u and v are the source and target vertices, respectively, $t_i^{\mathrm{s}}$ is the time at which the edge becomes active, and $t_i^{\mathrm{e}}$ is time at which the event ends, with $t_i^{\mathrm{e}}\ge t_i^{\mathrm{s}}$. This definition is equivalent to the ones of interval graphs (7) or link streams (9) and can also be used to describe more restrictive definitions of temporal networks with instantaneous events or as sequences of static graphs. A more general model of temporal networks, the stream graph model (9), also takes into account nodes with specific activation times. Our framework does not distinguish nodes that are absent from nodes that are present but inactive. We want to find a partition of the network in c nonoverlapping communities that describes well its structure. The N × c indicator matrix, H, records which vertex belongs to which community; e.g., each row of H is all zeros except for a one indicating the cluster to which the vertex belongs.

We consider an RW process starting on all nodes of the network at time t₁ with a density probability described by the 1 × N row vector p(t₁) and ending at t₂ (t₁ < t₂) with a density p(t₂). The RW evolution is restricted by the activation of the network’s edges, and the transition probability matrix of the RW, T(t₁, t₂), is such that p(t₂) = p(t₁)T(t₁, t₂) (see Materials and Methods). RWs are at the core of a variety of methods for community detection on static networks. However, their direct application to a temporal setting does not necessarily provide a satisfying answer. As an illustration, consider the framework of Markov stability, which clusters a network in groups of nodes where the random walkers are likely to remain for a given time. This can be achieved by clustering the covariance matrix of the process that encodes probabilities for walkers to start on a given node and end on another after a certain time minus the same probability for independent walkers (32). For a general, not necessarily stationary RW on a temporal network, the N × N covariance matrix between t₁ and t₂ is given by (see Methods and Materials)

$$\mathbf{S}(t_1,t_2)=\mathbf{P}(t_1)\mathbf{T}(t_1,t_2)-\mathbf{p}{(t_1)}^{\mathrm{T}}\mathbf{p}(t_2)$$ (1)

where P(t₁) = diag (p(t₁)). In the case of static networks, and taking p(t₁) = p(t₂) = π to be the stationary distribution of the RW process (which is defined if the graph is strongly connected), this expression reduces to the framework of Markov stability (32, 35).

In a temporal setting, a stationary state does not necessarily exist, and it is, in general, ill defined in the case of a network with a finite time window. For this reason, the initial distribution is not uniquely defined, and we argue that it can be chosen by the user depending on its purposes. This framework provides the ground to detect relevant multiscale structures in temporal networks and opens the door for a more general understanding of clustering in networks with nonstationary processes. However, constructing a quality function using Eq. 1 directly does not satisfyingly solve the temporal community detection problem, and this quality function needs some slight, yet conceptually important, modification.

To show so, we focus on the case of temporal networks with undirected events. Whether the events of the temporal networks have a direction or not, the transition matrix of the RW between two times is, in general, asymmetric. The time ordering of events can result in different probabilities for going from a particular node i at t₁ to a node j at t₂ than going from j at t₁ to i at t₂ (37), even if each event allows walkers to travel in both directions. As a consequence the covariance matrix S(t₁, t₂) is also asymmetric in general. For temporal network, the concept of community needs to take into account the temporal evolution of the network and the temporal asymmetry potentially arising from it. The element (i, j) of the covariance S(t₁, t₂) (Eq. 1) gives the probability that a walker is on node i at t₁ and on node j at t₂ minus the same probability for two independent walkers. Directly clustering S(t₁, t₂) in diagonal blocks would force a symmetric relation between nodes based on the RW state at two different times, as rows of S(t₁, t₂) refer to the state in t₁ and columns of S(t₁, t₂) to the state in t₂. By construction, S(t₁, t₂) considers the positions of the RW at different times and thus builds communities across time that are not synchronous, i.e., that aggregate nodes by comparing their states at different times.

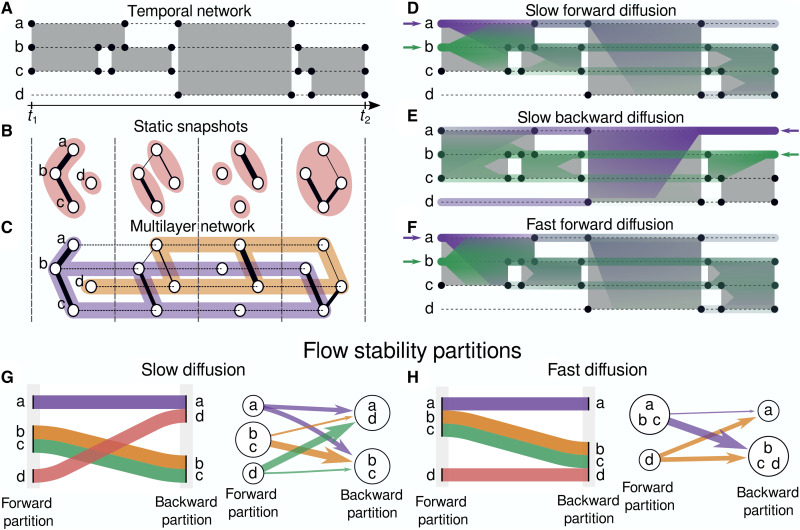
To make the similarity between the nodes synchronous and, concurrently, to capture the network evolution from t₁ to t₂, we propose to consider two partitions, effectively clustering the rows and columns of covariances separately and grouping together nodes based on their simultaneous state time and on the forward or backward evolution of the RW process (see Supplementary Text, “Relations with coclustering” section). This idea builds on the concept of dynamical embeddings of network (36) but generalized to temporal networks. We consider that two nodes are in the same forward community if the random walkers starting on them at t₁ tend to stay on the same nodes during the evolution of the network until t₂. To capture the temporal asymmetry, we also consider backward communities. A first possibility is to define backward communities by considering the random process that started at t₁ and saying that two nodes are in the same backward community if the random walkers that end on them at t₂ tended to stay on the same nodes from t₁ to t₂. A second possibility is to consider the reverse evolution of the network, where random walkers start at t₂ and diffuse until t₁. In this case, the backward communities are defined as the forward communities but by reversing the direction of time. Figure 1 illustrates the concept of the flow stability method on a simple example and compares it with other temporal community detection methods.

Fig. 1. Schematic representation of the flow stability compared to other temporal community detection methods.

(A) Example of a temporal network with four nodes (a, b, c, and d) and events joining pairs of nodes for different durations in continuous time. (B) A representation of the temporal network as four static networks each representing the aggregated edge activity over the corresponding time window. The communities found by modularity optimization are overlayed. (C) Multilayer representation of the sequence of static networks with interlayer links added in-between layers. The communities found by optimizing the multilayer modularity (6) (in orange and purple) extend over several layers. (D to F) Schematic representation of a diffusion process starting on nodes a (purple) and b (green) in forward time (D) and backward time (E). The probability density of the process at time t, computed with the transition probability matrix T(t₁, t) for the forward time and T_rev(t₂, t) for the backward time, is represented by the transparency of the colors. Using a faster diffusion rate (F), the process explores larger areas faster, and earlier events become more important. The flow stability method groups nodes together on the basis of the similarity of the diffusion processes starting on them and takes into account the ordering of the events and the dynamics of the network. (G) Two representations of the forward and backward partitions found with the flow stability method: an alluvial diagram (left) showing how nodes move between communities and a graph (right) showing the communities as meta nodes and the transition probabilities of the RW process between them as directed edges. Even by varying the aggregation window length, the initial and final static partitions cannot fully reproduce the results of the flow stability (see table S1). (H) Using a faster diffusion rate, nodes a and b are clustered together in the forward partition.

To find nodes from which random walkers tend to end up on the same node, we consider the process following the evolution of the network from t₁ to t > t₁ and followed by the inverse process going from t to t₁. The transition probability matrix corresponding to the inverse process, defined as the matrix T^inv(t, t₁) satisfying p(t)T^inv(t, t₁) = p(t₁), is given by Bayes’ theorem as T^inv(t, t₁) = P(t)⁻¹T(t₁, t)^TP(t₁) (38), where p(t) = p(t₁)T(t₁, t). The T^inv(t, t₁) matrix encodes the transitions probabilities to go from a state p(t) of a specific process back to the initial condition of this same process p(t₁), e.g., going backward in time in Fig. 1 (D or F). The corresponding covariance is

$$\begin{array}{c}{\mathbf{S}}_{\text{forw}}(t_1,t)=\mathbf{P}(t_1)\mathbf{T}({\mathrm{t}}_1,t){\mathbf{T}}^{\text{inv}}(t,t_1)-\mathbf{p}{(t_1)}^{\mathrm{T}}\mathbf{p}(t_1)=\\ \mathbf{P}(t_1)\mathbf{T}(t_1,t)\mathbf{P}{(t)}^{-1}\mathbf{T}{(t_1,t)}^T\mathbf{P}(t_1)-\mathbf{p}{(t_1)}^{\mathrm{T}}\mathbf{p}(t_1)\end{array}$$ (2)

which is symmetric by construction and has element (i, j) giving the probability that two random walkers starting in i and j at t₁ finish on the same node at t minus the probability that two independent walkers start in i and j at t₁. The matrix S_forw(t₁, t) contains the product of T(t₁, t) and T(t₁, t)^T and can be seen as a matrix measuring the similarity of the rows of T(t₁, t). Our method can be seen as a way to perform a coclustering of the transition matrix (see Supplementary Text, “Relations with coclustering” section). Moreover, this matrix is properly normalized; i.e., each row and column sum to zero, which is necessary for optimization method such as the Louvain algorithm (39).

Similarly, we can define a backward process by reversing time, which results in the following covariance matrix

$$\begin{array}{c}{\mathbf{S}}_{\text{back}}(t_2,t)=\mathbf{P}(t_2){\mathbf{T}}_{\text{rev}}(t_2,t){\mathbf{T}}_{\text{rev}}^{\text{inv}}(t,t_2)-\mathbf{p}{(t_2)}^{\mathrm{T}}\mathbf{p}(t_2)=\\ \mathbf{P}(t_2){\mathbf{T}}_{\text{rev}}(t_2,t)\mathbf{P}{(t)}^{-1}{\mathbf{T}}_{\text{rev}}{(t_2,t)}^{\mathrm{T}}\mathbf{P}(t_2)-\mathbf{p}{(t_2)}^{\mathrm{T}}\mathbf{p}(t_2)\end{array}$$ (3)

whose element (i, j) gives the probability that two random walkers starting in i and j at t₂ and following the reversed evolution of the network finish on the same node at t₁ minus the probability that two independent walkers start in i and j at t₂. Here, T_rev(t₂, t) is computed as T(t₁, t) but by considering the reversed evolution of the network since t < t₂ (see Materials and Methods). Figure 1E shows an example of this backward diffusion process. Similarly to the forward case, ${\mathbf{T}}_{\text{rev}}^{\text{inv}}(t,t_2)$ is given by Bayes’ theorem and encodes the transition probabilities to go from a state p(t) of a specific backward process back to the initial condition, p(t₂), of this process. This can be seen as going forward in time in Fig. 1E.

In this study, we consider S_forw(t₁, t) and S_back(t₂, t) for t₁ < t < t₂ with two corresponding initial conditions p(t₁) and p(t₂) taken as uniform distributions over all nodes, i.e., the maximum entropy distribution, for the general study of the dynamics of a temporal network between t₁ and t₂. This allows one to consider the forward and backward partitions independently as they both depend on their own process. We also investigate an example of clustering of a specific random process defined by a nonuniform initial probability distribution (see the “Uncovering the physical influences of network scientists” section). We discuss in Supplementary Text (“Covariances of inverse processes” section) an alternative definition of the backward covariance based on the same process than for the forward covariance.

We define the forward and backward flow stability functions as

$$I_{\text{forw}}^{\text{flow}}(t_1,t_2;{\mathbf{H}}_{\mathrm{f}})=\frac{1}{t_2-t_1}\text{trace}[{\mathbf{H}}_{\mathrm{f}}^T{\displaystyle {\int }_{t_1}^{t_2}}{\mathbf{S}}_{\text{forw}}(t_1,t)\mathit{dt}{\mathbf{H}}_{\mathrm{f}}]$$ (4)

and

$$I_{\text{back}}^{\text{flow}}(t_1,t_2;{\mathbf{H}}_{\mathrm{b}})=\frac{1}{t_2-t_1}\text{trace}[{\mathbf{H}}_{\mathrm{b}}^T{\displaystyle {\int }_{t_2}^{t_1}}{\mathbf{S}}_{\text{back}}(t_2,t)\mathit{dt}{\mathbf{H}}_{\mathrm{b}}]$$ (5)

The two partitions that maximize the forward and the backward flow stability functions, described by H_f and H_b, respectively, describe the temporal evolution of the network structure between t₁ and t₂. By taking the integral of the covariance over t, we find the most persistent communities during the entire time interval and give more weight to early times for the forward stability, or late times in the case of the backward stability, assuring that the time ordering of events is captured by both partitions. The integration correctly captures the time ordering even when a different ordering of the events results in the same final transition matrix, i.e., when interevent transition matrices commute.

The weight of early times compared to later time in the forward partition, or late times compared to early times in the backward partition, can be controlled by varying the rate of the RW process. We illustrate this effect with an analytic example in Supplementary Text (“Importance of early and late times on the optimal partitions” section) and fig. S1. However, our method gives a simplified description of the entire evolution of a network during a time interval with only two partitions and from the point of view of the starting and ending times of the interval. Details about the structure and dynamics in the middle of the interval may therefore be lost in the coarse graining procedure. When details about the dynamics happening in the middle of the interval are wanted, the time interval can be divided in a series of time windows for each of which two partitions are computed. In this case, compared to other methods that represent a temporal network as a sequence of static aggregated time windows (see Fig. 1, B and C), our approach has the advantage of preserving information about the dynamics inside each time window. We give an example of such an approach in the “Free-ranging house mice contact network” section. We also give results of the flow stability clustering applied on typical dynamic community events in fig. S2.

Example of temporal network with asymmetric temporal paths

As a simple model of temporal network where the time ordering of events leads to relations between nodes that could not be captured by a temporal aggregation in a static network, we consider the following network made of three groups of nine vertices each. Vertices are activated at random times drawn from an exponential distribution with parameter λ_activ (Poisson process). When a vertex is activated, it chooses another vertex according to a certain rule, and the duration of the interaction is drawn from another exponential distribution with parameter λ_inter. The system follows two types of successive interactions: (I1) during Δt₁, the vertices of two of the groups interact with one another with probability p₁ > 1/2 and with any other vertices in the network with probability 1 − p₁, while the vertices of the third group only interact with each other; and (I2) during Δt₂, each vertex interacts with other vertices of its group with a probability p₂ > 1/2 and with any vertices in the network with probability 1 − p₂. We generate a realization of the temporal network by running a simulation composed of three phases of interactions I1 separated by I2 phases as shown in Fig. 2A). During the first I1 phase, groups 1 and 2 interact; during the second I1 phase, groups 2 and 3 interact; and last, during the third I1 phase, groups 1 and 3 interact. If it were not for the small probability to reach any node in the network (if p₁ = p₂ = 1), the temporal paths in this network would not all be transitive; i.e., the existence of time-respecting paths from a node i to a node j and from node j to a node k would not guarantee the existence of a time-respecting path from node i to k. With p₁ < 1 and p₂ < 1, the situation is less marked, but the ordering of interactions creates temporal paths with asymmetric probabilities: For example, there are many paths that start in group 1, are in group 2 at the end of the first I1 phase, and are in group 3 at the end of the second I1 phase. However, there are almost no paths starting from group 3 going to group 2 and group 1 during the same time lapse. Defining communities in this temporal network is not straightforward. If we were to discard the temporal dimension, we would find that nodes are more densely connected with other nodes of the same group; however, the temporal pattern of interactions between groups would be lost. A good temporal partition in communities should offer a simplified description of the network structure and its evolution. In this case, the three groups and the ordering of their interactions should be identified. We show that we are able to achieve this by defining communities in terms of the flow of random walkers restricted by the edges activations. We run a simulation with the following parameters: λ_activ = 1, λ_inter = 1, p₁ = 0.95, p₂ = 0.95, Δt₁ = 120, and Δt₂ = 40.

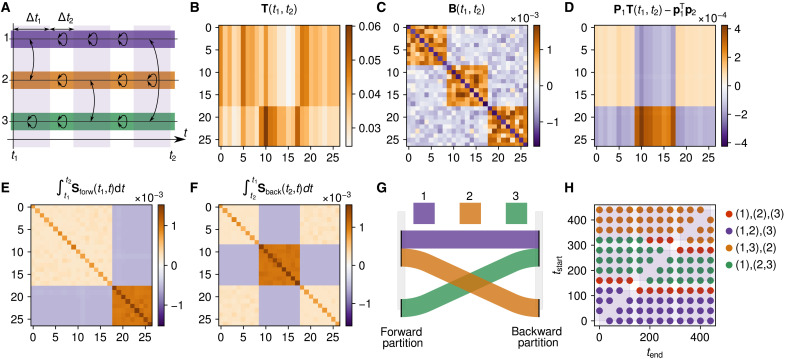
Fig. 2. Flow clustering of a synthetic network with asymmetric temporal paths.

(A) Representation of the different phases of interactions between the three groups of nodes. (B) RW transition matrix computed between the start, t₁, and the end of the three phases, t₂. (C) Modularity matrix computed on the aggregated network ($\mathbf{B}\mathit{=}\mathbf{A}-\frac{{\mathbf{k}}^{\mathit{T}}\mathbf{k}}{\mathbf{2}\mathit{m}}$, where A is the aggregated adjacency matrix, k=A1, and 2m = ∑_ik_i). (D) Covariance matrix, S(t₁, t₂), of the RW process defined in Eq. 12. (E) Integral of the forward process covariance matrix (Eq. 2). (F) Integral of the backward process covariance matrix (Eq. 3). (G) Representation of the forward and backward process in an alluvial diagram. (H) Best partitions found when varying the starting and ending times of the considered interval.

Figure 2B shows the transition matrix, T(t₁, t₂) computed from the resulting realization of the temporal network, between the start and the end of the three phases, using a continuous-time RW (CTRW) model (see Materials and Methods), and Fig. 2C shows the modularity matrix obtained when aggregating the temporal dimension. As expected, when aggregating the temporal activity, the temporal pattern of interaction is lost, and only the three groups are visible. Figure 2D shows the covariance matrix S(t₁, t₂) (Eq. 12). The temporal asymmetry of the system evolution is captured by the asymmetry of S(t₁, t₂). The two symmetric matrices corresponding to the forward and backward integrals of the symmetrized covariances (Eqs. 2 and 3, respectively) are shown in Fig. 2 (E and F). They capture the similarities between the rows and columns of S(t₁, t₂), integrated over the entire system evolution. The partitions that best describe them are found by optimizing the forward and backward flow stability functions (Eqs. 4 and 5, respectively) and are represented in Fig. 2G in an alluvial diagram (40). The forward and back partitions, and the relation between them, capture the three groups and the fact that groups 1 and 2 interact together at the beginning, groups 1 and 3 interact together at the end, while groups 2 and 3 “exchange” their position with group 1 during the evolution of the network. Figure 2H shows the best partition found with our method by varying the starting and ending times of the considered interval. When t_start < t_end (below the diagonal), the best partition is the forward partition (Eq. 4), and when t_start > t_end (above the diagonal), the best partition is the backward partition (Eq. 5). The alluvial diagram in Fig. 2G captures the global structure and dynamic of the system during its entire evolution, while Fig. 2H reveals the detailed timing of the interactions between groups.

Temporal multiscale community detection

An important point concerning community detection methods based on the optimization of a quality function, such as modularity optimization, is that the quality function implicitly restrict the size of the communities maximizing it (41). Quality functions including an explicit resolution parameter permit to overcome this problem. For example, the time parameter of the Markov stability framework serves as a resolution parameter that generalizes the modularity (32, 35) and allows to find communities at all scales in the network (42). In the case of temporal network, the concept of scale must take into account both the speed at which the network changes and the different sizes of its structures.

Here, the rate at which random walkers jump from nodes to nodes serves as a natural resolution parameter that controls how far walkers move during a certain time window. We use a CTRW on networks, which can also be described as a continuous-time Markov chain (43, 3), and we assume that, when an edge is active, walkers have a constant probability of jumping per unit of time given by the rate λ, or equivalently an average waiting time τ_w = 1/λ, even if the topology of the network is changing with time. The transition matrix therefore depends on the evolution of the network and on the RW waiting time; i.e., we have T(t₁, t₂) = T(t₁, t₂; τ_w). In the case of a temporal network where all edges are constant in time, i.e., a homogeneous Markov Chain, we have

$$\mathbf{T}(t_1,t_2;{\mathrm{\tau }}_{\mathrm{w}})=e^{-\frac{t_2-t_1}{{\mathrm{\tau }}_{\mathrm{w}}}\mathbf{L}}=\mathbf{I}+{\displaystyle \sum _{n=1}^{\infty }}\frac{{(-{\mathrm{\lambda }}^{\star }\mathbf{L})}^n}{n!}$$ (6)

where L = I − D⁻¹A is the RW Laplacian of the network (3) and ${\mathrm{\lambda }}^{\star }=\frac{t_2-t_1}{{\mathrm{\tau }}_{\mathrm{w}}}$ is a normalized RW rate. When computing the adjacency matrix A, we add self-loops on isolated nodes to keep the transition matrix stochastic. In the case where the network topology is changing in time, the transition matrix is computed as the time-respecting product of interevent transition matrices (see the details in Materials and Methods). We observe that varying τ_w in Eq. 6 allows to “zoom” in or out on the network. For λ^⋆ = 0 (or τ_w → ∞), i.e., for extremely slow walkers, T(t₁, t₂; τ_w) = I and walkers simply stay on their current nodes. When λ^⋆ = 1 (τ_w = t₂ − t₁), on average, walkers will have had the time to only jump to their direct neighbors. For λ^⋆ ≫ 1 (τ_w ≪ t₂ − t₁), i.e., for very fast walkers, the walker will have explored their entire reachable surroundings and, unless the RW is periodic, reached stationarity.

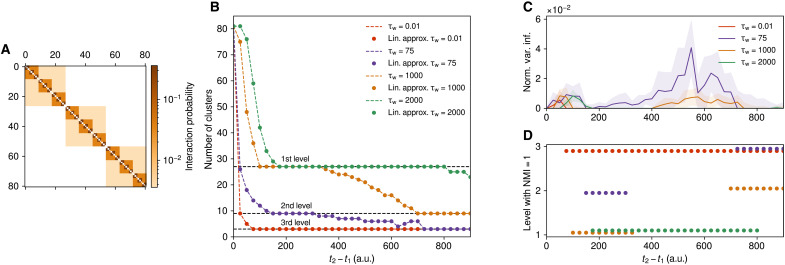
Figure 3 shows an example of the multiscale detection capabilities of our method and a comparison of the results obtained using the matrix exponential formulation to compute the transition matrices (Eq. 6) with the linearized version (see Materials and Methods, Eq. 14). For this example, we modeled temporal networks with 81 nodes using the same principle than for previous example with parameters λ_activ = 1/10 and λ_inter = 1/10. At each activation time, a node selects another node to interact with given different probabilities. The interaction probabilities, shown in Fig. 3A, define a hierarchical structure with a first level of 27 groups of 3 nodes, a second level with 9 groups of 9 nodes, and a third level with 3 groups of 27 nodes. We choose the interaction probabilities such that p₁/p₂ = 10, p₁/p₃ = 100, and p₄ = 0, where p₁ is the probability of a node to interact with nodes of the same first-level group, p₂ is the probability to interact with a node of the same second-level group, p₃ is the probability to interact with nodes of the same third-level group, and p₄ is the probability to interact with any other nodes. Figure 3B displays the number of communities found by our method, with the computation using the matrix exponential and the linear approximation, for different values of the average RW waiting time (τ_w) as a function of the time interval considered. We run 10 simulations and display the number of communities of the most common optimal partition found among the 10 simulations. To find the optimal partition, we run the Louvain algorithm (39) 50 times for each simulation and keep the partition maximizing the forward integral flow stability (Eq. 4). In this case, the network evolution is stationary, and therefore, using the backward integral flow stability gives similar results. The normalized variation of information (NVI) computed from the ensemble of partitions found by the Louvain algorithm is shown in Fig. 3C. Minima in NVI indicate the intrinsic scales of the system (35) and therefore allows to choose the relevant resolution parameters, i.e., the RW characteristic waiting times. We observe that depending on the time interval considered, we are able to recover the three scales of the system using different combinations of the waiting time parameter and that they correspond to minima in NVI. Figure 3D shows when the optimal partition found by our method corresponds exactly to one of three levels partition, measured by the normalized mutual information. For a given time interval, a slower RW discovers the finer level (27 communities), while faster RWs discover the coarser levels (9 and 3 communities). As time progresses, RWs go from the first level to the second level (e.g., τ_w = 1000 in Fig. 3) or from the second to the third level (e.g., τ_w = 75 in Fig. 3), discovering coarser and coarser scales. Figure 3B also shows that the linear approximation (circles) agrees very well with the computation using the matrix exponential (dashed lines) and allows to detect the different scales similarly in both regimes of the approximation (Eq. 14). Here, the average duration between changes in the network is ≃0.1 time units, so on average, λ^⋆ < 1 for τ_w > 0.1 and λ^⋆ > 1 for τ_w < 0.1.

Fig. 3. Multiscale temporal network clustering with the flow stability.

(A) Interaction probabilities of the synthetic temporal block model showing a hierarchical structure with three levels. (B) Number of clusters as a function of the time interval length for different values of the characteristic waiting time, τ_w. (C) Average NVI as a function of the time interval duration. Minima of the NVI indicate when the solutions of the optimization are robust. The filled band show the SD computed across the 10 simulations. (D) Correspondence between the optimal partitions found and the different levels of the network hierarchical structure. NMI, normalized mutual information; a.u., arbitrary units.

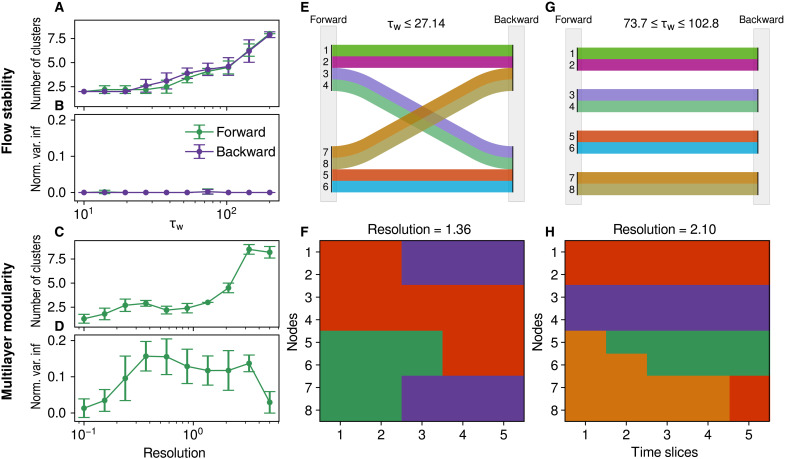
As the RW process is evolving with the temporal network, varying the rate of the RW can capture not only different coexisting structural scales but also gradual dynamic changes in structure. To demonstrate this, we run 10 simulations of our synthetic temporal network model with eight nodes and interaction probabilities that change linearly from the structure in two communities (1, 2, 3, 4) and (5, 6, 7, 8) at t = 0 to a structure with the two communities (1, 2, 7, 8) and (3, 4, 5, 6) at t = 100. Inside each community, the interaction probabilities are uniform. The activation rate of the nodes also change linearly between t = 0 and t = 100 from λ_activ = 1 to λ_activ = 2 for nodes 1, 2, 3, and 4 and from λ_activ = 2 to λ_activ = 1 for nodes 5, 6, 7, and 8. The event duration distribution is kept constant at λ_inter = 1. We apply the flow stability method over the entire time interval t = 0 to t = 100 and compare it with results obtained with the multilayer modularity (6) [optimized using the Leiden algorithm (44, 45)] applied to multilayer representations of the 10 networks with five layers containing the aggregated activity of the edges over five time windows. The interlayer coupling parameter is first fixed at $\frac{1}{10}$ of the global average edge weight. Figure 4 (A and C) shows the average and SD, taken across the 10 simulations, of the number of communities found by both methods as a function of the resolution parameter (i.e., the characteristic waiting time for the flow stability). For both methods, 50 runs of the optimization algorithm are performed, and the partition with the largest value of the objective function is kept. Figure 4 (B and D) shows the NVI of the 50 partitions as a function of the resolution. The NVI measures the variation in the set of 50 partitions found by the algorithms at each resolution. The average and SD are again computed across the 10 simulations. We see that the multilayer modularity shows a high value of the average NVI and of its SD for nontrivial partitions, while almost all the flow stability partitions have an average NVI of 0 with SD of 0. Two points have very small nonzero values. This indicates that the multilayer modularity has difficulties dealing with gradual changes and does not find consistent partitions when run several times on the same realization of the simulation. On the other hand, the flow stability shows very consistent results across all resolutions. Figure 4 (E to H) shows partitions at two different resolutions for both methods. For the flow stability, the partitions are also consistent across simulations, for τ_w = 10; the result displayed in Fig. 4E is found for all simulations and correctly captures the large scale dynamic of the system. This solution stays the most frequent across simulations until τ_w = 27.14, where this forward partition is found in 8 of 10 of the simulations and the backward partition in 5 of 10. The partitions shown in Fig. 4G, capturing the small-scale evolution, are found in 9 of 10 simulations for the forward partition, 8 of 10 for the backward at τ_w = 73.7, and 6 of 10 simulations for the forward and backward partitions at τ_w = 102.8. The partitions found with the multilayer modularity shown in Fig. 4 (F and H) correspond to the two resolutions with similar average NVI that are a local minima of the NVI curve. While Fig. 4F captures features of the evolution of the network structure, the multilayer modularity shows a large variability over repeated run of the optimization (large NVI) and over different realizations of the simulation. The partition shown in Fig. 4F is the most common among the different simulations and appears in 3 of 10 simulations. For the resolution shown in Fig. 4H, the 10 simulations result in 10 different optimal partitions (we show the one for the simulation that has the smallest NVI). Similar behaviors are observed by increasing or decreasing the number of time slices. When only two time slices are used, partitions with the initial and final configurations are found for the two slices, however still with a large NVI as the optimization hesitates between two configurations [(1, 2, 3, 4) in the first slice connected to (1, 2, 7, 8) in the second slice or (1, 2, 3, 4) connected to (3, 4, 5, 6)] in unequal proportions. In this case, a solution with a smaller NVI is given by the partition in four elongated communities similar to Fig. 4G. Increasing or decreasing the interslice coupling weight also results in high NVI until the same structure in four constant communities is found for large values of the interslice coupling. This example demonstrates that, without a priori knowledge of the real underlying dynamics, extracting the dynamic communities of continuously changing networks with multilayer methods is challenging. On the other hand, the flow stability method can consistently uncover dynamical changes in the structure of temporal networks within a single interval by only varying one parameter, the RW waiting time. Methods such as the multilayer modularity have more difficulties finding robust solutions and require tuning many parameters (resolution, number of slices, and interslice coupling).

Fig. 4. Comparison of the flow stability method with the multilayer modularity on synthetic network with a continuously changing structure.

The connections of the eight nodes change linearly from an initial structure in two communities: (1, 2, 3, 4) and (5, 6, 7, 8), to a final structure: (1, 2, 7, 8) and (3, 4, 5, 6). (A and C) Average and SD of the number of clusters as a function of the resolution parameter for the flow stability and multilayer modularity, respectively. (B and D) Average and SD of the NVI as a function of the resolution parameter for the flow stability and multilayer modularity, respectively. (E and G) Forward and backward partitions found with the flow stability for two different ranges of values of the resolution parameter that capture the two dynamic scales of the temporal network. (F and H) Partitions found with the multilayer modularity at two different values of the resolution parameter corresponding to local minima of the NVI.

Real-world examples

Primary school contact network

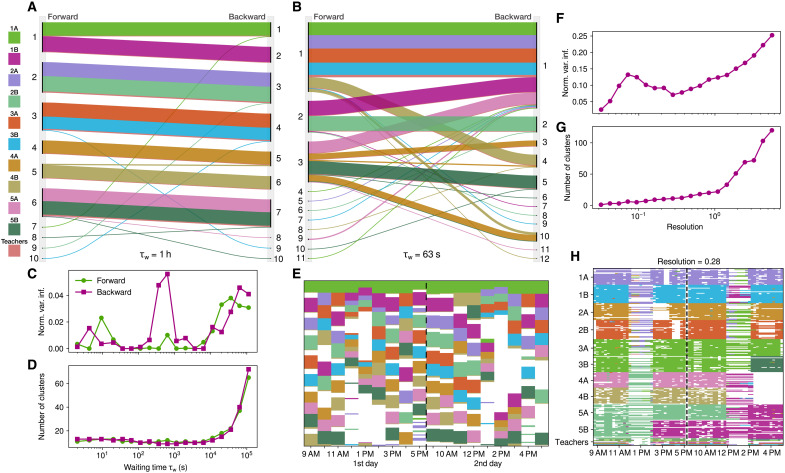
As a first real-world application of our method, we use the high-resolution measurements of face-to-face contact patterns recorded in a French primary school in the context of the sociopattern project (46). Face-to-face contacts between 232 children and 10 teachers were recorded for 2 days with the help of radio-frequency identification (RFID) devices, worn on the chests of participants, with a 20-s resolution. This dataset is well suited for validating temporal clustering method as the contacts are naturally restricted by the separation in five grades with two classes per grade. Each class has an assigned room and an assigned teacher; however, during morning, lunch, and afternoon breaks, children mix in the playground or in the canteen. As these common spaces do not have enough capacity to host all the students at the same time, only two or three classes have breaks at the same time, and lunches are taken in two consecutive turns (46).

We apply our method using the linear approximation of the transition matrices (Eq. 14) and perform 50 optimizations of the forward and backward flow stability functions with the Louvain algorithm for different RW characteristic waiting times. The NVI of the ensemble of partitions and the number of clusters of the best partition at each scale is shown in Fig. 5 (C and D, respectively). The NVI shows two minima, revealing the existence of two natural dynamical scales in the system, at τ_w = 63 s and τ_w = 1 hour. The forward and backward flow stability partitions corresponding to these two scales are shown in Fig. 5 (A and B) as alluvial diagrams.

Fig. 5. Flow stability clustering of face-to-face contacts in a primary school.

(A and B) Alluvial diagram representing the forward and backward partitions at two different scales corresponding to RW rates of (1 hour)⁻¹ and (63 s)⁻¹, respectively. (C and D) NVI and number of clusters of the best partition for different values of the characteristic waiting time. (E) Static clustering of hourly aggregated interactions using standard modularity optimization. (F and G) NVI and number of clusters found with the generalized multilayer modularity (6) as a function of the resolution parameter. (H) Multilayer partition of the network corresponding to the minima in NVI in (F).

The flow stability partitions found with an RW rate of (1 hour)⁻¹ (Fig. 5A) have 10 clusters for the forward partition and 10 clusters for the backward partition that mostly group children of the same grades together but with some additional details. Both partitions have also singleton clusters that correspond to children that were not present during the first day, for the forward partition, or second day, for the backward partition (see table S2). Classes 1A and 1B are clustered together in the forward partition but separately in the backward partition, indicating that they spent less time together near the end of the time interval than near the beginning. Classes 4A and 4B are separated in both the forward and backward partitions, revealing that they spent less time together than other classes of the same grade. All the other classes (2A, 2B, 3A, 3B, 5A, and 5B) are clustered in pairs, per grade, in both the forward and backward partitions. Figure 5E shows the static clustering of hourly aggregated interactions using standard modularity optimization (with a resolution parameter corresponding to the minimum NVI taken over all hourly slices). Although this method removes all the temporal details within each hourly slice, it allows to coarsely represent the interactions among children during the 2 days because the structures in this dataset change according to the school hourly schedule. This hourly clustering allows to verify the consistency of the flow clustering obtained over the entire period. We see that, indeed, classes 1A and 1B had lunch together during the first day, they are in the same static cluster at 12, 13, and 14 hours on the first day, but they were separated during the lunch break of the second day. We also see that classes 4A and 4B are separated during the morning and afternoon breaks of the first day and the morning and lunch breaks of the second day. In terms of cumulative time of the contacts between all individuals of two different classes of the same grade, classes 4A and 4B are indeed the classes in the grade with the lowest cumulative contact time (439.3 min) followed by classes 1A and 1B (582.7 min) [see table 3 in (46)]. All other grades have cumulative contact time between their classes above 966.7 min.

Figure 5B shows the forward and backward partitions maximizing the flow stability with an RW rate of (63 s)⁻¹ that capture changes happening at faster scales than in Fig. 5A. There are more forward and backward clusters with a small size than in Fig. 5A as they include not only children who missed the first or last day but also children, or small groups of children, who missed the morning of the first day or the afternoon of the second day (see table S3). The largest forward cluster contains classes 1A, 2A, 3A, and 4B. Figure 5E shows that these classes are often together during breaks of the first day, in particular during the morning break of the first day. The backward partition contains a similar cluster with the addition of classes 1B and 5A and without class 4B. Most of the children of class 4B leave after the lunch break of the second day, which is captured in the backward cluster 4 in Fig. 5B, with an average last contact time of 12:52 PM, while the last contact time in cluster 1 is 05:07 PM (see table S3). Classes 1B and 5A join the largest cluster in the backward partition. Figure 5E shows that they are often clustered together during the second day and join the other classes of the first cluster during the last hour. We also see that, while class 4A is in cluster 3 with classes 5A and 5B in the forward partition, it is split in two separated clusters (3 and 10) in the backward partition. Table S3 shows that the average last contact times for backward clusters 3 and 10 are 11:58 AM and 2:18 PM, respectively. The split in two clusters of class 4A is therefore due to the fact that a part of the class left before lunch, while the rest left after.

As a comparison to our method, we apply the generalization of the modularity to multilayer networks developed in (6). We create network layers corresponding to an aggregation in windows of 15 min, with edge weights equal to the cumulative contact times during each time window. The interslice weight is set to the average edge weight across all layers. Figure 5 (F and G) shows the NVI and the number of clusters found by running the Leiden (45) algorithm 50 times with the generalized multilayer modularity for each value of the resolution parameter. Here, only one minimum of the NVI is found, and the corresponding partition is shown in Fig. 5H. The partition captures the separation in grades and most of the separation in classes as well as some of the dynamics between classes. The scale and resolution in this case do not include the concept of time but consider the different layers as part of a larger static network. In our method, the different scales correspond to different speeds at which the network is traversed, and the two partitions correspond to the different directions of the temporal evolution of the network. We see that this allows us to discover two natural scales that describe the temporal network at two different levels: At the scale of 1 hour, we find the separation in different grades, while at the scale of 63 s, we find a coarser scale describing the interactions in-between grades and classes. Community detection performed on the multilayer representation of the network is useful for detecting the timing of the changes during the time interval considered. In our method, the temporal dynamic is captured in the two covariance matrices (Eqs. 2 and 3) in terms of probabilities of following a given path, and the RW rate plays the role of a filtering parameter that controls which spatiotemporal scales are considered. However, two partitions cannot represent the entire dynamics in a time interval when the dynamics change multiple times. In this case, the interval can be sliced in several time windows and the flow stability applied on each slice. We show such an example in the next section.

Free-ranging house mice contact network

As a second example of real-world application, we study an open population of house mice (Mus musculus domesticus) living freely in a barn of approximately 72 m² near Zurich, Switzerland. The barn is equipped with 40 nest boxes for the mice to rest and breed. Water and food are provided at 12 feeding trays inside the barn. The activity of the mice is monitored thanks to subcutaneously implanted RFID transponders and antennas situated at the entrance of each nest box (47). The time of the entering and leaving of the nest boxes is recorded, along with the identity of the corresponding animal.

Male and female mice of at least 18 g are implanted with new transponders with a unique RFID tag. The presence of litters in the nest boxes is also monitored weekly. The experiment has been initiated in 2002, and the continuous automatic reading and recording of the RFID transponders is in operation since 2007. We use a dataset recording the mice activity from 28 February to 1 May 2017, which captures the transition from winter to spring. A temporal network is reconstructed with 437 nodes representing all the mice recorded in the dataset and temporal events between two mice representing their simultaneous presence in the same nest box. There are more than 5.75 million events recorded with a millisecond resolution. The distribution of event durations is very broad with a median at 64 s, a 25 percentile at 7 s, and a 75 percentile at 6 hours and 25 min.

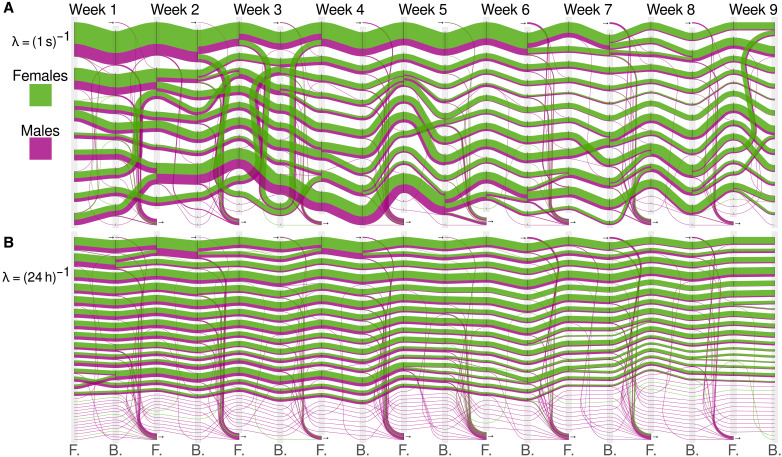
To observe the evolution of the community structure, we divide the period in nine intervals of 1 week each. For each week, we apply our method, using the linear approximation of the matrix exponential, and vary the RW rate to explore different dynamic scales. This results in nine pairs of forward and backward partitions that represent the evolution in each week. Figure 6 shows the nine backward and forward partitions represented as an alluvial diagram for the random rates of λ = (1 s)⁻¹ (Fig. 6A) and λ = (24 hours)⁻¹ (Fig. 6B). Figure 7 (A and B) shows the NVI of the partitions and the number of groups (i.e., communities) found with 50 runs of the Louvain algorithm as a function of the RW characteristic waiting time (τ_w = 1/λ). The average and SD taken over the nine forward and backward partitions is displayed. Minima in the NVI are visible for τ_w values of 1 s, 60 s, and 24 hours. These values indicate robust optimal partitions that correspond to intrinsic dynamic scales of the system.

Fig. 6. Flow stability clustering of a contact network of free-ranging wild house mice.

(A and B) Alluvial diagram representing the forward and backward partitions at two different scales corresponding to RW rates of (1 s)⁻¹ and (24 hours)⁻¹, respectively. The flow corresponding to females is indicated in green, and the one corresponding to males is in purple. The community dynamics at a rate of (1 s)⁻¹ (A) reveals the existence of large communities during the first weeks corresponding to the end of February and beginning of March, which split in smaller communities as spring arrives. At an RW rate of (24 hours)⁻¹ (B), a finer description of the dynamics is revealed with the presence of smaller social groups with compositions and sizes that are very stable over the entire observation period.

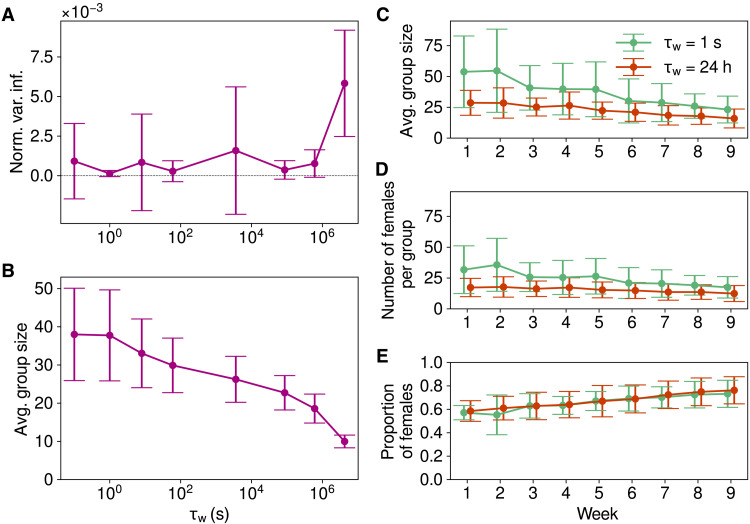
Fig. 7. Flow stability clustering statistics of the contact network of free-ranging wild house mice.

(A) NVI of the set of partitions found by the stochastic optimization algorithm as a function of the RW characteristic waiting time. (B) Community sizes as a function of the RW characteristic waiting time. In (A) and (B), the average and SD computed across the nine pairs of forward and backward partitions are shown. (C) Group, or community, sizes as a function of the week. (D) Number of females in each group as a function of the week. (E) Proportion of females in each group as a function of the week. In (C) to (E), the average and SD across the forward and backward communities of each week are shown.

The community dynamics at a rate of (1 s)⁻¹ (Fig. 6A) reveals the existence of large communities with a high proportion of males (Fig. 7E) during the first weeks corresponding to the end of February and beginning of March. As spring arrives, the large groups split in smaller communities (see Fig. 7C), and the proportion of females in groups increase as many males exit the system. In the mouse population, the transition from winter to spring corresponds to a transition from low reproduction to high reproduction (48). In this case, there were no weaned pups sampled until April. The average daily temperature in the barn also increased from freezing temperatures in February to temperatures around 20°C at the end of May. The presence of larger groups in winter may be explained by the benefit of thermoregulation (winter huddles) and by the lower competition for reproduction (49). At an RW rate of (24 hours)⁻¹ (Fig. 6B), a finer description of the dynamics is revealed with the presence of smaller social groups with compositions and sizes that are very stable over the entire observation period (see Fig. 7C). While the average number of females per group stays extremely stable (see Fig. 7D), the proportion of males decreases similarly than for the coarser partition (Fig. 7E), suggesting that the females are forming the cores of the different social groups.

We compare these results with results obtained by two other dynamic community detection methods typically used in temporal network. The first method consists of aggregating the activity over time windows to form a sequence of static networks. A static community detection method is then applied to each slice, and the evolution of the communities from slice to slice is tracked. Here, we use time windows of a half week to have the same number of partition than with the flow stability method, and we follow the methodology of Liechti et al. (49) who have studied the same mice population but over a different time frame. Communities are found at each slice with the hierarchical Infomap algorithm (50), and their evolution is tracked with an evolutionary clustering method (29). While this approach allows one to detect a coarse-grained and fine-grained evolution of the system (see fig. S3), an issue arises as the method does not necessarily detect the same number of hierarchical level in all slices. This renders the comparison of communities from slice to slice unclear. When tracking the number of communities per slice (see fig. S3A), large variations are observed without knowing whether they are due to real variations in the system or to the fact that the method found hierarchical levels at different scales. The flow stability method, in addition to keeping temporal information within each time window, uses a resolution parameter with a physical meaning, the rate of the RW, which allows a principled comparison of slices at the same dynamical scale and results in a smooth variation of the number of communities per week (see fig. S3B). The second method we compare our results with is the multilayer Infomap method applied to temporal networks (30, 21). This approach allows one to perform a hierarchical clustering considering the entire network evolution and therefore find scales relevant across time points. We represent the contact network as a multilayer network with 18 layers being formed by the static aggregations with a window length of a half week. This approach detects five levels of hierarchy; however, the communities at each level are all elongated in time (see fig. S4), and the dynamics of splitting of the large communities into smaller communities is not recovered. Here, we show that by using the flow stability method, we are able to retain temporal information within each slice and detect relevant dynamical scales, revealing both the splitting of the communities in smaller groups at the arrival of spring and the existence of underlying smaller stable social groups.

Uncovering the physical influences of network scientists

As a last example, we demonstrate the possibility of our method to cluster nonstationary diffusion processes to investigate the diffusion of ideas in a network of coauthorship of articles published in journals of the American Physical Society (APS) between 1970 and 2010. Scientists from many disciplines, including sociology, computer science, and mathematics, contributed to the emergence of the academic discipline of network science. In the late 1990s to early 2000s, several physicists started to study complex networks and made a number of important contributions to the field. We are interested in finding the influences in the field of physics that led these scientists to the study of complex networks. The collaboration network has 194,451 nodes that correspond to authors and 1,337,929 events corresponding to the coauthorship of two authors of the same article (see Materials and Methods). We consider that events represent collaborations between two authors and set their length to 1 year and their ending times to the date of the article publication. The event times are set on a monthly grid, and we divide our investigation period in decades. We search all authors who have published an article in one of the APS journals between 2000 and 2010 with a keyword related to complex networks in the title or the abstract (the list of keywords is given in table S5). We find 1108 authors, among which 1048 are in the largest connected component of the network. We compute an RW process with a homogeneous initial condition on the 1108 authors of complex network articles starting in 2010. The initial probability distribution is zero on all other nodes. We then let the RW diffuse backward in time until 1970 with a characteristic waiting time of 10 years (Eq. 8). We compute the monthly interevent transition matrices using the matrix exponential of the interevent Laplacians. For each decade, we find the best backward flow stability partition (Eq. 5) using the probability distributions of the RW process starting in 2010. We assigned a main country based on most frequent country of their affiliations. As APS journals Physical Reviews (Phys. Rev.) A, B, C, D, and E are organized according to specific subjects in physics, we associate each author to the journal, among those five, in which they published the most articles and use it as an indication of their main specialty in physics. If an author only published in journals that cover the full scope of physics disciplines (e.g., Physical Review Letters and Review of Modern Physics), then we associate them with a category “other.” When considering the backward diffusion process, over an interval (t₁, t₂), t₁ < t₂, the covariance matrix is non-null only for the nodes where p(t₂) > 0 (Eq. 3). For each decade, we only consider authors who were active, i.e., who published at least one article during the decade, and who have a probability density at the end of the decade, i.e., t₂, superior than zero.

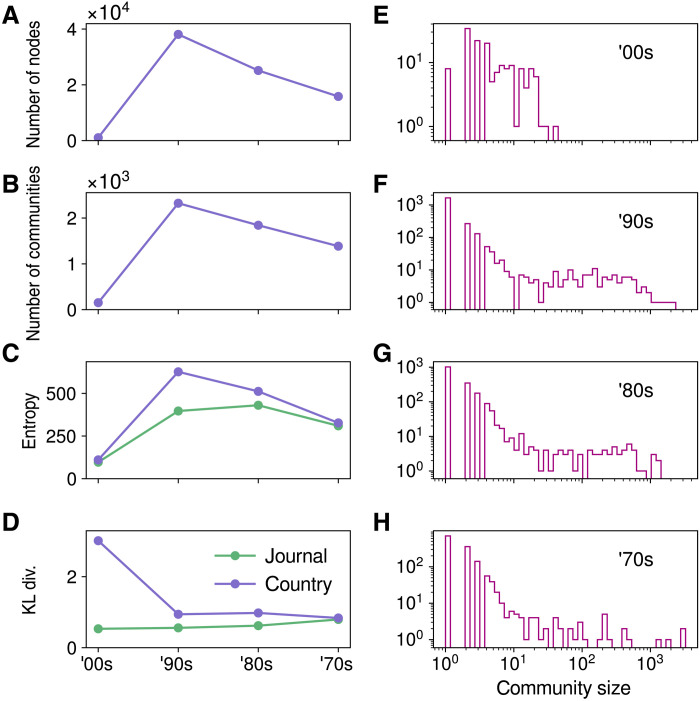
Figure 8 (A and B) shows the number of nodes and communities for each decade, revealing a drastic increase in 1990s compared to the initial condition in the 2000s. Although the process is diffusive, and the support of the probability distribution expands as it evolves because the network size is decreasing as we go back in time, the number of nodes considered decreases in the ‘80s and ‘70s. Histograms of the community sizes for each decade are shown in Fig. 8 (E to H). We compute the total entropy of the clusterings with respect to the journal and country labels of each node, which reveals that the diversity of the communities peaked in the 1990s and that communities are, in general, more diverse in terms of country than journals (Fig. 8C). This may be expected because edges in this network link authors publishing in the same journal. To better understand how the diversity of the communities differ from each other, we compute the Kullback-Leibler divergence (KLD) of the clustering as the weighted average of the KLD between the distribution of labels of each community and the distribution of labels of the union of all communities per decade (Fig. 8D). The average KLD reveals that the distribution of countries in the initial communities from the 2000s is very different than the global distribution of countries of authors of complex network articles. On the other hand, the average KLD of the distribution of journals is much smaller. Most of the initial authors (71%) are associated to the journal Phys. Rev. E, and therefore, the communities do not show a large diversity in terms of journals; however, the large KLD reveals that they are very diverse in terms of country distribution (the most common author country is the United States, with 20% of the authors). As the diffusion process moves backward in time, the average KLD of the country distributions stays larger than the KLD of the journal distributions; however, their difference becomes smaller and smaller.

Fig. 8. Flow stability clustering statistics of the APS collaboration dataset.

(A) Number of authors that were active and have a nonzero probability of participating in the diffusion process per decade. (B) Number of backward communities per decade. (C) Total entropy of the clustering. (D) Average KLD of the clustering compared to the label distribution of the active nodes per decade. (E to H) Histograms of the communities’ sizes for each decade.

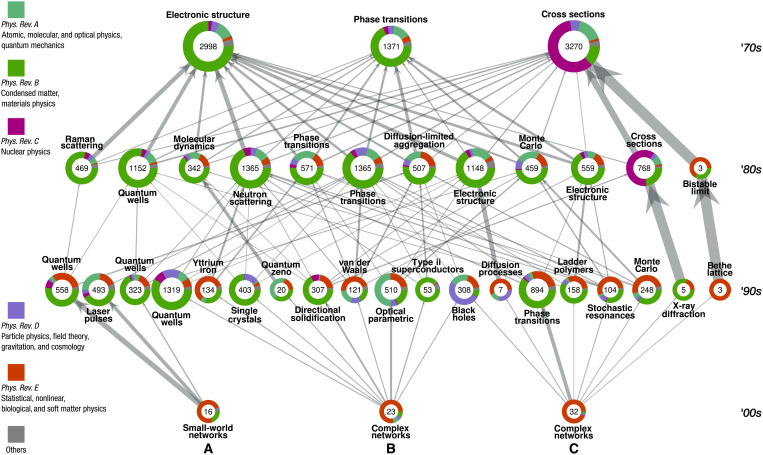
It is interesting to understand the relation between communities of different decades. Here, contrary to the previous examples, we are not interested in necessarily following the same nodes across intervals to understand how communities evolved but rather in following the diffusion process. We can link communities from one decade to another by clustering the transition matrix computed between those two decades (see Materials and Methods) and following the transitions with the highest probabilities. To illustrate this process, we selected three initial communities from the 2000s that had different country distributions: community A (50% USA and 44% Hungary), community B (30% UK, 22% Finland, and 17% Spain), and community C (34% Italy, 22% USA, and 19% Spain). The names, countries, and journals of all authors in these communities are given in table S6. The list of “ancestor” communities of the 1990s is found as the communities toward which the transition probability of the RW process, starting from one of the three initial communities, is larger than 5%. Similarly, we find the ancestor communities of the 1980s and 1970s. Figure 9 shows the three initial communities and their ancestor communities at each decade along with the transition probabilities between each community and the distribution of authors’ main journals in each community. Figure S5 shows the communities together with the distribution of authors’ main countries in each community. We discover that the three initial communities have different influence communities in the ‘90s (only communities B and C have one common ancestor at this stage) when considering transition probabilities larger than 5%. Community A has only three ancestors in the ‘90s, which are dominated by Phys. Rev. B (condensed matter and material physics) but with different distributions of secondary journals. The most frequent pair of words in the articles’ titles reveals that two communities are mostly focused on quantum wells and the third one on laser pulses. Figure S5 shows that the two quantum well communities differ in their country distribution, one of them having a large portion of authors with affiliations in the United Kingdom. Community B has the largest number of ancestors in the ‘90s, which are also the most diverse in terms of journal distributions. The main topics of each community are also very diverse, ranging from van der Waals forces to black holes. Last, community C also has a wide range of influences in the ‘90s, which is dominated by the journals Phys. Rev. B and E (statistical, nonlinear, biological, and soft matter physics), with topics such as diffusion processes, phase transitions, and Monte Carlo methods. As we follow influences in the ‘80s and ‘70s, more common ancestor communities are found that have a substantial proportion of Phys. Rev. B but focused on different topics. Three communities are found in the 1970s: Two have relatively similar journal compositions (dominated by Phys. Rev. B) but focus on different topics (electronic structure and phase transitions), and the third one is dominated by Phys. Rev. C (nuclear physics) and the topic of cross sections. The third community is only a significant ancestor (probability of transition >5%) of community C. We note that the three communities of the ‘70s are among the four largest communities of this decade (see Fig. 8H). This can be expected as larger communities have a higher probability of being on an RW, but this also reveals that there is another community, as important as those three, that does not have a significant influence on these three initial communities of network scientists. Note also that to study the transmission of influences from the 1970s to the 2000s using the same diffusion process, one would use the inverse forward covariance (see the section “Covariances of inverse processes” in the Supplementary Text). With this example, we demonstrate an original usage of our method for clustering nonstationary processes in temporal networks that allows us to uncover new insights about the influences, in the field of physics, of network scientists.

Fig. 9. Influential communities of authors of articles published in the APS journals for three communities of network scientists in the 2000s.

Each node represents a community, and its size is indicated in the center. The colors represent the distribution of journals inside each community where each author is associated to the journal in which they published the most (except large-scope journals). The pair of words next to each node indicate one of the most frequent pair of words of all the titles of the articles belonging to the community. Arrows between the communities represent probability transitions (>5%) from community to community of the diffusive process starting in 2010 and finishing in 1970.

DISCUSSION

The classical static definition of communities as clusters of densely connected nodes does not generalize well to temporal networks without resorting to temporal aggregations over some time windows to evaluate the “connectedness” of groups of nodes. In many cases, this aggregation does not prevent the detection of communities and their temporal evolution. However, many processes can be occurring simultaneously in a system described by a temporal network and each of them at different rates. We showed that the aggregation of temporal networks over time windows can lead to a loss of information at certain dynamical scales and render the detection of processes occurring at certain scales impossible. Here, we propose a framework based on the clustering of the flow of random walkers evolving with the network that allows us to define communities in temporal networks while keeping temporal information of time-respecting paths without resorting to temporal aggregation and without assuming the existence of a stationary state of the flow. To capture the asymmetric relations between nodes due to the temporal evolution of the network, we describe the communities over a given time interval with two partitions: the forward partition, which groups nodes in the same community if the flow of random walkers starting on them tend to stay together until the end of the interval, and the backward partition, which groups nodes in the same community if the flow of random walkers that ends on them tended to stay together since the beginning of the interval. Time symmetry is an essential concept in theoretical physics, associated to energy conservation through Noether’s theorem and to the emergence of an arrow of time through thermodynamics. While this work does not aim at modeling a physical system directly, it provides an interesting viewpoint that should be explored further. We model systems that show time asymmetry at the microscopic level, the RW process being diffusive and nonreversible in general, yet that can capture time symmetry at the mesoscopic level of communities when the forward and backward partitions are similar.

Our framework provides a natural way to explore the different natural dynamical scales present in a system by varying the rate of the RW, which plays the role of a dynamical resolution parameter. In terms of the classification by Rossetti and Cazabet (27), each partition taken alone could be classified in the temporal trade-off category. The forward partition depends on the network topology at time t and also on the future topology, while the backward partition depends on the topology at time t and in the past. The two partitions taken together could then be classified in the cross-time category, depending on the entire evolution of the network in a given time interval. The temporal flow stability is also a natural generalization of static networks concepts such as modularity and Markov stability and draws links with clustering methods for directed networks (see Supplementary Text, “Relations with coclustering” section). An advantage of our method is that, for a given time interval, the method has only one parameter with a principled meaning, the RW rate, while other approaches may require the tuning of several parameters [e.g., slice resolution parameter and interslice coupling (6)]. In static networks, the concept of Markov stability has already been expressed in terms of a filtering process in the framework of graph signal processing (51, 52). Here, the RW process can be seen as a spatiotemporal filter on the temporal network that weights the importance of interactions depending on their duration and frequency. Other types of filters could be designed to focus on particular processes such as cyclical activity, for example. The usage of different Laplacians, defining different diffusion processes, or time kernels modulating the importance of different temporal patterns in the objective functions could be used to design new methods. Our framework opens the door for the definition of new concepts for temporal networks in terms of RW probabilities and flows that may help to disentangle the complex processes simultaneously occurring in systems described as temporal networks.

MATERIALS AND METHODS

Flow modeling

We consider the temporal network with N vertices and M undirected events defined in the “Temporal flow stability” section. We define the ordered set of distinct event times, Tⁱ, as the union of the sets of starting times, T^s, and ending times, T^e. The event times effectively defines new events at a higher-temporal resolution such that there is no change in the network between two consecutive times (e.g., in Fig. 1A, the event times are indicated by black dots). One can compute the transition matrix between two arbitrary times from the product of the transition matrices for each interevent time interval. On this new temporal grid, one finds for the transition probability matrix between to arbitrary times t₁ and t₂ (t₁ < t₂)

$$\mathbf{T}(t_1,t_2)=\widehat{\mathbf{T}}(t_1,t_m)[{\displaystyle \prod _{k=m}^{n-1}}\widehat{\mathbf{T}}(t_k,t_{k+1})]\widehat{\mathbf{T}}(t_n,t_2)$$ (7)

with m < n, t_m ≥ t₁ being the time of the first event after, or at, t₁ and t_n < t₂ the time of the last event before t₂. To compute the transition matrix corresponding to the time-reversed evolution of the network, from t₂ to t₁, we perform the matrix product in the reversed order

$${\mathbf{T}}_{\text{rev}}(t_2,t_1)=\widehat{\mathbf{T}}(t_2,t_n)[{\displaystyle \prod _{k=n}^{m+1}}\widehat{\mathbf{T}}(t_k,t_{k-1})]\widehat{\mathbf{T}}(t_m,t_1)$$ (8)

To ensure that the transition probability matrix satisfies the Chapman-Kolmogorov equation T(t₁, t₃) = T(t₁, t₂)T(t₂, t₃) for arbitrary times t₁ < t₂ < t₃, one must ensure that in particular, $\widehat{\mathbf{T}}(t_k,t_{k+1})=\widehat{\mathbf{T}}(t_k,t_l)\widehat{\mathbf{T}}(t_l,t_{k+1})$, where t_k < t_l < t_{k + 1} and t_k and t_{k + 1} are consecutive times on the high-resolution temporal grid. Assuming that walkers have a constant probability of jumping per unit of time given by the rate λ, this is uniquely satisfied by the solution $\widehat{\mathbf{T}}(t_k,t_{k+1})=e^{-\mathrm{\lambda }\mathbf{L}(t_k){\mathrm{\tau }}_k}$ with τ_k = t_{k + 1} − t_k and where L = I − D(t)⁻¹(A(t) + S(t)) is the RW graph Laplacian at time t, A(t) is the adjacency matrix at time t, S(t) is the self-loops matrix at time t, with zeros everywhere except on the diagonal element i corresponding to nodes with zero out-degree, k(t)_i, and D(t) is the diagonal matrix with D(t)_ii = k(t)_i if k(t)_i > 0 and D(t)_ii = 1 otherwise. The element (i, j) of L(t) is therefore given by

$${(\mathbf{L}(t))}_{\mathit{ij}}=\{\begin{array}{cc}-\frac{a{(t)}_{\mathit{ij}}}{\text{max} (k{(t)}_i,1)}& \text{if} i\ne j,\\ 1-\mathrm{\delta }(k{(t)}_i,0)& \text{if} i=j\end{array}$$ (9)

We have L(t)1 = 0, i.e., ${\mathbf{u}}_{\mathbf{1}}=\frac{1}{N}\mathbf{1}$ is a right eigenvector of L associated with the eigenvalue ϵ₁ = 0. Note that for t > 0, e^{−λL(t_k)τ_k} may contain nonzero nondiagonal terms that are equal to zero in L (or A), i.e., e^{−λL(t_k)τ_k} takes into account trajectories with multiple steps.

Covariance of nonstationary RW

To find a relevant partition of the nodes between two time points t₁ and t₂ (t₁ < t₂), we consider the covariance of a flow of random walkers, performing a CTRW (53) on the network constrained by the activation of edges between the different clusters (32, 35). A partition that is well aligned with this flow will correspond to high values of the covariance inside each cluster.

Following the framework of the stability of a network partition (32) but in the case of a temporal network and without assuming an ergodic and reversible Markov chain with a stationarity distribution, we assign a different real value α_i (i = 1, …, c) to the vertices of each of the c clusters and consider the values α_i observed by a random walker as a stochastic process (X_t)_{t ∈ ℝ}, which is not necessarily Markovian and not necessarily stationary. The covariance of this process evaluated between t₁ and t₂ is given by

$$\text{cov}[\mathit{X}(t_1)\mathit{X}(t_2)]=\mathrm{E}[\mathit{X}(t_1)\mathit{X}(t_2)]-\mathrm{E}[\mathit{X}(t_1)]\mathrm{E}[\mathit{X}(t_2)]$$ (10)

where E[X(t)] represents the expectation of the random variable X(t).

Introducing p(t), the 1 × N row vector with element p_i(t) equal to the probability of finding a random walker on node i at time t, and using the N × N transition matrix T(t₁, t₂) defined in Eq. 6, where element (i, j) is equal to the conditional probability for a random walker to be on node j at t₂; if it was on node i at t₁, then we find

$$\begin{array}{c}\text{cov}[\mathit{X}(t_1)\mathit{X}(t_2)]={\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}{\mathrm{\alpha }}_i{p}_i(t_1)T_{i,j}(t_1,t_2){\mathrm{\alpha }}_j-\\ ({\displaystyle \sum _{i=1}^N}{\mathrm{\alpha }}_i{p}_i(t_1))({\displaystyle \sum _{i=1}^M}{\mathrm{\alpha }}_i{p}_i(t_2))=\\ {\displaystyle \sum _{\mathrm{\ell },m=1}^c}{\mathrm{\alpha }}_{\mathrm{\ell }}{\mathrm{\alpha }}_m{\displaystyle \sum _{i,j=1}^N}\mathrm{\delta }(\mathrm{\ell },c_i)(p_i(t_1)T_{i,j}(t_1,t_2)-\\ p_i(t_1)p_j(t_2))\mathrm{\delta }(c_j,m)={\mathbf{\alpha }}^{\mathrm{T}}\mathbf{R}(t_1,t_2)\mathbf{\alpha }\end{array}$$ (11)

where α is the 1 × c column vector of labels of the c communities and

$$\mathbf{R}(t_1,t_2;H)={\mathbf{H}}^{\mathrm{T}}[\mathbf{P}(t_1)\mathbf{T}(t_1,t_2)-\mathbf{p}{(t_1)}^{\mathrm{T}}\mathbf{p}(t_2)]\mathbf{H}={\mathbf{H}}^{\mathrm{T}}\mathbf{S}(t_1,t_2)\mathbf{H}$$ (12)

is the c × c clustered covariance matrix between t₁ and t₂ with P(t) = diag (p(t)) ∀ t ∈ [t₁, t₂] and

$$\mathbf{S}(t_1,t_2)=\mathbf{P}(t_1)\mathbf{T}(t_1,t_2)-\mathbf{p}{(t_1)}^{\mathrm{T}}\mathbf{p}(t_2)$$ (13)

is the N × N covariance matrix between t₁ and t₂. R(t₁, t₂; H) only depends on the network and its partition, and not on the specific, yet arbitrary, values of α.

This expression can then be used to find a partition clustering the covariance in blocks where the random walkers are likely to remain for a long time, i.e., where the covariance is high. In the case of static networks, this expression reduces to the framework of Markov stability (32, 35), where the random walkers eventually reach a stationary distribution. See Supplementary Text (“Relations with community detection in static networks,” “Relations with coclustering,” and “Special cases of the RW covariances in static networks” sections) as well as table S4 for the relations between our approach and well-known static networks heuristics such as modularity optimization. In the case of temporal networks, the activity-driven model has been used to approximate a stationary distribution and generalize the Markov stability framework (22). Another approach for temporal networks consists of treating them as multilayer networks and considering an RW that moves inside layers and in-between layers, effectively disregarding the direction of time and the causality of random walkers’ paths (6).

Linearization of the transition matrix and computation of the covariances

As the computation of the matrix exponential can be relatively time costly for large network, we introduce a linearization of Eq. 6 using two linear interpolations

$$\tilde{\mathbf{T}}(t_1,t_2;{\mathrm{\tau }}_{\mathrm{w}})=\{\begin{array}{cc}(1-{\mathrm{\lambda }}^{\star })\mathbf{I}+{\mathrm{\lambda }}^{\star }{\mathbf{T}}_{\text{DT}}& \text{for} 0\le {\mathrm{\lambda }}^{\star }\le 1,\\ \frac{1}{1-{\mathrm{\lambda }}^s}[({\mathrm{\lambda }}^{\star }-{\mathrm{\lambda }}^s){\mathbf{T}}_{\text{DT}}+(1-{\mathrm{\lambda }}^{\star })\mathbf{W}]& \text{for} 1<{\mathrm{\lambda }}^{\star }\le {\mathrm{\lambda }}^s,\\ \mathbf{W}& \text{for} {\mathrm{\lambda }}^{\star }>{\mathrm{\lambda }}^s\end{array}$$ (14)

where T_DT = I − L is the one-step discrete time RW transition matrix, ${\mathrm{\lambda }}^{\star }=\frac{t_2-t_1}{{\mathrm{\tau }}_{\mathrm{w}}}$, $\mathbf{W}={\text{lim}}_{n\to \infty }{\mathbf{T}}_{\text{DT}}^n$ is the limiting transition matrix, and λ^s = t_s/τ_w, with t_s the time taken by the RW to reach stationarity. In all the examples in this article, we use λ^s = 10.

To compute the linear approximation of the transition matrix T(t₁, t₂) of a time-evolving network (Eq. 7), we first compute the linear approximation of each interevent transition matrix with Eq. 14. The limiting transition matrix W can be easily computed for undirected network. The matrix W has nonzero values only in diagonal blocks that correspond to each connected component of the graph. The stationary distribution of the n^th connected component is π_n, with element π_ni = k_i/N_n, where k_i is the degree of node i and N_n is the size of component n. The N_n rows of the nth block of W are then all copies of the vector π_n.

For large networks, our method is limited to cases where the number of edges being active simultaneously remains small, which is usually the case in temporal networks. In this case, we find that the computations are greatly simplified by the fact that interevent Laplacians are usually extremely sparse, and one can compute the matrix exponential of each connected component independently.

The integral of the forward covariance is obtained by performing the integral ${\int }_{t_1}^{t_2}(\mathbf{T}(t,t_1)\mathbf{P}{(t)}^{-1/2}){(\mathbf{T}(t,t_1)\mathbf{P}{(t)}^{-1/2})}^{\mathrm{T}}\mathit{dt}$ and then multiplying its rows and columns by p(t₁). The integrand can be efficiently computed as a sparse gram matrix, and only its upper (or lower) triangular values need to be computed and stored as it is symmetric. The outer product of p(t₁) in Eq. 2 is a rank 1 matrix and therefore can be efficiently stored using only a vector.

The computational cost is small for network sizes N where N × N matrices can be stored in memory (e.g., ∼6 GB for a N = 4 × 10⁴ double-precision floats symmetric matrix). For large networks, the main limitation is the fact that the total transition matrix and the integral of the covariance may start to become less sparse. All elements of these matrices that are inside connected components have a nonzero value. As the integration interval increases, for very large networks, the connected components sizes increases, which slows down the matrix operations and may require large memory storage. This is a limit of our method and to scale it to larger networks, we keep the matrices sparse by neglecting RW paths with very low probabilities. We keep only values of these matrices with probabilities above a certain value. We applied this strategy in the case of the physical influences of network scientists (see below).

Tracking scientific influences in the APS coauthorship dataset

Similarly to (54), we consider only articles having 10 or less authors in the APS dataset to exclude articles from “big science” projects that do not correspond to the concept of collaboration that we are investigating. We also consider only articles with at least two authors because we are interested in the diffusion of ideas between coauthors. We use the author name disambiguation provided in (54). The countries corresponding to the authors’ affiliations were extracted by first examining the affiliations’ most common trigrams and bigrams that contain names of known institutions and locations. This allows us to extract the countries corresponding to 96% of the affiliations. The countries of the remaining affiliations are extracted by using three approaches: with the named entity extraction library (https://github.com/iwpnd/flashgeotext), by fuzzy matching the bigrams and trigrams (allowing the n-gram Jaro-Winkler similarity to be ≥0.95) to allow slight mispellings, and lastly by using the OpenStreetMap Nominatim geocoder (https://github.com/geopy/geopy). Over the initial 224,992 unique affiliations, we were unable to assign a country to only 89 affiliations. The full mapping and the code used to produce it are available at https://doi.org/10.7910/DVN/I87AXV.

We compute the interevent transition matrices without the linear approximation on a monthly resolution. We use sparse matrix representations and compute the matrix exponential on each connected component of the Laplacian matrix in parallel to limit memory and computation time. Moreover, we threshold the transition matrices (values smaller than 1 × 10⁻⁶ of the maximum) and of covariance integrals (absolute values smaller than 1 × 10⁻⁹ of the maximum) to further limit memory usage.

The transition probabilities between the backward communities of decade d and the ones of the previous decade d − 1 are computed as

$${\mathbf{T}}_{d\to d-1}={\mathbf{C}}_{b,d}^{-1}{\mathbf{H}}_{b,d}^T\mathbf{T}(t_d,t_{d-1}){\mathbf{H}}_{b,d-1}$$ (15)

where H_{b, d} d∈ {‘00s, ‘90s, ‘80s, and ‘70s} are the indicator matrices encoding the backward communities and T(t_d, t_{d − 1}) is the transition matrix of the RW process starting at the end of the decade d and ending at the end of decade d-1, e.g., 2010 to 2000 for d=‘00s and d − 1=‘90s. The matrix ${\mathbf{C}}_{b,d}=\text{diag}(\mathbf{1}{\mathrm{H}}_{b,d})$ is the diagonal matrix containing the sizes of each communities in H_{b, d}. Last, the transition probabilities between the ‘00s and all earlier decades are found by multiplying, in time-reversed order, the matrices for each decade.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S5

Tables S1 to S6

References