Classification and clustering of RNA crosslink-ligation data reveal complex structures and homodimers

Abstract

The recent development and application of methods based on the general principle of “crosslinking and proximity ligation” (crosslink-ligation) are revolutionizing RNA structure studies in living cells. However, extracting structure information from such data presents unique challenges. Here, we introduce a set of computational tools for the systematic analysis of data from a wide variety of crosslink-ligation methods, specifically focusing on read mapping, alignment classification, and clustering. We design a new strategy to map short reads with irregular gaps at high sensitivity and specificity. Analysis of previously published data reveals distinct properties and bias caused by the crosslinking reactions. We perform rigorous and exhaustive classification of alignments and discover eight types of arrangements that provide distinct information on RNA structures and interactions. To deconvolve the dense and intertwined gapped alignments, we develop a network/graph-based tool Crosslinked RNA Secondary Structure Analysis using Network Techniques (CRSSANT), which enables clustering of gapped alignments and discovery of new alternative and dynamic conformations. We discover that multiple crosslinking and ligation events can occur on the same RNA, generating multisegment alignments to report complex high-level RNA structures and multi-RNA interactions. We find that alignments with overlapped segments are produced from potential homodimers and develop a new method for their de novo identification. Analysis of overlapping alignments revealed potential new homodimers in cellular noncoding RNAs and RNA virus genomes in the Picornaviridae family. Together, this suite of computational tools enables rapid and efficient analysis of RNA structure and interaction data in living cells.

RNA forms complex structures and interactions to execute a wide variety of biological functions. The information-structure duality of RNA underlies its pioneering position in the early evolution of life on earth (Higgs and Lehman 2015). In addition to acting as the messenger between the genetic blueprint and the protein products, structured RNA molecules play extensive roles in scaffolding, regulation, and catalysis in the modern RNA world (Cech and Steitz 2014; Guil and Esteller 2015). Given the importance of this biopolymer, many methods have been developed to determine its structures. Predicting the base-pairing of nucleotides, or RNA secondary structure, has long been the goal of algorithms that calculate minimal free energy conformations or exhaustively search for conserved structural motifs in multiple alignments of nucleotide sequences (Gutell 1993; Mathews 2006). Various energy- and statistics-based computational tools have been developed to predict RNA 3D structures (Das et al. 2010; Weinreb et al. 2016; Miao and Westhof 2017; Sun et al. 2017). On the other hand, classical physical methods, such as X-ray crystallography, nuclear magnetic resonance (NMR) spectroscopy, and cryo-electron microscopy (EM) have made significant progress in recent years toward solving more complex 3D structures of RNAs and their complexes (Batey et al. 1999; Bai et al. 2015).

In the last few decades, a host of chemical methods were invented to probe the flexibility and accessibility of individual nucleotides, which are indicative of their structural context (Weeks 2010; Lu and Chang 2016; Velema and Kool 2020). These methods typically yield indirect one-dimension information that assists secondary and tertiary structure prediction. More recently, several crosslinking-based methods, including CLASH, hiCLIP, PARIS, LIGR-seq, SPLASH, fRIP, and COMRADES, have been advanced to provide direct physical evidence for spatial proximity among RNA fragments (Kudla et al. 2011; Helwak et al. 2013; Sugimoto et al. 2015; Aw et al. 2016; Hendrickson et al. 2016; Lu et al. 2016, 2018, 2020; Nguyen et al. 2016; Sharma et al. 2016; Ziv et al. 2018; Zhang et al. 2021). These methods employ a variety of crosslinkers, such as psoralens that only react with staggered uridines and cytidines in opposing strands, ultraviolet light (UV) that induces reactions between proteins and RNAs in direct contacts, and formaldehyde that crosslinks all types of primary amine-containing molecules that are close to each other (Lu and Chang 2018). After crosslinking and purification/enrichment, covalently attached RNA fragments are ligated and sequenced in high throughput, yielding hybrid reads, where each segment comes from a distinct region in an RNA, or from entirely different RNA molecules. In the simplest form, the crosslink-ligation experiments reveal RNA hetero-duplexes on a transcriptome-wide scale (Fig. 1A). In reality, hetero-duplexes with two arms are not the only form of structures in RNA structures and interactions, other types of complex arrangements are also common and critical for the formation of high-level structures (here, arms and segments are used interchangeably).

Figure 1.

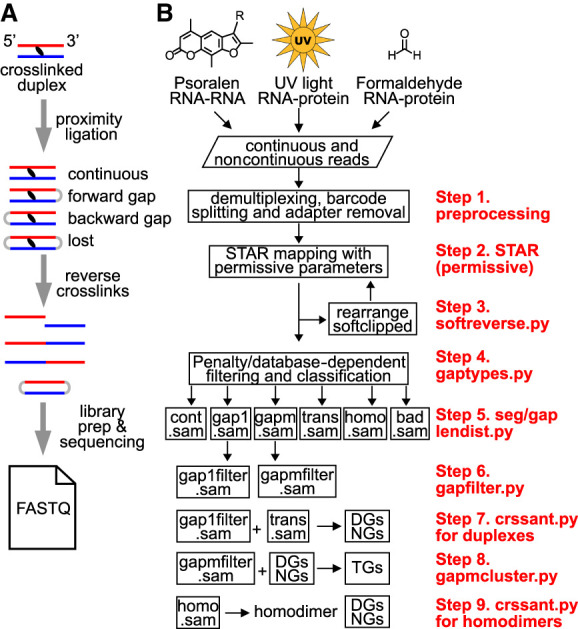
Overview of RNA crosslink-ligation experiments and analysis pipeline. (A) Outline of a typical crosslink-ligation experiment leading to FASTQ output files. The proximity ligation of crosslinked duplexes can produce both forward and backward arrangements. Circularized RNAs are rare and lost during library preparation because they cannot be ligated to adaptors. Similarly, concurrent crosslinking at multiple locations and subsequent ligation of them produce multigapped reads (gapm in panel B). (B) Several different types of crosslinking methods, such as psoralen, UV, and formaldehyde, together with proximity ligation produces noncontinuous reads that can be used to determine RNA structures. Newly developed computational tools and optimized parameters are listed on the right in nine steps (steps 1–9). Sequencing data that include both continuous and noncontinuous reads are demultiplexed, and the adapter/primer sequences are removed using published tools, for example, FASTX and Trimmomatic (step 1). The processed reads are mapped to genome references using optimized STAR parameters (permissive parameters, step 2). After the first round of STAR mapping, continuous alignments with softclips (indicating unmapped segments) are rearranged for a second round of STAR mapping (step 3). All alignments from the two rounds of STAR mapping are combined and filtered based on the gap penalty and a database of gapped alignments with longer segments, and then classified into six alignment types, including continuous (cont.sam in SAM format), one-gap (gap1), multigap (gapm), trans interactions (trans), homotypic interactions (homodimers, or homo), and miscellaneous bad alignments (bad) (step 4, using the gaptypes.py script) (see details in Fig. 3A–D; Supplemental Fig. S4). Data quality is checked using seglendist.py and gaplendist.py scripts, which calculate segment and gap length distributions (step 5). After removal of splicing events and reverse transcription artifacts, for example, short 1- to 2-nt gaps (step 6, using gapfilter.py), each of these alignment types is further processed to extract information for duplexes (step 7) (see Fig. 4 for details), high-level structures (step 8) (see Fig. 5 for details), and RNA homodimers (step 9, homo.sam) (see Fig. 6 for details). In step 7, two types of alignments, gap1filter.sam and trans.sam, are used to generate duplex groups and non-overlapping groups (DGs and NGs). In step 8, gapmfilter.sam alignments and the precomputed DGs and NGs are used to build trisegment groups (TGs). In step 9, overlapping chimeras are used to build potential homodimers. Detailed descriptions of these steps are in the Methods section and Supplemental Material.

First, within the same molecule, high-level structures include extended helices with various internal loops, multihelix junctions, pseudoknots, and even triple helices. In the past 50 yr, in vitro studies have shed light on the exquisite folding of a number of RNAs and their complexes, such as the ribosome, RNase P, RMRP, telomerase, mascRNA, and viral IRES elements, each employing unique combinations of the aforementioned high-level structures (Wilusz et al. 2012; Anger et al. 2013; Quade et al. 2015; Zhang et al. 2017; Wu et al. 2018; Kastner et al. 2019; Yan et al. 2019). However, direct in vivo observation of these complex structures and interactions has been more difficult, despite their demonstrated functional significance in well-studied examples.

Second, between different RNA molecules, homodimers are also possible besides heterodimers, yet very few RNA homodimers have been studied, despite the high stability of the base-pairing interactions (Bou-Nader and Zhang 2020). Examples have been reported in a variety of contexts, including viral RNA genomes, such as HIV, HCV, coronaviruses and bacteriophages (Clever et al. 2002; Shetty et al. 2010; Ishimaru et al. 2013; Dubois et al. 2018), ribozymes and riboswitches (Bou-Nader and Zhang 2020), mRNAs (Wagner et al. 2004; Jambor et al. 2011; Little et al. 2015; Trcek et al. 2015), trinucleotide/hexanucleotide repeats (Ciesiolka et al. 2017; Jain and Vale 2017), and tRNA mutant and fragment dimers/tetramers (Wittenhagen and Kelley 2002; Roy et al. 2005; Lyons et al. 2017; Tosar et al. 2018). In vitro, synthetic RNAs have also been made to dimerize or multimerize to prepare nanomachines (Severcan et al. 2009; Geary et al. 2011). These homodimers play important roles in virus genome packaging, stress response, translational regulation, liquid-liquid phase separation, and human genetic diseases. Again, de novo identification of homodimers remains challenging.

Despite the rapid progress in crosslink-ligation experimental techniques, there are three major challenges in the data analysis. First, the random RNA fragmentation by RNases or divalent cations and subsequent proximity ligation generates short reads with irregular gaps. Longer reads can be mapped to references with higher accuracy, but the resolution of secondary structure models is lower. Shorter reads increase the model resolution, but mapping accuracy is lower. Several short-read mappers have been developed with the ability to handle gaps. For example, Bowtie 2 applies affine penalty to gaps, which discourages gap opening and extension (Langmead and Salzberg 2012). Multistep mapping protocols based on Bowtie 2 reduces sensitivity for shorter segments that cannot be mapped uniquely to the genomes (Lu and Matera 2014; Travis et al. 2014; Lu et al. 2015b; Sharma et al. 2016). STAR can inherently map noncontinuous reads, but the parameters were optimized for the identification of splicing and gene fusion events (Dobin et al. 2013; Haas et al. 2019), and performances were suboptimal on crosslink-ligation data (Aw et al. 2016; Lu et al. 2016; Ziv et al. 2018). For example, splice junctions have unique sequence consensus to facilitate opening of gaps and assignment of extension penalty; in addition, splice junction databases can be used to help mapping, reducing the unnecessary penalty and increasing the efficiency. Noncontinuous reads from crosslink-ligation experiments, however, are far more random in gap sequence and length, making it difficult to determine the appropriate penalty. To solve this problem, we systematically optimized the STAR parameters in this study and designed a set of filtering criteria that significantly improved the sensitivity and specificity of mapping short reads with irregular gaps.

Second, in addition to simple duplexes, the complex crosslinking and proximity ligation reactions produce many different types of reads/alignments that remain poorly characterized. Our exhaustive classification uncovered eight categories of alignments, which we rearrange and combine to five distinct types, including continuous (cont for short), two-segment (1 gap, or gap1), multisegment (>1 gaps or >2 segments, gapm), homodimers (overlapped segments, homo), and trans interactions (two segments on different strands or chromosomes). Each type of noncontinuous alignments reveals distinct new structures and interactions, especially composite structures, and homodimers. The rearrangements also enable the visualization and of complex alignments in genome browsers and facilitate intuitive understanding of their corresponding structures.

Third, densely packed noncontinuous alignments are difficult to deconvolve into distinct groups that support individual RNA duplexes, because most RNA duplexes are very short and close to each other. This is further complicated by the multitude of alternative/dynamic conformations, where one RNA region can base pair with multiple other regions. To resolve the complex structure conformations encoded in noncontinuous alignments, we developed a method to cluster alignments based on a network representation, termed CRSSANT. Alignments are assigned to duplex groups (DGs) based on segment overlap ratios, and then DGs can be used to constrain secondary structure modeling. This new method is automatic and separates alternative conformations from each other. Using DGs as the foundation, we further developed a method to build trisegment groups (TGs) that reveal high-level structures and interactions among RNAs.

Using these newly developed tools, we systematically characterized published crosslink-ligation methods, revealing their basic properties and bias. For example, we noticed that psoralen monoadducts lead reverse transcription errors and overrepresentation of uridine deletions in some of these crosslink-ligation methods. Our classification and clustering of various types of alignments led to the discovery of high-level structures and interactions and RNA homodimers in various cellular and viral RNAs. Together, this suite of tools greatly expanded the capabilities of crosslink-ligation experimental methods.

Results

Overview of the computational pipeline

In general, crosslink-ligation experiments produce several types of reads, including continuous and noncontinuous, where the continuous reads could be due to failed crosslinking or failed ligation, and noncontinuous ones may contain two or more segments (Fig. 1A, showing two-segment reads as examples). To extract all possible types of structures from crosslink-ligation data, we established a general strategy that is applicable to different types of experimental strategies, including, but not limited to, psoralen, UV, or formaldehyde crosslinking (Fig. 1B; Supplemental Code; Kudla et al. 2011; Sugimoto et al. 2015; Aw et al. 2016; Hendrickson et al. 2016; Lu et al. 2016; Sharma et al. 2016; Van Nostrand et al. 2016; Ziv et al. 2018; Cai et al. 2020). The sequenced reads are first processed to remove adapters and barcodes and demultiplexed using common tools (step 1, e.g., FASTX and Trimmomatic) (Bolger et al. 2014). Processed reads are mapped to genome references using STAR (Dobin et al. 2013) and a set of parameters that we specifically optimized for noncontinuous reads (step 2) (see Fig. 2; Supplemental Fig. S1 for details). Softclipped alignments that cannot be mapped as chimeras are rearranged for a second round of STAR mapping to improve the detection of backward chimeras (step 3). The optimized STAR method and subsequent filtering maximize the sensitivity and specificity in the analysis of short segments with irregular gaps. Alignments are filtered to remove low-confidence segments, rearranged, and classified into six categories (step 4) (see Fig. 3; Supplemental Fig. S3 for details). In addition to simple RNA duplexes, these different types of alignments provide new information such as high-level structures (multigap alignments, or gapm), and RNA homodimers (homotypic interactions, or homo). Segment and gap length distribution and gap nucleotide properties are summarized to serve as quality controls (step 5). Gapped alignments (with one or more gaps) are filtered to remove splicing junctions and short 1- to 2-nt gaps that are likely artifacts (step 6). The filtered noncontinuous alignments are clustered into duplex groups and nonoverlapping groups (NGs, for visualization in genome browsers) (step 7) (see Fig. 4; Supplemental Fig. S3 for details). The alternative conformations (conflicting DGs) suggest the existence of dynamic RNA structures and functions. Multigap alignments together with DGs are further clustered into TGs that support more complex structures and interactions (step 8) (see Fig. 5 for details). Alignments with overlapping segments (homo.sam) are used to identify potential homodimers (step 9) (see Fig. 6 for details). Altogether, this pipeline optimizes and integrates all the known steps in the analysis of crosslink-ligation data.

Figure 2.

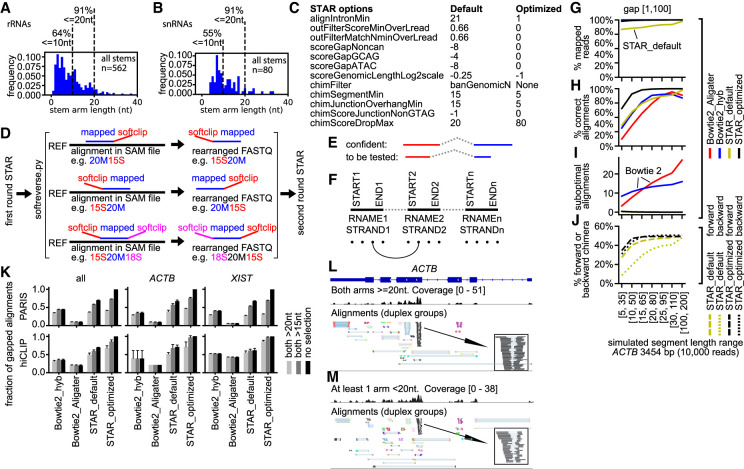
Optimization of short-read mapping from crosslink-ligation experiments. (A,B) RNA stems were extracted from the human cytoplasmic and mitochondrial ribosome and spliceosome crystal or cryo-EM structures. The following RNAs are included: 12S, 16S, 5S, 5.8S, 18S, 28S, U1, U2, U4, U6, U5, U11, U12, U4atac, and U6atac. (C) List of critical STAR parameters that are optimized to map noncontinuous reads. The default value for chimSegmentMin is unset, whereas setting this value to any positive integer triggers chimeric alignments. The recommended value of 15 is used here as the “default.” (D) Strategy for the two-round STAR mapping. After the first round of optimized STAR mapping, continuous alignments with softclips (“S” in CIGAR) are rearranged and then mapped again using the optimized STAR parameters. (E,F) Strategies for filtering alignments after STAR mapping. (E) Confident alignments: all segments or arms are uniquely mapped to the genome. Alignments with shorter segments that cannot be mapped uniquely are to be tested against confident ones. (F) Filtering method for the less confident alignments: all arms of the confident alignments are built into a database of connections between segments, in five nucleotide intervals (dots shown at the bottom). The connection database consists of reference name (RNAME), strand (STRAND), and coordinates between start and end (START, END). Then, the less confident alignments are tested against this database. (G–J) Benchmarking four mapping strategies on simulated reads for the human ACTB gene. Alignments are quantified on the following four aspects: (G) % mapped reads, that is, reads that are mappable to hg38 primary genome; (H) % correct alignments, that is, alignments with the same mapped positions and gap lengths as the simulated values, allowing 10-nt differences in positions or lengths due to ambiguities at the ends of reads; (I) Suboptimal alignments per read, defined as alignments that are not mapped to the correct locations; (J) % forward or backward chimera. In theory, both forward and backward chimera should be ∼50% (randomly assigned during simulation, so they are not precisely 50%). Here, only STAR alignments are calculated. (K) Gap1 (one gap, i.e., two segments) alignments in PARIS and hiCLIP data were recovered by various mapping methods and segment-length selections. Fractions for the highest-performing method (STAR_optimized) are set to 1. For STAR analysis, sequencing reads were mapped to the genome (hg38 primary); then alignments were filtered and classified into six categories using gaptypes.py. The gap1 alignments were filtered to remove short gaps and splicing alignments (gapfilter.py). Primary alignments were extracted from all alignments and used for analysis. For Bowtie 2 mapping, previously reported parameters (hyb and Aligater) were used. Unique alignments with deletions (D in SAM CIGAR string) were extracted and alignments were converted to join the multiple segments (bowtie2chim.py). Then, the alignments were classified using gaptypes.py. The gap1 alignments were filtered to remove short gaps and splicing alignments (gapfilter.py). The selection of alignments with both arms > 15 nt or 20 nt mimics the mapping and chaining strategy in previous studies that employ Bowtie 2 (hyb and Aligater). (L,M) Alignments in the ACTB mRNA from PARIS data in HEK cells were separated into ones where both arms (or segments) are at least 20 nt (L), or at least one arm is shorter than 20 nt (M). The inset boxes show DGs that support the same duplex regardless of segment length.

Figure 3.

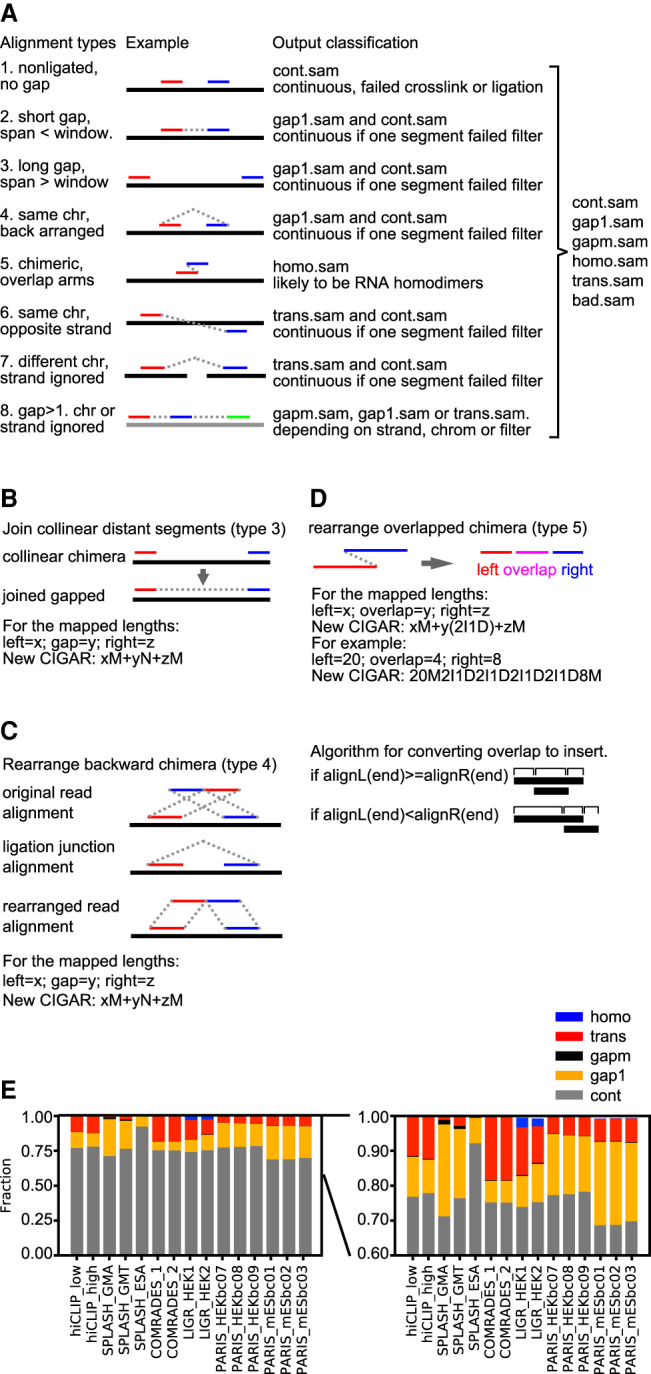
Classification and processing of alignments from crosslink-ligation experiments. (A) Types of alignments and classification after processing. This diagram presents a unified model for data from all types of crosslink-ligation experiments, and the terms are defined as follows. A read: one piece of sequence from the sequencing machine, and it may have one or multiple alignments to the reference; segment or arm: part of an alignment with no “N” in the CIGAR substring; continuous alignments: type 1, with only one segment or arm, either from non-crosslinked or crosslinked but not ligated RNA; gapped: forward arrangement, with one or more gaps, including gap1 and gapm (types 2 and some of type 8); chimeric: noncontinuous alignments similar to the definition from the STAR method, including types 3–7 and some of type 8; noncontinuous: including both gapped and chimeric alignments; homotypic: chimeric alignments where the arms overlap, suggesting RNA homodimers; trans: segments mapped to different chromosomes or strands (types 6–7 and some of type 8). In SAM files, each record describes one alignment, and it is represented by one CIGAR string. For example, a CIGAR string of “20M25N21M” (M for match, N for gap) has two segments or arms, 20 nt and 21 nt, separated by a 25-nt gap. In type 1, these two segments are from two different reads, and therefore represented by two records in SAM files (two CIGAR strings, e.g., “20M” and “21M”). Type 1 alignments are output to cont.sam. In type 2, these two segments are from the same read and therefore represented by one record in SAM files (one CIGAR string, e.g., “20M25N21M”). This alignment is either output to gap1.sam, or cont.sam if it does not pass the filtering (e.g., the gap corresponds to a splice junction). In type 3, the two segments are from the same read but still represented by two records in SAM files because they are mapped beyond the alignment window in STAR (two CIGAR strings, e.g., “20M” and “21M”). Type 3 alignments are rearranged and output to gap1.sam, or cont.sam if it does not pass the filtering. In type 4, the two segments are from the same read but mapped in reverse order and cannot be represented by one record because reverse order is not allowed in the CIGAR string (therefore represented by two records). Type 4 alignments are rearranged and output to gap1.sam, or cont.sam if it does not pass the filtering. In type 5, the two segments are from one read but overlap each other, which cannot be represented by one CIGAR string and therefore must be represented by two records in SAM files. Type 5 alignments are rearranged and output to homo.sam. In types 6 and 7, the two segments are from the same read but mapped to opposite strands of the same chromosome (type 6) or different chromosomes regardless of strand (type 7), and therefore must be represented by two records in SAM files. Type 6 and 7 alignments are output to trans.sam, or cont.sam if they do not pass filtering. In type 8, the multiple segments are from the same read but are mapped either to the same strand or to different strands or chromosomes. These arrangements are represented either by one record or multiple records in SAM files. Type 8 alignments are rearranged and output to gapm.sam, gap1.sam, or trans.sam, depending on their relative mapping locations. (B) Diagram for joining collinear distant segments into gapped alignments. The two segments are connected so that the two arms are represented by one record in SAM format, where xM and zM are the two arms, and yN is the gap. (C) Diagram for rearranging backward chimeric alignments to normal gapped alignments. The 5′ and 3′ arms are switched so that the two segments can be represented by one record in SAM format, where xM and zM are the two arms, and yN is the gap. (D) Diagram for rearranging overlapped chimera. The two arms are converted to three segments: left overhang, overlap, and right overhang. The new alignment can be represented by one record in SAM format, where y(2I1D) represents the overlapped region. (E) Classification of alignments from previously published crosslink-ligation experiments, in which the low abundance categories are magnified on the right.

Figure 4.

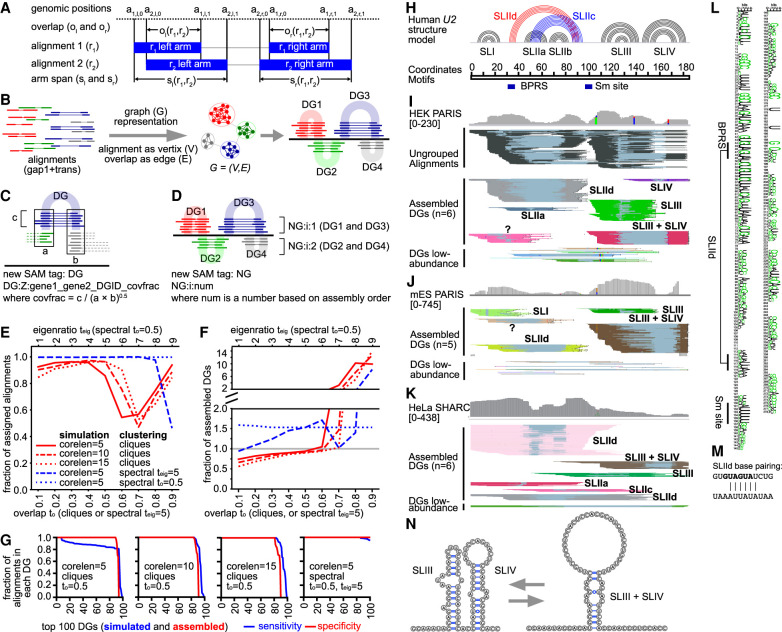
Network/graph-based method for automatic assembly of duplex groups underlying RNA structures and interactions (CRSSANT). (A) Overlap and span calculation for a pair of alignments. Two alignments r₁ and r₂ each comprising a left and right arm (solid blue bars), share left and right overlaps o_l, o_r, respectively, and left and right spans s_l, s_r, respectively. The arm start and stop positions of read/alignment i are represented by the 4-tuple (a_i,l,0, a_i,l,1, a_i,r,0, a_i,r,1). The two arms can be on the same chromosome and strand (gap1.sam), or different ones (trans.sam). (B) Diagram for network/graph-based clustering. All alignments with a single gap (gap1 and trans) are represented as a graph where each alignment is a vertex and the relative overlap ratio between the arms is the edge. Highly connected vertices cluster together forming subgraphs, corresponding to individual DGs. (C) Diagram for the DG tag information. The string after DG:Z includes the names of the two genes that the DG connects (gene1 and gene2). gene1 and gene2 are identical when the DG describes intramolecular structures or homodimers. DGID is a number based on assembly order. covfrac (coverage fraction) is defined as the number of alignments in this DG divided by the geometric mean of the coverages at the two arms. (D) Diagram for NG assembly. Non-overlapping DGs (e.g., DG1 and DG3, DG2 and DG4) are combined into NGs for visualization in genome browers like IGV. (E,F) Benchmarking CRSSANT clustering on 100 simulated DGs. All alignments map to Chr 1: 1–1000 and consist of cores 5, 10, or 15 nt (corelen = 5, 10 or 15), and random extensions on each side between 5 and 15 nt. Gaps between the two cores are at least 50 nt and at most the length of the Chr 1: 1–1000. Each DG contains between 10 and 100 alignments. The alignments were clustered using cliques or spectral algorithms. For cliques, overlap threshold t_o was varied between 0.1 and 0.9. For spectral clustering, t_o was varied between 0.1 and 0.9 when the eigenratio threshold was set at t_eig = 5. Alternatively, for spectral clustering, t_eig was varied between 1 and 10 when t_o was set at 0.5. The fraction of assigned alignments (out of 5335 input) was plotted in panel E. The fraction of assembled DGs (against 100 input) was plotted in panel F. (G) For each simulated DG data set and clustering parameter combination, the sensitivity and specificity of DG assembly was calculated for each of the top 100 DGs. The sensitivity of DG assembly is defined as the fraction of remaining alignments in each DG after CRSSANT assembly. The specificity is defined as the fraction of alignments from the dominant simulated DG. (H) Human U2 snRNA structure model based on previous studies. (I,J) Human HEK and mouse ES PARIS data were clustered using CRSSANT. The DGs were labeled corresponding to the secondary structure models in panel H. Alignments are grouped in IGV using the NG tag. “?” is a new duplex not in the known structure model. (K) Human HeLa SHARC data were clustered using CRSSANT, and the DGs were labeled as above. (L) The duplex SLIId is conserved from human down to yeast based on multiple sequence alignment of 208 seed sequences (Rfam: RF00004, in WebLogo format). (M) SLIId model; top strand is the 5′ arm, and the bottom is the 3′. Black letters, GUAUGA, indicate the BPRS masked by SLIId. (N) The alternative SLIII + SLIV structure models.

Figure 5.

Multisegment alignments support higher level structures and interactions. (A) Distributions of the numbers of arms/segments in gapm alignments. (B) Numbers of RNAs involved in each gapm alignment. Gapm alignments with three arms are shown. R1, R2, and R3 represent three different RNAs. (C) Gapm alignments with three arms indicate the coexistence of two helical regions. Sequential helices joined by gapm alignments indicate two separate stem–loops (left). Interlocked helices joined by gapm alignments indicate pseudoknots (middle). Overlapping helices joined by gapm alignments indicate triplexes. (D) Strategy to cluster gapm alignments, assuming that all TGs should be combinations of DGs. Alignments with more than two gaps are ignored for now. The DGs were produced by CRSSANT using gap1.sam and trans.sam alignments. The boundaries for each arm are the medians for the DGs. For the TGs, the merged middle arm is the redefined as boundaries of both DGs. Alignments from gapm.sam are then matched to the TGs so that each arm is overlapped. (E) Gapm alignment number distribution for TGs on the human 28S rRNA. PARIS2 HEK293 gapm alignments were assembled directly on the DGs (blue) or shuffled randomly across the 28S rRNA before assembly (red). The shuffling preserves the distances among the segments in each gapm read (i.e., the same CIGAR string). The crossing point (242, 14) indicates that the first 242 TGs each contain at least 14 gapm alignments. (F) Coverage of reads along the 28S rRNA for (1) all DGs, (2) only DGs that support the TGs, (3) TGs from original PARIS2 gapm alignments, and (4) TGs from shuffled gapm alignments. Coverage depth is indicated in the brackets. (G) For the top ranked 242 TGs either from the original gapm alignments (left) or the shuffled gapm alignments (right), the numbers of alignments (x-axis) were plotted against the geometric means of the numbers of alignments in the two DGs that support each TG (y-axis). Alignment numbers are log₁₀-transformed before plotting and calculation of Pearson's correlation. (H) gapm alignments mapped to the human 5.8S rRNA. Top track: base-pairing secondary structure model in arc format. (I) Mapping the three segments to the secondary structure model. The three segments are color-coded in panels H,I.

Figure 6.

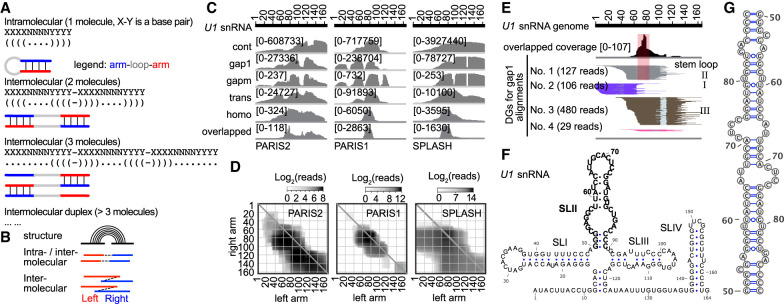
Identification of potential RNA homodimers using homotypic alignments. (A) The same base-pairing interactions can mediate intramolecular stem–loops (top) and homotypic interactions between two (middle) or more (bottom) copies of the same molecule. (B) Diagram showing alignments with gapped or overlapped arms, suggesting RNA stem–loops or homodimers. (C) Coverage of five different types of alignments on U1. The overlapped part of homo alignments is shown individually at the bottom. (D) Heat map of U1 snRNA homo alignments in three data sets. (E) PARIS2 data showing overlapped regions and corresponding local stem–loop (SLII). DGs were assembled from 1000 total alignments. (F) Secondary structure of U1homo interaction, with the SLII in bold letters. (G) Secondary structure model for the SLII homodimer.

Optimized short read mapping and filtering of crosslink-ligation sequencing data

The first critical step in analyzing crosslink-ligation data is mapping short reads with high sensitivity and specificity. To demonstrate the relevance of read length in structure modeling, we examined RNA duplexes in well-studied structures, the human ribosome and spliceosome (Fig. 2A,B; Supplemental Fig. S1A; Supplemental Data; Petrov et al. 2014; Yan et al. 2019). We found that ∼91% of arms are ≤20 nt, and more than 50% of them are ≤10 nt. Bowtie 2 can map parts of reads and the separately mapped segments can be chained to identify the gaps. The multistep mapping strategy results in low sensitivity because both segments need to be long enough (e.g., ≥20 nt) for unique mapping. The gap penalty is linear to gap size, making it difficult to accommodate long gaps. STAR considers the multiple segments together when calculating alignment scores. In addition, gap penalty calculation is more flexible, making it possible to retain short segments. Several previous studies used minimally modified STAR parameters (Ramani et al. 2015; Aw et al. 2016), whereas others used Bowtie 2 and additional postprocessing (Supplemental Table S1; Sugimoto et al. 2015; Nguyen et al. 2016; Sharma et al. 2016; https://mariotools.ucsd.edu/html/).

Here, we used STAR to develop a new strategy to identify gapped reads with high sensitivity and specificity. In principle, STAR searches for maximal mappable prefixes (MMPs) sequentially from fragments of the sequencing read, starting from the first base (Dobin et al. 2013). Here, junctions are detected naturally during the iterative search process and all types of junctions or gaps are included. After MMPs are detected, they are clustered, stitched, and scored in the second step. All seeds that are within the user-defined genomic windows are stitched (default: winBin = 2¹⁶, and window = 9 × winBin = 589824). The principle for our new strategy is that we allow mapping of short fragments by (1) removing the penalty for gap opening (scoreGap* parameters in STAR), (2) changing the penalty for gap extension (scoreGenomicLengthLog2scale in gap extension penalty calculation in STAR), and (3) allowing chimeric alignments with short fragments (Fig. 2C; Supplemental Table S2; Methods section “Optimized STAR mapping”; Supplemental Material). Traditionally, STAR considers two types of gaps: (1) short gaps from sequencing errors (“D” in CIGAR in SAM files); and (2) long gaps from splicing (“N” in CIGAR). We removed this distinction to simplify penalty calculation (changing alignIntronMin from 21 to 1). This combination of new parameters effectively treats all gaps like splicing junctions.

In theory, numbers of forward and backward gapped alignments should be similar because the proximity ligation could randomly occur on either the proximal or distal ends (shown in Fig. 1A). While analyzing the STAR alignments with short arms, we observed significantly fewer backward chimeras than forward ones. For example, a normal alignment with CIGAR string 20M10N5M can be mapped, but switching positions of the two arms will render it unmappable (only mapping the 20M part, leading to 5S20M). Given that forward and backward chimeric alignments are scored differently (a higher penalty for chimera), we rearranged alignments with softclips (unmapped parts, “S” in CIGAR) for a second round of STAR mapping (Fig. 2D). The rearrangement allows potential backward alignments to be scored as normal forward gapped alignments, which further increased the sensitivity.

After mapping, the alignments are filtered based on (1) segment length, and (2) overlap of less-confident shorter segments with confident longer ones (Fig. 2E,F). If shorter segments are close to long segments, they are very likely to be unique and bona fide, even though their presence in the entire genome is not unique. If shorter segments overlap longer ones, they are also considered confident. For example, an alignment with CIGAR string 20M30N10M (20-nt match, 30-nt gap, and 10-nt match) is likely to be real, because the 10M segment is very close to the 20M segment. The permissive STAR parameters and the two-step mapping strategy enable recovery of shorter fragments.

Systematic benchmarking of optimized STAR and analysis of crosslink-ligation data

To benchmark the performance of the optimized STAR, we first established a strategy to simulate noncontinuous alignments. We generated random forward and backward noncontinuous alignments on three genes with various characteristics, including ACTB, a ∼3.4-kb protein-coding gene, XIST, a ∼32-kb lncRNA gene, and TTN, a ∼281-kb gene that encodes the largest human protein titin. In particular, the XIST RNA contains many repetitive elements across the entire transcript, making it challenging to analyze. The simulated reads cover the full length of these three genes, including both exons and introns (Supplemental Fig. S1B). We focused on two-segment alignments, which are the dominant types. The segment and gap lengths were each randomly chosen in a range based on the distributions of real crosslink-ligation data (Supplemental Fig. S2). After simulation, the reads were mapped back to the human genome (hg38 primary assembly), and the alignments were quantified on the following four aspects: (1) % mapped reads, that is, reads mapped to the genome regardless of whether they are correct; (2) % correct alignments, that is, reads mapped to the correct simulated locations; (3) suboptimal alignments, that is, number of incorrect alignments per read; and (4) % forward or backward chimeras, that is, alignments with ligation junctions at the proximal or distal ends (Supplemental Fig. S1C).

We compared published Bowtie 2, default STAR (default in STAR except the activation of the chimeric alignments), and optimized settings. Whereas most reads could be mapped to the genome using the four methods (Fig. 2G; Supplemental Data), STAR optimized parameters (black line) outperformed all other methods in the correct alignment rate (Fig. 2H; see results for all parameter combinations on three genes in Supplemental Fig. S1D–H). When segments were short, the correct alignment rates were low across all the combinations of parameters (∼60%–70% for STAR_optimized). This is expected because short segments cannot be mapped uniquely. For longer segment lengths, the correct alignment rates all approached 100% for STAR and above 80% for Bowtie 2. Bowtie 2 correct mapping rates dropped when the segment lengths were above the [20,80] range. This is because the longer segments have more substrings that can be mapped to many locations across the genome. Bowtie 2 seeks to reseed the unmapped segment multiple times (e.g., up to 20 times) and may not find the perfect match within the specified number of reseeding attempts. Bowtie 2 outputs many more suboptimal alignments per read (with lower scores than the best chimera) (Fig. 2I; Supplemental Fig. S1F). This behavior may be useful for certain circumstances, for example, when some of these could be real. However, this benefit is at the cost of more noise in the background, especially for longer segments. The higher numbers of suboptimal alignments with longer segment lengths are due to the possibility of matching more subsequences in these long segments. On the other hand, STAR outputs very few suboptimal alignments on average, even though we set the outFilterMultimapNmax parameter to 10 (Fig. 2I; Supplemental Fig. S1F,H). Finally, the STAR default parameters resulted in more alignments in the forward than backward arrangements (broken yellow line vs. dotted yellow line), even though both should be ∼50% in theory (Fig. 2J; Supplemental Fig. S1G). The optimized parameters with the two-round mapping increased the backward chimera to near the forward chimera (dotted black line vs. broken black line). This improvement is especially high for the short segments, whereas both are mapped at near 50% when the segments are between 100 and 200 nt (Fig. 2J; Supplemental Fig. S1G).

To systematically evaluate published crosslink-ligation methods and the new mapping strategy, we processed data using uniform procedures (Supplemental Fig. S2A). After mapping using the optimized STAR parameters, we classified and rearranged alignments into six categories (see details later) and removed spliced alignments. The mapped segments and gaps follow a wide range of distributions (Supplemental Fig. S2B,C). PARIS data have a median segment size of 24 nt, followed by hiCLIP at 31 nt. For PARIS, ∼95% of the segments are shorter than 40 nt, and a significant portion of them, ∼13.8%, at or below 15 nt. Other crosslink-ligation data have median segment sizes above 40 nt, almost twice the size of PARIS data. We found that 1- to 2-nt gaps were present in a significant portion of all noncontinuous alignments (Supplemental Fig. S2C). In SPLASH, 1- to 2-nt gaps are present in 61% of alignments, whereas only 11% of gaps in PARIS are 1- to 2-nt.

To determine whether the short gaps are artifacts, we analyzed nucleotide frequencies in the gaps (Supplemental Fig. S2D). For data with more 1- to 2-nt gaps, uridine is significantly overrepresented (Supplemental Fig. S2E,F). SPLASH and COMRADES have significantly higher bias than PARIS and LIGR. SPLASH and COMRADES used biotinylated psoralens for enrichment, where monoadducts at uridines are the dominant products, rather than the crosslinks. In LIGR and PARIS, enrichment of crosslinked fragments was achieved using RNase R and 2D gels, respectively, where the monoadducts are much lower. We speculated that such 1- to 2-nt gaps are due to reverse transcription errors on psoralen-uridine monoadducts, and therefore we removed them before further analysis. The gap and segment length and composition analysis provided valuable information about the library quality and should serve as important guides for future applications and optimizations. Together, this analysis shows that PARIS and hiCLIP produced shorter segments that are more useful for higher resolution structure modeling and lower fractions of 1- to 2-nt gaps from reverse transcription errors.

Next, we tested the optimized STAR mapping strategy on real crosslink-ligation data. The optimized STAR mapping improved recovery of all alignments over all other methods (black bars, Fig. 2K). For example, among the mapped alignments in PARIS, roughly 50% of them have both arms > 20 nt, which is the commonly used cutoff in multistep mapping procedures in other studies. From the most stringent condition (default with both arms > 20 nt), to the most sensitive condition (optimized with no size selection), the mapped noncontinuous alignments increased 2.75-fold. To make sure that the differences in mappability are not due to artifacts, we examined the alignments mapped to two RNAs, ACTB and XIST. The results are consistent with global comparison, despite differences in sequence composition and presence of complex repeats in XIST (Lu et al. 2016). For data with longer segments, optimized STAR can still improve mapping, although not as much as for the data for the shorter segments (Supplemental Fig. S2G). As an example, we separated the gapped alignments on the ACTB mRNA from PARIS data into two groups, where both arms are ≥20 nt (Fig. 2L) or at least one arm is <20 nt (Fig. 2M). Alignments in both length ranges are clustered into duplex groups and compared side by side. We found that the DGs are similar between the different size ranges (see the inset boxes). In fact, the shortest segments in the alignments mapped to ACTB mRNA are only 8 nt, yet they are still mapped with high confidence. In summary, we showed that different crosslink-ligation protocols produce noncontinuous alignments with drastic differences in segment and gap properties. The optimized parameters and postprocessing for STAR mapping significantly improved the recovery of short segments that are most valuable for building high-resolution structure models.

Rearrangement and classification of alignments

The complex reactions of crosslink-ligation produce complex arrangements in each read. Through exhaustive classification, we divided alignments into eight types (Fig. 3A, left side, alignment types). Nongapped alignments from non-crosslinked RNA fragments or failed ligations, that is, crosslinked but not ligated, are type 1. Local collinear gapped alignments, within the predefined window, are type 2. Here, a window is defined in STAR by the parameters ‐‐winBinNbits (default 16) and ‐‐winAnchorDistNbins (default 9). The use of a window in calling gapped alignments in STAR was motivated by the need to capture spliced alignments, where intron lengths are typically within a limited range (e.g., default window = winAnchorDistNbins × 2^winBinNbits= 9 × 2¹⁶= 589,824). Alignment segments that are too distant from each other (beyond the STAR genomic window), even though collinear, are considered as one type of chimera (type 3). Types 2 and 3 are artificially separated because STAR treats local and distal segments in different ways. Chimeric alignments also include ones with reversed orders (backward chimera, type 4; ligation can occur on either end) (see Fig. 1A), two arms overlapped (type 5), located on opposite strands of the same chromosome (type 6), or different chromosomes regardless of strand (type 7). Multisegment alignments are also possible, arising from multiple proximity ligations or a combination of splicing and multiple proximity ligations (type 8). Type 8 alignments can be mapped to the same strand and same chromosome or different strands and/or chromosomes. In theory, the CIGAR string in the SAM format can only accommodate collinear arrangements with positive gaps (“D” and “N”, gap length > 0), that is, types 1–4, but not overlaps (gap length < 0) and noncollinear ones (undefined gap lengths). In STAR, types 4–7 and some of type 8 are all considered as chimeric and therefore represented by two or more records each in SAM files. Even though this exhaustive classification is based on the output from STAR, they are generally applicable to alignments from other types of short read mappers, with minor differences—for example, local versus distal gapped in types 2 and 3—and therefore should facilitate more sophisticated studies of RNA structures and interactions.

The complex arrangements of the alignments make them difficult to analyze and visualize. Therefore, we developed tools to filter, rearrange, and reclassify the eight types of alignments into five types (excluding bad ones, e.g., homopolymers, etc.), each providing a distinct type of information for inferring RNA structures and interactions (Fig. 3A, the right-side classification output; Fig. 3B–D; see flowchart in Supplemental Fig. S3; details in Methods and Supplemental Material). Distant collinear chimeras (type 3) are converted to normal chimeras, gap1 (type 2) by joining the two segments (Fig. 3B). Backward chimeras (type 4) are converted to normal chimeras, gap1 (type 2) by switching the two segments (Fig. 3C). Overlapped chimeras (type 5) are converted to homotypic chimeras (homo) by redefining the overlapped part as a combination of insertions and deletions (Fig. 3D). After conversion, these types can be processed and visualized as normal gapped alignments. Trans alignments and some of the multigap alignments that map to different chromosomes and/or different strands, cannot be combined into single records (single CIGAR strings) and are processed separately (see Fig. 5; Methods). We applied the alignment, filtering, and rearrangement methods to published data sets (Fig. 3E; Supplemental Data). Each experiment produced variable amounts of alignments in the five types (except the bad.sam, which are very rare). Even though most homo (overlapping arms) and gam (multisegment) alignments represent a small percentage of total number of alignments, they are significant because they reveal important new structures and interactions, and only a few reads/alignments are sufficient to call a specific RNA duplex (see details below).

Network-based duplex group assembly of single-gapped alignments

Among the five rearranged alignment types, gap1, gapm, trans, and homo support distinct RNA structures and interactions. To assemble alignments into groups that support individual structures, we developed a method CRSSANT to cluster single-gap alignments, including gap1 and trans, to duplex groups (see later sections for further processing of gapm and homo alignments). CRSSANT leverages network analysis techniques—also frequently referred to as “graph” techniques—to automate analysis of sequencing reads produced by crosslink-ligation methods. The well-developed graph theory in discrete mathematics studies pairwise interactions among objects, making it well-suited for the analysis of RNA structures from crosslink-ligation data, where nucleotides or RNA fragments are represented as “nodes” and their interactions are represented as “edges.” To determine the relationship among alignments, we defined the overlap ratios between any pair of alignments on both arms, o_l(r₁,r₂)/s_l(r₁,r₂) and o_r(r₁,r₂)/s_r(r₁,r₂), where r₁ and r₂ represent the two alignments, and the ratios should be in the range of [0,1] (Fig. 4A). Then, the gap1/trans alignments were converted to a network based on their overlap ratios, and the network is clustered using two alternative approaches, cliques-finding and spectral (Fig. 4B; Supplemental Fig. S4; Methods; Supplemental Materials, section 5). In particular, the cliques-finding approach searches for groups of alignment, where every alignment overlaps other alignments on both arms above a threshold t_o (0 < t_o ≤ 1). On the other hand, spectral clustering finds groups of alignments, such as overlaps within the group that are larger than overlaps between groups (see Supplemental Materials, section 5.3 for details of the clustering methods). The clustered subgraphs correspond to individual DGs, each containing highly similar alignments. The clustering produces two types of output, tagged SAM alignments and summary of DG information, which can be used for subsequent visualization and secondary structure prediction. A new DG tag is appended to each alignment in the SAM file to describe where this DG is assembled and its fractional coverage (covfrac) relative to all the noncontinuous alignments overlapping it (Fig. 4C). In addition, non-overlapping DGs are further clustered to make non-overlapping groups (also appended to the alignments in the SAM file), which facilitates compact visualization of the clustered alignments (Fig. 4D).

In crosslink-ligation experiments, crosslinking and ligation efficiencies vary greatly depending on sequence and structure contexts. More importantly, in vivo golden standard structure models do not exist for the vast majority of cellular RNAs because in vitro methods such as cryo-EM, crystallography, and NMR only capture a subset of stable conformations under artificial conditions. Therefore, we benchmarked the CRSSANT method on simulated DGs with gap1 alignments (Supplemental Fig. S5A,B; Methods; Supplemental Materials). On an artificial chromosome of defined length (e.g., 1000 bp), 100 simulated DGs were randomly positioned with defined core length, random extensions on each side of the core, random gap length, and random numbers of alignments in each DG. Then, we clustered the simulated alignments into DGs using the cliques and spectral algorithms and various parameters, including the overlap ratio threshold t_o for both cliques and spectral, and eigenratio threshold t_eig for spectral. t_o was varied between 0.1 to 0.9, where a higher value requires more overlap among alignments, which leads to larger numbers of DGs. t_eig was varied between 1 and 9, where higher values lead to smaller numbers of DGs. We calculated the fraction of input alignments assigned to assembled DGs (Fig. 4E), numbers of DGs assembled from the 100 simulated DGs (Fig. 4F), specificity, and sensitivity (Fig. 4G),

Over 80% of alignments were assembled into DGs with t_o between 0.1 and 0.5 using various simulation settings and both clustering algorithms (out of 5335 simulated alignments) (Fig. 4E; Supplemental Data). CRSSANT assembly produced between 50 and 200 DGs from the input 100 simulated DGs with t_o between 0.1 and 0.5 (Fig. 4F). As expected, higher t_o (>0.5) reduced assembled alignments and increased total assembled DGs. Spectral clustering consistently outperforms cliques at the recovery of alignments (Fig. 4E) but at the expense of increasing assembled DGs (in Fig. 4F, the horizontal line at 1.0 indicates the 100 simulated DGs), leading to unnecessary DG splitting. At t_o above 0.5, performance of both methods dropped, whereas t_eig did not affect the spectral clustering at all values tested (up to t_eig = 100, at which point, 99.8% of alignments were assembled, producing 145 DGs, or 145% of input DGs). Using the optimal settings for the two algorithms (t_o = 0.5 and t_eig = 5), we examined individual CRSSANT-assembled DGs (Fig. 4G). More than 80% of the top 100 DGs are consistently assembled with high sensitivity and specificity; that is, the original simulated alignments are mostly assembled into DGs (sensitivity), and the membership in the assembled DGs are correct (specificity) (all parameter combinations in Supplemental Fig. S5C,D). Visual inspection of the assembled DGs confirmed the better performance of the cliques method; the minor reduction of DG numbers compared to simulated input was due to merging of DGs that showed significant overlap at the two arms (Supplemental Fig. S6A–C). Even though the spectral method increased recovery of alignments, about 50 of the simulated DGs were split into overlapping smaller DGs (Supplemental Fig. S6D). The excessive splitting of DGs is undesirable as it produces multiple DGs that support the same RNA structures.

We tested the speed of CRSSANT by varying the simulation and clustering parameters on a standard laptop computer. Increasing alignment numbers in each DG extended running time nearly quadratically because pairwise comparison of overlapping alignments is the bottleneck (Supplemental Fig. S7A,B). Consistent with this, increasing genome length while maintaining alignment numbers (effectively reducing alignment density) significantly lowered running time (Supplemental Fig. S7C). The choice of clustering parameters did not affect running time at reasonable overlap thresholds (t_o between 0.1 and 0.5) (Supplemental Fig. S7D). Together, we identified the cliques as the preferred clustering algorithm and showed that t_o moderately affects clustering performance.

To validate CRSSANT on cellular RNAs, we analyzed the snRNA U2 and the snoRNA U3 using published PARIS data from human HEK and mouse ES cells (Fig. 4H–N; Supplemental Fig. S8; Supplemental Table S3; Supplemental Material; Lu et al. 2016). Ungrouped alignments on U2 are densely packed, making it difficult to recognize the structures (Fig. 4H). After clustering, DGs have an average dispersion (standard deviations of the left-start, left-end, right-start, and right-end positions) of 5.0 nt for each DG, compared to 44 nt for all alignments on U2, showing that the clustering resulted in tightly packed DGs (Fig. 4I). In other words, the coordinates for the four positions (left-start, left-end, right-start, and right-end) are closer to each other among the alignments in each group after clustering, compared to all alignments before clustering (e.g., a_1,I,0, a_2,l,0, … a_i,l,0 are closer to each other in the group, with an overall standard deviation of 5.0 for the U2 snRNA). We identified four previously known stem–loops SLI, SLIIa, SLIII, and SLIV (Patel and Steitz 2003; Hilliker et al. 2007; Perriman and Ares 2007). SLIIb and SLIIc were missed due to the lack of psoralen-crosslinkable staggered uridines (Supplemental Fig. S8A). In addition, we recovered DGs that suggest new conformations: SLIId and SLIII + SLIV, both of which are conserved between human and mouse (Fig. 4I,J). The low-abundance DGs may have come from other less stable conformations (bottom of Fig. 4I,J). SLIId is an alternative duplex to SLIIc, masking the branchpoint recognition sequence (BPRS), suggesting a function in regulating U2 recognition of introns. SLIId blocking of BPRS may act as a structural switch to reduce spurious binding and increase splicing fidelity.

To further validate the U2 alternative conformations, we used an orthogonal crosslinking method, Selective 2′-Hydroxyl Acylation Reversible Crosslinking (SHARC) (Van Damme et al. 2022). SHARC reagents crosslink RNA nucleotides in spatial proximity (not base-pairing) at the 2′-OH positions, and the crosslinking is reversible by mild alkaline hydrolysis. Therefore, the SHARC reagents can be incorporated into a standard crosslink-ligation experimental pipeline, like PARIS. Analysis of the SHARC sequencing data revealed similar alternative conformations, including SLIId and SLIII + SLIV (Fig. 4K). Further analysis of SLIId in U2 homologs revealed a strongly conserved duplex from human to yeast (Fig. 4L,M). The near complete overlap of the left arms of SLIII and SLIII + SLIV, and the overlap of the right arms of SLIV and SLIII + SLIV in human and mouse suggest that these conformations are alternative to each other (Fig. 4I–K; Supplemental Fig. S8B). The left arm of SLIII and right arm of SLIV form a 7-bp bulged stem with staggered uridine crosslinking sites, supporting its validity (Fig. 4N). Together, the analysis of U2 snRNA validates the CRSSANT clustering strategy, confirming previously known structures and nominating new conformations that reveal previously unknown mechanisms in splicing regulation.

To further validate CRSSANT on more complex RNAs and on data from other crosslink-ligation methods, we analyzed the 28S rRNA structures in four psoralen crosslinking and one formaldehyde indirect crosslinking method, PARIS, COMRADES, LIGR, SPLASH, and RIC. The 28S rRNA contains 132 helices based on cryo-EM (Anger et al. 2013). From 300,000 gap1 alignments, between 280 and 1200 DGs were assembled (reads ≥ 10 in each DG) (Supplemental Fig. S9A). The differences in numbers of DGs are caused by different crosslinking, fragmentation, enrichment, and ligation methods. For example, longer reads in RIC increase overlap on the two arms and cause more reads to be collapsed to the same DG. The in vivo crosslink-ligation methods capture the entire life cycle of the ribosome, from biogenesis to maturation and turnover, therefore producing more DGs than observed in the cryo-EM model. Long duplexes, for example, the expansion segments, which measure up to 180 bps, can be represented by multiple DGs, further increasing the number of DGs. These methods captured between 58 and 78 of the 132 known duplexes (Supplemental Fig. S9B), where the missed ones are likely due to their short arms and lack of crosslinkable sites (Fig. 2A,B; Supplemental Fig. S1A).

To determine whether the assembled DGs captured the base-pairing and spatial proximities in the ribosome, we compared DGs with bins of base pairs and spatial proximal nucleotides using the ROC curve (Supplemental Fig. S9C,D). Areas under the curve (AUC) are in the ranges of 0.77–0.91 and 0.83–0.90, demonstrating high specificity and sensitivity, despite the larger numbers of DGs and the missed duplexes. Notably, some of the DGs that do not correspond to any structures in the cryo-EM model were observed in several different crosslink-ligation data sets, suggesting that they are real in cells (Supplemental Fig. S9E). Spatial proximal regions that do not base pair were not captured efficiently, as expected (Supplemental Fig. S9F; Lu et al. 2016). Inspection of the common DGs among the different methods further confirmed the differences in segment lengths (Supplemental Figs. S2, S9G,H). Together, the tests on simulated and experimental data from multiple crosslink-ligation methods demonstrated the solid performance of CRSSANT in DG assembly.

Multisegment alignments provide evidence for complex structures and interactions

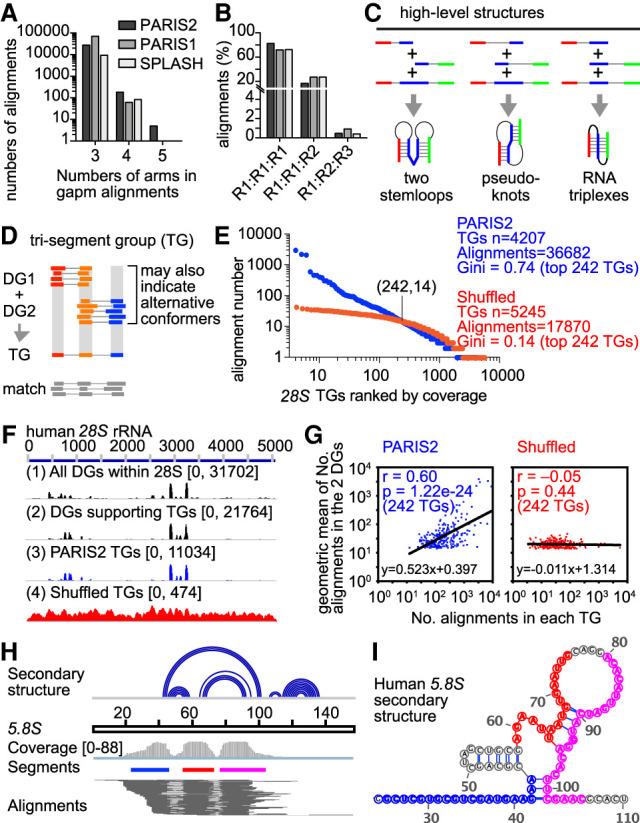
Both crosslinking and proximity ligation are inefficient; however, multiple events may occur simultaneously in some RNA regions, leading to reads and alignments with multiple gaps (referred to as gapm, with gaps ≥ 2 or segments ≥ 3) (Fig. 3). Further analysis of these alignments showed that three-segment alignments are the majority, accounting for >99% of them, whereas alignments with more segments were exceedingly rare (Fig. 5A; Supplemental Data). Among three-segment alignments, ∼70%–80% of them were mapped within one RNA, whereas 20%–25% of them are mapped to two RNAs simultaneously, indicating RNA-RNA interactions (Fig. 5B). A small fraction of them were mapped to three different RNAs, suggesting the existence of multi-RNA complexes.

These gapm alignments could indicate several types of structural topology, such as sequential or concentric helices, pseudoknots, and even triple helices (Fig. 5C, examples in one RNA). For example, we previously showed that interlocking helices suggest pseudoknots, but an alternative explanation is that the two helices could exist in separate RNA molecules (Lu et al. 2016). Alignments connecting the two helices are strong evidence that both helices occur on one RNA, therefore proving the pseudoknot structure. The complex structures could be either intramolecular or intermolecular, indicating complex interactions. Such high-level structures are hard to predict or validate in cells using conventional methods. Focusing on these three-segment (two-gap) alignments, we developed a method to cluster them into trisegment groups (Fig. 5D). Given that TGs are combinations of DGs, we first used CRSSANT-assembled DGs to build a list of DG pairs with one overlapping arm. Gapm alignments with three segments were then assigned to DG pairs based on overlap with each arm. Three-segment alignments that group together are defined as a TG.

Clustering of TGs from published data sets revealed a large number of complex structures, particularly in the most abundant cellular RNAs, for example, the rRNAs and snRNAs, and they are consistent with the combinations of DGs (Fig. 5E; Supplemental Fig. S10). Out of the 43,389 gapm alignments, 36,682, or 84.5%, of them are assembled into TGs (Fig. 5E). In particular, the top-ranked TG contains 3865 alignments (Fig. 5E, first blue dot on the left). This one TG takes up 10.5% of the total 36,682 alignments in all 4207 TGs (Fig. 5E), suggesting that it is highly specific. To test whether TGs correlate with DGs, we shuffled the gapm alignments across the 28S rRNA and then re-assembled them into TGs. Only 48.7% of the shuffled gapm alignments (17,870/36,682) can now be assigned. The alignment numbers in each shuffled TG are more uniformly distributed (Fig. 5E, red dots), with the maximal coverage at 46, compared to 3865 in the original data. The two distributions crossed at (242,14), where the top 242 TGs contains 75.2% alignments in the original data, but only 27.7% in the shuffled data. This result suggests that the TG alignments are not randomly derived from the rRNAs but rather correspond to combinations of DGs that describe the tightly packed structures (as shown in the diagram, Fig. 5D), supporting the validity of identified TGs. We then calculated the Gini indices, which measure statistical dispersion of gapm alignments among TGs, either from the original data or after shuffling for the top 242 TGs. For the original data, the Gini index is 0.74, showing highly uneven distribution, and it drops down to 0.14 after shuffling. To further determine whether the numbers of gapm alignments in TGs correlate with those of DGs that support the TG, we plotted the geometric mean of the DG alignment numbers (DG1_number × DG2_number)^0.5 versus the TG alignment numbers (DG1, DG2, and TG as defined in Fig. 5D). In the original TGs, there is a strong positive correlation, which is lost after shuffling (Fig. 5F,G; Supplemental Fig. S10A).

For example, in the 5.8S rRNA, we observed a TG that corresponds to a three-way junction (Fig. 5H,I). Some of the complex structures are supported by more than one TG. For instance, two concentric helices are supported by three different TGs because the RNase cleaved at different locations in the RNA structure before proximity ligation (Supplemental Fig. S10C). In addition to intramolecular interactions, we also discovered more complex intermolecular interactions. We previously showed that snoRNAs U8 and U13 form a dynamic network of intermolecular interactions with rRNA precursors during rRNA processing (Zhang et al. 2021). Here, we found that gapm alignments connect U8, U13, and the rRNA precursor together, suggesting that these interactions occur simultaneously in cells (Supplemental Fig. S10F–H; Supplemental Tables S4, S5). Together, these analyses revealed more complex structures than possible before.

Identifying alignments with overlapped segments indicating potential RNA homodimers

Base-pairing can drive the formation of intramolecular RNA duplexes as well as intermolecular interactions using the exact same sequences. For example, a stem–loop can also form an alternative conformation of homodimer with nearly identical base pairs (Fig. 6A, top and middle). The intermolecular interactions may contain two molecules, or even more, forming a daisy-chain complex (Fig. 6A, bottom). Given the prevalence of RNA stem–loops and the high concentration of many essential ncRNAs, and the sequestration of mRNAs into RNP granules (Protter and Parker 2016), it is conceivable that such RNA homodimers are widely present in cells. However, homodimers are difficult to detect using conventional methods. Here, we found that alignments with overlapping segments enable de novo discovery of such interactions. Normal gapped reads without overlaps between the two arms may come from one RNA molecule or two identical molecules (Fig. 6B). Gapped reads with overlaps between them could only have come from a homodimer (Fig. 6B). Because of this, such alignments are definitive evidence for homodimers. Such analysis provides an underestimation of the abundance of intermolecular duplexes because some normal gapped alignments (gap1) may also come from homodimers.

While testing the STAR parameters to discover RNA homodimers, we noticed that the mapping of overlapping chimeras was inefficient when the dimerization region was close to the 5′ or 3′ ends of the reference (e.g., the ends of the chromosome or a contig), or the flanking sequences were homopolymers of “N” (using the U8 snoRNA as an example test) (Supplemental Fig. S11A,B; more details below). Mapping was efficient when the flanking sequences contain at least 50 nt of normal genomic context (non “N”), or homopolymers of A, C, G, T, or random sequences, or when the chimFilter option was set to None (Supplemental Fig. S11C). This context-dependence was not obvious for other types of chimeras, for example, heterotypic intermolecular interactions (U8:U35A and U8:28S heterodimers) (Supplemental Fig. S11A,B; Supplemental Fig. S11D,E), and cannot be alleviated by adjusting the windowing parameters in STAR (Supplemental Fig. S11F). Therefore, to detect RNA homodimers, the reference sequences should be adjusted to contain 100 or more nucleotides of flanking sequences, or the chimFilter option set to None.

To determine whether cellular RNA can form homodimers, we analyzed published crosslink-ligation data (summary in Fig. 3E). First, we filtered homotypic alignments to remove short 1- to 2-nt insertions that may come from RNA damages or sequencing errors and repetitive sequences that may come from enzyme slippage during reverse transcription or PCR. To determine the significance of homodimers, we calculated the ratio of overlapping alignments versus nonoverlapping ones in the same RNA. Overlapped regions extend to >60 nt among various data sets (Supplemental Fig. S12A). In general, overlapping alignments are rare, but a few noncoding RNAs have high proportions of overlapping alignments (Supplemental Table S6). The most highly enriched RNA is U8, a snoRNA previously shown to be essential for rRNA processing (Peculis and Steitz 1993), mutations in which cause a neurological disease LCC (Labrune et al. 1996; Jenkinson et al. 2016; Iwama et al. 2017). We recently reported this dimer and showed that it is part of five alternative conformations for the U8 snoRNA structure, and this dimer is disrupted by LCC patient mutations (see Fig. 4 and Supplemental Figs. S20 and S21 in Zhang et al. 2021) (Supplemental Fig. S12B–D). In addition to U8, dimers also are likely to form for U1 and U2 snRNAs (Fig. 6C,D; Supplemental Fig. 12E–I; Supplemental Data). In U1, we detected a specific dimerization region in the SLII from three different psoralen crosslinking data sets. This specific enrichment compared to broader distributions of other types of alignments further suggests that this homodimer is real, despite the low abundance (Fig. 6C). The homo alignments localize to the same sequences as gap1 alignments at the local stem–loop (Fig. 6E), consistent with them as alternative conformations to each other (Fig. 6F,G). Similarly, we detected potential dimerization regions in the SLIII of U2 snRNA, mitochondrial tRNAs, and expansion segments in ribosomal RNAs (Supplemental Fig. S12J–P). Overlapping alignments in the mRNAs, however, were not abundant enough to allow the identification of local enrichment sites that indicate dimerization sequences (Supplemental Table S6). Homodimerization in other noncoding RNAs may also have been missed due to limited sequencing coverage.

Homodimers have been reported in a variety of RNA viruses. To detect potential homodimers, we analyzed our recently published PARIS2 data on two single-stranded RNA virus genomes (Supplemental Fig. S13; Zhang et al. 2021). In both US47 (US/MO/14-18947 and VR1197 (F02-3607 Corn), two strains of EV-D68, we detected local peaks of overlapping alignments. Whereas some of these peaks coincide with local stem–loops detected by PARIS2, others were not, suggesting alternative base-pairing mechanisms in the interactions (Supplemental Fig. S13A,D). The ratio of homotypic alignments over all gapped ones is only ∼1% (Supplemental Table S6), yet the overlapped regions are rather extended (Supplemental Fig. S13B,C,E,F). The top-ranked peaks were not conserved between the two viral strains due the rapid evolution of these RNA viruses. Additional dimerization sites may exist that cannot be captured by our method which relies on the identification of local hairpins. Together, these studies demonstrate the ability of our new computational pipeline in the identification of potential RNA homodimers in a variety of contexts.

To validate the newly discovered homodimers, we developed an experimental strategy based on convergent and divergent PCR and tested the U8 homodimer (Supplemental Fig. S14A). First, RNA was purified from cells with or without AMT crosslinking. For the crosslinked RNA, half were ligated proximally and the other half nonligated. U8 was then enriched from the three RNA samples using biotinylated antisense probes (Zhang et al. 2021), ligated to a 3′ end adapter, reverse-crosslinked with 254-nm UV light, and reverse-transcribed into cDNA. We designed a set of divergent PCR primers on U8, which should not lead to any products on non-crosslinked or nonligated RNA. However, in an RNA homodimer that was crosslinked and ligated, the divergent primers can now converge on the ligation junction to amplify the junction region. Given that the adapter ligation step may randomly join two non-crosslinked U8 molecules in solution, low levels of PCR amplification are expected from the non-crosslinked and nonligated samples. Indeed, PCR resulted in significantly higher amounts of products from the crosslinked and ligated samples (Supplemental Fig. S14B,C). Together, the de novo discovery by CRSSANT in crosslink-ligation experiments, our previous in vitro validation (Zhang et al. 2021), and the PCR validation in crosslinked cells confirmed the U8 homodimer.

Discussion

The recent development of crosslink-ligation methods has changed the field of in vivo RNA structure studies. Despite the progress in experimental techniques, computational processing of such data remains challenging. Previously developed computational tools have focused on simple cases, that is, identification of single-gapped alignments and building duplex structures from them (Travis et al. 2014; Sharma et al. 2016; Lu et al. 2018; Zhou et al. 2020). In this study, we performed exhaustive analysis of data from crosslink-ligation experiments, identified limitations of previous computational methods, and designed a set of tools to address several fundamental problems in the analysis pipeline and to realize the full potential of such experimental techniques.

Specifically, we focused on the mapping, classification, and clustering of sequencing reads: (1) we optimized a set of STAR mapping parameters, together with a new filtering strategy to maximize sensitivity and specificity of aligning short segments (Fig. 2). This improvement is particularly beneficial for building higher resolution secondary structure models that require shorter segments; (2) we developed a strategy to exhaustively classify alignments into eight categories, which are then rearranged into five types (Fig. 3). The newly developed tools are particularly useful for the analysis of alignments where the two segments can be converted to a single SAM record for visualization in genome browsers (Lu et al. 2016); (3) we developed a network-based method, CRSSANT, for clustering noncontinuous alignments to discrete groups that represent the underlying RNA duplexes, for simple gapped alignments (gap1 and trans, Fig. 4), complex alignments (gapm, Fig. 5), and homodimers (homo, Fig. 6). We benchmarked each step of the pipeline and demonstrated its applications in various real-world examples. The files output by CRSSANT concisely summarize information that is crucial to the RNA structural biologists and are prepared in file formats commonly used by the structural biology community to facilitate cross-platform analysis. Altogether, this pipeline greatly facilitates the analysis and interpretation of data from a wide variety of crosslink-ligation experiments.

Our systematic analysis of alignment properties such as the segment length, gap length, and gap nucleotide frequencies revealed previously unknown problems that help guide future improvement of crosslink-ligation methods. In particular, we show that the segment length distributions vary greatly across the methods, which has a major impact on the secondary structure modeling. Even with the shortest segments in hiCLIP and PARIS (Sugimoto et al. 2015; Lu et al. 2016), the median segment lengths of ∼20 nt far exceed those of the well-studied RNAs such as the ribosome and spliceosome (Fig. 2A), and it remains challenging to determine the exact base pairs. Future improvements to pinpoint crosslinking sites are necessary for unambiguous modeling. The discovery of psoralen-monoadduct-induced uridine deletions, especially in the 1- to 2-nt range, revealed concerns over some of the crosslinking methods. We suggest that these short-gap alignments should be removed before any subsequent analysis.

Even though recent studies have paid attention to alternative conformations in RNA secondary structure modeling from crosslink-ligation data, detailed analysis of individual RNAs is still challenging. In the CRSSANT method, we systematically tested clustering algorithms and parameters on simulated data sets and applied them to published data sets. This benchmarking provides important guidelines for applications on experimental data. As examples, our analysis revealed new conformations, even for well-studied noncoding RNAs, such as U2 and U3. The combination of different types of crosslinking data and phylogenetic analysis support the validity of these new conformations. Nevertheless, deeper studies are needed to understand their functions and mechanisms of dynamic interconversions.

RNAs in cells are known to form highly sophisticated machines, and our current understanding remains limited to a few well-behaving RNAs and their complexes that can be purified for characterizations. Our exhaustive classification allowed us to discover complex structures and RNA homodimers de novo, further expanding the capabilities of these experimental techniques. In a recent study, we have significantly improved the crosslinking and overall efficiency of crosslink-ligation experiments (>4000-fold) (Zhang et al. 2021); however, the low proximity ligation efficiency remains a major bottleneck for crosslink-ligation methods. This problem made it difficult to capture the multisegment structures and interactions. For example, at 10% ligation efficiency, reads with n segments are less than 1 in 10ⁿ. Improvement in proximity ligation and the ever-increasing sequencing power should solve this problem to allow the discovery of other complex structures.

The discovery of homodimers is particularly interesting because it opens new directions for future research. The small fraction of RNAs with overlapping fragments suggests that homodimers based on local palindrome-like sequences are rare. We discovered strong homodimers in the U8 snoRNA, and U1 and U2 snRNAs. These homodimers were detected across different data sets, even though their abundances vary considerably. In the most stable homodimer U8, the overlapping alignments are even more abundant than the intramolecular duplexes in one data set. Based on the de novo discovery in crosslink-ligation data, our recent in vitro validation (Zhang et al. 2021), and current in vivo validation of U8 homodimer, we believe that at least a subset of the predicted homodimers are real. The discovery of human patient mutations that disrupt the dimers points to the functional significance of such interactions (Labrune et al. 1996; Jenkinson et al. 2016; Iwama et al. 2017; Zhang et al. 2021). While this manuscript was in preparation, the Kudla group published a similar approach and confirmed our discovery of homodimers in the snRNAs and snoRNAs (Gabryelska et al. 2022).

We note that, in contrast to typical gapped alignments, where shorter segments lead to higher resolution structural modeling, longer segments are needed for efficient detection of overlapping alignments and potential homodimers. In the extreme case of the 5′ end of one copy binding to the 3′ end of another copy of the same RNA, full-length RNAs are necessary to detect such dimers. Alternatively, we propose a genetics-based method to detect homodimers, which is not limited by the sequence distance between the two segments (Supplemental Fig. S14D). When RNA molecules from two different genetic backgrounds (red and blue lines) exist in the same cell, for example, during co-infection of two RNA virus strains with sufficient genetic distance between them, or in the F1 generation of a hybrid organism, nucleotide sequence variants allow us to accurately map the fragments to the RNA of origin. When the two fragments are derived from the same genetic origin, the duplex could be either intra- or intermolecular. However, if the two fragments are from two different genetic backgrounds, then the duplex should be intermolecular, that is, a homodimer. Two caveats should be considered in this approach. First, some sequence variations may alter the structures and interactions and lead to artifacts. High enough sequence variation may redefine the homodimer to heterodimer. Secondly and specifically for RNA viruses, genome recombination may break the linkage of variants and confound the analysis of intermolecular homodimers.

In this study we focused on the mapping, classification, and clustering of crosslink-ligation data. Subsequent crosslink-guided structure modeling can be achieved using many previously published tools based on free energy minimization and multiple sequence alignments, but it is not a trivial task for several reasons (Eddy 2004; Lu et al. 2016). Even with the shortest fragments available in PARIS, there is ambiguity in determining the exact base pairs. In addition to the problems with the experimental constraints, energy- and conservation-based computational prediction approaches are still being optimized. As such, manual inspection is still needed for individual RNAs or regions before such models are used to guide deeper functional and mechanistic studies. For longer RNAs, it is even more challenging to stitch together all the models derived from individual DGs. Our discovery of the gapm alignments helps resolve certain complex conformations by providing evidence for the coexistence of helices. However, ambiguities also exist in the determination of which fragment base-pairs with the other two or more fragments in the same alignment (Fig. 5C). In a recent study, we reported a new method using computationally enumerated ensembles of RNA conformations and Bayesian statistics to identify optimal ones that match experimentally determined constraints (Zhou et al. 2020). Further optimization and integration of these various methods has the potential to reveal global conformations for larger RNAs.

In summary, we have developed a new computational pipeline to automate the otherwise laborious tasks of reads mapping, classification, and clustering. In addition, we systematically benchmarked the performance of the pipeline and validated the newly discovered structures and interactions. We envision that the pipeline will find broad use in the field as crosslink-ligation-based methods are applied to a wide variety of RNA biology problems.

Methods

Data access and preprocessing (Fig. 1B, step 1)

All sequencing data used in this study were previously published and listed with NCBI (https://www.ncbi.nlm.nih.gov/) accession numbers as follows: PARIS: GSE74353 HEK and mES and GSE149493 HEK (Lu et al. 2016; Zhang et al. 2021); LIGR: SRR3361013 HEK (Sharma et al. 2016); SPLASH_GMA: SRR3404937, GM12892, polyA. SPLASH_GMT SRR3404942, GM12892 total; SPLASH_ESA: hES (Aw et al. 2016); COMRADES: ZIKV (Ziv et al. 2018); hiCLIP: all data (Sugimoto et al. 2015). Sequencing data from these published crosslink-ligation methods were processed according to the original designs in each study. Briefly, 5′ and 3′ end adapter sequences were removed. Duplicates were removed based on the randomized universal molecular indices.

Optimized STAR mapping (Fig. 1B, step 2)

The default and optimized formulae for calculating alignment scores are as follows: the major changes are the deletion (deletion), gapopen (gap open), gapext (gap extension), and chimeric junction penalties

$$\mathrm{scor}{\mathrm{e}}_{\mathrm{default}}=\mathrm{matches}+\mathrm{mis}+\mathrm{ins}+\mathrm{del}+\mathrm{gapopen}+\mathrm{gapext}+\mathrm{chim}.$$

$$\mathrm{scor}{\mathrm{e}}_{\mathrm{optimized}}=\mathrm{matches}+\mathrm{mis}+\mathrm{ins}+\mathrm{gapext}.$$

Explanations are as follows: Matches – length of matched sequences (+1 for each nt); mis – length of mismatched sequences (−1 for each nt). Both matches and mismatches are represented by “M” in the CIGAR string in SAM, in which the mismatches are further identified in the “MD:Z:?” tag. del: deletion penalty (−2 for deletion opening, −2 for each nt extension in the default setting). del was disabled by alignIntronMin = 1 after optimization, so that all deletions and gaps are considered equal. In other words, deletions are treated like splicing junctions to facilitate the calculation of penalty. ins: insertion penalty (−2 for insertion opening and −2 for each nt insertion extention, not changed in optimization). gapopen: gap open penalty (scoreGapNoncan = −8, scoreGapGCAG = −4, scoreGapATAC = −8). gapopen was disabled after optimization because the gaps are not due to splicing. gapext: gap extension penalty, scoreGenomicLengthLog2scale × log2(genomicLength), changed after optimization. The higher penalty reduces low-confidence mapped segments. In normal gapped alignments, genomicLength = L1 + L2 + … + Li, where L is the length of each segment. In chimeric alignments, genomicLength = L1 × L2 × … × Li. This difference results in significantly higher penalty for chimeric alignments. chim: penalty for nonchimeric alignment (chimScoreJunctionNonGTAG = −1).

In the final output where all alignments are in the Aligned.out.sam, the counts are defined as follows: primary = unique + chimeric (primary only) + multimapped (excluding ones mapped to too many loci). Here, primary alignments can be extracted and counted using samtools view -F 0 × 900 (Li et al. 2009). An example optimized setting for STAR (Dobin et al. 2013) mapping of noncontinuous reads are as follows: ‐‐runThreadN 1 (set based on resources) ‐‐genomeLoad NoSharedMemory (set based on resources) ‐‐outReadsUnmapped Fastx ‐‐outFilterMultimapNmax 10 ‐‐outFilterScoreMinOverLread 0 ‐‐outFilterMatchNminOverLread 0 ‐‐outSAMattributes All ‐‐outSAMtype BAM Unsorted SortedByCoordinate ‐‐alignIntronMin 1 ‐‐scoreGap 0 ‐‐scoreGapNoncan 0 ‐‐scoreGapGCAG 0 ‐‐scoreGapATAC 0 ‐‐scoreGenomicLengthLog2scale −1 ‐‐chimFilter None ‐‐chimOutType WithinBAM HardClip ‐‐chimSegmentMin 5 ‐‐chimJunctionOverhangMin 5 ‐‐chimScoreJunctionNonGTAG 0 ‐‐chimScoreDropMax 80 ‐‐chimNonchimScoreDropMin 20.

Rearrangement of softclipped continuous alignments for second round STAR mapping (Fig. 1B, step 3)

Mapping score calculation is biased against backward arranged chimeric reads (type 4 in Fig. 3A), which are generated from proximity ligation on the distal ends. To discover these alignments more efficiently, the softclipped continuous alignments (with “S” operator in CIGAR) are rearranged so that the positions of the two segments (arms) switched. The output FASTQ file is subject to a second round STAR mapping using the optimized parameters listed above (see Supplemental Fig. S1 for details).

Filtering, classification, and rearrangement of alignments (Fig. 1B, step 4).

The filtering and classification methods are implemented in two scripts, gaptypes.py and gapfilter.py. In gaptypes.py, STAR alignments are filtered to remove low-confidence segments and rearranged and classified into six distinct categories. These six different group alignments were: continous alignments (cont.sam), noncontinuous alignments with 1 gap (gap1.sam), noncontinuous alignments with multiple gaps (gapm.sam), noncontinuous alignments with the two arms on different strands or chromosomes (trans.sam), noncontinuous alignments with the two arms overlapping each other (homo.sam), and noncontinuous alignments with complex combinations of indels and gaps (bad.sam). In particular, the fields FLAG, START, SEQ, and QUAL are adjusted after arrangement, whereas the optional tag fields are left unchanged, except that the ch:A and SA:Z fields that indicate chimeric alignments are removed. See Supplemental Materials for details of the methods.

Analysis of segment and gap properties (Fig. 1B, step 5)

After mapping and classification, the segment and gap properties are analyzed as a quality control for the data. Specifically, for alignments in SAM format, the gap length and segment lengths are summarized and plotted as cumulative densities. At the same time, all sequences in the gap region are summarized to count nucleotide frequencies.

Removing short and spliced gaps (Fig. 1B, step 6)

In eukaryotes, splicing generates noncontinuous reads and alignments, and they need to be separated from the ones generated by proximity ligation. We used the annotated splicing junctions to filter the sequencing data as follows: in gap1.sam and gapm .sam, if an alignment only has gaps that are identical to splicing junctions (upper panel), it is removed. If an alignment has at least one gap that is not the same as the splicing junction (lower panel), it is retained. At the same time, all gaps ≤2 nt are also removed, because these are highly likely to be artifacts caused by crosslinking-induced RNA damage.

Duplex group assembly (Fig. 1B, step 7)

Filtered gap1filter.sam and transfilter.sam alignments are combined as the input. Additional input files are gene annotations in BED format, where only the first six fields are needed, and genome files that list sizes of chromosomes. Alignments are assigned to gene pairs based on genome coordinates. If one alignment is contained within one gene (e.g., gene1), then the pair is (gene1, gene1). If the alignment spans gene1 and gene2, then it is mapped to the pair (gene1, gene2). Alignments mapped to each gene pair are processed separately in parallel to speed up the analysis. Regions with alignments higher than a predefined value are subsampled to speed up the processing, and the unused alignments are added back to the assembled DGs. BEDTools is used to produce a genome coverage file from all the two-segment noncontinuous alignments (gap1filter.sam and transfilter.sam). The coverage file is then used to calculate the confidence of each DG. See Supplemental Materials for details about the algorithm.

Assembly of trisegment groups (Fig. 1B, step 8)

Alignments with more than two gaps or three segments are ignored for now due to their extremely low abundance. The DGs were produced by CRSSANT using gap1.sam and trans.sam alignments. The boundaries for each arm are the medians for the DGs. For the TGs, the merged middle arm is redefined as boundaries of both DGs. Alignments from gapm.sam are then matched to the TGs so that each arm is overlapped.

Specifically, the gapm alignments (mapped to hg38/mm10 primary genome assemblies) were globally annotated using gapm_anno.py script. To study the RNA:RNA:RNA structures and intermolecular interactions from PARIS data, the reads were mapped to selected subsets of RNAs, including snRNAs (U1, U2, U4, U6, U5, U11, U12, U4atac, and U6atac), highly abundant snoRNAs (U3, U8, U13, and U35), and rRNAs. These selected RNAs were assembled into one small “chromosome.” After mapping, alignments classification, and short gap filtering, gap1 alignment was used to call the RNA:RNA duplex.

The majority of the human and mice genomes is duplicated sequence, such as repetitive DNA and genes with multiple copies. This makes unambiguous identification of RNA:RNA:RNA interactions very difficult on a genomic scale. To identify the RNA-RNA-RNA structures and interactions from PARIS data, the reads were mapped to selected subsets of RNAs, including snRNAs (U1, U2, U4, U6, U5, U11, U12, U4atac, and U6atac), highly abundant snoRNAs (U3, U8, U13, and U35), and rRNAs. These selected RNAs were assembled to one small “chromosome.” After mapping using the STAR program, alignments were classified into six groups. Filtered gap1 alignments (gap length > 2 nt) were used to call DGs. The assembled gap1 DGs were further used to cluster gapm alignments. The curated DGs were used for TGs assembly for gapm alignments. U8:U13:28S intermolecular interactions were analyzed using PARIS1 mES data (GEO: GSM1917758, GSM1917759, and GSM1917760) (Zhang et al. 2021).

RNA homodimer analysis (homo.sam, Fig. 6, step 9)

To ensure the identification of RNA homodimers using STAR mapping and gaptypes.py classification, the RNAs of interest must be flanked by additional non-N sequences. This condition is satisfied when the RNA is located in the middle of long sequence, or as a standalone mini-chromosome (i.e., the RNA itself), where additional sequences are padded to the 5′ or 3′ ends. For example, for RNAs with multiple gene copies in the genome, a single copy is taken out and padded with 100 “As” on each side. Alternatively, the chimFilter option should be set as None to disable the filtering. To cluster homo.sam alignments, crssant.py is applied in the same way as for gap1/trans alignments.

Homo alignments (homo.sam) with <2 nt overlapping between two arms were filtered out to avoid potential artifacts. The distance between two arms was calculated,

$$\mathrm{overlap}=min\left(\mathrm{arm}1\mathrm{\_}\mathrm{end},\mathrm{arm}2\mathrm{\_}\mathrm{end}\right)-\max \left(\mathrm{arm}1\mathrm{\_}\mathrm{start},\mathrm{arm}2\mathrm{\_}\mathrm{start}\right).$$

To understand the relationship between RNA homodimers and RNA stem–loop structures, RNA stem–loops were identified using local gap1 alignments. The length of two arms should be >15 nt and the loop length (gap length) should be <20 nt.

Bowtie 2 mapping of alignments and subsequent processing

To compare the STAR and Bowtie 2 mapping protocols, we designed the following general pipeline to map reads using Bowtie 2 and process the alignments. First, the reads were mapped using two sets of published parameters (Travis et al. 2014; Sharma et al. 2016). The alignments were converted to chimeric format using bowtie2chim.py, a custom script to rearrange chimeric alignments. The rearranged alignments were filtered using gapfil terbt2.py to remove splicing events, and unique alignments with deletion (D in CIGAR) >2 are counted. Similar to the STAR mapped data, the gaptypes.py script was used here to classify the alignments.

A brief description of the Bowtie 2 parameters is as follows: D – seed extension attempts; R – reseeding attempts; N – max mismatches; L – seed length; k – max number of valid alignments to search; i – score-min: ma: match bonus; np – N penalty; mp – mismatch penalty; rdg – affine read gap penalty; rfg – affine reference gap penalty. For end-to-end mode, the minimum should be −0.6–0.6 × L, where L is the length of the read. For local mode, the minimum should be 20 + 8 × ln(L). The commonly used setup in Bowtie 2:

•   ‐‐very-fast-local Same as: -D 5 -R 1 -N 0 -L 25 -i S,1,2.00

•   ‐‐fast-local Same as: -D 10 -R 2 -N 0 -L 22 -i S,1,1.75

•   ‐‐sensitive-local Same as: -D 15 -R 2 -N 0 -L 20 -i S,1,0.75 (default in ‐‐local mode)

•   ‐‐very-sensitive-local Same as: -D 20 -R 3 -N 0 -L 20 -i S,1,0.50

The primary assembly of hg38 and combinations of the Rfam and annotated mRNAs were used to build the Bowtie 2 indices (Lu et al. 2016). The Bowtie 2 parameters from the hyb package are as follows (Travis et al. 2014): bowtie2 -p 20 -D 20 -R 3 -N 0 -L 16 -k 20 ‐‐local -i S,1,0.50 ‐‐score-min L,18,0 ‐‐ma 1 ‐‐np 0 ‐‐mp 2,2 ‐‐rdg 5,1 ‐‐rfg 5,1 -x hg38pri -U xxx.fastq -S xxx.sam. The Bowtie 2 parameters from the Aligater package are as follows (Sharma et al. 2016): bowtie2 -p 20 -k 50 -R 3 -N 0 -L 16 -i S,1,0.50 ‐‐local -x hg38pri -U xxx.fastq -S xxx.sam. Default for the other parameters are as follows: -D 15 -score-min G,20,8 ‐‐ma 2 ‐‐np 1 ‐‐mp 6,2 ‐‐rdg 5,3 ‐‐rfg 5,3. The rdg and rfg setting in the default is much stronger.

Bowtie 2 does not produce supplemental alignments like STAR. It has one primary and multiple secondary alignments (“FLAG 256”). In the unsorted SAM output, the first is always the primary alignment. We developed the following strategy to combine the primary and secondary alignments (bowtie2 chim.py). If any of the secondary alignments can combine with the primary, with at most overlap (e.g., 2 nt) in the query, then we consider the pair as a chimera and modify the two alignments with tags “ch:A:1\tSA:Z:A”. If multiple loci for secondary alignments can be matched to the primary, keep one for simplicity. Only reads without linkers are considered to be comparable to a typical STAR run. The linkers can be easily removed before the STAR mapping step.

Simulation of gapped reads to benchmark optimized STAR alignment parameters

First, a region is extracted from the human genome, for example, the ACTB protein-coding gene. A simulated gapped read with two segments is randomly positioned across the selected region, where the gap length is randomly set within a range (e.g., between 1 and 100 nt), and the length of each segment is randomly set within a range (e.g., between 5 and 35 nt). In each read, at least one segment is set ≥20 nt to guarantee a unique match. The two segments are randomly assigned to be linked either on the proximal ends (forward gapped) or on the distal ends (backward gapped). The simulated reads are mapped to the entire human genome (hg38 primary assembly) using the four settings described above (Bowtie2_hyb, Bowtie2_Aligater, STAR_default, STAR_optimized). The alignments are then compared to the simulated positions to check the accuracy of mapping. The mapping is considered accurate if the start position and the gap length of an alignment are not more than 10 nt different from the simulated values (to account for ambiguities at the ends of each arm).

Simulation of DGs to benchmark CRSSANT

First, on an artificial chromosome of Chr 1: 0–1000, made of nucleotides “N” in one gene GENE1: 0–1000, pairs of core intervals of a specified length (corelen, e.g., 5, 10, or 15 nt) are selected, in the range of Chr 1: 100–900. The first 10 kb of hg38 Chr 1 happens to be a stretch of “N”, so the results can be viewed on hg38. The two intervals of each pair are at least a coregap away from each other (e.g., coregap = 50), and within a specific distance (e.g., corewithin = 1000, for Chr 1: 0–1000). Each side of the two cores are extended by a random length (e.g., in the range [5,15]) to make one alignment. Each pair of core intervals are expanded to a set number of alignments that make up one DG, and the number of alignments in each DG is randomly set in a specific range, for example, DGlower = 10, DGupper = 100. A set number of DGs are generated (e.g., 100), and overlap between DG cores are allowed for, at most, one arm, but not both. Pseudo random numbers were generated with seeds to ensure reproducibility. This script, dgsim.py, generates a simple set of alignments in DGs to test crssant.py.

CRSSANT analysis of rRNA structures from various crosslink-ligation methods

Watson-Crick base pairs and non-Watson-Crick interactions in the human ribosome cryo-EM model (PDB:4V6X) were extracted using DSSR (Lu et al. 2015a). The CRSSANT output DGs from 300,000 gap1 alignments on the rRNAs in each data set were used to generate the ROC curves. The structures in every 20-nt or 5-nt pairwise bin in 28S rRNA were identified and used as a gold standard to evaluate different crosslink-ligation data sets. For ROC analysis of the accuracy and specificity of secondary structures, the base pairs of each 20-nt pairwise bin were calculated. For ROC analysis of the accuracy and specificity of spatial proximity, the true-positive pairwise 5-nt bin was defined by the average Euclidean distance of the pairs being within 25 Å (roughly the width of an RNA duplex) of cryo-EM 28S rRNA structure. The missing expansion segments in cryo-EM model were excluded for the ROC analysis. Because COMRADES was performed on virus-infected cells and viral RNAs were enriched, fewer reads were mapped to the human genome. The 300,000 hs45S alignments from COMRADES data were gathered from all samples. For other data sets, the 300,000 reads were randomly chosen. DGs were assembled from the merged file of five different data sets and then later split, so that the DGs can be directly compared among the samples.

Analysis of correlation between DG and TG (Fig. 5)

To determine whether TGs correlate with the DGs that support them, human HEK293 cell PARIS data gapm alignments (with two gaps, or three segments) were randomly shuffled across the 28S rRNA while maintaining the organization of alignment (i.e., gap lengths were not changed). TGs were assembled from the original gapm alignments or the shuffled alignments. Pearson's correlation was calculated between the numbers of alignments in each TG and the geometric mean of the numbers of alignments in each pair of DGs that support the TG ((DG1_coverage × DG2_coverage)^0.5). Genomic coverages of alignments for the DGs, original TGs, and shuffled TGs were plotted in the Integrative Genomics Viewer (IGV, v2.8.13) (Robinson et al. 2011).

Experimental validation of U8 homodimer

HEK293 cells were crosslinked with 0.5 mg/mL AMT, or non-crosslinked, and total RNA from each condition was collected for U8 enrichment using five biotinylated antisense oligos (GGATTATCCCACCTGACGAT, CTCCGGAGGAGGAACAGGTA, CTCCAATCATCATGTTCTAA, GTTAATCACGTTTCATGCAT, and CAGGGTGTTGCAAGTCCTGA), designed using the published ChIRP method (Chu et al. 2012). The enriched target RNAs were treated with the mRNA decapping enzyme (NEB #M0608S). Ends of the enriched RNA were then ligated via proximity ligation by Mth RNA Ligase (NEB #M2611), followed by reverse crosslinking and adapter ligation (Zhang et al. 2021). cDNA was synthesized using a primer complementary to the adapter. PCR was performed using primer sets: F, GGACTTGCAACACCCTGATT; R, CGGAGGAGGAACAGGTAAGG. The positive PCR products from U8-U8 homodimer should be 72 bp.

RNA secondary structure modeling and visualization

In general, base-pairing was predicated using ViennaRNA Package (v 2.1.9) (Lorenz et al. 2011). DGs and TGs alignments were visualized by IGV. The curated seed alignments were turned into a WebLogo (https://weblogo.berkeley.edu/logo.cgi). Each arm of gapm and homo alignments were mapped to human 28S rRNA cryo-EM structure (PDB ID: 4V6X), U1 snRNP cryo-EM structure (PDB ID: 3CW1), and U2/U5/U6 snRNP cryo-EM structure (PDB ID: 7ABI).

Software availability

Source code for the software developed in this study is available from GitHub (https://github.com/zhipenglu/CRSSANT) and in Supplemental Code. Source data for the figures, including assembled DGs, TGs, and potential RNA homodimers from published crosslink-ligation data are also available in GitHub, as well as Supplemental Data.

Competing interest statement

The authors declare no competing interests.