Abstract
The rapid development of single-cell DNA sequencing (scDNA-seq) technology has greatly enhanced the resolution of tumor cell profiling, providing an unprecedented perspective in characterizing intra-tumoral heterogeneity and understanding tumor progression and metastasis. However, prominent algorithms for constructing tumor phylogeny based on scDNA-seq data usually only take single nucleotide variations (SNVs) as markers, failing to consider the effect caused by copy number alterations (CNAs). Here, we propose BiTSC , Bayesian inference of Tumor clonal Tree by joint analysis of Single-Cell SNV and CNA data. BiTSC
, Bayesian inference of Tumor clonal Tree by joint analysis of Single-Cell SNV and CNA data. BiTSC takes raw reads from scDNA-seq as input, accounts for the overlapping of CNA and SNV, models allelic dropout rate, sequencing errors and missing rate, as well as assigns single cells into subclones. By applying Markov Chain Monte Carlo sampling, BiTSC
takes raw reads from scDNA-seq as input, accounts for the overlapping of CNA and SNV, models allelic dropout rate, sequencing errors and missing rate, as well as assigns single cells into subclones. By applying Markov Chain Monte Carlo sampling, BiTSC can simultaneously estimate the subclonal scCNA and scSNV genotype matrices, subclonal assignments and tumor subclonal evolutionary tree. In comparison with existing methods on synthetic and real tumor data, BiTSC
can simultaneously estimate the subclonal scCNA and scSNV genotype matrices, subclonal assignments and tumor subclonal evolutionary tree. In comparison with existing methods on synthetic and real tumor data, BiTSC shows high accuracy in genotype recovery, subclonal assignment and tree reconstruction. BiTSC
shows high accuracy in genotype recovery, subclonal assignment and tree reconstruction. BiTSC also performs robustly in dealing with scDNA-seq data with low sequencing depth and variant missing rate. BiTSC
also performs robustly in dealing with scDNA-seq data with low sequencing depth and variant missing rate. BiTSC software is available at https://github.com/ucasdp/BiTSC2.
software is available at https://github.com/ucasdp/BiTSC2.
Keywords: single-cell DNA sequencing, intra-tumor heterogeneity, single nucleotide variation, copy number alteration, Bayesian modeling, cancer evolution
Introduction
The rapid development of single-cell DNA sequencing (scDNA-seq) technology has provided a refined perspective for unveiling the evolutionary mechanisms underlying cancer progression and characterizing intra-tumor heterogeneity (ITH) [1, 2]. Although promising, the major single-cell whole-genome amplification methods, e.g. DOP-PCR, MDA and MALBAC, still encounter various technical bottlenecks. These limitations will result in a high incidence of errors, such as missing bases, false positives or false negatives in the sequenced single-cell DNA, which poses additional challenges for the downstream ITH inferences [3].
Early single-cell studies utilize information from single-cell single nucleotide variant (scSNV) or single-cell copy number alteration (scCNA) to infer tumor evolution with classic phylogenetic methods [4–7]. In recent years, many computational methods have emerged for inferring the evolutionary histories of tumors from single-cell data. CHISEL [8], SCICoNE [9] and MEDALT [10] are the few methods that perform scCNA detection and also infer evolutionary histories. RobustClone [11] is a model free method that takes raw scSNV or scCNA genotype matrix as input to recover clone genotypes and infer tumor clone tree. BEAM is a Bayesian evolution-aware method based on scSNV data, which improves the quality of single-cell sequences by using the intrinsic evolutionary information under a classic molecular phylogenetic framework [12]. Many other methods based on scSNV data build maximum likelihood or Bayesian-based models to account for sequencing noise as well as reconstruct tumor clone/cell tree. SCITE [13], OncoNEM [14], SCI [15], CellPhy [16] make infinite site assumption in their models, that is, mutation may only occur once at any locus and only binary genotypes are allowed in scSNV sites. SiFit [17] and SiCloneFit [18] construct their models under the finite site assumption, which allows mutations to happen more than once at any locus.
[15], CellPhy [16] make infinite site assumption in their models, that is, mutation may only occur once at any locus and only binary genotypes are allowed in scSNV sites. SiFit [17] and SiCloneFit [18] construct their models under the finite site assumption, which allows mutations to happen more than once at any locus.
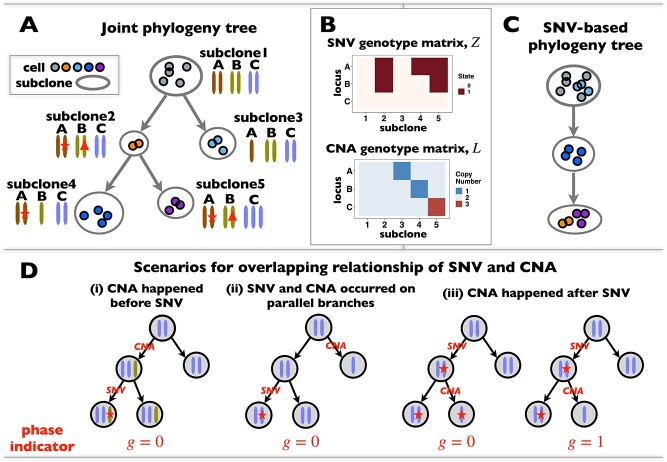
These single-cell based methods can only take into account one source of information, either from scSNV or scCNA. In fact, these two types of markers all play important role in tumor generation, progression and metastasis, and they constitute crucial traits in characterizing tumor heterogeneity [19]. Evolutionary inference with only one type of markers may lead to biased estimate. For example, suppose there is a true evolutionary process as shown in Figure 1A. The tumor tree 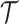 has five subclones, where the root node subclone1 is comprised of normal cells only, and the other nodes are cancerous subclones caused by point mutations and/or CNAs on three loci A, B and C. The SNV and CNA genotypes of these subclones are shown in Figure 1B. The two SNVs occur at loci A and B give rise to subclone2. The loss of the mutant copy on locus B further generates subclone4 based on the genotype of subclone2. If one infers the tumor clone tree with only SNV data
has five subclones, where the root node subclone1 is comprised of normal cells only, and the other nodes are cancerous subclones caused by point mutations and/or CNAs on three loci A, B and C. The SNV and CNA genotypes of these subclones are shown in Figure 1B. The two SNVs occur at loci A and B give rise to subclone2. The loss of the mutant copy on locus B further generates subclone4 based on the genotype of subclone2. If one infers the tumor clone tree with only SNV data 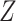 , one will most probably recover a linear evolutionary history as in Figure 1C. However, this is biased as it misses the identification of the two extra subclones (3 and 5), which respectively generated by a copy loss at locus A and a copy gain at locus C. Also, ignoring the CNA-driven loss of SNV at locus B in subclone4 may lead to misplacement of cells in subclone4 as the ancestor of cells in subclone2 and 5 on the SNV-based clone tree (Figure 1C). In such case, the full history can only be resolved by taking into account of information from both SNV (
, one will most probably recover a linear evolutionary history as in Figure 1C. However, this is biased as it misses the identification of the two extra subclones (3 and 5), which respectively generated by a copy loss at locus A and a copy gain at locus C. Also, ignoring the CNA-driven loss of SNV at locus B in subclone4 may lead to misplacement of cells in subclone4 as the ancestor of cells in subclone2 and 5 on the SNV-based clone tree (Figure 1C). In such case, the full history can only be resolved by taking into account of information from both SNV (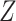 ) and CNA (
) and CNA (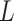 ).
).
Figure 1.
ScDNA-seq data display tumor heterogeneity. (A) Joint tumor phylogeny tree by SNV and CNA, where the gray node represents normal cells and the other nodes are cancerous cells. The letters A, B, and C are mutation loci. The bars under each letter represent alleles, and the bars with red stars and triangles are mutated. (B) The SNV genotype matrix,  , and the CNA genotype matrix,
, and the CNA genotype matrix,  , where rows represent loci and columns are subclones. (C) The phylogeny tree generally obtained by SNV-based algorithms. (D) Three possible scenarios for the overlapping relationship of SNV and CNA along the tree.
, where rows represent loci and columns are subclones. (C) The phylogeny tree generally obtained by SNV-based algorithms. (D) Three possible scenarios for the overlapping relationship of SNV and CNA along the tree.
In fact, joint analysis of SNV and CNA in characterizing ITH is common with bulk sequencing. PyClone [20] applies Bayesian clustering to identify tumor clones/subclones based on SNVs and clonal CNAs (CNAs carried by all cancer cells). It provides insights to temporal ordering of mutations and subclones, but does not make inference to the tree structure. PhyloWGS [21] also employs a Bayesian framework with a tree structured stick breaking process as prior, which infers subclone cluster as well as the tree relationship of the subclones. Canopy [22] is a Markov Chain Monte Carlo (MCMC) algorithm for tumor evolution history inference, which accounts for both point mutations and raw copy number (CN) information. Recently, [23] proposed a unified Bayesian feature allocation model, SIFA, on raw bulk sequencing reads. It provides a generating model that incorporates SNV and CNA to infer tumor phylogenetic tree.
To the best of our knowledge, the only method for tumor tree inference from scDNA-seq data that integrates SNV and CNA information is SCARLET [24]. SCARLET optimizes for a loss-supported phylogeny. It inputs a copy number tree constructed with existing methods and then refines such tree by resolving the multifurcations using point mutation profiles of the observed cells [24].
In this study, we propose Bayesian inference of Tumor clone Tree by joint analysis of Single-Cell SNV and CNA, termed BiTSC . It is the first method that fully models SNV and CNA states from raw reads of scDNA-seq data. It generalizes the SIFA model to account for the overlapping of CNA and SNV states comprehensively, and models allelic dropout (ADO) rate, missing rate and sequencing errors in scDNA-seq data. BiTSC
. It is the first method that fully models SNV and CNA states from raw reads of scDNA-seq data. It generalizes the SIFA model to account for the overlapping of CNA and SNV states comprehensively, and models allelic dropout (ADO) rate, missing rate and sequencing errors in scDNA-seq data. BiTSC takes the observed total reads and mutant reads at multiple loci in single cells as input and assigns cells to subclones. By applying MCMC sampling, BiTSC
takes the observed total reads and mutant reads at multiple loci in single cells as input and assigns cells to subclones. By applying MCMC sampling, BiTSC can simultaneously estimate the subclonal CNA and SNV genotypes, the overlapping relationship of CNA and SNV, the subclonal assignments of cells and the tumor evolutionary tree. In comparison with existing methods on synthetic and real tumor data, BiTSC
can simultaneously estimate the subclonal CNA and SNV genotypes, the overlapping relationship of CNA and SNV, the subclonal assignments of cells and the tumor evolutionary tree. In comparison with existing methods on synthetic and real tumor data, BiTSC shows high accuracy in genotype recovery, subclonal assignment and clone tree reconstruction. It is worth noting that BiTSC
shows high accuracy in genotype recovery, subclonal assignment and clone tree reconstruction. It is worth noting that BiTSC is also robust in dealing with scDNA-seq data with low sequencing depth.
is also robust in dealing with scDNA-seq data with low sequencing depth.
Methods
Overview of BiTSC
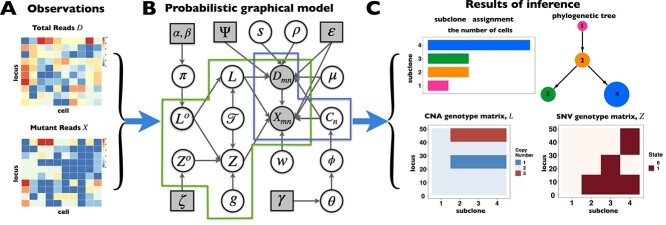
We give a brief introduction to BiTSC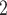 in this section, the general flowchart is shown in Figure 2. The definitions of all parameters in Figure 2B and examples of main parameters in Figure 1A can refer to Table S1, and the more model details can be found in following subsection and in supplementary notes.
in this section, the general flowchart is shown in Figure 2. The definitions of all parameters in Figure 2B and examples of main parameters in Figure 1A can refer to Table S1, and the more model details can be found in following subsection and in supplementary notes.
Figure 2.
Overview of the computational framework of BiTSC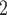 that identifies subclones, recovers subclonal genotypes of CNA and SNV, as well as reconstructs subclonal evolutionary trees using tumor scDNA-seq read count data. (A)The input of the algorithm, total reads matrix
that identifies subclones, recovers subclonal genotypes of CNA and SNV, as well as reconstructs subclonal evolutionary trees using tumor scDNA-seq read count data. (A)The input of the algorithm, total reads matrix 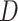 and mutant reads matrix
and mutant reads matrix 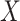 . (B) The probabilistic graphical model shows the dependency among parameters, where the shade nodes stand for observed or fixed values, the unshaded nodes represent the latent parameters. (C) The inference output of the algorithm, mainly containing subclone assignment (
. (B) The probabilistic graphical model shows the dependency among parameters, where the shade nodes stand for observed or fixed values, the unshaded nodes represent the latent parameters. (C) The inference output of the algorithm, mainly containing subclone assignment (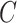 ), subclonal phylogenetic tree (
), subclonal phylogenetic tree (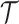 ), genotype matrix of CNA (
), genotype matrix of CNA (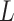 ) and SNV (
) and SNV (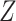 ), phase indicator
), phase indicator 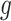 and other parameters, such as missing rate (
and other parameters, such as missing rate (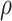 ), ADO rate (
), ADO rate (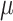 ) and so on.
) and so on.
BiTSC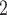 is a Bayesian model, which takes input of raw total and mutant read counts matrices
is a Bayesian model, which takes input of raw total and mutant read counts matrices 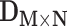 and
and 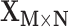 measured at
measured at 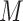 loci of
loci of 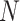 cells (Figure 2A). Due to the sharing of genetic information among homogeneous cells, we assume that there are
cells (Figure 2A). Due to the sharing of genetic information among homogeneous cells, we assume that there are 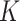 latent subclones in the cells drawn for sequencing (
latent subclones in the cells drawn for sequencing (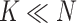 ). Here, we define subclone as a group of cells with identical genotypes and distinct subclones differ in SNV or CNA markers on at least one of the
). Here, we define subclone as a group of cells with identical genotypes and distinct subclones differ in SNV or CNA markers on at least one of the 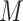 measured loci. We further assume the latent states follow a categorical distribution with parameter
measured loci. We further assume the latent states follow a categorical distribution with parameter 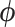 representing the prevalence of subclones and denote the state of cell
representing the prevalence of subclones and denote the state of cell 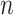 by
by 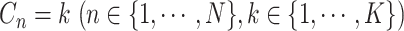 (the blue box in Figure 2B). BiTSC
(the blue box in Figure 2B). BiTSC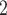 employs a tree coupled generating model to generate the raw total and mutant read count matrices, where the point mutation profiles
employs a tree coupled generating model to generate the raw total and mutant read count matrices, where the point mutation profiles 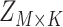 and the CN profiles
and the CN profiles 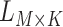 of subclones are jointly modeled, with their context and relationships coupled by the clone tree
of subclones are jointly modeled, with their context and relationships coupled by the clone tree 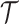 (the green box in Figure 2B).
(the green box in Figure 2B).
We consider three possible scenarios for the overlapping relationship of SNV and CNA along the tree: (i) CNA event happens before SNV on the same lineage; (ii) CNA and SNV occur in the same genomic region but on separate branches of the tree, thus affecting distinct clones; (iii) SNV happens before CNA on the same lineage (Figure 1D). For the first two scenarios, the overlapping of SNV and CNA does not affect the number of mutant alleles. For scenario (iii), we introduce an phase indication vector 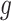 of length
of length 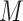 (the green box in Figure 2B), where
(the green box in Figure 2B), where 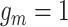 indicates CNA happened on the mutant allele at locus
indicates CNA happened on the mutant allele at locus 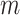 , thus affecting the number of mutant copy, and
, thus affecting the number of mutant copy, and 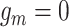 otherwise (Figure 1D). For example, in the toy model in Figure 1A, the phase indicator for locus B is
otherwise (Figure 1D). For example, in the toy model in Figure 1A, the phase indicator for locus B is 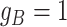 , since the copy loss on this locus occurs on mutant allele, which gives rise to subclone4. For locus A, the SNV arises in subclone2, which is parallel to the CNA occurring in subclone3. In such case, CNA does not affect the number of the mutant copy, thus
, since the copy loss on this locus occurs on mutant allele, which gives rise to subclone4. For locus A, the SNV arises in subclone2, which is parallel to the CNA occurring in subclone3. In such case, CNA does not affect the number of the mutant copy, thus 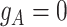 . For locus C, as there is only a CNA event, so
. For locus C, as there is only a CNA event, so 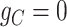 . Then the phase indicator
. Then the phase indicator 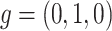 for the toy model in Figure 1A (Table S1).
for the toy model in Figure 1A (Table S1).
In addition, as single-cell sequencing data is prone to high technical errors, our model also accounts for sequencing error rate (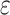 ), missing rate (
), missing rate (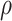 ) and ADO rate
) and ADO rate 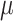 (Figure 2B).
(Figure 2B).
The ultimate goal of BiTSC is to infer the subclone prevalence
is to infer the subclone prevalence 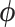 , the subclone assignment of cells
, the subclone assignment of cells 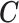 (a vector of length
(a vector of length 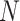 ), the SNV and CNA genotypes of subclones
), the SNV and CNA genotypes of subclones 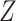 and
and 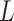 , the subclone tree
, the subclone tree 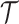 , the missing rate
, the missing rate 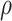 and also ADO rate
and also ADO rate 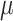 (Figure 2C). By assigning priors to
(Figure 2C). By assigning priors to 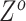 ,
, 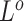 ,
, 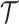 ,
, 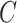 ,
, 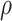 ,
, 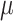 ,
, 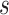 and
and 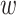 (the dispersion parameters for generating total reads
(the dispersion parameters for generating total reads 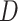 and mutant reads
and mutant reads 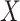 ), and given read depths of the sequencing cells
), and given read depths of the sequencing cells 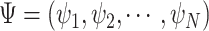 , and a sequencing error rate
, and a sequencing error rate 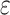 , these can be estimated from a posterior distribution
, these can be estimated from a posterior distribution 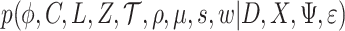 , which corresponds to
, which corresponds to 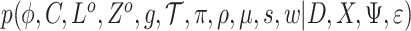 (Figure 2, see below and supplementary notes for details).
(Figure 2, see below and supplementary notes for details).
Tree coupled generating model of genotypes
The subclone genotypes 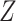 and
and 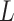 are generated according to the SNV and CNA origin matrices
are generated according to the SNV and CNA origin matrices 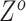 ,
, 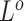 and the clone tree
and the clone tree 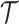 as well as phase indicator
as well as phase indicator 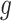 (the green box in the Figure 2B). By assuming a total of
(the green box in the Figure 2B). By assuming a total of 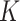 subclones on the tree,
subclones on the tree, 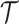 is represented by a length-
is represented by a length-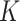 vector, where
vector, where 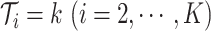 indicates the parent of subclone
indicates the parent of subclone 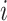 is
is 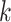 . We fix subclone
. We fix subclone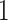 to normal cell and place it at the root of the tree (
to normal cell and place it at the root of the tree (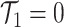 ). We assign a uniform prior to all possible trees with
). We assign a uniform prior to all possible trees with 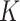 nodes.
nodes.
As the first model for joint analysis of CNA and SNV states from the raw reads of scDNA-seq data, considering the complexity of the model, BiTSC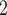 assumes CNA and SNV mutations arise independently. And each mutation (including SNV and CNA) originates only once in a specific subclone besides normal subclone. In general, the mutation will be inherited by all descendant subclones after its origination, with the exception that the mutant allele is affected by subsequent overlapping CNA (with phase indicator
assumes CNA and SNV mutations arise independently. And each mutation (including SNV and CNA) originates only once in a specific subclone besides normal subclone. In general, the mutation will be inherited by all descendant subclones after its origination, with the exception that the mutant allele is affected by subsequent overlapping CNA (with phase indicator 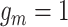 ), resulting in the increase or loss of such mutation at the locus. We use
), resulting in the increase or loss of such mutation at the locus. We use 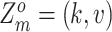 and
and 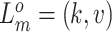 to represent the originations of SNV and CNA changes at locus
to represent the originations of SNV and CNA changes at locus 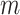 , that is,
, that is, 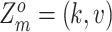 indicates mutation at locus
indicates mutation at locus 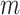 occurs from subclone
occurs from subclone 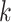 and gains
and gains 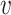 mutant copies, and
mutant copies, and 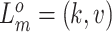 indicates the CNA arises in subclone
indicates the CNA arises in subclone 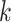 and gains (or losses if
and gains (or losses if 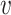 is negative)
is negative) 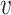 normal or mutant copies.
normal or mutant copies.
For SNV state, we take the prior of 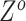 as
as 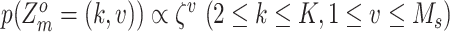 , where
, where 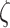 is the somatic point mutation rate and is predetermined within range of
is the somatic point mutation rate and is predetermined within range of 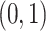 ,
, 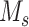 represents the maximum number of possible mutant copies [23]. In this study, we restrict
represents the maximum number of possible mutant copies [23]. In this study, we restrict 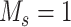 . However, such restriction may be relaxed if multiple mutations are allowed to hit one site. The specification of the mutation probability is independent of
. However, such restriction may be relaxed if multiple mutations are allowed to hit one site. The specification of the mutation probability is independent of 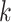 , which makes it equally likely for the SNV to originate from any subclones (besides the normal subclone).
, which makes it equally likely for the SNV to originate from any subclones (besides the normal subclone).
For CNAs, since they span genome intervals, if the genomic segmentation information is available, it will improve the inference of CNA status. There are many existing methods that can be applied to estimate the segment information, such as HMMcopy, copynumber, etc.[25, 26]. We thus model CNA status in segment level in a way similar to SIFA [23]. We sort the loci according to their chromosomal positions and divide the genome into 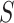 segments,
segments, 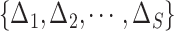 . If loci
. If loci 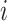 and
and 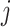 are located on the same segment, we assume they share the same CNA status. We let
are located on the same segment, we assume they share the same CNA status. We let 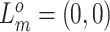 represent no CNA event at locus
represent no CNA event at locus 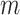 . For each genome segment,
. For each genome segment, 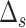 , we assign a prior probability
, we assign a prior probability 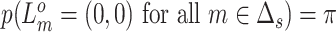 for no CNA, and uniform prior probabilities for other possible combinations of
for no CNA, and uniform prior probabilities for other possible combinations of 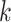 and
and 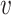 (e.g.,
(e.g., 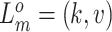 , for
, for 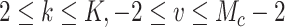 ), with
), with 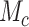 as the maximum possible number of total copies. The probability
as the maximum possible number of total copies. The probability 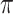 is further generated from a prior distribution
is further generated from a prior distribution 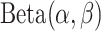 with given hyperparameters.
with given hyperparameters.
The independent origination of SNVs (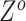 ) and CNAs (
) and CNAs (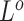 ) coupled with the structure of the
) coupled with the structure of the 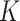 -node clone tree
-node clone tree 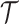 and phase indicator
and phase indicator 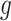 will derive the
will derive the 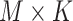 genotype matrices
genotype matrices 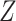 and
and 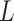 . The elements
. The elements 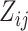 represent the number of mutant copies at the
represent the number of mutant copies at the 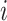 -th locus of the
-th locus of the 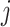 -th subclone, and
-th subclone, and 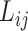 represent the total number of copies at the
represent the total number of copies at the 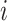 -th locus of the
-th locus of the 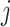 -th subclone. The CN matrix
-th subclone. The CN matrix 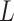 can be obtained according to
can be obtained according to 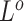 and
and 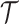 . The point mutation matrix
. The point mutation matrix 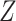 is determined by
is determined by 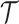 ,
, 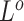 and
and 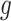 . For example, for locus B in Figure 1A, SNV and CNA with a copy loss arise in subclone2 and sublcone4 on the clone tree
. For example, for locus B in Figure 1A, SNV and CNA with a copy loss arise in subclone2 and sublcone4 on the clone tree 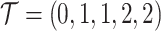 , respectively. Then
, respectively. Then 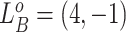 , thus the CNA genotypes on locue
, thus the CNA genotypes on locue  are
are 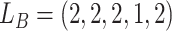 (Table S1). For SNV,
(Table S1). For SNV, 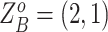 and the CNA occurs on the mutant allele, thus
and the CNA occurs on the mutant allele, thus 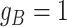 and
and 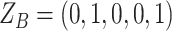 (Table S1).
(Table S1).
The optimal number of subclones 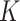 is selected based on a modified Bayesian Information Criterion (BIC, see Supplementary Note 4 for details).
is selected based on a modified Bayesian Information Criterion (BIC, see Supplementary Note 4 for details).
Zero-inflated modeling of single-cell sequencing reads
Next, we introduce the likelihood model of observing the total reads 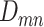 and the mutant reads
and the mutant reads 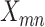 at locus
at locus 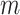 of cell
of cell 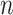 .
.
By given the latent subclone state 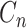 , e.g.
, e.g. 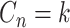 , the total reads
, the total reads 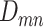 should be positively correlated with CN
should be positively correlated with CN 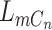 and the cell-specific diploid average coverage
and the cell-specific diploid average coverage 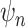 (which should be given a priori) for cell
(which should be given a priori) for cell 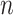 [23, 27, 28]. Here, we model the total reads by negative binomial distribution [29] as:
[23, 27, 28]. Here, we model the total reads by negative binomial distribution [29] as:
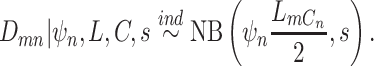 |
We parameterize the mean of negative binomial distribution to be 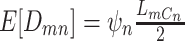 , which is equal to
, which is equal to 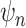 when the total CN of the single cell is
when the total CN of the single cell is 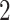 . The
. The 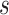 is the dispersion parameter that can control nonuniformity degree of coverage across the genome and that
is the dispersion parameter that can control nonuniformity degree of coverage across the genome and that 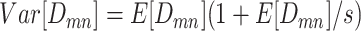 . The distribution reduces to Poisson as
. The distribution reduces to Poisson as 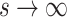 .
.
Since there often exist three major sources of noises in scDNA-seq, namely missing base, ADO or sequencing error, especially at low sequencing depth. We model them explicitly by introducing the zero-inflation parameter 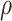 , the ADO rate
, the ADO rate 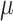 and the sequencing error rate
and the sequencing error rate 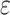 . For total reads
. For total reads 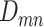 , we apply the zero-inflated negative binomial (ZINB) distribution, which introduces an additional probability
, we apply the zero-inflated negative binomial (ZINB) distribution, which introduces an additional probability 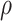 when no reads are observed (e.g.
when no reads are observed (e.g. 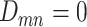 ), in order to control the amount of excessive zero reads due to missing [30]. Also, we model the false positives when all copies are lost, e.g.
), in order to control the amount of excessive zero reads due to missing [30]. Also, we model the false positives when all copies are lost, e.g. 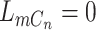 , by a small probability
, by a small probability 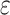 due to sequencing error. Moreover, the allelic amplification bias in scDNA-seq may result in random nonamplification of one allele, often referred as ADO [15]. To account for ADO events for each cell, we introduce the mixture probability with ADO rate
due to sequencing error. Moreover, the allelic amplification bias in scDNA-seq may result in random nonamplification of one allele, often referred as ADO [15]. To account for ADO events for each cell, we introduce the mixture probability with ADO rate 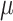 for the likelihood of the total reads. Finally, the ZINB likelihood of
for the likelihood of the total reads. Finally, the ZINB likelihood of 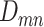 , which accounts for various sources of noises can thus be defined as in Eq. 1,
, which accounts for various sources of noises can thus be defined as in Eq. 1,
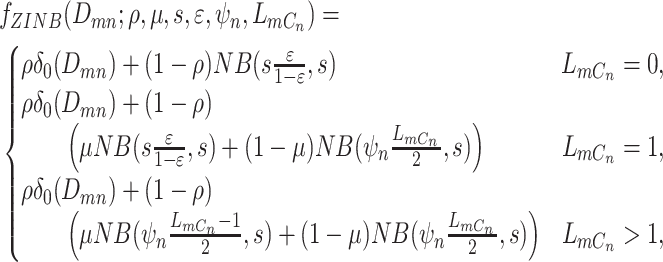 |
(1) |
where,
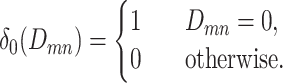 |
We then denote the expected probability of observing a mutant allele at locus 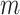 for cell
for cell 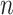 as
as 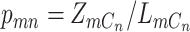 . We model the likelihood of observing
. We model the likelihood of observing 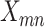 reads of the mutant allele by beta-binomial distribution [15] as:
reads of the mutant allele by beta-binomial distribution [15] as:
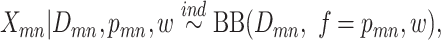 |
(2) |
where 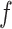 is the mean frequency of observing mutant reads and
is the mean frequency of observing mutant reads and 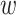 is the overdispersion term determining the shape of the distribution, which decreases with increasing variance [15].
is the overdispersion term determining the shape of the distribution, which decreases with increasing variance [15].
The integrated likelihood model of mutant reads 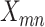 that also accounts for ADO rate
that also accounts for ADO rate 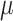 and sequencing error
and sequencing error 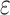 can be similarly defined as in Eq. 3. For modeling sequencing error in mutant counts, we assume that if mutation
can be similarly defined as in Eq. 3. For modeling sequencing error in mutant counts, we assume that if mutation 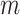 is absent in cell
is absent in cell 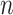 , i.e.
, i.e. 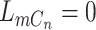 and/or
and/or 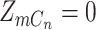 , the probability of observing a variant read corresponds to the per-nucleotide rate of sequencing error
, the probability of observing a variant read corresponds to the per-nucleotide rate of sequencing error 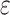 . If mutation
. If mutation 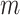 presents in cell
presents in cell 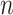 and
and 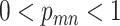 , the probability of sampling the mutant allele type
, the probability of sampling the mutant allele type 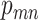 is corrected by sequencing errors in producing any of the other two bases [15]. If mutation
is corrected by sequencing errors in producing any of the other two bases [15]. If mutation 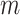 presents with
presents with 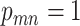 , that is,
, that is, 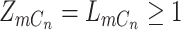 , there will also be a small probability
, there will also be a small probability 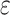 of sequencing error. In addition, ADO may happen when there is at least one copy present on the locus (
of sequencing error. In addition, ADO may happen when there is at least one copy present on the locus (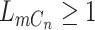 ). When ADO happens in the case of
). When ADO happens in the case of 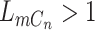 , there will be two possibilities, with probability
, there will be two possibilities, with probability 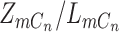 to drop the mutant allele or with probability
to drop the mutant allele or with probability 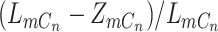 to drop the wild-type allele. The probability of sampling a mutant read will also vary according to the ADO events. We denote
to drop the wild-type allele. The probability of sampling a mutant read will also vary according to the ADO events. We denote 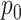 as the probability of sampling a mutant read without ADO events.
as the probability of sampling a mutant read without ADO events. 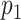 and
and 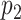 denote the probability of sampling a mutant read with an ADO event on the mutant allele and on the wild-type allele, respectively.
denote the probability of sampling a mutant read with an ADO event on the mutant allele and on the wild-type allele, respectively.
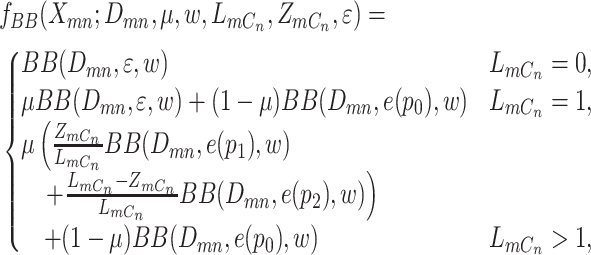 |
(3) |
where 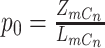 ,
, 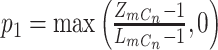 ,
, 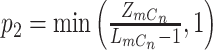 , and
, and
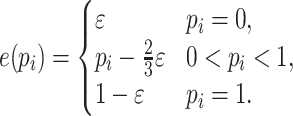 |
Inference
We apply the MCMC procedure to estimate the unknown parameters in BiTSC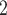 . The posteriors of the unknowns are sampled with differed strategies. Here we only briefly introduce our sampling procedures; the sampling details of each parameter can be found in Supplementary Note 1.
. The posteriors of the unknowns are sampled with differed strategies. Here we only briefly introduce our sampling procedures; the sampling details of each parameter can be found in Supplementary Note 1.
For genotype origin matrices 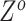 and
and 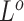 , we update one locus at a time by applying Gibbs sampler, where new states are sampled from the full conditional distribution. If the CNAs are in a segmented form, then at each step we will update all loci within the same segment. The hyper-parameter
, we update one locus at a time by applying Gibbs sampler, where new states are sampled from the full conditional distribution. If the CNAs are in a segmented form, then at each step we will update all loci within the same segment. The hyper-parameter 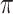 of
of 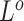 is also sampled by Gibbs sampler. Under scenarios where CNA happens after SNV at overlapping locus
is also sampled by Gibbs sampler. Under scenarios where CNA happens after SNV at overlapping locus 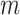 , we calculate the full conditional distribution by integrating over all possible values of phase indicator
, we calculate the full conditional distribution by integrating over all possible values of phase indicator 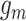 . That is with
. That is with 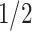 probability the subsequent CNA happens on the wild-type allele (
probability the subsequent CNA happens on the wild-type allele (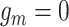 ) and with
) and with 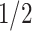 probability the CNA occurs on the mutant allele (
probability the CNA occurs on the mutant allele (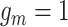 , see Supplementary Note 1 for details). After performing Gibbs sampling on
, see Supplementary Note 1 for details). After performing Gibbs sampling on  and
and 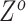 , we estimate each element of
, we estimate each element of 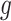 with the maximum probability at each locus.
with the maximum probability at each locus.
For the dispersion parameters 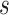 and
and 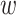 of the negative binomial distribution and beta-binomial distribution, we use Metropolis sampling with Gamma prior [31]. For missing rate
of the negative binomial distribution and beta-binomial distribution, we use Metropolis sampling with Gamma prior [31]. For missing rate 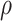 and ADO rate
and ADO rate 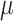 , since it is difficult to sample from its full conditional distribution, we adopt Metropolis sampling step with a uniform proposal of
, since it is difficult to sample from its full conditional distribution, we adopt Metropolis sampling step with a uniform proposal of 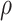 and
and 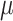 in the interval
in the interval 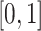 . We apply a mixed sampling strategy for
. We apply a mixed sampling strategy for 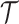 as in [23], where the tree is updated by randomly applying a Metropolis–Hastings sampler or a slice sampler.
as in [23], where the tree is updated by randomly applying a Metropolis–Hastings sampler or a slice sampler.
In sampling of the subclone prevalence, instead of updating the entire vector 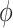 at once, we sample additional Gamma parameters
at once, we sample additional Gamma parameters 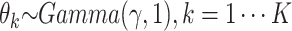 , one at a time. And let
, one at a time. And let 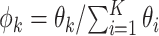 . This move is equivalent to sampling
. This move is equivalent to sampling 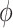 with prior
with prior 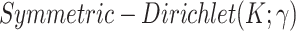 , and often leads to better mixing of the MCMC [23]. Each
, and often leads to better mixing of the MCMC [23]. Each 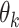 is updated by Metropolis–Hastings sampling with a Gamma proposal and an adaptive step size. Each element
is updated by Metropolis–Hastings sampling with a Gamma proposal and an adaptive step size. Each element 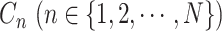 of
of 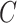 is taken from the Categorical distribution with parameter
is taken from the Categorical distribution with parameter 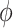 . We employ Gibbs sampling to update each
. We employ Gibbs sampling to update each 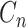 one by one.
one by one.
In order to avoid Markov Chain being trapped at some local optimum states, we adopt the parallel tempering technique, which runs multiple chains with different temperatures and exchanges samples between them [23, 32]. We use heuristic initialization for each parallel chain before MCMC sampling (Supplementary Note 2). The derivation of the fully conditional distribution for all model parameters can refer to Supplementary Note 3. The optimal number of subclones 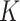 is selected by performing a modified BIC (Supplementary Note 4). We use the posterior mode for
is selected by performing a modified BIC (Supplementary Note 4). We use the posterior mode for 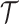 ,
, 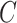 ,
, 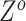 , and
, and 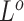 as the final estimates. We obtain the inference of
as the final estimates. We obtain the inference of 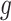 with the maximum probability at each locus, as well as
with the maximum probability at each locus, as well as 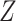 and
and 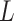 according to the final estimates of
according to the final estimates of 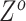 ,
, 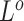 ,
, 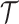 and
and 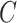 .
.
Benchmark BiTSC
Simulation data
To test the ability of BiTSC in identification of subclones that generated by only CNA changes, we simulated 10 datasets, denoted as G1. Figure S1 shows the ground truth of the datasets, which contains the phylogenetic tree and subclonal genotype matrices of CNA and SNV. We also simulated another 10 datasets, named G2, to assess the accuracy of BiTSC
in identification of subclones that generated by only CNA changes, we simulated 10 datasets, denoted as G1. Figure S1 shows the ground truth of the datasets, which contains the phylogenetic tree and subclonal genotype matrices of CNA and SNV. We also simulated another 10 datasets, named G2, to assess the accuracy of BiTSC and the competing algorithms when the overlapping CNA affects the state of SNVs in cells. Figure S2 shows the ground truth information of G2. There are CNA driven-loss of SNVs and CNA driven-gain of SNVs events in subclone4 and subclone5, respectively.
and the competing algorithms when the overlapping CNA affects the state of SNVs in cells. Figure S2 shows the ground truth information of G2. There are CNA driven-loss of SNVs and CNA driven-gain of SNVs events in subclone4 and subclone5, respectively.
We also systematically evaluate BiTSC in scenarios when topological structure of the clone tree can be fully recovered by SNV markers (Figure S3). We simulate 150 datasets with variant number of cells (
in scenarios when topological structure of the clone tree can be fully recovered by SNV markers (Figure S3). We simulate 150 datasets with variant number of cells (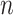 ), sequencing depths (
), sequencing depths (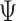 ), missing rate (
), missing rate (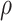 ) as well as the number of loci (
) as well as the number of loci (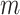 ) and the number of subclones (
) and the number of subclones (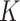 ). The 150 datasets are divided into five groups (denoted G3–G7), each of which contains 30 datasets. In each group we change one parameter and keep other parameters fixed. Under each parameter setting, we generate 10 replicates with different total reads matrix
). The 150 datasets are divided into five groups (denoted G3–G7), each of which contains 30 datasets. In each group we change one parameter and keep other parameters fixed. Under each parameter setting, we generate 10 replicates with different total reads matrix 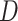 and mutant reads matrix
and mutant reads matrix 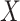 . In addition to the variable parameter, we set the default parameters in each group as follows: number of cells (
. In addition to the variable parameter, we set the default parameters in each group as follows: number of cells (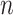 ) is 100, number of loci (
) is 100, number of loci (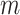 ) is 100, ADO rate (
) is 100, ADO rate (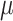 ) is 10%, missing rate (
) is 10%, missing rate (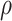 ) is 20%, sequencing depths of all single cells (
) is 20%, sequencing depths of all single cells (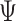 ) are 3, and the number of subclones (
) are 3, and the number of subclones (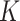 ) is 4. The ground truth (including genotype matrices
) is 4. The ground truth (including genotype matrices 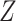 ,
, 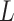 and tree structure
and tree structure 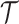 ) of G3–G5 is shown in Figure S4, and the ground truth of G6 and G7 is shown in Figure S5 and S6, respectively. To simulate coverage heterogeneity caused by amplification noise under different sequencing depths [3], we set the divergence parameter of negative binomial distribution,
) of G3–G5 is shown in Figure S4, and the ground truth of G6 and G7 is shown in Figure S5 and S6, respectively. To simulate coverage heterogeneity caused by amplification noise under different sequencing depths [3], we set the divergence parameter of negative binomial distribution, 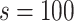 when generating total reads. Under the ground truth of G5, we show examples of simulated data of total reads under different sequencing depths. The large variance of simulated data shows high false positive and false negative rates due to nonuniform amplification (Figure S7). The detailed simulation process can be found in Supplementary Note 5, and the specific parameter settings of G3–G7 can refer to Table S2.
when generating total reads. Under the ground truth of G5, we show examples of simulated data of total reads under different sequencing depths. The large variance of simulated data shows high false positive and false negative rates due to nonuniform amplification (Figure S7). The detailed simulation process can be found in Supplementary Note 5, and the specific parameter settings of G3–G7 can refer to Table S2.
Real data
In addition to simulation data, we also test BiTSC on two sets of real scDNA-seq data. One is from the metastatic colorectal cancer patient CRC2 in [33], which includes 141 cells from the primary colorectal tumor and 45 cells from a matched liver metastasis by single cell DNA target sequencing of 1000 cancer genes with an average sequencing depth of 137
on two sets of real scDNA-seq data. One is from the metastatic colorectal cancer patient CRC2 in [33], which includes 141 cells from the primary colorectal tumor and 45 cells from a matched liver metastasis by single cell DNA target sequencing of 1000 cancer genes with an average sequencing depth of 137 . The sequencing data are available in NCBI Sequence Read Archive under accession number SRP074289. The other one is the single nuclei exome sequencing data of estrogen-receptor positive (ER1
. The sequencing data are available in NCBI Sequence Read Archive under accession number SRP074289. The other one is the single nuclei exome sequencing data of estrogen-receptor positive (ER1 /PR1
/PR1 /Her22−) breast cancer (ERBC) patient in [5] and [34], denoted as ERBC dataset. We use the 55 cells, include 45 tumor cells and 10 matched normal cells, studied in [34]. The data are available in Sequence Read Archive under accession number SRA053195.
/Her22−) breast cancer (ERBC) patient in [5] and [34], denoted as ERBC dataset. We use the 55 cells, include 45 tumor cells and 10 matched normal cells, studied in [34]. The data are available in Sequence Read Archive under accession number SRA053195.
Evaluations
We compare the performance of our algorithm to RobustClone, SCITE[11, 13], BEAM [11, 12], SiFit [11, 17] and SCARLET [24], five recent algorithms that perform single cell DNA genotype recovery and tumor tree analysis. Our evaluation metrics include: (1) the error rate of the recovered scSNV genotype matrix; (2) adjusted Rand Index (ARI) [35, 36], the similarity of subclone assignment between ground truth and the estimates (details can refer to Supplementary Note 6); (3) MP3 similarity [37], the similarity measure of the reconstructed tree and the true tree. Since RobustClone and BEAM do not make explicit infinite site assumption, we choose MP3 similarity as the metric for tree reconstruction, which allows mutations to occur multiple times on the tree.
Results
BiTSC jointly infers both SNV and CNA states
jointly infers both SNV and CNA states
Since BiTSC models both single-cell SNV and CNA data jointly, we design two sets simulations: one set corresponds to the case where CNAs do not affect SNV states but induce extra observable subclone genotype(s) on the tree (Figure S1 and G1, scenario (iii) in Figure 1D with
models both single-cell SNV and CNA data jointly, we design two sets simulations: one set corresponds to the case where CNAs do not affect SNV states but induce extra observable subclone genotype(s) on the tree (Figure S1 and G1, scenario (iii) in Figure 1D with 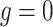 ); the other set includes CNAs that overlap with SNVs and result in gain or loss of mutant copies (Figure S2 and G2, scenario (iii) in Figure 1D with
); the other set includes CNAs that overlap with SNVs and result in gain or loss of mutant copies (Figure S2 and G2, scenario (iii) in Figure 1D with 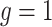 ). We simulate ten replicates for each setting. We compare the performance of BiTSC
). We simulate ten replicates for each setting. We compare the performance of BiTSC to SCARLET, the only algorithm of tumor tree inference that accounts for SNV loss caused by CNA. In addition, we also add RobustClone, SCITE, BEAM and SiFit, four recent methods to infer clone/cell/mutation tree with only one source of marker (SNV), in the comparison. As SCARLET needs an inferred CN tree for summarization of supported loss set as input, we provide it with the true CN tree. We provide BiTSC
to SCARLET, the only algorithm of tumor tree inference that accounts for SNV loss caused by CNA. In addition, we also add RobustClone, SCITE, BEAM and SiFit, four recent methods to infer clone/cell/mutation tree with only one source of marker (SNV), in the comparison. As SCARLET needs an inferred CN tree for summarization of supported loss set as input, we provide it with the true CN tree. We provide BiTSC the real segmentation information. The prior settings and the MCMC configurations of BiTSC
the real segmentation information. The prior settings and the MCMC configurations of BiTSC for analyzing these simulation datasets are in Tables S3 and S4. We perform BiTSC
for analyzing these simulation datasets are in Tables S3 and S4. We perform BiTSC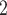 with the number of subclones
with the number of subclones 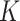 in range from 3 to 10, and select the best fitted
in range from 3 to 10, and select the best fitted 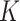 according to the modified BIC (Methods and Supplementary Note 4).
according to the modified BIC (Methods and Supplementary Note 4).
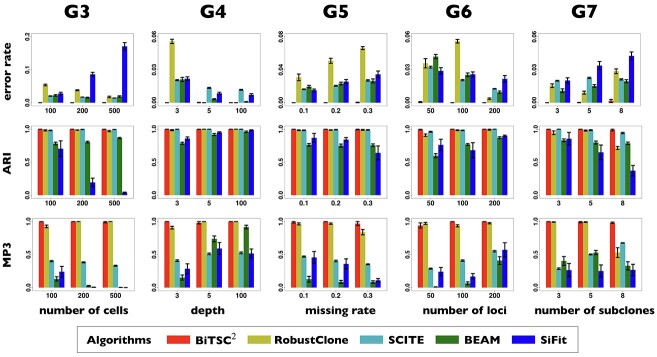
In the first group (G1) of simulations, we use a simple bifurcation structure as ground truth, which includes a branch of clone derived by a CN change (Figure S1). Figure 3A shows the comparison results of simulations in G1. For tree reconstruction, we apply MP3 similarity [37]. BiTSC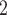 and RobustClone all display satisfactory accuracies (Figure 3A). Since MP3 measures tree similarity based only on SNV triplet structures, the CNA- (only) induced lineage in the simulation does not affect the measurement. Thus, RobustClone shows slightly less variance in performance. However, SCARLET shows large variance for tree reconstruction. The subclone assignment results of BiTSC
and RobustClone all display satisfactory accuracies (Figure 3A). Since MP3 measures tree similarity based only on SNV triplet structures, the CNA- (only) induced lineage in the simulation does not affect the measurement. Thus, RobustClone shows slightly less variance in performance. However, SCARLET shows large variance for tree reconstruction. The subclone assignment results of BiTSC are more consistent with the ground truth than that of RobustClone, SCITE, BEAM and SiFit, which only analyze one source of data (SNV)(Figure 3A). Since SiFit and SCITE do not output subclone assignment information, we apply K-medoids clustering based on the distance of cell along their reconstructed cell lineage tree (SiFit) or mutation tree (SCITE) to cluster cells into subclones as shown in [11]. As SCARLET does not cluster cell with two source markers in its final output, we exclude it in the evaluation of subclone assignment. Among all compared algorithms, only BiTSC
are more consistent with the ground truth than that of RobustClone, SCITE, BEAM and SiFit, which only analyze one source of data (SNV)(Figure 3A). Since SiFit and SCITE do not output subclone assignment information, we apply K-medoids clustering based on the distance of cell along their reconstructed cell lineage tree (SiFit) or mutation tree (SCITE) to cluster cells into subclones as shown in [11]. As SCARLET does not cluster cell with two source markers in its final output, we exclude it in the evaluation of subclone assignment. Among all compared algorithms, only BiTSC is able to reliably recover the CNA states with accuracy of 100% (Figure S8). For SNV genotype recovery, BiTSC
is able to reliably recover the CNA states with accuracy of 100% (Figure S8). For SNV genotype recovery, BiTSC also shows higher accuracy than others (Figure 3A).
also shows higher accuracy than others (Figure 3A).
Figure 3.
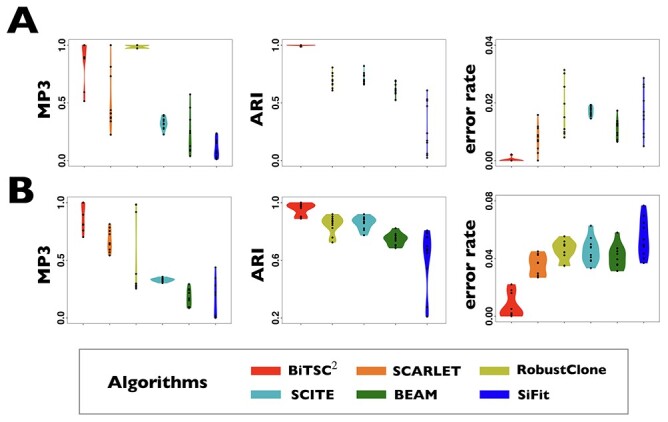
Comparison of performance on G1 and G2 for scSNV genotype recovery, subclone assignment and tree reconstruction. (A) The violin plot of BiTSC with real segments as input, SCARLET with true CN tree and supported loss set as input, RobustClone, SCITE, BEAM and SiFit for error rate of recovered scSNV genotype matrix, ARI of subclone assignment and MP3 similarity on G1 dataset, where 0, 1 and 1 indicate best performance for error rate, ARI and MP3 similarity, respectively. (B) The violin plot of BiTSC
with real segments as input, SCARLET with true CN tree and supported loss set as input, RobustClone, SCITE, BEAM and SiFit for error rate of recovered scSNV genotype matrix, ARI of subclone assignment and MP3 similarity on G1 dataset, where 0, 1 and 1 indicate best performance for error rate, ARI and MP3 similarity, respectively. (B) The violin plot of BiTSC with real segments as input, SCARLET with true CN tree and supported loss set as input, RobustClone, SCITE, BEAM and SiFit for error rate of recovered scSNV genotype matrix, ARI of subclone assignment and MP3 similarity on G2 dataset, where 0, 1 and 1 indicate best performance for error rate, ARI and MP3 distance, respectively.
with real segments as input, SCARLET with true CN tree and supported loss set as input, RobustClone, SCITE, BEAM and SiFit for error rate of recovered scSNV genotype matrix, ARI of subclone assignment and MP3 similarity on G2 dataset, where 0, 1 and 1 indicate best performance for error rate, ARI and MP3 distance, respectively.
Next, we evaluate BiTSC under more complex scenario. In this group, the data are generated from a tumor tree with six subclones, in which SNV states are partly affected by overlapping CNAs (gain and/or loss of mutant copy caused by CNAs, Figure S2). Both BiTSC
under more complex scenario. In this group, the data are generated from a tumor tree with six subclones, in which SNV states are partly affected by overlapping CNAs (gain and/or loss of mutant copy caused by CNAs, Figure S2). Both BiTSC and SCARLET show their advantages in joint modeling of the two sources of data (Figure 3B, Figure S9). BiTSC
and SCARLET show their advantages in joint modeling of the two sources of data (Figure 3B, Figure S9). BiTSC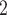 performs best in tree reconstruction. In most cases, it almost fully recovers the true tree structure. SCARLET, owing to the given CNA information, also shows consistent performance. We note that, in this comparison we only provide BiTSC
performs best in tree reconstruction. In most cases, it almost fully recovers the true tree structure. SCARLET, owing to the given CNA information, also shows consistent performance. We note that, in this comparison we only provide BiTSC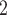 the segmentation information, and it has higher MP3 similarity than SCARLET in 9 out of 10 simulations. In addition, BiTSC
the segmentation information, and it has higher MP3 similarity than SCARLET in 9 out of 10 simulations. In addition, BiTSC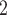 is able to successfully recover the CN profiles with mean accuracy of 99.32%, thus resulting in a more accurate subclone assignment (Figure 3B, Figure S9). More importantly, BiTSC
is able to successfully recover the CN profiles with mean accuracy of 99.32%, thus resulting in a more accurate subclone assignment (Figure 3B, Figure S9). More importantly, BiTSC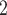 can also correctly infer the phase indicator (fully recovered in 7 out of 10 simulations), which reflects the detailed overlapping relationship of SNVs and CNAs (Figure S10).
can also correctly infer the phase indicator (fully recovered in 7 out of 10 simulations), which reflects the detailed overlapping relationship of SNVs and CNAs (Figure S10).
The SNV recovery errors of BiTSC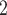 are significantly lower than other methods. The results are comparable for RobustClone, SCITE, BEAM, SiFit and SCARLET, where SCARLET is slightly better than the other four single source only methods. Although SCARLET accounts for CNA information in its algorithm, the CNA states as well as the CN tree have to be inferred by extra methods and packages. When providing true segmentation information to BiTSC
are significantly lower than other methods. The results are comparable for RobustClone, SCITE, BEAM, SiFit and SCARLET, where SCARLET is slightly better than the other four single source only methods. Although SCARLET accounts for CNA information in its algorithm, the CNA states as well as the CN tree have to be inferred by extra methods and packages. When providing true segmentation information to BiTSC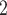 , it outperforms SCARLET (Figure 3B). We also apply BiTSC
, it outperforms SCARLET (Figure 3B). We also apply BiTSC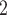 without real segmentation information (each locus as independent segment), it still shows comparable tree reconstruction performance and excellent genotype recovery ability (Figure S11).
without real segmentation information (each locus as independent segment), it still shows comparable tree reconstruction performance and excellent genotype recovery ability (Figure S11).
BiTSC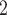 recovers SNV genotypes and assigns cells with high accuracy on synthetic datasets
recovers SNV genotypes and assigns cells with high accuracy on synthetic datasets
We further conduct five groups of simulations where CNA states do not explicitly affect SNV states and clone tree topology. In other words, in these sets of simulations, CNAs do not provide much extra information to the tree reconstruction (Figures S4–S6, including scenarios (i) and (ii) in Figure 1D with 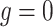 ). We compare BiTSC
). We compare BiTSC mainly to the four single source methods, RobustClone, SCITE, BEAM and SiFit. We evaluate their performance under change of settings such as, number of cells, sequencing depth, missing rate, number of loci and number of subclones (see Methods for details). Still, we provide BiTSC
mainly to the four single source methods, RobustClone, SCITE, BEAM and SiFit. We evaluate their performance under change of settings such as, number of cells, sequencing depth, missing rate, number of loci and number of subclones (see Methods for details). Still, we provide BiTSC the real segmentation information. The prior settings together with MCMC and model selection configurations of BiTSC
the real segmentation information. The prior settings together with MCMC and model selection configurations of BiTSC can refer to Tables S3 and S4 and Supplementary Note 4.
can refer to Tables S3 and S4 and Supplementary Note 4.
Figure 4 shows the detailed comparison performance of 5 algorithms in G3–G7 with three measurements. The overall benchmarks at differed settings are displayed in Figure S12. In general, compared with the other four algorithms, BiTSC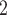 has high accuracy in recovering SNV genotypes (top row in Figure 4 and Figure S12), high robustness in subclone assignments (2nd row in Figure 4 and Figure S12), and high power in clone tree reconstruction (3rd row in Figure 4 and Figure S12).
has high accuracy in recovering SNV genotypes (top row in Figure 4 and Figure S12), high robustness in subclone assignments (2nd row in Figure 4 and Figure S12), and high power in clone tree reconstruction (3rd row in Figure 4 and Figure S12).
Figure 4.
Comparison of detailed performance on G3-G7 for scSNV genotype recovery, subclone assignment and tree reconstruction among BiTSC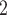 with real segments as input, RobustClone, SCITE, BEAM and SiFit, where 0, 1 and 1 indicate best performance for error rate, ARI and MP3 similarity, respectively.
with real segments as input, RobustClone, SCITE, BEAM and SiFit, where 0, 1 and 1 indicate best performance for error rate, ARI and MP3 similarity, respectively.
Specifically, BiTSC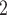 recovers SNV genotypes with little error rate in almost all simulation settings where the default sequencing depth (
recovers SNV genotypes with little error rate in almost all simulation settings where the default sequencing depth (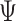 ) is set to 3. The accuracies of RobustClone and BEAM get significantly improved as the sequencing depths increase (G4 in Figure 4). The accuracies of SCITE and SiFit also show improved performance with increasing the sequencing depths (G4 in Figure 4). For default depth, RobustClone, SCITE, BEAM get lower error rates when more cells (
) is set to 3. The accuracies of RobustClone and BEAM get significantly improved as the sequencing depths increase (G4 in Figure 4). The accuracies of SCITE and SiFit also show improved performance with increasing the sequencing depths (G4 in Figure 4). For default depth, RobustClone, SCITE, BEAM get lower error rates when more cells (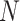 ) are sampled and/or more loci (
) are sampled and/or more loci (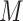 ) are sequenced, but shows reduced accuracy as the missing rates (
) are sequenced, but shows reduced accuracy as the missing rates (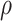 ) and the number of subclones rise. Different from these three algorithms, SiFit shows increasing error rates with more cells (
) and the number of subclones rise. Different from these three algorithms, SiFit shows increasing error rates with more cells (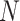 ).
).
The subclone assignment results of BiTSC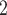 , RobustClone and SCITE are mostly consistent with the ground truth. BEAM and SiFit are slightly less consistent (2nd row in Figure S12), but BEAM gets improved with the increase of number of cells (
, RobustClone and SCITE are mostly consistent with the ground truth. BEAM and SiFit are slightly less consistent (2nd row in Figure S12), but BEAM gets improved with the increase of number of cells (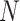 ), number of loci (
), number of loci (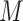 ) and/or sequencing depths (
) and/or sequencing depths (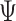 ) and SiFit performs better with less cells (
) and SiFit performs better with less cells (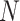 ), more loci (
), more loci (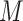 ) and/or deeper sequencing depths (
) and/or deeper sequencing depths (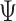 ) (2nd row in Figure 4). The tree reconstruction accuracies, which are measured in MP3 similarity, are almost over 0.9 in all cases for BiTSC
) (2nd row in Figure 4). The tree reconstruction accuracies, which are measured in MP3 similarity, are almost over 0.9 in all cases for BiTSC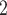 . For RobustClone, the tree reconstruction performance is also good in simulations with moderate missing rates and fewer subclones. The MP3 similarities between real tree and tree recovered by SCITE mostly near 0.5, but the similarity increases with the increase of sequencing depth(
. For RobustClone, the tree reconstruction performance is also good in simulations with moderate missing rates and fewer subclones. The MP3 similarities between real tree and tree recovered by SCITE mostly near 0.5, but the similarity increases with the increase of sequencing depth(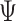 ), number of loci (
), number of loci (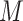 ) and number of subclones (
) and number of subclones (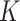 ). BEAM and SiFit are very sensitive to number of cell, sequencing depth and number of loci. And BEAM only performs satisfactorily in scenarios with sequencing depth over 5.
). BEAM and SiFit are very sensitive to number of cell, sequencing depth and number of loci. And BEAM only performs satisfactorily in scenarios with sequencing depth over 5.
In the above comparisons BiTSC was given the real segmentation information as input. Reliable segmentation may offer extra information and jointly updating CNA states of multiple loci with in the same segment could greatly improve the likelihood of the model. However, this information may not always be reliably estimated. In that case, we can either take the more refined raw bins (the bins after binning step before segmentation and CNA calling) as segments or use locus specific segments (each gene/SNV locus as a segment). Here we additionally evaluate BiTSC
was given the real segmentation information as input. Reliable segmentation may offer extra information and jointly updating CNA states of multiple loci with in the same segment could greatly improve the likelihood of the model. However, this information may not always be reliably estimated. In that case, we can either take the more refined raw bins (the bins after binning step before segmentation and CNA calling) as segments or use locus specific segments (each gene/SNV locus as a segment). Here we additionally evaluate BiTSC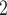 under locus-specific configuration, where the
under locus-specific configuration, where the 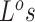 are updated one locus at a time. Although the performance results of BiTSC
are updated one locus at a time. Although the performance results of BiTSC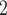 reduce slightly as compared with cases where correct segmentation information is provided, the overall accuracies are still consistently good (Figures S13 and S14).
reduce slightly as compared with cases where correct segmentation information is provided, the overall accuracies are still consistently good (Figures S13 and S14).
BiTSC recovers single-cell phylogeny of metastatic colorectal cancer
recovers single-cell phylogeny of metastatic colorectal cancer
We apply BiTSC to real scDNA-seq data of colorectal cancer patient CRC2 in [33], which includes both primary and metastatic samples. After filtering for some low-coverage data, the sequencing data of 182 single cells with 36 SNV loci were retained for further analysis. We directly input the raw reads covering these loci to BiTSC
to real scDNA-seq data of colorectal cancer patient CRC2 in [33], which includes both primary and metastatic samples. After filtering for some low-coverage data, the sequencing data of 182 single cells with 36 SNV loci were retained for further analysis. We directly input the raw reads covering these loci to BiTSC and use locus-specific segment setting for CNAs. The cell-specific sequencing depth of each single cells can be found in the Supplementary Table S4 in [33]. The priors and MCMC settings for running BiTSC
and use locus-specific segment setting for CNAs. The cell-specific sequencing depth of each single cells can be found in the Supplementary Table S4 in [33]. The priors and MCMC settings for running BiTSC are shown in Tables S5 and S6.
are shown in Tables S5 and S6.
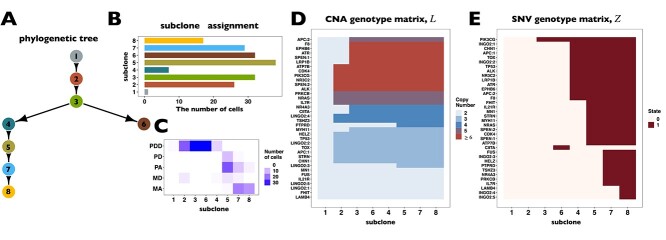
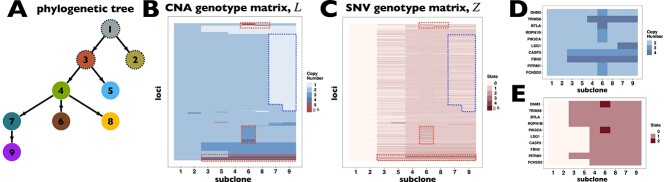
BiTSC fits a clone tree with 8 subclones as shown in Figure 5A (see Figure S15 for the BIC values). Figure 5B displays the prevalence of cells in each subclone. The metastatic aneuploid cells are mainly distributed in subclones 7 and 8, whereas the primary aneuploid cells are predominantly clustered in subclone5 (Figure 5C). Although the cells occupied the other subclones were labeled diploid in [33], we still find considerable CNA events occurring in these targeted genes (Figure 5D). Extensive point mutations are identified in primary (subclone5) and metastatic (subclones 7 and 8) tumor cells (Figure 5E).
fits a clone tree with 8 subclones as shown in Figure 5A (see Figure S15 for the BIC values). Figure 5B displays the prevalence of cells in each subclone. The metastatic aneuploid cells are mainly distributed in subclones 7 and 8, whereas the primary aneuploid cells are predominantly clustered in subclone5 (Figure 5C). Although the cells occupied the other subclones were labeled diploid in [33], we still find considerable CNA events occurring in these targeted genes (Figure 5D). Extensive point mutations are identified in primary (subclone5) and metastatic (subclones 7 and 8) tumor cells (Figure 5E).
Figure 5.
BiTSC reconstructs tumor phylogeny of metastatic colorectal cancer. (A) The phylogeny tree of metastatic colorectal cancer reconstructed by BiTSC
reconstructs tumor phylogeny of metastatic colorectal cancer. (A) The phylogeny tree of metastatic colorectal cancer reconstructed by BiTSC . (B) The subclone assignment. (C) The number of overlapped cells contained in subclones identified by BiTSC
. (B) The subclone assignment. (C) The number of overlapped cells contained in subclones identified by BiTSC and cells contained in the targeted region, where PD stands for Primary Diploid, PA stands for Primary Aneuploid, MD stands for Metastatic Diploid, and MA stands for Metastatic Aneuploid in [33]. (D) The CNA subclonal genotype matrix estimated by BiTSC
and cells contained in the targeted region, where PD stands for Primary Diploid, PA stands for Primary Aneuploid, MD stands for Metastatic Diploid, and MA stands for Metastatic Aneuploid in [33]. (D) The CNA subclonal genotype matrix estimated by BiTSC , where LINGO2: 1–5 represent different loci in the genomic region of LINGO2 on the chromosome, as well as SPEN:1-2 and APC:1-2. (E) The SNV subclonal genotype matrix estimated by BiTSC
, where LINGO2: 1–5 represent different loci in the genomic region of LINGO2 on the chromosome, as well as SPEN:1-2 and APC:1-2. (E) The SNV subclonal genotype matrix estimated by BiTSC .
.
Interestingly, our inferred tumor clone tree and genotypes show that metastatic cells (subclones 7 and 8) mainly share the same CNA events on PTPRD and LINGO2:3, which arise from primary sites (subclone5). Contrary to the polyclonal seeding (i.e. two independent clones with different mutations migrate from primary colon cancer to liver metastases at different time points) conclusion based on SCITE tree in the original study [33], our result indicates that the liver metastasis from colon is a single event, which supports the monoclonal seeding hypothesis and is consistent with the inference based on the SCARLET tree (Figure S16) [24].
Besides the metastatic lineage, we also identified another lineages with unique mutations. The lineage leads to subclone6, which consists of a small proportion of cells that carries point mutations on CIITA and PIK3CG. Such lineage was also identified by SCITE and SCARLET trees (Figure S16AB).
BiTSC recovers single-cell phylogeny of breast cancer
recovers single-cell phylogeny of breast cancer
We additionally perform BiTSC on the ERBC dataset, which contains 55 cells. The raw single-cell sequencing dataset are retrieved from the Sequence Read Archive (No. 053195) in FASTQ format [5, 34]. The information of mean sequencing depths for individual samples can refer to Table S1 of [34]. We adopt the pipeline given by [34] in their Supplementary Note to preprocess the raw data (Supplementary Note 7 for brief steps). After preprocessing, a total of 1137 gold-standard SNV loci with their raw mutant and total reads are extracted and used for downstream analysis. The priors and MCMC settings for running BiTSC
on the ERBC dataset, which contains 55 cells. The raw single-cell sequencing dataset are retrieved from the Sequence Read Archive (No. 053195) in FASTQ format [5, 34]. The information of mean sequencing depths for individual samples can refer to Table S1 of [34]. We adopt the pipeline given by [34] in their Supplementary Note to preprocess the raw data (Supplementary Note 7 for brief steps). After preprocessing, a total of 1137 gold-standard SNV loci with their raw mutant and total reads are extracted and used for downstream analysis. The priors and MCMC settings for running BiTSC are shown in Tables S6 and S7.
are shown in Tables S6 and S7.
We apply BiTSC to the processed ERBC dataset and infer a best fit clone tree with 9 subclones (Figure 6A). The BIC values for 3–10 subclones can be found in Figure S17. Subclones 1, 2 and 3 are inferred to be ancestor clones with no cells assigned in. Subclones 4 and 8 contain only normal cells, and subclones 5 and 6 are tumor only clones. With only one cell assigned to subclone5, the majority of tumor cells are concentrated in subclone6. The other tumor cells are distributed in subclones 7 and 9. Note that BiTSC
to the processed ERBC dataset and infer a best fit clone tree with 9 subclones (Figure 6A). The BIC values for 3–10 subclones can be found in Figure S17. Subclones 1, 2 and 3 are inferred to be ancestor clones with no cells assigned in. Subclones 4 and 8 contain only normal cells, and subclones 5 and 6 are tumor only clones. With only one cell assigned to subclone5, the majority of tumor cells are concentrated in subclone6. The other tumor cells are distributed in subclones 7 and 9. Note that BiTSC is not aim for labeling tumor or normal cells; the labels of tumor cell or normal cell are from [5] according to the sampling sites. The normal cells are most possibly from matched adjacent normal tissue, which may already possess many somatic mutations. In the study by [34], they also identified many somatic mutations in the normal cells with the same dataset (Figure 6 in [34]). Figure 6BC show the inferred CNA and SNV genotype matrices by BiTSC
is not aim for labeling tumor or normal cells; the labels of tumor cell or normal cell are from [5] according to the sampling sites. The normal cells are most possibly from matched adjacent normal tissue, which may already possess many somatic mutations. In the study by [34], they also identified many somatic mutations in the normal cells with the same dataset (Figure 6 in [34]). Figure 6BC show the inferred CNA and SNV genotype matrices by BiTSC (
(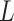 and
and  ). From the results we can see some CN events shared by most subclones (3–9 and 4–9, Figure 6B), which confirming the findings that somatic CNAs are acquired early on during breast cancer development [5]. We further find many loci with increased CN occur on the mutant alleles in the major tumor clone (subclone6). In addition, there are also some CNA-driven loss of mutations in subclones 7 and 9 (Figure 6BC). We then investigate previously reported non-synonymous mutations in [5, 34]. We find that all these mutations are inferred to have overlapped copy gains, to some extent, in the same region (Figure 6D). Moreover, by combining CNA and SNV genotypes together with the phase indicator, we infer that the copy gain happened in DNM3 and PIK3CA in tumor subclone6 possibly occurred on their mutant allele (Figure 6DE).
). From the results we can see some CN events shared by most subclones (3–9 and 4–9, Figure 6B), which confirming the findings that somatic CNAs are acquired early on during breast cancer development [5]. We further find many loci with increased CN occur on the mutant alleles in the major tumor clone (subclone6). In addition, there are also some CNA-driven loss of mutations in subclones 7 and 9 (Figure 6BC). We then investigate previously reported non-synonymous mutations in [5, 34]. We find that all these mutations are inferred to have overlapped copy gains, to some extent, in the same region (Figure 6D). Moreover, by combining CNA and SNV genotypes together with the phase indicator, we infer that the copy gain happened in DNM3 and PIK3CA in tumor subclone6 possibly occurred on their mutant allele (Figure 6DE).
Figure 6.
BiTSC reconstructs tumor phylogeny of breast cancer. (A) The phylogeny tree of breast cancer reconstructed by BiTSC
reconstructs tumor phylogeny of breast cancer. (A) The phylogeny tree of breast cancer reconstructed by BiTSC . (B) The CNA subclonal genotype matrix estimated by BiTSC
. (B) The CNA subclonal genotype matrix estimated by BiTSC . (C) The SNV subclonal genotype matrix estimated by BiTSC
. (C) The SNV subclonal genotype matrix estimated by BiTSC . (D) The CNA subclonal genotype matrix of 10 previously reported nonsynonymous mutations. (E) The SNV subclonal genotype matrix of 10 previously reported nonsynonymous mutations.
. (D) The CNA subclonal genotype matrix of 10 previously reported nonsynonymous mutations. (E) The SNV subclonal genotype matrix of 10 previously reported nonsynonymous mutations.
Discussion
Computational method based scDNA-seq data for tumor ITH and evolutionary history inference can provide important insights to the understanding of tumor progression and metastasis mechanism and provide guidance to tumor treatment and response. Most of such methods only utilize one source of information, either SNV or CNA, which may lead to biased estimation of the true evolution history of cancer. In this study, we propose BiTSC , a Bayesian-based method that integrates SNV and CNA markers from scDNA-seq data to jointly infer tumor clone tree. BiTSC
, a Bayesian-based method that integrates SNV and CNA markers from scDNA-seq data to jointly infer tumor clone tree. BiTSC is a unified Bayesian framework, which takes the raw total reads and mutant reads of single cells generated by sequencing as input and takes into account sequencing errors and models ADO rate, as well as missing rate. It also optimizes SNV and CNA subclonal genotype matrices, assigns cells to subclones and constructs subclonal tree. It can also estimate the overlapping relationship between CNA and SNV. BiTSC
is a unified Bayesian framework, which takes the raw total reads and mutant reads of single cells generated by sequencing as input and takes into account sequencing errors and models ADO rate, as well as missing rate. It also optimizes SNV and CNA subclonal genotype matrices, assigns cells to subclones and constructs subclonal tree. It can also estimate the overlapping relationship between CNA and SNV. BiTSC has a high accuracy for subclone assignment and SNV subclonal genotypes matrix recovery compared with existing methods such as RobustClone, BEAM and SCARLET. BiTSC
has a high accuracy for subclone assignment and SNV subclonal genotypes matrix recovery compared with existing methods such as RobustClone, BEAM and SCARLET. BiTSC can handle low-depth single-cell sequencing data with strong performance. BiTSC
can handle low-depth single-cell sequencing data with strong performance. BiTSC also provides high accurate and robust estimation of the missing rate in scDNA-seq data (Figure S18).
also provides high accurate and robust estimation of the missing rate in scDNA-seq data (Figure S18).
The simulations designed in this study simplified the SNV distribution along the chromosomes. While in reality SNVs occur randomly on all genomic regions, they were simulated in a neatly arranged manner. Since we assume SNVs arise independently between different loci and infer the genotype of SNV locus by locus. As long as the SNVs generated are informative in distinguishing subclones, whether they occur randomly on chromosomes will not affect the inference of our model. We have tested BiTSC on an exemplar simulation with 10 replicates, where SNVs randomly and uniformly occur on all genomic regions (Figure S19A). BiTSC
on an exemplar simulation with 10 replicates, where SNVs randomly and uniformly occur on all genomic regions (Figure S19A). BiTSC can fully recover the SNV and CNA genotypes of cells and accurately assign cells into subclones (results not show). Moreover, SNVs could be also sparsely and nonuniformly distributed within each CNA segment. We additionally performed an simulation with sparsely distributed SNVs as in Figure S19B. BiTSC
can fully recover the SNV and CNA genotypes of cells and accurately assign cells into subclones (results not show). Moreover, SNVs could be also sparsely and nonuniformly distributed within each CNA segment. We additionally performed an simulation with sparsely distributed SNVs as in Figure S19B. BiTSC also works robustly, when provided the CNA segment information, BiTSC
also works robustly, when provided the CNA segment information, BiTSC could fully recover the SNV and CNA genotypes of cells and accurately assign cells into subclones (results not show).
could fully recover the SNV and CNA genotypes of cells and accurately assign cells into subclones (results not show).
In general, BiTSC prefers to update all the loci in the same CNA segment together, since loci in the same segment share CNA status. There are many existing methods can be applied to perform segmentation, for example, HMMcopy, copy number, etc. [26]. In cases when segment information can not be reliably obtained, BiTSC
prefers to update all the loci in the same CNA segment together, since loci in the same segment share CNA status. There are many existing methods can be applied to perform segmentation, for example, HMMcopy, copy number, etc. [26]. In cases when segment information can not be reliably obtained, BiTSC can also update
can also update 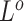 and
and 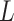 locus by locus in the same way as updating
locus by locus in the same way as updating 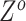 and
and 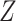 . In the results on synthetic data, we show that the accuracy and robustness of updating one locus at a time are still higher than RobustClone and BEAM in most cases (see Section 3.2, Figure S11, Figures S13 and S14). In this way, BiTSC
. In the results on synthetic data, we show that the accuracy and robustness of updating one locus at a time are still higher than RobustClone and BEAM in most cases (see Section 3.2, Figure S11, Figures S13 and S14). In this way, BiTSC may provide a raw estimation of CNA segments based on the inferred CNA genotype matrix
may provide a raw estimation of CNA segments based on the inferred CNA genotype matrix  .
.
At a given number of subclones, BiTSC will place each cell into the most likely subclones according to their mutation profiles (both SNV and CNA) and make inference to subclone genotypes. The number of subclones
will place each cell into the most likely subclones according to their mutation profiles (both SNV and CNA) and make inference to subclone genotypes. The number of subclones  is determined by model selection procedure. In some cases, BiTSC
is determined by model selection procedure. In some cases, BiTSC may recover a few empty subclones under the selected number of
may recover a few empty subclones under the selected number of 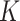 . These subclones are possibly latent subclones, that are either un-sampled or extinct ancestors of all other descendent subclones. Such subclones may be pruned in the final results if only the observed subclones are being interested.
. These subclones are possibly latent subclones, that are either un-sampled or extinct ancestors of all other descendent subclones. Such subclones may be pruned in the final results if only the observed subclones are being interested.
The full probabilistic model in BiTSC describes the generating process in a comprehensive manner. Especially, we purposed the phase indicator, which reflects the overlapping relationship of SNV and CNA in the same genomic region. Under such setting, our model can detect both gains and losses of mutant copy due to CNA. In contrast, the stepwise construct and refine approach (i.e. SCARLET) could not recover gains of mutant copy from the data. In addition, the optimization of SCARLET may fall into local optimum with integer-linear programming and the subtree root may be misplaced during the refinement [24]. For example, in the toy model of Figure 1A, SCARLET misplaces cells in subclone4 as the siblings of cells in subclone2. Thus, it failed to reconstruct the most parsimonious tree as shown in ground truth (Figure S20). In contrast, BiTSC
describes the generating process in a comprehensive manner. Especially, we purposed the phase indicator, which reflects the overlapping relationship of SNV and CNA in the same genomic region. Under such setting, our model can detect both gains and losses of mutant copy due to CNA. In contrast, the stepwise construct and refine approach (i.e. SCARLET) could not recover gains of mutant copy from the data. In addition, the optimization of SCARLET may fall into local optimum with integer-linear programming and the subtree root may be misplaced during the refinement [24]. For example, in the toy model of Figure 1A, SCARLET misplaces cells in subclone4 as the siblings of cells in subclone2. Thus, it failed to reconstruct the most parsimonious tree as shown in ground truth (Figure S20). In contrast, BiTSC can fully recover the topological structure in the true tree.
can fully recover the topological structure in the true tree.
Indeed, different values of 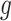 will indicate whether CNA affects the CN of the mutant allele on overlapping locus. This will affect the genotype matrix
will indicate whether CNA affects the CN of the mutant allele on overlapping locus. This will affect the genotype matrix 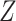 , thereby affecting the likelihood computation of mutant reads (Eq. 3), and further affecting the sampling of parameters
, thereby affecting the likelihood computation of mutant reads (Eq. 3), and further affecting the sampling of parameters 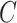 ,
, 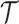 ,
, 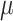 and
and 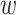 (the posterior computation in Supplementary Note 3). In the example of Figure 1A, the CNA occurs on the mutant allele on locus
(the posterior computation in Supplementary Note 3). In the example of Figure 1A, the CNA occurs on the mutant allele on locus 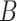 under the ground truth, then
under the ground truth, then 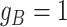 and the mutation states are
and the mutation states are 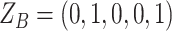 (the 2nd row of
(the 2nd row of 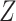 in Table S1). However, if the phase indicator is erroneously estimated as
in Table S1). However, if the phase indicator is erroneously estimated as 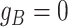 , the SNV states of locus B will be derived as
, the SNV states of locus B will be derived as 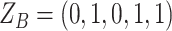 . Thus, it will directly affect the likelihood computation in Eq. 3 in turn impact the sampling of other parameters.
. Thus, it will directly affect the likelihood computation in Eq. 3 in turn impact the sampling of other parameters.
Despite the application of phase indicator and the comprehensive design of BiTSC , its model assumptions are still a simplified version of the reality. In our model, we assume SNV and/or CNA mutations occur independently among different loci and each mutation (including SNV and CNA) originates only once in a specific subclone, i.e. the infinite site assumption. In practice, however, such assumption may be violated. Multiple (point) mutations may hit the same site in the genome. Moreover, CN changes may happen in overlap or nested regions on the genome [22]. In addition, the effects of epistatic interactions among genes may induce extra correlations between different SNVs or CNAs. These complications are beyond the discussion of our present model. However, working on relaxing one or more assumptions in joint modeling of single cell SNV and/or CNA data can be a promising future direction.
, its model assumptions are still a simplified version of the reality. In our model, we assume SNV and/or CNA mutations occur independently among different loci and each mutation (including SNV and CNA) originates only once in a specific subclone, i.e. the infinite site assumption. In practice, however, such assumption may be violated. Multiple (point) mutations may hit the same site in the genome. Moreover, CN changes may happen in overlap or nested regions on the genome [22]. In addition, the effects of epistatic interactions among genes may induce extra correlations between different SNVs or CNAs. These complications are beyond the discussion of our present model. However, working on relaxing one or more assumptions in joint modeling of single cell SNV and/or CNA data can be a promising future direction.
Key Points
We proposed Bayesian method, BiTSC
 , for tumor clone tree inference by joint analysis of single-cell SNV and CNA data.
, for tumor clone tree inference by joint analysis of single-cell SNV and CNA data.BiTSC
 employs a tree coupled generating model that accounts for allelic dropout rate, sequencing errors and missing rate, as well as assigns single cells into subclones.
employs a tree coupled generating model that accounts for allelic dropout rate, sequencing errors and missing rate, as well as assigns single cells into subclones.BiTSC
 involves phase indicator in its model that models the overlapping relationship of SNV and CNA on the tumor tree.
involves phase indicator in its model that models the overlapping relationship of SNV and CNA on the tumor tree.BiTSC
 shows high accuracy in genotype recovery, subclonal assignment and tree reconstruction on synthetic and real tumor data.
shows high accuracy in genotype recovery, subclonal assignment and tree reconstruction on synthetic and real tumor data.
Conflict of interest
We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
Author contributions statement
Z.C., F.G., L.W. and L.M. conceived the model, Z.C. conducted the experiments, Z.C., W.L. and L.M. analyzed the results. Z.C., F.G., L.W. and L.M. wrote and reviewed the manuscript.
Supplementary Material
Funding
National Key Research and Development Program of China (grant nos. 2019YFA0709501, 2018YFB0704304); National Natural Science Foundation of China Grants (grant nos. 11971459, 12071466); National Center for Mathematics and Interdisciplinary Sciences (NCMIS) of Chinese Academy of Sciences; Key Laboratory of Systems and Control (LSC) of Chinese Academy of Sciences.
Author Biographies
Ziwei Chen is a Phd candidate in Academy of Mathematics and System Sciences, Chinese Academy of Sciences. Her research focuses on computational biology, systems biology, and data science.
Fuzhou Gong is a professor in the National Center for Mathematics and Interdisciplinary Sciences at Academy of Mathematics and Systems Science, Chinese Academy of Sciences. He is also a faculty member in the School of Mathematical Sciences at University of Chinese Academy of Sciences, China. His research focuses on probability theory, stochastic analysis, and applied mathematics.
Lin Wan is a professor in the National Center for Mathematics and Interdisciplinary Sciences at Academy of Mathematics and Systems Science, Chinese Academy of Sciences. He is also a faculty member in the School of Mathematical Sciences at University of Chinese Academy of Sciences, China. His research focuses on computational biology, systems biology, and data science.
Liang Ma is an assistant professor in Key Laboratory of Zoological Systematics and Evolution at Institute of Zoology, Chinese Academy of Sciences. His research focuses on computational biology, statistical learning, evolution and population genetics.
References
- 1. Navin NE. Cancer genomics: one cell at a time. Genome Biol 2014;15(8):452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Lawson DA, Kessenbrock K, Davis RT, et al. . Tumour heterogeneity and metastasis at single-cell resolution. Nat Cell Biol 2018;20(12):1349–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Gawad C, Koh W, Quake SR. Single-cell genome sequencing: current state of the science. Nat Rev Genet 2016;17, 175(3). [DOI] [PubMed] [Google Scholar]
- 4. Navin N, Kendall J, Troge J, et al. . Tumour evolution inferred by single-cell sequencing. Nature 2011;472(7341):90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Wang Y, Waters J, Leung ML, et al. . Clonal evolution in breast cancer revealed by single nucleus genome sequencing. Nature 2014;512(7513):155–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Xun X, Hou Y, Yin X, et al. . Single-cell exome sequencing reveals single-nucleotide mutation characteristics of a kidney tumor. Cell 2012;148(5):886–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Chang Y, Jun Y, Yao X, et al. . Discovery of biclonal origin and a novel oncogene slc12a5 in colon cancer by single-cell sequencing. Cell Res 2014;24(6):701–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Zaccaria S, Raphael BJ. Characterizing allele-and haplotype-specific copy numbers in single cells with chisel. Nat Biotechnol 2020;39(2):1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Kuipers J, Tuncel MA, Ferreira P, et al. . Single-cell copy number calling and event history reconstruction. bioRxiv 2020. [Google Scholar]
- 10. Wang F, Wang Q, Mohanty V, et al. . Medalt: single-cell copy number lineage tracing enabling gene discovery. Genome Biol 2021;22(1):1–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Chen Z, Gong F, Wan L, et al. . Robustclone: a robust PCA method for tumor clone and evolution inference from single-cell sequencing data. Bioinformatics 2020;36(11):3299–306. [DOI] [PubMed] [Google Scholar]
- 12. Miura S, Huuki LA, Buturla T, et al. . Computational enhancement of single-cell sequences for inferring tumor evolution. Bioinformatics 2018;34(17):i917–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Jahn K, Kuipers J, Beerenwinkel N. Tree inference for single-cell data. Genome Biol 2016;17(1):1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Ross EM, Markowetz F. Onconem: inferring tumor evolution from single-cell sequencing data. Genome Biol 2016;17(1):1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Singer J, Kuipers J, Jahn K, et al. . Single-cell mutation identification via phylogenetic inference. Nat Commun 2018;9(1):1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Kozlov A, Alves J, Stamatakis A, et al. . Cellphy: Accurate and Fast Probabilistic Inference of Single-Cell Phylogenies From scDNA-seq Data, 2020. [DOI] [PMC free article] [PubMed]
- 17. Zafar H, Tzen A, Navin N, et al. . Sifit: inferring tumor trees from single-cell sequencing data under finite-sites models. Genome Biol 2017;18(1):1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Zafar H, Navin N, Chen K, et al. . Siclonefit: Bayesian inference of population structure, genotype, and phylogeny of tumor clones from single-cell genome sequencing data. Genome Res 2019;29(11):1847–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Schwartz R, Schäffer AA. The evolution of tumour phylogenetics: principles and practice. Nat Rev Genet 2017;18(4):213–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Roth A, Khattra J, Yap D, et al. . Pyclone: statistical inference of clonal population structure in cancer. Nat Methods 2014;11(4):396–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Deshwar AG, Vembu S, Yung CK, et al. . Phylowgs: reconstructing subclonal composition and evolution from whole-genome sequencing of tumors. Genome Biol 2015;16(1):1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Jiang Y, Yu Q, Minn AJ, et al. . Assessing intratumor heterogeneity and tracking longitudinal and spatial clonal evolutionary history by next-generation sequencing. Proc Natl Acad Sci 2016;113(37):E5528–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Zeng L, Warren JL, Zhao H, et al. . Phylogeny-based tumor subclone identification using a bayesian feature allocation model. Ann Appl Stat 2019;13(2):1212–41. [Google Scholar]
- 24. Satas G, Zaccaria S, Mon G, et al. . Scarlet: single-cell tumor phylogeny inference with copy-number constrained mutation losses. Cell Syst 2020;10(4):323–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Shah SP, Xuan X, DeLeeuw RJ, et al. . Integrating copy number polymorphisms into array cgh analysis using a robust hmm. Bioinformatics 2006;22(14):e431–9. [DOI] [PubMed] [Google Scholar]
- 26. Mallory XF, Edrisi M, Navin N, et al. . Methods for copy number aberration detection from single-cell DNA-sequencing data. Genome Biol 2020;21(1):1–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Lee J, Mueller P, Gulukota K, et al. . A Bayesian feature allocation model for tumor heterogeneity. Ann Appl Stat 2015;9(2):621–39. [Google Scholar]
- 28. Klambauer G, Schwarzbauer K, Mayr A, et al. . Cn. Mops: mixture of poissons for discovering copy number variations in next-generation sequencing data with a low false discovery rate. Nucleic Acids Res 2012;40(9):e69–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Grün D, Kester L, Van Oudenaarden A. Validation of noise models for single-cell transcriptomics. Nat Methods 2014;11(6):637–40. [DOI] [PubMed] [Google Scholar]
- 30. Grønbech CH, Vording MF, Timshel PN, et al. . Scvae: Variational auto-encoders for single-cell gene expression data. Bioinformatics 2020;36(16):4415–22. [DOI] [PubMed] [Google Scholar]
- 31. Marass F, Mouliere F, Yuan K, et al. . A phylogenetic latent feature model for clonal deconvolution. Ann Appl Stat 2016;10(4):2377–404. [Google Scholar]
- 32. Geyer CJ. Markov chain Monte Carlo maximum likelihood, 1991.
- 33. Leung ML, Davis A, Gao R, et al. . Single-cell DNA sequencing reveals a late-dissemination model in metastatic colorectal cancer. Genome Res 2017;27(8):1287–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Alves JM, Posada D. Sensitivity to sequencing depth in single-cell cancer genomics. Genome Med 2018;10(1):1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Rand WM. Objective criteria for the evaluation of clustering methods. J Am Stat Assoc 1971;66(336):846–50. [Google Scholar]
- 36. Qiu X, Mao Q, Tang Y, et al. . Reversed graph embedding resolves complex single-cell trajectories. Nat Methods 2017;14(10):979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Ciccolella S, Bernardini G, Denti L, et al. . Triplet-based similarity score for fully multi-labeled trees with poly-occurring labels. Bioinformatics 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.