Polygenic risk for prostate cancer: Decreasing relative risk with age but little impact on absolute risk

Summary

Polygenic risk scores (PRSs) for a variety of diseases have recently been shown to have relative risks that depend on age, and genetic relative risks decrease with increasing age. A refined understanding of the age dependency of PRSs for a disease is important for personalized risk predictions and risk stratification. To further evaluate how the PRS relative risk for prostate cancer depends on age, we refined analyses for a validated PRS for prostate cancer by using 64,274 prostate cancer cases and 46,432 controls of diverse ancestry (82.8% European, 9.8% African American, 3.8% Latino, 2.8% Asian, and 0.8% Ghanaian). Our strategy applied a novel weighted proportional hazards model to case-control data to fully utilize age to refine how the relative risk decreased with age. We found significantly greater relative risks for younger men (age 30–55 years) compared with older men (70–88 years) for both relative risk per standard deviation of the PRS and dichotomized according to the upper 90^th percentile of the PRS distribution. For the largest European ancestral group that could provide reliable resolution, the log-relative risk decreased approximately linearly from age 50 to age 75. Despite strong evidence of age-dependent genetic relative risk, our results suggest that absolute risk predictions differed little from predictions that assumed a constant relative risk over ages, from short-term to long-term predictions, simplifying implementation of risk discussions into clinical practice.

Introduction

Polygenic risk scores (PRSs), also called genomic risk scores, provide a single measure of a large number of genetic variants associated with common diseases and have potential to improve personalized medical care and public health by informing subjects of their future risk of developing disease. Because common diseases increase with age with increasing impact of lifetime exposures, it is critical to evaluate whether the association of a PRS with disease changes with age and the practical implications of ignoring age-dependent risks. As stressed by others,¹ understanding the age dependency of PRSs for a disease is important not only for personalized medical care and population health but also to improve understanding of disease etiology.

A PRS for an individual is a weighted sum over the doses of selected risk variants, on the order of hundreds to millions of genetic variants,² and so creation of a PRS depends on which variants are chosen and how weights are assigned. A variety of methods to create a PRS have been developed,^{3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13} many of which result in a large number of selected variants. The purpose of this report is to propose a strategy to evaluate a PRS for clinical risk predictions by determining whether the relative risk for a PRS depends on age and whether age-dependent relative risks have practical implications. Our empirical evaluations are based on a PRS for prostate cancer that was developed on a large number of men of diverse ancestry and has been replicated. Hence, our starting point is based on a chosen PRS and not development of a new PRS.

Conti et al.¹⁴ developed a PRS for prostate cancer based on a multi-ancestry meta-analysis of genome-wide association summary statistics from a total of 107,247 cases and 127,006 controls with European, African, East Asian, and Hispanic ancestries. They discovered a total of 269 variants associated with prostate cancer risk and constructed a PRS by using multi-ancestry weights. Although 269 variants might seem like a small number for a PRS, these variants were selected on the basis of stepwise selection to determine independent associations within each genomic region as well as fine-mapping with joint analysis of marginal summary statistics (JAM)¹⁵ to determine population-specific variants that were independently associated with prostate cancer. This PRS was validated in an independent study of 13,628 US men.¹⁶

Conti et al.¹⁴ found that men with prostate cancer in the top 10% of the PRS distribution were diagnosed 2.84 years younger than men in the bottom 10% of the distribution. Others have also reported that larger values of PRS based on 110 genetic variants were associated with younger age of prostate cancer diagnosis for white men.¹⁷ These observations raise concerns regarding whether statistical models to predict prostate cancer should allow for PRS relative risks to depend on age. A complication is that even if the relative risk for a PRS is constant over all ages, the men with highest risk will succumb to disease at earlier ages, resulting in observations that men with larger values of PRS tend to be diagnosed at younger ages. See supplemental information for theoretical derivations and Figure S1 for numerical illustration. Hence, because odds ratios and relative risks are used to predict future risk of disease, it is important to evaluate whether these risk parameters change with age. Nonetheless, Conti et al.¹⁴ found that among men of European ancestry, those with PRSs in the top decile of the PRS distribution had an odds ratio of 6.71 (95% CI, 5.99–7.52), compared with PRSs in the 40^th–60^th percentile, for men aged $\le 55$ years in contrast to a smaller odds ratio of 4.39 (95% CI, 4.19–4.60) for men older than 55 years.

The observation of weakening association of PRS with disease risk as age increases has been observed for breast cancer¹⁸ and for cardiovascular disease, particularly when many non-genetic risk factors are known to have effects at older ages.¹⁹ Furthermore, by a study of genetic relative risk for 24 common diseases within the British ancestry subset of the UK Biobank, Jiang²⁰ found evidence for age-varying relative risk for hypertension, skin cancer, atherosclerotic heart disease, hypothyroidism, and calculus of gallbladder. The predominant pattern was genetic risk largest at younger ages, and relative risk decreased as age increased. Because risk due to a PRS can change with age, it is important to understand the full impact of age on risk predictions, including future absolute risk of disease, conditional on current age and PRS.

In addition to the influence of age, it is critical to consider the influence of ancestry. Large genome-wide association studies (GWASs) are needed to determine the most relevant genetic variants and their weights, and many GWASs have focused on European ancestry.²¹ The work by Conti et al.¹⁴ attempted to overcome this limitation by gathering as much GWAS summary statistics as possible across different ancestries. They found that the distribution of PRSs varied across different ancestral populations, even for controls. This is expected when allele frequencies of the variants in the PRSs differ across different populations. It can be shown that the distribution of the PRSs in controls is a normal distribution with mean $\mu$ and variance ${\sigma }^2$ that both depend on the allele frequencies and the PRS weights.¹⁸ Furthermore, if the risk of disease is due to a large number of alleles of small effect, combining multiplicatively, the distribution among cases is also a normal distribution with the same variance as for controls, but with a mean among cases that is approximately $\mu +{\sigma }^2$, illustrating that the distribution among cases is shifted to larger values. Because of these theoretical expectations and empirical data that support these expectations, it is critical to account for not only the association of PRSs with prostate cancer in different populations but also the difference in distribution of PRSs across different populations.

In summary, multiple factors complicate the modeling of the effect of PRSs on prostate cancer risk: the population distribution of PRSs, which depends on ancestry; the influence of PRSs on prostate cancer risk, which depends on age; and family history of prostate cancer, which can be confounded with age of diagnosis. Men with a family history of prostate cancer tend to have a younger age of diagnosis,¹⁷ and a younger age of diagnosis has been reported when a close relative had prostate cancer.^22,23 In this report, we refined the analyses reported by Conti et al. by a more extensive evaluation of age, beyond the dichotomy of $\le$ 55 years versus >55 years, and adjusting for the differences in distribution of PRSs across different ancestries. Furthermore, we evaluated the role of family history in addition to effects of age. Finally, following the recommendation to convey absolute risks to lay people in order to simplify interpretation of personal risks,^24,25 we evaluated the impact of a PRS relative risk changing over ages on predicting the future absolute risk of prostate cancer.

Material and methods

Studies

Prostate cancer case-control GWASs were obtained from dbGaP after approval of project request # 25202 “Development and Testing of Polygenic Risk Scores for Prostate Cancer.” All data were de-identified, and by dbGaP policy, no review by an institutional review board was necessary. The seven case-controls studies are illustrated in Table S1 and described detail in the supplemental information. Advantages of these studies are their large size and diverse ancestry. Note that some of the studies were used to develop the PRS by Conti et al.,¹⁴ so our results should not be viewed as an independent validation of the original PRS.

Genotype quality control and imputation

Genotype quality control (QC) prior to imputation was conducted separately for each study and each genotyping platform. We removed SNPs with a call rate < 98%, indels, duplicate SNPs, or monomorphic SNPs and men with a call rate < 95%. SNPs were also excluded if they failed Hardy-Weinberg equilibration (HWE) test p value < 10⁻⁶. Because admixture of different ancestries can influence tests of HWE, we applied the software ADMIXTURE²⁶ to the genetic data to classify men into major ancestral groups (European, African, Amerindian, East Asian, South Asian) and then tested HWE within major ancestral groups. Genetic sex was verified by PLINK with markers on the X and Y chromosomes, and subjects that were not consistent with male were excluded. Samples were removed if they displayed a call rate < 80% on any given chromosome or if they had unusually low heterozygosity ratio < 0.4 (observed/expected heterozygosity) on any chromosome, presuming poor quality genotype data that would unduly influence imputation. The relatedness between each pair of men was evaluated by estimation of the kinship coefficient via King robust²⁷ that is implemented in the R package SNPRelate. We randomly removed one subject from each strongly related pair (i.e., duplicates, parent-offspring, full siblings, and third-degree relatives, with an estimated kinship coefficient at least 0.0442). This approach allowed us to identify men whose samples were included in more than one study and remove duplicates.

After the above QC processing, samples were uploaded to the TOPMed imputation server,^28,29 where additional QC steps were completed including removal of multi-allelic SNPs, removal of indels, removal of monomorphic SNPs, and removal of SNPs with large allele frequency differences compared with the TOPMed Imputation Reference panel. Imputed variants with an imputation R² ≥ 0.3 were retained.

Data harmonization

The Breast and Prostate Cancer Cohort Consortium (BPC3) data included both men and women; women were excluded from our analyses. The set of variables that were common across all dbGaP studies were case-control status, ancestry, family history of prostate cancer, and age (age of disease diagnosis for cases and age of study enrollment for controls). Age was recorded differently across studies. Some studies recorded exact age, others recorded in 5-year intervals, and others recorded in 10-year intervals. To determine a common set of intervals, 10-year intervals were recoded as the last 5 years of an interval. For example, 50–59 was recoded to 55–59. For analyses that used yearly ages, we used the mid-point of an age interval when exact age was missing.

Polygenic risk score

Conti et al.¹⁴ developed a trans-ethnic PRS based on 269 SNPs and their associations with prostate cancer across four ancestries: European, African, East Asian, and Hispanic. The variants and weights used to create the PRS are available from their Table S4 and also at https://www.pgscatalog.org/publication/PGP000122/. After QC and imputation in our data, there were 220 variants that overlapped with our imputed data. Because the distribution of PRSs differs across different ancestries, we evaluated different approaches to correct for ancestry (see supplemental information) and chose to center and scale the PRS within each ancestry group by using the mean and standard deviation for controls within each ancestry group.

Age-specific incidence rates for prostate cancer and for death

We used age-specific prostate cancer incidence (hazard) rates to create weights for Cox proportional hazards models as well as combine with death hazard rates to compute absolute risks. Prostate cancer incidence rates were downloaded from the CDC US Cancer Statistics (https://www.cdc.gov/cancer/uscs/dataviz/download_data.htm). The cancer rates were reported for 5-year intervals, and we used linear interpolation to determine the rate at each year of age from age 30 to 87 years. CDC rates were available for ancestries of US White, Latino, African American, and Asian. We used the incidence rates of US African American men for men from Ghana. Figure S3 in the supplemental information illustrates how the incidence rates and cumulative risk for prostate cancer vary over ages for different ancestries.

Death incidence rates were obtained from CDC Health Statistics (https://ftp.cdc.gov/pub/Health_Statistics/NCHS/Publications/NVSR/61_03/) with documentation from https://www.cdc.gov/nchs/products/life_tables.htm. The life tables for 2008 were for each sex and race (White, non-Hispanic White, Black, non-Hispanic Black, and Hispanic). Based on life analytic methods, the death hazard rate at age t, $h_t$ was calculated according to $h_t=q_t/\left(1-q_t/2\right)$, where $q_t$ is the life table probability of dying between ages $t$ and $t+1$. The division by 2 assumes deaths on average occur mid-way during each year.³⁰ We used non-Hispanic White death rates for Asian ancestry.

Statistical methods

Statistical analyses were conducted with R version 4.0.3. The associations between PRS and age of disease diagnosis were estimated by weighted Cox regression models. Although logistic regression is typically used to analyze case-control studies, the resulting odds ratios are an approximation of the relative risk estimated in studies when disease is rare, yet odds ratios over-estimate the relative risk,³¹ which impacts models to estimate absolute risk. Furthermore, additional information about the risk of disease at different ages is potentially available from the age of diagnosis, and the age at which controls are free of disease. Studies have shown that applying Cox regression models to case-control data, using age information, can lead to greater power than logistic regression,³² although a naive analysis that fails to account for over-sampling of cases in case-control studies can lead to biased estimates of the relative risks.³³ For these reasons, we estimated relative risks by use of the Cox model with sampling weights based on population incidence rates to account for how cases and controls were sampled.^{34, 35, 36} We assigned weights of 1 to cases and weights of $1/in{c}_t$ to controls, where $in{c}_t$ is the age-specific incidence rate of prostate cancer in a defined ancestry group. In addition, we used the survSplit function in the survival package to fit piece-wise proportional hazards models to allow the relative risks to differ across different age categories, as well as the time-transform functions of coxph to model continuous time-dependent coefficients. Methods to compute the future absolute risk of disease, conditional on a man alive and free of disease at a specified age and with a standardize PRS, are described in Appendix A.

Results

The cases and controls included in analyses are characterized in Table 1. Details about how samples were evaluated for quality of genetic results, how genetically related men were removed, and selection criteria to exclude men with missing age (N = 2,800), missing ancestry (N = 27), or young age < 30 years (N = 39) and characteristics of men according to study are provided in the supplemental information (see Tables S2, S3,and S4). There were 64,274 prostate cancer cases and 46,432 controls included in analyses. The ancestry groups in Table 1 are based on self-report, with 82.8% European, 9.8% African American, 3.8% Latino, 2.8% Asian, and 0.8% Ghanaian. Overall, 19% reported a family history of prostate cancer. However, family history varied across the studies with the International Consortium for Prostate Cancer Genetics (ICPCG) reporting the largest fraction with family history (69.6%) because the ICPCG group focused on ascertaining cases with a family history; some studies failed to collect family history information (see Table S4). For this reason, analyses that focused on family history were considered secondary. The median age of diagnosis of prostate cancer for cases was 66 years and the median age of blood collection for controls was 62 years.

Table 1.

Characteristics of men by case-control status

	Case (No. = 64,274)	Control (No. = 46,432)	Total (No. = 110,706)
Ancestry group
African American	5,505 (8.6%)	5,370 (11.6%)	10,875 (9.8%)
Asian	1,574 (2.4%)	1,483 (3.2%)	3,057 (2.8%)
European	54,564 (84.9%)	37,059 (79.8%)	91,623 (82.8%)
Ghanaian	461 (0.7%)	452 (1.0%)	913 (0.8%)
Latino	2,170 (3.4%)	2,068 (4.5%)	4,238 (3.8%)
Family history of prostate cancer
Unknown	25,094	16,016	41,110
No	29,206 (74.5%)	27,189 (89.4%)	56,395 (81.0%)
Yes	9,974 (25.5%)	3,227 (10.6%)	13,201 (19.0%)
Age group, years
[30,45)	330 (0.5%)	991 (2.1%)	1,321 (1.2%)
[45,50)	1,290 (2.0%)	1,707 (3.7%)	2,997 (2.7%)
[50,55)	4,288 (6.7%)	4,945 (10.6%)	9,233 (8.3%)
[55,60)	10,122 (15.7%)	8,740 (18.8%)	18,862 (17.0%)
[60,65)	12,586 (19.6%)	10,840 (23.3%)	23,426 (21.2%)
[65,70)	15,769 (24.5%)	9,635 (20.8%)	25,404 (22.9%)
[70,75)	11,335 (17.6%)	5,631 (12.1%)	16,966 (15.3%)
[75,88)	8,554 (13.3%)	3,943 (8.5%)	12,497 (11.3%)
Age, year: median (range)	66 (30–87)	62 (30–87)	64 (30–87)

Excludes men with missing age, age < 30 years, or missing ancestry.

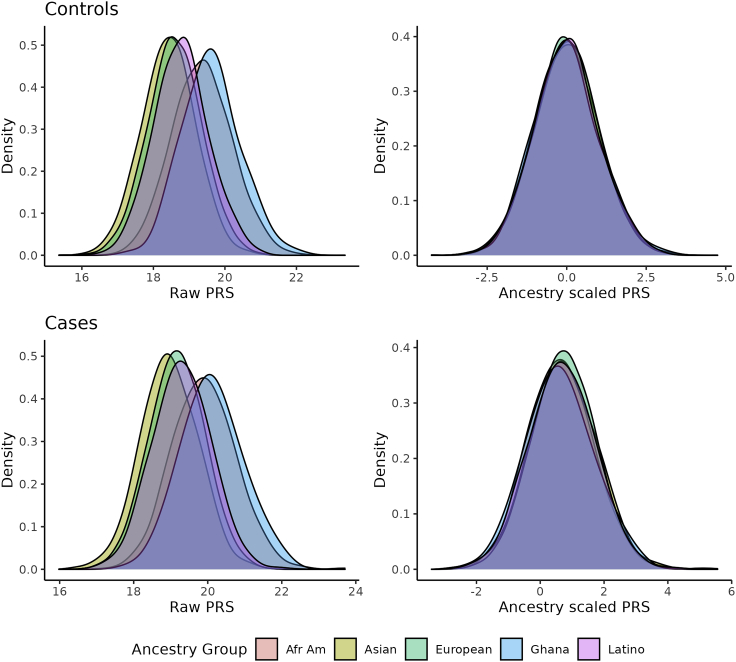
The distribution of the PRSs is illustrated in Figure 1 for cases and controls of different ancestries, both the raw PRS and the PRS standardized by the mean and standard deviation within controls of each ancestry group. This figure illustrates that the distribution of the PRS is shifted to larger values for men of African American and Ghanaian ancestry, shifted to smaller values for men of Asian ancestry, and similar distributions for men of European and Latino ancestries. These shifted distributions occurred for both controls and cases, emphasizing the impact of the allele frequency differences across different ancestries. In contrast, when the PRS was centered and scaled according to the controls of each ancestry group, the distributions of the PRS overlap for the different ancestral groups. Note that the distributions were centered at zero for controls, as expected, while the distributions for the cases were shifted to greater values.

Figure 1.

Distribution of PRSs by ancestry and disease status before and after adjustment for ancestry by centering and scaling according to mean and standard deviation within controls of each ancestry

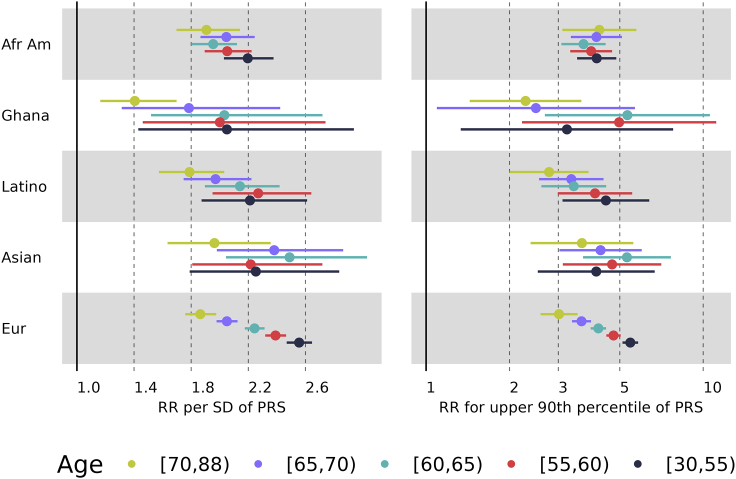
The association of the standardized PRS with age of onset of prostate cancer in the pool of all data, assessed by a weighted Cox proportional hazards model assuming a constant hazard ratio, estimated a relative risk of 2.14 per standard deviation (SD) of the PRS (95% confidence interval, CI, 2.09–2.19), allowing for adjusting covariates ancestry group and dbGaP study. Sensitivity analyses of the weights showed that a 10-fold decrease or increase in the weights had little impact on results (relative risks of 1.93 and 2.17, respectively). More refined weights that attempted to account for potential preferential sampling of cases at different ages (see supplemental information) gave results identical to the initial proposed weights. Relative risks for each ancestry are presented in Figure 2 for relative risks per PRS SD as well as for PRS dichotomized according to the upper 90^th percentile. These results show that relative risks per PRS SD were similar for European, African American, and Asian ancestries, slightly less for Latino, and much less for Ghanaian men (heterogeneity p value = 0.008). The relative risks for the upper 90^th percentile were much larger than the relative risk per SD, as expected, and less heterogeneity of relative risks (p value = 0.308), although the larger standard errors of the estimates for the upper 90^th percentile relative risks decreased power to detect heterogeneity. See Table S7 for the log-relative risk estimates and their standard errors.

Figure 2.

Relative risk per PRS SD (left panel) and for upper 90^th percentile cutoff of PRS (right panel) according to ancestry

The bars represent 95% confidence intervals.

Because the pooled analysis of all men showed a strong departure from a constant relative risk (p < 2e−16), we performed piece-wise proportional hazards analyses by partitioning age into five age groups and found significant differences in the relative risks across the age groups (p < 1e−30). Piece-wise proportional hazards were fit separately for each ancestry group and results in Figure 3 illustrate that relative risks per SD were greatest for the youngest age group (30–55 years) and least for the oldest age group (70–88 years). For European ancestry, there was a clear trend of decreasing risk with age, from a relative risk of 2.56 for 30–55 years old (95% CI 2.47–2.65) to a relative risk of 1.86 for 70–88 years old (95% CI 1.76–1.98), with no overlapping confidence intervals throughout the different age groups. The relative risks for European ancestry differed statistically across the age groups (p < 0.001). The other ancestries in Figure 3 showed that the youngest and oldest age groups had different relative risks, but the patterns of risk in the intermediate age groups were not as distinct as for European ancestry, presumably because of the much smaller sample sizes of the other ancestry groups. For these non-European ancestries, the relative risks were not statistically significantly different across the age groups (see Tables S8 and S9 for details).

Figure 3.

Relative risk per PRS SD (left panel) and for upper 90^th percentile cutoff of PRS (right panel) for age groups according to ancestry

The bars represent 95% confidence intervals.

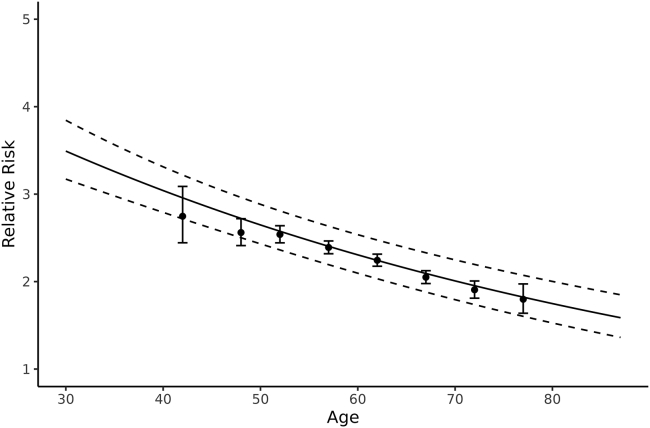
We performed a similar analysis with the PRS dichotomized according to the upper 90^th percentile and similar patterns of relative risk decreasing with age were found, as illustrated in Figure 3. The relative risks implied by the upper 90^th percentile ranged 3–5 for most ancestries and age groups, except the lesser relative risks for Ghanaian men. The wide confidence intervals for this group reflect the small sample size. These relative risks differed significantly across the age groups (p < 0.001) for European ancestry but not for the non-European ancestries (see Tables S8 and S9 for details).Because of the large number of men with European ancestry, we were able to refine analyses of the age dependence of relative risk. We created the age group 30–45-year olds, then groups in 5-year intervals (45–50, to 70–75, then 75–88) and fit-piece-wise hazard ratios for each age group. We also fit a model with the log-relative risk depending linear on age: ${\beta }_{0}PRS+{\beta }_1\left(a-30\right)PRS$, where age $a$ ranged 30–87 and we offset by the minimum age of 30 years in our dataset. The estimated effect of PRS was ${\beta }_0=1.2504$ (SE = 0.049) and the estimated gradient of age was ${\beta }_1=-0.0138$ (SE = 0.0015). The estimated relative risks and their 95% confidence intervals for the piecewise and linear models are presented in Figure 4, showing that the log-relative risk decreased approximately linearly from age 50 to age 75. We developed methods to account for preferential inclusion of cases at different ages, to evaluate the sensitivity of the Cox model weights (see supplemental information), and found results identical to the proposed weights. These results were also consistent with fitting logistic regression models to the case-control data (see supplemental information). To compare this linear decrease across different diseases and populations, one can estimate for the relative risk per adjusted standard error (OPERA)³⁷ per year of age, which is exp(−0.0138/.00155) = 0.00014.

Figure 4.

Piece-wise relative risk models and log-relative risk modeled as linear with age for European ancestry

The solid line is the model assuming log-relative risk depends linearly on age and dashed lines are the 95% confidence interval over ages. The estimated dependence on age was 1.2504-0.0138^∗(age-30). The piece-wise relative risks are represented as “^∗” and their 95% confidence intervals represented as whiskers. The piece-wise results are positioned on the x axis at the median value of age within each age group.

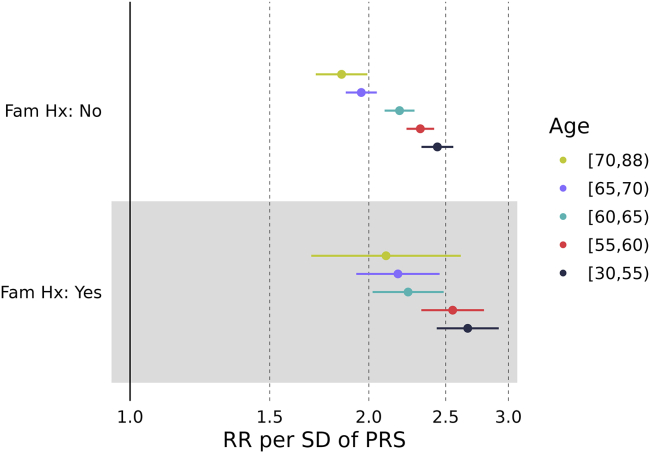
Because men with a family history of prostate cancer have been reported to have a younger age of diagnosis,¹⁷ we performed secondary analyses to attempt to sort out the role of family history. Secondary analyses were necessary because of the relatively large number of men without family history information. For this focus, we subset to men with European ancestry to obtain sufficient sample size. The results in Figure 5 illustrate that men with a family history of prostate cancer had greater relative risks associated with PRS at all ages compared with men with a negative family history (p value = 0.007) and that relative risks decreased with increasing age for both men with a family history of prostate cancer (heterogeneity of relative risks over ages, p value = 0.015) and men without a family history of prostate cancer (p value < 0.001). See Table S10 for more details. The gradient of the log-relative risk with increasing age was −0.0108 (SE = 0.0045) for men with a family history and −0.0122 (SE = 0.0019) for men with a negative family history, and these gradients were not statistically significantly different (p value = 0.78). The greater relative risk among men with a family history of prostate cancer across all ages emphasizes the importance of obtaining family history information when attempting to predict future risk of prostate cancer with PRSs.

Figure 5.

Relative risk per PRS SD according to age groups and family history for European ancestry

The bars represent 95% confidence intervals.

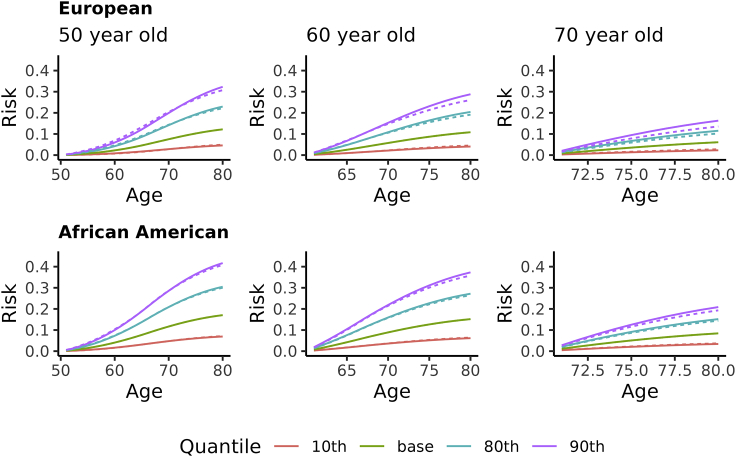
Given the decreasing relative risk of PRS with increasing age, it is important to evaluate how much the decreasing relative risk impacts prediction of future risk when attempting to use PRS for personalized medical recommendations. To view this, we computed the future prostate cancer absolute risk, conditional on men’s current age and value of a standardized PRS. These future risks are based on the relative risks estimated from our data, population disease incidence rates, as well as death rates to account for competing risks. We present in Figure 6 the future absolute risk for men of European and of African American ancestry, assuming current ages of 50, 60, and 70 years, for future remaining years at 1-year increments until age 80 years. These results illustrate that even though our results show strong evidence of relative risks due to PRS decreasing with increasing age, predicting future absolute risk while allowing for decreasing relative risk differed little from predictions that assumed a constant relative risk over ages. The largest difference was 2.7% for future predictions for a 70-year-old man of European ancestry.

Figure 6.

Future absolute risk of prostate cancer for European ancestry (left three panels) and African American ancestry (right three panels) conditional on current age and quantile of PRS

The solid lines assume a relative risk constant over ages, and the broken lines assume piece-wise relative risks to account for relative risks changing over ages. The quantiles (10, 80, 90) are for a standard normal distribution as expected for a standardized PRS in a population. The baseline represents the absolute risk assuming the PRS is unknown.

Discussion

Based on a large number of men of diverse ancestry with publicly available genome-wide genetic variants, we demonstrated decreasing PRS relative risks for prostate cancer as age increased. Our results were most accurate for men of European ancestry because of the large number of men in this group. By applying a novel weighted proportional hazards model to case-control data, we were able to fully utilize age information (diagnosis among cases; enrollment age among controls) to refine how the genetic relative risk decreased with age. For men of European ancestry, we observed a linear decrease of the log-relative risk from age 50 to 75, the ages at which most men are diagnosed with prostate cancer. Thomas et al. also observed a linear decrease of the log-relative risk for colorectal cancer with age, for age > 50 years with 72,791 subjects of European ancestry and with 1,311 colorectal cancer cases.^38,39 This reduced risk could result from non-genetic risk factors accumulating over a lifetime such that genetic effects that influence developmental pathways at younger ages have relatively less influence as non-genetic risk factors accumulate. Although a reduction in genetic relative risk with increasing age is expected when the highest risk individuals succumb to disease at younger ages, and hence are preferentially removed from the at-risk population at older ages,⁴⁰ it is important to evaluate the implications of age-varying risk. In contrast to prostate and colon cancers, breast cancer has not shown a declining risk with age for ER-negative disease, and only a weak decline has been observed for ER-positive disease.⁴¹

Despite the accumulating environmental risk with age, we observed that men of European ancestry had increased genetic relative risks at all ages if they had a family history of prostate cancer compared with a negative family history, suggesting that additional unmeasured genetic risk factors could be causing this difference, or perhaps clustering of environmental risk factors within families. This also emphasizes the importance of obtaining accurate pedigree disease information to combine with a PRS to improve age-dependent risk predictions.⁴²

As with most GWASs conducted to date, our data had a limited number of subjects with non-European ancestry, making it difficult to accurately refine how genetic relative risk decreased with age in other ancestries. Nonetheless, ancestries of Ghanaian, African American, Asian, and Latino all showed the PRS relative risk to be greatest for the youngest age group (30–55 years) and least for the oldest age group (70–88 years). These pattens were observed for both the relative risk per SD of the PRSs and binary classification based on the upper 90^th percentile of the PRS distribution.

The influence of a decreasing genetic relative risk with age on personalized medical decisions should consider how the risk will be used. Categorizing into highest risk, such as above the 90^th percentile of the PRS distribution, is a common approach, yet the amount of risk also depends on a man’s current age, as our results show. Because absolute risks are important for interpretation of personal risks,^24,25 we evaluated the impact of decreasing genetic relative risk with age on predicting future absolute risk. Despite strong evidence of age-dependent genetic relative risk, our results suggest that absolute risk predictions differed little between predictions that assumed a constant relative risk and those that allowed relatives risks to decrease with age. These findings covered a broad range, from short-term (e.g., 1 year) to long-term (e.g., to age 80). This may be due to the calculation of absolute risk depending on both the relative risk and the baseline incidence rates; large relative risks at younger ages have less impact on absolute risk because the incidence of prostate cancer is much smaller at young ages. Assuming a constant relative risk over age simplifies the approach to calculate and present risk predictions to lay persons as well as simplifies implementation of risk discussions into clinical practice. Our strategy to evaluate how genetic relative risks vary with age and the impact of changing relative risks with age on absolute risk predictions is worth considering for other common diseases.

Published: March 29, 2022

Appendix A

The future absolute risk of disease up to age $a_h$, conditional on a man alive and free of disease at age $a_l$ and with a standardized PRS of $z$, depends on the baseline population age-specific incidence of disease, ${\lambda }_o\left(t\right)$, the population age-specific death rate, ${\delta }_o\left(t\right)$, and the log hazard ratio estimated by Cox regression, ${\beta }_t$. For our purposes, we use the subscript $t$ to account for piece-wise proportional hazards (e.g., ${\beta }_t$ constant over an interval), or ${\beta }_t$ could be constant over all time. From this information, we calculate the future risk that a man will have disease by age $a_h$, given he is free of disease at $a_l$, as

$$Risk\left(a_h|a_l,z\right)=\frac{F\left(a_h|z\right)-F\left(a_l|z\right)}{S_{disease}\left(a_l\right)S_{death}\left(a_l\right)},$$

where $F\left(a|z\right)=\sum _{t=0}^a{e}^{{\beta }_{t}z}{\lambda }_o\left(t\right)S_{disease}\left(t|z\right)S_{death}\left(t\right)$ is the cumulative probability of disease up to age $a$ accounting for competing risk of death, $S_{disease}\left(a|z\right)=\mathit{exp}\left[-\sum _{t=0}^a{e}^{{\beta }_{t}z}{\lambda }_o\left(t\right)\right]$ is the probability of being free of disease at age $a$, and $S_{death}\left(a\right)=\mathit{exp}\left[-\sum _{t=0}^a{\delta }_o\left(t\right)\right]$ is the probability of being alive at age $a$. Absolute risk calculations were achieved by estimates of ${\beta }_t$ determined in our data.

Data and code availability

All data are available through dbGaP (https://www.ncbi.nlm.nih.gov/gap/) based on the dbGaP Study accession numbers provided in the supplemental information in Table S1. Code was written in the R statistical language and linux shell commands in multiple scripts that are available upon request from the corresponding author.